Vortex-Induced Vibration Predictions of a Circular Cylinder Using an Efficient Pseudo-Time Code-Coupling Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Governing Equations
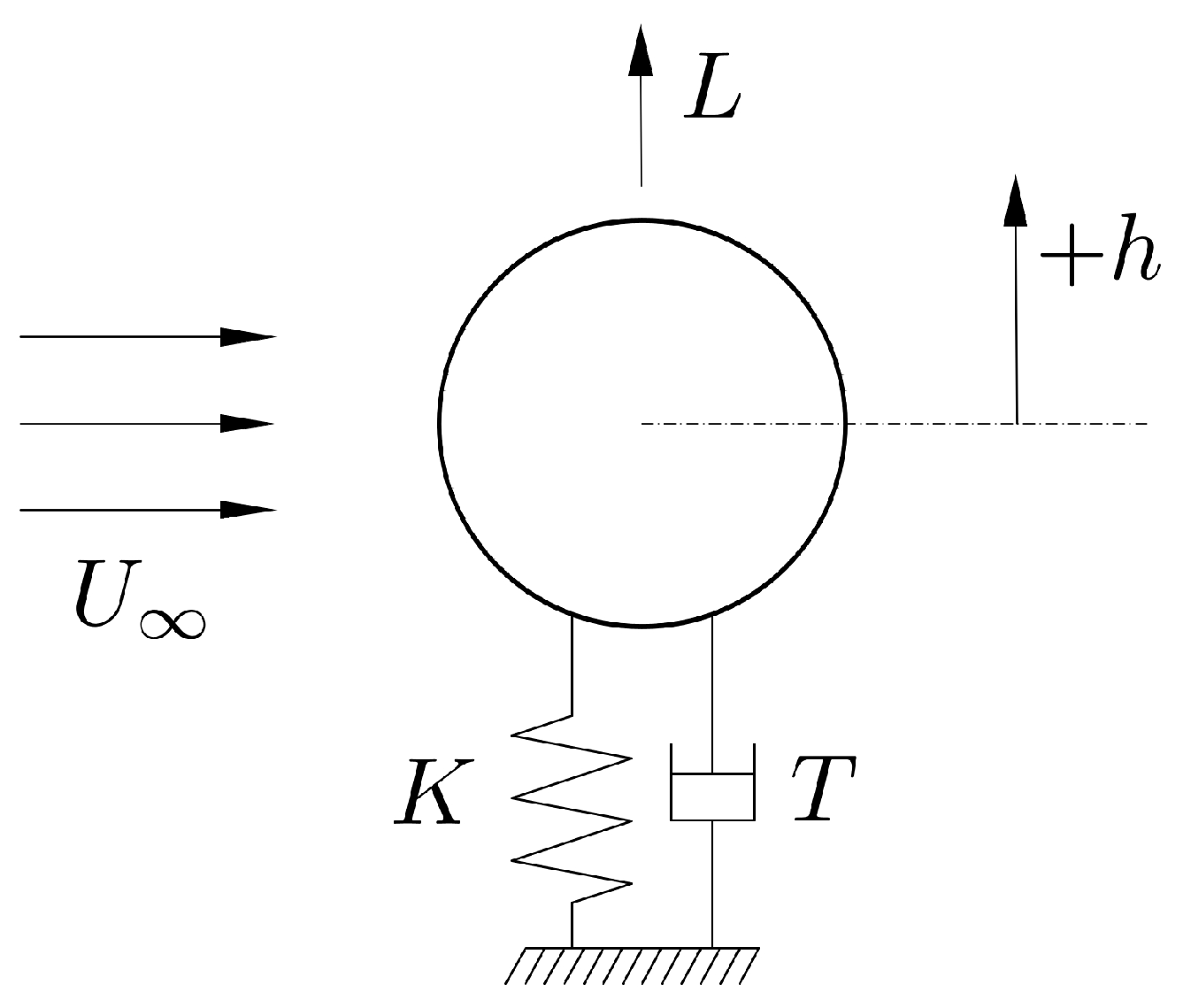
2.1.1. The One-DOF VIV Model
2.1.2. The Unsteady Flow Solver
2.2. The One-Shot Method
2.2.1. The High-Dimensional Harmonic Balance Technique
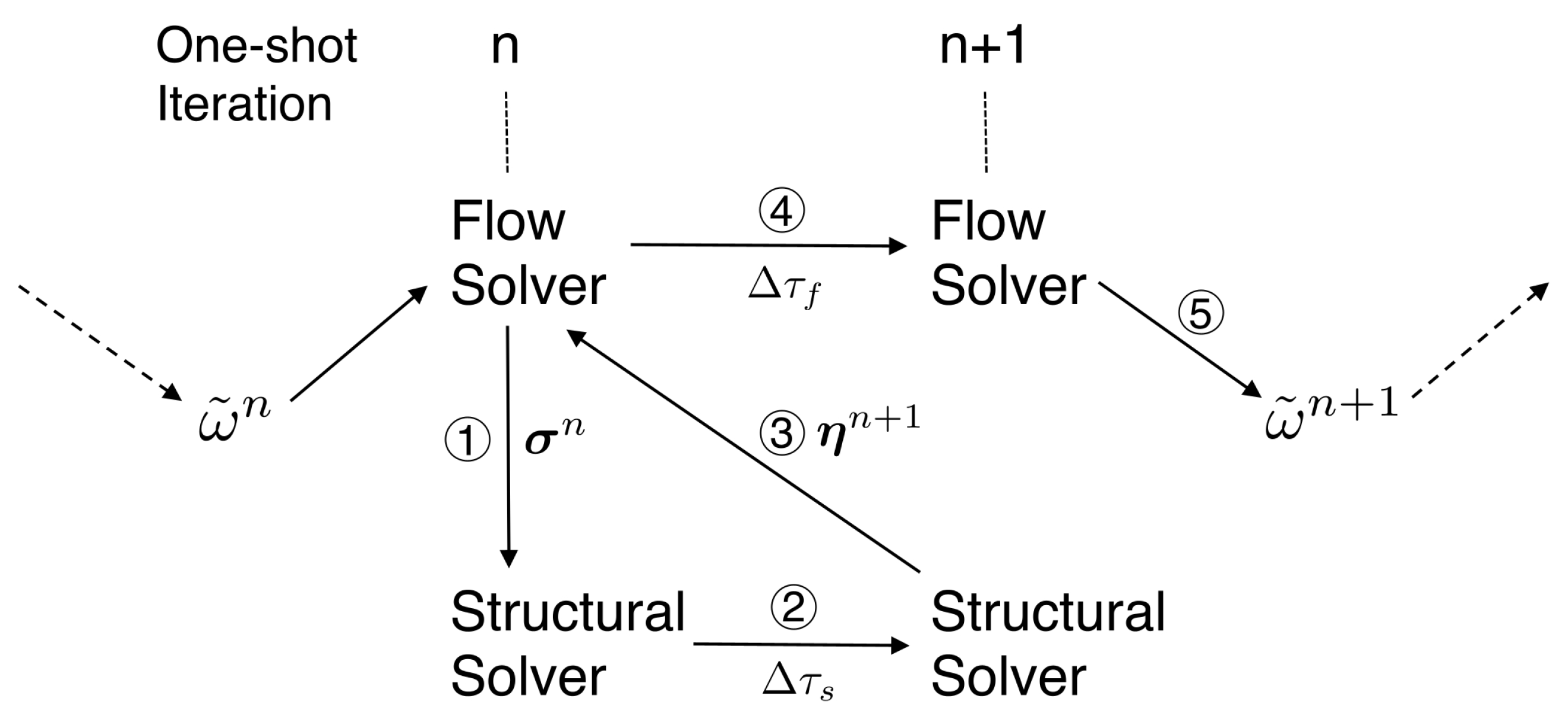
2.2.2. Fluid–Structure Code-Coupling in Pseudo-Time
3. Results and Discussion
3.1. Validation and Verification of the HB-CFD Solver
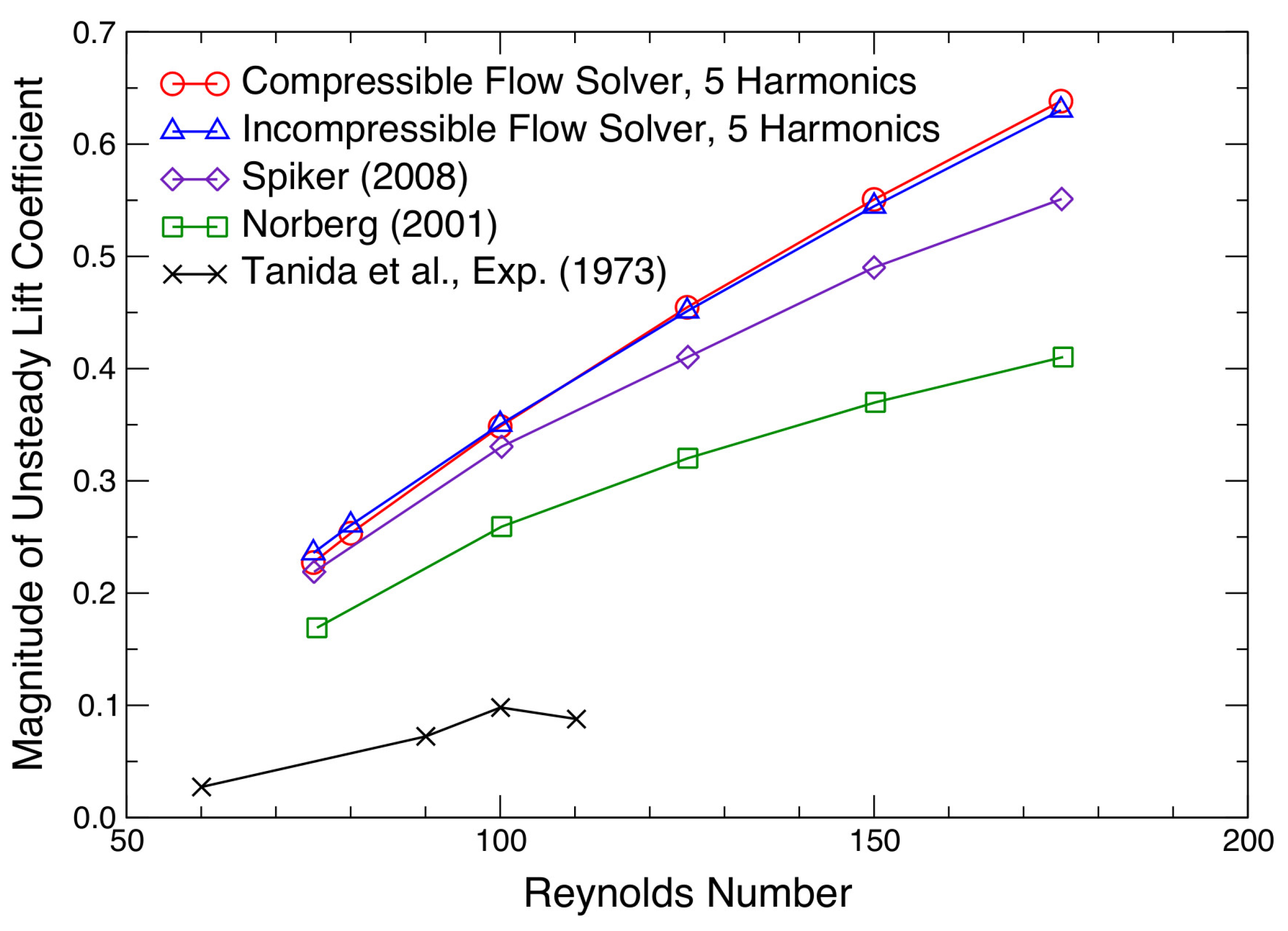
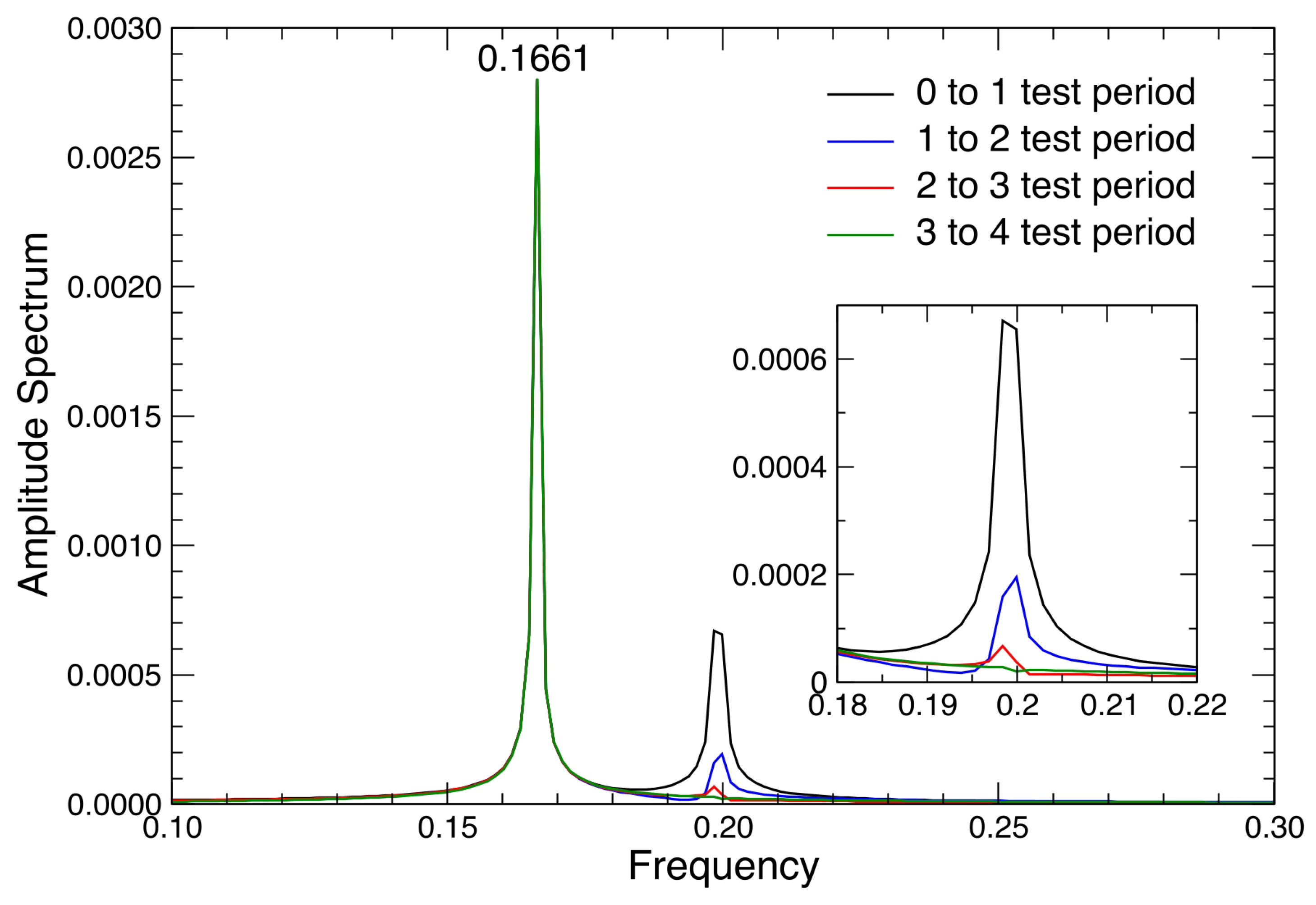
3.2. The VIV Results
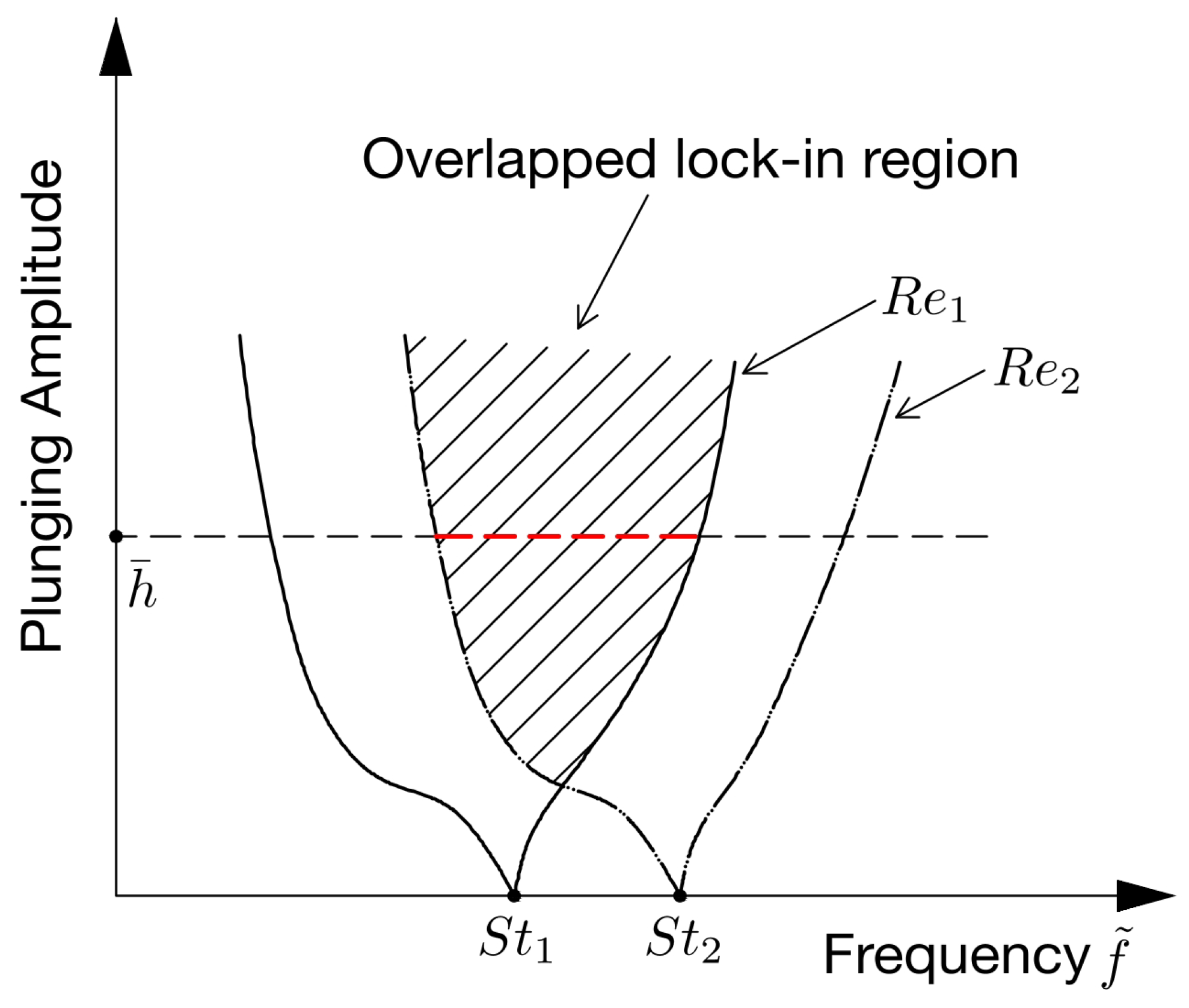
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| structural matrices in state-space form | |
| lift and drag coefficients, respectively | |
| pseudo-spectral matrix | |
| D | cylinder diameter |
| discrete Fourier and inverse Fourier transformation matrices, respectively | |
| flux vectors in x and y directions, respectively | |
| f | regular frequency, |
| reduced regular frequency based on cylinder diameter, | |
| structural natural frequencies of plunging in hertz (Hz) | |
| H | total enthalpy |
| h | plunge displacement |
| K | plunge stiffness of cylinder |
| L | fluid dynamic lift |
| free-stream Mach number | |
| m | mass of the plunging cylinder |
| mass ratio, | |
| N | number of harmonics |
| n | index number of harmonic mode or numerical iteration |
| p | local pressure |
| free-stream dynamic pressure, | |
| free stream Reynolds number | |
| Strouhal number, the of vortex shedding associated with the stationary cylinder | |
| s | cylinder span |
| T | plunge damping of cylinder |
| t | physical time |
| free-stream velocity | |
| conservation variables of fluid equation | |
| Fourier coefficients of conservation variables | |
| Cartesian velocity components | |
| Cartesian coordinates | |
| Z | figure-of-merit for frequency search |
| plunge coordinate damping coefficient, | |
| vector of dependent structure variables | |
| a control parameter in the cylinder VIV problem | |
| freestream kinetic viscosity | |
| local and free-stream densities, respectively | |
| vector of aerodynamic forces | |
| shear stress | |
| pseudo-time for fluid and structure solvers, respectively | |
| phase of plunging vibration | |
| angular frequency, | |
| reduced angular frequency based on cylinder diameter, | |
| structural natural frequencies of plunging, | |
| Superscripts and accents | |
| * | variable in sub-time levels (except for the mass ratio) |
| ^ | Fourier coefficients |
| · | dimensional time derivative |
| ′ | non-dimensional time derivative |
| ˜ | variable in reduced form |
| ¯ | amplitude of variable |
| Subscripts | |
| 0 | mean value |
| initial condition | |
| value at VIV condition |
References
- Williamson, C.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Hao, Z.; Sun, C.; Lu, Y.; Bi, K.; Zhou, T. Suppression of vortex-induced vibration and phase-averaged analysis of the wake generated by a circular cylinder covered with helical grooves. Fluids 2022, 7, 194. [Google Scholar] [CrossRef]
- Wu, Y.; Lien, F.S.; Yee, E.; Chen, G. Numerical investigation of flow-induced vibration for cylinder-plate assembly at low Reynolds number. Fluids 2023, 8, 118. [Google Scholar] [CrossRef]
- Xiao, D.; Hao, Z.; Zhou, T.; Zhu, H. Experimental Studies on Vortex-Induced Vibration of a Piggyback Pipeline. Fluids 2024, 9, 39. [Google Scholar] [CrossRef]
- Cao, D.; He, J.; Zeng, H.; Zhu, Y.; Chan, S.Z.; Williams, M.R.; Khor, I.Z.L.; Yalla, O.V.; Sunny, M.R.; Ghoshal, R.; et al. A Review of Oscillators in Hydrokinetic Energy Harnessing Through Vortex-Induced Vibrations. Fluids 2025, 10, 78. [Google Scholar] [CrossRef]
- Anagnostopoulos, P.; Bearman, P. Response characteristics of a vortex-excited cylinder at low Reynolds numbers. J. Fluids Struct. 1992, 6, 39–50. [Google Scholar] [CrossRef]
- Nomura, T. Finite element analysis of vortex-induced vibrations of bluff cylinders. J. Wind. Eng. Ind. Aerodyn. 1993, 46, 587–594. [Google Scholar] [CrossRef]
- Nomura, T. ALE finite element computations of fluid-structure interaction problems. Comput. Methods Appl. Mech. Eng. 1994, 112, 291–308. [Google Scholar] [CrossRef]
- Anagnostopoulos, P. Numerical investigation of response and wake characteristics of a vortex-excited cylinder in a uniform stream. J. Fluids Struct. 1994, 8, 367–390. [Google Scholar] [CrossRef]
- Wei, R.; Sekine, A.; Shimura, M. Numerical analysis of 2D vortex-induced oscillations of a circular cylinder. Int. J. Numer. Methods Fluids 1995, 21, 993–1005. [Google Scholar] [CrossRef]
- Anagnostopoulos, P. Numerical study of the flow past a cylinder excited transversely to the incident stream. Part 1: Lock-in zone, hydrodynamic forces and wake geometry. J. Fluids Struct. 2000, 14, 819–851. [Google Scholar] [CrossRef]
- Anagnostopoulos, P. Numerical study of the flow past a cylinder excited transversely to the incident stream. Part 2: Timing of vortex shedding, aperiodic phenomena and wake parameters. J. Fluids Struct. 2000, 14, 853–882. [Google Scholar] [CrossRef]
- Bahmani, M.; Akbari, M. Effects of mass and damping ratios on VIV of a circular cylinder. Ocean. Eng. 2010, 37, 511–519. [Google Scholar] [CrossRef]
- Prasanth, T.; Premchandran, V.; Mittal, S. Hysteresis in vortex-induced vibrations: Critical blockage and effect of m. J. Fluid Mech. 2011, 671, 207–225. [Google Scholar] [CrossRef]
- Yang, F.L.; Chen, C.; Young, D. A novel mesh regeneration algorithm for 2D FEM simulations of flows with moving boundary. J. Comput. Phys. 2011, 230, 3276–3301. [Google Scholar] [CrossRef]
- Tang, G.; Lu, L.; Teng, B.; Liu, M. Numerical simulation of vortex-induced vibration with three-step finite element method and arbitrary Lagrangian-Eulerian formulation. Adv. Mech. Eng. 2013, 5, 890423. [Google Scholar] [CrossRef]
- Kaneko, S.; Hong, G.; Mitsume, N.; Yamada, T.; Yoshimura, S. Partitioned-coupling FSI analysis with active control. Comput. Mech. 2017, 60, 549–558. [Google Scholar] [CrossRef]
- Al Manthari, M.; Azeez, C.; Sankar, M.; Pushpa, B. Numerical Study of Laminar Flow and Vortex-Induced Vibration on Cylinder Subjects to Free and Forced Oscillation at Low Reynolds Numbers. Fluids 2024, 9, 175. [Google Scholar] [CrossRef]
- Ning, W.; He, L. Computation of unsteady flows around oscillating blades using linear and nonlinear harmonic Euler methods. J. Turbomach. 1998, 120, 508–514. [Google Scholar] [CrossRef]
- Hall, K.C.; Thomas, J.P.; Clark, W.S. Computation of Unsteady Nonlinear Flows in Cascades Using a Harmonic Balance Technique. AIAA J. 2002, 40, 879–886. [Google Scholar] [CrossRef]
- McMullen, M.; Jameson, A.; Alonso, J. Application of a Non-Linear Frequency Domain Solver to the Euler and Navier-Stokes Equations. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. AIAA Paper 2002–0120. [Google Scholar] [CrossRef]
- Nadarajah, S.K. Convergence studies of the time accurate and non-linear frequency domain methods for optimum shape design. Int. J. Comput. Fluid Dyn. 2007, 21, 189–207. [Google Scholar] [CrossRef]
- Zhang, W.; Xi, G.; Zhang, C.; Huang, Z. A high-accuracy temporal–spatial pseudospectral method for time-periodic unsteady fluid flow and heat transfer problems. Int. J. Comput. Fluid Dyn. 2011, 25, 191–206. [Google Scholar] [CrossRef]
- Ekici, K.; Huang, H. An assessment of frequency-domain and time-domain techniques for turbomachinery aeromechanics. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, New Orleans, LA, USA, 25–28 June 2012. AIAA Paper 2012-3126. [Google Scholar] [CrossRef]
- Hall, K.C.; Ekici, K.; Thomas, J.P.; Dowell, E.H. Harmonic Balance Methods Applied to Computational Fluid Dynamics Problems. Int. J. Comput. Fluid Dyn. 2013, 27, 52–67. [Google Scholar] [CrossRef]
- Carlson, H.; Feng, J.; Thomas, J.; Kielb, R.; Hall, K.; Dowell, E. Computational models for nonlinear aeroelasticity. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005; p. 1085. [Google Scholar] [CrossRef]
- Thomas, J.P.; Dowell, E.H.; Hall, K.C. Nonlinear Inviscid Aerodynamic Effects on Transonic Divergence, Flutter, and Limit-Cycle Oscillations. AIAA J. 2002, 40, 638–646. [Google Scholar] [CrossRef]
- Kielb, R.E.; Hall, K.C.; Spiker, M.; Thomas, J.P.; Pratt, E.T., Jr.; Jeffries, R. Non-Synchronous Vibration of Turbomachinery Airfoils; Technical Report; Department of Mechanical Engineering and Materials Science, Duke University: Durham, NC, USA, 2006. [Google Scholar]
- Dowell, E.H.; Hall, K.C.; Thomas, J.P.; Kielb, R.E.; Spiker, M.A.; Denegri, C.M. A new solution method for unsteady flows around oscillating bluff bodies. In Proceedings of the IUTAM Symposium on Fluid-Structure Interaction in Ocean Engineering, Hamburg, Germany, 23–26 July 2008; Springer: Dordrecht, The Netherlands, 2008; pp. 37–44. [Google Scholar] [CrossRef]
- Spiker, M.A. Development of an Efficient Design Method for Non-Synchronous Vibrations. Ph.D. Thesis, Duke University, Durham, NC, USA, 2008. [Google Scholar]
- Clark, S.T. Design for Coupled-Mode Flutter and Non-Synchronous Vibration in Turbomachinery. Ph.D. Thesis, Duke University, Durham, NC, USA, 2013. [Google Scholar]
- Besem, F.M. Aeroelastic Instabilities due to Unsteady Aerodynamics. Ph.D. Thesis, Duke University, Durham, NC, USA, 2015. [Google Scholar]
- Besem, F.M.; Thomas, J.P.; Kielb, R.E.; Dowell, E.H. An aeroelastic model for vortex-induced vibrating cylinders subject to frequency lock-in. J. Fluids Struct. 2016, 61, 42–59. [Google Scholar] [CrossRef]
- Thomas, J.; Dowell, E. A fixed point iteration approach for harmonic balance based aeroelastic computations. In Proceedings of the AIAA Aerospace Sciences Meeting & Exhibit, Kissimmee, FL, USA, 8–12 January 2018. AIAA Paper 2018–14462018. [Google Scholar] [CrossRef]
- Blanc, F.; Roux, F.; Jouhaud, J. Harmonic-Balance-Based Code-Coupling Algorithm for Aeroelastic Systems Subjected to Forced Excitation. AIAA J. 2010, 48, 2472–2481. [Google Scholar] [CrossRef]
- Berci, M.; Dimitriadis, G. A combined Multiple Time Scales and Harmonic Balance approach for the transient and steady-state response of nonlinear aeroelastic systems. J. Fluids Struct. 2018, 80, 132–144. [Google Scholar] [CrossRef]
- Yao, W.; Jaiman, R.K. A harmonic balance technique for the reduced-order computation of vortex-induced vibration. J. Fluids Struct. 2016, 65, 313–332. [Google Scholar] [CrossRef]
- Nardini, M.; Illingworth, S.J.; Sandberg, R.D. Nonlinear reduced-order modeling of the forced and autonomous aeroelastic response of a membrane wing using Harmonic Balance methods. J. Fluids Struct. 2019, 91, 102699. [Google Scholar] [CrossRef]
- He, S.; Jonsson, E.; Mader, C.A.; Martins, J.R.R.A. A coupled Newton–Krylov time spectral solver for flutter prediction. In Proceedings of the AIAA Aerospace Sciences Meeting & Exhibit, Kissimmee, FL, USA, 8–12 January 2018. AIAA Paper 2018–2149. [Google Scholar] [CrossRef]
- He, S.; Jonsson, E.; Mader, C.A.; Martins, J. Aerodynamic Shape Optimization with Time Spectral Flutter Adjoint. In Proceedings of the AIAA Aerospace Sciences Meeting & Exhibit, San Diego, CA, USA, 7–11 January 2019. AIAA Paper 2019–0697. [Google Scholar] [CrossRef]
- He, S.; Jonsson, E.; Mader, C.A.; Martins, J.R.R.A. A Coupled Newton–Krylov Time-Spectral Solver for Wing Flutter and LCO Prediction. In Proceedings of the AIAA AVIATION Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Maljaars, P.; Kaminski, M.; den Besten, J. A new approach for computing the steady state fluid–structure interaction response of periodic problems. J. Fluids Struct. 2019, 84, 140–152. [Google Scholar] [CrossRef]
- Ekici, K.; Hall, K.C. Harmonic Balance Analysis of Limit Cycle Oscillations in Turbomachinery. AIAA J. 2011, 49, 1478–1487. [Google Scholar] [CrossRef]
- Li, H.; Ekici, K. Revisiting the One-shot Method for Modeling Limit Cycle Oscillations: Extension to Two-degree-of-freedom Systems. Aerosp. Sci. Technol. 2017, 69, 686–699. [Google Scholar] [CrossRef]
- Li, H.; Ekici, K. Improved One-shot approach for modeling viscous transonic limit cycle oscillations. AIAA J. 2018, 56, 3138–3152. [Google Scholar] [CrossRef]
- Li, H.; Ekici, K. A novel approach for flutter prediction of pitch-plunge airfoils using an efficient One-shot method. J. Fluids Struct. 2018, 82, 651–671. [Google Scholar] [CrossRef]
- Li, H.; Ekici, K. Aeroelastic Modeling of the AGARD 445.6 Wing Using the Harmonic-Balance-Based One-shot Method. AIAA J. 2019, 57, 4885–4902. [Google Scholar] [CrossRef]
- Navrose; Mittal, S. Lock-in in vortex-induced vibration. J. Fluid Mech. 2016, 794, 565–594. [Google Scholar] [CrossRef]
- Sabino, D.; Fabre, D.; Leontini, J.; Jacono, D.L. Vortex-induced vibration prediction via an impedance criterion. J. Fluid Mech. 2020, 890, A4. [Google Scholar] [CrossRef]
- Jameson, A. A Vertex Based Multigrid Algorithm for Three Dimensional Compressible Flow Calculations. In Numerical Methods for Compressible Flows–Finite Difference, Element and Volume Techniques; AMD: New York, NY, USA, 1986; Volume 78. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Jameson, A.; Schmidt, W.; Turkel, E. Numerical Solution of the Euler Equations by Finite Volume Methods Using Runge-Kutta Time Stepping Schemes. In Proceedings of the AIAA Aerospace Sciences Meeting & Exhibit, St. Louis, MO, USA, 12–15 January 1981. AIAA Paper 81–1259. [Google Scholar] [CrossRef]
- Jameson, A. Solution of the Euler Equations for Two Dimensional Transonic Flow by a Multigrid Method. Appl. Math. Comput. 1983, 13, 327–355. [Google Scholar] [CrossRef]
- Huang, H.; Ekici, K. Stabilization of high-dimensional harmonic balance solvers using time spectral viscosity. AIAA J. 2014, 52, 1784–1794. [Google Scholar] [CrossRef]
- Chorin, A.J. A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 1997, 135, 118–125. [Google Scholar] [CrossRef]
- Ekici, K.; Hall, K.C. Nonlinear analysis of unsteady flows in multistage turbomachines using harmonic balance. AIAA J. 2007, 45, 1047–1057. [Google Scholar] [CrossRef]
- Nimmagadda, S.; Economon, T.D.; Alonso, J.J.; da Silva Ilario, C.R. Robust uniform time sampling approach for the harmonic balance method. In Proceedings of the AIAA Aerospace Sciences Meeting & Exhibit, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016–3966. [Google Scholar] [CrossRef]
- Li, H. The One-shot Aeroelastic Method: A Highly Efficient Modeling Approach Based on the Harmonic Balance Technique. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2019. [Google Scholar]
- Li, H.; Ekici, K. Supplemental-frequency harmonic balance: A new approach for modeling aperiodic aerodynamic response. J. Comput. Phys. 2021, 436, 110278. [Google Scholar] [CrossRef]
- Williamson, C.H. Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 1988, 31, 2742–2744. [Google Scholar] [CrossRef]
- Tanida, Y.; Okajima, A.; Watanabe, Y. Stability of a circular cylinder oscillating in uniform flow or in a wake. J. Fluid Mech. 1973, 61, 769–784. [Google Scholar] [CrossRef]
- Keefe, R.T. Investigation of the fluctuating forces acting on a stationary circular cylinder in a subsonic stream and of the associated sound field. J. Acoust. Soc. Am. 1962, 34, 1711–1714. [Google Scholar] [CrossRef]
- Djeddi, R.; Ekici, K. Resolution of Gibbs phenomenon using a modified pseudo-spectral operator in harmonic balance CFD solvers. Int. J. Comput. Fluid Dyn. 2016, 30, 495–515. [Google Scholar] [CrossRef]
- Norberg, C. Flow around a circular cylinder: Aspects of fluctuating lift. J. Fluids Struct. 2001, 15, 459–469. [Google Scholar] [CrossRef]
- He, T.; Zhou, D.; Bao, Y. Combined interface boundary condition method for fluid–rigid body interaction. Comput. Methods Appl. Mech. Eng. 2012, 223, 81–102. [Google Scholar] [CrossRef]
- He, T.; Zhou, D.; Han, Z.; Tu, J.; Ma, J. Partitioned subiterative coupling schemes for aeroelasticity using combined interface boundary condition method. Int. J. Comput. Fluid Dyn. 2014, 28, 272–300. [Google Scholar] [CrossRef]
- He, T.; Zhang, K.; Wang, T. AC-CBS-based partitioned semi-implicit coupling algorithm for fluid-structure interaction using stabilized second-order pressure scheme. Commun. Comput. Phys. 2017, 21, 1449–1474. [Google Scholar] [CrossRef]
- Williamson, C.H.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Nestor, R.M.; Quinlan, N.J. Application of the meshless finite volume particle method to flow-induced motion of a rigid body. Comput. Fluids 2013, 88, 386–399. [Google Scholar] [CrossRef]
- Bahmani, M.; Akbari, M. Response characteristics of a vortex-excited circular cylinder in laminar flow. J. Mech. Sci. Technol. 2011, 25, 125–133. [Google Scholar] [CrossRef]
- Geuzaine, P.; van der Zee, K.; Farhat, C. Second-Order Time-Accurate Loosely-Coupled Solution Algorithms for Nonlinear FSI Problems. In Proceedings of the European Congress on Computational Mechanics in Applied Sciences and Engineering, Barcelona, Spain, 20–25 July 2004. [Google Scholar]
- He, T. On the mesh insensitivity of the edge-based smoothed finite element method for moving-domain problems. Comput. Methods Appl. Mech. Eng. 2025, 440, 117917. [Google Scholar] [CrossRef]
- Dettmer, W.; Perić, D. A computational framework for fluid–rigid body interaction: Finite element formulation and applications. Comput. Methods Appl. Mech. Eng. 2006, 195, 1633–1666. [Google Scholar] [CrossRef]
- Tan, W.; Wu, H.; Zhu, G. Fluid-structure interaction using Lattice Boltzmann method: Moving boundary treatment and discussion of compressible effect. Chem. Eng. Sci. 2018, 184, 273–284. [Google Scholar] [CrossRef]

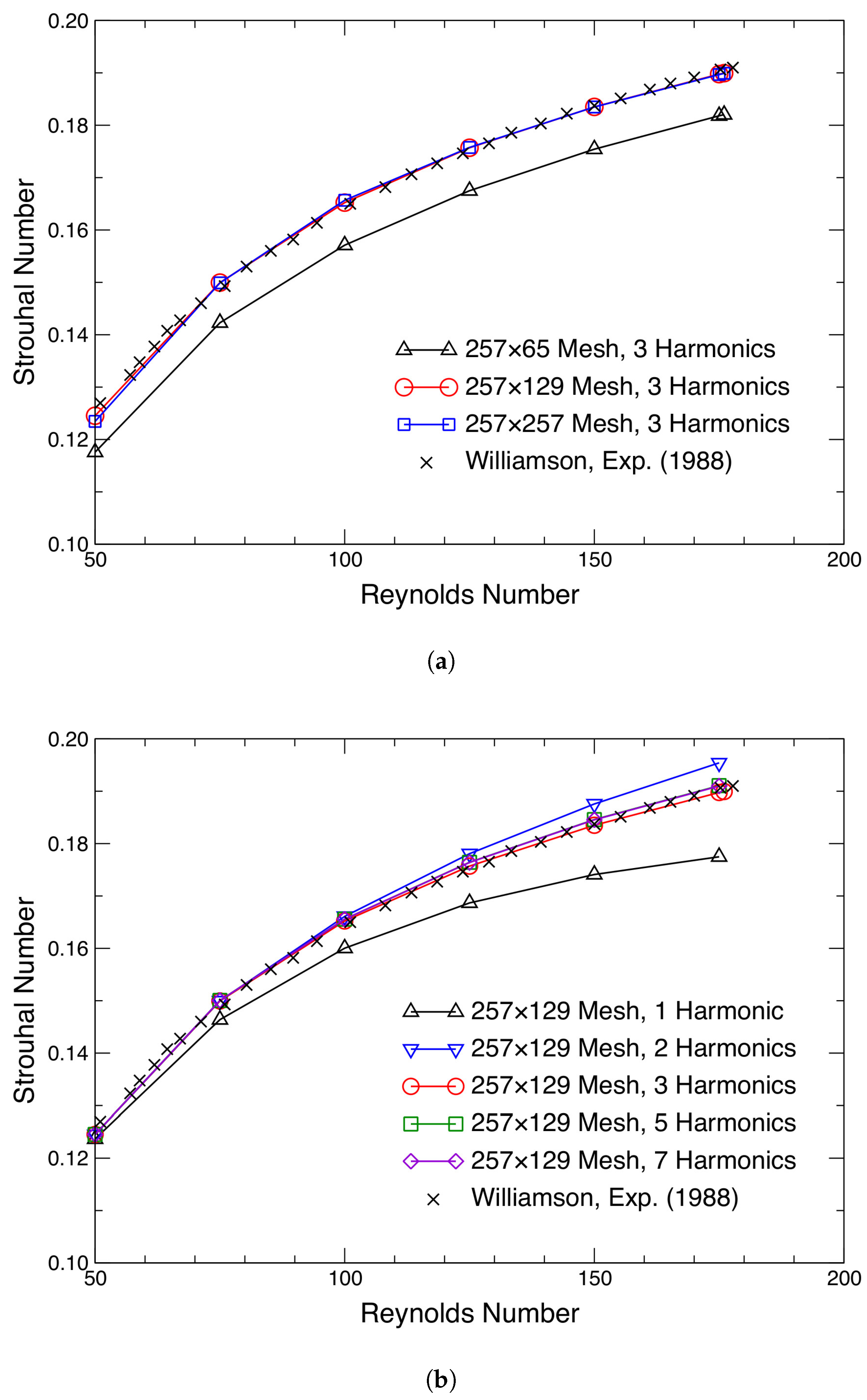

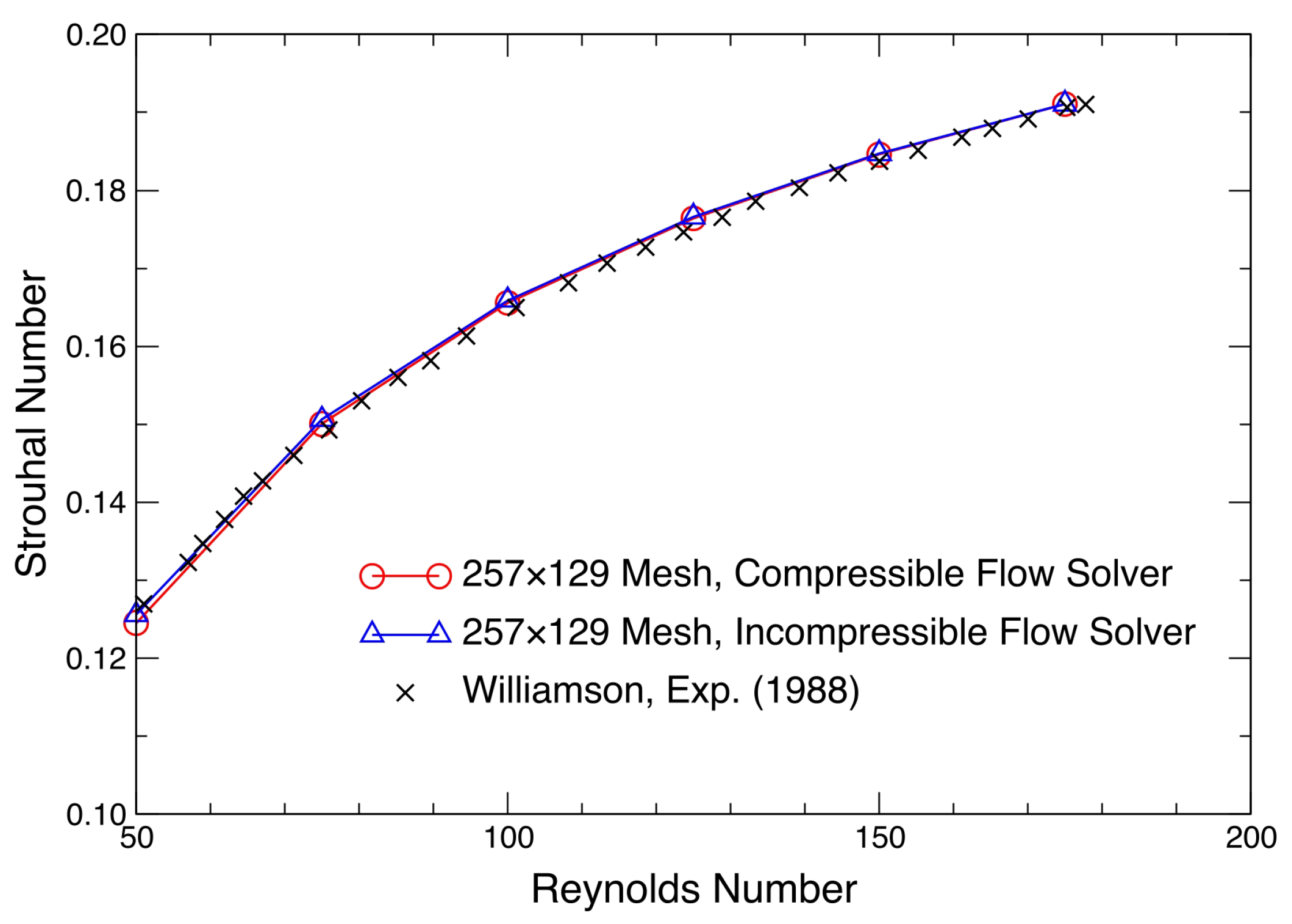

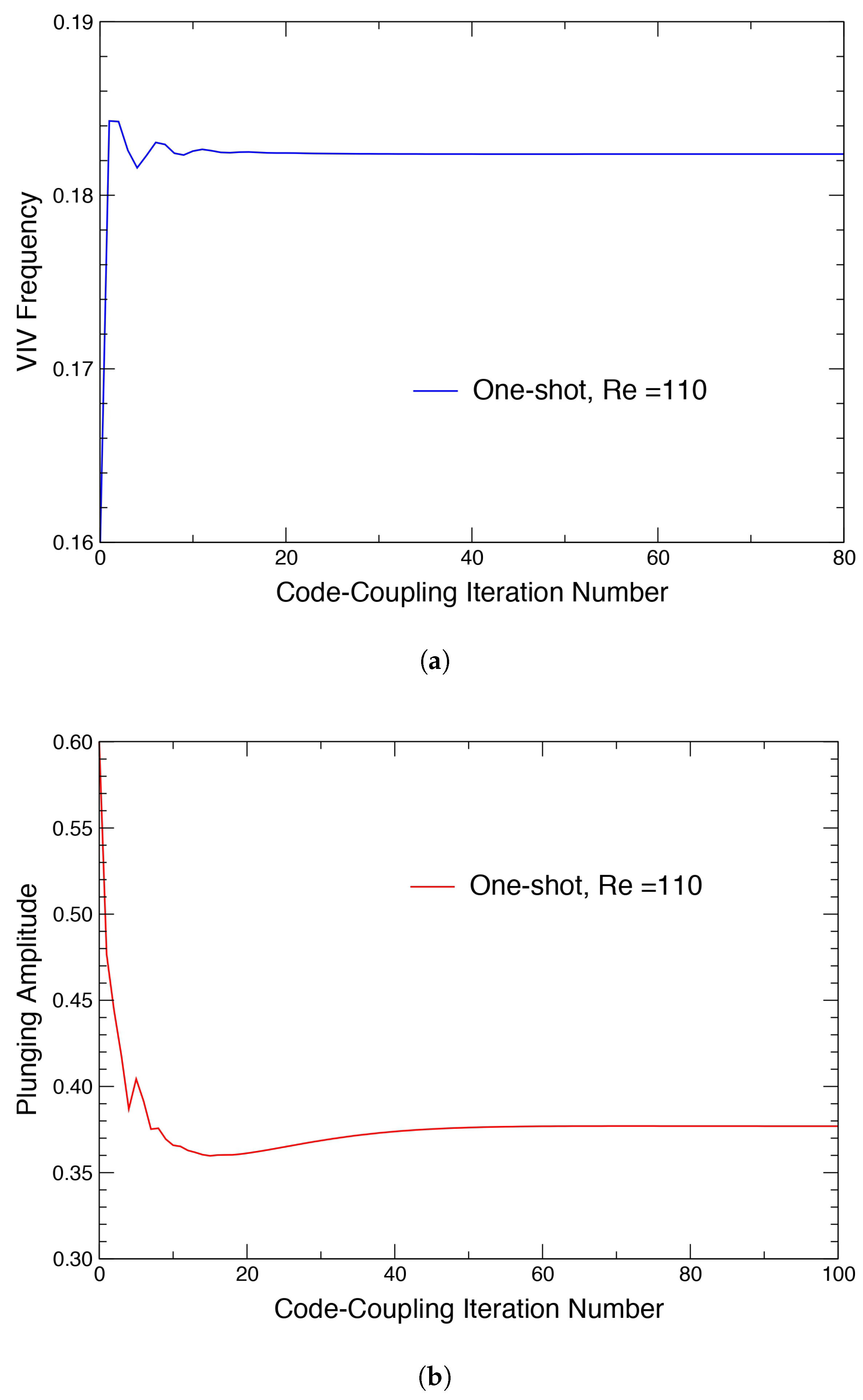
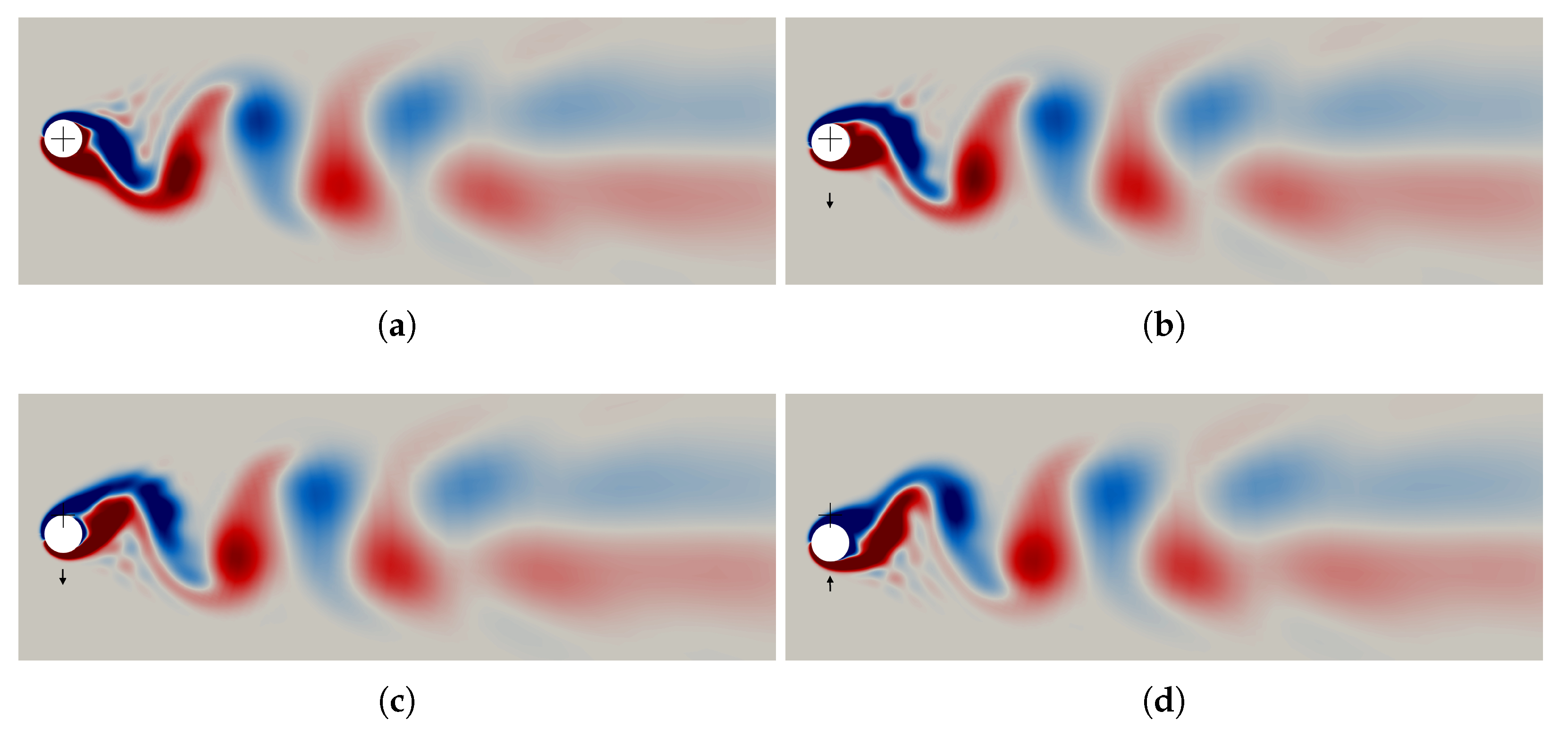
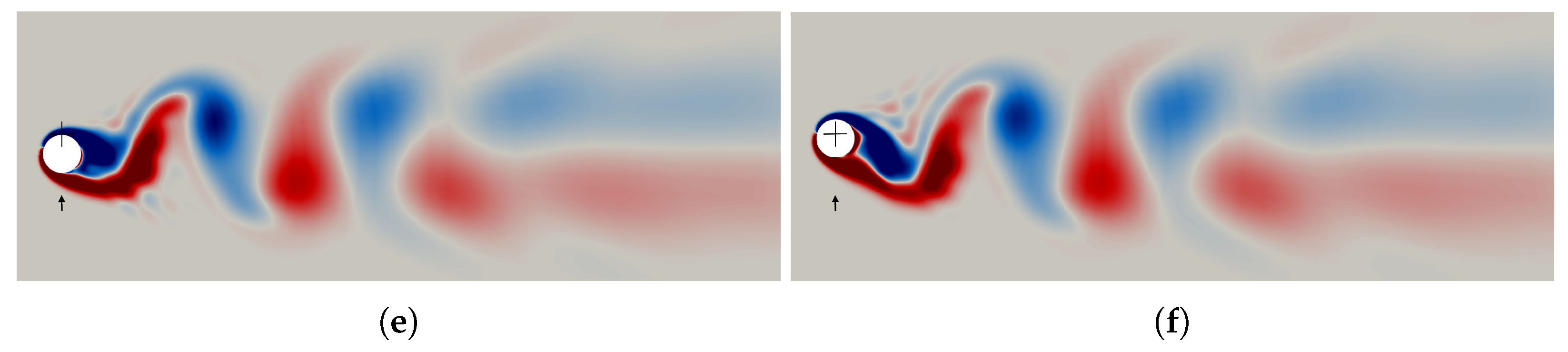
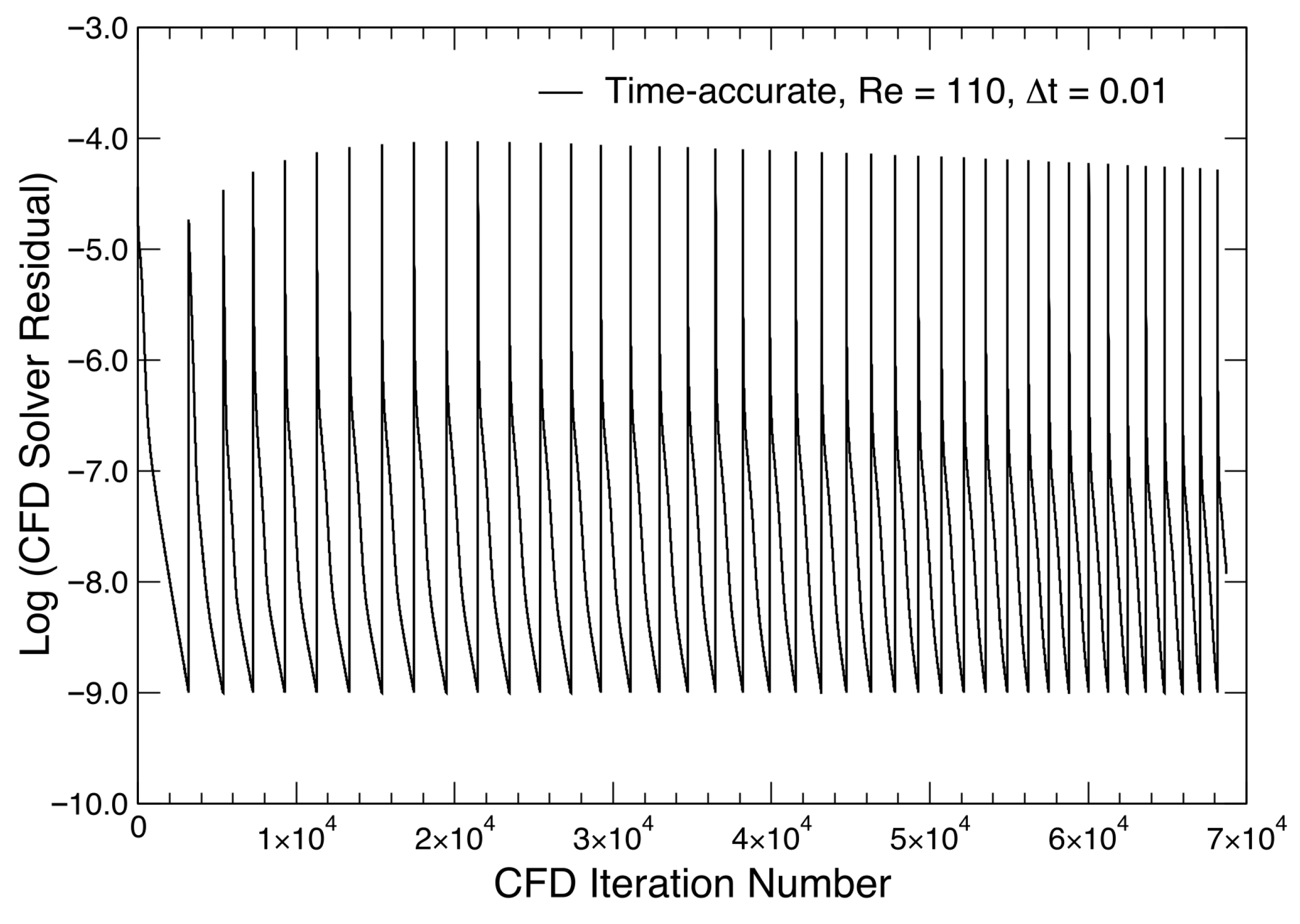
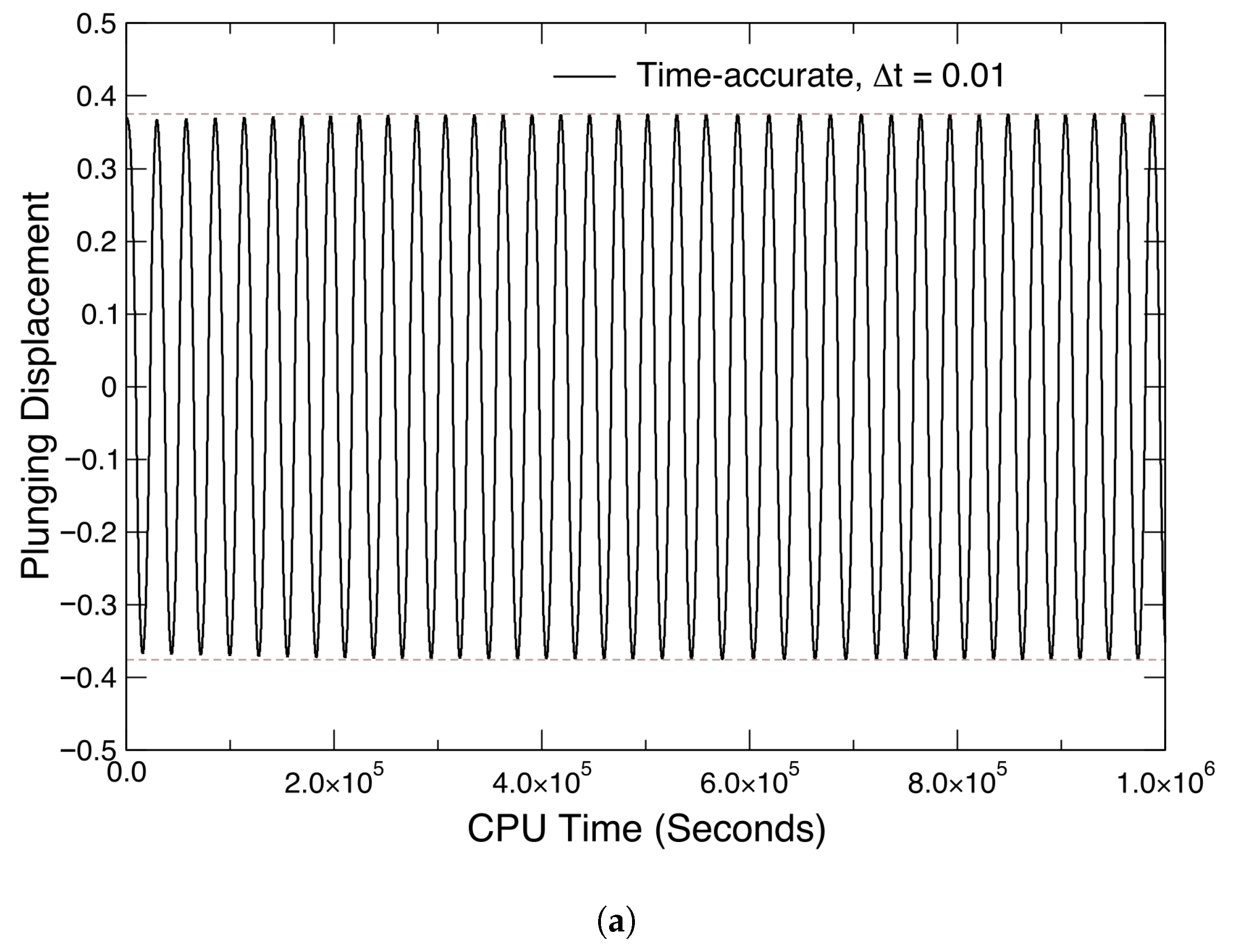
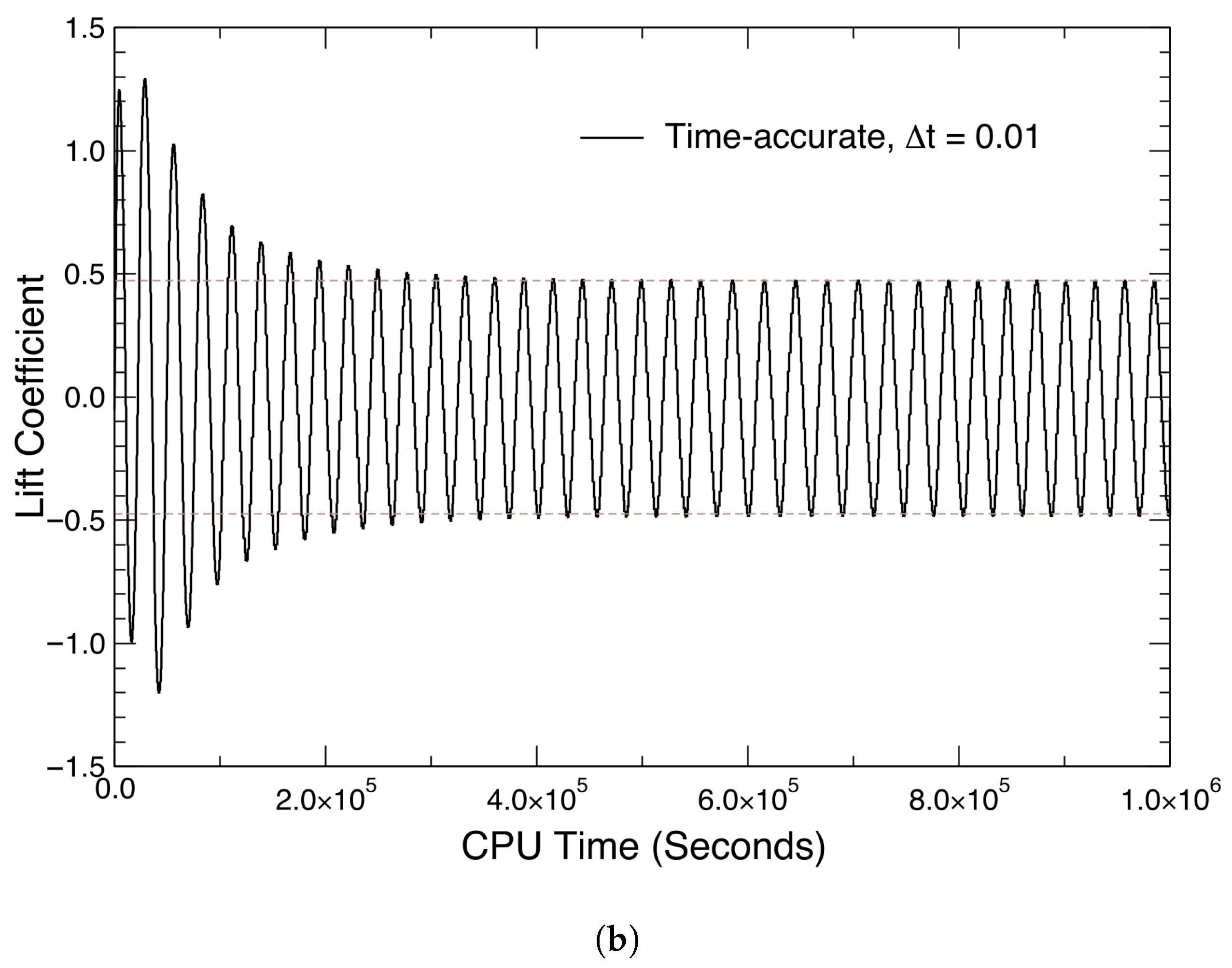

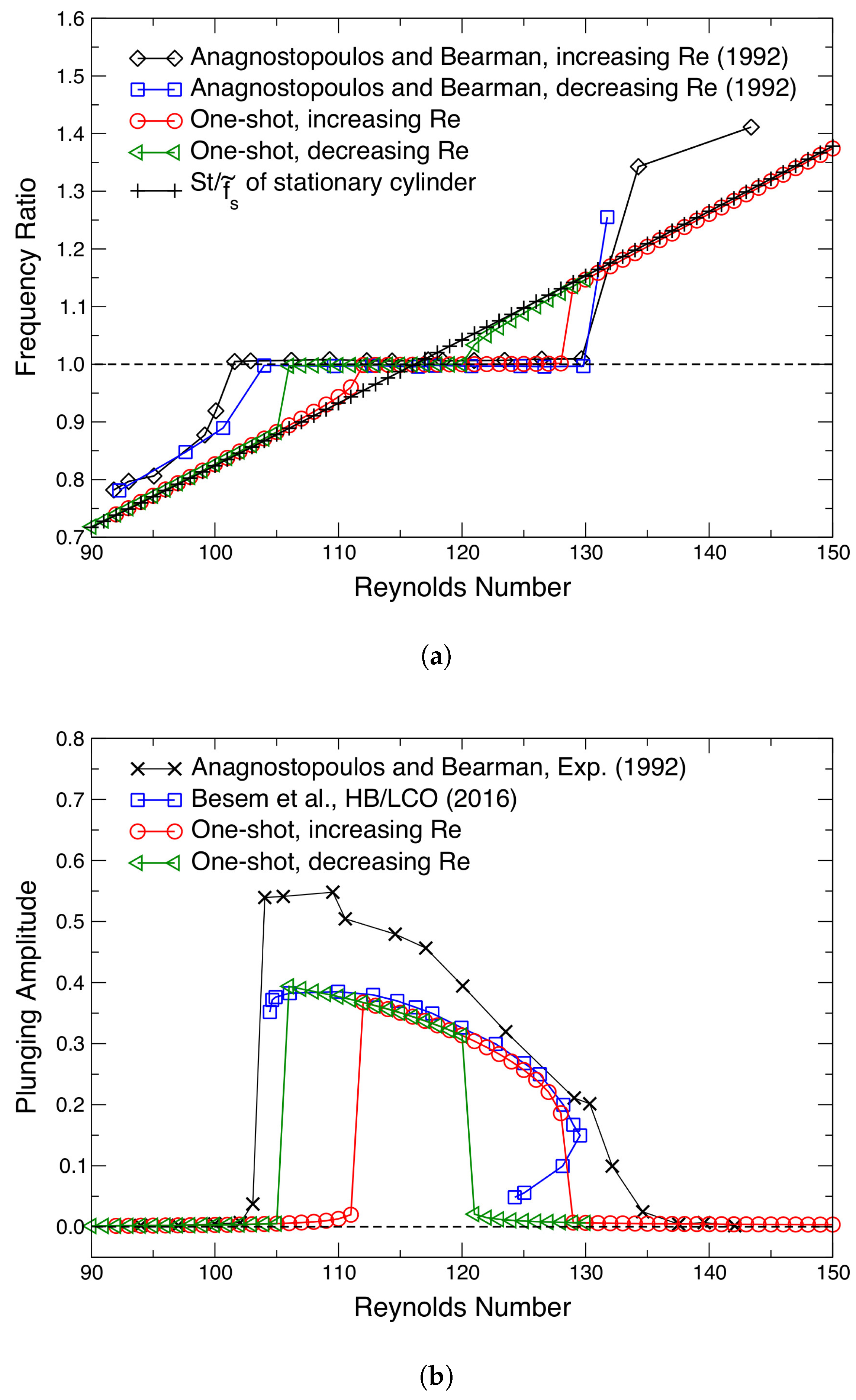
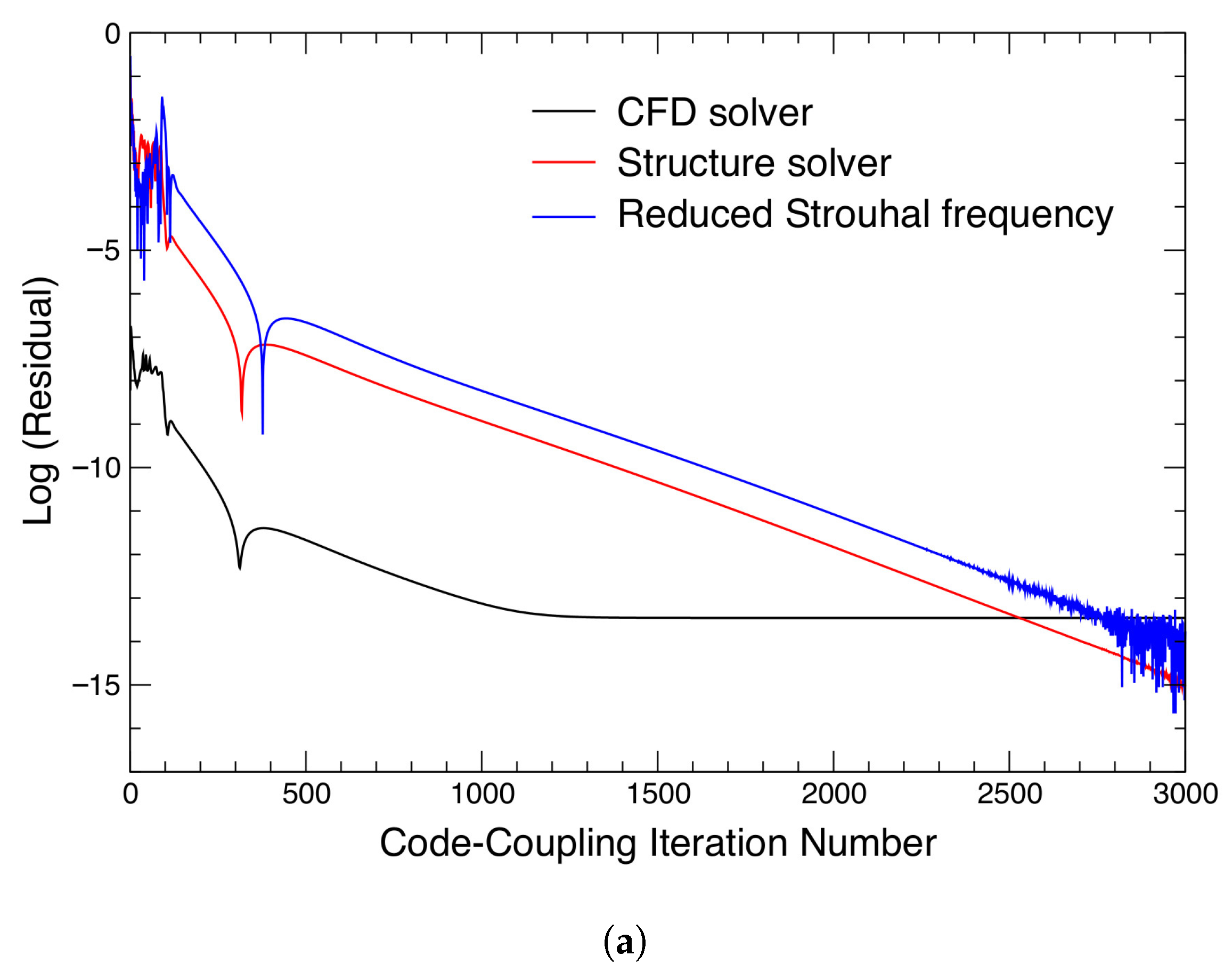
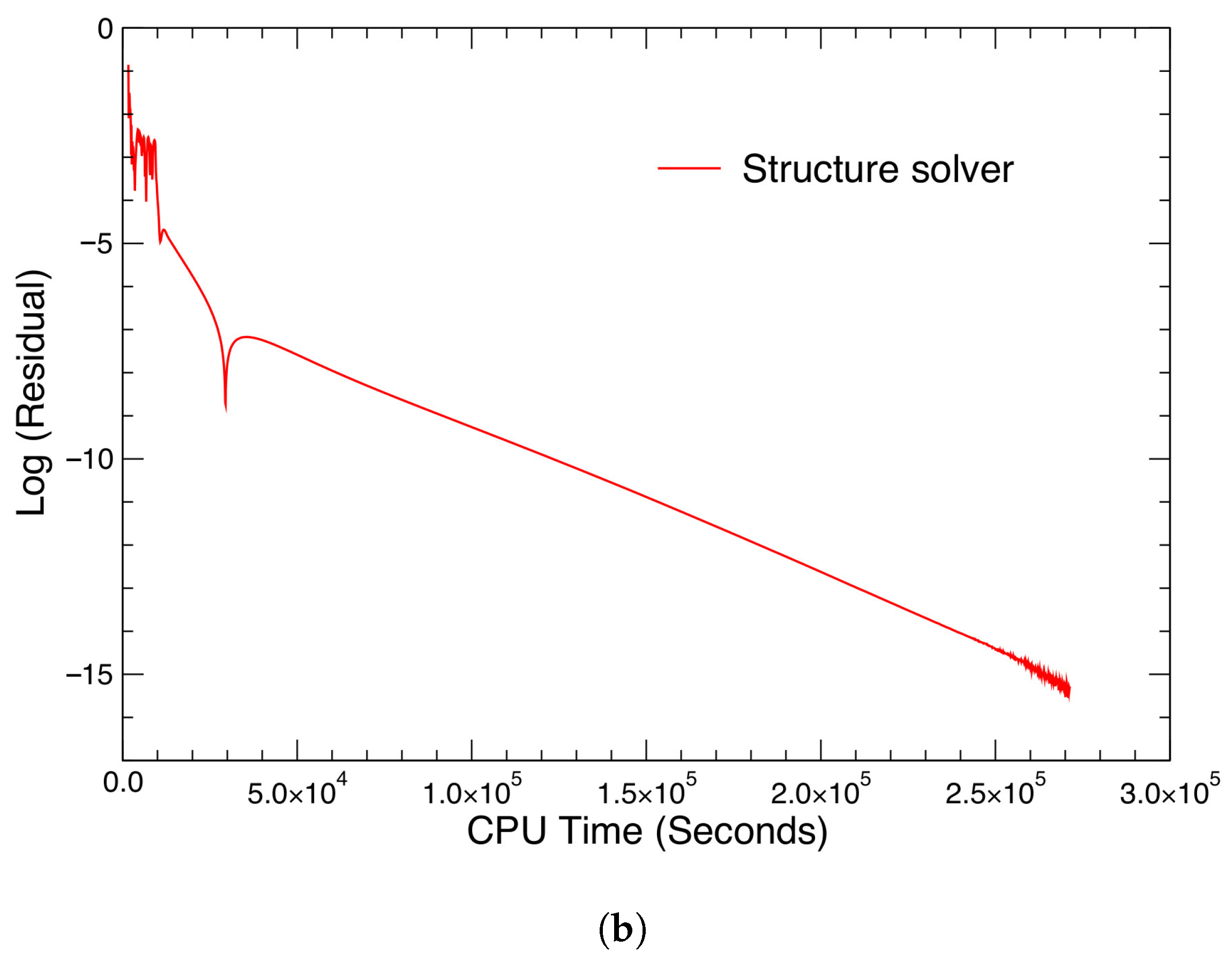
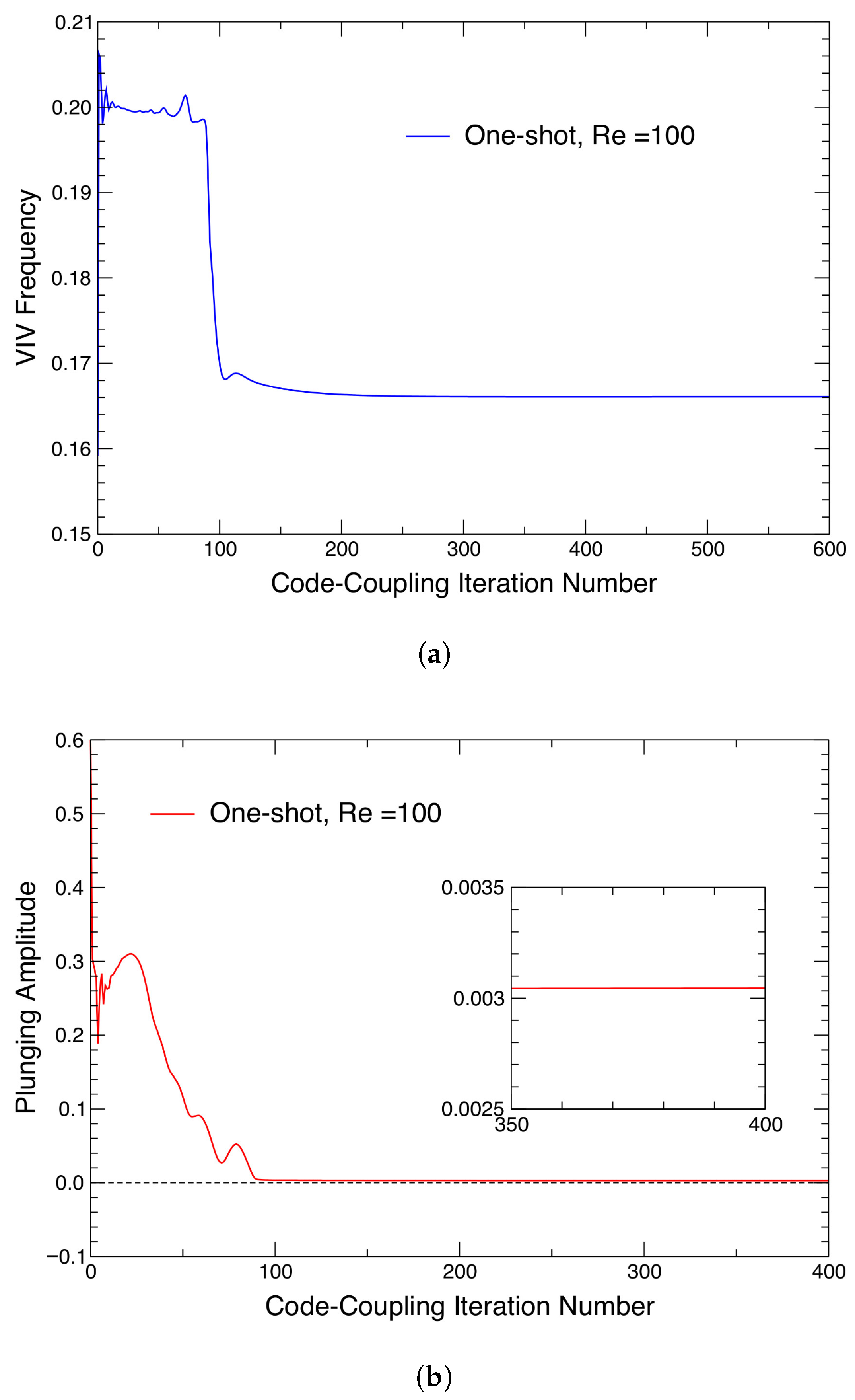
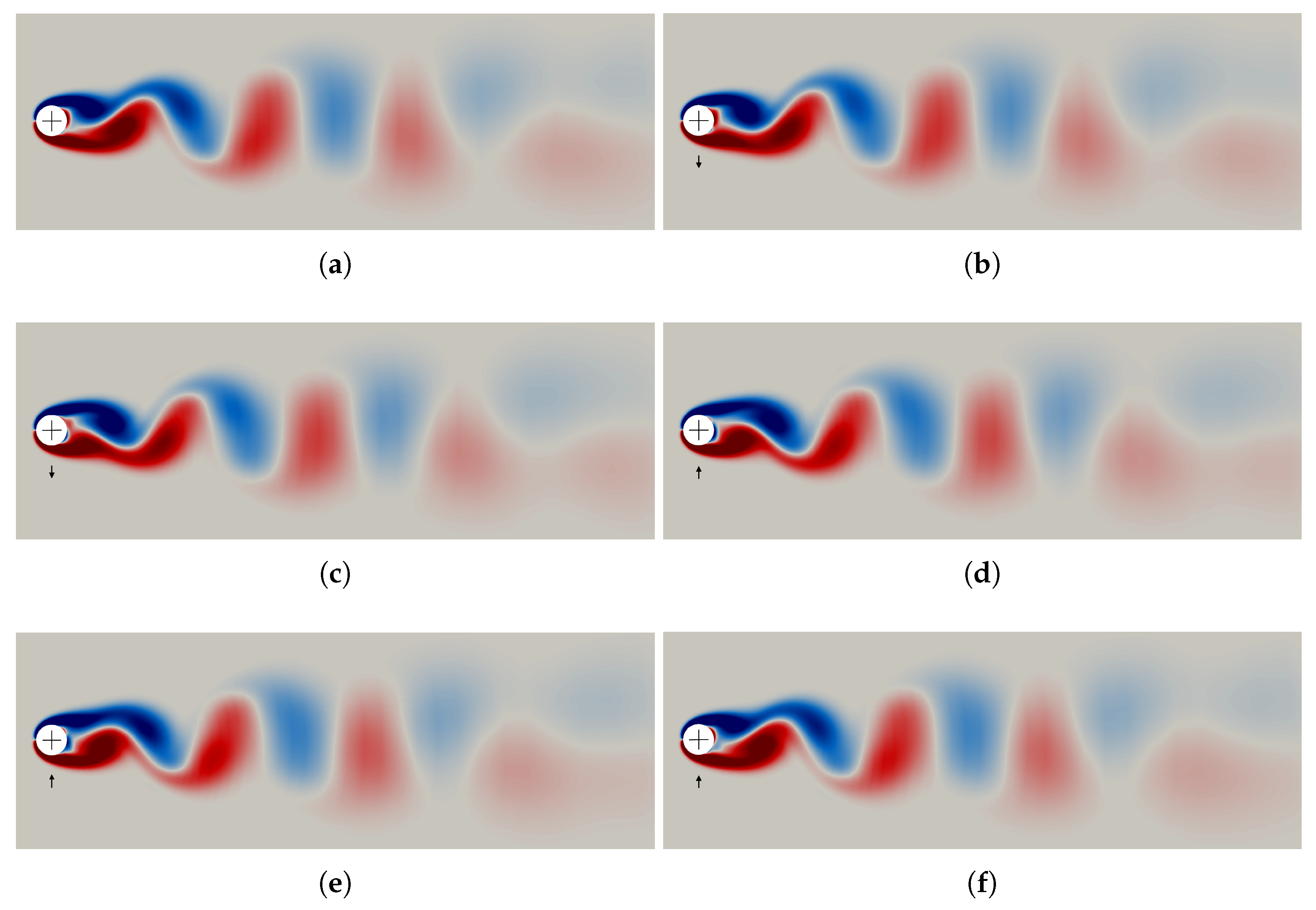
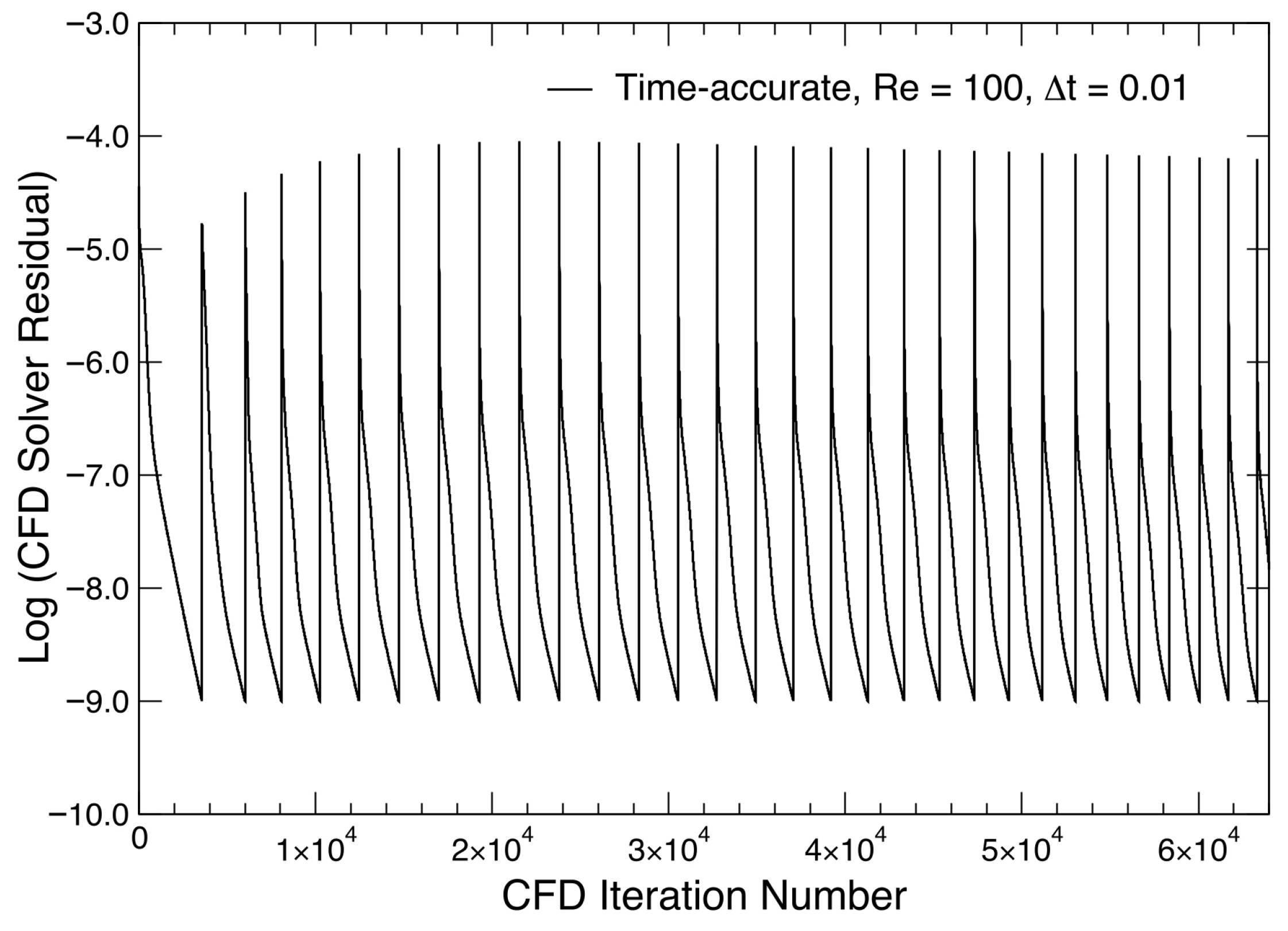
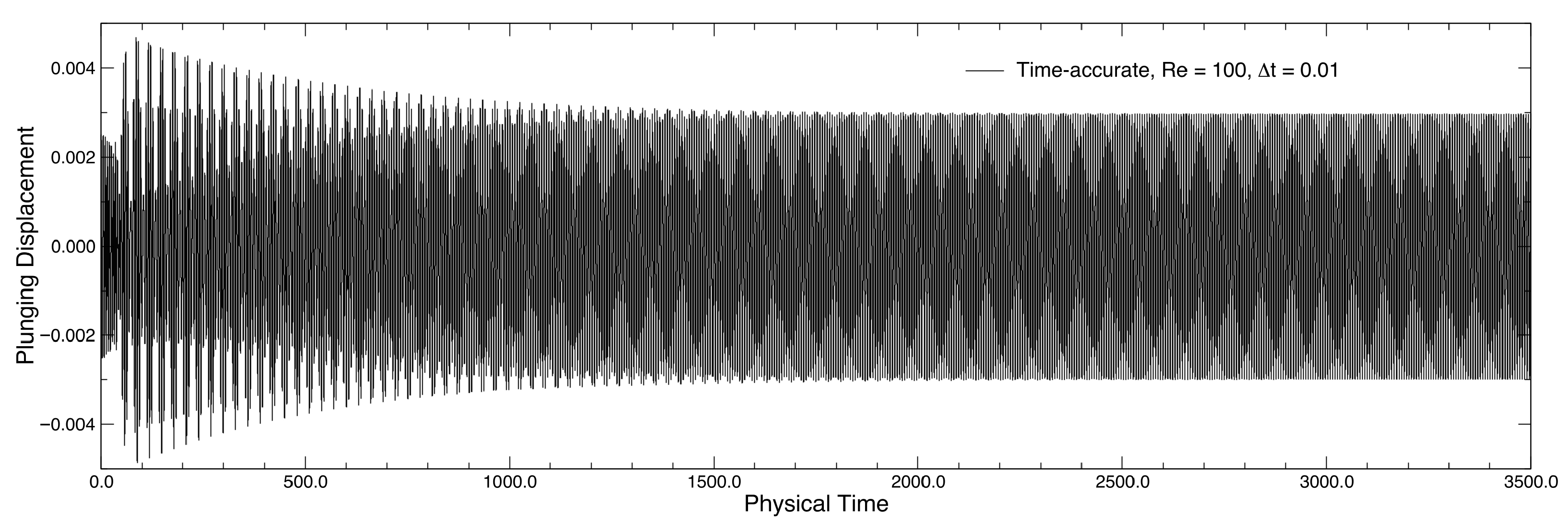
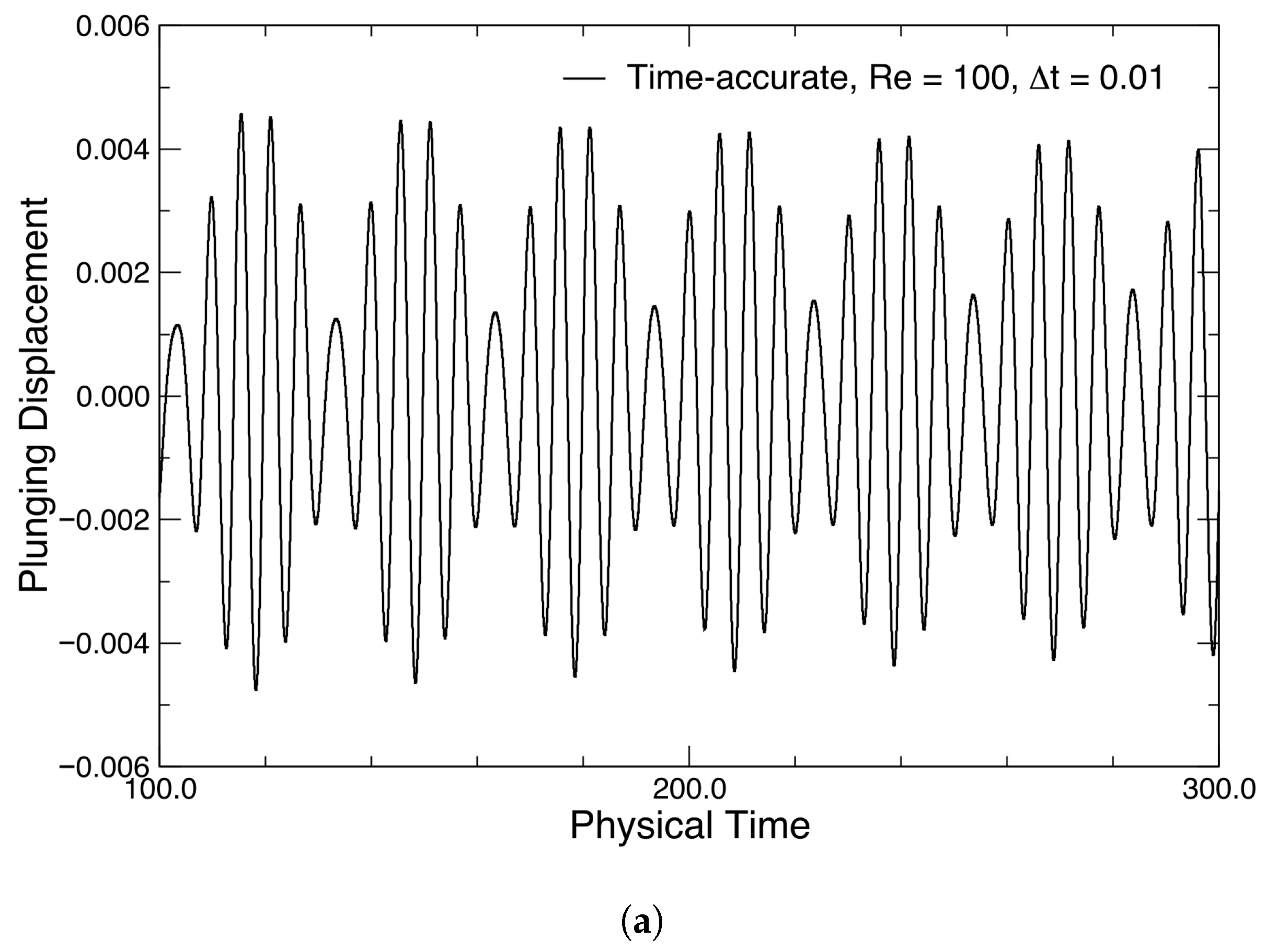


| Parameter | Value |
|---|---|
| Inner iterations of the implicit CSD solver | 1 |
| Pseudo-time step size of the CSD solver, | 40 |
| Inner iterations of the explicit CSD solver | 100 |
| Initial amplitude, | 0.6 |
| Initial phase, | 0.0 |
| Initial frequency, | 0.159 () |
| CPU Time (Seconds) | |||
|---|---|---|---|
| One-shot | 0.1824 | 0.3769 | |
| Time-accurate | 0.1825 | 0.3759 |
| One-shot | 0.1661 | 0.003048 |
| Time-accurate | 0.1661 | 0.002986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Ekici, K. Vortex-Induced Vibration Predictions of a Circular Cylinder Using an Efficient Pseudo-Time Code-Coupling Approach. Fluids 2025, 10, 182. https://doi.org/10.3390/fluids10070182
Li H, Ekici K. Vortex-Induced Vibration Predictions of a Circular Cylinder Using an Efficient Pseudo-Time Code-Coupling Approach. Fluids. 2025; 10(7):182. https://doi.org/10.3390/fluids10070182
Chicago/Turabian StyleLi, Hang, and Kivanc Ekici. 2025. "Vortex-Induced Vibration Predictions of a Circular Cylinder Using an Efficient Pseudo-Time Code-Coupling Approach" Fluids 10, no. 7: 182. https://doi.org/10.3390/fluids10070182
APA StyleLi, H., & Ekici, K. (2025). Vortex-Induced Vibration Predictions of a Circular Cylinder Using an Efficient Pseudo-Time Code-Coupling Approach. Fluids, 10(7), 182. https://doi.org/10.3390/fluids10070182







