Zeta Potential as a Key Indicator of Network Structure and Rheological Behavior in Smectite Clay Dispersions
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
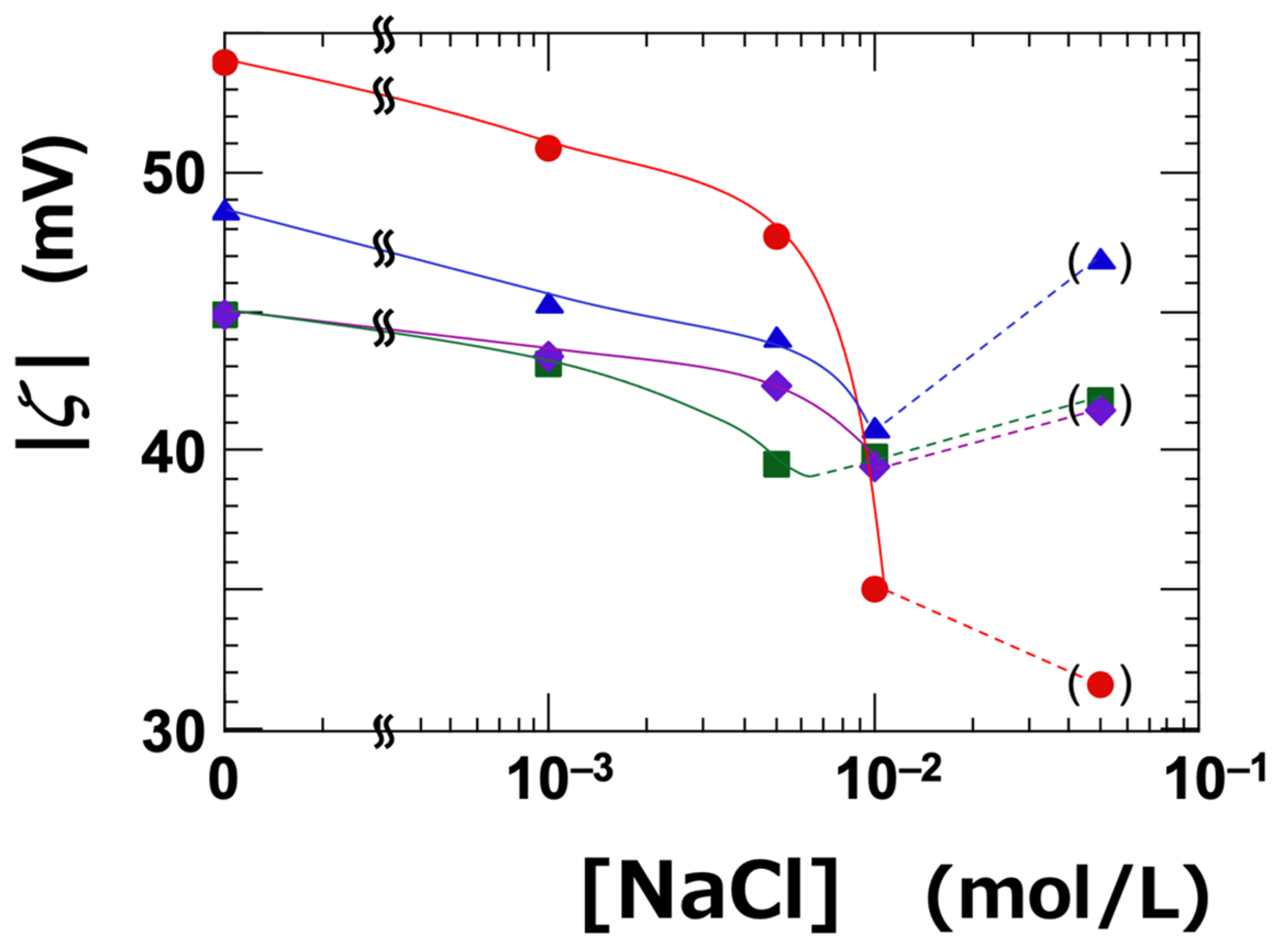
3.1. Cation Exchange Capacity, Zeta Potential, and Electrical Conductivity of Dispersions
3.2. DLVO Potential Curves for Clay Particles in Aqueous Media
3.3. Rheological Measurements
3.3.1. Steady-State (Static) Shear Measurements
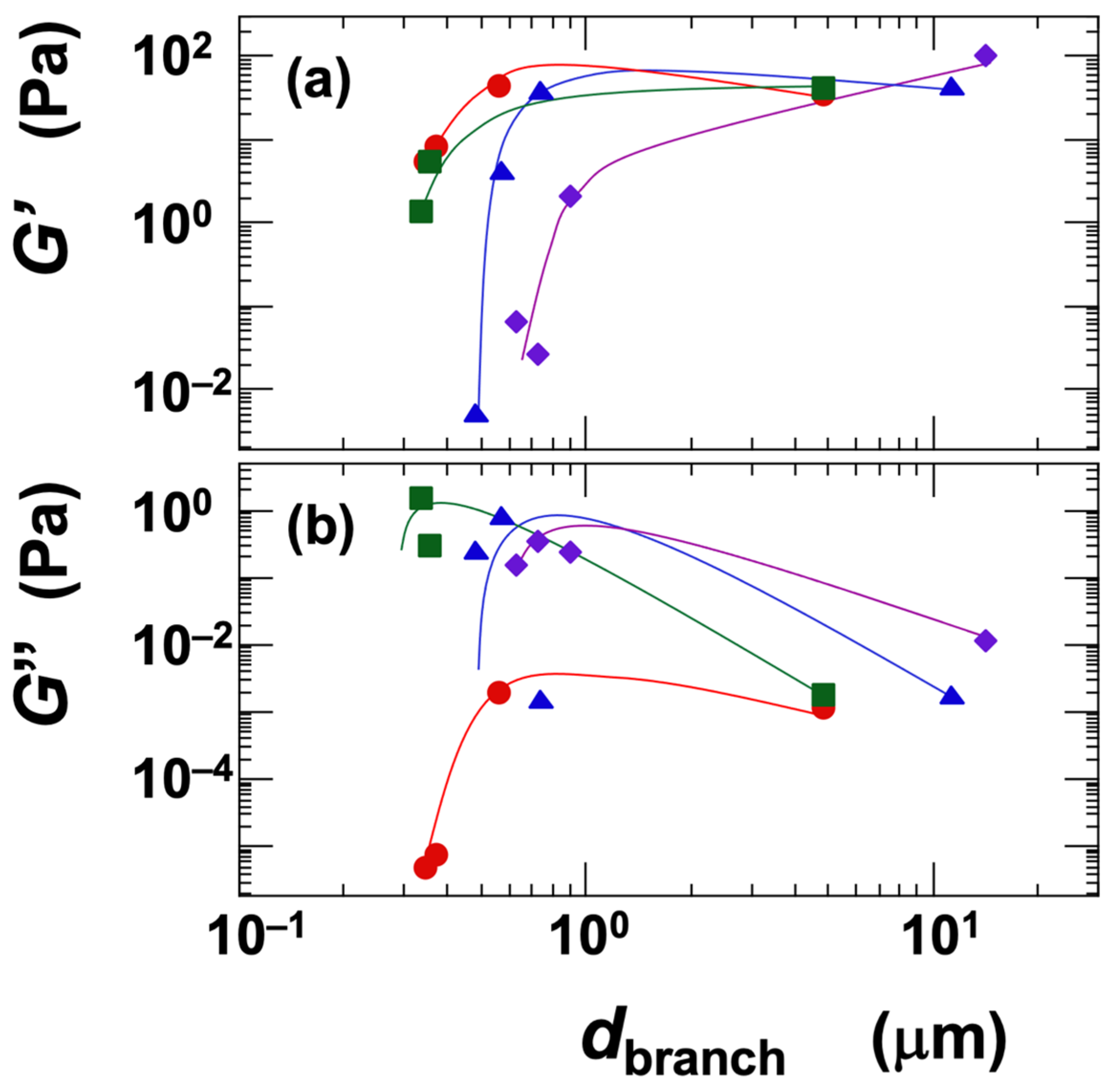
3.3.2. Dynamic (Oscillatory) Rheological Measurements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Olphen, H. An Introduction to Clay Colloid Chemistry, 2nd ed.; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Freundlich, H. About thixotropy (Über Thixotropie). Kolloid-Z. 1928, 46, 289–299. (In German) [Google Scholar] [CrossRef]
- Mourchid, A.; Delville, A.; Levitz, P. Sol–gel transition of colloidal suspensions of anisotropic particles of laponite. Faraday Discuss. 1995, 101, 275–285. [Google Scholar] [CrossRef]
- Kroon, M.; Vos, W.L.; Wegdam, G.H. Structure and formation of a gel of colloidal discs. Phys. Rev. E 1998, 57, 1962–1970. [Google Scholar] [CrossRef]
- Larson, R.G.; Wei, Y. A review of thixotropy and its rheological modeling. J. Rheol. 2019, 63, 477–501. [Google Scholar] [CrossRef]
- Kimura, H. Deionization-induced colorless transparency in physical gels formed by clay aqueous dispersions. Appl. Clay Sci. 2024, 249, 107261. [Google Scholar] [CrossRef]
- Kleinfeld, E.R.; Ferguson, G.S. Stepwise formation of multilayered nanostructural films from macromolecular precursors. Science 1994, 265, 370–373. [Google Scholar] [CrossRef] [PubMed]
- Thompson, D.W.; Butterworth, J.T. The nature of Laponite and its aqueous dispersions. J. Colloid Interface Sci. 1992, 151, 236–243. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, W.; Jin, X.; Su, G. A diffusion model for the swelling of compacted Na–montmorillonite in water. Appl. Clay Sci. 2021, 214, 106301. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Sprik, M.; Cheng, J.; Meijer, E.J.; Wang, R. Acidity of edge surface sites of montmorillonite and kaolinite. Clay Miner. 2011, 46, 209–228. [Google Scholar] [CrossRef]
- Tournassat, C.; Davis, J.A.; Chiaberge, C.; Grangeon, S.; Bourg, I.C. Modeling the acid–base properties of montmorillonite edge surfaces. Environ. Sci. Technol. 2016, 50, 13436–13445. [Google Scholar] [CrossRef]
- Gao, P.; Liu, X.; Guo, Z.; Tournassat, C. Acid–base properties of cis-vacant montmorillonite edge surfaces: A combined first-principles molecular dynamics and surface complexation modeling approach. Environ. Sci. Technol. 2023, 57, 1342–1352. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M.; Hansen, J.-P.; Madden, P.A. Statistical model for the structure and gelation of smectite clay suspensions. Phys. Rev. E 1997, 55, 3044–3053. [Google Scholar] [CrossRef]
- Pignon, F.; Piau, J.M.; Magnin, A. Structure and pertinent length scale of a discotic clay gel. Phys. Rev. Lett. 1996, 76, 4857–4860. [Google Scholar] [CrossRef] [PubMed]
- Pignon, F.; Magnin, A.; Piau, J.M.; Cabane, B.; Lindner, P.; Diat, O. Yield stress thixotropic clay suspension: Investigations of structure by light, neutron, and X-ray scattering. Phys. Rev. E 1997, 56, 3281–3289. [Google Scholar] [CrossRef]
- Ramsey, J.D.F. Colloidal properties of synthetic hectorite clay dispersions: I. Rheology. J. Colloid Interface Sci. 1986, 109, 441–447. [Google Scholar] [CrossRef]
- Durán, J.D.G.; Ramos-Tejada, M.M.; Arroyo, F.J.; González-Caballero, F. Rheological and electrokinetic properties of sodium montmorillonite suspensions: I. Rheological properties and interparticle energy of interaction. J. Colloid Interface Sci. 2000, 229, 107–117. [Google Scholar] [CrossRef]
- Tombácz, E.; Szekeres, M. Colloidal behavior of aqueous montmorillonite suspensions: The specific role of pH in the presence of indifferent electrolytes. Appl. Clay Sci. 2004, 27, 75–94. [Google Scholar] [CrossRef]
- Ali, S.; Bandyopadhyay, R. Effect of electrolyte on the microstructure and yielding of aqueous dispersions of colloidal clay. Soft Matter 2015, 11, 5774–5782. [Google Scholar] [CrossRef]
- Lin, Y.; Qin, H.; Guo, J.; Chen, J. Rheology of bentonite dispersions: Role of ionic strength and solid content. Appl. Clay Sci. 2021, 214, 106275. [Google Scholar] [CrossRef]
- Schofield, R.K. Ionic forces in thick films of liquid between charged surfaces. Trans. Faraday Soc. 1946, 42, 219–228. [Google Scholar] [CrossRef]
- Kimura, H. Influence of sol–gel state in smectite aqueous dispersions on drying patterns of droplets. Materials 2024, 17, 2891. [Google Scholar] [CrossRef] [PubMed]
- Bonn, D.; Tanaka, H.; Wegdam, G.; Kellay, H.; Meunier, J. Aging of a colloidal “Wigner” glass. Europhys. Lett. 1998, 45, 52–57. [Google Scholar] [CrossRef]
- Mourchid, A.; Levitz, P. Long-term gelation of Laponite aqueous dispersions. Phys. Rev. E 1998, 57, R4887–R4890. [Google Scholar] [CrossRef]
- Cummins, H.Z. Liquid, glass, gel: The phases of colloidal Laponite. J. Non-Cryst. Solids 2007, 353, 3891–3905. [Google Scholar] [CrossRef]
- Abu-Jdayil, B. Rheology of sodium and calcium bentonite–water dispersions: Effect of electrolytes and aging time. Int. J. Miner. Process. 2011, 98, 208–213. [Google Scholar] [CrossRef]
- Au, P.-I.; Leong, Y.-K. Surface chemistry and rheology of Laponite dispersions: Zeta potential, yield stress, ageing, fractal dimension and pyrophosphate. Appl. Clay Sci. 2015, 107, 36–45. [Google Scholar]
- Leong, Y.K.; Clode, P.L. Time-dependent clay gels: Stepdown shear rate behavior, microstructure, ageing, and phase state ambiguity. Phys. Fluids 2023, 35, 123329. [Google Scholar] [CrossRef]
- Lin, Y.; Cheah, L.K.-J.; Phan-Thien, N.; Khoo, B.C. Effect of temperature on rheological behavior of kaolinite and bentonite suspensions. Colloids Surf. A 2016, 506, 1–5. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd ed.; Butterworths: London, UK, 1959. [Google Scholar]
- Yamamoto, M. Derivation of Onsager’s equation for the electrical conductivity of strong electrolytes. Rev. Polarogr. 2022, 68, 47–50. (In Japanese) [Google Scholar]
- Atkins, P.W. Physical Chemistry, 5th ed.; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Jiang, C.; Wang, Y.; Wang, D.; Zhang, G. Effects of inorganic and organic anions on the stability of illite and quartz soil colloids in Na-, Ca- and mixed Na–Ca systems. Colloids Surf. A Physicochem. Eng. Asp. 2012, 415, 134–141. [Google Scholar] [CrossRef]
- Luckham, P.F.; Rossi, S. The colloidal and rheological properties of bentonite suspensions. Adv. Colloid Interface Sci. 1999, 82, 43–92. [Google Scholar] [CrossRef]
- Mpofu, P.; Addai-Mensah, J.; Ralston, J. Interfacial chemistry, particle interactions and improved dewatering behaviour of smectite clay dispersions. Int. J. Miner. Process. 2005, 75, 155–174. [Google Scholar] [CrossRef]
- Chorom, M.; Rengasamy, P. Dispersion and zeta potential of pure clays as related to net particle charge under varying pH, electrolyte concentration and cation type. Eur. J. Soil Sci. 1995, 46, 657–665. [Google Scholar] [CrossRef]
- Marry, V.; Le Crom, S.; Ferrage, E.; Michot, L.; Farago, B.; Delville, A.; Dubois, E. Role of cationic organization on water dynamics in saponite clays. J. Phys. Chem. C 2024, 128, 4233–4244. [Google Scholar] [CrossRef]
- Yoonessi, M.; Toghiani, H.; Kingery, W.L.; Pittman, C.U., Jr. Preparation, characterization, and properties of exfoliated/delaminated organically modified clay/dicyclopentadiene resin nanocomposites. Macromolecules 2004, 37, 2511–2518. [Google Scholar] [CrossRef]
- Stöter, M.; Rosenfeldt, S.; Breu, J. Tunable exfoliation of synthetic clays. Annu. Rev. Mater. Res. 2015, 45, 129–151. [Google Scholar] [CrossRef]
- Jennings, B.R.; Parslow, K. Particle size measurement: The equivalent spherical diameter. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1988, 419, 137–149. [Google Scholar]
- Derjaguin, B.; Landau, L.D. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Physicochim. URSS 1941, 14, 633–662. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Hunter, R.J. Foundations of Colloid Science, 2nd ed.; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: London, UK, 2011. [Google Scholar]
- Kimura, H. Influence of alternating electric field on electrorheological effect of aqueous dispersions of stevensite. Appl. Clay Sci. 2024, 254, 107393. [Google Scholar] [CrossRef]
- Tadros, T. General principles of colloid stability and the role of surface forces. In Colloid Stability: The Role of Surface Forces; Wiley-VCH: Weinheim, Germany, 2011; pp. 1–45. [Google Scholar]
- Yoon, R.-H.; Kwon, T. The effect of non-DLVO forces on the stability of colloidal suspensions. Colloids Surf. A 1996, 114, 267–276. [Google Scholar]
- Barnes, H.A. The yield stress—A review or ‘panta roi’—Everything flows? J. Non-Newtonian Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Sciortino, F.; Buldyrev, S.V.; De Michele, C.; Foffi, G.; Ghofraniha, N.; La Nave, E.; Moreno, A.; Mossa, S.; Saika-Voivod, I.; Tartaglia, P.; et al. Routes to colloidal gel formation. Comput. Phys. Commun. 2005, 169, 166–171. [Google Scholar] [CrossRef]
- Abend, S.; Lagaly, G. Sol–gel transitions of sodium montmorillonite dispersions. Appl. Clay Sci. 2000, 16, 201–227. [Google Scholar] [CrossRef]
- Armstrong, M.J.; Beris, A.N.; Rogers, S.A.; Wagner, N.J. Dynamic shear rheology of a thixotropic suspension: Comparison of an improved structure-based model with large amplitude oscillatory shear experiments. J. Rheol. 2016, 60, 433–450. [Google Scholar] [CrossRef]
- Trappe, V.; Weitz, D.A. Scaling of the viscoelasticity of weakly attractive particles. Phys. Rev. Lett. 2000, 85, 449–452. [Google Scholar] [CrossRef]
- Zaccarelli, E. Colloidal gels: Equilibrium and non-equilibrium routes. J. Phys. Condens. Matter 2007, 19, 323101. [Google Scholar] [CrossRef]
- Adachi, Y.; Tsujimoto Kawashima, Y.; Ghazali, M.E.B. Rheology and sedimentation of aqueous suspension of Na-montmorillonite in the very dilute domain. KONA Powder Part. J. 2020, 37, 145–165. [Google Scholar] [CrossRef]









| Clay | d | Thickness | CEC | |ζ|(*1) |
|---|---|---|---|---|
| (nm) | (nm) | (meq/100 g) | (mV) | |
| Ht-F | 40 | 1 | 70 | 54 |
| Stv | 46 | 1 | 32 | 45 |
| Ht | 79 | 1 | 49 | 48 |
| Sap | 108 | 1 | 70 | 45 |
| Clay | d | CEC | κ | |ζ| (*1) | η (*2) | σ y(*3) | Gel Region | G’ (*3) | Tr |
|---|---|---|---|---|---|---|---|---|---|
 | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kimura, H.; Tanabe, H.; Shinoki, S. Zeta Potential as a Key Indicator of Network Structure and Rheological Behavior in Smectite Clay Dispersions. Fluids 2025, 10, 178. https://doi.org/10.3390/fluids10070178
Kimura H, Tanabe H, Shinoki S. Zeta Potential as a Key Indicator of Network Structure and Rheological Behavior in Smectite Clay Dispersions. Fluids. 2025; 10(7):178. https://doi.org/10.3390/fluids10070178
Chicago/Turabian StyleKimura, Hiroshi, Haruka Tanabe, and Susumu Shinoki. 2025. "Zeta Potential as a Key Indicator of Network Structure and Rheological Behavior in Smectite Clay Dispersions" Fluids 10, no. 7: 178. https://doi.org/10.3390/fluids10070178
APA StyleKimura, H., Tanabe, H., & Shinoki, S. (2025). Zeta Potential as a Key Indicator of Network Structure and Rheological Behavior in Smectite Clay Dispersions. Fluids, 10(7), 178. https://doi.org/10.3390/fluids10070178






