Effect of Pore-Scale Anisotropic and Heterogeneous Structure on Rarefied Gas Flow in Three-Dimensional Porous Media
Abstract
1. Introduction
2. Numerical Method
2.1. Lattice Boltzmann Method with Multiple Relaxation Time Collision Operator
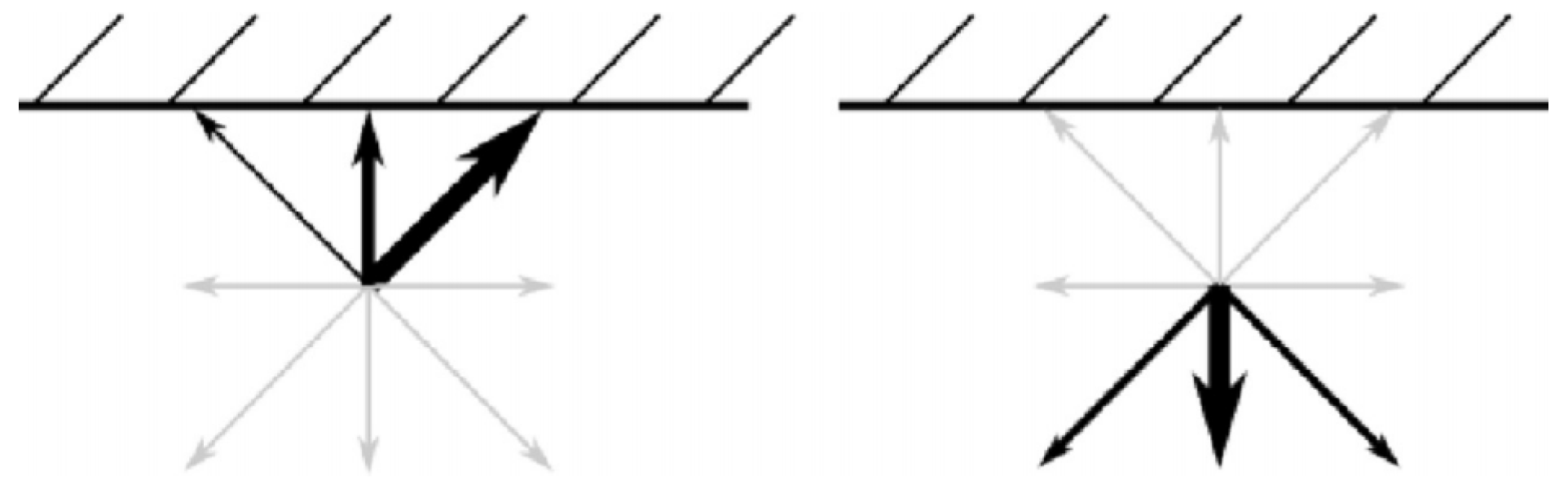
2.2. Boundary Condition
2.3. Unit Conversion
2.4. Permeability Calculation
3. Validation of the MRT-LBM
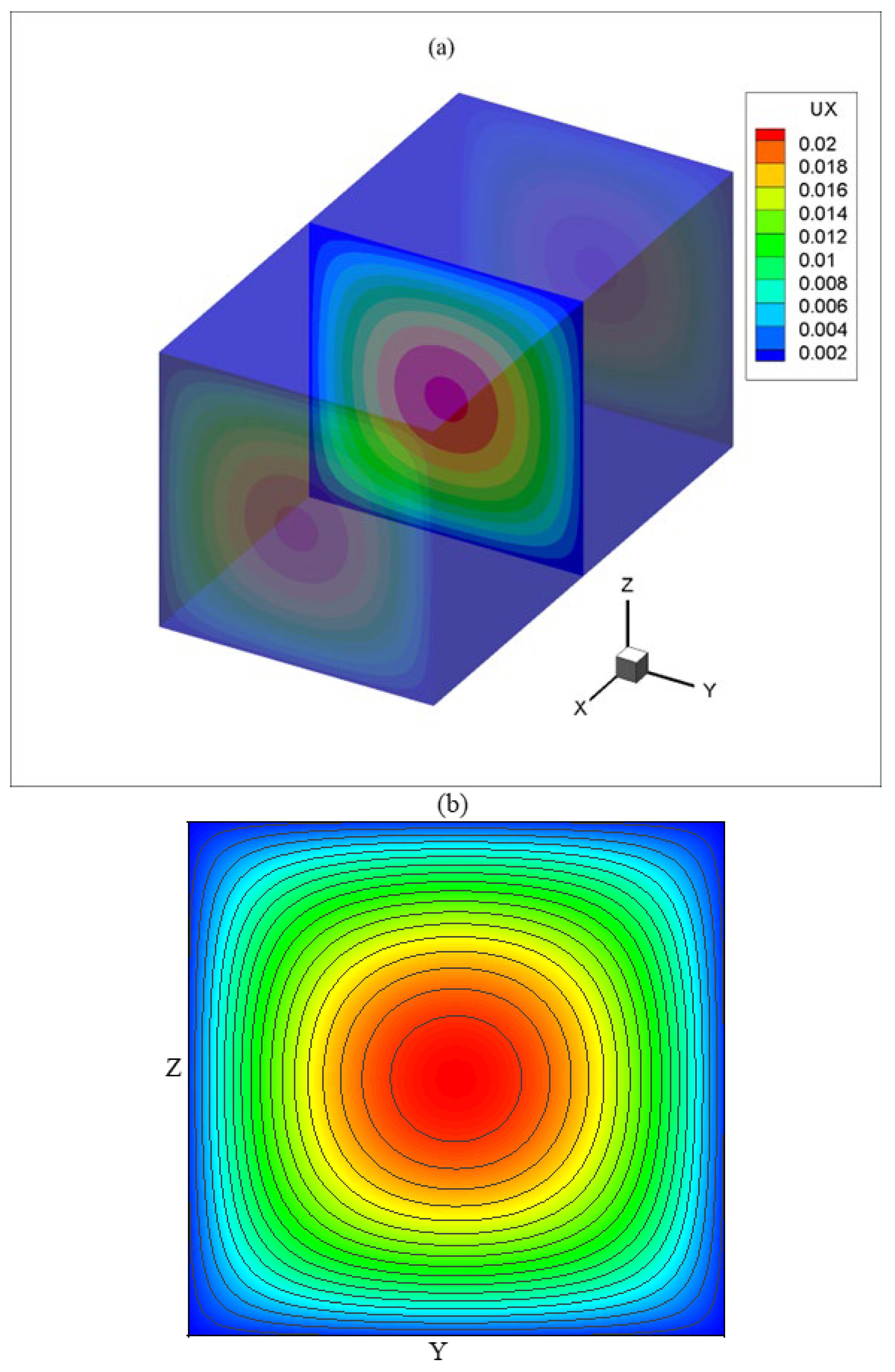
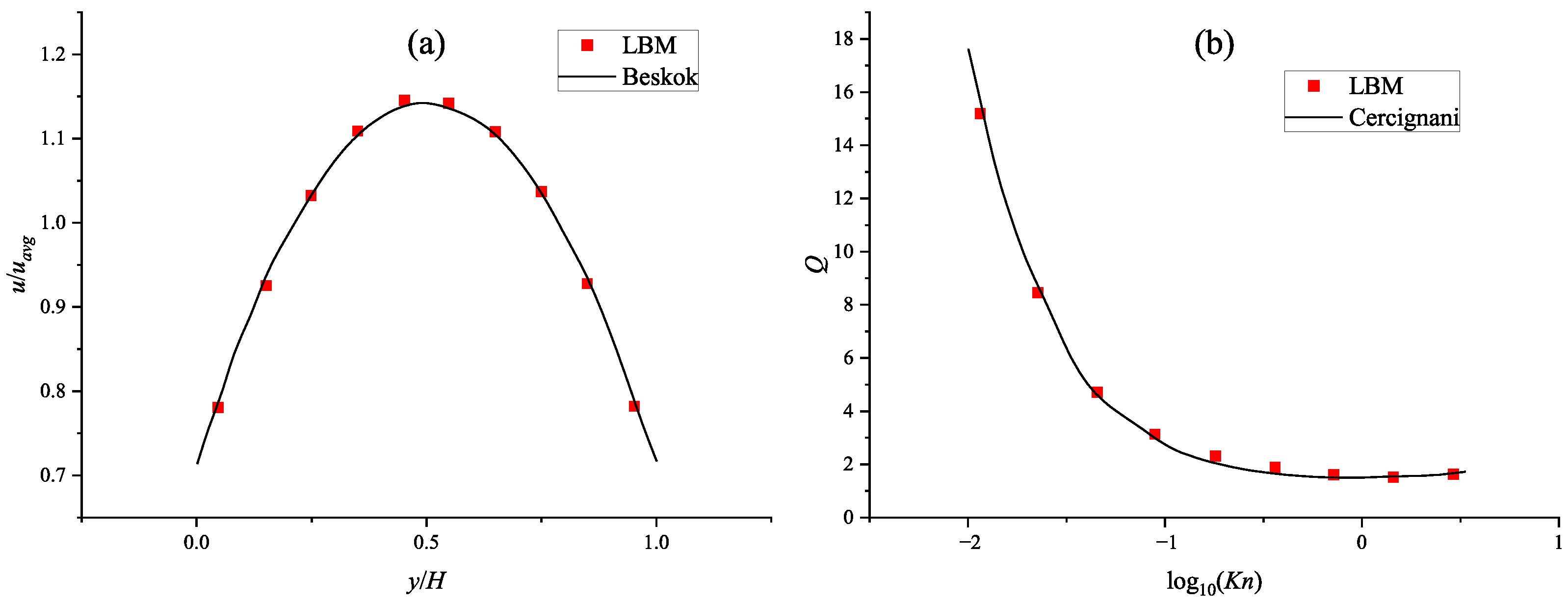
3.1. Poiseuille Flow in a 3D Square Channel
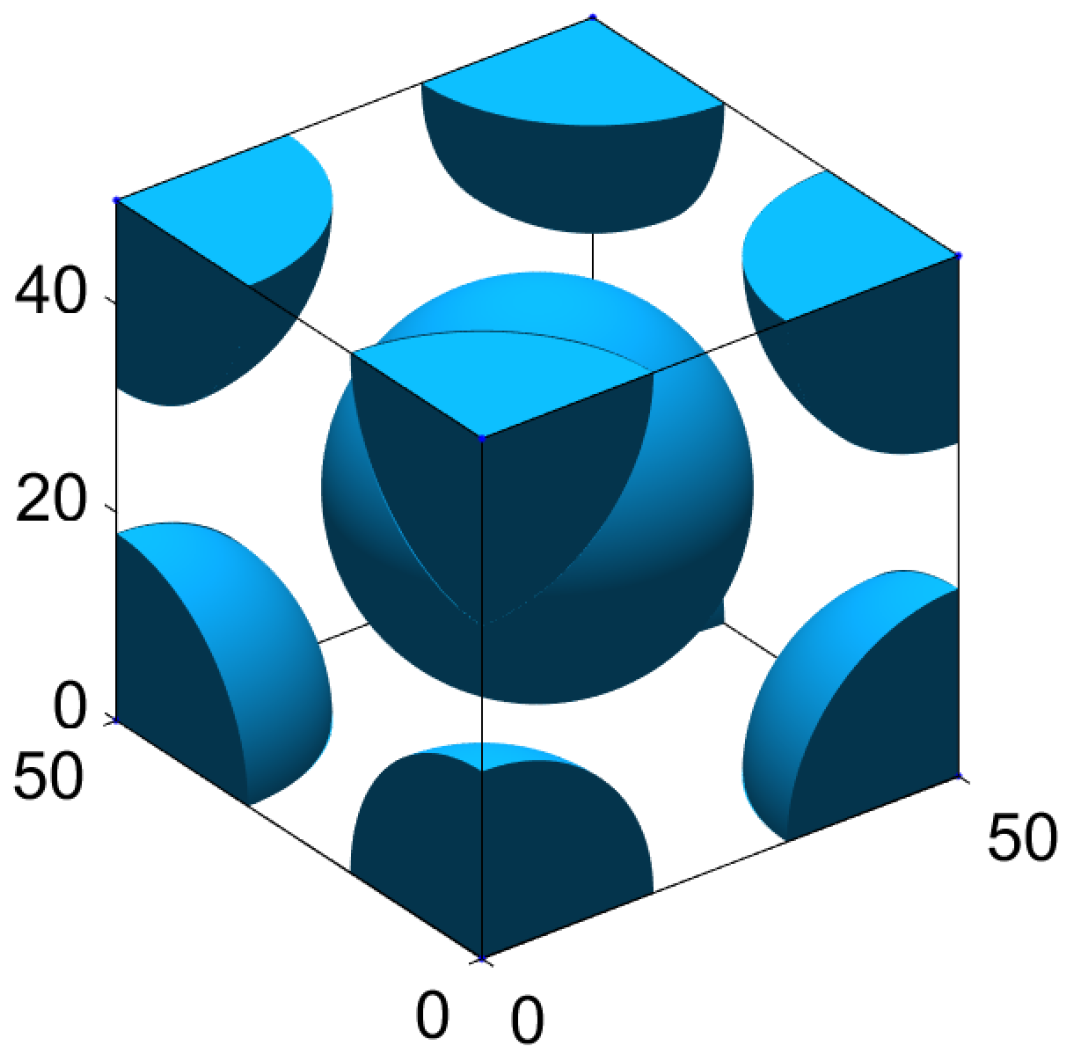
3.2. Flow Through a Body-Centered Cubic Array of Spheres
3.3. Mircochannel Flow at High Kn Number
4. Flow in Porous Media
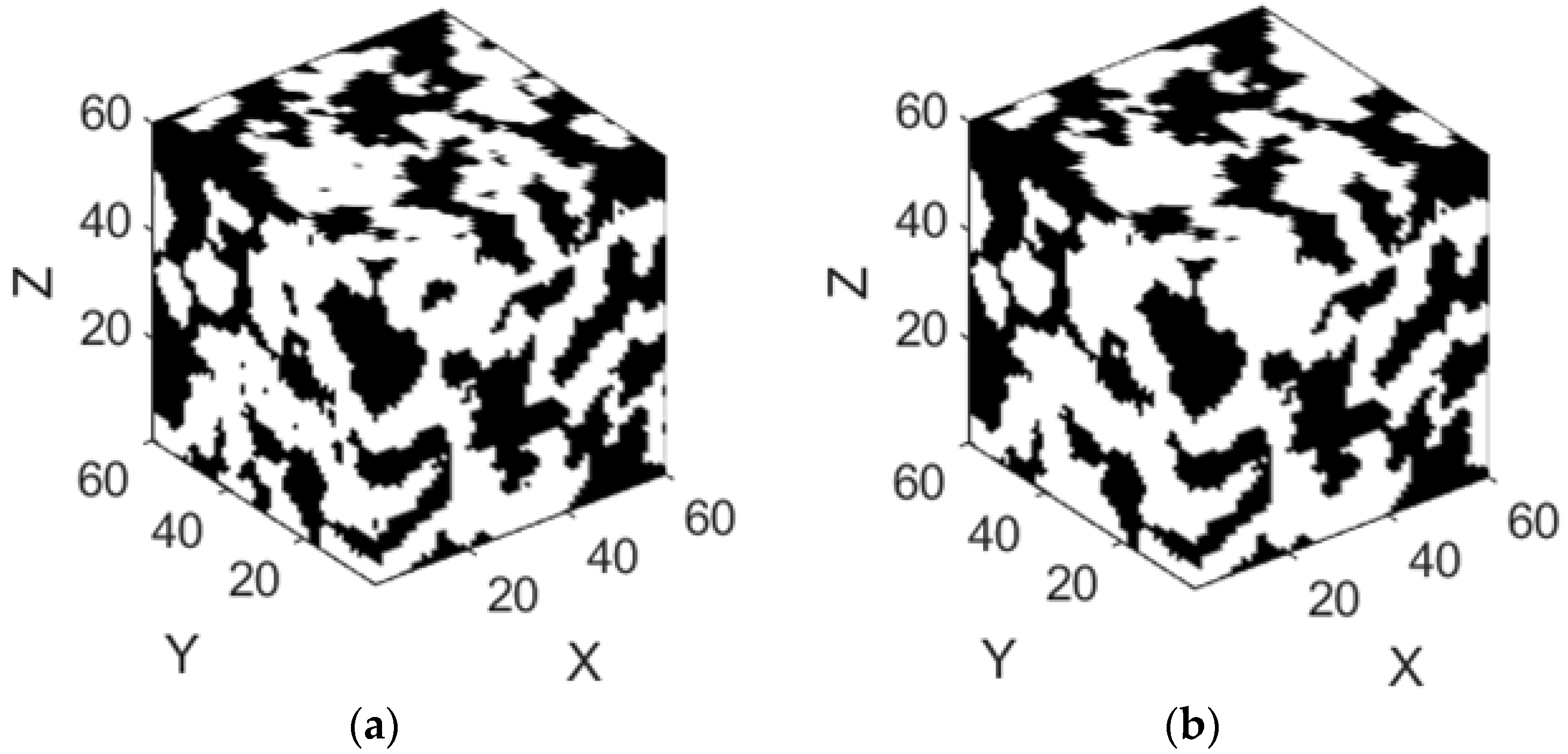
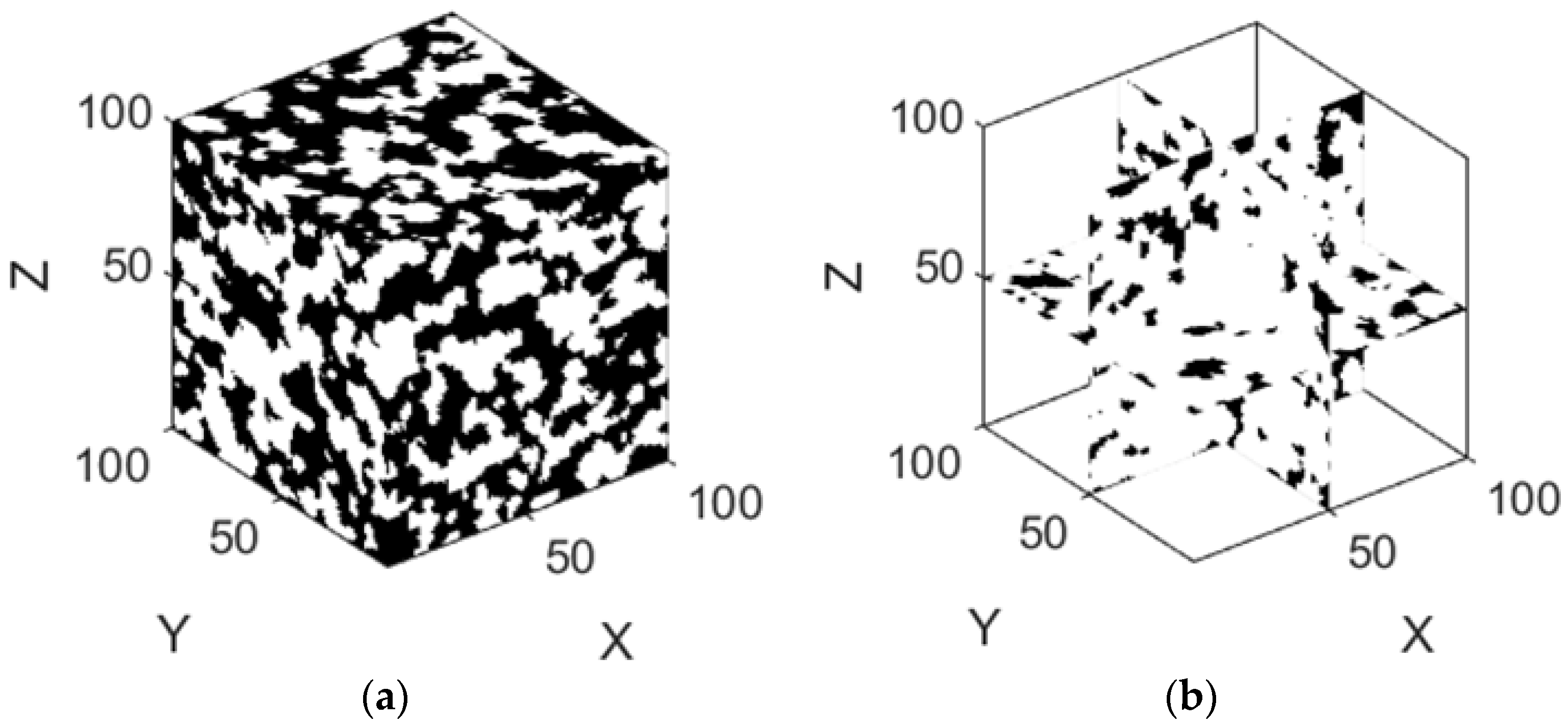
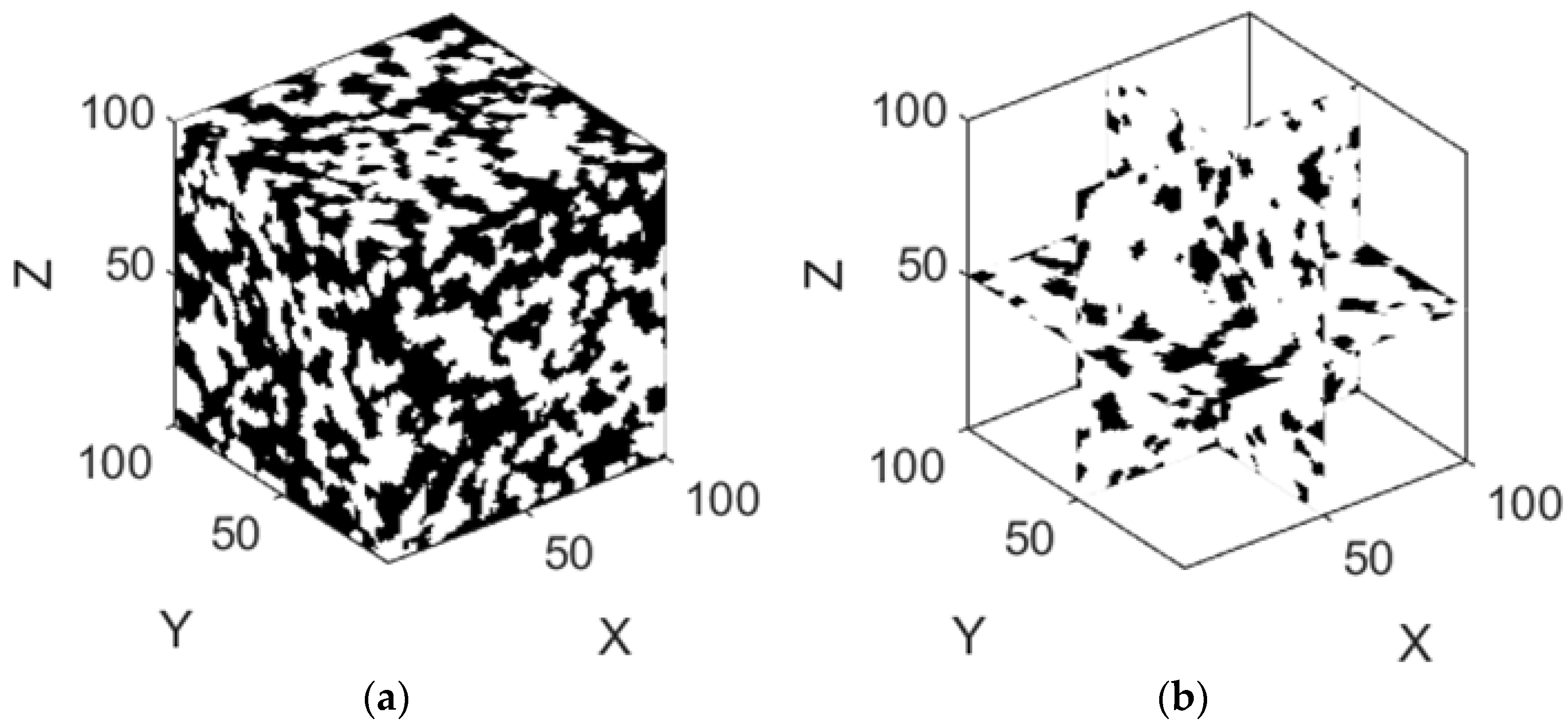
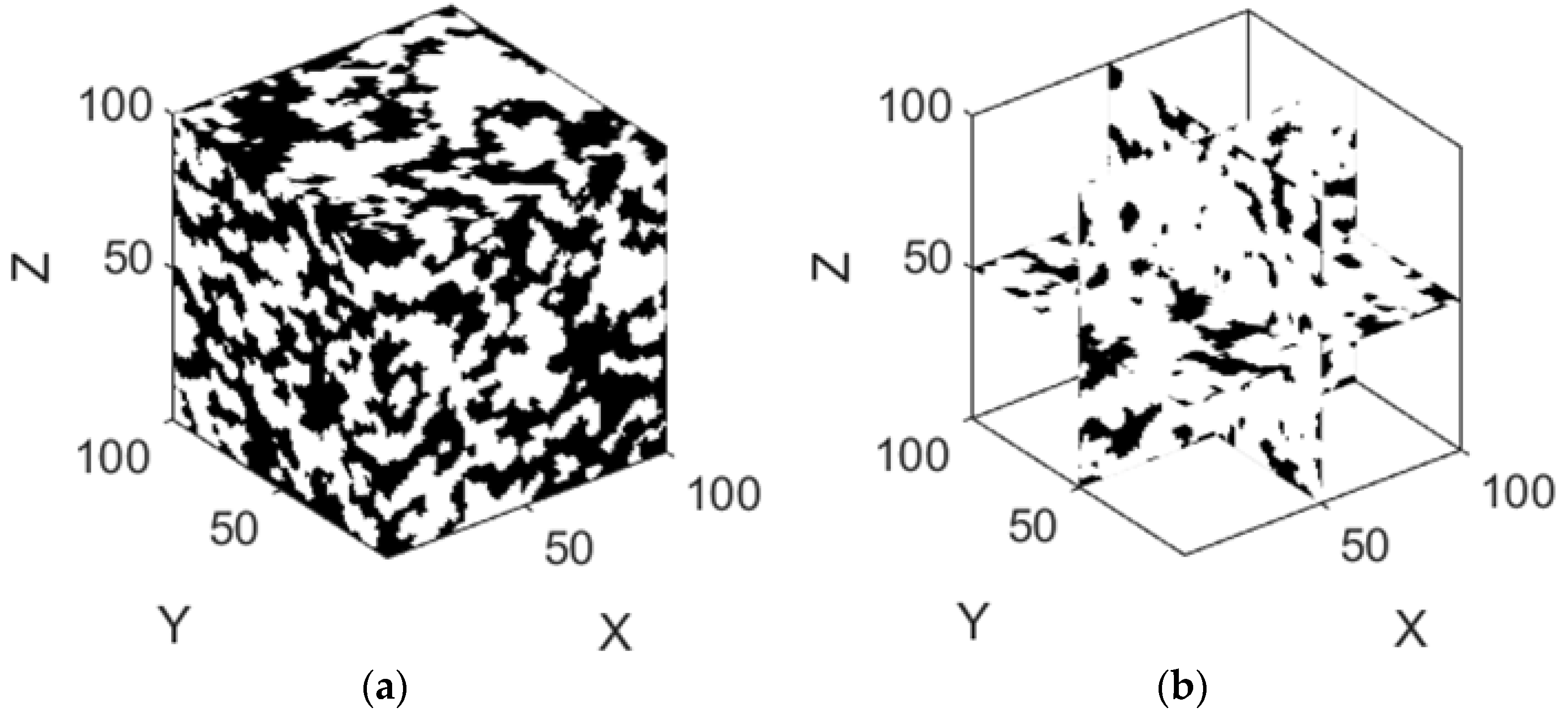
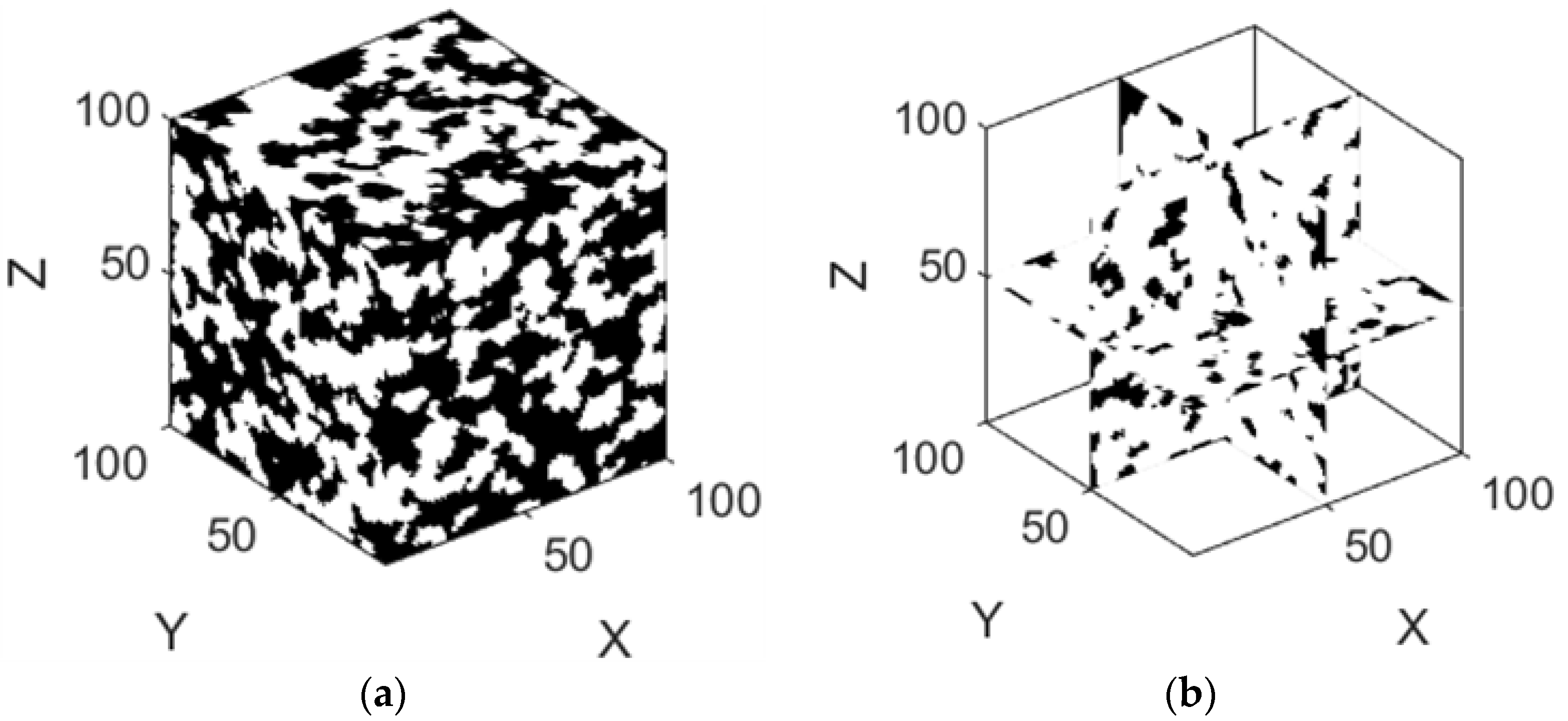
4.1. Porous Structure Reconstruction
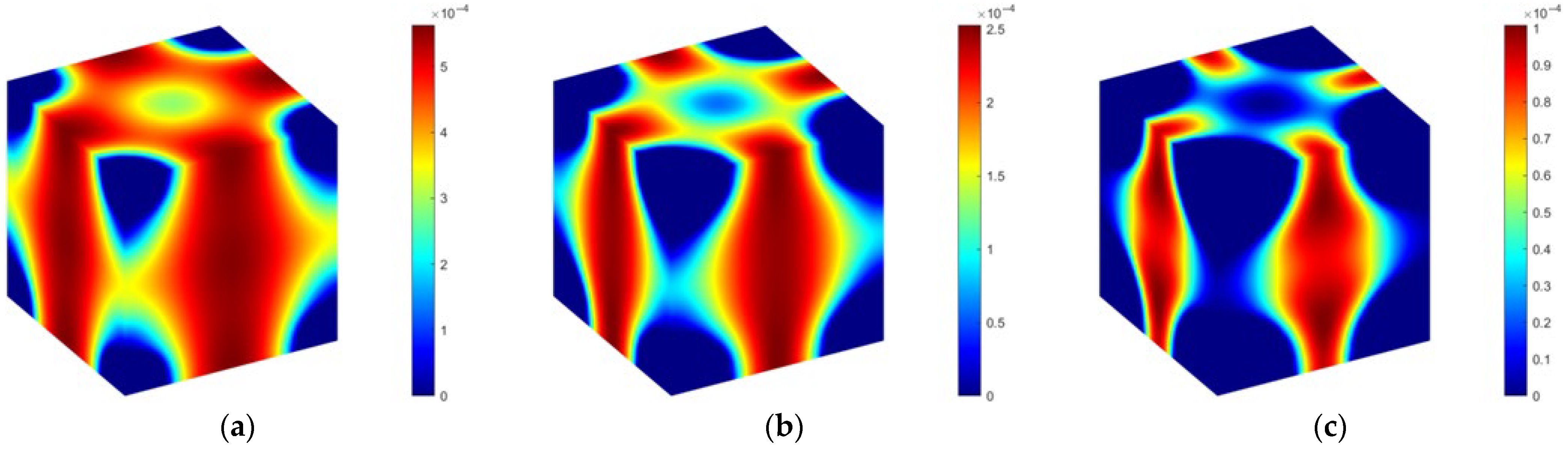
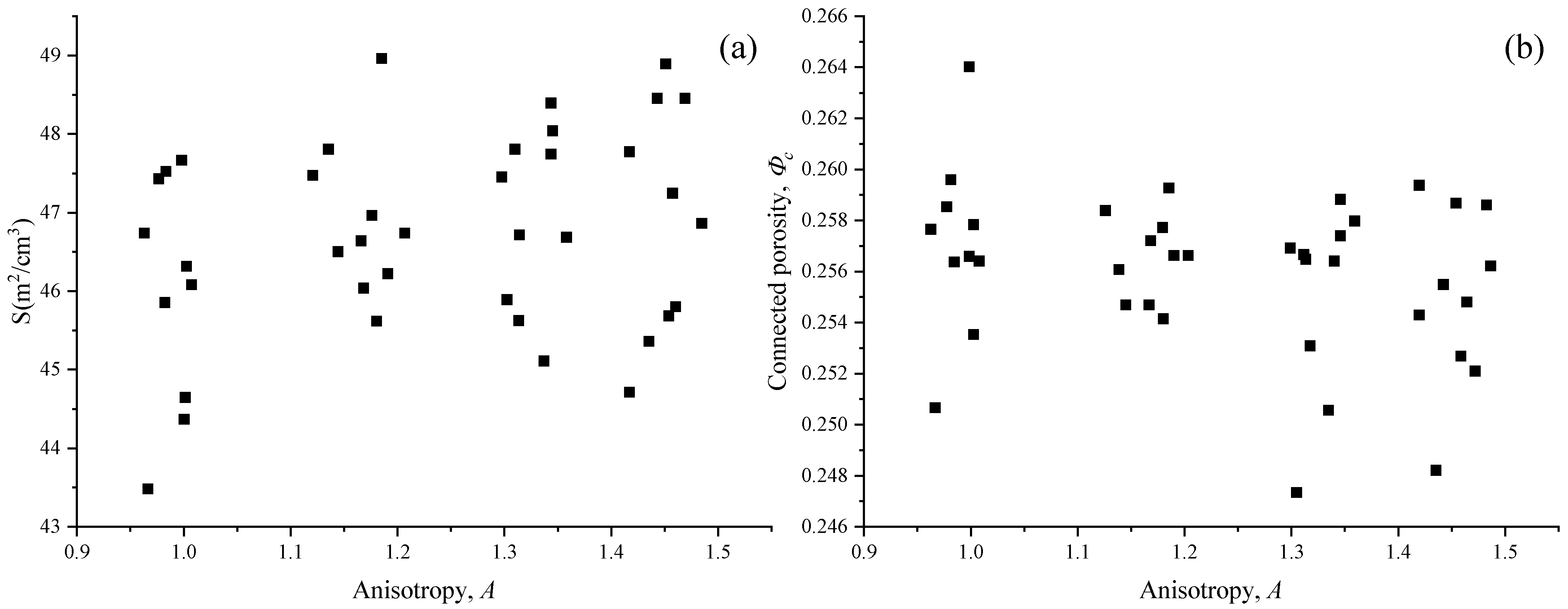
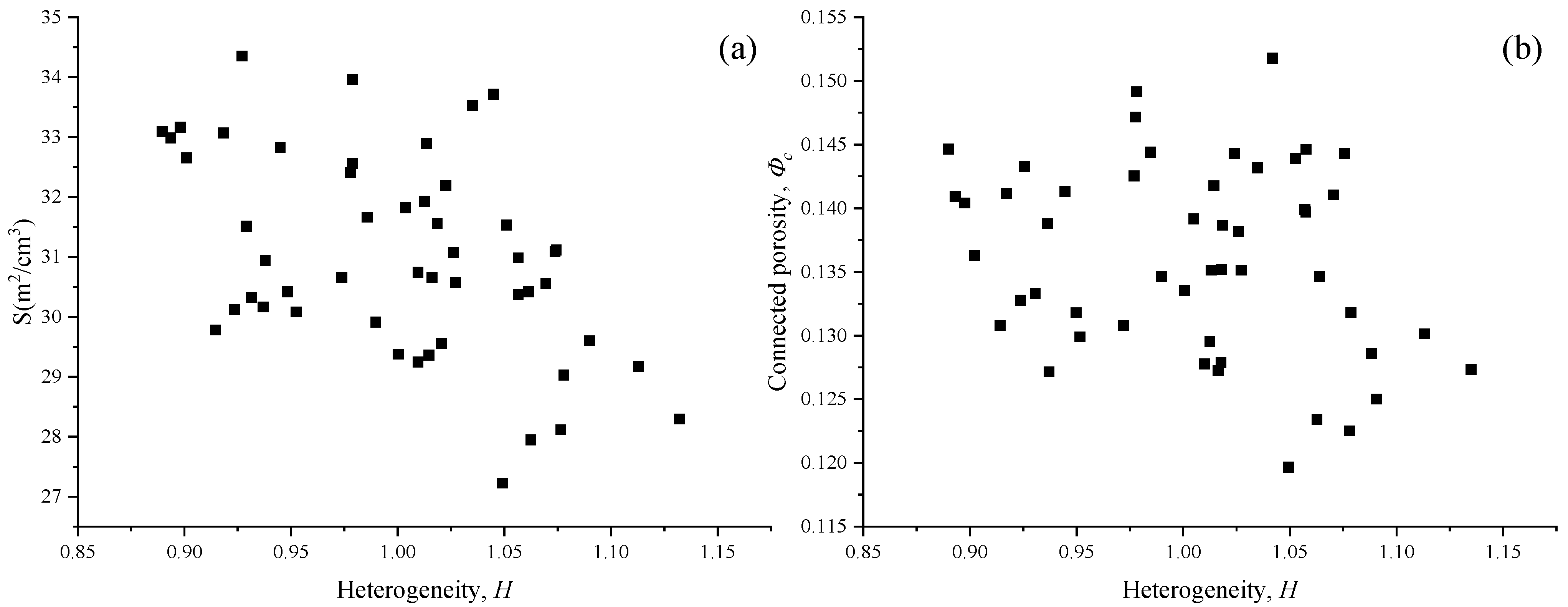
4.2. Effect of Anisotropy and Heterogeneity
4.3. Effect of Slip
5. Conclusions
- (1)
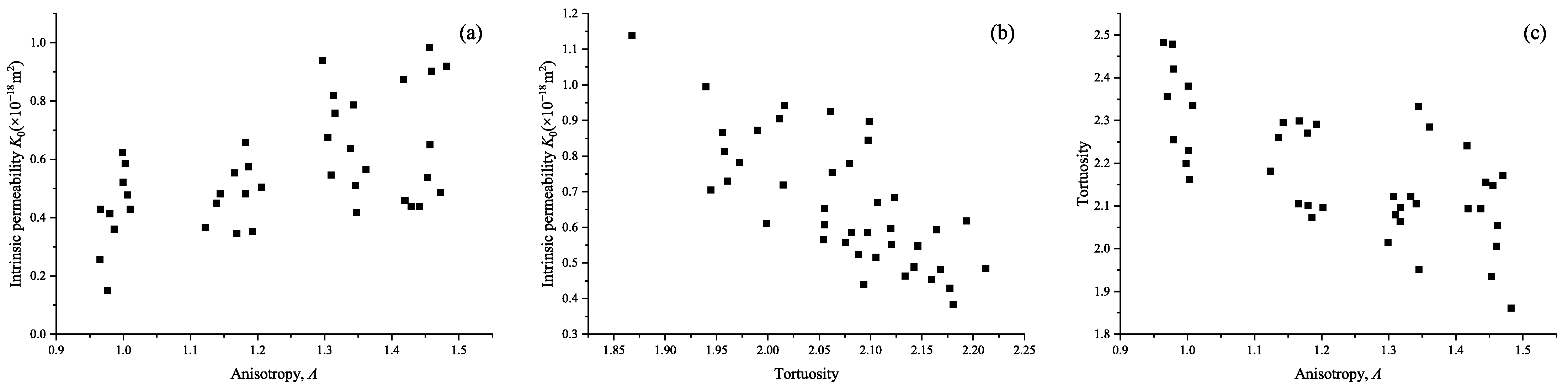
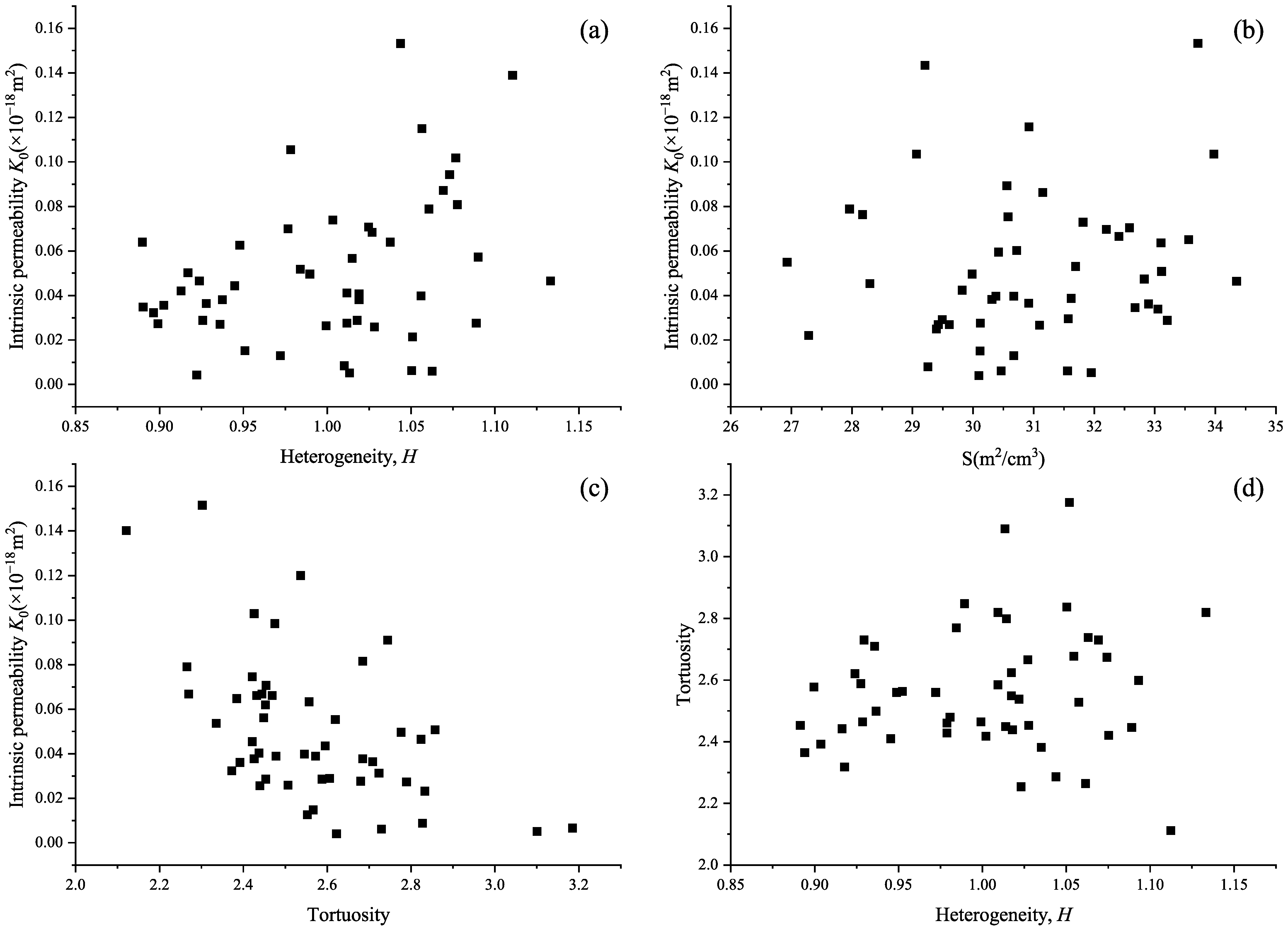
- The intrinsic permeability of anisotropic porous media is positively correlated with anisotropy factor and negatively correlated with tortuosity. Tortuosity is negatively correlated with anisotropy factor. The intrinsic permeability of heterogeneous porous media is positively correlated with the heterogeneity factor of pore distribution, but has no obvious correlation with the ratio of surface area to volume, and has an obvious negative correlation with tortuosity. There is no obvious correlation between tortuosity and the heterogeneity factor.
- (2)
- The pore-scale anisotropy significantly affects the tortuosity of porous media, and the heterogeneity of pore distribution significantly affects the specific surface area, and then significantly affects the flow in porous media. The strong correlation between tortuosity and anisotropy is the fundamental reason why anisotropy affects permeability. With the increase in heterogeneity of pore distribution, the ratio of surface area to volume decreases significantly, the wall friction resistance of fluid flowing through porous media decreases, and the permeability of porous media increases.
- (3)
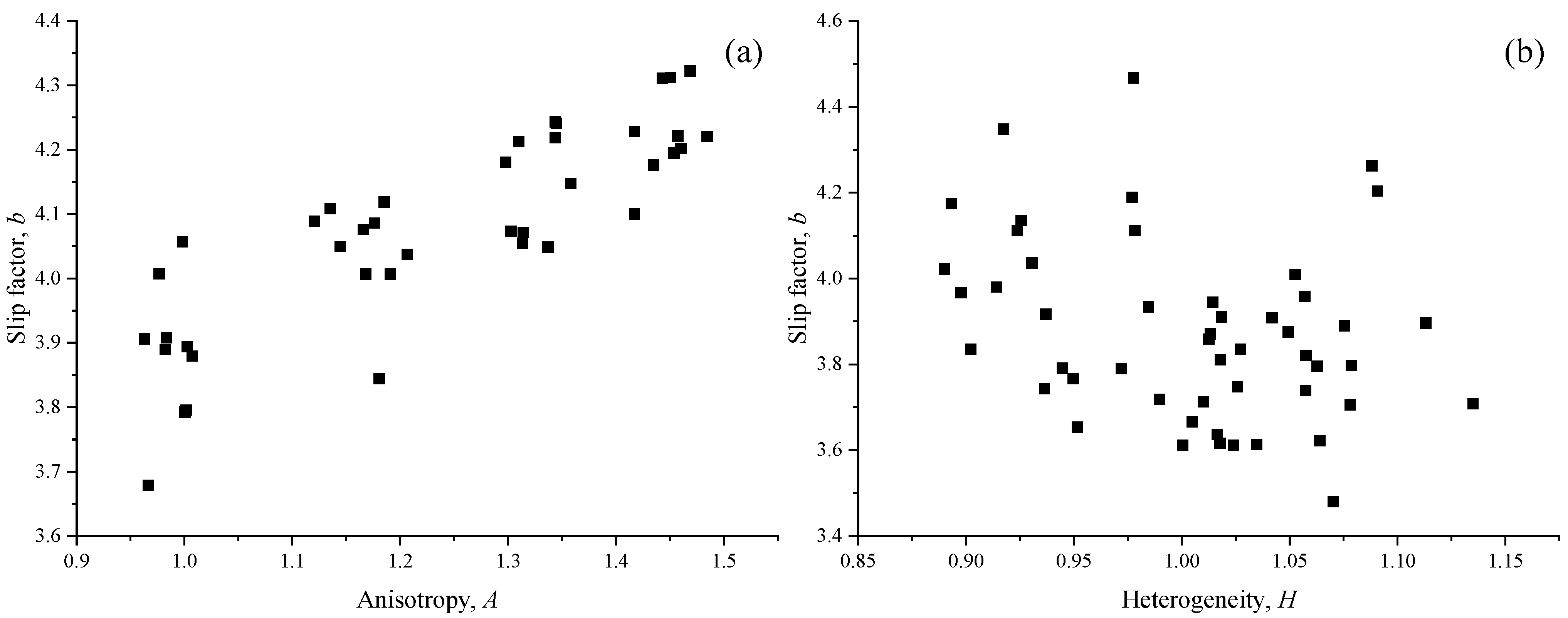
- The slip factor is positively correlated with the anisotropic factor, which means that the high Kn effect is stronger in anisotropic structures. There is no obvious correlation between the slip factor and heterogeneity factor. With the enhancement of heterogeneity, the randomness of the distribution position may lead to the random change in tortuosity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Poovathingal, S.; Stern, E.C.; Nompelis, I.; Schwartzentruber, T.E.; Candler, G.V. Nonequilibrium flow through porous thermal protection materials, Part II: Oxidation and pyrolysis. J. Comput. Phys. 2019, 380, 427–441. [Google Scholar] [CrossRef]
- Van Foreest, A.; Sippel, M.; Gülhan, A.; Esser, B.; Ambrosius, B.A.; Sudmeijer, K.J. Transpiration cooling using liquid water. J. Thermophys. Heat Transf. 2009, 23, 693–702. [Google Scholar] [CrossRef]
- Glass, D. Ceramic matrix composite (CMC) thermal protection systems (TPS) and hot structures for hypersonic vehicles. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008; American Institute of Aeronautics and Astronautics: Dayton, OH, USA, 2008; p. 2682. [Google Scholar]
- Khabbazi, A.E.; Hinebaugh, J.; Bazylak, A. Determining the impact of rectangular grain aspect ratio on tortuosity-porosity correlations of two-dimensional stochastically generated porous media. Sci. Bull. 2016, 61, 601–611. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Kang, Q.; Rahman, S.S. The lattice Boltzmann method for isothermal micro-gaseous flow and its application in shale gas flow: A review. Int. J. Heat Mass Transf. 2016, 95, 94–108. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Sappa, G. Numerical and experimental study of fluid flow and heat transfer in porous media: A review article. Energies 2025, 18, 976. [Google Scholar] [CrossRef]
- D’Orazio, A.; Karimipour, A.; Ranjbarzadeh, R. Lattice Boltzmann modelling of fluid flow through porous media: A comparison between pore-structure and representative elementary volume methods. Energies 2023, 16, 5354. [Google Scholar] [CrossRef]
- Zahid, F.; Cunningham, J.A. Review of the Color Gradient Lattice Boltzmann Method for Simulating Multi-Phase Flow in Porous Media: Viscosity, Gradient Calculation, and Fluid Acceleration. Fluids 2025, 10, 128. [Google Scholar] [CrossRef]
- Ho, M.; Tucny, J.-M.; Ammar, S.; Leclaire, S.; Reggio, M.; Trépanier, J.-Y. Lattice Boltzmann Model for Rarefied Gaseous Mixture Flows in Three-Dimensional Porous Media Including Knudsen Diffusion. Fluids 2024, 9, 237. [Google Scholar] [CrossRef]
- Atykhan, M.; Dauyeshova, B.K.; Monaco, E.; Rojas-Solórzano, L.R. Modeling Immiscible Fluid Displacement in a Porous Medium Using Lattice Boltzmann Method. Fluids 2021, 6, 89. [Google Scholar] [CrossRef]
- Lei, G.; Liu, T.; Liao, Q.; He, X. Estimating permeability of porous media from 2D digital images. J. Mar. Sci. Eng. 2023, 11, 1614. [Google Scholar] [CrossRef]
- Farahani, M.V.; Nezhad, M.M. On the effect of flow regime and pore structure on the flow signatures in porous media. Phys. Fluids 2022, 34, 115139. [Google Scholar] [CrossRef]
- Farahani, M.V.; Foroughi, S.; Norouzi, S.; Jamshidi, S. Mechanistic study of fines migration in porous media using lattice Boltzmann method coupled with rigid body physics engine. J. Energy Resour. Technol. 2019, 141, 123001. [Google Scholar] [CrossRef]
- Chalmers, G.R.; Bustin, R.M.; Power, I.M. Characterization of gas shale pore systems by porosimetry, pycnometry, surface area, and field emission scanning electron microscopy/transmission electron microscopy image analyses: Examples from the Barnett, Woodford, Haynesville, Marcellus, and Doig units. AAPG Bull. 2012, 96, 1099–1119. [Google Scholar]
- Succi, S. The Lattice-Boltzmann Equation; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Tao, S.; Guo, Z. Boundary condition for lattice Boltzmann modeling of microscale gas flows with curved walls in the slip regime. Phys. Rev. E 2015, 91, 043305. [Google Scholar] [CrossRef] [PubMed]
- Ansumali, S.; Karlin, I.V. Kinetic boundary conditions in the lattice Boltzmann method. Phys. Rev. E 2002, 66, 026311. [Google Scholar] [CrossRef]
- Zhao, J.; Yao, J.; Li, A.; Zhang, M.; Zhang, L.; Yang, Y.; Sun, H. Simulation of microscale gas flow in heterogeneous porous media based on the lattice Boltzmann method. J. Appl. Phys. 2016, 120, 579. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C. Analysis of Lattice Boltzmann Equation for Microscale Gas Flows: Relaxation Times, Boundary Conditions and the Knudsen Layer; Taylor & Francis, Inc.: Abingdon, UK, 2008. [Google Scholar]
- Succi, S. Mesoscopic modeling of slip motion at fluid-solid interfaces with heterogeneous catalysis. Phys. Rev. Lett. 2002, 89, 064502. [Google Scholar] [CrossRef]
- Verhaeghe, F.; Luo, L.; Blanpain, B. Lattice Boltzmann modeling of microchannel flow in slip flow regime. J. Comput. Phys. 2009, 228, 147–157. [Google Scholar] [CrossRef]
- Eu, B.C.; Khayat, R.E.; Billing, G.D.; Nyeland, C. Nonlinear transport coefficients and plane Couette flow of a viscous, heat-conducting gas between two plates at different temperatures. Can. J. Phys. 1987, 65, 1090–1103. [Google Scholar] [CrossRef]
- Myong, R. A generalized hydrodynamic computational model for rarefied and microscale diatomic gas flows. J. Comput. Phys. 2004, 195, 655–676. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.H.; Zhang, R.L.; Wang, C.; Xiong, Y.; Zheng, X.; Li, S.; Jin, K.; Rui, Z. Review of multi-scale and multi-physical simulation technologies for shale and tight gas reservoirs. J. Nat. Gas. Sci. Eng. 2017, 37, 560–578. [Google Scholar] [CrossRef]
- Michalis, V.K.; Kalarakis, A.N.; Skouras, E.D.; Burganos, V.N. Rarefaction effects on gas viscosity in the Knudsen transition regime. Microfluid. Nanofluidics 2010, 9, 847–853. [Google Scholar] [CrossRef]
- Li, Q.; He, Y.L.; Tang, G.H.; Tao, W.-Q. Lattice Boltzmann modeling of microchannel flows in the transition flow regime. Microfluid. Nanofluidics 2011, 10, 607–618. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Jin, X.; Wang, X.Q.; Sun, L.; Wang, M. Pore-scale geometry effects on gas permeability in shale. J. Nat. Gas. Sci. Eng. 2016, 34, 948–957. [Google Scholar] [CrossRef]
- Zheng, Q.; Yu, B.M.; Duan, Y.G.; Fang, Q. A fractal model for gas slippage factor in porous media in slip flow regime. Chem. Eng. Sci. 2013, 87, 209–215. [Google Scholar] [CrossRef]
- Ren, X.; Li, A.; Wang, Y.; Jiang, K.; Chen, M. Gas Permeability Experimental Study of Low Permeability Core Considering Effect of Gas Slippage. Nat. Gas. Geosci. 2015, 26, 733–736. [Google Scholar]
- Zhu, Y.; Tao, G.; Fang, W.; Wang, S. Research progress of the Klinkenberg Effect in Tight Gas Reservoir. Progress. Geophys. 2007, 22, 1591–1596. [Google Scholar]
- Duan, Q.; Yang, X.; Chen, J. Gas Permeability And Klinkenberg Effect Of Fault Rocks. Seismol. Geol. 2014, 36, 964–975. [Google Scholar]
- Civan, F. Effective Correlation of Apparent Gas Permeability in Tight Porous Media. Transp. Porous Media 2010, 82, 375–384. [Google Scholar] [CrossRef]
- Fang, Y. Reconstruction of Coal’s Microstructure and Simulation of Coal Bed Methane Migration Using LBM. Master’s Thesis, Jiangnan University, Wuxi, China, 2016. [Google Scholar]
- wan der Hoef, M.A.; Beetstra, R.; Kuipers, J.A.M. Lattice-Boltzmann simulations of low-Reynolds-number flow past mono- and bidisperse arrays of spheres: Results for the permeability and drag force. J. Fluid Mech. 2005, 528, 233–254. [Google Scholar] [CrossRef]
- Wang, M.R.; Pan, N. Numerical analyses of effective dielectric constant of multiphase micro-porous media. J. Appl. Phys. 2007, 101, 114102-1–114120-8. [Google Scholar] [CrossRef]
- Lou, D.; Chen, Z.; Zhang, Y.; Yu, Y.; Fang, L.; Tan, P.; Hu, Z. A novel micro-scale structure reconstruction approach for porous media and characterization analysis: An application in ceramics-based diesel particulate filter. Process Saf. Environ. Prot. 2024, 186, 679–693. [Google Scholar] [CrossRef]
- Cai, P.C.; Que, Y.; Jiang, Z.L.; Yang, P.F. Lattice Boltzmann meso-seepage research of reconstructed soil based on the quartet structure generation set. Hydrogeol. Eng. Geol. 2022, 49, 33–42. [Google Scholar]
- Zhang, M.Z. Multiscale Lattice Boltzmann-Finite Element Modelling of Transport Properties in Cement-Based Materials. Doctoral Dissertation, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Pan, C.; Luo, L.S.; Miller, C.T. An evaluation of lattice Boltzmann schemes for porous medim flow simulation. Comput. Fluids 2006, 35, 898–909. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice; Springer: Berlin/Heidelberg, Germany, 2017; pp. 105–119. [Google Scholar]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific Publishing: Singapore, 2013; pp. 19–25. [Google Scholar]
- Junk, M.; Klar, A. Discretizations for the incompressible Navier-Stokes equations based on the lattice Boltzmann method. SIAM J. Sci. Comput. 2000, 22, 1–19. [Google Scholar] [CrossRef]
- Junk, M.; Yong, W.-A. Rigorous Navier-Stokes limit of the lattice Boltzmann equation. Asymptot. Anal. 2003, 35, 165–185. [Google Scholar] [CrossRef]
- He, X.; Zou, Q.; Luo, L.; Dembo, M. Analytic solutions of simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann BGK model. J. Stat. Phys. 1997, 87, 115–136. [Google Scholar] [CrossRef]
- Krastins, I.; Kao, A.; Pericleous, K.; Reis, T. Moment-based boundary conditions for straight on-grid boundaries in three-dimensional lattice Boltzmann simulations. Int. J. Numer. Meth Fluids 2020, 92, 1948–1974. [Google Scholar] [CrossRef]
- Yang, P.; Wen, Z.; Dou, R.; Liu, X. Permeability in multi-sized structures of random packed porous media using three-dimensional lattice Boltzmann method. Int. J. Heat Mass Transf. 2017, 106, 1368–1375. [Google Scholar] [CrossRef]
- Sangani, A.S.; Acrivos, A. Slow flow through a periodic array of spheres. Int. J. Multiph. Flow. 1982, 8, 343–360. [Google Scholar] [CrossRef]
- Ahrenholz, B.; Tolke, J.; Krafczyk, M. Lattice-Boltzmann simulations in reconstructed parametrized porous media. Int. J. Comput. Fluid Dyn. 2006, 20, 369–377. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophys. Eng. 1999, 3, 43–77. [Google Scholar]
- Cercignani, C.; Lampis, M.; Lorenzani, S. Variational approach to gas flows in microchannels. Phys. Fluids 2004, 16, 3426–3437. [Google Scholar] [CrossRef]
- Wang, J.; Kang, Q.; Wang, Y.; Pawar, R.; Rahman, S.S. Simulation of gas flow in micro-porous media with the regularized lattice Boltzmann method. Fuel 2017, 205, 232–246. [Google Scholar] [CrossRef]


| Radius | Porosity | Moment-Based Boundary | NEBB Boundary | Analytical Solution | Δ1 | Δ2 |
|---|---|---|---|---|---|---|
| 11 | 0.9136 | 0.035485 | 0.035486 | 0.034529 | 2.77% | 2.77% |
| 12 | 0.88813 | 0.027233 | 0.027233 | 0.026392 | 3.19% | 3.19% |
| 13 | 0.85696 | 0.02049 | 0.02049 | 0.019931 | 2.80% | 2.80% |
| 14 | 0.82099 | 0.015207 | 0.015208 | 0.014806 | 2.71% | 2.72% |
| 15 | 0.77786 | 0.010921 | 0.010921 | 0.010762 | 1.48% | 1.48% |
| 16 | 0.73101 | 0.007771 | 0.007771 | 0.007605 | 2.18% | 2.18% |
| 17 | 0.67808 | 0.005346 | 0.005347 | 0.005185 | 3.11% | 3.12% |
| 18 | 0.61798 | 0.003497 | 0.003497 | 0.003377 | 3.55% | 3.55% |
| 19 | 0.5495 | 0.002144 | 0.002144 | 0.002078 | 3.18% | 3.18% |
| 20 | 0.47418 | 0.001232 | 0.001232 | 0.001192 | 3.36% | 3.36% |
| Parameter | Anisotropic Structure | Heterogeneous Structure |
|---|---|---|
| Core distribution probability, Pcd | 0.005 | Refined structure: 0.005 Coarse structure (×10−5): 9, 7, 5, 3, 1 |
| Porosity, Φ | 0.3 | 0.2 (Porosity for refined structure, ΦR = 0.4) |
| Grid resolution | 100 × 100 × 100 | 100 × 100 × 100 |
| Cell scale | 20 nm | 20 nm |
| Growth rate along X, Dx | 0.01 | 0.01 |
| Growth rate along Y, Dy | 0.01 | 0.01 |
| Growth rate along Z, Dz | 0.01, 0.005, 0.0025, 0.00125 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Zhao, J.; Wang, G.; Fang, M.; Zhu, K. Effect of Pore-Scale Anisotropic and Heterogeneous Structure on Rarefied Gas Flow in Three-Dimensional Porous Media. Fluids 2025, 10, 175. https://doi.org/10.3390/fluids10070175
Guo W, Zhao J, Wang G, Fang M, Zhu K. Effect of Pore-Scale Anisotropic and Heterogeneous Structure on Rarefied Gas Flow in Three-Dimensional Porous Media. Fluids. 2025; 10(7):175. https://doi.org/10.3390/fluids10070175
Chicago/Turabian StyleGuo, Wenqiang, Jinshan Zhao, Gang Wang, Ming Fang, and Ke Zhu. 2025. "Effect of Pore-Scale Anisotropic and Heterogeneous Structure on Rarefied Gas Flow in Three-Dimensional Porous Media" Fluids 10, no. 7: 175. https://doi.org/10.3390/fluids10070175
APA StyleGuo, W., Zhao, J., Wang, G., Fang, M., & Zhu, K. (2025). Effect of Pore-Scale Anisotropic and Heterogeneous Structure on Rarefied Gas Flow in Three-Dimensional Porous Media. Fluids, 10(7), 175. https://doi.org/10.3390/fluids10070175






