Abstract
Both the excess and alteration of bed sediments in river systems can cause socioeconomic and environmental damage; thus, the quantification of bedload transport is an important tool to assess the health of rivers and help in decision-making imposed by the agencies responsible for water resource management. This work aims to evaluate the efficiency of pressure-difference samplers (Helley–Smith) qualitatively and quantitatively when used in environments with sandy characteristics. The experiments were carried out in a stream with full transparency and two pressure-difference samplers with nozzle dimensions of 7.20 × 7.20 cm and 8.89 × 7.50 cm. The Particle Image Velocimetry technique was used to analyze the sampler efficiency simultaneously with an Acoustic Doppler Current Profiler. Qualitative results showed that the way the equipment is allocated at the bottom of the river can generate overestimated or underestimated sediment transport measurements. Additionally, evaluating it quantitatively, we see that the collection efficiency of the equipment varied between 15.45% and 534.78% when compared to the results obtained by the Particle Image Velocimetry technique.
1. Introduction
Some time ago, bottom sediments were seen only as a physical problem responsible for reducing the capacity of reservoirs and silting rivers and streams, making navigability difficult and decreasing water availability. Nowadays, it is understood that the presence of bottom sediments in aquatic environments corroborates the balance of the ecosystem, creating an environment rich in nutrients and favorable to the proliferation of benthic and autotrophic organisms, which form the basis of the food chain. However, enhanced bottom sediment transport inhibits the proliferation of photosynthetic organisms by increasing the turbidity of water, and the movement of substrates alters and/or precludes the location and proliferation of benthos along sandy riverbeds [1].
Data published from the US Environmental Protection Agency (EPA) classify excess sediment as the factor second most responsible for degradation of the aquatic environments of rivers and streams in the United States [2,3]. The high capacity which sediments have in the degradation of fluvial environments generates economic and environmental losses in the order of USD 7 billion per year for North American rivers [4]. The total amount of damage within the socioeconomic and environmental framework makes the quantification of sediments in river systems an irreplaceable indicator for water resource management to trace effective qualitative and quantitative protection strategies aimed at reducing sedimentation loading into the drainage system. Mechanically, the incipient motion of bed sediments occurs when the hydraulic conditions exceed the critical bed shear stress above forces resisting the movement of particles [5,6,7]. On the other hand, estimating bedload transport rates in natural environments is complicated due to the complex variations in the transport rates for similar hydraulic conditions [8,9,10,11,12].
Historically, bedload transport data have become increasingly scarce, as their collection and quantification is a difficult, laborious, and costly process. Various methodologies have been developed to quantify bedload transport. However, the efficacy of each method is limited according to the granulometric and hydraulic characteristics of each environment [7,8,9,10,11,12,13,14]. In this paper, we describe three distinct methods for quantifying bedload transport for predominantly sand-bed rivers: those that are indirect, non-intrusive, and intrusive.
Indirect methods are represented by numerous theoretical and empirical equations (see, for example, Refs. [5,15,16,17], among others). However, despite being easy to use, bedload transport estimates for equations are problematic because they tend to represent one-dimensional sediment displacement, and the acquisition of reliable data for sediment inputs that needed for the equations can be problematic [18,19].
Non-intrusive methods using Acoustic Doppler Current Profilers (ADCPs) to estimate moving-bed velocities for estimating the rate of bedload transport have been widely explored [20,21,22,23,24,25]. This body of research indicates that data produced by ADCPs can be used to infer bed-sediment displacements in predominantly sand-bed rivers [21,23]. However, this technique has not yet become operationally common and further scientific assessments are being carried out [26,27,28].
Manually intrusive methods are considered the most common means for producing bedload transport data [8,12,29,30]. They entail using the dry mass of sediments captured by a bedload sampler of a known width resting on the bed for a specified duration to calculate an average bedload transport rate. Helley and Smith [31] developed a bedload sampler operating on a pressure difference, with a flair ratio of 3.54, mainly for use in rivers with granulometric characteristics of coarse sands and gravel (2 to 10 mm). This sampler and subsequent variations have been evaluated for efficiency in rivers and flumes with distinct morphological and hydraulic characteristics [12,32,33,34], and it was noted that when used in sand-bed rivers, some variables such as grain size [31], mesh size [35,36], and nozzle-wall thickness [11] may affect the sampling efficiency, causing uncertainty in calculated bedload transport measurements. Despite showing uncertainties, the pressure-difference sampler is still one of the tools most used by researchers and professionals [12,13,29], and it was used by [20,37,38,39,40,41] for bedload measurements in sand-bed rivers.
According to Edwards and Glysson [32], tests using pressure-difference samplers with a smaller flare ratio (1.40) than the original Helley–Smith device (3.54) showed a hydraulic efficiency close to 100% for all bedload transport rates and particle sizes. Thus, the pressure-difference sampler called BL-84, with a flair ratio of 1.40, was accepted as a standard tool to measure bedload transport by U.S. Federal Agencies. However, (1) there is a large amount of historical data collected by pressure-difference samplers that requires verification; (2) pressure-difference samplers are still being used in many places, regardless of guidance from the US Federal Interagency Sedimentation Project; and (3) according to [42], even if there are pressure-difference samplers with a hydraulic efficiency near 100%, this is not a straightforward measure of sampling efficiency.
The objective of this study was to quantify the uncertainties of two pressure-difference samplers (with flare ratios of 1.95 and 3.47) in a natural stream by simultaneously using Particle Image Velocimetry (PIV) techniques on bed-particle movements observed with an underwater camera mounted on top of the pressure-difference samplers. The PIV technique has been widely used, in a non-intrusive way, to evaluate this phenomenon [26,27,43,44,45,46,47,48,49,50,51]. This technique has the advantage of estimating the velocity fields of sediment displacement under various conditions. Thus, using PIV techniques to assess pressure-difference samplers can help to gain a better understanding of the uncertainties in sampling instances.
2. Review of Pressure-Difference Sampler Efficiency
In 1971, a report was published on the development and calibration of a bedload sampler, whose authors Edward J. Helley and Winchell Smith described the pressure-difference sampler dimensions and flair ratio of 3.54 and their hydrodynamic calibration. In the tests, the sampler was effective when used in channels with grain size characteristics of coarse sediments (>0.5 mm). However, when used in places with sand granulometric characteristics (<0.5 mm), it deviated by 50% compared to the Meyer-Peter and Mueller equation [31]. In addition, it was described that there was an increase in the fluid velocity when the flow approached the collector opening; thus, the ratio between the natural fluid velocity and the fluid velocity close to the collector could be different and non-linear [31].
Due to numerous uncertainties when using pressure-difference samplers, [36] performed hydraulic calibration of a sampler in the laboratory. It was noted that the ratio between the average flow velocity at the sampler entrance and the average natural flow velocity was found to be 1.54. It was also identified that the higher the ratio between the exit and entry areas of the equipment, the larger the increase in the ratio between the intake and natural flow velocities. Additionally, the sampler efficiency (), defined by [52] as the rate between the sediment weight sampled by a pressure-difference sampler (mHS) in a time period and the bedload weight that would be displaced without the sampler (M) at the same location and in the same time period, presented a decrease caused by sediments with diameters smaller than the mesh size, which were responsible for obstructing the openings, indeterminately altering the efficiency.
Ref. [53] performed calibration of the Helley–Smith sampler in the field at East Fork River near Pinedale, Wyoming, USA. In this study, the author compared bedload transport estimates using the Helley–Smith sampler and a conveyor-belt. The results showed that for particle sizes between 0.25 and 0.50 mm, the water flow ranged between 2.04 and 41.5 m3 s−1, and the mean velocity ranged between 0.57 and 1.41 m s−1; the Helley–Smith sampler had an efficiency of 175%.
Another feature that affects the sampling efficiency is the volume of the collection bag. In rivers with sandy granulometry and the presence of organic matter, the particles may block the mesh of the bag, reducing the hydraulic efficiency. Ref. [35] compared the standard 1950 cm3 bag with a 6000 cm3 bag for sampling on predominantly sandy beds. The author concluded that there is a 76% efficiency in the first minute of sampling when using the standard bag, while when using the 6000 cm3 bag, the efficiency is 100% up to an 8 min sampling period. Ref. [11] investigated the trapping efficiency of two pressure-difference samplers which differed only in their nozzle-wall thicknesses, 1.5 mm and 6.3 mm. For an average granulometry of 1.0 mm, their results showed that the sampler that had the thinnest entry plates collected up to twice as much sediment as the thicker plate sampler.
Ref. [12] described that there are sources of interference that can also alter the efficiency of pressure-difference sampling in gravel-bed rivers. These sources of interference are associated with the channel-bed morphology and the way the equipment is arranged at the collection time and may even make the collection of data unfeasible.
More recently, Ref. [42] ran hydraulic efficiency tests of three pressure-difference samplers, TR2, Elwha, and BL-84, with flair ratios of 1.40, 1.45, and 1.39, respectively. In their laboratory experiments (flume) to analyze the hydraulic efficiency, the flow velocities were changed. Mesh bags with openings of 0.25, 0.50, 1.0, 2.0, and 3.6 mm and 30% and 50% filling were used. The results showed that the parameters of sampler entrance area, fluid velocity, and percentage of the bag filled influenced the hydraulic efficiency with the same magnitude. Moreover, the authors suggest that the equipment’s width also affected sampler hydraulic efficiency. Table 1 presents important variables considered in each study and the ones used in this research.

Table 1.
Summary of bedload sampler characteristics and the experimental conditions used to assess their efficiency.
3. Methods
3.1. Study Area
The Guariroba Stream Basin (GB) is located east of the Campo Grande city, Mato Grosso do Sul, Brazil (Figure 1). It has an area of approximately 360 km2 and an altimetric range from 440 to 660 m. According to Köppen–Geiger [54], the climate classification is represented by Aw (tropical savannah), humid tropical, with an average temperature and precipitation of 23.4 °C and 1449 mm, respectively. The rainy season is concentrated between October and March (summer season), and the dry season is concentrated between April and September (winter season).
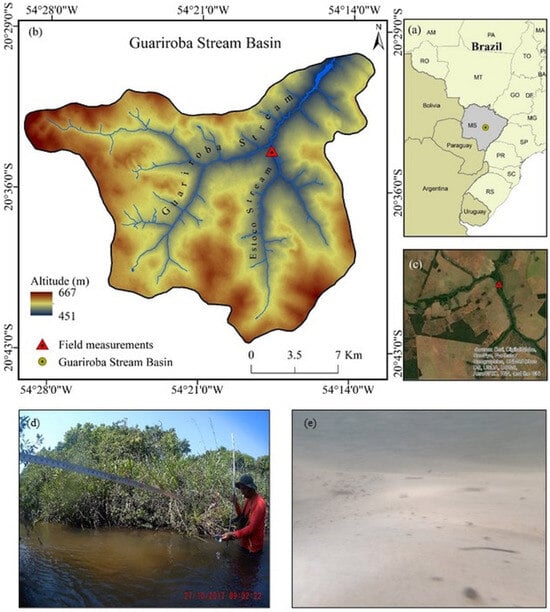
Figure 1.
(a) Location of the Guariroba Stream Basin in the central region of Mato Grosso do Sul, Campo Grande City, Brazil; (b) Guariroba Stream Basin and the monitoring point in the Estoco Stream; (c) monitored cross-section of the Estoco Stream; (d) monitoring the cross-section of the Estoco Stream; (e) example of bed-sediment view of the Estoco Stream during high flow.
The soil of GB has a sandy texture and consists of Ortic Quartz-Sand Neosol, Red Latosol, and Hydromorphic Quartz-Sand (95.71, 0.52, and 3.77%, respectively). Moreover, its average slope, with a value of 3.7%, favors a high rate of infiltration and a decreased surface runoff rate [55]. Thus, the streams in the GB drainage system have suspended sediment concentrations ranging from 0.57 mg l−1 to 66.83 mg l−1 and an average of 24.51 mg l−1, resulting in low turbidity, thus allowing observations of the bed-sediment displacement by video recording.
The experiments were performed in a cross-section in the Estoco Stream. Between April 2017 and January 2018, ten sedimentological monitoring campaigns were conducted, generating prior knowledge of hydraulic and sedimentological characteristics of the section under consideration, enhancing the development of the experiment (Figure 2). The cross-section had an almost rectangular shape over the entire period of field measurements. Sedimentological surveys were performed at two points of the cross-section using a Helley–Smith sampler (understood as a pressure-difference sampler) for bedload transport measurement. Bed-material characterization was performed by a BMH-53 device, and a mechanical current meter was used for water-flow measurements using the mean section method, dividing the cross-section into eight verticals. After field measurements, the sediment analysis was performed in the HEROS Laboratory (Hydrology, Erosion, and Sediment), located at the Federal University of Mato Grosso do Sul. Firstly, sediment samples were dried for 24 h at 120 °C, then shaken in mechanical sieve equipment for 15 min.
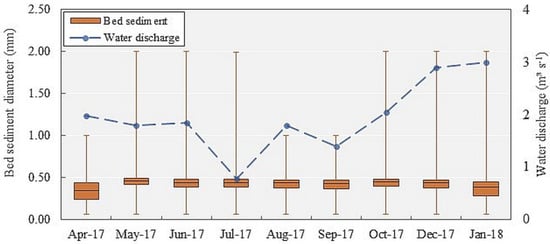
Figure 2.
Background of hydrosedimentological monitoring in the Estoco Stream. The left axis shows the bed-material characteristics, and the right axis shows the amplitude of streamflow between April 2017 and January 2018.
The results showed (Figure 2) that, during the sampling period, the Estoco Stream water discharge ranged from 0.78 to 2.99 m3 s−1, with an average depth of 0.73 to 1.06 m; surface-widths from 3.3 to 4.4 m; and bed-sediment granulometry with a representative diameter (D50) ranging from 0.35 to 0.46 mm, with an average standard deviation of 0.07 mm.
3.2. Experiment
Design and Implementation of Field Measurements
The experiment required using underwater filming equipment to provide us with a better view of sediment displacement near the samplers’ openings. In order to carry out the measurements, some particularities were needed to avoid uncertainties in data processing and to adapt them to the objective of the study. A camera was attached to each structure so that it was perpendicular to the entrance of the Helley–Smith samplers, and a diffuse illumination system for homogeneous images was an important factor to improve the PIV processing (Figure 3). Additionally, a cloth hanging over the cross-section shaded the measurement area to decrease the intensity of solar illumination on the water surface. We divided the experiment into two field measurements, both performed in the same cross-section of the Estoco Stream (Table 2).
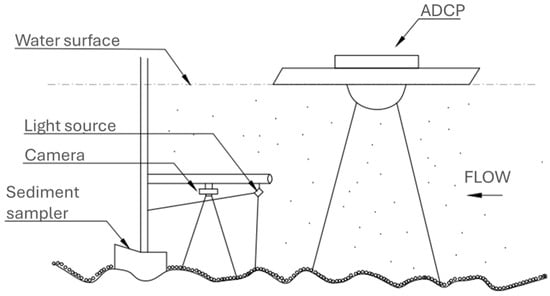
Figure 3.
Schematic of the experimental design.

Table 2.
Organization of the measurements of the experiment performed.
First measurement: The Helley–Smith handheld (hs) and video-recording system was used for further evaluation and PIV processing, and a mechanical current meter (the Newton model produced by the Hidromec Company, Rio de Janeiro, Brazil) was used to establish the velocity profile throughout the cross-section and the flow estimation. First, we established our sampling point with maximum water velocities and then filmed it with the hs at the time of sampling. The SJcam 4000 camera (SJcam, Shenzhen, China) was placed at a distance of 15 cm from the lower edge of the hs, and the video length totaled 15 min, filmed at 4K resolution (3840 × 2160 px), 24 fps, and with a linear field of view to eliminate optical distortion, resulting in a movie frame of 15 × 8 cm, totaling 10,800 sequential images. Additionally, bed material (BM) was collected with a BMH-53 sampler for bed-material characterization.
Second measurement: Two Helley–Smith models were used: the hs and another one weighing 30 Kg and with a 3.47 flare ratio (HS). The configuration of the video recording system for further evaluation and PIV processing was the same, and we used the ADCP Sontek M9 to measure velocity profiles along the cross-section and to compute the discharge. First, we identified the location with the highest water velocity to define our collection point. Later, we filmed the respective Helley–Smith samplers at the time they collected the sediments while using the ADCP in static mode for moving-bed tests. A GoPro Hero 6 camera was placed at a distance of 23 cm from the bottom edge of both samplers. Each video lasted 15 min and had a 2.7K resolution (2704 × 2032 px), 60 fps, and a linear field of view to eliminate optical distortion, resulting in a 35 × 26.3 cm movie frame. Additionally, bed material was collected using a BMH-53 sampler for bed-material characterization.
3.3. Stream Velocity, Bed Mobility, and Sediment Size Characteristics
In this study, we used a mechanical current meter (1st measurement) and the ADCP Sontek M9 (2nd measurement) to obtain velocity and flow information at the point with the highest streamwise velocity.
The ADCP used in this study has two sets of four transducers, one set of 1.0 MHz and another set of 3.0 MHz, plus a 0.5 MHz echo-sounder to determine the depth and to perform the moving-bed test. Calculation of the water velocity profile using an ADCP is a vector algebra problem that depends on the water velocity and the boat velocity [56]. When the ADCP is used on a moving boat, the absolute water velocity is calculated by the difference between the instrument reference-frame velocity and the boat velocity [57].
The boat velocity is the most sensitive operational variable required to obtain coherent water profiling velocities and can be estimated by two methods: the bottom-track (vBT) or the DGPS method (vDGPS). The DGPS method determines the boat velocity by measuring its position using a DGPS georeferencing system. The bottom-track method uses the Doppler signals from the bed to determine the velocity of the boat relative to the bed. This method is accurate when good Doppler signals can be obtained from the bed, which is usually the case for sandy beds. The moving-bed test keeps the ADCP in a fixed position (anchored or otherwise attached to some structure) and thus estimates the average velocity at which the bed particles are moving (va). It can be defined according to Equation (1) [24].
Ref. [24] pointed out that we must be careful to use the va estimated by the ADCP because this may detect the velocity of suspended particles. Subsequently, Ref. [21] developed investigations to evaluate the reliability of the va estimated by ADCP in different environments, concluding that these estimates are reliable for bed-particle displacement velocities below 0.6 m s−1.
For ambient experimental conditions, a river with total transparency and the ADCP standing perfectly still (vDGPS ≈ 0) during the experiments, tensioned by ropes attached to each edge of the cross-section, generates the va equivalent to vBT [58].
In addition to the hydraulic characteristics, particle-size distributions of bed material were analyzed using samples collected by the BMH-53 and the sediments transported and collected by the Helley–Smith samplers. The samples were placed in an oven at 120 °C for 24 h and then mechanically shaken by a series of standard sieves for 15 min (Table 3).

Table 3.
Natural characteristics of the Estoco Stream at the time of the experiment.
The granulometry of the Estoco Stream bed is predominantly one of medium sand, and the results of both measurements for bed material (BM) show that 93% for the particle sizes range from 0.25 to 0.50 mm. The standard deviations, 0.12 and 0.35, respectively, represent a low degree of dispersion for the collected sediment, a fact also indicated by the degree-of-sorting value, corresponding to grains with similar characteristics. Moreover, it is interesting to observe how the physical sampling of the bedload presents a data set with other characteristics noted for all evaluated parameters.
3.4. PIV Technique
Particle Image Velocimetry (PIV) techniques correlate predominant features (particles, particle clouds, dye colors, etc.) of two consecutive digital images to compute their displacement in time through cross-correlation algorithms. Using these techniques on images divided into a grid (interrogation windows) and using interpolation methods for regions without sufficient features enables the derivation of a velocity vector field for each set of images. The processing of acquired images was performed using the PIVlab software version 2.2. This MatLab version R2013b application is easy to handle, even for inexperienced users; however, for proper frame processing, the operator needs to know the theory and its limitations so that incorrect data are not produced [59].
3.4.1. Image Pre-Processing and PIV Settings
The PIV technique can obtain better measurements of bed-particle displacement when there are images with high contrast, low noise, and density relevant to the analysis; however, images are usually subject to non-uniform illumination, contrast limitation, and water impurity [26,49]. Thus, pre-processing is one of the most important steps in PIV analysis [59]. This approach improves measurements of particle displacement [60] (Figure 4).
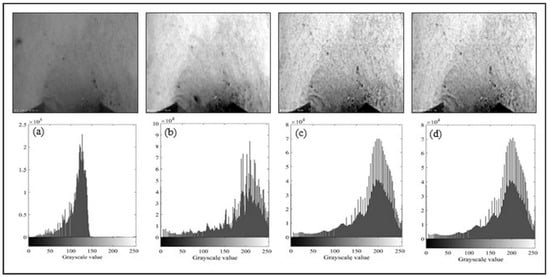
Figure 4.
Examples of image pre-processing with algorithms implemented in PIVlab software and its histograms. (a) Original image without any pre-processing. (b) Image with only intensity capping filter. (c) Image with only CLAHE filter. (d) Image with intensity capping and CLAHE filters.
The experiments were conducted in a natural stream with full transparency. The bed sediments in the Estoco Stream are considered homogeneous, characterized predominantly as non-spherical quartz sediment particles with an average nominal diameter between 0.44 and 0.45 mm (in the 1st and 2nd measurements, respectively); therefore, the images have a texture limited to the natural conditions of the experiment (Figure 5).

Figure 5.
Variation in color, shape, and size of the bed particles found in the Estoco Stream during the experiment.
Since the velocity vectors in the PIV method are estimated from a statistical correlation of interrogation windows (IWs), errors may occur due to particle density, interrogation-window size, and image resolution [45,61]. Before processing the data, image enhancement should be performed so that the results are more representative [60].
The images obtained do not always have homogeneous illumination. Therefore, some algorithms were used to correct image imperfections that could have decreased the accuracy of the PIV processing. The methods used were contrast-limited adaptative histogram equalization (CLAHE) and intensity capping filters.
CLAHE is responsible for redistributing the most-frequent image intensities through small areas (tiles), rearranging the data in a range from 0 to 255 [59]. This increases the texture of images, and, for experimental conditions, the use of CLAHE can lead to identifying valid vectors by 4.7 ± 3.2% [60]. The visual difference in our images can be observed before (Figure 6a,c) and after (Figure 6b,d) using CLAHE.

Figure 6.
Representation of a small area of an image obtained from the bed of the Estoco Stream (width 460px ≈ 5.9 cm) before and after processing using CLAHE and intensity capping. (a) Image without any processing. (b) Image after pre-processing. There is a higher contrast. (c,d) Greyscale values of the same regions of the images before and after pre-processing, respectively. We noticed changes in the amplitude of the values in the information matrix, resulting in better cross-correlation processing.
Since natural grain shapes are not spherical, the reflectance of the particles, caused by sunlight and the inserted diffuser, may vary as particle displacement occurs and may randomly result in bright particles. Particles with excessive light intensity can mask the actual correlation peaks of IWs and create unrealistic vector-magnitude estimates in the data processing. Intensity capping filters help to avoid this problem. If a light intensity from a bright particle shows a substantial deviation from the intensity of the nearby particles, it will be reallocated to an intensity consistent with that region, thus generating a realistic vector magnitude to the movement [60].
The choice of interrogation-window dimensions significantly impacts PIV accuracy, as it influences vector estimation [49,59,61,62,63]. To ensure robust cross-correlation, each interrogation window should ideally contain at least 10 particles, with densities above 5 particles per window and particle displacements within 25% of the IW size [63].
Table 4 summarizes the settings and results for both measurements, including camera distances, image resolutions, particle counts, and IW dimensions. Given similar hydraulic and granulometric conditions across cross-sections, we used multipass FFT interrogation windows of varying dimensions to ensure that particle displacements remained below 25% of the IW size, meeting PIV processing standards.

Table 4.
Experimental setup.
In the first measurement campaign, as we did not use ADCP to estimate the bed-particle velocity, the processing was only for qualitative analysis of the Helley–Smith sampling, so the interrogation-window frame dimensions were made from the data produced in the second measurement of the experiment, given that the hydraulic and granulometric characteristics of the cross-section were equivalent. In the second measurement campaign, the analyses were qualitative and quantitative, and for the dimensions of the IWs we used the va estimated by ADCP, according to [26,28]. The value of va in the second measurement was 0.0140 m s−1, resulting in an average bed-particle displacement equal to 2 px. Taking into account that the D50 diameter of the particles is equivalent to 4 px, that the number of particles required by IW is >10, and that the displaced material must travel a distance less than 25% of the IW, the minimum dimension for the IW must be greater than 25 × 25 px. Considering the large e frames, 35 × 26.3 cm and 15 × 8 cm, and that larger IWs correspond to more representative velocities even though they decrease spatial detail, for our experiment we used multipass FFT IWs of 256 × 256, 128 × 128, and 64 × 64 px for both studies.
3.4.2. Post-Processing of the Data
We used the width of the lower edge already known from the Helley–Smith sampler to perform the conversion of frame-per-pixel results to meters per second. Some factors, such as low particle density due to a high-velocity gradient and the identification of particles with displacement outside the analyzed plane, can generate outliers (spurious vectors) [49,62]. For our experimental conditions in the Estoco Stream, we realized that the cross-correlation algorithm identified and processed particles that were moving out of the riverbed plane, causing outliers, requiring post-processing exclusions of these vectors.
PIVlab software enables us to use two outlier exclusion methods: the standard deviation filter and the local medium filter. The standard deviation filter enables restraint of the velocity magnitude from a variable, n, linked to the standard deviation of the average velocity (Equation (2)). Velocities that do not fit this restriction are excluded from the result.
where v is the velocity in m s−1, is the average velocity in m s−1, n is the number of standard deviations used in the outlier exclusion, and σv is the standard deviation of the velocity.
Using the adjustment from trial and observation of the recorded video, n equal to 3 was considered to obtain a realistic vector magnitude for the displacement of bed sediments. The local medium filter [64] has a more localized action. In PIVlab, this algorithm evaluates floating velocities from a 3 × 3 set of the surrounding neighborhood. If the vector magnitude exceeds the average value, it is automatically reallocated to local conditions [59]. In our experiments, we also used a standard deviation of 3 for the local medium filter. Using both filters created results consistent with the average va estimated by the ADCP.
3.5. Sediment Transport
The mass of bed sediments collected with a Helley–Smith sampler allows a direct evaluation of the sediment that is being transported, the bedload transport rate, and the bed-particle velocity. However, sampling in sand-bed rivers may be overestimated by 50% [31], and material transported in suspension may be accumulated [53]. Moreover, the authors are not aware of the correction factor for collections with Helley–Smith samplers in predominantly sand-bed rivers. To calculate the bedload transport using the samples collected with the Helley–Smith sampler, we used Equation (3). In addition, we used Equation (3) to calculate the average velocity of the sediments collected by the Helley–Smith sampler.
where p is the mass of the dry sample at point (kg); Eam is the efficiency of the sampler in retaining sediment, which for Helley–Smith can be considered equal to 1 [65]; l is the width of the sampler’s entry (m); t is the sampling time (minutes); and qHS is the bedload transport (Kg s m−1).
For the vertical collected in the 2nd measurement, we performed an ADCP moving-bed test for a period equivalent to 900 s. Thus, we were able to estimate the bedload transport rate per unit width (qADCP) through a kinematic model (Equation (4)) [30]. This model is a function of (i) bed-particle velocity—ub; (ii) the thickness of the active layer of the riverbed—δb; and (iii) the concentration of sediment in this layer—cb.
where ub is the apparent bedload velocity (m s−1), δb is the thickness of the active layer of the moving sediment (2.D50) (m), and cb is the sediment concentration in the active layer ≈ 0.4 (porosity for sand).
Additionally, as a comparison, we used the bed-particle velocity (vPIV) processed by the PIV technique to estimate the bedload transport rate by the kinematic model (qPIV). The aim of this comparison was to directly assess the potential of both non-intrusive methods.
4. Results and Discussion
The presented results are exclusively about the analysis of the granular flow and the influence of the 1.94- and 3.47-flare ratio Helley–Smith samplers on the particle displacement at the moment of the sampling. We did not quantify the hydrodynamic changes caused by the insertion of the Helley–Smith samplers. Additionally, we observed that the Helley–Smith samplers were placed at the stream bed in two different ways. We define the first one as an insertion below the bedload thickness layer and the second as one above the bedload thickness layer.
4.1. First Measurement
One of the sources of uncertainty during sampling using intrusive equipment described for gravel-bed rivers is the way the equipment is inserted into the bed of the river [12]. Given this description and the morphology in sand-bed rivers, we paid attention to observe if there was any uncertainty associated with the Helley–Smith sampling given the way the sampler was placed on the bed. During the first measurement campaign, the Helley–Smith sampler was placed below the bedload thickness layer (Figure 7).

Figure 7.
(a) Helley–Smith sampler at the time of sampling, top view. (b) Lower edges below the transported bed-sediment layer).
The insertion of a device under a certain flow intensity may cause changes in the velocity vectors. Ref. [31] identified an increase in the velocity of water flow due to the approximation of the sampler’s entrance and that, for each flow intensity, there is a non-unity ratio between the ambient velocity and the velocity near the sampler.
The PIV processing of a sampling lasting 7.5 min with a total of 10,800 frames shows the effect of increased velocity on sediment displacement (Figure 8).
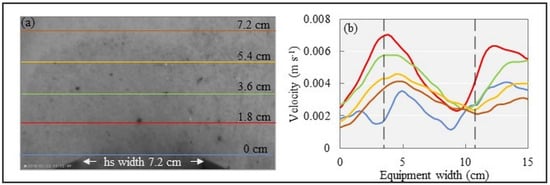
Figure 8.
(a) The gray dotted lines represent the projection of the sampler’s edges. (b) Different colored lines represent the velocity magnitude at distances from 0, 1.8, 3.6, 5.4, and 7.2 cm parallel to the entrance of the Helley–Smith sampler.
The velocity profiles of the bedload sediments, when approaching the sampler, were susceptible to an acceleration process. The average displacement velocity for a distance of 7.2 cm was equal to 0.0028 m s−1, and, successively, at 5.4 cm it was equal to 0.0034 m s−1, at 3.6 cm to 0.0042 m s−1, at 1.8 cm to 0.0048 m s−1, and at 0 (the sampler entrance) to 0.0026 m s−1. There was an average increase in velocity (upstream to downstream) of 19% every 1.8 cm to the 1.8 cm position. Between 1.8 and 0, there was a decrease of 46%. Through the PIV processing of the images, it can be observed that changes in velocity also influence the direction of sediment flow (Figure 9).
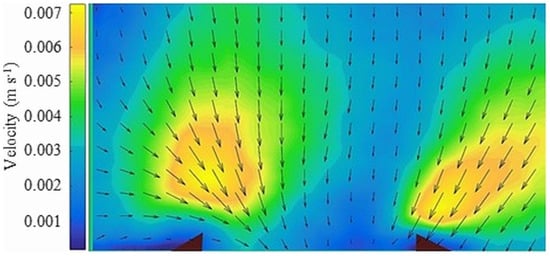
Figure 9.
Top view. Velocity magnitude (colors, m s−1) and velocity field (vectors) of bed-sediment movements upstream and around the Helley–Smith sampler. Temporal average of 7.5 min. Triangles with reddish shades are added masks for image processing and match the locations of the sampler edges.
This processing identified a convergence of material transported to the sampler, with velocities ranging between 0.0035 and 0.007 m s−1 under hydraulic conditions, where the mean water velocity measured by the current meter 20 cm near the bed was 0.91 m s−1.
Furthermore, from the images, we can see an intermittent zone with circular movements in the sediment displacement, especially near the edges of the Helley–Smith sampler. From the same number of frames, a vorticity graph was processed (Figure 10).
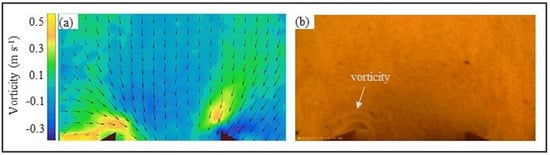
Figure 10.
Top view. (a) Vorticity (colors) and velocity (vectors) fields of bed-sediment movements upstream and around the Helley–Smith sampler. Temporal average of 7.5 min. Triangles with reddish shades are added masks for image processing and match the locations of the sampler edges. (b) Frame represents the vorticity near the hs edge.
The vorticity location was consistent with the rotational movements in the video (Figure 10). The region near the sampler’s edge had a vorticity ranging from 0.2 s−1 to 0.5 s−1 on the left edge and from −0.1 s−1 to −0.3 s−1 on the right edge. This phenomenon mobilized the sediment that was on the side of the equipment and even that located behind the input of the equipment, into it, which is another factor that contributes to overestimation in Helley–Smith collections in predominantly sand-bed rivers. We also note that the vorticity values above zero s−1 were located near the convergence and velocity-increase regions.
4.2. Second Measurement
The first measurement showed an overestimation of sediment sampling caused by sampling below the bedload thickness in the riverbed, that is, the lower edge of the sampler was below the surface of the bed such that it was possible to collect the transported bed sediments.
In the second measurement of the experiment, we observed other aspects at the sampling moment. The first was related to the local characteristics of each body of water and the presence of organic matter. The collection performed in the Estoco Stream showed us the inability of the hydrosedimentologist to evaluate the quality of their samples. In this case, due to blockage of the entry of the sampler by leaves contained in the body of water, sediment was prevented from naturally entering the sampler (Figure 11a). There was an underestimation of the actual bedload transport rate.

Figure 11.
(a) Presence of organic material blocking the entry of the equipment and interfering with the sampling. (b) Absence of contact between entry and bed.
The second characteristic we observed is considered to exist in any river or stream that has a bed with a sandy granulometry, the presence of bed forms. These can be seen as dunes or ripples consisting of sandy material that are formed due to the velocity intensity close to the bed having a crest (highest elevation) and a trough (region of lowest elevation). In fact, we observed that for the collections made in the second measurement, the Helley–Smith sampler was located above the crest of the existing bedforms in the channel, such that its lower edge was far from the riverbed, thus invalidating the bedload sampling with intrusive equipment (Figure 11b).
From these two observations, which theoretically would have caused underestimation and or invalidation of the sampling, we evaluated all our samples following the hypothesis that the usually unknown positioning of the sampler on the bed has a significant influence on the measurement results and may generate anomalous data compared to the realistic bedload transport rate. The proof of this hypothesis would be an essential acquisition of knowledge, considering that many types of research try to evaluate methods that estimate the bedload transport rate from data collected using intrusive equipment.
Therefore, we processed the PIV data from minute to minute, for a total of 5 min of processing, to evaluate sediment transport behavior and its possible changes when the sampler was placed above the bedload thickness layer of the Helley–Smith sampler in the riverbed. The results show a comparison of maps of natural transport (without the presence of equipment) and velocities obtained using the hs and the HS, all at the same collection point (Figure 12).
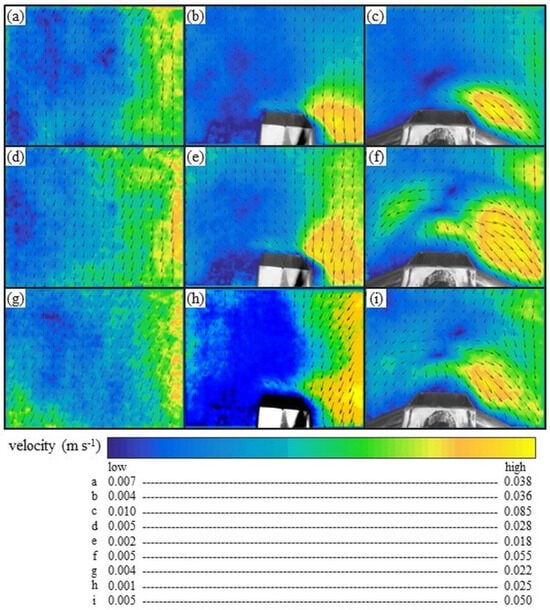
Figure 12.
Spatial and temporal velocity behavior of the sediment displacement, with and without the insertion of intrusive equipment for bed-sediment sampling. The velocity maps show the same dimensions, 35 × 26.3 cm (x and y axes, respectively): (a–c) after the first minute of processing; (d–f) after the third minute of processing; (g–i) after the fifth minute of processing. Different legends to each figure were needed to visualize the behaviors of the sediment velocities. In addition, a single figure legend is presented in Appendix A.
We observed that for natural (real) displacement of the sediments (first column), there was homogeneity in the direction and variation in the velocities, the right side presenting a higher intensity with a variation of 0.025 to 0.038 m.s−1 and the left side with a variation of 0.004 to 0.015 m.s−1, showing that even for small dimensions there is a marked amplitude in the magnitude of sediment displacement, which raises the challenge of quantifying this rate in the water body.
The insertion of the hs above the bedload thickness layer produced different results compared to those from the first measurement campaign (second column). We noted the absence of sediment convergence zones for the sampler’s access; however, there was a tendency of increasing sediment velocities ranging from 0.025 to 0.036 m s−1 on the right side of the sampler. For the collections made with the HS, we noticed that, in addition to an increase in velocity on the right side of the sampler, which varied between 0.04 and 0.085 m s−1, there was a change in the local morphology near the sampler opening, showing an abrupt change in the sediment trajectory.
To assess the changes caused by the intrusive equipment, we extracted the mean velocity values of the sediment displacement transversely over a period of 5 min in three positions: at the top, where we believed that there would be less influence on the sediment displacement caused by the intrusion of the equipment because, according to [36,42], hydrodynamics increases near the opening of the equipment with different behavior depending on the flair-ratio dimension; at the middle and the entrance, where there may have been abnormal changes in sediment transport due to the presence of the equipment (Figure 13). We noticed that the percentual difference in velocity between the top and the entrance lines increased with the presence of the intrusive equipment with a larger flair ratio. The results showed percentual differences in velocity of 4.91% (b), 10.75% (c), and 36.05% (d) for natural sediment displacement, the hs, and the HS, respectively.
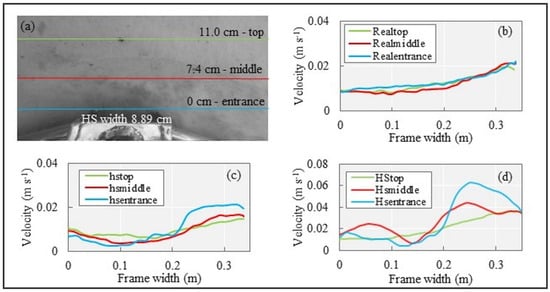
Figure 13.
(a) Locations of the velocities extracted from the image. (b) Velocities without the presence of a pressure-difference sampler. (c) Velocities with the hs located in the bed (river bottom). (d) Velocities with the HS located in the bed.
When evaluating the vorticity (Figure 14), we checked to see whether there was the same overestimation effect due to the unnatural movement of sediment into the sampler as shown in the first measurement. We noted in the analysis of granular flow without the presence of the sampler that there were small spatially distributed spots that represented small spatial and temporal variations in vorticity, with a uniform spread amplitude from −0.6 s−1 to +1.1 s−1. When we inserted the hs, we noticed that the vorticity ranged from −0.4 s−1 to +1.6 s−1. However, this feature increased when the sediment approached the sampler’s input, ranging from +0.6 s−1 to +1.6 s−1. The same characteristic of the spatial presence of vorticity was observed when sampling with the HS. In the proximity of the entrance of the sampler, the variation ranged from +1.5 s−1 to +3.5 s−1, with the rest of the map ranging from −1.3 s−1 to +1.5 s−1. Moreover, there was a spatial change in vorticity values, which changed along with the sampling precisely where the vectors changed their direction from upstream to downstream, resulting in a divergent displacement.
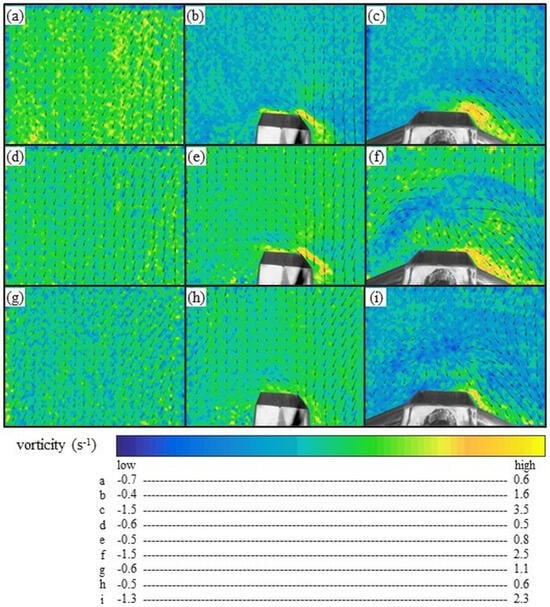
Figure 14.
Spatial and temporal behavior of the vorticity in the sediment displacement, with and without the inclusion of intrusive equipment. The vorticity maps show the same dimensions, 35 × 26.3 cm (x and y axes, respectively): (a–c) after the first minute of processing; (d–f) after the third minute of processing; (g–i) after the fifth minute of processing. A single figure legend is presented in Appendix A.
The analysis of the average vorticity over 5 min of processing showed that one way the equipment is placed at the bottom of the river causes changes in the displacement of the sediment. Moreover, the second measurement showed that the equipment was placed with the lower edge above the thickness zone, and this evidence reinforces the physical difficulties in using pressure-difference equipment. Figure 15a represents an analysis without the sampler which showed that the amplitude and vorticity between the top, middle, and entrance positions had the same magnitude.
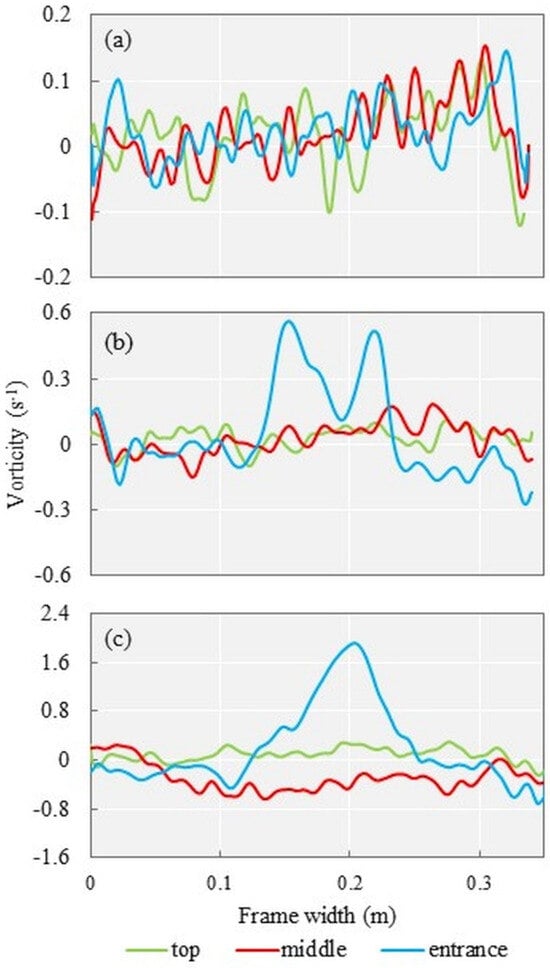
Figure 15.
(a) Vorticities without pressure-difference sampler. (b) Vorticities with hs located on bed. (c) Vorticities with HS located on bed.
On the other hand, Figure 15b,c, representing analyses with the hs and the HS, respectively, showed changes in the average of vorticity mainly in the entrance line.
The observation of the recorded video helps to understand the dynamics that occur between water and sediment. The insertion of the HS above the ridge of a roughness, at a certain distance from the bed, created a turbulent zone between the lower edge of the equipment and the riverbed. This change in the field of water velocity modified the local bed morphology along the sediment sampling (Figure 16).
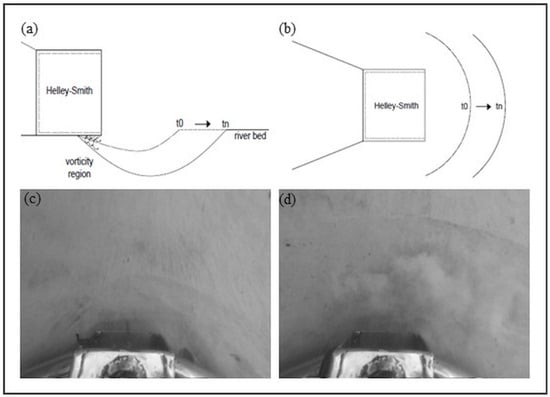
Figure 16.
Vorticity effect between the bed surface and the lower area of the equipment. (a) Sampling period and changes in canal morphology at time t0 and tn (side view). (b) Top view of the phenomenon caused by the insertion of the equipment at times t0 and tn. (c) Image of the sampling moment at time t0 (top view). (d) Image of the sampling moment at time tn (top view).
These modifications occurred gradually, increasing the distance between the collector’s input and the bottom and also creating a sediment barrier preventing the natural flow of transport from continuing to reach the sampler (Figure 16b). Figure 16c,d represent the sampling times t0 and tn, as shown in (a) and (b). Moreover, we identified a sediment suspension zone in (d), possibly caused by turbulence. We understand that there was a change in the local morphology of the riverbed due to the incorrect insertion of the equipment and that there may have been a change in the natural displacement of sediments; thus, we evaluated the divergence maps in Figure 17.
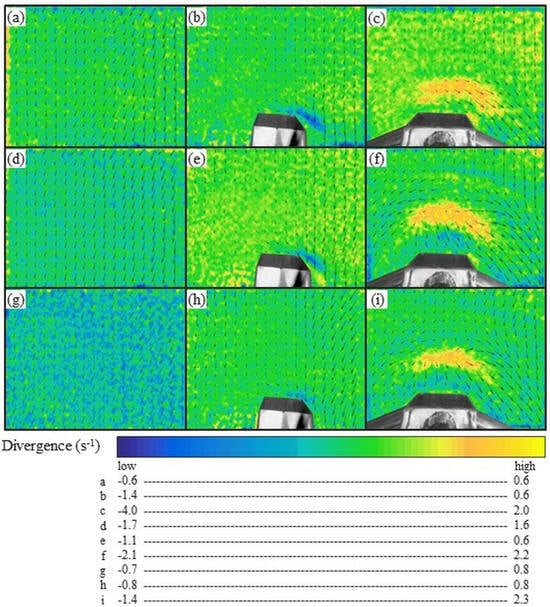
Figure 17.
Spatial and temporal behavior of sediment displacement divergence, with and without the insertion of intrusive equipment for bed-sediment sampling. The divergence maps show the same dimensions, 35 × 26.3 cm (x and y axes, respectively): (a–c) after the first minute of processing; (d–f) after the third minute of processing; (g–i) after the fifth minute of processing. A single figure legend is presented in Appendix A.
We noticed differences in the divergence analyses between the natural granular flow and the one modified because of the sampling. In maps representing the natural flow of sediments, homogeneity in the displacement of upstream and downstream particles with no change in divergence was visible (Figure 17a,d,g).
In this experiment, when we placed the hs on the bed, we observed that its lower edge was located close to the bed surface, and we did not identify the morphological changes (Figure 17b,e,h), as we did when we used the HS, resulting in differences when evaluating the divergences between them (Figure 17c,f,i). For the hs, we noticed small zones of divergence near the right edge of the equipment. The HS presented larger zones of divergence in sediment displacement, and these divergence zones followed the movement of morphological changes caused by turbulence, attributed to the most substantial distance between the lower edge of the sampler and the bed.
This item described the fragility of the sediment sampling using intrusive equipment. We have seen that for the same vertical with similar hydraulic characteristics, sampling with this type of equipment depends on various factors that are imperceptible to the eyes of the hydrosedimentologist. Therefore, we were unable to evaluate the quality of our samples, which may have produced anomalous data or may not correspond to a realistic displacement of sediments in the situation in question, thus creating erroneous transport estimates. In the second measurement, all these factors that led to uncertainty in the samplings were confirmed by a large difference in the masses sampled by the hs and the HS, 2.10 and 0.248 Kg, respectively.
Figure 18 shows the average of the divergence variation in the collections performed without a sampler and with a sampler over a period of 5 min. We noticed more anomalous behavior in the divergence when we analyzed the collections with the samplers: in (b), the divergence zones follow the location of the vorticity zones caused by the hs. In (c), it is interesting to note that the variation in the divergence is in the central line, which reflects the local morphological changes due to the presence of the HS and the moving bed. On the other hand, the analysis performed without the presence of equipment shows a more equalized (standardized) behavior pattern. In fact, the figures and graphs above reflect the importance of knowing how the equipment is located on the bed of the river, whether it is above or below the sediment displacement, because, depending on how the equipment is located, there is a tendency to overestimate or underestimate the measurements.
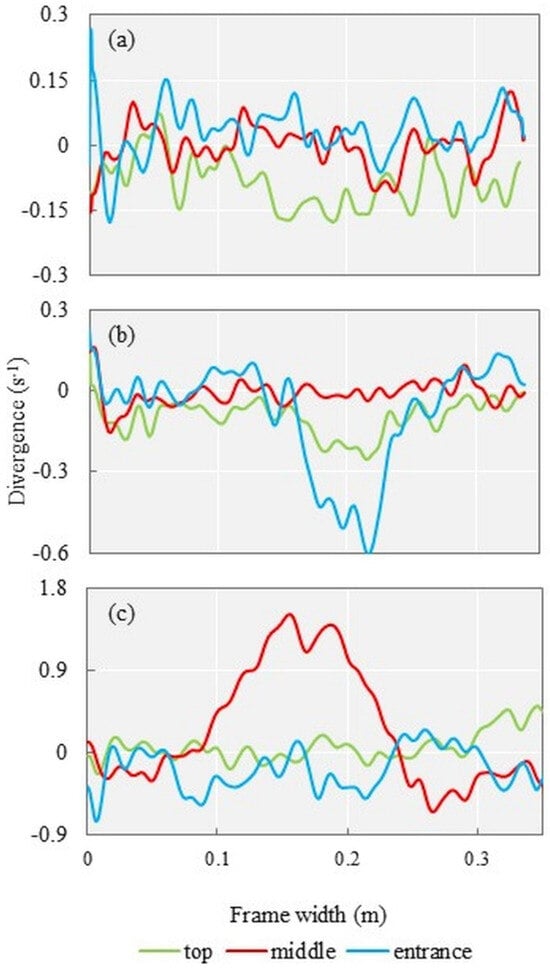
Figure 18.
(a) Divergences without pressure-difference sampler. (b) Divergences with hs located on bed. (c) Divergences with HS located on bed.
4.3. Bedload Transport Analysis
The aim of this section is to evaluate the difference between the bedload transport rates obtained by the different methodologies, intrusive and non-intrusive ones. We analyzed the results obtained with the two Helley–Smith samplers with different dimensions, the estimates made from the moving-bed test performed with an ADCP, and the estimates made using the average velocity of the bed particles calculated using PIV processing (Table 5).

Table 5.
Hydraulic and sediment characteristics in the Estoco Stream during the experiments.
It is noteworthy that for the two measurement campaigns we found similar hydraulic conditions and granulometric characteristics: mean D50 values with a difference of 0.01 mm, equal D90 values, and vm values with a difference of 0.03 m s−1. However, we do not intend to perform data analysis between both measurement campaigns but to analyze the result of each one. In the first measurement, we did not perform video recording without the Helley–Smith sampler; however, for the application of the kinematic model to calculate the qPIV, we used the average velocity values of the particles that were the furthest from the equipment opening so that there would be no interference with the velocity. Thus, the value found for the efficiency (534.78%) indicated a high overestimation of the hs sampler when it was placed below the bedload thickness layer. The high efficiency was explained for convergence and vorticity zones found at the sampler opening.
In the second measurement, we observed the difference between the estimates obtained by the two Helley–Smith samplers. Although the equipment was used for the same hydraulic and granulometric conditions, the percentage error in the estimate of bedload transport between the hs and the HS was 910.53%. This difference is explained by all the factors evaluated with the PIV results. Although the two devices were located above the bedload transport layer, the fact that the hs and the HS were at different distances from the bedload transport layer resulted in this significant percentage difference.
Ref. [21] developed research to assess the reliability of bedload transport estimates using ADCP in different environments, concluding that these estimates are reliable for bed-particle displacement velocities below 0.6 m s−1. Bearing in mind that in these conditions they respected the conclusions of the research carried out, we consider that the estimates that originated in the velocity data obtained from the moving-bed tests are realistic. The direct comparison between vADCP and vPIV showed a percentage error of only 3.55%, showing the potential of this technique for qualitative and quantitative analyses of this experiment. Using the respective velocities to estimate the bedload transport rate using the kinematic model, we found a percentage error of only 3.36%.
5. Conclusions
In this work, we used the Particle Image Velocimetry technique (PIV) to qualitatively and quantitatively evaluate the use of the Helley–Smith sampler in a sand-bed stream. At the sampling time, we described two possibilities regarding the insertion of the equipment. When the bottom face of the equipment was located below the bedload transport layer, the equipment was able to collect the sediments that were being transported by rolling and sliding. On the other hand, if the equipment was placed on the bed with its bottom face above the sediment transport layer, at an undetermined distance, it was impossible for sediments that were transported by rolling and sliding to enter it.
When the equipment was placed below the bedload transport layer, unreal sediment displacements were identified in the vicinity of the equipment, resulting in an overestimation of the collection. When the equipment was placed above the bedload thickness layer, morphological changes were identified due to the turbulence region caused by the distance between the lower area of the equipment and the riverbed, creating a region of abrupt divergence in sediment displacement, invalidating the sample. When comparing the masses of bed sediments collected by the hs and the HS at the same point, we found a difference of 910.53% even with the two samplers located above the bedload transport layer, making the qualitative evaluation of the samples even more difficult. In addition, the presence of organic matter may have obstructed sediment entering the sampler, causing uncertainty during the measurement that we were unable to measure.
Therefore, to avoid measurement errors during sampling, we recommend the following when using Helley–Smith-type load samplers:
- (a)
- Different modes of locating a Helley–Smith sampler in a riverbed can significantly change the total mass of the sampled sediment, leading to unrealistic estimates of bedload transport. To assess bed-sediment sampling, installing cameras to check the position and flow conditions, as well as the general characteristics of bedload transport and organic matter, is highly recommended.
- (b)
- In the second measurement, we identified temporal variation in sediment transport velocities minute by minute. To carry out better measurements, we recommend sampling over long time periods and repeatedly at each position to reduce uncertainties by increasing sample numbers.
- (c)
- Each piece of equipment, intrusive or non-intrusive, used for estimating bedload transport in sandy rivers has its limits and uncertainties. Performing measurements along with other methodologies, such as moving-bed tests with ADCP or dune tracking is a necessary option.
- (d)
- In addition, from the filming, we were able to qualitatively and quantitatively evaluate the bedload transport and thus improve data analysis in post-processing, whether using PIV or other algorithms.
- (e)
- Future research is recommended in testing both methods (pressure-difference samplers and acoustic methods using ADCPs) simultaneously in either large laboratory flumes or more controlled field experiments.
Author Contributions
Conceptualization, R.B.P.; Methodology, G.A.C.; Investigation, P.A.P.Z.; Data curation, L.W.; Visualization, F.V.G.; Supervision, T.B. and J.G.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CAPES, and support for equipment (ADCPs and Helley–Smith samplers acquired and built through financing from CAPES and CNPq, respectively) was received from PPGTA, Federal University of Mato Grosso do Sul, to carry out the related field measurements in this research (01/23/2018 and 13/06/2018). Tobias Bleninger acknowledges a productivity stipend from the National Council for Scientific and Technological Development, CNPq (grant no. 313491/2023-2, call no. 09/2023). This study was financed in part by the Universidade Federal de Mato Grosso do Sul–Brasil (UFMS)–Finance Code 001 and the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior–Brasil (CAPES)–Finance Code 001.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
We would like to thank the USGS and the Federal University of Paraná for the possibility of interacting with their researchers in conducting research and sharing knowledge. We specially thank John S. Gray for providing insights that improved the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Glossary
| ADCP | Acoustic Doppler Current Profiler |
| Aw | Tropical savannah |
| BM | Bed material |
| BMH-53 | Bed-material sampler |
| D50 | Median particle diameters (mm) |
| D90 | Particle diameter bigger than 90% (mm) |
| e | Sampler efficiency (%) |
| GB | Guariroba Stream Basin |
| HEROS | Hydrology, Erosion, and Sediment Laboratory |
| HS | Helley–Smith (flair ratio equal to 3.47) |
| hs | Helley–Smith handheld (flair ratio equal to 1.95) |
| M | Bedload weight displaced without sampler (Kg) |
| mHS | Sediment weight sampled by Helley–Smith (Kg) |
| PIV | Particle Image Velocimetry |
| Q | Water discharge rate (m3 s m−1) |
| qADCP | Bedload transport rate sampled by ADCP (Kg min−1) |
| qhs | Bedload transport rate sampled by hs (Kg min−1) |
| qHS | Bedload transport rate sampled by HS (Kg min−1) |
| qPIV | Bedload transport rate sampled by PIV (Kg min−1) |
| RTK | Real-Time Kinematics |
| va | Apparent bed-particle velocity (m s−1) |
| vADCP | Bed-particle velocity sampled by ADCP (m s−1) |
| vBT | Bottom-track velocity (m s−1) |
| vDGPS | Differential Global Positioning System velocity (m s−1) |
| vhs | Bed-particle velocity sampled by hs (m s−1) |
| vHS | Bed-particle velocity sampled by HS (m s−1) |
| vm | Depth-averaged vertical velocity (m s−1) |
| vPIV | Bed-particle velocity sampled by PIV (m s−1) |
Appendix A
Here, we present the figures that show the behavior analysis of the velocities, vorticities, and divergence of sediments using only one legend. We note that the application of only one caption with high-amplitude causes visual loss with respect to the sediment behavior minute by minute.
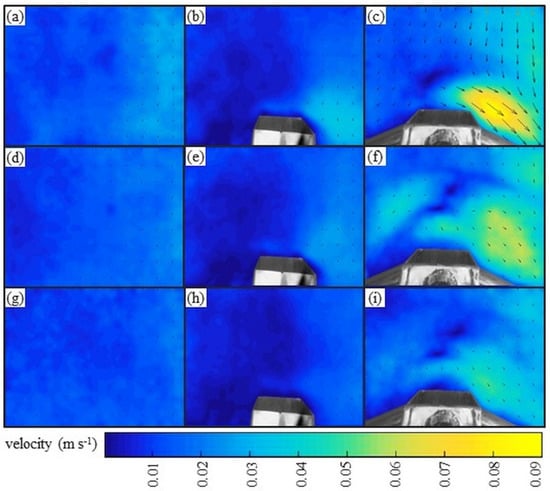
Figure A1.
Spatial and temporal behavior of sediment displacement velocity, with and without the insertion of intrusive equipment for bed-sediment sampling. The divergence maps show the same dimensions, 35 × 26.3 cm (x and y axes, respectively): (a–c) after the first minute of processing; (d–f) after the third minute of processing; (g–i) after the fifth minute of processing.
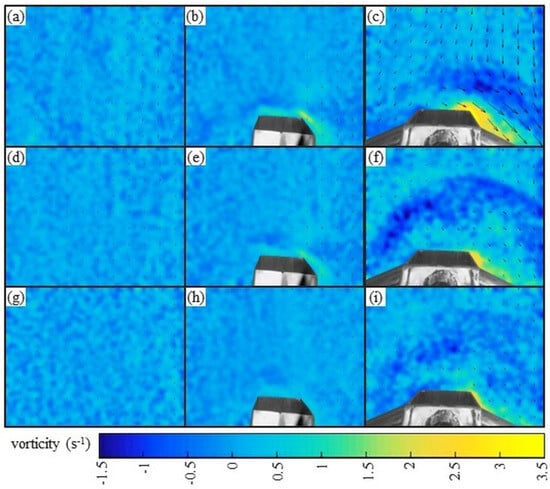
Figure A2.
Spatial and temporal behavior of sediment displacement vorticity, with and without the insertion of intrusive equipment for bed-sediment sampling. The divergence maps show the same dimensions, 35 × 26.3 cm (x and y axes, respectively): (a–c) after the first minute of processing; (d–f) after the third minute of processing; (g–i) after the fifth minute of processing.
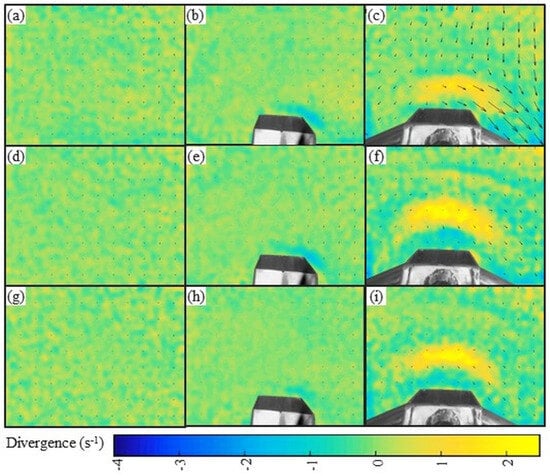
Figure A3.
Spatial and temporal behavior of sediment displacement divergence, with and without the insertion of intrusive equipment for bed-sediment sampling. The divergence maps show the same dimensions, 35 × 26.3 cm (x and y axes, respectively): (a–c) after the first minute of processing; (d–f) after the third minute of processing; (g–i) after the fifth minute of processing.
References
- Atkinson, B.L.; Grace, M.R.; Hart, B.T.; Vanderkruk, K.E.N. Sediment Instability Affects the Rate and Location of Primary Production and Respiration in a Sand-Bed Stream. J. N. Am. Benthol. Soc. 2008, 27, 581–592. [Google Scholar] [CrossRef]
- Larsen, M.C.; Gellis, A.C.; Glysson, G.D.; Gray, J.R.; Horowitz, A.J. Fluvial Sediment in Teh Enviroment: A National Challenge. In Proceedings of the Joint Federal Interagency Conference 2010: Hydrology and Sedimentation for a Changing Future: Existing and Emerging Issues; Cambridge University Press: Cambridge, UK, 2010; 14p. [Google Scholar] [CrossRef]
- USEPA. Causes of Impairment in Assessed Rivers and Streams; USEPA: Washington, DC, USA, 2019.
- Pimentel, D.; Harvey, C.A.; Resosudarmo, P.; Sinclair, K.; Kurz, D.; Mcnair, M.; Crist, S.; Shpritz, L.; Fitton, L.; Saffouri, R.; et al. Environmental and Economic Costs of Soil Erosion and Conservation Benefits. Science 1995, 267, 1117–1123. [Google Scholar] [CrossRef] [PubMed]
- Bagnold, R.A. An Approach to the Sediment Transport Problem From General Physics; Geological Survey Professional Paper 422-I; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Chen, Y.; Bai, Y.; Xu, D. On the Mechanisms of the Saltating Motion of Bedload. Int. J. Sediment Res. 2017, 32, 53–59. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment Transport, Part I: Bed Load Transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Claude, N.; Rodrigues, S.; Bustillo, V.; Bréhéret, J.G.; Macaire, J.J.; Jugé, P. Estimating Bedload Transport in a Large Sand-Gravel Bed River from Direct Sampling, Dune Tracking and Empirical Formulas. Geomorphology 2012, 179, 40–57. [Google Scholar] [CrossRef]
- Gaweesh, M.T.K.; Van Rijn, L.C. Bed-Load Sampling in Sand-Bed Rivers. J. Hydraul. Eng. 1994, 120, 1364–1384. [Google Scholar] [CrossRef]
- Gomez, B.; Church, M. An Assessment of Bed Load Sediment Transport. Water Resour. Res. 1989, 25, 1161–1186. [Google Scholar] [CrossRef]
- Pitlick, J. Variability of Bed Load Measurement. Water Resour. Res. 1988, 24, 173–177. [Google Scholar] [CrossRef]
- Vericat, D.; Church, M.; Batalla, R.J. Bed Load Bias: Comparison of Measurements Obtained Using Two (76 and 152 Mm) Helley-Smith Samplers in a Gravel Bed River. Water Resour. Res. 2006, 42, W10423. [Google Scholar] [CrossRef]
- Gomez, B. Bedload Transport. Earth Sci. Rev. 1991, 31, 89–132. [Google Scholar] [CrossRef]
- Gray, J.R.; Laronne, J.B.; Marr, J.D.G. Bedload-Surrogate Monitoring Technologies; U.S. Geological Survey Scientific Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2010; Volume 5091, pp. 1–37.
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; United States Department of Agriculture, Soil, and Conservation Service: Portland, OR, USA, 1950; p. 1026.
- Kalinske, A.A. Movement of Sediment as Bed Load in Rivers. Trans. Am. Geophys. Union 1947, 28, 615–620. [Google Scholar]
- Meyer-Peter, E.; Muller, R. Formulas for Bed-Load Transport. Int. Assoc. Hydraul. Struct. Res. 1948. Available online: https://repository.tudelft.nl/record/uuid:4fda9b61-be28-4703-ab06-43cdc2a21bd7 (accessed on 22 August 2024).
- Gomez, B.; Naff, R.L.; Hubbell, D.W. Temporal Variations in Bedload Transport Rates Associated with the Migration of Bedforms. Earth Surf. Process. Landforms 1989, 14, 135–156. [Google Scholar] [CrossRef]
- Gray, J.R.; Simões, F.J.M. Estimating Sediment Discharge. In Sedimentation Engineering—Processes, Measurements, Modeling, and Practice: American Society of Civil Engineers Manuals and Reports on Engineering Practice; United States Department of the Interior, Geological Survey-Water Resources Division: Reston, VA, USA, 2008; pp. 1067–1088. [Google Scholar] [CrossRef]
- Gaeuman, D.; Jacobson, R.B. Acoustic Bed Velocity and Bed Load Dynamics in a Large Sand Bed River. J. Geophys. Res. Earth Surf. 2006, 111, 1–14. [Google Scholar] [CrossRef]
- Jamieson, E.C.; Asce, S.M.; Rennie, C.D.; Asce, M.; Jacobson, R.B.; Townsend, R.D. Evaluation of ADCP Apparent Bed Load Velocity in a Large Sand-Bed River: Moving versus Stationary Boat Conditions. J. Hydraul. Eng. 2011, 137, 1064–1072. [Google Scholar] [CrossRef]
- Villard, P.V.; Church, M.A.; Kostaschuk, R. Estimating Bedload in Sand-Bed Channels Using Bottom Tracking from an Acoustic Doppler Profiler. In Fluvial Sedimentology VII; Blackwell Publishing Ltd.: Malden, MA, USA; Oxford, UK; Carlton, VIC, Australia, 2005; pp. 197–209. [Google Scholar] [CrossRef]
- Latosinski, F.; Nicolás, R.; Guerrero, M.; Amsler, L.; Vionnet, C. The ADCP’s Bottom Track Capability for Bedload Prediction: Evidence on Method Reliability from Sandy River Applications. Flow Meas. Instrum. 2017, 54, 124–135. [Google Scholar] [CrossRef]
- Rennie, C.D.; Millar, R.G.; Church, M.A. Measurement of Bed Load Velocity Using an Acoustic Doppler Current Profiler. J. Hydraul. Eng. 2002, 128, 473–483. [Google Scholar] [CrossRef]
- Rennie, C.D.; Villard, P.V. Site Specificity of Bed Load Measurement Using an Acoustic Doppler Current Profiler. J. Geophys. Res. 2004, 109, F03003. [Google Scholar] [CrossRef]
- Conevski, S.; Guerrero, M.; Ruther, N.; Rennie, C.D.; Asce, M. Laboratory Investigation of Apparent Bedload Velocity Measured by ADCPs under Different Transport Conditions. J. Hydraul. Eng. 2019, 145, 04019036. [Google Scholar] [CrossRef]
- Conevski, S.; Guerrero, M.; Rennie, C.D.; Ruther, N. Towards an Evaluation of Bedload Transport Characteristics by Using Doppler and Backscatter Outputs from ADCPs. J. Hydraul. Res. 2021, 59, 703–723. [Google Scholar] [CrossRef]
- Conevski, S.; Guerrero, M.; Winterscheid, A.; Faltis, D.; Rennie, C.D.; Ruther, N. Analysis of the Riverbed Backscattered Signal Registered by ADCPs in Different Bedload Transport Conditions–Field Application. J. Hydraul. Res. 2023, 61, 532–551. [Google Scholar] [CrossRef]
- Frings, R.M.; Vollmer, S. Guidelines for Sampling Bedload Transport with Minimum Uncertainty. Sedimentology 2017, 64, 1630–1645. [Google Scholar] [CrossRef]
- Kostaschuk, R.; Best, J.; Villard, P.; Peakall, J.; Franklin, M. Measuring Flow Velocity and Sediment Transport with an Acoustic Doppler Current Profiler. Geomorphology 2005, 68, 25–37. [Google Scholar] [CrossRef]
- Helley, E.J.; Smith, W. Development and Calibration of a Pressure-Difference Bedload Sampler; USGS Open-File Report; United States Department of the Interior, Geological Survey-Water Resources Division: Reston, VA, USA, 1971; 18p.
- Edwards, T.E.; Glysson, G.D. Field Methods for Collection of Fluvial Sediment. Tech. Water-Resour. Investig. 1999, 3, 89. [Google Scholar] [CrossRef]
- Gray, J.R.; Schwarz, G.E.; Czuba, J.A.; Strom, K.; Diplas, P.; Survey, U.S.G.; Survey, U.S.G.; Engineering, B.S.; Tech, V.; Tech, V.; et al. Facilities, Data, and Analytical Methods Used to Derive Sand- and Gravel-Trapping Efficiencies for Four Types of Pressure. Differ. Bedload Sampl. 2019, 1993, 1–2. [Google Scholar]
- Marr, J.D.G.; Gray, J.R.; Davis, B.E.; Ellis, C.; Johnson, S. Large-Scale Laboratory Testing of Bedload-Monitoring Technologies: Overview of the StreamLab06 Experiments. 2010, pp. 266–282. Available online: https://api.semanticscholar.org/CorpusID:110130184 (accessed on 22 August 2024).
- Beschta, R.L. Increased Bag Size Improves Helley-Smith Bed Load Sampler for Use in Streams with High Sand and Organic Matter Transport. Eros. Sediment Transp. Meas. 1981, 133, 17–26. [Google Scholar]
- Druffel, L.; Emmett, W.W.; Schneider, V.R.; Skinner, J.V. Laboratory Hydraulic Calibration of the Helley- Smith Bedload Sediment Sampler; US Geological Survey: Reston, VA, USA, 1976; pp. 76–752.
- Billi, P. Flash Flood Sediment Transport in a Steep Sand-Bed Ephemeral Stream. Int. J. Sediment Res. 2011, 26, 193–209. [Google Scholar] [CrossRef]
- Boyer, C.; Roy, A.G.; Best, J.L. Dynamics of a River Channel Confluence with Discordant Beds: Flow Turbulence, Bed Load Sediment Transport, and Bed Morphology. J. Geophys. Res. Earth Surf. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Kasvi, E.; Vaaja, M.; Kaartinen, H.; Kukko, A.; Jaakkola, A.; Flener, C.; Hyyppä, H.; Hyyppä, J.; Alho, P. Geomorphology Sub-Bend Scale Flow—Sediment Interaction of Meander Bends—A Combined Approach of Fi Eld Observations, Close-Range Remote Sensing and Computational Modelling. Geomorphology 2015, 238, 119–134. [Google Scholar] [CrossRef]
- Makaske, B.; Smith, D.G.; Berendsen, H.J.A.; de Boer, A.G.; van Nielen-Kiezebrink, M.F.; Locking, T. Hydraulic and Sedimentary Processes Causing Anastomosing Morphology of the Upper Columbia River, British Columbia, Canada. Geomorphology 2009, 111, 194–205. [Google Scholar] [CrossRef]
- Venditti, J.G.; Church, M.; Bennett, S.J. Morphodynamics of Small-Scale Superimposed Sand Waves over Migrating Dune Bed Forms. Water Resour. Res. 2005, 41, 1–14. [Google Scholar] [CrossRef]
- Bunte, K.; Klema, M.; Hogan, T.; Thornton, C. Testing the Hydraulic Efficiency of Pressure Difference Samplers While Varying Mesh Size and Type Technical Committee of the Federal Interagency Sedimentation Project; Colorado State University, Engineering Research Center: Fort Collins, CO, USA, 2017. [Google Scholar]
- Sawadogo, O.; Basson, G.R. 3D fully coupled numerical modelling of local sediment flushing scour at dam bottom outlets for sustainable hydropower operation. In River Sedimentation; CRC Press: Boca Raton, FL, USA, 2017; pp. 1154–1160. [Google Scholar]
- Frank-Gilchrist, D.P.; Penko, A.; Calantoni, J. Investigation of Sand Ripple Dynamics with Combined Particle Image and Tracking Velocimetry. J. Atmos. Ocean Technol. 2019, 35, 2019–2036. [Google Scholar] [CrossRef]
- Gollin, D.; Brevis, W.; Bowman, E.T.; Shepley, P. Performance of PIV and PTV for Granular Flow Measurements. Granul. Matter 2017, 19, 42. [Google Scholar] [CrossRef]
- Lueptow, R.M.; Akonur, A.; Shinbrot, T. PIV for Granular Flows. Exp. Fluids 2000, 28, 183–186. [Google Scholar] [CrossRef]
- Sarno, L.; Carravetta, A.; Tai, Y.; Martino, R.; Papa, M.N.; Kuo, C. Measuring the Velocity Fields of Granular Flows—Employment of a Multi-Pass Two-Dimensional Particle Image Velocimetry (2D-PIV) Approach. Adv. Powder Technol. 2018, 29, 3107–3123. [Google Scholar] [CrossRef]
- Van Scheltinga, R.C.T.; Friedrich, H. Sand Particle Velocities over a Subaqueous Dune Slope Using High-Frequency Image Capturing. Earth Surf. Process. Landf. 2019, 44, 1881–1894. [Google Scholar] [CrossRef]
- Senatore, C.; Wulfmeier, M.; Vlahinić, I.; Andrade, J.; Iagnemma, K. Design and Implementation of a Particle Image Velocimetry Method for Analysis of Running Gear-Soil Interaction. J. Terramech. 2013, 50, 311–326. [Google Scholar] [CrossRef]
- Tsubaki, R.; Baranya, S.; Muste, M.; Toda, Y. Spatio-Temporal Patterns of Sediment Particle Movement on 2D and 3D Bedforms. Exp. Fluids 2018, 59, 93. [Google Scholar] [CrossRef]
- Ermilov, A.A.; Fleit, G.; Conevski, S.; Guerrero, M.; Baranya, S.; Rüther, N. Bedload Transport Analysis Using Image Processing Techniques. Acta Geophys. 2022, 70, 2341–2360. [Google Scholar] [CrossRef]
- Hubbell, D.W. Apparatus and Techniques for Measuring Bedload; U.S. Geological Survey Water-Supply Paper; U.S. Government Publishing Office: Washington, WA, USA, 1964; Volume 1748, p. 74.
- Emmett, W.W. A Field Calibration of the Sediment-Trapping Characteristics of the Helley-Smith Bedlaod Sampler; U.S. Geological survey professional paper; United States Government Printing Office: Washington, WA, USA, 1980; p. 1139.
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Long-Term Rates of Mass Wasting in Mesters Vig, Northeast Greenland: Notes on a Re-Survey. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Valle Junior, L.C.G.; Rodrigues, D.B.B.; Oliveira, P.T.S. Initial Abstraction Ratio and Curve Number Estimation Using Rainfall and Runoff Data from a Tropical Watershed. Rev. Bras. Recur. Hidr. 2019, 24, 1–9. [Google Scholar] [CrossRef]
- Wagner, C.R.; Mueller, D.S. Comparison of Bottom-Track to Global Positioning System Referenced Discharges Measured Using an Acoustic Doppler Current Profiler. J. Hydrol. 2011, 401, 250–258. [Google Scholar] [CrossRef]
- Rennie, C.D.; Rainville, F. Case Study of Precision of GPS Differential Correction Strategies: Influence on aDcp Velocity and Discharge Estimates. J. Hydraul. Eng. 2006, 132, 225–234. [Google Scholar] [CrossRef]
- Mueller, D.S. QRev—Software for Computation and Quality Assurance of Acoustic Doppler Current Profiler Moving-Boat Streamflow Measurements—User’s Manual for Version 2.8; U.S. Geological Survey Open-File Report 2016-1052; U.S. Geological Survey: Reston, VA, USA, 2016. [CrossRef]
- Thielicke, W.; Stamhuis, E.J. PIVlab—Towards User-Friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, 30. [Google Scholar] [CrossRef]
- Shavit, U.; Lowe, R.J.; Steinbuck, J.V. Intensity Capping: A Simple Method to Improve Cross-Correlation PIV Results. Exp. Fluids 2007, 42, 225–240. [Google Scholar] [CrossRef]
- Hart, D.P. PIV Error Correction. Exp. Fluids 2000, 29, 13–22. [Google Scholar] [CrossRef]
- Huang, H.; Daribi, D.; Gharibi, M. On Errors of Digital Particle Image Velocimetry. Meas. Sci. Technol. 1997, 8, 1427–1440. [Google Scholar] [CrossRef]
- Keane, R.D.; Adrian, R.J. Theory of Cross-Correlation Analysis of PIV Images. Appl. Sci. Res. 1992, 49, 191–215. [Google Scholar] [CrossRef]
- Westerweel, J.; Scarano, F. Universal Outlier Detection for PIV Data. Exp. Fluids 2005, 39, 1096–1100. [Google Scholar] [CrossRef]
- Carvalho, N.D.O.; Ide, C.N.; do Val, L.A.A.; Rondon, M.A.C.; Barbedo, A.G.A.; Cybis, L.F.d.A. Causas Do Assoeramento Dos Rios Da Bacia Do Alto Paragui e Os Efeitos Decorrentes Nas Cheias. In Proceedings of the VIII Encontro Nacional de Engenharia de Sedimentos, Campo Grande, Brazil, 2–8 November 2008; pp. 1–18. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).