Slow Translation and Rotation of a Composite Sphere Parallel to One or Two Planar Walls
Abstract
1. Introduction
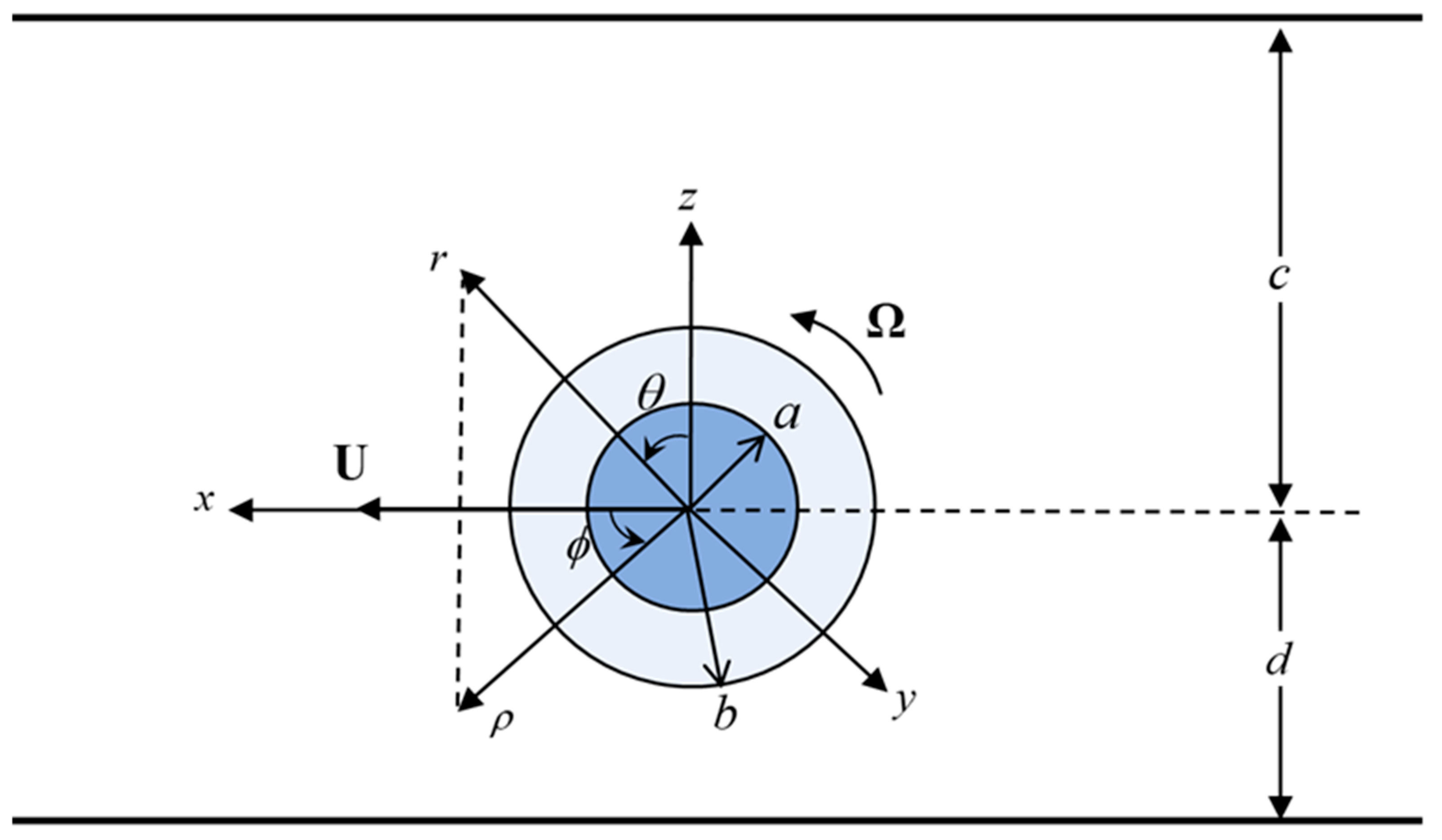
2. Analysis
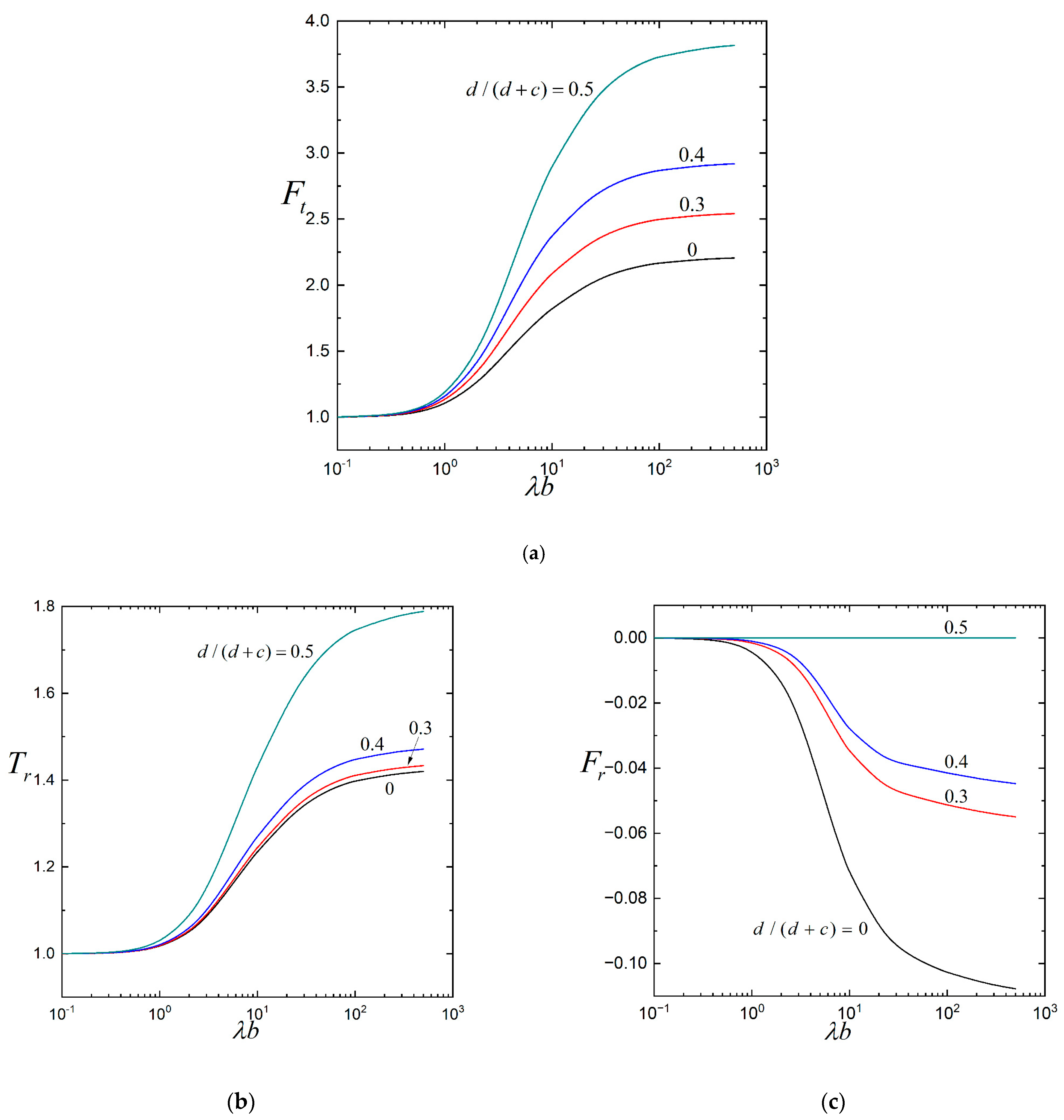
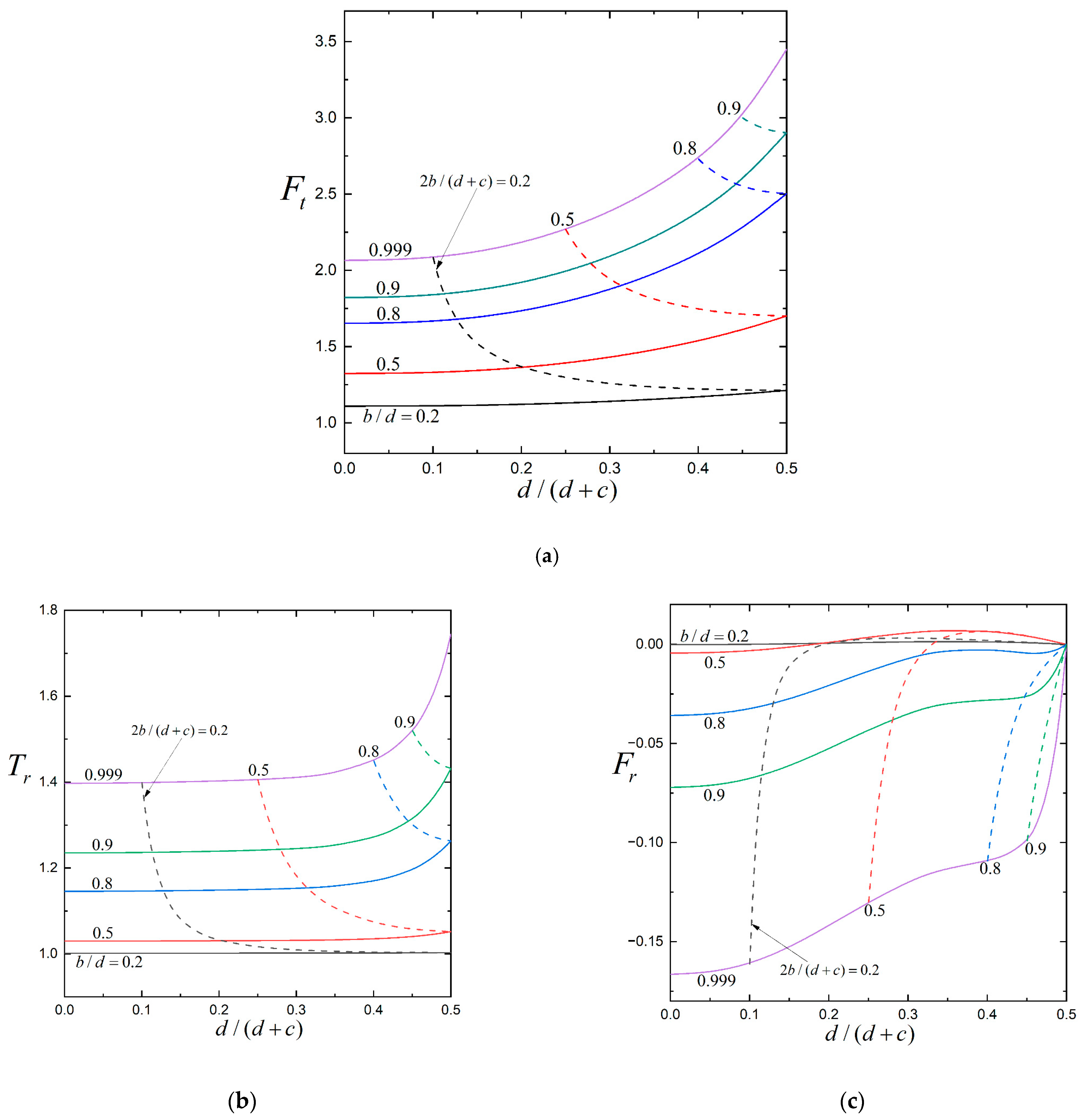
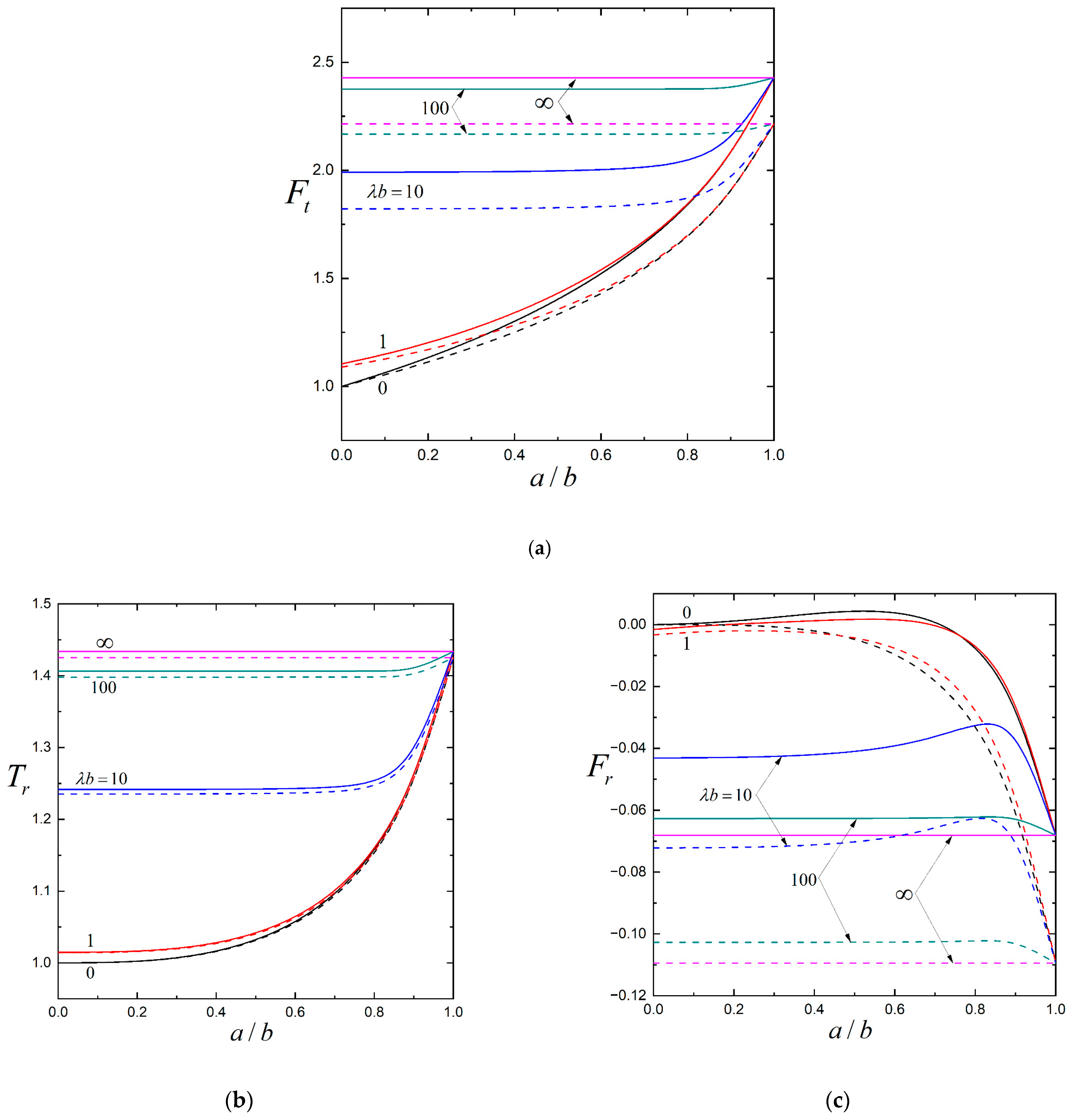
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Stokes, G.G. On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids. Trans. Camb. Phil. Soc. 1845, 8, 287–319. [Google Scholar]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Cambridge Phil. Soc. 1851, 9, 8–106. [Google Scholar]
- Masliyah, J.H.; Neale, G.; Malysa, K.; van de Ven, T.G.M. Creeping flow over a composite sphere: Solid core with porous shell. Chem. Eng. Sci. 1987, 42, 245–253. [Google Scholar] [CrossRef]
- Keh, H.J.; Chou, J. Creeping motion of a composite sphere in a concentric spherical cavity. Chem. Eng. Sci. 2004, 59, 407–415. [Google Scholar] [CrossRef]
- Wunderlich, R.W. The effects of surface structure on the electrophoretic mobilities of large particles. J. Colloid Interface Sci. 1982, 88, 385–397. [Google Scholar] [CrossRef]
- Anderson, J.L.; Solomentsev, Y. Hydrodynamic effects of surface layer on colloidal particles. Chem. Eng. Comm. 1996, 148–150, 291–314. [Google Scholar] [CrossRef]
- Napper, D.H. Polymeric Stabilization of Colloidal Dispersions; Academic Press: London, UK, 1983. [Google Scholar]
- Neale, G.; Epstein, N.; Nader, W. Creeping flow relative to permeable spheres. Chem. Eng. Sci. 1973, 28, 1865–1874. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Nijhoff: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Anderson, J.L. Colloid transport by interfacial forces. Ann. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Romanò, F.; des Boscs, P.-E.; Kuhlmann, H.C. Forces and torques on a sphere moving near a dihedral corner in creeping flow. Eur. J. Mech. B Fluids 2020, 84, 110–121. [Google Scholar] [CrossRef]
- Goldman, A.J.; Cox, R.G.; Brenner, H. Slow viscous motion of a sphere parallel to a plane wall-I. Motion through a quiescent fluid. Chem. Eng. Sci. 1967, 22, 637–651. [Google Scholar] [CrossRef]
- Ganatos, P.; Pfeffer, R.; Weinbaum, S. A strong interaction theory for the creeping motion of a sphere between plane parallel boundaries. Part 2. Parallel motion. J. Fluid Mech. 1980, 99, 755–783. [Google Scholar] [CrossRef]
- Chen, P.Y.; Keh, H.J. Slow motion of a slip spherical particle parallel to one or two plane walls. J. Chin. Inst. Chem. Engrs. 2003, 34, 123–133. [Google Scholar]
- Sherief, H.H.; Faltas, M.S.; Ashmawy, E.A.; Nashwan, M.G. Slow motion of a slip spherical particle along the axis of a circular cylindrical pore in a micropolar fluid. J. Mol. Liq. 2014, 200, 273–282. [Google Scholar] [CrossRef]
- Papavassiliou, D.; Alexander, G.P. Exact solutions for hydrodynamic interactions of two squirming spheres. J. Fluid Mech. 2017, 813, 618–646. [Google Scholar] [CrossRef]
- Chou, C.Y.; Keh, H.J. Slow rotation of a spherical particle in an eccentric spherical cavity with slip surfaces. Eur. J. Mech. B Fluids 2021, 86, 150–156. [Google Scholar] [CrossRef]
- Lee, M.C.; Keh, H.J. Slow axisymmetric rotation of a sphere in a circular tube with slip surfaces. Fluid Dyn. Res. 2021, 53, 065502. [Google Scholar] [CrossRef]
- Nashwan, M.G.; Ragab, K.E.; Faltas, M.S. Axisymmetric slow motion of a non-deformable spherical droplet or slip particle toward an orifice in a plane wall. Phys. Fluids 2022, 34, 083106. [Google Scholar] [CrossRef]
- Liao, J.C.; Keh, H.J. Slow rotation of a sphere about its diameter normal to two planes with slip surfaces. Fluid Dyn. Res. 2022, 54, 035502. [Google Scholar] [CrossRef]
- Madasu, K.P. Boundary effects of slow flow past a fluid coated sphere. Phys. Fluids 2025, 37, 031908. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Krishna Prasad, M. Steady rotation of a composite sphere in a concentric spherical cavity. Acta Mech. Sin. 2012, 28, 653–658. [Google Scholar] [CrossRef]
- Prakash, J.; Raja Sekhar, G.P. Slow motion of a porous spherical particle with a rigid core in a spherical fluid cavity. Meccanica 2017, 52, 91–105. [Google Scholar] [CrossRef]
- Chou, C.Y.; Keh, H.J. Low-Reynolds-number rotation of a soft particle inside an eccentric cavity. Eur. J. Mech. B Fluids 2022, 91, 194–201. [Google Scholar] [CrossRef]
- Chen, Y.C.; Keh, H.J. Slow translation of a composite sphere in an eccentric spherical cavity. Fluids 2024, 9, 154. [Google Scholar] [CrossRef]
- Chen, Y.C.; Keh, H.J. Slow translation and rotation of a composite sphere within a nonconcentric spherical cavity normal to their common diameter. Fluid Dyn. Res. 2025, 54, 035502. [Google Scholar] [CrossRef]
- Jhuang, L.J.; Keh, H.J. Slow axisymmetric rotation of a soft sphere in a circular cylinder. Eur. J. Mech. B Fluids 2022, 95, 205–211. [Google Scholar] [CrossRef]
- Chen, S.B.; Ye, X. Boundary effect on slow motion of a composite sphere perpendicular to two parallel impermeable plates. Chem. Eng. Sci. 2000, 55, 2441–2453. [Google Scholar] [CrossRef]
- Chang, C.L.; Keh, H.J. Slow rotation of a soft colloidal sphere normal to two plane walls. Colloids Interfaces 2023, 7, 18. [Google Scholar] [CrossRef]
- Koplik, J.; Levine, H.; Zee, A. Viscosity renormalization in the Brinkman equation. Phys. Fluids 1983, 26, 2864–2870. [Google Scholar] [CrossRef]

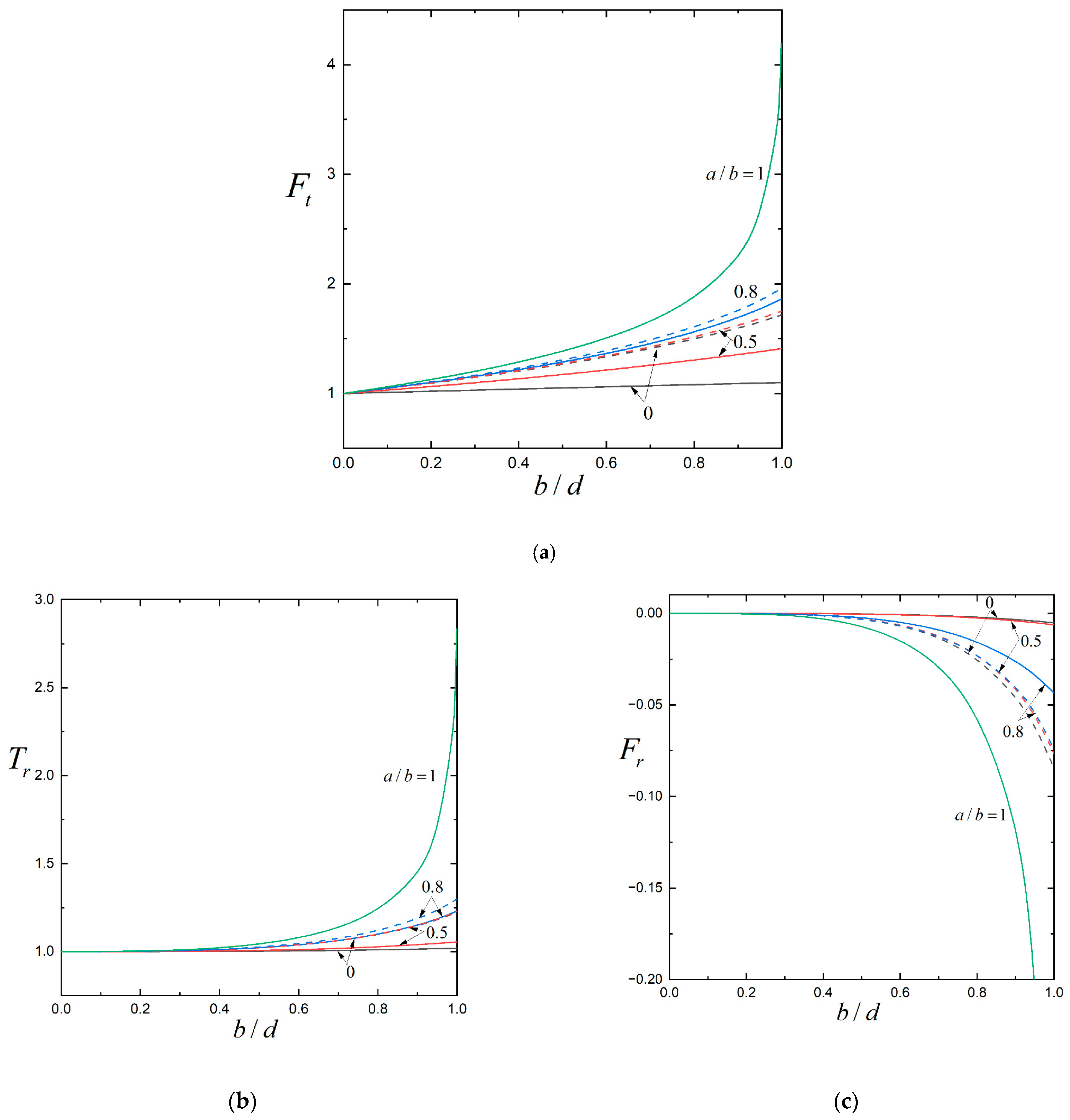
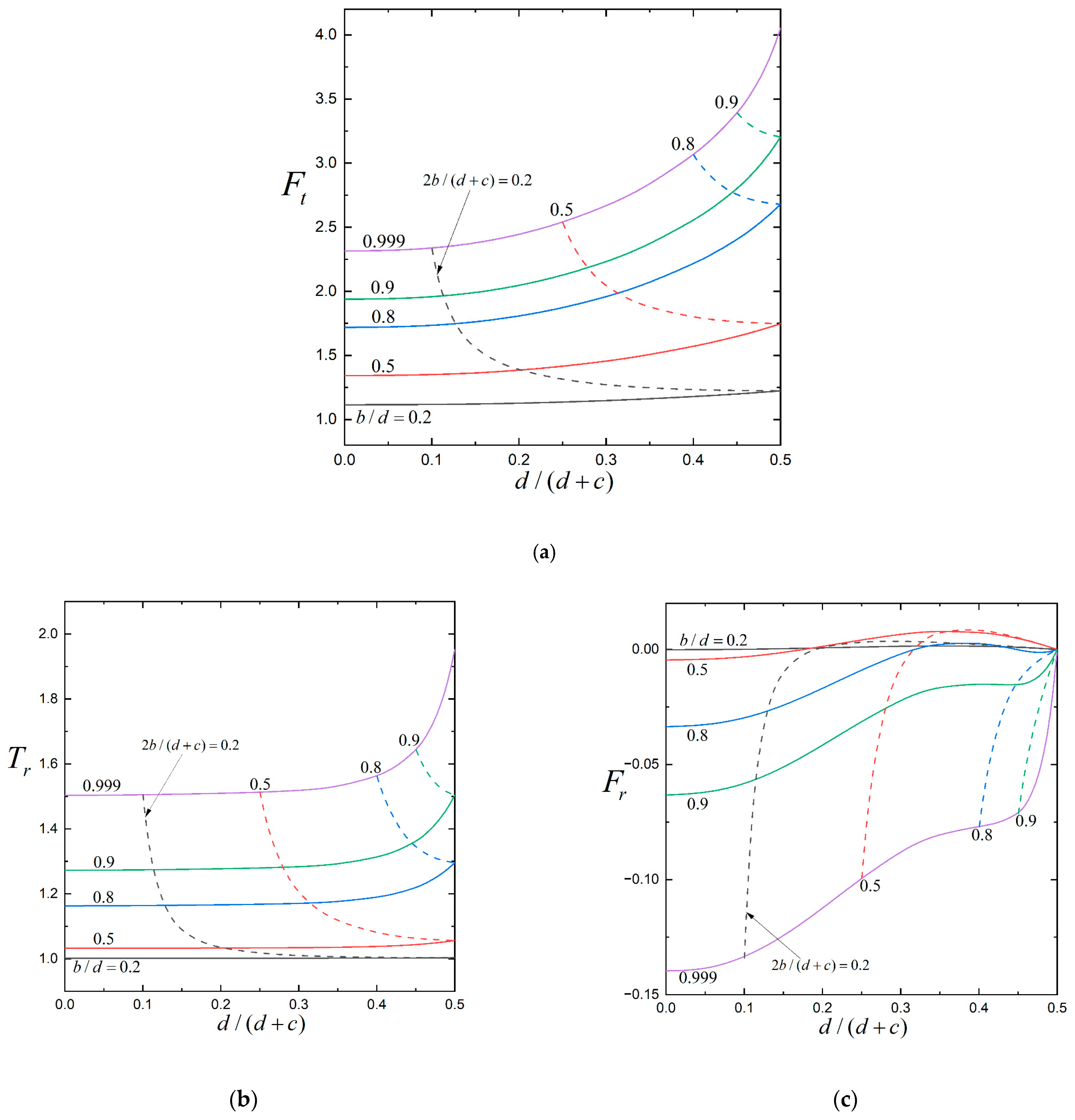
| d/(d+c) | b/d | Ft | ||||
|---|---|---|---|---|---|---|
| λb = 1 | λb = 10 | λb = 100 | λb = 300 | λb→∞ | ||
| 0 | 0.1 | 1.0100 | 1.0525 | 1.0588 | 1.0593 | 1.0595 |
| 0.2 | 1.0200 | 1.1103 | 1.1244 | 1.1254 | 1.1259 | |
| 0.3 | 1.0302 | 1.1740 | 1.1979 | 1.1995 | 1.2003 | |
| 0.4 | 1.0403 | 1.2448 | 1.2810 | 1.2835 | 1.2847 | |
| 0.5 | 1.0503 | 1.3243 | 1.3773 | 1.3810 | 1.3828 | |
| 0.6 | 1.0602 | 1.4154 | 1.4926 | 1.4980 | 1.5006 | |
| 0.7 | 1.0700 | 1.5225 | 1.6380 | 1.6463 | 1.6503 | |
| 0.8 | 1.0797 | 1.6531 | 1.8381 | 1.8522 | 1.8591 | |
| 0.9 | 1.0893 | 1.8219 | 2.1672 | 2.1995 | 2.2152 | |
| 0.99 | 1.0980 | 2.0377 | 2.9709 | 3.2285 | 3.3975 | |
| 0.999 | 1.0988 | 2.0656 | 3.2048 | 3.6843 | 4.1929 | |
| 0.25 | 0.1 | 1.0116 | 1.0614 | 1.0689 | 1.0694 | 1.0697 |
| 0.2 | 1.0233 | 1.1302 | 1.1471 | 1.1483 | 1.1489 | |
| 0.3 | 1.0352 | 1.2071 | 1.2361 | 1.2381 | 1.2391 | |
| 0.4 | 1.0470 | 1.2936 | 1.3382 | 1.3412 | 1.3427 | |
| 0.5 | 1.0588 | 1.3916 | 1.4568 | 1.4613 | 1.4635 | |
| 0.6 | 1.0704 | 1.5039 | 1.5983 | 1.6048 | 1.6080 | |
| 0.7 | 1.0818 | 1.6351 | 1.7738 | 1.7836 | 1.7884 | |
| 0.8 | 1.0931 | 1.7927 | 2.0082 | 2.0243 | 2.0322 | |
| 0.9 | 1.1042 | 1.9912 | 2.3759 | 2.4109 | 2.4279 | |
| 0.99 | 1.1142 | 2.2359 | 3.2183 | 3.4792 | 3.6724 | |
| 0.999 | 1.1152 | 2.2668 | 3.4570 | 3.9392 | 4.4494 | |
| 0.5 | 0.1 | 1.0179 | 1.0975 | 1.1099 | 1.1107 | 1.1111 |
| 0.2 | 1.0362 | 1.2134 | 1.2432 | 1.2452 | 1.2462 | |
| 0.3 | 1.0545 | 1.3504 | 1.4041 | 1.4078 | 1.4096 | |
| 0.4 | 1.0727 | 1.5114 | 1.5980 | 1.6039 | 1.6068 | |
| 0.5 | 1.0904 | 1.7002 | 1.8324 | 1.8413 | 1.8458 | |
| 0.6 | 1.1074 | 1.9222 | 2.1194 | 2.1329 | 2.1395 | |
| 0.7 | 1.1236 | 2.1854 | 2.4818 | 2.5024 | 2.5124 | |
| 0.8 | 1.1387 | 2.5033 | 2.9690 | 3.0029 | 3.0194 | |
| 0.9 | 1.1530 | 2.9019 | 3.7294 | 3.8019 | 3.8369 | |
| 0.99 | 1.1652 | 3.3877 | 5.4403 | 5.9675 | 6.2597 | |
| 0.999 | 1.1664 | 3.4488 | 5.9201 | 6.8900 | 7.6253 | |
| d/(d+c) | b/d | Tr | ||||
|---|---|---|---|---|---|---|
| λb = 1 | λb = 10 | λb = 100 | λb = 300 | λb→∞ | ||
| 0 | 0.1 | 1.0000 | 1.0002 | 1.0003 | 1.0003 | 1.0003 |
| 0.2 | 1.0002 | 1.0018 | 1.0024 | 1.0025 | 1.0025 | |
| 0.3 | 1.0005 | 1.0062 | 1.0083 | 1.0085 | 1.0086 | |
| 0.4 | 1.0012 | 1.0149 | 1.0200 | 1.0205 | 1.0207 | |
| 0.5 | 1.0024 | 1.0299 | 1.0405 | 1.0413 | 1.0418 | |
| 0.6 | 1.0041 | 1.0536 | 1.0737 | 1.0754 | 1.0763 | |
| 0.7 | 1.0066 | 1.0899 | 1.1274 | 1.1307 | 1.1324 | |
| 0.8 | 1.0099 | 1.1457 | 1.2182 | 1.2249 | 1.2283 | |
| 0.9 | 1.0142 | 1.2352 | 1.3980 | 1.4161 | 1.4253 | |
| 0.99 | 1.0190 | 1.3768 | 1.9369 | 2.1072 | 2.2233 | |
| 0.999 | 1.0195 | 1.3974 | 2.1150 | 2.4519 | 2.8341 | |
| 0.25 | 0.1 | 1.0000 | 1.0002 | 1.0003 | 1.0003 | 1.0003 |
| 0.2 | 1.0002 | 1.0019 | 1.0025 | 1.0026 | 1.0026 | |
| 0.3 | 1.0005 | 1.0065 | 1.0086 | 1.0088 | 1.0089 | |
| 0.4 | 1.0013 | 1.0155 | 1.0208 | 1.0213 | 1.0215 | |
| 0.5 | 1.0025 | 1.0310 | 1.0420 | 1.0429 | 1.0433 | |
| 0.6 | 1.0043 | 1.0555 | 1.0763 | 1.0781 | 1.0789 | |
| 0.7 | 1.0068 | 1.0929 | 1.1314 | 1.1348 | 1.1365 | |
| 0.8 | 1.0103 | 1.1502 | 1.2241 | 1.2309 | 1.2344 | |
| 0.9 | 1.0147 | 1.2415 | 1.4062 | 1.4244 | 1.4337 | |
| 0.99 | 1.0197 | 1.3850 | 1.9476 | 2.1182 | 2.2463 | |
| 0.999 | 1.0203 | 1.4057 | 2.1262 | 2.4631 | 2.8455 | |
| 0.5 | 0.1 | 1.0000 | 1.0004 | 1.0005 | 1.0005 | 1.0005 |
| 0.2 | 1.0003 | 1.0031 | 1.0042 | 1.0043 | 1.0043 | |
| 0.3 | 1.0009 | 1.0107 | 1.0143 | 1.0146 | 1.0147 | |
| 0.4 | 1.0021 | 1.0258 | 1.0347 | 1.0354 | 1.0358 | |
| 0.5 | 1.0041 | 1.0519 | 1.0707 | 1.0722 | 1.0730 | |
| 0.6 | 1.0071 | 1.0940 | 1.1304 | 1.1335 | 1.1351 | |
| 0.7 | 1.0113 | 1.1598 | 1.2289 | 1.2350 | 1.2381 | |
| 0.8 | 1.0170 | 1.2629 | 1.3996 | 1.4123 | 1.4188 | |
| 0.9 | 1.0243 | 1.4318 | 1.7463 | 1.7815 | 1.7994 | |
| 0.99 | 1.0327 | 1.7046 | 2.8108 | 3.1503 | 3.3477 | |
| 0.999 | 1.0336 | 1.7446 | 3.1658 | 3.8382 | 4.3955 | |
| d/(d+c) | b/d | Fr | ||||
|---|---|---|---|---|---|---|
| λb = 1 | λb = 10 | λb = 100 | λb = 300 | λb→∞ | ||
| 0 | 0.1 | −4.7 × 10−7 | −7.4 × 10−6 | −1.1 × 10−5 | −1.2 × 10−5 | −1.2 × 10−5 |
| 0.2 | −7.5 × 10−6 | −1.2 × 10−4 | −1.8 × 10−4 | −1.8 × 10−4 | −1.8 × 10−4 | |
| 0.3 | −3.8 × 10−5 | −5.7 × 10−4 | −8.6 × 10−4 | −8.9 × 10−4 | −9.0 × 10−4 | |
| 0.4 | −1.2 × 10−4 | −0.0018 | −0.0026 | −0.0027 | −0.0028 | |
| 0.5 | −3.0 × 10−4 | −0.0044 | −0.0064 | −0.0066 | −0.0067 | |
| 0.6 | −6.3 × 10−4 | −0.0094 | −0.0134 | −0.0138 | −0.0141 | |
| 0.7 | −0.0012 | −0.0186 | −0.0261 | −0.0270 | −0.0275 | |
| 0.8 | −0.0020 | −0.0359 | −0.0499 | −0.0517 | −0.0527 | |
| 0.9 | −0.0033 | −0.0722 | −0.1027 | −0.1067 | −0.1095 | |
| 0.99 | −0.0049 | −0.1526 | −0.3486 | −0.3640 | −0.3852 | |
| 0.999 | −0.0051 | −0.1665 | −0.4881 | −0.6124 | −0.8240 | |
| 0.25 | 0.1 | 2.0 × 10−5 | 2.5 × 10−4 | 3.3 × 10−4 | 3.4 × 10−4 | 3.4 × 10−4 |
| 0.2 | 7.6 × 10−5 | 9.9 × 10−4 | 0.0013 | 0.0013 | 0.0013 | |
| 0.3 | 1.5 × 10−4 | 0.0020 | 0.0027 | 0.0027 | 0.0028 | |
| 0.4 | 2.2 × 10−4 | 0.0031 | 0.0040 | 0.0041 | 0.0041 | |
| 0.5 | 2.3 × 10−4 | 0.0036 | 0.0045 | 0.0045 | 0.0046 | |
| 0.6 | 1.4 × 10−4 | 0.0026 | 0.0029 | 0.0028 | 0.0028 | |
| 0.7 | −1.2 × 10−4 | −0.0018 | −0.0031 | −0.0035 | −0.0037 | |
| 0.8 | −6.6 × 10−4 | −0.0134 | −0.0190 | −0.0201 | −0.0209 | |
| 0.9 | −0.0016 | −0.0431 | −0.0627 | −0.0658 | −0.0681 | |
| 0.99 | −0.0028 | −0.1169 | −0.2994 | −0.3136 | −0.3121 | |
| 0.999 | −0.0030 | −0.1301 | −0.4384 | −0.5610 | −0.7720 | |
| d/(d+c) | b/d | a/b = 0.8 | a/b = 0.95 | ||||
|---|---|---|---|---|---|---|---|
| Ft | Tr | Fr | Ft | Tr | Fr | ||
| 0 | 0.1 | 1.0472 | 1.0002 | −4.0 × 10−6 | 1.0564 | 1.0003 | −9.3 × 10−6 |
| 0.2 | 1.0987 | 1.0013 | −6.3 × 10−5 | 1.1189 | 1.0022 | −1.4 × 10−4 | |
| 0.3 | 1.1551 | 1.0044 | −3.1 × 10−4 | 1.1885 | 1.0073 | −7.0 × 10−4 | |
| 0.4 | 1.2170 | 1.0105 | −9.5 × 10−4 | 1.2669 | 1.0176 | −0.0022 | |
| 0.5 | 1.2857 | 1.0209 | −0.0023 | 1.3567 | 1.0355 | −0.0052 | |
| 0.6 | 1.3632 | 1.0371 | −0.0046 | 1.4627 | 1.0642 | −0.0108 | |
| 0.7 | 1.4523 | 1.0612 | −0.0087 | 1.5932 | 1.1095 | −0.0208 | |
| 0.8 | 1.5581 | 1.0966 | −0.0152 | 1.7655 | 1.1831 | −0.0385 | |
| 0.9 | 1.6893 | 1.1493 | −0.0257 | 2.0243 | 1.3154 | −0.0734 | |
| 0.99 | 1.8435 | 1.2215 | −0.0413 | 2.4836 | 1.5924 | −0.1525 | |
| 0.999 | 1.8617 | 1.2307 | −0.0434 | 2.5641 | 1.6447 | −0.1681 | |
| 0.25 | 0.1 | 1.0552 | 1.0002 | 1.8 × 10−4 | 1.0660 | 1.0003 | 2.9 × 10−4 |
| 0.2 | 1.1163 | 1.0013 | 7.1 × 10−4 | 1.1405 | 1.0022 | 0.0012 | |
| 0.3 | 1.1841 | 1.0046 | 0.0015 | 1.2248 | 1.0076 | 0.0024 | |
| 0.4 | 1.2595 | 1.0109 | 0.0025 | 1.3208 | 1.0183 | 0.0037 | |
| 0.5 | 1.3439 | 1.0217 | 0.0033 | 1.4314 | 1.0368 | 0.0044 | |
| 0.6 | 1.4394 | 1.0384 | 0.0037 | 1.5616 | 1.0665 | 0.0035 | |
| 0.7 | 1.5490 | 1.0633 | 0.0030 | 1.7200 | 1.1131 | −6.4 × 10−4 | |
| 0.8 | 1.6778 | 1.0998 | 0.0006 | 1.9241 | 1.1883 | −0.0115 | |
| 0.9 | 1.8346 | 1.1538 | −0.0053 | 2.2186 | 1.3227 | −0.0383 | |
| 0.99 | 2.0144 | 1.2274 | −0.0161 | 2.7136 | 1.6019 | −0.1093 | |
| 0.999 | 2.0353 | 1.2367 | −0.0177 | 2.7979 | 1.6545 | −0.1239 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou, Y.F.; Keh, H.J. Slow Translation and Rotation of a Composite Sphere Parallel to One or Two Planar Walls. Fluids 2025, 10, 154. https://doi.org/10.3390/fluids10060154
Chou YF, Keh HJ. Slow Translation and Rotation of a Composite Sphere Parallel to One or Two Planar Walls. Fluids. 2025; 10(6):154. https://doi.org/10.3390/fluids10060154
Chicago/Turabian StyleChou, Yu F., and Huan J. Keh. 2025. "Slow Translation and Rotation of a Composite Sphere Parallel to One or Two Planar Walls" Fluids 10, no. 6: 154. https://doi.org/10.3390/fluids10060154
APA StyleChou, Y. F., & Keh, H. J. (2025). Slow Translation and Rotation of a Composite Sphere Parallel to One or Two Planar Walls. Fluids, 10(6), 154. https://doi.org/10.3390/fluids10060154






