Numerical Analysis of Submerged Horizontal Plate Wave Energy Converter Device Considering Float Effects
Abstract
1. Introduction
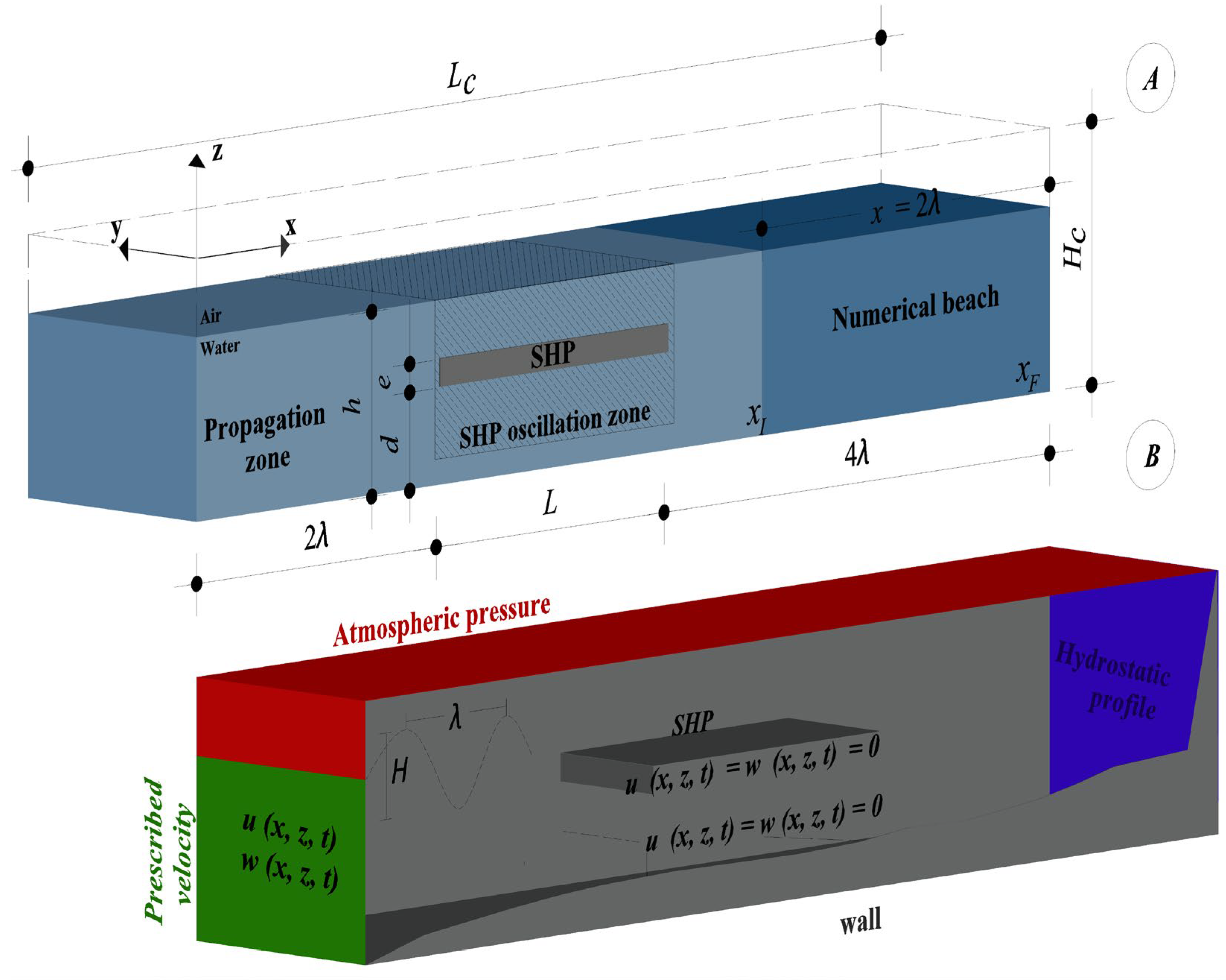
2. Computational Modeling
2.1. Volume of Fluid Model (VOF)
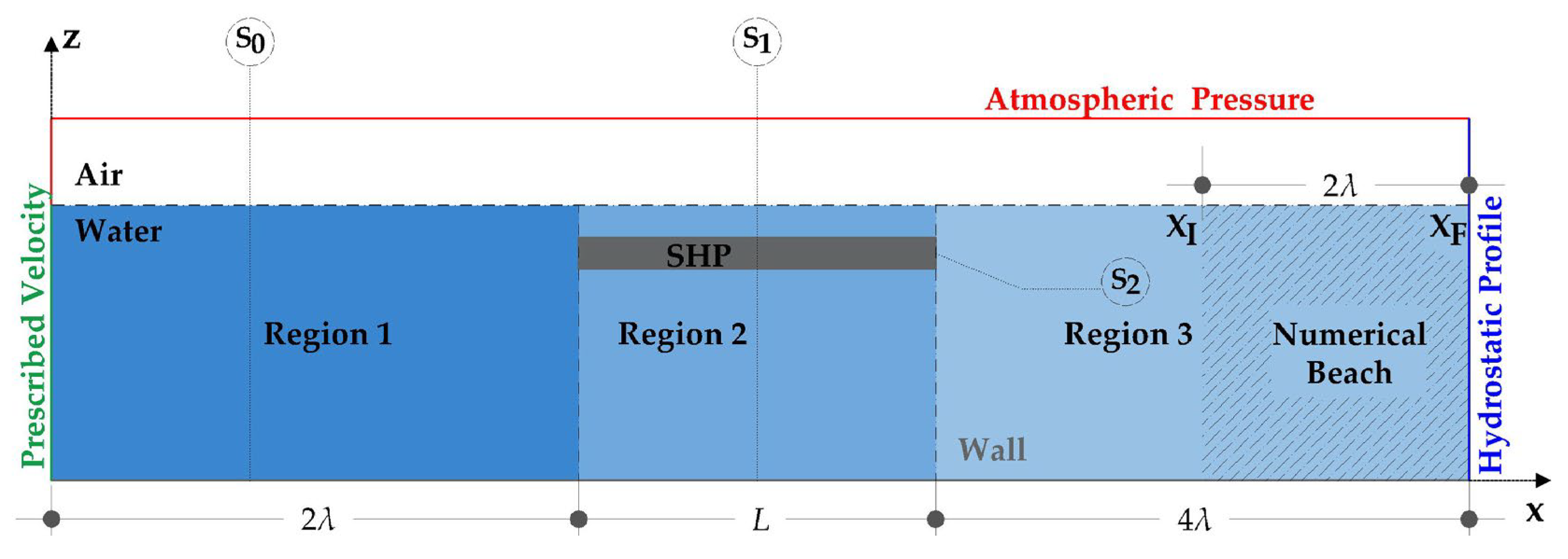
2.2. Boundary Conditions
2.3. Numerical Methods
2.4. Numerical Errors
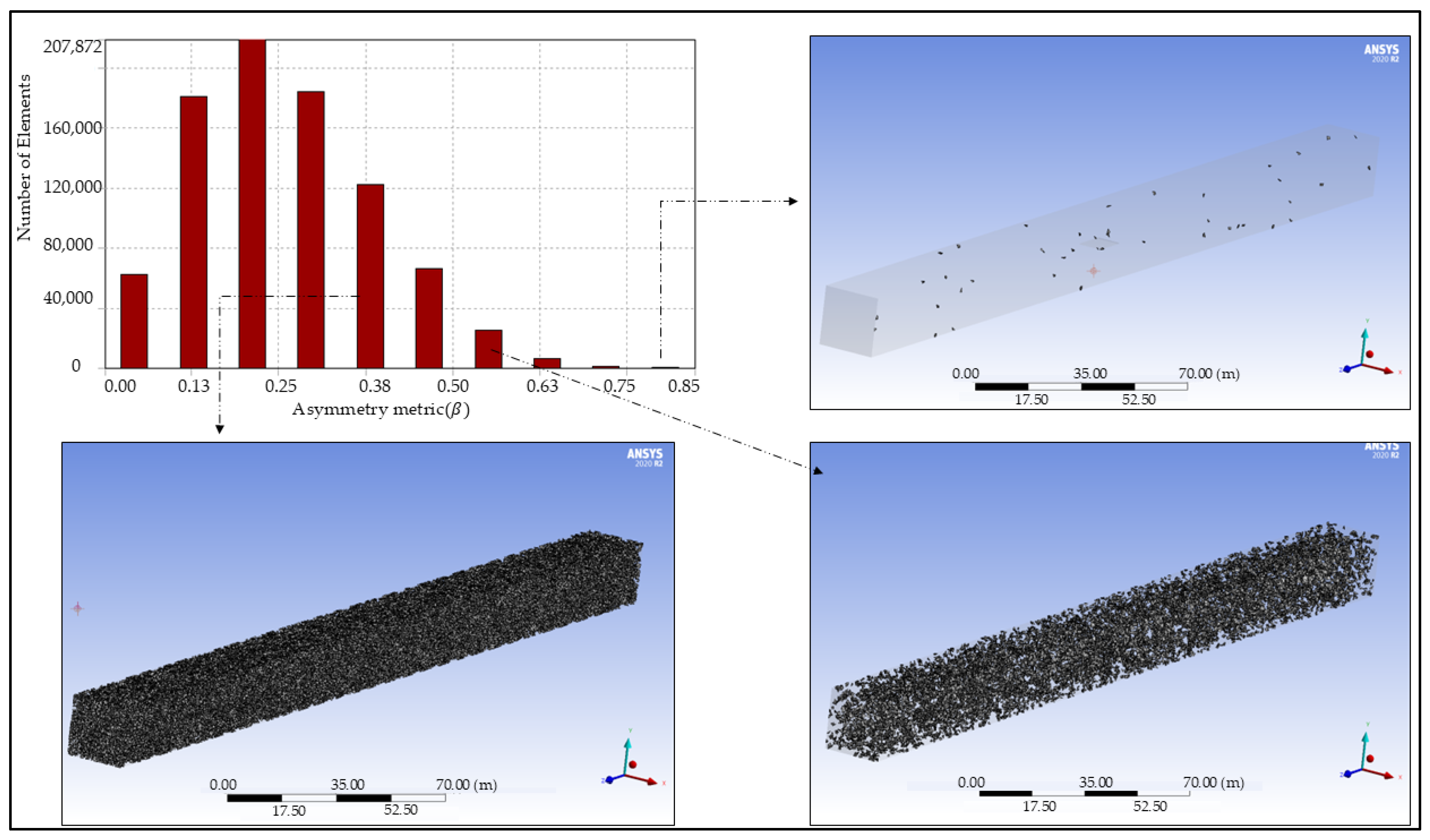
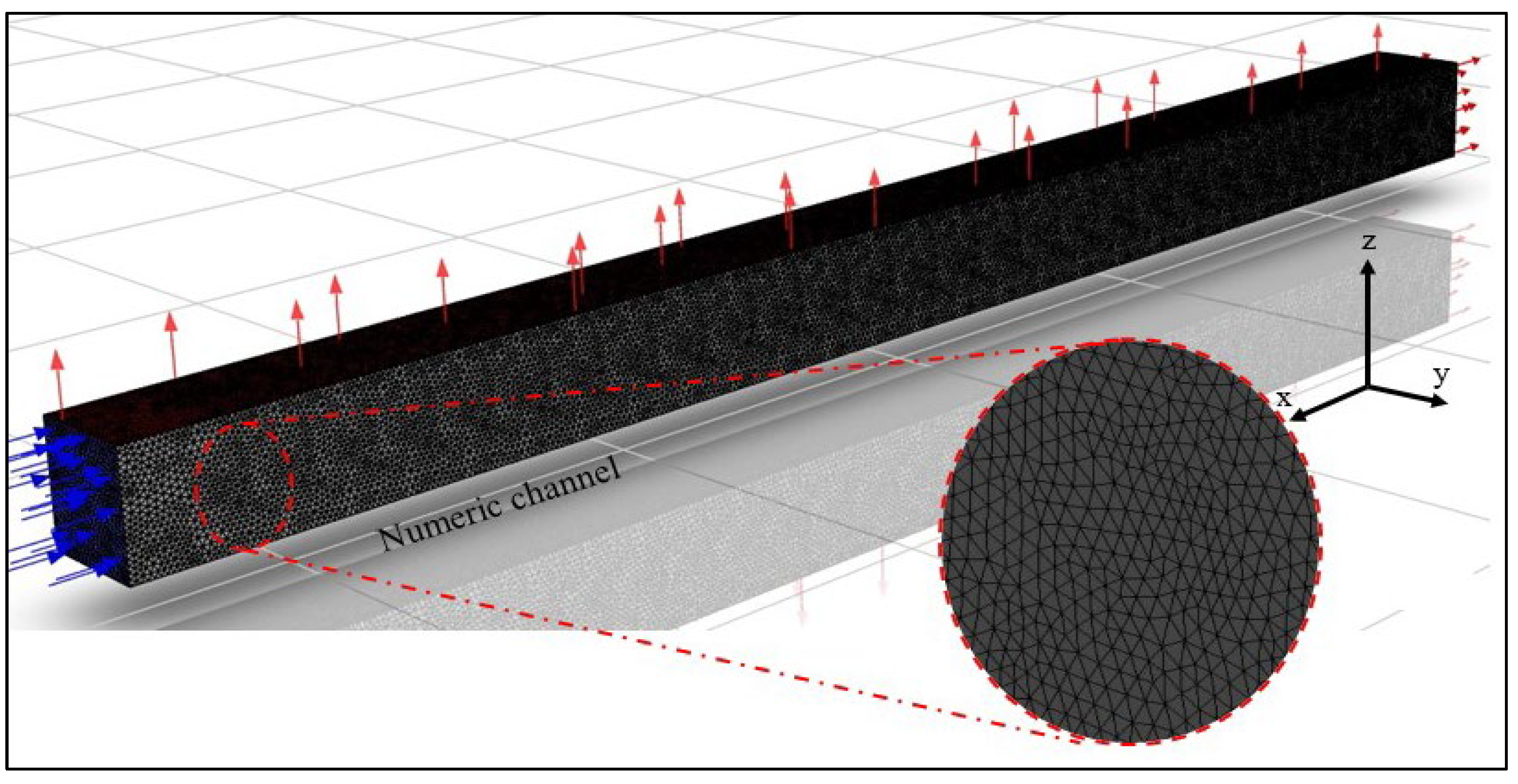
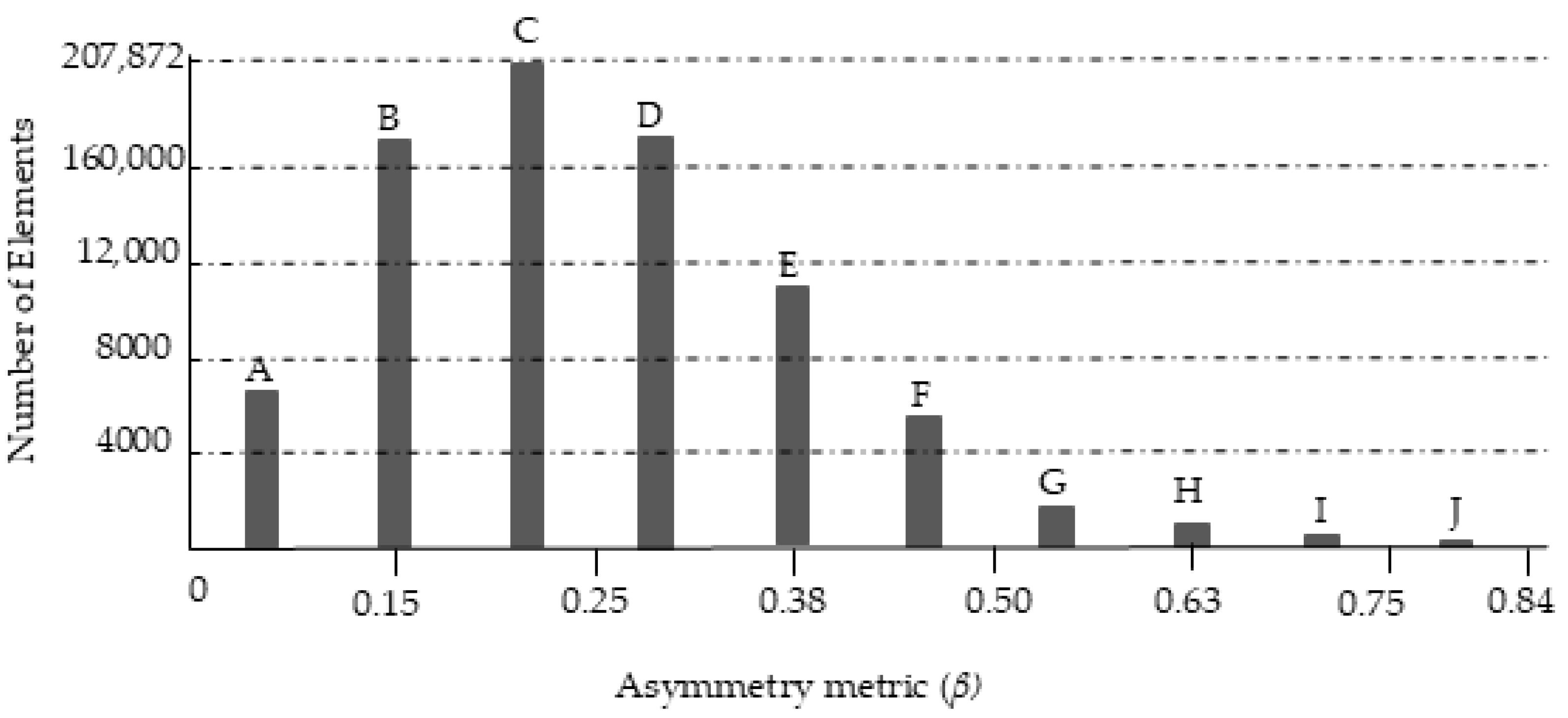
2.5. Domain Discretization
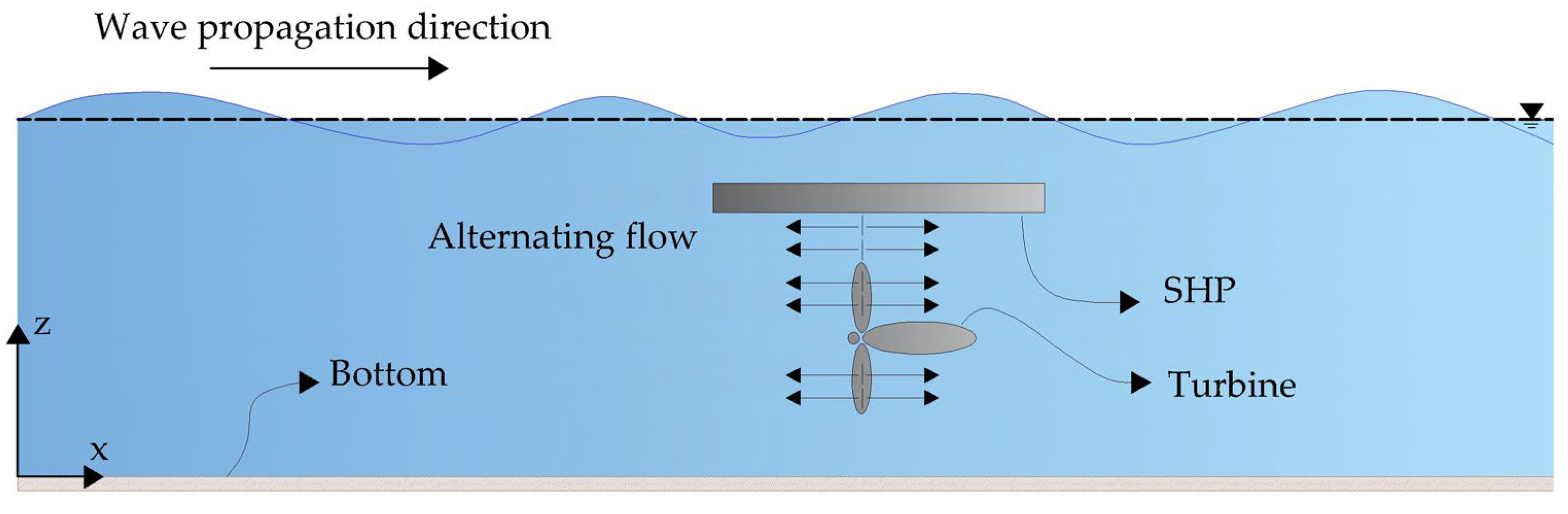
2.6. Parameters of Interest
3. Results and Discussion
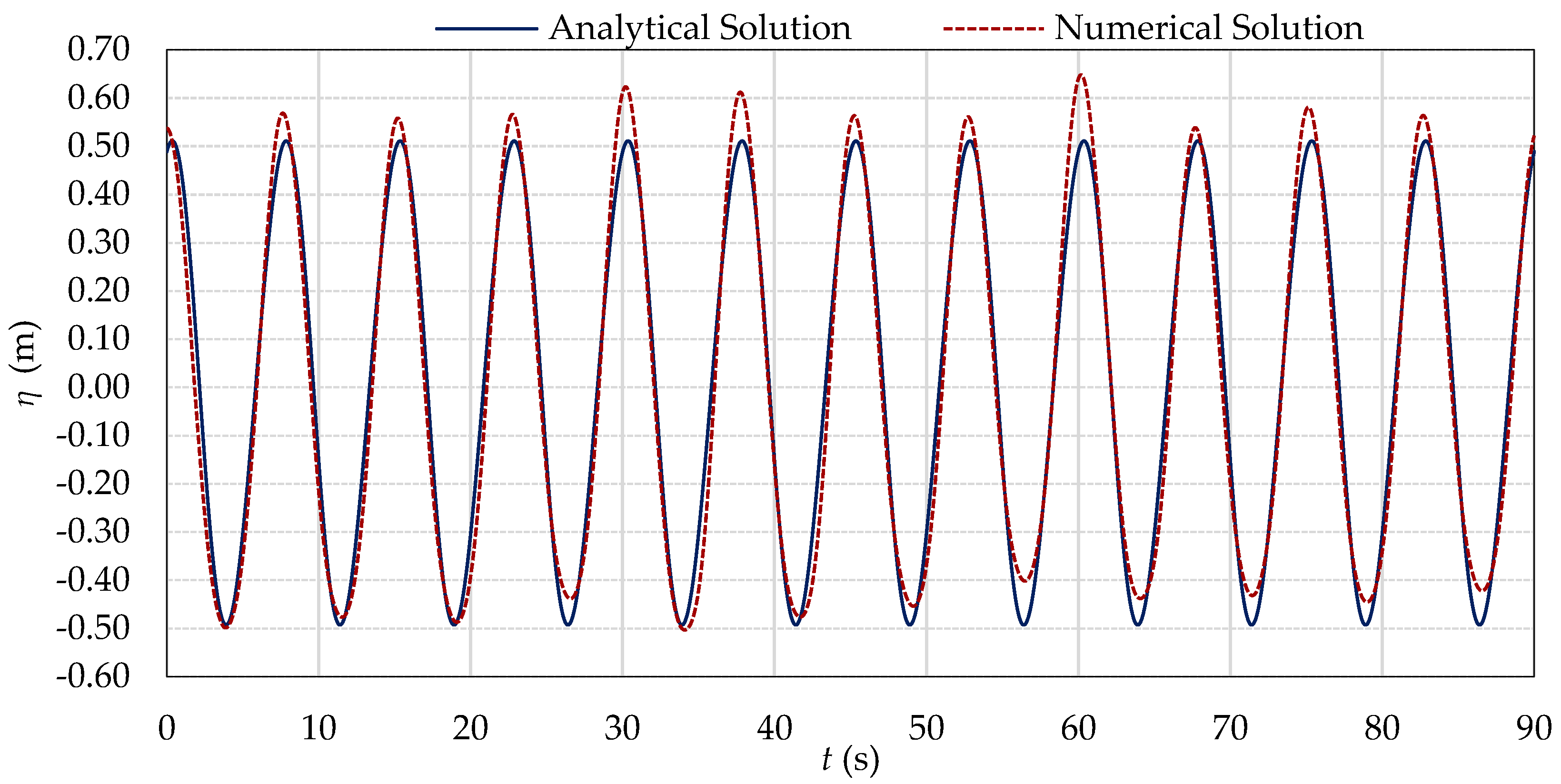
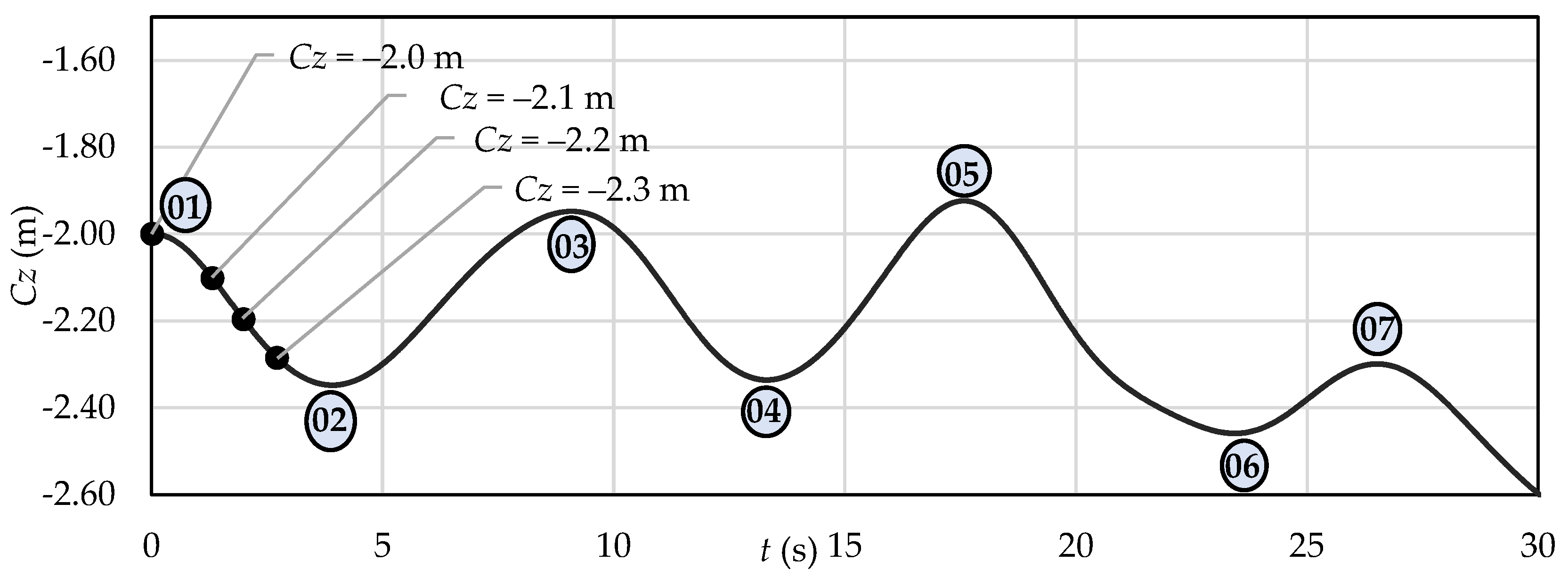
3.1. Verification of the Numerical Model
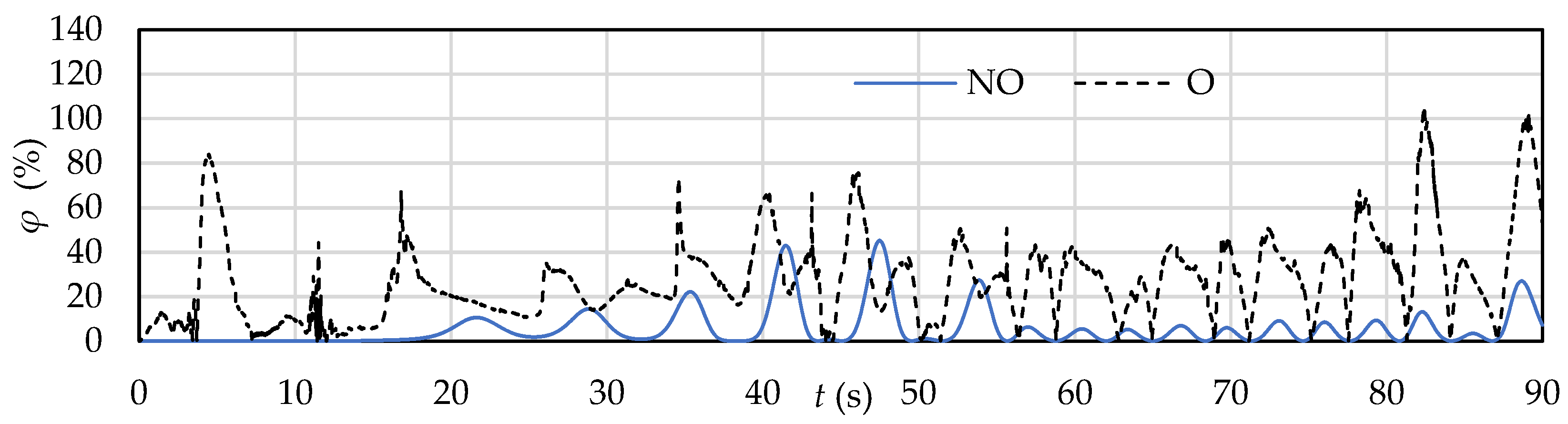
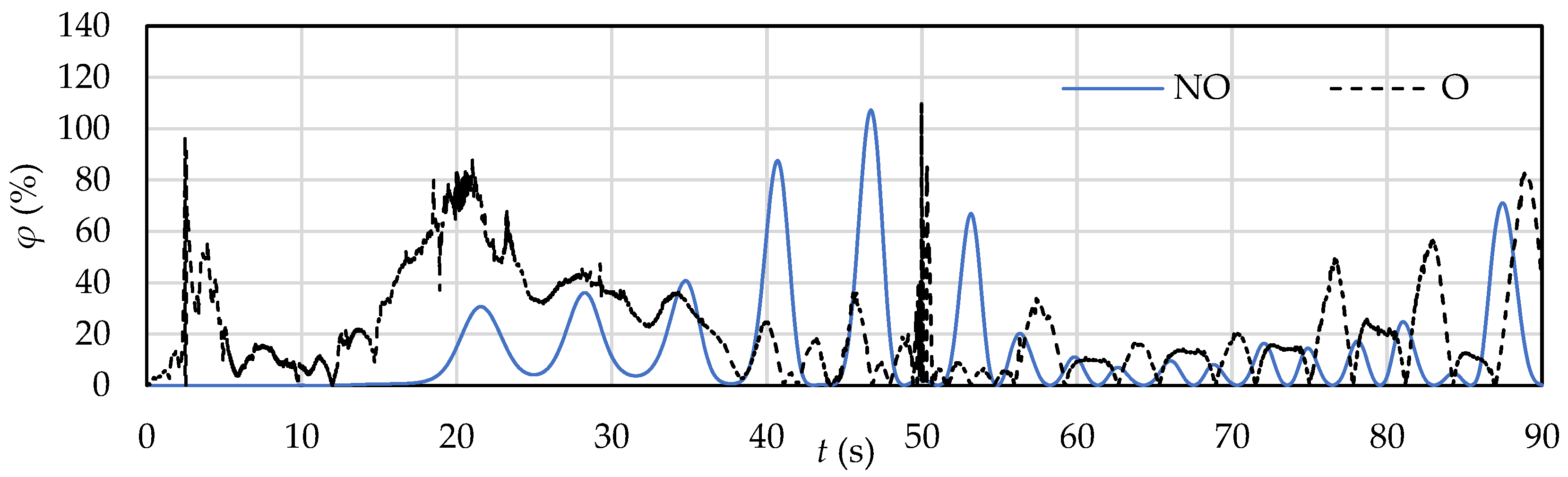
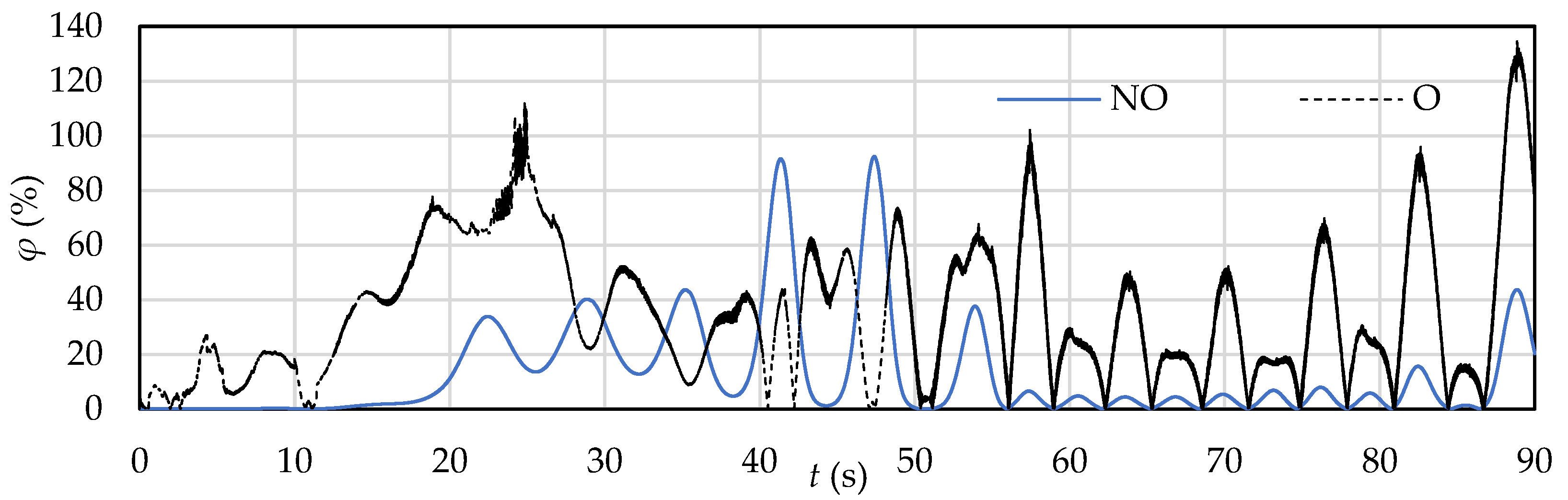
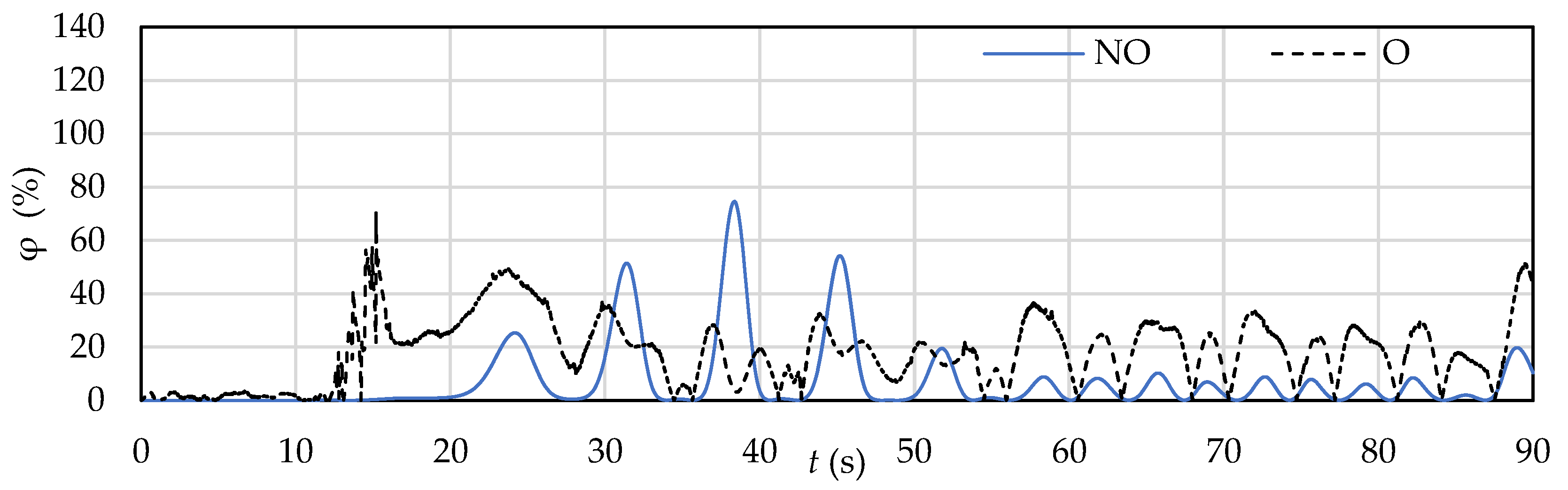
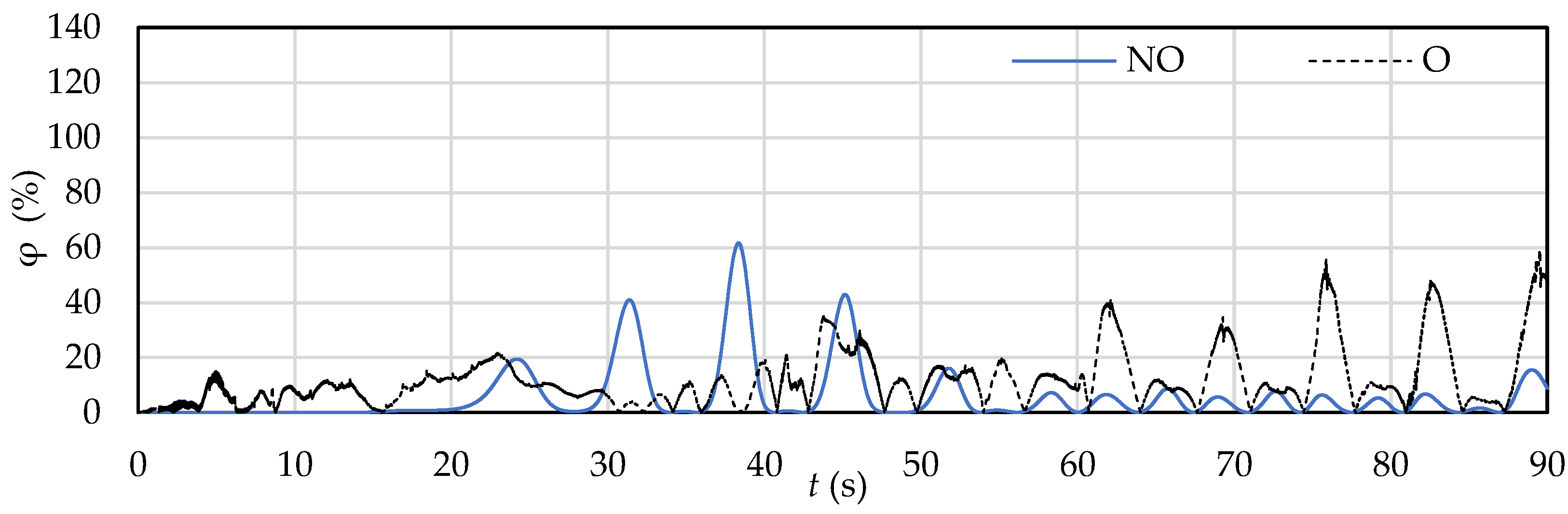
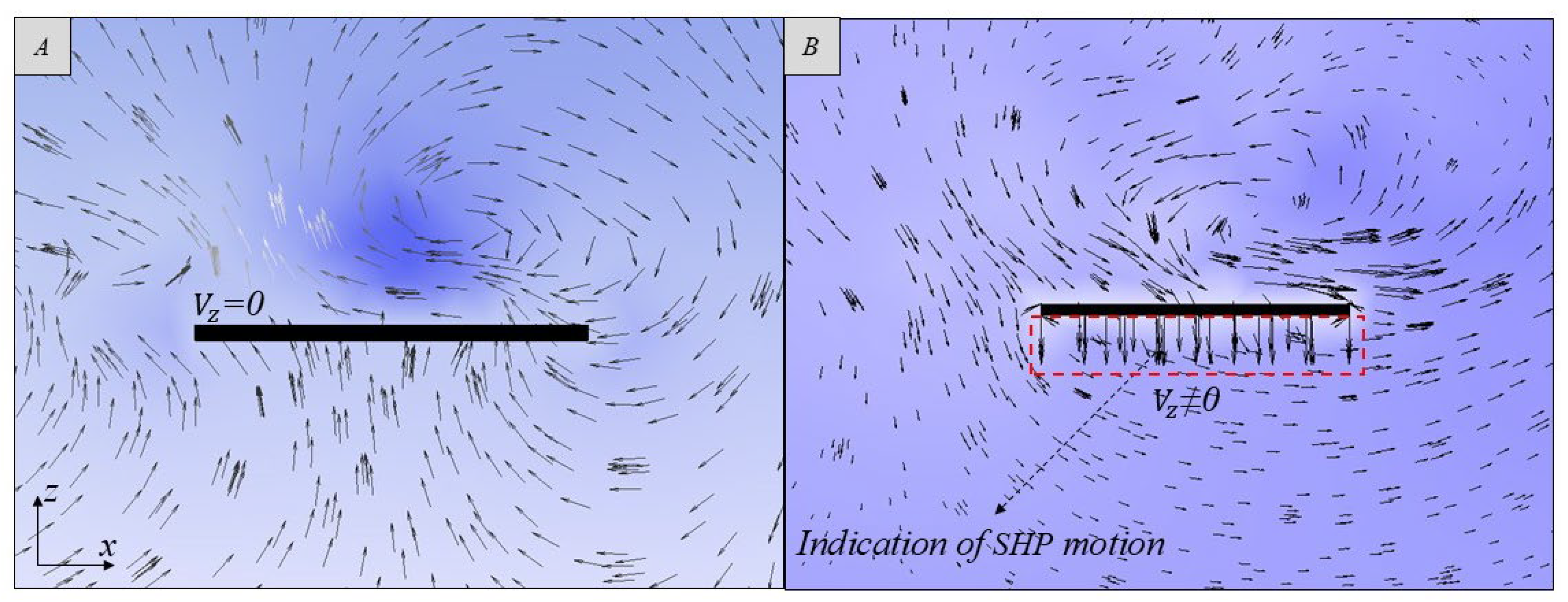
3.2. Evaluation of the Efficiency of the SHP Device in Non-Oscillating and Oscillating Modes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Code UDF #include “udf.h” DEFINE_SDOF_PROPERTIES (stage, prop, dt, time, dtime) { // Define the mass of the rigid body prop[SDOF_MASS] = Mass; // Defining the SHP mass // Define moments of inertia as zero prop[SDOF_IXX] = 0; // Moment of Inertia about the X-axis (zero) prop[SDOF_IYY] = 0; // Moment of Inertia about the Y-axis (zero) prop[SDOF_IZZ] = 0; // Moment of Inertia about the Z-axis (zero) // Define the acting loads as needed prop[SDOF_LOAD_F_Z] = load; // Z-axis force // Displacement constraints prop[SDOF_ZERO_TRANS_X] = TRUE; // Movement restricted along the X-axis prop[SDOF_ZERO_TRANS_Y] = TRUE; // Movement restricted along the Y-axis prop[SDOF_ZERO_TRANS_Z] = FALSE; // Allows movement in the Z direction // Rotation restrictions prop[SDOF_ZERO_ROT_X] = TRUE; // Rotation restricted around X-axis prop[SDOF_ZERO_ROT_Y] = TRUE; // Rotation restricted around Y-axis prop[SDOF_ZERO_ROT_Z] = TRUE; // Rotation restricted around Z-axis } |
References
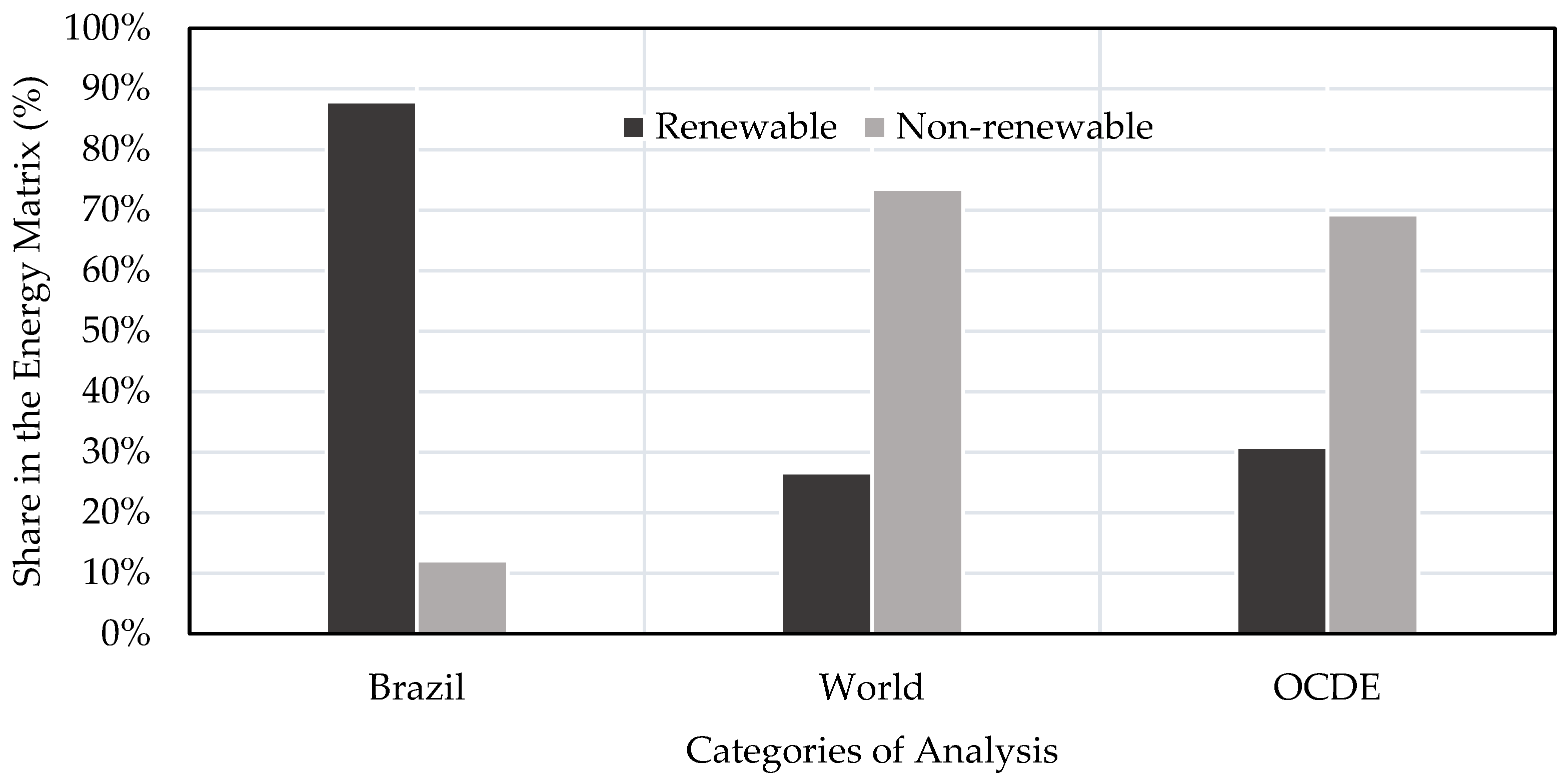
- Corrales-gonzalez, M.; Lavidas, G.; Besio, G. Feasibility of Wave Energy Harvesting in the Ligurian Sea, Italy. Sustainability 2023, 15, 9113. [Google Scholar] [CrossRef]
- International Energy Agency (IEA); International Renewable Energy Agency (IRENA); United Nations Statistics Division (UNSD); World Bank; World Health Organization (WHO). Tracking SDG 7: The Energy Progress Report; World Bank: Washington, DC, USA, 2023. [Google Scholar]
- EPE—Energy Research Company. Summary Report of the National Energy Balance 2023: Base Year 2022. Rio de Janeiro. 2022. Available online: https://www.epe.gov.br/sites-pt/publicacoes-dados-abertos/publicacoes/PublicacoesArquivos/publicacao-748/topico-681/BEN_S%C3%ADntese_2023_PT.pdf (accessed on 5 January 2023).
- International Energy Agency—IEA. Implementing agreement on ocean energy systems (IEA-OES). In Annual Report; IEA: Paris, France, 2012. [Google Scholar]
- Jusoh, M.A.; Ibrahim, M.Z.; Daud, M.Z.; Albani, A.; Mohd Yusop, Z. Hydraulic power take-off concepts for wave energy conversion system: A review. Energies 2019, 12, 4510. [Google Scholar] [CrossRef]
- IBGE—Brazilian Institute of Geography and Statistics. Geographic Data. 2021. Available online: https://www.ibge.gov.br/geociencias/organizacao-do-territorio/estrutura-territorial/34330-municipios-costeiros.html (accessed on 22 January 2024).
- IBGE—Brazilian Institute of Geography and Statistics. Territorial Structures. 2021. Available online: https://agenciadenoticias.ibge.gov.br/agencia-noticias/2012-agencia-de-noticias/noticias/31090-ibge-atualiza-municipios-de-fronteira-e-defrontantes-com-o-mar-devido-a-mudancas-de-limites (accessed on 13 August 2023).
- Bastos, A.S.; Souza, T.R.C.D.; Ribeiro, D.S.; Melo, M.D.L.N.M.; Martinez, C.B. Wave Energy Generation in Brazil: A Georeferenced Oscillating Water Column Inventory. Energies 2023, 16, 3409. [Google Scholar] [CrossRef]
- Falcão, A.F.O. Wave energy utilization: A review of the Technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Sheng, W. Wave energy conversion and hydrodynamics modelling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Gayathri, R.; Chang, J.Y.; Tsai, C.C.; Hsu, T.W. Wave Energy Conversion through Oscillating Water Columns: A Review. J. Mar. Sci. Eng. 2024, 12, 342. [Google Scholar] [CrossRef]
- Straub, J. In search of technology readiness level (TRL) 10. Aerosp. Sci. Technol. 2015, 46, 312–320. [Google Scholar] [CrossRef]
- Seibt, F.M.; de Camargo, F.V.; dos Santos, E.D.; Gomes, M.N.; Rocha, L.A.O.; Isoldi, L.A.; Fragassa, C. Numerical evaluation on the efficiency of the submerged horizontal plate type wave energy converter. FME Trans. 2019, 47, 543–551. [Google Scholar] [CrossRef]
- Tian, X.; Wang, Q.; Liu, G.; Deng, W.; Gao, Z. Numerical and experimental studies on a three-dimensional numerical wave tank. IEEE Access 2018, 6, 6585–6593. [Google Scholar] [CrossRef]
- Yu, J.; Yao, C.; Liu, L.; Dong, G.; Zhang, Z. Numerical study on wave-structure interaction based on functional decomposition method. Ocean Eng. 2022, 266, 113067. [Google Scholar] [CrossRef]
- Mackay, E.; Johanning, L. Comparison of analytical and numerical solutions for wave interaction with a vertical porous barrier. Ocean Eng. 2020, 199, 107032. [Google Scholar] [CrossRef]
- Oliveira, D.; de Almeida, J.L.; Santiago, A.; Rigueiro, C. Development of a CFD-based numerical wave tank of a novel multipurpose wave energy converter. Renew. Energy 2022, 199, 226–245. [Google Scholar] [CrossRef]
- Orer, G.; Ozdamar, A. An experimental study on the efficiency of the submerged plate wave energy converter. Renew. Energy 2007, 32, 1317–1327. [Google Scholar] [CrossRef]
- Goulart, M.M.; Martins, J.C.; Gomes, A.P.; Puhl, E.; Rocha, L.A.O.; Isoldi, L.A.; dos Santos, E.D. Experimental and numerical analysis of the geometry of a laboratory-scale overtopping wave energy converter using constructal design. Renew. Energy 2024, 236, 121497. [Google Scholar] [CrossRef]
- Lin, Z.; Qian, L.; Bai, W.; Ma, Z.; Chen, H.; Zhou, J.G.; Gu, H. A finite volume based fully nonlinear potential flow model for water wave problems. Appl. Ocean Res. 2021, 106, 102445. [Google Scholar] [CrossRef]
- Bihs, H.; Kamath, A.; Chella, M.A.; Aggarwal, A.; Arntsen, Ø.A. A new level set numerical wave tank with improved density interpolation for complex wave hydrodynamics. Comput. Fluids 2016, 140, 191–208. [Google Scholar] [CrossRef]
- Tutar, M.; Mendi, M. A performance study of a horizontal-axis micro-turbine in a numerical wave flume. Energy Procedia 2017, 112, 83–91. [Google Scholar] [CrossRef]
- Tang, H.J.; Huang, C.C.; Chen, W.M. Dynamics of dual pontoon floating structure for cage aquaculture in a two-dimensional numerical wave tank. J. Fluids Struct. 2011, 27, 918–936. [Google Scholar] [CrossRef]
- Dong, J.; Xue, L.; Cheng, K.; Shi, J.; Zhang, C. An experimental investigation of wave forces on a submerged horizontal plate over a simple slope. J. Mar. Sci. Eng. 2020, 8, 507. [Google Scholar] [CrossRef]
- Cummins, C.P.; Scarlett, G.T.; Windt, C. Numerical analysis of wave–structure interaction of regular waves with surface-piercing inclined plates. J. Ocean Eng. Mar. Energy 2022, 8, 99–115. [Google Scholar] [CrossRef]
- Seibt, F.M.; dos Santos, E.D.; Isoldi, L.A.; Rocha, L.A.O. Constructal Design on full-scale numerical model of a submerged horizontal plate-type wave energy converter. Mar. Syst. Ocean Technol. 2023, 18, 1–13. [Google Scholar] [CrossRef]
- Motta, V.E.; Thum, G.Ü.; Gonçalves, R.A.A.C.; Rocha, L.A.O.; dos Santos, E.D.; Machado, B.N.; Isoldi, L.A. Numerical Study of Inclined Geometric Configurations of a Submerged Plate-Type Device as Breakwater and Wave Energy Converter in a Full-Scale Wave Channel. J. Exp. Theor. Anal. 2025, 3, 3. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 1991; Volume 2. [Google Scholar]
- Short, A.D.; Klein, A.H.d.F. (Eds.) Brazilian Beach Systems. Coast. Res. Libr. 2016, 17, 573–608. [Google Scholar]
- Araújo, J.D.P.; Miranda, J.M.; Pinto, A.M.F.R.; Campos, J.B.L.M. Wide-ranging survey on the laminar flow of individual Taylor bubbles rising through stagnant Newtonian liquids. Int. J. Multiph. Flow 2012, 43, 131–148. [Google Scholar] [CrossRef]
- Kashyap, P.V.; Duguet, Y.; Dauchot, O. Flow statistics in the transitional regime of plane channel flow. Entropy 2020, 22, 1001. [Google Scholar] [CrossRef]
- Sano, M.; Tamai, K. A universal transition to turbulence in channel flow. Nat. Phys. 2016, 12, 249–253. [Google Scholar] [CrossRef]
- Opoku, F.; Uddin, M.N.; Atkinson, M. A review of computational methods for studying oscillating water columns–the Navier-Stokes based equation approach. Renew. Sustain. Energy Rev. 2023, 174, 113124. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Garoosi, F.; Hooman, K. Numerical simulation of multiphase flows using an enhanced Volume-of-Fluid (VOF) method. Int. J. Mech. Sci. 2022, 215, 106956. [Google Scholar] [CrossRef]
- Garoosi, F.; Kantzas, A.; Irani, M. Numerical simulation of wave interaction with porous structure using the coupled Volume-Of-Fluid (VOF) and Darcy-Brinkman-Forchheimer model. Eng. Anal. Bound. Elem. 2024, 166, 105866. [Google Scholar] [CrossRef]
- Rafiee, A.; Dutykh, D.; Dias, F. Numerical simulation of wave impact on a rigid wall using a two–phase compressible SPH method. Procedia IUTAM 2015, 18, 123–137. [Google Scholar] [CrossRef]
- Srinivasan, V.; Salazar, A.J.; Saito, K. Modeling the disintegration of modulated liquid jets using volume-of-fluid (VOF) methodology. Appl. Math. Mod. 2011, 35, 3710–3730. [Google Scholar] [CrossRef]
- Horko, M. CFD Optimisation of an Oscillating Water Column Energy Converter. Master’s Thesis, The University of Western, Perth, Australia, 2007. [Google Scholar]
- Hübner, R.G.; Oleinik, P.H.; Marques, W.C.; Gomes, M.N.; dos Santos, E.D.; Machado, B.N.; Isoldi, L.A. Numerical Study Comparing the Incidence Influence Between Realistic Wave and Regular Wave Over an Overtopping Device. Rev. De Eng. Térmica 2019, 18, 46–49. [Google Scholar] [CrossRef]
- Lima, F.M.S. Using surface integrals for checking Archimedes’ law of buoyancy. Eur. J. Phys. 2011, 33, 101. [Google Scholar] [CrossRef]
- Machado, B.N.; Oleinik, P.H.; Kirinus, E.D.P.; Domingues Dos Santos, E.; Rocha, L.A.O.; Gomes, M.D.N.; Isoldi, L.A. WaveMIMO Methodology: Numerical Wave Generation of a Realistic Sea State. J. Appl. Comput. Mech. 2021, 7, 2129–2148. [Google Scholar]
- Carneiro, D.M. Sequência de Ensino Investigativo Através da Construção de um Túnel de Vento de Baixo Custo. Master’s Thesis, The Federal University of Western Pará, Belem, Brazil, 2020. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education: London, UK, 2007. [Google Scholar]
- Martins, J.; Goulart, M.; Gomes, M.D.N.; Souza, J.A.; Rocha, L.A.O.; Isoldi, L.; Dos Santos, E. Geometric evaluation of the main operational principle of an overtopping wave energy converter by means of Constructal Design. Renew. Energy 2018, 118, 727–741. [Google Scholar] [CrossRef]
- Coimbra, A.L.S.C.; Telles, W.R.; Ferreira, F.F.; Junior, J.L. Solução de um problema de transporte de contaminante em corpos hídricos utilizando o método dos volumes finitos. Rev. Cereus 2021, 13, 199–216. [Google Scholar]
- Hou, D.; Li, Q.M. Damage boundaries on shock response spectrum based on an elastic single-degree-of-freedom structural model. Int. J. Impact Eng. 2023, 173, 104435. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin, Germany, 1997; p. 423. [Google Scholar]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Zollanvari, A.; Dougherty, E.R. Moments and root-mean-square error of the Bayesian MMSE estimator of classification error in the Gaussian model. Pattern Recognit. 2014, 47, 2178–2192. [Google Scholar] [CrossRef]
- Asprone, D.; Auricchio, F.; Manfredi, G.; Prota, A.; Reali, A.; Sangalli, G. Particle methods for a 1 d elastic model problem: Error analysis and development of a second-order accurate formulation. Comput. Model. Eng. Sci. (CMES) 2010, 62, 1–21. [Google Scholar]
- Chen, G.; Wang, R. Triangular Mesh Surface Subdivision Based on Graph Neural Network. Appl. Sci. 2024, 14, 11378. [Google Scholar] [CrossRef]
- Rezaiee-pajand, M.; Yaghoobi, M. A robust triangular membrane element. Lat. Am. J. Solids Struct. 2014, 11, 2648–2671. [Google Scholar] [CrossRef]
- Moreira, P.A.V. Projeto de Produção de Tubo Elíptico em Aço Avançado de Elevada Resistência Para Uma Serra de Arco. Master’s Thesis, University of Minho, Braga, Portuguese, 2015. [Google Scholar]
- Graw, K.U. Wellenenergie—Eine Hydromechanische Analyse; Bericht Nr. 8, Lehrund Forschungsgebietes Wasserbau und Wasserwirtschaft; Institut fur Grundbau, Abfall- und Wasserwesen; Bergische Universitaet–Gesamthochschule Wuppertal: Berlin, Germany, 1995. [Google Scholar]
- Mccormick, M.E. Ocean Wave Energy Conversion; Dover Publications, Inc.: New York, NY, USA, 1981. [Google Scholar]
- Carter, R.W. Wave Energy Converters and a Submerged Horizontal Plate. Master’s Thesis, University of Hawai’i, Honolulu, HI, USA, 2005. [Google Scholar]
- DizadjI, N.; Sajadian, S.E. Modeling and optimization of the chamber of OWC system. Energy 2011, 36, 2360–2366. [Google Scholar] [CrossRef]
- Mocellin, A.P.G.; da Silveira Paiva, M.; dos Santos, E.D.; Rocha, L.A.O.; Isoldi, L.A.; Ziebell, J.S.; Machado, B.N. Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Device Using Representative Regular Waves of the Sea State Found in Tramandaí, Brazil. Processes 2024, 12, 2352. [Google Scholar] [CrossRef]
- Brito, M.; Ferreira, R.M.; Teixeira, L.; Neves, M.G.; Gil, L. Experimental investigation of the flow field in the vicinity of an oscillating wave surge converter. J. Mar. Sci. Eng. 2020, 8, 976. [Google Scholar] [CrossRef]
- Fleming, A.; Penesis, I.; Macfarlane, G.; Bose, N.; Denniss, T. Energy balance analysis for an oscillating water column wave energy converter. Ocean Eng. 2012, 54, 26–33. [Google Scholar] [CrossRef]








| Parameters | Input Data | |
|---|---|---|
| Solution | Pressure Based | |
| Pressure–velocity Coupling | PISO | |
| Spatial Discretization | Gradient Evaluation | Least Squares Cell Based |
| Pressure | PRESTO | |
| Momentum | First Order Upwind | |
| Volume fraction | Geo-Reconstruct | |
| Temporal Differencing Scheme | First Order Implicit | |
| Flow regime | Laminar | |
| Under-Relaxation Factors | Pressure | 0.3 |
| Momentum | 0.7 | |
| Residual | Continuity | 10−6 |
| x-velocity | ||
| z-velocity | ||
| Open channel initialization method | Wave |
| Element Quality | |
|---|---|
| 1 | Degenerate |
| 0.90 < < 1.00 | Poor |
| 0.75 < ≤ 0.90 | Weak |
| 0.50 < ≤ 0.75 | Acceptable |
| 0.25 < ≤ 0.5 | Good |
| 0.00 < ≤ 0.25 | Excellent |
| 0.00 | Equilateral |
| Element Quality | Categority | Number of Elements | |
|---|---|---|---|
| 1.00 | Degenerate | – | – |
| 0.90 < < 1.00 | Poor | – | – |
| 0.75 < ≤ 0.90 | Weak | J | 95.00 |
| 0.50 < ≤ 0.75 | Acceptable | G/H/I | 22,003.00 |
| 0.25 < ≤ 0.5 | Good | D/E/F | 332,000.00 |
| 0.00 < ≤ 0.25 | Excellent | A/B/C | 453,950.00 |
| 0.00 | Equilateral | – | – |
| Error | Values (m) | ||||
|---|---|---|---|---|---|
| 0 to 90 s | 20 to 40 s | 40 to 60 s | 60 to 80 s | 80 to 90 s | |
| MAE | 0.0467 | 0.0507 | 0.0472 | 0.0439 | 0.0405 |
| RMSE | 0.0575 | 0.0626 | 0.0595 | 0.0532 | 0.0456 |
| Difference of infinity norms | 0.1371 | 0.1122 | 0.1290 | 0.1371 | 0.0526 |
| Numerical errors RMS | 0.0575 | 0.0626 | 0.0595 | 0.0532 | 0.0456 |
| Caso | (m) | H (m) | L (m) | B (m) | e (m) |
|---|---|---|---|---|---|
| 1 | 60.4 | 10.0 | 8.0 | 0.32 | |
| 2 | 10.0 | 8.0 | 0.16 | ||
| 3 | 8.0 | 8.0 | 0.32 | ||
| 4 | 8.0 | 8.0 | 0.16 | ||
| 5 | 70.4 | 1.0 | 12.0 | 8.0 | 0.32 |
| 6 | 12.0 | 8.0 | 0.16 | ||
| 7 | 70.4 | 1.5 | 8.0 | 12.0 | 0.32 |
| Case | NO | O | ||
|---|---|---|---|---|
| 1 | 7741.68 | 42,923.05 | 7741.68 | 212,760.59 |
| 2 | 7741.68 | 95,790.61 | 7741.68 | 175,569.85 |
| 3 | 7741.68 | 73,423.44 | 7741.68 | 144,999.09 |
| 4 | 2385.13 | 29,986.57 | 2385.13 | 85,118.55 |
| 5 | 9556.36 | 66,288.80 | 9556.36 | 172,909.44 |
| 6 | 9556.36 | 53,274.93 | 9556.36 | 112,288.62 |
| 7 | 21,561.24 | 147,343.50 | 21,561.24 | 123,825.84 |
| Case | ||||
|---|---|---|---|---|
| 1 | 1.61 | 7.82 | 5.54 | 27.48 |
| 2 | 7.66 | 7.53 | 12.37 | 22.67 |
| 3 | 6.95 | 6.38 | 9.48 | 18.73 |
| 4 | 4.90 | 6.90 | 12.57 | 35.68 |
| 5 | 6.21 | 7.32 | 6.94 | 18.09 |
| 6 | 5.74 | 6.48 | 5.57 | 11.75 |
| 7 | 8.34 | 6.13 | 6.83 | 5.74 |
| Case | ||
|---|---|---|
| 1 | 4.72 | 23.66 |
| 2 | 23.21 | 21.87 |
| 3 | 21.26 | 21.43 |
| 4 | 14.66 | 88.09 |
| 5 | 22.03 | 22.86 |
| 6 | 20.64 | 18.86 |
| 7 | 28.94 | 21.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batista, R.C.; Oliveira, M.R.d.; Santos, E.D.d.; Rocha, L.A.O.; Isoldi, L.A.; Gomes, M.d.N. Numerical Analysis of Submerged Horizontal Plate Wave Energy Converter Device Considering Float Effects. Fluids 2025, 10, 136. https://doi.org/10.3390/fluids10050136
Batista RC, Oliveira MRd, Santos EDd, Rocha LAO, Isoldi LA, Gomes MdN. Numerical Analysis of Submerged Horizontal Plate Wave Energy Converter Device Considering Float Effects. Fluids. 2025; 10(5):136. https://doi.org/10.3390/fluids10050136
Chicago/Turabian StyleBatista, Rodrigo Costa, Marla Rodrigues de Oliveira, Elizaldo Domingues dos Santos, Luiz Alberto Oliveira Rocha, Liércio André Isoldi, and Mateus das Neves Gomes. 2025. "Numerical Analysis of Submerged Horizontal Plate Wave Energy Converter Device Considering Float Effects" Fluids 10, no. 5: 136. https://doi.org/10.3390/fluids10050136
APA StyleBatista, R. C., Oliveira, M. R. d., Santos, E. D. d., Rocha, L. A. O., Isoldi, L. A., & Gomes, M. d. N. (2025). Numerical Analysis of Submerged Horizontal Plate Wave Energy Converter Device Considering Float Effects. Fluids, 10(5), 136. https://doi.org/10.3390/fluids10050136










