Recent Developments in the Immersed Boundary Method for Complex Fluid–Structure Interactions: A Review

Abstract

The “immersed boundary method (IBM)” is considered to be the most efficacious and versatile technique to solve flow problems associated with intricate geometries. The first part of this review examines recent advancements in IBM, essential for the simulation of “fluid–structure interactions (FSIs)” in sophisticated systems. This review highlights significant developments in turbulence modeling, adaptive mesh refinement, and complex geometric simulations, demonstrating IB methods’ capacity to seamlessly integrate arbitrary geometries into structured computational grids while preserving computational efficiency. Various IB techniques are analyzed for enforcing boundary conditions on dynamic immersed boundaries, with notable breakthroughs in managing velocity discontinuities, spurious oscillations, and large-scale deformations. Recent findings illustrate the versatility of IB methods, with applications encompassing biological fluid dynamics, turbulent multiphase flows, and cavitating flows. These innovations not only enhance computational performance but also address evolving challenges across engineering and scientific fields, establishing IB methods as a robust tool for resolving complex, multidisciplinary problems with high accuracy and efficiency.

1. Introduction

“Fluid–structure interactions (FSIs)” are vital in many technological fields, namely aerospace, biomedical, civil, ocean, and energy engineering. They play a key role in understanding complex processes like the aerodynamic behavior of aircraft, the performance of wind turbine blades, and the movement of biological fluids, such as the operation of synthetic heart valves and blood flow in blood vessels. FSIs are also critical for tackling issues related to the dynamic response of structures like bridges and skyscrapers to wind forces, as well as the interactions occurring within wind farms.

The “immersed boundary method (IBM)” offers a different technique for handling FSI problems that involves complicated geometries and large, unpredictable deformations. Initially developed by Peskin [1] to model the flow of blood in the heart, the immersed boundary (IB) approach solves the Navier–Stokes (N-S) equations based on a static background grid, which can take various forms such as unstructured, cartesian, or curvilinear. The fluid–structure boundary is depicted by separate surface meshes, and its impact on the flow is explained in different IB formulations, either by locally altering the background grid or by adding artificial forces to governing equations. In contrast, with “arbitrary Lagrangian–Eulerian (ALE) methods”, IB techniques offer two key advantages: (1) quick mesh generation without needing to align the mesh with the fluid–structure boundary, which may have a highly intricate shape or undergo sizable deformations, and (2) the ability to handle high-performance flow solvers to resolve the governing equations on a fixed mesh.

Over the past two decades, numerous reviews have examined IBM, each offering valuable insights into different aspects of the field. Notably, Iaccarino and Verzicco [2] reviewed the use of IB techniques in turbulent flow simulations, highlighting their ability to handle complex geometries in turbulence modeling. Mittal and Iaccarino [3] provided a comprehensive overview of IB methods, focusing on their evolution and application to fluid dynamics, particularly in cases involving moving or deforming boundaries. Sotiropoulos and Yang [4] emphasized the use of IB methods in FSI, with a special focus on aerospace applications and the challenges of accurately modeling interactions between fluids and flexible structures. Kim and Choi [5] offered a detailed review of advances in IB methods for FSI, covering a wide range of applications, from biological systems to engineering solutions. The book by Roy et al. [6] served as an in-depth resource on IB methods, exploring their theoretical foundations, numerical techniques, and diverse applications in fields like engineering and biology. Griffith and Patankar [7] discussed the latest developments in IB methods for FSI, emphasizing improvements in computational efficiency and their application in both biological and engineering contexts. In their work, Mittal and Bhardwaj [8] delve into the use of IB methods for thermo-fluid problems, with a particular focus on heat transfer and fluid dynamics simulations. Recently, Verzicco [9] provided a historical perspective on IB methods, tracing their development and offering insights into future directions, with a special emphasis on advancing computational techniques and expanding their use in complex fluid dynamics.

One of the key gaps identified in the literature is the limited focus on recent developments in immersed boundary methods (IBMs) beyond 2020. While several reviews have provided comprehensive insights into various aspects of IBM, the rapid advancements in computational techniques, numerical solvers, and turbulence modeling necessitate a more up-to-date analysis of the field. In the present review, a total of 131 articles post 2020 are analyzed. While our focus is on the post-2020 literature, a discussion on earlier works remains essential for contextualizing these developments within the broader evolution of the field. The foundational contributions to IBM, particularly in turbulence modeling and fluid–structure interactions, have shaped current methodologies and computational frameworks. Furthermore, earlier research provides a benchmark for assessing improvements in numerical accuracy, computational efficiency, and boundary condition enforcement. The challenges identified in pre-2020 studies, such as instability in IBM formulations for highly turbulent flows and difficulties in capturing thin boundary layers, directly inform the motivations behind more recent algorithmic enhancements.

A critical aspect of IBM is its interplay with turbulence modeling, where different flow solvers such as Reynolds-Averaged Navier–Stokes (RANS), Large Eddy Simulation (LES), and Direct Numerical Simulation (DNS) play a crucial role in formulating boundary conditions and accurately resolving flow structures. The integration of IBM with these solvers requires advancements in numerical schemes to ensure stability, accuracy, and computational feasibility, particularly in high-Reynolds-number flows and multi-physics scenarios. Moreover, despite the increasing adoption of IBM in engineering and biomedical applications, challenges remain in improving the stability and accuracy of immersed boundary formulations for highly deformable structures and complex geometries. Thus, it is important to understand how IBM has evolved and where further advancements are still needed for next-generation simulations in fluid dynamics, biomechanics, and aerodynamics.

In this current review, we build on these foundational works by examining the latest trends and applications of IB methods. Our focus includes key areas such as turbulence modeling and complex geometries. The current review provides a multidisciplinary perspective, offering cutting-edge insights and techniques relevant to each of these fields. It bridges gaps between fluid dynamics, computational methods, and real-world applications, enabling professionals from diverse domains to leverage IB methods in their work.

2. Overview of Numerical Framework

A simple overview of the implementation of the IBM is provided. The equations governing the fluid are given by the Navier–Stokes (N-S) Equation (1) and Continuity Equation (2).

$$\rho \left({\displaystyle \frac{\partial \mathit{u}}{\partial t}}+\left(\mathit{u}·\mathbf{\nabla }\mathit{u}\right)\right)=-\nabla p+\mu {\mathbf{\nabla }}^2\mathit{u}+\mathit{f}$$

(1)

$$\mathbf{\nabla }·\mathit{u}=0$$

(2)

where

u (x, t) is the fluid velocity (m/s) at position x (m) and time t (s). p (x, t) is the pressure in Pa, $\rho$ is the density in (kg/m³), $\mu$ is the dynamic viscosity in (Pa·s), and f (x, t) is the body force per unit volume, which represents the presence of the immersed structure in (N/m³).

The immersed structure is often represented as a set of discrete points, typically denoted as X (s, t), where s is the Lagrangian coordinate of the structure. The motion of these points is governed by Newton’s Laws of Motion Equation (3),

$${\rho }_s{\displaystyle \frac{{\partial }^2\mathit{X}}{\partial t^2}}={\mathit{F}}_{\mathit{s}}+{\mathit{F}}_{\mathit{e}}$$

(3)

where

the structural density is given by ${\rho }_s$ in (kg/m³), F_s is the restoring elastic force of the structure in (N), and F_e is the external forces including the fluid force acting on the structure in (N).

The fluid–structure interactions are enforced by velocity interpolation (Equation (4)) and force distribution (Equation (5)).

$$\mathit{U}\left(\mathit{s},\mathit{t}\right)=\int \mathit{u}\left(\mathit{x},t\right)\delta \left(\mathit{x}-\mathit{X}\left(\mathit{s},t\right)\right)\mathit{d}\mathit{x}$$

(4)

$$\mathit{f}\left(\mathit{x},t\right)=\int \mathit{F}\left(\mathit{s},t\right)\delta \left(\mathit{x}-\mathit{X}\left(\mathit{s},t\right)\right)\mathit{d}\mathit{s}$$

(5)

where

U (s, t) is the Lagrangian velocity in (m/s) and F (s, t) is the structural force in (N).

The force distribution and velocity interpolation are carried out using the Dirac delta function $\delta$. In the IB method, the structure is modeled using a Lagrangian mesh and the fluid with an Eulerian mesh. The N-S equations are solved on a uniform Cartesian grid using finite difference, finite volume, or spectral methods. The IB method is executed in a time-stepping framework. The fluid velocity and pressure are advanced in time using the N-S equations. The structural forces are determined, and the position of the IB is updated. Coupling is enforced by computing the interaction forces (f) and velocity interpolation (U) between the fluid and structure.

3. Application

3.1. Turbulence Modeling

Initially developed to focus on fluid flow around complex geometries without requiring body-fitted meshes, IBM has since been felicitous for a wide range of applications. The method’s adaptability lies in its ability to efficiently handle moving and deformable boundaries within a fluid domain, making it ideal for capturing the convoluted interactions that occur in turbulent flows. In turbulence, where the flow is often chaotic and multiscale in nature, it presents a significant computational challenge. IBM provides a robust framework for incorporating complex boundary conditions while maintaining accuracy. It is important to understand how fluid solvers impact IBM formulations in turbulence modeling.

Table 1. Recent application of fluid solvers in IBM formulations pertaining to turbulent and high-speed flow scenarios.

Authors and Reference	Fluid Solver	IBM Methodology	Description	Application Area	Year
Choi et al. [10]	RANS (METIS)	Level-set IBM with power-law wall model	High-order schemes for 3D incompressible flows	High-Re turbulent flows	2007
De Tullio et al. [11]	RANS	Sharp-interface IBM with AMR	Local mesh refinement for compressible flows	Compressible steady flow past an NACA-0012 airfoil	2007
Ghosh et al. [12]	Hybrid LES/RANS	Perforated surface IBM	Shock–BL interaction with bleed modeling	Supersonic flows (Mach 2.5)	2010
Capizzano [13]	RANS	Two-layer wall-modeled IBM	Enhanced near-wall turbulence modeling	High-Re wall-bounded flows	2011
Bai et al. [14]	LES	Basic IBM-FVM coupling	Free surface MCT simulations	Marine turbines	2014
Specklin and Delauré [15]	OpenFOAM Hybrid LES/RANS	Penalization-based sharp IB	Verified with Wannier flow	Complex moving geometries	2018
Tamaki and Imamura [16]	RANS (METIS)	Wall-function IBM	Transonic turbulent flow solver	High-angle separation	2018
Xu et al. [17]	LBM	Adaptive-refinement IB-LBM	Geometry-adaptive grids	Wide-Re range flows	2018
Specklin et al. [18]	OpenFOAM (PIMPLE) + LBM	FSI-IBM coupling	Rag motion in rotating flows	Wastewater pumps	2019
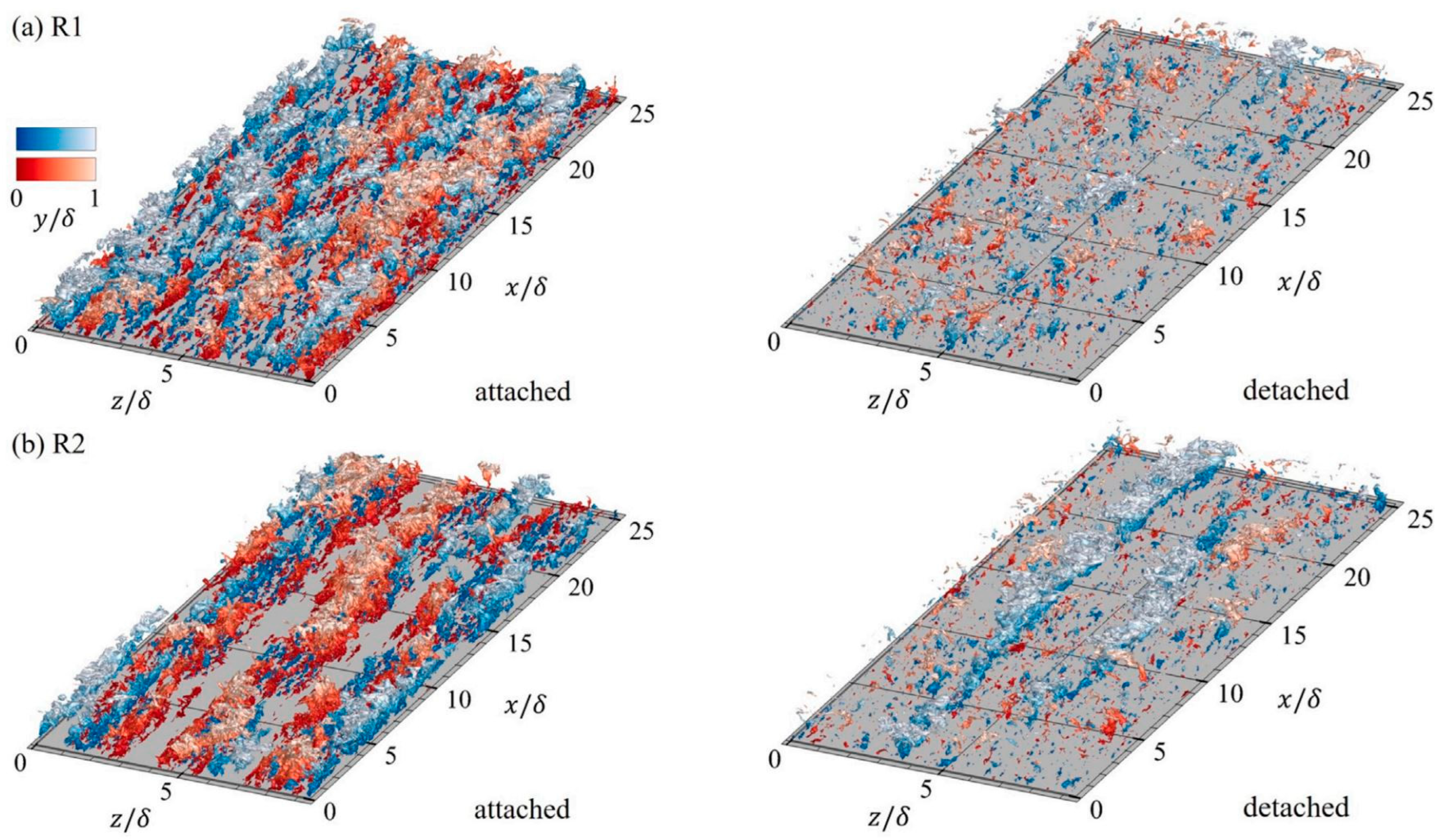
Yoon et al. [19]	DNS	Wall-attached structure analysis	Classified turbulent structures in boundary layers	Turbulent boundary layers	2020
Wiersema et al. [20]	WRF Model	LES-IBM coupling	Enhanced urban terrain simulations	Weather forecasting	2020
Arthur et al. [21]	WRF Model	Velocity reconstruction IBM	Evaluated IB implementations in WRF	Atmospheric flows	2020
Wang et al. [22]	DNS	Wave–turbulence interaction	Studied energy transfer mechanisms	Surface wave flows	2020
Zhou et al. [23]	DNS	Lagrangian particle tracking	Investigated particle-laden flows	Channel turbulence	2020
Agarwal et al. [24]	LBM	IB-LBM with LES	Simulated flow past square cylinder	Turbulent duct flows	2020
Ma et al. [25]	DNS	Rough wall modeling	Examined roughness effects	Turbulent rough walls	2020
Hwang et al. [26]	DNS	Attached-eddy hypothesis	Analyzed TNTI structures	Wall turbulence	2020
Yang et al. [27]	DNS	TNTI analysis	Studied adverse pressure gradients	Boundary layers	2020
Wang et al. [28]	OpenFOAM (rhoCentralFoam)	Sharp-interface IBM	High-speed compressible flows	Hypersonic	2020
Zhang et al. [29]	Adaptive Tsinghua Turbulence Laboratory Large Eddy Simulation (ATTLES)	Weighted least square IBM	Hypersonic flow discontinuities	Shock waves	2020
Tsvetkova et al. [30]	Navier–Stokes system with Brinkman penalty	Topology-free IBM	Unstructured mesh adaptation	Moving bodies	2020
Onishi and Tsubokura [31]	LES	Ghost-cell TF-IBM	“Dirty” CAD geometry handling	Industrial flows	2021
Tamaki and Imamura [32]	Roe’s approximate Riemann solver	Dimension-by-dimension reconstruction	Quadrature modified flux	NACA Airfoil	2018
Chen et al. [33]	URANS	Tamaki wall–model IBM	Rotor/stator interactions	Turbomachinery	2021
Liao and Yang [34]	Newton-Krylov	CURVIB method	Near-wall turbulence prediction	Curvilinear flows	2021
Cai et al. [35]	SA-fv3	Wall–model coupling	High-Re modifications	Cartesian grids	2021
Ma et al. [36]	LES	Hybrid IBM–wall model	High-Re turbulent flows	Wall-bounded flows	2021
Xu and Liu [37]	RANS	y+-adaptive IBM	Smooth wall shear stress	Complex geometries	2021
Wang and Gorlé [38]	LES	Direct forcing IBM	Atmospheric boundary layer	Wake dynamics	2024
Kang et al. [39]	DNS	Many-core optimization	Intel Xeon Phi implementation	High-performance CFD	2021
Choung et al. [40]	Euler Equation solver	NWIBM	Nonlinear weighting process	Compressible flows	2021
Constant et al. [41]	RANS	Improved Cartesian IBM	Spurious oscillation reduction	Turbulent flows	2021
Wang et al. [42]	LES	Wavy boundary analysis	Wall-attached structures	Traveling waves	2021
Bale et al. [43]	Second-order accurate pressure projection algorithm	MLS one-sided IBM	Simplified meshing approach	Fluid interactions	2021
Giannenas and Laizet [44]	DNS	Cubic spline IBM	Fixed/moving objects	Cartesian meshes	2021
Kubo et al. [45]	RANS (k-ω SST)	Level-set topology IBM	2D turbulent flow optimization	Aerodynamics	2021
Troldborg et al. [46]	RANS/DES	Tree skeleton IBM	Wind force prediction	Forest meteorology	2021
Kasbaoui et al. [47]	DNS	Semi-implicit MIBM	Swirling von Kármán flow	Vortex dynamics	2021
Cui et al. [48]	DNS	Particle tracking IBM	Fiber/disk alignment	Multiphase flows	2021
Sugaya et al. [49]	RANS/DDES-p	High-order scheme IBM	Moving Cartesian grids	Unsteady flows	2021
Lin et al. [50]	HLCC Riemann solver	Transient flow IBM	Solid rocket motors	Combustion chambers	2021
Cao and Huang [51]	Exact Riemann solver	Bayesian calibration IBM	Unscented Kalman filter for uncertainty analysis	Transonic buffeting	2021
Secchi et al. [52]	DNS	IBM vs. PFA comparison	Jet impingement on rough plates	Turbulent jets	2021
Atmani et al. [53]	LES	Hybrid IBM-LES	High-Re pipe flows on coarse grids	Wall-bounded turbulence	2021
Kang and Masud [54]	GMRES	Variational IBM	Weak boundary enforcement	Train aerodynamics	2021
Giannenas et al. [55]	InCompact3D	ADR-IBM with CAD/ALM	1D cubic spline reconstruction	Rotor aerodynamics	2021
Shallcross et al. [56]	Navier–Stokes system with Brinkman penalty	Characteristic-based penalization	Compressible Euler/NS equations	Hypersonic	2021
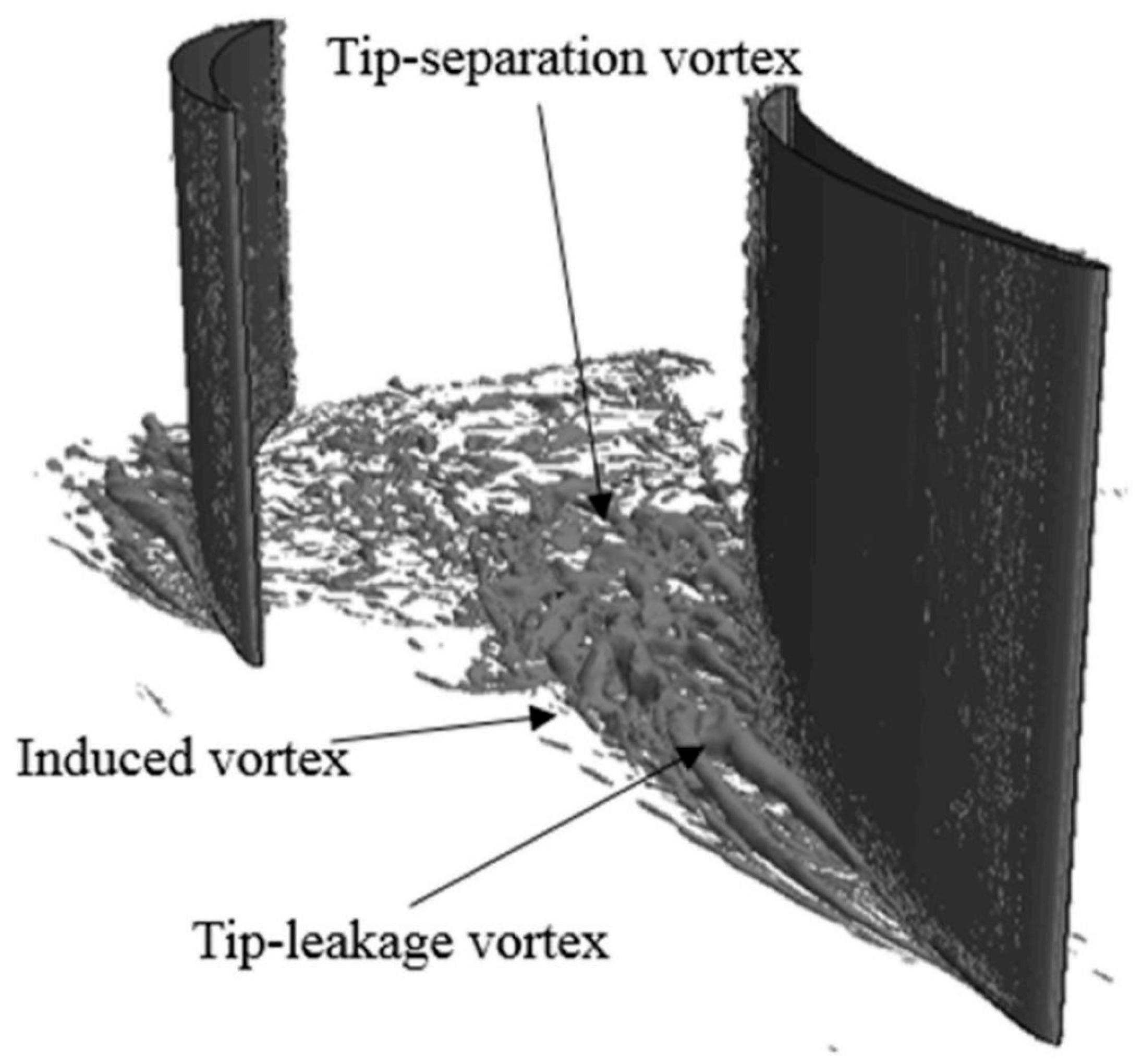
Jiang et al. [57]	LES	Tip-gap flow IBM	TLV trajectory analysis	Turbomachinery	2021
Park et al. [58]	OpenFOAM Hybrid LES/RANS	Wall-function IBM	Rotorcraft/ship air wakes	High-Re external flows	2021
Troldborg et al. [59]	RANS	Two wall-function IBM	Near-wall flow modeling	Aerodynamics	2021
de Albuquerque et al. [60]	RANS	IMERSPEC	IMERSPEC combined with the Spalart–Allmaras turbulence model	Fully developed channel flow	2021
Du et al. [61]	RANS	DI-IBM with auxiliary layers	High-Re turbulent flows	Boundary layers	2022
Van Noordt et al. [62]	WMLES	Hypersonic IBM	Shock–boundary layer interaction	Hypersonic flows	2022
Mitkov et al. [63]	RANS	IBOFlow® solver	Urban wind simulations	Microclimate	2022
Unglehrt et al. [64]	MGLET	Symmetry-preserving IBM	3D extension with cell merging	General CFD	2022
Capuano et al. [65]	OpenFOAM (PIMPLE)	Comparative IBM study	Sphere flow at Re = 3700	Separated flows	2022
	/Nek5000)
Ryan et al. [66]	RANS	Cartesian mesh IBM	CBR dispersion modeling	Public safety	2022
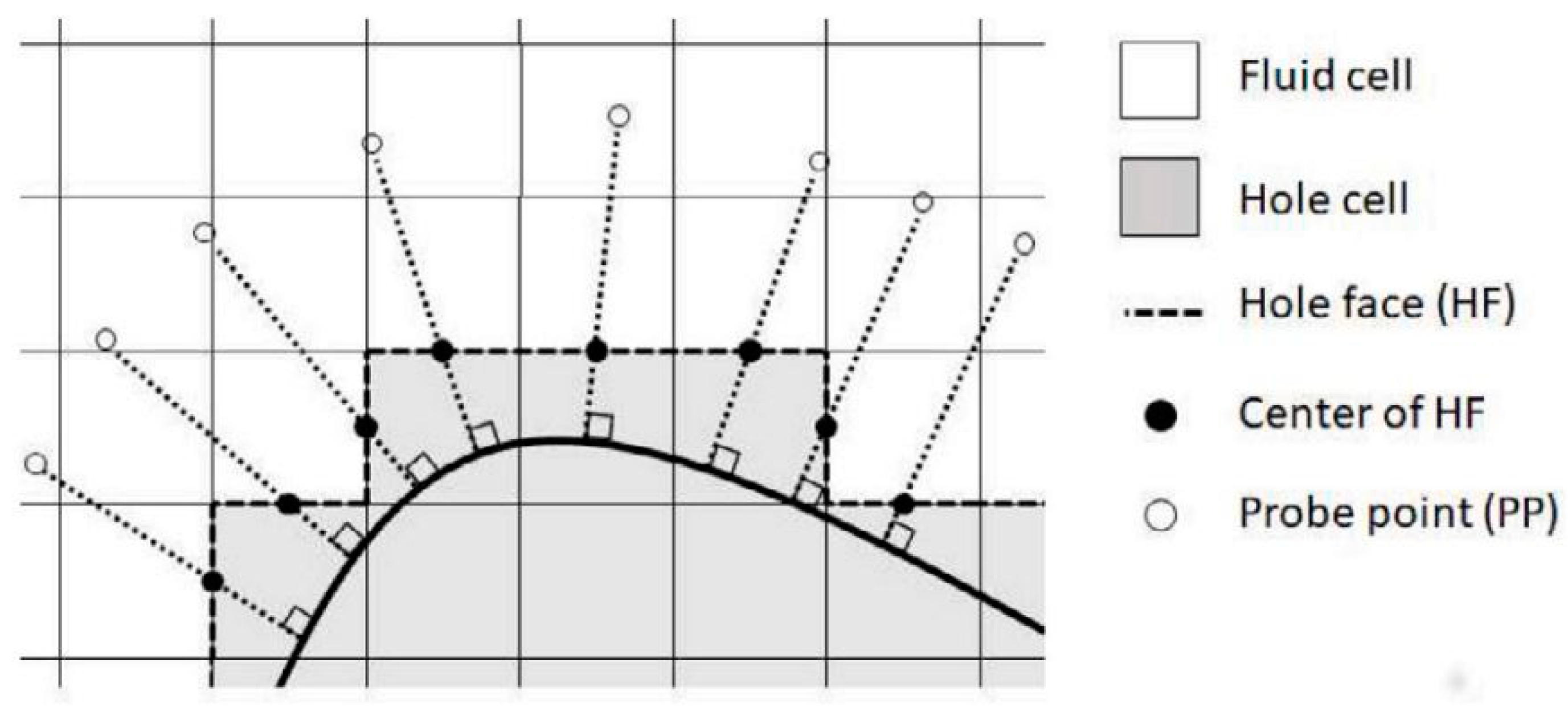
Kubíčková and Isoz [67]	OpenFOAM (SIMPLE)	HFDIB method	Topology optimization	Geometry simplification	2022
Chen et al. [68]	URANS	Wall-function IBM	ANCF rotor validation	Fan aerodynamics	2022
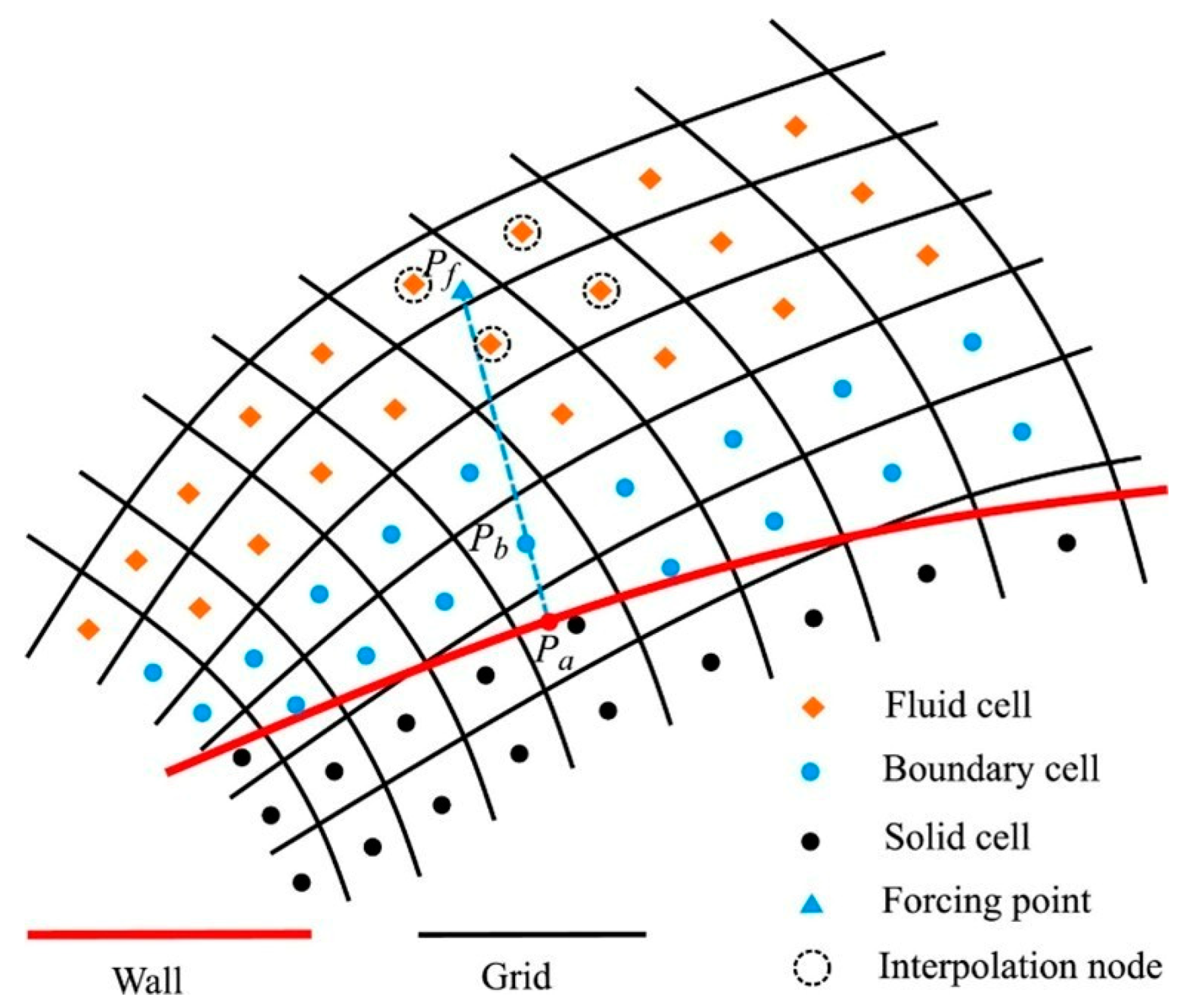
Wang et al. [69]	URANS	AFD-IBM technique	Aero-engine internal flows	Turbomachinery	2022
Cai et al. [70]	Hybrid RANS-LES	Wall-modeled IBM	Spurious oscillation reduction	Complex geometries	2022
Ma et al. [71]	LES	Roughness IBM	3D bump effects	Channel flows	2022
Ma et al. [72]	DNS	Roughness IBM	Secondary motion analysis	Wall turbulence	2022
Lin et al. [73]	HLCC Riemann solver	3D fixed-boundary IBM	Solid rocket motors	Combustion	2023
Cheylan et al. [74]	LBM	Lagrangian weight IBM	20% error reduction in FSI	Moving boundaries	2023
Başkaya et al. [75]	Mutation++	CNE/GSI IBM	Atmospheric entry	Hypersonic re-entry	2023
De Vanna et al. [76]	WMLES	SI-IBM with Cartesian grids	High-speed complex flows	Aerospace	2023

illustrates the application of fluid solvers in an IBM formulation pertaining to turbulent and high-speed flow scenarios.

3.1.1. Large Eddy Simulation (LES)

Large Eddy Simulation (LES) has emerged as a pivotal tool in computational fluid dynamics (CFD), particularly when combined with the immersed boundary method (IBM) to handle complex geometries and high-speed flows. The synergy between LES and IBM enables high-fidelity simulations of turbulent flows while bypassing the challenges of body-fitted meshing, making it especially attractive for applications involving moving boundaries, intricate geometries, and shock-dominated environments. The LES-IBM framework resolves large-scale turbulent structures while modeling subgrid-scale (SGS) effects, providing an efficient yet accurate approach for high-Reynolds-number flows where traditional methods may struggle.

One of the primary advantages of LES in IBM implementations is its ability to handle turbulence in high-speed flows, where shock waves, boundary layer interactions, and flow separation introduce significant complexities. For instance, Zhang et al. [29] employed an adaptive LES solver with a weighted least square IBM to capture hypersonic flow discontinuities, demonstrating the method’s robustness in resolving shock waves without excessive grid refinement. Similarly, Van Noordt et al. [62] utilized a wall-modeled LES (WMLES) approach with a hypersonic IBM to study shock–boundary layer interactions (SBLIs), highlighting the method’s capability to maintain accuracy on relatively coarse grids. Authors have developed hypersonic IBM for shock–boundary layer interaction studies, as illustrated in Figure 1. The method has been successfully tested in various scenarios, including a turbulent channel for basic validation, “a hypersonic transitional boundary layer”, “a hypersonic shock wave–boundary layer interaction” (Figure 2), and “a hypersonic compression ramp”.

The IBM’s flexibility in handling complex and moving geometries further enhances LES applications in industrial and aerospace settings. Onishi and Tsubokura [31] demonstrated this by using a ghost-cell-based IBM with LES to simulate flows around “dirty” CAD geometries, which are often problematic for conventional mesh generation. Meanwhile, De Vanna et al. [76] applied a sharp-interface IBM (SI-IBM) within a Cartesian grid framework to simulate high-speed flows in aerospace applications, where traditional meshing would be prohibitively expensive. The technique involved combining a wall-modeling technique for LES with an SI-IBM, as shown in Figure 3. Both of these techniques were powered by high-precision numerical schemes. This combination enabled accurate near-wall flow modelling without having to micromanage every detail, as well as effortless handling of complex shapes using simple Cartesian grids, as illustrated by bulk-scaled velocity contours in Figure 4.

These implementations highlight how LES-IBM combinations can streamline simulations of real-world engineering problems without sacrificing accuracy.

In atmospheric and environmental flows, Arthur et al. [21] evaluated different IBM implementations within the WRF model, focusing on velocity reconstruction techniques for atmospheric boundary layer simulations. Their work demonstrated that IBM could effectively handle terrain-induced turbulence while maintaining compatibility with weather prediction models. Wang and Gorle [38] further extended LES-IBM applications to atmospheric boundary layer flows, using a direct-forcing IBM to study wake dynamics behind obstacles, which is critical for urban wind engineering and pollutant dispersion studies.

For wall-bounded flows, LES-IBM frameworks have been particularly effective in addressing the challenges of high-Reynolds-number turbulence. Ma et al. [36] developed a hybrid IBM-wall model within an LES solver to simulate turbulent channel flows, demonstrating that the approach could accurately capture near-wall dynamics without excessive resolution requirements. Expanding on this, Ma et al. [71] later introduced a roughness-resolving IBM within an LES framework to analyze three-dimensional bump effects in channel flows, showing that the method could replicate surface-induced flow modifications with high fidelity. Similarly, Atmani et al. [53] combined IBM with LES to study pipe flows at high Reynolds numbers, showing that the method remains viable even on coarse grids. These studies illustrate how LES-IBM methodologies can bridge the gap between computational efficiency and physical fidelity in wall-bounded turbulence.

In turbomachinery applications, Jiang et al. [57] resolved complex tip gap flows, offering detailed analyses of tip leakage vortex (TLV)-induced losses in axial compressors and turbines (Figure 5). Various aero foils with different “section parameters”, “pitch angles”, and “tip gap sizes” were analyzed to understand their effects on the “mean flow field”, “turbulence statistics”, and the “trajectory of the “tip leakage vortex (TLV)”, as shown in Figure 6 and Figure 7, respectively. The study identified the gap width as a key parameter influencing TLV, with “larger chords and thicknesses” effectively suppressing TLV, while pitch angle had a minor impact. This approach enabled engineers to optimize rotating machinery performance by understanding intricate fluid dynamics at microscopic scales.

Their work demonstrated the method’s capability to resolve complex vortex interactions near blade tips, which are crucial for performance optimization. Meanwhile, Wang et al. [42] used LES with a wavy boundary analysis technique to study wall-attached coherent structures in traveling wave scenarios, providing insights into flow control mechanisms in both engineering and geophysical contexts.

Beyond aerodynamics, LES-IBM has found applications in marine engineering and atmospheric sciences. Bai et al. [14] employed a basic IBM-FVM coupling within an LES framework to simulate free surface flows around marine turbines, while Wiersema et al. [20] integrated LES-IBM into the Weather Research and Forecasting (WRF) model to enhance urban terrain simulations for weather forecasting. These diverse applications demonstrate the adaptability of LES-IBM across different flow regimes and physical scales.

In conclusion, the integration of LES with IBM has significantly expanded the scope of CFD simulations, particularly in high-speed and turbulent flows. By leveraging LES for turbulence resolution and IBM for geometric flexibility, researchers have been able to tackle complex problems in aerospace, industrial flows, and environmental fluid dynamics with unprecedented efficiency. Future advancements in SGS modeling, adaptive mesh refinement, and high-performance computing will further enhance the capabilities of LES-IBM frameworks, solidifying their role as a cornerstone of modern computational fluid dynamics.

3.1.2. Direct Numerical Simulation (DNS)

Direct Numerical Simulation (DNS) represents the highest-fidelity approach in computational fluid dynamics, resolving all relevant turbulent scales without modeling approximations. When combined with the immersed boundary method (IBM), DNS provides an unparalleled tool for investigating fundamental turbulence physics in complex geometries. This powerful combination has enabled breakthroughs in understanding wall-bounded turbulence, multiphase flows, and vortex dynamics, where an exact representation of boundary effects is crucial. Unlike LES or RANS approaches, DNS-IBM captures the complete spectrum of turbulent structures while maintaining geometric flexibility, making it indispensable for fundamental research despite its computational intensity.

The DNS-IBM framework has proven particularly valuable for studying wall turbulence and boundary layer dynamics. Yoon et al. [19] employed DNS with IBM to classify turbulent structures in boundary layers, revealing new insights into the organization of near-wall turbulence. Their work demonstrated how IBM can accurately represent wall effects while maintaining the resolution required for DNS. This capability was further extended by Ma et al. [25] and Ma et al. [72], who developed roughness-resolving IBM techniques within DNS to examine both primary and secondary flow motions induced by rough walls. The study examined a homogeneous random arrangement and a clustered arrangement, both compared to a smooth wall. Although there were minimal differences in the mean streamwise velocity variation, the clustered arrangement generated large-scale secondary motions resulting in alternating high-momentum pathways and low-momentum pathways in the time-averaged velocity (Figure 8).

These studies provide fundamental knowledge about the roughness effects that inform turbulence modeling across various applications. The analysis of turbulent/non-turbulent interfaces (TNTIs) by Hwang et al. [26] and Yang et al. [27] further showcased DNS-IBM’s ability to capture intricate flow features, particularly in boundary layers with adverse pressure gradients where traditional methods often struggle.

In multiphase and particle-laden flows, DNS-IBM has enabled an unprecedented examination of fluid–particle interactions. Zhou et al. [23] implemented Lagrangian particle tracking within a DNS-IBM framework to study particle dispersion in channel turbulence, revealing complex modulation mechanisms between particles and turbulent structures. Cui et al. [48] expanded this approach to investigate fiber and disk alignment in turbulent flows, demonstrating how IBM can handle complex particle shapes while maintaining DNS accuracy. These studies highlight DNS-IBM’s unique capability to resolve both the smallest flow scales and intricate boundary conditions simultaneously, a requirement for understanding multiphase turbulence.

Vortex dynamics and complex flow patterns represent another area where DNS-IBM has made significant contributions. Kasbaoui et al. [47] developed a semi-implicit moving IBM (MIBM) for DNS of swirling von Kármán flows, capturing intricate vortex interactions that would be challenging with conventional methods. Giannenas and Laizet [44] introduced a cubic spline IBM within a DNS framework capable of handling both fixed and moving objects on Cartesian meshes, significantly improving accuracy for complex geometries. These implementations demonstrate how DNS-IBM can maintain high fidelity while simulating flows with moving boundaries and strong vortical structures.

The method has also advanced the understanding of wave–turbulence interactions and jet flows. Wang et al. [22] used DNS-IBM to study energy transfer mechanisms in surface wave flows, providing new insights into this complex interaction. Secchi et al. [52] conducted a direct comparison between IBM and penalization methods (PFAs) for turbulent jet impingement on rough plates, establishing best practices for DNS of such flows. These applications underscore DNS-IBM’s versatility across different flow regimes, from wall-bounded turbulence to free shear flows.

From an implementation perspective, DNS-IBM presents unique computational challenges that have driven innovations in high-performance computing. Kang et al. [39] optimized DNS-IBM for many-core architectures like Intel Xeon Phi, demonstrating how algorithmic improvements can make these computationally intensive simulations more feasible. Such advancements are crucial as the scientific community pushes DNS-IBM toward higher Reynolds numbers and more complex geometries.

In conclusion, the integration of DNS with IBM has created a powerful paradigm for fundamental turbulence research. By providing exact solutions to the Navier–Stokes equations while handling complex boundaries, DNS-IBM has yielded transformative insights into wall turbulence, multiphase flows, and vortex dynamics that would be unattainable with other methods. While computational costs remain significant, ongoing advancements in numerical algorithms and high-performance computing continue to expand the frontiers of DNS-IBM applications. As these capabilities grow, DNS-IBM will remain essential for uncovering the fundamental physics of turbulence and validating modeling approaches across the spectrum of computational fluid dynamics.

3.1.3. Reynolds-Averaged Navier–Stokes Equations (RANS)

The combination of Reynolds-Averaged Navier–Stokes (RANS) solvers with immersed boundary methods (IBMs) has emerged as a powerful and computationally efficient approach for simulating turbulent flows around complex geometries. This hybrid methodology bridges the gap between geometric flexibility and turbulence modeling, making it particularly valuable for industrial applications where both accuracy and computational efficiency are paramount. Unlike DNS or LES approaches that resolve turbulent structures directly, RANS-IBM frameworks rely on turbulence modeling while maintaining the geometric advantages of IBM, creating a practical solution for engineering-scale problems.

The development of wall treatment strategies has been central to advancing RANS-IBM capabilities for high-Reynolds-number flows. Choi et al. [10] pioneered this approach by integrating a level-set IBM with power-law wall modeling, demonstrating how RANS could be effectively coupled with IBM for three-dimensional incompressible flows. This work laid the foundation for subsequent advancements in near-wall treatment, including Capizzano’s [13] two-layer wall-modeled IBM that significantly improved turbulence predictions for wall-bounded flows. The importance of proper wall modeling was further emphasized by Tamaki and Imamura [16], who developed a wall-function IBM specifically for transonic flows with high-angle separation, showcasing the method’s ability to handle challenging aerodynamic conditions. These developments collectively addressed one of the most critical challenges in RANS-IBM implementations—accurate near-wall turbulence prediction without explicit boundary-conforming meshes. These works were subsequently refined by researchers like Troldborg et al. [59], who developed specialized wall-function IBM implementations for aerodynamic applications. The method incorporated two different wall functions to simulate near-wall flow and the k − ω − SST turbulence model, as shown in Figure 9. The aerodynamics co-efficient predicted on the body-conforming mesh is provided in Figure 10.

Recent work by Cai et al. [35] has significantly advanced wall-model coupling techniques for high-Reynolds-number flows on Cartesian grids, demonstrating improved accuracy in the SA-fv3 framework. Similarly, Chen et al. [68] made important contributions to fan aerodynamics through their URANS implementation with wall-function IBM for ANCF rotor validation. These studies highlight ongoing innovations in turbulence modeling within RANS-IBM frameworks. The geometric flexibility of RANS-IBM has enabled its application across diverse flow regimes, from internal flows to external aerodynamics. In turbomachinery applications, Chen et al. [33] and Wang et al. [69] demonstrated the effectiveness of URANS-IBM approaches for capturing rotor–stator interactions and aero-engine internal flows, respectively. The approach combined a hybrid mesh strategy that uses a structured mesh and single block to represent the physical domain while employing the IB method to model internal walls, as shown in Figure 11. To handle situations where large-aspect-ratio cells are near the walls, an “Adaptive Forcing Distance (AFD)” technique was introduced which determines the forcing point locations. This extension of the IB method to curvilinear grids allowed the domain boundaries to be determined by a body-fitted mesh.

The method’s ability to handle complex moving boundaries proved particularly valuable in these applications. Similarly, in external aerodynamics, Kubo et al. [45] implemented a level-set topology IBM with k-ω SST turbulence modeling for two-dimensional flow optimization, while Troldborg et al. [46] extended the approach to forest meteorology applications using specialized wall-function implementations. These varied applications underscore the adaptability of RANS-IBM frameworks to different physical domains and engineering requirements.

Recent advancements have focused on improving numerical robustness and accuracy in RANS-IBM implementations. Constant et al. [41] and Cai et al. [70] both addressed the critical issue of spurious oscillations in turbulent flow simulations, developing improved Cartesian IBM formulations that maintain solution fidelity. Xu and Liu [37] contributed to these efforts with their y+-adaptive IBM that provided smooth wall shear stress predictions on complex geometries. Meanwhile, Du et al. [61] introduced a novel DI-IBM with auxiliary layers specifically designed for high-Reynolds-number boundary layer simulations. These methodological improvements have significantly enhanced the reliability of RANS-IBM for industrial applications, where solution quality cannot be compromised.

The RANS-IBM approach has shown particular promise in handling compressible and supersonic flow regimes. Ghosh et al. [12] developed a hybrid LES/RANS-IBM framework for shock–boundary layer interaction at Mach 2.5, incorporating innovative bleed modeling for perforated surfaces. De Tullio et al. [11] earlier demonstrated the potential of sharp-interface IBM with adaptive mesh refinement (AMR) for compressible flows, establishing a template for later developments. These implementations highlight how RANS-IBM can be extended beyond traditional incompressible flow applications to more challenging high-speed regimes.

Urban and environmental applications have also benefited from RANS-IBM methodologies. Mitkov et al. [63] implemented the IBOFlow^® solver for urban wind simulations, addressing the complex microclimate challenges posed by building clusters. Ryan et al. [66] applied a Cartesian mesh IBM to chemical, biological, and radiological (CBR) dispersion modeling, demonstrating the method’s utility for public safety applications, as shown in Figure 12. It emphasized the use of CFD for dispersion modeling of gases, particularly the combination of structured Cartesian meshes and IBM to reduce modeling efforts.

The temporal resolution of unsteady flows represents another area where RANS-IBM has made significant contributions. Specklin and Delauré [15] and Sugaya et al. [49] both developed approaches for moving geometries, with the latter implementing high-order schemes on moving Cartesian grids. Park et al. [58] extended these capabilities to rotorcraft and ship air wake simulations using a wall-function IBM within a hybrid LES/RANS framework. These developments have expanded the applicability of RANS-IBM to time-dependent problems traditionally considered challenging for RANS approaches.

Looking forward, the work of de Albuquerque et al. [60] on IMERSPEC combined with the Spalart–Allmaras model points to ongoing innovations in RANS-IBM methodologies. Their approach to fully developed channel flow demonstrates the continued potential for improving the fundamental accuracy of these simulations. As computational resources grow and algorithms advance, RANS-IBM frameworks are poised to become even more prevalent in industrial CFD applications.

In conclusion, the integration of RANS solvers with immersed boundary methods has created a versatile and practical framework for turbulent flow simulations across numerous engineering disciplines. By combining the computational efficiency of RANS turbulence modeling with the geometric flexibility of IBM, researchers and engineers can tackle complex flow problems that would be prohibitively expensive with traditional body-fitted approaches. The continued development of wall treatments, numerical schemes, and turbulence modeling adaptations ensures that RANS-IBM will remain at the forefront of industrial CFD applications, providing reliable solutions for challenges ranging from aerodynamics to urban flow modeling. As the methodology matures, we can expect further refinements that will expand its applicability to even more demanding flow conditions and complex geometries.

3.1.4. Hybrid Solvers

The implementation of immersed boundary methods (IBMs) across diverse fluid solvers has revolutionized computational fluid dynamics by enabling the efficient simulation of complex geometries while maintaining solution accuracy. This versatility stems from the ability to adapt IBM to various numerical frameworks, from lattice Boltzmann methods (LBMs) to traditional Navier–Stokes solvers, each offering unique advantages for specific flow regimes. The coupling between fluid solvers and IBM techniques has proven particularly valuable for turbulent flow simulations, where accurate boundary representation is crucial yet traditional body-fitted meshes become computationally prohibitive.

Lattice Boltzmann methods have emerged as particularly effective partners for IBM, benefiting from their inherent parallelizability and particle-based nature. Xu et al. [17] demonstrated this synergy through their adaptive-refinement IB-LBM approach, which efficiently handled a wide range of Reynolds numbers by dynamically adjusting grid resolution near boundaries. This capability was further enhanced by Agarwal et al. [24], who combined IB-LBM with LES modeling for turbulent duct flows past square cylinders, showing how the method could capture complex vortex shedding patterns. The flexibility of LBM-IBM systems was extended to fluid–structure interaction problems by Specklin et al. [18] in wastewater pump applications, and later refined by Cheylan et al. [74], whose Lagrangian weight IBM achieved significant error reduction in moving boundary simulations. They achieved a remarkable 20% error reduction in fluid–structure interaction problems using Lagrangian weight IBM (Figure 13) with isosurface representation, as shown in Figure 14.

These developments highlight how LBM’s kinetic theory foundation complements IBM’s geometric flexibility for both laminar and turbulent flow regimes.

For high-speed compressible flows, traditional finite-volume and finite-difference solvers paired with IBM have demonstrated remarkable capabilities. Wang et al. [28] implemented a sharp-interface IBM within OpenFOAM’s rhoCentralFoam solver for hypersonic applications, preserving shock-capturing accuracy while avoiding body-fitted mesh generation. Similarly, Shallcross et al. [56] developed a characteristic-based penalization method for compressible Navier–Stokes equations, maintaining numerical stability in hypersonic regimes. The treatment of compressible flows was further advanced by Choung et al. [40] through their nonlinear weighting process (NWIBM) for Euler equation solvers, demonstrating improved boundary layer resolution. These implementations showcase how IBM can maintain solution fidelity in compressible flow solvers where shock–boundary interactions are critical.

Specialized Riemann solvers have also proven effective when combined with IBM frameworks, particularly for combustion and propulsion applications. Lin et al. [50,73] implemented HLCC Riemann solvers with IBM for solid rocket motor simulations, capturing complex flow features in combustion chambers. Cao and Huang [51] enhanced this approach by incorporating Bayesian calibration with an exact Riemann solver, enabling uncertainty quantification in transonic buffeting predictions. The non-conforming mesh used in embedded boundary framework and AGARD transonic buffeting illustrations of the fluid–structure solution at t = 0.025 s, t = 0.05 s, t = 0.075 s, t = 0.10 s (left to right) with Mach contour in the fluid and pressure coefficient on the wing are provided in Figure 15 and Figure 16, respectively.

The treatment of turbulent flows has particularly benefited from advanced IBM implementations in Navier–Stokes solvers. Liao and Yang [34] developed the CURVIB method within a Newton–Krylov framework, significantly improving near-wall turbulence predictions for curvilinear flows. Unglehrt et al. [64] extended these capabilities through their symmetry-preserving IBM in the MGLET solver, enabling accurate Large Eddy Simulations with complex geometries. For industrial applications, Giannenas et al. [55] combined CAD modeling with their ADR-IBM implementation in InCompact3D, achieving high-fidelity simulations of rotor aerodynamics. These approaches demonstrate how IBM can bridge the gap between accurate turbulence modeling and practical engineering geometries.

Recent advancements have focused on improving numerical robustness and mesh flexibility. Tsvetkova et al. [30] and Bale et al. [43] developed topology-free and moving-least squares IBM approaches, respectively, simplifying mesh generation while maintaining accuracy. Kubíčková and Isoz [67] implemented their HFDIB method in OpenFOAM’s SIMPLE solver for topology optimization, demonstrating IBM’s potential for design applications. These methodological innovations have expanded IBM’s applicability to increasingly complex engineering problems, where traditional meshing approaches would be impractical.

Hypersonic flow simulations represent another area where fluid solver–IBM combinations have shown remarkable success. Başkaya et al. [75] coupled their CNE/GSI IBM with the Mutation++ solver for atmospheric re-entry simulations, capturing nonequilibrium chemistry effects. This work builds upon earlier compressible flow implementations by demonstrating IBM’s capability to handle coupled physico-chemical phenomena at extreme conditions. The method’s geometric flexibility proves particularly valuable for re-entry vehicle analysis where ablation and shape change complicate traditional mesh approaches.

For fundamental turbulence studies, Capuano et al. [65] conducted a comprehensive comparison of IBM implementations across OpenFOAM and Nek5000 solvers for separated flows, providing valuable benchmarks for the community. Their work on sphere flow at Re = 3700 established best practices for the IBM treatment of separation and wake dynamics. Similarly, Kang and Masud [54] developed a variational IBM within a GMRES framework for train aerodynamics, demonstrating how solver–IBM combinations can be optimized for specific industrial applications. The integration points for volume and surface are provided in Figure 17, and instantaneous velocity fields along the train surface are provided in Figure 18.

The evolution of fluid solver–IBM combinations has also addressed critical numerical challenges. Tamaki and Imamura [32] improved flux reconstruction accuracy in their Roe solver implementation. These developments have progressively removed the traditional limitations associated with non-body-conformal methods, making IBM an increasingly attractive option for industrial CFD applications.

In conclusion, the integration of immersed boundary methods with diverse fluid solvers has created a powerful paradigm for turbulent flow simulations across engineering and scientific applications. From LBM’s particle-based approaches to specialized Riemann solvers for combustion, each fluid solver brings unique advantages that IBM enhances through geometric flexibility. The methodology has proven particularly valuable for high-speed flows, complex geometries, and moving boundary problems, where traditional meshing approaches struggle. As solver technologies advance and IBM formulations become more sophisticated, this synergy will continue to expand the frontiers of computational fluid dynamics, enabling accurate simulations of increasingly complex physical phenomena while reducing preprocessing overhead. Future developments will likely focus on enhanced turbulence modeling, multiphysics coupling, and uncertainty quantification within IBM frameworks, further solidifying their role in industrial and scientific computing.

3.1.5. Influence of Fluid Solver on IBM Formulation

The implementation of the immersed boundary method (IBM) is heavily influenced by the choice of fluid solvers, which directly impact numerical accuracy, computational efficiency, and adaptability to complex geometries. Various fluid solvers and discretization schemes, including finite volume, finite difference, lattice Boltzmann, and DNS/pseudo-spectral methods, have been integrated with IBMs to tackle challenging flow problems. High-resolution methods like WENO and spectral DNS have improved IBM’s accuracy in resolving turbulent flows, while Large Eddy Simulations (LESs) and wall-modeled LES (WMLESs) have enhanced IBM’s capability for high-Reynolds-number applications. Additionally, OpenFOAM-based IBM implementations have gained traction for industrial applications due to their flexibility in handling moving boundaries and unstructured meshes. Application-wise, IBM advancements have enabled breakthroughs in high-speed aerodynamics, atmospheric flows, turbomachinery, and biofluid dynamics. For instance, IBM implementations in LES and DNS frameworks have provided deeper insights into wall-bounded turbulence, roughness effects, and shock–boundary layer interactions in hypersonic and aerospace flows. Moreover, IBM’s role in environmental and engineering applications has expanded, with studies on urban wind simulations, rotor aerodynamics, and combustion modeling demonstrating its potential in tackling real-world fluid dynamics challenges. The continuous evolution of IBM methodologies, supported by advanced fluid solvers, signifies its growing impact across scientific and engineering disciplines.

3.2. Complex Rigid Geometries

In computational methods, IBM delivers a unique solution for handling boundary conditions and complex geometries that would otherwise require sophisticated mesh generation. The method’s competency to immerse arbitrary geometries into a systemized grid makes it highly efficient for handling problems in aerodynamics, biomechanics, and environmental fluid dynamics. This section examines the boundary treatment and diverse applications of the IBM across computational fields, featuring its contributions to enhancements in accuracy, reductions in computational costs, and aiding in more realistic simulations.

3.2.1. Diffuse Interface

The diffuse interface approach to immersed boundary methods (IBMs) has emerged as a powerful paradigm for simulating complex fluid–structure interaction (FSI) problems, offering distinct advantages over sharp-interface methods in handling moving boundaries, complex geometries, and multiphase systems. This methodology, characterized by its smoothed representation of boundaries across multiple grid points, has been successfully implemented across a spectrum of fluid solvers, each contributing unique capabilities tailored to specific application requirements. The fundamental philosophy of diffuse IBMs lie in their distribution of boundary effects over a finite thickness region, enabling robust handling of problems where boundary motion, deformation, or topological changes would challenge traditional sharp-interface approaches.

Table 2. Recent advancement pertaining to DI-IBM for handling complex geometries.

Authors and Reference	Fluid Solver	Summary	Application Area	Year
Lai and Peskin [79]	Spectral	Second-order IBM with reduced numerical viscosity	General CFD	2000
Griffith and Peskin [80]	Projection Method	Higher-order accuracy analysis for smooth problems	FSI	2005
Pan [81]	Fractional Step	Volume-of-body function approach	Incompressible flows	2005
Taira and Colonius [82]	Fractional Step	Immersed boundary projection approach	General CFD	2007
Shin et al. [83]	Fractional Step	Assessment of regularized delta functions	IB forcing schemes	2008
Ji et al. [84]	Fractional Step	Iterative direct-forcing IB method	Finite volume	2012
Valero-Lara [85]	Lattice Boltzmann	GPU-accelerated IB-LBM	Solid–fluid interaction	2014
Dash et al. [86]	Lattice Boltzmann	Flexible forcing 3D IB-LBM	Flow past spheres	2014
Valero-Lara et al. [87]	Lattice Boltzmann	Heterogeneous platform acceleration	Solid–fluid interaction	2014
Valero-Lara et al. [88]	Lattice Boltzmann	Optimized for NVIDIA GPUs/Xeon Phi	Solid–fluid interaction	2015
Wang et al. [89]	LES	Implicit direct forcing IBM for complex flows	Moving boundaries	2017
Kefayati et al. [90]	Lattice Boltzmann	IB-FD-LBM for viscoplastic fluids	Fluid–structure interaction	2018
Stein et al. [91]	Spectral	Immersed boundary smooth extension	Polymeric flows	2019
Dash [92]	Lattice Boltzmann	Flexible forcing IB-SLBM	2D/3D FSI	2019
Tao et al. [93]	Lattice Boltzmann	Non-iterative IB-LBM	Fluid–solid flows	2019
Peng et al. [94,95]	Lattice Boltzmann	IBM vs. bounce-back schemes	Curved surfaces	2019
Vadala-Roth et al. [96]	IBAMR	Stabilized hyperelastic IBM	Large deformation	2020
Ma et al. [97]	Lattice Boltzmann	IB-LBM for viscoelastic fluids	Complex FSI	2020
Bale et al. [98]	Projection Method	Constraint IBM with stencil penalization	Neumann BCs	2020
Zhang et al. [99]	Lattice Boltzmann	Relaxed multi-direct-forcing IB-LBM	GPU acceleration	2020
Zhou et al. [100]	Fractional Step	Divergence-free IBM	Incompressible flows	2020
Wang et al. [101]	Implicit velocity decoupling	Monolithic framework for FSI	Constrained problems	2020
Huang et al. [102]	Spectral	IB smooth extension method	Stefan problems	2021
Wang et al. [103]	Lattice Boltzmann	IB-LBM with Navier-slip	Solid–fluid interaction	2021
Zhao et al. [104]	LBM	Efficient BC-enforced IBM	Moving boundaries	2021
Sela et al. [105]	SIMPLE	Semi-implicit direct forcing IBM	Moving bodies	2021
Abbati et al. [106]	Lattice Boltzmann	Diffuse interface IBM	Particulate flows	2022
Wang and Cao [107]	LES	IBM for bridge aerodynamics	Wind engineering	2022
Yu and Pantano [108]	Half-explicit Runge–Kutta	IBM with implicit body force	Compressible flows	2022
Dardé et al. [109]	CEM (Finite Element)	IBM for EIT	Electrode modeling	2023
Sikdar et al. [110]	Lattice Boltzmann	Flexible forcing IB-LBM	2D FSI	2023
Zhang et al. [111]	Lattice Boltzmann	Stability improvement	IB-LBM coupling	2023
Cong et al. [112]	Lattice Boltzmann	VOS-based IB-LBM with level-set function	Moving boundaries	2023
Fang and Tan [113]	LBM	Efficient multi-direct forcing	IBM optimization	2023
Chen and Peskin [114]	Fourier Spectral	Spectral IBM	Viscous flows	2024
Gruninger et al. [115]	IBAMR	IBM benchmarking for viscoelastic flows	Complex geometries	2024

summarizes the recent literature pertaining to DI-IBM, along with its corresponding application areas.

The historical development of diffuse IBM owes much to foundational work by Lai and Peskin [79], whose second-order spectral method with reduced numerical viscosity established key principles for accurate boundary treatment in general CFD applications. This early work influenced subsequent developments in regularization techniques, including Shin et al.’s [83] comprehensive assessment of delta functions for IB forcing schemes, which provided critical guidance for implementing diffuse boundaries across different numerical frameworks. Ji et al. [84] built upon these foundations with their iterative direct-forcing IB method for finite volume solvers, demonstrating how diffuse IBM could be effectively adapted to industrial CFD codes.

Lattice Boltzmann method (LBM) solvers have demonstrated particular synergy with diffuse IBM implementations, owing to their kinetic theory foundation and natural parallelism. Valero-Lara’s pioneering work [85,87,88] established GPU-accelerated IB-LBM frameworks that revolutionized solid–fluid interaction simulations by distributing boundary forces across lattice nodes near immersed surfaces. This approach was extended by Dash [86,92] through flexible forcing schemes that improved accuracy for flow past spheres and general FSI problems. Tao et al. [93], through their non-iterative IB-LBM, significantly improved computational efficiency for fluid–solid flows while maintaining solution accuracy. Zhang et al. [99] further enhanced these capabilities with their relaxed multi-direct-forcing IB-LBM, achieving superior performance on GPU architectures through optimized force distribution schemes. The diffuse nature of these LBM-IBM implementations proved especially valuable for viscoplastic fluid simulations, as demonstrated by Kefayati et al. [90], where the method successfully captured yield stress behavior and fluid–structure coupling. Recent advancements by Wang et al. [103] incorporated Navier-slip conditions into IB-LBM, enabling the more accurate treatment of solid–fluid interaction problems, where slip boundary effects are significant. Further advancements by Zhang et al. [111] and Cong et al. [112] have enhanced stability and moving boundary treatment in IB-LBM, incorporating level-set functions and volume-of-solid approaches to better define the diffuse interface region.

For Large Eddy Simulations of complex flows, Wang et al. [89] developed an implicit direct-forcing IBM that successfully handled moving boundaries while maintaining LES solution fidelity. This approach demonstrated how diffuse IBM concepts could be extended to turbulent flow simulations where both boundary motion and subgrid-scale modeling must be addressed simultaneously. The treatment of constrained FSI problems was advanced by Wang et al. [101] through their monolithic framework combining implicit velocity decoupling with diffuse IBM principles, offering improved stability for problems involving strong fluid–structure coupling.

Recent innovations in boundary condition enforcement have further expanded diffuse IBM capabilities. Zhao et al. [104] developed an efficient BC-enforced IBM within LBM frameworks that improved accuracy for moving boundary problems while maintaining computational efficiency. For industrial applications using finite-volume methods, Sela et al. [105] implemented a semi-implicit direct forcing IBM in SIMPLE-based solvers, demonstrating robust performance for moving-body simulations in practical engineering contexts. These developments collectively showcase how diffuse IBM implementations have evolved to address diverse application needs while maintaining numerical robustness.

Spectral methods have contributed significantly to diffuse IBM development, particularly through the immersed boundary smooth extension (IBSE) approach. Stein et al. [91] and Huang et al. [102] implemented this methodology for polymeric flows and Stefan problems, respectively, demonstrating how spectral accuracy can be maintained despite the diffuse boundary representation. The IBSE framework preserves high-order convergence by smoothly extending the solution across the immersed boundary, a feature particularly valuable for problems requiring the precise resolution of boundary layers or phase interfaces.

For finite-element and finite-volume implementations, the diffuse IBM has enabled new capabilities in handling complex boundary conditions. Bale et al. [98] developed a constraint IBM with stencil penalization that effectively enforced Neumann boundary conditions in projection method solvers, while Vadala-Roth et al. [96] created a stabilized hyperelastic IBM within the IBAMR framework, capable of handling large deformations. These implementations showcase how a diffuse IBM can be adapted to different numerical frameworks while maintaining essential conservation properties. The fractional step method has proven particularly amenable to diffuse IBMs, as evidenced by Pan’s volume-of-body function approach [81] and Taira and Colonius’s immersed boundary projection method [82], both of which achieved robust solutions for incompressible flows with moving boundaries.

The application spectrum of diffuse IBMs reveals their remarkable versatility across engineering and scientific domains. In biomedical flows, the method’s ability to handle flexible boundaries has enabled breakthroughs in large-deformation FSI simulations, as demonstrated by Ma et al. [97] for viscoelastic fluids. For particulate flows, Abbati et al. [106] developed a diffuse interface IBM that accurately resolved particle–fluid interactions without explicit boundary tracking. Wind engineering applications have benefited from Wang and Cao’s [107] LES-based diffuse IBM for bridge aerodynamics, where the method captured complex vortex–structure interactions. In emerging fields like electrical impedance tomography, Dardé et al. [109] adapted diffuse IBM principles to electrode modeling, demonstrating the methodology’s cross-disciplinary potential.

The performance and accuracy of diffuse IBM implementations are deeply intertwined with their underlying fluid solvers. LBM-based approaches, such as those by Peng et al. [94,95] and Sikdar et al. [110], excel in parallel scalability and complex boundary handling but may face challenges in compressible flow regimes. In contrast, spectral methods like those of Chen and Peskin [114] offer superior accuracy for smooth problems but require structured grids. Projection and fractional step methods, exemplified by Griffith and Peskin [80] and Zhou et al. [100], provide robust incompressible flow solutions with good conservation properties, making them ideal for industrial FSI applications. The choice of solver–IBM combination ultimately depends on the target application’s specific requirements for accuracy, computational efficiency, and boundary complexity.

Recent trends in diffuse IBM development focus on enhancing stability and efficiency for challenging flow regimes. Yu and Pantano’s [108] half-explicit Runge–Kutta approach with implicit body force treatment improved performance for compressible flows, while Fang and Tan’s [113] efficient multi-direct forcing scheme optimized LBM-based IBM for large-scale simulations. Recent work by Gruninger et al. [115] provides comprehensive benchmarking for viscoelastic flows, establishing best practices for complex geometries, as shown in Figure 19 and Figure 20, respectively.

In conclusion, diffuse immersed boundary methods have evolved into a versatile framework for tackling some of the most challenging problems in computational fluid dynamics. By distributing boundary effects across a finite region and leveraging the strengths of diverse fluid solvers, these methods successfully bridge the gap between geometric complexity and numerical efficiency. The continued development of LBM, spectral, and finite-volume-based diffuse IBM implementations promises to further expand the methodology’s applicability to emerging challenges in multiphysics simulations, high-performance computing, and complex FSI problems. As computational resources grow and algorithms mature, diffuse IBMs are poised to become an increasingly indispensable tool across scientific and engineering disciplines, offering a robust alternative to traditional boundary-conforming approaches while maintaining high fidelity in flow prediction. Future research directions will likely focus on improved boundary layer resolution, enhanced stability for extreme deformation cases, and tighter integration with machine learning techniques for adaptive boundary treatment.

3.2.2. Sharp Interface

Sharp-interface immersed boundary methods (IBMs) have established themselves as a powerful computational framework for simulating complex fluid flows with intricate geometries, offering distinct advantages in accuracy and boundary condition enforcement compared to their diffuse counterparts. These methods maintain a precise, non-smoothed representation of immersed boundaries while operating on non-conformal grids, making them particularly valuable for problems requiring exact boundary condition satisfaction. The development of sharp IBM implementations across various fluid solvers has created a rich ecosystem of numerical approaches tailored to specific application requirements, from incompressible flows to compressible shock-dominated scenarios.

Table 3. Recent advancement pertaining to SI-IBM for handling complex geometries.

Authors and Reference	Fluid Solver	Summary	Application Area	Year
Fadlun et al. [116]	Fractional Step	3D complex flow simulations with immersed boundaries	Complex geometries	2000
Kim et al. [117]	Fractional Step	IB-FV method for complex geometries	Complex flows	2001
Gilmanov et al. [118]	Fractional Step	General reconstruction algorithm for 3D immersed boundaries	Cartesian grids	2003
Gilmanov and Sotiropoulos [119]	Artificial Compressibility	Method for 3D complex moving bodies	Moving boundaries	2005
Kim and Choi [120]	Fractional Step	IB method for arbitrarily moving bodies	Moving bodies	2006
Zhang and Zheng [121]	Fractional Step	Improved direct-forcing IB method	Finite differences	2007
Husain and Floryan [122]	Spectral	IB conditions for unsteady Laplace problems	Unsteady flows	2007
Mittal et al. [123]	Fractional Step	Versatile sharp-interface IB method	Complex boundaries	2008
Husain and Floryan [124]	Spectral	Implicit spectrally accurate moving boundary method	Moving boundaries	2008
Husain et al. [125]	Spectral	Over-determined IB conditions method	General CFD	2009
Husain and Floryan [126]	Spectral	Spectrally accurate moving boundary algorithm	Navier–Stokes flow	2010
Husain and Floryan [127]	Spectral	Efficient over-determined IB implementation	Fluid dynamics	2014
Kumar and Roy [128]	Fractional Step	SI-IBM addressing pressure fluctuations	Moving/deformable bodies	2016
Sakib et al. [129]	Spectral	3D spectral analysis with immersed BCs	Rough boundary flows	2017
Wu [130]	Fractional Step	Local domain-free discretization IBM	Moving boundaries	2018
Yuan and Zhong [131]	Gas-Kinetic BGK	IBM for compressible/incompressible flows	Complex boundaries	2018
Yousefzadeh and Battiato [132]	SIMPLE	High-order ghost-cell IBM	Generalized BCs	2019
Zhang et al. [133]	Fractional Step	Improved ghost-cell IBM	Shock/obstacle interactions	2019
Shah et al. [134]	Fractional Step	OpenMP parallelized IBM	FSI acceleration	2019
Lin et al. [135]	Projection Method	Target-fixed IB for rigid body FSI	Flow-structure interaction	2020
Sundaresan and Ghosh [136]	REACTMB	Surface data reconstruction	Pressure interpolation	2020
Kettemann et al. [137]	OpenFOAM (PIMPLE)	Verification of static/moving geometries	Turbulent flows	2021
Liu et al. [138]	Fractional Step	Volume of solid implicit forcing IBM	Navier–Stokes	2021
Hoover and Kumar [139]	Finite Element	Thin shell analysis	Complex geometries	2021
Boustani et al. [140]	Finite Element	Thin compliant shell structures	FSI	2021
Carraturo et al. [141]	Finite Cell	Residual stress evaluation	Additive manufacturing	2021
Stavropoulos et al. [142]	RANS	Direct forcing IBM	Cavitating flows	2021
Wang and Zhang [143]	Brinkman penalization	Variable-extended IBM	Reactive flows	2021
Su et al. [144]	Fractional Step	Well-defined grid line IBM	Incompressible flow	2021
Yan et al. [145]	Two-phase flow model	Algebraic forcing-point-searching	Water impact	2021
Tian et al. [146]	Finite Element fluid solver	Improved penalty IBM	Transient FSI	2021
Jost and Glockner [147]	Projection using spectral elements	Ghost-cell IBM improvements	Cartesian grids	2021
Hong et al. [148]	Composite Implicit Time Integration	Ghost-cell IBM for zero-thickness	Large CFL numbers	2021
Gsell and Favier [149]	LBM	DF-IBM with slip correction	Boundary errors	2021
Zhang et al. [150]	SIMPLE	Ghost-cell IBM with momentum interpolation	Incompressible flows	2021
Billo et al. [151,152]	Projection Method	Penalized DF-IBM	Thin obstacles	2022
Wang et al. [153]	Riemann Solver	Ghost-cell with hybrid reconstruction	Compressible flows	2022
Lauber et al. [154]	Fractional Step	Boundary data immersion method	Thin membranes	2022
Hoover and Kumar [155]	Finite Element	Mindlin–Reissner shell element	Composite shells	2022
Nair and Goza [156]	Finite Element	Strongly coupled IBM	FSI efficiency	2022
Kingora and Sadat-Hosseini [157]	Implicit Euler	Interpolation-free sharp-interface IBM	Incompressible flows	2022
Barbeau et al. [158]	Pressure-Stabilizing/Petrov–Galerkin (PSPG)	High-order sharp-interface IBM	Incompressible flows	2022
Ong et al. [159]	Projection Method	IB projection method	Fluid–rigid body	2022
Ou et al. [160]	DNS	Directional ghost-cell IBM	Reacting flows	2022
Tewolde et al. [161]	Projection Method	DF-IBM for thin bodies	Volumeless bodies	2022
Funada and Imamura [162]	Flux Reconstruction	High-order IBM	Inviscid flows	2023
Kristoffersen et al. [163]	Fourth Order Runge–Kutta	3D sharp-interface ghost node IBM	Compressible flows	2023
Raj et al. [164]	Marker and Cell Method	GPU-accelerated SI-IBM	Versatile geometries	2023
Keslerová et al. [165]	SIMPLE	Novel solver for branching channels	Incompressible flows	2023
Zhang et al. [166]	Fractional Step	Divergence-free IBM for rigid boundaries	FSI stability	2023
Lauber et al. [167]	Projection Method	IBM-FEM for membranes/shells	Large deformation FSI	2023
Xu et al. [168]	CgLES	Discretized IBM (DIBM)	Moving/deforming solids	2023
Li et al. [169]	Roe approximate Riemann solver	SI-IBM for thin-walled geometries	Compressible flows	2023
Chiu [170]	Projection Method	Convolution kernel DFIBM (cDFIB)	Time-varying geometries	2023
Yildiran et al. [171]	Fractional Step	Pressure BCs for IBM	Slip-error reduction	2024

summarizes the recent literature pertaining to SI-IBM, along with its corresponding application areas.

The fractional step method has served as a foundational framework for many sharp IBM implementations, particularly for incompressible flow simulations. Fadlun et al. [116] pioneered this approach with their three-dimensional complex flow simulations, demonstrating how sharp IBM could handle intricate geometries without body-fitted meshes. This work was extended by Kim et al. [117] through their IB-FV method, which improved geometric flexibility while maintaining solution accuracy. Gilmanov et al. [118,119] made significant contributions to the field with their general reconstruction algorithms for three-dimensional immersed boundaries, enabling accurate simulations on Cartesian grids for both stationary and moving bodies. The versatility of fractional step-based sharp IBM was further demonstrated by Kim and Choi [120] for arbitrarily moving bodies and Zhang and Zheng [121] through their improved direct-forcing approach, which enhanced numerical stability for finite difference schemes. This work was extended by Mittal et al. [123], who developed a versatile sharp-interface IB method capable of handling complex boundaries with improved accuracy. The versatility of fractional step-based sharp IBM was further demonstrated by Su et al. [144] through their well-defined grid line IBM, which provided enhanced accuracy for incompressible flow simulations, and Lauber et al. [154], who implemented a boundary data immersion method specifically designed for thin membranes.

Spectral methods have played a crucial role in advancing high-accuracy sharp IBM implementations, particularly for problems requiring precise boundary layer resolution. Husain and Floryan [122,124,126,127] developed a series of spectrally accurate moving boundary algorithms that set new standards for numerical precision in unsteady flow simulations. Their work on over-determined IB conditions [125] and implicit spectrally accurate methods demonstrated how spectral solvers could maintain exceptional accuracy even with complex immersed boundaries. Sakib et al. [129] later extended these concepts to the three-dimensional spectral analysis of rough boundary flows, showcasing the method’s capability for challenging surface geometries.

For compressible flow applications, sharp IBM implementations have demonstrated remarkable success in handling shock–boundary interactions. Zhang et al. [133] developed an improved ghost-cell IBM within a fractional step framework specifically designed for shock/obstacle interactions, while Wang et al. [153] implemented a ghost-cell method with hybrid reconstruction in a Riemann solver for general compressible flows. These approaches maintain sharp-interface representation while accommodating the unique challenges of compressible flow physics. Kristoffersen et al. [163] pushed these capabilities further with their three-dimensional sharp-interface ghost node IBM for compressible flows, demonstrating high-order accuracy in challenging flow regimes. Yuan and Zhong [131] developed a gas-kinetic BGK-based IBM that uniquely handled both compressible and incompressible flows with complex boundaries, while Ou et al. [160] created a directional ghost-cell IBM specifically optimized for reacting flows in DNS simulations. These approaches maintain sharp-interface representation while accommodating the unique challenges of compressible flow physics, with Li et al. [169] later extending these capabilities through their sharp-interface IBM for thin-walled geometries in compressible flows using a Roe approximate Riemann solver (Figure 21 and Figure 22).

The treatment of fluid–structure interaction (FSI) problems has particularly benefited from advanced sharp IBM implementations. Kumar and Roy [128] addressed persistent pressure fluctuation issues in moving/deformable body simulations through their semi-implicit IBM, significantly improving solution stability. Lin et al. [135] developed a target-fixed IB approach for rigid body FSIs within a projection method framework, offering enhanced accuracy for flow–structure coupling. More recently, Nair and Goza [156] created a strongly coupled IBM in a finite element framework that improved FSI simulation efficiency, while Lauber et al. [167] combined an IBM with finite element methods for membrane and shell structures undergoing large deformations. Tian et al. [146] improved a penalty IBM within a finite element fluid solver for transient FSI problems, demonstrating superior stability for strongly coupled simulations. Xu et al. [168] later developed a discretized IBM (DIBM) within a CgLES framework that improved the handling of moving and deforming solids. These specialized implementations addressed long-standing challenges in FSI simulations with sharp interfaces.

Industrial applications of sharp IBM have driven innovations in computational efficiency and parallel implementation. Shah et al. [134] developed an OpenMP parallelized IBM that significantly accelerated FSI simulations, making the method more practical for large-scale engineering problems. Raj et al. [164] implemented a GPU-accelerated sharp-interface IBM using the marker and cell method, demonstrating impressive performance gains for versatile geometries. This method utilized a modified signed distance algorithm for accurate geometry tracking, as shown in Figure 23.

The vortical structures of the robotic butterfly for different mean positions are shown in Figure 24 and Figure 25, respectively. These advancements have been crucial for adopting sharp IBM in industrial CFD workflows, where both accuracy and computational efficiency are paramount. Yousefzadeh and Battiato [132] implemented a high-order ghost-cell IBM in SIMPLE solvers that handled generalized boundary conditions with improved accuracy, while Gsell and Favier [149] developed a direct-forcing IBM with slip correction in LBM frameworks that significantly reduced boundary errors. Keslerová et al. [165] later created a novel SIMPLE-based solver with sharp IBM capabilities optimized for branching channel flows, demonstrating the method’s adaptability to specific industrial configurations.

Recent developments in sharp IBM have focused on specialized applications and improved boundary treatments. Stavropoulos et al. [142] applied direct forcing IBM to cavitating flows within a RANS framework, successfully capturing complex phase change phenomena near sharp boundaries. Wang and Zhang [143] developed a variable-extended IBM for reactive flows using Brinkman penalization, enabling the accurate simulation of combustion processes near immersed surfaces. For thin structure simulations, Billo et al. [151,152] and Tewolde et al. [161] created specialized IBM formulations that accurately represented volumeless and thin bodies without numerical artifacts. Carraturo et al. [141] applied finite cell sharp IBM to residual stress evaluation in additive manufacturing, showcasing the method’s potential for materials engineering applications. Sundaresan and Ghosh [136] developed sophisticated surface data reconstruction techniques within their REACTMB solver that improved pressure interpolation accuracy near immersed boundaries. For inviscid flows, Kingora and Sadat-Hosseini [157] created an interpolation-free sharp-interface IBM that maintained excellent accuracy in incompressible flow simulations.

The role of different fluid solvers in sharp IBM implementations reveals interesting trade-offs between accuracy, flexibility, and computational efficiency. Fractional step methods, as demonstrated by Wu [130] and Liu et al. [138], offer robust performance for incompressible flows with moving boundaries. Finite element approaches, such as those by Hoover and Kumar [139,155] and Boustani et al. [140], provide superior geometric flexibility for complex structures and thin shells. Projection methods have proven particularly effective for fluid–rigid body interactions, as shown by Ong et al. [159] and Jost and Glockner [147], while spectral element implementations maintain exceptional accuracy for smooth problems.

High-order accuracy has been a persistent focus in sharp IBM development. Barbeau et al. [158] implemented a high-order sharp-interface IBM using Pressure-Stabilizing/Petrov-Galerkin formulation, while Funada and Imamura [162] developed a flux reconstruction-based high-order IBM for inviscid flows. These approaches demonstrate how modern numerical techniques can be combined with sharp IBM to achieve superior convergence properties while maintaining geometric flexibility.

Specialized boundary treatments have expanded sharp IBM’s applicability to unique flow scenarios. Yan et al. [145] developed an algebraic forcing point searching method for water impact problems within a two-phase flow model, successfully capturing violent free surface phenomena. Hong et al. [148] created a ghost-cell IBM capable of handling zero-thickness boundaries at large CFL numbers, addressing a long-standing challenge in explicit time integration schemes. These innovations demonstrate the method’s adaptability to diverse physical scenarios.

For industrial CFD applications, sharp IBM implementations in standard solvers like OpenFOAM and SIMPLE have significantly improved practicality. Kettemann et al. [137] verified sharp IBM performance for static and moving geometries in turbulent flows using OpenFOAM’s PIMPLE algorithm, while Zhang et al. [150] implemented a ghost-cell IBM with momentum interpolation in a SIMPLE-based solver for incompressible flows. These implementations have helped bridge the gap between academic research and industrial applications of sharp IBM methodologies.

Recent advances in sharp IBM have addressed persistent challenges in boundary condition enforcement and numerical stability. Yildiran et al. [171] developed improved pressure boundary conditions for fractional-step IBM that reduced slip errors, while Zhang et al. [166] created a divergence-free IBM for rigid boundaries that enhanced FSI stability. The introduction of the convolution “kernel-based direct forcing immersed boundary method (cDFIB)” by Chiu [170] successfully mitigated “Spurious Force Oscillations (SFOs)” for various time step sizes, thereby improving stability in flow–structure interaction scenarios, as presented in Figure 26 and Figure 27.

In conclusion, sharp immersed boundary methods have evolved into a sophisticated and versatile framework for computational fluid dynamics, offering precise boundary representation across a wide range of flow regimes and applications. The method’s success stems from its integration with diverse fluid solvers, each contributing unique strengths to address specific challenges in accuracy, efficiency, or geometric complexity. From spectral methods offering exceptional precision to fractional step approaches providing robust performance for moving boundaries, the sharp IBM ecosystem continues to expand and mature. Future developments will likely focus on enhanced parallel scalability, improved boundary condition treatments for multiphysics applications, and tighter integration with machine learning techniques for adaptive grid refinement. As computational resources grow and algorithms advance, sharp IBM is poised to become an increasingly indispensable tool for both academic research and industrial CFD applications, particularly in areas requiring precise boundary layer resolution or handling of complex moving geometries. The continued cross-pollination between different numerical frameworks and sharp IBM implementations promises to yield further innovations in this vibrant field of computational fluid dynamics.

3.2.3. Hybrid Boundary Treatments

The evolution of immersed boundary methods (IBMs) has reached an inflection point, with the emergence of hybrid approaches that strategically combine elements from sharp-interface, diffuse-interface, and novel computational techniques. This synthesis has produced methodologies capable of addressing limitations inherent in pure formulations while leveraging their respective strengths. Hybrid IBM distinguishes itself through its adaptive blending of numerical strategies, often combining the geometric fidelity of sharp-interface methods with the computational flexibility of diffuse approaches. Thekkethil and Sharma’s [176] level-set immersed interface method exemplifies this paradigm, merging interface tracking precision with finite element flexibility for complex FSI problems. Such hybridizations have proven particularly valuable for multiscale phenomena where no single traditional approach provides optimal performance across all relevant lengths and time scales [177].

The most transformative hybrid IBM developments have emerged from multi-physics integration and spectral solvers [178,179,180]. IBM stability improved drastically with Fourier analysis to solve N-S equations [181]. Ataei et al. [182] demonstrated this through their hybrid LBM-MD-IBM framework for polymer foaming simulations, seamlessly bridging molecular dynamics with continuum-scale hydrodynamics. This approach overcame traditional limitations in modeling phase change dynamics while maintaining computational tractability. Similarly, Yan et al. [183] developed an explicit velocity correction IB for fish swimming dynamics that coupled fluid mechanics with biomechanical models, enabling the unprecedented analysis of aquatic locomotion. Figure 28 illustrates the changes in swimming speed and displacement along the X direction. The fish quickly accelerated from t = 0 s to t = 2 s, after which the rate of acceleration decreased and stabilized by t = 4 s. The fish ultimately reached the left boundary at roughly t = 7 s. Due to the periodic nature of the muscle force, the swimming speed also fluctuated periodically. To examine the intricate FSI and the fish’s dynamic response, the vortex contours from t = 4.20 s to t = 4.60 s are illustrated in Figure 29, and the specific hydrodynamic factors such as fish morphology, hydrodynamic force, swimming velocity, and tail displacement during one period are shown in Figure 30.

These multi-physics capabilities were extended by Ferrer et al. [184] through their HORSES3D spectral element solver, which integrated hybrid IBM with advanced turbulence modeling for aerospace applications. The framework’s ability to handle complex geometry while maintaining spectral accuracy represented a significant leap forward for high-fidelity simulations of practical engineering systems. Mascio and Zaghi [185] achieved breakthrough accuracy for compressible flows by combining high-order WENO schemes with immersed boundary treatments, while Yu et al. [186] developed generalized harmonic polynomial methods that improved Navier–Stokes solution fidelity. These approaches demonstrated how hybrid methodologies could enhance traditional finite difference/volume schemes without sacrificing computational efficiency.

Adaptive mesh refinement (AMR) has particularly benefited from hybrid IBM integration. Saravanan et al. [187] and Liu et al. [188] developed AMR-IBM frameworks that dynamically adjusted computational resolution to critical flow regions, dramatically improving efficiency for complex geometry simulations. Zaghi et al. [189] accelerated these approaches through GPU implementations, enabling practical application to industrial-scale problems. The intersection of IBM with machine learning represents one of the most promising recent developments. Fang and Tan [190] pioneered physics-informed machine learning hybrids that learned optimal forcing strategies from high-fidelity simulation data, significantly improving fluid–solid coupling accuracy. Han et al. [191] applied reinforcement learning to active flow control within an IBM framework, demonstrating autonomous drag reduction strategies that outperformed traditional control approaches. These data-driven methods complement more traditional numerical improvements like those of Llorente et al. [192], who developed modified equation analysis techniques to systematically improve IBM accuracy. The combination of analytical rigor with data science approaches points toward a new generation of self-optimizing hybrid IBM implementations.

Hybrid IBM has driven significant advances in computational efficiency through targeted HPC implementations. Kozubskaya et al. [193] developed unstructured mesh adaptation techniques for moving bodies that maintained solution quality while minimizing computational overhead. Hedayat and Borazjani’s [194] Overset-CURVIB framework demonstrated how careful grid hybridization could enable the efficient simulation of extremely complex flows. These developments have made previously intractable simulations feasible, such as the large-scale viscoelastic flow analyses by Li and Qu [195] and Li et al. [196], and the dynamic fracture simulations of Ni et al. [197] using IB–Material Point Methods. The flexibility of hybrid IBM has enabled customized solver development for specific application needs. Manueco et al. [198] created wall-modeled IB approaches with curvilinear grids that improved accuracy for turbomachinery applications. Huang and Wang [199] developed moving least-square IBMs for compressible viscous flows, addressing long-standing challenges in aerospace CFD. Marussig et al. [200] contributed fast IBM implementations using weighted quadrature that accelerated higher-order computations, while Beer and Duenser [201] demonstrated how isogeometric boundary element methods could be effectively immersed for geotechnical applications. These specialized implementations showcase hybrid IBM’s adaptability to diverse engineering challenges.

Hybrid IBM has revolutionized biological flow simulations through its ability to handle complex, deforming geometries. Ya et al. [202] and Yang et al. [203] developed peridynamic IB-LBM hybrids that enabled coupled analysis of fluid dynamics and structural fracture, providing new insights into cardiovascular pathologies. Shahmardi et al. [204] advanced contact line dynamics modeling through Eulerian hybrid IB/phase-field methods, with applications in microfluidic drug delivery systems. The method’s multiscale capabilities have been particularly valuable in biomedical contexts. Wells et al. [205] immersed finite element formulations to enable the detailed analysis of soft tissue mechanics, while Tirri et al. [206] provided crucial linear stability analysis for cardiovascular device design. Yousefzadeh and Battiato [207] developed level-set IBM for reactive transport in porous media, with applications in enhanced oil recovery. Chen et al. [208] improved force calculation accuracy for simple geometries relevant to heat exchanger design, while Goncharuk et al. [209] adapted SIMPLE-IBM hybrids for industrial incompressible flow analysis. Jiang et al. [210] created signed distance field IBM implementations optimized for tidal turbine simulations, whereas Luo and Zhang [211] developed an σ-coordinate IBM for free surface flows in hydroelectric systems. As shown in Figure 31, this problem can be further streamlined to assess whether a ray intersects with a triangular mesh element in three-dimensional space. The cells within the boundary are identified as solid cells, whereas those outside are classified as fluid. The characteristics and variables of the solid cells are dictated by the movement of the solid body, while the flow in the fluid cells is resolved through discretized governing equations. Cells that are outside the boundary but adjacent to at least one solid cell are designated as IB cells. These IB cells serve as intermediaries for transferring numerical information between solid and fluid cells. To enforce the boundary conditions, virtual boundary forces are applied to the IB cells, as illustrated in Figure 32 and Figure 33, respectively. The IBM is incorporated by introducing a virtual boundary force into the momentum equations, which helps in simulating the natural boundary conditions.

Bourantas et al. [212] developed meshless vector potential-vorticity solvers for complex material flows. Wang et al. [213] advanced thin-walled structure analysis through moving least square IBM, with applications in additive manufacturing. These implementations have significantly reduced the prototyping costs for advanced materials, as demonstrated by Dave et al. [214] in their volume-filtering IBM for static/moving boundaries in composite material processing. More recently, the research of Yu and Pantano [215] presented a novel regularized IBM that employs Tikhonov regularization to overcome challenges associated with accurate boundary force calculations, especially in cases of refined grids, as shown in Figure 34.

3.2.4. Impact of Various Boundary Treatments

The treatment of boundaries in immersed boundary methods (IBMs) plays a crucial role in ensuring numerical stability, accuracy, and efficiency, particularly for complex geometries and moving boundaries. Recent advances have focused on improving sharp-interface methods, hybrid approaches, and diffuse-interface techniques to enhance performance across various fluid–structure interaction (FSI) problems. Studies have introduced high-order ghost-cell IBM and divergence-free IBM to address pressure fluctuations and shock interactions. Hybrid methods, such as those integrating finite volume, finite element, and lattice Boltzmann models, have improved adaptability for reactive flows and viscoelastic fluids. Moreover, application-driven developments have targeted aerodynamics, biomedical flows, and additive manufacturing, with significant contributions in GPU-accelerated implementations and thin-shell structures. The trend indicates a push toward machine learning-assisted IBM optimization and AMR-based IBM frameworks, demonstrating the method’s expanding capabilities in handling increasingly complex FSI scenarios. These innovations reinforce the IBM’s relevance in computational fluid dynamics (CFD) applications, driving its evolution toward more robust and efficient implementations.

4. Limitations

The immersed boundary method (IBM) has become an indispensable tool in computational fluid dynamics, yet several persistent challenges continue to limit its accuracy and computational efficiency. Important among them is the method’s difficulty in accurately resolving near-wall turbulence and high-Reynolds-number flows, where conventional interpolation schemes introduce problematic diffusion errors that compromise solution quality. Recent advances employing wall-modeled LES, adaptive mesh refinement, and high-order numerical schemes have shown promise in addressing these limitations. The inherent numerical instability of Cartesian grid-based implementations, manifested through spurious oscillations, has been partially mitigated through sophisticated filtering techniques and advanced interpolation approaches, though challenges remain in maintaining both stability and accuracy. Computational expense presents another significant barrier, particularly for large-scale industrial applications requiring high-fidelity simulations, prompting researchers to explore hybrid modeling approaches, GPU acceleration, and machine learning-assisted optimization strategies. The method’s treatment of complex geometries and moving boundaries continues to pose difficulties, with issues ranging from force representation inconsistencies to artificial stiffness in fluid–structure interactions—problems that have seen incremental improvements through Lagrangian tracking methods and energy-conserving formulations. Perhaps most crucially, the validation of IBM results against experimental data remains an ongoing concern, driving the development of more robust calibration and uncertainty quantification techniques. These collective challenges highlight both the current limitations and future potential of IBM as it evolves to meet the demands of increasingly complex fluid dynamics applications across engineering and scientific disciplines.

5. Summary

Recent advancements in the immersed boundary method (IBM) from 2020 to 2024 have significantly enhanced its accuracy, efficiency, and versatility in handling complex fluid–structure interaction problems. The method’s performance has been greatly influenced by the choice of fluid solvers, including high-resolution techniques such as WENO schemes, spectral DNS, and LES, which have improved turbulence modeling and high-Reynolds-number simulations. Concurrently, developments in boundary treatment strategies—such as high-order ghost-cell methods, divergence-free formulations, and hybrid approaches—have addressed key challenges in pressure stability and shock interactions. The growing adoption of OpenFOAM-based IBM frameworks and GPU-accelerated implementations has further expanded their industrial applicability, particularly for moving boundaries and unstructured meshes. Meanwhile, emerging trends like machine learning-assisted optimization and AMR-enhanced IBM frameworks are pushing the boundaries of computational efficiency and adaptive resolution. These advancements have enabled breakthroughs across diverse fields, from high-speed aerodynamics and biofluid dynamics to environmental flows and additive manufacturing, solidifying IBM’s role as a powerful tool in modern computational fluid dynamics for both scientific and engineering applications.

6. Future Scope and Concluding Remarks

The future of IBM holds immense potential for addressing emerging challenges in FSI and expanding their applicability across diverse fields. Advancing computational efficiency for large-scale simulations remains a critical area of focus, particularly for problems involving highly intricate geometries or multi-physics phenomena. Enhancing the accuracy of IB methods in capturing fine-scale interactions, such as those in turbulent flows or systems with soft or flexible structures, presents another promising avenue. Integrating IB methods with machine learning techniques could enable real-time applications and adaptive modeling, while leveraging next-generation computing architectures could revolutionize high-resolution simulations. These directions underscore the need for continued innovation in numerical techniques and cross-disciplinary collaboration to unlock new capabilities.

This review has provided a comprehensive overview of recent advancements in IB methods, with a focus on turbulence modeling and complex geometric handling. By building on foundational works and exploring recent innovations, it demonstrates the versatility and effectiveness of IBMs in addressing intricate FSI challenges across engineering and scientific domains. With ongoing research and technological progress, IB methods are poised to become even more integral to addressing the intricate challenges of modern science and engineering.