Abstract
Mesh adaptation techniques can significantly impact Computational Fluid Dynamics by improving solution accuracy and reducing computational costs. In this review, we begin by defining the concept of mesh adaptation, its core components and the terminology commonly used in the community. We then categorise and evaluate the main adaptation strategies, focusing both on error estimation and mesh modification techniques. In particular, we analyse the two most prominent families of error estimation: feature-based techniques, which target regions of high physical gradients and goal-oriented adjoint methods, which aim to reduce the error in a specific integral quantity of interest. Feature-based methods are advantageous due to their reduced computational cost: they do not require adjoint solvers, and they have a natural ability to introduce anisotropy. A substantial portion of the literature relies on second-order derivatives of scalar flow quantities to construct sensors that can be equidistributed to minimise discretisation error. However, when used carelessly, these methods can lead to over-refinement, and they are generally outperformed by adjoint-based techniques when improving specific target quantities. Goal-oriented methods typically achieve higher accuracy in fewer adaptation steps with coarser meshes. It will be seen that various approaches have been developed to incorporate anisotropy into adjoint-based adaptation, including hybrid error sensors that combine feature-based and goal-oriented indicators, sequential strategies and adjoint weighting of fluxes. After years of limited progress, recent work has demonstrated promising results, including certifiable solutions and applications to increasingly complex cases such as transonic compressor blades and film-cooled turbines. Despite these advances, several critical challenges remain: efficient parallelisation, robust geometry integration, application to unsteady flows and deployment in high-order discretisation frameworks. Finally, examples of the potential role of artificial intelligence in guiding or accelerating mesh adaptation are also discussed.
1. Introduction
1.1. Background and Motivation
The use of Computational Fluid Dynamics (CFD) has steadily grown as improvements in computer hardware, numerical accuracy and general reliability have been accomplished. As a consequence, it is now employed on a daily basis in industrial settings, such as Airbus, Boeing and Rolls-Royce, in the design process of a wide variety of components. As highlighted by [1], the simulation of steady, transonic/supersonic flows may be considered a solved problem, for which reason CFD is consistently utilised for preliminary aerodynamic design. For example, Refs. [1,2] report aircraft development cases where computer simulations have or are predicted to aid the design process. In particular, during the Boeing 777 design process, CFD use was mainly related to the wing at high-speed, fuselage and engine/wing interfaces. Interestingly, the cab design was entirely carried out utilising computer simulations, and no further modifications were required after wind-tunnel experiments. This meant that experimental testing would be unnecessary for future cab design. Additionally, the authors state that the steady increase in CFD simulations has allowed a consistent reduction in wind-tunnel testing in an ever-decreasing number of wing designs. These developments have, therefore, allowed significant costs and time savings.
Concerning jet engine manufacturing, ref. [3] describes the current status of the usage of CFD on various components of a modern turbofan jet engine. In particular, the authors report a reduction in the experimental testing of high-pressure compressors at Pratt & Whitney as a result of CFD simulations. Similarly, ref. [4] shows how a Reynolds-Averaged Navier-Stokes (RANS) study favoured the improvement of fan and low-pressure compressor efficiency by and , respectively, with savings of 20 M$ in rig testing.
Despite these successes, a more pessimistic view was given by [5]: if CFD fails to correctly predict the performance of turbomachinery components, the redesign and retesting process cost can be of the order of 100 M$. In particular, they give an idea of the accuracy range required in today’s designs of high-pressure turbines and compressors. For the first item, a reduction in the cooling rate will result in cycle efficiency increase in the gas turbine, while for the second, improving the adiabatic efficiency by will yield an overall cycle efficiency increase of . These performance gains are becoming more difficult to obtain, and thus, accuracy is of paramount importance. For example, the 3rd Drag-Prediction Workshop results showed significant scatter in the drag coefficient () predictions from various codes using different turbulence models and meshes. As noted by [6,7], a variation of just in computations can represent up to passengers in payload capacity for a civil aircraft. Additionally, they highlight how the same CFD code employing the same turbulence model gave dissimilar results in mesh independence studies starting from different grids. As stated by [8], it is very difficult to achieve a CFD solution that properly resolves all flow features. The authors give a twofold explanation as to why this is the case. Firstly, grid generation, having always been an issue, has become even more intricate due to the greater complexity of the geometries modelled today. Additionally, this will also augment the burden on the flow solver, as many more smaller flow complexities will start to appear. The second reason for CFD shortcomings is related to the nonlinear nature of fluid flow and the model Navier–Stokes (NS) relations. For these reasons, the authors argue that multiple mesh independence studies are required to achieve a reliable solution for a single case. In terms of time consumption, it should be noted that a complete refinement of a grid will increase the simulation time sixteen-fold. Therefore, it can be concluded that the use of an automatic approach to modify a grid to reliably compute the flow solution would solve the issue. Moreover, as pointed out by [9], a successful mesh adaptation and error estimation technique would allow for the reaching of an asymptotic convergence of the flow solution, and thus reliability, on coarser grids. This, in turn, would have a positive outcome on a variety of aspects of a generic aerodynamic design process, such as reducing user/expert interaction, improved final design due to more accurate solutions, increased widespread employment of CFD and so on.
1.2. Objectives of the Review
With the need for mesh adaptation technology having been justified, the aim of this review is to critically examine the development, implementation and future potential of mesh adaptation techniques in CFD. The aims and objectives are as follows:
- To introduce the fundamental concepts behind mesh adaptation: error estimation, adaptation mechanics and optimality criteria.
- To classify and evaluate the most successful mesh adaptation methodologies, generally revolving around the feature-based and goal-oriented approaches.
- To critically assess the advantages and limitations of each adaptation technique, including aspects such as anisotropy, solver integration and industrial deployment.
- To highlight recent advances in mesh adaptation, such as the use of fully tetrahedral mesh regeneration for viscous flows, solution certification and industrial applications.
- To identify challenges and future research directions that could enable the more widespread adoption of mesh adaptation, including the role of artificial intelligence, high-order methods, unsteady flows and parallel computations.
By fulfilling these points, this paper aims to provide a reference for researchers who wish to implement mesh adaptation techniques in their CFD workflows.
This paper is an updated version of the material presented in the first author’s thesis [10].
2. Understanding Mesh Adaptation
The birth of mesh adaptation as an individual research theme dates back to the early 1980s, with the first conferences dedicated to this subject taking place in 1982 [11]. It consists of the automatic modification of a grid based on some sensor to reduce the discretisation error (de) without the need to refine the mesh uniformly. According to [12,13], this type of error is the most difficult to estimate and the main source of inaccuracy in a CFD solution, with others being round-off, iterative and statistical sampling errors. In a more general framework, ref. [14] also includes modelling inaccuracies, input uncertainties and post-processing errors as causes of solution inexactness.
The de of a partial differential equation (pde) is defined as the difference between the continuous analytical solution and that of the discretised system [12]. The very same author is able to show how this quantity acts as a local source of error than for the NS relations and is then transported via the convection terms throughout the domain. To this end, two different test cases to show this behaviour are illustrated: in subsonic flow, the de is propagated along the streamlines, while, for hypersonic cases, it is convected along Mach lines.
Apart from the automated accuracy improvement with minimal node count, optimal mesh adaptation can be beneficial to other aspects. As stated by [15], without mesh adaptation, the grid generation process is far too complex. In fact, if it is not employed in the overall CFD procedure, a significant amount of time has to be spent by the engineer to generate an appropriate mesh. Moreover, unless the user has a basic knowledge of the test-case aerodynamics and the flow solver’s numerical performance, the overall process can require iteratively modifying the grid and running the solver to achieve an appreciable level of convergence of the parameters of interest and resolution of the main flow features.
There are two main branches concerning mesh adaptation. These are divided according to the flow solution availability: a-priori techniques do not utilise any data other than the grid itself, while a-posteriori approaches will require an initial evaluation of the flow solution. The former techniques concern mainly the geometric characteristics of the mesh, such as cell aspect ratio, skewness and size transition. Due to the fact that important regions of the flow are unknown, it is not possible to add, remove or move nodes strategically, which is why these techniques have found limited use. On the other hand, a-posteriori procedures have shown consistent solution improvement with limited node addition, as they target the flow regions where most complex features appear. The latter mesh adaptation process can be considered a classical closed-loop feedback system, as shown in Figure 1. In fact, once the flow solution is evaluated, an error estimation procedure follows. This is where the main diversity of the mesh adaptation technology resides, with a large number of possible strategies being currently available from published work. Once the error has been determined, it is employed to add/remove/move nodes in the domain or regenerate the mesh entirely, with the procedure being repeated for a user-specified number of iterations or error convergence level.
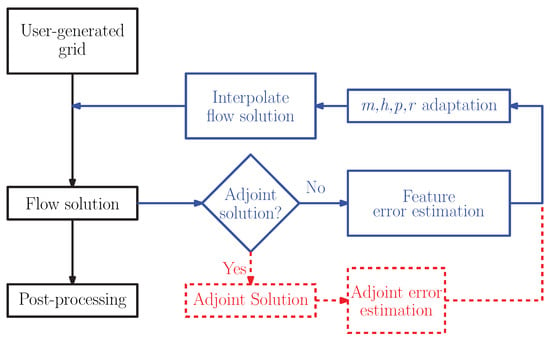
Figure 1.
CFD process augmented with an a-posteriori mesh adaptation feedback system. Blue arrows relate to feature-based approaches, red to goal-oriented ones.
In general, mesh adaptation can be seen as an automated control system to drive a car. The fact that it has to remain within the carriage delimiters and avoid hitting the opposing traffic on one side or the pedestrian pavement on the other represents the stability limits of the flow solver. Repeated readings from the vehicle status allow the control algorithm to limit the car’s movement within the boundaries equidistant from each side, with slight over- and under-shoots being corrected. Similarly, the iterative application of the grid modification technique should achieve flow accuracy convergence, with the solution oscillating within the limits of flow solver stability. Historically, this last point has represented one of the main complexities when employing mesh adaptation techniques. In fact, often, the initial flow solution is not in asymptotic range; i.e., it does not capture all the physical features present in the flow (regardless of their sharpness). Grid modification in one region may cause new, previously undetected complexities to appear. These may distort the mesh too much or fall in portions of the mesh that are unsuitable for solver stability, therefore impeding any further analysis. This has probably been one of the main reasons behind the limited use of mesh adaptation in industrial settings. Nowadays, however, this issue has been, for a particular meshing strategy and modelling, solved, and it will be discussed later on in more detail.
The overall mesh adaptation process can be split into three components [11]:
- Optimal mesh determination;
- Error estimation;
- Adaptation mechanics.
2.1. Optimality Criteria
To appropriately modify a mesh, it is necessary to be able to determine when it reaches its optimal state. This means that the solution is sufficiently accurate that no further change is required. In fact, the user will generally not know when this point has been reached, as the location and intensity of flow characteristics may only be guessed in either case, requiring a significant amount of experience.
In general, all techniques do employ the so-called error-equidistribution principle. This states that the optimal mesh is reached once the error sensor employed is equal over all elements in the mesh [16]. Here, the author also reviews the proof of this concept. From a more intuitive point of view, ref. [15] expresses it as a mapping from the physical space, where cell sizes may have any value, to a computational domain, where the grid elements have uniform size. During the mesh adaptation process, a threshold is then determined to equidistribute the inaccuracies in the grid, and once the statistical average error in the mesh has a relatively constant behaviour, it is possible to terminate the procedure (see, e.g., [17] for a feature-based approach and [18] for an adjoint-related case). A statistical analysis is not always employed, though. In fact, a final inaccuracy level may be determined starting with the application of the equidistribution principle ([19]), while in other cases, a limit on the number of adaptation steps or final node count may be preferred. This is sometimes referred to as complexity, and the use of such philosophy to control the adaptation process may be found in [20]. In [21], the adaptation stopping criteria considered were the variation in the quantities of interest (i.e., lift coefficient, pressure and viscous drag) over three consecutive adaptation cycles: if this was below to (depending on the quantity), the adaptation was stopped.
2.2. Error Estimation
In general terms, there are two popular branches of error estimation techniques published in the literature. The oldest of these two methods is the feature-based approach. In this case, the data of interest relate to physical values of the nonlinear flow, such as density or static pressure, to capture shocks present in the solution. Ideally, the best parameter to apply is one that enables the identification of all the flow intricacies, thus allowing node clustering to occur where they appear. On the other hand, the chosen physical variable should also be able to identify where fewer nodes are needed, as the solution has a linear behaviour and thus can be easily replicated using a coarser grid.
The other main mesh error estimation is generically called goal-oriented and makes use of adjoint technology. Originally, this technique was devised to optimise geometry with an attenuated computational effort with respect to (wrt) other approaches, such as the finite-difference method (FDM). Once the nonlinear flow solution has been achieved, an adjoint solver is employed to determine the sensitivity of an integral quantity of interest (e.g., lift) wrt multiple design parameters. This is written as follows:
where the adjoint state vector is , f is the quantity to be optimised, such as lift or drag, is the residual vector and is the vector of conservative variables. As Figure 2 shows, the overarching philosophy of the adjoint method is visible. Instead of perturbing a design variable, , and observing how this propagates through the system (via the NS relations) in forward mode to affect a functionalf, the method works in reverse. This means that it perturbs f to determine which changes in would influence it most. In general, there are more design parameters, , than there are performance quantities f; therefore the adjoint approach allows for a reduction in computations. As will be seen later, this extra computation can provide an indication as to where solution imbalances are most influential on the functional level; therefore, it specifies which regions of the mesh ought to be modified.
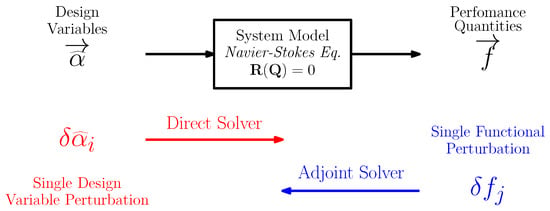
Figure 2.
Direct and adjoint sensitivity computation. From [10].
At this point, it should be highlighted that feature-based approaches will attempt to improve the overall flow solution, while adjoint techniques will only better the quantity they were evaluated for. Naively, it is easy to conclude that the former approaches should be pursued, as they are designed to modify the mesh to predict the overall flow solution more accurately, not just a single value. Significant research has shown, however, that adjoint approaches are more reliable and end up generating coarser grids (see, for example, [20,22,23,24]).
In this section, feature and goal-based methods have been touched upon, providing the generic definition. Due to their importance and the large number of applications, a more in-depth analysis will be provided in Section 3 and Section 4, respectively. A summary of the main characteristics of both approaches is provided in Table 1.
Another class of mesh adaptation sensors is truncation error (te)-based, with this being defined as the difference between the continuous pde and the discretised version [13]. It may be determined by employing the Taylor-Series expansion, but this can be quite complicated and long-winded unless the pde at hand is relatively simple [25]. To this end, [26,27] employed the Taylor-Series to derive expressions relating mesh quality and te for typical 2D and 3D CFD grids. Despite the validity of the technique elaborated, it is relatively complex even in its 2D formulation. The te effect was studied in detail by [12]. In his work, the author showed how this quantity is actually a source of error that arises for the NS relations and is then transported to other regions of the domain. To this end, the Continuous and Discrete versions of the Linear Error Transport Equation were derived. The first te estimation approach suggested by the author would require either the exact continuous solution or, in its absence, a Richardson Extrapolation. The second technique necessitates the construction of the continuous operator. While this process is feasible for the case of Finite Element Method (FEM) discretisations, for FDM and the Finite Volume Method (FVM), the procedure is more involved, as it would require a curve fitting process. Another example of the te-based error estimation procedure is the so-called methodology [28], related to multigrid approaches [25]. For other material concerning te-based approaches, the interested reader is referred to the references in [29], while other examples relating the te to adjoint adapted techniques can be found in [30].
A final mention should be made regarding the difference between isotropic and anisotropic approaches. Both words are derived from the Greek language with the prefix iso-, meaning identical, and ani-, meaning different. The suffix -tropos translates to direction. Therefore, in a mesh adaptation setting, the use of these words refers to the directionality of the error estimation and the grid modification technique. In fact, isotropic mesh adaptation will lead to the same error in all three directions, while an anisotropic technique will be able to differentiate whether one direction has a greater error/requires more clustering wrt others. Again, it is easy to understand that the latter will be more efficient, only refining/clustering nodes in the main direction, not in all.
2.3. Adaptation Mechanics
According to [11], there are mainly 4 grid modification approaches:
- r-methods ⇒ nodal movement;
- h-methods ⇒ refinement and coarsening;
- p-methods ⇒ order enrichment;
- m-methods ⇒ regeneration.
As discussed by [31], a mesh movement algorithm comprises three components:
- Monitor function ⇒ quantity driving the node relocation (error);
- Mesh equations ⇒ map between computational and physical domains;
- Interpolation ⇒ solution estimate at the new nodal position.
The monitor function may be determined in three ways: a-priori (see Figure 3), a-posteriori and based on physical arguments [32]. In the case of an isotropic movement, the node relocation driving quantity is a scalar, as it does not convey any directionality information. On the other hand, to achieve anisotropy a matrix-valued quantity is required. Once the monitor function has been determined, it is necessary to equidistribute it over the physical domain. This can be achieved in different manners, i.e., geometric conservation laws, optimal transport or moving mesh pdes [32]. The resulting equation is then discretised and can be solved simultaneously with the physical problem at hand. Alternatively, it can be evaluated sequentially. It is clear that it is the latter approach that requires the interpolation of the flow field. Once the movement equation has been solved, it will produce either the node velocity or location for the adapted mesh.
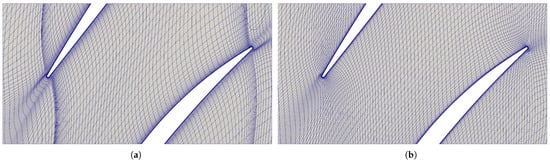
Figure 3.
Example of a-priori mesh movement using control volume-based Laplacian smoothing as the monitor function: (a) Before. (b) After. From [10].
As described by [33], an alternative approach to equidistribution to derive mesh equations is that employing error direct minimisation. By formulating the minimisation in terms of node locations and pde variables, an extra equation may be solved simultaneously with those of the problem at hand. This adds a further unknown to the overall system, i.e., the node position. This technique is generally known as the Moving FEM. One of the most successful mesh movement methods employs a spring-stiffness approach (Figure 4). In this case, the grid edge lengths are the spring-stiffness, while the error can be seen as the potential energy at each node [34]:
where is the spring-stiffness representing the error between nodes , j is the list of neighbours connected to node i through edges and is each node’s displacement vector. Minimising this quantity and considering a smooth relocation of each node to its optimal position leads to the following:
with being a user-defined relaxation factor. Equidistribution is achieved by determining the node locations to achieve system equilibrium. The spring potential energy equations are solved separately from that of the NS relations and in an iterative fashion. Therefore, they will require interpolation of the flow solution or error quantity. An example of its usage on a mesh at mid-span of a transonic compressor blade is reported in Figure 5: the right mesh shows clustering towards a shock. According to [11], there is a further r-adaptation approach: once the error has been determined, this may be employed in an optimisation approach determining the node location minimising the error. An example of such a method is that employed by [35].
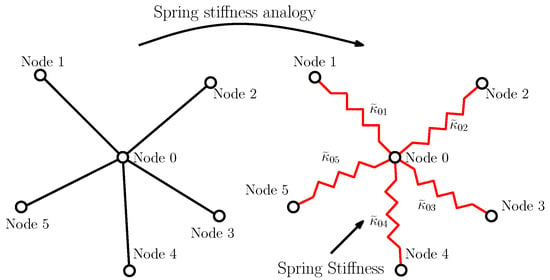
Figure 4.
Mesh movement spring analogy. From [10].

Figure 5.
Initial and mesh-movement anisotropic-adapted meshes. From [10].
A final mention should be made for the mesh movement/deformation methods devised to account for geometry changes. In fact, this may apply in the case of optimisation, or in an unsteady simulation with moving items (e.g., to study fluid-structure interaction). Examples of these techniques are the linear spring method and elasticity, Laplacian smoothing and procedures using the interpolation analogy [36]. The very same authors also provide an overview and classification of the various methodologies.
From a historical perspective, refinement (Figure 6) and coarsening (Figure 7 and Figure 8) methods are possibly the most popular mesh adaptation approaches, having found widespread use in the CFD community. A while back, ref. [37] summarised the advantages of h-adaptation as follows:
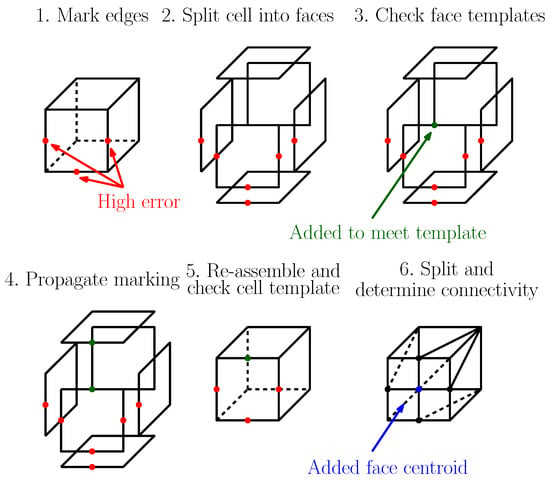
Figure 6.
Mesh refinement procedure example. From [10].
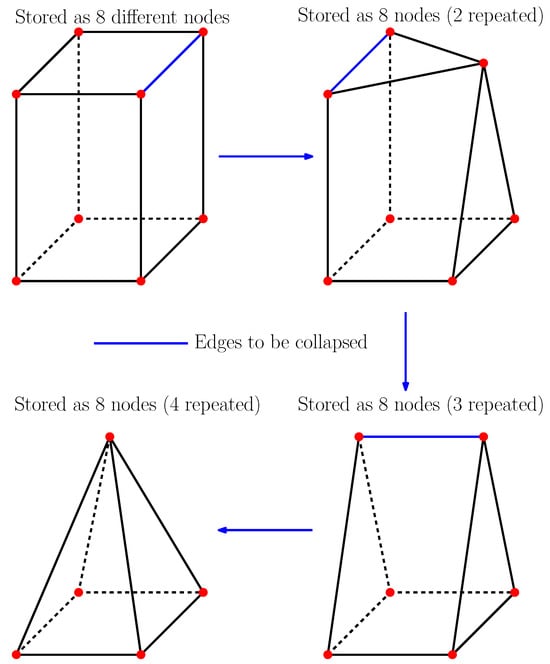
Figure 7.
Repeated mesh coarsening by means of edge collapse. From [10].

Figure 8.
Example of mesh coarsening via repeated edge collapsing: (a) Hand-generated mesh. (b) Coarsening step 1. (c) Coarsening step 2. (d) Final coarsening step. From [10].
- Physical conservation of quantities;
- Robustness;
- Parallelisation.
In their study on tetrahedral meshes, only 3 refinement patterns were allowed. In the subsequent splitting, these templates would be further constrained. The aim was to maintain mesh quality. On the other hand, for the coarsening, they allowed more possibilities, independently of whether adaptation had been previously applied to the cells. An interesting point concerning their work, is the effort to try to reduce the amount of information stored from the previous grid in an attempt to minimise the memory burden.
Again employing tetrahedral grids, ref. [38] studied the refinement effect on the resulting element’s quality and showed that, regardless of the number of adaptation steps, a limited set of similar tetrahedra can be created.
Shortly afterwards, ref. [39] attempted to refine fully tetrahedral grids in an isotropic fashion to improve control over mesh quality. One of the author’s conclusions relates to the difficulty in employing the refinement of simplicial elements while achieving alignment with the flow anisotropy. Therefore, they concluded that hexahedral elements would be better suited for this purpose. Moreover, in a later article [40], they claimed that, by using these cell types, a gain is achieved in terms of accuracy and resulting grid quality. In this work, an anisotropic h-refinement strategy was developed: edges below a user-defined threshold would be removed (coarsening), while those above it would be split (refinement). It should be noted that the coarsening of the grid was only carried out on elements marked to be removed that appeared as a consequence of previous adaptation steps’ refinement. This means that no parts of the mesh were coarser than the starting grid. Additionally, to avoid hanging nodes, hybrid elements were employed at the interface between finer and coarser regions of the mesh. If these elements required subdivision in future refinement steps, they were removed, and the starting hexahedra would be split instead. An important mention concerns the refinement propagation into undesired regions: in fact, it was noted that extra edges would be marked in an attempt to fulfil the splitting templates available. To avoid this issue, unless the edge marking allowed hexahedra to be split into smaller hexahedra, the cell was subdivided into 6 pyramids by placing a node at its centroid.
As for the previous case, ref. [41] used a hierarchical approach requiring template-splitting definition. Concerning tetrahedral volumes, only three valid configurations were chosen: each of these cell types could only be refined once without splitting it in an isotropic fashion. A similar approach was chosen for hexahedral elements; these could only be split into smaller cubes unless they formed the interface between fine and coarse mesh zones. In total, the refinement algorithm allowed 8 possible subdivisions of hexahedral and pyramidal cells, while 9 were permitted for prisms. The actual code implementation consisted of splitting each volume into its faces and determining the new cells according to the face marking combinations. To avoid coding repeated templates for different orientations of each cell, a rotation of their connectivity data was applied. In [42,43], the authors developed a methodology to be able to refine a fully hexahedral mesh without introducing new types of cells, yet they maintained the grid conformal (see Figure 9). This was an extension of the approach discussed in [44,45]. The process consisted of splitting each edge of a hexahedron into three and applying a “shrinking” of the hexahedral layers. In the final step, the grid connectivity was updated. Shortly afterwards, [46] extended the method just outlined by allowing the local refinement of either nodes, edges, faces and cells, thus increasing the flexibility. As a progression of this work, [47], included the possibility of coarsening, maintaining a conformal grid with solely hexahedral elements. Two ways of doing this were proposed; the first one, a global process, consisted of removing a sheet of connected cells. However, given that this could cause issues further away from the actual coarsening region, they also devised a local operation. In [48], a further improvement of the sheet-refinement algorithm of [46] was achieved by including the element-by-element enrichment approach of [44].
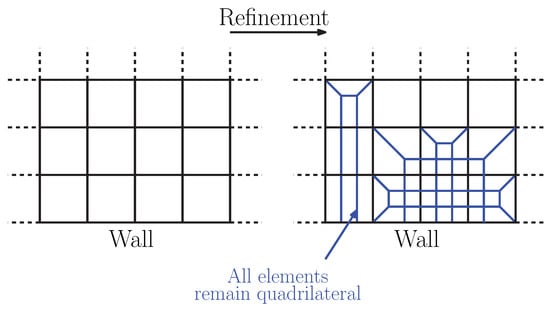
Figure 9.
Example of quadrilateral-to-quadrilateral refinement. Valid in 3D also.
The issue relating to the generation of hanging nodes and different levels of refinement when fully hexahedral grids are employed was also discussed by [49]. As in previous cases, the interface elements between finer and coarser regions were never refined: in subsequent adaptation steps, they would be removed to minimise poor quality. Moreover, the authors managed to reduce the amount of possible transition cases between the two different mesh-density regions.
The effect of over-refinement due to the error directionality not being parallel to the cell faces was discussed by [49]. In this case, the refinement templates were defined by their edges, but the constraints on the possible combinations were governed by the faces; e.g., in their case, they allowed a quadrilateral to have all 4, 2 parallel or 2 adjacent (i.e., sharing a node) and a single edge to be marked, but not 3, and in this case, the fourth would be forced to be split, propagating the refinement. Again, as in previous articles, the authors decided to remove any interface element between the refined hexahedral and the coarser mesh regions at the start of the next adaptation step. Another publication of interest is [50]: here, a discussion of the differences between splitting edges of a fully hexahedral mesh into 2 or 3 sub-edges is explored, with particular attention to the parallel implementation of the former. In fact, once the domain has been split, it is difficult to achieve the same refined mesh, regardless of how the parallel division is carried out. Another refinement methodology of interest is that relating to Cartesian meshes: in this case, starting from a fully quadrilateral or hexahedral grid, it is possible to maintain the element type even after adaptation (see Figure 10). This requires a modification of the solver to be able to handle hanging nodes. Successful examples of Cartesian mesh adaptation are [51,52,53]. An important advantage of these methods relates to their speed. p-methods are sometimes called order enrichment, and they consist of the increase or reduction in the polynomial order in the flow solver. From an intuitive point of view, it is a “flow solver refinement” process, as no change is applied to the physical grid. These techniques are generally applicable to high-order methods (in general high-order methods have an order greater than 2, i.e., that of standard FVM approaches). These methods include FEM or related methods (e.g., Spectral Elements). For this reason, according to [11], in the past, they have found limited use in CFD since, in general, higher-order solvers involve greater complications in terms of monotonicity near discontinuities and in turbulent flow (examples as to how these have been solved can be found in [54] for incompressible flows and [55] for compressible ones). Additionally, the author states that they are more difficult to code since there are more possible templates for each type of cell. Nevertheless, in more recent years, much of the flow solver-related research has been carried out with high-order methods, meaning that p-adaptation techniques have started to gain more and more momentum. Examples of the use of order enrichment can be found in [6,14].
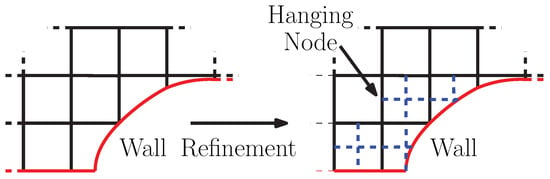
Figure 10.
Example of Cartesian mesh refinement.
Mesh regeneration is now considered the best choice for grid adaptation, as it allows the greatest freedom, flexibility and accuracy in achieving a suitably modified mesh for a given amount of nodes. As discussed by [56], there are several paths one may take. The simplest approach consists of a partial regeneration of the grid. Once features have been detected, portions of the starting mesh are removed and filled with good-quality elements, ideally aligned with the feature. An example of such an approach is provided by [57]. In their work, the authors employed a sensor to determine the feature location and then locally reconstructed the mesh around it using an advancing front approach. Effectively, extracting flow complexities and defining them as geometrical entities, allows this information to be employed in a complete mesh regeneration process. Therefore, the procedure may consist of placing a good-quality, aligned quadrilateral/hexahedral mesh around the flagged complexity. The rest of the domain can then be filled with any combination of hybrid elements, as long as no hanging nodes or negative volumes appear. Examples of mesh regeneration treating the flow features as geometrical entities and regenerating the entire mesh are [58,59,60].
Over time, fully triangular/tetrahedral approaches to mesh regeneration have started to gain popularity due to the shape flexibility in handling very complex solutions and the feasibility of coding such methods. Unlike the previously mentioned techniques, these do not require any pseudo-geometrical information identifying the location of shocks or wakes; they simply employ a continuous metric field, as is described in Section 3. In this approach, given a number of nodes, the distribution of the elements may be optimised to allow alignment and clustering towards the regions of interest. For a detailed, up-to-date analysis of these techniques, the reader is referred to [61,62].
3. Feature-Based Mesh Adaptation
Possibly the most popular feature-related techniques attempt to highlight solution complexities as sources of inaccuracies. Therefore, flow quantities, such as density or Mach number, are generally utilised as sensors. According to [11], common feature-based approaches are differences in variables, the Hessian matrix of flow quantities or a comparison of derivatives.
An example of the calculation of the Hessian of the Mach number at the mid-span of a compressor blade before and after adaptation is shown in Figure 11: clearly, the adaptation has sharpened the sensor where the flow features are (shock, its interaction with the boundary layer and shear layers). One of the main issues regarding these techniques was the inability to handle complexities of different magnitudes [11,15,63]. From a physical standpoint, there is no single flow quantity that has a significant variation over all possible features appearing. For example, in a turbulent transonic flow, the Mach number is able to capture the shock, wake and boundary layer, but is uniformly zero at the wall. Therefore, it would miss, for example, the shock propagation at the wall, unlike the static pressure. On the other hand, this quantity does not vary across any wake, separation and boundary layer present in the solution. To this end, refs. [11,15] suggest using multiple flow parameters with non-dimensionalisation of each indicator. In particular [63], merges multiple flow quantities into a single mesh metric with a local rather than global approach, while [58] utilises the static pressure and Mach number to capture all flow quantities. A similar approach is taken by [59,60], where shocks and wakes are extracted separately by employing a combination of velocity, density, Mach number and static pressure. The solution to this particular problem was provided by [64]: the authors developed the metric definition, such that multiscale phenomena (e.g., turbulence and shock/boundary interaction) could be captured via a unique error sensor.
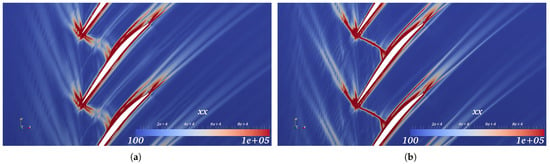
Figure 11.
-component of the Mach number Hessian matrix: (a) Before adaptation. (b) After adaptation. From [10].
One of the main characteristics of feature-based approaches relates to the amount of research that has been carried out to determine anisotropic error sensors. In fact, most flow features display directionality in the sense that variations in quantities across them is far greater than in the tangential direction. Moreover, the ability to align the grid with solution complexities such as shocks will allow for the satisfaction of Rankine–Hugoniot relationships, thus improving accuracy [58]. Being able to determine a directional error estimator will allow for the achievement of a higher density of nodes where they are actually needed, hence also improving the solution. On the other hand, isotropic approaches do not place any relative importance on the error directionality. This is not a disadvantage in terms of achieving improved accuracy, but it concerns the larger amount of nodes required to achieve the same solution wrt anisotropic approaches. It is, therefore, mainly a question of the efficiency of the resulting adapted grid that has pushed the research community towards these techniques. As discussed by [61], the concept of anisotropic mesh adaptation appeared towards the end of the 1980s in [65]. In this case, grid generation was modified to be able to produce elements with different stretching in 2D. Three-dimensional versions were developed a few years later, in [66,67], but according to [61], the visible anisotropy was minimal. A far more powerful approach to capturing the flow features directions was developed by [68]. In this case, the authors argued that the absolute value of the Hessian matrix of a scalar quantity of the flow could be adopted to map the edge length to a Riemannian metric. Obviously, the Hessian matrix represents the error in the linear interpolation over an element [34]. Considering a flow scalar quantity, q, the Hessian matrix, H, can be written as follows:
This can be eigen-decomposed into eigenvalues and eigenvectors as follows:
where the absolute value of eigenvalues, , is considered to ensure positive semi-definiteness to achieve a Riemannian metric. The eigenvectors now indicate the directionality of the error, while the eigenvalues are the error magnitude.
Since then, this technique has been the source of significant research. This process was later employed by [69] in a combined movement and refinement development. The fact that this error estimator can be deployed to move the grid nodes and generate an anisotropic grid makes it suitable in a structured data setting, as no connectivity between the elements is changed. Therefore, [34] made use of it to determine a new edge length that could be fed into a spring-stiffness-based mesh movement procedure, thus allowing equidistribution. Their results showed that the starting mesh had been significantly stretched and clustered towards the main flow features. As previously mentioned, flow quantities are difficult to utilise on their own to adapt the mesh successfully. Therefore, ref. [63] not only combined the metrics of multiple variables but also modified these at the wall and in its vicinity to achieve good orthogonality and allow the user to select a certain wall distance. The finalised error was then used in an edge swap, collapse, split and movement process. The same strategy in terms of grid mechanics, but without any artificial modification of the Hessian matrix or derived metrics, was employed by [17,70,71,72,73]. In their work, they iteratively applied the mesh adaptation process based on the Riemannian metric and were able to show how, starting from different grids, the same final solution could be achieved. Moreover, the final adapted grid produced the same answer when utilised with different flow solvers. However, they did note that, throughout the adaptation process, the solver settings had to be changed to include higher artificial damping to allow satisfactory convergence on the poor initial grids that were created. This requirement was then unnecessary for the resulting grid. In particular, in [17], they show the initial and final error distribution over the mesh. It is clear from the curves that this has been appropriately equidistributed over the domain. Later, in [71], they actually employed the strategy they had devised for 3D flows, yet they were not able to show the same sort of improvement as for the 2D cases they had analysed until then. One of the possible reasons behind the reduced performance is the treatment of turbulent regions near the wall. In fact, as is generally the case, wall functions are used and require suitable grid spacing in order to appropriately capture the entire velocity profile. This is generally not known during the grid generation process and, therefore, should be taken into account in the adaptation process. This was the central aspect of the work in [74]. Here, the authors proposed modifying the near-wall metric derived from the Hessian matrix in two different ways to accommodate cases where wall functions are employed and cases where they are not. To this end, they devised two separate strategies. In cases where the near-wall velocity profile was modelled, they forced the near-wall layers to employ a spacing equal to that specified by the user. In regions such as stagnation points, the requirement was neglected, as it would be too small, and the actual error metric derived was employed instead. For cases where the wall functions were not used, e.g., fully tetrahedral grids, the wall metric was modified to employ the largest eigenvalue perpendicular to the surface, while the other two were aligned tangentially to the wall itself. Another approach employing the Riemannian metric and applying special modifications to the grid in the near wall region is discussed in [75,76].
A different Riemannian metric-based approach to refinement and movement was proposed by [42,43]. In fact, nodes were added while managing to keep the grid fully quadrilateral (in 2D or hexahedral in 3D) without any hanging nodes, thus deploying the mesh movement to smooth out the overall grid. They employed the so-called pillowing approach, as described by [45], alongside the ideas of [44].
Given the successful results obtained by deploying Hessian metrics to adapt the grids, mesh regeneration techniques based on this quantity started to be favoured. It should be clear that two different approaches may be undertaken. The first flags domain features and attempts to build a fully quadrilateral/hexahedral block around it, essentially treating it as a geometrical entity. The remainder of the computational field may then be filled up with a combination of hybrid elements. Another approach which appears to have gained more popularity is the complete grid regeneration employing the Hessian metric to guide the location, size and orientation of tetrahedral elements. Examples of mesh generation employing quadrilateral blocks where the detected flow features can be found in [56,58], whilst a 3D extension of the work is reported in [59]. One of the test cases considered in [58] showed how the grid was regenerated with good-quality quadrilateral blocks around the aerofoil, wake and shock, while the remnant of the domain was filled with relatively smooth triangular elements. The main advantage of the latter approach resides in the fact that triangular/tetrahedral elements allow greater flexibility when attempting to mesh a generic complex domain. For this reason, these latter approaches have been pursued further.
Concerning the complete 3D mesh regeneration with tetrahedral elements, much work has been carried out at the Institut National De Recherche en Informatique et Automatique (INRIA, France), where significant developments in the methodology have been researched. Following the metric definition employing the Hessian matrix, they managed to determine an upper bound to the interpolation error that is independent of the problem at hand [77]. Moreover, they have related the anisotropic measure to the shape, size and orientation of a tetrahedral element. However, the error field is discrete in the sense that it is only available at the points where the solution has been evaluated using the flow solver. Given that regenerating the mesh to cluster points according to the metric will place them in different locations, a continuous version of the field is required. To this end [78] employs interpolation techniques to achieve this continuous representation, while in other publications, [79,80,81], rigorous mathematical derivations, along with applications, are provided. Within the mesh regeneration process, an optimisation step has been included in order to be able to produce a grid that minimises the linear interpolation error for a given amount of nodes [82].
One of the main characteristics of the Hessian matrix computation is the difficulty of being able to achieve a smooth and accurate field. This is, in part, due to the test-case complexity, along with the starting mesh resolution and the accuracy of the flow solver (most FVM codes are accurate; therefore, the derivatives are at the limit of the flow solver’s capability). A comparison of various approaches to carrying out the Hessian-matrix determination is reported in [83,84]. Nevertheless, it is often necessary to employ artificial strategies in order to be able to smooth the derivatives or the metric itself. Examples of various techniques are provided by [85,86,87,88].
A comparison between the user-time requirements to generate fixed meshes by means of best-practice guidelines and feature adaptation procedures utilising the Hessian of the Mach number was presented by [89]. While the two types of procedures yielded similar drag estimates, it was reported that the former approach would require three weeks, while that for a coarse starting mesh for the adaptation procedure would be less than 2 days. In terms of actual gains in the feature-adapted meshes wrt the user-generated grids presented by [90], the authors reported reaching the same level of accuracy with a staggering 75-times coarse mesh.
An interesting application of the anisotropic continuous meshing framework of [80] was discussed by [91]. The authors had a look at adapting meshes for the High-Lift Common Research Model and the JAXA Standard Model at various angles of attack: it is known that lift prediction near a stall is complex when using RANS solvers. The grid modification strategy used a log-Euclidean interpolation of the initial metric field (Mach number-based) with modifications to consider near-wall requirements. In all cases, they showed that the quantities of interest converged later on user-generated meshes than on the automatically adapted ones; moreover, the latter generally ended up being much coarser (roughly 7 times smaller). In particular, they also highlighted how, during the adaptation process, the solver did not always reach the desired level of residuals but crucially never diverged over the 12∼13 automatic adaptation cycles. A comparison of various adaptation and flow solver codes was carried out by [20]. In this case, in an attempt to simplify the convergence comparison with a standard mesh-independent solution, the High-lift Common Research Model was considered. A particularly important point that was highlighted in this work relates to the nonlinearity of the mesh adaptation process. In other words, starting from a coarse mesh each adaptation step will require a number of adaptation sub-iterations (usually 5 to 10) where the number of mesh nodes is kept constant to improve the process robustness. A recent publication [21] outlined a complete change in philosophy: the fact that fully tetrahedral meshes cannot be used for viscous CFD high-fidelity studies is a misconception related to the existence of a boundary layer that is localised and highly anisotropic. They proceed to employ fully tetrahedral meshes and at every adaptation cycle regenerate the mesh once the or norm multiscale errors have been computed. This significantly simplifies the mesh adaptation procedure for complex geometries. Starting from a generic initial coarse mesh, they were able to show that the solution-adaptive process converges to the same solution regardless of the initial mesh or the error estimate, i.e., a certified mesh-independent solution. They also stated that the norm was a better option than the one. An important aspect that was highlighted was the importance of modifying the flow solver in terms of stability/robustness to be able to carry out this procedure. Some of the upgrades concerned using a combined FVM-FEM discretisation and implicit time-stepping. A critical aspect that was mentioned in the last paragraph relates to achieving a certified solution. The first example of code verification related to feature-based mesh adaptation was presented by [92]; the authors compared different codes using the interpolation error of a scalar function on simple problems such as linear advection–diffusion and laminar flow over a delta wing. A verification of feature-based approaches relying on the linear interpolation of the Mach number and norm errors for the well-known ONERA M6 case was carried out by [93]. In their work, they utilised different mesh adaptation and flow solver codes and managed to show that forces and pitching moments would converge to the same value sooner than fixed meshes designed by means of best-practice guidelines. In particular, they also confirmed that the norm error allows for faster convergence of the quantities of interest. The flow solvers employed in the study utilised three different discretisations: FEM, FVM and mixed FVM/FEM, and found that the FEM solver converged to the final solution sooner.
A particular area that has received a significant amount of interest over the recent decade is mesh adaptation for turbomachinery. The first tests were carried out by [71], who adapted a hybrid prismatic-tetrahedral mesh for a viscous NASA Rotor 37 simulation, run with the turbulence model. They employed the relative Mach number as their sensor to form the Hessian matrix. A combination of movement, edge collapse, swap and split was used to adapt the grid. Despite improving the clustering towards the main features of the flow, the results were not completely satisfactory. More recently, ref. [82] considered the LS89 turbine blade in 2D and NASA Rotor 37 in 3D and regenerated the mesh for both cases. In particular, in the latter case, the authors employed prismatic elements in the boundary layer, that were left untouched by the adaptation. The rest of the domain was filled up with tetrahedral cells, that were actually regenerated employing a Riemannian-metric. Of note, is also the fact that they did not modify the periodic boundary of the starting mesh, that had a node count of 2.8 M. The resulting adapted meshes show how the main flow features are captured, however, there is no indication of how the final grid performs in terms of quantities of interest (such as efficiency or pressure ratio). Regarding the periodic boundary, in [94], the same research group demonstrated the necessary upgrades to be able to handle periodic boundary mesh re-generation for gas turbine components using fully tetrahedral meshes without hexahedral/prismatic elements. Another application of feature-based adaptation applied to jet engines is presented in [95]: here they considered flow separation in a nacelle under cross-wind conditions using isotropic and anisotropic adaptation with two different solvers tuned to the different approaches. An important consideration the authors make is that within the turbomachinery community, mesh adaptation has found limited use due to the heavy use of structured multi-block meshes (Figure 12) that allow good resolution of boundary layers and wakes. This particular industry has now gained a significant experience with these methods. The authors argue, however, that other strategies are needed to be able to handle the increase in complexity. Their results show that both grid modification strategies provide accurate predictions starting from coarse meshes, however, the anisotropic counterpart achieves similar accuracy at size of the isotropic counterpart. Another key statement from this publication is that mesh adaptation is more expensive than 1 shot simulation. A very interesting turbomachinery problem was first considered in [96,97], i.e., a film-cooled nozzle guide vane. The authors employed feature-based Mach number interpolation error in the , and despite the complexity of the case, they achieved flow solver and mesh convergence to obtain a certifiable numerical solution. The ability to apply the same adaptation strategy to another challenging gas turbine configuration was recently seen in [98], where multistage and mixing planes were employed in the modelling. Still regarding this application area, ref. [99] utilised Hessian-based mesh movement in a geometrical optimisation loop of the NASA Rotor 37 test-case.
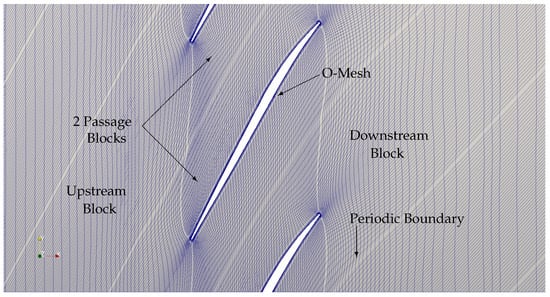
Figure 12.
Example of a structured multi-block mesh generated for a compressor blade.
4. Goal-Oriented Mesh Adaptation
Adjoint error estimation and grid adaptation techniques appeared towards the mid-90s (see, e.g., [100,101]). They attracted particular interest, as, unlike feature-based approaches, they allow the definition of an error threshold [102] and are more reliable in determining an accurate quantity of interest. In fact, feature-related techniques tend to cluster nodes in parts of the flow such as shocks, shear/boundary layers, and wakes, not taking into account the error that may originate in other regions of the flow [103]. Moreover, the same author argued that even te procedures do not consider the relative local effect that this may have on the global quantity. By including the adjoint weighting into the error analysis, ref. [103] showed that it is possible to relate the te in the solution to that of the quantity of interest. In particular, the superconvergent property was proven for FEM, through which the functional achieves double the rate of convergence towards the exact solution wrt the flow quantities. At a later stage, [104] achieved the superconvergence of the performance parameter for all types of discretisation, FDM, FVM and FEM, for both linear and nonlinear problems.
The same approach of weighting the flow residuals vector by the adjoint solution was later employed by [105]. This was applied to a 2D subsonic/transonic flow over NACA 0012 profile. In particular, they attempted to smooth out the flow residuals due to checkerboard behaviour they experienced by introducing a control volume gather and scatter approach. Unfortunately, there appeared to be issues in deciding the amount of smoothing iterations that may be applied, as too many caused solution degradation. Nevertheless, they did show better performance of the adjoint-weighted methods wrt feature and residual-only sensors, as these were incapable of detecting all sources of inaccuracies in the domain.
In the meantime, in a series of articles [19,22,102,106], another adjoint-based adaptation process was presented and applied to FVM solvers. Their work was based on that of [104], with the main difference being that the error on a grid with average spacing was evaluated on an embedded grid with spacing . They determined two types of error: computable correction and non-computable correction. The former is defined as follows:
where both the adjoint and residual vectors are evaluated on a fine mesh, after having been interpolated from a coarse grid solution. This quantity can then be used to improve the functional estimate as follows:
The non-computable counterpart has a much more involved formulation at
where, once again, the flow and adjoint solution are interpolated from a coarse to a fine mesh, but in this case, it is achieved with a linear and quadratic operator and the adjoint residuals on the fine mesh are computed as well. Operations are carried out in a node-wise fashion.
An example of their computation at the mid-span of a transonic compressor blade is reported in Figure 13. It may be seen that the non-computable counterpart tends to weight much more adjoint features, unlike the computable counterpart that contains both. Both of them were evaluated on the embedded grid, with the former simply being the flow residuals vector multiplied by the adjoint. The non-computable correction term is an estimation of the remaining error due to the prolongation of the adjoint solution, instead of using the exact quantity. They argued that, as the computable version could be reliably calculated if the grid were in asymptotic range and used to improve the functional estimate, the non-computable version should be employed for the actual cell-based refinement. It is important to note that their non-computable sensor is composed of the average of both primal and dual computations of the remaining error and, therefore, can be used to reduce the duality gap, thus highlighting nonlinearities present in the flow. One of the requirements for evaluating the error is the need to interpolate both flow and adjoint solutions linearly and quadratically. In [22], they also proved significant benefits wrt Hessian-metric-based procedures for 2D inviscid flows. In an attempt to improve the drag evaluated on the lower aerofoil in a tandem-aerofoil configuration, they proved how a pressure-sensor significantly over-refines the grid trying to sufficiently resolve all the flow features, thus wasting valuable resources. On the other hand, adjoint-based processes only flagged regions where the functional was affected by errors. In particular, they highlighted how the leading edge of the two aerofoils was refined in a different manner by the adjoint error estimate and identically by the feature-based approach. In their final article concerning adjoint adaptation [19], viscous flow conditions were considered. In their previous work, the mesh adaptation had been carried out by regenerating fully triangular grids by determining each element’s size using the non-computable term. In this case, they included anisotropy in the grid regeneration procedure. This was done utilising the standard Hessian-based Riemannian-metric calculation (see [61,63,65,72] for examples of this error computation). In their case, they employed the Mach number as the flow quantity of interest to be able to determine the stretching and orientation of the mesh cells. On the other hand, the element size was computed by equidistributing the remaining error in the adjoint adaptation formulation. One of the test cases they employed was the RAE 2822 in turbulent flow. They were able to show the improvement of the devised methodology wrt the pure Hessian-based mesh regeneration. In particular, it was consistently proven that the quantity of interest is better approximated with fewer nodes when taking the adjoint error into account. The adjoint-related processes were better at reducing the inaccuracies in the inviscid part of the flow and also improving the wake resolution. It should be noted that the latter clustering is probably due to the combination of the Hessian with the flow solution residuals present in the remaining error. In fact, adjoint approaches do not tend to highlight downstream regions as those requiring refinement. On the other hand, the pure Hessian technique tends to over-cluster the regions near the geometry, thus neglecting any inaccuracy due to the rest of the domain. A similar approach was taken by [107,108]. They employed a method to include the adjoint error estimate as derived by [109] into a Riemannian metric formulated through the Hessian for FEM solvers. They also managed to combine the metrics of different quantities.
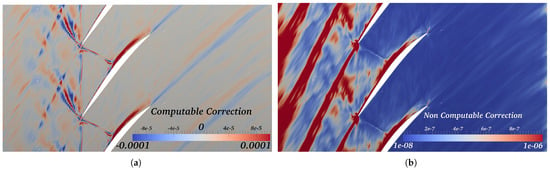
Figure 13.
Adjoint error evaluated a mid-span of a transonic compressor blade according to the method of [22]: (a) Computable correction. (b) Non-computable correction. From [10].
The first successful attempts at adapting the mesh based on the adjoint error in 3D were those of [110] for inviscid simulations and [111] for viscous simulations. In [110], the author paid particular attention to the interpolation scheme employed to transfer the flow and adjoint solutions from coarse to embedded grids. In fact, while the linear prolongation can be carried out by simply averaging values along edges, faces or cells, the quadratic is more involved. Ref. [19] had originally proposed local-least squares process with error minimisation on the coarse mesh, thus achieving a discontinuous quadratic reconstruction. The embedded node values were then determined by averaging the coarse grid parameters of the points to which they were connected. Ref. [110] instead proposed using a cubic fit along each edge employing the gradients determined with the least-squares approach (see [112] for how the gradient is calculated). However, the main finding concerned the effect that using the linear or high-order interpolation had on the computable error term. In the test case considered (ONERA M6), it was seen how using the lower-accuracy interpolation for the correction factor would improve the functional estimate but not as much as using the quadratic operator.
In [111], anisotropy was merged with the adjoint error analysis, as in [19]. This was done by employing the Mach number Hessian and scaling the maximum eigenvalue of each node’s second derivatives matrix by the adjoint sensor. Results for the ONERA M6 inviscid transonic case showed that this approach tends to converge to a more accurate result sooner and with fewer nodes wrt the procedure formulated in [110]. The results reported confirmed the improvement obtained by combining the adjoint with the feature-based adaptation technique: it was clear that the proposed methods resulted in a coarser mesh. It is of interest to note, however, that the inclusion of anisotropy did not cause any visible refinement around the shock, unlike the isotropic approach, where part of the shock structure was clearly visible. The author suggested that the cause of this may be related to the shock location being more important than its resolution to appropriately determine the functional of interest.
Concerning the viscous case analysed, this consisted of the extruded NACA 0012, with the functional of interest being drag. In this case as well, the author was able to show how the adjoint error combined with the anisotropic approach successfully reduced the error in the performance quantity. However, it was observed that the computable correction evaluated on the fine grid was not as accurate as in the inviscid cases due to oscillations in the interpolation that caused non-physical negative turbulent viscosity to appear.
A different approach combining adjoint error calculations with feature-based approaches to achieve anisotropy was proposed by [113,114]. In this case, the user-generated grid was repeatedly adapted using the approach of [34] to move grid nodes. Once this had converged, the adjoint sensor developed by [109] would be computed and used in an isotropic fashion to refine the mesh. The authors reported significant benefits using the feature preliminary step at no extra cost in terms of nodal addition (Figure 14).

Figure 14.
Reduction effect of feature-based adaptation on the computable correction [102]: (a) Before adaptation. (b) After adaptation. From [10].
A detailed study on the effect of interpolation techniques relative to the adjoint solution for computable and non-computable errors was carried out in [115]. In their simulation, they employed an embedded-boundary Cartesian method. They applied two sets of interpolation techniques for the adjoint solution from coarse to fine grids: a piecewise constant and a higher-order reconstruction involving the gradients calculated using a least squares solver with a Barth–Jespersen limiter [116]; the second procedure made use of trilinear and triquadratic polynomials. Their results showed that using the better interpolation approach (tricubic) improved the error correction estimate, but it was sufficient to use linear interpolation to determine the adaptation parameter. Additionally, they also compared the error estimate using the adjoint solution solved on the fine grid. From the data, they concluded that the error correction is better estimated this way, but the tricubic interpolation is close in terms of performance. Of note is also the fact that their refinement algorithm was cell-based and that they started the adaptation process by adding a small amount of nodes progressively increasing the quantity. They argued that, at the start, the error will not be as accurate; therefore, limiting the node addition will avoid wasting resources. To this end, the very same authors in [18] employed the varying threshold philosophy in an attempt to devise a robust and generic strategy. Utilising a similar philosophy to [117], they were able to show, for an inviscid transonic ONERA M6 simulation, that employing a varying threshold achieved the same accuracy of the final grid with fewer nodes wrt a constant-threshold approach. In fact, their technique attempted to equidistribute the error over the entire mesh by attacking the highest sources of it in the first few adaptation steps. By gradually reducing the value, more and more low-error cells were split. This procedure also allowed for relatively limited refinement in the beginning, and only in the last few adaptation steps did the node count substantially increase. It was clear that the changing threshold procedure always resulted in a lower node count wrt the constant valued procedure, still reaching the same error level. This then resulted in a reduced run time.
As the complexity of the cases grew, there was the necessity to parallelise the adaptation process. In fact, the need for an embedded mesh, along with linear and quadratically prolonged flow and adjoint solutions, requires significant computational memory capabilities. To this end, [118] were the first to employ a parallel-mesh adaptation code. In particular, it is interesting to note that they modified the non-computable correction term to include the quadratically interpolated flow and adjoint solution residuals. According to the authors, this allowed a much more accurate error map, although at the expense of the technique’s robustness. Of note is that, as they did not have flux limiters available in the adjoint solver, the adaptation process had to be halted due to poor convergence performance. Nevertheless, they applied the adjoint procedure to the DLR F6 case in turbulent flow. The reported error maps showed a very noisy sensor, but in general, it did present a combination of both flow and adjoint features.
Investigations into methods to reduce the noisiness of the sensor map were carried out by [119]. In particular, the cases of interest were the ONERA M5 and M6, simulated with an Euler solver. Concerning the adaptation procedure chosen, they employed the computable error correction due to the extra burden that computing the fine grid adjoint residuals would cause in terms of memory consumption. This was combined with its standard deviation to determine an error threshold. The interpolation parameters from a coarse to a fine grid were those employed by [110]. The actual refinement was carried out by marking nodes with high error on the fine mesh and consequently any cell on the coarse mesh containing them. There were two interesting aspects reported by their research. Firstly, they employed the volume-weighted gather and scatter approach used by [105] to smooth out the flow residuals, as high-frequency noise due to the interpolation was present. This allowed them to improve the computable-correction estimate. It was seen that there was an optimal number of residual smoothing iterations: too few, and the high-frequency interpolation will dominate the computable error; too many, and the smoothing will dampen it. Additionally, they also showed that using multiple refinement steps to generate the grid onto which to interpolate and evaluate the error helps achieve a more accurate solution. Additionally, the error calculated using linear or quadratic prolongation, with or without smoothing, is always improved by using multiple layers of refinement.
Despite their very promising findings, the same authors were unable to show the same improvement for viscous flow computations [120]. The performance quantity of interest for their study was drag for the ONERA M6 case, simulated with the Spalart–Allmaras (SA) turbulence model. The main finding of this work concerned the use of the residuals smoothing approach. In fact, they stated that even one iteration of it would significantly dampen the error map and remove significant features that were necessary for appropriate adaptation.
Adjoint mesh adaptation procedures related to the technique developed by [109] require the starting grid to be in the asymptotic range of the exact solution. This requirement is necessary due to the interpolation to the embedded mesh (just as for the Richardson extrapolation process [16]). While this requirement is true in a strict sense, [121] was able to show that the process would work even when the starting mesh was too coarse. In particular, they employed the strategy outlined by [109] to adapt a 3D Euler flow around various conical configurations in order to accurately predict the pressure signal at a certain location in the domain. Despite starting from a grid with a limited node count, the authors were able to successfully adapt it. What is interesting is that they always found that the first few adaptation steps would have relatively strong error oscillations. The reason behind this, they claim, relates to the starting mesh not being in asymptotic range wrt the correct solution, and therefore, the calculated error will not decrease monotonically, as in [19,22,106].
A detailed comparison of feature and the adjoint-based error estimation (as developed by [109]) in 3D inviscid/viscous flows can be found in [23]. The main change wrt the approach of [109] was the calculation of the interpolated solution to the fine grid: this was done using a moving least squares approach (e.g., see [122]). Additionally, they did not employ mesh regeneration but, rather, isotropic refinement, as each primal volume was marked to be split if the average of its nodal adjoint error values was greater than the threshold. Their work showed how the adjoint adaptation procedure consistently outperformed that using the feature-related approach. Moreover, they also discussed how the latter was much more sensitive to the starting grid wrt the adjoint-related technique.
Similarly, ref. [123] analysed inviscid flow around the NACA 0012, ONERA M6 and DLR F6 wing–nacelle–pylon configuration with the DLR flow solver TAU and reached the same conclusions. In particular, they showed how the technique proposed by [102] with the interpolation suggested by [110] outperformed feature-based approaches in terms of accuracy and final node count. As in [23], they too concluded that adjoint techniques are far superior if the starting mesh is very coarse. Additionally, they compared the computable and non-computable error effectiveness for the adaptation. In particular, they removed the adjoint residuals multiplied by the difference of interpolated flow quantities in the non-computable correction evaluation. From their results, they concluded that non-computable correction is the best option for grid refinement, as it consistently created coarser meshes to match the desired accuracy.
The burden of time and memory usage for adjoint adaptation techniques described by [22] was considered by [124]. In their work, they devised two strategies to be able to overcome this issue. The first consisted of what they call adaptation sub-iterations. These were employed within the overall mesh improvement process by alternating them with the standard and more accurate technique. The error for the sub-iterations was evaluated using the approximate flow and adjoint solution of the adapted mesh. As usual, these are then interpolated to an embedded grid, where the adjoint quantities are smoothed using a block-Jacobi process. The sensor formulation they considered was that consisting of the flow residuals multiplied by the difference of low and high-order prolonged dual solutions. While the smoothed adjoint formed the lower accuracy term, the other was constructed in a different manner. In fact, for every complete error estimation step, as per [22], they actually solved the embedded grid adjoint to remove the remaining error. This expensive solution was then recycled and interpolated to the following adaptation step’s embedded grid to be used as the high-order term. This cheaper technique was successfully applied to a 2D and 3D extruded NACA 0012 case, simulated using a Discontinuous Galerkin (DG, see [125] for an overview of the methodology) steady solver. In all cases, they were able to show the gain in terms of time without any final loss in accuracy.
The second method they proposed to reduce time and memory consumption consisted of modifying the process of [109] by interpolating from the starting grid to a coarser one. For their work, they utilised a lower-order interpolation state, rather than coarsening the physical mesh. The test case used was an unsteady 2D advection Gaussian wave with inflow on the lower and left-hand side of a quadrilateral domain. This was simulated using the Active-Flux methodology [126] and showed positive results.
A separate mention is required for cases where the base strategy of [22] was modified. Ref. [127] combined the use of adjoint error techniques with a defect error correction approach. While the former employed flow and adjoint solutions, duly interpolated to a fine grid, to increase the functional accuracy by one order of magnitude, the latter would attempt to improve the overall flow solution. To be able to employ the defect correction approach, a reconstructed flow solution was required (in this case, they employed cubic splines), which was then fed into an iterative process to determine the base solution’s accuracy or improve the functional’s estimate. However, coupling the two techniques allowed for the achievement of a higher order of accuracy wrt the reconstruction procedure. In particular, they proved this concept for linear and nonlinear quasi-1D and 2D inviscid problems.
Ref. [128] studied the effects of using a continuous or discrete formulation of the adjoint solver in the grid error calculation proposed by [102]. They showed that the presence of shocks is negligible in the mesh adaptation process for both continuous and discrete adjoint formulations. Concerning the performance of the two different dual solver formulations, they concluded that the discrete approach was possibly the best option, as, unless the grid was suitably fine, the continuous counterpart would underperform.
Ref. [129] attempted to overcome the issue of having different errors occurring when perturbing the input, thus allowing to produce insensitive grids. This is particularly important for uncertainty quantification purposes, as these require varying the system parameters to be able to carry out a statistical analysis. Their procedure consisted in modifying the techniques of [22] by introducing unknown perturbations. Therefore, minimising the error equations would also allow a reduction in the discretisation error variability. Again, the refinement process was cell-based.
Finally, ref. [130] considered the effect of constraints in the error reduction in a function of interest, while ref. [131] managed to combine the errors of multiple functionals and ref. [132] employed adjoint error estimation techniques with the turbulence model.
Up to this point, methods and applications related to the work of [19,22,102,104] have been outlined. As pointed out in the literature, it is an expensive process due to its need for an embedded grid, two interpolation operators, two flow and adjoint solutions with their relative residuals. A few attempts have been made to try to reduce the burden of it, as previously described, however, other researchers devised completely different adjoint-based error estimators.
One of the most original techniques is that developed by [133,134]. In this case, the error indicator was based on the idea that artificial dissipation can be the cause of up to of the error in a function of interest [134]. The analysis was based on the Jameson–Schmidt–Turkel (JST, [135]) flux reconstruction scheme, where the and coefficients dampen the higher-order terms where the shock switch detects a flow complexity. In fact, where strong variation in quantities or discontinuities appear, the inclusion of high-order terms causes oscillations that can eventually lead to instability and divergence of the solution. Apart from the error reduction, this procedure presented other advantages, such as avoiding the generation of a fine grid and the consequent interpolation onto it. However, not all flow solvers employ JST flux discretisation, and actually, there are more accurate schemes wrt this, questioning the main idea behind the error formulation [134].
To avoid the necessity to run the adjoint solver and have separate adaptation processes, ref. [136] devised a method involving entropy variables. In their work, they showed that these satisfy an adjoint relation, able to target regions with numerical dissipation. The procedure to actually determine the error is equivalent to that of the computable correction calculated by [102]; however, given the flow solver nature (DG), the embedded mesh interpolation was substituted with the injection of the solution into a higher-order state. Once the error had been computed, cells were marked for refinement, with all their edges being split. The procedure was tested on a NACA 0012 case, with a low Mach number in either inviscid or viscous conditions. In both cases, an improvement in the flow solution was shown, especially wrt traditional adjoint techniques. In particular, the entropy-adjoint approach refined the grid in a noticeably different manner wrt the other adjoint cases. Issues did arise when they adapted the same test-case run in transonic flow conditions. In fact, the shock presence caused problems in terms of entropy production, as it was no longer conserved. To be noted is the fact that their traditional adjoint adaptation cycles showed oscillatory behaviour, and in some cases, they had difficulty adapting the wake, due to the adjoint weighting.
Refs. [35,137] attempted to devise a process to be able to achieve anisotropic adjoint mesh movement. Firstly, they defined the functional error as the difference between the coarse value and the corrected embedded grid one, as calculated in [109]. To be noted is the linear interpolation they employed for the prolongation of quantities from coarse to fine mesh. Following this, they formulated a Lagrangian relationship, containing both the error value and the NS equations as the constraint. Minimising this wrt the grid coordinates, allowed it to be combined with the original error equation, thus producing a modified adjoint relation. The result of this may then be utilised in a steepest descent search algorithm to minimise the overall mesh error by moving the nodes. The procedure they devised included also global refinement if the change in the fine grid estimate was sufficiently small. They successfully applied it to a 2D Poisson problem and an inviscid subsonic diverging nozzle. The procedure appeared to face greater difficulty when the case was transonic, with the authors arguing that this was due to the shock presence. Nevertheless, apart from the functional of interest’s adjoint, the process required an additional adjoint solution for the error sensitivity wrt the mesh coordinates and the steepest descent algorithm for each adaptation step.
A different approach was developed by [138,139,140,141], generally known as “Mesh Optimization via Error Sampling and Synthesis” or “MOESS” within the community. This relates to a high-order discretisation whereby the error is computed according to the localised dual-weighted residual [100] computed using the flow and adjoint solutions at polynomial order p and . The error is then cast in a continuous mesh model allowing the calculation of an optimised metric used to regenerate the mesh in an anisotropic fashion. As mentioned in Section 3, ref. [20] compared different mesh adaptation strategies applied to the 2D High-Lift Common Research Model to study consistency. The authors also employed the adjoint-based adaptation using the different approaches of [19,80,138]. The MOESS-based methods were the fastest at reaching the mesh converged results, with this being particularly visible on the coarser meshes. Although, when the user-defined error levels were decreased, the difference between the adjoint-based methods becomes noticeable. Of note is that the adjoint-based approach had the characteristic of resolving the stagnation streamlines, while the others, as seen many times in the literature (e.g., [19]) also refined the wakes. The authors also noticed a large variation in normal wall spacing. Finally, another major aspect that was highlighted in this study was the rate of mesh convergence. The trajectories were different; however, the adjoint-based approaches always outperformed the other methods. A recent publication employing the MOESS error formulation was presented in [142]. The main focus related to a comparison of the mesh adaptation in the continuous and discontinuous Galerkin formulations for both high-order and linear representations of the mesh. They were able to show that, when using second- and third-order solutions, it is possible to achieve accurate outputs with an order of magnitude less in computational time wrt first-order methods (especially considering continuous discretisation). The study also showed that adapted meshes do not necessarily adhere to best-practice boundary-layer meshing requirements: along the wall a appeared in some regions and did not hinder the accuracy. Finally, regarding the geometry representation, high-order methods can improve the accuracy when combined with mesh adaptation of linear and curved surfaces, with the latter having a better performance in terms of error performance.
Special mention is required for the methodology outlined in [143]: the authors developed a different methodology to couple anisotropy and goal-oriented error estimates. In fact, the former can be seen as a local geometric error estimate, while the latter indicates non-local errors. The combination of the two was achieved by weighting the inviscid fluxes by the adjoint derivatives, which was then written in the continuous mesh form. A calculus of variations was then employed to minimise the error that could be fed into a metric-based mesh generator. The methodology was successfully applied to 3D Euler flows around supersonic and transonic jets. Of note is that the authors also utilised the a-priori and a-posteriori terminology in their manuscript: this relates to a different formulation of the adjoint error. In fact, the former relates to the use of the continuous formulation, while the latter refers to the discrete version. Later on, this was then upgraded to viscous formulations by [144]: apart from the inviscid flux interpolation error, now, the metric includes the viscous and temperature terms. The proposed sensor estimate was then applied to a series of 2D and 3D aerofoils in steady, low-Reynolds-number conditions in subsonic, transonic and supersonic regimes. The function of interest was seen to converge within 5∼10 adaptation steps. Of note is that they did not include any turbulence model in their error formulation. An improved version of this error sensor was then provided by [21]: to start with, the adjoint preconditioner was strengthened to be able to include the turbulence model terms in the error formulation. Finally, in [94] periodic boundary conditions were dealt with and turbomachinery applications were considered.
An example of the verification of adjoint-based mesh adaptation was carried out by [145]. As a first step, the various mesh adaptation strategies considered were verified using analytical flow and adjoint solutions to be able to decouple any solver effects and simply compare the different formulations. The various techniques were seen to have a consistent convergence.
In the series of articles, refs. [146,147,148,149,150,151], the first use of the mesh adjoint output was employed to adapt a grid. The mesh adjoint vector is defined as follows:
In ref. [146], the functional sensitivity wrt the grid coordinates was modified by removing the normal components to the surface of integration of the quantity of interest. The authors claimed that this was required to avoid unnecessarily strong clustering in this region. Moreover, they also forced to 0 the sensitivity at sharp geometrical corners, but the value in the remainder of the flow was left untouched. They showed the validity of their approach by optimising a grid for the Poisson equation with a steepest-descent algorithm. Interestingly, from their first tests, they realised that there was a need for smoothing of the overall sensitivity, as nodal relocation at the leading edge of the inviscid NACA 0012 test case proved to be erratic. Despite only allowing the relocation of small parts of the domain, the authors showed how the functional sensitivity to the mesh reduced after the adaptation. Shortly after, in ref. [147], the refinement of the grid was added into the overall adaptation by adding nodes where the mesh adjoint output was strongest. Again, as in the previous case, the flow was set as inviscid, but most importantly, as the adaptation progressed, they were able to confirm their previous finding, i.e., a reduction in the mesh sensitivity once the grid had been adapted. In a later stage, ref. [148] employed the previous findings to develop a structured mesh regeneration strategy based on mesh adjoint sensitivity. In particular, once the functional derivative wrt the mesh coordinates had been modified according to [146], this was multiplied by the edge length to determine a quantity that would be fed into the elliptic mesh generation algorithm. Finally, ref. [150] was able to apply the method that had been developed to unstructured grids and showed the results for an inviscid NACA 0012 case. Interestingly, the comparison of the final adapted grid with those obtained by [22,134] proved that their grid regeneration strategy was able to produce clustering in the same regions of the flow. Another separate effort in utilising the mesh adjoint to adapt the grid may be seen in [152,153]. In this case, the anisotropy of the adjoint sensor was achieved by approximating the Hessian matrix by applying a gradient operator such as Green–Gauss or least-squares onto the mesh sensitivities. The resulting second-order derivative was then fed into a mesh movement strategy (an example of the error is shown in Figure 15). Significant benefits were reported when compared with the equivalent feature-based approach. Of interest are also the test cases considered: in fact, mesh adaptation was applied to demanding high-Reynolds turbomachinery components.

Figure 15.
Mesh adjoint error. From [10].
Finally, on a slightly different note, refs. [154,155] carried out simultaneous adjoint mesh adaptation and geometry optimisation. Adjoint code capabilities have been developed to be able to optimise a geometry in a more efficient fashion. Given the availability of an adjoint solution, it is then natural to employ it as an error estimate to improve the mesh and provide a more accurate performance quantification. This will, in turn, help improve the design optimisation loop’s robustness.

Table 1.
Summary and comparison of feature and goal-oriented error estimation.
Table 1.
Summary and comparison of feature and goal-oriented error estimation.
| Main Characteristics | Variants | Applications | |
|---|---|---|---|
| Feature-Based |
|
|
|
| Goal-Oriented |
|
|
|
5. Future Mesh Adaptation Research Trends
Today, considerable mesh adaptation improvements have been showcased [21], with the methods being applied to increasingly complex geometries for steady turbulent flows [94,97]. Moreover, a good level of automation and process consistency has been seen [20]. Nevertheless, there are still many areas of mesh adaptation that require a significant amount of research.
Geometry representation is one of them, as the mesh adaptation software requires this information to be able to provide a modified mesh that is the most truthful copy of what is being modelled. As seen in [156], adaptive processes require more stringent tolerances than the grid generation process. Ref. [157] identified one of the problems as being a lack of standard geometry format within the mesh adaptation community, with “IGES” and “STEP” being the most widespread formats. Additionally, they provide two reasons as to why there is poor integration of the geometry information within mesh adaptation: model complexity and geometry construction artefacts. Moreover, to be able to correct any inaccuracies in the model representation, there is no consistent method in the CFD community. With the increase in popularity of high-order methods, it will become increasingly crucial to be able to achieve a robust and automated approach to interfacing with the geometry.
An area of development that will become crucial in the future deals with code parallelisation. In fact, more and more detailed flow features are being resolved on larger configurations. Additionally, there is a growing interest for unsteady modelling with implicit Large Eddy (iLES) and, in some cases, Direct Numerical Simulation (DNS) resolution. Therefore, being able to speed-up the adaptation mechanics procedure becomes crucial. As stated by [158] anisotropic grid adaptation is still in its infancy, unlike isotropic mesh generation. This generally splits the domain into sub-problems that may have varying levels of communication and synchronisation (tightly, partially, weakly or decoupled). The authors also outline 5 points that are crucial to interface the code with new hardware and thus for methodology development:
- Stability ⇒ parallel and sequential executions should generate similar if not identical meshes.
- Reproducibility ⇒ this can be split into strong and weak, depending on how stringent is the requirement that the code produce identical results when restarted with the same input.
- Robustness ⇒ the code should correctly and efficiently process any input data.
- Scalability ⇒ the ratio of sequential to parallel run-time.
- Code Reuse ⇒ this depends on the code implementation strategy.
The literature does describe various successful applications of mesh adaptation in parallel. For example, [159] presented an isotropic hybrid strategy refining and coarsening all standard cell types (tetrahedra, prisms, pyramids and hexahedra). Once the mesh had been modified, load balancing between the processors is carried out. The method’s robustness was proven by application to a fighter aircraft with missiles and pylons. An example of parallel mesh adaptation algorithm involving only tetrahedral meshes to ensure maximum flexibility was reported in [160]. This work is of particular interest as the authors report speed-up gains in parallel; however, they do indicate that the adaptation cost is ∼60% of the runtime, with mesh smoothing being the most time-consuming. Their adaptation algorithm used a combination of refinement/coarsening, along with smoothing. As mentioned, parallel mesh adaptation is particularly crucial for unsteady simulations. A recent example of the successful application was presented in [161]. In this, they employ a Cartesian mesh with feature-based error estimation. They claim an “embarrassingly” parallel algorithm able to scale up to 4000 cores: to achieve this, they split the simulation into time-frames, each adapted simultaneously, rather than sequentially. Another important aspect relates to “time-step” refinement: most of this paper has dealt with spatial discretisation, as these are the only errors present in RANS. However, unsteady simulations will also introduce a time discretisation error, and thus the adaptation must be 4D. More recently, ref. [162] presented an anisotropic adaptation approach carried out in parallel. The approach employed the second derivatives of a flow quantity to refine and coarsen the mesh. A different parallelisation approach was presented in [163]. They utilised refinement/coarsening and smoothing with a Hessian-based metric determination and geometry integration. However, the main interest resides in the so-called “speculative parallelism”, and an efficiency of more than was reported. This particular technique attempts to maximise concurrency without rigidly pre-partitioning the mesh or relying on global synchronisation, typical in many domain-decomposition methods. Each thread attempts to acquire the necessary data dependencies on the fly.
Until now, the discussion has mostly revolved around linear FEM or FVM, with high-order discretisations not really mentioned. These methods are becoming increasingly important, as they allow the same level of resolution to be reached with fewer degrees of freedom compared to standard second-order spatial reconstructions. This results in reduced run times (and thus costs) [164]. Recently, these techniques have gained significant interest due to an increased accuracy requirement within industrial settings. In fact, they allow for unsteady iLES if not DNS at a reduced cost. This type of modelling is needed to handle the intrinsic deterministic and chaotic unsteadiness present in flows [165]. As mentioned in Section 2, high-order discretisations allow for polynomial order enrichment. Examples of its use for an open-source spectral/hp code can be found in [166,167,168,169]. In the first case, a goal-oriented strategy was employed, whereby the error was determined by means of a higher polynomial order. This was then utilised to determine in which elements the solver order had to be increased. Interpolation error bounds were subsequently analysed for high-order curved finite elements. Later on, a field-guided quadrilateral mesh generation method that produces naturally curved, high-order valid meshes using an adaptive spectral element solve was shown. The authors solved the Laplace equations, thus replacing traditional cross fields and avoiding the smoothing requirement. More recently, a combination of polynomial-order and mesh movement was used. A metric-based anisotropic adaptation for high-order interpolation was shown by [170], thus extending traditional Hessian-driven techniques beyond linear interpolation. After, [171] developed an continuous mesh framework for DG schemes. [172] also used a continuous mesh model with a DG discretisation, but this had anisotropic refinement and isotropic polynomial adaptation. [173] focused on understanding the concept of metric conforming meshes with curved elements and extended the work of [138,139] from linear elements to curved, high-order ones in 1D. Later on, [174] compared the original, linear FEM MOESS and the high-order version (called HOLMES or High-Order MOESS) and found that the latter offered a better metric-field, improved the handling of the curved geometry and was more accurate. As expected, though the cost increased.
As mentioned earlier on, unsteady adaptation is becoming increasingly important, and examples of its usage are present in the literature. For example, [175] used multiscale continuous mesh model adaptation for cases with moving boundaries, including time discretisation in error formulation. In terms of grid mechanics, they utilised smoothing and swapping, such that large deformations could be handled without any remeshing. The very same group extended the mesh adaptation to local remeshing for inviscid flows [176], parallelising the adaptation loop. Later on, [53] utilised a combination of user-specified and pressure-based Hessian refinement on very large grids (70M∼250M cells) for Detached Eddy Simulations (DESs) and Unsteady RANS (URANS). It was found that adaptation was critical to capturing vortex onset and progression, as without it, the turbulent kinetic energy and vortex strength were grossly under- or over-predicted. In particular, URANS models caused vortex diffusion without proper mesh resolution. Concerning different unsteady turbulence modelling, ref. [177] utilised the -norm interpolation error over space and time to carry out adaptation. In space, these norms are preferred to the counterpart, as they allow a more balanced targeting of smooth and unsmooth features. Of note is that the Mach number Hessian averaged over multiple time steps was utilised. Transition zones between RANS and LES were targeted via the adaptation, and they found that LES-based metrics enabled a smoother RANS-to-LES transition for Delayed DES (DDES) and better pressure predictions than DDES on RANS-adapted or coarser meshes.
The more recent research topic in mesh adaptation concerns the use of machine learning techniques. A physics-informed, semi-supervised adaptive mesh refinement model was proposed by [178]. Its aim was to predict the accurate solution on an adaptively refined mesh using low-resolution solutions. It was shown that, despite its training on three canonical flows, it was able to generalise to different boundary conditions and unseen geometries with a consequent speed-up when compared to standard CFD methods. Graph Neural Networks (GNNs) were employed by [179] to generate the initial mesh and carry out physics-informed anisotropic adaptation using only open-source tools. The flow solution was predicted in the end. GNNs were also used by [180] in a bid to predict the flow solution without using any flow or structural solver. The mesh morphing in the resulting solutions following the features’ directionality is clearly visible. Anisotropic mesh generation employing machine learning was attempted by [181] in a bid to avoid flow and adjoint solutions. The model was seen to perform well when compared to the MOESS meshes, refining the boundary layer and waking 10∼15 times faster. It was also able to deal with different Reynolds/Mach numbers and angles of attack. Due to a lack of shocks in the training data, the model did not perform well when these were present. Ref. [182] managed to remove the need to compute costly adjoints using Graph Convolutional networks (GCNs) to predict the local error estimator for each cell on an advection–diffusion problem, while [183] employed a small feedforward neural network to determine the anisotropy using MOESS data for training. It was seen that the trained model outperformed MOESS, showing less sensitivity to noisy flow and adjoint solutions, and was generalisable to unseen geometries. Moreover, MOESS required more iterations, as it had to discover the features. A different approach to adaptive mesh refinement was discussed by [184]. In their work, they employed a Markov decision process and then deep reinforcement learning to learn mesh refinement policies. Finally, ref. [185] employed unsupervised learning, along with Gaussian Mixture Models, to split the domain into inviscid/irrotational regions and viscous/turbulent ones. The adaptation then varied the polynomial order in a DG framework.
6. Conclusions
In this paper, a review and analysis of mesh adaptation techniques applied to CFD have been presented. The need for and importance of automated grid modification strategies were discussed, quantifying their significance in an industrial setting. Following this, the main aspects, definitions and terminology were discussed, highlighting two solution error calculations, namely feature-based and goal-oriented. These now form the bulk of the research, showing very promising results for widespread use. Another important concept that has been discussed is anisotropy: this relates to the error having directionality, thus allowing the grid to be modified more strategically and resulting in coarser meshes. Four different grid modification strategies have been outlined: refinement/coarsening, movement, polynomial order increase and grid regeneration. The first two have been extensively utilised in the past, sometimes in combination. However, as complete mesh regeneration approaches have matured, these have appeared more and more frequently, as they allow for the greatest level of flexibility without leading to issues such as over-refinement or problematic cells. The final method, p-adaptation, is limited to high-order flow solvers: while there are some important examples of its usage, more work is required in this area. This will be crucial in the future as industry starts to adopt these types of discretisations to carry out unsteady iLES/DNS modelling.
Two whole sections have then been presented, discussing in more detail various feature and goal-oriented approaches. The two methods have shown a significant amount of success but do have important differences in terms of development and performance. Regarding the first, the literature points to the second-order derivatives of flow quantities using the multiscale error as a strong candidate. The combination of this with the continuous mesh concept allows for full mesh regeneration by means of tetrahedral elements. These would be shaped and oriented by the error, i.e., achieving anisotropy, which is more naturally achieved using feature-based methods. This aspect is more complex to achieve when using adjoint-based methods, but nonetheless, various attempts have been carried out, showcasing one important aspect: adjoint approaches allow the error reduction in a quantity of interest with reduced node counts, fewer adaptation steps and greater reliability than their feature-based counterparts, which can waste resources when high derivatives occur. However, the latter does not require an additional solution (i.e., adjoint), is easier to develop and attempts to improve the solution globally, not for a single quantity of interest. In the past, a lot of research has been undertaken relative to the method of deploying an embedded grid to calculate the adjoint computable or non-computable correction. While this has shown very positive results, its use has gradually reduced favouring methods that do not rely on interpolations and finer grid computations.
An important aspect that requires mention is the continued increase in complexity of the test cases considered. In particular, from an industrial perspective, cases such as wings, full aircraft configurations and gas turbine compressors/turbines have been successfully adapted. These results were achieved with minimal, if any, solver convergence issues, with this having probably been one of the main barriers to the widespread use of mesh adaptation technology.
A final mention concerns future trends: some are issues that need solving, while others have the potential to improve current practices. As mentioned earlier, high-order mesh adaptation needs to be further developed. This will introduce even more challenges when it comes to geometry integration: this is a known problem due to inconsistent file formats and the lack of a standard approach to “clean” the surface representation without introducing errors. As computational power continues to grow, CFD has started to use increasingly finer meshes in both steady and unsteady simulations run on multi-core architectures. Including grid adaptation in the overall modelling pipeline will necessarily require these algorithms to handle mesh partitioning in an efficient and repeatable way. Most of the mesh adaptation literature has revolved around RANS modelling. As unsteady simulations become more and more feasible, grid modification will have to be developed further and applied to these to ensure minimal spatial discretisation errors, such that the user can extract valid and accurate information. Finally, with the rise of artificial intelligence, methods to automatically modify or predict the grid using such techniques have begun to appear and are expected to have a growing impact on improving the CFD modelling pipeline.
Author Contributions
Conceptualization, G.V.; formal analysis, G.V.; investigation, G.V.; resources, N.Q. and S.S.; data curation, G.V.; writing—original draft preparation, G.V.; writing—review and editing, G.V., N.Q. and S.S.; supervision, N.Q. and S.S.; project administration, N.Q. and S.S.; funding acquisition, N.Q. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Rolls-Royce plc grant number 5002531676.
Acknowledgments
Funding for this work was provided by Rolls-Royce plc (grant number 5002531676) and carried out at the University of Sheffield. The authors would also like to express their gratitude to Rolls-Royce plc for the permission to publish.
Conflicts of Interest
Author Shahrokh Shahpar was employed by the company Rolls-Royce Plc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational fluid dynamics |
| DDES | Delayed DES |
| de | Discretisation error |
| DES | Detached Eddy Simulation |
| DG | Discontinuous Galerkin |
| DNS | Direct numerical simulation |
| FDM | Finite difference method |
| FEM | Finite element method |
| FVM | Finite volume method |
| GCN | Graph convolutional networks |
| GMM | Gaussian mixture model |
| GNN | Graph neural networks |
| h-methods | Mesh refinement and coarsening |
| HOLMES | High-Order MOESS |
| iLES | Implicit Large Eddy Simulation |
| INRIA | Institut National de Recherche en Informatique et en Automatique (France) |
| JST | Jameson Schmidt Turkel |
| m-methods | Mesh regeneration |
| MOESS | Mesh optimization via error sampling and synthesis |
| NS | Navier–Stokes |
| p-methods | Polynomial order enrichment |
| pde | Partial differential equation |
| r-methods | Mesh adaptation via node relocation |
| RANS | Reynolds-averaged Navier–Stokes |
| SA | Spalart Allmaras |
| te | Truncation error |
| URANS | Unsteady RANS |
| wrt | wrt |
| Drag coefficient | |
| Functional sensitivity to mesh coordinates | |
| Number of edges connected to node i | |
| f | Functional or quantity of interest |
| Coarse and fine grid spacing | |
| H | Hessian matrix |
| Spring-stiffness coefficient between nodes i and j | |
| Error norms | |
| Potential energy at node i | |
| q | Generic scalar field |
| Navier–Stokes conservative variables vector | |
| Navier–Stokes residual vector | |
| Eigenvectors | |
| Node displacement vector | |
| Wall-normal distance | |
| Design variable | |
| Eigenvalue | |
| Adjoint vector | |
| Relaxation parameter | |
| Linear interpolation operator | |
| Quadratic interpolation operator |
References
- Witherden, F.D.; Jameson, A. Future Directions in Computational Fluid Dynamics. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3791. [Google Scholar]
- Johnson, F.T.; Tinoco, E.N.; Yu, N.J. Thirty years of development and application of CFD at Boeing Commercial Airplanes, Seattle. Comput. Fluids 2005, 34, 1115–1151. [Google Scholar] [CrossRef]
- Laskowski, G.M.; Kopriva, J.; Michelassi, V.; Shankaran, S.; Paliath, U.; Bhaskaran, R.; Wang, Q.; Talnikar, C.; Wang, Z.J.; Jia, F. Future Directions of High Fidelity CFD for Aerothermal Turbomachinery Analysis and Design. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3322. [Google Scholar]
- Fischberg, C.J.; Rhie, C.M.; Zacharias, R.M.; Bradley, P.C.; DesSureault, T.M. Using hundreds of workstations for production running of parallel CFD applications. In Parallel Computational Fluid Dynamics 1995; Elsevier: Amsterdam, The Netherlands, 1996; pp. 9–22. [Google Scholar]
- Sandberg, R.D.; Michelassi, V. The current state of high-fidelity simulations for main gas path turbomachinery components and their industrial impact. Flow Turbul. Combust. 2019, 102, 797–848. [Google Scholar] [CrossRef]
- Fidkowski, K.J.; Darmofal, D.L. Review of output-based error estimation and mesh adaptation in computational fluid dynamics. AIAA J. 2011, 49, 673–694. [Google Scholar] [CrossRef]
- Fidkowski, K.J. A Simplex Cut-Cell Adaptive Method for High-Order Discretizations of the Compressible Navier-Stokes Equations. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Alauzet, F.; Loseille, A. A decade of progress on anisotropic mesh adaptation for computational fluid dynamics. Comput.-Aided Des. 2016, 72, 13–39. [Google Scholar] [CrossRef]
- Park, M.A.; Krakos, J.A.; Michal, T.; Loseille, A.; Alonso, J.J. Unstructured Grid Adaptation: Status, Potential Impacts, and Recommended Investments Toward CFD Vision 2030. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Vivarelli, G. Anisotropic & Edgewise Adjoint Error Estimation & Grid Adaptation with Applications to Turbomachinery Flows. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2019. [Google Scholar]
- Löhner, R. Mesh adaptation in fluid mechanics. Eng. Fract. Mech. 1995, 50, 819–847. [Google Scholar] [CrossRef]
- Roy, C. Strategies for driving mesh adaptation in CFD. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 1302. [Google Scholar]
- Roy, C. Review of discretization error estimators in scientific computing. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4 January 2010; p. 126. [Google Scholar]
- Fidkowski, K.J. Output Based Error Estimation and Mesh Adaptation for Steady and Unsteady Flow Problems. In 38th Advanced CFD Lectures Series; von Karman Institute for Fluid Dynamics (September 14–16, 2015); Deconinck, H., Horvath, T., Eds.; von Karman Institute for Fluid Dynamics: Saint-Genesius-Rode, Belgium, 2015. [Google Scholar]
- Baker, T.J. Mesh adaptation strategies for problems in fluid dynamics. Finite Elem. Anal. Des. 1997, 25, 243–273. [Google Scholar] [CrossRef]
- Baker, T.J. Mesh generation: Art or Science? Prog. Aerosp. Sci. 2005, 41, 29–63. [Google Scholar] [CrossRef]
- Habashi, W.G.; Dompierre, J.; Bourgault, Y.; Fortin, M.; Vallet, M.G. Certifiable computational fluid dynamics through mesh optimization. AIAA J. 1998, 36, 703–711. [Google Scholar] [CrossRef]
- Nemec, M.; Aftosmis, M.; Wintzer, M. Adjoint-based adaptive mesh refinement for complex geometries. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 725. [Google Scholar]
- Venditti, D.A.; Darmofal, D.L. Anisotropic grid adaptation for functional outputs: Application to two-dimensional viscous flows. J. Comput. Phys. 2003, 187, 22–46. [Google Scholar] [CrossRef]
- Michal, T.; Krakos, J.; Kamenetskiy, D.; Galbraith, M.; Ursachi, C.I.; Park, M.A.; Anderson, W.K.; Alauzet, F.; Loseille, A. Comparing unstructured adaptive mesh solutions for the high lift common research airfoil. AIAA J. 2021, 59, 3566–3584. [Google Scholar] [CrossRef]
- Alauzet, F.; Frazza, L. Feature-based and goal-oriented anisotropic mesh adaptation for RANS applications in aeronautics and aerospace. J. Comput. Phys. 2021, 439, 110340. [Google Scholar] [CrossRef]
- Venditti, D.A.; Darmofal, D.L. Grid adaptation for functional outputs: Application to two-dimensional inviscid flows. J. Comput. Phys. 2002, 176, 40–69. [Google Scholar] [CrossRef]
- Balasubramanian, R.; Newman, J.C. Comparison of adjoint-based and feature-based grid adaptation for functional outputs. Int. J. Numer. Methods Fluids 2007, 53, 1541–1569. [Google Scholar] [CrossRef]
- Balan, A.; Park, M.A.; Wood, S.L.; Anderson, W.K.; Rangarajan, A.; Sanjaya, D.P.; May, G. A review and comparison of error estimators for anisotropic mesh adaptation for flow simulations. Comput. Fluids 2022, 234, 105259. [Google Scholar] [CrossRef]
- Fraysse, F.; Valero, E.; Ponsín, J. Comparison of mesh adaptation using the adjoint methodology and truncation error estimates. AIAA J. 2012, 50, 1920–1932. [Google Scholar] [CrossRef]
- Kallinderis, Y.; Kontzialis, C. A priori mesh quality estimation via direct relation between truncation error and mesh distortion. J. Comput. Phys. 2009, 228, 881–902. [Google Scholar] [CrossRef]
- Kallinderis, Y.; Fotia, S. A priori mesh quality metrics for three-dimensional hybrid grids. J. Comput. Phys. 2015, 280, 465–488. [Google Scholar] [CrossRef]
- Brandt, A.; Livne, O.E. Multigrid Techniques: 1984 Guide with Applications to Fluid Dynamics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2011; Volume 67. [Google Scholar]
- Fraysse, F. Numerical Error Prediction and Its Applications in CFD Using τ-Estimation. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2012. [Google Scholar]
- Derlaga, J.M. Application of Improved Truncation Error Estimation Techniques to Adjoint Based Error Estimation and Grid Adaptation. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2015. [Google Scholar]
- Tang, T. Moving mesh methods for computational fluid dynamics. Contemp. Math. 2005, 383, 141–174. [Google Scholar]
- Budd, C.J.; Huang, W.; Russell, R.D. Adaptivity with moving grids. Acta Numer. 2009, 18, 111–241. [Google Scholar] [CrossRef]
- Baines, M.J. Grid adaptation via node movement. Appl. Numer. Math. 1998, 26, 77–96. [Google Scholar] [CrossRef]
- Ait-Ali-Yahia, D.; Habashi, W.G.; Tam, A.; Vallet, M.G.; Fortin, M. A Directionally Adaptive Methodology Using an Edge-Based Error Estimate on Quadrilateral Grids. Int. J. Numer. Methods Fluids 1996, 23, 673–690. [Google Scholar] [CrossRef]
- Diskin, B.; Yamaleev, N. Grid Adaptation using Adjoint-Based Error Minimization. In Proceedings of the 20th AIAA Computational Fluid Dynamics Conference, Honolulu, HI, USA, 27–30 June 2011; p. 3986. [Google Scholar]
- Selim, M.M.; Koomullil, R.P. Mesh deformation approaches—A survey. J. Phys. Math. 2016, 7, 1–9. [Google Scholar]
- Löhner, R.; Baum, J.D. Adaptive h-refinement on 3D unstructured grids for transient problems. Int. J. Numer. Methods Fluids 1992, 14, 1407–1419. [Google Scholar] [CrossRef]
- Liu, A.; Joe, B. Quality local refinement of tetrahedral meshes based on 8-subtetrahedron subdivision. Math. Comput. Am. Math. Soc. 1996, 65, 1183–1200. [Google Scholar] [CrossRef]
- Biswas, R.; Strawn, R.C. Mesh quality control for multiply-refined tetrahedral grids. Appl. Numer. Math. 1996, 20, 337–348. [Google Scholar] [CrossRef]
- Biswas, R.; Strawn, R.C. Tetrahedral and hexahedral mesh adaptation for CFD problems. Appl. Numer. Math. 1998, 26, 135–151. [Google Scholar] [CrossRef]
- Mavriplis, D.J. Adaptive meshing techniques for viscous flow calculations on mixed element unstructured meshes. Int. J. Numer. Methods Fluids 2000, 34, 93–111. [Google Scholar] [CrossRef]
- Tchon, K.F.; Dompierre, J.; Camarero, R. Conformal refinement of all-quadrilateral and all-hexahedral meshes according to an anisotropic metric. In Proceedings of the 11th International Meshing Roundtable, Ithaca, NY, USA, 15–18 September 2002. [Google Scholar]
- Tchon, K.F.; Dompierre, J.; Scamarero, R. Automated refinement of conformal quadrilateral and hexahedral meshes. Int. J. Numer. Methods Eng. 2004, 59, 1539–1562. [Google Scholar] [CrossRef]
- Schneiders, R. A grid-based algorithm for the generation of hexahedral element meshes. Eng. Comput. 1996, 12, 168–177. [Google Scholar] [CrossRef]
- Mitchell, S.A.; Tautges, T.J. Pillowing doublets: Refining a mesh to ensure that faces share at most one edge. In Proceedings of the 4th International Meshing Roundtable, Albuquerque, NM, USA, 16–17 October 1995; pp. 231–240. [Google Scholar]
- Harris, N.J.; Benzley, S.E.; Owen, S.J. Conformal Refinement of All-Hexahedral Element Meshes Based on Multiple Twist Plane Insertion. In Proceedings of the International Meshing Roundtable, Williamsburg, VA, USA, 19–22 September 2004; pp. 157–168. [Google Scholar]
- Benzley, S.E.; Harris, N.J.; Scott, M.; Borden, M.; Owen, S.J. Conformal refinement and coarsening of unstructured hexahedral meshes. J. Comput. Inf. Sci. Eng. 2005, 5, 330–337. [Google Scholar] [CrossRef]
- Parrish, M.; Borden, M.; Staten, M.; Benzley, S. A selective approach to conformal refinement of unstructured hexahedral finite element meshes. In Proceedings of the 16th International Meshing Roundtable, Seattle, WA, USA, 14–17 October 2007; Springer: Berlin/Heidelberg, Germany, 2008; pp. 251–268. [Google Scholar]
- Nicolas, G.; Fouquet, T.; Geniaut, S.; Cuvilliez, S. Improved adaptive mesh refinement for conformal hexahedral meshes. Adv. Eng. Softw. 2016, 102, 14–28. [Google Scholar] [CrossRef]
- Owen, S.J.; Shih, R.M. A Template-Based Approach for Parallel Hexahedral Two-Refinement. Procedia Eng. 2015, 124, 31–43. [Google Scholar] [CrossRef]
- Wintzer, M.; Nemec, M.; Aftosmis, M. Adjoint-based adaptive mesh refinement for sonic boom prediction. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008; p. 6593. [Google Scholar]
- Wackers, J.; Deng, G.; Guilmineau, E.; Leroyer, A.; Queutey, P.; Visonneau, M. Combined refinement criteria for anisotropic grid refinement in free-surface flow simulation. Comput. Fluids 2014, 92, 209–222. [Google Scholar] [CrossRef]
- Bhushan, S.; Yoon, H.; Stern, F.; Guilmineau, E.; Visonneau, M.; Toxopeus, S.; Simonsen, C.; Aram, S.; Kim, S.; Grigoropoulos, G. Assessment of computational fluid dynamic for surface combatant 5415 at straight ahead and static drift β = 20 deg. J. Fluids Eng. 2019, 141, 051101. [Google Scholar] [CrossRef]
- Kirby, R.M.; Sherwin, S.J. Stabilisation of spectral/hp element methods through spectral vanishing viscosity: Application to fluid mechanics modelling. Comput. Methods Appl. Mech. Eng. 2006, 195, 3128–3144. [Google Scholar] [CrossRef]
- Moro, D.; Nguyen, N.C.; Peraire, J. Dilation-based shock capturing for high-order methods. Int. J. Numer. Methods Fluids 2016, 82, 398–416. [Google Scholar] [CrossRef]
- Harris, M.J. Flow Feature Aligned Mesh Generation and Adaptation. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2013. [Google Scholar]
- Ito, Y.; Shih, A.M.; Koomullil, R.P.; Soni, B.K. A solution-based adaptive redistribution method for unstructured meshes. In Proceedings of the 15th International Meshing Roundtable, Birmingham, Al, USA, 17–20 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 147–161. [Google Scholar]
- Qin, N.; Liu, X. Flow feature aligned grid adaptation. Int. J. Numer. Methods Eng. 2006, 67, 787–814. [Google Scholar] [CrossRef]
- Harris, M.J.; Qin, N. Geometric representation of flow features using the medial axis for mesh generation. AIAA J. 2014, 53, 246–259. [Google Scholar] [CrossRef]
- Harris, M.J.; Qin, N. Using the medial axis to represent flow features for feature-aligned unstructured quad-dominant mesh generation. Comput. Fluids 2014, 102, 1–14. [Google Scholar] [CrossRef]
- Alauzet, F. Metric Based Anisotropic Mesh Adaptation; CEA-EDF-INRIA Schools: Numerical Analysis Summer School; CEA: Cadarache, France, 2010. [Google Scholar]
- Loseille, A. Unstructured Mesh Generation and Adaptation. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2017; Volume 18, pp. 263–302. [Google Scholar]
- Castro-Díaz, M.J.; Hecht, F.; Mohammadi, B.; Pironneau, O. Anisotropic unstructured mesh adaption for flow simulations. Int. J. Numer. Methods Fluids 1997, 25, 475–491. [Google Scholar] [CrossRef]
- Hecht, F.; Mohammadi, B.; Hecht, F.; Mohammadi, B. Mesh adaption by metric control for multi-scale phenomena and turbulence. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997; p. 859. [Google Scholar]
- Peraire, J.; Vahdati, M.; Morgan, K.; Zienkiewicz, O.C. Adaptive remeshing for compressible flow computations. J. Comput. Phys. 1987, 72, 449–466. [Google Scholar] [CrossRef]
- Löhner, R. Three-dimensional fluid-structure interaction using a finite element solver and adaptive remeshing. Comput. Syst. Eng. 1990, 1, 257–272. [Google Scholar] [CrossRef]
- Peraire, J.; Peiro, J.; Morgan, K. Adaptive remeshing for three-dimensional compressible flow computations. J. Comput. Phys. 1992, 103, 269–285. [Google Scholar] [CrossRef]
- George, P.L.; Hecht, F.; Vallet, M.G. Creation of internal points in Voronoi’s type method. Control adaptation. Adv. Eng. Softw. Work. 1991, 13, 303–312. [Google Scholar] [CrossRef]
- Fortin, M.; Vallet, M.G.; Poirier, D.; Habashi, W.G. Error Estimation and Directionally-Adaptive Meshing. In Proceedings of the 25th AIAA Fluid Dynamics Conference, Colorado Springs, CO, USA, 20–23 June 1994. [Google Scholar]
- Habashi, W.G.; Fortin, M.; Dompierre, J.; Vallet, M.G.; Bourgault, Y. Anisotropic mesh adaptation: A step towards a mesh-independent and user-independent CFD. In Barriers and Challenges in Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 99–117. [Google Scholar]
- Robichaud, M.; Ait-Ali-Yahia, D.; Peeters, M.; Baruzzi, G.; Kozel, V.; Habashi, W. 3-D anisotropic adaptation for external and turbomachinery flows on hybrid unstructured grids. In Proceedings of the Fluids 2000 Conference and Exhibit, Denver, CO, USA, 19–22 June 2000. [Google Scholar]
- Habashi, W.G.; Dompierre, J.; Bourgault, Y.; Ait-Ali-Yahia, D.; Fortin, M.; Vallet, M.G. Anisotropic mesh adaptation: Towards user-independent, mesh-independent and solver-independent CFD. Part I: General principles. Int. J. Numer. Methods Fluids 2000, 32, 725–744. [Google Scholar] [CrossRef]
- Ait-Ali-Yahia, D.; Baruzzi, G.; Habashi, W.G.; Fortin, M.; Dompierre, J.; Vallet, M.G. Anisotropic mesh adaptation: towards user-independent, mesh-independent and solver-independent CFD. Part II. Structured grids. Int. J. Numer. Methods Fluids 2002, 39, 657–673. [Google Scholar] [CrossRef]
- Suerich-Gulick, F.; Lepage, C.; Habashi, W.G. Anisotropic 3-D Mesh Adaptation for Turbulent Flows. In Proceedings of the 34th AIAA Fluid Dynamics Conference and Exhibit, Portland, OR, USA, 28 June–1 July 2004; p. 2533. [Google Scholar]
- Sahni, O.; Jansen, K.E.; Shephard, M.S.; Taylor, C.A.; Beall, M.W. Adaptive boundary layer meshing for viscous flow simulations. Eng. Comput. 2008, 24, 267. [Google Scholar] [CrossRef]
- Chitale, K.C. Anisotropic Mesh Adaptivity for Turbulent Flows with Boundary Layers. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2013. [Google Scholar]
- Frey, P.J.; Alauzet, F. Anisotropic mesh adaptation for CFD computations. Comput. Methods Appl. Mech. Eng. 2005, 194, 5068–5082. [Google Scholar] [CrossRef]
- Loseille, A.; Dervieux, A.; Frey, P.; Alauzet, F. Achievement of global second order mesh convergence for discontinuous flows with adapted unstructured meshes. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007; p. 4186. [Google Scholar]
- Mesri, Y.; Alauzet, F.; Loseille, A.; Hascoët, L.; Koobus, B.; Dervieux, A. Continuous mesh adaptation models for CFD. CFD J. 2008, 16, 346–355. [Google Scholar]
- Loseille, A.; Alauzet, F. Continuous mesh framework part I: Well-posed continuous interpolation error. SIAM J. Numer. Anal. 2011, 49, 38–60. [Google Scholar] [CrossRef]
- Loseille, A.; Alauzet, F. Continuous mesh framework part II: Validations and applications. SIAM J. Numer. Anal. 2011, 49, 61–86. [Google Scholar] [CrossRef]
- Frazza, L.; Loseille, A.; Alauzet, F. Anisotropic mesh adaptation for turbomachinery applications. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3299. [Google Scholar]
- Vallet, M.G.; Manole, C.M.; Dompierre, J.; Dufour, S.; Guibault, F. Numerical comparison of some Hessian recovery techniques. Int. J. Numer. Methods Eng. 2007, 72, 987–1007. [Google Scholar] [CrossRef]
- Picasso, M.; Alauzet, F.; Borouchaki, H.; George, P.L. A numerical study of some Hessian recovery techniques on isotropic and anisotropic meshes. SIAM J. Sci. Comput. 2011, 33, 1058–1076. [Google Scholar] [CrossRef]
- Borouchaki, H.; Hecht, F.; Frey, P.J. Mesh gradation control. Int. J. Numer. Methods Eng. 1998, 43, 1143–1165. [Google Scholar] [CrossRef]
- Li, X.; Remacle, J.F.; Chevaugeon, N.; Shephard, M.S. Anisotropic Mesh Gradation Control. In Proceedings of the International Meshing Roundtable, Williamsburg, VA, USA, 19–22 September 2004; pp. 401–412. [Google Scholar]
- Alauzet, F. Size gradation control of anisotropic meshes. Finite Elem. Anal. Des. 2010, 46, 181–202. [Google Scholar] [CrossRef]
- Joubarne, E.; Guibault, F. 3D Metric-based anisotropic mesh adaptation for vortex capture. Math. Comput. Simul. 2011, 82, 163–180. [Google Scholar] [CrossRef]
- Michal, T.; Babcock, D.; Kamenetskiy, D.; Krakos, J.; Mani, M.; Glasby, R.; Erwin, T.; Stefanski, D.L. Comparison of fixed and adaptive unstructured grid results for drag prediction workshop 6. J. Aircr. 2018, 55, 1420–1432. [Google Scholar] [CrossRef]
- Alauzet, F.; Clerici, F.; Loseille, A.; Tarsia-Morisco, C.; Vanharen, J. Some progress on CFD high lift prediction using metric-based anisotropic mesh adaptation. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0388. [Google Scholar]
- Michal, T.R.; Kamenetskiy, D.S.; Krakos, J. Anisotropic Adaptive Mesh Results for the Third High Lift Prediction Workshop (HiLiftPW-3). In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 1257. [Google Scholar]
- Park, M.A.; Balan, A.; Anderson, W.K.; Galbraith, M.C.; Caplan, P.; Carson, H.A.; Michal, T.R.; Krakos, J.A.; Kamenetskiy, D.S.; Loseille, A.; et al. Verification of unstructured grid adaptation components. In Proceedings of the AIAA Scitech 2019 forum, San Diego, CA, USA, 7–11 January 2019; p. 1723. [Google Scholar]
- Balan, A.; Park, M.A.; Anderson, W.K.; Kamenetskiy, D.S.; Krakos, J.A.; Michal, T.; Alauzet, F. Verification of anisotropic mesh adaptation for turbulent simulations over ONERA M6 wing. AIAA J. 2020, 58, 1550–1565. [Google Scholar] [CrossRef]
- Alauzet, F.; Frazza, L.; Papadogiannis, D. Periodic adjoints and anisotropic mesh adaptation in rotating frame for high-fidelity RANS turbomachinery applications. J. Comput. Phys. 2022, 450, 110814. [Google Scholar] [CrossRef]
- Laure, B.; Dimitrios, P.; Frédéric, A. Isotropic and anisotropic mesh adaptation for rans simulations of a nacelle under crosswind conditions. J. Glob. Power Propuls. Soc. 2023, 7, 188–199. [Google Scholar] [CrossRef]
- Alauzet, F.; Papadogiannis, D.; Billon, L. Evaluation of heat transfer performance of a film-cooled turbine vane using metric-based anisotropic mesh adaptation. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 1399. [Google Scholar]
- Alauzet, F.; Parente, E.; Remigi, A. High-Fidelity Film-Cooled Rotor High Pressure Turbine Simulation using Metric-Based Anisotropic Mesh Adaptation. In Proceedings of the Global Power and Propulsion Society, GPPS Chania24, Chania, Crete, 4–6 September 2024. ISSN-Nr: 2504-4400. [Google Scholar]
- Remigi, A.; Philit, M.; Alauzet, F.; Guilbert, E. Evaluation of tandem transonic compressor performances with mixing plane and metric-based mesh adaptation. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 0523. [Google Scholar]
- John, A.; Vivarelli, G.; Qin, N.; Shahpar, S. Using Feature-Based Mesh Adaptation to Improve the Adjoint Optimisation of Transonic Compressor Blades. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air. American Society of Mechanical Engineers, Virtual, 21–25 September 2020; Volume 84089, p. V02CT35A036. [Google Scholar]
- Becker, R.; Rannacher, R. Weighted a posteriori error control in FE methods. In Proceedings of the Lecture at ENUMATH-95, Paris, France, 18–22 September 1995; pp. 621–637. [Google Scholar]
- Giles, M.B.; Larson, M.; Levenstam, M.; Suli, E. Adaptive Error Control for Finite Element Approximations of the Lift and Drag Coefficients in Viscous Flow; Technical report; University of Oxford: Oxford, UK, 1997. [Google Scholar]
- Venditti, D.A.; Darmofal, D.L. A multilevel error estimation and grid adaptive strategy for improving the accuracy of integral outputs. In Proceedings of the 14th Computational Fluid Dynamics Conference, Norfolk, VA, USA, 1–5 November 1999; p. 3292. [Google Scholar]
- Giles, M.B. On adjoint equations for error analysis and optimal grid adaptation in CFD. In Frontiers of Computational Fluid Dynamics 1998; World Scientific: Singapore, 1998; pp. 155–169. [Google Scholar]
- Pierce, N.A.; Giles, M.B. Adjoint recovery of superconvergent functionals from PDE approximations. SIAM Rev. 2000, 42, 247–264. [Google Scholar] [CrossRef]
- Müller, J.D.; Giles, M. Solution adaptive mesh refinement using adjoint error analysis. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; p. 2550. [Google Scholar]
- Venditti, D.A.; Darmofal, D.L. Adjoint error estimation and grid adaptation for functional outputs: Application to quasi-one-dimensional flow. J. Comput. Phys. 2000, 164, 204–227. [Google Scholar] [CrossRef]
- Power, P.W.; Piggott, M.D.; Fang, F.; Gorman, G.J.; Pain, C.C.; Marshall, D.P.; Goddard, A.J.H.; Navon, I.M. Adjoint goal-based error norms for adaptive mesh ocean modelling. Ocean. Model. 2006, 15, 3–38. [Google Scholar] [CrossRef]
- Power, P.W.; Pain, C.C.; Piggott, M.D.; Fang, F.; Gorman, G.J.; Umpleby, A.P.; Goddard, A.J.H.; Navon, I.M. Adjoint a posteriori error measures for anisotropic mesh optimisation. Comput. Math. Appl. 2006, 52, 1213–1242. [Google Scholar] [CrossRef]
- Venditti, D.A. Grid Adaptation for Functional Outputs of Compressible Flow Simulations. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2002. [Google Scholar]
- Park, M.A. Adjoint-based, three-dimensional error prediction and grid adaptation. AIAA J. 2004, 42, 1854–1862. [Google Scholar] [CrossRef]
- Park, M. Three-dimensional turbulent RANS adjoint-based error correction. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3849. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2001; p. 2001. ISBN 0080430090. [Google Scholar]
- Vivarelli, G.; Qin, N.; Shahpar, S. Combined Hessian and Adjoint Error-Based Anisotropic Mesh Adaptation for Turbomachinery Flows. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 1946. [Google Scholar]
- Vivarelli, G.; Qin, N.; Shahpar, S.; Radford, D. Sequential feature-based mesh movement and adjoint error-based mesh refinement. Int. J. Numer. Methods Fluids 2021, 93, 249–272. [Google Scholar] [CrossRef]
- Nemec, M.; Aftosmis, M. Adjoint error estimation and adaptive refinement for embedded-boundary Cartesian meshes. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007; p. 4187. [Google Scholar]
- Barth, T.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989; p. 366. [Google Scholar]
- Aftosmis, M.; Berger, M. Multilevel error estimation and adaptive h-refinement for cartesian meshes with embedded boundaries. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 863. [Google Scholar]
- Lee-Rausch, E.; Park, M.; Jones, W.; Hammond, D.; Nielsen, E. Application of parallel adjoint-based error estimation and anisotropic grid adaptation for three-dimensional aerospace configurations. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference, Toronto, OT, Canada, 6–9 June 2005; p. 4842. [Google Scholar]
- Kim, H.J.; Takano, Y.; Nakahashi, K. Error estimation and grid adaptation using Euler adjoint method. J. Aircr. 2006, 43, 1317–1324. [Google Scholar] [CrossRef]
- Kim, H.J.; Nakahashi, K. Output-based error estimation and adaptive mesh refinement using viscous adjoint method. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 1395. [Google Scholar]
- Jones, W.; Nielsen, E.; Park, M. Validation of 3D adjoint based error estimation and mesh adaptation for sonic boom prediction. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 1150. [Google Scholar]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Ponsin, J.; Caloto, A.; Andrés, E.; Bitrián, P.; Lozano, C. Implementation of an Adjoint-Based Error Estimation and Grid Adaptation Module in the DLR TAU Code. In Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences, Nice, France, 19–24 September 2010. [Google Scholar]
- Ding, K.; Fidkowski, K.J.; Roe, P.L. Acceleration Techniques for Adjoint-Based Error Estimation and Mesh Adaptation. In Proceedings of the Eighth International Conference on Computational Fluid Dynamics (ICCFD8) ICCFD8-2014-0249, Chengdu, China, 14–18 July 2014. [Google Scholar]
- Fidkowski, K.J. High-Order Output-Based Adaptive Methods for Steady and Unsteady Aerodynamics. In 37th Advanced CFD Lectures Series; von Karman Institute for Fluid Dynamics (December 9–12 2013); Deconinck, H., Abgrall, R., Eds.; von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2013. [Google Scholar]
- Eymann, T.A. Active Flux Schemes. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2013. [Google Scholar]
- Pierce, N.A.; Giles, M.B. Adjoint and defect error bounding and correction for functional estimates. J. Comput. Phys. 2004, 200, 769–794. [Google Scholar] [CrossRef]
- Duraisamy, K.; Alonso, J.J.; Chandrasekhar, P.; Palacios, F. Error estimation for high speed flows using continuous and discrete adjoints. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 128. [Google Scholar]
- Palacios, F.; Duraisamy, K.; Alonso, J.J.; Zuazua, E. Robust grid adaptation for efficient uncertainty quantification. AIAA J. 2012, 50, 1538–1546. [Google Scholar] [CrossRef]
- Rothacker, B.A.; Ceze, M.; Fidkowski, K. Adjoint-based error estimation and mesh adaptation for problems with output constraints. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2576. [Google Scholar]
- Hartmann, R. Multitarget error estimation and adaptivity in aerodynamic flow simulations. SIAM J. Sci. Comput. 2008, 31, 708–731. [Google Scholar] [CrossRef]
- Hartmann, R.; Held, J.; Leicht, T. Adjoint-based error estimation and adaptive mesh refinement for the RANS and k–ω turbulence model equations. J. Comput. Phys. 2011, 230, 4268–4284. [Google Scholar] [CrossRef]
- Dwight, R.P. Goal-oriented mesh adaptation for finite volume methods using a dissipation-based error indicator. Int. J. Numer. Methods Fluids 2008, 56, 1193–1200. [Google Scholar] [CrossRef]
- Dwight, R.P. Heuristic a posteriori estimation of error due to dissipation in finite volume schemes and application to mesh adaptation. J. Comput. Phys. 2008, 227, 2845–2863. [Google Scholar] [CrossRef][Green Version]
- Jameson, A.; Schmidt, W.; Turkel, E. Numerical solution of the Euler equations by finite volume methods using Runge Kutta time stepping schemes. In Proceedings of the 14th Fluid and Plasma Dynamics Conference, Palo Alto, CA, USA, 23–25 June 1981; p. 1259. [Google Scholar]
- Fidkowski, K.F.; Roe, P.L. Entropy-based mesh refinement, I: The entropy adjoint approach. In Proceedings of the 19th AIAA Computational Fluid Dynamics, San Antonio, TX, USA, 22–25 June 2009; p. 3790. [Google Scholar]
- Yamaleev, N.; Diskin, B.; Pathak, K. Error minimization via adjoint-based anisotropic grid adaptation. In Proceedings of the 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010; p. 4436. [Google Scholar]
- Yano, M.; Modisette, J.; Darmofal, D. The importance of mesh adaptation for higher-order discretizations of aerodynamic flows. In Proceedings of the 20th AIAA Computational Fluid Dynamics Conference, Honolulu, HI, USA, 27–30 June 2011; p. 3852. [Google Scholar]
- Yano, M.; Darmofal, D.L. An optimization-based framework for anisotropic simplex mesh adaptation. J. Comput. Phys. 2012, 231, 7626–7649. [Google Scholar] [CrossRef]
- Carson, H.A.; Huang, A.C.; Galbraith, M.C.; Allmaras, S.R.; Darmofal, D.L. Anisotropic mesh adaptation for continuous finite element discretization through mesh optimization via error sampling and synthesis. J. Comput. Phys. 2020, 420, 109620. [Google Scholar] [CrossRef]
- Carson, H.A.; Huang, A.C.; Galbraith, M.C.; Allmaras, S.R.; Darmofal, D.L. Mesh optimization via error sampling and synthesis: An update. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0087. [Google Scholar]
- Ursachi, C.I.; Galbraith, M.; Allmaras, S.R.; Darmofal, D. Output-based adaptive RANS solutions using higher-order FEM on a multi-element airfoil. In Proceedings of the AIAA Aviation 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 3220. [Google Scholar]
- Loseille, A.; Dervieux, A.; Alauzet, F. Fully anisotropic goal-oriented mesh adaptation for 3D steady Euler equations. J. Comput. Phys. 2010, 229, 2866–2897. [Google Scholar] [CrossRef]
- Belme, A.; Alauzet, F.; Dervieux, A. An a priori anisotropic goal-oriented error estimate for viscous compressible flow and application to mesh adaptation. J. Comput. Phys. 2019, 376, 1051–1088. [Google Scholar] [CrossRef]
- Park, M.A.; Balan, A.; Clerici, F.; Alauzet, F.; Loseille, A.; Kamenetskiy, D.S.; Krakos, J.A.; Michal, T.R.; Galbraith, M.C. Verification of viscous goal-based anisotropic mesh adaptation. In Proceedings of the AIAA Scitech 2021 Forum, Orlando, FL, USA, 12–16 January 2021; p. 1362. [Google Scholar]
- Peter, J.; Nguyen-Dinh, M.; Trontin, P. Goal oriented mesh adaptation using total derivative of aerodynamic functions wrt mesh coordinates. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 158. [Google Scholar]
- Peter, J.; Nguyen-Dinh, M.; Trontin, P. Goal oriented mesh adaptation using total derivative of aerodynamic functions wrt mesh coordinates—With applications to Euler flows. Comput. Fluids 2012, 66, 194–214. [Google Scholar] [CrossRef]
- Nguyen-Dinh, M.; Peter, J.; Sauvage, R.; Meaux, M.; Désidéri, J.A. Mesh quality assessment based on aerodynamic functional output total derivatives. Eur. J. Mech.-B/Fluids 2014, 45, 51–71. [Google Scholar] [CrossRef]
- Peter, J.E.; Desideri, J.A. Unstructured mesh adaptation for functional outputs. With application to two dimensionnal inviscid flows. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1930. [Google Scholar]
- Todarello, G.; Vonck, F.; Bourasseau, S.; Peter, J.; Désidéri, J.A. Finite-volume goal-oriented mesh adaptation for aerodynamics using functional derivative wrt nodal coordinates. J. Comput. Phys. 2016, 313, 799–819. [Google Scholar] [CrossRef]
- Resmini, A.; Peter, J.; Lucor, D. Mono-block and non-matching multi-block structured mesh adaptation based on aerodynamic functional total derivatives for RANS flow. Int. J. Numer. Methods Fluids 2017, 83, 866–884. [Google Scholar] [CrossRef]
- Vivarelli, G.; Qin, N.; Shahpar, S.; Radford, D. Efficient Adjoint-Based Mesh Adaptation Applied to Turbo-Machinery Flows. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Vivarelli, G.; Qin, N.; Shahpar, S.; Radford, D. Anisotropic adjoint sensitivity-based mesh movement for industrial applications. Comput. Fluids 2021, 221, 104929. [Google Scholar] [CrossRef]
- Ordaz, I.; Rallabhandi, S.K.; Nielsen, E.J.; Diskin, B. Mitigation of engine inlet distortion through adjoint-based design. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3410. [Google Scholar]
- Nemec, M.; Rodriguez, D.L.; Aftosmis, M.J. Adjoint-based mesh adaptation and shape optimization for simulations with propulsion. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3488. [Google Scholar]
- Michal, T.R.; Kamenetskiy, D.S.; Krakos, J. Generation of Anisotropic Adaptive Meshes for the First AIAA Geometry and Mesh Generation Workshop. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0658. [Google Scholar]
- Park, M.A.; Kleb, W.L.; Jones, W.T.; Krakos, J.A.; Michal, T.R.; Loseille, A.; Haimes, R.; Dannenhoffer, J. Geometry modeling for unstructured mesh adaptation. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 2946. [Google Scholar]
- Tsolakis, C.; Chrisochoides, N.; Park, M.A.; Loseille, A.; Michal, T. Parallel anisotropic unstructured grid adaptation. AIAA J. 2021, 59, 4764–4776. [Google Scholar] [CrossRef]
- Tang, J.; Cui, P.; Li, B.; Zhang, Y.; Si, H. Parallel hybrid mesh adaptation by refinement and coarsening. Graph. Model. 2020, 111, 101084. [Google Scholar] [CrossRef]
- Menon, S.; Mooney, K.G.; Stapf, K.; Schmidt, D.P. Parallel adaptive simplical re-meshing for deforming domain CFD computations. J. Comput. Phys. 2015, 298, 62–78. [Google Scholar] [CrossRef]
- Spurlock, W.M.; Aftosmis, M.J.; Chiew, J.J.; Nemec, M. Parallel Mesh Adaptation for Unsteady Blast Simulations on Cartesian Meshes. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 1792. [Google Scholar]
- Sahni, O.; Brown, C.S.; Gica, M.; Kaur, S.; Salazar, G.; Keistler, P. In-Memory Parallel Anisotropic Mesh Adaptation for Unsteady Hypersonic Problems. In Proceedings of the AIAA Aviation Forum and Ascend 2024, Las Vegas, NV, USA, 29 July–2 August 2024; p. 4258. [Google Scholar]
- Tsolakis, C.; Chrisochoides, N. Parallel Metric-based Anisotropic Mesh Adaptation using Speculative Execution on Shared Memory. arXiv 2024, preprint. [Google Scholar]
- Wang, Z. High-order computational fluid dynamics tools for aircraft design. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130318. [Google Scholar] [CrossRef]
- Michelassi, V. Turbomachinery research and design: The role of DNS and LES in industry. In Progress in Hybrid RANS-LES Modelling: Papers Contributed to the 7th Symposium on Hybrid RANS-LES Methods, Berlin, Germany 17–19 September 2018; Springer: Berlin/Heidelberg, Germany, 2020; pp. 55–69. [Google Scholar]
- Ekelschot, D.; Moxey, D.; Sherwin, S.; Peiró, J. A p-adaptation method for compressible flow problems using a goal-based error indicator. Comput. Struct. 2017, 181, 55–69. [Google Scholar] [CrossRef]
- Moxey, D.; Sastry, S.P.; Kirby, R.M. Interpolation error bounds for curvilinear finite elements and their implications on adaptive mesh refinement. J. Sci. Comput. 2019, 78, 1045–1062. [Google Scholar] [CrossRef]
- Marcon, J.; Kopriva, D.A.; Sherwin, S.J.; Peiró, J. Naturally curved quadrilateral mesh generation using an adaptive spectral element solver. arXiv 2019, preprint. [Google Scholar]
- Marcon, J.; Castiglioni, G.; Moxey, D.; Sherwin, S.J.; Peiró, J. rp-adaptation for compressible flows. Int. J. Numer. Methods Eng. 2020, 121, 5405–5425. [Google Scholar] [CrossRef]
- Coulaud, O.; Loseille, A. Very high order anisotropic metric-based mesh adaptation in 3D. Procedia Eng. 2016, 163, 353–365. [Google Scholar] [CrossRef]
- Dolejší, V.; May, G.; Rangarajan, A. A continuous hp-mesh model for adaptive discontinuous Galerkin schemes. Appl. Numer. Math. 2018, 124, 1–21. [Google Scholar] [CrossRef]
- Rangarajan, A.; Balan, A.; May, G. Mesh optimization for discontinuous Galerkin methods using a continuous mesh model. AIAA J. 2018, 56, 4060–4073. [Google Scholar] [CrossRef]
- Sanjaya, D.P.; Fidkowski, K.; Diosady, L.T.; Murman, S.M. Error minimization via metric-based curved-mesh adaptation. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017; p. 3099. [Google Scholar]
- Sanjaya, D.P.; Fidkowski, K.; Murman, S.M. Comparison of algorithms for high-order, metric-based mesh optimization. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1141. [Google Scholar]
- Barral, N.; Olivier, G.; Alauzet, F. Time-accurate anisotropic mesh adaptation for three-dimensional time-dependent problems with body-fitted moving geometries. J. Comput. Phys. 2017, 331, 157–187. [Google Scholar] [CrossRef]
- Alauzet, F.; Loseille, A.; Olivier, G. Time-accurate multi-scale anisotropic mesh adaptation for unsteady flows in CFD. J. Comput. Phys. 2018, 373, 28–63. [Google Scholar] [CrossRef]
- Park, M.A.; Kleb, W.L.; Anderson, W.K.; Wood, S.L.; Balan, A.; Zhou, B.Y.; Gauger, N.R. Exploring Unstructured Mesh Adaptation for Hybrid Reynolds-Averaged Navier–Stokes/Large Eddy Simulation. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1139. [Google Scholar]
- Obiols-Sales, O.; Vishnu, A.; Malaya, N.; Chandramowlishwaran, A. ADARNet: Deep Learning Predicts Adaptive Mesh Refinement. In Proceedings of the 52nd International Conference on Parallel Processing, Salt Lake City, UT, USA, 7–10 August 2023; pp. 524–534. [Google Scholar]
- Pelissier, U.; Parret-Fréaud, A.; Bordeu, F.; Mesri, Y. Graph Neural Networks for Mesh Generation and Adaptation in Structural and Fluid Mechanics. Mathematics 2024, 12, 2933. [Google Scholar] [CrossRef]
- Pfaff, T.; Fortunato, M.; Sanchez-Gonzalez, A.; Battaglia, P. Learning mesh-based simulation with graph networks. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar]
- Ojha, V.; Chen, G.; Fidkowski, K. Initial mesh generation for solution-adaptive methods using machine learning. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1244. [Google Scholar]
- Ghosh, K.; Mehul, B.; Pandya, K.; Kain, D.; Balan, A.; Rangarajan, A. Machine Learning Driven Metric Based Mesh Adaptation. In Proceedings of the International Conference on Applied AI and Scientific Machine Learning, Bangalore, India, 14–18 December 2024. [Google Scholar]
- Fidkowski, K.J.; Chen, G. Metric-based, goal-oriented mesh adaptation using machine learning. J. Comput. Phys. 2021, 426, 109957. [Google Scholar] [CrossRef]
- Yang, J.; Dzanic, T.; Petersen, B.; Kudo, J.; Mittal, K.; Tomov, V.; Camier, J.S.; Zhao, T.; Zha, H.; Kolev, T.; et al. Reinforcement learning for adaptive mesh refinement. In Proceedings of the International conference on artificial intelligence and statistics. PMLR, Valencia, Spain, 25–27 April 2023; pp. 5997–6014. [Google Scholar]
- Tlales, K.; Otmani, K.E.; Ntoukas, G.; Rubio, G.; Ferrer, E. Machine learning mesh-adaptation for laminar and turbulent flows: Applications to high-order discontinuous Galerkin solvers. Eng. Comput. 2024, 40, 2947–2969. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).