Droplets at Liquid-Fluid Interfaces: Stages Leading to Coalescence

Abstract

Droplet coalescence at interfaces affects industrial and natural processes. Previous studies focused on droplet stability and thin film drainage. We use meticulous experiments to infer the evolution of coalescence for both ascending and descending droplets under different conditions. Images show the anticipatory deformation of the interface and dimple formation during the approach phase. While the droplet rests at the interface, the two surfaces interact through the draining thin film, and the effective interfacial tension can be higher than twice the interfacial tension between the two fluids, suggesting not only concurrent action but also potential changes in interfacial tension in thin films. Following the film breakage, the unbalanced force propels the droplet into the continuous phase, i.e., the slingshot effect. Multiple droplets may coexist at the interface and collectively contribute to its deformation, which in turn pushes the droplets together. The various stages of droplet coalescence are influenced by the droplet and host fluid viscosities, densities, interfacial tension, size, and initial interface curvature.

1. Introduction

Droplets deform and coalesce at interfaces in a wide range of industrial and technological applications, including emulsion stability [1], drug delivery [2,3], food preparation [4], cosmetics [5], painting [6], oil separation from produced water [7], and the formation of stable Pickering emulsions with particle coatings [8,9]. In general, the presence of surfactants, electrolytes or impurities at the interface affects coalescence [10,11].

Previous studies focused on the stability of droplets resting at the interface and the drainage of the thin fluid film that separates the droplet from the interface [12,13,14,15,16,17]. Typically, analytical models are based on the lubrication and thin-film theories [18,19,20,21,22,23,24]; still, the time to coalescence is inherently stochastic and statistical data are required to fully describe the phenomenon. Furthermore, questions remain related to the stages of coalescence, the effect of initially curved interfaces, and implications associated with multiple concurrent droplets.

Moreover, several important questions remain unresolved. In particular, there is a need for a deeper understanding of the different stages involved in coalescence, the role of initially curved or deformed interfaces, and the dynamic interactions that occur when multiple droplets are present simultaneously at the interface. These factors can significantly alter the progression and outcome of coalescence events, but they have received limited attention.

The objective of this study is to advance the understanding of droplet–interface interactions and the mechanics of coalescence under controlled conditions. We use meticulous experiments and detailed image analysis to track the evolution of the coalescence process for both ascending light droplets and descending heavy droplets under various fluid and interfacial conditions. Particular attention is given to characterizing the interface deformation during the approach, the formation of dimples, the drainage of the thin film, and the rapid dynamics following film rupture, including the slingshot effect observed when unbalanced interfacial forces accelerate the droplet into the continuous phase. In addition, we investigate how multiple droplets at an interface can interact through collective deformation, promoting coalescence. By systematically exploring these aspects, this study contributes new experimental insights into the physics of droplet coalescence, laying the groundwork for improved models and applications where control of droplet behavior is essential.

2. Experimental Method

The test involved silicone oils of different viscosities, mineral oil, hexane, glycerol, and deionized water (properties in

Table 1. Fluid used in this study—properties.

Material	Density [g/cm3]	Refractive Index	Viscosity [cP]	IFT [mN/m]
Silicone oil 10 cP	0.93	1.40	10	32.0 b
Silicone oil 100 cP	0.96	1.40	100	33.7 b
Silicone oil 1000 cP	0.97	1.40	1000	34.4 b
Silicone oil 10,000 cP	0.971	1.40	10,000	35.5 b
Hexane	0.655	1.37	0.29	29.3 c
Mineral oil light	0.85	1.47	96	28.9 d
Glycerol	1.261	1.47	1412 a	63.4 d
Deionized water	1.000	1.33	0.89	72.0 d
Glycerol-water (35% g + 65% w)	1.080	1.37	2.8 a	47.7 d
Glycerol-water (55% g + 45% w)	1.142	1.40	7.2 a	65.6 d

Note: Glycerol-water mixtures defined by mass. ^a data from [25]. ^b IFT measured in glycerol–water 55% w/w. ^c IFT measured in glycerol–water 35% g + 65% w. ^d IFT measured in air. Fluids used in this study were purchased at Sigma-Aldrich, Inc., St. Louis, MO 63178, USA.

). The initial water-oil column sat in a square glass container to minimize parallax effects. Then, oil droplets injected from the bottom rose through the water column towards the interface, while water droplets injected at the top fell through the oil column to reach the interface. A high-resolution digital camera (Biolin theta light: 1920 × 1200 pixels, pixel size 5.86 µm) recorded the droplet evolution from the initial approach to final coalescence.

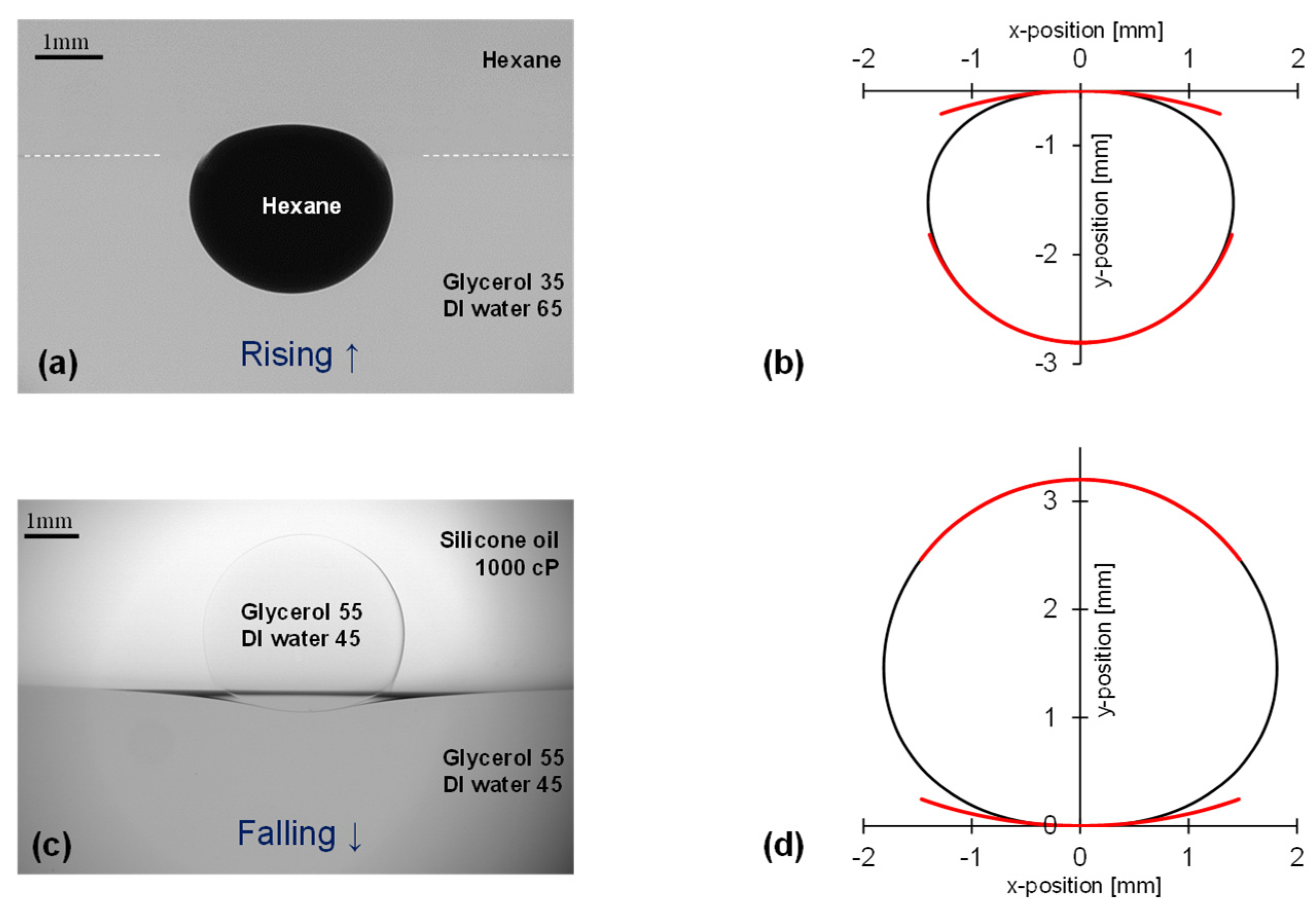
Some tests were conducted with matched refractive index fluids to observe the liquid droplet resting at the interface with minimal distortion. In such cases, we varied the composition of water-glycerol solutions until the interface between the aqueous solution and oil faded away. The resulting liquid systems are hexane over a 35% glycerol and 65% water solution (by mass), and a 55% glycerol and 45% water solution over silicone oil (100 cP). A lipophilic “oil red” dye was added to hexane, and a hydrophilic fluorescein dye to water to form visible droplets against the invisible interfaces.

3. Results: Physical Observations and Analyses

3.1. Droplet Migration Towards the Interface—Dimple

The released droplet promptly reached terminal velocity as it migrated towards the interface (see droplet deformation in viscous fluids in [26]). Our experimental observations show that the terminal velocity is a function of the buoyant force determined by differences in density ${\rho }_{drop}-{\rho }_{host}$, and is inversely proportional to the host fluid viscosity in agreement with Stokes drag. The gravity-driven droplet migration creates a hydrodynamic pressure field around the droplet and induces fluid displacement, including interface distortion as the droplet approached the interface (Figure 1a); the magnitude of the interface anticipatory deformation depended on factors such as droplet size, relative densities, host fluid viscosity, and interfacial tension (Figure 1a and Supplementary Figure S1—see also [27,28,29]). There are visible interface oscillations in some cases [30].

The formation of a dimple and transient fluid trapping may occur as the droplet approaches the interface [13,14,31,32]. We observed dimples when the water droplets descending through the 10 cP silicone oil host fluid, but no visible dimple forms when the droplet falls slowly through the high-viscosity 10,000 cP oil (Figure 1b—additional images in Supplementary Figure S2). The host fluid viscosity plays a dual role: it enables faster droplet migration, which favors trapping, but also promotes faster fluid drainage between the droplet and the interface, which hinders trapping. Evidently, droplet deformation, dimple formation, and transient fluid trapping in liquid–liquid systems require an appropriate combination of viscosities, density difference, and droplet size.

3.2. Quiescent Droplet at the Interface: Curvature and Effective Interfacial Tension

The determination of local curvatures along the droplet surface and the oil-water interface is remarkably nuanced and prone to noticeable variability [33]. Instead, we determined the curvatures at the top and bottom apices along the axis of symmetry by locally fitting a circle. Then, the mean curvature K [m⁻¹] at each apex was computed from the radius R [m] of the locally fitted circle as K = 1/R.

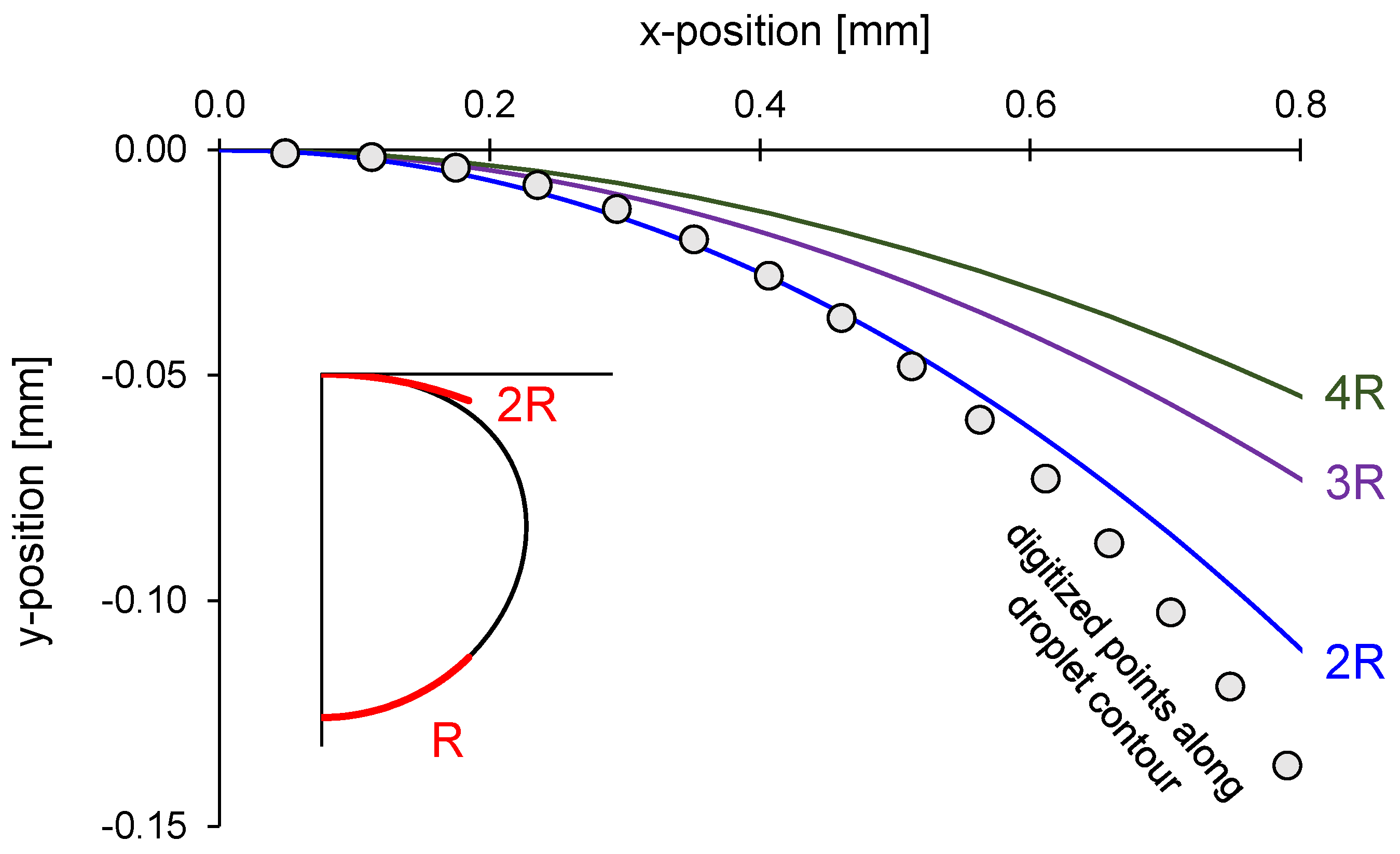
Figure 2 shows the photographs, digitized contours and locally fitted circles for a rising “light” droplet and a falling “heavy” droplet resting at a liquid interface before coalescence (Note: we obtained 70-to-200 points around the 2-to-3 mm diameter droplets). The curvature along the free apex K_free is very well defined. However, this is not the case for the apex at the liquid interface K_inter: Figure 3 shows the digitized points and several fitted circles ranging from twice the free apex radius R_inter = 2R_free to four times larger R_inter = 4R_free. The inferred curvature depends on the length scale selected for the fitting circle.

The capillary pressure $p_c=\gamma K$ [Pa] is the pressure difference across a curved interface and is proportional to the mean curvature K and the interfacial tension $\gamma$ [N/m] [34,35]. Under hydrostatic conditions, the difference in capillary pressure $\Delta p_c$ between the top and bottom apices separated by a distance $z$ is related to the difference in fluid densities $\Delta \rho \left[\mathrm{k}\mathrm{g}/{\mathrm{m}}^3\right]$ between the droplet and the host fluid:

$$\Delta p_c=({\rho }_{drop}-{\rho }_{host})g·\Delta z$$

(1)

The deformed droplet shape resting at the interface reflects the interaction between the two interfaces across the thin film. In the absence of a dimple, a droplet is concave everywhere. The interface in the liquid column has similar curvature near the centerline; however, it becomes convex near the edges of the thin film (note: mirrored situations apply to both light and heavy droplets). From the droplet perspective, the interaction between the liquid interface and the droplet surface can be captured as an “effective interfacial tension”${\gamma }_{eff} [\mathrm{N}/\mathrm{m}]$. Taking the free apex curvature K_free as a reference value, the local effective surface tension is as follows:

$${\gamma }_{eff}(z)={\displaystyle \frac{p_c\left(z\right)}{K\left(z\right)}}={\displaystyle \frac{K_{free} \gamma \pm ∆\rho g ∆z}{K_{inter}}}$$

(2)

The calculated effective interfacial tension at the centerline for both ascending light droplets and descending heavy droplets is at least γ_eff ≥ 2γ the actual interfacial tension γ between the two fluids (refer to Figure 3—see an early study in [36]). A value of γ_eff = 2γ implies the concurrent action of the two interfaces on the droplet shape; values potentially larger than γ_eff ≥ 2γ would suggest changes in interfacial tension when fluids are involved in thin films [37].

3.3. Initially Curved Interfaces

Our tests and published studies show that the time to coalescence increases for high host fluid viscosity and long drainage lengths such as in large droplets with low surface tension. Furthermore, we observed that curved interfaces affect the contact length, drainage and the time to coalesce. Interfaces are curved when the liquid column exists in a narrow gap between walls—noticeable at the millimeter to centimeter scale. In particular, the interface curves up when the lower fluid wets the wall.

We investigated the effect of interface curvature using square glass containers of various sizes, and a liquid column made of DI-water beneath mineral oil. The water-wet walls created a convex interface in all the cases. We released 70 μL water droplets from the top and analyzed their stability from the video recordings obtained at 139 frames per second. We repeated the test 100 times for each interface curvature.

The results show quasi “instantaneous” coalescence—shorter than the frame rate ~7 ms—when the droplets approach a flat interface. However, the droplets remain for a noticeable time before coalescence as the interface curvature is within two orders of magnitude of the droplet curvature (the statistics of instantaneous coalescence as a function of interface curvature are summarized in Supplementary Figure S3). The effect of interface curvature may explain differences among previous studies [27,38].

3.4. Coalescence: Slingshot Effect

Van der Waals attraction gains relevance and accelerates the thin film rupture as the film thickness reduces to bellow ~50 nm [39,40,41]. If a dimple forms, the distance between the droplet and the interface is minimal along the outer dimple shoulder where breakthrough nucleates [32,42,43,44].

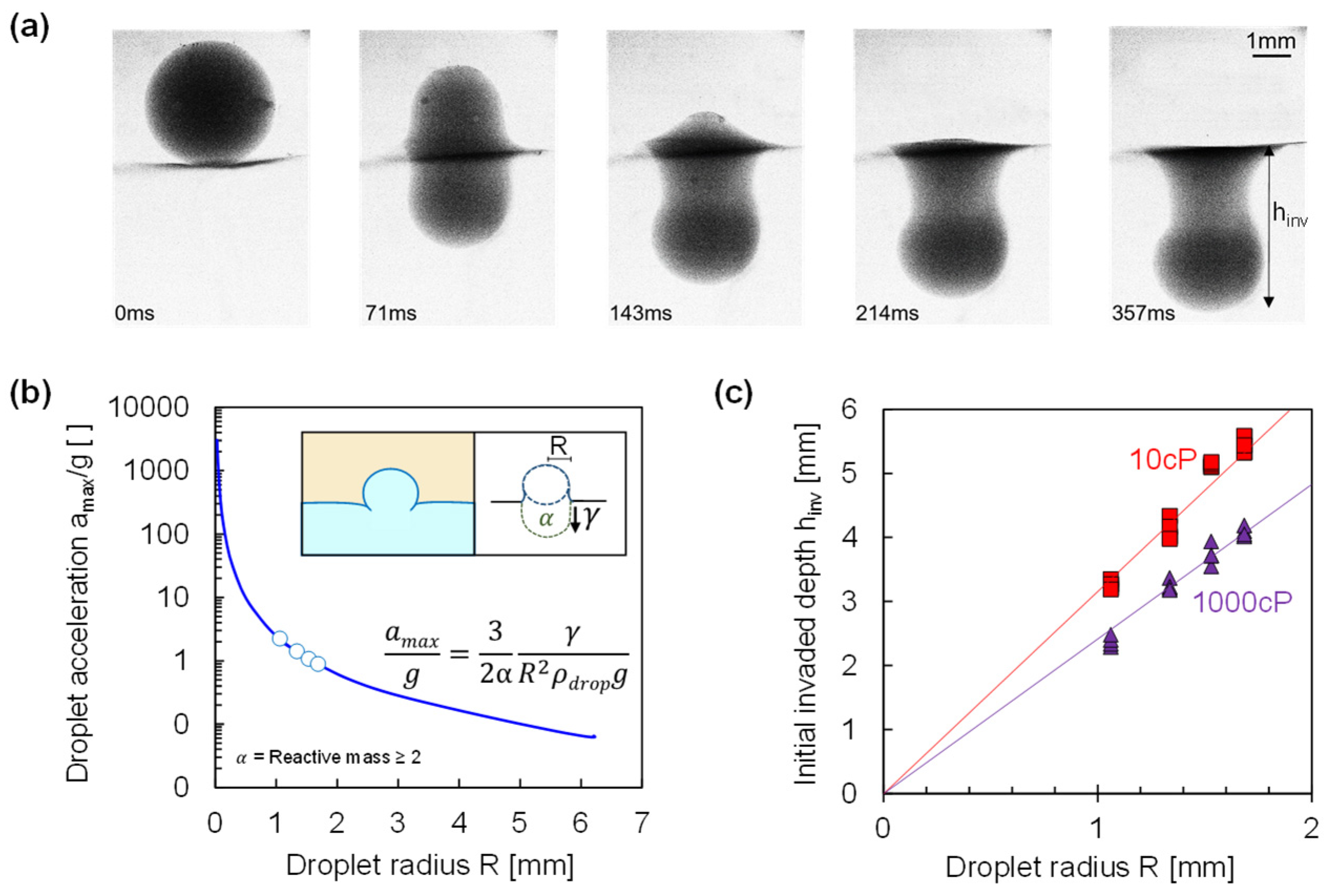
Once the thin film breaks, surface tension around the droplet perimeter creates an unbalanced force that accelerates the initially stationary droplet, effectively producing a slingshot effect that pulls the droplet into the continuous phase (Figure 4a). The initial acceleration $a=F/m$ before viscous drag arises is a function of the droplet radius and the interfacial tension:

$${\displaystyle \frac{a_{max}}{g}}={\displaystyle \frac{3}{2\alpha }}{\displaystyle \frac{\gamma }{R^2{\rho }_{drop}g}}$$

(3)

Fluids both ahead of and behind the droplet must also be accelerated. In the absence of formal hydrodynamic simulations, we assume the effective reactive mass to be α-times the droplet mass. The droplets in our tests experienced initial accelerations between $a_{max}$ = 0.9 g and 2.2 g (Figure 4b—we assumed α = 2 drawing inspiration from Saint-Venant’s Principle in solid mechanics). Equation (3) predicts high acceleration for small droplets leading to a rapid droplet disappearance into the continuous phase.

There was rapid mass transfer as the droplet broke through the thin film (see implications for contaminant or species transport in [45,46]). The initial invaded depth $h_{inv}$ before the droplet decisively disperses into the continuous phase was defined as the vertical distance the droplet mass penetrates into the continuous phase immediately after film rupture (measured from the interface midplane and within the first 139 frames, or less than 1 s). The data in Figure 4c show that the initial invaded depth was proportional to the droplet size $h_{inv}$ ≈ 2-to-3R. The lower end corresponds to volume replacement: a sphere size 2R resting above the interface will sink just below it, reaching an invasion depth $h_{inv}$ = 2R; this simple geometric analysis accounts for the basic scaling of invasion with droplet size. Further invasion results from the slingshot acceleration but is hindered by viscous drag; as a result, the droplet’s invasion depth into the continuous phase increases in low viscosity fluids (Figure 4c).

Finally, we note the occurrence of “partial coalescence” events, where only a portion of the droplet merges into the continuous phase leaving a smaller droplet behind. Partial coalescence occurs when the capillary retraction is rapid enough to pinch the droplet neck before full drainage. Therefore, it is dependent on the viscosity of the fluids involved, the droplet size and the interfacial tension [47,48,49].

3.5. Concurrent Droplets

Multiple droplets can arrive and coexist at the interface before coalescence. Their combined action increases the interface deformation, which in turn brings the droplets close together (Figure 5). Consequently, we observed both droplet-droplet and droplet–interface coalescence events. Typically, the dynamics generated by a droplet coalescence triggers a domino effect that causes multiple subsequent coalescence events.

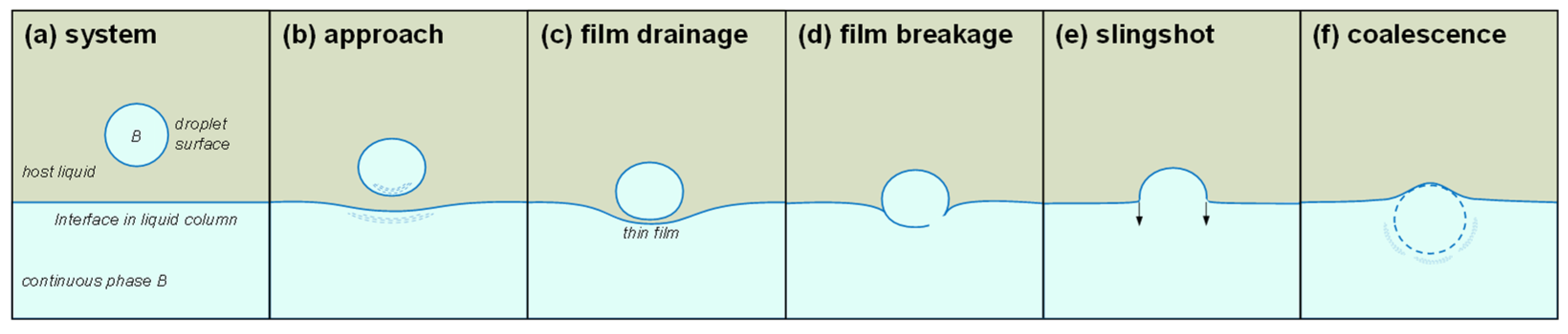
3.6. Summary: The Stages of Coalescence

The results from this study and previous observations in the literature allow us to piece together the sequence of events that lead to droplet coalescence at the interface between immiscible fluids (Figure 6—see also: [29,50,51,52,53,54,55,56]):

• Initial approach to the interface and ensuing droplet and interface deformation prompted by gravity, viscous and interfacial forces (Figure 6a,b); initially trapped fluids may form a dimple in the droplet towards the center of the contact line.
• A period of apparent quiescence conditions as the thin film drains driven by the pressure gradient along the film (Figure 6c).
• Eventually, attractive Van der Waals intermolecular forces gain relevance, the process accelerates and the film breaks (Figure 6d).
• The droplet mass accelerates towards the continuous phase driven by the surface tension around the contact line (slingshot—Figure 6e,f); the rapid mass transfer is accompanied by interface oscillations.
• This sequence of events is common to both ascending light droplets and descending heavy droplets and may involve multiple concurrent droplets at the interface.

Figure 6. Stages of coalescence: the case of a heavy droplet falling through a lighter viscous fluid. (a) System definition. (b) Falling droplet and anticipatory deformation of both the droplet and the interface. (c) Droplet resting at the interface while the thin film drains. (d) Film breaks. (e) Driven by the peripheral interfacial tension, the droplet accelerates towards the continuous phase and invades it. (f) Coalescence. Note: vertically mirrored images apply to light droplets rising through a heavier fluid.

Figure 6. Stages of coalescence: the case of a heavy droplet falling through a lighter viscous fluid. (a) System definition. (b) Falling droplet and anticipatory deformation of both the droplet and the interface. (c) Droplet resting at the interface while the thin film drains. (d) Film breaks. (e) Driven by the peripheral interfacial tension, the droplet accelerates towards the continuous phase and invades it. (f) Coalescence. Note: vertically mirrored images apply to light droplets rising through a heavier fluid.

4. Conclusions

A migrating droplet may temporarily rest at interfaces before coalescing into the continuous fluid phase. The process starts with the droplet migration velocity, causes anticipatory interface deformation and even dimple formation, evolves by gradual thin film drainage and breakage, and ends with the slingshot droplet acceleration and mass transfer into the continuous phase. The viscosities and densities of both the droplet and host fluid, their interfacial tension, droplet size, and initial interface curvature affect the various stages.

The droplet shape is a proxy measurement of fluid—fluid interaction. Accurate measurements require optical techniques such as matched refractive index to render the liquid column interface invisible, dyed droplets for clear visualization, and square tubes to minimize parallax.

Under quasi-static conditions—when the droplet rests at the interface before coalescence—the interface in the liquid column and the droplet surface interact through the thin film. The effective interfacial tension can be higher than twice the interfacial tension between the two fluids. A value of γ_eff = 2γ highlights the concurrent action of the two interfaces on the droplet shape; a value larger than γ_eff ≥ 2γ suggests changes in the interfacial tension when fluids form thin films.

Once the thin film breaks, the unbalance force propels the droplet into the continuous phase. The slingshot acceleration is inversely proportional to the droplet size $R^2$; the initial invasion length into the continuous phase scales with the droplet size and is inversely proportional to the continuous phase viscosity.

Curved interfaces in narrow gaps embrace the droplet leading to longer drainage lengths and coalescence times.

Multiple droplets may coexist at the interface and collectively contribute to its deformation, which in turn pushes the droplets together. Then, both droplet-droplet and droplet-interface coalescence events can take place. The dynamics initiated by the coalescence of one droplet can trigger a domino effect leading to multiple subsequent coalescence events.