Abstract
Computational fluid dynamics (CFD) is an instrumental tool used in tackling the challenges of flow behavior and safety within nuclear reactor cores. Traditional CFD methods like finite volume, finite element, and finite difference have driven significant progress in nuclear engineering, particularly in single-phase and two-phase flow modeling, multiscale analysis, and multiphysics coupling. However, the Lattice Boltzmann Method (LBM), an advancing CFD tool for nuclear reactor subchannel study, remains underexplored in this field. LBM takes a unique mesoscopic approach by modeling particle distributions on a discrete lattice, offering a bridge between microscopic dynamics and macroscopic continuum behavior. Since the integration of LBM into the Lattice Bhatnagar–Gross–Krook (LBGK) model, it has significantly advanced, proving its efficiency in handling complex flow conditions. This review explores the potential of LBM in nuclear reactor subchannel applications. This study emphasizes LBM as a robust computational tool for subchannel study by highlighting its strengths, limitations, and future possibilities.
1. Introduction
Global environmental concerns such as greenhouse gas emissions and ozone layer depletion have brought nuclear energy to the forefront as a vital component in terms of energy efficiency and sustainability [1]. While renewable energy sources like solar, hydro, and wind are essential for a low-carbon future, their unpredictability creates difficulties in maintaining a consistent power supply [2]. Nuclear energy, with its ability to provide consistent power, offers a complement to these renewable sources, helping to stabilize the energy grid and also supporting the transition towards a more sustainable energy landscape [3]. In recent times, the role of nuclear energy is considered within the context of its safety and reliability. The safety standards for nuclear reactor systems must satisfy several ranges of conditions for operation, such as design, operational modes, and severe emergency scenarios [4].
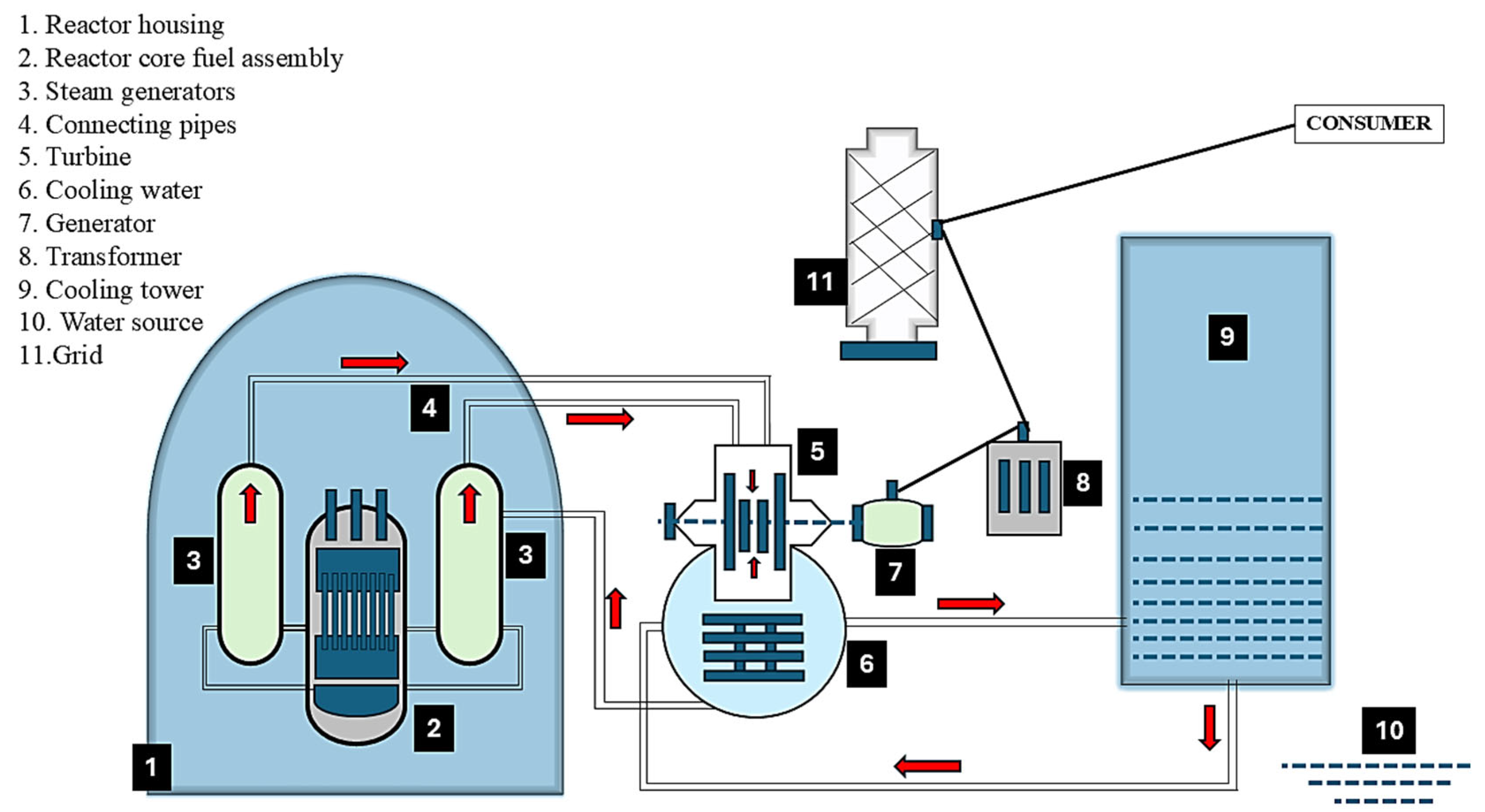
A nuclear reactor, in the context of nuclear engineering, is a thermoelectric facility used to generate energy from radioactive minerals (uranium) during fission in nuclear chain reactions [5]. Nuclear reactors can be classified into several types, such as Gas-Cooled Reactors (GCRs), Light Water Reactors (LWRs), Small Modular Reactors (SMRs), and Heavy Water Reactors (HWRs), depending on their design, fuel use, cooling methods, operational principles, and applications [6]. These nuclear reactors operate within two different loops, the primary and secondary loop, based on their specific functions. The loops separate heat transfer in the reactor core from the steam turbines and generators for efficient power generation, as shown in Figure 1.
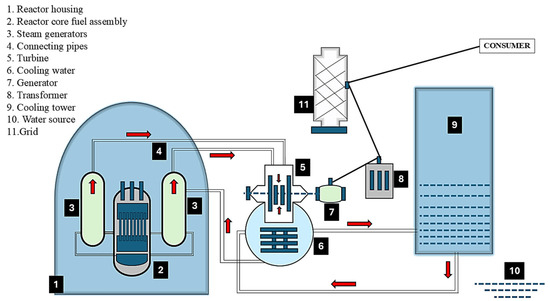
Figure 1.
Structural component of a nuclear plant facility.
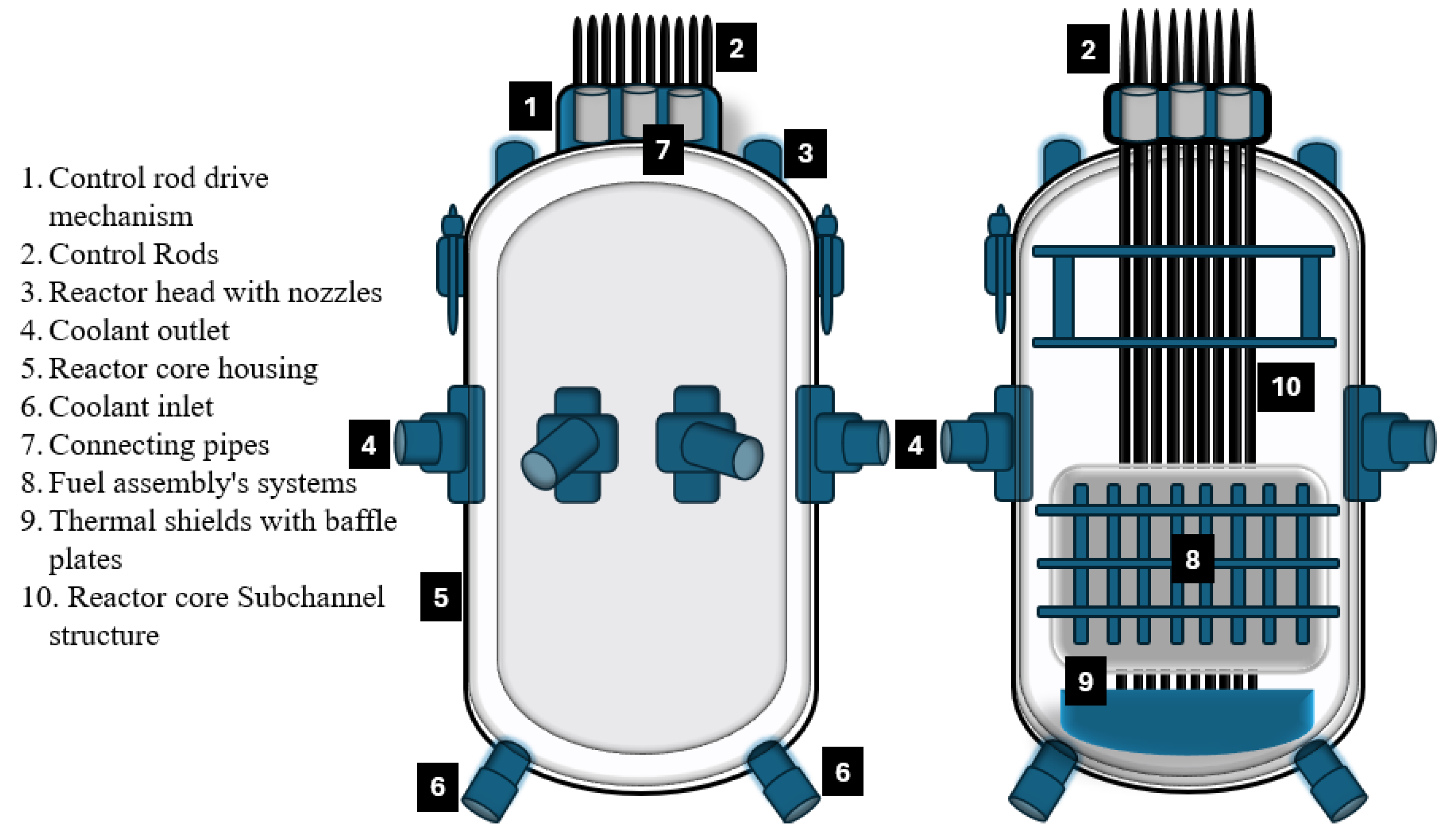
In reactor core analysis, subchannels refer to a series of multiple flow paths within the reactor’s fuel assembly, typically between two adjacent fuel rods, where coolant circulates to dissipate heat (energy) generated during nuclear fission [7]. Subchannel analysis in reactor study involves studying the dynamic characteristics of coolant, heat transfer processes, and temperature distributions within the flow paths of fuel assemblies [8], as shown in Figure 2.
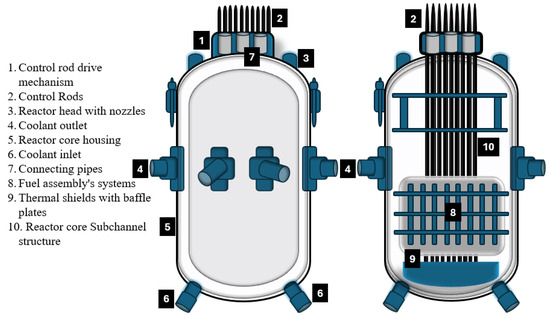
Figure 2.
The layout of nuclear reactor vessel.
In view of this, computational simulations and models are instrumental for reactor core research and analysis study [9]. Therefore, to design, evaluate, and simulate the multiphysics of the complex reactor core, efficient numerical tools and techniques are required. As nuclear reactors are evolving to enhance safety and efficiency, computational fluid dynamics (CFDs), a highly advanced computational method, has been used over the years for simulating the complex nature of the reactor cores [10]. These CFD simulations are essential for understanding the dynamic behavior of coolants in the intricate geometries of the subchannel fuel assemblies, which is vital for optimizing thermal transfer and safety operations.
Over the years, an effective method for simulating, modeling, and investigating coolant flow dynamics is the use of computational fluid dynamics [11]. The evolution of CFDs in nuclear reactor subchannel analysis was needed to address the complex thermal–hydraulic challenges within nuclear fuel assemblies [12]. Conventionally, CFD methods such as the Finite Volume Method (FVM) and Finite Element Method (FEM) have been used to model fluid flow and heat transfer in nuclear reactors [12]. While these methods are well-established and widely used, they sometimes face challenges in handling the complex geometries and multi-phase flow dynamics typically found in nuclear reactor cores (subchannels) [13]. One limitation of conventional CFD methods is the difficulty of accurately capturing intricate interactions within subchannels, which leads to uncertainties in safety assessments and performance predictions. Unlike the conventional CFD approach that relies on the Navier–Stokes equation (NSE) to model reactor core problems, the Lattice Boltzmann Method (LBM), a relatively new subset of conventional CFD methods, has not been thoroughly explored in nuclear reactor applications yet [14]. The Lattice Boltzmann Method (LBM) uses a mesoscale approach which depends on the discretized Boltzmann equation (BE) and Lattice Gas Automata (LGA) to bridge the gap between microscopic particle dynamics and macroscopic flow behavior by simulating particle distributions on a discrete lattice.
In recent times, computing capabilities have increased due to interest in numerical methods applied in fluid dynamics [13]. This phenomenon has influenced applications in nuclear areas like subchannel analysis (predicting coolant flow behavior and heat distribution techniques). The LBM framework provides several advantages, such as the ability to easily implement complex boundary conditions, parallelization, and flexibility in modeling multiphase flows [13]. Currently, research into the Lattice Boltzmann Method is novel in the field of nuclear reactor core applications. There are scant reviews on the Lattice Boltzmann Method applied as a CFD method in the nuclear reactor core (subchannel analysis study) [15]. Existing research on neutronic coupling and thermal–hydraulic analysis provides insights for multiphysics study. However, it does not address the applications of LBM in reactor core analyses. Examining the relevance of the Lattice Boltzmann Method applications in reactor study is necessary due to its advantages.
In view of this, our review aims to provide insight into the applications and advancements of Lattice Boltzmann Methods, particularly in subchannel analyses, to identify problems within reactor cores, and their adaptability when applied in nuclear reactor studies. From this study, individuals and researchers will gain significant insights into LBM and its application in the subchannel analysis study of the nuclear reactor plant.
1.1. Basic Principles and Relations Governing Computational Fluid Dynamics and Lattice Boltzmann Method
This section provides an overview of the fundamental principles governing computational fluid dynamics and the Lattice Boltzmann Method, as well as the relationship between the two. This fundamental study on CFD and LBM aims to highlight and familiarize researchers with the mathematical models, concepts, and developments governing them, without delving into details or their extensive mathematical derivations. Detailed knowledge can be found in the referenced resource material [16,17,18].
In nuclear reactor core analysis, subchannel studies on reactor behavior, such as the type of fluid flow and thermal transfer in the continuum, influences the accuracy, efficiency, and practicality of simulations. Simulation of the reactor core for subchannel studies is mostly performed using prominent fluid dynamics tools like computational fluid dynamics. Although CFD have been and still are proficient in the field of nuclear core simulation, LBM has gained attention in fluid dynamics and multiphysics simulations in recent times. While both address mass and thermal transfer problems, their fundamental principles, numerical frameworks, and computational benefits differ significantly.
1.1.1. Computational Fluid Dynamics
Computational fluid dynamics (CFD) is an aspect of fluid simulation systems that uses computational, numerical, and mathematical algorithms to investigate, evaluate, and solve fluid flow problems. The fundamental principles of CFDs depend on the laws of mass, momentum, and energy conservation, which are mathematically expressed through the Navier–Stokes equation:
where denote the velocity, pressure, density, kinematic viscosity, and external force, respectfully [17].
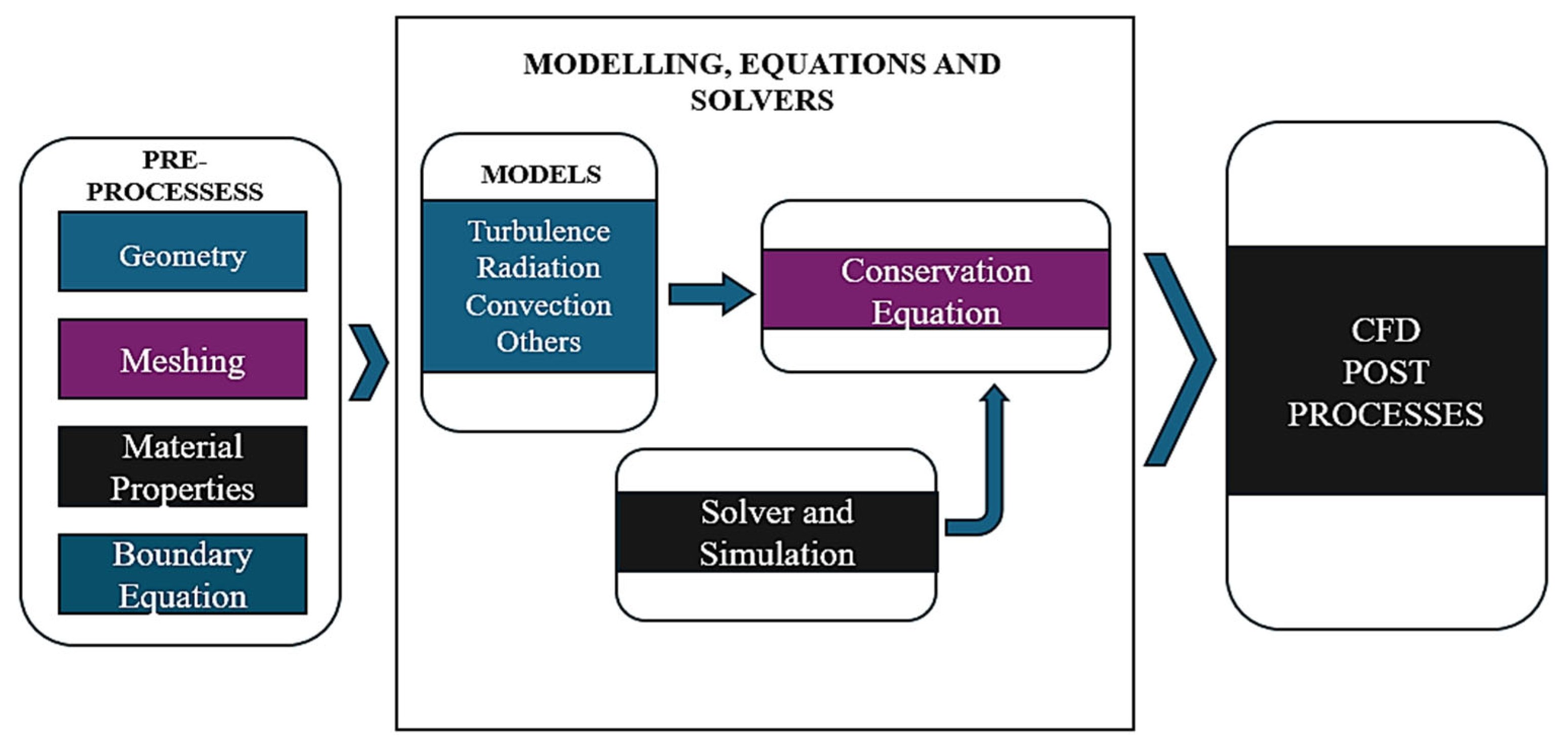
The Navier–Stokes CFD equations form the mathematical foundation for simulating coolant flow phenomena such as heat and mass transfer [16]. These governing equations iteratively solve and describe how fluids in motion are influenced by various fluid properties, such as viscosity, pressure, and temperature [19]. Following the development of the Navier–Stokes equations by Claude-Louis Navier and George Gabriel Stokes in 1822, CFD has since emerged as a simulation tool [20]. The Navier–Stokes equation has been the foundation for the CFD framework, which explains the flow of viscous fluids in terms of fluid dynamics. The CFD framework involves several approaches, such as the Finite Difference Method (FDM) [21], the Finite Volume Method (FVM) [22], the Finite Element Method (FEM) [23], and the Lattice Boltzmann Method (LBM) [24]. CFD has found extensive application across industries and scientific disciplines, including nuclear engineering [17]. CFD has become an indispensable tool for modeling complex physical phenomena, predicting flow patterns, and optimizing reactor designs, based on the workflow shown in Figure 3 [16].
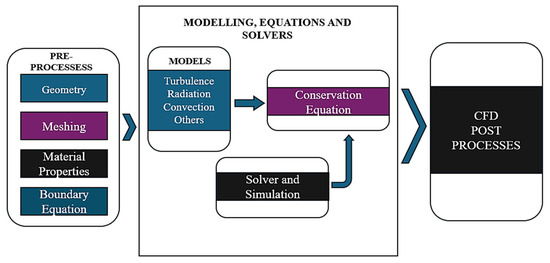
Figure 3.
Workflow of a conventional computational fluid dynamics (CFD) framework.
1.1.2. Lattice Boltzmann Method
The Lattice Boltzmann Method (LBM) has advanced as a fluid dynamics tool which uses computational approaches to solve fluid mechanics problems [25]. In recent times, the Lattice Boltzmann Method (LBM) has gained significant recognition as an alternative computational approach to traditional CFD methods [26]. Unlike conventional CFD, which directly solves the Navier–Stokes equations, the LBM uses a mesoscopic approach to model the time evolution of particle distributions by simulating the behavior of fluid particles on a discrete lattice [27].
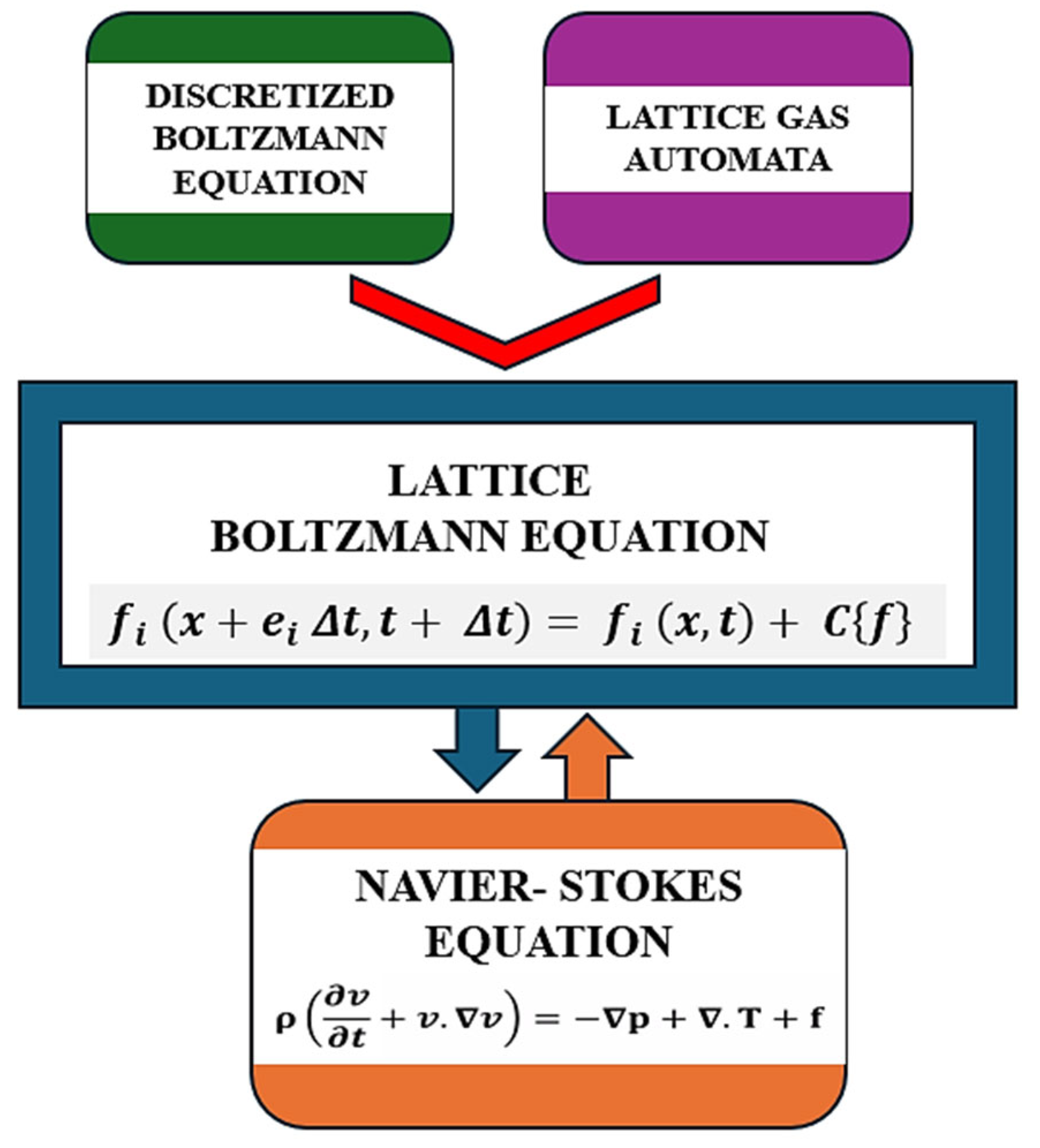
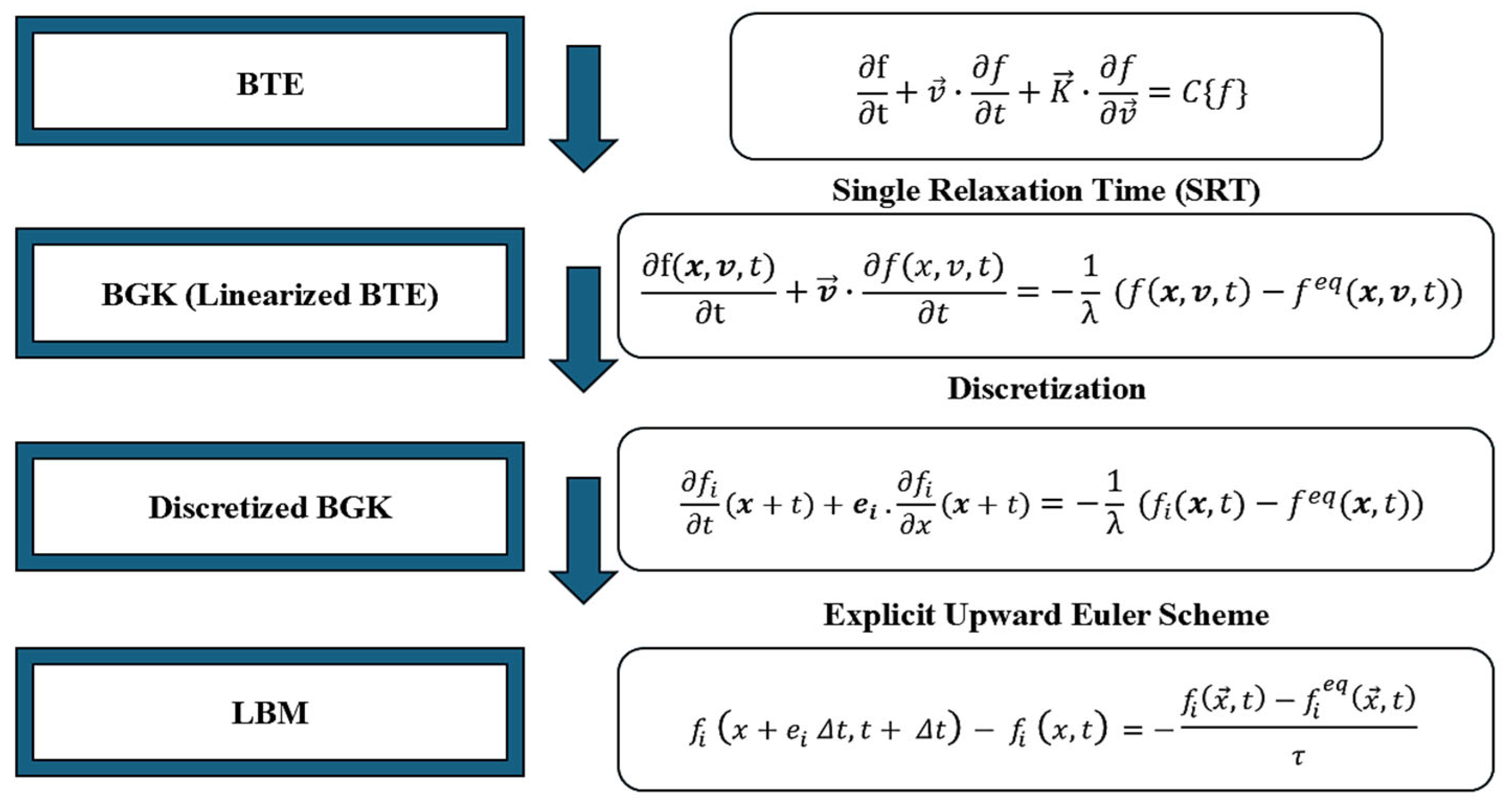
LBM has its roots in the Lattice Gas Automata (LGA) and discretized Boltzmann equation (BE) [28]. The LBM operates on a lattice grid principle and uses the discretized Boltzmann Transport Equation (BTE) and Lattice Gas Automata (LGA) to simulate fluid particle dynamics, making it suitable for high-performance computing and applications [21]. The foundational models of LGA and discretized BE in Figure 4 are based on the mass law, momentum, and energy conservation principles which form the Navier–Stokes equations (NSE) [28].
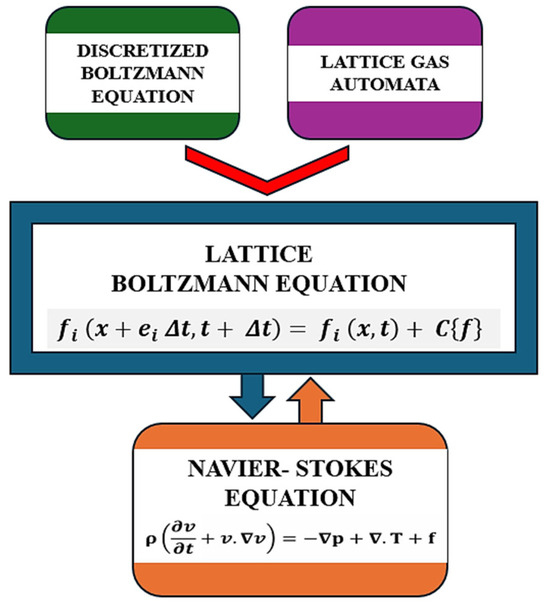
Figure 4.
Discretized Boltzmann equation (BE) with Lattice Gas Automata (LGA).
Although the Lattice Gas Automata model developed was limited due to statistical noise, velocity-dependent pressure, and an absence of Galilean invariance, the Lattice Boltzmann Method addresses these shortcomings by introducing probabilistic particle distributions and a linearized collision operator: the Bhatnagar–Gross–Krook model (BGK) [29]. This is because the macroscopic flow properties that develop from the microscopic relations of multiple molecular particles do not influence the overall macroscopic fluid behavior [29].
LBM models fluid behavior using a discretized set of particle velocities defined on a unit lattice grid. The overall particle distribution is expressed by the density distribution function given in the following equation:
where indicates the likelihood of a particle in position with velocity at time occurring, respectively [17].
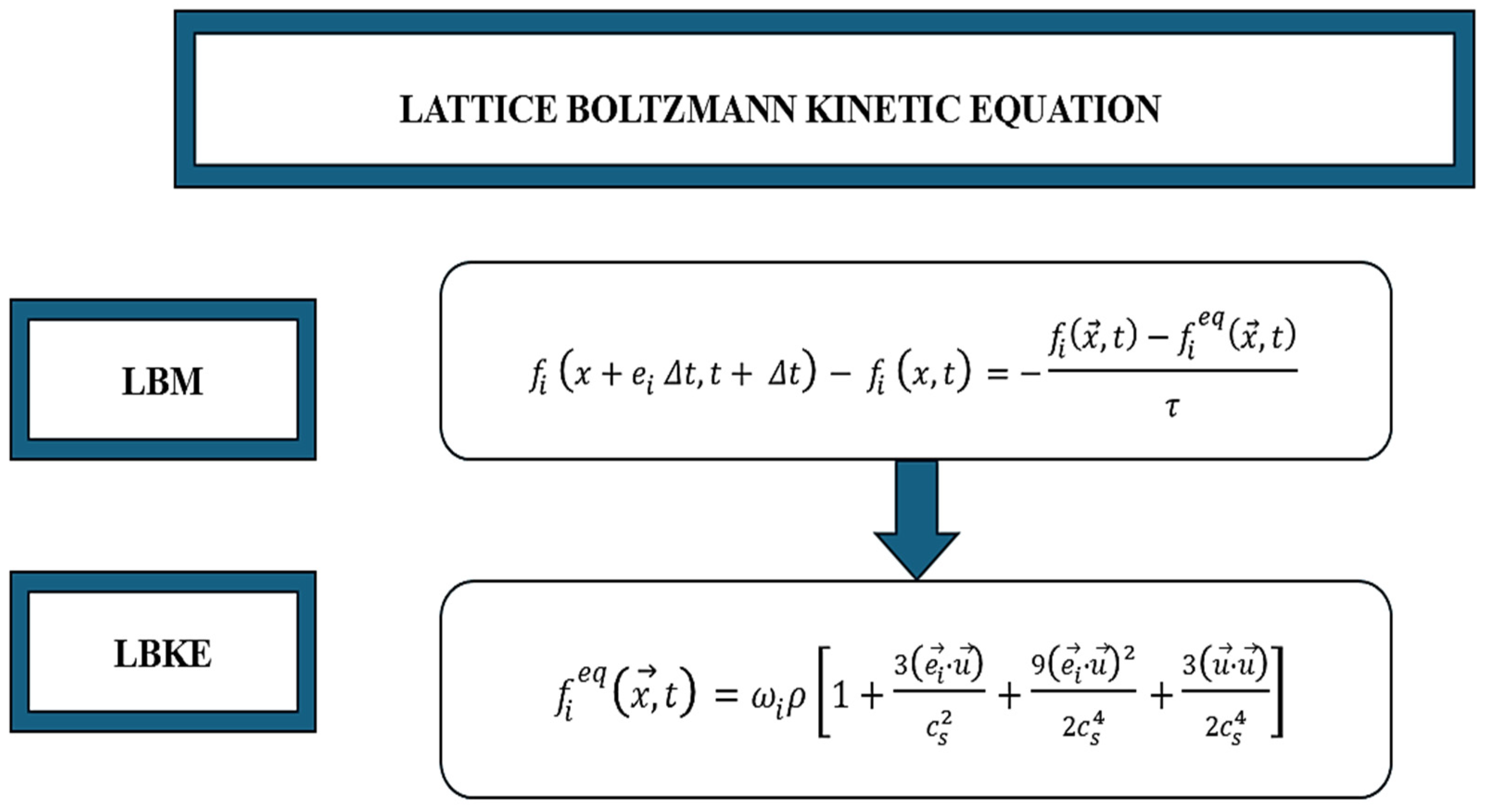
At each lattice node, the likelihood of a particle occurring in a particular discretized direction describes the principles of the particle distribution function [17]. The behavior of the fluid is governed by the Lattice Boltzmann Kinetic Equation (LBKE), obtained from the discretized Boltzmann equation [25]. The method uses the BGK (Bhatnagar–Gross–Krook) approximation to model particle collisions.
The BGK approximation assumes that particles relax towards an equilibrium distribution over a characteristic time step by simplifying the calculation of particle interactions while maintaining accuracy [30]. For each distribution velocity with th direction, linearized the Boltzmann Transport Equation (BTE) and BGK approximation of the time domain is discretized as the Lattice Boltzmann Kinetic Equation (LBKE) in Figure 5 and Figure 6 below:
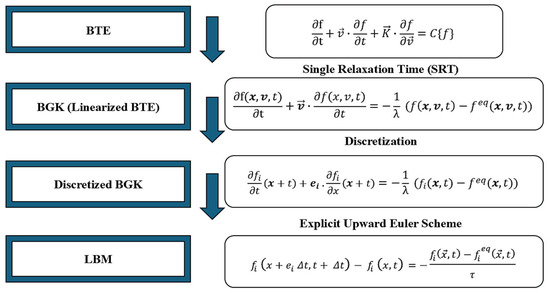
Figure 5.
Lattice Boltzmann framework: represents particle distribution function, represents discrete velocity, represents time step, and represents the collision operator (modeled using the BGK approximation).
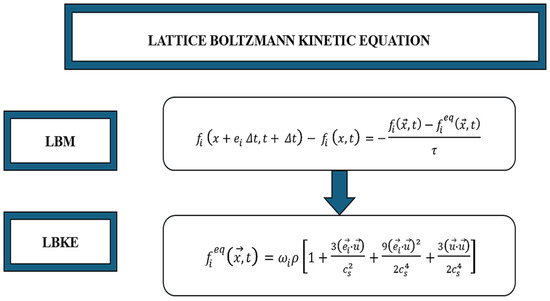
Figure 6.
Lattice Boltzmann Kinetic Equation: . Particle distribution function for velocity: . Equilibrium distribution function: . Relaxation time and , , , weight factor of the distribution velocity, density, fluid velocity, and speed of sound.
The Lattice Boltzmann Method, although a CFD subset, differs fundamentally from the traditional CFD approach [28]. LBM operates on a square or rectangular lattice mode, which divides the computational domain into a grid of nodes [28]. Each node represents a spatial point, associated with distribution functions which describe the probability of particles moving in specific discrete directions at a given velocity. These discrete velocity directions are predetermined based on the lattice structure, and are integral to LBM’s ability to model fluid flow.
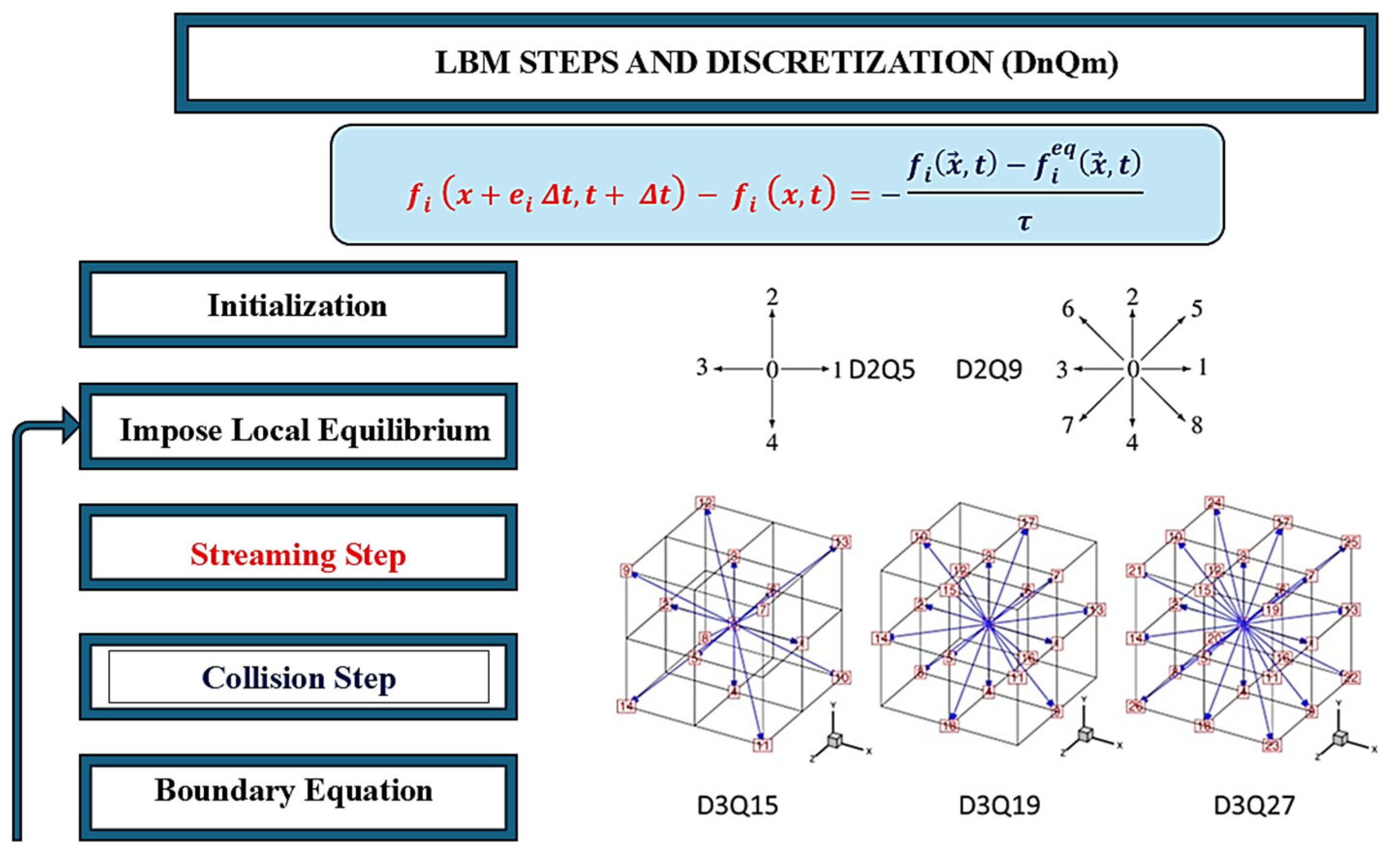
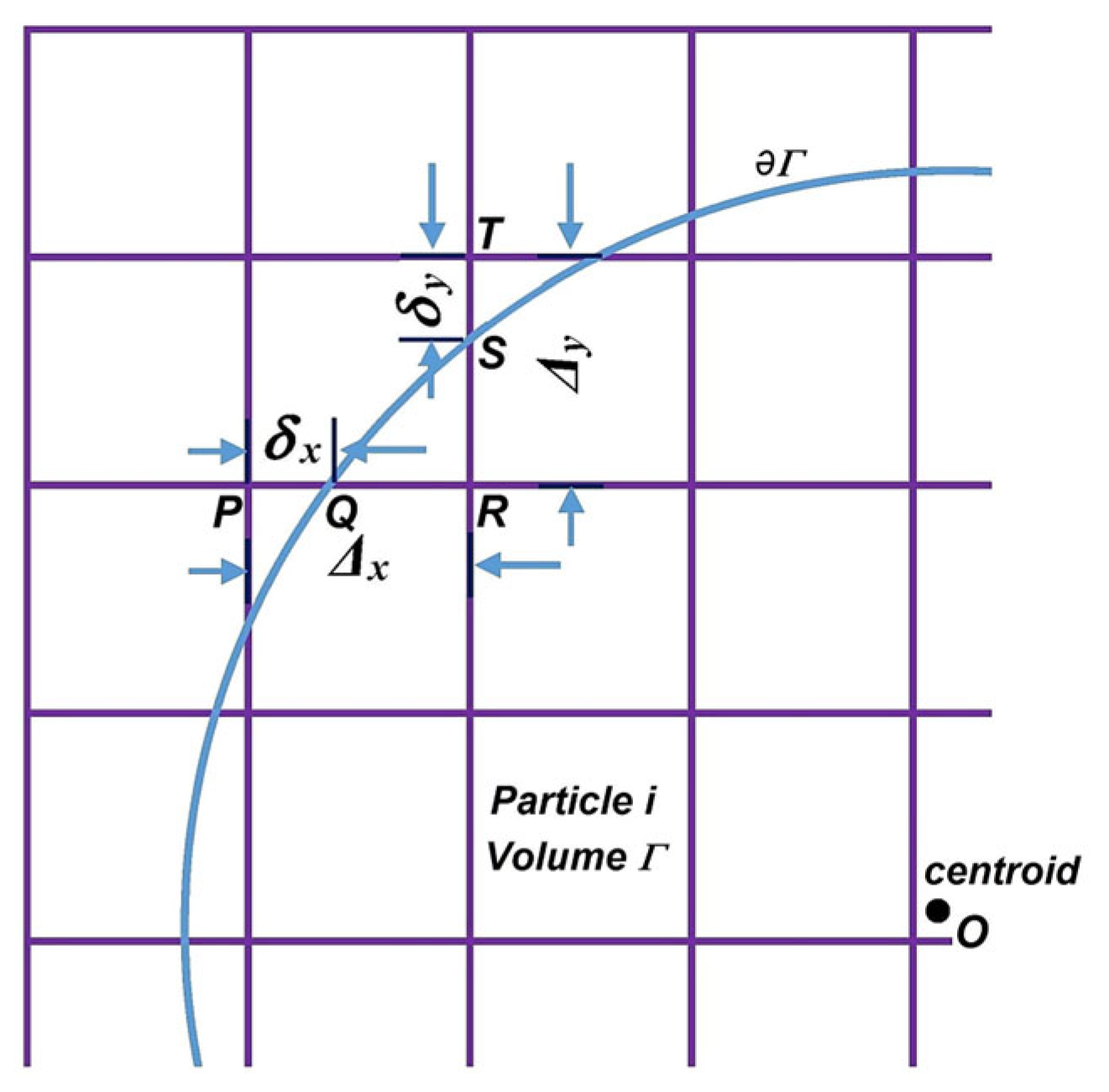
To implement the Lattice Boltzmann Kinetic Equation (LBKE) in an n-dimensional model for real-world problems with the BGK operator, as in Figure 7, the density distribution function in Equation (2) is modeled as , where “” is the dimensions and “” is the unit velocity at a lattice node [31].
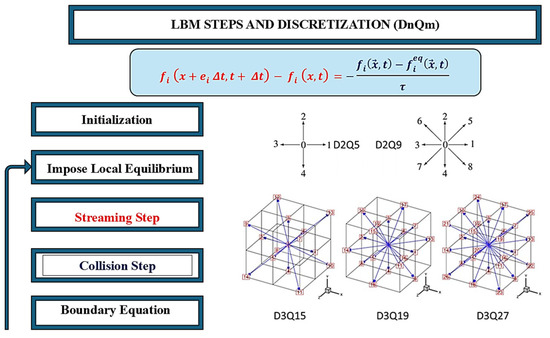
Figure 7.
LBM Steps and square lattice grids of LBM with the discretized distribution velocities ().
1.2. Tabular Comparision Between Computational Fluid Dynamics Method and Lattice Boltzmann Method
The comparison highlights their fundamental differences, strengths, and weaknesses in the context of fluid dynamics simulations, particularly for nuclear reactor analysis study and applications. The detailed comparison is outlined in Table 1 given below.

Table 1.
Comparative relation between computational fluid dynamics method and Lattice Boltzmann Method.
2. Methodology
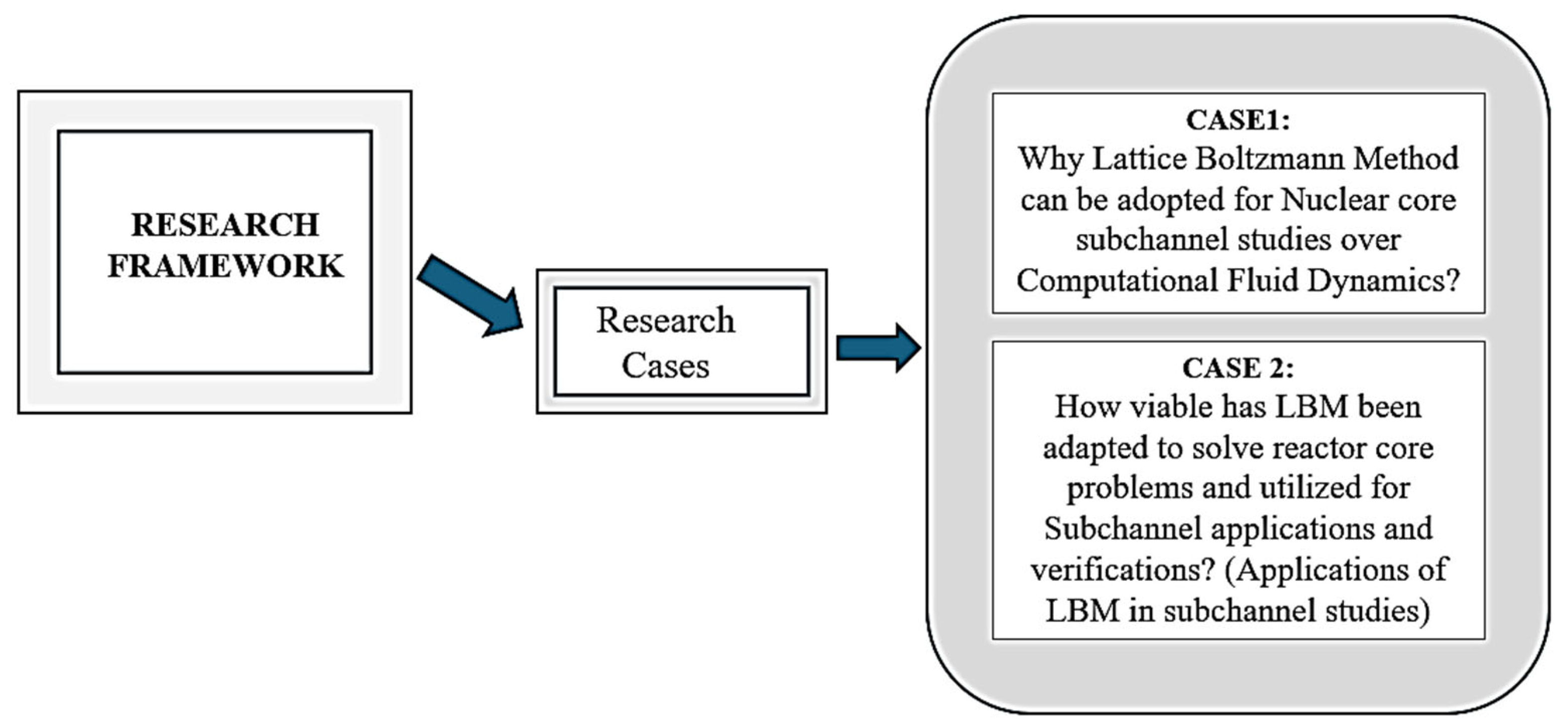
This section outlines the methodology adopted for this comprehensive review, which aimed to synthesize relevant research materials and provide insights into both computational fluid dynamics and the Lattice Boltzmann Method in the context of nuclear reactor cores. It explores articles and research materials on the Lattice Boltzmann Method, and evaluates its effectiveness and suitability compared to conventional CFD methods. The structured steps are outlined in Figure 8.
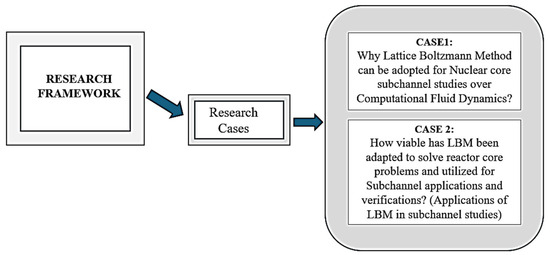
Figure 8.
Structured research cases.
The layout in Figure 8 summarizes the comprehensive case by case approach taken in this review, highlighting key phases from resources based on the categorization of CFD and LBM studies, comparative analysis, and their application in reactor subchannel studies. This structured research case will ensure comprehensive coverage of existing research while identifying gaps and potential advancements in the application of LBM for subchannel analysis in nuclear reactor cores.
3. Results: Addressing Research Cases
Over the decades, CFD has emerged as a high technological approach for investigating complex fluid flow and thermal transfer phenomena across various engineering disciplines [16]. Conventional CFD methods and codes have been extensively applied in modeling and simulating fluid dynamics behaviors in reactor cores, specifically for subchannel analysis [32]. However, reactor designs and safety have become more sophisticated, hence there is a demand for better and advanced simulation methods and modeling techniques to meet the demand [33].
LBM, a computational tool from traditional CFD, has emerged as an alternative, offering significant advantages over conventional CFD methods [29]. The LBM stands out due to its unique approach to simulating fluid dynamics, which differs fundamentally from the macroscopic continuum-based Navier–Stokes equations used in CFD [18]. The LBM operates on a mesoscopic scale, utilizing a particle-based approach that models flow characteristics using the evolution of probability distribution functions on discrete lattice units. This unique methodology enables LBM to handle complex geometries, multiphase flows, and turbulent interactions more effectively than traditional CFD approaches [34].
3.1. Case 1: Why Lattice Boltzmann Method Can Be Adopted for Nuclear Core Subchannel Studies over Computational Fluid Dynamics?
In the context of nuclear subchannel analysis, the utilization of the Lattice Boltzmann Method over traditional computational fluid dynamics methods offers several distinct advantages according to our research findings. To address the research question mentioned above, below is a relevant review study on why LBM is a better choice over the traditional CFD method.
3.1.1. Simple Algorithmic Implementation
One primary advantage of LBM is its relatively simple algorithmic implementation [17]. Unlike traditional CFD methods, which often require complex numerical models to solve the NS equations, LBM operates on a straightforward lattice structure [26]. This simplicity allows for easier modeling and debugging of numerical models [26].
In 2014, a review paper titled “A Comparative Study of Lattice Boltzmann Models for Incompressible Flow” [35] evaluated various lattice Boltzmann method (LBM) models to determine their effectiveness in simulating incompressible fluid flows. They focused on the simplicity of algorithm implementation, computational efficiency, and the accuracy of these models. The study provided insights into the trade-offs between simplicity and performance, guiding the selection of appropriate LBMs for specific incompressible flow simulations. While the specific details the authors find from other papers demonstrate a simple algorithm schematic of LBM, they concluded in their studies that LBM algorithm implementations are straightforward, which is simple for incompressible flow implementation, unlike the traditional CFD codes [35].
Sauro Succi (2001), in “The Lattice Boltzmann Equation for Fluid Dynamics and Beyond”, emphasized the simplicity of the LBM as a computational tool for fluid flow studies [36]. Succi highlighted that LBM distinguishes itself by being a mesoscopic method rooted in statistical mechanics, which allows it to bypass some of the complexities inherent in calculating the NS equations directly [36]. This means that LBM uses simple collision and streaming steps on a discrete lattice, making its implementation straightforward compared to the conventional CFD approach. The authors stated that LBM operates locally, which eliminates the need for solving complex equations of conventional CFD. Succi underscored the mesoscopic nature of LBM and concluded that LBM bridges the gap between microscopic kinetic theory (Boltzmann equation) and macroscopic continuum mechanics (Navier–Stokes equations), and also uses simple update rules based on collision and streaming steps by avoiding the need for iterative solvers for pressure–velocity coupling [36].
Guo et al.’s (2014) paper, “Lattice Boltzmann Method and Its Applications in Engineering”, highlighted the effectiveness of the LBM in representing physical processes, boundary conditions, and fluid interactions [37]. Guo et al.’s (2014) work particularly emphasized how LBM’s kinetic theory foundation facilitates its adaptability to simulate various complex geometries in fluid dynamics [37]. They stated that the LBM has a structured framework which enables accurate numerical modeling and the efficient implementation of boundary conditions, such as Dirichlet and Neumann types, which are crucial in fluid and thermal dynamics studies. In conclusion, the authors stated that LBM’s advantage lies in its ability to simplify pre- and post-processing through discretization on regular lattice grids, thereby making it suitable for multiphysics problems [37].
3.1.2. Efficient Meshing and Grid Refinement
Unlike traditional CFDs, LBM has a structured lattice grid, which simplifies the meshing process. Traditional CFD methods often require complex mesh generation techniques, especially for intricate geometries in nuclear reactors [33]. In contrast, LBM operates on a discrete lattice, which is more flexible and computationally efficient without the need of fine mesh generation [33]. The grid used in LBM can be easily refined or adapted without the need to re-mesh the entire domain, making it more time efficient, making this phenomenon applicable in nuclear reactor analysis, where the reactor core geometry is highly intricate [38].
Li-Shi Luo, Manfred Krafczyk, and Wei Shyy published a paper on “Lattice Boltzmann Method (LBM) in computational fluid dynamics (CFD)”, where they emphasized that efficient meshing and grid refinement is a critical strength of LBM [39]. The authors explained that LBM is inherently designed for structured grids, which simplifies the process of grid generation and makes it computationally efficient. Unlike traditional CFD methods that may require unstructured or hybrid grids to handle complex geometries, LBM employs uniform lattice grids that allow for straightforward meshing [39].
Further, Li-Shi Luo, Manfred Krafczyk, and Wei Shyy stated that LBM is compatible with Adaptive Mesh Refinement (AMR) techniques, which allow for localized grid refinement where higher resolution is needed, such as near boundaries, shocks, or interfaces in multiphase flows. They concluded that the simplicity of LBM meshing and grid refinements significantly reduced the pre-processing time for simulations, making LBM particularly useful and applicable to problems where quick setup and deployment are critical [39].
In 2020 [33], a paper titled “Discrete effects on boundary conditions of the lattice Boltzmann method for fluid flows with curved no-slip walls” by Wang et al. examined how meshing and grid refinement impact the accuracy of boundary conditions during LBM simulations involving no-slip curved walls. They highlighted that the discrete nature of the lattice grid can introduce errors when representing curved boundaries, leading to inaccuracies in simulating fluid flows near these walls. To address this limitation, the authors discussed the importance of refining the grid near curved boundaries to better capture their geometry and improve the precision of boundary condition implementation. They also explored various meshing strategies to enhance the representation of curved surfaces within the lattice framework. Their findings suggested that careful attention to meshing, and grid refinement, is crucial for accurately modeling fluid flows with curved no-slip walls using the Lattice Boltzmann Method [33].
3.1.3. High Parallelization Capabilities
One of the major challenges faced by traditional CFD methods is their computational cost, particularly for large-scale simulations [40]. CFD methods often require solving complex Partial Differential Equations (PDEs) over large domains, which are computationally expensive and can be difficult to parallelize [16]. In contrast, LBM is parallelizable due to its localized nature. Each lattice node in LBM only interacts with its nearest neighboring node, making it well-suited for parallel computing like multi-core CPUs and GPUs [17]. In nuclear reactor analysis, where simulations often involve modeling large and complex systems (reactor core with subchannel models), LBM’s ability to distribute the calculations across multiple processors can significantly reduce computation time [15].
The authors of the paper “Parallel fluid flow control and optimization with lattice Boltzmann methods and automatic differentiation”, Mathias J. Krause and Vincent Heuveline, discussed the integration of parallel computing with LBM for flow controls and optimization [41]. Their research leveraged automatic differentiation to optimize flow problems and used joint Lattice Boltzmann Methods for shape optimization and control. Their implementations demonstrated efficient parallel performance, enabling simulations on complex geometries and achieving results with high computational efficiency in a distributed system. Mathias J. Krause and Vincent Heuveline’s research demonstrated an exceptional scalability across large simulations, showing LBM’s strength in handling complex geometries and high-resolution computations effectively [41].
Yan Su, Tiniao Ng, and Jane H. Davidson conducted a study on “A Parallel Non-Dimensional Lattice Boltzmann Method for Fluid Flow and Heat Transfer with Solid–Liquid Phase Change” [42]. The authors highlighted that the parallelization efficiency of the LBM is highly parallelizable, making it efficient for large-scale simulations. They stated that LBM leverages the n-dimensional Lattice Boltzmann Model to handle flow and thermal transfer problems. Additionally, the parallelization of LBM enables it to tackle complex geometries and varying thermal conditions with ease. They concluded that LBM’s parallelization feature makes the method adaptable to different flow regimes, boundary conditions, and even varying physical properties during phase changes [42].
3.1.4. Integrated Multiphysics Coupling and Multiphase Flow
Multiphysics coupling and the ability to model multiphase flow are two most important factors in nuclear reactor analysis [43]. In nuclear reactor cooling, fluids may exhibit multiphase behavior such as gas–liquid or liquid–liquid interactions. Modeling this multiphase flow in the reactor core for subchannel study is necessary for understanding heat transfer dynamics [32].
A study by Yahui Wang, Ming Xie, and Yu Ma, titled “Neutron transport solution of lattice Boltzmann method and streaming-based block-structured adaptive mesh refinement”, highlighted integrated multiphysics coupling and multiphase flow in the context of neutron transport simulations [44]. Their study emphasized the ability of LBM to couple neutron transport with other physical phenomena, such as heat transfer and fluid dynamics. By combining LBM with Adaptive Mesh Refinement techniques, they stated that the model can handle the complexities of multiphysics systems. This integration can allow for a more accurate representation of the interactions between neutrons, fluid flow, and heat transport, which are critical in nuclear reactor simulations [44].
The paper also discussed the application of LBM to simulate multiphase flows. Traditional CFD methods often require a separate framework for fluid dynamics, heat transfer, and neutronics. In contrast, LBM enables multiphysics coupling within a single framework, which simplifies the process of integrating different physical phenomena. By using multiple overlapping lattices such as fluid lattices, thermal lattices, and neutronic lattices [21,43], LBM allows for the seamless integration of thermal–hydraulic and neutronic analyses in reactor simulations. While the primary focus is on neutron transport, LBM’s inherent capabilities in handling multiphase allow it to model complex systems. They concluded that LBM is particularly useful when the neutron transport process is influenced by multiphase systems, such as those found in nuclear reactors, where coolant behavior and phase changes significantly impact reactor performance [17].
3.1.5. Flexibility and Hybridization
Unlike traditional CFD, flexibility and hybridization efficiency are important features of the Lattice Boltzmann Method [45]. LBM can be easily integrated into hybrid schemes where traditional CFD methods like FVM or FEM can be combined with the LBM to increase the strengths of both methods. For example, turbulence models can be integrated with LBM to handle high Reynolds number flows in reactor cores while using LBM’s simple mesoscopic approach for fluid dynamics and heat transfer [12]. This flexibility allows researchers to tackle a broader range of problems in nuclear reactor simulations, from complex geometries to high-fidelity turbulence modeling [46].
A paper published by Mengke Wen, Weidong Li, and Zhangyan Zhao on “A hybrid scheme coupling Lattice Boltzmann method and Finite-volume Lattice Boltzmann method for steady incompressible flows” highlighted a hybridized approach that combined LBM with the Finite Volume Lattice Boltzmann Method (FV-LBM) to increase the rate of simulation of steady incompressible fluid flows [47]. According to the authors, the FV-LBM combination allowed for better numerical stability and accuracy in simulating incompressible fluid flows compared to using each method independently. Again, they stated that, by coupling LBM and FV-LBM, the hybrid model leverages the mesh flexibility of the LBM and the conservation properties of the FV-LBM, thereby reducing computational costs while ensuring that fluid flow properties are accurately captured [47].
A study on “Neutron transport solution of lattice Boltzmann method and streaming-based block-structured adaptive mesh refinement” by Yahui Wang, Ming Xie, and Yu Ma also highlighted the flexibility and hybridization of LBM in addressing complex simulation challenges [44]. They stated that the hybridization of LBM with Adaptive Mesh Refinement enabled it to handle highly localized phenomena effectively. This hybrid method adapted mesh resolution dynamically, refined it in regions with steep gradients or complex interactions, such as near boundaries or phase interfaces, and coarsened it in simpler areas. By hybridizing LBM with AMR, the technique achieved optimal computational efficiency, which ensures that high computational resources were focused on areas that require detailed resolution (regions where neutron transport or fluid dynamics undergo significant changes) [44].
The paper “A hybrid lattice Boltzmann/Immersed Boundary Method/Finite-Difference Model for thermal fluid-solid interactions” by Farshad Gharibi, Seyed Ali Hosseini, and Dominique Thévenin proposed a novel hybrid method combining the Lattice Boltzmann Method (LBM), Immersed Boundary Method (IBM), and Finite Difference Method (FDM) models to simulate thermal fluid–solid interactions effectively [48]. Their study successfully integrated the strengths of LBM, the IB method, and FD techniques to handle complex thermal fluid–solid interactions. LBM was used for fluid flow simulation, the IB method was employed to manage the interaction between fluid and solid boundaries, and FDM was utilized for solving energy equations. This hybrid approach allowed for more accurate and efficient modeling of complex geometries and heat transfer processes [48]. They concluded that the hybrid approach offers significant improvements in simulating thermal fluid–solid systems, especially for complex geometries and conditions. By combining the strengths of LBM, IB, and FD, the model efficiently handled the coupled fluid dynamics and heat transfer processes. This makes LBM a powerful tool for applications involving heat exchangers, thermal management in industrial systems, and other systems with significant thermal–fluid interactions [48].
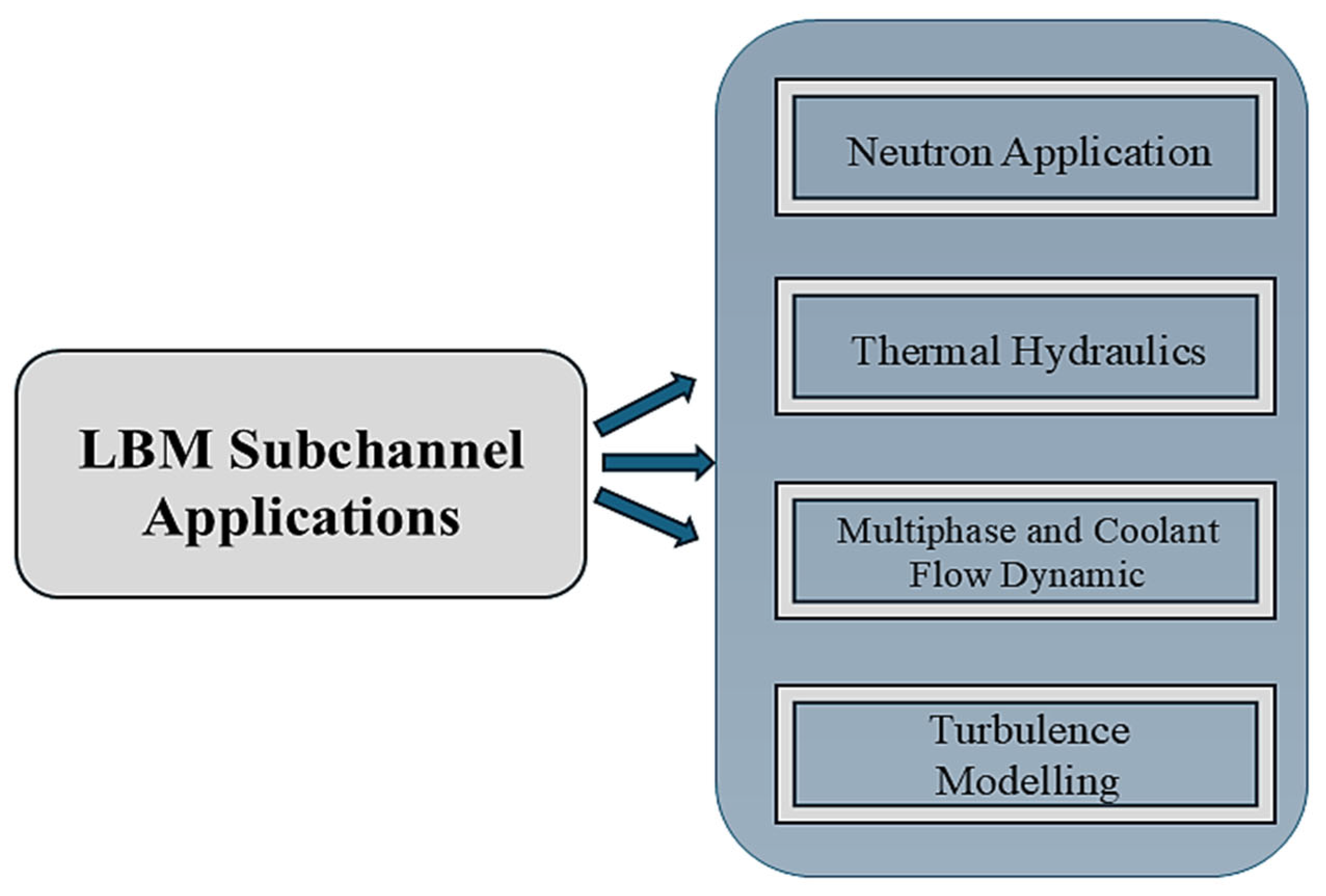
3.2. Case 2: How Viably Has LBM Been Adapted to Solve Reactor Core Problems and Utilized for Subchannel Applications and Verifications? (Applications of LBM in Subchannel Reactor Studies)
To simulate the behavior of fluid flow in subchannel analysis studies, computational and numerical methods with effective modeling paradigms contribute to the nuclear reactor’s design and sustainable applications. Subchannel analysis involves detailed examination of coolant flow and heat transfer behaviors within the closely packed fuel assemblies of a reactor core. The subchannel analysis of a nuclear reactor core focuses on fluid dynamics and heat removal between fuel rods in the reactor core, which is crucial in the reactor operation.
Over decades, conventional CFD methods have been applied to study these complex phenomena. However, in recent years, LBM, with its unique applications, has gained prominence as an alternative approach in handling complex reactor analysis problems. In the section below, Figure 9 shows our findings on various aspects of the reactor’s subchannels where LBM has been applied in place of CFDs to increase improvement in nuclear reactor modeling methods.
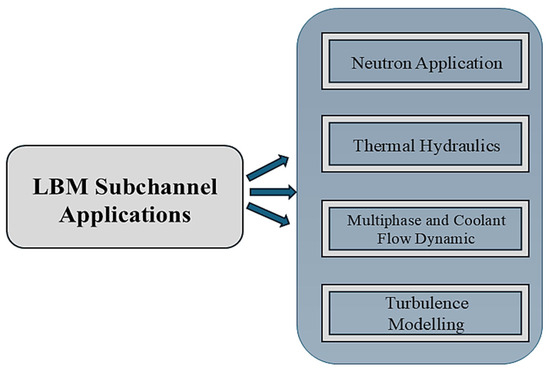
Figure 9.
Various aspects where LBM have been applied in subchannel studies.
The studies below demonstrate the viability of how LBM has been applied in addressing key challenges in subchannel analysis.
3.2.1. Neutron Transport Modeling
The LBM in neutron transport modeling and application has become an alternative to traditional CFD numerical methods due to the flexibility and efficiency in simulating complex reactor geometries and multiphysics phenomena [15]. A series of studies by [49,50,51,52] have explored the potential of LBM in addressing neutron transport challenges in various reactor settings, including Pressurized Water Reactors (PWRs), Molten Salt Reactors, and heterogeneous core configurations. Their studies do not only focus on the capabilities of LBM in solving neutron transport equations, but also investigate its integration with other physical models, such as heat transfer, to provide a more comprehensive understanding of reactor behavior.
Wang et al.’s (2019) study on “Neutron Discrete Velocity Boltzmann Equation and its Finite Volume Lattice Boltzmann Scheme” conducted research on neutron transport in steady-state and transient scenarios in two-dimensional and three-dimensional (2D and 3D) geometries [52]. Their work emphasized the application of LBM into neutron transport with asymmetric source configurations. A key finding of their study is the lattice-independent nature of LBM, particularly its ability to handle high angular discretization, which is crucial for achieving accurate solutions across a wide range of reactor configurations, from simple geometries to complex heterogeneous systems. The authors demonstrated that in high-scattering media, LBM is capable of capturing neutron transport behaviors with high fidelity. They highlighted that the flexibility of LBM to work with both triangular and quadrilateral meshes was viable, making it a valuable tool for simulating reactors with intricate geometries. Despite its advantages, the study pointed out challenges such as ray effects, which can cause inaccuracies in regions far from the neutron source. The authors concluded that the limitation, however, can be mitigated by increasing the angular discretization, ensuring more accurate results, particularly in high-scattering environments like reactor cores [52].
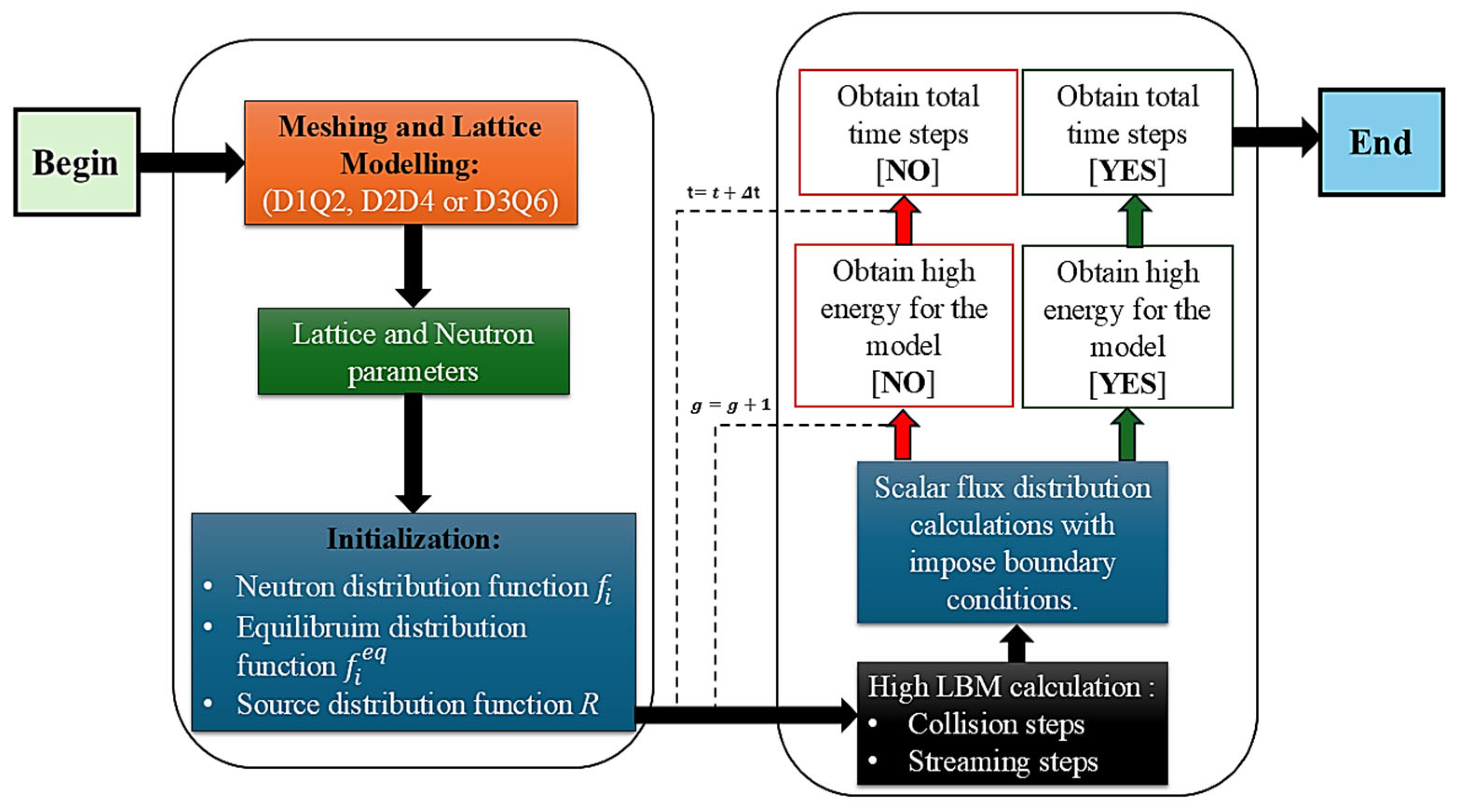
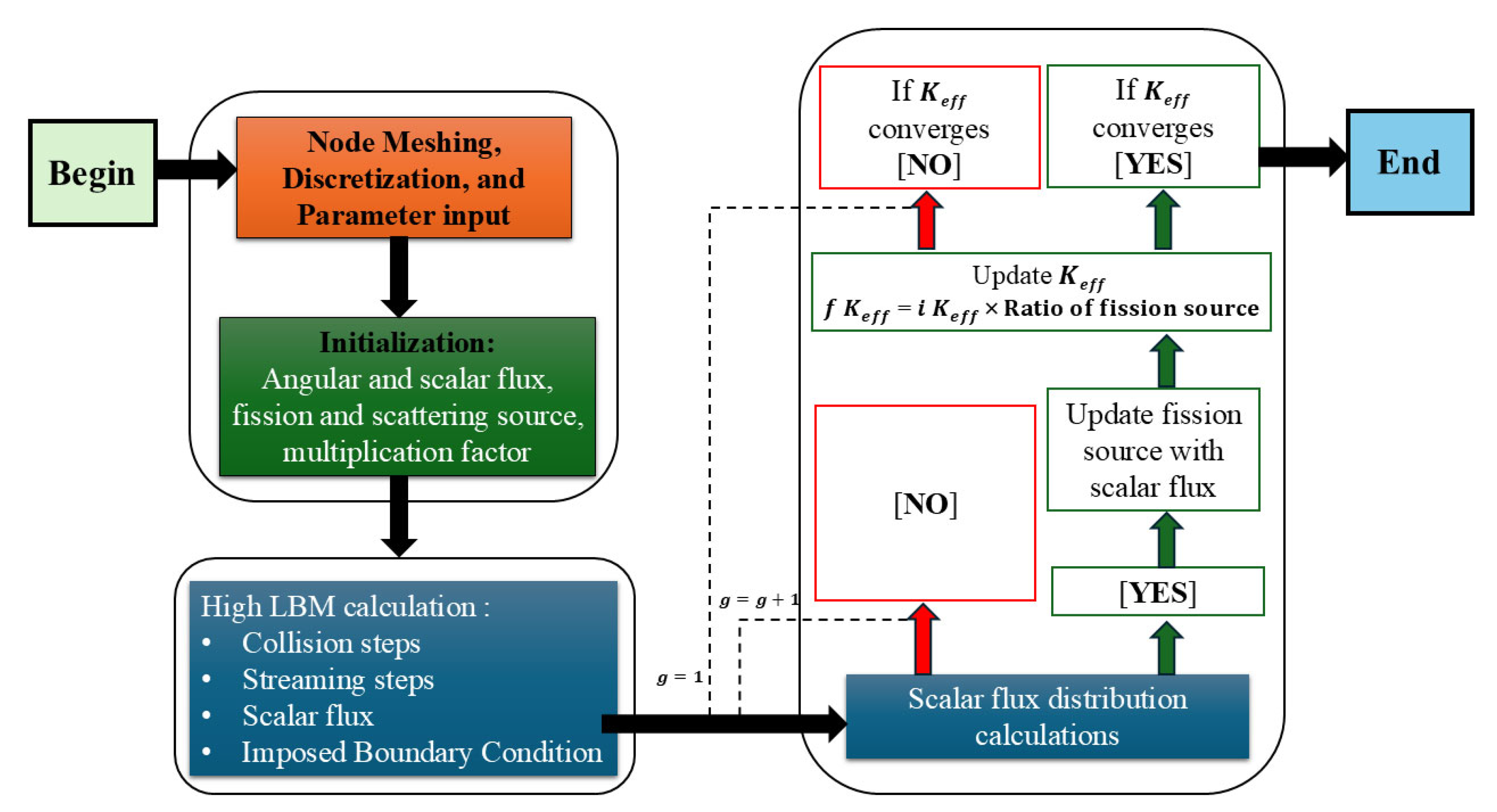
A follow-up study by Wang et al. (2019) on “High-order lattice Boltzmann method for multi-group neutron diffusion solution” examined the neutron diffusion of Pressurized Water Reactors (PWRs) and heterogeneous reactor cores, specifically focusing on the comparison of different LBM variants in 2D and 3D setups [51]. The study made a significant contribution by highlighting the superior performance of high-order LBM (HLBM, particularly P1-LBM) compared to conventional LBM and other numerical methods, such as Finite Element Methods (FEMs) and Finite Difference Methods (FDMs) [51]. The higher-order LBM provides greater accuracy and reduces truncation errors, especially in complex simulations where conventional methods might struggle with precision. Their research also integrated 3D simulations, further showcasing LBM’s ability to handle more realistic reactor models. The accuracy of LBM in 3D geometries was validated through comparisons with established neutron transport techniques, proving that LBM could be a reliable tool in simulating neutron behavior in reactors in Figure 10. However, in Figure 11 and Figure 12, while LBM shows promise in 2D and 3D, computational efficiency remains a challenge, particularly in large-scale simulations involving complex materials and geometries [51].
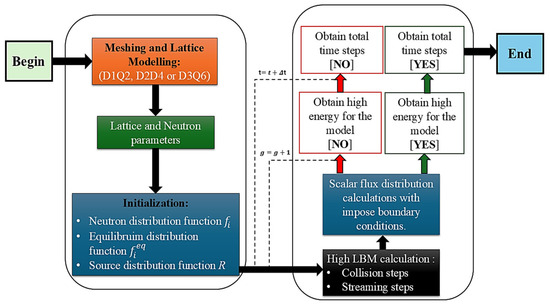
Figure 10.
Schematic flowchart application of high LBM for neutron diffusion transient problems.
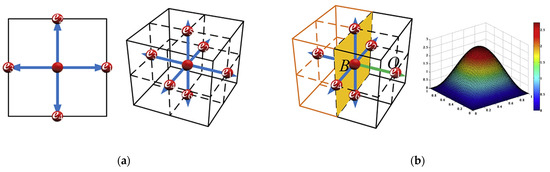
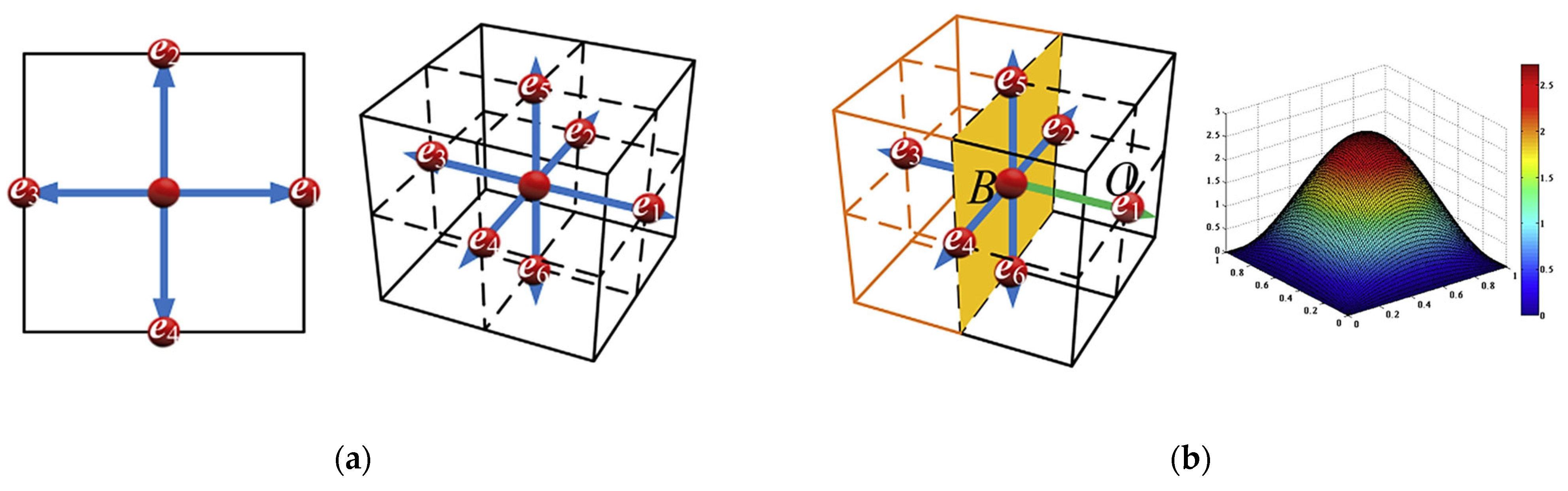
Figure 11.
(a) Schematics of lattice models (D2Q4 and D3Q6) [51]; (b) schematics of boundary conditions for D3Q6 lattice model used for HLBM and neutron distribution from center to boundaries [51].
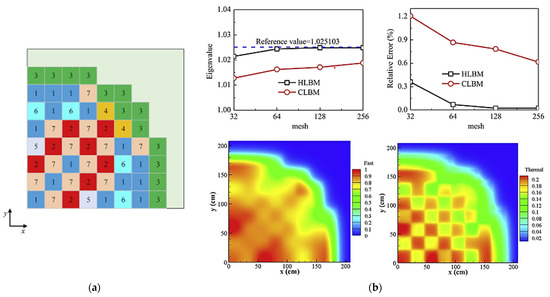
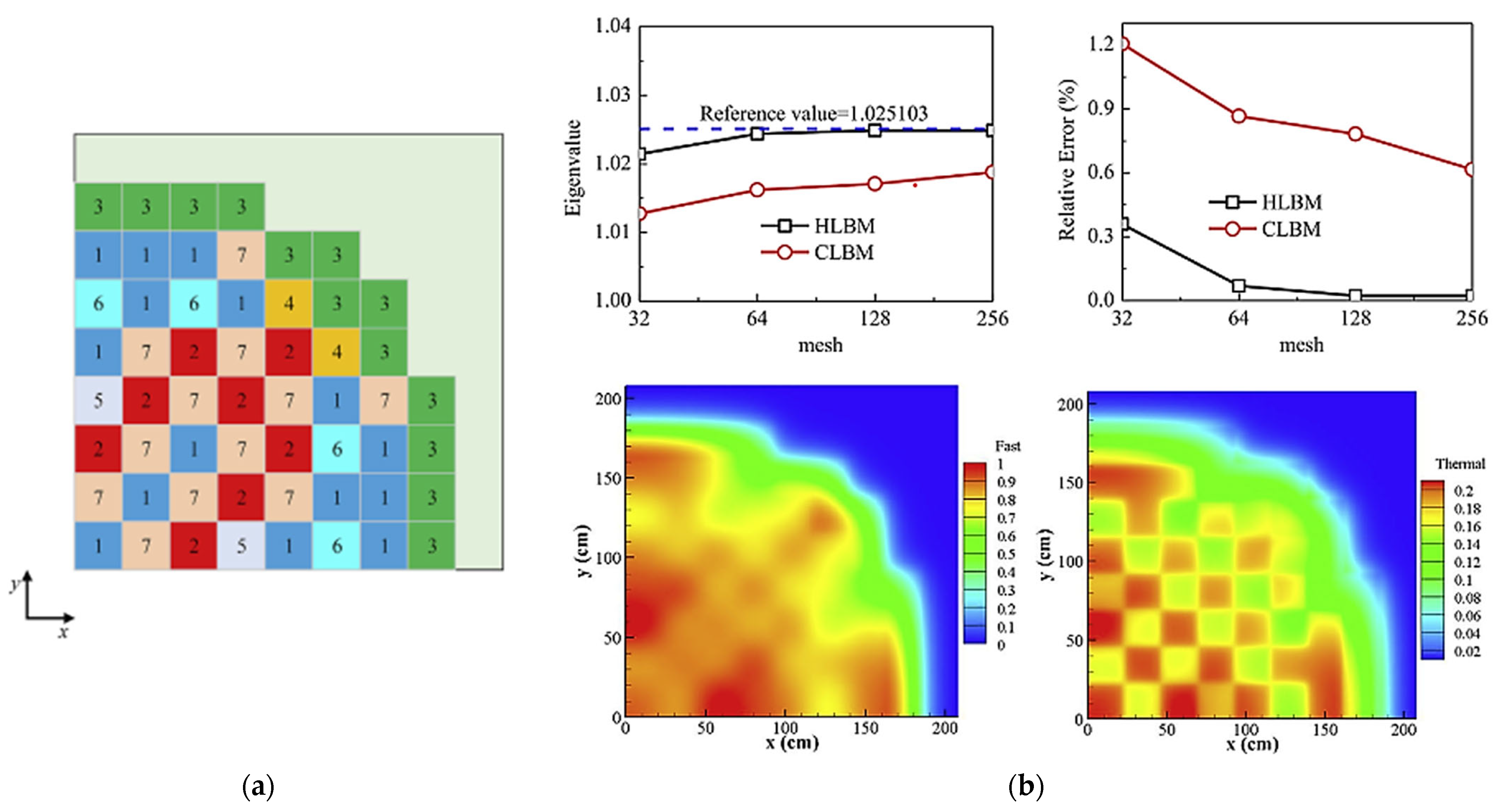
Figure 12.
(a) The 2D model of PWR benchmark schematics; (b) solution of using HLBM for the 2D PWR benchmark problem [51].
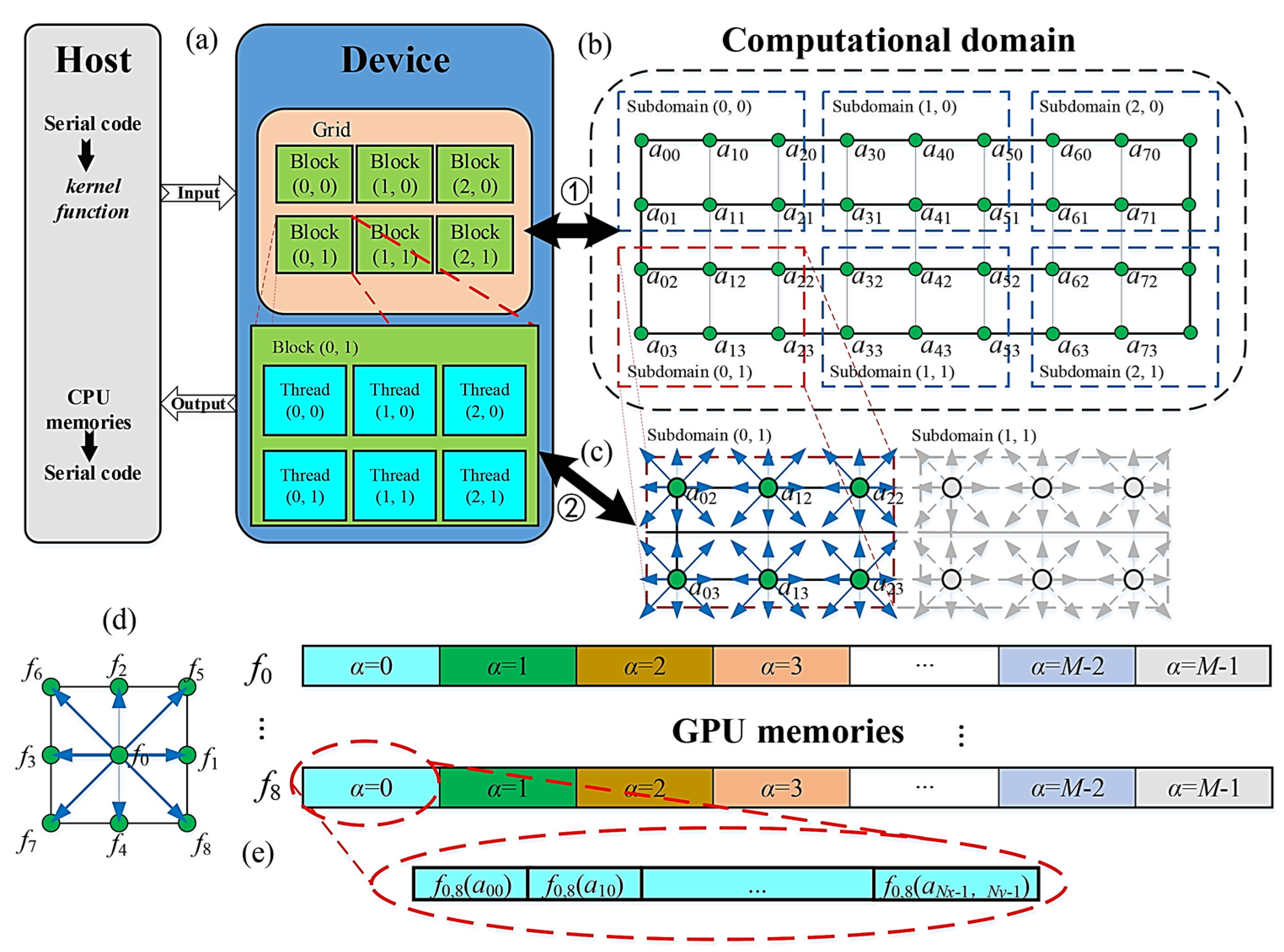
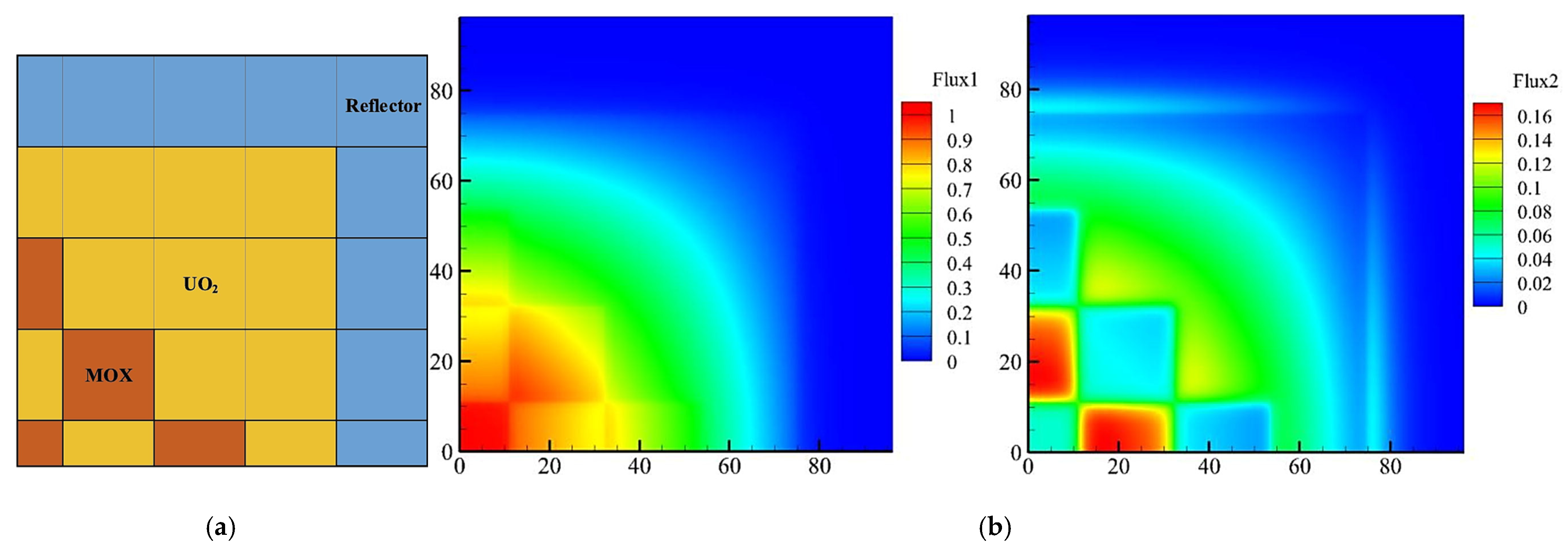
In Wang et al.’s (2019) paper “GPU accelerated lattice Boltzmann method in neutron kinetics problems II Neutron transport calculation”, the authors applied LBM to simulate neutron transport in a MOX (mixed oxide) reactor and a reed cell, using both one-dimensional and two-dimensional (1D and 2D) models. Their research introduced a key advancement in neutron transport simulation by employing spatial–angular parallelization to optimize the computational efficiency of LBM. The incorporation of spatial–angular parallelization substantially decreased the computational time and improved the accuracy of the neutron transport simulations, which is particularly important when simulating reactor cores with complex geometries and angular variations. Additionally, their study employed discrete ordinate Sn-LBM, which was necessary for accurately modeling neutron flux in regions where scattering is high, and angular discretization plays a vital role in achieving precise results [50]. The computational efficiency of NT-LBM used in Figure 13 and Figure 14 shows the flexibility of LBM, which was proven to be effective for simulating neutron transport in heterogeneous reactors, making it a valuable tool for reactor design and analysis [50].
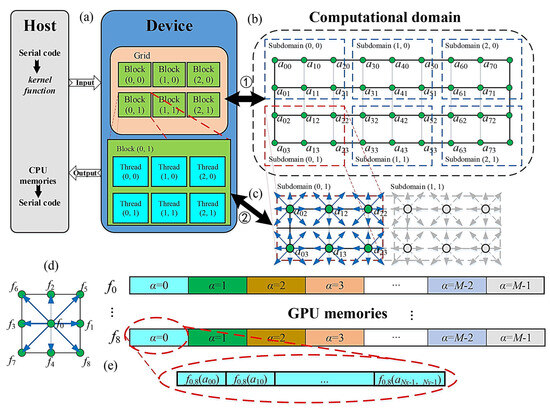
Figure 13.
GPU-accelerated NT-LBM schematics. (a) The hybrid GPU framework. (b) Computational geometry. (c) Computational subdomain geometry. (d) The 2D D2Q9 lattice model. (e) GPU storage [50].
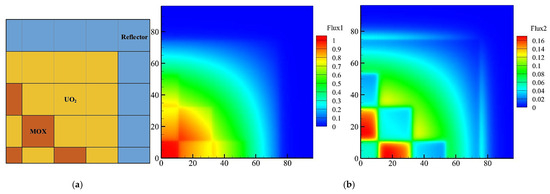
Figure 14.
(a) A MOX reactor geometry for a GPU–NTLBM problem. (b) A neutron distribution of a NT-LBM normalized steady state simulation [50].
Agarwal et al. (2020), in “Multi-group lattice Boltzmann method for criticality problems”, explored the application of the Lattice Boltzmann Method (LBM) in neutron transport for homogeneous thin media, such as materials used in reactor shielding [49]. The study emphasized the importance of high angular discretization in improving the accuracy of simulations for thin materials, where neutron scattering was typically homogeneous, as shown in Figure 15. The authors found that LBM, combined with high angular discretization, was able to converge more rapidly in criticality problems, making it an ideal choice for modeling reactors and other systems where neutron behavior is critical [49].
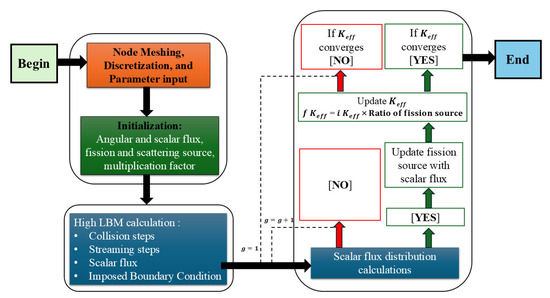
Figure 15.
A schematic layout for implementing the neutron transport equation of the LBM one-dimensional steady state eigenvalue.
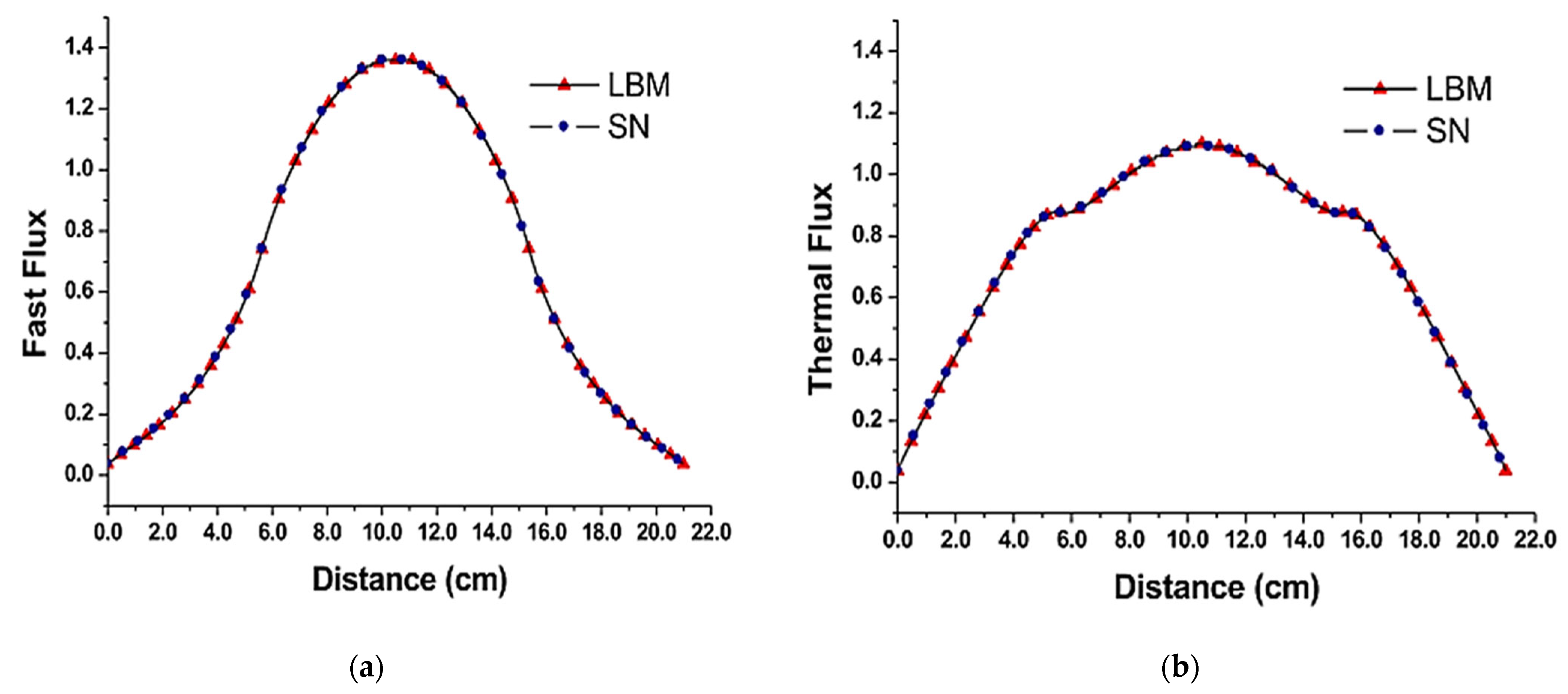
A study by [49] also provided insight into the advantages of LBM for neutron transport simulations in thin media. The method was shown to offer better convergence and more accurate results in cases involving complex scattering behavior, which is a common feature in reactor shielding materials. However, in Figure 16, while LBM excels in thin media, its application in more complex reactor geometries still requires further refinement to address potential challenges like ray effects and computational resource demands. Table 2 gives a summary of LBM advances in nuclear/neutron applications.
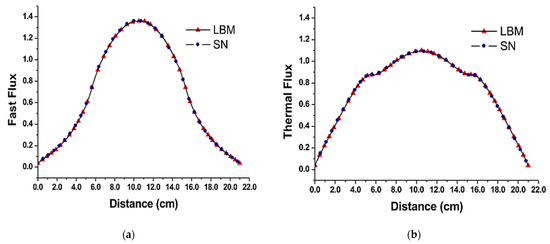
Figure 16.
(a) A neutron flux profile (fast flux) of LBM’s physical phenomenon for neutron reflections across a distance in one-dimensional steady state. (b) A thermal neutron flux profile of LBM’s physical phenomenon for neutron reflections across a distance in a one-dimensional steady state [49].

Table 2.
Summary of Lattice Boltzmann Method (LBM) in nuclear/neutron application.
The table above provides a summarized research overview concerning reactor problems where the Lattice Boltzmann Method has been applied, the lattice and models used, and the validation and insight gained from each study in neutron application.
3.2.2. Thermal–Hydraulic Applications
In nuclear reactor performance analysis, thermal–hydraulic simulations are necessary for fluid flow dynamics and behavior in the subchannel. LBM plays a significant role in resolving flow and heat transfer behaviors in reactor coolant systems.
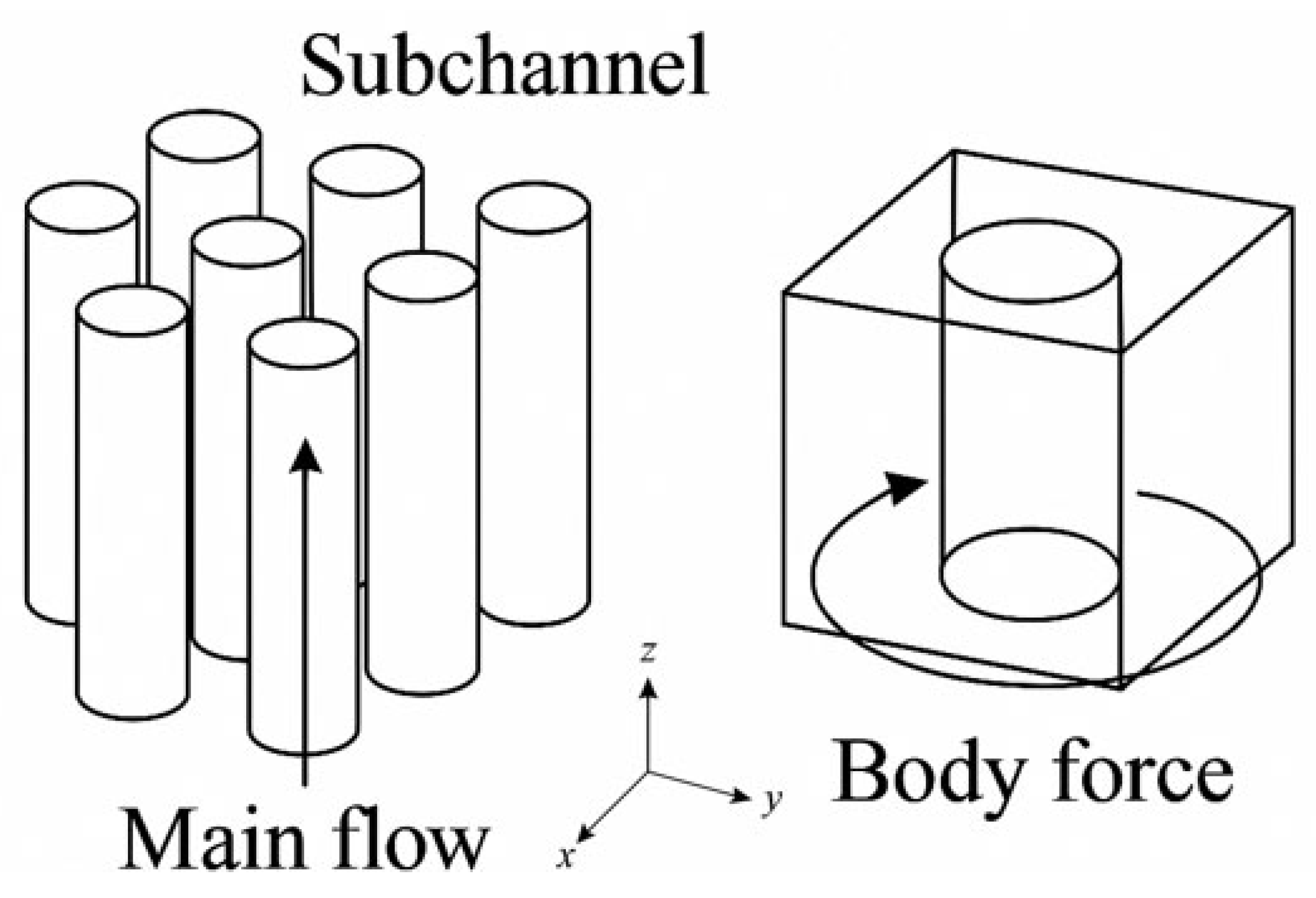
Mayer and Házi (2005) [53] modeled flux around fuel rods in PWR and VVER-440 reactors with the LES (Smagorinsky) turbulence model. Their study revealed a high dependency on flow characteristics, specifically secondary flows and pulsations, and a change in reactor geometry, using the D3Q27 BGK lattice operator in Figure 17. Their findings showed that LBM can accurately be used in modeling turbulent flows, positioning it as a viable alternative to traditional CFD approaches.
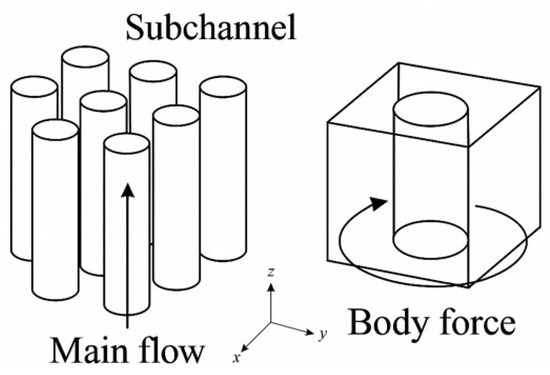
Figure 17.
A cylindrical arranged array (left) and a computational geometry of reactor domain using the D3Q27 LBM lattice model (right) [54].
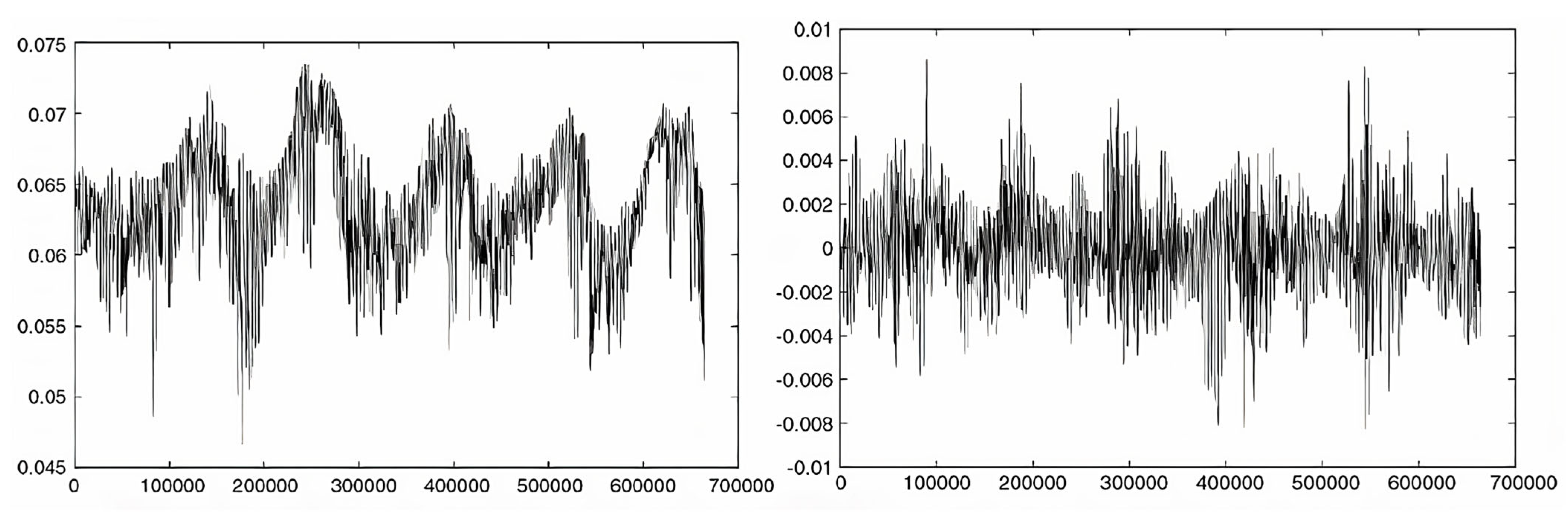
Further, Mayer and Házi (2006) [54] compared D3Q19 and D3Q27 lattice operators and found that only the latter produced accurate flux results under turbulent flow conditions. They further emphasized that LBM, especially with the D3Q27 lattice, is effective in simulating complex geometries within the reactor and capturing flow patterns in the turbulent nature when coupled with DNS and LES, as shown in Figure 18 and Figure 19. Their work was validated against experimental data, including axial velocities and Reynolds stresses, where they identified systematic errors in normal stress computations, and resolved the need for refinement in turbulence models.
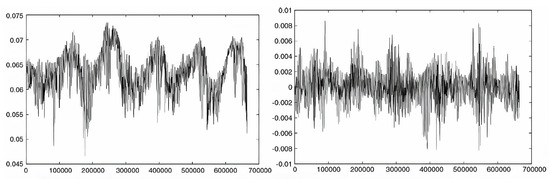
Figure 18.
Time evolution of axial and lateral velocity simulation for developed heat and turbulence based on DNS and LBM coupling [54].
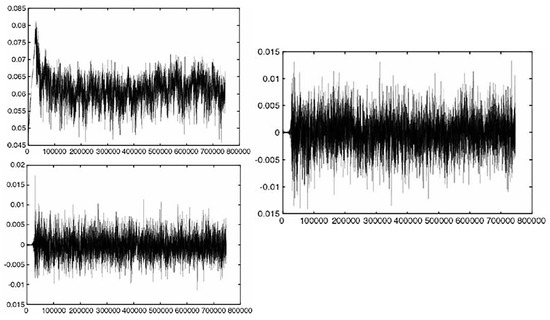
Figure 19.
Time evolution of axial and lateral velocity simulation for developed heat and turbulence based on LES and LBM coupling [54].
The works of Fan et al. (2009) and Kaufman et al. (2009) [55,56] focused on the fast cooling of the reaction chamber after a Loss-of-Coolant Accident (LOCA) in PWRs. Their simulations revealed the accumulation of cold plumes within the reactor core, a phenomenon crucial for understanding heat transfer during emergency cooling scenarios.
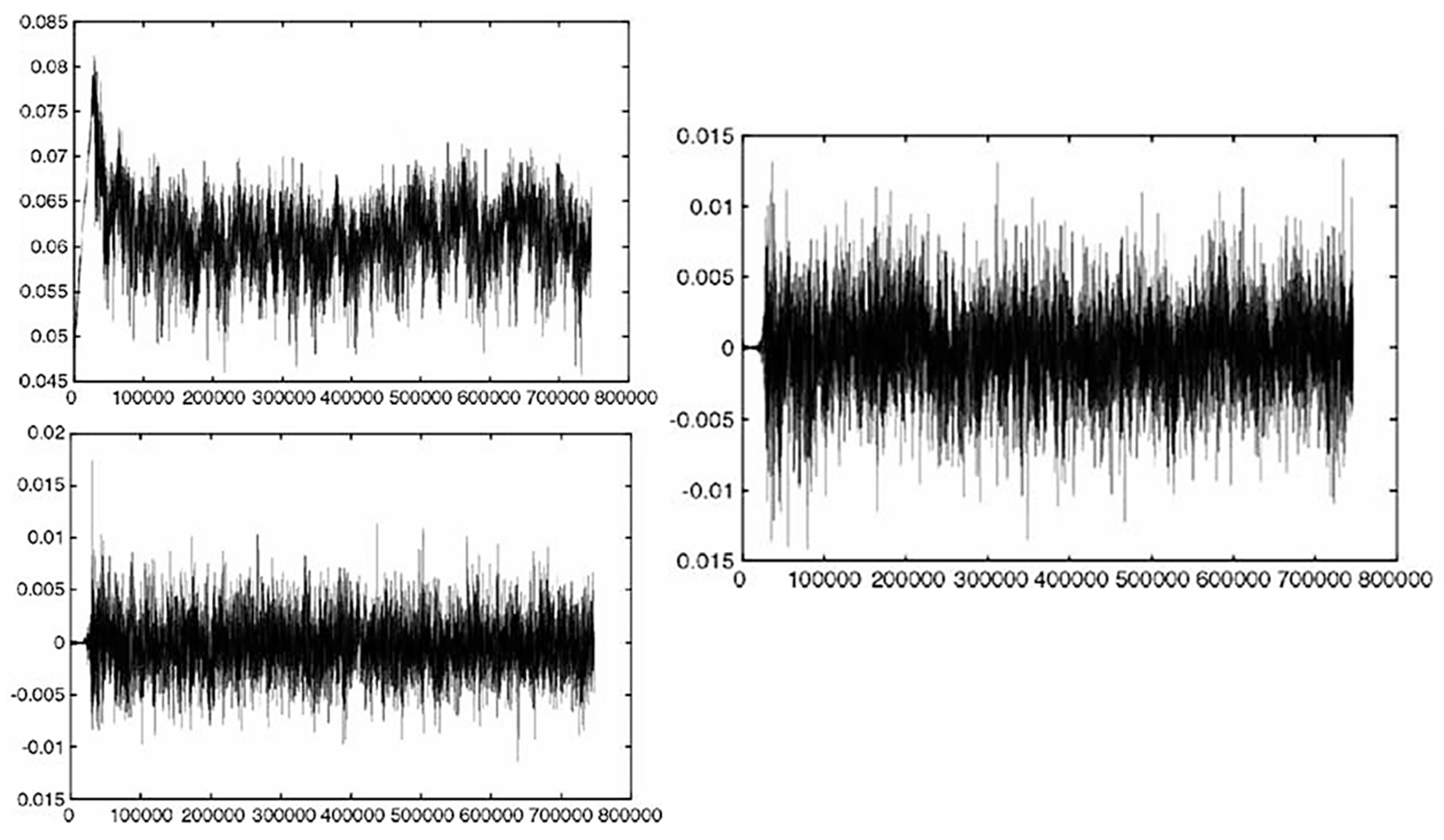
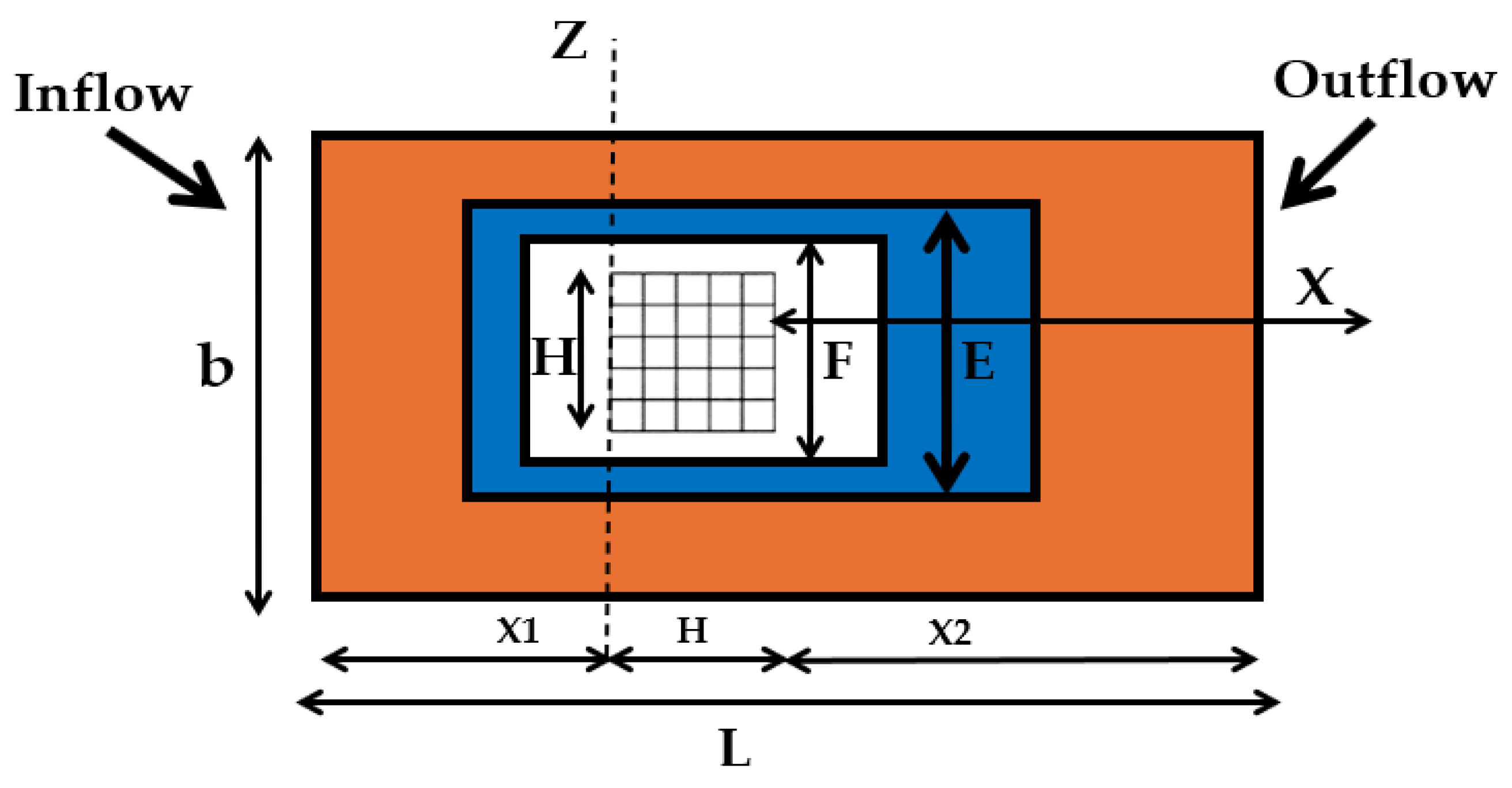
Tiftikci and Kocar [57] used LBM to model wire-wrapped fuel bundles, validating turbulent flow predictions and heat transfer modules against experimental friction factor data and showcasing LBM’s adaptability to unconventional reactor designs, shown in Figure 20 and Figure 21. These findings underscore LBM’s potential to address thermal–hydraulic complexities in both traditional and advanced reactor types.

Figure 20.
Schematics of wire-wrapped lattice grid fuel bundles in a cross-flow and inflow direction [57].
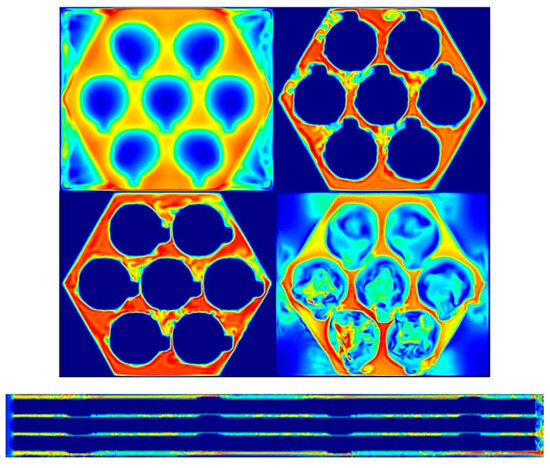
Figure 21.
Simulation of axial thermal dynamics and velocity profiles presented at five points; before the inlet (top-left), 260 mm inside the channel (top-right), 340 mm inside it (bottom-left), at the channel exit (bottom-right), and along the bundle axis (bottom) [57].
3.2.3. Multiphase Flow Dynamics
The simulation of multiphase flow phenomena, such as phase changes and coolant mixing, has an influence on the flow dynamics of the fluid in the reactor core.
Park (2011) [58] used the D3Q9 MRT lattice to study flux in the lower plenum of Very-High-Temperature Reactors (VHTRs). The study conducted found that the simulation results were in qualitative accordance with flow dynamics observed in the benchmark data for both low and high Reynolds numbers. However, discrepancies were noted at the reactor walls, which suggested that the wall needs grid refinement for more accurate simulations at higher Reynolds numbers.
In the context of liquid metal reactors, Tiftikci and Kocar (2015) [57] applied LBM to study flux around fuel rods in sodium-cooled fast breeder reactors (LMFBRs) using a hexagonal primitive cell and D3Q27 BGK lattice operator. They found that the inclusion of the Very Large Eddy Simulation (VLES) model provided better agreement with experimental data, particularly in the validation of velocity profiles, friction factors, and Reynolds stresses. This work further confirmed the feasibility of LBM in simulating complex fluid–structure interactions in LMFBRs. Their findings also highlighted the ability of LBM to handle heat transfer and flow characteristics in reactors with intricate geometries and flow patterns.
Tamura et al. (2018) [59] extended the applicability of LBM to impurity precipitation and cold trap simulations in mesh wire matrices of fast breeder reactors. Their findings validated the Low-Re LR-LKS model with experimental results, showing that LBM can be used to simulate complex phenomena such as impurity precipitation and its effect on reactor performance, as well as optimizing reactor stability by reducing computational time.
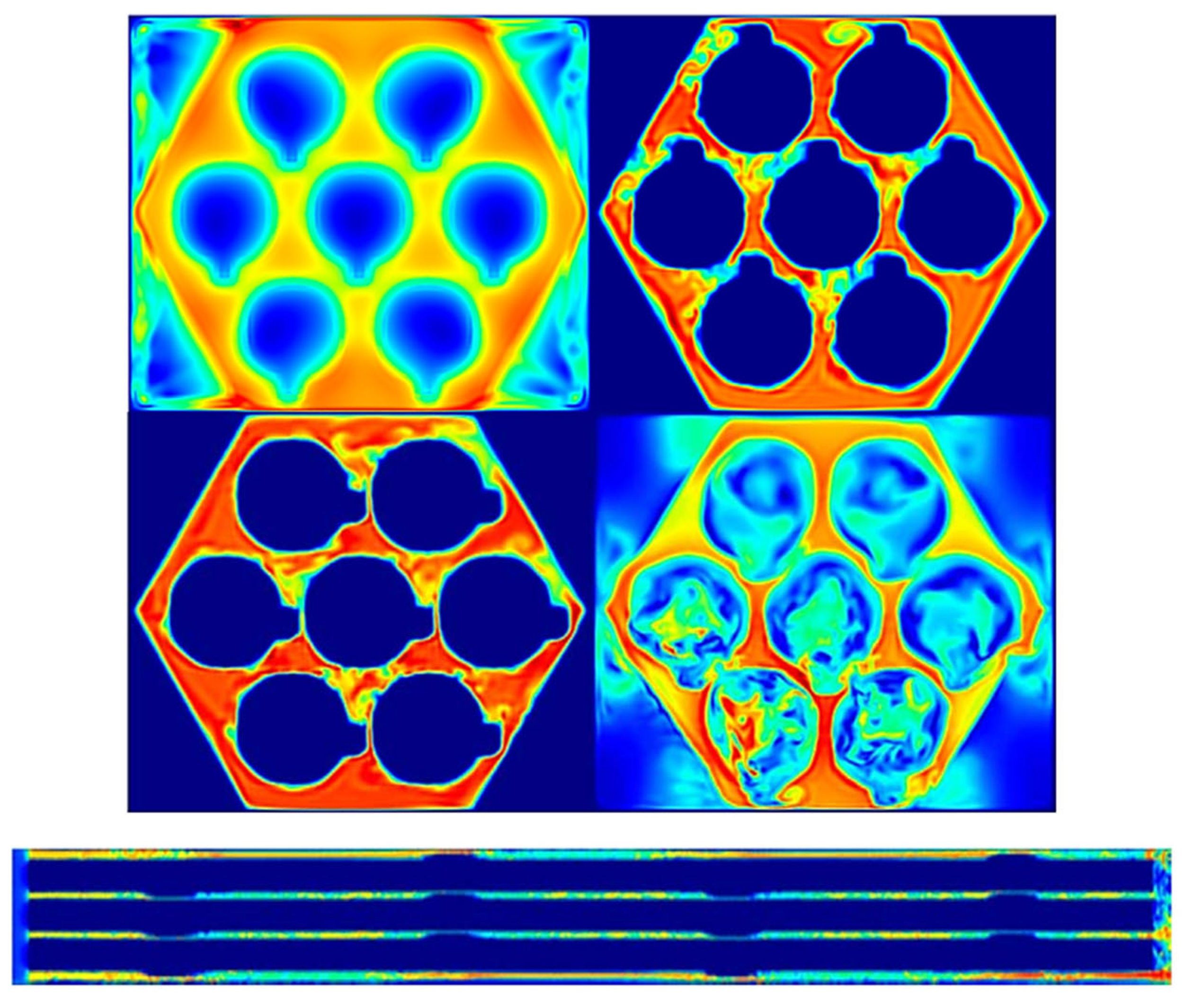
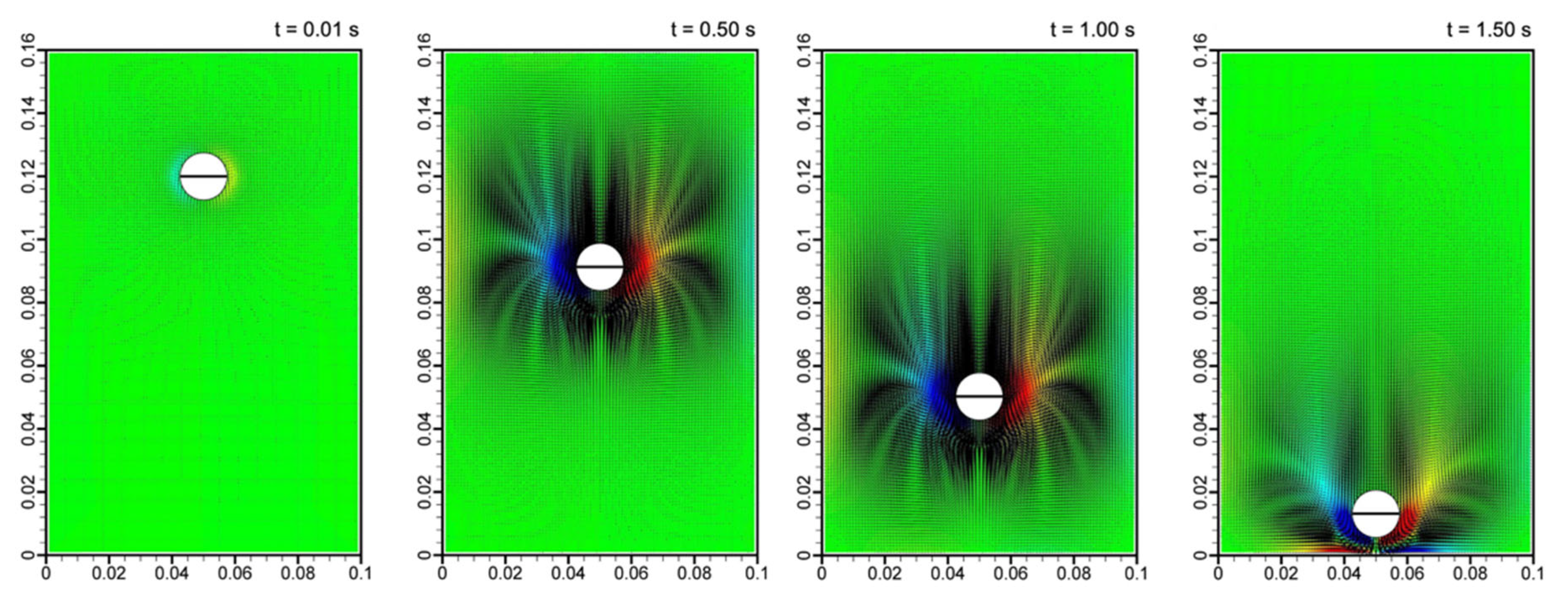
Gui et al. (2019) [60], in their studies, used LBM coupled with Immersed Boundary Methods (IBMs) and Discrete Element Methods (DEMs) to study pebble recirculation in High-Temperature Gas-Cooled Reactors (HTGRs) based on their multiphase in Figure 22 and Figure 23, by revealing complex fluid–particle interactions and their impact on reactor core system stability.
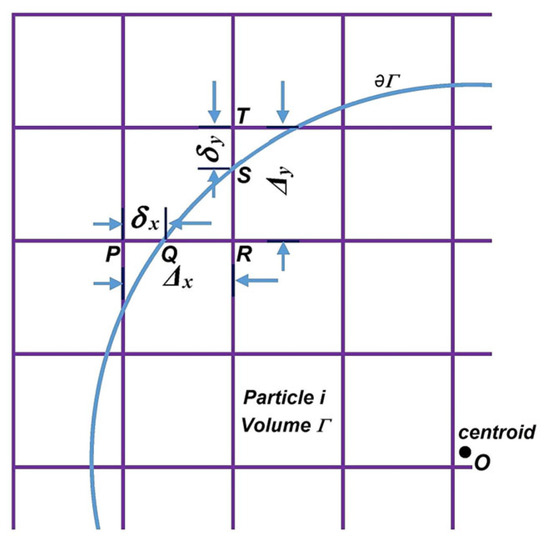
Figure 22.
Schematic sketch of Immersed Boundary Method interphase coupling approach [60].
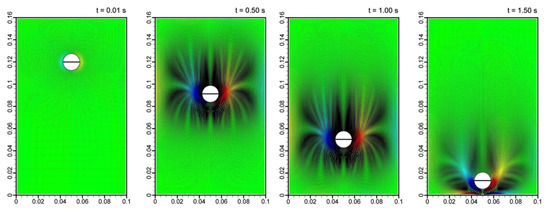
Figure 23.
Multiphase velocity snapshots of the momentum field in HTGR simulation [60].
De Rosis and Coreixas (2020) [61] demonstrated the effectiveness of Central Moments (CM-LBM) in a D3Q19 lattice model, providing new insights into flow patterns and heat transfer mechanisms in nuclear reactors. Their study focused on multiphysics flows, ensuring stability and accuracy in simulations, with new formulations for equilibrium and external forces.
In addition, Wang et al. (2023) [26] introduced an LB framework to simulate natural and forced convection in the Radiation–Convection heat transfer of a lattice D2Q9 model, showcasing the LBM’s ability to handle coupled heat and mass transfer models in multiphase systems. These studies highlight LBM’s strength in resolving fluid–solid interactions and capturing the intricacies of multiphase flows in nuclear reactor environments. Coupled radiation–convection research works in Table 3 applied LBM as CFD in various thermal and multiphase subchannel applications.

Table 3.
Summary of Lattice Boltzmann Method for computational fluid dynamics in subchannel applications of reactor core of nuclear plant.
This table summarizes studies where LBM has been used as computational fluid dynamics to simulate coolant behavior, turbulence, and multiphase dynamics in advanced reactor subchannels. It summarizes key reactor applications, lattice configurations, and validation approaches used by different authors.
3.2.4. Turbulence Modeling
Turbulence modeling remains a critical challenge in thermal–hydraulic simulations, where accurate predictions of flow instabilities and heat transfer are necessary [32]. Several turbulence models have been integrated into the LBM framework to enhance its ability to simulate turbulent flows. Among the most widely used models are Large Eddy Simulation (LES) and Reynolds-Averaged Navier–Stokes (RANS) models [46].
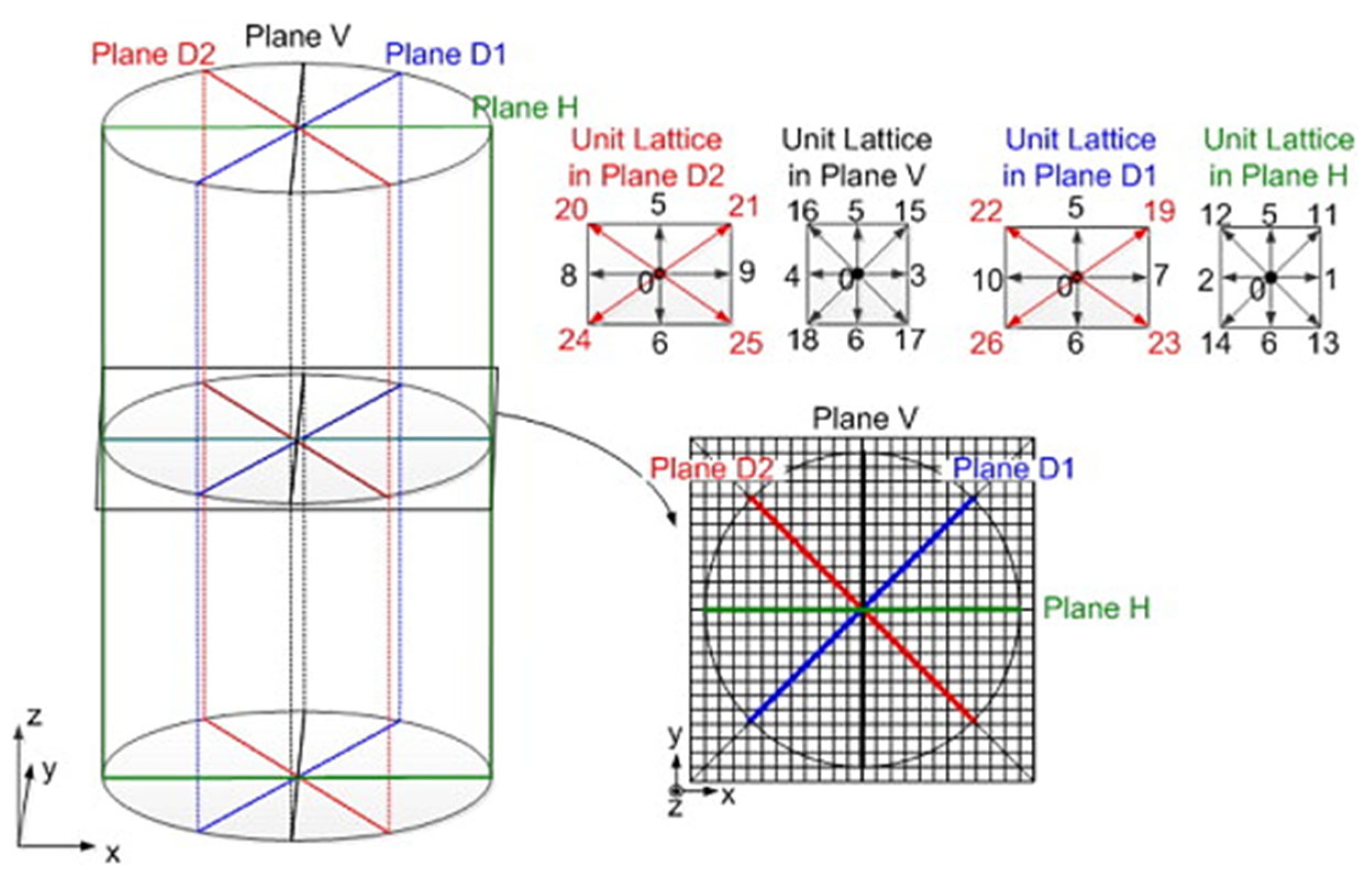
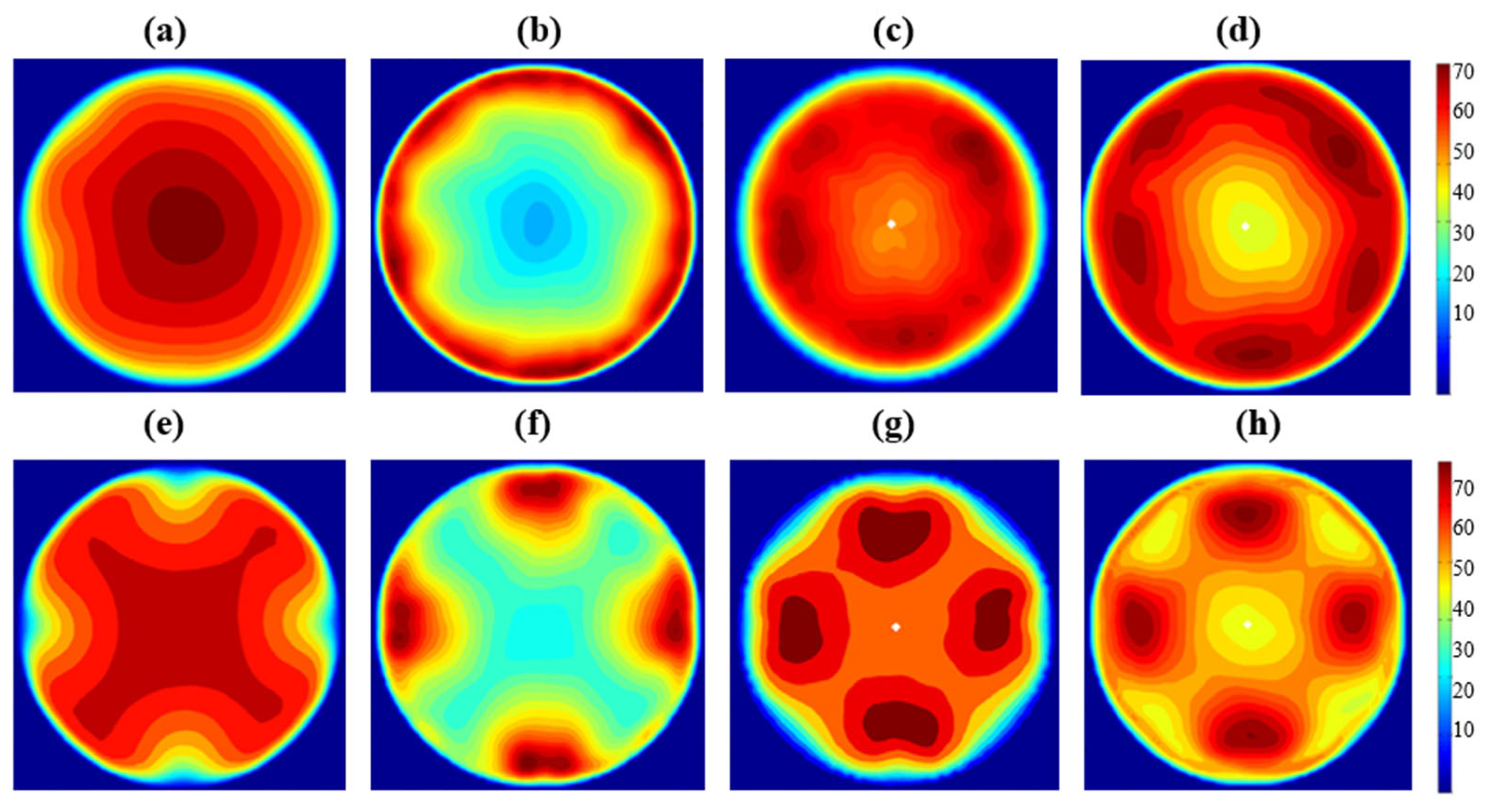
The study “The Effect of Lattice Models within the Lattice Boltzmann Method in the Simulation of Wall-Bounded Turbulent Flows” by Kang and Hassan explored the effectiveness of various lattice models used in simulating complex turbulent fluid behaviors [70]. The authors compared lattice models with varying numbers of velocity directions, such as D2Q9, D3Q15, and D3Q19, and highlighted how these configurations impact the accuracy of turbulent flow predictions, particularly in near-wall regions [70]. The higher-order models, like D3Q19, demonstrate superior performance in capturing the fine-scale turbulent structures near boundaries, compared to the simpler D2Q9 model. Furthermore, their study integrated the Wall-Adapting Local Eddy turbulence model (LES-WALE) within the LBM framework. LES-WALE enhanced LBM’s ability to resolve small eddies, particularly in the inner-wall region, by improving the accuracy of the simulation in capturing complex turbulence behaviors. This combination of LBM with turbulence models like LES in Figure 24 and Figure 25 is particularly applicable in reactor simulations, where small-scale turbulent structures play an important role in heat transfer and overall reactor performance.
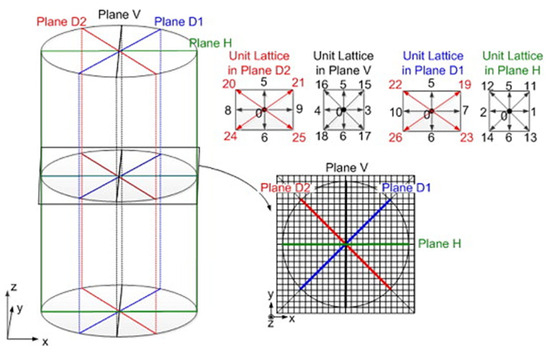
Figure 24.
LBM unit lattices of a cylindrical vessel geometry for turbulence modeling [70].
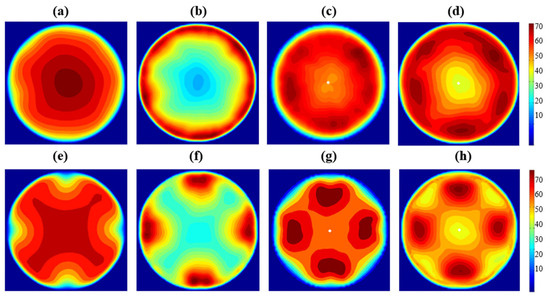
Figure 25.
Velocity contour plots from turbulence modeling of the LBMs D3Q27 lattice model (a–d) and D3Q19 model (e–h) [70].
Kang and Hassan’s work [70], “The effect of lattice models within the lattice Boltzmann method in the simulation of wall-bounded turbulent flows”, underscored the potential of LBM in capturing turbulent flow dynamics, particularly in applications like reactor simulations. The integration of advanced turbulence models like LES-WALE allowed for more precise predictions, while the choice of lattice model directly affects both the accuracy and computational cost of the simulation.
In “Investigation of the LES WALE Turbulence Model within the Lattice Boltzmann Framework” by [71], the authors integrated the Large Eddy Simulation model with the Wall-Adapting Local Eddy turbulence model into the LBM framework for the modeling and simulation of turbulent flows in the reactor core. According to their study, the WALE model, which is designed to resolve finer scales of turbulence, was particularly effective in capturing the small eddies that form in boundary layers, which are critical in determining heat transfer and fluid mixing in applications such as reactor cores. Their study emphasized a delicate balance between computational cost and the accuracy of simulations, particularly when applying Large Eddy Simulation (LES) models, as in Figure 26 and Figure 27 [71]. The authors concluded that, by using the WALE model within LBM, they reduced the computational burden while maintaining high accuracy, especially in the near-wall regions [71].
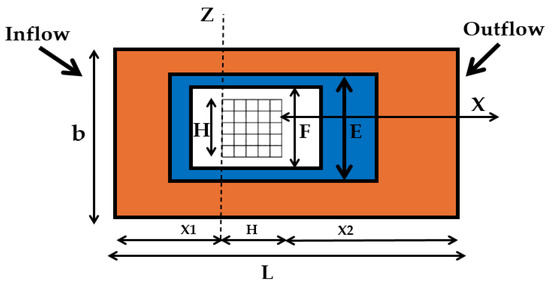
Figure 26.
Computational geometry for turbulent LBM simulation with high Reynolds number [71].

Figure 27.
Turbulent flow viscosity of the geometry with white lines symbolizing the phase between the LES WALE LBM model between different grid resolutions [71].
Han et al. (2021) investigated the “Effects of Wall Function Model in Lattice Boltzmann Method-Based Large-Eddy Simulation on Built Environment Flows” in LBM- based Large Eddy Simulation (LES) on built environment flows [72]. In this study, the authors investigated how various wall function models are necessary for handling boundary conditions in turbulence simulations.
Further, the paper “Multiscale Lattice Boltzmann Schemes with Turbulence Modeling” by O. Filippova et al. (2014) [73] focused on combining LBM with turbulence models to capture the complexities of fluid flow dynamics at various scales. The authors proposed a multiscale approach to the Lattice Boltzmann Method to address the need for modeling turbulence at both small and large scales in an efficient and accurate manner. Their study highlighted the use of Large Eddy Simulation (LES) models, such as the Smagorinsky model, within the LB framework. They integrated LES and LBM to allow for a more accurate and computationally efficient way of simulating turbulence in complex flow geometries. The authors noted that LES provides a good balance between computational cost and the need for accurate representations of turbulent flows, particularly when direct numerical simulations (DNSs) would be too computationally expensive [73]. The research works listed in Table 4 applied LBM as CFD in various turbulence models.

Table 4.
Summary of Lattice Boltzmann Method (LBM) in turbulence modeling.
The table above summarizes studies where LBM was integrated with turbulence models to simulate wall-bounded and reactor-scale turbulent flows. It highlights how different lattice setups and advanced turbulence models have been employed to improve near-wall predictions and resolve multiscale reactor problems.
From the review of the Lattice Boltzmann Method (LBM) in various subchannel applications, the integration of LBM together with other models into nuclear reactor studies has the ability to transform the simulation landscape, offering precise and efficient tools for addressing complex problems in neutron transport, thermal–hydraulic behavior, multiphase flows, and turbulence modeling.
Recent advancements in computational frameworks, such as GPU parallelization and hybrid methods, have further expanded LBM’s applicability, enabling the resolution of multiphysics phenomena critical to reactor safety and design. The LBM has been used as a computational fluid dynamics tool that has been applied in subchannel analysis of nuclear reactors due to its flexibility in handling complex geometries and multiphase flow.
LBM’s unique advantages, such as implementation, parallelizability, and ability to model complex boundary conditions, make it particularly suitable for investigating coolant flow and thermal transfer dynamics in subchannels. The validation of numerical models for reactor studies is essential for evaluating the efficiency, reliability, and accuracy of computational methods like the Lattice Boltzmann Method for subchannel analysis. However, the validation and verification of Lattice Boltzmann Methods remain limited and require more improvements. Hence, the validation of most LBM models in Table 2, Table 3 and Table 4 was benchmarked against experimental, numerical, analytical, and some subchannel methods. Through its adaptability and computational power, LBM can continue to provide innovative solutions to the subchannel challenges of nuclear reactor analysis.
3.2.5. Lattice Boltzmann Method’s Application in Advanced Reactor Designs
The global nuclear industry, in recent times, has shifted toward a more compact, efficient, and advanced reactors system for clean energy generation. The recent advancements in nuclear reactor field have introduced advanced reactors such as Generation-IV reactors and Small Modular Reactors (SMRs), which have unique flow and heat characteristics. Although these reactors exhibit unique coolant flow behaviors, and multiphase interactions, due to their compact geometries, and alternative reactor coolants (non-water coolants), thermal–hydraulic within reactor subchannel remains a challenge [74].
Reactors like Generation-IV reactors and Small Modular Reactors are designed to operate under diverse thermal and fluid dynamic conditions that differ significantly from traditional reactors like Light Water Reactors. In advance reactors like SMRs, coolant channels are often small and more intricately arranged than in conventional large-scale reactors [75]. To address some of these challenges, the Lattice Boltzmann Method (LBM), with its capability to handle complex geometries and multiphysics, has been used in some advanced reactor applications to mitigate the challenges.
Freile et al. (2023), in “Lattice Boltzmann Solidification Modelling of Forced Convection Internal Flows applied to Gen-IV Nuclear reactor Coolants”, discovered that Gen IV coolants have relatively high melting points, and their solidification process poses safety risks in various loop sections and cooling systems of the reactor [76]. In their study, they utilized a Double Distribution Function Lattice Boltzmann Method (DDF–LBM) to solve coupled momentum and enthalpy equations for heat transfer and velocity fields in the reactor. They also used an LBM-based method to model the solid–liquid interface during coolant solidification. In conclusion, they stated that LBM proved a suitable performance for solidification risk analysis and heat dynamics in Gen-IV reactor–coolant systems [76].
Sitompul et al. (2024), in “Gas Entrainment Simulation for Fast Reactors using Free-surface Lattice Boltzmann Method”, using a Japan Sodium-Cooled Fast reactor (JSFR), used the Lattice Boltzmann Method [77]. In their findings, free-surface vortices near the coolant inlet entrained argon gases into the coolant (sodium), posing a risk to heat transfer efficiency in the reactor. To overcome this challenge, the authors used a Free-Surface Lattice Boltzmann method with a D3Q27 lattice to simulate the gas entrainment due to vortex formation. The LBM was coupled with a cumulant collision model for numerical stability at increasing Reynolds numbers. In conclusion, they confirmed that the LBM demonstrated suitability for simulating flows with vortical structures in large-scale reactor geometries. Also, the simulation offered better accuracy and lower computational costs [77].
Wang and Ma (2022), in “Coupled Neutronics-Thermal-Hydraulics Simulation Using LBM for Molten Salt Reactors”, analyzed the multiphysics interactions in Molten Salt Reactors (MSRs) with an LBM-based model for coupled neutronics and thermal–hydraulics simulations [78]. In their study, they modeled a lattice Boltzmann framework for unified multiphysical components such as neutron transport, heat transfer, heat flow, and precursor transport in a generalized equation using a common distribution function to solve neutron transport and heat transfer equations. In their findings, they stated that the LBM handled multiphysical coupling efficiently by avoiding external interpolations. Agan, they confirmed that LBMs for MSRs showed remarkable temperature dynamics which increased the coolant distribution at various temperature and velocity profiles [78].
4. Discussion
The Lattice Boltzmann Method (LBM) has emerged as a transformative computational tool in the nuclear reactor core study, particularly in the context of neutron transport and thermal–hydraulic analysis. This review has highlighted the unique advantages of the Lattice Boltzmann Method and its application as a CFD tool for subchannel study. The findings reviewed from papers indicate that LBM is an innovative computational fluid dynamics (CFD) tool, capable of addressing the inherent complexities of heat and mass transfer (thermal complexities) within reactor cores.
Traditional CFD methods have long been used for reactor core analysis; however, studies have shown that LBM distinguishes itself through its unique mesoscopic algorithmic structure, which directly models fluid dynamics at particle distribution level. This distinct feature allows LBM to bridge micro-scale interactions and macro-scale phenomena, offering flexibility and improved accuracy when simulating thermal–hydraulic processes in nuclear reactor subchannels. Moreover, the use of lattice discretization schemes in LBM, such as the model, allows for effective modeling of the reactor’s subchannel geometries, including those with complex boundary conditions.
From our study, we observed that LBM can efficiently handle one-, two-, and three-dimensional simulations (1D, 2D, and 3D), showcasing its versatility in addressing a diverse range of reactor configurations. Again, we observed that the implementation of LBM algorithms is straightforward, and their compatibility with parallel computing at high resolution simulation is exceptional. Hence, LBMs can be validated with existing CFD data, benchmark problems, and some experimental results, demonstrating their applicability in subchannel applications.
One of the primary research questions guiding this study was, “How applicable and effective is the lattice Boltzmann computational fluid dynamics method for subchannel fuel assemblies in reactor cores?” Based on the research we reviewed, it can be observed that the Lattice Boltzmann Method (LBM) not only demonstrates applicability to subchannel analysis, but also exhibits distinct advantages over traditional methods. The following two points are the major advantages LBM has over CFD.
- Enhanced Resolution of Complex Geometries
The discrete and localized nature of LBM makes it particularly effective for simulating the intricate geometries of subchannel fuel assemblies. Unlike conventional CFD approaches, LBM readily adapts to the irregular boundaries and flow obstacles that characterize fuel rod arrangements and spacer grids in reactor cores. Also, the integration of mesh refinement strategies within LBM can enhance its computational efficiency, particularly in complex geometries. By optimizing grid resolution and adapting to the intricacies of reactor designs, LBM significantly reduces computational costs while maintaining accuracy. Additionally, the potential to combine hybrid schemes, such as Finite Volume-LBM (FV-LBM), allows for effective handling of unstructured meshes, optimizing the modeling of complex reactor domains.
- 2.
- Efficient Multiphysics Coupling
LBM has proven adept at solving the coupled phenomena of heat transfer and fluid flow simultaneously. This capability is necessary in reactor subchannel analysis, where accurate predictions of temperature distribution and velocity profiles are essential to ensuring safe reactor operation. With LBM, the ability to couple neutron transport modeling with thermal–hydraulic simulations within a single framework is phenomenal. Previous studies have demonstrated that LBM can recover macroscopic equations, such as the Navier–Stokes equations and neutron transport equations, from its foundational principles. This theoretical robustness positions LBM as a suitable numerical tool for comprehensive simulations in fluid dynamics, heat transfer, and neutron behavior in nuclear reactors.
- 3.
- Parallel Scalability
LBM algorithms are inherently parallelizable, making them well-suited for large-scale, high-resolution simulations. These characteristics address one of the key challenges in nuclear engineering, where high computational demands often limit the scope of traditional CFD methods.
The observations made across the reviewed studies highlight several critical insights into the behavior of thermal–hydraulic processes within subchannel fuel assemblies. For instance, LBM simulations reveal detailed patterns of temperature gradients and fluid velocity distributions under a wide range of operating conditions. These patterns provide valuable information for optimizing fuel assembly designs to minimize thermal hotspots and maximize heat transfer efficiency. Moreover, LBM has shown its ability to capture flow instabilities and turbulence effects, which are often overlooked or poorly resolved by conventional methods. This is particularly beneficial in areas with steep gradients or intricate flow patterns, where traditional CFD methods may struggle.
Regardless of these advantages, our findings indicate that the validation and benchmarking of LBM in nuclear applications remain significant challenges. Many studies have not established comprehensive comparisons between LBM results and experimental data or established numerical methods, which is crucial for validating the reliability of LBM in critical applications. While some comparisons have been made with benchmark solutions from other well-established numerical methods, such as the Finite Volume Method (FVM), there is a need for more extensive validation against experimental data relevant to complex reactor scenarios. Although reactors operate under strict environmental and safety regulations, the feasibility of direct experimental validations is significantly limited. In order to bridge this gap, we propose the following reactor scenarios and experimental setups, which can be adopted as the basis for an LBM-based subchannel analysis validation, in Table 5.

Table 5.
Proposed reactor scenarios and experimental setups for LBM-based subchannel analysis validation.
The above table presents our proposed reactor scenarios and experimental setups for LBM-based subchannel validations; to validate the LBM simulations of single-phase coolant flow within a nuclear reactor subchannel, a scaled-down experimental model must be constructed. The model should mimic the geometry of a subchannel typically found in Pressurized Water Reactors (PWRs), such as a transparent cylindrical or rectangular flow channel with surrogate fuel rods. A primary measurement technique like Particle Image Velocimetry (PIV) or a Laser Doppler Anemometer can be adopted for checking fluid flow field measurement. Data collection can be performed using a data acquisition system, which can help record flow patterns, velocity profiles, and pressure drops. For multiphase flow dynamics, a lab-scale multiphase flow reactor system with steam (gas) interacting with a liquid phase (coolant) can be created. A high-speed camera can be used to capture coolant behavior and bubble dynamics can be visualized using image processing software to analyze interfacial behaviors. PIVs can be used to analyze flow velocities and temperature fields, and the results can be compared to other benchmarks. For heat transfer validations, a lab-scale thermal–hydraulic reactor model like a Continuous Stirred-Tank Reactor (CSTR) can be created with embedded heaters. Infrared thermography or thermocouples can be set up to monitor mixing and thermal dynamics profiling. Data collection tools can be used to collect data readings, visualized and benchmarked against other validation models. Uncertainties in PIV (±2%) and pressure sensors (±0.5%) can be quantified through standard calibration and analysis.
Notwithstanding these strengths of LB methods, LBMs do have limitations in maintaining numerical stability at very high Reynolds numbers, managing complex geometries with non-uniform grids, and resolving high steep gradients in velocity and thermal flow fields.
In recent years, these gaps in LBM have led to the development of non-standard LBM approaches, which extends its capabilities beyond the Lattice Boltzmann Method. A notable advancing non-standard LBM which seeks to address the shortcomings of LBM is the Discrete Unified Gas Kinetic Scheme (DUGKS). Unlike standard LBM, DUGKS adopts a finite-volume formulation based on kinetic theory, enabling it to decouple the physical and velocity spaces and thereby offer greater flexibility in mesh handling and numerical stability. DUGKS has demonstrated improved performance in simulating heat and mass transfer in domains with complex geometries.
Tao et al. (2021), in “Discrete Unified Gas Kinetic Scheme Simulation of Conjugate Heat Transfer Problems in Complex Geometries by a Ghost-Cell Interface Method” employed the Discrete Unified Gas Kinetic Scheme (DUGKS), a non-standard LBM, to simulate conjugate heat transfer problems in complex geometries [79]. The study demonstrated the application of DUGKS to simulate conjugate heat transfer in complex geometries, which involved irregularly shaped objects with complex boundary conditions. This phenomenon, adopted by the authors, increased accuracy in the prediction of temperature fields and heat fluxes in heat transfer complex systems [79].
In the context of subchannel reactor analysis, the emergence of DUGKS can offer promising capabilities. Therefore, to enhance the scope of LBM applications in reactor studies, future studies can also consider the potential of non-standard LBMs like DUGKS.
In terms of answering the research question, the following conclusions can be drawn:
- Applicability
LBM is highly applicable to subchannel analysis in PWRs, as demonstrated by its ability to handle complex boundary conditions, irregular geometries, and multiscale phenomena with ease.
- Effectiveness
The method is effective in providing accurate and high-resolution data for thermal and fluidic behavior, offering insights that are critical to reactor safety and efficiency.
- Advantages over Traditional CFD
Compared to conventional CFD, LBM offers better adaptability to modern computational infrastructure, faster prototyping of models, and enhanced capabilities for simulating transient behaviors.
5. Conclusions
In conclusion, the Lattice Boltzmann Method (LBM) represents a significant advancement in the computational analysis of nuclear reactor cores, particularly its application towards neutron transport and thermal–hydraulic interactions. Our study has demonstrated that LBM’s unique characteristics, such as its ability to simplify complex neutron transport phenomena, its efficient handling of intricate geometries, and its strong parallelization capabilities make it an efficient numerical tool for addressing multifaceted and complex challenges in nuclear reactor applications.
While LBM shows great advantages in its applications, it has limitations that need to be addressed for future applications relating to nuclear reactor core studies. Limitations such as high computational resource requirements for large-scale simulations make LBM capital-demanding. Although LBM is inherently parallelizable, the need for extensive computational infrastructure remains a barrier, especially for high-fidelity reactor simulations. Additionally, the benchmarking of experimental validation for LBMs in nuclear engineering is limited, and it narrows the strength of LBMs in terms of reliability.
As the nuclear engineering landscape continues to evolve, LBM plays a significant role in enhancing reactor safety, efficiency, and performance.
To address these challenges, we suggest that future research must be conducted in the following areas.
- Developing hybrid methods that combine LBM with traditional CFD approaches to leverage the strengths of both methodologies;
- Enhancing algorithmic efficiency through advanced lattice schemes and adaptive meshing techniques;
- Increasing experimental validation efforts to ensure the accuracy and reliability of LBM-based models in predicting real-world reactor behavior.
To briefly outline the future directions in developing hybrid numerical simulation methods, coupling the Lattice Boltzmann Method (LBM) with other CFD numerical techniques, such as finite difference, finite element, or finite volume method, can increase efficiency in solving macroscopic flow problems by leveraging the complementary strengths of each technique. Additionally, integrating machine learning techniques to optimize LBM parameters and model performance can also serve as a robust hybrid method for predicting subchannel behavior more accurately, since real-world reactor behavior and operations include uncertainties.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMR | Adaptive Mesh Refinement |
| BE | Boltzmann Equation |
| BEM | Boundary Element Method |
| BGK | Bhatnagar Gross Krook |
| BIM | Boundary Immersed Method |
| BWR | Boiling Water Reactor |
| CFD | Computational Fluid Dynamics |
| CM | Central Moments |
| CPU | Computer Processing Unit |
| CSTR | Continuous Stirred-Tank Reactor |
| DDF | Double Distribution Function |
| DEM | Discrete Element Method |
| DNS | Direct Numerical Simulation |
| DOM | Discrete Ordinate Method |
| DUGKS | Discrete Unified Gas Kinetic Scheme |
| FDM | Finite Difference Method |
| FEM | Finite Element Method |
| FVM | Finite Volume Method |
| GCR | Gas-Cooled Reactor |
| GPU | Graphics Processing Unit |
| HLBM | High-Order Hybrid LBM |
| HTGR | High-Temperature Gas Reactor |
| HWR | Heavy Water Reactor |
| IBM | Immersed Boundary Equation |
| JSFR | Japan Sodium Fast Reactor |
| LB | Lattice Boltzmann |
| LBM | Lattice Boltzmann Method |
| LDA | Laser Doppler Anemometer |
| LES | Large Eddy Simulation |
| LGA | Lattice Gas Automata |
| LMFBR | Liquid Metal Fast Breeder Reactor |
| LOCA | Loss of Coolant Accident |
| LKS | Lattice Kinetic Scheme |
| LR | Lattice Refinement |
| LR | Low Reynolds Number |
| LWR | Light Water Reactor |
| MOX | Mixed Oxide |
| MRT | Multiple Relaxation Time |
| MSR | Molten Salt Reactor |
| NS | Navier–Stokes |
| NSE | Navier–Stokes Equations |
| NT | Neutron Transport |
| PDE | Partial Differential Equation |
| PIV | Particle Image Velocimeter |
| PWR | Pressurized Water Reactor |
| RANS | Reynolds Averaged Navier–Stokes |
| SAMR | Structured Adaptive Mesh Refinement |
| SMR | Small Modular Reactor |
| SSAMR | Streaming Based Block Structured Adaptive Mesh Refinement |
| VHTR | Very-High-Temperature Reactor |
| VLES | Very Large Eddies Simulation |
| VVER | Vodo Vodyanoi Energetichesky Reactor |
| WALE | Wall Adapting Local Eddy Viscosity Equation |
| Symbols | |
| Adaptive Mesh Refinement | |
| Density | |
| Pressure | |
| Kinematic viscosity | |
| External force vector | |
| Distribution function | |
| Equilibrium distribution function | |
| Discrete velocity | |
| Weight factor of velocity | |
| Time step | |
| Spatial lattice resolution | |
| Reynolds number | |
| Prandtl number | |
| Thermal conductivity | |
| Temperature | |
| Collision operator | |
| Relaxation time | |
| Speed of sound | |
| Subscripts | |
| direction in the discrete velocity space | |
| Equilibrium state | |
| Number of spatial dimensions in discretization | |
| Discrete velocities in lattice | |
| Inlet conditions | |
| Outlet conditions | |
| Boundary wall | |
| Average condition | |
| Maximum value |
References
- Wang, J.; Azam, W. Natural resource scarcity, fossil fuel energy consumption, and total greenhouse gas emissions in top emitting countries. Geosci. Front. 2024, 15, 101757. [Google Scholar] [CrossRef]
- Kabeyi, M.J.B.; Olanrewaju, O.A. Sustainable energy transition for renewable and low carbon grid electricity generation and supply. Front. Energy Res. 2022, 9, 743114. [Google Scholar] [CrossRef]
- Obaidurrahman, K.; Arul, A.J.; Ramakrishnan, M.; Singh, O.P. Nuclear reactor safety. In Physics of Nuclear Reactors; Elsevier: Amsterdam, The Netherlands, 2021; pp. 449–510. Available online: https://linkinghub.elsevier.com/retrieve/pii/B9780128224410000157 (accessed on 17 December 2024).
- Alameri, S.A.; Alkaabi, A.K. Fundamentals of nuclear reactors. In Nuclear Reactor Technology Development and Utilization; Elsevier: Amsterdam, The Netherlands, 2020; pp. 27–60. Available online: https://linkinghub.elsevier.com/retrieve/pii/B9780128184837000019 (accessed on 17 December 2024).
- Pioro, I.; Duffey, R.B.; Kirillov, P.L.; Dort-Goltz, N. Current status of reactors deployment and small modular reactors development in the world. J. Nucl. Eng. Radiat. Sci. 2020, 6, 044001. [Google Scholar] [CrossRef]
- Mollah, A.S. Recent advances in computational convective heat transfer study in a sub-channel for nuclear power reactor and future directions. WSEAS Trans. Heat Mass Transf. 2023, 18, 162–181. [Google Scholar] [CrossRef]
- Yang, B.-W.; Ninokata, H.; Long, J.; Liu, A.; Han, B. Subchannel analysis—Current practice and development for the future. Nucl. Eng. Des. 2021, 385, 111477. [Google Scholar] [CrossRef]
- Wu, Y.; Song, J.; Zheng, H.; Sun, G.; Hao, L.; Long, P.; Hu, L. CAD-based Monte Carlo program for integrated simulation of nuclear system SuperMC. Ann. Nucl. Energy 2015, 82, 161–168. [Google Scholar] [CrossRef]
- Hassan, Y. An overview of computational fluid dynamics and nuclear applications. In Thermal-Hydraulics of Water Cooled Nuclear Reactors; Elsevier: Amsterdam, The Netherlands, 2017; pp. 729–829. Available online: https://linkinghub.elsevier.com/retrieve/pii/B9780081006627000129 (accessed on 17 December 2024).
- Wang, M.; Wang, Y.; Tian, W.; Qiu, S.; Su, G.H. Recent progress of CFD applications in PWR thermal hydraulics study and future directions. Ann. Nucl. Energy 2021, 150, 107836. [Google Scholar] [CrossRef]
- Verma, G.; Sinha, S.L.; Verma, S.K.; Verma, T.N. A review of cfd advancements toward thermal-hydraulic analysis of prototypical flow conditions in pwr subchannels. Nucl. Technol. 2024, 210, 1–44. [Google Scholar] [CrossRef]
- Reddy, J.N.; Anand, N.K.; Roy, P. Finite Element and Finite Volume Methods for Heat Transfer and Fluid Dynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2022; Available online: https://www.cambridge.org/highereducation/product/9781009275453/book (accessed on 17 December 2024).
- Drikakis, D.; Frank, M.; Tabor, G. Multiscale computational fluid dynamics. Energies 2019, 12, 3272. [Google Scholar] [CrossRef]
- Petersen, K.J.; Brinkerhoff, J.R. On the lattice Boltzmann method and its application to turbulent, multiphase flows of various fluids including cryogens: A review. Phys. Fluids 2021, 33, 041302. [Google Scholar] [CrossRef]
- Bocanegra Cifuentes, J.A.; Borelli, D.; Cammi, A.; Lomonaco, G.; Misale, M. Lattice boltzmann method applied to nuclear reactors—A systematic literature review. Sustainability 2020, 12, 7835. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 3rd ed.; Butterworth-Heinemann: Amsterdam, The Netherlands, 2015; ISBN 978-0-08-099995-1. [Google Scholar]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method: Principles and Practice (Graduate Texts in Physics); Springer: Cham, Switzerland, 2017; Available online: http://link.springer.com/10.1007/978-3-319-44649-3 (accessed on 17 December 2024).
- Maliska, C.R. Fundamentals of Computational Fluid Dynamics: The Finite Volume Method (Fluid Mechanics and Its Applications); Springer: Cham, Switzerland, 2023; ISBN 978-3-031-18234-1. [Google Scholar]
- Wendt, J.F. (Ed.) Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2009; Available online: http://link.springer.com/10.1007/978-3-540-85056-4 (accessed on 17 December 2024).
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer: Cham, Switzerland, 2020; Available online: http://link.springer.com/10.1007/978-3-319-99693-6 (accessed on 17 December 2024).
- Chen, L.; Feng, Y.-L.; Song, C.-X.; Chen, L.; He, Y.-L.; Tao, W.-Q. Multi-scale modeling of proton exchange membrane fuel cell by coupling finite volume method and lattice Boltzmann method. Int. J. Heat Mass Transf. 2013, 63, 268–283. [Google Scholar] [CrossRef]
- Jin, P.; Xie, B.; Xiao, F. Multi-moment finite volume method for incompressible flows on unstructured moving grids and its application to fluid-rigid body interactions. Comput. Struct. 2019, 221, 91–110. [Google Scholar] [CrossRef]
- Tong, Z.-X.; He, Y.-L.; Tao, W.-Q. A review of current progress in multiscale simulations for fluid flow and heat transfer problems: The frameworks, coupling techniques and future perspectives. Int. J. Heat Mass Transf. 2019, 137, 1263–1289. [Google Scholar] [CrossRef]
- Bistafa, S.R. On the development of the navier-stokes equation by navier. Rev. Bras. Ensino Física 2017, 40, e2603. Available online: http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1806-11172018000200703&lng=en&tlng=en (accessed on 17 December 2024). [CrossRef]
- O’Connor, J.; Day, P.; Mandal, P.; Revell, A. Computational fluid dynamics in the microcirculation and microfluidics: What role can the lattice Boltzmann method play? Integr. Biol. 2016, 8, 589–602. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Rajamuni, M. Recent progress of lattice Boltzmann method and its applications in fluid-structure interaction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 2461–2484. [Google Scholar] [CrossRef]
- Marquardt, J.E.; Krause, M.J. A review of the homogenized lattice boltzmann method for particulate flow simulations: From fundamentals to applications. Powders 2024, 3, 500–530. [Google Scholar] [CrossRef]
- Naaktgeboren, C.; De Andrade, F.N. Lattice nomenclature survey from lga to modern lbm. engrXiv 2020, engrXiv:489k2. Available online: https://engrxiv.org/index.php/engrxiv/preprint/view/1079 (accessed on 17 December 2024).
- Sharma, K.V.; Straka, R.; Tavares, F.W. Current status of Lattice Boltzmann Methods applied to aerodynamic, aeroacoustic, and thermal flows. Prog. Aerosp. Sci. 2020, 115, 100616. [Google Scholar] [CrossRef]
- Salimi, M.R.; Taeibi-Rahni, M.; Jam, F. Heat transfer analysis of a porously covered heated square cylinder, using a hybrid Navier–Stokes–lattice Boltzmann numerical method. Int. J. Therm. Sci. 2015, 91, 59–75. [Google Scholar] [CrossRef]
- Philippi, P.C.; Hegele, L.A.; Dos Santos, L.O.E.; Surmas, R. From the continuous to the lattice Boltzmann equation: The discretization problem and thermal models. Phys. Rev. E 2006, 73, 056702. [Google Scholar] [CrossRef] [PubMed]
- Moorthi, A.; Kumar Sharma, A.; Velusamy, K. A review of sub-channel thermal hydraulic codes for nuclear reactor core and future directions. Nucl. Eng. Des. 2018, 332, 329–344. [Google Scholar] [CrossRef]
- Wang, L.; Tao, S.; Meng, X.; Zhang, K.; Lu, G. Discrete effects on boundary conditions of the lattice Boltzmann method for fluid flows with curved no-slip walls. Phys. Rev. E 2020, 101, 063307. [Google Scholar] [CrossRef]
- Dietzel, M.; Ernst, M.; Sommerfeld, M. Application of the lattice-boltzmann method for particle-laden flows: Point-particles and fully resolved particles. Flow Turbul. Combust. 2016, 97, 539–570. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Xie, H.; Zhang, Y.; Lu, Y.; Yoshikawa, A.; Mizuseki, H.; Kawazoe, Y. A comparative study of lattice Boltzmann models for incompressible flow. Comput. Math. Appl. 2014, 68, 1446–1466. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond (Numerical Mathematics and Scientific Computation); Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 2001; ISBN 978-0-19-850398-9. [Google Scholar]
- Guo, Z. Lattice Boltzmann Method and Its Application in Engineering (Advances in Computational Fluid Dynamics Ser); World Scientific Publishing Co. Pte. Ltd.: Singapore, 2014; ISBN 978-981-4508-29-2. [Google Scholar]
- Eitel-Amor, G.; Meinke, M.; Schröder, W. A lattice-Boltzmann method with hierarchically refined meshes. Comput. Fluids 2013, 75, 127–139. [Google Scholar] [CrossRef]
- Luo, L.; Krafczyk, M.; Shyy, W. Lattice boltzmann method for computational fluid dynamics. In Encyclopedia of Aerospace Engineering; Blockley, R., Shyy, W., Eds.; Wiley: Hoboken, NJ, USA, 2010; Available online: https://onlinelibrary.wiley.com/doi/10.1002/9780470686652.eae064 (accessed on 18 December 2024).
- Blocken, B. Computational Fluid Dynamics for urban physics: Importance, scales, possibilities, limitations and ten tips and tricks towards accurate and reliable simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Krause, M.J.; Heuveline, V. Parallel fluid flow control and optimisation with lattice Boltzmann methods and automatic differentiation. Comput. Fluids 2013, 80, 28–36. [Google Scholar] [CrossRef]
- Su, Y.; Ng, T.; Davidson, J.H. A Parallel Non-Dimensional Lattice Boltzmann Method for fluid flow and heat transfer with solid–liquid phase change. Int. J. Heat Mass Transf. 2017, 106, 503–517. [Google Scholar] [CrossRef]
- Zerkak, O.; Kozlowski, T.; Gajev, I. Review of multi-physics temporal coupling methods for analysis of nuclear reactors. Ann. Nucl. Energy 2015, 84, 225–233. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, M.; Ma, Y. Neutron transport solution of lattice Boltzmann method and streaming-based block-structured adaptive mesh refinement. Ann. Nucl. Energy 2018, 118, 249–259. [Google Scholar] [CrossRef]
- Di Ilio, G.; Chiappini, D.; Ubertini, S.; Bella, G.; Succi, S. Hybrid lattice Boltzmann method on overlapping grids. Phys. Rev. E 2017, 95, 013309. [Google Scholar] [CrossRef] [PubMed]
- Merzari, E.; Obabko, A.; Fischer, P.; Halford, N.; Walker, J.; Siegel, A.; Yu, Y. Large-scale large eddy simulation of nuclear reactor flows: Issues and perspectives. Nucl. Eng. Des. 2017, 312, 86–98. [Google Scholar] [CrossRef]
- Wen, M.; Li, W.; Zhao, Z. A hybrid scheme coupling lattice Boltzmann method and finite-volume lattice Boltzmann method for steady incompressible flows. Phys. Fluids 2022, 34, 037114. [Google Scholar] [CrossRef]
- Gharibi, F.; Hosseini, S.A.; Thévenin, D. A hybrid lattice Boltzmann/immersed boundary method/finite-difference model for thermal fluid-solid interactions. Int. Commun. Heat Mass Transf. 2024, 155, 107525. [Google Scholar] [CrossRef]
- Agarwal, G.; Singh, S.; Bindra, H. Multi-group lattice Boltzmann method for criticality problems. Ann. Nucl. Energy 2020, 140, 107260. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y.; Xie, M. GPU accelerated lattice Boltzmann method in neutron kinetics problems II: Neutron transport calculation. Ann. Nucl. Energy 2019, 134, 305–317. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y.; Xie, M. High-order lattice Boltzmann method for multi-group neutron diffusion solution. Prog. Nucl. Energy 2019, 110, 341–353. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, M.; Ma, Y. Neutron discrete velocity boltzmann equation and its finite volume lattice boltzmann scheme. Commun. Comput. Phys. 2019, 25, 1446–1468. [Google Scholar] [CrossRef]
- Házi, G.; Mayer, G. Flow in rod bundles. In Proceedings of the International Conference Nuclear Energy for New Europe, Blend, Slovenia, 5–8 September 2005; pp. 118.1–118.10. Available online: https://inis.iaea.org/records/6eyyv-bdq13 (accessed on 20 February 2025).
- Mayer, G.; Házi, G. Direct numerical and large eddy simulation of longitudinal flow along triangular array of rods using the lattice Boltzmann method. Math. Comput. Simul. 2006, 72, 173–178. [Google Scholar] [CrossRef]
- Fan, Z.; Kuo, Y.-C.; Zhao, Y.; Qiu, F.; Kaufman, A.; Arcieri, W. Visual simulation of thermal fluid dynamics in a pressurized water reactor. Vis. Comput. 2009, 25, 985–996. [Google Scholar] [CrossRef]
- Kaufman, A.; Fan, Z.; Petkov, K. Implementing the lattice Boltzmann model on commodity graphics hardware. J. Stat. Mech. Theory Exp. 2009, 2009, P06016. [Google Scholar] [CrossRef]
- Tiftikci, A.; Kocar, C. Turbulent Flow Simulations of Wire-Wrapped Fuel Pin Bundle of Sodium Cooled Fast Reactor in Lattice-Boltzmann Framework. In Proceedings of the International Conference Nuclear Energy for New Europe, Portorož, Slovenia, 14–17 September 2015; Available online: https://www.semanticscholar.org/paper/Turbulent-Flow-Simulations-of-Wire-wrapped-Fuel-Pin-Tiftikci-Kocar/d585d414525c24dae1479cda421895f3f2f23630 (accessed on 20 February 2025).
- Park, J.W. Application of mesh free lattice Boltzmann method to the analysis of very high temperature reactor lower plenum. ATW. Int. Z. Fuer Kernenerg. 2011, 57, 636–640. [Google Scholar]
- Tamura, A.; Takahashi, S.; Nakata, H.; Takota, A. A Numerical Analysis Method of Impurity Precipitation on Mesh Wire of Cold Trap in Fast Breeder Reactor. J. Nucl. Eng. Radiat. Sci. 2018, 4, 031015. [Google Scholar] [CrossRef]
- Gui, N.; Li, Z.; Zhang, Z.; Yang, X.; Tu, J.; Jiang, S. Numerical study of pebble recirculation in a two-dimensional pebble bed of stationary atmosphere using LB-IB-DEM coupled method. Ann. Nucl. Energy 2019, 124, 58–68. [Google Scholar] [CrossRef]
- De Rosis, A.; Coreixas, C. Multiphysics flow simulations using D3Q19 lattice Boltzmann methods based on central moments. arXiv 2020, arXiv:2010.01628. Available online: https://arxiv.org/abs/2010.01628v2 (accessed on 20 February 2025). [CrossRef]
- Mayer, G.; Páles, J.; Házi, G. Large eddy simulation of subchannels using the lattice Boltzmann method. Ann. Nucl. Energy 2007, 34, 140–149. [Google Scholar] [CrossRef]
- Li, Z. Simulation of the CRUD Formation Process Using the Lattice Boltzmann Method. Master’s Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2011. Available online: https://hdl.handle.net/2142/29727 (accessed on 20 February 2025).
- Park, J.W. Development of two-dimensional lattice Boltzmann code DG2LBM for computational fluid dynamic problems in nuclear reactor safety component design. ATW Int. Z. Fuer Kernenerg. 2012, 58, 176–181. Available online: https://www.osti.gov/etdeweb/biblio/21568537 (accessed on 20 February 2025).
- Carrasco Boix, A. Application of the Lattice Boltzmann Method to Issues of Coolant Flows in Nuclear Power Reactors. Master’s Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2013. Available online: https://www.semanticscholar.org/paper/Application-of-the-Lattice-Boltzmann-Method-to-of-Boix/bf89a1448931c73b7f86951340dd72453f3ec639 (accessed on 20 February 2025).
- Takahashi, S.; Tamura, A.; Nakata, H.; Takota, A. Development of Evaluation Method for Cold Trap in Fast Breeder Reactor: Part 2—Analytical Evaluation of Impurity Capturing Capacity in Cold Trap; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Wahba, M.A.; Abdelrahman, A.A.; El-Sahlamy, N.M.; Rabb, M.F.A. Double SRT Thermal Lattice Boltzmann Method for Simulating Natural Convection of Low Prandtl Number Fluids. Int. J. Eng. Sci. IJES 2017, 6, 21–35. [Google Scholar]
- Tiftikçi, A.; Kocar, C. Investigation of turbulence models for a fully-periodic LWR unit-cell in lattice-Boltzmann framework. Prog. Nucl. Energy 2018, 104, 160–171. [Google Scholar] [CrossRef]
- Hudear, H.R.; Shehab, S.N. Cross Flow Characteristics and Heat Transfer of Staggered Tubes Bundle: A Numerical Study. Front. Heat Mass Transf. 2023, 21, 367–383. [Google Scholar] [CrossRef]
- Kang, S.K.; Hassan, Y.A. The effect of lattice models within the lattice Boltzmann method in the simulation of wall-bounded turbulent flows. J. Comput. Phys. 2013, 232, 100–117. [Google Scholar] [CrossRef]
- Weickert, M.; Teike, G.; Schmidt, O.; Sommerfeld, M. Investigation of the LES WALE turbulence model within the lattice Boltzmann framework. Comput. Math. Appl. 2010, 59, 2200–2214. [Google Scholar] [CrossRef]
- Han, M.; Ooka, R.; Kikumoto, H. Effects of wall function model in lattice Boltzmann method-based large-eddy simulation on built environment flows. Build. Environ. 2021, 195, 107764. [Google Scholar] [CrossRef]
- Filippova, O.; Succi, S.; Mazzocco, F.; Arrighetti, C.; Bella, G.; Hänel, D. Multiscale lattice boltzmann schemes with turbulence modeling. J. Comput. Phys. 2001, 170, 812–829. [Google Scholar] [CrossRef]
- Dunlap, R.A. Generation IV Nuclear Reactors: Design, Operation and Prospects for Future Energy Production; IOP Publishing: Bristol, UK, 2024; Available online: https://iopscience.iop.org/book/mono/978-0-7503-6069-2 (accessed on 15 April 2025).
- Nøland, J.K.; Hjelmeland, M.N.; Hartmann, C.; Tjernberg, L.B.; Korpås, M. Overview of Small Modular and Advanced Nuclear Reactors and Their Role in the Energy Transition. In Proceedings of the IEEE Transactions on Energy Conversion (Early Access), Piscataway, NJ, USA, 14 January 2025; pp. 1–12. [Google Scholar] [CrossRef]
- Freile, R.; Tano, M.E.; Ragusa, J.C. Lattice Boltzmann solidification modeling of forced convection internal flows applied to Gen-IV nuclear reactor coolants. Prog. Nucl. Energy 2023, 163, 104785. [Google Scholar] [CrossRef]
- Sitompul, Y.; Sugihara, K.; Onodera, N.; Idomura, Y. Gas entrainment simulation for fast reactors using freesurface lattice boltzmann method. EPJ Web Conf. 2024, 302, 05004. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Y. Coupled Neutronics-thermal-hydraulics Simulation of Nuclear Reactor Based on Lattice Boltzmann Method. At. Energy Sci. Technol. 2022, 56, 308–315. [Google Scholar] [CrossRef]
- Tao, S.; He, Q.; Wang, L.; Chen, B.; Chen, J.; Lin, Y. Discrete unified gas kinetic scheme simulation of conjugate heat transfer problems in complex geometries by a ghost-cell interface method. Appl. Math. Comput. 2021, 404, 126228. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).