CFD Analysis of Hydrodynamic Loads on Jack-Up Platforms Using Buoyancy-Modified k-ω SST Turbulence Model
Abstract
1. Introduction
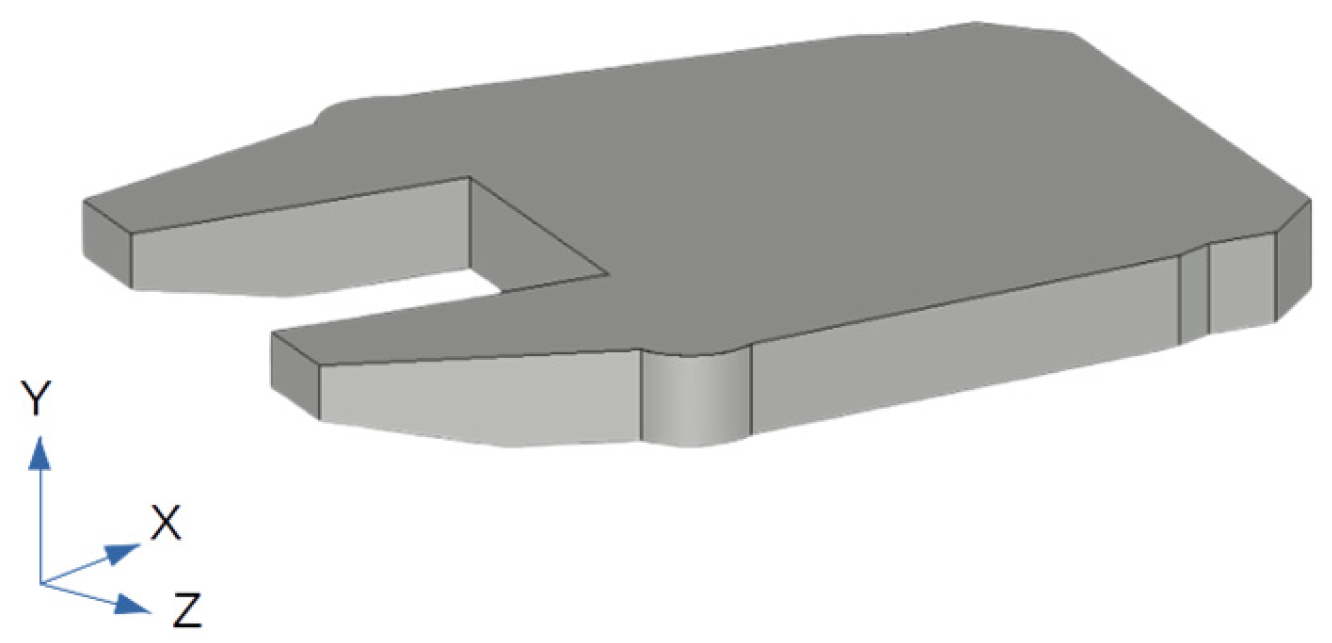
2. Jack-Up Platform Configuration
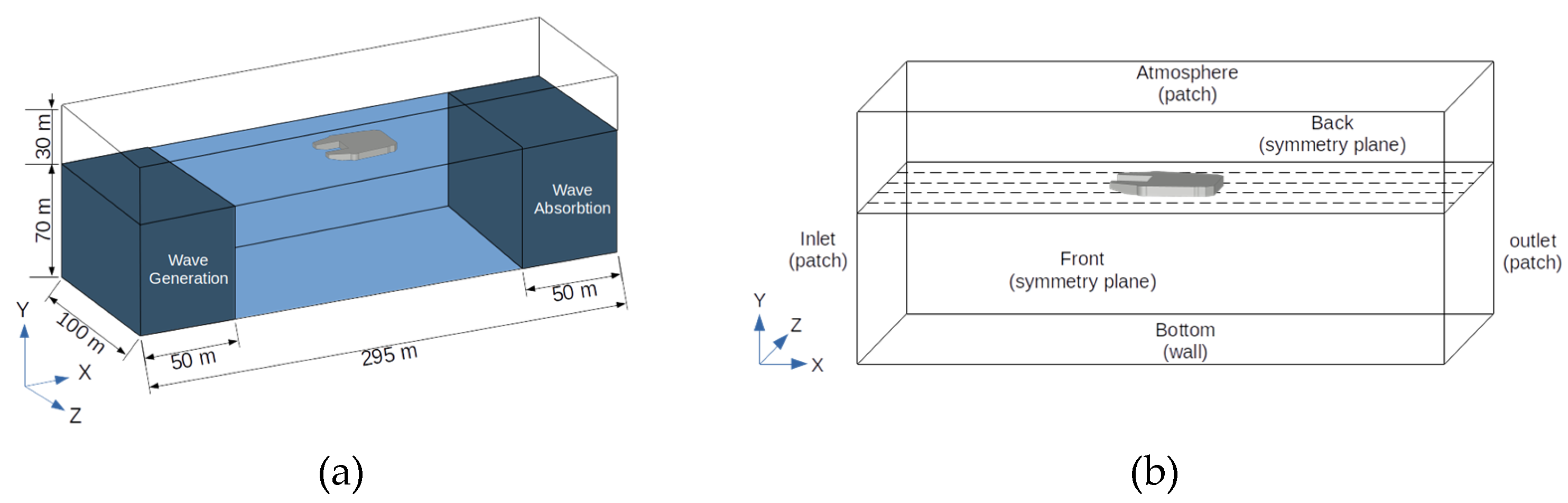
2.1. Jack-Up Platform Geometric and Domain
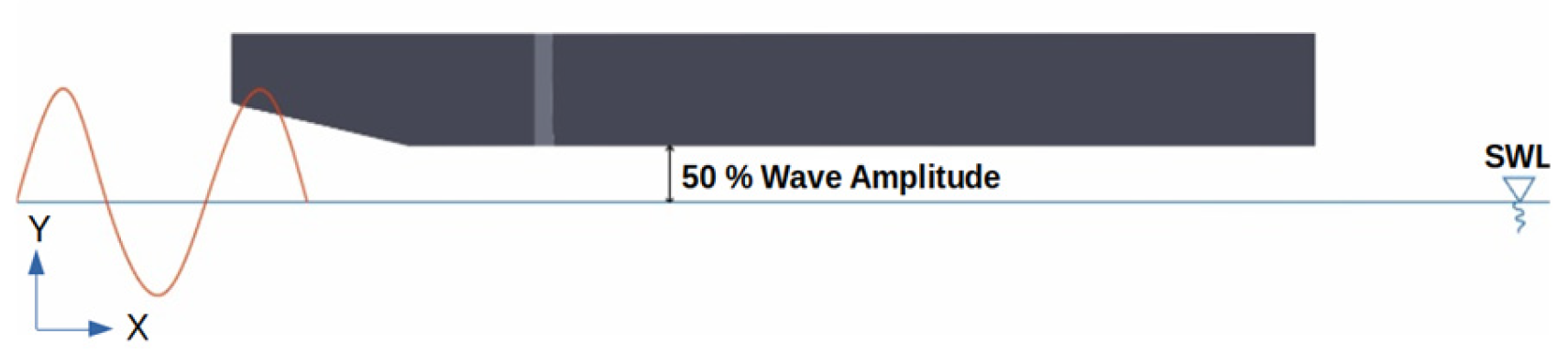
2.2. Meshing and Boundary Condition
- Case B serves as the reference case.
- Case A explores conditions with a higher wave height and longer wave periods compared to Case B.
- Case C examines scenarios with a lower wave height and shorter wave periods than Case B.
- Case D investigates the impact of varying wave heights while maintaining a constant wave period.
| Case | Wave Height (m) | Wave Periods (s) |
|---|---|---|
| A | 5.4 | 5.9 |
| B | 4.6 | 5.5 |
| C | 4 | 5.1 |
| D | 3.7 | 5.5 |
3. Numerical Method
3.1. Governing Equation
3.2. Volume of Fluid
3.3. Froude Scaling
3.4. Turbulence Model
4. Results and Discussion
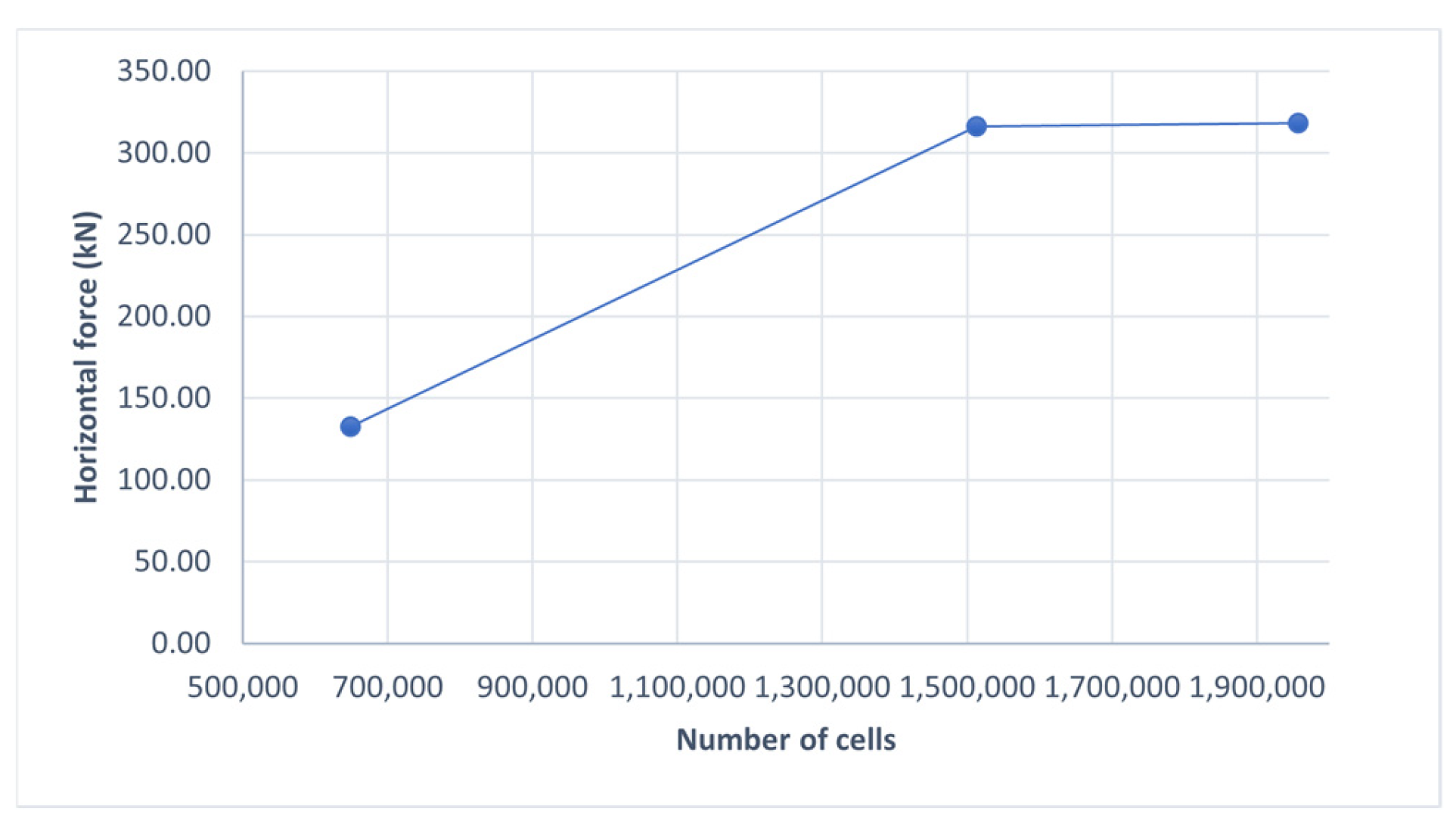
4.1. Verification
4.2. Wave Behavior on the Jack-Up Production Platform Hull Structures
4.3. Wave Loads on Jack-Up Production Platform Structure
5. Conclusions
- The force load experienced by the jack-up production platform structure correlates directly with the magnitude of wave height and the wave period. Notably, the research identified the maximum wave load in test case A (H = 5.4 m and T = 5.9 s) and the minimum wave load in test case D (H = 3.7 m and T = 5.5 s). As the wave height and period increase, the mass of water impacting the walls of the jack-up production platform amplifies accordingly.
- Due to the geometric positioning of the jack-up production platform above the Still Water Level (SWL), the predominant forces acting on the platform walls manifest predominantly in the vertical direction.
- The study revealed that the vertical force along the negative axis exhibits a significant magnitude, primarily induced by the rebounding of water waves from the jack-up production platform’s walls after the initial collision. This phenomenon causes a vacuum effect, generating negative pressure on the bottom wall of the jack-up production platform.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Scale ratio |
| Dω | Cross diffusion term |
| g | Gravitational acceleration |
| F1, F2 | blending function that helps transition between different turbulence models |
| Gω | Generation of ω due to turbulence |
| Gk | Generation of k due to shear in the velocity field |
| k | Turbulence kinetic energy |
| L | Length |
| S | Strain rate magnitude |
| V | Velocity |
| Yk | Rate at which turbulent kinetic energy is converted into thermal energy due to viscosity |
| Yω | Destruction (dissipation) of ω due to viscosity effects. |
| α | Empirical model constants |
| β | Model constant |
| Effective diffusivity for turbulent kinetic energy | |
| Effective diffusivity of ω | |
| Wave length | |
| μ | Viscosity |
| σ | Turbulence model constant |
| ω | Turbulence specific dissipation rate |
| Superscript | |
| T | Transpose |
| Superscript | |
| m | Model scale |
| p | Real scale |
| t | Turbulent (turbulent eddy) |
References
- BP. BP Statistical Review of World Energy, 68th ed.; BP: London, UK, 2019; Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2019-full-report.pdf (accessed on 24 January 2024).
- BP. BP Statistical Review of World Energy, 72nd ed.; BP: London, UK, 2023; Available online: https://www.bp.com/statisticalreview (accessed on 24 January 2024).
- Randall, R.E. Elements of Ocean Engineering, 2nd ed.; Society of Naval Architects: College Station, TX, USA, 2010. [Google Scholar]
- Azman, N.U.; Abu Husain, M.K.; Mohd Zaki, N.I.; Mat Soom, E.; Mukhlas, N.A.; Syed Ahmad, S.Z.A. Structural Integrity of Fixed Offshore Platforms by Incorporating Wave-in-Deck. J. Mar. Sci. Eng. 2021, 9, 1027. [Google Scholar] [CrossRef]
- Ghazi, Z.M.; Abbood, I.S.; Hejazi, F. Dynamic Evaluation of Jack-up Platform Structure under Wave, Wind, Earthquake and Tsunami Loads. J. Ocean. Eng. Sci. 2022, 7, 41–57. [Google Scholar] [CrossRef]
- Kagita, G.; Addala, M.B.; Achary, G.G.S.; Sripada, S.V.R. Evaluation of Impact Loads on Offshore Jacket Platform during Float-over Mating Operation. Int. Conf. Ocean. Offshore Arct. Eng. 2019, 1, V001T01A013. [Google Scholar] [CrossRef]
- Luo-Theilen, X.; Rung, T. Numerical Analysis of the Installation Procedures of Offshore Structures. Ocean. Eng. 2019, 179, 116–127. [Google Scholar] [CrossRef]
- Ye, H.; Yu, D.; Ye, J.; Yang, Z. Numerical Analysis of Dynamics of Jack-Up Offshore Platform and Its Seabed Foundation under Ocean Wave. Appl. Sci. 2022, 12, 3299. [Google Scholar] [CrossRef]
- Tang, W.; Zhuang, H.; Tang, Z.; Guo, S.; Yan, F. Mooring Positioning Performance of Jack-up Platform. Ships Offshore Struct. 2020, 15, 633–644. [Google Scholar] [CrossRef]
- Abdel Raheem, S.E. Nonlinear Behaviour of Steel Fixed Offshore Platform under Environmental Loads. Ships Offshore Struct. 2014, 11, 1–15. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, J.; Li, X.; Tian, X.; Liu, G.; Leng, D. Experimental Study on Hydrodynamic Characteristics of Three Truss-Type Legs of Jack-up Offshore Platform. Ocean. Eng. 2021, 234, 109305. [Google Scholar] [CrossRef]
- Wu, Y.-S. Multiphase Fluid Flow in Porous and Fractured Reservoirs; Gulf Professional Publishing: Houston, TX, USA, 2016. [Google Scholar]
- Zhou, Y.; Xiao, Q.; Liu, Y.; Incecik, A.; Peyrard, C.; Wan, D.; Pan, G.; Li, S. Exploring Inflow Wind Condition on Floating Offshore Wind Turbine Aerodynamic Characterisation and Platform Motion Prediction Using Blade Resolved CFD Simulation. Renew. Energy 2022, 182, 1060–1079. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, G.; Zhu, Y.; Li, X.; Shen, X.; He, R. Real-Time Risk Assessment of Explosion on Offshore Platform Using Bayesian Network and CFD. J. Loss Prev. Process Ind. 2021, 72, 104518. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Experimental and Numerical Measurements of Wave Forces on a 3D Offshore Stationary OWC Wave Energy Converter. Ocean. Eng. 2017, 144, 98–117. [Google Scholar] [CrossRef]
- Nematollahi, M.; Moghim, M.N. Numerical Simulation of Spatial Distribution of Wave Overtopping on Non-Reshaping Berm Breakwaters. J. Marine. Sci. Appl. 2020, 19, 301–316. [Google Scholar] [CrossRef]
- Cui, F.; Daskiran, C.; King, T.; Robinson, B.; Lee, K.; Katz, J.; Boufadel, M.C. Modeling Oil Dispersion under Breaking Waves. Part I: Wave Hydrodynamics. Environ. Fluid Mech. 2020, 20, 1527–1551. [Google Scholar] [CrossRef]
- Yao, Y.; Chen, X.; Xu, C.; Jia, M.; Jiang, C. Modeling Solitary Wave Transformation and Run-up over Fringing Reefs with Large Bottom Roughness. Ocean. Eng. 2020, 218, 108208. [Google Scholar] [CrossRef]
- Aggarwal, A.; Chella, M.A.; Bihs, H.; Arntsen, Ø.A. Numerical Study of Irregular Breaking Wave Forces on a Monopile for Offshore Wind Turbines. Energy Procedia 2017, 137, 246–254. [Google Scholar] [CrossRef]
- Chella, A.M.; Bihs, H.; Myrhaug, D. Wave Impact Pressure and Kinematics Due to Breaking Wave Impingement on a Monopile. J. Fluids Struct. 2019, 86, 94–123. [Google Scholar] [CrossRef]
- Leftheriotis, G.A.; Chalmoukis, I.A.; Oyarzun, G.; Dimas, A.A. A Hybrid Parallel Numerical Model for Wave-Induced Free-Surface Flow. Fluids 2021, 6, 350. [Google Scholar] [CrossRef]
- Wang, W.; Bihs, H.; Kamath, A.; Arntsen, Ø.A. Multi-Directional Irregular Wave Modelling with CFD. In Proceedings of the Fourth International Conference in Ocean Engineering (ICOE2018); Murali, K., Sriram, V., Samad, A., Saha, N., Eds.; Lecture Notes in Civil Engineering. Springer: Singapore, 2019; Volume 22, pp. 521–529. [Google Scholar] [CrossRef]
- Frantzis, C.; Grigoriadis, D.G.E.; Dimas, A.A. Numerical Study of Solitary Waves Past Slotted Breakwaters with a Single Row of Vertical Piles: Wave Processes and Flow Behavior. Ocean. Eng. 2020, 211, 107667. [Google Scholar] [CrossRef]
- Nizamani, M.; Nizamani, Z.; Nakayama, A.; Osman, M. Analysis of Loads Caused by Waves on the Deck near the Free Surface of the Offshore Platform Using Computational Fluid Dynamics. Ships Offshore Struct. 2022, 17, 1964–1974. [Google Scholar] [CrossRef]
- Dong, G.; Gao, X.; Ma, X.; Ma, Y. Energy Properties of Regular Water Waves over Horizontal Bottom with Increasing Nonlinearity. Ocean. Eng. 2020, 218, 108159. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Application of a Buoyancy-Modified k-ω SST Turbulence Model to Simulate Wave Run-up around a Monopile Subjected to Regular Waves Using OpenFOAM ®®. Coast. Eng. 2017, 125, 81–94. [Google Scholar] [CrossRef]
- Huo, S.; Deng, S.; Song, Z.; Zhao, W.; Wan, D. On the Hydrodynamic Response and Slamming Impact of a Cylindrical FPSO in Combined Wave-Current Flows. Ocean. Eng. 2023, 275, 114139. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A Wave Generation Toolbox for the Open-source CFD Library: OpenFoam®®. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Karola, A.; Tavakoli, S.; Mikkola, T.; Matusiak, J.; Hirdaris, S. The Influence of Wave Modelling on the Motions of Floating Bodies. Ocean Eng. 2024, 306, 118067. [Google Scholar] [CrossRef]
- Brown, S.A.; Greaves, D.M.; Magar, V.; Conley, D.C. Evaluation of Turbulence Closure Models under Spilling and Plunging Breakers in the Surf Zone. Coast. Eng. 2016, 114, 177–193. [Google Scholar] [CrossRef]
- Islam, H.; Guedes Soares, C. Assessment of Uncertainty in the CFD Simulation of the Wave-Induced Loads on a Vertical Cylinder. Mar. Struct. 2021, 80, 103088. [Google Scholar] [CrossRef]
- Bruinsma, N. Validation and Application of a Fully Nonlinear Numerical Wave Tank; Delft University of Technology: Delft, The Netherlands, 2016. [Google Scholar]
- Sayigh, A. Comprehensive Renewable Energy, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Keser, R. Block-Coupled Solution Algorithms for 2-Equation Turbulence Models; Fakultet Strojarstva i Brodogradnje: Zagreb, Croatia, 2016; p. 110. [Google Scholar]
- Devolder, B.; Troch, P.; Rauwoens, P. Performance of a Buoyancy-Modified k-ω and k-ω SST Turbulence Model for Simulating Wave Breaking under Regular Waves Using OpenFOAM®®. Coast. Eng. 2018, 138, 49–65. [Google Scholar] [CrossRef]
- Kumar, R.; Dewan, A. Assessment of Buoyancy-Corrected Turbulence Models for Thermal Plumes. Eng. Appl. Comput. Fluid Mech. 2013, 7, 239–249. [Google Scholar] [CrossRef][Green Version]
- Devolder, B. Hydrodynamic Modelling of Wave Energy Converter Arrays; KU LEUVEN: Leuven, Belgium, 2018. [Google Scholar]
- Jasak, H.; Vukčević, V.; Gatin, I. Numerical Simulation of Wave Loading on Static Offshore Structures. In CFD for Wind and Tidal Offshore Turbines; Springer International Publishing: Cham, Switzerland, 2015; pp. 95–105. [Google Scholar]
- Liu, B.; Park, S. CFD Simulations of the Effects of Wave and Current on Power Performance of a Horizontal Axis Tidal Stream Turbine. J. Mar. Sci. Eng. 2023, 11, 425. [Google Scholar] [CrossRef]
- Chen, Z.; Jiao, J.; Jiang, C.; Si, H.; Chen, S. Scale Effects on Wave Loads and Slamming Loads in Ship Hydroelasticity Simulation by CFD-FEM Method. Ocean Eng. 2024, 314, 119718. [Google Scholar] [CrossRef]



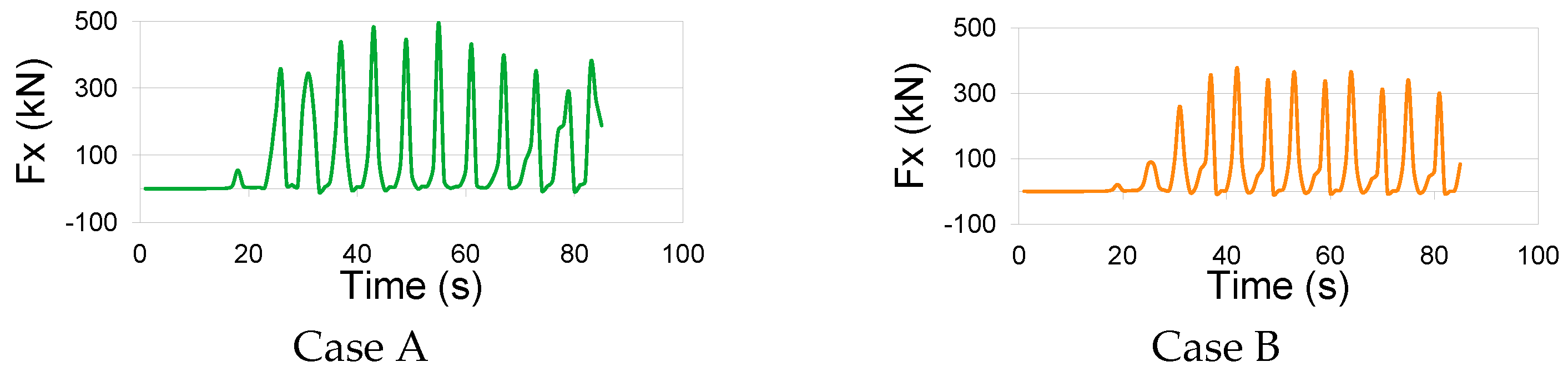
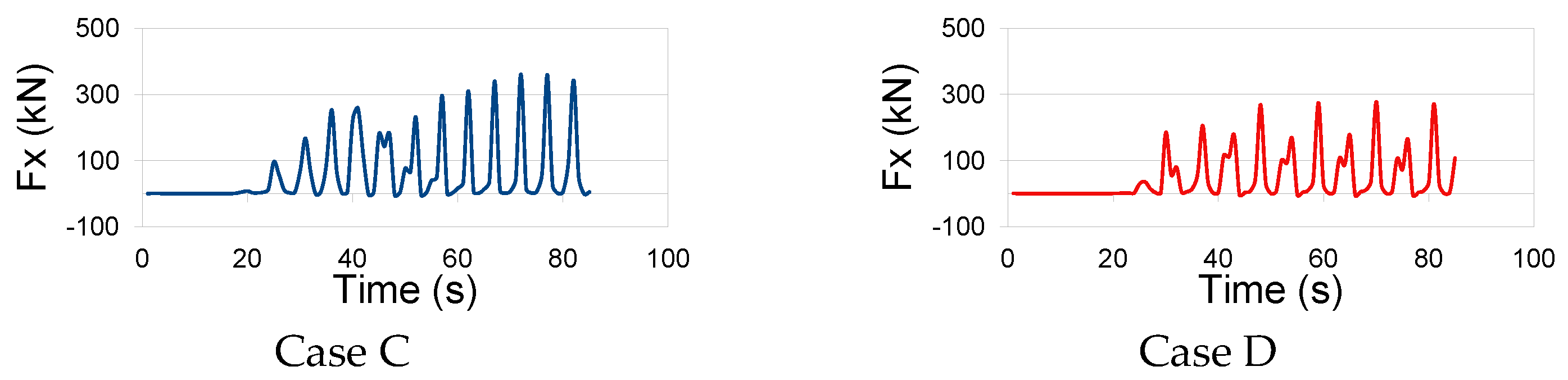
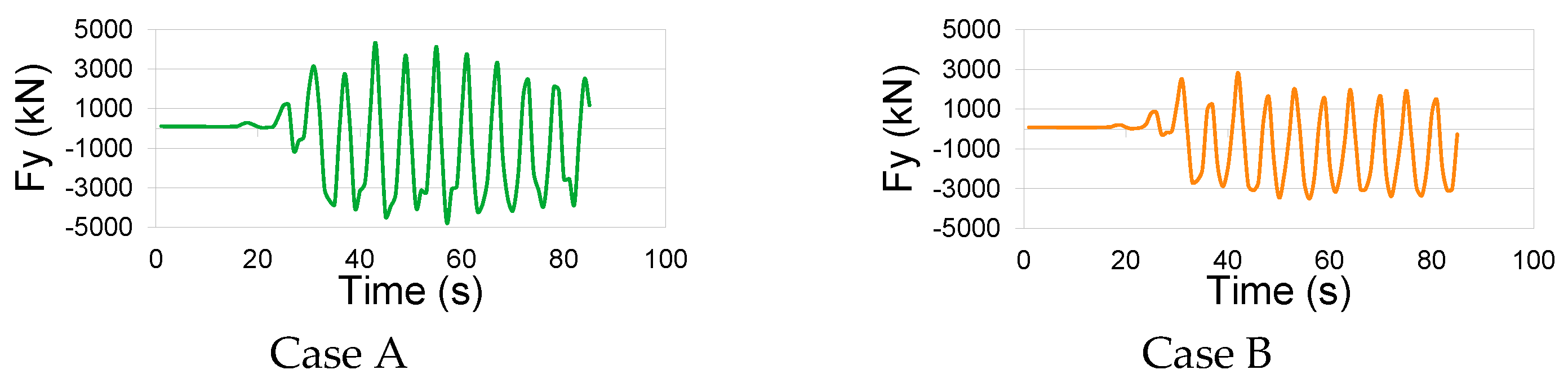
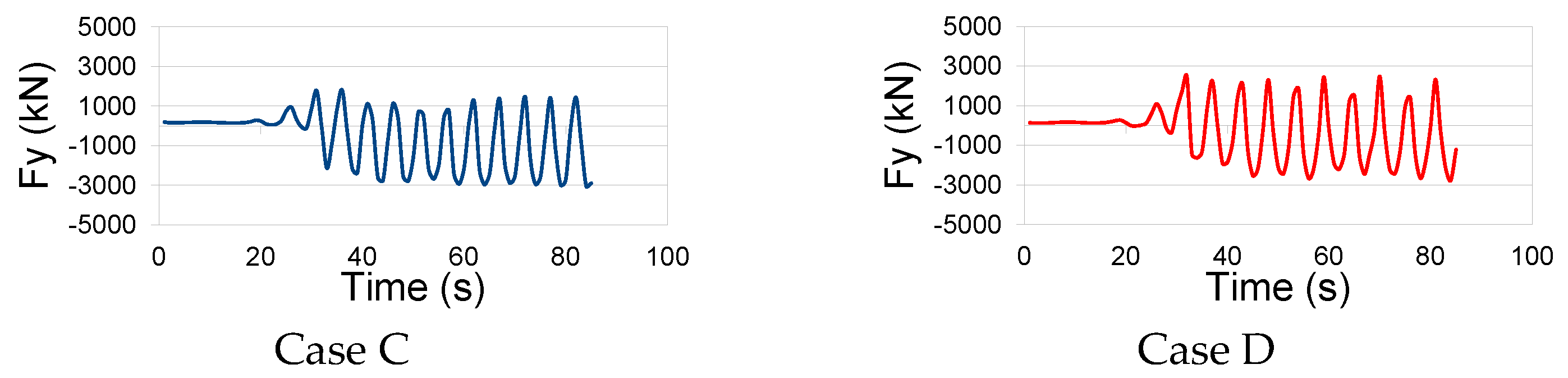

| Variable | Unit | Scale Factor |
|---|---|---|
| Length | m | |
| Wave Height | m | |
| Wave Length | m | |
| Wave Period | s | |
| Force | N | |
| Mass | Kg | |
| Pressure | Pa | |
| Moment | Nm |
| Wave Steepness | Simulation Results | Exact Solution Results | Error (%) |
|---|---|---|---|
| Low (H = 0.12 m and T = 1.6 s) | 5.048 N | 5.104 N | 1.1% |
| High (H = 0.12 m and T = 1.05 s) | 4.448 N | 4.459 N | 0.25% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arini, N.R.; Muhammad, G.; Ilman, E.C.; Ariwibowo, T.H.; Moshrefi-Torbati, M.; Saputra, D. CFD Analysis of Hydrodynamic Loads on Jack-Up Platforms Using Buoyancy-Modified k-ω SST Turbulence Model. Fluids 2025, 10, 96. https://doi.org/10.3390/fluids10040096
Arini NR, Muhammad G, Ilman EC, Ariwibowo TH, Moshrefi-Torbati M, Saputra D. CFD Analysis of Hydrodynamic Loads on Jack-Up Platforms Using Buoyancy-Modified k-ω SST Turbulence Model. Fluids. 2025; 10(4):96. https://doi.org/10.3390/fluids10040096
Chicago/Turabian StyleArini, Nu Rhahida, Gilang Muhammad, Eko Charnius Ilman, Teguh Hady Ariwibowo, Mohamed Moshrefi-Torbati, and Deni Saputra. 2025. "CFD Analysis of Hydrodynamic Loads on Jack-Up Platforms Using Buoyancy-Modified k-ω SST Turbulence Model" Fluids 10, no. 4: 96. https://doi.org/10.3390/fluids10040096
APA StyleArini, N. R., Muhammad, G., Ilman, E. C., Ariwibowo, T. H., Moshrefi-Torbati, M., & Saputra, D. (2025). CFD Analysis of Hydrodynamic Loads on Jack-Up Platforms Using Buoyancy-Modified k-ω SST Turbulence Model. Fluids, 10(4), 96. https://doi.org/10.3390/fluids10040096









