Experimental Investigations of Capillary Flow in Three-Dimensional-Printed Microchannels
Abstract
1. Introduction
2. Materials and Methods
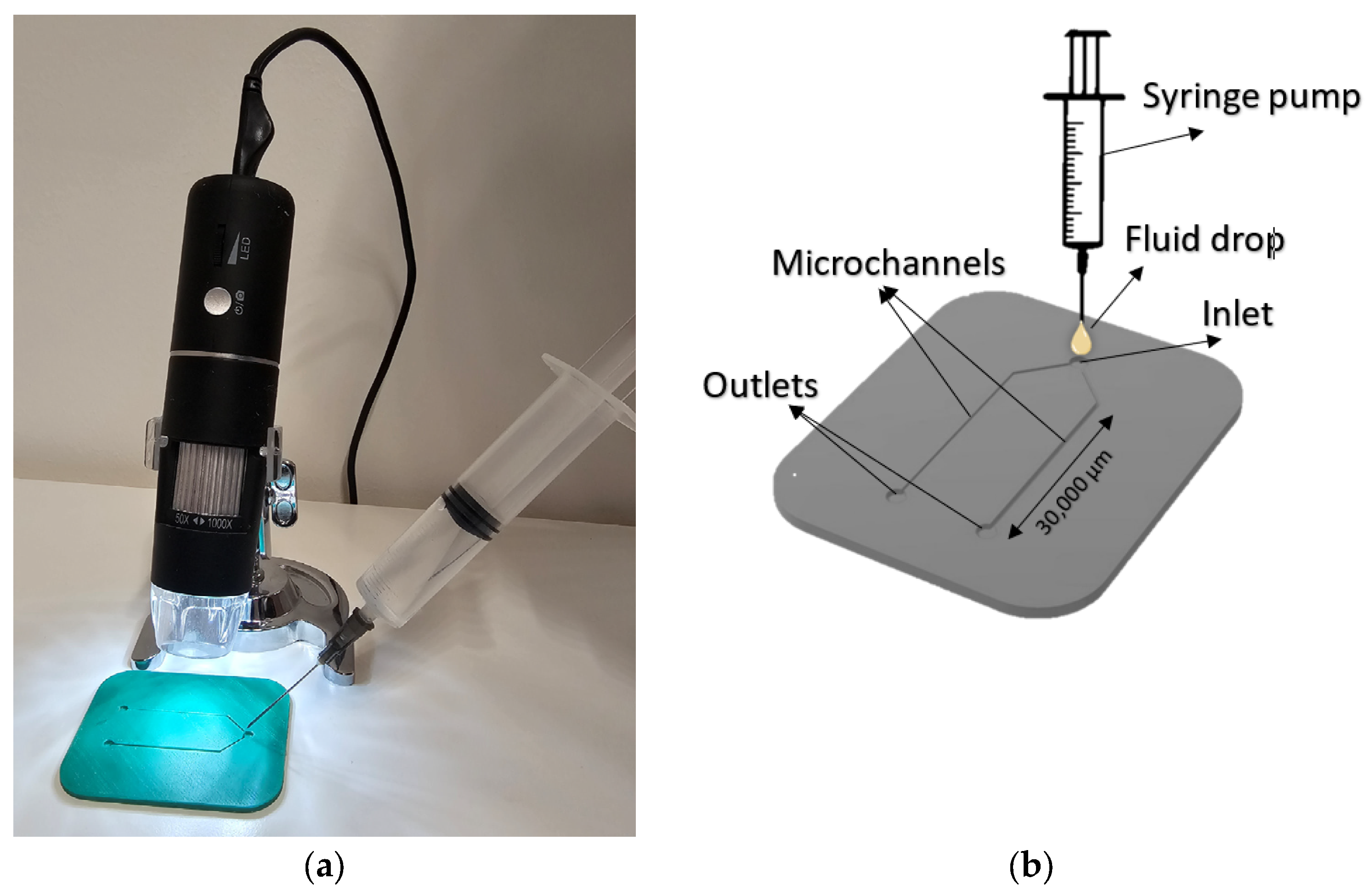
2.1. Experimental Setup
2.2. 3D Model Development
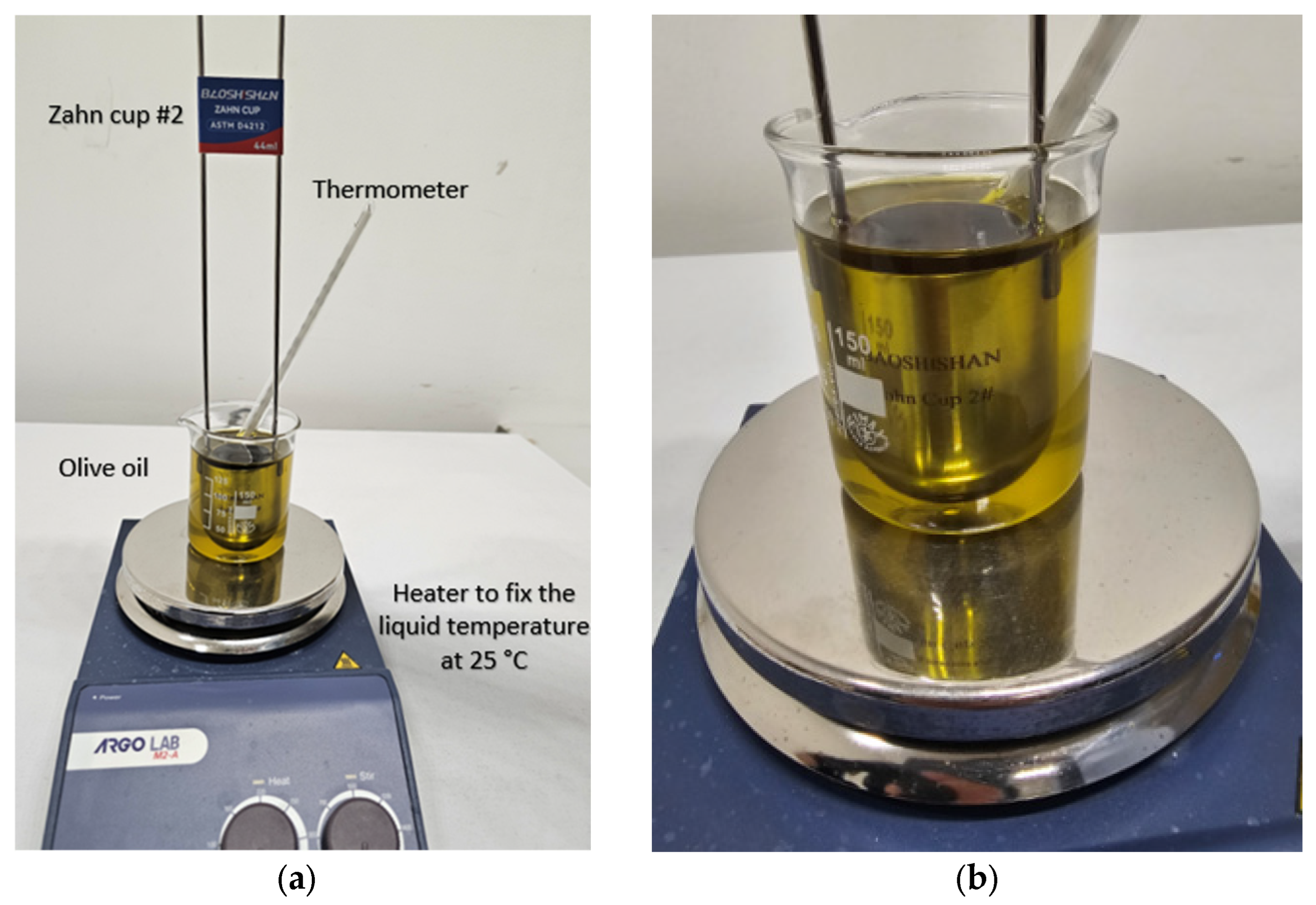
2.3. Selected Materials’ Properties
2.4. Theoretical Analysis
3. Results and Discussion
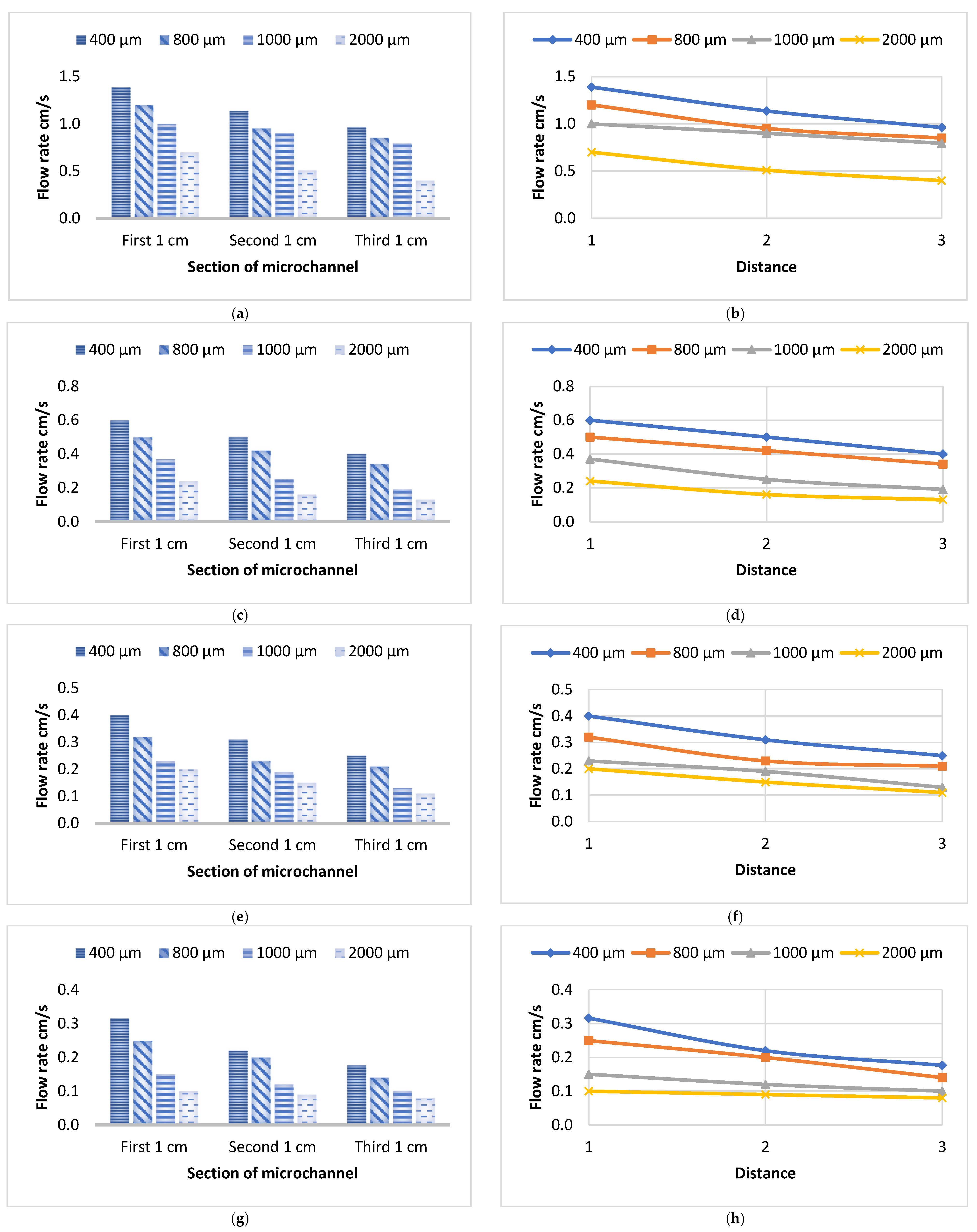
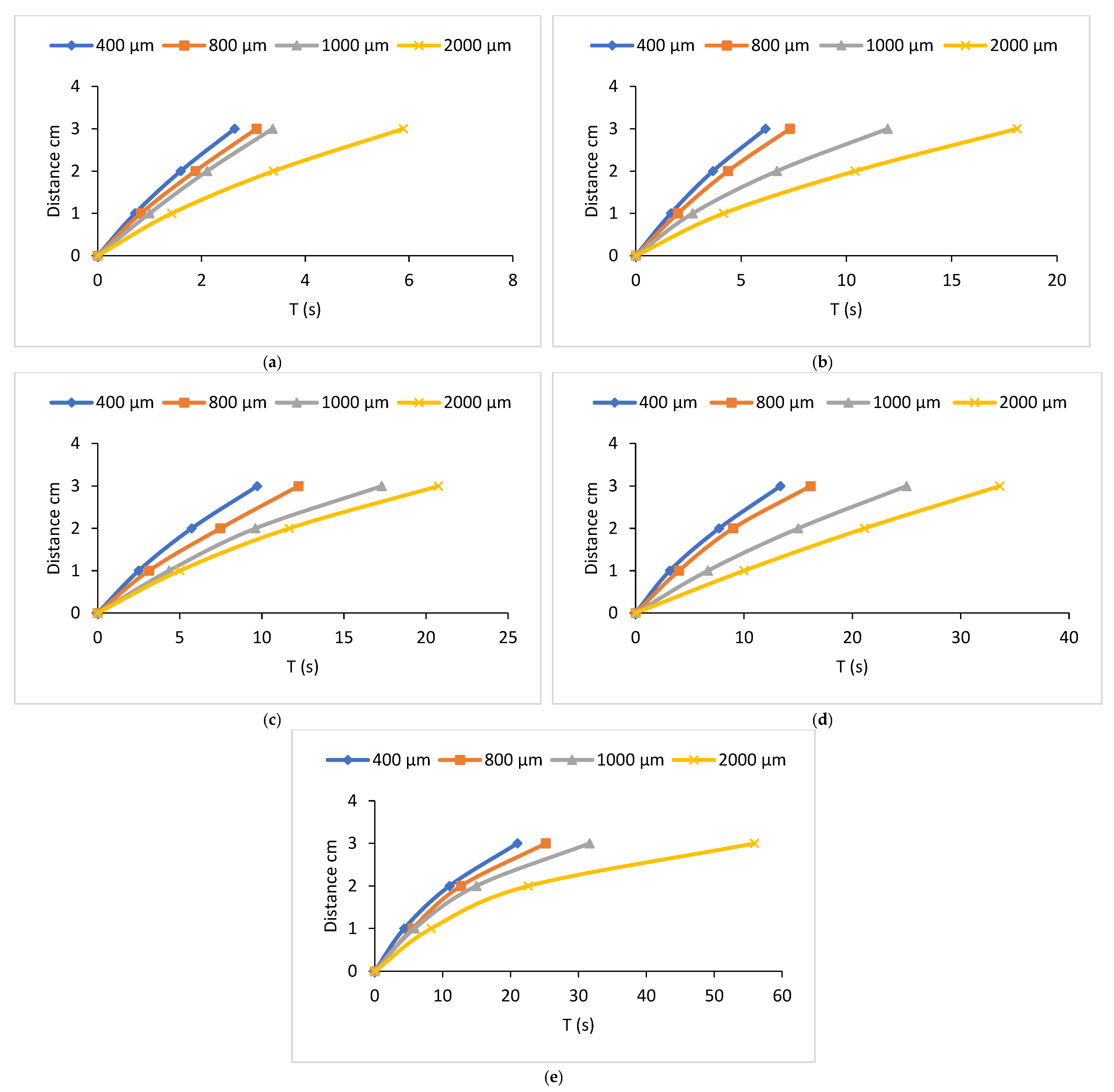
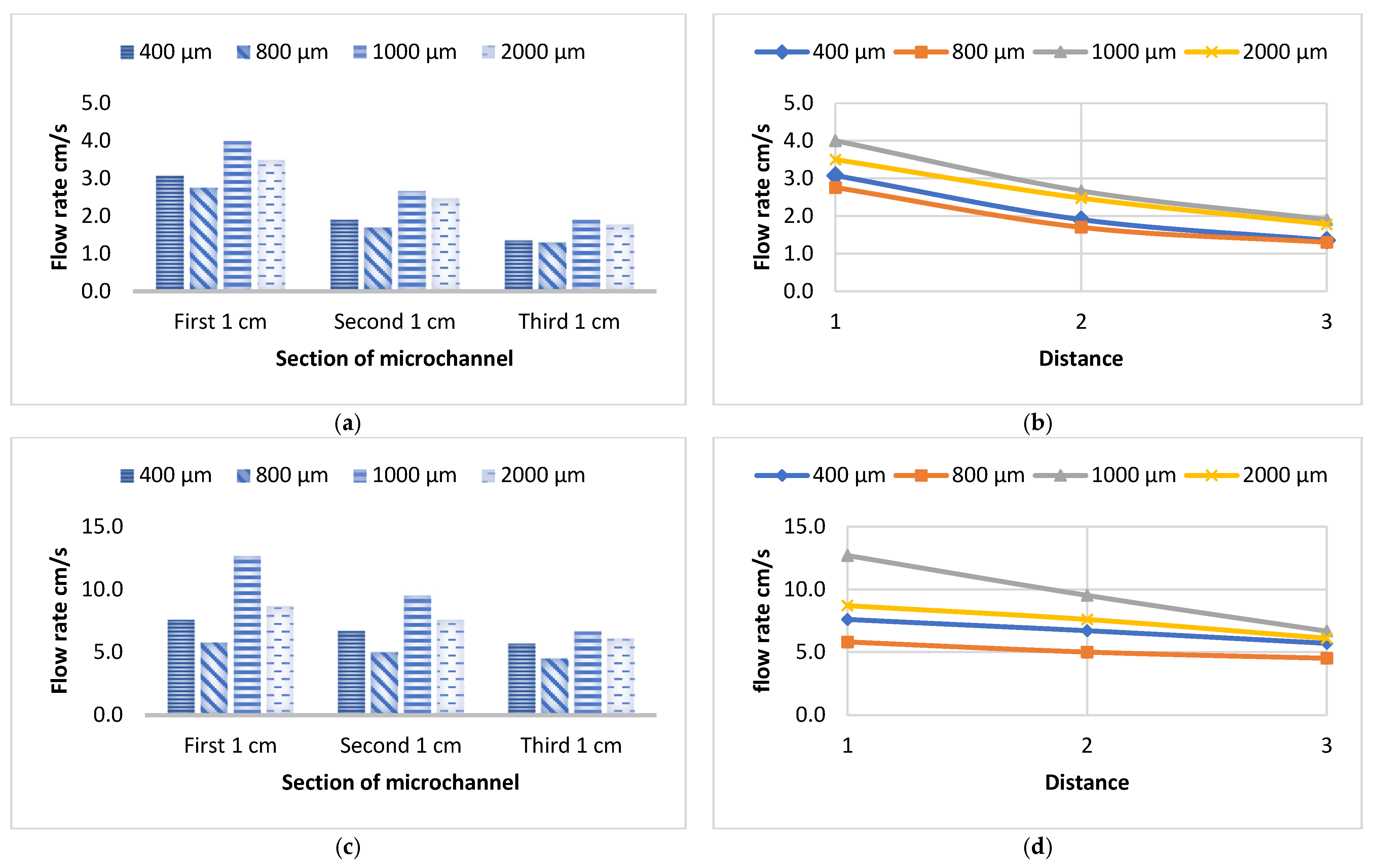
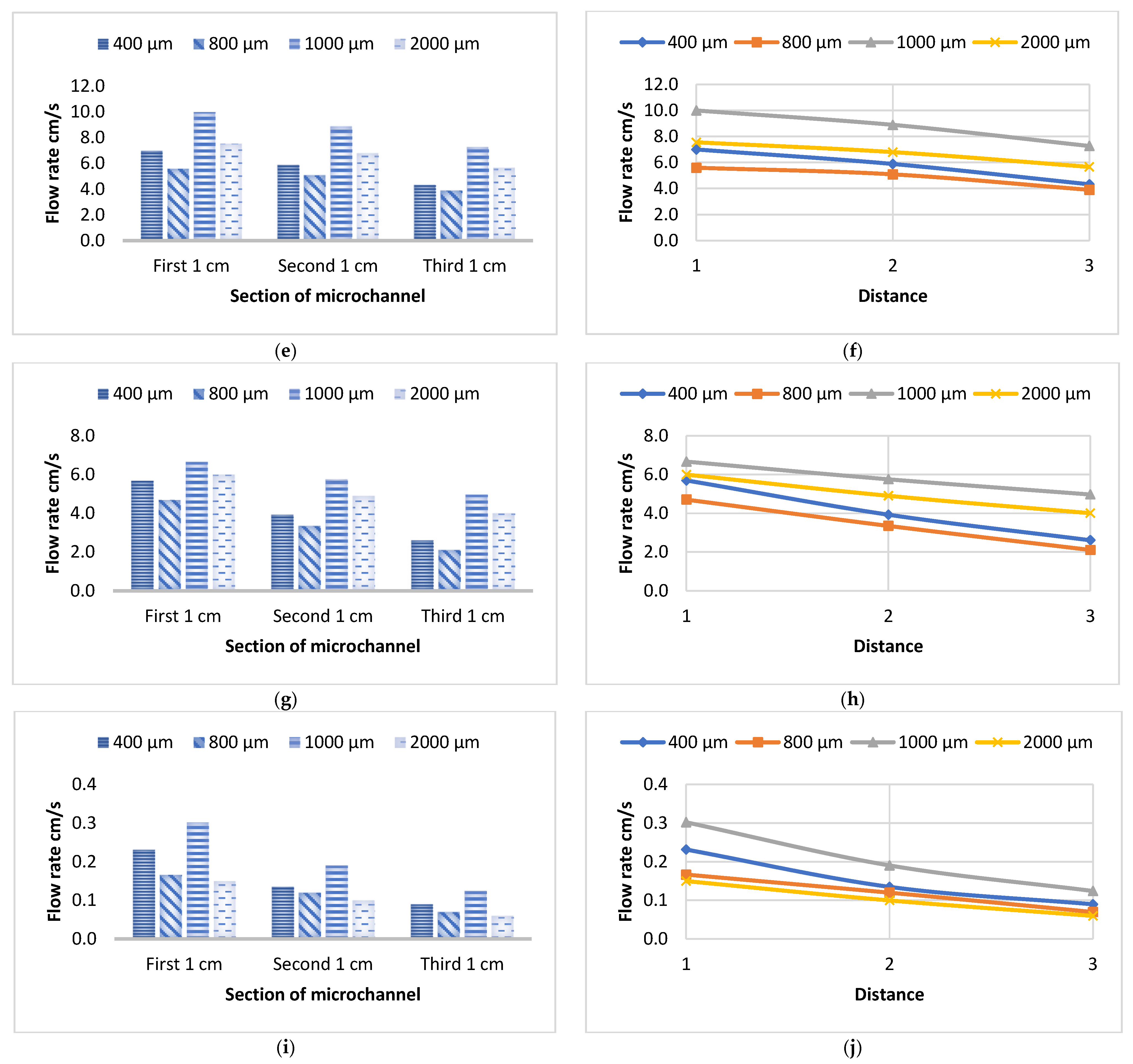
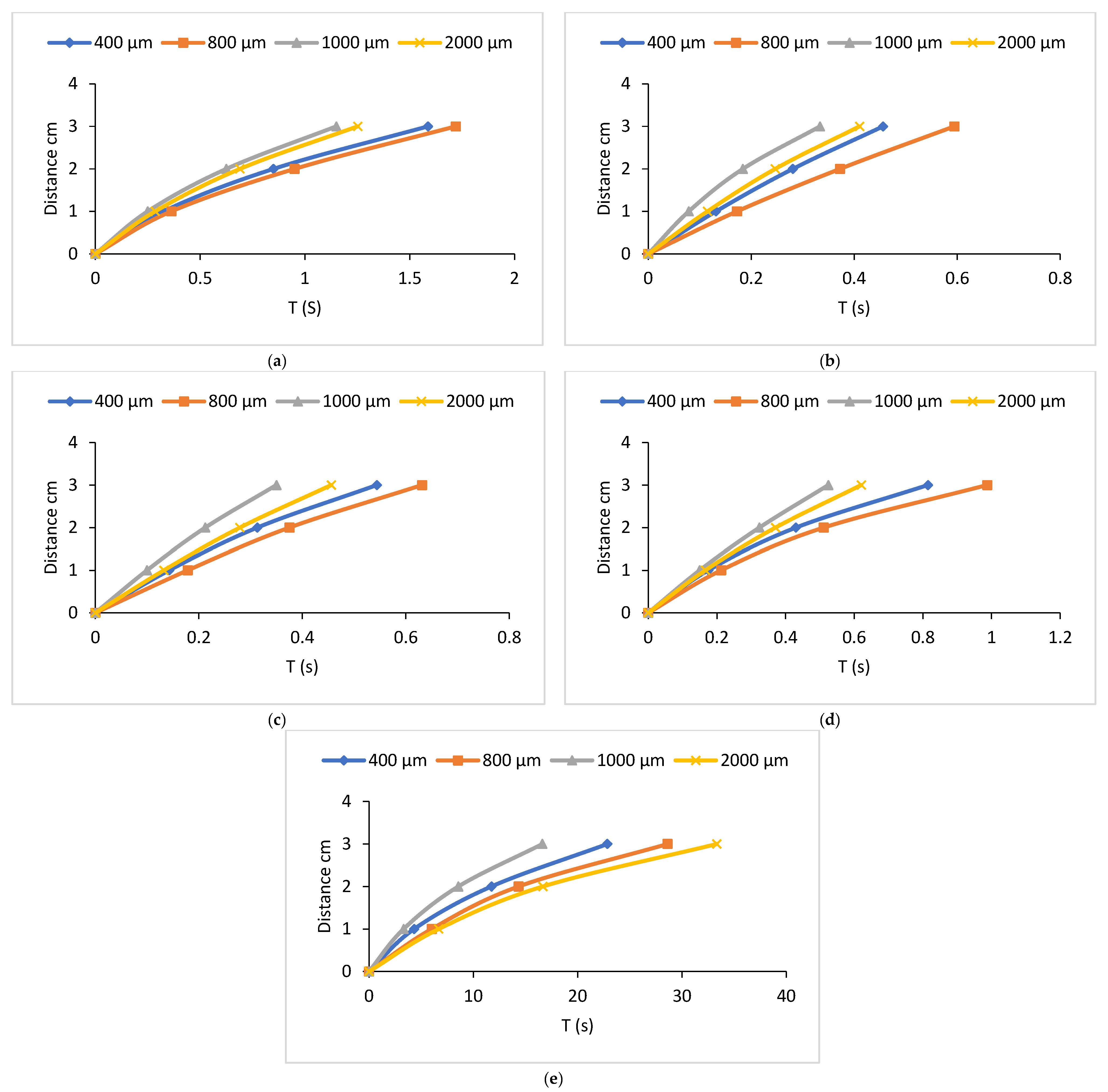
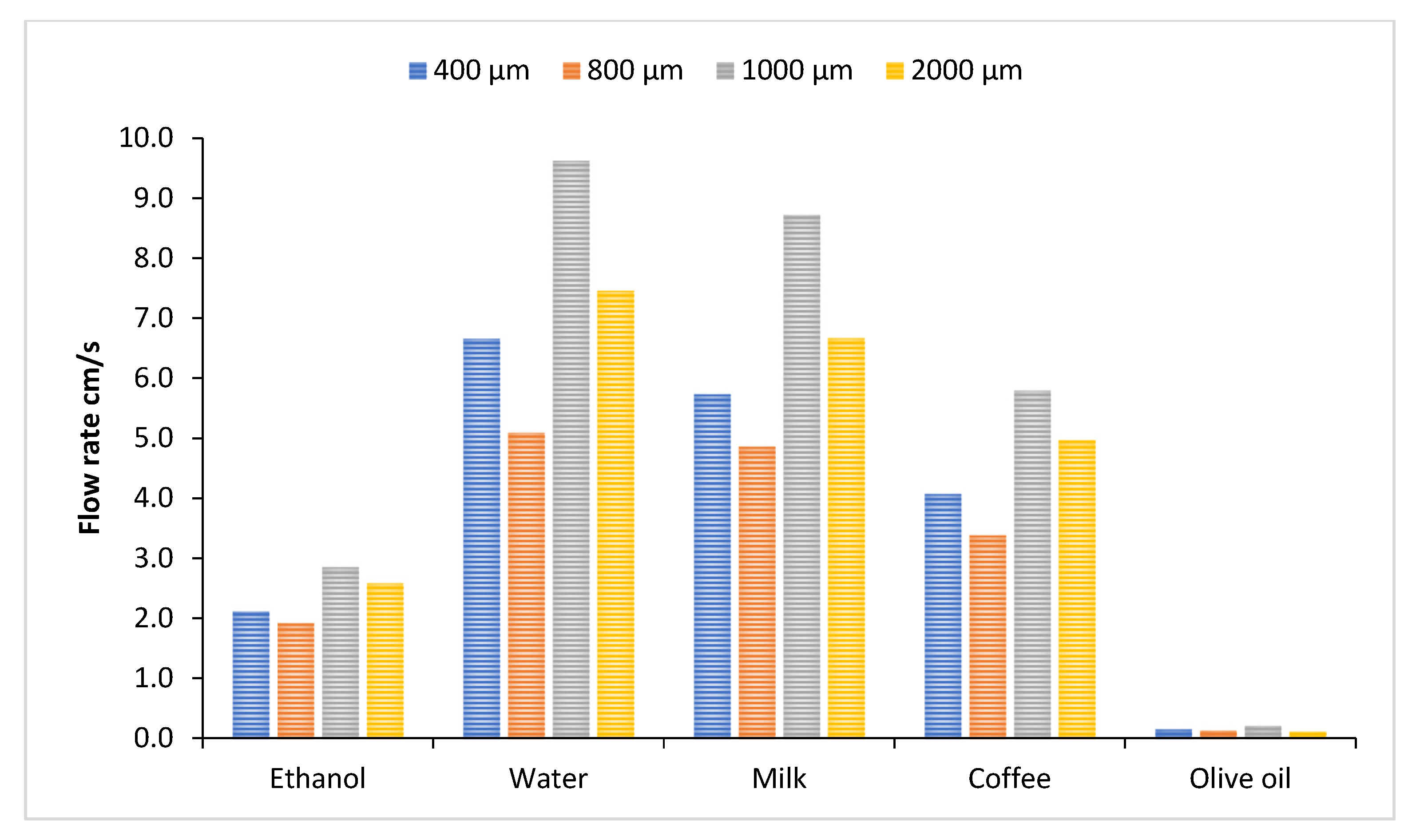
3.1. Flow Velocity of Various Liquids Along Four Sizes of Open Microchannels
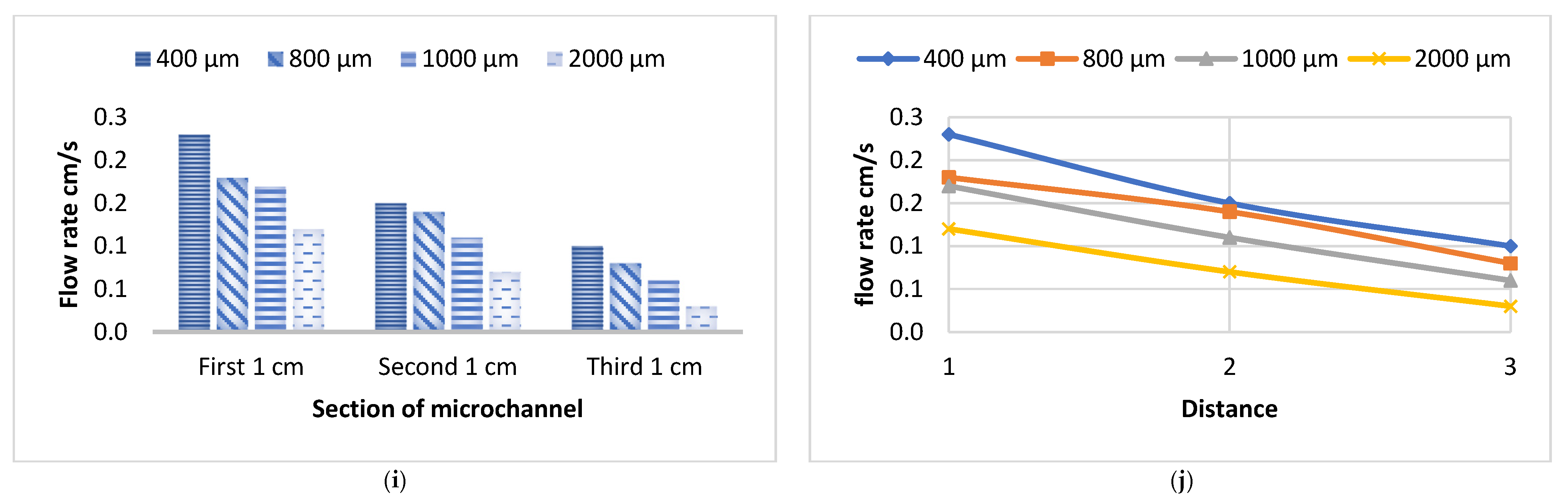
3.2. Flow Velocity of Various Liquids Along Four Sizes of Closed Microchannels
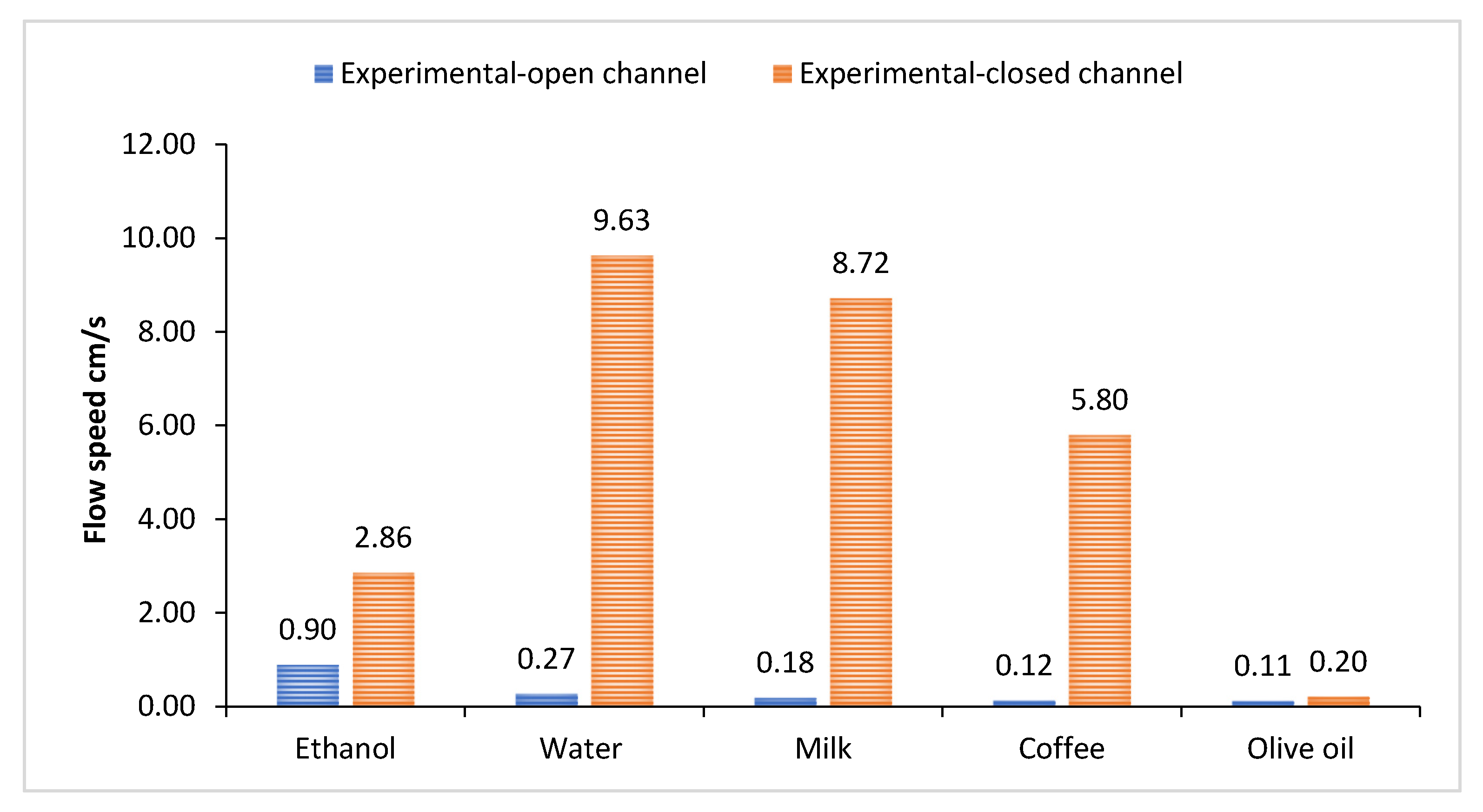
3.3. Theoretical and Experimental Comparisons
3.4. The Factors Affecting the Analysis of 3D Printer-Based Microchannels and Possible Applications
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3D | Three-dimensional |
| CAD | Computer-Aided Design |
| FDM | Fused deposition modeling |
| FPS | Frames per second |
| HMDS | Hexamethyldisilazane |
| MJM | MultiJet modeling |
| PDMS | Polydimethylsiloxane |
| PLA | Polylactic Acid |
| SLA | Stereolithography |
| SLS | Selective laser sintering |
References
- Nielsen, J.B.; Hanson, R.L.; Almughamsi, H.M.; Pang, C.; Fish, T.R.; Woolley, A.T. Microfluidics: Innovations in materials and their fabrication and functionalization. Anal. Chem. 2020, 92, 150–168. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, M. Refreshable microfluidic channels constructed using an inkjet printer. Sens. Actuators B Chem. 2007, 122, 141–147. [Google Scholar] [CrossRef]
- Maria, M.S.; Rakesh, P.E.; Chandra, T.S.; Sen, A.K. Capillary flow-driven microfluidic device with wettability gradient and sedimentation effects for blood plasma separation. Sci. Rep. 2017, 7, 43457. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yang, C.; Xiao, Y.; Yan, X.; Hu, L.; Eggersdorfer, M.; Chen, D.; Weitz, D.A.; Ye, F. Millifluidics, microfluidics, and nanofluidics: Manipulating fluids at varying length scales. Mater. Today Nano 2021, 16, 100136. [Google Scholar] [CrossRef]
- Bhattacharjee, N.; Urrios, A.; Kang, S.; Folch, A. The upcoming 3D-printing revolution in microfluidics. Lab Chip 2016, 16, 1720–1742. [Google Scholar] [CrossRef]
- Koo, D.; So, H. Facile microfabrication of three dimensional-patterned micromixers using additive manufacturing technology. Sci. Rep. 2022, 12, 6346. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Kim, B.J.; Sung, H.J. Two-fluid mixing in a microchannel. Int. J. Heat Fluid Flow 2004, 25, 986–995. [Google Scholar] [CrossRef]
- Schwesinger, N.; Frank, T.; Wurmus, H. A modular microfluid system with an integrated micromixer. J. Micromech. Microeng. 1996, 6, 99–102. [Google Scholar] [CrossRef]
- Di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef]
- Harrison, D.J.; Fluri, K.; Seiler, K.; Fan, Z.; Effenhauser, C.S.; Manz, A. Micromachining a miniaturized capillary electrophoresis-based chemical analysis system on a chip. Science 1993, 261, 895–897. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I.; Carbone, M.; Garofalo, G.; Lanza, L.G.; Piro, P. Influence of stratigraphy and slope on the drainage capacity of permeable pavements: Laboratory results. Urban Water J. 2015, 12, 394–403. [Google Scholar] [CrossRef]
- Piro, P.; Carbone, M. A modelling approach to assessing variations of total suspended solids (tss) mass fluxes during storm events. Hydrol. Process. 2014, 28, 2419–2426. [Google Scholar] [CrossRef]
- MacDonald, E.; Wicker, R. Multiprocess 3D printing for increasing component functionality. Science 2016, 353, aaf2093. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wu, Y.; Fu, J.Z.; Gao, Q.; Qiu, J.J. Developments of 3D Printing Microfluidics and Applications in Chemistry and Biology: A Review. Electroanalysis 2016, 28, 1658–1678. [Google Scholar] [CrossRef]
- Yang, X.; Tang, Q.; Lai, C.; Wu, K.; Shi, X. Applications and Prospects of Microfluidic Chips in Orthopaedic Diseases. Front. Mater. 2021, 7, 610558. [Google Scholar] [CrossRef]
- Fan, X.Y.; Deng, Z.F.; Yan, Y.Y.; Orel, V.E.; Shypko, A.; Orel, V.B.; Ivanova, D.; Pilarsky, C.; Tang, J.; Chen, Z.S.; et al. Application of microfluidic chips in anticancer drug screening. Bosn. J. Basic Med. Sci. 2022, 22, 302–314. [Google Scholar] [CrossRef]
- Illath, K.; Kar, S.; Gupta, P.; Shinde, A.; Wankhar, S.; Tseng, F.G.; Lim, K.T.; Nagai, M.; Santra, T.S. Microfluidic nanomaterials: From synthesis to biomedical applications. Biomaterials 2022, 280, 121247. [Google Scholar] [CrossRef]
- Kolliopoulos, P.; Jochem, K.S.; Johnson, D.; Suszynski, W.J.; Francis, L.F.; Kumar, S. Capillary-flow dynamics in open rectangular microchannels. J. Fluid Mech. 2021, 911, A32. [Google Scholar] [CrossRef]
- Kolliopoulos, P.; Kumar, S. Capillary flow of liquids in open microchannels: Overview and recent advances. npj Microgravity 2021, 7, 51. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Olanrewaju, A.; Beaugrand, M.; Yafia, M.; Juncker, D. Capillary microfluidics in microchannels: From microfluidic networks to capillaric circuits. Lab Chip 2018, 18, 2323–2347. [Google Scholar] [CrossRef] [PubMed]
- Gorthi, S.R.; Gaikwad, H.S.; Mondal, P.K.; Biswas, G. Surface Tension Driven Filling in a Soft Microchannel: Role of Streaming Potential. Ind. Eng. Chem. Res. 2020, 59, 3839–3853. [Google Scholar] [CrossRef]
- Bernetski, K.A.; An, H.T.; Maki, K.L.; Schertzer, M.J. Predicting actuated contact line pinning forces and the elimination of hysteresis under AC electrowetting. Microfluid. Nanofluidics 2022, 26, 94. [Google Scholar] [CrossRef]
- Keshmiri, K.; Huang, H.; Jemere, A.B.; Nazemifard, N. Investigation of Capillary Filling Dynamics of Multicomponent Fluids in Straight and Periodically Constricted Microchannels. Langmuir 2020, 36, 6304–6313. [Google Scholar] [CrossRef]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Yang, D.; Krasowska, M.; Priest, C.; Popescu, M.N.; Ralston, J. Dynamics of capillary-driven flow in open microchannels. J. Phys. Chem. C 2011, 115, 18761–18769. [Google Scholar] [CrossRef]
- Bao, J.; Nagayama, G. Optimization for ultrafast capillary-driven flow in open rectangular microchannels. Int. J. Heat Mass Transf. 2023, 201, 123629. [Google Scholar] [CrossRef]
- Lade, R.K.; Hippchen, E.J.; Macosko, C.W.; Francis, L.F. Dynamics of Capillary-Driven Flow in 3D Printed Open Microchannels. Langmuir 2017, 33, 2949–2964. [Google Scholar] [CrossRef]
- Truesdell, S.L.; Saunders, M.M. A low-cost 3D printed pumping system for generating oscillatory flow in a multicellular lab-on-a-chip device. Microfluid. Nanofluidics 2023, 27, 42. [Google Scholar] [CrossRef]
- ASTM D4212 Standard Test Method for Viscosity by Dip-Type Viscosity Cups. Available online: https://cdn.standards.iteh.ai/samples/115972/31778e8b1a4b497e8b2e5fa689129c34/ASTM-D4212-16-2023-.pdf (accessed on 2 February 2025).
- Hauner, I.M.; Deblais, A.; Beattie, J.K.; Kellay, H.; Bonn, D. The Dynamic Surface Tension of Water. J. Phys. Chem. Lett. 2017, 8, 1599–1603. [Google Scholar] [CrossRef]
- Tümer, E.H.; Erbil, H.Y.; Akdoǧan, N. Wetting of Superhydrophobic Polylactic Acid Micropillared Patterns. Langmuir 2022, 38, 10052–10064. [Google Scholar] [CrossRef] [PubMed]
- Ferner, R.E.; Chambers, J. Alcohol intake: Measure for measure. BMJ 2001, 323, 1439–1440. [Google Scholar] [CrossRef] [PubMed]
- Adamson, A.W.; Klerer, J. Physical Chemistry of Surfaces. J. Electrochem. Soc. 1977, 124, 192C. [Google Scholar] [CrossRef]
- Bertsch, A.J. Surface tension of whole and skim-milk between 18 and 135 C. J. Dairy Res. 1983, 50, 259–267. [Google Scholar] [CrossRef]
- Gmoser, R.; Bordes, R.; Nilsson, G.; Altskär, A.; Stading, M.; Lorén, N.; Berta, M. Effect of dispersed particles on instant coffee foam stability and rheological properties. Eur. Food Res. Technol. 2017, 243, 115–121. [Google Scholar] [CrossRef]
- Illy, E.; Navarini, L. Neglected Food Bubbles: The Espresso Coffee Foam. Food Biophys. 2011, 6, 335–348. [Google Scholar] [CrossRef]
- Calligaris, S.; Mirolo, G.; Da Pieve, S.; Arrighetti, G.; Nicoli, M.C. Effect of Oil Type on Formation, Structure and Thermal Properties of γ-oryzanol and β-sitosterol-Based Organogels. Food Biophys. 2014, 9, 69–75. [Google Scholar] [CrossRef]
- Pirouz, B.; Javadi Nejad, H.; Chirillo, A.S.; Naghib, S.N.; Piro, P. Enhancing the Design of Microdevices: The Role of Computational Fluid Dynamics and Experimental Investigation. Micromachines 2025, 16, 316. [Google Scholar] [CrossRef]
- Lucas, R. Ueber das Zeitgesetz des kapillaren Aufstiegs von Flüssigkeiten. Kolloid-Z. 1918, 23, 15–22. [Google Scholar] [CrossRef]
- Cai, J.; Jin, T.; Kou, J.; Zou, S.; Xiao, J.; Meng, Q. Lucas-Washburn Equation-Based Modeling of Capillary-Driven Flow in Porous Systems. Langmuir 2021, 37, 1623–1636. [Google Scholar] [CrossRef]
- Tokihiro, J.C.; McManamen, A.M.; Phan, D.N.; Thongpang, S.; Blake, T.D.; Theberge, A.B.; Berthier, J. On the Dynamic Contact Angle of Capillary-Driven Microflows in Open Channels. Langmuir 2024, 40, 7215–7224. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, N.P.; Cabot, J.M.; Smejkal, P.; Guijt, R.M.; Paull, B.; Breadmore, M.C. Comparing Microfluidic Performance of Three-Dimensional (3D) Printing Platforms. Anal. Chem. 2017, 89, 3858–3866. [Google Scholar] [CrossRef] [PubMed]
- Ratner, B.D. Surface modification of polymers: Chemical, biological and surface analytical challenges. Biosens. Bioelectron. 1995, 10, 797–804. [Google Scholar] [CrossRef] [PubMed]
- Burg, K.J.L.; Holder, W.D.; Culberson, C.R.; Beiler, R.J.; Greene, K.G.; Loebsack, A.B.; Roland, W.D.; Mooney, D.J.; Halberstadt, C.R. Parameters affecting cellular adhesion to polylactide films. J. Biomater. Sci. Polym. Ed. 1999, 10, 147–161. [Google Scholar] [CrossRef]
- Jiang, Y.; Islam, M.N.; He, R.; Huang, X.; Cao, P.F.; Advincula, R.C.; Dahotre, N.; Dong, P.; Wu, H.F.; Choi, W. Recent Advances in 3D Printed Sensors: Materials, Design, and Manufacturing. Adv. Mater. Technol. 2023, 8, 2200492. [Google Scholar] [CrossRef]
- Jakupi, K.; Dukovski, V.; Hodolli, G. Surface Roughness Modeling of Material Extrusion PLA Flat Surfaces. Int. J. Polym. Sci. 2023, 2023, 844626. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Sánchez-Casas, X.; Luis-Pérez, C.J. Analysis of am parameters on surface roughness obtained in pla parts printed with fff technology. Polymers 2021, 13, 2384. [Google Scholar] [CrossRef]
- Alsoufi, M.S.; Elsayed, A.E. How Surface Roughness Performance of Printed Parts Manufactured by Desktop FDM 3D Printer with PLA+ is Influenced by Measuring Direction. Am. J. Mech. Eng. 2017, 5, 211–222. [Google Scholar] [CrossRef]
- Fountas, N.A.; Kitsakis, K.; Aslani, K.E.; Kechagias, J.D.; Vaxevanidis, N.M. An experimental investigation of surface roughness in 3D-printed PLA items using design of experiments. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 1979–1984. [Google Scholar] [CrossRef]
- Silvestri, L.; Saraceni, M.; Bongioannini Cerlini, P. Quality management system and design of an integrated mesoscale meteorological network in Central Italy. Meteorol. Appl. 2022, 29, e2060. [Google Scholar] [CrossRef]
- Ambrosia, M.S.; Ha, M.Y. A molecular dynamics study of Wenzel state water droplets on anisotropic surfaces. Comput. Fluids 2018, 163, 1–6. [Google Scholar]
- Ouali, F.F.; McHale, G.; Javed, H.; Trabi, C.; Shirtcliffe, N.J.; Newton, M.I. Wetting considerations in capillary rise and imbibition in closed square tubes and open rectangular cross-section channels. Microfluid. Nanofluidics 2013, 15, 309–326. [Google Scholar] [CrossRef]
- Liu, H.; Lan, L.; Abrigo, J.; Ip, H.L.; Soo, Y.; Zheng, D.; Wong, K.S.; Wang, D.; Shi, L.; Leung, T.W.; et al. Comparison of Newtonian and Non-newtonian Fluid Models in Blood Flow Simulation in Patients With Intracranial Arterial Stenosis. Front. Physiol. 2021, 12, 718540. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Pan, T.W.; Glowinski, R. Three-dimensional numerical simulation of red blood cell motion in Poiseuille flows. Int. J. Numer. Methods Fluids 2014, 76, 397–415. [Google Scholar] [CrossRef]
- Goetting-Minesky, M.P.; Mullin, B.C. Differential gene expression in an actinorhizal symbiosis: Evidence for a nodule-specific cysteine proteinase. Proc. Natl. Acad. Sci. USA 1994, 91, 9891–9895. [Google Scholar] [CrossRef]
- Tabeling, P. Introduction to Microfluidics; Oxford University Press: Oxford, UK, 2023; ISBN 9780192845306. [Google Scholar]
- Grolsman, A.; Stelnberg, V. Elastic turbulence in a polymer solution flow. Nature 2000, 405, 53–55. [Google Scholar] [CrossRef]
- Boi, S.; Mazzino, A.; Pralits, J.O. Minimal model for zero-inertia instabilities in shear-dominated non-Newtonian flows. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2013, 88, 033007. [Google Scholar] [CrossRef]








| Material | Viscosity (mPa.s) | Surface Tension [mNm−1] | Density [g/mL] | Refs. |
|---|---|---|---|---|
| Distilled water | 1 | 72 | 1 | [31,32] |
| Ethanol | 1.3 | 22.5 | 0.8 | [33,34] |
| Milk | 2 | 46.4 | 1.1 | [35] |
| Espresso coffee | 6 | 46–50 | 1 | [36,37] |
| Olive oil | 78 | 32 | 0.92 | [38] |
| Type of Microchannel | Material | (1) Experimental Velocity | (2) Theoretical Velocity (Dynamic Contact Angle) | (3) Theoretical Velocity (Static Contact Angle) | Relative Error | ||
|---|---|---|---|---|---|---|---|
| (cm/s) | (cm/s) | (cm/s) | 2 vs. 1 | 3 vs. 1 | 3 vs. 2 | ||
| Open | Ethanol | 0.9 | 35.2 | 44.4 | 38.3 | 48.6 | 0.3 |
| Water | 0.3 | 47.5 | 140.5 | 174.9 | 519.5 | 2.0 | |
| Milk | 0.2 | 15.3 | 48.6 | 82.7 | 263.9 | 2.2 | |
| Coffee | 0.1 | 7.0 | 13.1 | 55.7 | 105.6 | 0.9 | |
| Olive oil | 0.1 | 0.7 | 1.0 | 5.5 | 7.7 | 0.3 | |
| Closed | Ethanol | 2.9 | 4.0 | 44.4 | 0.4 | 14.6 | 10.1 |
| Water | 9.6 | 16.0 | 117.9 | 0.7 | 11.2 | 6.4 | |
| Milk | 8.7 | 10.3 | 41.9 | 0.2 | 3.8 | 3.1 | |
| Coffee | 5.8 | 6.0 | 11.7 | 0.0 | 1.0 | 1.0 | |
| Olive oil | 0.2 | 0.5 | 0.9 | 1.6 | 3.6 | 0.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirouz, B.; Naghib, S.N.; Chirillo, D.; Javadi Nejad, H.; Piro, P. Experimental Investigations of Capillary Flow in Three-Dimensional-Printed Microchannels. Fluids 2025, 10, 91. https://doi.org/10.3390/fluids10040091
Pirouz B, Naghib SN, Chirillo D, Javadi Nejad H, Piro P. Experimental Investigations of Capillary Flow in Three-Dimensional-Printed Microchannels. Fluids. 2025; 10(4):91. https://doi.org/10.3390/fluids10040091
Chicago/Turabian StylePirouz, Behrouz, Seyed Navid Naghib, Diamante Chirillo, Hana Javadi Nejad, and Patrizia Piro. 2025. "Experimental Investigations of Capillary Flow in Three-Dimensional-Printed Microchannels" Fluids 10, no. 4: 91. https://doi.org/10.3390/fluids10040091
APA StylePirouz, B., Naghib, S. N., Chirillo, D., Javadi Nejad, H., & Piro, P. (2025). Experimental Investigations of Capillary Flow in Three-Dimensional-Printed Microchannels. Fluids, 10(4), 91. https://doi.org/10.3390/fluids10040091









