A Review of Oscillators in Hydrokinetic Energy Harnessing Through Vortex-Induced Vibrations
Abstract
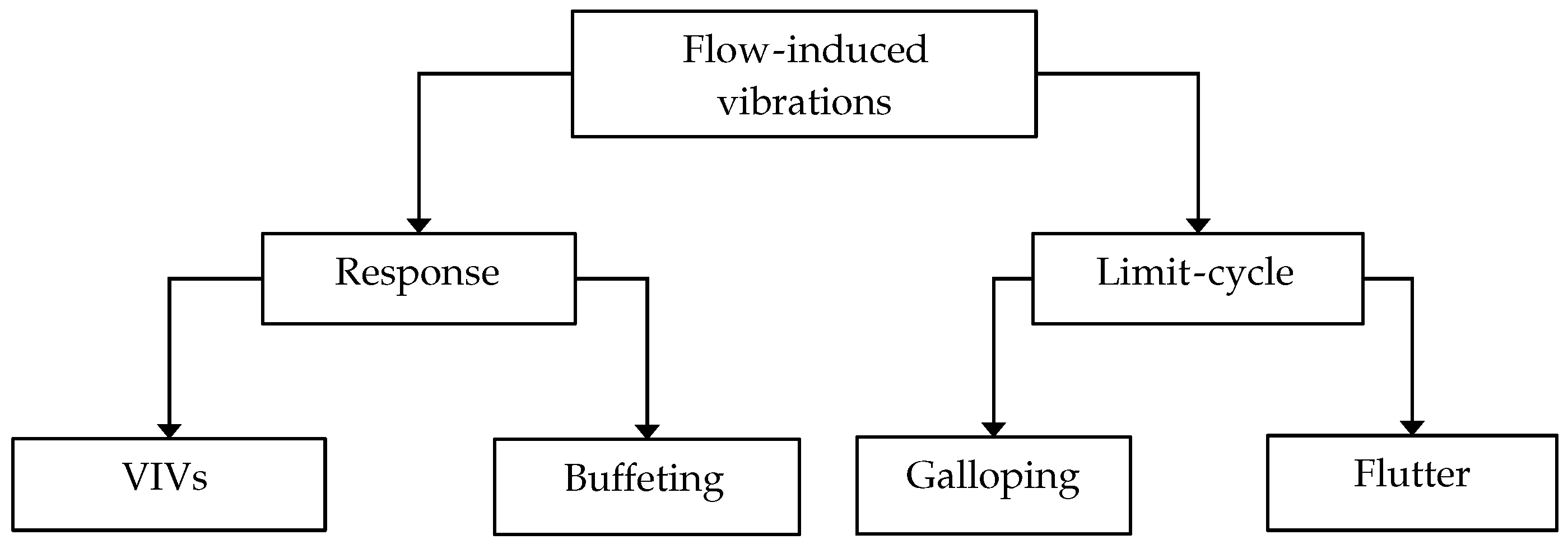
1. Introduction
2. Working Principles
3. Applications of VIV
3.1. Proposed Applications
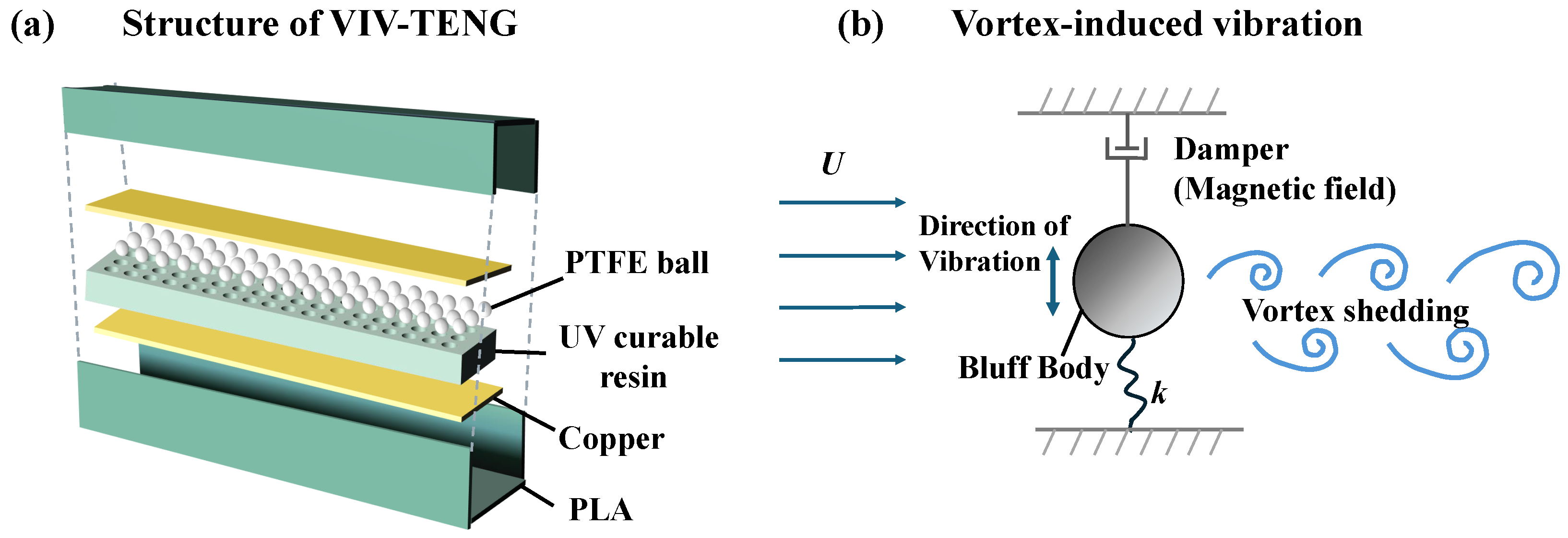
3.1.1. Vortex-Induced Vibration Triboelectric Nanogenerator (VIV-TENG)
3.1.2. Ocean Wave-Induced Vortex-Induced Vibration Piezoelectric Energy Harvester (Wave-VIVPEH)
3.2. Commercialised Applications
3.2.1. Vortex-Induced Vibration Aquatic Clean Energy (VIVACE)
3.2.2. Other Demonstration Projects
4. Design Optimisation
4.1. Bluff Body Design
4.1.1. Shape and Geometry
4.1.2. Surface Roughness
4.1.3. Splitter Plates
4.1.4. Grooves
4.1.5. Mass
4.2. Bluff Body Arrangements
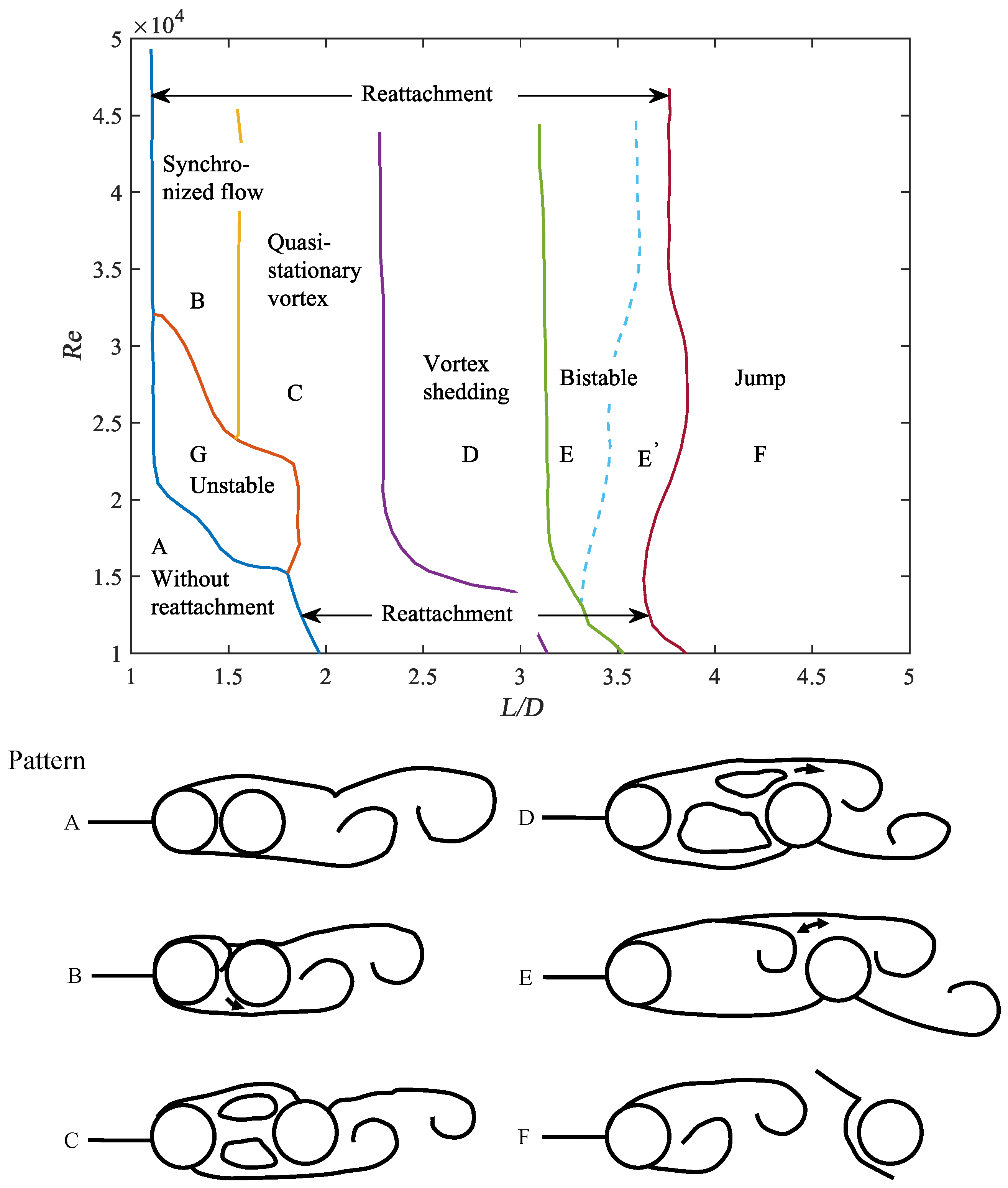
4.2.1. Tandem Configuration
4.2.2. Side-by-Side Configuration
4.2.3. Staggered Configuration
4.3. Virtual Spring Damper Systems
4.4. Nonlinear System Improvements
4.4.1. Nonlinear Damping Systems
4.4.2. Bio-Inspired Adaptive Damping
4.4.3. Variable Stiffness
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FIV | Flow-Induced Vibration |
| VIV | Vorte-Induced Vibration |
| USD | United States Dollar |
| CFD | Computational Fluid Dynamics |
| EM | Electromagnetic |
| PE | Piezoelectric |
| TE | Triboelectric |
| VIV-TENG | Vortex-Induced Vibration Triboelectric Nanogenerator |
| Wave-VIVPEH | Wave Vortex-Induced Vibration Piezoelectric Energy Harvester |
| OWC | Oscillating Water Column |
| VIVACE | Vortex-Induced Vibration Aquatic Clean Energy |
| PTFE | Polytetrafluoroethylene |
| MR | Magnetorheologica |
| NES | Nonlinear Energy Sink |
| CPFD | Cyber-Physical Fluid Dynamics |
| 1-DOF | One Degree Of Freedom |
| WEC | Wave Energy Converter |
| DRL | Deep Reinforcement Learning |
| PTC | Passive Turbulence Control |
| PTFE | Polytetrafluoroethylene |
| RMS | Root Mean Square |
| IL | Inline |
| CF | Crossflow |
| Nomenclature | |
| Angle of incidence | |
| Average roughness height | |
| Damping ratio | |
| c | Damping coefficient |
| Added mass coefficient | |
| Drag coefficient | |
| D | Diameter of cylinder |
| G | Gap width |
| k | Stiffness coefficient |
| L | Streamwise distance |
| m | Oscillating structure’s mass |
| Mass ratio | |
| Displaced fluid mass | |
| P | Centre-to-centre pitch |
| Renolds number | |
| Strouhal number | |
| T | Cross-stream distance |
References
- Armandei, M.; Fernandes, A.C.; Rostami, A.B. Hydroelastic buffeting assessment over a vertically hinged flat plate. Exp. Tech. 2016, 40, 833–839. [Google Scholar] [CrossRef]
- Bearman, P.W. Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Williamson, C.H.; Roshko, A. Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 1988, 2, 355–381. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibration; Krieger Publishing Company: Malabar, FL, USA, 1977. [Google Scholar]
- Wang, J.s.; Fan, D.; Lin, K. A review on flow-induced vibration of offshore circular cylinders. J. Hydrodyn. 2020, 32, 415–440. [Google Scholar] [CrossRef]
- Majumdar, A.; Adhikary, B.R. Mitigation of Vortex-Induced Vibration in Offshore Structures. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, SPE, Muscat, Oman, 22–24 April 2024; p. SPE-218591-MS. [Google Scholar]
- Falnes, J.; Kurniawan, A. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2020; Volume 8. [Google Scholar]
- Chhaparwal, G.; Dayal, R. Vortex-induced vibrations for energy harvesting: A review. In Emerging Trends in Energy Conversion and Thermo-Fluid Systems: Select Proceedings of iCONECTS 2021; Springer: Singapore, 2022; pp. 275–284. [Google Scholar]
- Razaviyn, Z.; Heidari, M.; Thangavel, S.; Verma, V.; Kumar, A.; Yadav, A.K. Marine energy harvesting from fluid flow via vortex induced vibrations. Int. J. Thermofluids 2025, 25, 101015. [Google Scholar] [CrossRef]
- Schmider, A.; Kerhervé, F.; Spohn, A.; Cordier, L. Improved VIV energy harvesting with a virtual damper–spring system. Ocean Eng. 2024, 293, 116668. [Google Scholar] [CrossRef]
- Rehman, U.U.; Munir, A.; Khan, N.B.; Zhao, M.; Kashif, M.; Islam, M.S.; Saeed, Z.; Ali, M.A. Numerical investigation of vortex-induced vibrations (VIV) of a rotating cylinder in in-line and cross-flow directions subjected to oscillatory flow. Ocean Eng. 2024, 304, 117917. [Google Scholar] [CrossRef]
- Constantinides, Y.; Oakley, O.H., Jr. Numerical prediction of VIV and comparison with field experiments. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; Volume 48227, pp. 577–583. [Google Scholar]
- Wang, E.; Xiao, Q.; Incecik, A. CFD simulation of vortex-induced vibration of a vertical riser. In Proceedings of the 9th International Workshop on Ship & Marine Hydrodynamics, Glasgow, UK, 26–28 August 2015. [Google Scholar]
- Feng, Y.; Li, S.; Chen, D.; Xiao, Q. Predictions for combined In-Line and Cross-Flow VIV responses with a novel model for estimation of tension. Ocean Eng. 2019, 191, 106531. [Google Scholar] [CrossRef]
- Ge, F.; Long, X.; Wang, L.; Hong, Y. Flow-induced vibrations of long circular cylinders modeled by coupled nonlinear oscillators. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 1086–1093. [Google Scholar] [CrossRef]
- Gu, J.j.; An, C.; Levi, C.; Su, J. Prediction of vortex-induced vibration of long flexible cylinders modeled by a coupled nonlinear oscillator: Integral transform solution. J. Hydrodyn. 2012, 24, 888–898. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, J.; Zhao, H.; Gao, Y. Experimental study on the vortex-induced vibration of a catenary flexible riser under sheared flows. Int. J. Offshore Polar Eng. 2021, 31, 283–292. [Google Scholar] [CrossRef]
- Edwards, P. Mass-Spring-Damper Systems: The Theory; Bournemouth University: Poole, UK, 2001. [Google Scholar]
- Wang, D.A.; Chiu, C.Y.; Pham, H.T. Electromagnetic energy harvesting from vibrations induced by Kármán vortex street. Mechatronics 2012, 22, 746–756. [Google Scholar] [CrossRef]
- Mehmood, A.; Abdelkefi, A.; Hajj, M.; Nayfeh, A.; Akhtar, I.; Nuhait, A. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder. J. Sound Vib. 2013, 332, 4656–4667. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Li, Z.; Guo, H.; Gong, Y.; Zhang, D.; Zhang, D.; Zhang, Q.; Wang, B.; Peng, Y. Vortex-induced vibration triboelectric nanogenerator for energy harvesting from low-frequency water flow. Energy Convers. Manag. 2023, 292, 117383. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Raghavan, K.; Ben-Simon, Y.; Garcia, E. VIVACE (vortex induced vibration aquatic clean energy): A new concept in generation of clean and renewable energy from fluid flow. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 4–9 June 2006; Volume 47470, pp. 619–637. [Google Scholar]
- Sun, H.; Kim, E.S.; Nowakowski, G.; Mauer, E.; Bernitsas, M.M. Effect of mass-ratio, damping, and stiffness on optimal hydrokinetic energy conversion of a single, rough cylinder in flow induced motions. Renew. Energy 2016, 99, 936–959. [Google Scholar] [CrossRef]
- Sun, H.; Ma, C.; Kim, E.S.; Nowakowski, G.; Mauer, E.; Bernitsas, M.M. Hydrokinetic energy conversion by two rough tandem-cylinders in flow induced motions: Effect of spacing and stiffness. Renew. Energy 2017, 107, 61–80. [Google Scholar] [CrossRef]
- Erturk, A.; Vieira, W.G.R.; De Marqui, C.; Inman, D.J. On the energy harvesting potential of piezoaeroelastic systems. Appl. Phys. Lett. 2010, 96, 184103. [Google Scholar] [CrossRef]
- Liu, W.; Badel, A.; Formosa, F.; Zhu, Q.; Zhao, C.; Hu, G.D. A comprehensive analysis and modeling of the self-powered synchronous switching harvesting circuit with electronic breakers. IEEE Trans. Ind. Electron. 2017, 65, 3899–3909. [Google Scholar] [CrossRef]
- Liu, W.; Yuan, Z.; Zhang, S.; Zhu, Q. Enhanced broadband generator of dual buckled beams with simultaneous translational and torsional coupling. Appl. Energy 2019, 251, 113412. [Google Scholar] [CrossRef]
- Wang, Z.L. Triboelectric nanogenerators as new energy technology for self-powered systems and as active mechanical and chemical sensors. ACS Nano 2013, 7, 9533–9557. [Google Scholar] [CrossRef]
- Wang, Z.L.; Chen, J.; Lin, L. Progress in triboelectric nanogenerators as a new energy technology and self-powered sensors. Energy Environ. Sci. 2015, 8, 2250–2282. [Google Scholar] [CrossRef]
- Paul, S.; Chang, J. Design of novel electromagnetic energy harvester to power a deicing robot and monitoring sensors for transmission lines. Energy Convers. Manag. 2019, 197, 111868. [Google Scholar] [CrossRef]
- Sripadmanabhan Indira, S.; Aravind Vaithilingam, C.; Oruganti, K.S.P.; Mohd, F.; Rahman, S. Nanogenerators as a sustainable power source: State of art, applications, and challenges. Nanomaterials 2019, 9, 773. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L. From contact electrification to triboelectric nanogenerators. Rep. Prog. Phys. 2021, 84, 096502. [Google Scholar] [CrossRef]
- Shao, Z.; Zhou, T.; Zhu, H.; Zang, Z.; Zhao, W. Amplitude enhancement of flow-induced vibration for energy harnessing. In Proceedings of the 6th International Conference on Renewable Energy Technologies (ICRET 2020), Perth, Australia, 8–10 January 2020; Volume 160, p. 01005. [Google Scholar]
- Wang, Y.; Chen, T.; Sun, S.; Liu, X.; Hu, Z.; Lian, Z.; Liu, L.; Shi, Q.; Wang, H.; Mi, J.; et al. A humidity resistant and high performance triboelectric nanogenerator enabled by vortex-induced vibration for scavenging wind energy. Nano Res. 2022, 15, 3246–3253. [Google Scholar] [CrossRef]
- Du, X.; Wang, Y.; Chen, H.; Li, C.; Han, Y.; Yurchenko, D.; Wang, J.; Yu, H. Vortex-induced piezoelectric cantilever beam vibration for ocean wave energy harvesting via airflow from the orifice of oscillation water column chamber. Nano Energy 2022, 104, 107870. [Google Scholar] [CrossRef]
- Park, H. Mapping of Passive Turbulence Control to Flow Induced Motions of Circular Cylinders. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2012. [Google Scholar]
- Lee, J.; Xiros, N.; Bernitsas, M. Virtual damper–spring system for VIV experiments and hydrokinetic energy conversion. Ocean Eng. 2011, 38, 732–747. [Google Scholar] [CrossRef]
- Sun, H.; Soo Kim, E.; Bernitsas, M.P.; Bernitsas, M.M. Virtual spring–damping system for flow-induced motion experiments. J. Offshore Mech. Arct. Eng. 2015, 137, 061801. [Google Scholar] [CrossRef]
- Sun, W.; Jo, S.; Seok, J. Development of the optimal bluff body for wind energy harvesting using the synergetic effect of coupled vortex induced vibration and galloping phenomena. Int. J. Mech. Sci. 2019, 156, 435–445. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Gu, S.; Yang, K.; Li, H.; Lai, Y.; Yurchenko, D. Enhancement of low-speed piezoelectric wind energy harvesting by bluff body shapes: Spindle-like and butterfly-like cross-sections. Aerosp. Sci. Technol. 2020, 103, 105898. [Google Scholar] [CrossRef]
- Zhu, H.; Yao, J. Numerical evaluation of passive control of VIV by small control rods. Appl. Ocean Res. 2015, 51, 93–116. [Google Scholar]
- Zhu, H.; Yao, J.; Ma, Y.; Zhao, H.; Tang, Y. Simultaneous CFD evaluation of VIV suppression using smaller control cylinders. J. Fluids Struct. 2015, 57, 66–80. [Google Scholar]
- Ding, L.; Zhang, L.; Wu, C.; Mao, X.; Jiang, D. Flow induced motion and energy harvesting of bluff bodies with different cross sections. Energy Convers. Manag. 2015, 91, 416–426. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W.; Li, B. Numerical investigation on VIV energy harvesting of bluff bodies with different cross sections in tandem arrangement. Energy 2017, 133, 723–736. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Fallahi, R. Effects of cylinder cross-sectional geometry and blockage ratio on VIV-based mixing performance in two dimensional laminar channel flow. Chem. Eng. Process.-Process Intensif. 2022, 177, 108987. [Google Scholar]
- Wang, Q.; Li, M.; Xu, S. Experimental study on vortex induced vibration (VIV) of a wide-D-section cylinder in a cross flow. Theor. Appl. Mech. Lett. 2015, 5, 39–44. [Google Scholar]
- Achenbach, E. Influence of surface roughness on the cross-flow around a circular cylinder. J. Fluid Mech. 1971, 46, 321–335. [Google Scholar]
- Nakamura, Y.; Tomonari, Y. The effects of surface roughness on the flow past circular cylinders at high Reynolds numbers. J. Fluid Mech. 1982, 123, 363–378. [Google Scholar]
- Bearman, P.W.; Harvey, J. Control of circular cylinder flow by the use of dimples. AIAA J. 1993, 31, 1753–1756. [Google Scholar]
- Okajima, A.; Nagamori, T.; Matsunaga, F.E.; Kiwata, T. Some experiments on flow-induced vibration of a circular cylinder with surface roughness. J. Fluids Struct. 1999, 13, 853–864. [Google Scholar]
- Adrian, R.J. Hairpin vortex organization in wall turbulence. Phys. Fluids 2007, 19, 041301. [Google Scholar]
- ASME B46.1-2019; Surface Texture: Surface Roughness, Waviness and Lay. American Society of Mechanical Engineers: New York, NY, USA, 2003.
- Choi, K.S.; Fujisawa, N. Possibility of drag reduction using d-type roughness. Appl. Sci. Res. 1993, 50, 315–324. [Google Scholar] [CrossRef]
- Assi, G.R.; Bearman, P.W.; Kitney, N. Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 2009, 25, 666–675. [Google Scholar]
- Galvao, R.; Lee, E.; Farrell, D.; Hover, F.; Triantafyllou, M.; Kitney, N.; Beynet, P. Flow control in flow–structure interaction. J. Fluids Struct. 2008, 24, 1216–1226. [Google Scholar]
- Allen, D.W.; Lee, L.; Henning, D. Fairings vs. Helical Strakes for Suppression of Vortex-Induced Vibration: Technical Comparisons. In Proceedings of the Offshore Technology Conference, OTC, Houston, TX, USA, 5–8 May 2008; p. OTC-19373-MS. [Google Scholar]
- Law, Y.Z.; Jaiman, R.K. Wake stabilization mechanism of low-drag suppression devices for vortex-induced vibration. J. Fluids Struct. 2017, 70, 428–449. [Google Scholar] [CrossRef]
- Roshko, A. On the wake and drag of bluff bodies. J. Aeronaut. Sci. 1955, 22, 124–132. [Google Scholar] [CrossRef]
- Apelt, C.; West, G.; Szewczyk, A.A. The effects of wake splitter plates on the flow past a circular cylinder in the range 104 < R < 5× 104. J. Fluid Mech. 1973, 61, 187–198. [Google Scholar]
- Kwon, K.; Choi, H. Control of laminar vortex shedding behind a circular cylinder using splitter plates. Phys. Fluids 1996, 8, 479–486. [Google Scholar] [CrossRef]
- Anderson, E.; Szewczyk, A. Effects of a splitter plate on the near wake of a circular cylinder in 2 and 3-dimensional flow configurations. Exp. Fluids 1997, 23, 161–174. [Google Scholar]
- Hwang, J.Y.; Yang, K.S.; Sun, S.H. Reduction of flow-induced forces on a circular cylinder using a detached splitter plate. Phys. Fluids 2003, 15, 2433–2436. [Google Scholar]
- Hwang, J.Y.; Yang, K.S. Drag reduction on a circular cylinder using dual detached splitter plates. J. Wind Eng. Ind. Aerodyn. 2007, 95, 551–564. [Google Scholar] [CrossRef]
- Dehkordi, B.G.; Jafari, H.H. On the Suppression of Vortex Shedding From Circular Cylinders Using Detached Short Splitter-Plates. J. Fluids Eng.-Trans. Asme 2010, 132, 044501. [Google Scholar] [CrossRef]
- Cimbala, J.; Chen, K. Supercritical Reynolds number experiments on a freely rotatable cylinder/splitter plate body. Phys. Fluids 1994, 6, 2440–2445. [Google Scholar] [CrossRef]
- Cimbala, J.M.; Leon, J. Drag of freely rotatable cylinder/splitter-plate body at subcritical Reynolds number. AIAA J. 1996, 34, 2446–2448. [Google Scholar] [CrossRef]
- Cimbala, J.M.; Garg, S. Flow in the wake of a freely rotatable cylinder with splitter plate. AIAA J. 1991, 29, 1001–1003. [Google Scholar] [CrossRef]
- Huang, S. VIV suppression of a two-degree-of-freedom circular cylinder and drag reduction of a fixed circular cylinder by the use of helical grooves. J. Fluids Struct. 2011, 27, 1124–1133. [Google Scholar] [CrossRef]
- Zhou, Y.; Yiu, M. Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 2006, 548, 17–48. [Google Scholar] [CrossRef]
- Canpolat, C.; Sahin, B. Influence of single rectangular groove on the flow past a circular cylinder. Int. J. Heat Fluid Flow 2017, 64, 79–88. [Google Scholar] [CrossRef]
- Zhao, G.; Xu, J.; Duan, K.; Zhang, M.; Zhu, H.; Wang, J. Numerical analysis of hydroenergy harvesting from vortex-induced vibrations of a cylinder with groove structures. Ocean Eng. 2020, 218, 108219. [Google Scholar] [CrossRef]
- Wang, W.; Song, B.; Mao, Z.; Tian, W.; Zhang, T. Numerical investigation on VIV suppression of marine riser with triangle groove strips attached on its surface. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 875–882. [Google Scholar] [CrossRef]
- Mittal, S.; Kumar, V. Finite element study of vortex-induced cross-flow and in-line oscillations of a circular cylinder at low Reynolds numbers. Int. J. Numer. Methods Fluids 1999, 31, 1087–1120. [Google Scholar] [CrossRef]
- Sen, S.; Mittal, S. Effect of mass ratio on free vibrations of a square cylinder at low Reynolds numbers. J. Fluids Struct. 2015, 54, 661–678. [Google Scholar]
- Williamson, C.H.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Jauvtis, N.; Williamson, C. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 2004, 509, 23–62. [Google Scholar]
- Sun, L.; Wang, C.; Li, J.; Zhao, B.; Yanfang, L. Design and Analysis of Multi-Column Vortex Induced Vibration Power Generator Device. In Proceedings of the 2019 IEEE 2nd International Conference on Renewable Energy and Power Engineering (REPE), Toronto, ON, Canada, 2–4 November 2019; pp. 202–207. [Google Scholar]
- Zdravkovich, M. The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Gu, Z.; Sun, T. On interference between two circular cylinders in staggered arrangement at high subcritical Reynolds numbers. J. Wind Eng. Ind. Aerodyn. 1999, 80, 287–309. [Google Scholar]
- Zdravkovich, M.; Pridden, D. Interference between two circular cylinders; series of unexpected discontinuities. J. Wind Eng. Ind. Aerodyn. 1977, 2, 255–270. [Google Scholar]
- Igarashi, T. Characteristics of the flow around two circular cylinders arranged in tandem: 1st report. Bull. JSME 1981, 24, 323–331. [Google Scholar]
- Igarashi, T. Characteristics of the flow around two circular cylinders arranged in tandem: 2nd report, unique phenomenon at small spacing. Bull. JSME 1984, 27, 2380–2387. [Google Scholar] [CrossRef]
- Williamson, C. Evolution of a single wake behind a pair of bluff bodies. J. Fluid Mech. 1985, 159, 1–18. [Google Scholar]
- Kumada, M. Wake interference between three cylinders arranged side-by-side normal to a flow. Trans. JSME 1984, 50, 1699–1707. [Google Scholar]
- Sumner, D.; Price, S.; Paidoussis, M. Flow-pattern identification for two staggered circular cylinders in cross-flow. J. Fluid Mech. 2000, 411, 263–303. [Google Scholar] [CrossRef]
- Sumner, D. Two circular cylinders in cross-flow: A review. J. Fluids Struct. 2010, 26, 849–899. [Google Scholar]
- Alam, M.M.; Zhou, Y. Strouhal numbers, forces and flow structures around two tandem cylinders of different diameters. J. Fluids Struct. 2008, 24, 505–526. [Google Scholar]
- Liu, C.H.; Chen, J.M. Observations of hysteresis in flow around two square cylinders in a tandem arrangement. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1019–1050. [Google Scholar] [CrossRef]
- Lee, T.; Basu, S. Nonintrusive measurements of the boundary layer developing on a single and two circular cylinders. Exp. Fluids 1997, 23, 187–192. [Google Scholar]
- Xu, G.; Zhou, Y. Strouhal numbers in the wake of two inline cylinders. Exp. Fluids 2004, 37, 248–256. [Google Scholar] [CrossRef]
- Ljungkrona, L.; Norberg, C.; Sundén, B. Free-stream turbulence and tube spacing effects on surface pressure fluctuations for two tubes in an in-line arrangement. J. Fluids Struct. 1991, 5, 701–727. [Google Scholar] [CrossRef]
- Zdravkovich, M. Flow induced oscillations of two interfering circular cylinders. J. Sound Vib. 1985, 101, 511–521. [Google Scholar]
- Meneghini, J.R.; Saltara, F.; Siqueira, C.d.L.R.; Ferrari, J., Jr. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 2001, 15, 327–350. [Google Scholar]
- Lin, J.C.; Yang, Y.; Rockwell, D. Flow past two cylinders in tandem: Instantaneous and averaged flow structure. J. Fluids Struct. 2002, 16, 1059–1071. [Google Scholar] [CrossRef]
- Ishigai, S.; Nishikawa, E.; Nishimura, K.; Cho, K. Experimental study on structure of gas flow in tube banks with tube axes normal to flow: Part 1, Karman vortex flow from two tubes at various spacings. Bull. JSME 1972, 15, 949–956. [Google Scholar] [CrossRef]
- Alam, M.M.; Zhou, Y. Phase lag between vortex shedding from two tandem bluff bodies. J. Fluids Struct. 2007, 23, 339–347. [Google Scholar] [CrossRef]
- Biermann, D.; Herrnstein, W. The Interference Between Struts in Various Combinations; NACA R-468; NACA: Boston, MA, USA, 1933. [Google Scholar]
- Ishigai, S. Structures of Gas flow and vibration in tube banks with tube axes normal to flow. Proc. Int. Sym. Mar. Eng. 1973. Available online: https://cir.nii.ac.jp/crid/1571980076393320960#citations_container (accessed on 13 January 2025).
- Okajima, A. Flows around two tandem circular cylinders at very high Reynolds numbers. Bull. JSME 1979, 22, 504–511. [Google Scholar] [CrossRef]
- Tatsuno, M.; Taneda, S. Visual studies of wake structure behind two cylinders in tandem arrangement. Rep. Res. Inst. Appl. Mech. 1985, 32, 1–20. [Google Scholar]
- Jendrzejczyk, J.; Chen, S. Fluid Forces on Two Circular Cylinders in Crossflow; Technical report; Argonne National Lab. (ANL): Argonne, IL, USA, 1985. [Google Scholar]
- Wu, J.; Welch, L.; Welsh, M.; Sheridan, J.; Walker, G. Spanwise wake structures of a circular cylinder and two circular cylinders in tandem. Exp. Therm. Fluid Sci. 1994, 9, 299–308. [Google Scholar] [CrossRef]
- Zhao, M. Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150. Phys. Fluids 2013, 25, 123601. [Google Scholar] [CrossRef]
- Chen, W.; Ji, C.; Williams, J.; Xu, D.; Yang, L.; Cui, Y. Vortex-induced vibrations of three tandem cylinders in laminar cross-flow: Vibration response and galloping mechanism. J. Fluids Struct. 2018, 78, 215–238. [Google Scholar] [CrossRef]
- Yu, K.R.; Étienne, S.; Scolan, Y.M.; Hay, A.; Fontaine, E.; Pelletier, D. Flow-induced vibrations of in-line cylinder arrangements at low Reynolds numbers. J. Fluids Struct. 2016, 60, 37–61. [Google Scholar] [CrossRef]
- Dey, P. A Novel Arrangement of Multiple Cylinders of Different Structural Conditions Dictating Wind Energy Harvesting at Very Low Reynolds Number. J. Vib. Eng. Technol. 2024, 12, 151–170. [Google Scholar] [CrossRef]
- Zdravkovich, M.M.; Bearman, P.W. Flow Around Circular Cylinders—Volume 1: Fundamentals. J. Fluids Eng. 1998, 120, 216. [Google Scholar] [CrossRef]
- Bearman, P. The effect of base bleed on the flow behind a two-dimensional model with a blunt trailing edge. Aeronaut. Q. 1967, 18, 207–224. [Google Scholar] [CrossRef]
- Wood, C. Visualization of an incompressible wake with base bleed. J. Fluid Mech. 1967, 29, 259–272. [Google Scholar] [CrossRef]
- Sumner, D.; Wong, S.; Price, S.; Paidoussis, M. Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J. Fluids Struct. 1999, 13, 309–338. [Google Scholar] [CrossRef]
- Zhiwen, W.; Zhou, Y.; Li, H. Flow-visualization of a two side-by-side cylinder wake. J. Flow Vis. Image Process. 2002, 9, 123–138. [Google Scholar]
- Alam, M.M.; Zhou, Y. Flow around two side-by-side closely spaced circular cylinders. J. Fluids Struct. 2007, 23, 799–805. [Google Scholar] [CrossRef]
- Alam, M.M.; Moriya, M.; Sakamoto, H. Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. J. Fluids Struct. 2003, 18, 325–346. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, Y.; So, R. Reynolds number effects on the flow structure behind two side-by-side cylinders. Phys. Fluids 2003, 15, 1214–1219. [Google Scholar] [CrossRef]
- Zhou, C.; So, R.; Lam, K. Vortex-induced vibrations of an elastic circular cylinder. J. Fluids Struct. 1999, 13, 165–189. [Google Scholar] [CrossRef]
- Kim, H.; Durbin, P. Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation. Phys. Fluids 1988, 31, 3260–3265. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 1999, 13, 813–851. [Google Scholar] [CrossRef]
- Kim, H.J.; Durbin, P. Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 1988, 196, 431–448. [Google Scholar]
- Le Gal, P.; Chauve, M.; Lima, R.; Rezende, J. Coupled wakes behind two circular cylinders. Phys. Rev. A 1990, 41, 4566. [Google Scholar]
- Peschard, I.; Le Gal, P. Coupled wakes of cylinders. Phys. Rev. Lett. 1996, 77, 3122. [Google Scholar]
- Brun, C.; Tenchine, D.; Hopfinger, E.J. Role of the shear layer instability in the near wake behavior of two side-by-side circular cylinders. Exp. Fluids 2004, 36, 334–343. [Google Scholar]
- Kamemoto, K. Formation and interaction of two parallel vortex streets. Bull. JSME 1976, 19, 283–290. [Google Scholar]
- Spivack, H.M. Vortex frequency and flow pattern in the wake of two parallel cylinders at varied spacing normal to an air stream. J. Aeronaut. Sci. 1946, 13, 289–301. [Google Scholar] [CrossRef]
- Sun, T.; Gu, Z.; He, D.; Zhang, L. Fluctuating pressure on two circular cylinders at high Reynolds numbers. J. Wind Eng. Ind. Aerodyn. 1992, 41, 577–588. [Google Scholar]
- Zhou, Y.; So, R.; Liu, M.; Zhang, H. Complex turbulent wakes generated by two and three side-by-side cylinders. Int. J. Heat Fluid Flow 2000, 21, 125–133. [Google Scholar]
- Eastop, T. Air flow around three cylinders at various pitch-to-diameter ratio for both a longitudinal and transverse arrangement. Trans. Inst. Chem. Eng. 1982, 60, 359–363. [Google Scholar]
- Xu, X.; Ji, C.; Zhang, L.; Chen, W. Flow-induced vibrations of three side-by-side cylinders in laminar flow: Vibration response and near-wake patterns. Chin. J. Comput. Mech. 2018, 35, 643–649. [Google Scholar]
- Mittal, S.; Kumar, V. Flow-induced oscillations of two cylinders in tandem and staggered arrangements. J. Fluids Struct. 2001, 15, 717–736. [Google Scholar] [CrossRef]
- Bearman, P. Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 2011, 27, 648–658. [Google Scholar] [CrossRef]
- Alam, M.M.; Sakamoto, H. Investigation of Strouhal frequencies of two staggered bluff bodies and detection of multistable flow by wavelets. J. Fluids Struct. 2005, 20, 425–449. [Google Scholar]
- Sumner, D.; Richards, M. Some vortex-shedding characteristics of the staggered configuration of circular cylinders. J. Fluids Struct. 2003, 17, 345–350. [Google Scholar]
- Zhou, Y.; Feng, S.; Alam, M.M.; Bai, H. Reynolds number effect on the wake of two staggered cylinders. Phys. Fluids 2009, 21, 125105. [Google Scholar] [CrossRef]
- Wang, R.; He, Y.; Chen, L.; Zhu, Y.; Wei, Y. Numerical simulations of flow around three cylinders using momentum exchange-based immersed boundary-lattice Boltzmann method. Ocean Eng. 2022, 247, 110706. [Google Scholar] [CrossRef]
- Behara, S.; Ravikanth, B.; Chandra, V. Vortex-induced vibrations of three staggered circular cylinders at low Reynolds numbers. Phys. Fluids 2017, 29, 083606. [Google Scholar] [CrossRef]
- Ding, L.; He, H.; Song, T. Vortex-induced vibration and heat dissipation of multiple cylinders under opposed thermal buoyancy. Ocean Eng. 2023, 270, 113669. [Google Scholar]
- Ma, Y.; Xu, W.; Liu, B. Dynamic response of three long flexible cylinders subjected to flow-induced vibration (FIV) in an equilateral-triangular configuration. Ocean Eng. 2019, 183, 187–207. [Google Scholar] [CrossRef]
- Zhu, H.; Zhong, J.; Shao, Z.; Zhou, T.; Alam, M.M. Fluid-structure interaction among three tandem circular cylinders oscillating transversely at a low Reynolds number of 150. J. Fluids Struct. 2024, 130, 104204. [Google Scholar] [CrossRef]
- Feng, C. The Measurement of Vortex Induced Effects in Flow Past Stationary and Oscillating Circular and D-Section Cylinders. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1968. [Google Scholar]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Klamo, J.; Leonard, A.; Roshko, A. On the maximum amplitude for a freely vibrating cylinder in cross-flow. J. Fluids Struct. 2005, 21, 429–434. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C. Defining the ‘modified Griffin plot’ in vortex-induced vibration: Revealing the effect of Reynolds number using controlled damping. J. Fluid Mech. 2006, 561, 147–180. [Google Scholar] [CrossRef]
- Hover, F.; Miller, S.; Triantafyllou, M. Vortex-induced vibration of marine cables: Experiments using force feedback. J. Fluids Struct. 1997, 11, 307–326. [Google Scholar] [CrossRef]
- Mackowski, A.W.; Williamson, C.H. Developing a cyber-physical fluid dynamics facility for fluid–structure interaction studies. J. Fluids Struct. 2011, 27, 748–757. [Google Scholar] [CrossRef]
- Mackowski, A.; Williamson, C. An experimental investigation of vortex-induced vibration with nonlinear restoring forces. Phys. Fluids 2013, 25, 087101. [Google Scholar] [CrossRef]
- Wang, E.; Xu, W.; Gao, X.; Liu, L.; Xiao, Q.; Ramesh, K. The effect of cubic stiffness nonlinearity on the vortex-induced vibration of a circular cylinder at low Reynolds numbers. Ocean Eng. 2019, 173, 12–27. [Google Scholar] [CrossRef]
- Ye, M.; Zhang, C.; Ren, Y.; Liu, Z.; Haidn, O.J.; Hu, X. Adaptive optimization of wave energy conversion in oscillatory wave surge converters via SPH simulation and deep reinforcement learning. arXiv 2024, arXiv:2410.08871. [Google Scholar]
- Duan, J.; Zhou, J.; You, Y.; Wang, X. Time-domain analysis of vortex-induced vibration of a flexible mining riser transporting flow with various velocities and densities. Ocean Eng. 2021, 220, 108427. [Google Scholar]
- Hao, Z.; Sun, C.; Lu, Y.; Bi, K.; Zhou, T. Suppression of Vortex-Induced Vibration and Phase-Averaged Analysis of the Wake Generated by a Circular Cylinder Covered with Helical Grooves. Fluids 2022, 7, 194. [Google Scholar] [CrossRef]
- Lee, L.; Allen, D. Vibration frequency and lock-in bandwidth of tensioned, flexible cylinders experiencing vortex shedding. J. Fluids Struct. 2010, 26, 602–610. [Google Scholar]
- Hosotani, K.; Ishii, T.; Hirano, M. Vibration Characteristics of an Elastically Supported Single Circular Cylinder under Steady and Pulsating Flow Condition. Adv. Exp. Mech. 2016, 1, 9–14. [Google Scholar]
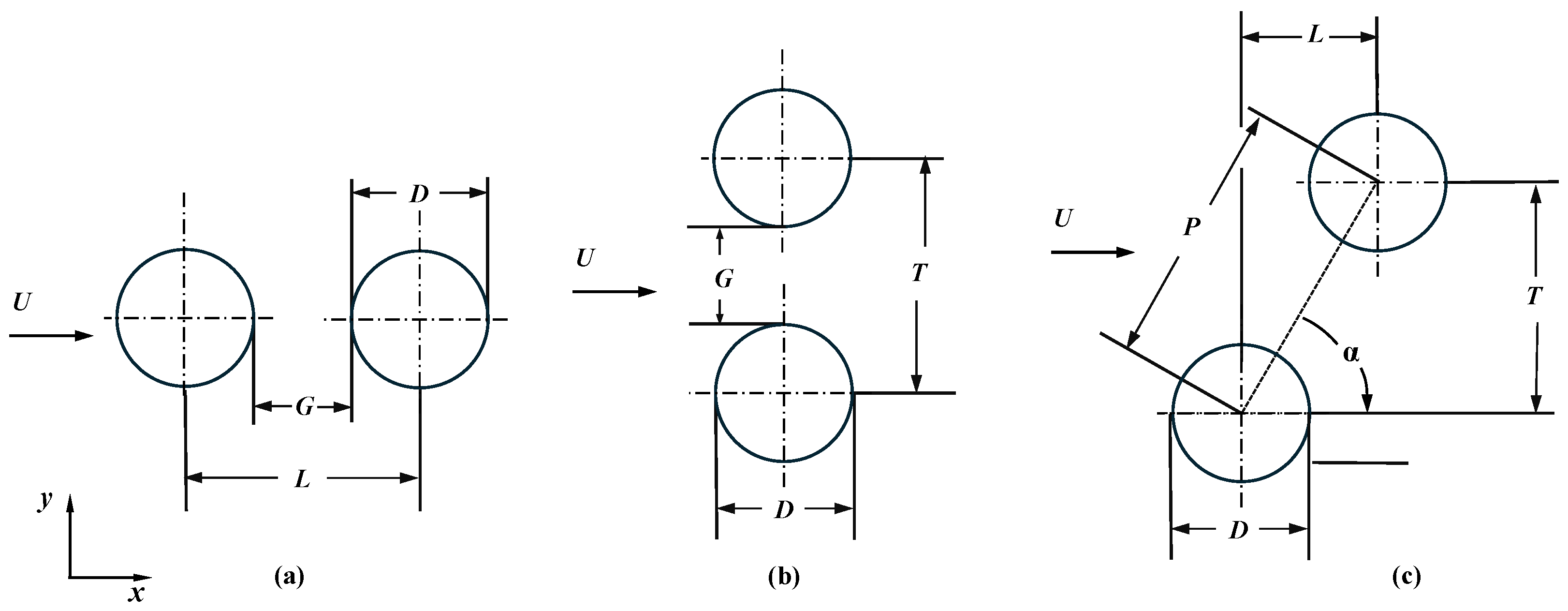
| Type | Power Output (mW) | Efficiency (%) | Frequency Range (Hz) | Real-World Application | References |
|---|---|---|---|---|---|
| EM | 100–500 | 15–30 | 1–10 | VIV-based energy harvester for ocean currents (e.g., VIVACE) | [22,23,24] |
| PE | 5–50 | 10–20 | 5–50 | Wind energy harvester using galloping vibrations | [25,26,27] |
| TE | 1–10 | 5–15 | 0.1–5 | Low-frequency water flow energy harvester (e.g., VIV-TENG) | [21,28,29] |
| Researchers | Contributions | ||
|---|---|---|---|
| Two cylinders in tandem | |||
| Igarashi [81] | – | 1–5 | Flow patterns with unsteady flow |
| Lin et al. [94] | 1.15–5.1 | Instantaneous and averaged flow structures | |
| Biermann and Herrnstein [97] | – | 1–9 | Interference effects in various combinations |
| Ishigai et al. [98] | – | 1–5 | Kármán vortex structure of two tubes in tube banks |
| Okajima [99] | – | 1.1–6.3 | Flow characteristics at high Reynolds numbers |
| Tatsuno et al. [100] | 100, 300, | 1.5–10 | Wake structure behind two tandem cylinders |
| Jendrzejcyk and Chen [101] | – | 1.4–10 | Measured fluid dynamics characteristics |
| Wu et al. [102] | , – | 3–7 | Cylinder spacing affects spanwise coherence |
| Zhao et al. [103] | 150 | 1.5–6 | Lock-in regime variation with spacing ratio |
| Three cylinders in tandem | |||
| Chen et al. [104] | 100 | 1.2–5 | Mechanism of VIV of three tandem cylinders |
| Yu et al. [105] | 100, 150 | 4 | Dynamic response of 3 cylinders differs from that of 2 cylinders |
| Prasenjit Dey [106] | 100 | 3, 6, 9 | Energy harvesting with multiple cylinders |
| Researchers | Contributions | ||
|---|---|---|---|
| Two side-by-side cylinders | |||
| Williamson [3] | 50–150, 200 | 1.2–6 | Evolution of single wake |
| Ishigai et al. [95] | – | 1.25–3 | Impact of tube spacing on Kármán vortex street |
| Sumner et al. [110] | 500– | 1–6 | Fluid behavior in steady flow |
| Alam and Zhou [112] | 1.1–1.2 | Flow structure changes of closely spaced cylinders | |
| Alam et al. [113] | 350, | 1.1–3.4 | Aerodynamic characteristics and vortex shedding phenomenon |
| Xu et al. [114] | 150– 300– | 1.2–1.6 | Reynolds number effects on flow structure |
| Kim and Durbin [118] | 1–3 | Flopping regime between two cylinders | |
| Le Gal et al. [119] | 110 | 1–7.5 | Flopping regime between two cylinders |
| Peschard and Le Gal [120] | 90–150 | 1–6 | Coupled wakes behind two side-by-side cylinders |
| Brun et al. [121] | – | 1.583 | Role of shear layer instability in near wake |
| Kamemoto [122] | 662 | 1.5–3 | Formation and interaction of two parallel vortex streets |
| Spivack [123] | – | 1–6 | Vortex frequency and flow pattern in wake |
| Sun et al. [124] | , | 2.2 | Fluctuating pressure at high Reynolds numbers |
| Zhou et al. [125] | 1.5–3 | Generation of complex turbulent wakes | |
| More than two cylinders | |||
| Kumada et al. [84] | – | 1–3.75 | Fluctuating pressure at high Reynolds numbers |
| Eastop and Turner [126] | – | 1.2–2.6 | Fluctuating pressure at high Reynolds numbers |
| Xu et al. [127] | 100 | 2-5 | Six near-wake patterns are observed |
| Researchers | Geometry | |
|---|---|---|
| Two staggered cylinders | ||
| Gu and Sun [79] | , – | P/D = 1.5–2, = 0–45°, P/D = 1.1–3.5, = 0–90° |
| Sumner et al. [85] | 850– | P/D = 1–5, = 0–90°, P/D = 1–4, = 0–90° |
| Alam et al. [130] | , 350 | P/D = 1.1–6, = 10–75° |
| Sumner and Richards [131] | – | P/D = 2–2.5, = 0–90° |
| Zhou et al. [132] | – | P/D = 1.2–4, = 0–90° |
| Three staggered cylinders | ||
| Wang et al. [133] | 10–200 | P/D = 0.1–8, = 45° |
| Behara et al. [134] | 60–160 | L/D = 5, T/D = 3 |
| Ding et al. [135] | 100 | P/D = 2, = 60° |
| Ma et al. [136] | – | P/D = 6, = 0–60° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, D.; He, J.; Zeng, H.; Zhu, Y.; Chan, S.Z.; Williams, M.R.; Khor, I.Z.L.; Yalla, O.V.; Sunny, M.R.; Ghoshal, R.; et al. A Review of Oscillators in Hydrokinetic Energy Harnessing Through Vortex-Induced Vibrations. Fluids 2025, 10, 78. https://doi.org/10.3390/fluids10040078
Cao D, He J, Zeng H, Zhu Y, Chan SZ, Williams MR, Khor IZL, Yalla OV, Sunny MR, Ghoshal R, et al. A Review of Oscillators in Hydrokinetic Energy Harnessing Through Vortex-Induced Vibrations. Fluids. 2025; 10(4):78. https://doi.org/10.3390/fluids10040078
Chicago/Turabian StyleCao, Deping, Jie He, Hanqi Zeng, Yijia Zhu, Sean Zixuan Chan, Mark Ravinpal Williams, Ivan Zhi Liang Khor, Omkar Venkata Yalla, Mohammed R. Sunny, Ritwik Ghoshal, and et al. 2025. "A Review of Oscillators in Hydrokinetic Energy Harnessing Through Vortex-Induced Vibrations" Fluids 10, no. 4: 78. https://doi.org/10.3390/fluids10040078
APA StyleCao, D., He, J., Zeng, H., Zhu, Y., Chan, S. Z., Williams, M. R., Khor, I. Z. L., Yalla, O. V., Sunny, M. R., Ghoshal, R., Bhattacharyya, A., Chowdhury, S. D., Lin, Z., Chin, C. S., & Chen, H. (2025). A Review of Oscillators in Hydrokinetic Energy Harnessing Through Vortex-Induced Vibrations. Fluids, 10(4), 78. https://doi.org/10.3390/fluids10040078









