Particle Tracking Velocimetry Measurements and Simulations of Internal Flow with Induced Swirl

Abstract

The downstream decay of induced swirling flow within an internal passage has implications for heat transfer enhancement, species mixing, and combustion processes. For this paper, swirling flow in an internal passage was investigated using both experimental and computational techniques. Two staggered rows of 8 vanes each with an NACA 0015 profile, intended to turn the near-wall flow 45° to the flow direction, were installed on the top and bottom surfaces of the Roughness Internal Flow Tunnel (RIFT) wind tunnel. The vanes induced opposite lateral components in—the flow near the upper and lower surfaces of the rectangular test section of the RIFT and induced a swirling flow pattern within the passage. A 4-camera tomographic particle tracking velocimetry (PTV) system was used to evaluate airflow within a 40 mm × 40 mm × 60 mm measurement volume at the tunnel midline 0.5 m downstream of the induced swirl. Mean flow velocity measurements were collected at hydraulic diameter-based Reynolds numbers of 10,000, 20,000, and 30,000. To validate PTV measurements, particularly the camera-plane normal component of velocity, traces across the measurement volume were taken using a five-hole probe. The results of both measurement methods were compared to a computational simulation of the entire RIFT test section using a shear stress transport (SST) k-ω, Improved Delayed Detached Eddy Simulation (IDDES) turbulence model. The combined particle tracking measurements and five-hole probe measurements provide a method of investigating the turbulent flow model and simulation results, which are needed for future simulations of flows found inside swirl-inducing combustor nozzles.

1. Introduction

Introducing swirl to internal flow has a wide range of engineering applications related to its ability to enhance heat transfer or chemical reactions between a fluid and the walls of the conduit, mix or separate fluid streams, and stabilize combustion processes. This investigation specifically examines swirl within a rectangular channel—a configuration with similarities to the non-circular cross-sections found in many gas turbine combustors.

Swirl-stabilized combustion is the most common approach in gas turbines for flame stabilization due to the swirling flow-induced central and corner recirculation zones that stabilize flow with proper fuel air mixing and continuous ignition [1,2,3]. Flame stabilization is critical for flame holding, static flame stability, flame extinction, flashback, thermo-acoustic instability, and turn-down ratio in all types of gas turbine combustion systems [2,4,5]. The degree of swirl achieved by adjusting the swirl flow velocity is also critical to forming proper local reactant mixture and thus achieving complete combustion with low emissions. The spiral motion of swirling flow is associated with axial and azimuthal velocity components, substantial shear stress, and highly turbulent flow layers [1,6]. Therefore, reconstructing the three-dimensional flow field of swirling flow, especially its defining lateral velocity component w, is significant for the investigation of the flame stability mechanism in a gas turbine combustor.

Once flow is directed to swirl within a channel, the rate of swirl will decay downstream unless a conduit is regularly lined with vanes, deflectors, or some other mechanism to maintain that motion. This makes downstream decay a key characteristic of swirling flow. For instance, in a swirl-stabilized combustor, the decay will directly affect the downstream fuel–air mixing and flame stability. By collecting measurements some distance downstream of the swirl causing vanes, a comparison between the experimental and computational results will reflect the model’s ability to accurately capture decay behavior.

Measuring flows, like those in swirl-stabilized combustion flames, presents experimental challenges. In stereoscopic PIV systems, measurements are made while seed particles remain inside a thin laser sheet. For swirling flows, which have a significant velocity component perpendicular to the laser sheet, the time during which particles pass through the sheet and may be measured is shortened. Image pairs must be captured more quickly to fit within the required window, and the necessary faster inter-image timing may not be optimal for observing seed particle motion. Measurements are less accurate if correlated displacement is reduced near the limits of camera resolution. Three-component laser Doppler systems are often used for three-dimensional flows, but just as with five-hole probes and other point-flow measurement devices, significant time is required to traverse the measurement system through the flow domain. Particle tracking approaches present an advantage in this regard: because the laser sheet is spread into an illumination volume, longer separation times may be employed. Additionally, larger and instantaneously characterized measurement volumes result in better temporal and spatially averaged flow quantities.

Swirling line vortices are also challenging for Computational Fluid Dynamics (CFD). For example, two-equation Reynolds-Averaged Navier–Stokes (RANS) models, which are standard in many industrial applications, typically use a linear eddy viscosity constitutive relation to calculate the Reynolds stresses. This constrains the Reynolds stresses to being aligned with the mean rate of strain, which is incorrect in a line vortex [7] and predicts an unphysically rapid vortex decay. Seven-equation RANS models, with an equation for each of the six Reynolds stress components and an additional equation for the Turbulent Dissipation Rate (TDR), are capable, at least in principle, of resolving line vortices. Line vortices also extend far from solid surfaces into the bulk flow where computational cell sizes typically become large, so that the vortex core is almost certain to be under-resolved in most computations, especially if the path of the vortex is not known in advance.

In the present flow, the difficulty is compounded further because many vortices interact with each other and with a nearby shear-dominated wall boundary layer. This complicated interaction, and the rich turbulent physics that result, motivate the use of a time-resolved, scale-resolving turbulence model. Detached Eddy Simulation (DES), whereby a grid-filtered Large Eddy Simulation (LES) turbulence model away from the solid surfaces is blended with a near-wall RANS model, is a practical choice for computations of engineering-scale flows in situations where turnaround time is an important consideration. In this effort, a swirling internal flow in the RIFT is simulated using the SST k-$\mathsf{\omega }$ Improved Delayed Detached Eddy Simulation (IDDES) turbulence model. Two steady RANS computations, one with a two-equation model and one with a seven-equation model, are also presented for comparison.

The purpose of this effort was to investigate the IDDES turbulence model’s ability to predict the behavior of swirling flow within a rectangular channel. While combustors are not typically rectangular, flows with significant lateral components may be used as representative of swirl-combustor flows. Experimental data was gathered using two approaches—particle tracking velocimetry (PTV) and a five-hole probe. The PTV system provided a volume of detailed mean velocity measurements to compare with the computational model some distance downstream from the induced swirl. The five-hole probe provided a check on the spanwise velocity components measured using the PTV system.

Early investigations of a decaying swirl focused on quantifying the downstream rate of decay and predicting it based on known flow parameters. Experimental studies of swirl decay rates represent a large body of work and include velocity measurements taken with pitot probes [8,9,10,11,12], hot film/wire probes [13,14,15,16], and LDV (laser Doppler velocimetry) [17], using both air and water as the fluid. The types of swirls considered in investigations of swirl decay rates were grouped into three categories—concentrated vortices, solid body, and wall jets—by Steenbergen and Voskamp [18]. They generally quantify flow rotation using a parameter such as the swirl number along a series of points downstream from where a swirl is introduced. The breadth of swirl decay studies stems from an attempt to predict swirl decay rates in a wide range of situations based on parameters such as Reynolds number, friction factor, and the angle at which fluid flow is directed to induce a swirl.

Flow conditions observed in this study most closely resemble solid body rotation, with fluid rotation largely uniform across the span of the channel. However, the rectangular cross-section of the RIFT with a 6.31 aspect ratio represents a significant difference from previously mentioned works, which almost exclusively studied flow in circular pipes. Studies of swirling flow within rectangular channels include Kazuyoshi et al. [19], Tang et al. [20], and Vashahi et al. [1]. Other notable investigations of swirling flow with unique geometry include Kitoh [21], who explored eccentric rotation occurring when axi-asymmetric flow is created within circular pipes, and Sobota and Marble [22], who examined swirling flow with the transition from circular to rectangular conduit.

Confined swirling flows are a natural application of DES. Widenhorn et al. [23,24] calculated the non-reacting flow-field in a swirl stabilized combustor using two DES models and saw good agreement with PIV measurements. Similarly, Mansouri et al. [25] used a Delayed-Detached Eddy Simulation model to predict annular swirling jet flow in a non-premixed swirl burner, also seeing close agreement in the time-averaged flow-field with PIV measurements. Paik and Sotiropoulos [26] used a Spalart–Allmaras DES model to simulate swirling flow through a cylindrical pipe with a sudden expansion. Chen et al. [27] used the SST k-$\mathsf{\omega }$ IDDES model to simulate a high-pressure swirling water jet used to break rocks in oil-drilling applications.

2. Materials and Methods

A channel flow tunnel, volumetric PTV system, and 5-hole probe were used as experimental apparatuses in this study. Additionally, flow through the wind tunnel was simulated using a turbulence model. These methods were selected to use results of the two experimental approaches in both the evaluation of flow with decaying swirl and assessing the validity of the model, which is not constrained to the measurement volume and provides a more comprehensive look at flow within the channel. Testing within the wind tunnel was conducted at $R{e}_{Dh}$ = 10,000, 20,000, and 30,000. Only conditions at $R{e}_{Dh}$ = 30,000 were simulated.

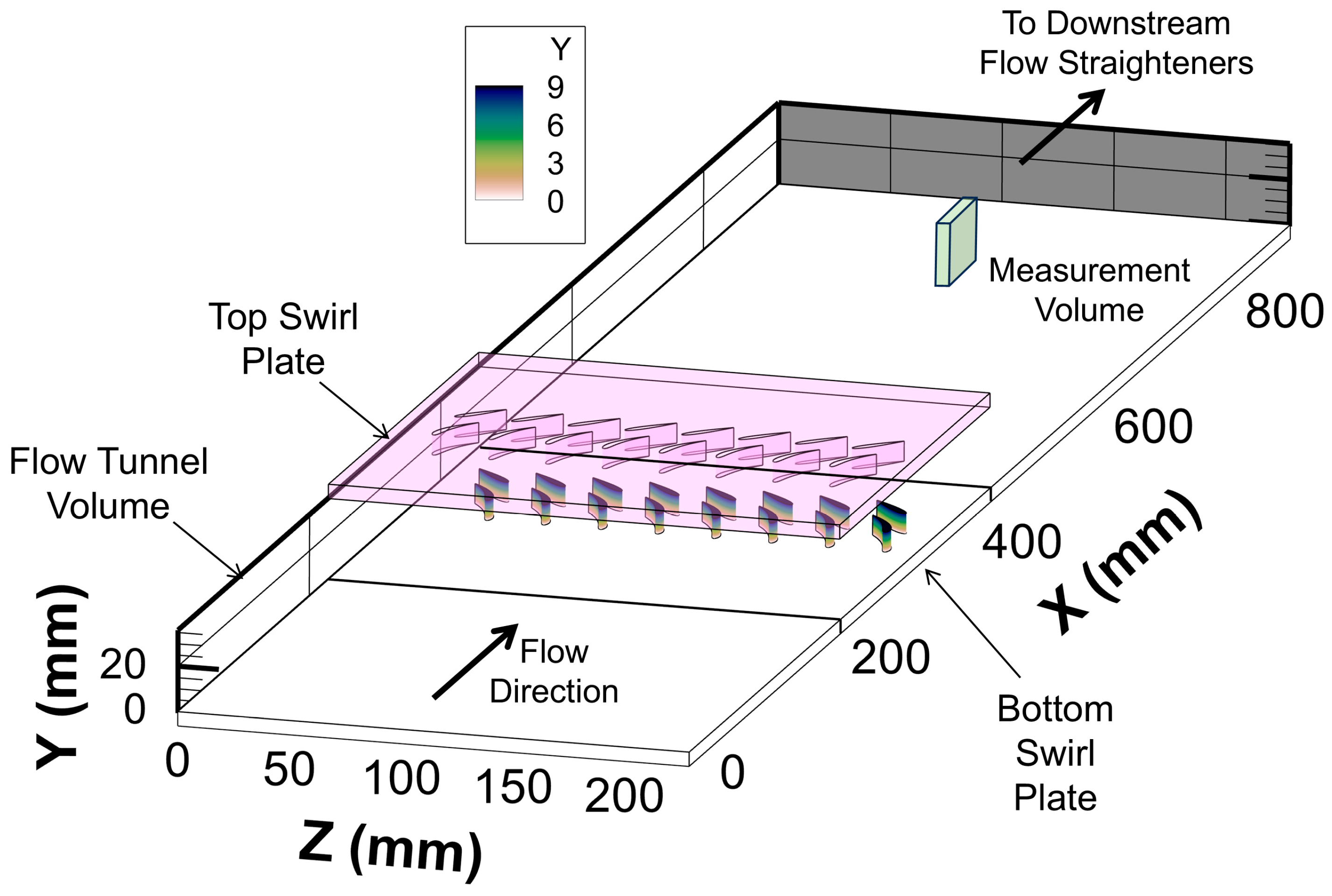
2.1. Roughness Internal Flow Tunnel (RIFT)

The Roughness Internal Flow Tunnel (RIFT) has been previously used in studies of flow over large additively manufactured roughness in the works of McClain et al. [28], Stafford et al. [29], and Boldt et al. [30,31]. In these studies, the RIFT was used to obtain experimental measurements of friction factors, heat transfer coefficients, and mean velocity profiles. Within its test section, the RIFT has dimensions of 228.6 mm by 35.56 mm, creating an aspect ratio of 6.3:1 and a hydraulic diameter of 62.3 mm. The total length of the test section is 914.4 mm and this distance is divided equally among four removable panels that make up the upper and lower walls of the RIFT. A centrifugal fan provides airflow through the RIFT; the fan can produce steady flow conditions up to $R{e}_{Dh}$ = 68,000. A fixed pitot probe, used for instrument calibration, is mounted inside the RIFT downstream of the test section and positioned in the center of the channel. The RIFT has flow straighteners at the inlet contraction and in the first settling chamber upstream of the test section. The second set of flow straighteners is approximately 500 mm upstream of the start of the RIFT test section.

The volumetric flow rate of air through the RIFT is measured using the pressure difference across the initial tunnel contraction—essentially treating the contraction as a venturi nozzle, as shown in Equation (1).

$$\begin{array}{c}Q=C_0{A}_{ts}\sqrt{{\displaystyle \frac{2\Delta P_v}{\rho }}}\end{array}$$

(1)

Flow through the RIFT was characterized using the hydraulic-diameter-based Reynolds number, as calculated in Equation (2).

$$\begin{array}{c}R{e}_{Dh}={\displaystyle \frac{\rho D_{h}Q}{\mu A_{ts}}}\end{array}$$

(2)

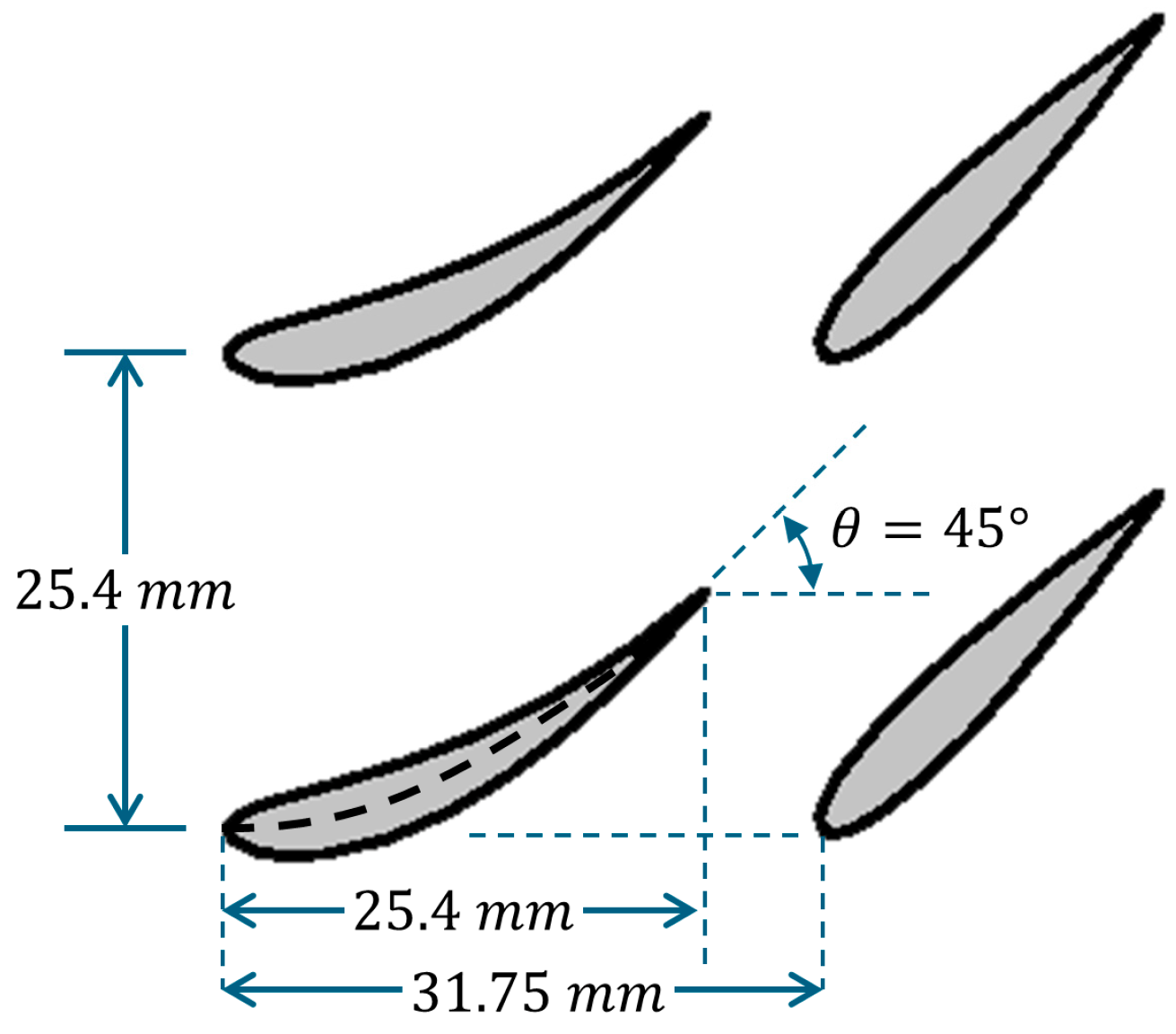
2.2. Swirl Plates

Two special test panels on the upper and lower walls of the wind tunnel induced swirling flow within the RIFT. Each test panel, referred to as a swirl plate, has two rows of 8 vanes, directing flow laterally. The swirl plates were additively manufactured in Acrylonitrile butadiene styrene (ABS) using an FDM printer. The leading edge of the first row of vanes is located at X = 343 mm and the leading edge of the second row is located at X = 374 mm. The first row of vanes turns the near-wall flow 45°, and the second row exhibits a straight profile angled at 45° to the flow direction. Each vane is based on an NACA 0015 profile and extends 8.9 mm from the wall of the wind tunnel. Based on this vane height, the middle 51% of the flow area is open between the turning vanes. Figure 1 presents a diagram of the vanes viewed from the top down and includes relevant dimensions.

The location of the two swirl plates within the test section and their relation to the PTV measurement volume are indicated in Figure 2. In Figure 1, the upper surface swirl plate is rendered transparent so that the lower surface may also be seen and the relationship between the two swirl plates is demonstrated.

Figure 1 and Figure 2 demonstrate the fact that the flow studied is a limited analog of true swirl-combustor flows. In most swirl-combustor flows, the primary flow is through a circular passage. Additionally, the swirling flow is typically generated by injecting gas through outside wall slats that are angled with the outside wall to generate azimuthal velocity. The use of vanes in this investigation also generates lateral flow within the test section. However, additional vortices from each individual vane are expected to be present within the larger swirling flow characterized in the measurement volume. Because of the different scales of swirling flow generated in the apparatus, the flow presents challenges for both measurement and simulation.

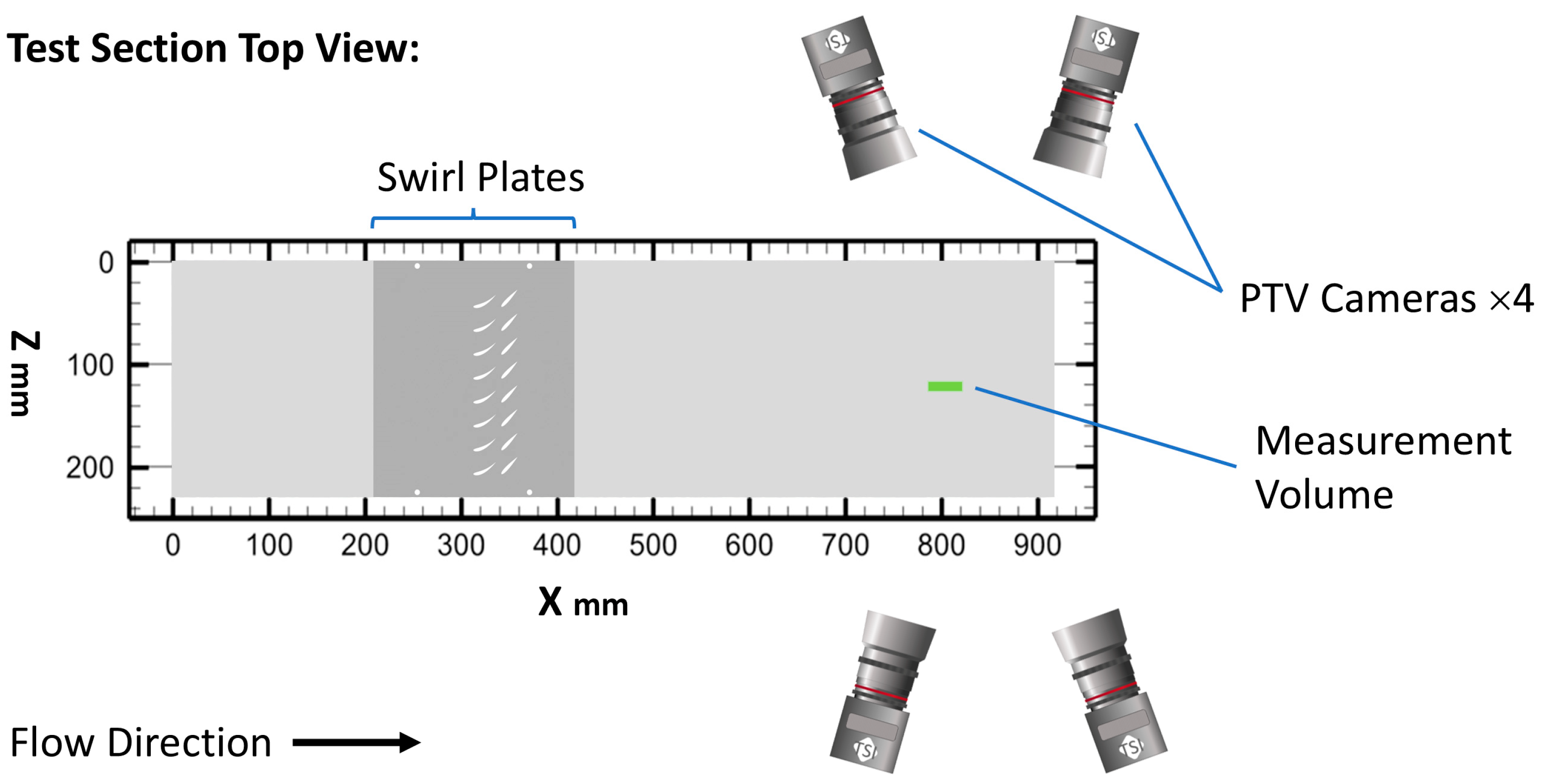
2.3. Particle Tracking Velocimetry (PTV) System

The particle tacking system used in this study has been previously used to investigate airflow over large additively manufactured roughness in the works of Boldt et al. [30,31]. Details of the PTV system’s development, calibration, and validation are provided in Boldt et al. [30]. The PTV system, from TSI, Inc., Shoreview, MN, USA, consists of a BG-1000 micro bubble generator which creates seed particles with a 15 $\mathsf{\mu }$m mean diameter, twin Nd:YAG lasers that emit 600 mJ pulses at a wavelength of 532 nm, and 4 8MP CCD cameras. Commercial PTV software [32] was used to facilitate image capture and perform initial data processing.

Figure 3 presents a top-down view of the RIFT test section and shows the orientation of the 4 PTV cameras around the measurement volume, which is indicated by a green rectangle. The measurement volume is illuminated using the laser from above or, using the context of Figure 3, by firing the laser into the page. Only the bottom swirl plate is shown in Figure 3. The upper swirl plate is identical but faces downwards and directs flow in the opposite direction.

To study mean flow through the RIFT, a series of instantaneous PTV measurements were performed and results were averaged together. The rate of instantaneous measurement collection was not affected by flow conditions so mean flow measurements were considered ensemble-averaged rather than time-averaged. An ensemble of 500 instantaneous measurements were taken to be averaged at each of the three flow conditions tested.

Before data collection, the PTV system was calibrated using a multiplane target with dimensions of 40 mm × 40 mm × 3 mm and a pattern of 361 markers. During the calibration process, a single image was taken of the calibration target with each PTV camera and used to create 4th-order polynomial mapping functions that related the camera’s view to the coordinate system of the PTV software.

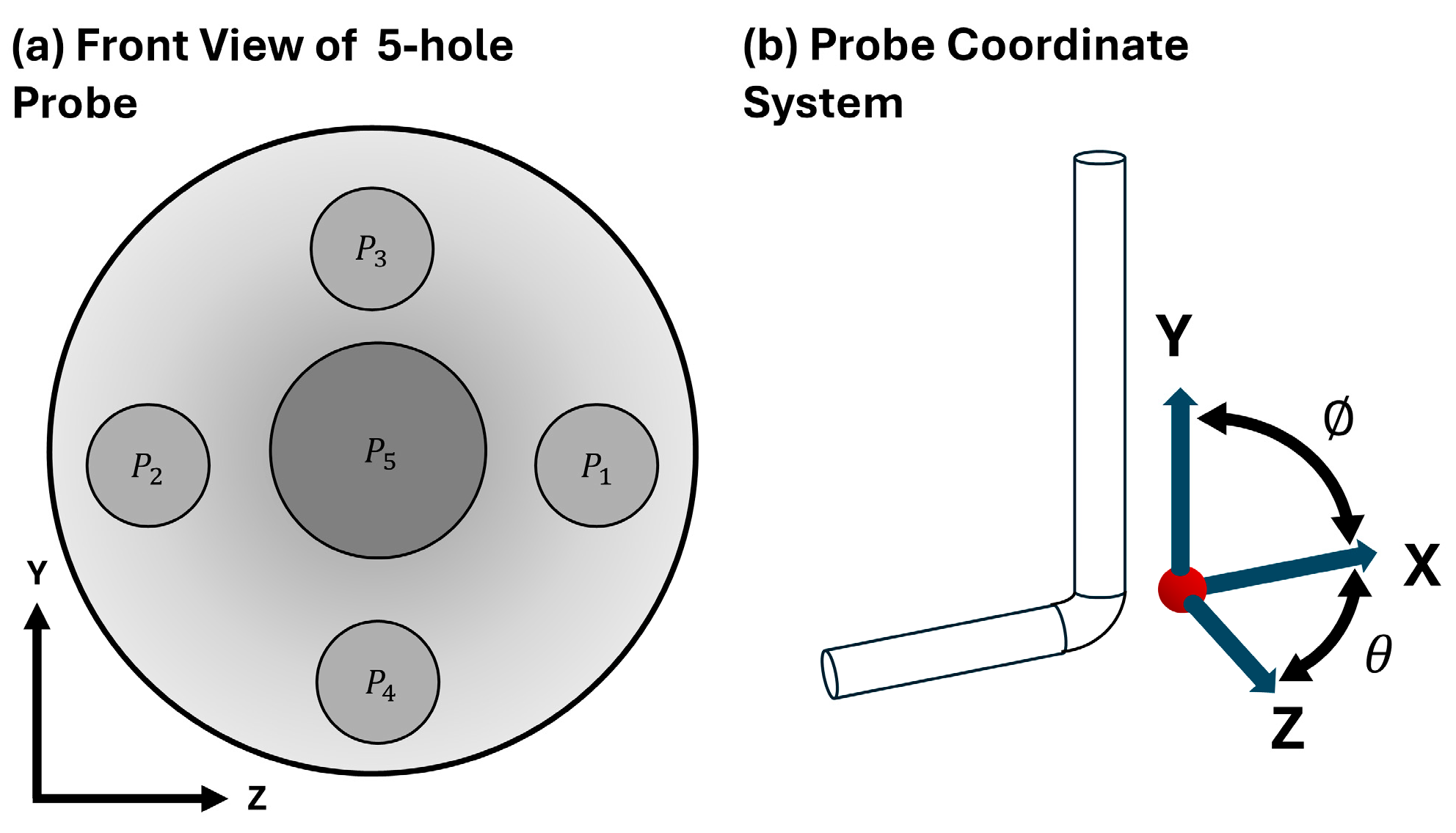
2.4. 5-Hole Probe

The PTV system was used and validated in previous studies of airflow over large AM roughness [30,31]. The use of swirl plates introduced a large lateral, or W, component to airflow within the RIFT that was not present in previous works and a 5-hole probe was included as an additional validation step to verify that this behavior was accurately captured by the PTV system. As noted by Lai et al. [33] and Hamed et al. [34] the uncertainty of PTV measurements is higher for velocity components aligned with the viewing direction of the system’s cameras. With the PTV apparatus used in this experiment, the direction of higher uncertainty corresponded to the lateral, or W, velocity component, giving the validation of such PTV measurements with the 5-hole probe additional importance.

The multi-hole probe used in this experiment is a 3.2 mm diameter, 5-hole L-shaped probe connected to a Scanivalve pressure transducer array with a pressure range of 10″ H₂O. The probe was calibrated using the non-nulling method by orientating the probe to the flow direction at angles between −15° and 15° within the RIFT across a Reynolds number range of 10,000–60,000 and recording the pressure values at each port. $P_o$, or the local stagnation pressure, was collected using the RIFT pitot static probe, which was located downstream of the test section at the center of the tunnel’s cross-section—in line with the 5-hole probe. The static pressure, $P_{static}$, is collected using pressure taps mounted on the RIFT’s sidewall at x = 978 mm. The pressure values from each port are labeled $P_1$ through $P_5$ and their position on the probe is indicated in Figure 4.

As the first step in creating a calibration, the average pressure across the surrounding ring of pressure ports was calculated using Equation (3).

$$\begin{array}{c}{P}_{avg}={\displaystyle \frac{P_1+P_2+P_3+P_4}{4}}\end{array}$$

(3)

Following the method of Morrison et al. [35], pressure data collected during the calibration process was collapsed into three coefficients—$C{p}_{\theta }$, $C{p}_{\varnothing }$, $C{p}_5$, and $C{p}_{avg}$—calculated using Equations (4)–(7), respectively.

$$\begin{array}{c}C{p}_{\theta }={\displaystyle \frac{P_2-P_1}{P_5-P_{avg}}}\end{array}$$

(4)

$$\begin{array}{c}C{p}_{\varnothing }={\displaystyle \frac{P_4-P_3}{P_5-P_{avg}}}\end{array}$$

(5)

$$\begin{array}{c}C{p}_5={\displaystyle \frac{P_5-P_{static}}{P_o-P_{static}}}\end{array}$$

(6)

$$\begin{array}{c}C{p}_{avg}={\displaystyle \frac{P_{avg}-P_{static}}{P_o-P_{staic}}}\end{array}$$

(7)

Using linear regression for $C{p}_{\theta }$ and quadratic regression for $C{p}_5$ and $C{p}_{avg}$, best fit curves were found to relate each pressure coefficient to the calibration angle such that $C{p}_x=f_x\left(\theta \right)$. Because their relation is linear, $\theta$ may be found as a function $C{p}_{\theta }$ such that $\theta ={f_{\theta }}^{-1}\left(C{p}_{\theta }\right)$. The axial symmetry of the probe allowed this relationship to also be used for calculating $\varnothing$. In other words, $\varnothing ={f_{\theta }}^{-1}\left(C{p}_{\varnothing }\right)$.

To process collected data after calibration, first, $P_{avg}$, $C{p}_{\theta }$, and $C{p}_{\varnothing }$ were calculated using Equations (5)–(7). Second, $\theta$ and $\varnothing$ were found using ${f_{\theta }}^{-1}\left(C{p}_{\theta }\right)$ and ${f_{\theta }}^{-1}\left(C{p}_{\varnothing }\right).$ Third, $C{p}_5$ and $C{p}_{avg}$ were found using $C{p}_5=f_5\left(\theta \right)$ and $C{p}_{avg}=f_{avg}\left(\theta \right)$. Using $C{p}_5$ and $C{p}_{avg}$, the magnitude of measured velocity was calculated using Equations (8)–(10).

$$\begin{array}{c}{P}_{static}={\displaystyle \frac{C{p}_5{P}_{avg}-C{p}_{avg}{P}_5}{C{p}_5-C{p}_{avg}}}\end{array}$$

(8)

$$\begin{array}{c}{P}_o=P_{static}+{\displaystyle \frac{P_5-P_{static}}{C{p}_5}}\end{array}$$

(9)

$$\begin{array}{c}V=\sqrt{{\displaystyle \frac{2\left(P_o-P_{static}\right)}{\rho }}}\end{array}$$

(10)

Finally, the velocity components $u$ and $w$ were calculated using the velocity magnitude $V$ and the two flow direction angles $\theta$ and $\varnothing$ as shown in Equations (11) and (12).

$$\begin{array}{c}u=V\cos \theta \cos \varnothing \end{array}$$

(11)

$$\begin{array}{c}w=V\sin \theta \end{array}$$

(12)

2.5. Swirl Number Calculation

Swirl number was calculated using the ratio of tangential and axial momentum flux within the channel, as shown in Equation (13). The method of calculating swirl number used in Equation (13) is considered acceptable for confined flows within a circular duct, as discussed by Guillaume et al. [36]; however, no attempt was made to account for the RIFT’s rectangular cross-section. Measurements of $\langle \overline{U}\rangle$ and $\langle \overline{W}\rangle$, as acquired using the five-hole probe, were used as ${\overline{U}}_x$ and ${\overline{U}}_{\theta },$ respectively. Equations (13) and (14) assume that rotation occurs around the channel center line.

$$\begin{array}{c}{S}_G={\displaystyle \frac{G_{\theta }}{H{G}_x}}={\displaystyle \frac{{\int }_0^H{\rho }_{air}{\overline{U}}_{\theta }{\overline{U}}_x{r}^{2}dr}{H{\int }_0^H{\rho }_{air}\left({{\overline{U}}_x}^2\frac{-1}{2}{{\overline{U}}_{\theta }}^2\right)rdr}}\end{array}$$

(13)

The ratio of tangential and axial bulk velocity was also evaluated to provide another indication of swirl strength. $U_{Bulk,\theta }$ was found by integrating the $\langle \overline{W}\rangle$ component of PTV data for flow across the lower half of the RIFT contained within the measurement volume. $U_{Bulk,x}$ was found using the volumetric flowrate provided by the RIFT venturi flow meter. The equation used in calculating the tangential and axial velocity ratios is provided below as Equation (14).

$$\begin{array}{c}{\displaystyle \frac{U_{Bulk,\theta }}{U_{bulk,x}}}={\displaystyle \frac{{\int }_0^H\langle \overline{W}\rangle dY A_{ts}}{HQ}}\end{array}$$

(14)

2.6. Uncertainty Analysis

The uncertainty propagation equation, presented as Equation (15), was used to calculate overall uncertainty in velocity measurements. The uncertainty propagation equation operates by multiplying the uncertainty of each variable by the partial derivative of the velocity equation with respect to that same variable.

$$\begin{array}{c}{P}_U={\left[{\left({\displaystyle \frac{\partial U}{\partial x_1}}{P}_{x_1}\right)}^2+{\left({\displaystyle \frac{\partial U}{\partial x_2}}{P}_{x_2}\right)}^2+{\left({\displaystyle \frac{\partial U}{\partial t_1}}{P}_{t_1}\right)}^2+{\left({\displaystyle \frac{\partial U}{\partial t_2}}{P}_{t_2}\right)}^2\right]}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\end{array}$$

(15)

For PTV measurements, velocity magnitude was found using the location of seed particles at $t_1$ and $t_2$ and dividing the change in location by the elapsed time. The velocity equation is provided as Equation (16).

$$\begin{array}{c}\left|\stackrel{\rightharpoonup }{U}\right|={\displaystyle \frac{\left|{\stackrel{\rightharpoonup }{x}}_2-{\stackrel{\rightharpoonup }{x}}_1\right|}{t_2-t_1}}\end{array}$$

(16)

The uncertainty of ${\stackrel{\rightharpoonup }{x}}_{\mathrm{x}}$ was considered 0.07 mm, as described by Lei et al. [37], for non-overlapping seed particles with a mean diameter of 15 $\mathsf{\mu }\mathrm{m}$. The uncertainty of $t_{\mathrm{x}}$ was considered to be the longest possible duration of each laser flash or 0.010 $\mathsf{\mu }\mathrm{s}$. As an example, using this method to find the uncertainty of a particle traveling at 5 $\mathrm{m}/\mathrm{s}$—approximately the bulk channel velocity when $R{e}_{Dh}$ = 20,000—results in an uncertainty of 0.31 $\mathrm{m}/\mathrm{s}$. Uncertainty can be reduced for mean velocity measurements to account for large sample size as described in the method of Coleman and Steele [38] and shown in Equation (17), where $R_x$ is the uncertainty of a single measurement and $N_i$ is the number of measurements.

$$\begin{array}{c}{R}_{\langle x\rangle }={\displaystyle \frac{1}{\sqrt{N_i}}}{R}_x\end{array}$$

(17)

$N_i$ is the number of samples and equals 500 for the number of instantaneous PTV measurements in the ensemble used to calculate mean velocity. This step reduces the calculated uncertainty for a measurement of 5 $\mathrm{m}/\mathrm{s}$ to just 0.014 $\mathrm{m}/\mathrm{s}$. As noted in the introduction, the velocity component aligned to the camera’s viewing direction, which in this case is the spanwise or $w$ component, will have an uncertainty 3–4 times higher than components within the camera’s viewing plane [34,37].

The uncertainty propagation equation was also used to calculate uncertainty for velocity measurements made using the 5-hole probe. However, the correlation of pressure coefficients as part of the calibration process and the many steps of data processing outlined in Equations (3)–(12) necessitated a different approach than the one that was used to evaluate uncertainty in the PTV measurements. Similarly to the approach described by Moffat [39], a perturbation method was used to determine the sensitivity of calculated velocity to variation in pressure and pressure coefficients. For example, for a velocity magnitude of $8.4 \mathrm{m}/\mathrm{s}$, uncertainty was determined to be 0.46 $\mathrm{m}/\mathrm{s}$.

2.7. Simulation Methodology

In addition to the measurements detailed above, swirling flow through the RIFT test section, from just upstream of the swirl vanes to 0.5 m downstream, was simulated computationally. A time-resolved Detached Eddy Simulation (DES), as well as two steady RANS simulations for comparison, were run at a Reynolds number of $R{e}_{Dh}$ = 30,000. The total flow-time simulated in the DES was 2 s, or ~27 flow-through times.

The simulations were run using Star-CCM+, a commercial CFD package with a large number of physical and numerical models; only the models relevant to these simulations are mentioned here.

The RIFT test section was discretized using an unstructured Cartesian mesh with uniform cubical elements filling the flow volume. Cells had a uniform side-length of 0.025″ (6.35 $\times {10}^{-4}$ m). Approximately 56 of these uniform cells covered the test section height. A 32-layer near-wall prism layer 0.2″ (0.005 m) deep provided near-wall anisotropic resolution with a stretching ratio of 1.1. The height of the first cell on all solid surfaces was ~1.2 $\times {10}^{-5}$ m; this provided a wall $y^{+}$ of ~0.25. The total cell count was approximately 56 million.

The working fluid was modeled as incompressible air at standard conditions. The spatial stencil was a second-order-accurate Bounded-Central difference scheme. Time advancement was achieved with an implicit, second-order-accurate backward-difference scheme with a time step of 6.3 $\times {10}^{-5}$ s, for an approximate bulk-flow Courant–Friedrichs–Lewy (CFL) number of unity. Velocity and pressure were coupled using the SIMPLEC algorithm.

DES near-wall turbulence was simulated using the Menter k-$\omega$ SST IDDES model [40]. The first RANS simulation used the Menter k-$\omega$ SST [41] two-equation model with the Durbin curvature correction [42] and a linear eddy viscosity constitutive model; the other used a seven-equation Reynolds stress transport model with an Elliptic Blending (EB-RSM) near-wall pressure-strain model developed by Manceau and Hanjalic [43] and revised by Lardeau and Manceau [44]. Menter k-$\omega$ SST is a standard two-equation model widely used in industry; seven-equation models are not widely used for industrial calculations, but the EB model is of interest in the present context as being one of the most applicable RANS models available. Many other RANS turbulence models have been developed over the years to specifically address line vortices [45,46], but testing all such models is beyond the scope of this work.

The three time-averaged velocity components, as well as three velocity variances ($\overline{u\prime u\prime }$, $\overline{v^{\prime }v\prime }$, and $\overline{w\prime w\prime }$) and three co-variances ($\overline{u\prime v\prime }$, $\overline{u^{\prime }w\prime }$, and $\overline{v\prime w\prime }$), were recorded on the entire flow domain. Results were interpolated onto a vertical line through the middle of the PTV measurement volume for comparison with experiment.

An auxiliary simulation upstream of the Test Section simulation produced a time-resolved (or steady, for the RANS simulations), fully developed rectangular channel turbulent velocity profile. This was accomplished by developing the flow under an applied pressure drop in a one-inch length of square duct with the RIFT cross-section, with the outflow recycled back to the inlet, thus modeling a rectangular duct of infinite length. Once this upstream simulation became fully developed, the velocity profile at the outlet face was point-mapped to the inlet boundary face for the main RIFT simulation at each time step. The downstream outlet boundary for the RIFT test section was modeled as a constant-pressure face.

3. Results

The results are presented and discussed in different subsections as follows. First, a PTV vector cloud is presented to demonstrate the nature of the collected measurements and the system’s ability to view $v$ and $w$ components of swirling flow. Second, the mean flow velocity profiles of the three simulations, PTV system, and five-hole probe are all compared. Third, flow visualizations of the entire RIFT test section are provided using simulation results and scaled Reynolds stress terms are plotted for the DES and EB-RSM models.

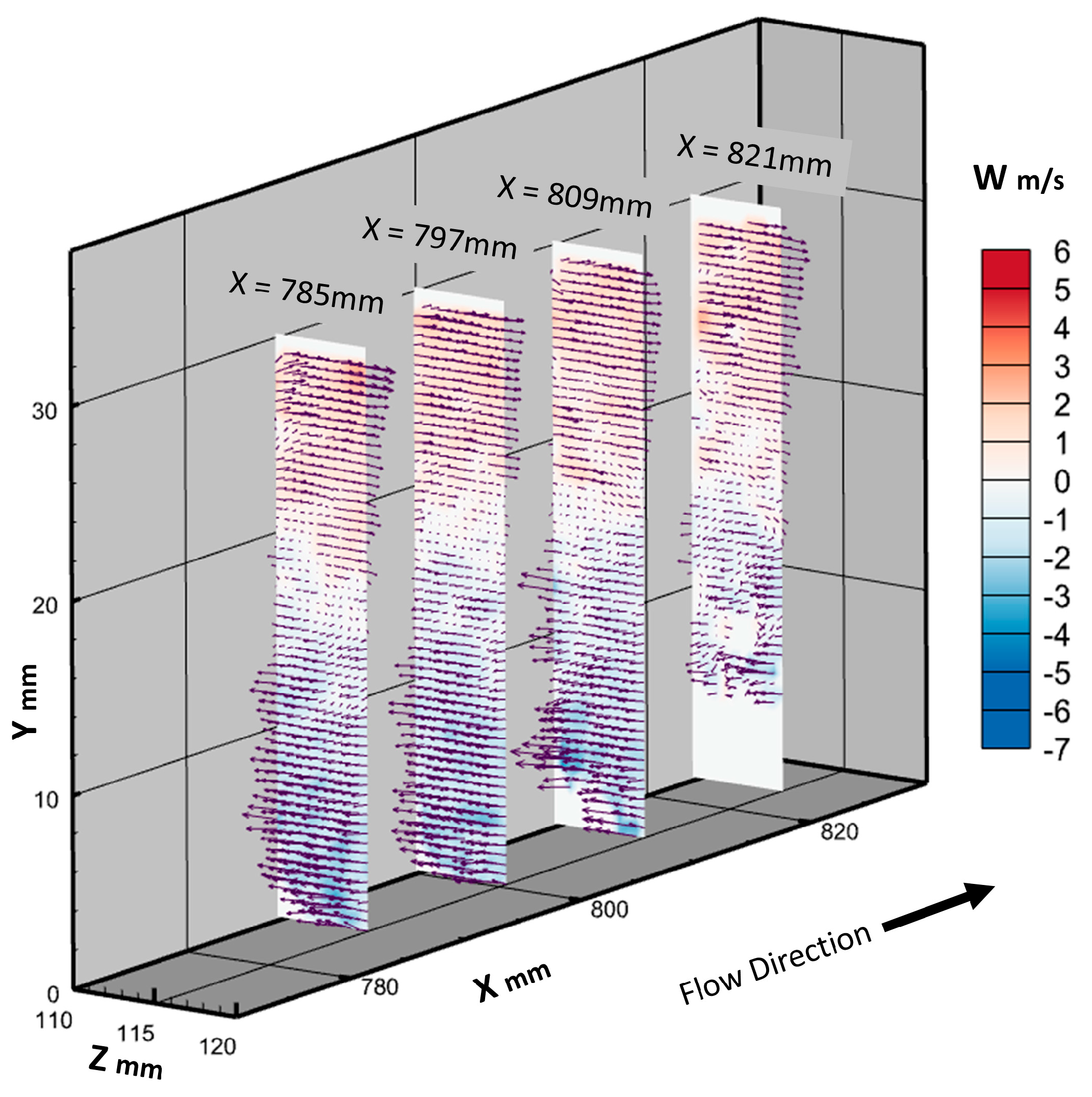
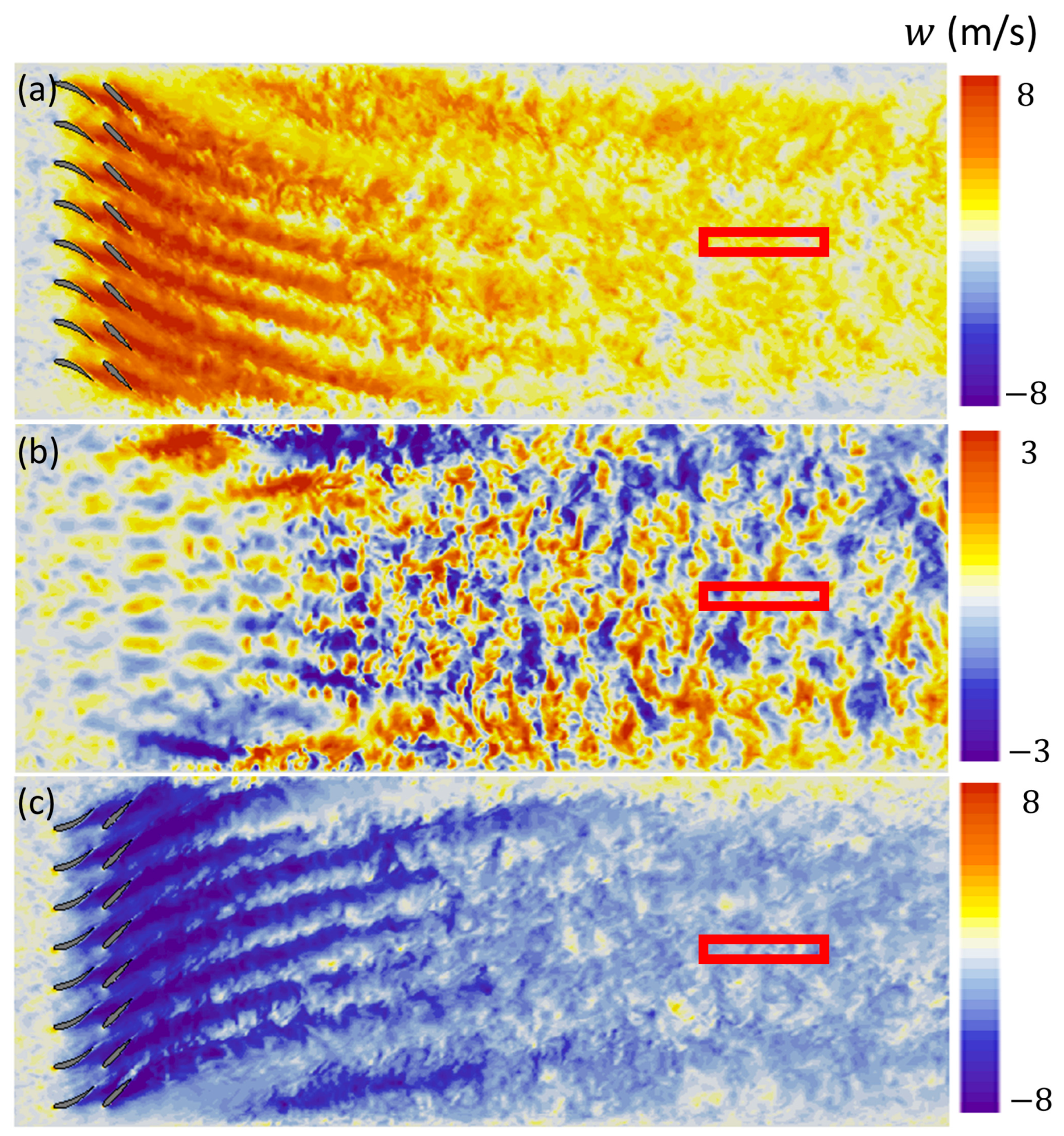
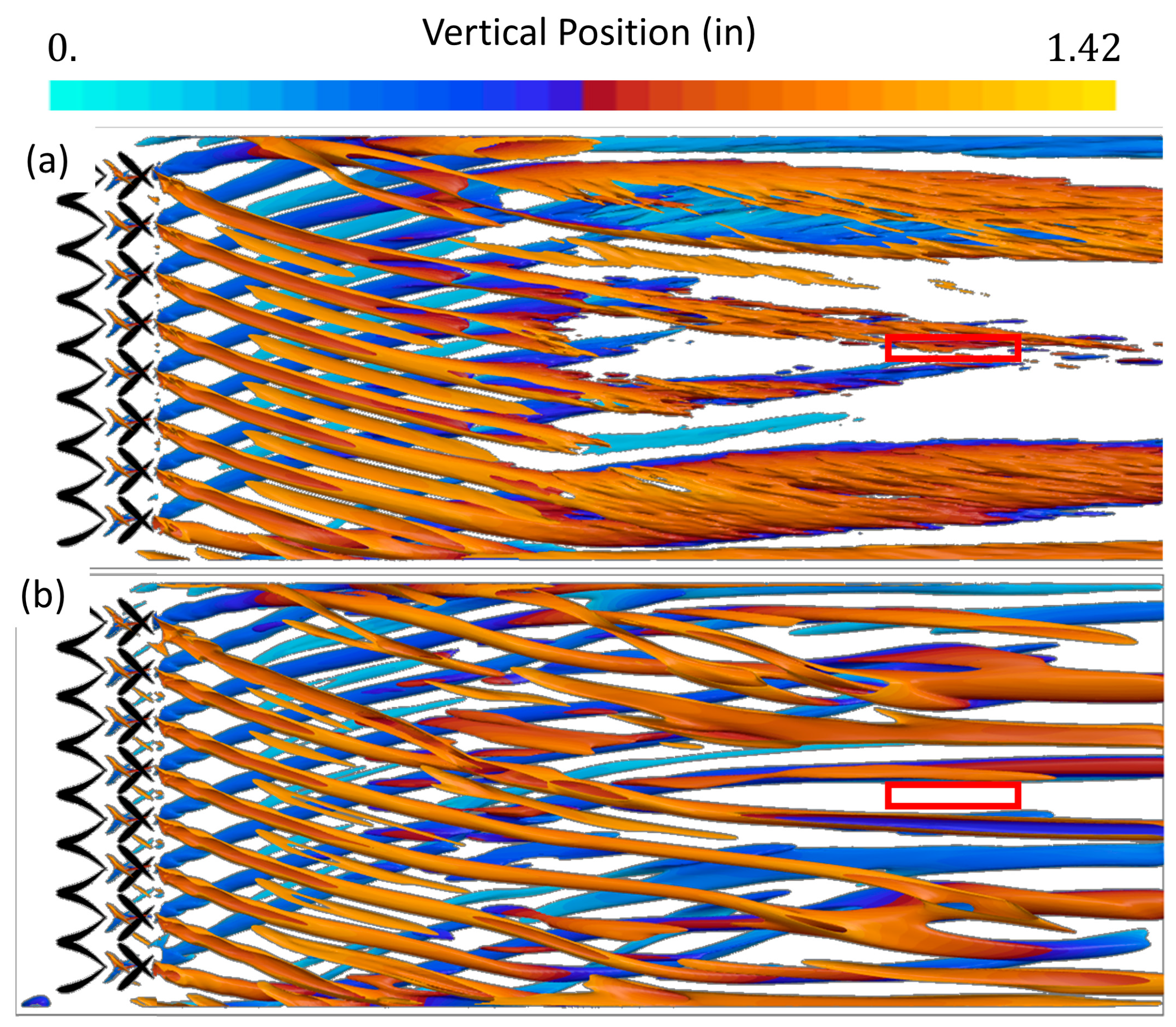
3.1. PTV Vector Clouds

The ensemble-averaged $v$ and $w$ components of flow along four Y-Z slices of the PTV measurement volume are plotted in Figure 5. The vectors in Figure 5 are colored to describe the spanwise, or $w$, component of flow, with positive velocities colored red and negative velocities colored blue. The vectors shown only correspond to individual voxels where particle velocities were evaluated; no spatial averaging was used to create Figure 5.

Figure 5 shows predominantly positive velocities above the channel’s mid-height and negative values below it, suggesting that the PTV system successfully measures spanwise flow associated with swirl. While small regions of the measurement volume did not contain a sufficient number of tracked particles to successfully indicate a velocity, as indicated in Figure 5 by white space without vectors, measurement density was still high.

The distribution of measured $w$ vector components across the measurement volume in PTV data shows that the spanwise movement of particles in swirling flow was detected. However, the increased uncertainty known to be present in measurements made normal to the viewing direction of cameras [33] made it desirable to further confirm the accuracy of collected measurements. The additional verification was provided by the five-hole probe measurements.

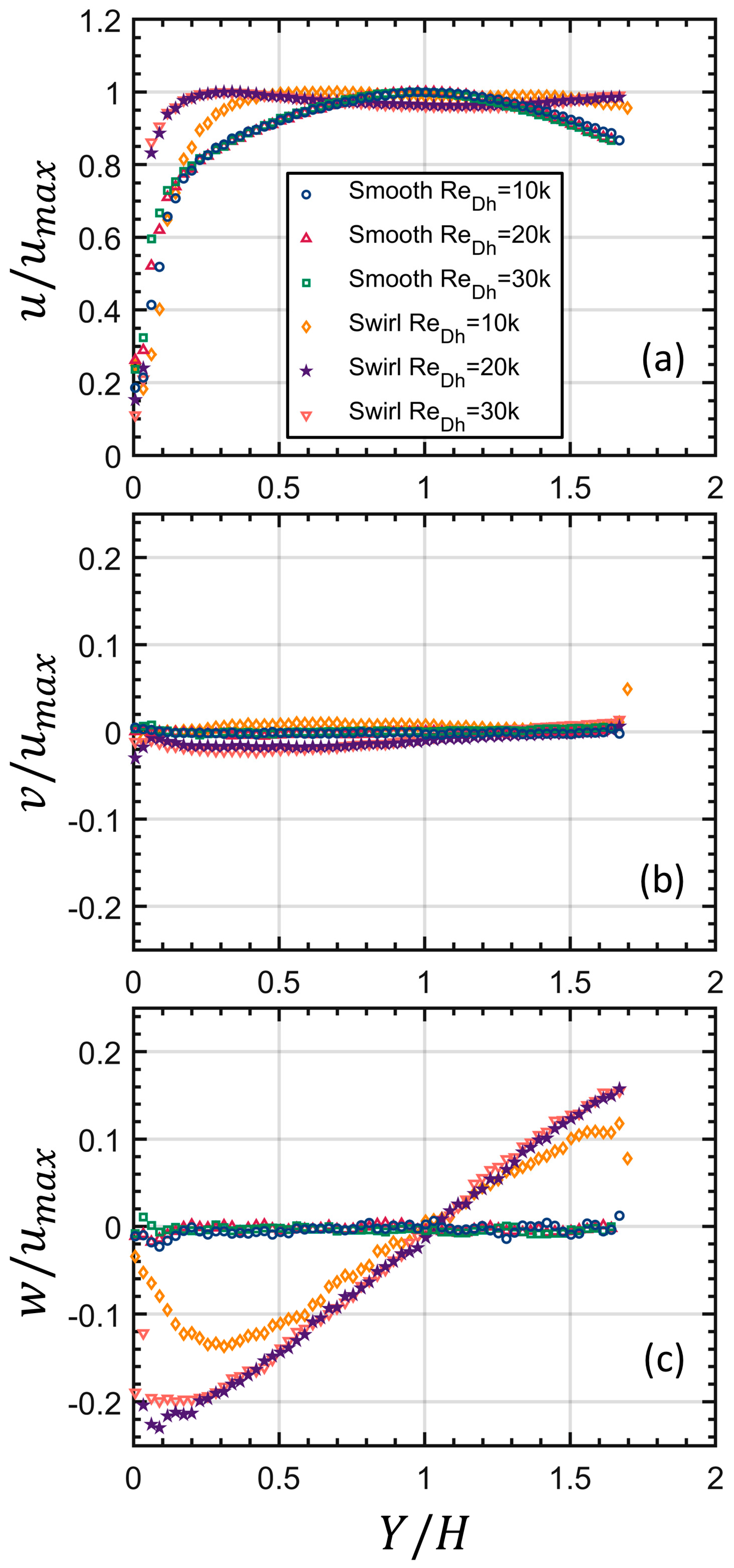
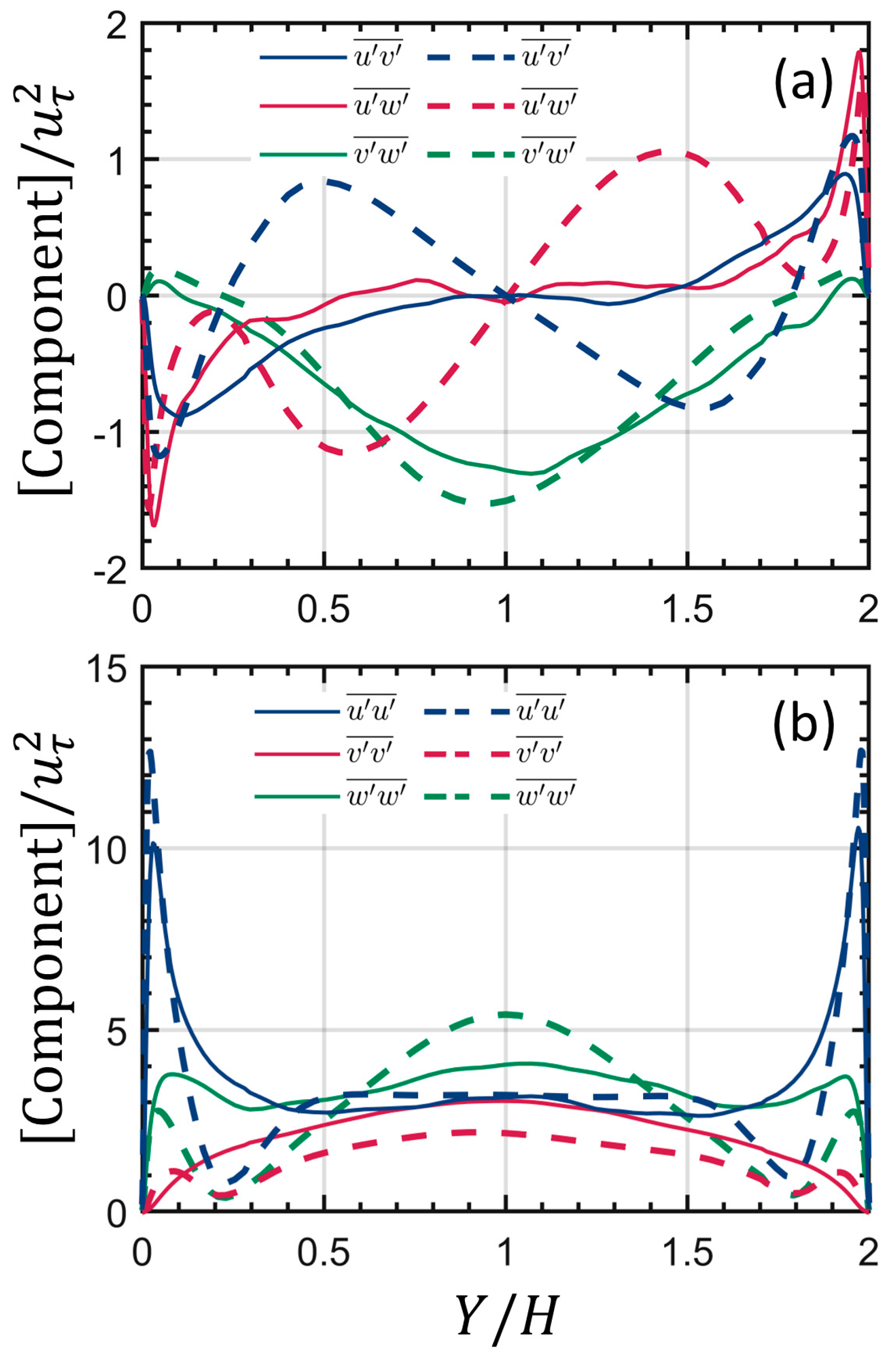
3.2. PTV Velocity Profiles

The mean flow velocity profiles of $u$, $v$, and $w$ components scaled by $u_{max}$ for the PTV system are presented in Figure 6. To create each velocity profile, PTV data was ensemble- and spatially averaged across the X-Z plane. Figure 6 presents PTV measurements within the RIFT both with and without the swirl plates installed at each $R{e}_{Dh}$ tested.

Velocity profiles for the flow direction, or axial component $u$, are shown in Figure 6a. Swirl plate $u$ profiles have a velocity peak near the wall and slightly lower values at the centerline. This behavior is less pronounced in the $R{e}_{Dh}$ = 10,000 case, which is notably different from the other two profiles and may not be fully turbulent.

The $v$ components, shown in Figure 6b, are essentially zero, both with and without the swirl plates. Without the swirl plates, no wall normal mean flow is expected, and none is observed. With the swirl plates installed, equal airflow is expected to travel upward and downward within the right and left sides of the measurement volume. When spatially averaged across the X-Z plane, these two trends should cancel out resulting in $v$ = 0. The slight negative values of $v$ shown in Figure 6b may indicate that the measurement volume is not perfectly centered within the test section but has shifted slightly left or in the negative-Z direction. Because the spatial averaging approach used to collapse PTV data hides trends within the vertical flow component, and the measurement volume is located centrally within a large aspect ratio channel, only $w$ or spanwise flow is emphasized as the swirl component in future discussion.

The $w$ components, shown in Figure 6c, are essentially zero without the swirl plates installed. With the swirl plates, values of $w$ are negative below the channel’s mid-height and positive above it. $w$ values measured without swirl plates are indicative of measurement noise since there should be no mean flow normal to the test section walls during these trials. PTV measurements taken with the swirl plates installed show clear rotation about the channel centerline. Like the axial component, $w$ profiles between the $R{e}_{Dh}$ = 20,000 and $R{e}_{Dh}$ = 30,000 cases appear nearly identical when scaled by $u_{max},$ while the $R{e}_{Dh}$ = 10,000 trial has a maximum $w$ value farther away from the wall.

A comparison of the PTV measurements to the five-hole probe measurements is presented in Figure 7. Mean-flow streamwise velocity (u) relative to the maximum streamwise velocity is presented in Figure 7a, and spanwise (w) velocity relative to the maximum streamwise velocity is shown in Figure 7b. Figure 7 demonstrates that the five-hole differs from the PTV measurements near the wall. However, these differences are generally within the uncertainties of the five-hole probe measurements. Most importantly, Figure 7 demonstrates that the PTV and the five-hole probe measurements report similar differences between the streamwise and spanwise velocities between the profiles. That is, the $R{e}_{Dh}=\mathrm{10,000}$ case presents different near-wall behavior than the other cases for both measurement techniques.

3.3. Swirl Strength

The swirl number and ratio of bulk axial to tangential velocity within the channel are presented in

Table 1. Indications of swirl strength at each tested $R{e}_{Dh}$.

$\mathit{R}{\mathit{e}}_{{\mathit{D}}_{\mathit{h}}}$	${\mathit{S}}_{\mathit{G}}$	${\mathit{U}}_{\mathit{B}\mathit{u}\mathit{l}\mathit{k},\mathit{\theta }}/{\mathit{U}}_{\mathit{b}\mathit{u}\mathit{l}\mathit{k},\mathit{x}}$
10,000	0.4070	0.1880
20,000	0.4893	0.3367
30,000	0.5556	0.3193

for each Reynolds number tested. The swirl number increases linearly with the Reynolds number over the range of conditions tested and the ratio of tangential and axial bulk velocity is lower in the $R{e}_{Dh}$ = 10,000 case and higher but roughly equal in the $R{e}_{Dh}$ = 20,000 and 30,000 cases. The shift in tangential and axial velocity ratios between the $R{e}_{Dh}$ = 10,000 case and the two higher Reynolds number tests is also visible in the scaled velocity profiles shown in Figure 6, where the W/U_max profile is shallower in the lowest Reynolds number case. The trend in swirl number indicates that swirl strength within the measurement volume increases with increased flow rate and the shift in tangential over axial bulk velocities indicates that swirl strength decays more significantly before reaching the measurement volume at the lowest Reynolds number tested.

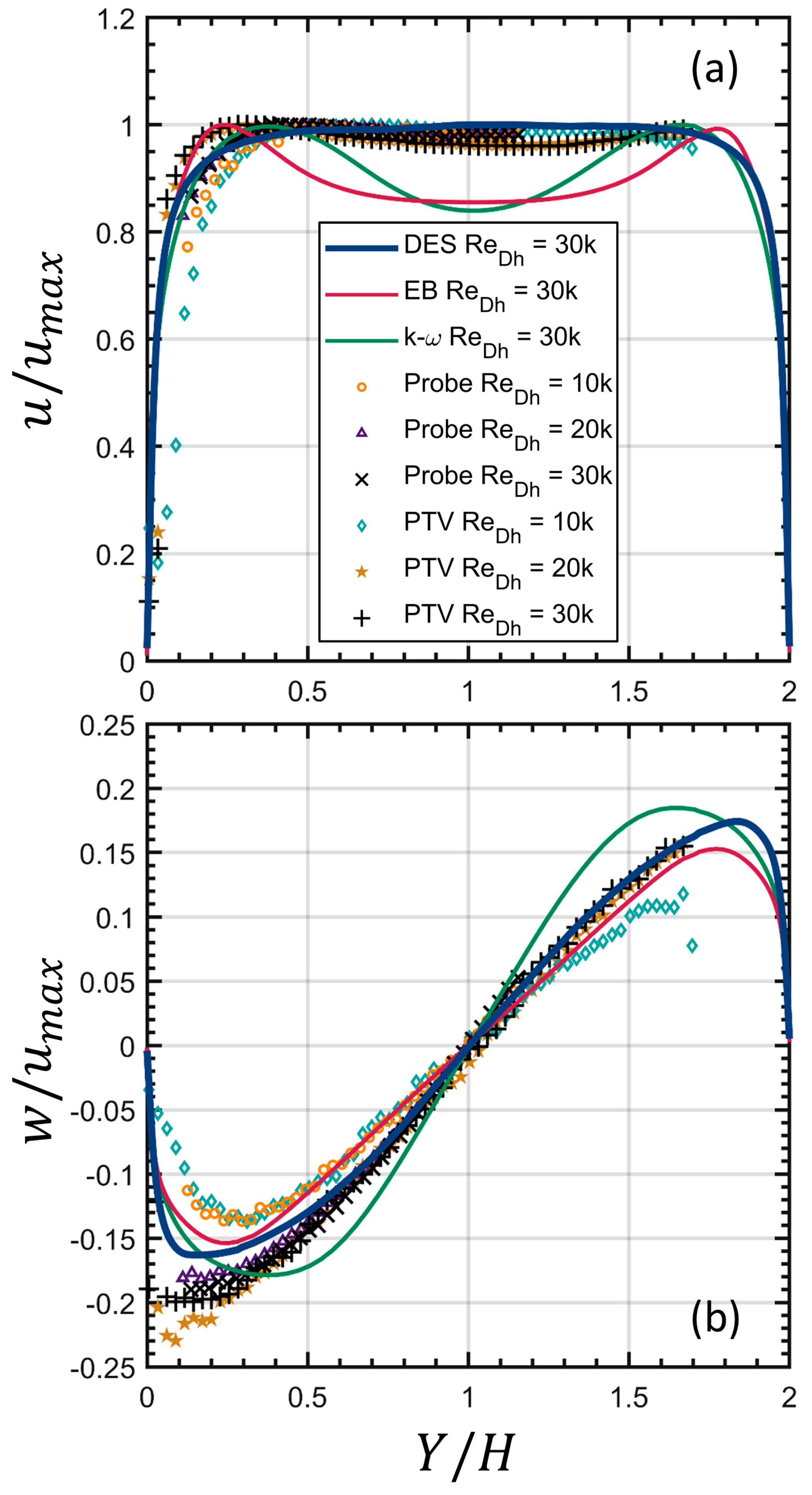
3.4. Simulation Results

Figure 7 also presents a comparison of the experimental flow measurements to the simulation results. The PTV and five-hole probe data are shown at the three measured Reynolds numbers. CFD velocity profiles for $R{e}_{Dh}=\mathrm{30,000}$ are superimposed onto the measured data.

The DES produces a velocity profile that closely matches the measurements in both the axial (u) and swirling (w) components, although it predicts a slightly lower maximum swirling component near the wall. By contrast, both RANS models produce an axial velocity deficit at mid-channel height: 15% below the maximum streamwise velocity for the EB-RSM computation and 17% below this value for the k-ω computation. In addition, the two-equation model smears the swirling component unphysically due to its intrinsic over-prediction of the effect of the turbulent stresses. The EB model captures the swirl component but under-predicts the maximum swirl velocity by 5% of the streamwise maximum velocity and moves the location of the maximum-swirl component away from the wall.

An instantaneous flow-field from the DES is visualized in Figure 8 on three planes (at 25%, 50%, and 75% of the channel height). Vortices from the top and bottom row of swirl vanes interact most strongly at the mid-plane. On the mid-plane, the flow passes through a region of coherent, well-defined vortices for roughly the first three inches downstream of the swirl vanes before turbulent mixing becomes dominant. Figure 9 shows a visualization of the time-averaged vortex structure for the DES and the EB-RSM simulations. A short distance downstream of the swirl vanes, interaction with the RIFT sidewalls causes the vorticity to merge into a pair of large vortices to either side of the centerline and two smaller vortices that pass through the PTV volume. The cross-channel velocity profile at the measurement volume is strongly sensitive to the location of these centerline vortices.

The Reynolds stress components are shown in Figure 10; they were evaluated from the DES and EB-RSM computations on a vertical line through the center of the PTV volume. The three diagonal components (bottom plot) show qualitative agreement between the two models. The swirling component, $\overline{v\prime w\prime }$, is shown in green in the top plot; this is the Reynolds stress involving interaction between vertical and cross-channel velocity fluctuations. The EB-RSM computation agrees qualitatively with the DES results for this component. The other two off-diagonal components, however, have very different shapes for EB-RSM compared with the DES in the mid-channel away from the solid surfaces. The over-prediction of $\overline{u\prime v\prime }$ and $\overline{u\prime w\prime }$ may be the reason that the EB-RSM predicts a mid-channel deficit in the axial velocity. Physically, these components represent interactions between axial turbulent fluctuations and the vertical and cross-stream fluctuations, respectively.

4. Conclusions

To investigate flows related to combustor flow physics and to investigate improved simulation methods for combustor flows using the SST k-ω IDDES turbulence model, swirling flow was generated and measured in a small wind tunnel. To create swirling flow within the RIFT, test panels were constructed and installed in the upstream portion of the test section for the purpose of studying swirling flow within a rectangular channel. The resulting flow, which was similar to flow within swirl-stabilized combustors, was characterized using two experimental approaches and predicted using computational methods. Mean velocity measurements were taken downstream of the induced swirl using a tomographic PTV system and a five-hole probe. Flow within the RIFT was simulated using three different approaches—one time-resolved DES and two steady RANS simulations using different closure models.

The primary takeaways from this work include the following:

(1)

The PTV system was employed to measure fluid rotation despite limitations in spanwise measurement uncertainty. The PTV measurements demonstrated similar variations as found in the five-hole probe measurements with the substantial benefit of characterizing an entire volume of ensemble-averaged swirling flow measurements.

(2)

The flow direction mean velocity profiles produced by the DES for flow within the measurement volume largely agree with measurements taken using the five-hole probe and PTV system.

(3)

Both RANS models underpredicted streamwise velocity at the channel midline.

(4)

The DES model underpredicts fluid rotation near the walls, but the maximum lateral flow agrees within 4% of the maximum channel streamwise (axial) flow.

(5)

The EB-RSM model predicts fluid rotation within 5% of the maximum channel streamwise flow despite underpredicting the centerline streamwise velocity by 15% of the maximum streamwise flow velocity.

The agreement between the PTV measurements and the five-hole probe measurements demonstrates the usefulness of both approaches for comparing simulations to time-averaged flow measurements. Additionally, the PTV results demonstrate the approach’s utility in characterizing swirling flow in volumes that will be important to future investigations of swirl-stabilized combustor-like flows. Comparisons of the measurement sets and simulation results demonstrate the ability of the DES in capturing the mean flow and the vortex structure. However, the RANS-based simulation results demonstrate additional research is needed to improve the vortex structure capturing and the time-averaged turbulent statistics for internal flows with surface feature-induced swirl.