Slow Motion of a Spherical Particle Perpendicular to Two Planar Walls with Slip Surfaces
Abstract
1. Introduction
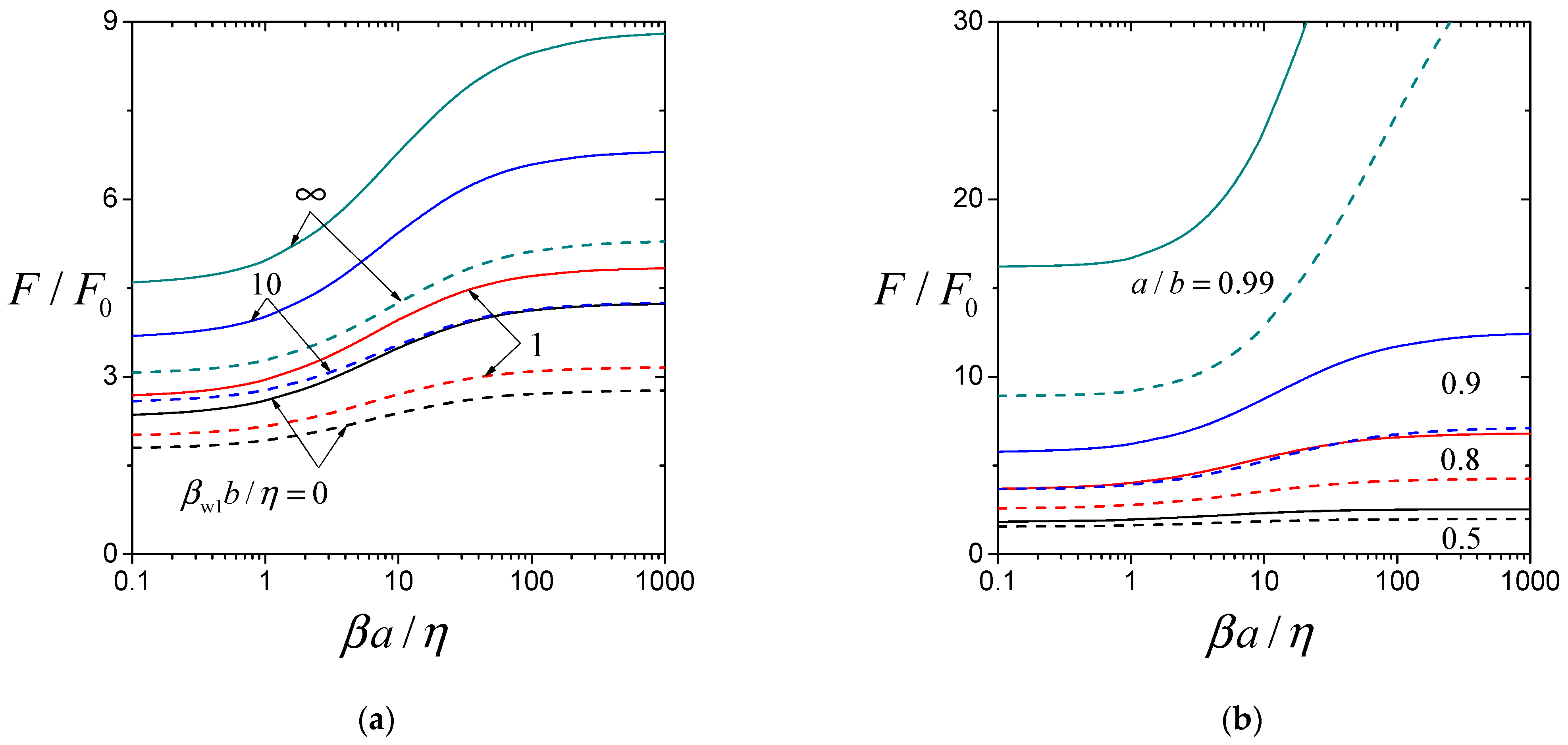
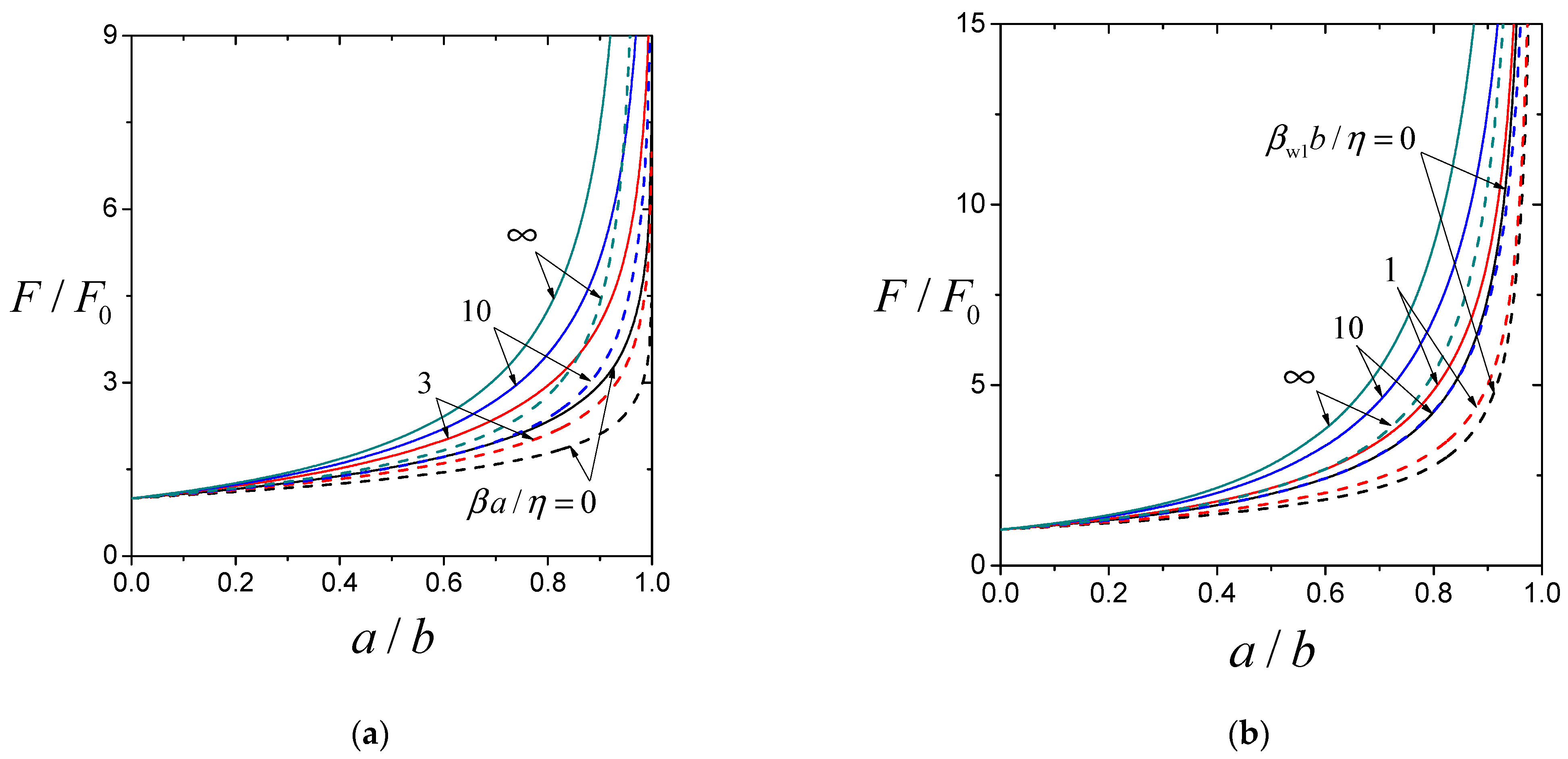
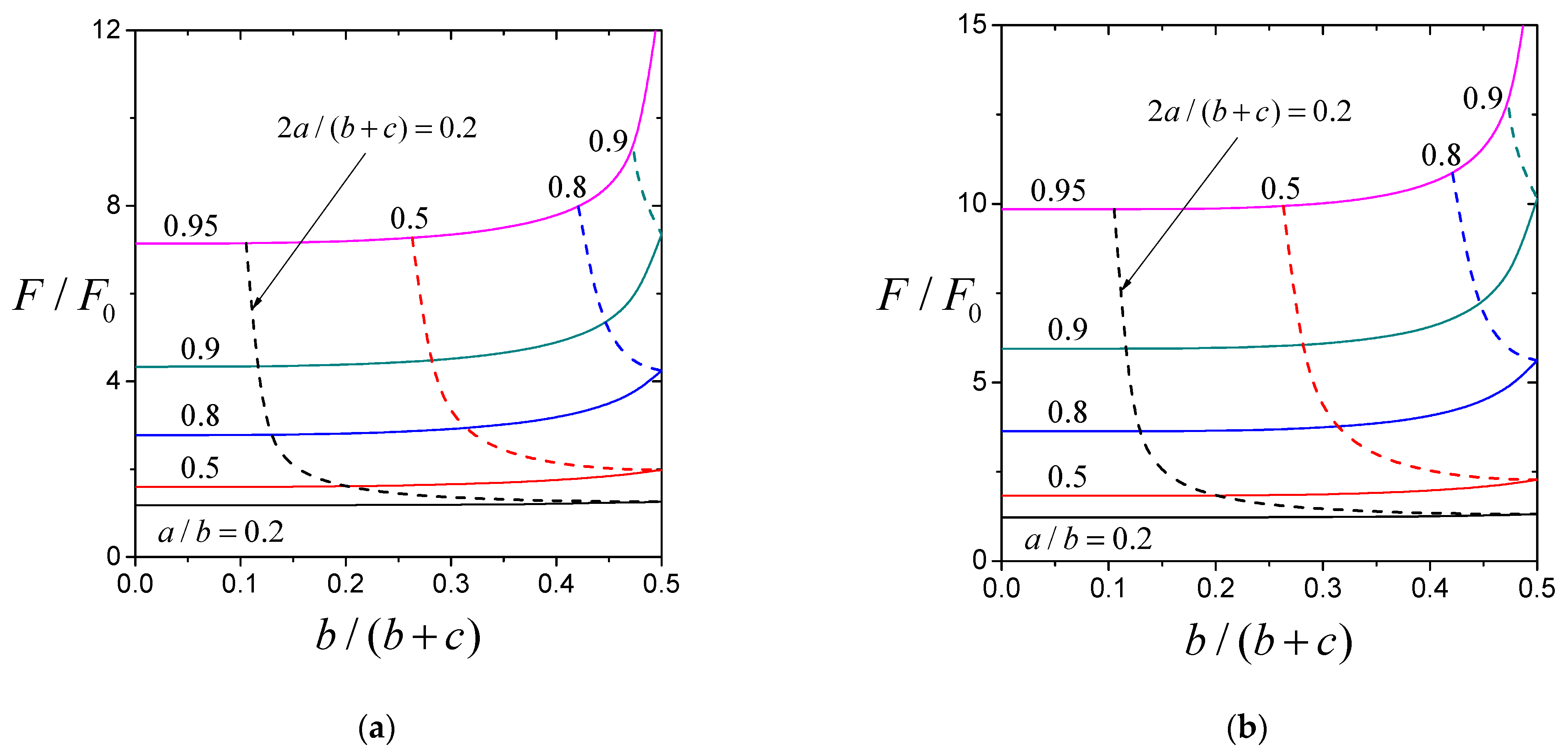
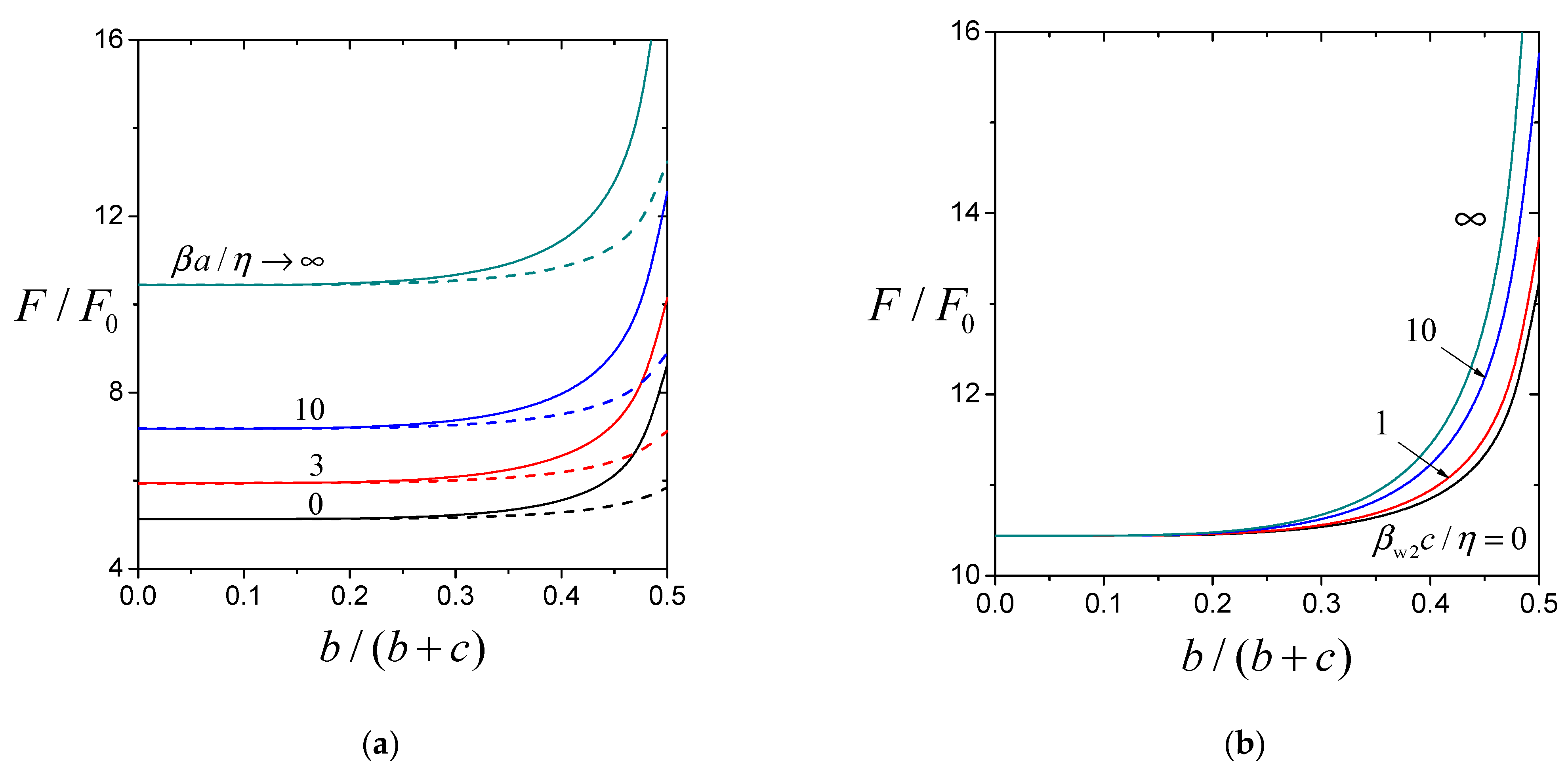
2. Analysis
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Some Functions in Section 2
References
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Philos. Soc. 1851, 9, 8–106. [Google Scholar]
- Pit, R.; Hervet, H.; Leger, L. Direct experimental evidence of slip in hexadecane: Solid interfaces. Phys. Rev. Lett. 2000, 85, 980–983. [Google Scholar] [CrossRef]
- Tretheway, D.C.; Meinhart, C.D. Apparent fluid slip at hydrophobic microchannel walls. Phys. Fluids 2002, 14, L9–L12. [Google Scholar] [CrossRef]
- Neto, C.; Evans, D.R.; Bonaccurso, E.; Butt, H.J.; Craig, V.S.J. Boundary slip in Newtonian liquids: A review of experimental studies. Rep. Prog. Phys. 2005, 68, 2859–2897. [Google Scholar] [CrossRef]
- Choi, C.H.; Ulmanella, U.; Kim, J.; Ho, C.M.; Kim, C.J. Effective slip and friction reduction in nanograted superhydrophobic microchannels. Phys. Fluids 2006, 18, 087105. [Google Scholar] [CrossRef]
- Beavers, G.S.; Joseph, D.D. Boundary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Nir, A. Linear shear flow past a porous particle. Appl. Sci. Res. 1976, 32, 313–325. [Google Scholar] [CrossRef]
- Hutchins, D.K.; Harper, M.H.; Felder, R.L. Slip correction measurements for solid spherical particles by modulated dynamic light scattering. Aerosol Sci. Technol. 1995, 22, 202–218. [Google Scholar] [CrossRef]
- Sharipov, F.; Kalempa, D. Velocity slip and temperature jump coefficients for gaseous mixtures. I. Viscous slip coefficient. Phys. Fluids 2003, 15, 1800–1806. [Google Scholar] [CrossRef]
- Myong, R.S.; Reese, J.M.; Barber, R.W.; Emerson, D.R. Velocity slip in microscale cylindrical Couette flow: The Langmuir model. Phys. Fluids 2005, 17, 087105. [Google Scholar] [CrossRef]
- Thompson, P.A.; Troian, S.M. A general boundary condition for liquid flow at solid surfaces. Nature 1997, 389, 360–362. [Google Scholar] [CrossRef]
- Lauga, E.; Brenner, M.P.; Stone, H.A. Microfluidics: The no-slip boundary condition. In Handbook of Experimental Fluid Mechanics; Springer: New York, NY, USA, 2005. [Google Scholar]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Nijhoff: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Basset, A.B. A Treatise on Hydrodynamics; Dover: New York, NY, USA, 1961; Volume 2. [Google Scholar]
- Anderson, J.L. Colloid transport by interfacial forces. Ann. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Romanò, F.; des Boscs, P.-E.; Kuhlmann, H.C. Forces and torques on a sphere moving near a dihedral corner in creeping flow. Eur. J. Mech. B Fluids 2020, 84, 110–121. [Google Scholar] [CrossRef]
- Reed, L.D.; Morrison, F.A. Particle interactions in viscous flow at small values of Knudsen number. J. Aerosol Sci. 1974, 5, 175–189. [Google Scholar] [CrossRef]
- Chen, S.H.; Keh, H.J. Axisymmetric motion of two spherical particles with slip surfaces. J. Colloid Interface Sci. 1995, 171, 63–72. [Google Scholar] [CrossRef]
- Keh, H.J.; Chang, J.H. Boundary effects on the creeping-flow and thermophoretic motions of an aerosol particle in a spherical cavity. Chem. Eng. Sci. 1998, 53, 2365–2377. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; El-Sapa, S. Hydrophobic effects on a solid sphere translating in a Brinkman couple stress fluid covered by a concentric spherical cavity. Phys. Fluids 2024, 36, 033113. [Google Scholar] [CrossRef]
- Gluckman, M.J.; Pfeffer, R.; Weinbaum, S. A new technique for treating multi-particle slow viscous flow: Axisymmetric flow past spheres and spheroids. J. Fluid Mech. 1971, 50, 705–740. [Google Scholar] [CrossRef]
- Leichtberg, S.; Pfeffer, R.; Weinbaum, S. Stokes flow past finite coaxial clusters of spheres in a circular cylinder. Int. J. Multiph. Flow 1976, 3, 147–169. [Google Scholar] [CrossRef]
- Ganatos, P.; Weinbaum, S.; Pfeffer, R. A strong interaction theory for the creeping motion of a sphere between plane parallel boundaries. Part 1. perpendicular motion. J. Fluid Mech. 1980, 99, 739–753. [Google Scholar] [CrossRef]
- Dagan, Z.; Weinbaum, S.; Pfeffer, R. General theory for the creeping motion of a finite sphere along the axis of a circular orifice. J. Fluid Mech. 1982, 117, 143–170. [Google Scholar] [CrossRef]
- Keh, H.J.; Lee, T.C. Axisymmetric creeping motion of a slip spherical particle in a nonconcentric spherical cavity. Theor. Comput. Fluid Dyn. 2010, 24, 497–510. [Google Scholar] [CrossRef]
- Lee, T.C.; Keh, H.J. Slow motion of a spherical particle in a spherical cavity with slip surfaces. Int. J. Eng. Sci. 2013, 69, 1–15. [Google Scholar] [CrossRef]
- Keh, H.J.; Chang, Y.C. Creeping motion of a slip spherical particle in a circular cylindrical pore. Int. J. Multiph. Flow 2007, 33, 726–741. [Google Scholar] [CrossRef]
- Sherief, H.H.; Faltas, M.S.; Ashmawy, E.A.; Nashwan, M.G. Slow motion of a slip spherical particle along the axis of a circular cylindrical pore in a micropolar fluid. J. Mol. Liq. 2014, 200, 273–282. [Google Scholar] [CrossRef]
- Nashwan, M.G.; Ragab, K.E.; Faltas, M.S. Axisymmetric slow motion of a non-deformable spherical droplet or slip particle toward an orifice in a plane wall. Phys. Fluids 2022, 34, 083106. [Google Scholar] [CrossRef]
- Chen, P.Y.; Keh, H.J. Slow motion of a slip spherical particle parallel to one or two plane walls. J. Chin. Inst. Chem. Eng. 2003, 34, 123–133. [Google Scholar]
- Chang, Y.C.; Keh, H.J. Slow motion of a slip spherical particle perpendicular to two plane walls. J. Fluids Struct. 2006, 22, 647–661. [Google Scholar] [CrossRef]
- Hocking, L.M. The effect of slip on the motion of a sphere close to a wall and of two adjacent spheres. J. Eng. Math. 1973, 7, 207–221. [Google Scholar] [CrossRef]
- Goren, S.L. The hydrodynamic force resisting the approach of a sphere to a plane wall in slip flow. J. Colloid Interface Sci. 1973, 44, 356–360. [Google Scholar] [CrossRef]
- Luo, H.; Pozrikidis, C. Effect of surface slip on Stokes flow past a spherical particle in infinite fluid and near a plane wall. J. Eng. Math. 2008, 62, 1–21. [Google Scholar] [CrossRef]
- Procopio, G.; Giona, M. On the theory of body motion in confined Stokesian fluids. J. Fluid Mech. 2024, 1000, A11. [Google Scholar] [CrossRef]
- Liao, J.C.; Keh, H.J. Slow rotation of a sphere about its diameter normal to two planes with slip surfaces. Fluid Dyn. Res. 2022, 54, 035502. [Google Scholar] [CrossRef]
- Keh, H.J.; Chen, S.H. Low Reynolds number hydrodynamic interactions in a suspension of spherical particles with slip surfaces. Chem. Eng. Sci. 1997, 52, 1789–1805. [Google Scholar] [CrossRef]
- Tsai, M.J.; Keh, H.J. Slow rotation of coaxial slip colloidal spheres about their axis. Colloids Interfaces 2023, 7, 63. [Google Scholar] [CrossRef]
- Park, J.; Youn, J.R.; Song, Y.S. Hydrodynamic metamaterial cloak for drag-free flow. Phys. Rev. Lett. 2019, 123, 074502. [Google Scholar] [CrossRef] [PubMed]
- Boyko, E.; Bacheva, V.; Eigenbrod, M.; Paratore, F.; Gat, A.D.; Hardt, S.; Bercovici, M. Microscale hydrodynamic cloaking and shielding via electro-osmosis. Phys. Rev. Lett. 2021, 126, 184502. [Google Scholar] [CrossRef]
- Wang, B.; Shih, T.-M.; Xu, L.; Dai, G.; Huang, J. Intangible hydrodynamic cloaks for convective flows. Phys. Rev. Appl. 2021, 15, 034014. [Google Scholar] [CrossRef]
- Chen, M.; Shen, X.; Xu, L. Realizing the thinnest hydrodynamic cloak in porous medium flow. Innovation 2022, 3, 100263. [Google Scholar] [CrossRef] [PubMed]


| 0 | 0.1 | 1.05264 | 1.06096 | 1.06776 | 1.07475 | 1.08110 |
| 0.3 | 1.17719 | 1.20910 | 1.23616 | 1.26502 | 1.29224 | |
| 0.5 | 1.34106 | 1.41233 | 1.47662 | 1.54966 | 1.62382 | |
| 0.7 | 1.58556 | 1.73194 | 1.87850 | 2.06633 | 2.29122 | |
| 0.8 | 1.77839 | 1.99546 | 2.23133 | 2.56687 | 3.04339 | |
| 0.9 | 2.10931 | 2.46421 | 2.90022 | 3.63713 | 5.13001 | |
| 0.95 | 2.44379 | 2.95120 | 3.63751 | 4.98083 | 9.08847 | |
| 0.99 | 3.23330 | 4.12306 | 5.51052 | 8.91686 | 39.5699 | |
| 0.995 | 3.57695 | 4.63695 | 6.35356 | 10.8302 | 77.2772 | |
| 0.999 | 4.37868 | 5.83819 | 8.34279 | 15.4916 | 375.817 | |
| 3 | 0.1 | 1.06661 | 1.07727 | 1.08599 | 1.09499 | 1.10318 |
| 0.3 | 1.22971 | 1.27173 | 1.30759 | 1.34605 | 1.38253 | |
| 0.5 | 1.45436 | 1.54840 | 1.63355 | 1.73090 | 1.83047 | |
| 0.7 | 1.81040 | 1.99734 | 2.18340 | 2.42163 | 2.70754 | |
| 0.8 | 2.10904 | 2.37635 | 2.66233 | 3.06505 | 3.63259 | |
| 0.9 | 2.65566 | 3.06589 | 3.55523 | 4.36109 | 5.94513 | |
| 0.95 | 3.24477 | 3.79945 | 4.52184 | 5.88503 | 9.84840 | |
| 0.99 | 4.72957 | 5.61545 | 6.93895 | 10.0551 | 36.1757 | |
| 0.995 | 5.39933 | 6.42583 | 8.02021 | 12.0138 | 67.2352 | |
| 0.999 | 6.97895 | 8.33568 | 10.5539 | 16.7214 | 308.200 | |
| 0.1 | 1.08096 | 1.09408 | 1.10487 | 1.11602 | 1.12619 | |
| 0.3 | 1.28781 | 1.34205 | 1.38884 | 1.43964 | 1.48843 | |
| 0.5 | 1.59668 | 1.72363 | 1.84125 | 1.97937 | 2.12554 | |
| 0.7 | 2.17078 | 2.43602 | 2.71051 | 3.08005 | 3.55939 | |
| 0.8 | 2.77242 | 3.16366 | 3.60266 | 4.26209 | 5.30532 | |
| 0.9 | 4.33307 | 4.95945 | 5.74884 | 7.15332 | 10.4405 | |
| 0.95 | 7.14158 | 8.01670 | 9.22199 | 11.6810 | 20.5762 | |
| 0.99 | 27.8594 | 29.3309 | 31.6397 | 37.4262 | 100.892 | |
| 0.995 | 53.1698 | 54.9006 | 57.7131 | 65.1576 | 201.028 | |
| 0.999 | 252.546 | 254.881 | 258.888 | 269.711 | 995.829 | |
| 0 | 0.1 | 1.07448 | 1.08259 | 1.09027 | 1.09883 | 1.10714 |
| 0.3 | 1.26260 | 1.29684 | 1.33053 | 1.36958 | 1.40911 | |
| 0.5 | 1.53229 | 1.61836 | 1.70793 | 1.81845 | 1.93887 | |
| 0.7 | 1.96739 | 2.17033 | 2.40129 | 2.72019 | 3.12597 | |
| 0.8 | 2.32772 | 2.65284 | 3.04895 | 3.65085 | 4.55048 | |
| 0.9 | 2.96524 | 3.54514 | 4.32675 | 5.71764 | 8.63955 | |
| 0.95 | 3.62238 | 4.49618 | 5.77069 | 8.36688 | 16.5126 | |
| 0.99 | 5.19212 | 6.82146 | 9.49163 | 16.2077 | 77.4399 | |
| 0.995 | 5.87829 | 7.84693 | 11.1697 | 20.0306 | 152.847 | |
| 0.999 | 7.48083 | 10.2390 | 15.1503 | 29.3489 | 749.987 | |
| 3 | 0.1 | 1.09473 | 1.10520 | 1.11515 | 1.12627 | 1.13710 |
| 0.3 | 1.34586 | 1.39171 | 1.43719 | 1.49035 | 1.54460 | |
| 0.5 | 1.72675 | 1.84159 | 1.96211 | 2.11220 | 2.27720 | |
| 0.7 | 2.37874 | 2.63651 | 2.93038 | 3.33719 | 3.85676 | |
| 0.8 | 2.94893 | 3.34311 | 3.82067 | 4.54221 | 5.61483 | |
| 0.9 | 4.01688 | 4.67066 | 5.53746 | 7.04987 | 10.1444 | |
| 0.95 | 5.18308 | 6.11195 | 7.43564 | 10.0545 | 17.9018 | |
| 0.99 | 8.14327 | 9.72311 | 12.2413 | 18.3596 | 70.5166 | |
| 0.995 | 9.48165 | 11.3360 | 14.3899 | 22.2729 | 132.628 | |
| 0.999 | 12.6405 | 15.1434 | 19.4922 | 31.6837 | 614.605 | |
| 0.1 | 1.11576 | 1.12878 | 1.14119 | 1.15511 | 1.16873 | |
| 0.3 | 1.44102 | 1.50180 | 1.56285 | 1.63513 | 1.70994 | |
| 0.5 | 1.98237 | 2.14363 | 2.31670 | 2.53798 | 2.78920 | |
| 0.7 | 3.06884 | 3.45148 | 3.90270 | 4.55654 | 5.45349 | |
| 0.8 | 4.24667 | 4.84996 | 5.61022 | 6.82698 | 8.84049 | |
| 0.9 | 7.34598 | 8.38578 | 9.82542 | 12.5142 | 19.0039 | |
| 0.95 | 12.9532 | 14.4727 | 16.7329 | 21.5216 | 39.2209 | |
| 0.99 | 54.3819 | 57.0794 | 61.5374 | 72.9733 | 199.811 | |
| 0.995 | 104.999 | 108.213 | 113.677 | 128.428 | 400.080 | |
| 0.999 | 503.860 | 508.290 | 516.140 | 539.033 | 1989.86 | |
| 0.25 | 0.1 | 1.08158 | 1.09257 | 1.10380 | 1.11616 | 1.12697 |
| 0.3 | 1.29424 | 1.33811 | 1.38539 | 1.44067 | 1.49232 | |
| 0.5 | 1.62840 | 1.72493 | 1.83757 | 1.98287 | 2.13595 | |
| 0.7 | 2.29990 | 2.48092 | 2.72188 | 3.08955 | 3.58165 | |
| 0.8 | 3.05486 | 3.29394 | 3.65204 | 4.28056 | 5.33622 | |
| 0.9 | 5.14486 | 5.42003 | 5.97088 | 7.21721 | 10.4823 | |
| 0.95 | 9.10527 | 9.23415 | 9.87781 | 11.8890 | 20.6243 | |
| 0.99 | 39.5885 | 37.0743 | 36.2084 | 39.2119 | 100.947 | |
| 0.995 | 77.2932 | 70.9251 | 67.2661 | 69.0240 | 201.097 | |
| 0.999 | 339.308 | 304.622 | 279.012 | 264.561 | 890.644 | |
| 0.5 | 0.1 | 1.09335 | 1.10609 | 1.11914 | 1.13353 | 1.14617 |
| 0.3 | 1.34485 | 1.39842 | 1.45660 | 1.52514 | 1.58953 | |
| 0.5 | 1.75332 | 1.87767 | 2.02393 | 2.21356 | 2.41307 | |
| 0.7 | 2.57623 | 2.82433 | 3.15333 | 3.65150 | 4.30551 | |
| 0.8 | 3.47593 | 3.82082 | 4.32559 | 5.19233 | 6.59805 | |
| 0.9 | 5.84750 | 6.30701 | 7.13339 | 8.89744 | 13.2406 | |
| 0.95 | 10.1171 | 10.5210 | 11.6000 | 14.5364 | 26.1588 | |
| 0.99 | 41.3694 | 39.3699 | 39.3916 | 44.6814 | 127.172 | |
| 0.995 | 79.4179 | 73.6746 | 71.1181 | 75.8685 | 252.616 | |
| 0.999 | 378.755 | 340.898 | 313.664 | 301.139 | 1247.08 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.C.; Keh, H.J. Slow Motion of a Spherical Particle Perpendicular to Two Planar Walls with Slip Surfaces. Fluids 2025, 10, 287. https://doi.org/10.3390/fluids10110287
Chen YC, Keh HJ. Slow Motion of a Spherical Particle Perpendicular to Two Planar Walls with Slip Surfaces. Fluids. 2025; 10(11):287. https://doi.org/10.3390/fluids10110287
Chicago/Turabian StyleChen, Yi C., and Huan J. Keh. 2025. "Slow Motion of a Spherical Particle Perpendicular to Two Planar Walls with Slip Surfaces" Fluids 10, no. 11: 287. https://doi.org/10.3390/fluids10110287
APA StyleChen, Y. C., & Keh, H. J. (2025). Slow Motion of a Spherical Particle Perpendicular to Two Planar Walls with Slip Surfaces. Fluids, 10(11), 287. https://doi.org/10.3390/fluids10110287






