Modeling of the Nose Landing Gear Shock Absorber for Carrier-Based Aircraft and Optimization of Oil Orifice Area Configuration

Abstract

To optimize and improve the nose landing gear shock absorber of a fixed-wing carrier-based aircraft, the cross-sectional area of the oil needle in the main oil orifice and the cross-sectional area of the oil return orifice shall be reconfigured. Firstly, a dynamic analysis of a single landing shock absorber system is conducted, with a focus on explaining the calculation methods for air spring force and oil damping force. Secondly, the shock absorber is modeled and its typical working processes are simulated, including calculations of shipboard landing buffering results under different sinking speeds and catapult extension results under different terminal drag speeds. Phenomena such as wheel transition oscillation and shock absorber hysteresis compression are interpreted. Finally, an orifice area configuration optimization scheme based on the work-energy diagram of the shock absorber system is proposed, with principles and necessary explanations for key steps in the scheme provided. The optimized scheme, which comprehensively considers buffering and extension performance, is applied to a single shock absorber system model for verification. The results show that the main orifice area should exhibit a slight increase near the critical stroke of the high and low pressure chambers. After optimizing the orifice area, under the ultimate sinking speed, the peak load of the shock absorber is reduced by 12.92%, the compression stroke is decreased by 2.91%, and the energy absorption efficiency is increased by 19.90%; the peak load of the tire is reduced by 12.17%, the compression stroke is decreased by 5.92%, and the energy absorption efficiency is increased by 12.28%.

1. Introduction

Most of the landing gear shock absorbers of modern aircraft adopt the form of air spring combined with oil damping. The research on their dynamic performance is relatively complex, but their dynamic models are all established on the classic platform of the two-mass spring-damper system [1]. In terms of the optimization of structural parameters and filling parameters, the goal is to make the aircraft adapt to its take-off and landing environment, coordinate the air spring force and oil damping force, reduce impact loads, and improve buffering efficiency and energy dissipation [2,3].

The FAR (Federal Aviation Regulations) [4] requires that the maximum sink rate of land-based aircraft shall be 3.05 m/s. However, fixed-wing carrier-based aircraft adopt the “impact” landing method. The U.S. Military Standard MIL-A-8863C [5] stipulates that the statistical mean value of the sink rate of carrier-based aircraft shall be 3.7 m/s with a standard deviation of 0.71 m/s, and the design shall be based on the maximum value (5.1 m/s) within the 95% confidence interval. Considering factors such as deck pitch and heave caused by night landing and adverse sea conditions, the sink rate relative to the ship under actual operating conditions will be even greater. The standard [5] further requires that the landing gear shock absorber shall take a safety factor of 1.5 into account during design. Therefore, when verifying structural reliability, the sink rate of many carrier-based aircraft reaches 11 m/s. In addition, for heavy carrier-based aircraft capable of catapult-assisted takeoff, at the end of the catapult stroke, the moment the catapult bar detaches from the catapult shuttle, the nose landing gear buffer system of the aircraft will perform an extension movement. That is, it releases as much elastic potential energy as possible on the remaining ten-odd meters of the flight deck at the bow to raise the nose and establish the initial angle of attack for takeoff from the ship. Therefore, the nose landing gear shock absorber of a carrier-based aircraft needs to have both buffering performance and extension performance, making its relevant parameters even more critical.

The main means to optimize the performance of the shock absorber is to control the flow rate of the oil, and the control of the oil flow rate mainly relies on the oil orifices. Foreign research teams have integrated buffering and retraction functions through an active oil injection system, which increases the aircraft’s crash-resistant load by 50%. At the same time, they optimize the oil orifice layout to reduce the transmission of impact energy [3]. They can also control the stroke change rate of the buffer strut within 25% during the extension process by optimizing the opening sequence of the oil orifice [6]. The latest adaptive variable orifice valve adjusts the damping orifice diameter in real time through mechanical feedback, which can control the buffer force fluctuation within ±5% without electronic components [7]. In addition, there have been corresponding breakthroughs in the improvement of buffer materials [8] and magnetorheological damper control technology [9]. While the aforementioned active control method is undoubtedly effective and has become one of the research directions in the industry, the traditional method—which changes the cross-sectional area of the main oil orifice by inserting an oil needle to passively control the oil damping characteristics—still remains a widely adopted solution for optimizing shock absorber performance in the industry. This is attributed to its advantages of simple structure, extremely low cost, and high safety and reliability.

For the nose landing gear shock absorber of an existing heavy carrier-based aircraft, its filling parameters and main structural parameters have been finalized, while the oil needle of the main oil orifice and the cross-sectional area of the oil return orifice need to be redesigned [10]. In the conventional design of shock absorber structural parameters, the area of the main oil orifice is usually determined based on experience for the values at the start and end of the stroke. Then, based on the basic trend assumption of the ideal oil orifice area curve given in Reference [11], improvements are made through certain optimization strategies. Domestic research teams have established a mathematical model targeting the extension time using the golden section optimization method [12,13]. By substituting the function of the oil orifice cross-sectional area changing with the stroke into the dynamic differential equation, the optimized extension displacement and velocity curves are better than those of the traditional constant-section oil orifice, which verifies the rationality of the variable-section design.

This paper analyzes the structure of the strut-type nose landing gear buffer system, conducts kinematic analysis and modeling for two typical working conditions—landing and extension—and interprets the simulation results, including the interpretation of the work-energy diagram and the causes of the wheel transient oscillation phenomenon. Subsequently, an oil orifice area configuration optimization scheme guided by the work-energy diagram is proposed, and the optimized parameters are introduced into the aircraft nose landing gear buffer system model for comparison, which verifies the rationality of the optimization scheme.

2. Dynamic Equations of the Landing Gear Buffer System

2.1. Overall Motion Equations

The nose landing gear shock absorber of a heavy fixed-wing carrier-based aircraft is simplified as a two-mass spring-damper system. The air, which is mainly used for energy absorption and barely dissipates energy, is simplified as a spring; the oil (for energy dissipation) and various friction-generating mechanisms are simplified as dampers [14]. The landing gear structure is divided into two lumped masses: sprung mass and unsprung mass.

Sprung mass (upper mass): The mass supported by the air spring, including the fuselage, wings, empennage, and outer cylinder of the shock absorber.

Unsprung mass (lower mass): The mass not supported by the air spring, including the piston rod of the shock absorber, brake disk, tires, and wheel carrier.

Unlike rocker arm landing gear, the force exerted by strut-type landing gear on the fuselage can be regarded as being always perpendicular to the ground. Therefore, when analyzing the motion of a single landing gear, it is only necessary to establish the axial motion differential equation. The force-bearing conditions and internal structure of the shock absorber are shown in Figure 1, and its typical working process can be divided into three phases: compression, rebound, and extension. Among these, compression and rebound correspond to the forward and reverse strokes of a single shock absorption process, respectively [15].

Take the center of the wheel as the origin and the downward direction as the positive direction to establish the landing gear coordinate system. The initial value of the vertical position of the unsprung mass is 0, and the initial value of the vertical position of the sprung mass is 0.6. The differential equation of motion of the shock absorber is as follows:

$$\left\{\begin{array}{l}{m}_1{\ddot{s}}_1=m_{1}g-N_f-F_L\\ m_2{\ddot{s}}_2=m_{2}g+N_f-F_t\end{array}\right.$$

(1)

The compression stroke $s$ refers to the relative displacement between the upper and lower mass blocks.

$$s=s_{\max }-\left(s_2-s_1\right)$$

(2)

There exist structural constraint conditions during the motion.

$$0\le s\le s_{\max }$$

(3)

In the equation,

• $s_1$—Vertical position of the sprung mass;
• $s_2$—Vertical position of the unsprung mass;
• $N_f$—Axial force of the shock absorber;
• $F_t$—Tire reaction force;
• $F_L$—Equivalent lift force of the nose landing gear;
• $s_{\max }$—Initial distance between the upper and lower mass blocks.

The first compression process starts at the moment when the wheel touches the deck. At this instant, the upper and lower mass blocks almost start moving downward simultaneously. During this process, the compression amount of the shock absorber increases continuously. When the velocities of the upper and lower mass blocks become equal, the shock absorber compresses to its limit position, and the rebound process begins accordingly. The rebound process continues until the shock absorber compresses again, marking the end of a single action cycle.

The initial conditions of the buffer motion are as follows:

$$\left\{\begin{array}{l}{s}_2=0\\ s_1=-s_{\max }\\ {\dot{s}}_1={\dot{s}}_2=v\end{array}\right.$$

(4)

In the equation, $v$ denotes the vertical velocity of the aircraft relative to the deck during landing.

At the start of the extension motion, $s_2$ and $s_1$ reach their maximum values (which occur before the sudden release of the catapult force) for the tire and the shock absorber, respectively. The extension motion ends when the nose wheel leaves the deck.

2.2. Calculation Methods for Axial Component Forces

When analyzing a single landing gear, the sprung mass is the result of distributing the total weight of the aircraft to the pivot axes of the nose landing gear and main landing gear in accordance with specific principles under static equilibrium conditions. The equivalent lift force ($F_L$) refers to the equivalent decomposition of the total aircraft lift force onto each individual landing gear. The tire reaction force ($F_t$) is determined based on the widely used TR-R-64 semi-empirical model for aircraft tires [16].

$$F_t=\left(1+c_T{\dot{s}}_2\right)f\left(s_2\right)$$

(5)

In the equation, $f\left(s_2\right)$ denotes the static pressure curve of the tire and $c_T$ represents the vertical vibration damping coefficient.

$N_f$ is mainly composed of three components: air spring force, oil damping force, and frictional damping force, i.e.,

$$N_f=F_a+F_{oil}+F_f$$

(6)

2.2.1. Air Spring Force

An air spring is a nonlinear spring that operates on the principle of gas compressibility. Within a specific stroke range, it compresses the gas, reduces the volume of the chamber, and increases the pressure inside the chamber to generate a rebound force [17]. Figure 2 schematically illustrates the compression process of the shock absorber. Among them, the shade of the color of the air chamber indicates the magnitude of the air pressure inside the chamber. The force analysis of the compressor piston throughout the process is based on the assumptions of neglecting its mass and maintaining equilibrium.

When the sprung mass is subjected to pressure, the low-pressure chamber starts to compress first. The compression process of the air spring is regarded as a polytropic process, where $P{V}^{\gamma }$ is a constant [18]. The compressor piston maintains equilibrium under the action of gas pressure on both sides and structural constraint forces. Excluding the influence of atmospheric pressure, according to the polytropic equation of gas, when only the low-pressure chamber is compressed, the expression of the air spring force is as follows:

$$F_a=A_L\cdot P_L=A_L\cdot \left[P_{L0}{({\displaystyle \frac{V_{L0}}{V_{L0}-A_{L}S}})}^y-P_{am}\right]$$

(7)

In the equation,

• $A_L$—Compressed gas area of the low-pressure chamber;
• $P_{L/L0}$—Real-time/initial pressure of the low-pressure chamber;
• $V_0$—Initial volume of the low-pressure chamber;
• $\gamma$—Gas polytropic exponent;
• $P_{atm}$—Atmospheric pressure.

When the pressure in the low-pressure chamber increases to a certain level while the compression stroke is not yet completed, and the pressure in the low-pressure chamber reaches the critical value $P_{L0}^{\prime }$, the forces acting on both sides of the separating piston between the high-pressure and low-pressure chambers become equal. At this point, the high-pressure and low-pressure chambers start coupled compression, and the critical compression amount of the shock absorber $s^{\prime }$ can be calculated using Equation (8).

$$\left\{\begin{array}{l}{P}_{L0}^{\prime }{A}_L=P_{H0}{A}_H\\ P_{L0}^{\prime }=P_{L0}^{\prime }{P}_{L0}{\left({\displaystyle \frac{V_{L0}}{V_{L0}-A_L{s}^{\prime }}}\right)}^y-P_{atm}\end{array}\right.$$

(8)

The subsequent positive stroke is the linkage compression stage. During this stage, the compressor piston maintains equilibrium only by relying on the gas pressure on its two sides. The respective compression strokes $s_H$ and $s_L$ of the high-pressure and low-pressure chambers satisfy the following relationship:

$$\left[P_{H0}{\left({\displaystyle \frac{V_{H0}}{V_{H0}-A_H{s}_H}}\right)}^y-P_{atm}\right]A_H=\left[P_{L0}^{\prime }{\left({\displaystyle \frac{V_{L0}^{\prime }}{V_{L0}^{\prime }-A_L{s}_L}}\right)}^y-P_{atm}\right]A_L$$

(9)

The equivalent stiffness coefficient $K$ of two air springs in series is as follows:

$$\left\{\begin{array}{l}K={\displaystyle \frac{K_H\cdot K_L}{K_H+K_L}}\\ K_H={\displaystyle \frac{A_H}{s_H}}\cdot \left[P_{H0}{\left({\displaystyle \frac{V_{H0}}{V_{H0}-A_H{s}_H}}\right)}^y-P_{atm}\right]\\ K_L={\displaystyle \frac{A_L}{s_L}}\cdot \left[P_{L0}^{\prime }{\left({\displaystyle \frac{V_{L0}^{\prime }}{V_{L0}^{\prime }-A_L{s}_L}}\right)}^y-P_{atm}\right]\end{array}\right.$$

(10)

Finally, the expression for the air spring force is as follows:

$$F_a=\left\{\begin{array}{l}{A}_L\cdot \left[P_{L0}{({\displaystyle \frac{V_{L0}}{V_{L0}-A_{L}s}})}^y-P_{atm}\right],s\le s^{\prime }\\ K(s-s^{\prime }),s>s^{\prime }\end{array}\right.$$

(11)

2.2.2. Oil Damping Force

When the volume of the low-pressure chamber changes, the oil-pressing piston forces the oil fluid to flow between different chambers through the oil holes. The oil damping force originates from the static pressure loss when the fluid flows through the oil holes. According to the Bernoulli equation in fluid mechanics, when the oil flows from $A$ side to $B$ side, the following condition is satisfied [19]:

$${\displaystyle \frac{P_A}{\rho g}}+{\displaystyle \frac{{v_A}^2}{2g}}+h_A={\displaystyle \frac{P_B}{\rho g}}+{\displaystyle \frac{{v_B}^2}{2{C_d}^{2}g}}+h_B$$

(12)

In the equation,

• $P_{A/B}$—Hydraulic pressure of the oil fluid on both sides;
• $v_{A/B}$—Average flow velocity of the oil fluid on both sides;
• $h_{A/B}$—Average height of the oil fluid on both sides;
• $C_d$—Oil fluid contraction coefficient (energy loss when flowing through the orifice).

For the shock absorber, $\Delta h$ can be neglected. Whether in the forward stroke or reverse stroke, the shock absorber velocity is always the average flow velocity on the oil outflow side, while the average flow velocity on the inflow side is the result of the oil being accelerated through the orifice. Taking the forward stroke shown in Figure 3 as an example, based on the assumption of incompressible oil and the assumption of fluid continuity [20], when the oil-pressing piston moves toward side A at velocity $\dot{s}$, the oil will flow toward side B at velocity ${\dot{s}}_d$, i.e., $v_A=\dot{s}$, $v_B={\dot{s}}_d$, and $A_h\cdot \dot{s}=A_d\cdot {\dot{s}}_d$. Thus, the expression of the oil damping force in the positive stroke is deduced as follows:

Figure 3. Mechanism of oil damping force generation.

Figure 3. Mechanism of oil damping force generation.

$$\begin{array}{cc}\hfill F_{oil}& =A_h\left(P_A-P_B\right)=A_h\cdot {\displaystyle \frac{\rho }{2}}\left({\displaystyle \frac{v_B^2}{{C_d}^2}}-v_A^2\right)\hfill \\ & =A_h\cdot {\displaystyle \frac{\rho {\dot{s}}^2}{2{A_d}^2}}\cdot \left({\displaystyle \frac{{A_h}^2}{{C_d}^2}}-{A_d}^2\right)\hfill \end{array}$$

(13)

In the equation,

• $A_{d/ds}$—Area of the main/return oil hole;
• $A_{h/hs}$—Area of the oil-pressing piston in the main/return oil chamber.

The area of the oil orifice generally accounts for approximately 1.5% of the area of the oil-pressing piston, and the oil flow contraction coefficient $C_d$ is less than 1. Therefore,

$${\displaystyle \frac{{A_h}^2}{C_d^2}}-A_d^2\approx {\displaystyle \frac{A_h^2}{C_d^2}}$$

(14)

Including the damping force of the return oil hole, the final expression for the oil damping force can be written as:

$$F_{oil}={\displaystyle \frac{\rho \left|\dot{s}\right|}{2\dot{s}}}\left({\displaystyle \frac{A_h^3{\dot{s}}^2}{C_d^2{A}_d^2}}+{\displaystyle \frac{A_{hs}^3{\dot{s}}^2}{C_{ds}^2{A}_{ds}^2}}\right)$$

(15)

The above equation is the quadratic damping formula for oil fluid, which is widely used in shock absorber design [18,19].

2.2.3. Frictional Damping Force

For the strut-type landing gear equipped on this aircraft model, the bending friction caused by the misalignment between the piston rod and the piston outer sleeve is neglected, and the cup friction caused by the compression of the air chamber wall is considered [21,22]. The empirical formula for frictional damping can be written as:

$$F_f=k_{fa}{F}_a{\displaystyle \frac{\left|\dot{s}\right|}{\dot{s}}}$$

(16)

The friction coefficient $K_{fa}$ is generally taken as approximately 0.15.

3. Simulation Analysis

MATLAB/Simulink software has the advantage of modular modeling. Relying on this platform, the modeling and simulation of the nose landing gear buffer system of a certain type of fixed-wing carrier-based aircraft are carried out. The main parameters of the buffer are shown in

Table 1. Example aircraft nose bumper parameters.

Parameter	Value	Parameter	Value
Maximum stroke	60 cm	Recommended working stroke	54 cm
Initial inflation pressure of low-pressure chamber	1.5 Mpa	Initial inflation pressure of high-pressure chamber	7.4 MPa
Initial volume of low-pressure chamber	4320 mL	Initial volume of high-pressure chamber	4550 mL
Compressed gas area of low-pressure chamber	113.1 cm2	Compressed gas area of high-pressure chamber	153.94 cm2
Gas polytropic exponent of low-pressure chamber	1.1	Gas polytropic exponent of high-pressure chamber	1.2
Area of main oil hole	variable cross-section	Area of return oil hole (forward stroke)	4 cm2
Oil contraction coefficient of main oil chamber	0.8	Area of return oil hole (reverse stroke)	1.2 cm2
Oil density	865 kg/m3	Oil contraction coefficient of return oil chamber	0.7
Oil-pressing area of main oil chamber	75.213 cm2	Oil-pressing area of return oil chamber	41.04 cm2

. Assume that the initial height difference between the upper and lower mass blocks of this aircraft is 1.5 m, where $m_1$ and $m_2$ are 3840 kg and 51.5 kg, respectively. The ode45 solver is used, with a maximum simulation step size of 0.001 s to ensure sufficient calculation accuracy [23].

3.1. Drop Shock Performance

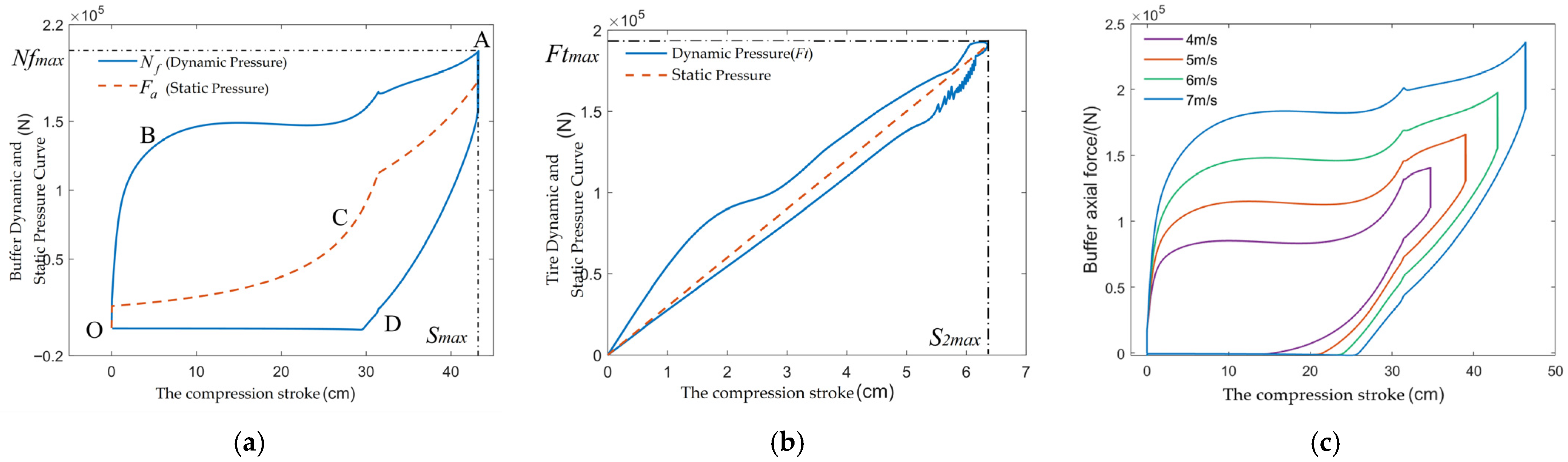
Under normal circumstances, the sink rate of this aircraft onto the ship is 6 m/s. The drop shock simulation results under this working condition shown in Figure 4a,b show the variation in vertical velocity and vertical position of $m_1$ and $m_2$, respectively. The maximum compression amount of the shock absorber reaches 41.542 cm, and the maximum compression amount of the tire is 6.523 cm. The shock absorber completes approximately two shock absorption cycles within 2 s, with the first shock absorption cycle lasting 0.532 s.

It is not difficult to see from Formula (11) that the air spring is a nonlinear spring. The movement of the compressor piston requires the pressure difference between its two sides to reach a certain threshold. When the compression stroke $s$ is 0, there is $F_{a\min }=A_L(P_{L0}-P_{atm})$. At the moment the wheel touches the ground, the tire begins to compress immediately, while the compressor piston is still restrained by the structural constraint forces. There is no relative movement between the inner and outer cylinders of the shock absorber. Only when the tire support reaction force increases to $F_t=F_{a\min }+m_{2}g+F_f$ will the shock absorber start to compress. There is an obvious time window $t_{del}$ between the tire’s second contact with the ship and the buffer’s second compression; this is also due to the fact that $F_t$ needs to reach the buffer’s compression threshold. In the first action cycle, this time window is not obvious because the sinking speed is very high.

Figure 4c shows the variation in each axial component force within the first shock absorption cycle. It can be observed that, due to the presence of the dual-air-chamber structure, all axial forces inside the buffer exhibit obvious phase characteristics at the same time. t1 and t4 are the transition moments between the actuation of the low-pressure chamber and the linkage of the dual chambers; the period from t2 to t3 is the transitional oscillation phase for the conversion between the positive and return strokes. The wheel leaves the deck at moment t5, after which the tire reaction force becomes zero.

The work-energy diagram can intuitively reflect the buffer’s ability to absorb and dissipate energy. Figure 5a shows the work-energy diagrams of the buffer under a sinking speed of 6 m/s. It can be observed that during the positive stroke, the axial force changes along the curve O-B-A; the air spring force changes along the curve O-C-A; and the difference between the two curves represents the magnitude of the damping force. Since energy is the integral of force over its acting distance, during the positive stroke, the integral of the axial force represents the energy absorbed by the buffer, and the area of the closed curve OBAC represents the work done by the damping force (i.e., the energy dissipated in the positive stroke). The return stroke starts from point A: the axial force changes along the curve A-D-O; the gas polytropic process does not dissipate energy, so the air spring force returns along the original path A-C-O; the area of the closed curve OCAD represents the energy dissipated in the return stroke. Similarly, during the return stroke, the integral of the axial force represents the energy released by the buffer, and the area of the closed curve OBAD is the total energy dissipated by the buffer in the first action cycle.

It is noted that the D-O segment of curve A-D-O is a horizontal line segment, corresponding to the period from time t5 to the end of a single shock absorber cycle. During this period, the tire is in a suspended state, the axial force of the shock absorber is 0, and the air spring force maintains a state of equilibrium with the resultant force of the oil damping and friction damping. However, the reverse stroke of the shock absorber continues, and the relative velocity between its inner and outer cylinders—i.e., the shock absorber extension speed—remains constant until the shock absorber is fully extended. At the end of the single operation cycle of the shock absorber, the wheel still does not touch the ground. Instead, as shown in Figure 4b, the second operation cycle of the shock absorber begins only after the tire touches the ground and the tire support reaction force reaches the compression threshold of the shock absorber.

Similar to the buffer, the tire is also an important energy-absorbing component. Figure 5b shows the work-energy diagrams of the tire. Obviously, the damping force of the tire is much smaller than its spring force, and the work-energy change in the rebound phase tends to be linear. Both the tire and the buffer play a role in energy absorption. The compression stroke, peak load, and energy absorption efficiency are important indicators for evaluating their performance. The calculation method of energy absorption efficiency $\eta$ is as follows [24,25]:

$$\eta =\left({\displaystyle {\int }_0^{S\max }{N}_{f}ds}\right)/\left(F_{\max }{S}_{\max }\right)$$

(17)

Figure 5c shows that under different sinking speeds, the work-energy diagrams of the buffer are roughly similar in shape, indicating that this model can reflect the authenticity of the buffer system model within a certain speed range.

Table 2. Nose gear landing performance.

Sinking Speed (m/s)	4	5	6	7
Buffer Compression Stroke (cm)	35.106	39.427	43.298	46.643
Buffer Peak Load (kN)	142.842	168.539	200.479	238.986
Buffer Energy Absorption (kJ)	32.449	47.885	66.062	86.658
Buffer Energy Absorption Efficiency (%)	64.71	72.06	76.11	77.74
Tire Compression Stroke (cm)	4.771	5.612	6.643	7.859
Tire Peak Load (kN)	143.431	169.205	201.279	239.964
Tire Energy Absorption (kJ)	3.899	5.548	7.838	11.082
Tire Energy Absorption Efficiency (%)	56.98	58.43	58.62	58.76

presents the load and energy absorption conditions of the buffer and tire under different sinking speeds. It can be observed that all indicators increase with the increase in sinking speed.

3.2. Extension Performance

The distance between the reverse stroke curve A–D in Figure 5a and the horizontal axis represents the axial force of the shock absorber during the reverse stroke, which can reflect the extension capability of the nose landing gear to a certain extent. However, there is an essential difference between the reverse stroke of the shock absorber and the extension of the nose landing gear:

In terms of the action process, the two have different initial conditions. Before the start of the extension movement, $m_1$ and $m_2$ are both at the limit compression position. When the catapult bar is disconnected, the tire and the shock absorber start to extend simultaneously. The reverse stroke of the shock absorber differs: it is not difficult to see from both Figure 4c and Figure 5b that the compression-rebound cycle of the shock absorber is significantly longer than that of the tire, and the two are out of sync. In terms of the research subject, the main focus of the extension movement is the vertical displacement of $m_1$, which provides the initial angle of attack for the carrier-based aircraft at the end of the catapult stroke [26]. Its value is the sum of the total extension length of both the shock absorber and the tire. However, the reverse stroke of the shock absorber mainly focuses on the relative distance between $m_1$ and $m_2$.

Figure 6 shows the variation in the extension speed of the upper and lower mass blocks under the conditions of a full-aircraft mass of 22.5 t, a final towing speed of 60 m/s, and a free taxiing distance of 12.5 m. The tire oscillation lasts only 0.025 s, indicating good performance.

Table 3. Nose gear protrusion performance.

Final Towing Speed (m/s)	55	60	65	70
Vertical Sudden Unloading Load (kN)	191.071	221.776	249.440	237.716
Extension Time (s)	0.221	0.202	0.188	0.174
Vertical Upward Displacement of Sprung Mass (cm)	46.968	48.875	51.316	51.069
Buffer Extension Stroke (cm)	29.531	28.823	28.189	26.952
Vertical Final Speed of Sprung Mass (m/s)	1.994	2.437	2.906	3.264
Angle of Attack Increment (deg)	3.807	3.960	4.157	4.137

reflects the extension movement results of the aircraft under different final towing speeds. It can be observed that the extension of the nose landing gear can bring an angle of attack increment of approximately 4° to the fuselage, which is quite significant during the takeoff phase. However, due to the short free taxiing distance, even at the minimum final towing speed, the elastic potential energy stored in the buffer system is not fully released. Additionally, the extension stroke of the buffer slightly decreases as the final towing speed increases—this proves that the higher the final towing speed, the smaller the proportion of the buffer’s extension in the vertical displacement of $m_1$. Furthermore, the higher the final towing speed, the greater the upward speed of the aircraft at the moment of leaving the ship. Nevertheless, the vertical displacement of $m_1$ does not increase accordingly. In terms of the angle of attack increment, a final speed of 65 m/s is more appropriate.

3.3. Wheel Oscillation Phenomenon

From the previous simulation results, obvious oscillation at the junction of the positive and return strokes can be clearly observed. Combined with Figure 4a, the following explanation can be provided from the perspective of the dynamic model:

0.143 s to 0.149 s: The upward speeds of $m_1$ and $m_2$ become equal at 0.143 s. After this moment, the buffer should theoretically enter the return stroke. However, due to the change in the movement direction of the pressure piston, $F_f$ exhibits a “step” change at its maximum value point, causing $N_f$ to decrease suddenly within $\Delta t$(a minuscule time). Since the value of $m_1$ is much larger than $m_2$, the resultant force acting on $m_2$ increases in a stepwise manner accordingly, leading to its upward “jump”. As a result, the buffer is forced to enter the compression phase again, and the frictional damping changes sign simultaneously. $N_f$ then increases suddenly, causing the speed of $m_2$ to quickly synchronize with that of $m_1$ again. Such a cycle repeats, resulting in the oscillation of the wheel at the end of the positive stroke. During this phase, the speed of $m_2$ is always upward, meaning the tire reaction force continuously decreases. Additionally, the damping force dissipates energy, leading to a continuous attenuation of the oscillation amplitude. Meanwhile, the buffer is forced to compress by a small distance. It is not until 0.149 s that the speed of $m_1$ catches up with the damped oscillation speed of $m_2$, and the first compression phase of the buffer truly ends.

0.149 s to 0.157 s: At 0.149 s, $F_a$ reaches its maximum value during the forced compression phase. At this moment, $N_f$ decreases in a stepwise manner, resulting in the resultant force acting on component $m_2$ becoming zero. During the subsequent time $\Delta t$, $F_f$ is forced to increase in a “step” manner, causing component $m_2$ to instantly obtain a downward acceleration. However, the buffer’s return stroke has already started, and $F_f$ decreases rapidly after increasing. Therefore, the upward speed of $m_2$ quickly catches up with that of $m_1$ again. The above process repeats at the moment when their speeds become equal. In this process, both $F_t$ and $N_f$ continuously decrease until the axial force—after increasing in a stepwise manner—makes the resultant force on $m_2$ zero. Only then does the oscillation process end, allowing the buffer to rebound smoothly. Figure 7 shows a schematic diagram of the force acting on $m_2$ during the transitional oscillation phase.

From the above analysis, it can be concluded that the cup friction in the axial direction of the buffer is the main cause of the excessive wheel oscillation phenomenon. When the friction coefficient in the model is set to 0, the oscillation phenomenon disappears accordingly. However, in practice, around the junction of the positive and return strokes, the friction force switches repeatedly between dynamic friction and static friction. In the model of this paper, the dynamic friction coefficient is used to replace the maximum value of the static friction coefficient. Additionally, other factors such as the instability of the oil flow contraction coefficient under low-speed conditions and the gas polytropic coefficient under high-pressure conditions are not considered. Therefore, the actual wheel oscillation time is longer and the amplitude is larger than the simulation results in this paper.

4. Optimization of Orifice Area Configuration

4.1. Optimization Objectives and Ideas

From the perspective of energy, there is an inherent contradiction between landing buffering and extension. Within a single cycle, for landing buffering, the more energy the buffer dissipates, the better; this means the [energy dissipation] curve should be as full as possible. For the extension process, it is desirable for the aircraft to release more energy; this means the curve A-D-O should be as close to the curve A-C-O as possible. The contradiction between the two lies in the work done by the damping force during the return stroke. Since the frictional damping force is directly related to the air spring force and almost unchangeable, dynamically adjusting the magnitude of the oil damping force is the key to optimizing the buffer’s performance. In general, the axial force is usually controlled by inserting a variable-section oil needle to realize the variation in orifice area with stroke, and mechanical valves are used to configure different oil return orifice areas for the positive and return strokes.

Considering the performance of both landing buffering and ejection extension comprehensively, an orifice area optimization scheme based on the buffer system’s work-energy diagram is proposed. The logic of this scheme is summarized in the following four steps:

(1)

Damping Force Curve: Under the condition that the gas polytropic parameters are determined, draw the ideal work-energy diagram of the buffer. Since the frictional damping force is a function of the air spring force, the ideal curve of oil damping force varying with buffer stroke is obtained accordingly.

(2)

Velocity Curve: Draw the ideal tire work-energy diagram. Assuming gravity and equivalent lift are constant, derive the corresponding relationship between the vertical velocity of each of the upper and lower mass blocks and the resultant force. Further, obtain the curve of buffer compression velocity varying with stroke.

(3)

Orifice Area Configuration: Based on the calculation formula of oil damping force, derive the constraint relationships among three elements: the curve of main orifice area varying with buffer stroke, and the oil return orifice areas corresponding to the positive and return strokes.

(4)

Difference Iteration: Import the orifice area parameters into the simulation model, and compare the simulated work-energy diagram of the buffer and the work-energy diagram of tire reaction force with the previously drawn ideal diagrams. Invert the difference and bring it into the ideal curve, and repeat the iteration several times until the difference falls within the acceptable range.

Figure 8 provides a brief description of the optimization steps. In the figure, “A–B” indicates the variation in variable A with variable B. In the figure, the yellow boxes represent the optimization objectives, and the pink boxes represent the optimized objects.

4.2. Optimization Steps

The drawing of the ideal work-energy diagram is the first step in design optimization and also the core part of this method. The following principles should be followed during the process:

(1)

The drawing of the ideal buffer work-energy diagram must be based on the gas polytropic curve, while the drawing of the ideal tire work-energy diagram must be based on the tire static pressure curve.

(2)

Due to the generally weak damping effect of aircraft tires, their action cycle is shorter than that of the buffer. However, this does not affect the selection and optimization of the area ratio. The reason is that only one of the positive or return strokes is required to generate the variation curve of the main orifice cross-section, and only a small segment (or even a single point) of each of the positive and return strokes is needed to proportion the oil return orifice area. Therefore, the drawn ideal buffer work-energy diagram can end when the tire leaves the ground, and it is not necessary to cover the entire buffering cycle.

(3)

Analyzing the buffering process from the perspective of energy, the total energy absorbed by the two major energy-absorbing components (the buffer and the tire) during a single positive stroke is

$${\displaystyle \int N_{f}ds}+{\displaystyle \int F_{t}d{s}_2}={\displaystyle \frac{1}{2}}\left(m_1+m_2\right)v_0^2+m_{1}g\Delta s_1+m_{2}g\Delta s_2-{\displaystyle \int F_{L}d{s}_1}$$

(18)

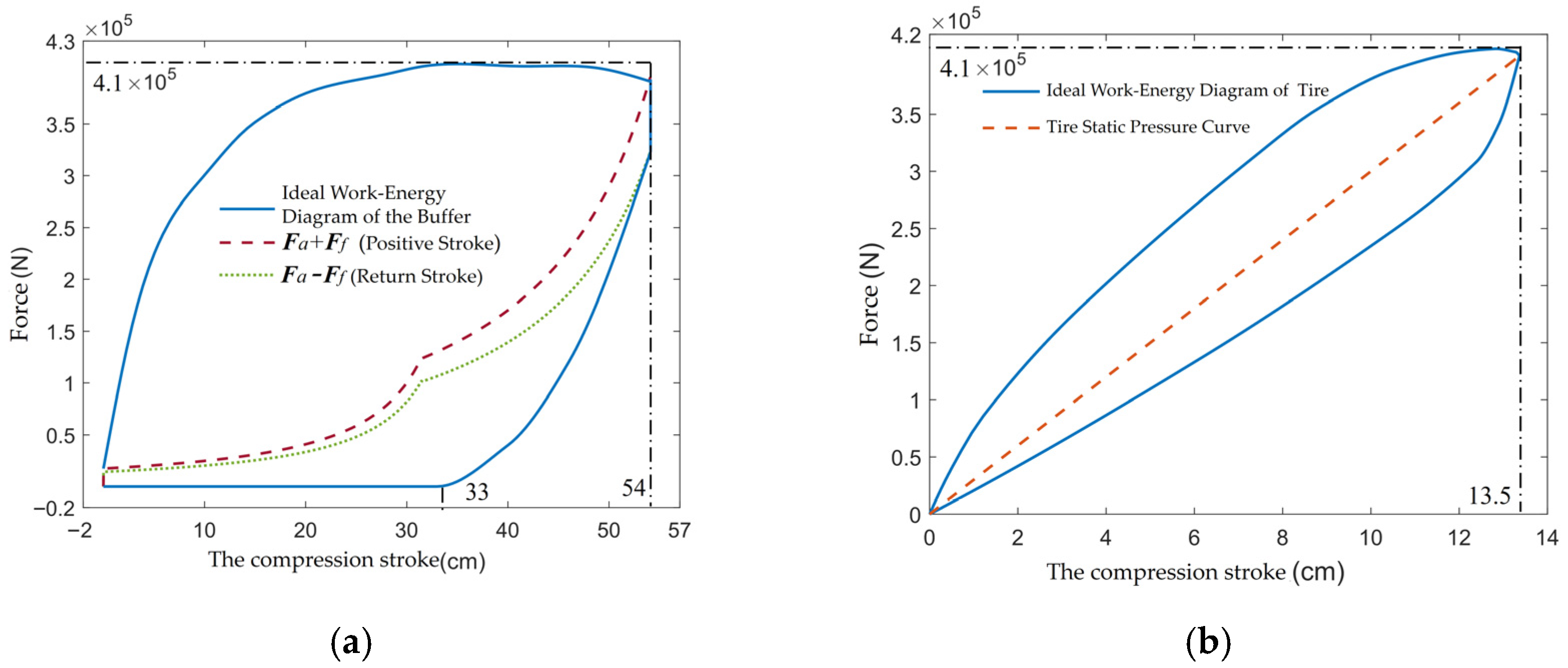
Among them, the difference between the change in gravitational potential energy and the work done by the equivalent lift is not significant; therefore, the integral of the work-energy diagram during the positive stroke should be kept constant. On this basis, to obtain the main orifice area values for the entire stroke, a sufficiently high speed should be selected to make the compression stroke reach the limit position. However, if the speed is too high, it will trigger the structural limits of the buffer, which changes the termination condition of the positive stroke and makes it impossible to inversely derive the variation in the main orifice area from the work-energy diagram. Thus, it is necessary to ensure that the compression stroke limit at the maximum sinking speed is 54 cm, the recommended maximum stroke.

(4)

During the positive stroke, both the axial force of the buffer and the tire reaction force reach their maximum values simultaneously. Since the tire damping is generally smaller than that of the buffer, the oscillation phenomenon should occur after the start of the return stroke. To ensure the differentiability of the tire work-energy diagram curve, the tangent of the curve at its compression limit should be parallel to the y-axis. Therefore, the maximum tire reaction force should be slightly greater than the maximum value of the static pressure curve and should appear before the end of the tire compression stroke. Meanwhile, the corresponding peak axial force of the buffer at this moment satisfies (zzzz) and occurs in the middle to later part of the buffer’s positive stroke. As a result, the work-energy diagram curve of the positive stroke first increases and then decreases, and should preferably maintain an upwardly convex shape—this enables higher buffering efficiency.

The following is the necessary explanation for the numbered steps in Figure 8:

(1)

Buffer Positive Stroke: $F_{oil}(s)=N_f-(1+k_{fa})F_a$

Buffer Return Stroke: $F_{oil}(s)=(1-k_{fa})F_a-N_f$

Tire Compression Speed: $v_2(s_2)=\left[F_t(s_2)/f(s_2)-1\right]/c_T$

(2)

The conversion process between $F_{itatal}-s_i$ and $v_i-s_i$ is as follows:

$$a={\displaystyle \frac{dv}{dt}}={\displaystyle \frac{dv}{ds}}{\displaystyle \frac{ds}{dt}}=v{\displaystyle \frac{dv}{ds}}$$

(19)

Therefore, the conversion relationship from $v_2-s_2$ to $F_{2total}-s_2$ is as follows:

$$F_{2total}=m_{2}a=m_2\nu (s_2){\displaystyle \frac{d{\nu }_2}{d{s}_2}}$$

(20)

Separate the variables in the separated form (16), and integrate both sides of the equation simultaneously to obtain the conversion relationship from $F_{1total}-s_1$ to $v_1-s_1$ as follows:

$$\begin{array}{cc}\hfill {{\displaystyle \int }}_{s_{10}}^{s_1}{F}_{1total}d{s}_1& =m_1{{\displaystyle \int }}_{v_{10}}^{v_1}vdv={\displaystyle \frac{1}{2}}{m}_1(v_1^2-v_{10}^2)\hfill \\ \hfill {\nu }_1^2& ={\nu }_{10}^2+({{\displaystyle \int }}_{s_{10}}^{s_1}{F}_{1total}d{s}_1)/m_1\hfill \end{array}$$

(21)

(3)

It can be derived from the calculation formula of the oil damping force that:

$$\left\{\begin{array}{cc}\hfill {\displaystyle \frac{F_{oil}(s)}{s\left|s\right|(s)}}& ={\displaystyle \frac{\rho }{2}}{\displaystyle \frac{A_h^3}{C_d^2{A}_d^2(s)}}+{\displaystyle \frac{\rho }{2}}{\displaystyle \frac{A_{hs}^3}{C_{ds}^2{A}_{ds}^2}}={\displaystyle \frac{C_1}{A_d^2(s)}}+{\displaystyle \frac{C_2}{A_{ds}^2}}\hfill \\ \hfill C_1& ={\displaystyle \frac{\rho }{2}}{\displaystyle \frac{A_h^3}{C_d^2}},C_2={\displaystyle \frac{\rho }{2}}{\displaystyle \frac{A_{hs}^3}{C_{ds}^2}}\hfill \end{array}\right.$$

(22)

Based on the above formula, the forward and reverse strokes each generate a constraint relationship, namely:

$$\left\{\begin{array}{ll}\hfill {\displaystyle \frac{F_{oil}\left(s\right)}{{\dot{s}}^2\left(s\right)}}& ={\displaystyle \frac{C_1}{A_d^2\left(s\right)}}+{\displaystyle \frac{C_2}{A_{ds+}^2}}\hfill \\ \hfill {\displaystyle \frac{F_{oil}\left(s\right)}{-{\dot{s}}^2\left(s\right)}}& ={\displaystyle \frac{C_1}{A_d^2\left(s\right)}}+{\displaystyle \frac{C_2}{A_{ds-}^2}}\hfill \end{array}\right.$$

(23)

When the areas of the positive and negative pressure oil chambers and the oil density remain constant, the values of $C_1$ and $C_2$ in the formula are always constants, thus deriving the constraint relationship among the three unknown quantities.

4.3. Simulated Results After Optimization

Assuming the maximum sinking speed of the aircraft relative to the ship is 11 m/s, the ideal work-energy diagrams of the buffer and the tire are drawn as shown in Figure 9, based on the recommended working stroke of the buffer (54 cm).

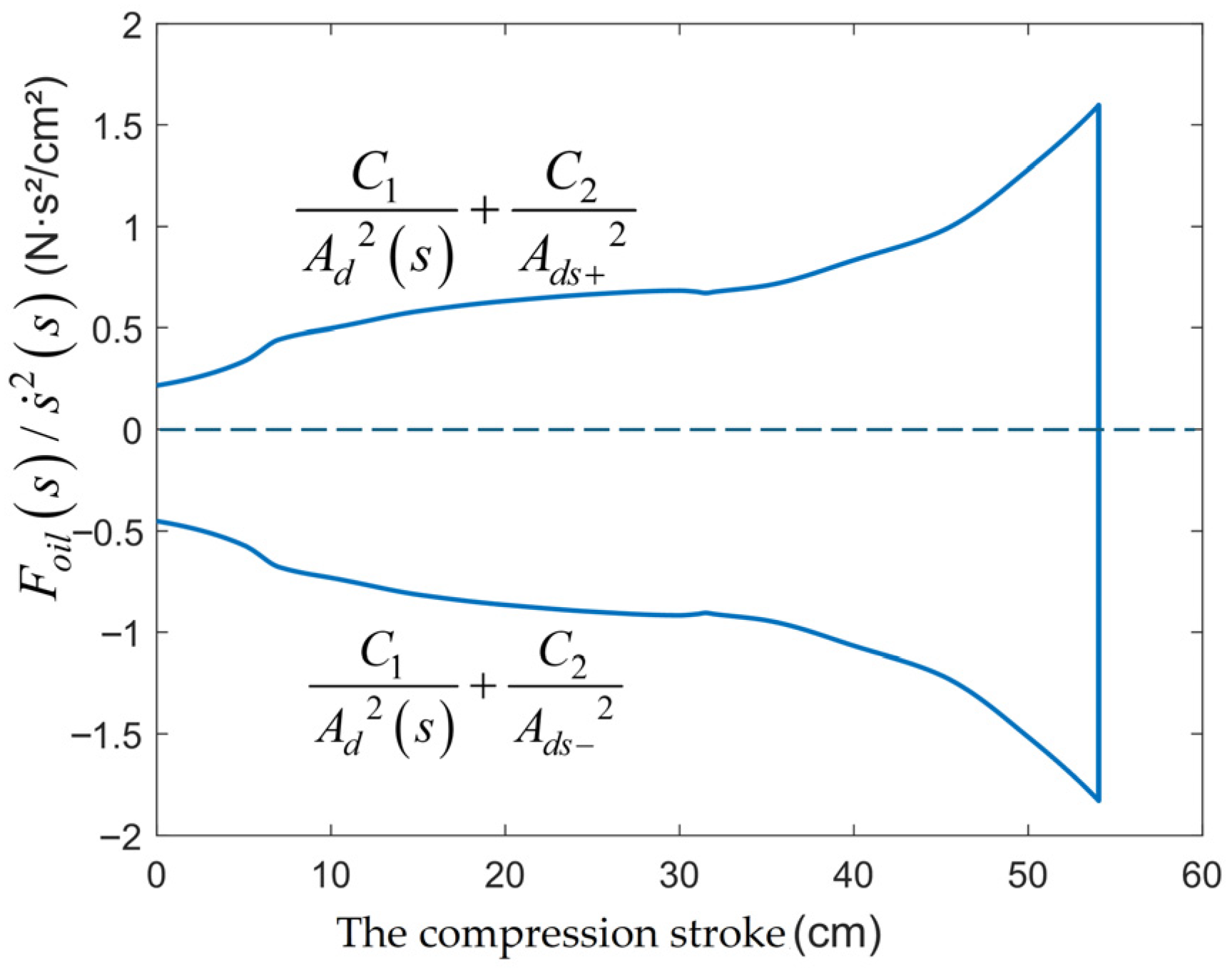
The optimized constraint relationships for the orifice area configuration are obtained as shown in Figure 10. Among them, the constants are $C_1$ = 2.8753 Ns²/cm²,$C_2$ = 0.6101 Ns²/cm².

The unknown quantities are a variable $A_d\left(s\right)$ that changes with the buffer stroke, and two constants $A_{ds+}$ and $A_{ds-}$. There are two constraint relationships as shown in Equation (23), resulting in an infinite number of solutions for the equation. Theoretically, any oil hole configuration that conforms to the oil flow contraction coefficient assumption in Table 1 and satisfies the constraint relationships of Equation (23) can achieve the optimization objective. Since the problem to be solved involves the modification of a specific model, structural parameters should be modified as little as possible. When the oil return hole area of the forward stroke is kept at 4 cm², there is no need to change the initial area of the main oil hole $A_d(0)$. 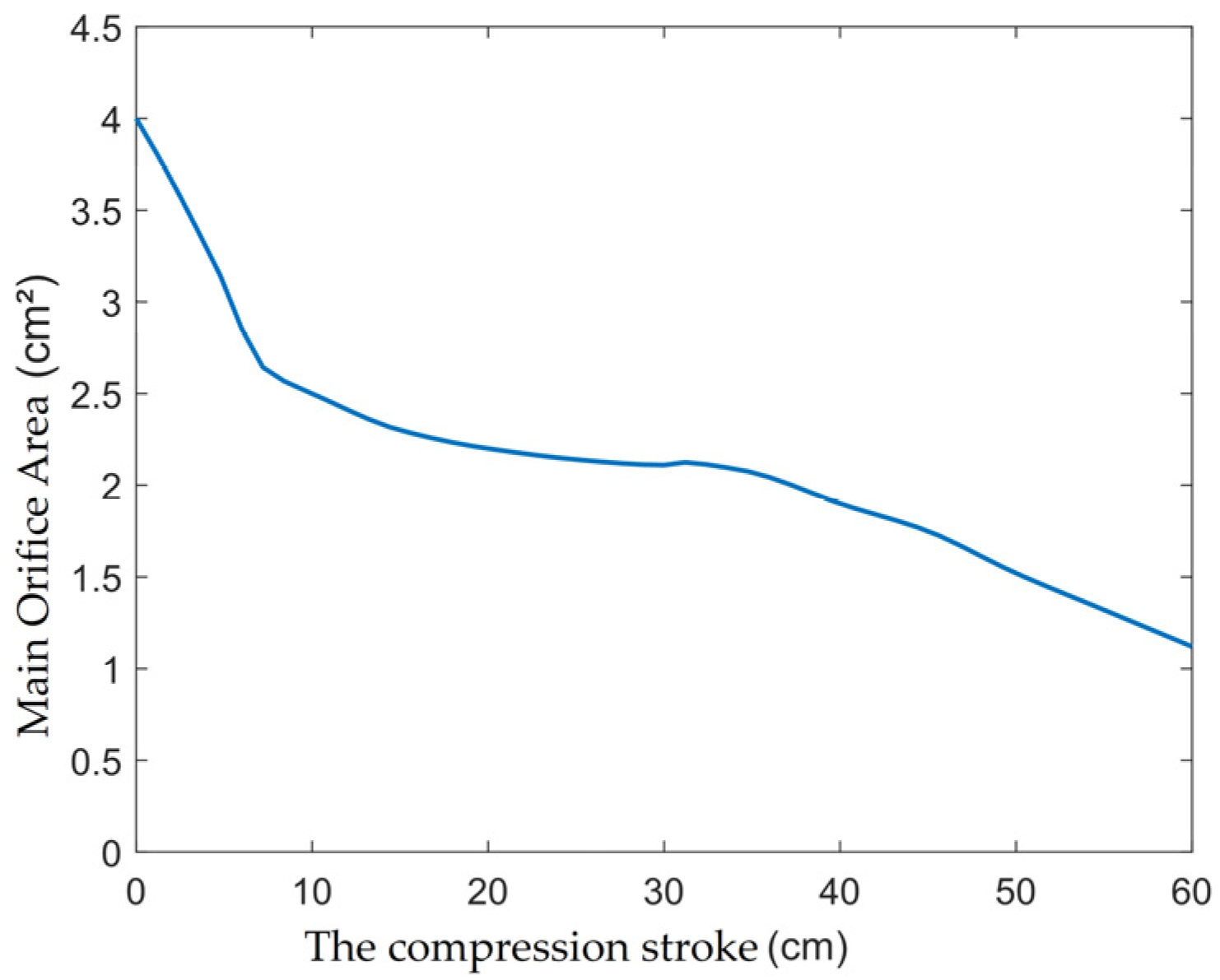The re-planning of the main oil hole area can be achieved only by changing the oil needle. After three interpolation iteration calculations, the optimized oil return hole area of the reverse stroke is 2.33 cm², and the area curve of the main oil hole is shown in Figure 11.

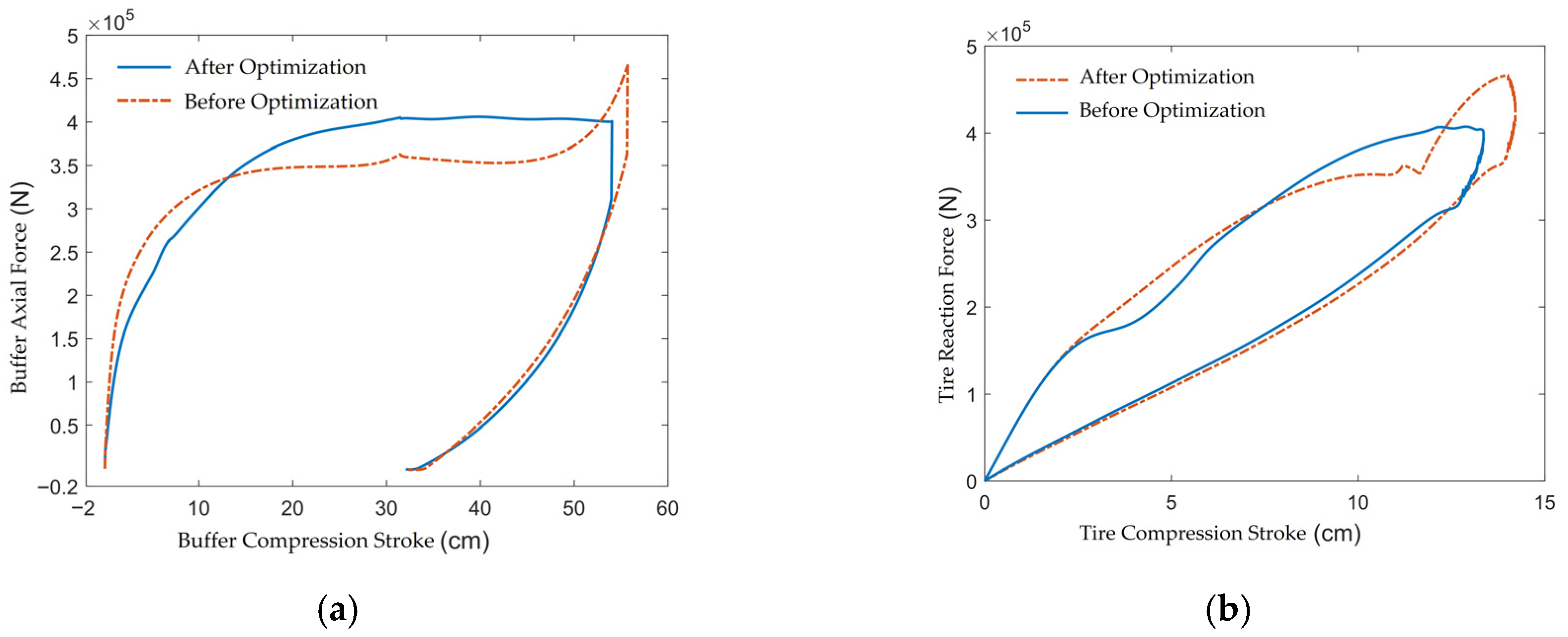
It can be seen that the orifice area of the dual-chamber buffer does not conform to the monotonically decreasing concave function form presented in [14]. Near the linked critical compression stroke of 31.5 cm, to make the axial force of the buffer more linear, the optimized main orifice area increases slightly and exhibits a convex function pattern during the linked compression phase. At a sinking speed of 11 m/s, the comparison of buffer performance before and after optimization is shown in Figure 12 and

Table 4. Performance Comparison of the Buffer System Before and After Optimization.

Indicator	Before Optimization	After Optimization	Improvement (%)
Buffer Peak Load (kN)	463.964	406.003	12.92
Tire Peak Load (kN)	466.247	407.486	12.17
Buffer Compression Stroke (cm)	55.66	54.04	2.91
Tire Compression Stroke (cm)	14.20	13.36	5.92
Buffer Energy Absorption Efficiency (%)	73.01	87.54	19.90
Tire Energy Absorption Efficiency (%)	58.55	65.74	12.28

. It is evident that this optimization scheme has a significant effect on reducing the peak load of the buffer, controlling the compression stroke, and improving the buffering efficiency.

5. Conclusions

The Main Research Results of This Paper:

(1)

The shock absorber system model established in this paper can intuitively reflect various motion characteristics of the aircraft during the carrier landing buffering and catapult extension processes, and has practical value. The model constructed based on the Simulink platform allows for easy modification of parameters and initial conditions.

(2)

Within a single buffering cycle, all axial component forces exhibit a phased pattern due to the dual-air-chamber structure; the cup friction between the inner and outer cylinders of the buffer is the main cause of the wheel transitional oscillation phenomenon. The higher the sinking speed, the higher the energy absorption efficiency of the buffer, while the extension effect reaches its optimum when the drag end speed is 65 m/s.

(3)

The orifice area configuration optimization scheme proposed in this paper can directly match the orifice area value according to the required buffer work-energy diagram. To improve buffering efficiency, the main orifice area should show a slight increase near the critical stroke. This optimization scheme has a significant effect on improving the performance of the buffer system.

Limitations and Future Research Directions:

(1)

The modeling process of the air spring force is overly simplified. In engineering practice, temperature has a significant impact on the air spring. The assumptions of neglecting the gas–liquid interaction and setting the gas polytropic coefficient as a constant are too idealized. A more accurate air spring force model with smaller errors will be established in future research.

(2)

This optimization scheme has limitations: “Interpolation iteration”, as a key step of the scheme, has not been summarized into standardized operating procedures that can guide practice in the paper. For this equipment case, the authors manually adjusted the main orifice area for the next iteration based on the difference between the work-energy diagram generated from the current main orifice area optimization result and the ideal work-energy diagram. After two adjustments, the deviation can be reduced to 0.5%. Determining how to standardize the difference iteration will be the focus of future research.