Abstract
Adjoint-based optimization methods, that were previously in the realm of computational fluid dynamics (CFD) research, are now available in commercial software. This work explores the use of adjoint-based optimization to maximize mixing and combustion efficiencies for a supersonic combustor. To this end, a two-dimensional combustor was considered with parallel hydrogen injection. Simulations were carried out based on the steady Reynolds-Averaged Navier–Stokes equations and optimization was performed using a simplified passive scalar field instead of the full reactive flow problem. The optimization of a triangle-shaped mixing element is considered in addition to a case allowing the entire bottom of the combustor to deform. The relatively small mixing element could not boost efficiency significantly. By comparison, the optimization of the combustor wall resulted in both mixing and combustion efficiency gains accompanied by total pressure loss penalty. The optimization achieved higher efficiency compared to the baseline by extending the total volume of the reaction zone. The presented proof-of-concept results are relevant for the design of hypersonic vehicle propulsion systems, such as scramjets.
1. Introduction
Hypersonic vehicles have been the subject of interest in the past century with the first manned atmospheric hypersonic flight achieved in the X-15 program in 1961 [1]. These vehicles could enable access-to-space in single-stage-to-orbit (SSTO) space planes [2] or significantly reduce intercontinental flight times. Accomplishing this is a technological challenge, as exemplified by the National Aerospace Plane (NASP) program back in the late 1980s. NASP was a U.S. program that aimed to develop a SSTO hydrogen aircraft with airbreathing propulsion. These hypersonic vehicles have to support high heat and mechanical loads and must be coupled with highly integrated propulsion systems. Interest in such a program was sparked by successful subscale scramjet tests, and by significant advances in computational fluid dynamics (CFD) as well as in structures and heat-resistant materials [3]. While progress in hypersonic product development was clear, in order to bring diverse technologies to a level of maturity that was sufficiently high to realize, such a program had proven to be an important hurdle. It led to the cancellation of the program in 1994.
Since the NASP era, CFD has gained an important place in general hypersonic vehicle design, especially in the last decade, which has been boosted by a more widespread availability of computational power with relative affordability. This development has made CFD a powerful tool to complement wind tunnel and flight testing. This trend is observable in the literature of the past two decades with hypersonic flight test programs such as the X43 [4], X51 [5], HyShot [6], HIFiRE [7], IXV [8,9] and the more recent BOLT program [10,11]. Moreover, commercial softwares have matured in recent years, offering users a wide variety of solvers for different applications as well as design methods including adjoint-based optimization. The growing availability of adjoint CFD solvers has also been observed in the CFD vision 2030 report [12,13]. Adjoint-based optimization efficiently computes sensitivities with a cost independent of the number of design variables (single flow solution needed), making it well-suited for aerodynamic shape optimization problems with few objectives and many design variables.
Adjoint-based aerodynamic shape optimization has been reported in design problems related to airfoils [14,15,16,17,18,19,20,21], three-dimensional wings [22,23,24], turbomachinery blades [21,25,26,27,28,29] and inlets [30,31]. Multi-disciplinary optimization problems have also been successfully tackled with the adjoint method in aero-structural [32,33,34] and aero-structural-acoustic designs [35]. However, the number of studies on the application of adjoint-based optimization on supersonic [36] and hypersonic [37,38,39] design problems remains limited. Adjoint-optimization has not been widely explored especially in high-speed flows with mixing and combustion because the derivation of the adjoint equation for each species cannot be easily generalized. A way to circumvent this is by relying on a passive scalar transport equation. This method has been adopted by Mosca et al. [40] in a T-mixer geometry and by Eggl et al. [41] in a stirring device. Another analysis [42] was conducted in a 2D channel under subsonic conditions to optimize the uniformity of particle distribution in the outlet, validating the strategy with numerical differentiation and quantifying the reduction in the calculation cost compared to traditional methods.
On the hypersonic air-breathing propulsion side, scramjet technology, where the flow remains supersonic throughout the whole internal flow path, has been identified as the enabling technology for hypersonic flight. Improving mixing and combustion efficiency in scramjets is extremely challenging (see, e.g., [43,44]), but crucial in making their use to propel hypersonic vehicles viable. Although operating at high speeds is critical for an efficient operation, the short time of mixing air–fuel within combustor can lead to incomplete combustion and reduction in efficiency [45]. A parallel wall injection strategy, such as in the experiment of Burrows and Kurkov [46], has the advantage of cooling the wall through the fuel but has a very limited mixing capability. A transverse injection mechanism such as in the HyShot II [47] has a higher penetration depth but induces higher total pressure losses due to the jet obstruction. Shock waves and shock wave boundary layer interactions are flow features that can have a positive or negative impact on scramjet mixing and combustion. When it comes to optimizing a given scramjet combustor with CFD, physics-based interventions are most commonly reported in the literature. Kummitha et al. [48,49,50,51,52] presented a series of work where obstacles are introduced in the flow or at walls to change the flow field dynamics of an existing experimentally studied combustor. Landsberg et al. [44,53] rely on jet-based flow field manipulations to improve a specific type of combustor flow path. The introduced changes in the aforementioned works are of empirical nature and only a small number of simulations are finally performed. Alternatively, Shenoy et al. [54,55] optimized a flushwall injector geometry through a surrogate model build based on a design of experiment type engineering approach. Kumar et al. [56] did also rely on surrogate modeling to find an optimal relative positioning of three strut injectors. While past studies demonstrate that geometric modifications, injection strategies, and physics-based interventions can significantly enhance scramjet mixing and combustion efficiency, these approaches are often case specific. The more generic surrogate modeling-based optimization workflow does treat the CFD as a black box with respect to the objective functions and therefore does not exploit the extensive information contained in the CFD flow field. Adjoint gradient-based optimization offers a systematic alternative by providing sensitivity information that directly links the flow field to performance metrics like mixing and combustion efficiency. To the authors’ knowledge, the potential of adjoint-based CFD to optimize supersonic combustors remains unquantified.
The present study sets out to assess the applicability of adjoint-based methods for supersonic combustor optimization based on the capabilities of readily available commercial CFD software. The investigated case is the classical supersonic hydrogen combustor experiment of Burrows and Kurkov [46] used here to present a proof of concept regarding the capabilities of CFD with adjoint-based optimization. Preliminary results were previously presented at the 3rd International Conference on High-Speed Vehicle Science and Technology [57]. Section 2 presents test case alongside the adjoint-based optimization strategy, loop-holing the need for multi-species formulation. Results and conclusions are discussed in Section 3 and Section 4, respectively.
2. Methods
2.1. Flow Configuration
In order to assess the capability of the adjoint-based optimization, the supersonic (non-)reacting wall jet experiment of Burrows and Kurkov [46] is adopted for simulations as shown in Figure 1. The experimental setup consists of hydrogen injected parallel to a vitiated air-stream behind a backward facing step. Two different stages are simulated: (I) mixing of various species (H2, H2O and N2); and (II) combustion taking place as a result of O2 being added to the airflow. The combustion stage is initialized with the solution of the mixing stage. Further details of the simulation strategy such as inflow conditions and reaction mechanisms are summarized in [58].
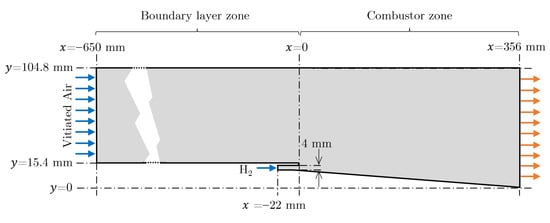
Figure 1.
Schematic of the Burrows–Kurkov supersonic combustion experiment [46]. Not to scale.
2.2. Formulation of the Optimization Problem
From an engineering point of view, the purpose of combustion chamber optimization might be to maximize thrust (typical in defense applications), to minimize emissions or to maximize combustion efficiency (typical in civil applications). The computational cost of adjoint-based optimization using reactive simulations is extremely high because of the relatively high cost of a single cost function evaluation. Furthermore, even the most recent commercial software do not have an adjoint formulation for generic reactive and multi-species flows [59,60], i.e., one adjoint equation per species transport equation. To overcome this limitation, an alternative formulation is suggested.
Adjoint-based optimization is used here based on passive scalar injection instead of multi-species flow simulation. Consequently, a compatible optimization target must be defined. In this case, mixing efficiency instead of combustion efficiency is used for optimization and it is hypothesized that enhanced mixing efficiency also results in boosted combustion efficiency. This approach is inspired by recent studies considering optimization problems emerging from passive scalar transport [40,41]. It is worth recognizing that passive scalar simulations cannot be used to maximize thrust originating inherently from the reaction of multiple species.
The passive scalar transport equation for the fuel concentration used in the adjoint-based optimization is
Here, and are the velocity vector and density, and is the unknown variable describing the spatial distribution of hydrogen concentration. The terms represent the linear eddy diffusivity with being the dynamic viscosity, the Schmidt number and the subindex t denoting turbulent quantities.
In order to enhance mixing, the optimization problem is set to maximize the variance of hydrogen at the outlet. The resulting cost function depends on the employed geometry (mesh) displacement vector field and the array of all field variables , including velocity components, pressure values, etc. Therefore, the J cost function to be minimized is
Here, is the variance of the hydrogen concentration at the outlet of the combustor given by
The mean hydrogen concentration value at the outlet is defined as
where mm is the height of the outlet section.
It is hereby pointed out that diverse strategies can be adopted to improve mixing, with different levels of geometrical modifications. A possible implementation is to introduce a small immersed obstacle at the mixing interface of the hydrogen and the air streams. Another possibility is to add a mounted obstacle to the wall in front of the injector. Both strategies have been considered in [58] and the results for a mounted triangle-shaped obstacle are revisited here. In addition, a setup where the diverging wall section is allowed to deform freely is explored.
The following geometric constraints are imposed mainly for the deformations direction and location. The triangle was placed between and 203 mm with a 3 mm long vertical side located at mm on the bottom wall of the combustor. In this case, the geometry is able to move freely only between and 203, and the vertical wall at mm can only move in the vertical direction (). This maintains the displacement between the length of obstacle and does not extend to the lower wall of the combustor. By comparison, the entire lower wall was optimized solely with vertical deformations between mm and 300 mm.
Previous analysis not presented here revealed that the obstacle positions from 80 mm and downwards have a positive impact on the outlet concentration [58]. Additionally, the 300 mm limit is to prevent deformation on the outlet wall. The resultant shapes are presented in Figure 2, where both the displacements and the direction of the deformation field are depicted. The geometrical constraints for the triangle are also visible in the vectors mainly on the vertical wall of the obstacle.
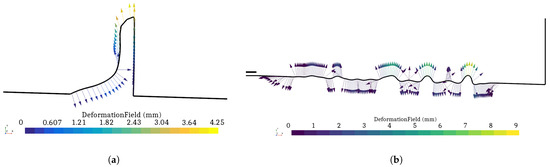
Figure 2.
Deformation field with displacements and direction for the two optimized cases: (a) triangle and (b) wall.
2.3. Numerical Approach
The steady-state coupled solver of Simcenter STAR-CCM+ 2206 [59] is used. Turbulence modeling is handled by the k- shear stress transport (SST) model [61]. This Reynolds-Averaged Navier–Stokes (RANS) model is used with default settings (SST-2003 following NASA’s naming convention [62]). Governing equations are discretized using second-order spatial discretization scheme. Inviscid fluxes are treated with the Advection Upstream Splitting Method (AUSM+) with Flux Vector Splitting (FVS) [63]. Convergence is assessed through a combination of residual levels, mass flow imbalance and relative change in measures such as the forces on the walls.
Modeling the mixing stage with a passive scalar entails differences in the flow field. Compared to the multispecies simulation with fuel injection, thermophysical properties of the flow are not influenced by passive scalar concentration. For this reason, the x-velocity profiles along different the combustor differ in the case of the multispecies and passive scalar simulation cases as depicted in Figure 3. Shear layers near the wall ( cm) are present in both cases but the profiles differ clearly, even though passive scalar simulations have been set up with the same properties as the multispecies simulations with matching inflow conditions. Note that the injector boundary conditions in the passive scalar case have been adapted in order to match the total pressure profiles of the multispecies simulations and the experiments in the reactive case. Additionally, Figure 4 shows the difference in the fuel concentration for the multispecies and passive scalar. Despite the differences in the presence of fuel along the domain for the two cases, caused by the non-influencing character of the passive scalar into the flow properties (for example in density and momentum), the fuel region is considered similar enough near the wall to be optimized.
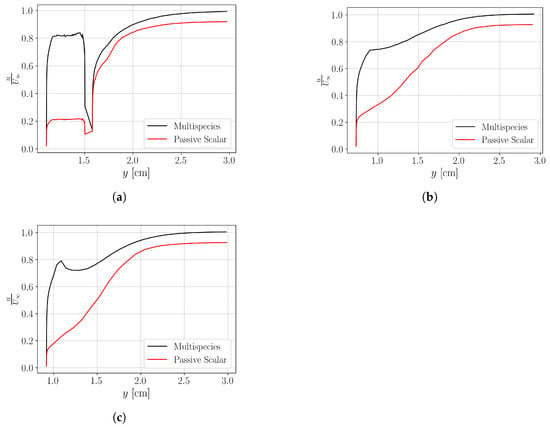
Figure 3.
Comparison of the x-directional velocity profiles (u) between the mixing stage with multispecies and passive scalar strategy at (a) mm, (b) mm and (c) mm. The velocity fields are normalized with the freestream velocity of the multispecies case .
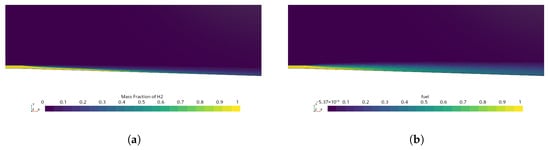
Figure 4.
Comparison of the fuel mass fraction flow field between multi-species mixing case (a) and passive scalar (b).
In spite of the depicted differences in shear layer evolution and fuel concentration, passive scalar simulations were found to be useful because some benefits of the identified favorable geometries translated to multi-species flow simulations. This can be seen in the results section (Section 3), where there is the comparison between the optimized cases with the baseline. The Peclet number based on the combustor length, hydrogen diffusivity and the air inflow velocity is . Accordingly, the flow is overwhelmingly dominated by advection underpinning the passive scalar simplification.
Regarding the adjoint optimization, the general minimum residual with deflated restarting (GMRES-DR) algorithm is used with a fix number of steps. Firstly, an initial flow solution is provided to then compute the sensibilities of the gradients with the adjoint solver. With these sensibilities, the deformation field is calculated, considering the geometric constrains previously mentioned, and a new flow solution is computed with the new geometry. This loop was split into 500 iterations of the adjoint solver and 500 iterations for the following CFD with the new deformed geometry, and run until the cost function found a constant value. In this case, since the objective was to maximize the fuel variance (see Equation (2)) at the outlet, when this variable reached a constant maxima. For the triangle optimization, around 400 iterations of the entire loop were necessary to reach convergence, whereas for the wall optimization, 600 due to the bigger area of deformation.
3. Results and Discussion
This section presents the results of the different optimization problems with adjoint-based CFD. Section 3.1 discusses the supersonic combustor. General comments on the methodology are provided in Section 3.2.
3.1. Scramjet Mixing Optimization
Figure 5 reports the validation of simulations with experimental data in the case of the reference geometry (referred to as baseline case) for both mixing and combustion stages. Further details of the validation are provided in [57,58]. In general, a good agreement is found, with predictions similar to what has been reported in the literature [64]. The same mixing and combustion configurations are used for the adjoint-based optimization simulations.
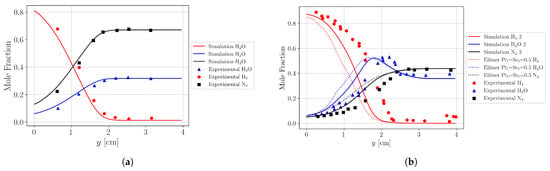
Figure 5.
Mole fraction at the outlet for the (a) non-reacting and (b) reacting combustor setup. The experimental data and Eilmer simulation results correspond to [46] and [64], respectively.
Figure 6 presents the comparison of both the mixing and reacting stages for the main variables used in the optimization. A clear effect of the optimization on the outlet concentration of hydrogen is shown, with an increase in its variance of around 15% for the optimized obstacle and more than double for the wall optimization. Therefore, the optimization conducted reached the objective imposed on maximizing the variance of H2 on the outlet of the mixing stage. The increase in mixing efficiency supports this optimization, where higher values of this variable correspond to higher variance, with an increase of 10% for the wall case (see Table 1). Additionally, the mixing stage results presented indicate that the use of a passive scalar to model H2 in the optimization is potentially beneficial for this type of setup.
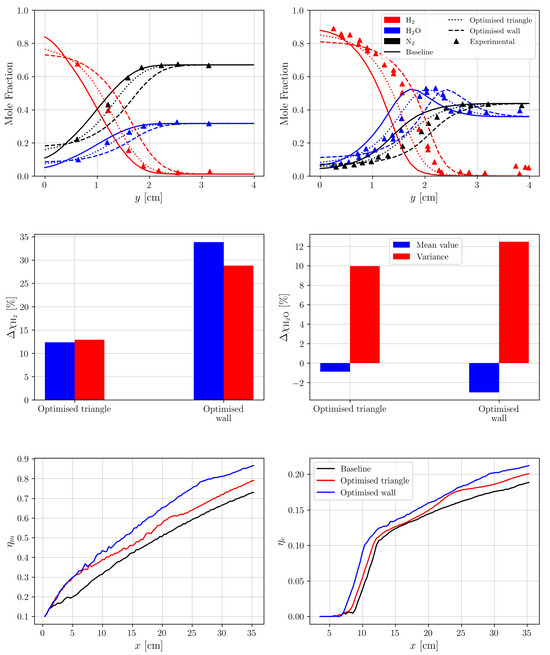
Figure 6.
Comparison between the baseline and optimized cases for mixing (left) and reacting (right) stages of the following: outlet concentration (top row); mean and variance hydrogen concentration differences compared to the baseline case at the outlet (middle row) and mixing and combustion efficiencies (bottom row).

Table 1.
Comparison between baseline and optimized cases for efficiency, pressure loss and thrust potential at both mixing and combustion stages.
When looking at how the modified geometry affects the combustion stage, the variance of the product of the reaction (H2O) does increase together with the combustion efficiency but only around 2% in the best case. In Figure 6, the effect of the obstacles in the combustion efficiency is depicted with a sharp increase in the variable after the position of the optimized triangle (200 mm) as opposed to the continuous increase in the baseline case. Overall, a strongly mixed limited combustion is still observed. The improvements are not as noticeable in the case of the optimized triangle which is analyzed in depth in previous studies [57,58]. Therefore this case is excluded from further analyzes here.
Figure 7c demonstrates the limitations of parallel injection in the baseline case corresponding to the exit species profiles of Figure 5b. Mixing is limited to a thin region elongated in the streamwise direction, and fuel does not reach deeper layers of the air stream. Two different optimization cases are investigated to compare them with the baseline case. The first optimization case proposed is by introducing a mounted obstacle to enhance the mixing of the species (referred to as optimized triangle case). Different shapes and positions were analyzed as mentioned previously, leading to an initial triangle shape to be optimized. The second optimization case allows the lower wall of the combustor to deform freely, in order to explore other potential strategies to improve mixing (referred to as optimized wall case). The optimized geometries are then used in a reacting setup with the same boundary conditions as the baseline case.
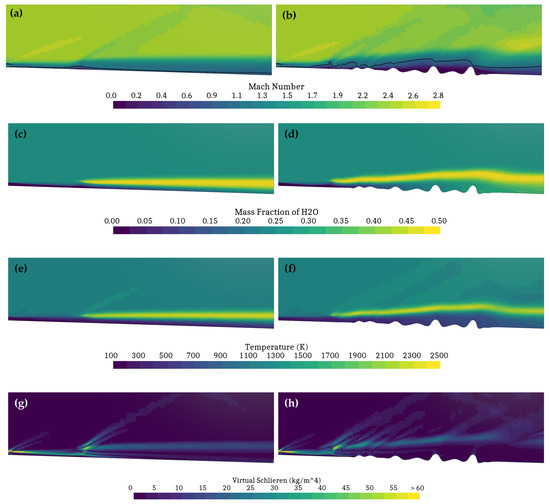
Figure 7.
Contour plots of field variables in the reacting case: baseline simulation (left column) and optimized wall (right column). Mach number with an isoline at Ma = 1 (a,b); H2O mass fraction (c,d); Temperature (e,f); virtual Schlieren (g,h). The field of view covers the region between the injector outlet and the domain outlet.
However, combustion in the optimized wall case shows promising improvement even in the reacting stage. The benefit of the optimized wall manifests into an increased combustion efficiency peaking at 21.8% at the outlet. By comparison, the maximum combustion efficiency in the baseline case is 19.9% so that the optimization results in a 9.5% overall improvement as detailed in Table 1. The optimized wall case results in a substantially elongated reaction zone thanks to the hills and valleys introduced by the adjoint-based optimization. Figure 6 indicates that the combustion efficiency increases monotonically in the combustor as the vertical extent of the reaction zone grows with the streamwise distance. Logically, the optimizations suggest that elongating the reaction zone is crucial to enhance mixing and combustion efficiencies when parallel injection is employed. Figure 7 provides a visual comparison between the baseline and wall optimized case for several flow variables. It is clear that the obstacles of the optimized wall are introducing a bigger mixing area (see Figure 7) which leads to an increase in the combustion region as well. This is depicted in Figure 7h, with an increment in bright zones of the virtual Schlieren (density gradient contour) where the reactive area is present, as well as an increment in the outlet area where high H2O concentration is found (Figure 7d).
Table 1 also provides the relative total pressure loss along the combustor evaluating the penalty caused by the obstacles. For both stages, the increment in pressure loss is around 2% for the best case. In the mixing stage this appears to be acceptable given the 10% efficiency increment. However, in the reacting stage, the improvement in combustion efficiency is comparable to the losses. As a final quantity of interest, the thrust potential (TP) [64,65], also known as combustor effectiveness concept [66], is computed. It is obtained by expanding one-dimensional flow quantities at a given streamwise location through an ideal (reversible), isentropic and adiabatic nozzle. As such, the TP is an indicator of the thrust that you could ideally generate by truncating the combustor. The TP is influenced by the losses in total pressure as well as by the chemical reactions [64]. In analogy to previous work [64,65], the computation assumes that flow is expended back to the free-stream static pressure which is presently taken as the inflow boundary pressure. The TP in Table 1 is provided based on a unit depth. In reacting conditions, the TP increases by 3.13 % and 2.27 % for the optimized triangle and wall, respectively. The TP of the optimized cases do indicate that the small increase in combustion efficiency (≈2%) is sufficient to balance the ≈2% increase in pressure losses.
3.2. Limitations
A grid independence study was carried out in a previous work [58] and it demonstrated that further refinement does not lead to improvements when baseline mixing and combustion simulations are compared to experimental results, as shown in Figure 5. Separate grid independence study was not carried out for simulations of the optimized geometry. From a flow physics perspective, the major changes observed in the present wall-based parallel injection case are in the extend of the mixing/reaction zone for which the baseline mesh independence study did indicate sufficient grid accuracy. Furthermore, results might be significantly impacted by the choice of turbulence model and boundary conditions. The authors acknowledge the importance of sensitivity analysis and uncertainty quantification regarding the aforementioned inputs of the simulation. However, a comprehensive uncertainty analysis is beyond the scope of the present study.
The specific choice of Menter’s SST turbulence model in the present work follows from its wider adoption in the hypersonic CFD community [44,48,49,50,51,52,65,67,68,69,70,71,72]. Note that variation in its usage does exist with combinations of modeling constants, source term formulations and practical implementations in CFD solvers, which makes it difficult to perform comparisons between codes. Moreover, recent work on a controlled RANS code-to-code comparison on hypersonic SWBLI cases [73] indicated a general scatter in predictions. Essentially, it is not possible to state that one turbulence model or turbulence model variation is consistently better over the other. This observation can be translated to the flow fields considered in the present work. The SST model, like other RANS models, fails when it comes to predict more detailed supersonic combustor dynamics for which scale-resolving simulations are better suited but at a significant increase in computational cost [74]. Certainly, large eddy simulations have gained popularity recently in supersonic combustion modeling [75,76]. However, with engineering design in mind, a RANS model such as the SST remains a valid choice for comparative studies.
The passive scalar approach has been used to circumvent the inherent limitation of adjoint-based solvers in multi-species conditions leading to one adjoint equation per governing equations (species equation included in this case). Due to this, the incoming fuel has to be modeled similarly to the incoming airflow as a single species air. This could induce changes in incoming fuel mass flow. Currently, the boundary conditions are kept the same as in the mixing simulation, except for the total pressure which is adapted to match experimental total pressure values at the step. Figure 3 illustrates the influence of this change on various axial velocity profiles.
The validity of the passive scalar optimization approach might depend on the type of injection mechanism and validations with other scramjet combustors, such as the HyShot II [69] or HIFiRE2 [68], should be performed. From a practical perspective, the adjoint method with passive scalar should, similarly to what is observed here, rely on flow field manipulations (shocks and mixing layers) to achieve its goal. In slotted injection cases such as the HyShot II with multiple injector spread across the transverse wall direction, constraints on the deformation of the holes could be linked to one another to avoid asymmetric optimization results (if not desired). In angled injection cases, as seen in the REST type engines [44], the method could be used to deform part of the wall boundaries in conjunction with other flow field manipulation methods such as cascade injectors [53].
The passive scalar optimization approach presented herein is oriented to improve non-reacting setups. This inherently limits the scope of physics which are present in comparison with a reacting setup where heat release plays an important role. From an engineering point of view, relying on non-reacting simulations to improve mixing is a common strategy which assumes that improved mixing behavior directly translates in improved combustion as exemplified by the work of Landsberg et al. [44,53]. The main motivation is a reduced computational cost obtained by omitting reactions and avoid the introduction of associated chemical kinetics and turbulence chemistry interaction modeling assumptions. Other strategies could be to reduce the computational cost of reacting simulations by simplifying the turbulent combustion physics [77]. This is however out of the scope of the present work.
Regarding the optimized geometries presented, the higher freedom of the optimizer could result in challenging shapes to manufacture. Specifically, to this combustor, as a cold hydrogen layer separates the combustor zone from the wall, additive manufacturing with existing materials can be achieved. However, this will not be the case in any type of combustor. Therefore, the optimization restrictions need to be carefully chosen, depending on the combustor’s constraints. It is worth mentioning that the full wall optimization case identifies key positions for an obstacle to be placed, which could potentially maximize the impact on the objective function and could alleviate the aforementioned manufacturing constraints. Manufacturing challenges are left to be explored in the future with the note that wire arc additive manufacturing [78] and roboforming [79] are found particularly promising for the creation of complex shapes like the ones proposed here.
4. Conclusions
The findings suggest that commercial CFD and adjoint-based optimization is sufficiently mature enough to consider reactive flows in the context of high-speed propulsion systems. In order to use the method in a multi-species CFD context, a proxy measure for mixing had to be considered. This is achieved through a passive-scalar representation of the fuel concentration.
Regarding mixing enhancement in a generic scramjet combustor with parallel fuel injection at the lower wall, the adjoint-based method together with passive scalar transport delivered two designs with an increase in the variance of the fuel concentration at the outlet. It is clear that with more deformation restrictions, the improvement is less noticeable (as seen in the triangle case) than when leaving more freedom. However, unconstrained optimization might result in configurations that are challenging to manufacture.
Nevertheless, the optimization of the wall presents insights on the case that can be used for a more accurate optimization. Substantial improvement in combustion efficiency was found only when a relatively large part of the combustor wall was altered. This resulted in a combustion efficiency of 21.8% compared to the baseline 19.9%. The improvement in combustion efficiency was accompanied with a decrease in total pressure loss which grew from 9.0% in the baseline case to 11.1% in the optimized case, suggesting that increasing efficiency required performance drop.
The optimization case underlines the maturity of adjoint-based optimization to reach desgin targets. It also highlights the bottlenecks of similar optimizations. Combustion efficiency was improved substantially by the optimization at the cost of higher total pressure drop. In short, efficiency was boosted by increasing losses inside the combustor.
The difference between baseline and optimized configurations is substantial but benefits are difficult to evaluate because of uncertainties associated with the employed RANS modeling framework. Future work might focus on quantifying and reducing such uncertainties and exploring more sophisticated direction and line search algorithms. Alternative parameterization of the geometry could also be considered for an increased control over the deformation including freeform deformation.
Author Contributions
Conceptualization, J.-J.O.E.H. and T.I.J.; methodology, C.R.S. and J.-J.O.E.H.; software, C.R.S.; validation, C.R.S.; formal analysis, C.R.S., J.-J.O.E.H. and T.I.J.; investigation, C.R.S., J.-J.O.E.H. and T.I.J.; resources, T.I.J.; data curation, T.I.J.; writing—original draft preparation, C.R.S. and N.J.P.; writing—review and editing, J.-J.O.E.H. and T.I.J.; visualization, C.R.S.; supervision, J.-J.O.E.H. and T.I.J.; funding acquisition, T.I.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are not publicly archived for privacy reasons but may be obtained from the corresponding author on reasonable request.
Acknowledgments
The authors would like to thank Marc Famada Vizcaino of Destinus and Alberto Simón Félix for valuable discussions during their MSc studies at Cranfield University.
Conflicts of Interest
Author Jimmy-John Olivier Etienne Hoste is employed by Destinus SA. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Anderson, J. Hypersonic and High Temperature Gas Dynamics, 2nd ed.; AIAA: Reston, VA, USA, 2006. [Google Scholar]
- Bruno, C.; Czysz, P. Future Spacecraft Propulsion Systems: Enabling Technologies for Space Exploration; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Guy, R. Hypersonic propulsion: Status and challenge. In AGARD, Hypersonic Combined Cycle Propulsion; NATO: Brussels, Belgium, 1990. [Google Scholar]
- McClinton, C. X-43-Scramjet power breaks the hypersonic barrier: Dryden lectureship in research for 2006. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 1. [Google Scholar]
- Hank, J.; Murphy, J.; Mutzman, R. The X-51A scramjet engine flight demonstration program. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008; p. 2540. [Google Scholar]
- Steelant, J.; Mack, A.; Hannemann, K.; Gardner, A. Comparison of Supersonic Combustion Tests with Shock Tunnels, Flight and CFD. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar]
- Bowcutt, K.; Paull, A.; Dolvin, D.; Smart, M. HIFiRE: An international collaboration to advance the science and technology of hypersonic flight. In Proceedings of the 28th International Congress of the Aeronautical Sciences, Leiden, The Netherlands, 23–28 September 2012; p. 998. [Google Scholar]
- Roncioni, P.; Ranuzzi, G.; Marini, M.; Battista, F.; Rufolo, G. CFD aerothermodynamic characterization of the IXV hypersonic vehicle. In Proceedings of the 7th European Symposium on Eerothermodynamics of Space Vehicles, Brugge, Belgium, 9–12 May 2011; pp. 9–12. [Google Scholar]
- Paris, S.; Charbonnier, D.; Tran, D. Experimental and numerical investigation of aerothermal characteristics of the IXV hypersonic vehicle. In Proceedings of the 7th European Symposium on Aerothermodynamics, Brugge, Belgium, 9–12 May 2011; Volume 692, p. 47. [Google Scholar]
- Berry, S.; Mason, M.; Greene, F.; King, R.; Rieken, E.; Basore, K. LaRC aerothermodynamic ground tests in support of BOLT flight experiment. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0091. [Google Scholar]
- Wheaton, B.; Berridge, D.; Wolf, T.; Araya, D.; Stevens, R.; McGrath, B.; Kemp, B.; Adamczak, D. Final design of the Boundary Layer Transition (BOLT) flight experiment. J. Spacecr. Rocket. 2021, 58, 6–17. [Google Scholar] [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; Technical Report; NASA: Washington, DC, USA, 2014.
- Cary, A.; Chawner, J.; Duque, E.; Gropp, W.; Kleb, B.; Kolonay, R.; Nielsen, E.; Smith, B. The CFD Vision 2030 Roadmap: 2020 Status Progress and Challenges. Technical Report. 2021. Available online: http://www.cfd2030.com/report (accessed on 1 June 2025).
- Srinath, D.; Mittal, S. An adjoint method for shape optimization in unsteady viscous flows. J. Comput. Phys. 2010, 229, 1994–2008. [Google Scholar]
- Kavvadias, I.; Papoutsis-Kiachagias, E.; Dimitrakopoulos, G.; Giannakoglou, K. The continuous adjoint approach to the k-ω SST turbulence model with applications in shape optimization. Eng. Optim. 2015, 47, 1523–1542. [Google Scholar] [CrossRef]
- Lei, J.; He, J. Adjoint-based aerodynamic shape optimization for low Reynolds number airfoils. J. Fluids Eng. Trans. ASME 2016, 138, 1–6. [Google Scholar]
- Halila, G.; Martins, J.; Fidkowski, K. Adjoint-based aerodynamic shape optimization including transition to turbulence effects. Aerosp. Sci. Technol. 2020, 107, 106243. [Google Scholar] [CrossRef]
- Rashad, R.; Zingg, D. Aerodynamic shape optimization for natural laminar flow using a discrete-adjoint approach. In Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 1–20 June 2015. [Google Scholar]
- Carpentieri, G.; Koren, B.; van Tooren, M. Adjoint-based aerodynamic shape optimization on unstructured meshes. J. Comput. Phys. 2007, 224, 267–287. [Google Scholar] [CrossRef]
- Kapsoulis, D.; Tsiakas, K.; Trompoukis, X.; Asouti, V.; Giannakoglou, K. A PCA-assisted hybrid algorithm combining EAs and adjoint methods for CFD-based optimization. Appl. Soft Comput. J. 2018, 73, 520–529. [Google Scholar] [CrossRef]
- Luo, J.; Xiong, J.; Liu, F. Aerodynamic design optimization by using a continuous adjoint method. Sci. China Phys. Mech. Astron. 2014, 57, 1363–1375. [Google Scholar] [CrossRef]
- Reuther, J.; Jameson, A. Supersonic Wing and Wing-Body Shape Optimization Using an Adjoint Formulation; American Society of Mechanical Engineers, Fluids Engineering Division (Publication) FED: New York, NY, USA, 1995; pp. 45–52. [Google Scholar]
- Jameson, A.; Martinelli, L.; Pierce, N.A. Optimum aerodynamic design using the Navier-Stokes equations. Theor. Comput. Fluid Dyn. 1998, 10, 213–237. [Google Scholar] [CrossRef]
- Ashikhmina, E.; Prosuntsov, P. Coupled CFD-based shape optimization of a wing of reusable space vehicle of tourist class. IOP Conf. Ser. Mater. Sci. Eng. 2020, 709, 022108. [Google Scholar]
- Wang, D.; He, L. Adjoint aerodynamic design optimization for blades in multistage turbomachines-Part I: Methodology and verification. J. Turbomach. 2010, 43161, 2141–2156. [Google Scholar] [CrossRef]
- Wang, D.; He, L.; Li, Y.; Wells, R. Adjoint aerodynamic design optimization for blades in multistage turbomachines-Part II: Validation and application. J. Turbomach. 2010, 43161, 2157–2169. [Google Scholar] [CrossRef]
- Luo, J.; Xiong, J.; Liu, F.; Power, A. Three-Dimensional Aerodynamic Design Optimization of a Turbine Blade by Using an Adjoint Method. Artic. J. Turbomach. 2010, 48883, 651–664. [Google Scholar] [CrossRef]
- Luo, J.; McBean, I.; Liu, F. Optimization of endwall contours of a turbine blade row using an adjoint method. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Vancouver, BC, Canada, 6–10 June 2011; Volume 54679, pp. 1335–1350. [Google Scholar]
- Chen, L.; Chen, J. Aerodynamic optimization design for high pressure turbines based on the adjoint approach. Chin. J. Aeronaut. 2015, 28, 757–769. [Google Scholar] [CrossRef]
- Yi, J.; Kim, C.; Lee, B. Adjoint-Based Design Optimization of Vortex Generator in an S-Shaped Subsonic Inlet. AIAA J. 2012, 50, 2492–2507. [Google Scholar] [CrossRef]
- Chanzy, Q.; Garnier, E.; Bur, R. Optimization of a Fluidic Vortex Generator’s Control in a Transonic Channel Flow. AIAA J. 2020, 58, 5216–5227. [Google Scholar] [CrossRef]
- Martins, J.; Kennedy, G. Enabling Large-scale Multidisciplinary Design Optimization through Adjoint Sensitivity Analysis. Struct. Multidiscip. Optim. 2021, 64, 2959–2974. [Google Scholar] [CrossRef]
- Dhert, T.; Ashuri, T.; Martins, J. Aerodynamic shape optimization of wind turbine blades using a Reynolds-averaged Navier–Stokes model and an adjoint method. Wind. Energy 2017, 20, 909–926. [Google Scholar] [CrossRef]
- He, S.; Jonsson, E.; Mader, C.; Martins, J. Aerodynamic shape optimization with time spectral flutter adjoint. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Mavriplis, D.; Fabiano, E.; Anderson, E. Recent advances in high-fidelity multidisciplinary adjoint-based optimization with the NSU3D flow solver framework. In Proceedings of the AIAA SciTech Forum—55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Martins, J.R.; Alonso, J.; Reuther, J. High-fidelity aerostructural design optimization of a supersonic business jet. J. Aircr. 2004, 41, 523–530. [Google Scholar] [CrossRef]
- Kline, H.; Palacios, F.; Economon, T.; Alonso, J. Adjoint-Based Optimization of a Hypersonic Inlet. In Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Kline, H.; Economon, T.; Alonso, J. Multi-objective optimization of a hypersonic inlet using generalized outflow boundary conditions in the continuous adjoint method. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Damm, K.; Gollan, R.; Jacobs, P.; Smart, M.; Lee, S.; Kim, E.; Kim, C. Discrete adjoint optimization of a hypersonic inlet. AIAA J. 2020, 58, 2621–2634. [Google Scholar] [CrossRef]
- Mosca, R. Adjoint-Based Passive Optimization of a Micro T-Mixer. Master’s Thesis, Politecnico Di Milano, Milan, Italy, 2017. [Google Scholar]
- Eggl, M.; Schmid, P. Mixing by stirring: Optimizing shapes and strategies. Phys. Rev. Fluids 2022, 7, 073904. [Google Scholar] [CrossRef]
- Helgason, E.; Krajnović, S. Implementation of an adjoint-based optimization with scalar transport. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Urzay, J. Supersonic combustion in air-breathing propulsion systems for hypersonic flight. Annu. Rev. Fluid Mech. 2018, 50, 593–627. [Google Scholar] [CrossRef]
- Landsberg, W.; Gibbons, N.; Wheatley, V.; Smart, M.; Veeraragavan, A. Improving scramjet performance through flow field manipulation. J. Propuls. Power 2018, 34, 578–590. [Google Scholar] [CrossRef]
- Garg, V.; Deshpande, L.; Swaraj, P.; Verma, T.; Vinay, D.; Raj, Y.; Gahlot, N.K.; Sharma, N.; Kumar, V.R.S. Optimizing Hypersonic Propulsion: Analysis of Angled Fuel Injection and Strut Geometries in Scramjet Combustors. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025. [Google Scholar]
- Burrows, M.; Kurkov, A. An analytical and experimental study of supersonic combustion of hydrogen in vitiated air stream. AIAA J. 1973, 11, 1217–1218. [Google Scholar] [CrossRef]
- Karl, S.; Hannemann, K.; Mack, A.; Steelant, J. CFD analysis of the HyShot II scramjet experiments in the HEG shock tunnel. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008; p. 2548. [Google Scholar]
- Kummitha, O. Numerical analysis of hydrogen fuel scramjet combustor with turbulence development inserts and with different turbulence models. Int. J. Hydrogen Energy 2017, 42, 6360–6368. [Google Scholar] [CrossRef]
- Kummitha, O.; Suneetha, L.; Pandey, K. Numerical analysis of scramjet combustor with innovative strut and fuel injection techniques. Int. J. Hydrogen Energy 2017, 42, 10524–10535. [Google Scholar] [CrossRef]
- Kummitha, O. Numerical analysis of passive techniques for optimizing the performance of scramjet combustor. Int. J. Hydrogen Energy 2017, 42, 10455–10465. [Google Scholar] [CrossRef]
- Kummitha, O.; Pandey, K.; Gupta, R. CFD analysis of a scramjet combustor with cavity based flame holders. Acta Astronaut. 2018, 144, 244–253. [Google Scholar] [CrossRef]
- Kummitha, O.; Pandey, K.; Gupta, R. Optimization of scramjet performance with different fuel injection techniques and flame holder cavities. Acta Astronaut. 2018, 152, 908–919. [Google Scholar] [CrossRef]
- Landsberg, W.; Wheatley, V.; Veeraragavan, A. Characteristics of cascaded fuel injectors within an accelerating scramjet combustor. AIAA J. 2016, 54, 3692–3700. [Google Scholar] [CrossRef]
- Shenoy, R.; Drozda, T.; Baurle, R.; Parker, P. Surrogate Modeling and Optimization of a Combustor with an Interdigitated Flushwall Injector. In Proceedings of the Programmatic and Industrial Base (PIB) Meeting, Dayton, OH, USA, 3–7 June 2019. number NF1676L-33632. [Google Scholar]
- Drozda, T.; Shenoy, R.; Axdahl, E.; Baurle, R. Numerical investigation and optimization of a flushwall injector for scramjet applications at hypervelocity flow conditions. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019; p. 4196. [Google Scholar]
- Kumar, S.; Das, S.; Sheelam, S. Application of CFD and the Kriging method for optimizing the performance of a generic scramjet combustor. Acta Astronaut. 2014, 101, 111–119. [Google Scholar] [CrossRef]
- Rovira Sala, C.; Famada Vizcaino, M.; Simon Felix, A.; Bernabeu-Vazquez, A.; Van Hove, B.; Józsa, T.I.; Hoste, J.J.O.E. An exploration of adjoint-based optimization for hypersonic vehicle- and propulsion design. In Proceedings of the 3rd International Conference on High-Speed Vehicle Science Technology (HiSST), Busan, Republic of Korea, 14–19 April 2024. [Google Scholar]
- Rovira Sala, C. Optimisation of a Generic Supersonic Hydrogen Combustor. Master’s Thesis, Cranfield University, Bedford, UK, 2023. [Google Scholar]
- Siemens Digital Industries Software. Simcenter STAR-CCM+, version 2206; Siemens: Munich, Germany, 2023; Available online: https://www.plm.automation.siemens.com/global/en/products/simcenter/STAR-CCM.html (accessed on 1 June 2025).
- ANSYS Inc. Fluent 2025 R1 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2025. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- NASA. Turbulence Modeling Resources. Available online: https://turbmodels.larc.nasa.gov (accessed on 12 June 2025).
- Liou, M. Ten years in the making - AUSM-family. In Proceedings of the 15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001; pp. 2001–2521. [Google Scholar]
- Hoste, J. Scramjet Combustion Modeling Using Eddy Dissipation Model. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2018. [Google Scholar]
- Drozda, T.G.; Baurle, R.A.; Drummond, J.P. Impact of Flight Enthalpy, Fuel Simulant, and Chemical Reactions on the Mixing Characteristics of Several Injectors at Hypervelocity Flow Conditions; Technical Report; NASA Langley Research Center: Hampton, VA, USA, 2016.
- Riggins, D.; McClinton, C.; Vitt, P. Thrust losses in hypersonic engines part 1: Methodology. J. Propuls. Power 1997, 13, 281–287. [Google Scholar] [CrossRef]
- Baurle, R.; Eklund, D. Analysis of dual-mode hydrocarbon scramjet operation at Mach 4-6.5. J. Propuls. Power 2002, 18, 990–1002. [Google Scholar] [CrossRef]
- Bynum, M.; Baurle, R. A design of experiments study for the HIFiRE flight 2 ground test computational fluid dynamics results. In Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, CA, USA, 11–14 April 2011; p. 2203. [Google Scholar]
- Karl, S. Numerical Investigation of a Generic Scramjet Configuration. Ph.D. Thesis, Saechsische Landesbibliothek-Staats-und Universitaetsbibliothek Dresden, Dresden, Germany, 2011. [Google Scholar]
- Pecnik, R.; Terrapon, V.; Ham, F.; Iaccarino, G.; Pitsch, H. Reynolds-averaged Navier-Stokes simulations of the HyShot II scramjet. AIAA J. 2012, 50, 1717–1732. [Google Scholar]
- Georgiadis, N.; Yoder, D.; Vyas, M.; Engblom, W. Status of turbulence modeling for hypersonic propulsion flowpaths. Theor. Comput. Fluid Dyn. 2014, 28, 295–318. [Google Scholar] [CrossRef]
- Georgiadis, N.; Mankbadi, M.; Vyas, M. Turbulence model effects on RANS simulations of the HIFiRE flight 2 ground test configurations. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 0624. [Google Scholar]
- Hoste, J.; Gibbons, N.; Ecker, T.; Amato, C.; Knight, D.; Sattarov, A.; Thiry, O.; Hickey, J.; Hizir, F.; Köktürk, T.; et al. A review of Reynolds-averaged Navier–Stokes modeling for hypersonic large cone–flares. Phys. Fluids 2025, 37, 025193. [Google Scholar]
- Fureby, C.; Sahut, G.; Ercole, A.; Nilsson, T. Large eddy simulation of combustion for high-speed airbreathing engines. Aerospace 2022, 9, 785. [Google Scholar] [CrossRef]
- Huang, Z.W.; He, G.Q.; Qin, F.; Wei, X.G. Large eddy simulation of flame structure and combustion mode in a hydrogen fueled supersonic combustor. Int. J. Hydrogen Energy 2015, 40, 9815–9824. [Google Scholar] [CrossRef]
- Huang, Z.W.; He, G.Q.; Wang, S.; Qin, F.; Wei, X.G.; Shi, L. Simulations of combustion oscillation and flame dynamics in a strut-based supersonic combustor. Int. J. Hydrogen Energy 2017, 42, 8278–8287. [Google Scholar] [CrossRef]
- Hoste, J.; Fossati, M.; Taylor, I.; Gollan, R. Characterisation of the eddy dissipation model for the analysis of hydrogen-fuelled scramjets. Aeronaut. J. 2019, 123, 536–565. [Google Scholar] [CrossRef]
- Chaturvedi, M.; Scutelnicu, E.; Rusu, C.C.; Mistodie, L.R.; Mihailescu, D.; Subbiah, A.V. Wire arc additive manufacturing: Review on recent findings and challenges in industrial applications and materials characterization. Metals 2021, 11, 939. [Google Scholar] [CrossRef]
- Keran, Z.; Runje, B.; Piljek, P.; Razumić, A. Roboforming in ISF-Characteristics, Development, and the Step Towards Industry 5.0. Sustainability 2025, 17, 2562. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).