Box Model for Confined Power-Law Viscous Gravity Currents Including Surface Tension Effects

Abstract

We consider the flow of a viscous fluid (power-law, non-Newtonian) injected into a gap of height H between two horizontal plates. When the viscosity of the ambient (displaced) fluid is negligible, the injected fluid forms a tail-slug in contact with both plates connected (at a moving grounding line) to a leading gravity current (GC) whose interface does not touch the top of the gap. Surface tension menisci may appear at the grounding line and nose of the GC. Such systems, of interest in the injection molding industry, have been investigated recently in the framework of the lubrication theory for the volume $\mathcal{V}=q{t}^{\alpha }$ (q and $\alpha$ are positive constants and t is time). Similarity appears for certain values of $\alpha$. The similarity solution of the lubrication model requires manipulations and numerical calculations, which obscure the underlying mechanisms and defy reliable interpretation, because the flow is dependent on four coupled parameters: viscosity exponent n, as well as J, $\sigma$, and ${\sigma }_N$ (the height ratio of the unconfined GC, grounding line meniscus, and nose meniscus to H, respectively). Here we present a significantly simpler box-model analysis, which provides straightforward insights and facilitates the quantitative predictions. Comparisons with the rigorous lubrication-model solution and with previously published data demonstrate that the box model provides a reliable physical description of the system, as well as a fairly accurate prediction of the propagation, for a wide range of parameters.

1. Introduction

Gravity current (GC) is a generic name for the buoyancy-driven flow of a fluid of one density, $\rho$, into an ambient fluid of a different density, ${\rho }_a$. The propagation of the GC is mostly in horizontal direction x (to be distinguished from the mostly vertical buoyancy-driven flows called plumes); see [1] and the references therein. The driving buoyancy mechanism is explained as follows: the hydrostatic pressure fields $p_j\propto - {\rho }_{j}gz$ produce a horizontal pressure gradient $\propto g^{\prime }=|\rho /{\rho }_a-1|g$, where g is the gravitational acceleration, z is the vertical upward coordinate, j denotes the ambient and current, and $g^{\prime }$ is the reduced gravity. The buoyancy is balanced by inertial or viscous effects. Here we consider the so-called viscous GC, dominated by a buoyancy–viscous dynamic balance, relevant to flows at a small Reynolds number. Viscous GCs have numerous applications in nature and industry. The systems of interest belong to various prototypes, such as Newtonian or non-Newtonian fluids, two-dimensional (2D) or cylindrical axisymmetric (AXI) propagation, fixed or time-varying (influxed) volume, liquid or porous medium. An important distinction is between unconfined and confined (gap) domain into which the GC propagates. Geostrophic and environmental GCs are often unconfined (e.g., spread of lava or oilspills), and have received significant attention.The confined GC occurs often in a gap where one viscous fluid displaces another viscous fluid in particular in the context of porous layers (e.g., [2,3,4,5] and the review [6]).

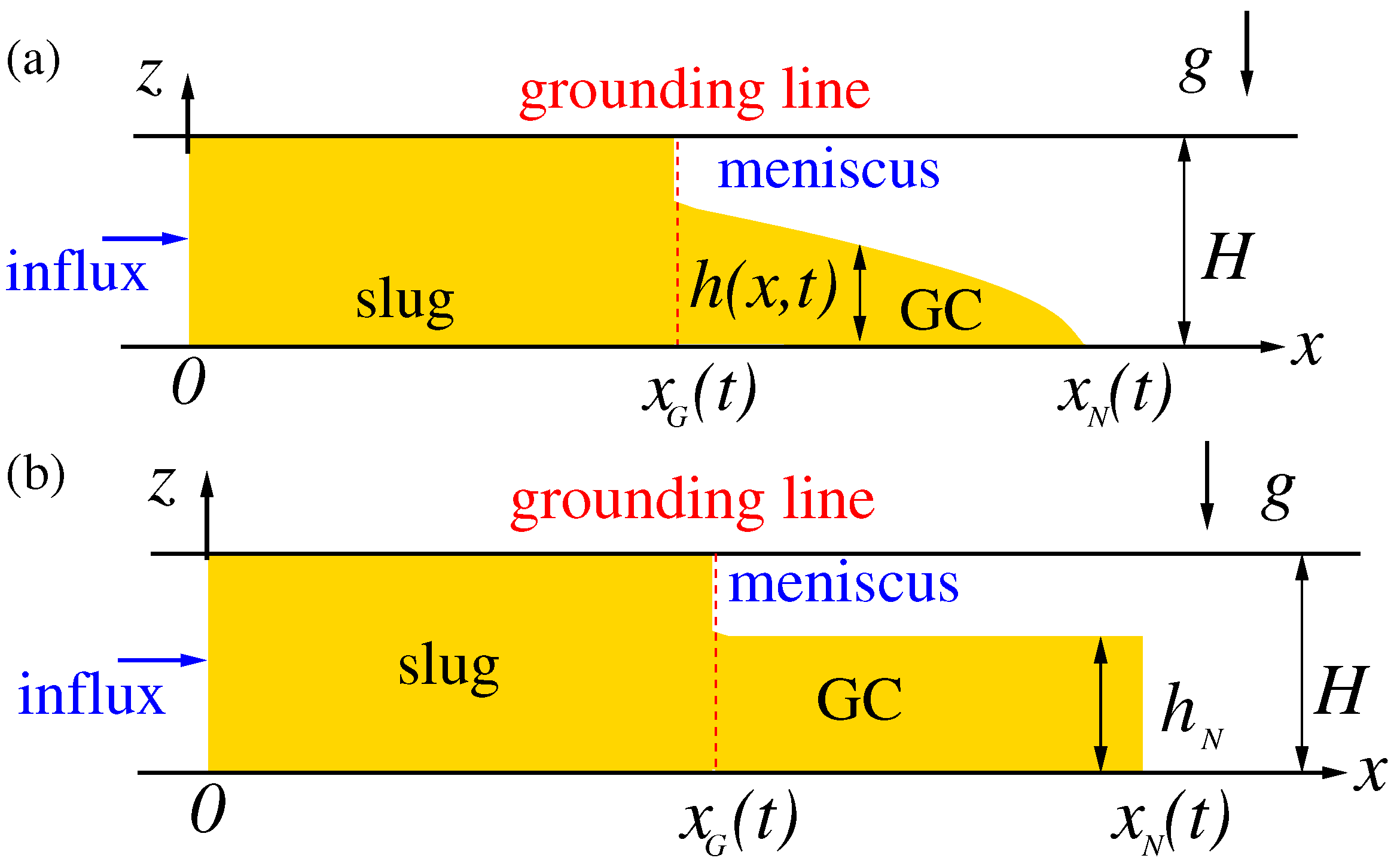
Recent investigations addressed the flow of confined viscous GCs, relevant to injection molding (see [7]); see Figure 1a. Consider the two-dimensional (2D) propagation of a viscous fluid injected into a small gap of height H between two horizontal plates. This system is a simplification of a realistic rectangular channel of width $\gg H$. We assume that the ambient fluid, displaced from the gap by the injected fluid, is less dense and significantly less viscous than the injected one (e.g., oil injected into air). In this case, the following type of flow may appear: the dense fluid forms a slug that fills the gap in $0<x\le x_G\left(t\right)$, while the fluid ahead of the slug, in $x_G\left(t\right)<x\le x_N\left(t\right)$, forms a viscous GC on the bottom while the interface is detached from the top of the gap. The subscripts G and N denote the “grounding line” and the nose of the GC. Moreover, when the injected volume is $\mathcal{V}=q{t}^{\alpha }$, such flows may be self-similar, in the sense that the GC elongates like $K{t}^{\beta }$ while the slug elongates as $y_{G}K{t}^{\beta }$, where $q, \alpha , K, \beta , y_G$ are positive constants and t is time. (The details of the source at $x=0$ are outside the scope of this study. In the laboratory and industry, the influx is supplied by a pump or similar mechanical device, which provides the volume rate and the pressure necessary for the flow in the $x>0$ domain. There is evidence that such systems work well, i.e., [8]).

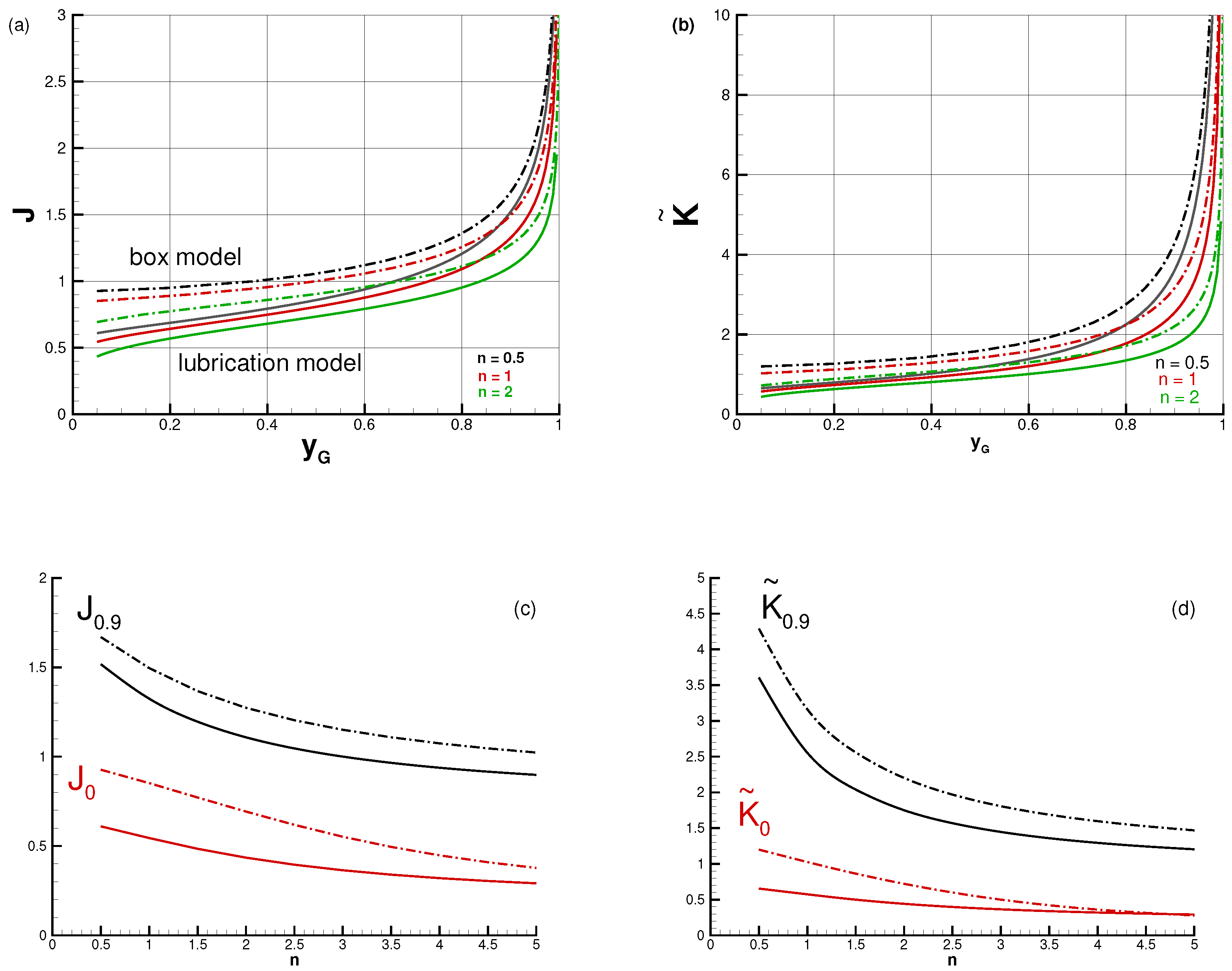
The stringent task is to determine the values of $\alpha , \beta , y_G$, and K for a given physical system. Moreover, it is important to suggest a convenient scaling to determine the governing dimensionless parameters and predict the trends of the flow upon the variation of the input conditions. In particular, it is clear that for a sufficiently large H, the confined GC can be considered unconfined; a sharp criterion for this transition is of interest. The need for an efficient prediction method motivated our study.

Ref. [8] considered the confined axisymmetric (AXI) flow of a Newtonian fluid (theoretically and experimentally). They used a lubrication-theory model (with no surface tension effects) to show that a constant influx, $\alpha =1$, produces self-similar propagation with power $\beta =1/2$, and the only governing dimensionless parameter is $J=l/H$, where l is the typical height of the corresponding unconfined GC. The associated experiments (using golden syrup in a gap of about 1 cm filled initially with air) supported the theory (with some small discrepancies). Ref. [9] (referred to below as U25) extended the theory to cover also two-dimensional (2D) and non-Newtonian power-law fluids with exponent n (the Newtonian fluid is recovered for $n=1$). The lubrication-theory framework indicates that a self-similar flow develops for select values of $\alpha$, determined by n; the power $\beta$ is equal to $\alpha$ in 2D case and $\alpha /2$ in AXI case. The detached interface of the GC displays an inclined profile (see Figure 1a) which is defined by a second-order ordinary differential equation subjected to boundary conditions at the nose and at the grounding line, which, in general, must be solved numerically. When surface tension effects are discarded, for a given fluid (specified by the viscosity exponent n), the scaled solution depends on only one dimensionless parameter, J. The theory provides a convenient scaling of variables, and a sharp prediction of the threshold value $J=J_0$ below which the confinement is irrelevant (the GC with the select $\alpha$ propagates on the bottom without touching the top of the gap).

The paper [10] revisits the system of [8], and it demonstrates that the discrepancies between theory and experiment can be attributed (mainly) to surface tension ($\mathsf{\Gamma }$) effects between the current and the ambient fluids at the grounding line. The Young–Laplace formulation predicts the existence of a meniscus at the grounding line of height of the order of the capillary length ${(\mathsf{\Gamma }/\rho g^{\prime })}^{1/2}$, but the details and boundary conditions are complicated and hence an accurate solution of the meniscus in practical systems is not feasible. However, by modelling this meniscus as a vertical jump of height $\sigma H$ (see Figure 1, where $\sigma \lesssim 0.5$ is a constant) the surface tension effect was added conveniently to the original lubrication-model. The main point is that the similarity behaviour is maintained, with unchanged $\alpha$ and $\beta$. The dependencies between $J, y_G$, and K are affected by $\sigma$. The theoretical solutions with small $\sigma$ show better agreement with experiments than the original $\sigma =0$ predictions. Although the exact value of $\sigma$ is not known a priori, this model provides valuable insights and can be applied with tentative theoretical or empirically estimated values. The study of [10] suggests that $\sigma ={(\mathsf{\Gamma }/\rho g^{\prime })}^{1/2}/H$ is a fair approximation. This promising extension of the original lubrication model similarity solution was derived and tested in [10] only for the a Newtonian fluid in AXI system ($n=1,\alpha =1,\beta =1/2$). Here we show that the $\sigma >0$ contribution can be also implemented conveniently in the theory of confined GCs of power-law fluids in both 2D and AXI systems.

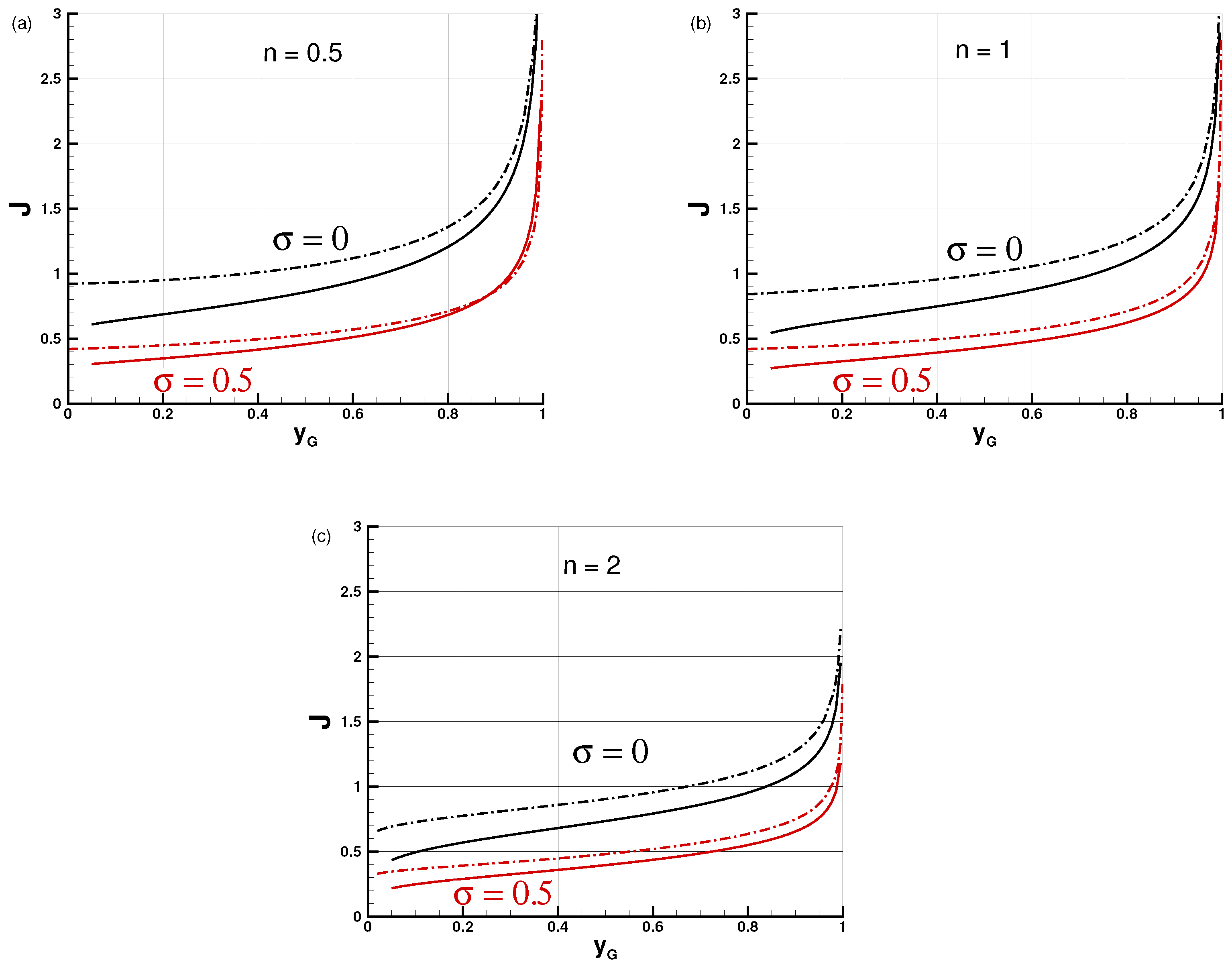
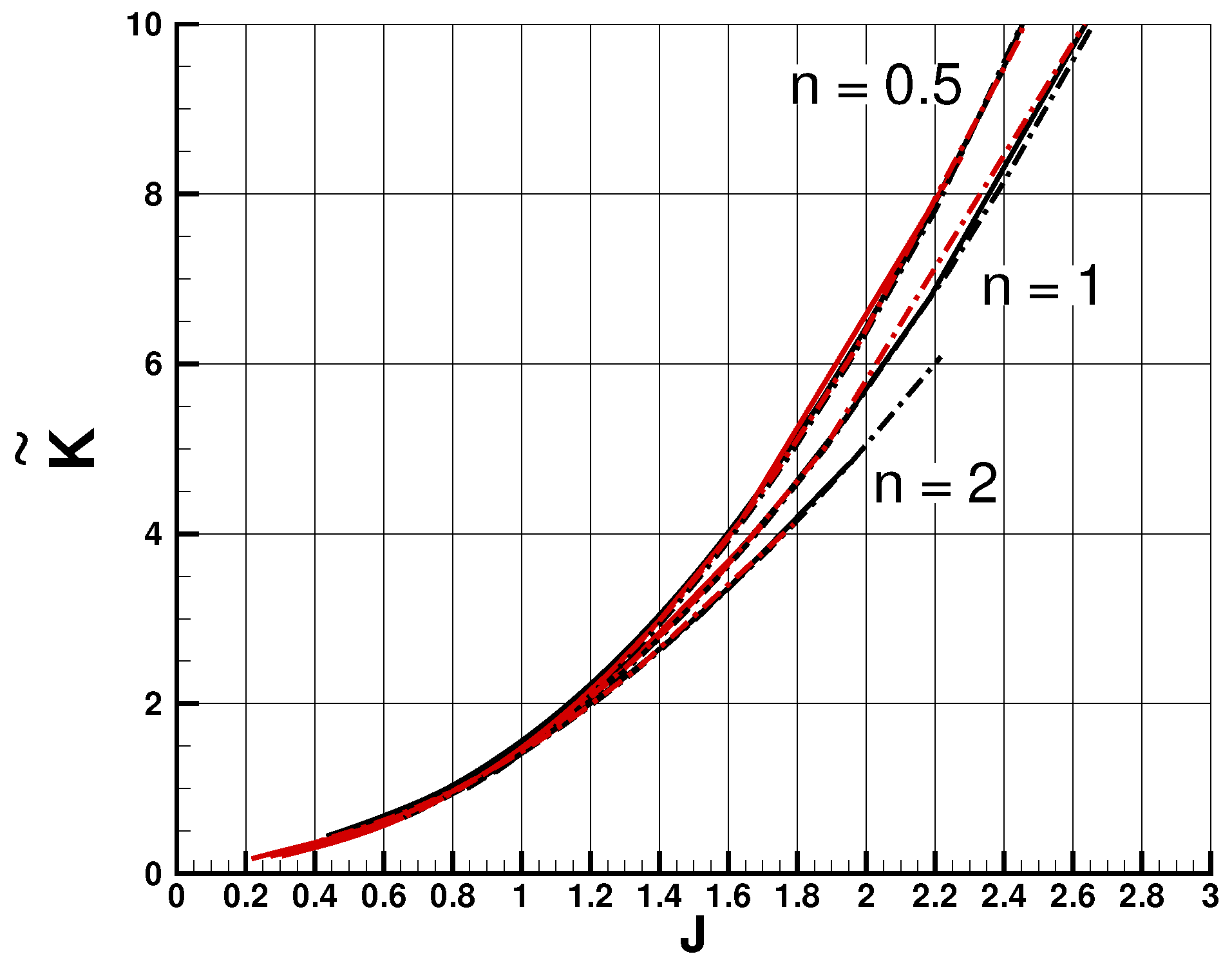
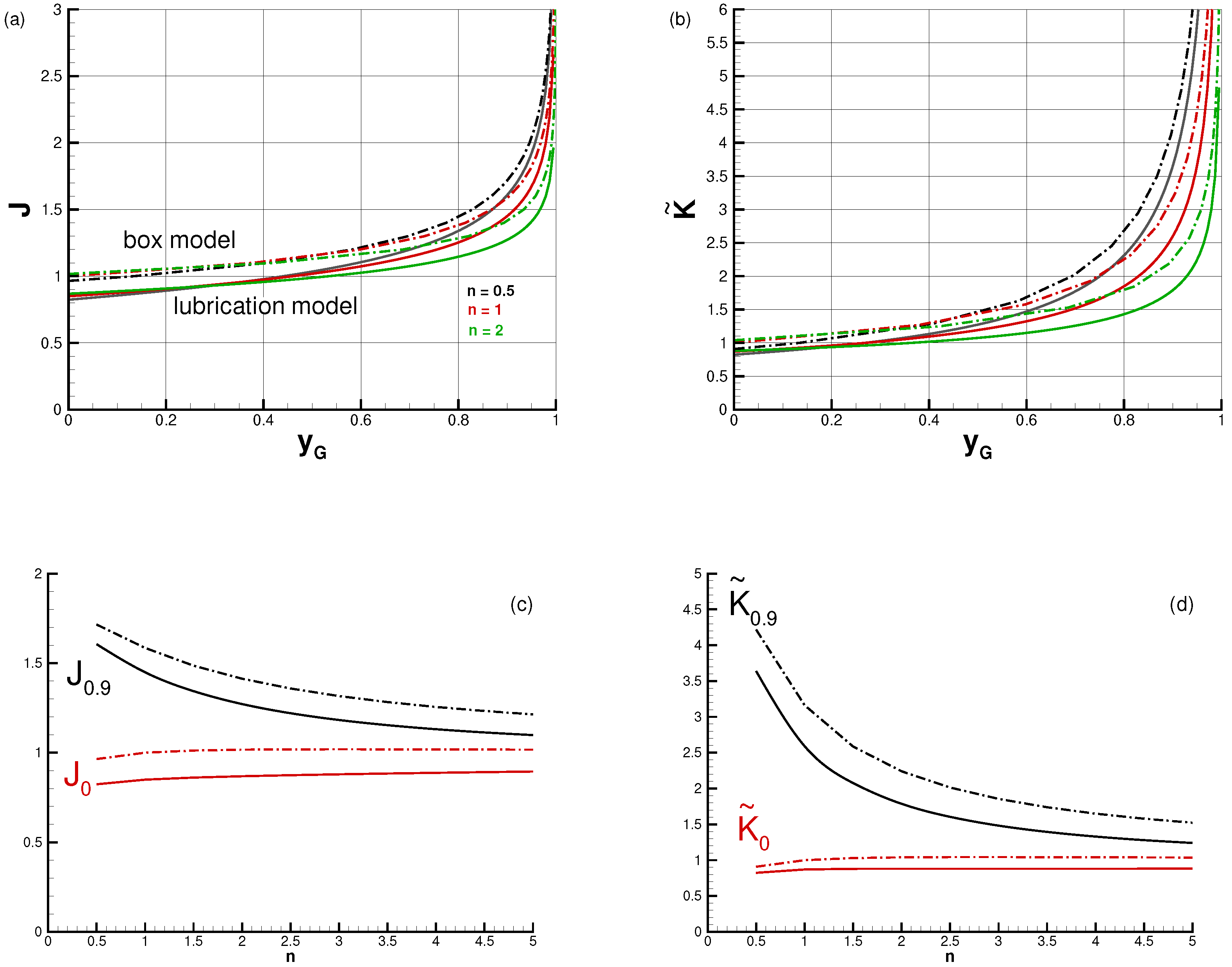
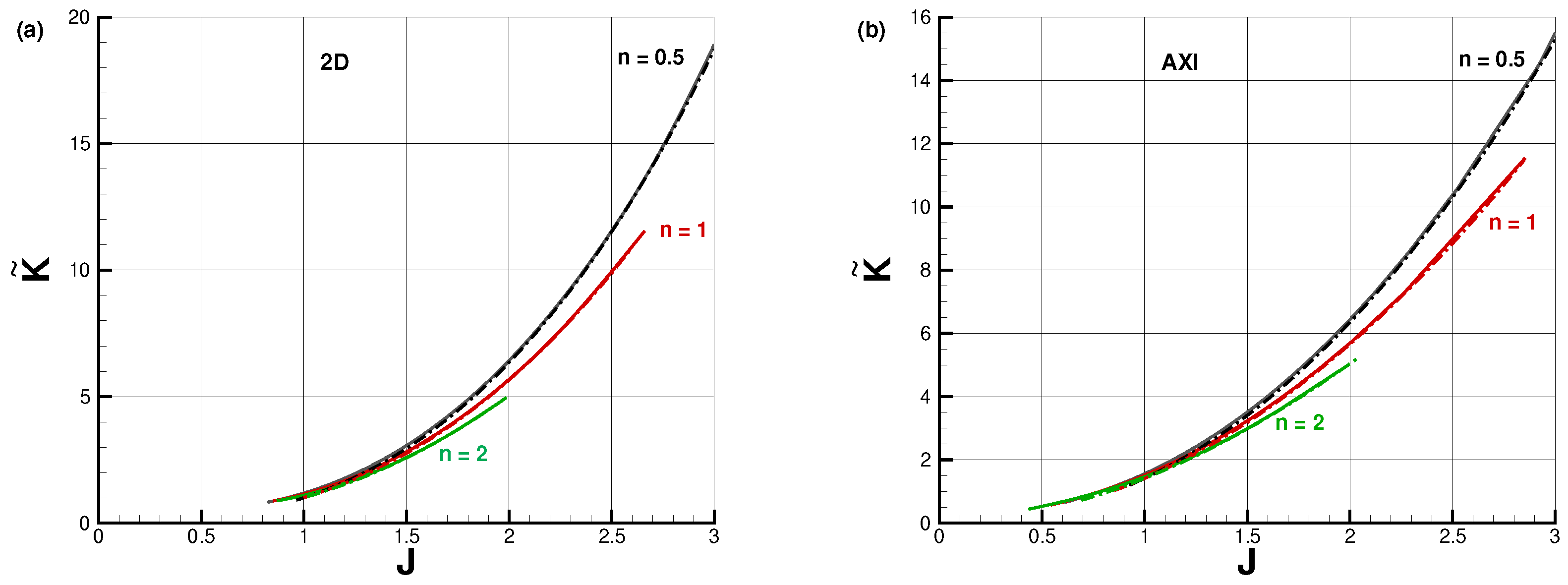
The advantage of these published theories, based on the lubrication simplification, is the rigour of the governing equations and of the mathematical solution. The similarity solution predicts analytically the time behaviour, but the spatial profiles must be compiled numerically. The numerical task is straightforward. The disadvantage of this solution is that the needed mathematical manipulations are cumbersome and the results lack analytical description. This precludes straightforward extraction of trends and obscures the physical insights. This difficulty is exacerbated for the confined flow of power-law fluids in the presence of surface tension effects, which is dependent on three major parameters, $J, \sigma , n$, and the geometry (2D and AXI). (An additional parameter, ${\sigma }_N$, associated with the nose meniscus, will be introduced later). For example, the value $J_0$ (for a given $\sigma$) is obtained from the numerical integration of a second-order ODE; a change of $\sigma$ requires a new integration. This motivated the search for a simpler mathematical model for the same physical problem.

A simpler model is expected to be beneficial for both research and applications. For this objective, in this paper, we develop and test a box-model solution. The box-model approximation makes bold assumptions about the details of the local behaviour of the flow field, and it applies integral balances of volume and momentum on the entire mass (the box) of the GC. Box models have been used successfully for influxed viscous GCs, but, to our knowledge, only for unconfined systems (e.g., [1,11,12,13,14,15]). A widely used simplification (also implemented here) is that the interface of the GC is horizontal, as seen in Figure 1b; this eliminates the calculation of the profile of the inclined interface, which is the major challenge in the lubrication model.

The present work is a significant extension of the improved box model presented in [15]. The previous model considers GCs in a very deep environment, i.e., the height of the container, H, is much larger than the height h of the current. In this configuration, called “unconfined,” the GC that propagates on the bottom is not influenced by the top boundary. In the present system, the GC is confined by the top. Moreover, here we take into account the surface tension effect, because there is evidence ([10]) that the meniscus about the grounding line in the confined flow affects the motion (see Figure 1). In other words, the present box model incorporates two novel physical effects: confinement and surface tension. The present paper demonstrates that the box model for the self-similar confined flow provides explicit simple and insightful results for both 2D and AXI systems with Newtonian and non-Newtonian power-law fluids, including surface tension effects.

The surface tension is expected to generate, in addition to the meniscus at the grounding line, a meniscus at the nose as well, i.e., a modification of the tip of the GC at the bottom position $x_N\left(t\right)$ in Figure 1a. This effect can be incorporated in both the lubrication and box models with an additional small parameter ${\sigma }_N$. However, the typical influence of this meniscus is significantly smaller than that of the grounding-line meniscus, and hence the main analysis and discussion of the paper ignore this detail. The quantitative justification will be given in Appendix A.

The structure of the paper is as follows. The box-model-governing equations are developed, and some useful analytical results are derived for the general system (including surface tension), for the 2D and AXI systems in Section 2.2 and Section 2.3, respectively. Results for the special (basic state) with excluded surface tension, $\sigma =0$, are presented in Section 3. At the end of each section, we perform stringent quantitative comparisons with the more rigorous lubrication-model solution and show that there is good agreement for a wide range of parameters. A brief comparison with published data is discussed in Section 4. Concluding remarks are given in Section 5. The effect of the nose meniscus (not included in the main text) is estimated in Appendix A. The method of solution of the lubrication model, which is compared with the box-model predictions, is briefly presented in Appendix B.

2. Formulation and Analysis

2.1. The Bottom-Shear Approximation

An essential component of the approximate model is a simple formula that connects the depth-averaged velocity of the GC with the resulting shear at the bottom. The analysis can be performed in a convenient compact form for both Newtonian and non-Newtonian (power-law) fluids. We use dimensional variables unless stated otherwise.

The dynamic and kinematic viscosities of the current are given by

$$\mu =m{\left|{\displaystyle \frac{\partial u}{\partial z}}\right|}^{n-1},\nu =m/\rho .$$

(1)

where m is the consistency index and n is the behaviour index (or exponent). A fluid is shear-thinning (pseudoplastic) if $n<1$, shear-thickening (dilatant) if $n>1$, and Newtonian if $n=1$ (in this case, $m=\mu$, the standard dynamic viscosity of the fluid and $\nu$ is the standard kinematic viscosity coefficient). The dimension of $\nu$ is ${\mathrm{cm}}^2{\mathrm{s}}^{\mathrm{n}-2}$.

The flow of the GC is as sketched in Figure 1a. Assume a 2D flow in x direction with velocity $u(x,z,t)$, and let $z=h(x,t)$ be the height of the interface above the bottom. The surface tension effects are confined to the small meniscus about $x_G$, and assumed to be negligible over the rest of the interface (because the capillary length is of the order of H, and the interface is much larger). The pressure in the thin-layer GC is hydrostatic, and hence the intrinsic driving force is given by $-g^{\prime }(\partial h/\partial x)$, referred to as the buoyancy. The driving force is balanced by the shear, as expressed by the lubrication–simplification momentum equation

$$0=-g^{\prime }{\displaystyle \frac{\partial h}{\partial x}}+\nu {\displaystyle \frac{\partial }{\partial z}}\left[{\left|{\displaystyle \frac{\partial u}{\partial z}}\right|}^{n-1}{\displaystyle \frac{\partial u}{\partial z}}\right].$$

(2)

This equation is integrated twice with respect to z to obtain $u(x,z,t)$. The constants of integration are determined by the boundary condition: (a) no slip, $u=0$, at the bottom $z=0$; (b) no shear, $(\partial u/\partial z)=0$, at the free interface $z=h$. We obtain

$$u(x,z,t)={\displaystyle \frac{n}{n+1}}{\mathcal{G}}^{1/n}{\left(-{\displaystyle \frac{\partial h}{\partial x}}\right)}^{1/n}{h}^{(n+1)/n}\left[1-{\left(1-{\displaystyle \frac{z}{h}}\right)}^{(n+1)/n}\right],$$

(3)

where

$$\mathcal{G}=g^{\prime }/\nu .$$

(4)

The depth-averaged velocity is

$$\overline{u}=\overline{u}(x,t)={\displaystyle \frac{1}{h}}{\int }_0^{h}u(x,z,t)dz={\displaystyle \frac{n}{2n+1}}{\mathcal{G}}^{1/n}{\left(-{\displaystyle \frac{\partial h}{\partial x}}\right)}^{1/n}{h}^{(n+1)/n}.$$

(5)

The shear stress at the bottom, $\mu (\partial u/\partial x)$ at $z=0$, can then be expressed as

$$\tau =\tau (x,t)=\rho \nu {\gamma }^n{\left({\displaystyle \frac{\overline{u}}{h}}\right)}^n,\mathrm{where}\gamma =2+1/n.$$

(6)

In the subsequent analysis, we drop the bar notation from the depth-averaged u. The box model adopts the result (6) as an approximation for the calculation of the total shear force, which balances the total buoyancy on the GC; the local balances are not satisfied because $\partial h/\partial x=0$ in Figure 1b. We also note that the results (1)–(6) carry over to the axisymmetric system upon changing x to the radial coordinate r.

2.2. Two Dimensional Confined Flow

The basic simplification of the box model is that the interface of the GC is horizontal, i.e., $h(x,t)=h_N\left(t\right)$; see Figure 1b. In the present case, the confinement requires that the interface be attached to the upper boundary by a meniscus of constant height at the moving grounding line $x_G\left(t\right)$. This is modelled by the following assumptions: the meniscus at the grounding line is a vertical jump of constant height $\sigma H$, and hence the horizontal interface is time-independent at the position $z=h=h_N=(1-\sigma )H$. (The x-dimension of the meniscus, $\sim H$, is negligible because the GC is assumed to be a thin layer, $H/x_N\ll 1$). Note that $u(x,t)$ of the box model represents the depth-averaged velocity. For definiteness, we assume $\sigma \le 0.5$, which means that the meniscus may be large, but not dominant.

We are interested in similarity propagation of the form

$$x_N\left(t\right)=K{t}^{\beta },u_N=\beta K{t}^{\beta -1},x_G\left(t\right)=y_G{x}_N\left(t\right)=y_{G}K{t}^{\beta },$$

(7)

where K, $\beta$, and $y_G$ are constants ($K,\beta >0,0<y_G<1$). The reason for this choice is that when the volume $\sim t^{\alpha }$, then $x_N$ and $x_G$ are expected to behave like t to some power, such as $t^{\beta }$ and $t^{\omega }$. As t increases, if $\omega <\beta$, then $x_G/x_N\to 0$ (i.e., unconfined GC), and if $\omega >\beta$, then $x_G/x_N\to 1$ (slug flow). Consequently, $\omega =\beta$ and the form $x_G=y_G{x}_N\left(t\right)$, with a constant $y_G\in (0,1)$, correspond to the confinement problem of interest here, which displays a clear-cut grounding line during a long propagation time and distance. We also note that the form (7) is compatible with the similarity solution of the lubrication model; see Appendix B.

The balances are performed per unit width. The volume of the injected fluid is $q{t}^{\alpha }$.

Consider the kinematic balances. The constant $h=h_N=(1-\sigma )H$ has two important implications. First, total volume conservation

$$x_{G}H+(x_N-x_G)h_N=q{t}^{\alpha },$$

(8)

upon use of (7), yields

$$\alpha =\beta ,$$

(9)

$$K={\displaystyle \frac{q}{H[1-\sigma (1-y_G)]}}.$$

(10)

Second, the continuity equation ${\left(uh\right)}_x=0$ imposes $u(x,t)=u_N\left(t\right)$ in the GC.

The dynamic balance is between the forces acting on the entire GC in the box from $x_G$ to $x_N$. (The force balance for the slug is unimportant in the present analysis. We assume that the source (pump) at $x=0$ provides the pressure necessary for sustaining the flow of the influxed fluid in the gap $x>0$). This is expressed as

$$F_V=F_B,$$

(11)

where the buoyancy force is given by

$$F_B=(1/2)\rho g^{\prime }{h}_N^2,$$

(12)

and the viscous force due to the shear at the bottom is approximated by

$$F_V={\int }_{x_G}^{x_N}\tau dx=\rho \nu {\gamma }^n{\left({\displaystyle \frac{u_N}{h_N}}\right)}^n{x}_N(1-y_G).$$

(13)

We used (6) and $u=u_N$ (justified above). The surface tension contributes a hindering (drag) force on the slug of dense fluid in the domain $x<x_G$, which is balanced by the buoyancy over the meniscus in the gap $h_N<z<H$. The GC in the domain $x>x_G$ is not directly affected by this force; however, the presence of the meniscus reduces $F_B$ of the GC because $h_N=(1-\sigma )H$; see (12).

In the assumed flow, $F_B$ is a constant. The force balance requires the same property for $F_V$. Inspection of (13) shows that this can be satisfied when

$$u_N^n{x}_N={\beta }^n{K}^{n+1}{t}^{(n+1)\beta -n}={\beta }^n{\displaystyle \frac{q^{n+1}}{H^{n+1}{[1-\sigma (1-y_G)]}^{n+1}}}{t}^{(n+1)\beta -n}=\mathrm{const}.$$

(14)

in which (7) and (10) were used. This yields

$$\beta =n/(n+1).$$

(15)

By combining Equations (11)–(15), setting $h_N=(1-\sigma )H$, and some algebra, we obtain

$${\displaystyle \frac{1-y_G}{{[1-\sigma (1-y_G)]}^{n+1}}}={(1-\sigma )}^{n+2}\varphi J^{-(2n+3)},$$

(16)

or

$$J={\left[{(1-\sigma )}^{n+2}\varphi {\displaystyle \frac{{[1-\sigma (1-y_G)]}^{n+1}}{1-y_G}}\right]}^{1/(2n+3)},$$

(17)

where

$$\varphi =\varphi \left(n\right)={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{n+1}{n}}\right)}^n,$$

(18)

$$J={\displaystyle \frac{l}{H}},l={\left[{\gamma }^n{q}^{n+1}{\mathcal{G}}^{-1}\right]}^{1/(2n+3)}.$$

(19)

The dimensionless parameter J is evidently the ratio of two lengths: l, the typical thickness of the unconstrained GC (with the corresponding influx conditions), and H, the height of the gap. The coefficient $\varphi$ is approximately 1 (increases from 0.7 to 1.3 for $n\in (0.2-10)$).

Equation (16) (or (17)) is a useful result of the box-model analysis. This equation expresses in a quite explicit dimensionless form the connections between the governing parameter J, grounding line position $y_G$, meniscus height $\sigma$, and viscosity law n. We recall that $0\le y_G\le 1$ and $0\le \sigma \lesssim 0.5$, while n is typically of the order of unity. We also keep in mind that $J\propto q/H$. Some parametric trends of the physical system of the confined GC can be inferred by inspection of these equations as follows: (1) In general, a larger J corresponds to a larger $y_G$. In other words, a stronger flux (or smaller gap) generate a longer filling slug. (2) For a fixed $y_G$, as the meniscus height $\sigma$ increases, J decreases.

It is convenient to define $J_0$ and $J_{0.9}$, which correspond to $y_G=0$ (the transition to unconfined flow) and $y_G$ = 0.9 (the confined slug occupies 90 % of the distance of propagation). The values are directly provided by (17). In particular,

$$J_0=(1-\sigma ){\varphi }^{1/(2n+3)};J_{0.9}={\left[10{(1-\sigma )}^{n+2}{(1-0.1\sigma )}^{n+1}\varphi \right]}^{1/(2n+3)}.$$

(20)

The presence of surface tension effects represented by $\sigma >0$ may reduce significantly the transition value $J_0$, as well as the value of $J_{0.9}$. This could be expected, because the meniscus reduces the effective gap.

We now estimate the effect of the grounding-line meniscus on the major behaviour of the confined 2D GC. First, we consider a fixed J and estimate the change $\mathsf{\Delta }{y}_G$ of $y_G$ when $\sigma$ increases from 0 (position $y_G$). The leading term of an expansion for small $\sigma$ of (16) gives

$$\mathsf{\Delta }{y}_G=(1-y_G)\left[2n+3-(n+1)y_G\right]\sigma \left(\mathrm{fixed}J\right).$$

(21)

For $y_G<0.5$, this is a very significant increase, ∼2$\sigma$.

Second, we consider a fixed $y_G$, and estimate the required change of J when $\sigma$ increases from zero. Equation (16) indicates that, for keeping $y_G$ fixed, $J^{2n+3}$ must decrease at least as ${(1-\sigma )}^{n+2}$. An expansion for small $\sigma$ yields

$${\displaystyle \frac{\mathsf{\Delta }J}{J}}=-\left[1-{\displaystyle \frac{n+1}{2n+3}}{y}_G\right]\sigma \left(\mathrm{fixed}{y}_G\right).$$

(22)

In particular, we note that $J_0$ is expected to decrease from about 1 to $1-\sigma$. Again, the interpretation is that the meniscus reduces the effective gap into which the GC is injected. For a larger $\sigma$, a smaller flux (smaller J) preserves the position $y_G$.

The coefficients of $\sigma$ in (21) and (22) are plotted in Figure 2. The box model predicts significant influence of $\sigma$ on the behaviour of the confined GC. The effect is most pronounced for small $y_G$ and larger n.

We switch to dimensionless variables denoted by an upper ∼. The scales for length, speed, and time are $H, U, T$, as follows:

$$U={\gamma }^{-1}{\mathcal{G}}^{1/n}{H}^{(n+1)/n},\mathrm{and}T=H/U.$$

(23)

The coefficient K (see (10)) is scaled with $H{T}^{-\beta }$. Now the propagation reads

$${\tilde{x}}_N=\tilde{K}{\tilde{t}}^{\beta },\tilde{K}={\displaystyle \frac{J^{(2n+3)/(n+1)}}{1-\sigma (1-y_G)}}.$$

(24)

The interpretation of $\tilde{K}$ requires some care: $y_G$ in the denominator is provided by (16), not an independent variable.

The box model solution has been completed. We determined that the similarity 2D flow exists for $\alpha =\beta =n/(n+1)$; this is identical with the prediction of the lubrication model (see Appendix B). For a given fluid (i.e., a fixed n), the only free parameters, which govern the values of $y_G$ and $\tilde{K}$, are J and $\sigma$. Qualitatively, this is also in agreement with the lubrication model.

A quantitative comparison between the box and lubrication models is shown in Figure 3 and Figure 4. We see that there is good agreement between the predictions of $y_G$ as a function of J and $\sigma$ for all tested values of n. For a given J, the box model predicts a smaller $y_G$ than the lubrication model. This could be anticipated because the constant h profile of the box produces a smaller shear per unit length, and hence requires a larger length $1-y_G$ for balancing the buoyancy driving force. Figure 4 shows a remarkably good agreement between the models concerning the prediction of $\tilde{K}$. The curves of $\tilde{K}$ vs. J of the box and lubrication models, for a given n, practically coincide; this holds for both $\sigma =0$ and $\sigma =0.5$. This demonstrates that the box model captures well the dominant mechanisms of the flow, and gives confidence into the present results.

2.3. Axisymmetric Confined Flow

We use dimensional variables unless stated otherwise. Again, the box model seen in Figure 1b, subject to the confinement condition, assumes $h(r,t)=h_N=(1-\sigma )H$. We shall keep the constant $h_N$ in our balances for a while, and at a later stage, we shall impose $h_N=(1-\sigma )H$. We are interested in similarity propagation of the form

$$r_N\left(t\right)=K{t}^{\beta },u_N=\beta K{t}^{\beta -1},r_G\left(t\right)=y_G{r}_N\left(t\right)=y_{G}K{t}^{\beta }.$$

(25)

The balances are formulated per radian (i.e., we omit the coefficient $2\pi$). The volume of the injected fluid is $q{t}^{\alpha }$. We assume a source at $r=0$, which is non-physical; a correction will be suggested later.

Consider the kinematic balances. First, total volume conservation

$$(1/2)\left[r_G^{2}H+(r_N^2-r_G^2)h_N\right]=q{t}^{\alpha },$$

(26)

upon use of (25), yields

$$\alpha =2\beta ,$$

(27)

$$K={\left[{\displaystyle \frac{2q}{H[1-\sigma (1-y_G^2)]}}\right]}^{1/2}.$$

(28)

Second, the continuity equation ${\left(ruh\right)}_r=0$ shows that in the GC

$$u(r,t)=u_N\left(t\right)r_N\left(t\right)/r.$$

(29)

The dynamic balance is again given by (11). The buoyancy force is

$$F_B=(1/2)\rho g^{\prime }{h}_N^2{r}_N.$$

(30)

The viscous force due to the shear at the bottom is expressed as

$$F_V={\int }_{r_G}^{r_N}\tau rdr=\rho \nu {\gamma }^n{\left({\displaystyle \frac{u_N}{h_N}}\right)}^n{r}_N^2{\int }_{y_G}^1{y}^{1-n}dy,$$

(31)

where $y=r/r_N$; we used (6) and (29).

Comparing $F_V$ with $F_B$ we deduce that compatibility requires

$$u_N^n{r}_N={\beta }^n{K}^{n+1}{t}^{(n+1)\beta -n}={\beta }^n{\left[{\displaystyle \frac{2q}{H[1-\sigma (1-y_G^2)]}}\right]}^{(n+1)/2}{t}^{(n+1)\beta -n}=\mathrm{const}.$$

(32)

where (25) and (28) were used. This yields

$$\beta =n/(n+1).$$

(33)

The force balance in view of the results (30)–(33), after some algebra, yields

$${\displaystyle \frac{1-y_G^{2-n}}{{[1-\sigma (1-y_G^2)]}^{(n+1)/2}}}={(1-\sigma )}^{n+2}(2-n)\mathsf{\Psi }{J}^{-(3n+5)/2}(n\ne 2),$$

(34)

$$ln{y}_G=-{(1-\sigma )}^4{[1-\sigma (1-y_G^2)]}^{3/2}\left({\displaystyle \frac{9}{16\sqrt{2}}}{J}^{-11/2}\right)(n=2),$$

(35)

where

$$\psi =\psi \left(n\right)=2^{-(n+1)/2}{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{n+1}{n}}\right)}^n=2^{-(n+1)/2}\varphi ,$$

(36)

$$J={\displaystyle \frac{l}{H}},l={\left[{\gamma }^n{q}^{(n+1)/2}{\mathcal{G}}^{-1}\right]}^{2/(3n+5)}.$$

(37)

The set (34)–(35) is continuous at about $n=2$. To show this, we divide (34) by $2-n=ϵ$, and note that ${lim}_{ϵ\to 0}(1-y_G^{ϵ})/ϵ=-ln{y}_G$.

The dimensionless parameter J is, again a ratio of two lengths, with the same physical interpretation as in the 2D case.

Equations (34) and (35) can be inverted to obtain explicit formulas for J as a function of $y_G$. However, the transition to the unconfined GC here is not straightforward at $y_G=0$ because the theoretical u is unbounded at the axis; see (29). The same difficulty was noted in the lubrication model U25, and the remedy is to define the transition (and hence $J_0$) at some small but finite $y_0=0.05$; this mimics a source of finite radius, which is unavoidable in practical systems.

We now estimate the effect of the grounding-line meniscus on the confined AXI GC. An expansion of (34) in powers of $\sigma$ yields, to leading order, the following changes from the basic flow ($\sigma =0$):

$$\mathsf{\Delta }{y}_G=y_G^{n-1}\left\{{\displaystyle \frac{1-y_G^{2-n}}{2-n}}\right\}{\displaystyle \frac{1}{2}}\left[3n+5-(n+1)y_G^2\right]\sigma \left(\mathrm{fixed}J\right).$$

(38)

The formula is valid for $n\ne 2$; for $n=2$, the term in the curly brackets is replaced by $-ln{y}_G$.

$${\displaystyle \frac{\mathsf{\Delta }J}{J}}=-\left[1-{\displaystyle \frac{n+1}{3n+5}}{y}_G^2\right]\sigma \left(\mathrm{fixed}{y}_G\right).$$

(39)

We note that for $y_G<0.5$, the relative change of J needed to keep a fixed $y_G$ is close to $-\sigma$, like in the 2D system. The change of $y_G$ with $\sigma$ is more complex in the diverging AXI flow. The coefficients of $\sigma$ in (38) and (39) are plotted in Figure 5. The box model predicts significant influence of $\sigma$ on the behaviour of the confined AXI GC. The effect is most pronounced for small $y_G$. For a fixed J and small $y_G$ the axisymmetric system is very sensitive to surface tension effects. This can be attributed to strong changes of the flow field near the axis.

We switch to dimensionless variables denoted by an upper ∼. The scales for length, speed, and time are $H,U,T$, as for the 2D case, see (23), and the coefficient K (see (28)) is scaled again with $H{T}^{-\beta }$. Now the propagation reads

$${\tilde{r}}_N=\tilde{K}{\tilde{t}}^{\beta },\tilde{K}={\displaystyle \frac{\sqrt{2}{J}^{(3n+5)/\left(2\right(n+1\left)\right)}}{{[1-\sigma (1-y_G^2)]}^{1/2}}}.$$

(40)

Again, the interpretation of $\tilde{K}$ requires some care: $y_G$ in the denominator is provided by (34), not an independent variable.

The box model solution has been completed. We determined that the similarity AXI flow exists for $\alpha =2n/(n+1)=2\beta$, identical with the prediction of the lubrication-model. The only free parameters, which governs the values of $y_G$ and $\tilde{K}$, are J and $\sigma$ (for a given fluid, i.e., a fixed n). Qualitatively, this is in agreement with the lubrication model. A quantitative comparison between the models is shown in Figure 6 and Figure 7. There is fair agreement in general, and the differences could be anticipated with the same arguments presented for the 2D flow. Again, there is a remarkably good agreement between the models concerning the value of $\tilde{K}$.

3. Results for $\mathit{\sigma }=\mathbf{0}$

The $\sigma =0$ (no surface tension effects) system merits a detailed discussion for several reasons. First, the formulas are amenable for simplifications, which enhance the understanding of the confined GC flow. Second, systems with small (negligible) surface tension may be of interest in experiments and application. Third, the $\sigma =0$ solution is a valuable reference (base) for the $\sigma >0$ behaviour. We have developed simple formulas for estimating the change from this base when $\sigma >0$ is present.

The $\sigma =0$ system can be regarded as the limit $\sigma \to 0$ of the analysis and results presented in the previous sections. The interface of the GC in the $x>x_G\left(t\right)$ domain (see Figure 1b) is approximated by a horizontal line $z=h_N=H^{-}$, i.e., very near to, but detached from, the top boundary. The tiny gap, $\sigma H$, is close to zero at the grounding line $x_G\left(t\right)$. The flow is governed by the parameter J; see (19) and (37). The values of $\alpha$ and $\beta$ are same as before.

3.1. 2D Confined Flow for $\sigma =0$

A good insight into the confinement effect is provided by Equation (16) with $\sigma =0$, i.e.,

$$y_G=1-\varphi J^{-(2n+3)},$$

(41)

which predicts the relative position $y_G$ of the grounding line for a given J (fixed n). Note that $J\propto q$. For $J>1$, the second term in the RHS of (41) decays faster than $J^{-3}$. For a large J, $y_G$ is close to 1, i.e., almost all the injected fluid propagates as a slug along the gap. As J decreases, $y_G$ becomes small, i.e., a significant part of the injected fluid is a GC over the bottom with a free interface below the top of the gap. Further decrease in J brings $y_G$ to zero (the slug domain disappears at $J=J_0$), and then to negative values. The non-physical $y_G<0$ indicates the failure of the confinement assumption; in other words, the influx conditions produce a GC with $h_N<H$, which propagates over the bottom of the gap without touching the top. Equation (41) also clarifies that the decay $J^{-(2n+3)}$ becomes faster as n increases, i.e., for a given J, the grounding $y_G$ is closer to 1 for larger n. The shear increases with n, and hence a shorter distance $1-y_G$ is needed for counteracting the buoyancy force.

Equation (41) can be rewritten as

$$J={[\varphi /(1-y_G)]}^{1/(2n+3)},(0\le y_G<1).$$

(42)

Since $\varphi \approx 1$, it is evident that, for $y_G=0$, $J_0$ is very close to 1 in general. This confirms the claim that l (see (19)) is the thickness of the unconfined GC.

The dimensionless propagation (see (24) and (42)) now reads

$${\tilde{x}}_N=\tilde{K}{\tilde{t}}^{\beta },\tilde{K}=J^{(2n+3)/(n+1)}={\left({\displaystyle \frac{\varphi }{1-y_G}}\right)}^{1/(n+1)}.$$

(43)

A quantitative comparison between the box and lubrication models with $\sigma =0$ is shown in Figure 8 and Figure 9. We see that there is fair quantitative agreement between the predictions. The differences could be anticipated because the constant h profile of the box produces a smaller shear per unit length, and can accommodate the same volume over a shorter $x_N$. Consequently, for a fixed J (i.e., fixed q), the box model is expected to predict a larger $y_G$ and smaller $\tilde{K}$ than the lubrication model (for the same n). The comparisons confirm these expectations. Moreover, the differences of $\tilde{K}$ for a given J are surprisingly small: Figure 9 shows that the lines of $\tilde{K}$ vs. J almost coincide for $J>1.3$ (the agreement increases with n). This demonstrates that the box model captures well the dominant mechanisms of the flow, and gives confidence into the present results.

3.2. AXI Confined Flow for $\sigma =0$

For obtaining a good insight into the confinement effect, we rearrange (34) for $\sigma =0$ and use an expansion in powers of the type ${(1+ϵ)}^p\approx 1+pϵ$, where $ϵ=\mathsf{\Psi }{J}^{-(3n+5)/2}$. We obtain

$$y_G\approx 1-\mathsf{\Psi }{J}^{-(3n+5)/2}=1-2^{-(n+1)/2}\varphi J^{-(3n+5)/2}.$$

(44)

This equation is exact for $n=1$ and, in general, a good approximation for $J>1$. We note that (44) is quite similar to the 2D counterpart (41); here, again, $J\propto q$, and the decay with J of the last RHS term is also strong, at least as $J^{-5/2}$. The arguments presented for the 2D confinement effect can be repeated here. For a large J (strong influx), $y_G$ is close to 1, and as J decreases (weak influx), $y_G$ tends to 0. However, in the AXI system, $r=0$ is a singular point, and hence the transition to unconfined flow is assumed to occur at a small but finite $y_G\approx 0.05$. The typical value of $J_0$ for $y_0=0.05$ is $0.7$ for a fairly large range of n; see Figure 10. This supports the claim that l given by (37) is the typical thickness of the unconfined GC. For $J<J_0$, the GC can be considered unconfined.

The dimensionless propagation (see (40)) with $\sigma =0$, reads

$${\tilde{r}}_N=\tilde{K}{\tilde{t}}^{\beta },\tilde{K}=\sqrt{2}{J}^{(3n+5)/\left(2\right(n+1\left)\right)}.$$

(45)

A quantitative comparison between the models with $\sigma =0$ is shown in Figure 9b and Figure 10. There is fair agreement in general, and the differences could be anticipated with the same arguments presented for the 2D flow. Again, the differences of $\tilde{K}$ for a given J are surprisingly small: Figure 9b shows that the lines of $\tilde{K}$ vs. J almost coincide when $J>1.2$ (the agreement increases with n).

4. Comparison with Data

A useful test for the validity of the box model is provided by a comparison of the present predictions with the experimental data presented in the papers of [8,10]. The laboratory system is AXI, the GC fluid is Newtonian ($n=1$) golden syrup, the ambient fluid is air (hence $g^{\prime }=g$), the gaps H are 0.71, 1.07, and 1.48 cm. The viscous fluid was influxed at a constant rate ($\alpha =1$) by a piston pump via a hole of 5.5 cm in diameter in the bottom plate and spread out in a quite axisymmetric pattern (the maximum $r_N$ was 27 cm). For sufficiently large influx rates, a clear separation between the slug and the GC, i.e. a clear grounding line, was observed. The propagation of the nose $r_N\left(t\right)$ and grounding line $r_G\left(t\right)$ (when present) were recorded for various constant volume fluxes. The absence of the grounding line indicates a free (unconfined) GC.

Refs. [8,10] use the same scaling as that used here for length, velocity, and time (see (23)) but employ the notations ${\eta }_N$ and ${\eta }_G$ as follows:

$${\tilde{r}}_N={\eta }_N{\tilde{t}}^{1/2};{\tilde{r}}_G={\eta }_G{\tilde{t}}^{1/2}.$$

(46)

In terms of our scaled solution (see (40)) the correspondence is $\beta =1/2$, ${\eta }_N=\tilde{K}$, ${\eta }_G/{\eta }_N=y_G$.

The definition of J here (37) for $n=1$ recovers the definition of J in these papers.

The box model predicts that for $n=1$, a self-similar propagation of the type (46) appears in the AXI system for $\alpha =1$. The experiments confirmed this prediction: the measured $r_N$ and $r_G$ fit that pattern very well. This allowed the calculation of the experimental ${\eta }_N$ and ${\eta }_G$ (the estimated error is $11\%$; the error of the experimental $y_G={\eta }_G/{\eta }_N$ is 22 %).

Table 1 of [8] provides values of the experimental ${\eta }_N$ and ${\eta }_G$ as functions of J for three different gaps H. Ref. [10], using available experimental values of the surface tension $\mathsf{\Gamma }$, pointed out that the three different gaps H also imply three different values of the parameter $S={(\mathsf{\Gamma }/\rho g)}^{1/2}/H=0.16,0.22,0.34$. The suggestion is to use the approximation $\sigma =S$ in the models. Figure 4 of [10] shows the experimental points ${\eta }_G$ and ${\eta }_N$ vs. J (symbols), as well as the corresponding predictions (curves) of the lubrication model, which takes into account the surface tension effect.

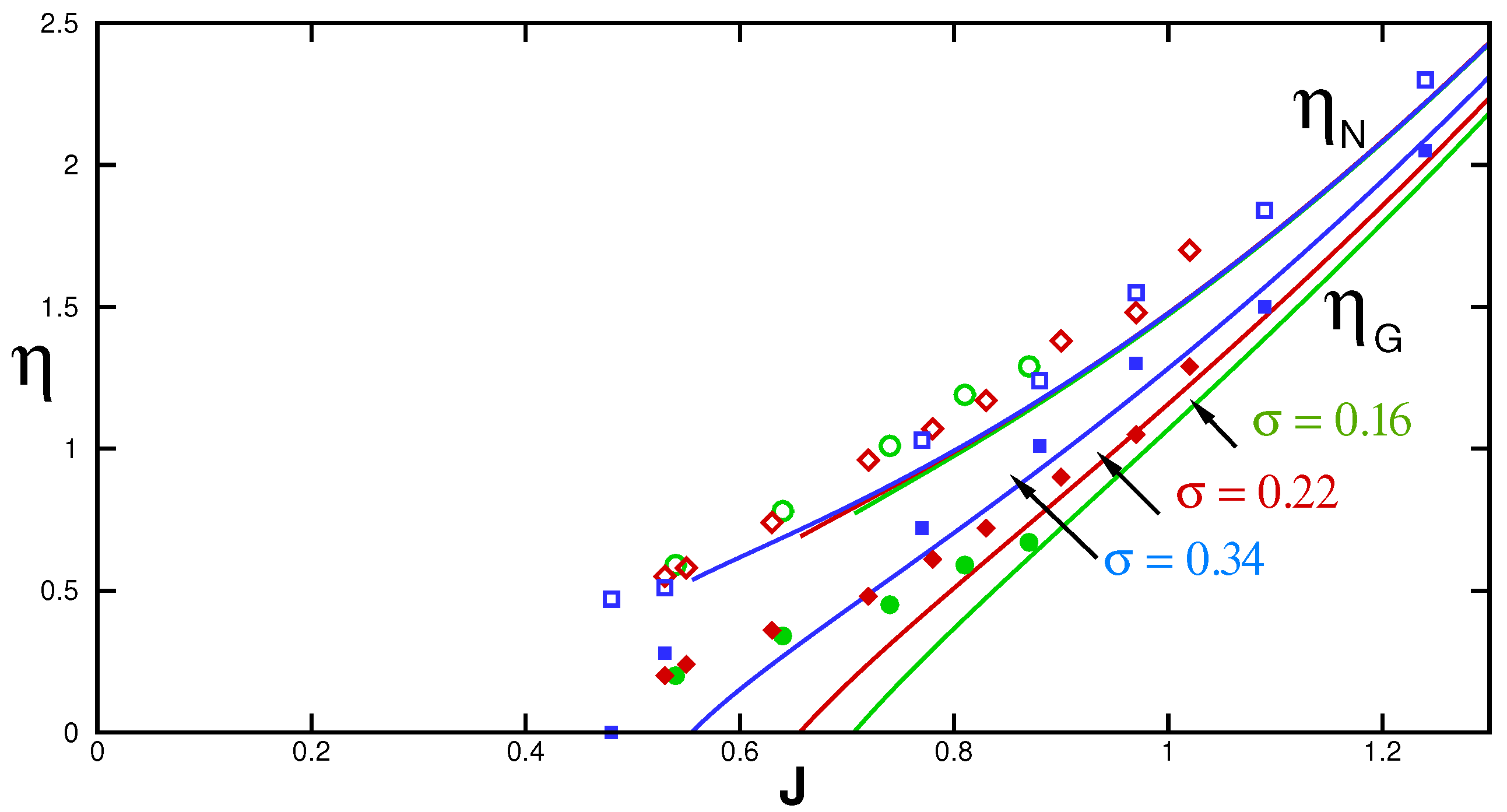
The box-model predictions for the tested flows are straightforward. For the AXI system with $n=1$, we obtain $\alpha =1,\beta =1/2$, (see (27) and (33)). For a given $\sigma$, the algebraic Equations (34) and (40) provide values of $\tilde{K}$ and $y_G$ for various J of interest. Using these results and the conversion ${\eta }_N=\tilde{K},{\eta }_G=y_G\tilde{K}$, we present in Figure 11 a similar plot to Figure 4 of [10]. The the lines are box-model predictions. There is a fair agreement of the predictions with the data. We see that the model predicts correctly the behaviours of ${\eta }_N$ and ${\eta }_G$. There is strong decay of ${\eta }_N$ as J decreases from 1.2 to 0.5 (approximately). However, the effect of $\sigma$ on this variable is remarkably small: the theoretical lines for the three values of $\sigma$ almost overlap, and the open symbols for the three values of $\sigma$ collapse on a smooth (imaginary) line. ${\eta }_G$ decreases faster than ${\eta }_N$ as J decreases. ${\eta }_G$ increases with $\sigma$, as seen in the prediction lines and in the filled symbols. (For $J<0.5$, the comparison with data is irrelevant because the GC is unconfined).

The box model provides the physical interpretation of these trends. The parameter J is proportional to $q/H$. When the influx rate decreases and/or the gap increases, the parameter J decreases, and in the physical system, the coefficients ${\eta }_G$ and ${\eta }_N$ of the propagation of the fronts (see (46)) are expected to decrease due to volume conservation. A larger $\sigma$ cause a smaller effective thickness $h_N$ (see Figure 1b) and a smaller buoyancy force $\sim h_N^2$. This allows a reduction of the bottom drag of the GC which is $\sim ({\eta }_N-{\eta }_G)$. Consequently, at a fixed J, a larger ${\eta }_G$ appears for a larger $\sigma$. The behaviour of ${\eta }_N$ is subtle. For a fixed J (fixed influx), a larger $\sigma$ renders a smaller effective thickness $h_N$; this would suggest an increase in ${\eta }_N$ to accommodate the volume. Here enters the second front. The larger $\sigma$ increases ${\eta }_G$, which means an increase in the radius of the slug. The larger slug absorbs a larger portion of the influxed fluid and counteracts the expected increase in ${\eta }_N$. The resulting flow displays a value of ${\eta }_N$, which is minimally affected by the variations of $\sigma$ in these data.

The quantitative discrepancies between the data and the theoretical predictions observed in our Figure 11 are, roughly, of the same magnitude for the present box model and the lubrication model used by [10] (Figure 4 in that paper). It is not possible to determine how much of the discrepancy is attributable to the box-model simplifications, because of the restricted data set, experimental errors, and uncertainty of the parameter $\sigma$. Taking into account the fact that the box model predicts correctly the values of $\alpha$ and $\beta$ of the experimental system, the overall predictions of the box model in this test seem to capture well the physical balances of the flow under consideration. In our opinion, this comparison provides support to the box model as a predictive tool for realistic systems, and motivates further tests in other systems, particularly power-law fluids.

5. Conclusions

We presented a box-model analysis of the flow of a viscous fluid injected into a horizontal gap of height H in rectangular 2D and cylindrical AXI geometries for a power-law non-Newtonian fluid ($\mu \sim {|\partial u/\partial z|}^{n-1}$). When the displaced (ambient) fluid is less dense and significantly less viscous than the injected one (a typical occurrence in molding industry), and the influx is sufficiently strong, the leading part of the flow is a GC while the tail fills the gap. We focused attention on the influxed volume $\mathcal{V}=q{t}^{\alpha }$. We showed that for certain values of $\alpha$ (depending on n), the flow is self-similar: the propagation of the nose and of the grounding line are like $K{t}^{\beta }$ and $y_{G}K{t}^{\beta }$. In general, $\beta =\alpha$ in 2D and $\beta =\alpha /2$ in AXI. We recall that the unconfined GCs display self-similar propagation for any $\alpha \ge 0$. The confinement restricts the similarity flow to $\alpha =n/(n+1)$ and $2n/(n+1)$ in 2D and AXI flows, respectively. We obtained explicit formulas for the stringent features of the flow field, like $y_G,\tilde{K},J_0,J_{0.9}$. All the results are in good agreement with the more rigorous lubrication-model solution (which does not assume a horizontal interface). In particular, we note identical prediction for the time-power coefficients $\alpha$ and $\beta$, as well as a surprisingly small discrepancy for the dimensionless prefactor $\tilde{K}$.

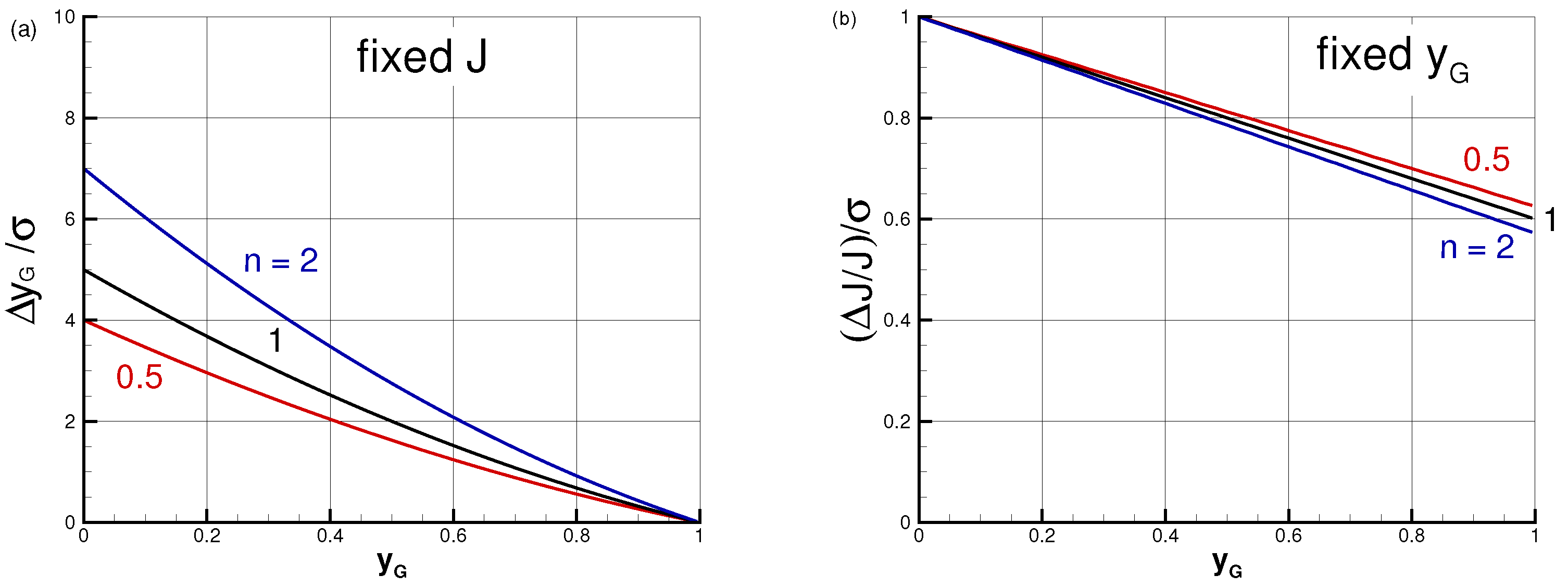
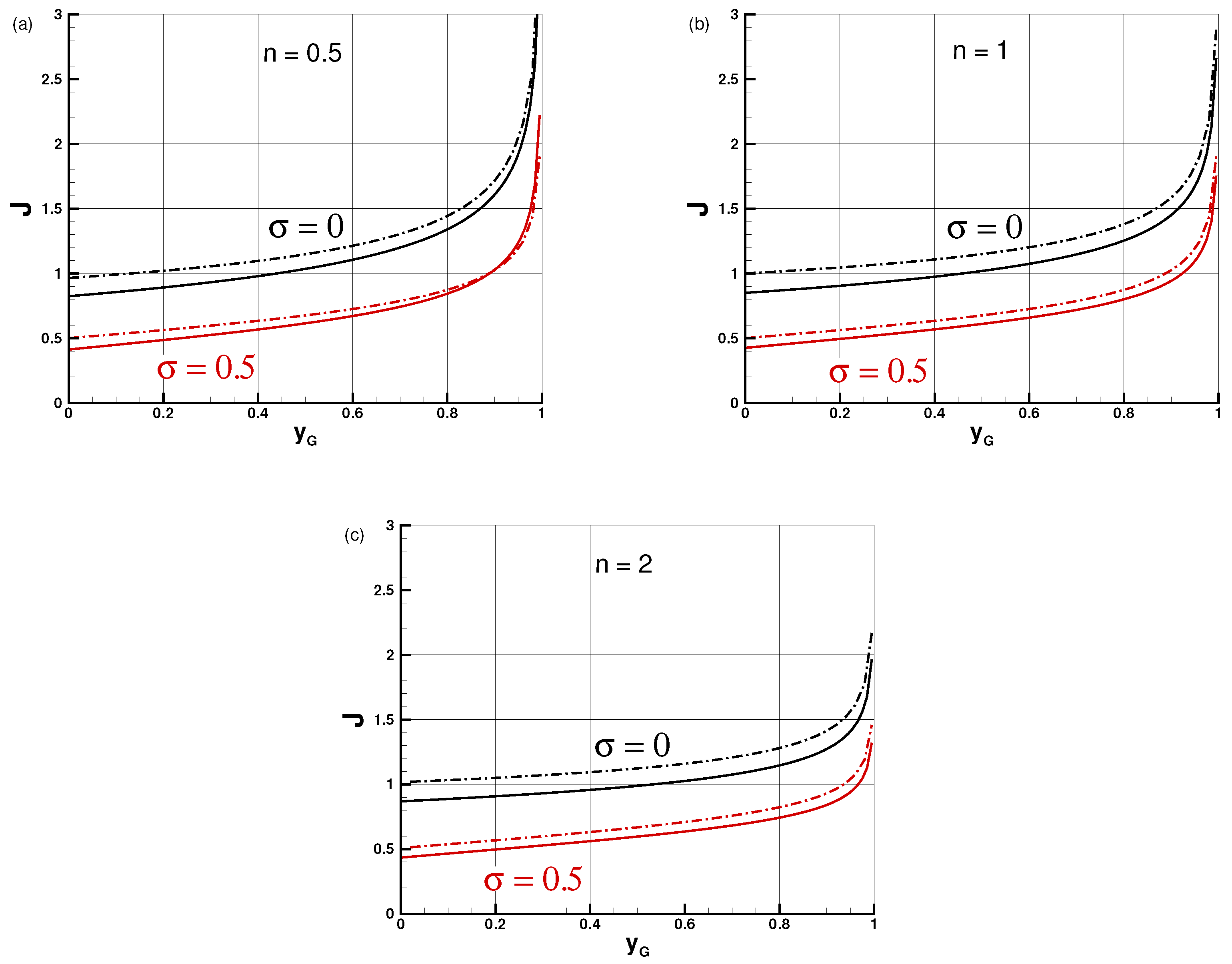
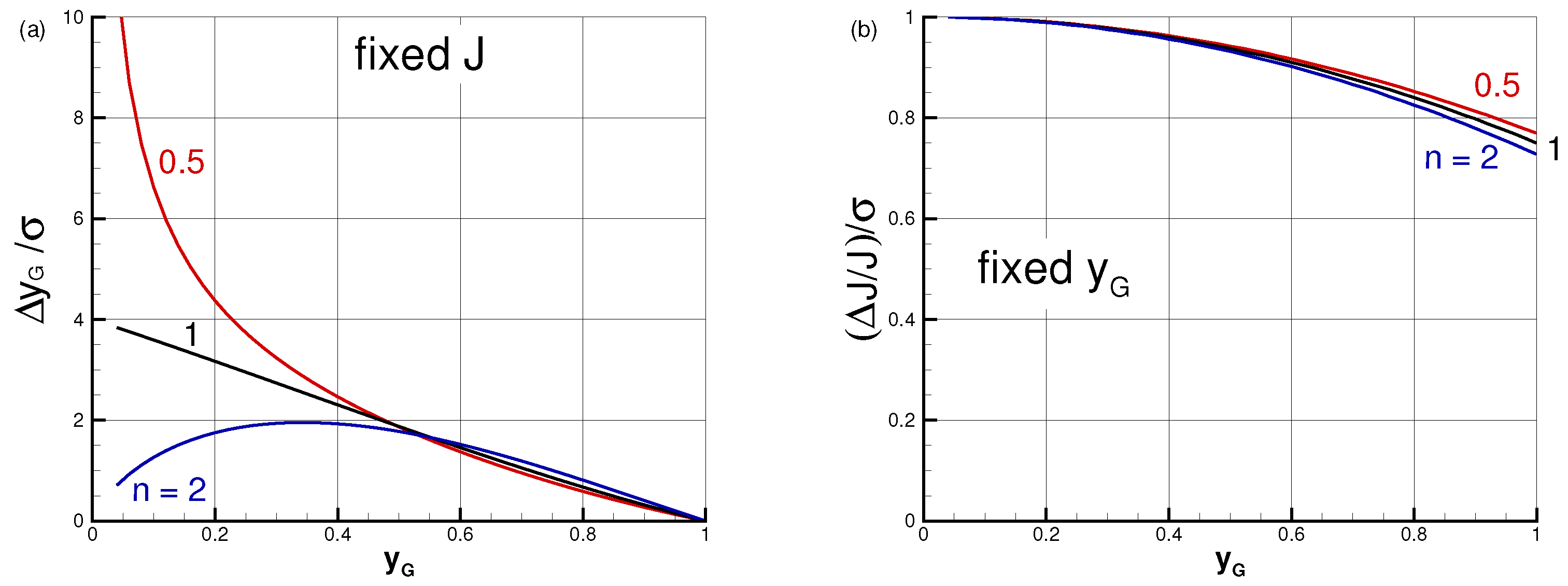
In general, the flow under consideration depends on four parameters: $J,n,\sigma$, and ${\sigma }_N$. The box model demonstrates that the dependencies are strongly coupled and non-linear, and hence a simple model is helpful for understanding the physical influence of each of the parameters.

The box model reveals that the main surface tension effects, $\propto \sigma$, are as follows: (a) for a fixed J, the position $y_G$ increases; (b) for maintaining a fixed $y_G$, J must be reduced. The effects of a nose meniscus are in the same direction, but $\propto {\sigma }_N^2$.

The restriction of the solution to special values of the influxed volume coefficient $\alpha$ reproduces a physical condition, not a mathematical simplification. We argue that the similarity behaviour corresponding to this $\alpha$ is essential in the present problem; influx with a different $\alpha$ is bound to produce a very different flow pattern. The present $\alpha$ keeps the grounding line between the inlet and the nose ($0<y_G<1$). In this case, the GC elongates, but maintains a constant average thickness. When $\alpha$ is reduced, the GC tends to become thinner with t, the grounding line moves toward the inlet, and an unconfined GC appears on the bottom of the gap. When $\alpha$ is increased, the GC tends to become thicker with t, the grounding line moves toward the nose, and all the injected fluid behaves like a slug in contact with both boundaries of the gap. It is remarkable that the similarity solution is robust: for a given geometry, the time powers $\alpha$ and $\beta$ depend on n, and are unaffected by the presence of surface tension effects represented by $\sigma$ and ${\sigma }_N$. This interesting prediction has been verified experimentally for the AXI system and $n=1$ ([10]), and further tests will be beneficial.

We recall that the accurate value of the surface tension parameter $\sigma$ is not available for practical systems. The comparisons of predictions with data, performed by [10] and here in Section 4, suggests that $\sigma ={(\mathsf{\Gamma }/\rho g^{\prime })}^{1/2}/H$ is a fair approximation. This is a good starting point for the practical use of the present models. However, we must keep in mind that the data set of [10] covers only AXI flow of a Newtonian fluid. For the assessment and improvement of the extended theory, a much wider experimental study is necessary. We expect that this will be reported in the near future.

The advantage of the box model is in the simplicity of the derivation and the predictions. We straightforwardly gain the insight that the kinematic (volume continuity) balances determine the relation between $\alpha$ and $\beta$, as well as the coefficient K; the dynamic force balance determine the values of $\beta$ and $y_G$. The interconnections between the dimensionless variables $y_G,\tilde{K},J,\sigma ,{\sigma }_N,n$ are expressed in explicit formulas, without any adjustable constants. The description of the flow has been reduced to a set of basic algebraic-substitution formulas. The influence of the surface tension meniscus at the grounding line (parameter $\sigma$) is well elucidated. The box model also clarifies that the effect of the nose meniscus (parameter ${\sigma }_N$) is typically negligible. These simplifications are expected to facilitate the analysis and design of various applications. Needless to say, the same information can be extracted from the more rigorous lubrication model, but this requires a more significant effort of programming, data processing, and interpretation.

We emphasise that, in general, the box model is an unreliable prediction tool, unless subjected to stringent verification against some more accurate results over a significant range of parameters. The present box model can be recommended because it has passed such tests (without using any adjustable constants), and we have reliable information about the expected error concerning the sign (under/over prediction) and order of magnitude. However, we keep in mind that this paper compares mostly between two theories based on simplifications (such as thin layer, hydrostatic pressure, sharp meniscus, and well-controlled influx). The convincing assessment of the models requires critical comparison with experimental data. (The comparison with the data of [10], which is in Section 4, is encouraging but covers a restricted domain, particularly $n=1$). In view of the large number of involved parameters, this is a challenging experimental task. We are confident that the present quite sharp theoretical predictions will facilitate the experimental verification.