RIM-PIV Measurements of Solid–Liquid Flow in a Stirred Tank Used for Mesenchymal Stem Cell Culture
Abstract
1. Introduction
2. Materials and Methods
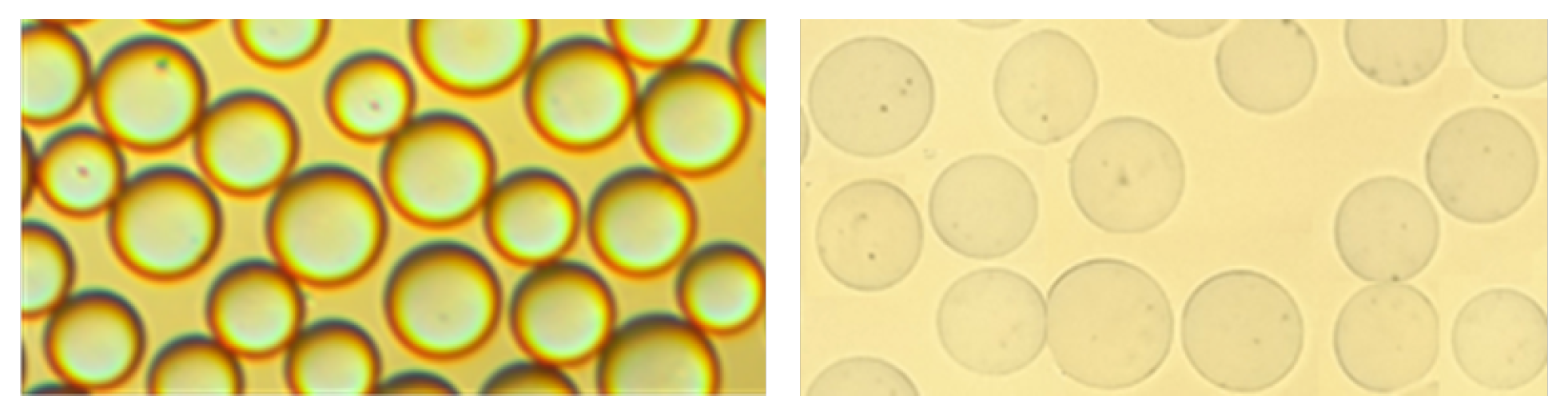
2.1. Solid–Liquid System Properties
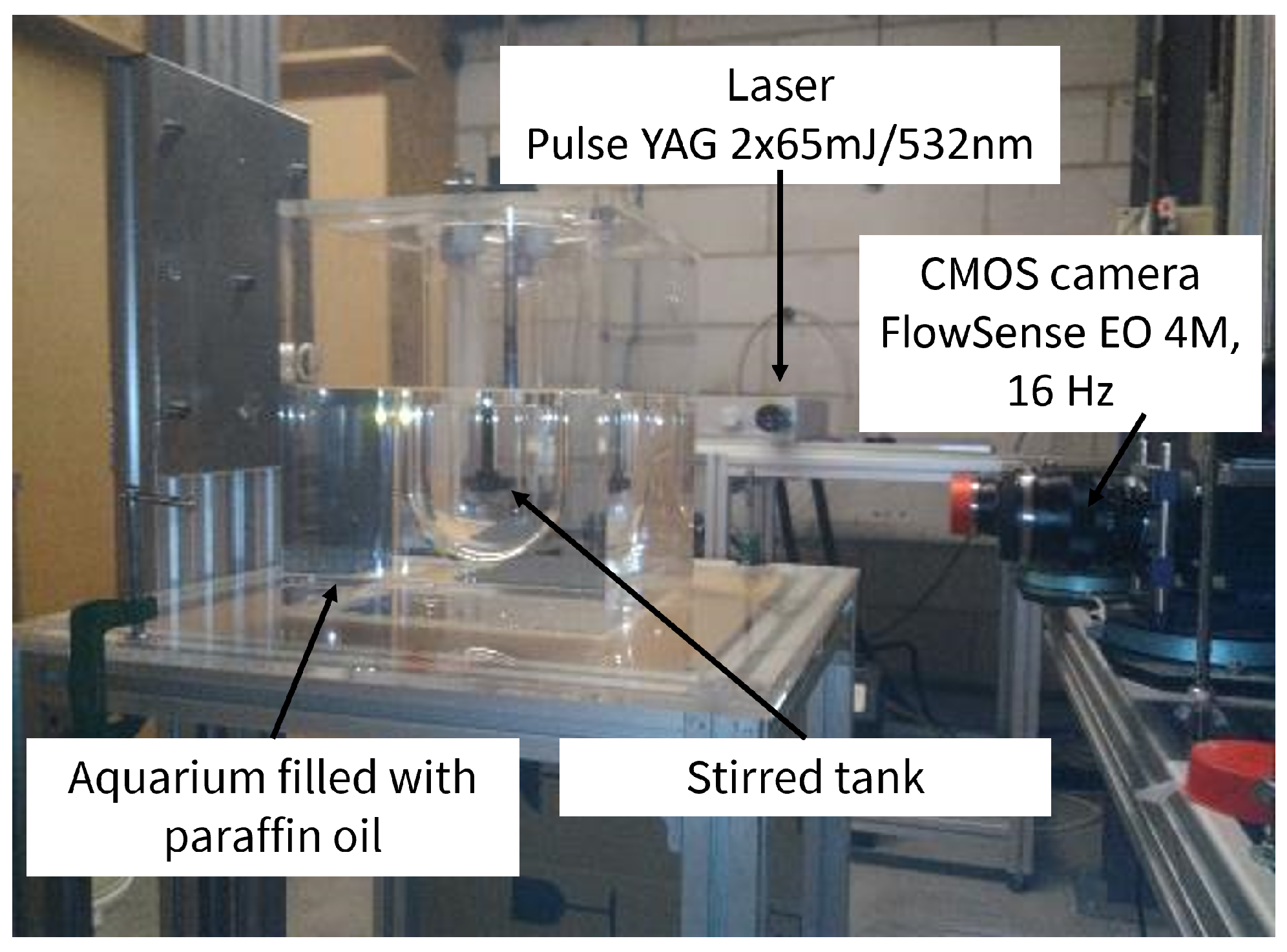
2.2. Stirred Tank and PIV Setup
2.3. Flow Properties
2.4. PIV Treatment and Post-Processing
3. Results and Discussions
3.1. PIV Treatment Assessment
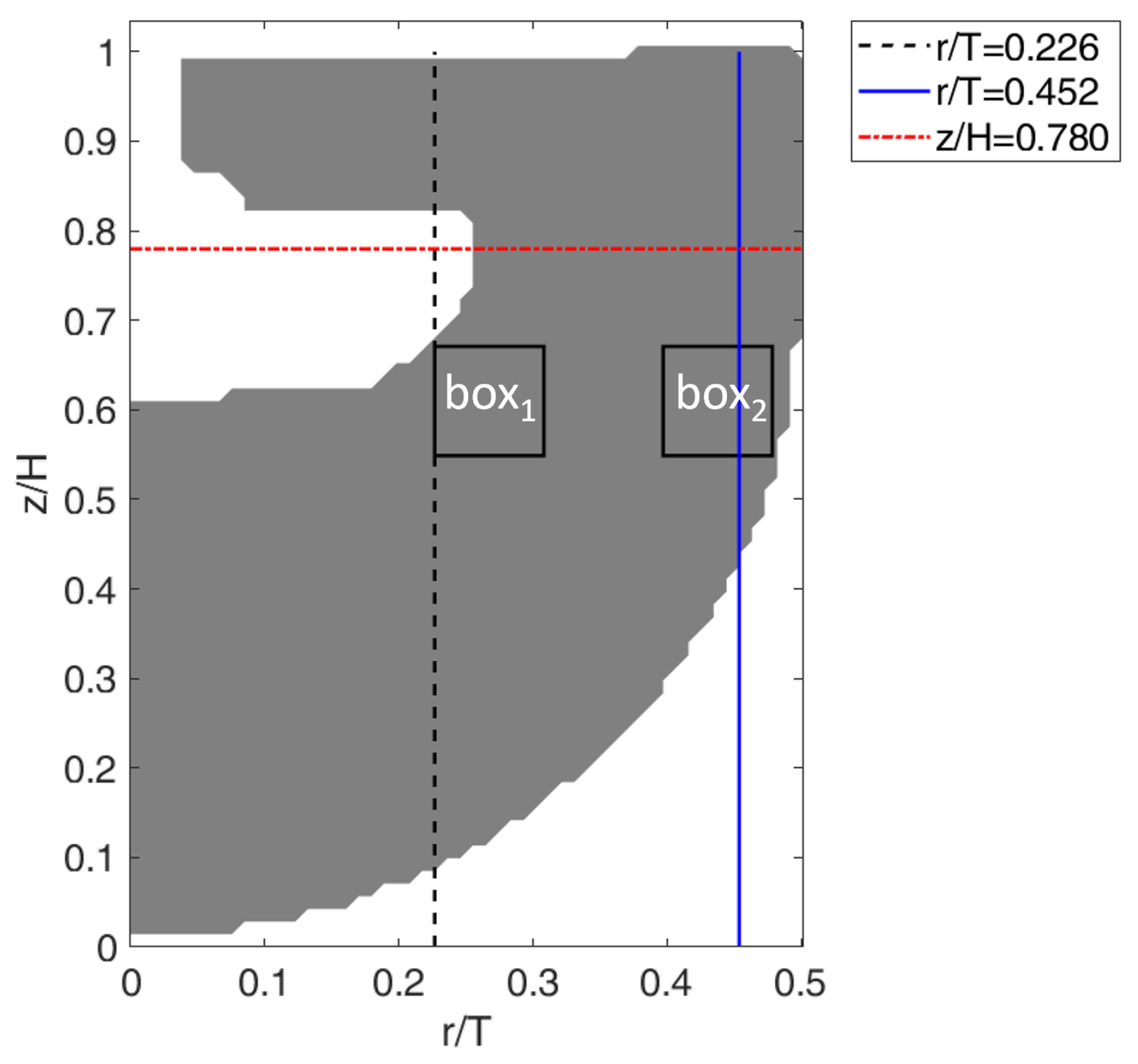
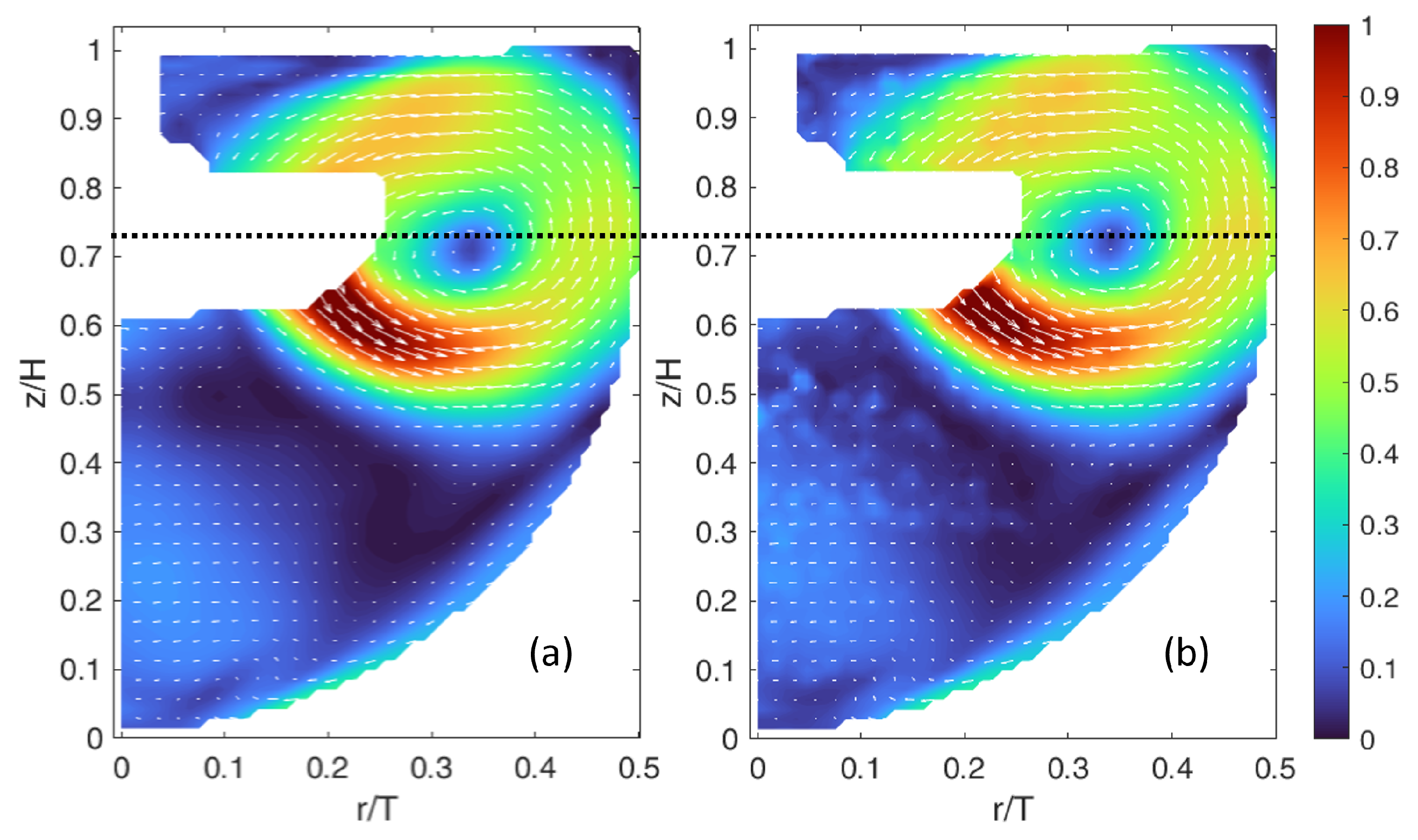
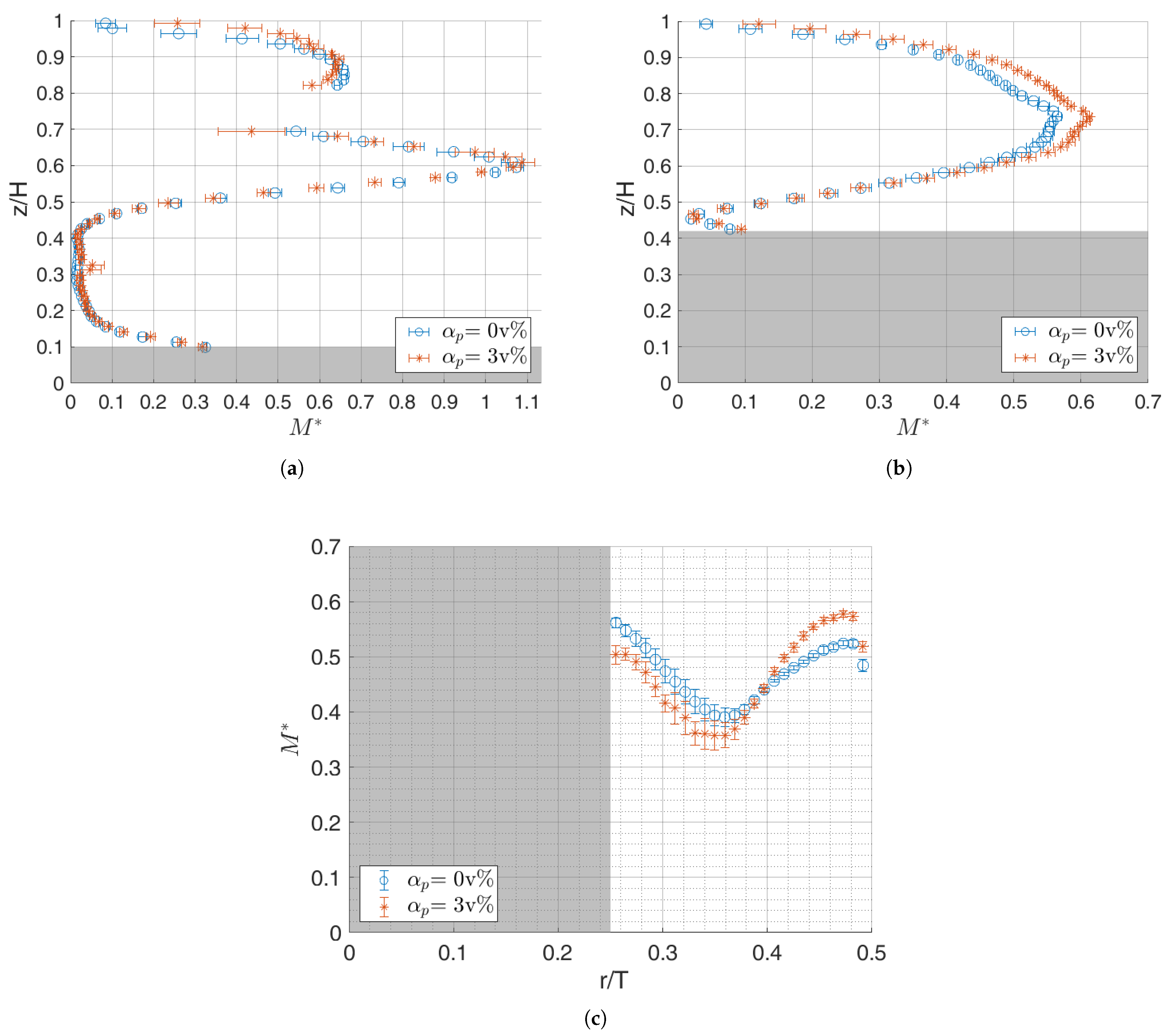
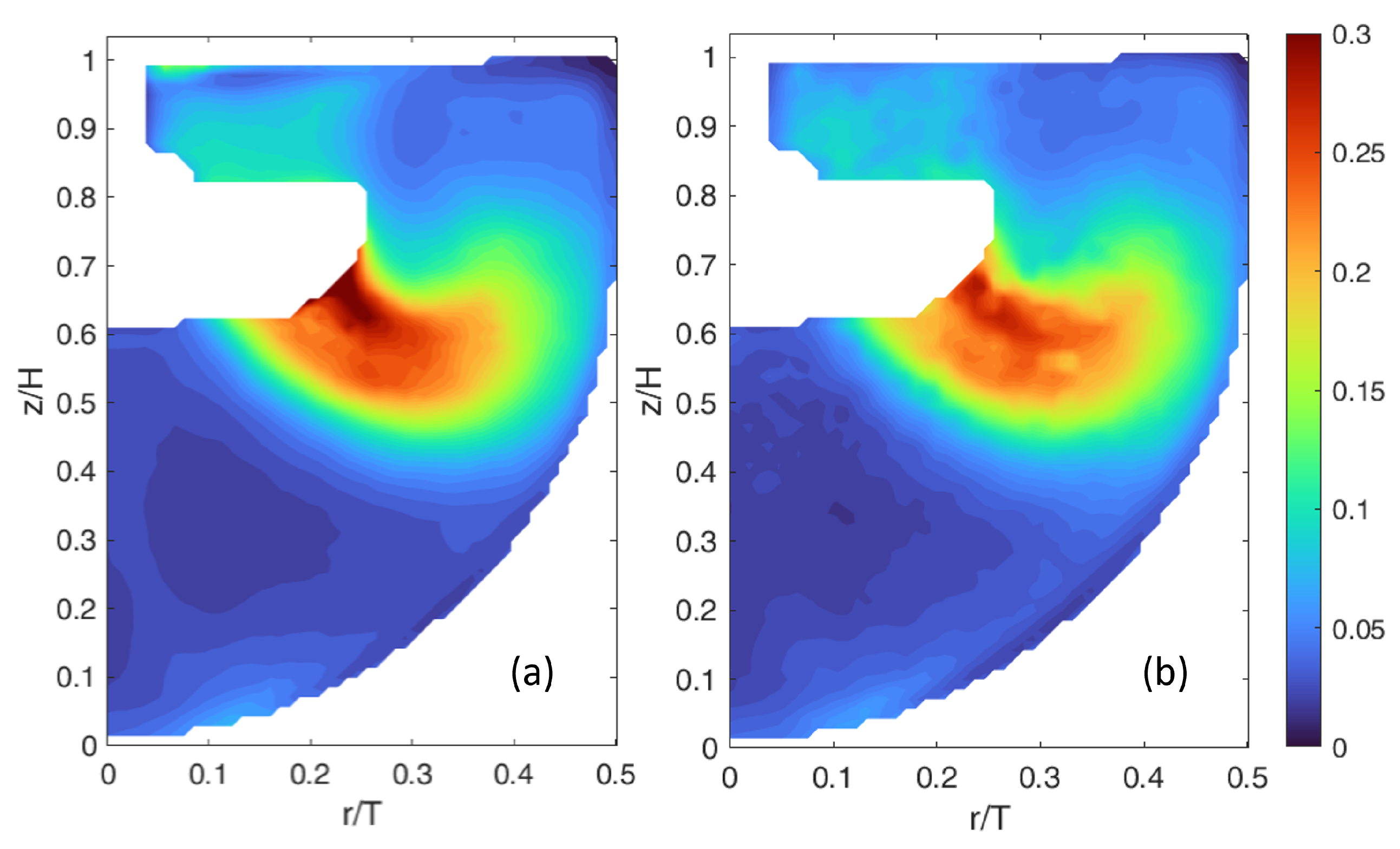
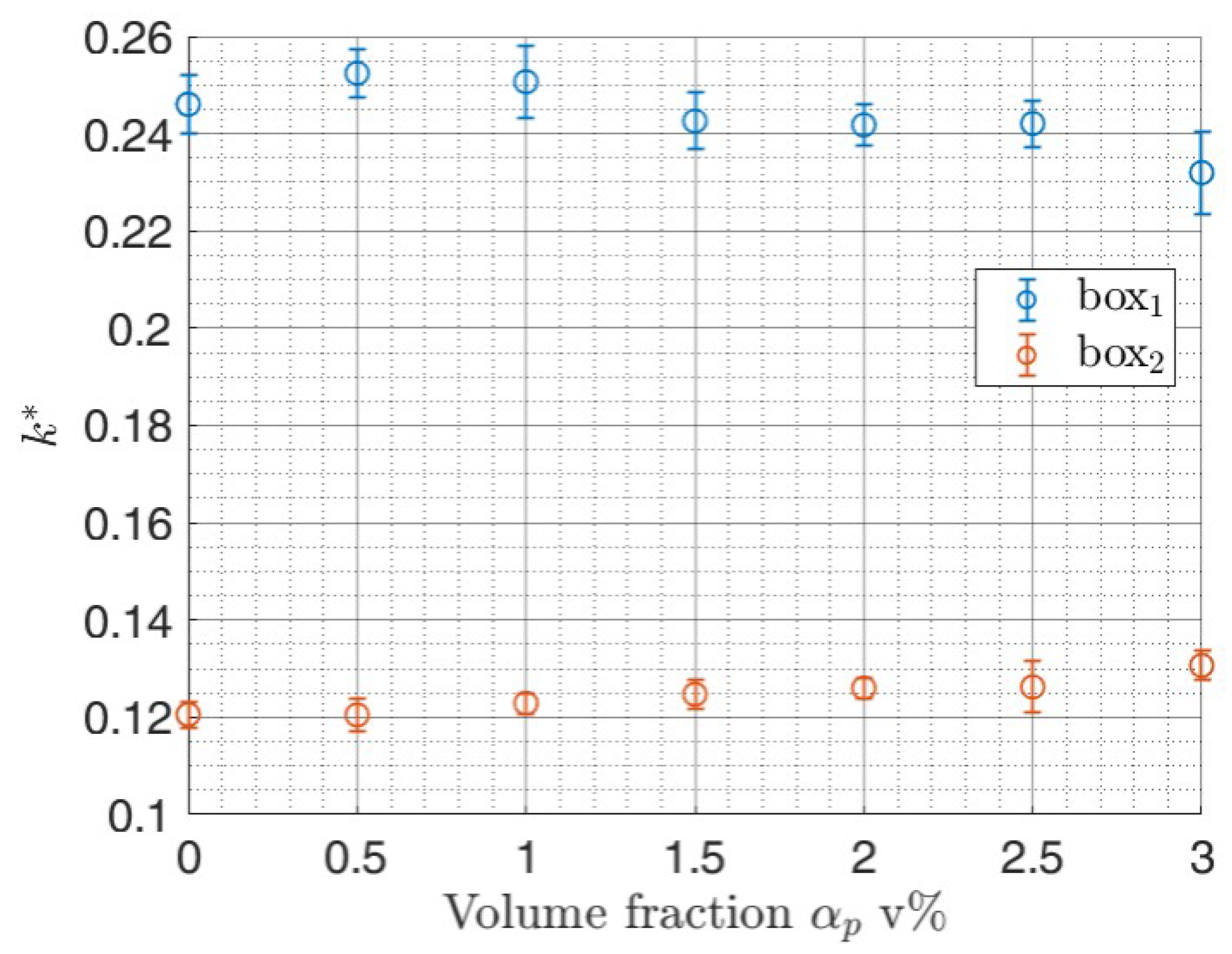
3.2. Flow Analysis
- r/T = 0.226, which cuts through the impeller tip to cover the beginning of the discharge flow and the ending phase of the recirculation loop;
- r/T = 0.452, near the wall, which covers the other half of the loop;
- z/H = 0.780, above the impeller, which covers the top of the recirculation loop.
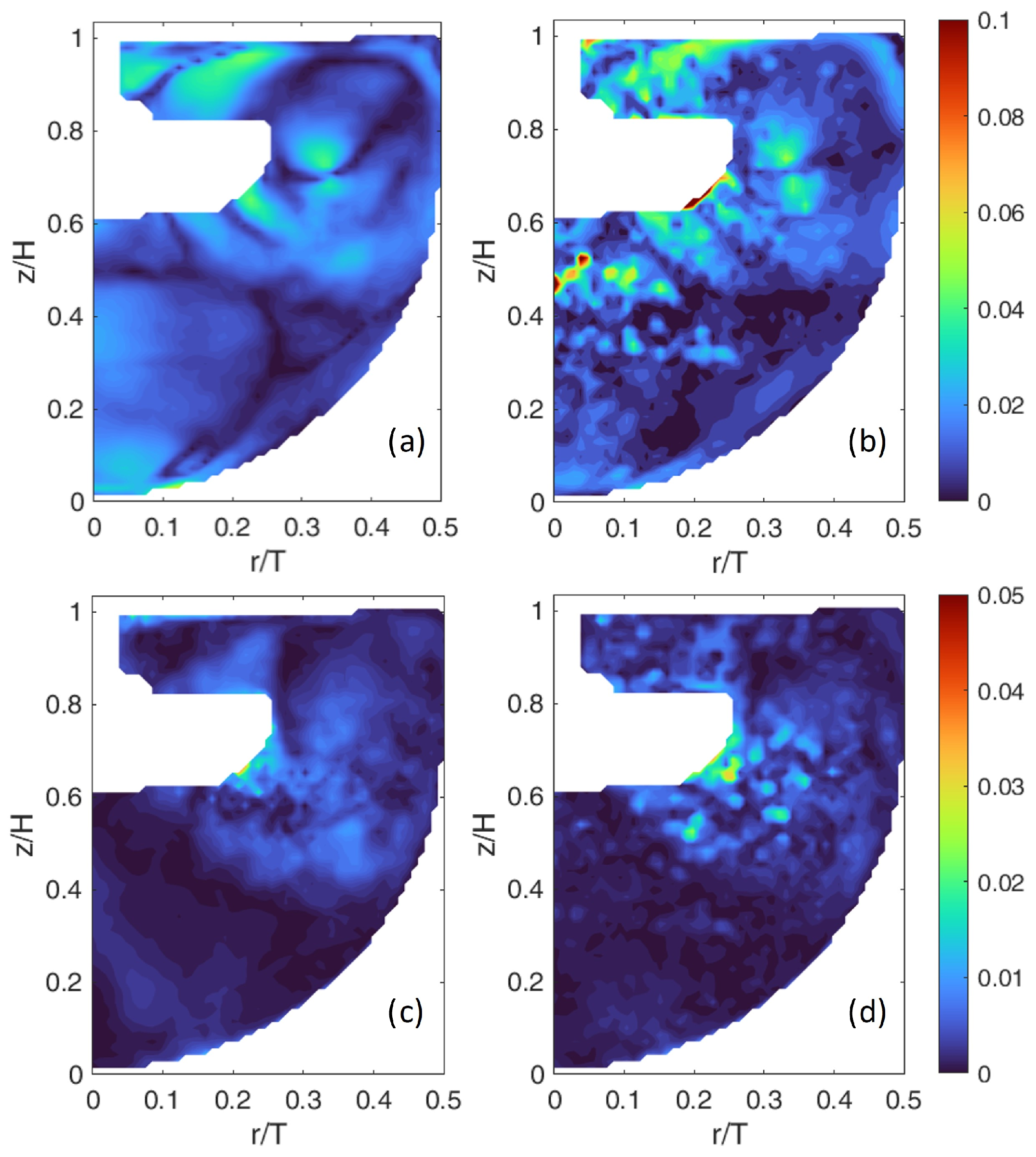
3.2.1. Mean Velocity Magnitude
3.2.2. Turbulent Kinetic Energy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LDA | Laser Doppler anemometry |
| MSC | Mesenchymal stem cell |
| PIV | Particle image velocimetry |
| RI | Refractive index |
| RIM | Refractive index matching |
| rms | Root mean square |
| TKE | Turbulent kinetic energy |
| Particle volume fraction, – | |
| Energy dissipation rate, m2/s3 | |
| Dynamic viscosity, Pa.s | |
| Kinematic viscosity, m2/s | |
| Density, kg/m3 | |
| Taylor length scale, m | |
| Kolmogorov length scale, m | |
| Time scale, s | |
| C | Impeller clearance, m |
| D | Impeller diameter, m |
| Particle diameter, m | |
| H | Liquid height, m |
| k | Turbulent kinetic energy, m2/s2 |
| Non-dimensional turbulent kinetic energy, – | |
| L | Integral length scale, m |
| M | Mean velocity magnitude, m/s |
| Non-dimensional mean velocity magnitude, – | |
| N | Impeller speed, rpm |
| T | Tank diameter, m |
| P | Power input, W |
| Power number, – | |
| r | Radial coordinate, m |
| Mean velocity, m/s | |
| Fluctuating velocity, m/s | |
| V | Fluid volume, m3 |
| z | Axial coordinate, m |
| Reynolds number, – | |
| Stokes number, – |
References
- Rodríguez-Fuentes, D.E.; Fernández-Garza, L.E.; Samia-Meza, J.A.; Barrera-Barrera, S.A.; Caplan, A.I.; Barrera-Saldaña, H.A. Mesenchymal stem cells current clinical applications: A systematic review. Arch. Med. Res. 2021, 52, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Beyer Nardi, N.; da Silva Meirelles, L. Mesenchymal Stem Cells: Isolation, In Vitro Expansion and Characterization. In Stem Cells; Wobus, A.M., Boheler, K.R., Eds.; Handbook of Experimental Pharmacology; Springer: Berlin/Heidelberg, Germany, 2006; pp. 249–282. [Google Scholar] [CrossRef]
- Frauenschuh, S.; Reichmann, E.; Ibold, Y.; Goetz, P.M.; Sittinger, M.; Ringe, J. A Microcarrier-Based Cultivation System for Expansion of Primary Mesenchymal Stem Cells. Biotechnol. Prog. 2007, 23, 187–193. [Google Scholar] [CrossRef]
- Schop, D.; Janssen, F.W.; Borgart, E.; de Bruijn, J.D.; van Dijkhuizen-Radersma, R. Expansion of mesenchymal stem cells using a microcarrier-based cultivation system: Growth and metabolism. J. Tissue Eng. Regen. Med. 2008, 2, 126–135. [Google Scholar] [CrossRef] [PubMed]
- Rafiq, Q.A.; Brosnan, K.M.; Coopman, K.; Nienow, A.W.; Hewitt, C.J. Culture of human mesenchymal stem cells on microcarriers in a 5 L stirred-tank bioreactor. Biotechnol. Lett. 2013, 35, 1233–1245. [Google Scholar] [CrossRef]
- Croughan, M.S.; Hamel, J.F.P.; Wang, D.I.C. Effects of microcarrier concentration in animal cell culture. Biotechnol. Bioeng. 1988, 32, 975–982. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/bit.260320805 (accessed on 13 October 2025). [CrossRef]
- Maul, T.M.; Chew, D.W.; Nieponice, A.; Vorp, D.A. Mechanical stimuli differentially control stem cell behavior: Morphology, proliferation, and differentiation. Biomech. Model. Mechanobiol. 2011, 10, 939–953. [Google Scholar] [CrossRef]
- Nienow, A.W. Reactor engineering in large scale animal cell culture. Cytotechnology 2006, 50, 9–33. [Google Scholar] [CrossRef]
- Godara, P.; McFarland, C.; Nordon, R. Design of bioreactors for mesenchymal stem cell tissue engineering. J. Chem. Technol. Biotechnol. 2008, 83, 408–420. [Google Scholar] [CrossRef]
- Jossen, V.; Pörtner, R.; Kaiser, S.C.; Kraume, M.; Eibl, D.; Eibl, R.; Jossen, V.; Pörtner, R.; Kaiser, S.C.; Kraume, M.; et al. Mass Production of Mesenchymal Stem Cells — Impact of Bioreactor Design and Flow Conditions on Proliferation and Differentiation. In Cells and Biomaterials in Regenerative Medicine; IntechOpen: London, UK, 2014. [Google Scholar] [CrossRef]
- Hutmacher, D.W.; Singh, H. Computational fluid dynamics for improved bioreactor design and 3D culture. Trends Biotechnol. 2008, 26, 166–172. [Google Scholar] [CrossRef]
- Rafiq, Q.A.; Coopman, K.; Nienow, A.W.; Hewitt, C.J. Systematic microcarrier screening and agitated culture conditions improves human mesenchymal stem cell yield in bioreactors. Biotechnol. J. 2016, 11, 473–486. [Google Scholar] [CrossRef] [PubMed]
- Collignon, M.L.; Delafosse, A.; Calvo, S.; Martin, C.; Marc, A.; Toye, D.; Olmos, E. Large-Eddy Simulations of microcarrier exposure to potentially damaging eddies inside mini-bioreactors. Biochem. Eng. J. 2016, 108, 30–43. [Google Scholar] [CrossRef]
- Loubière, C.; Delafosse, A.; Guedon, E.; Chevalot, I.; Toye, D.; Olmos, E. Dimensional analysis and CFD simulations of microcarrier ‘just-suspended’ state in mesenchymal stromal cells bioreactors. Chem. Eng. Sci. 2019, 203, 464–474. [Google Scholar] [CrossRef]
- Olmos, E.; Loubiere, K.; Martin, C.; Delaplace, G.; Marc, A. Critical agitation for microcarrier suspension in orbital shaken bioreactors: Experimental study and dimensional analysis. Chem. Eng. Sci. 2015, 122, 545–554. [Google Scholar] [CrossRef]
- Delafosse, A.; Loubière, C.; Calvo, S.; Toye, D.; Olmos, E. Solid-liquid suspension of microcarriers in stirred tank bioreactor – Experimental and numerical analysis. Chem. Eng. Sci. 2018, 180, 52–63. [Google Scholar] [CrossRef]
- Loubière, C.; Sion, C.; De Isla, N.; Reppel, L.; Guedon, E.; Chevalot, I.; Olmos, E. Impact of the type of microcarrier and agitation modes on the expansion performances of mesenchymal stem cells derived from umbilical cord. Biotechnol. Prog. 2019, 35, e2887. [Google Scholar] [CrossRef] [PubMed]
- Maillot, C.; De Isla, N.; Loubiere, C.; Toye, D.; Olmos, E. Impact of microcarrier concentration on mesenchymal stem cell growth and death: Experiments and modeling. Biotechnol. Bioeng. 2022, 119, 3537–3548. [Google Scholar] [CrossRef]
- Hewitt, C.J.; Lee, K.; Nienow, A.W.; Thomas, R.J.; Smith, M.; Thomas, C.R. Expansion of human mesenchymal stem cells on microcarriers. Biotechnol. Lett. 2011, 33, 2325–2335. [Google Scholar] [CrossRef]
- Northrup, M.A.; Kulp, T.J.; Angel, S.M. Fluorescent particle image velocimetry: Application to flow measurement in refractive index-matched porous media. Appl. Opt. 1991, 30, 3034–3040. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, L.; Kelly, J.; Wexler, A.; Prasad, A. Particle image velocimetry measurements in complex geometries. Exp. Fluids 2000, 29, 91–95. [Google Scholar] [CrossRef]
- Morgan, R.G.; Markides, C.N.; Zadrazil, I.; Hewitt, G.F. Characteristics of horizontal liquid–liquid flows in a circular pipe using simultaneous high-speed laser-induced fluorescence and particle velocimetry. Int. J. Multiph. Flow 2013, 49, 99–118. [Google Scholar] [CrossRef]
- Bluestein, A.M.; Bohl, D. Development and validation of a PIV processing routine for two-phase index-matched flows. J. Vis. 2020, 23, 951–970. [Google Scholar] [CrossRef]
- Virdung, T.; Rasmuson, A. Solid–Liquid Flow at Dilute Concentrations in an Axially Stirred Vessel Investigated Using Particle Image Velocimetry. Chem. Eng. Commun. 2008, 195, 18–34. [Google Scholar] [CrossRef]
- Unadkat, H.; Rielly, C.D.; Hargrave, G.K.; Nagy, Z.K. Application of fluorescent PIV and digital image analysis to measure turbulence properties of solid–liquid stirred suspensions. Chem. Eng. Res. Des. 2009, 87, 573–586. [Google Scholar] [CrossRef]
- Gabriele, A.; Tsoligkas, A.N.; Kings, I.N.; Simmons, M.J.H. Use of PIV to measure turbulence modulation in a high throughput stirred vessel with the addition of high Stokes number particles for both up- and down-pumping configurations. Chem. Eng. Sci. 2011, 66, 5862–5874. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Montante, G.; Paglianti, A.; Magelli, F. Analysis of dilute solid–liquid suspensions in turbulent stirred tanks. Chem. Eng. Res. Des. 2012, 90, 1448–1456. [Google Scholar] [CrossRef]
- Li, G.; Gao, Z.; Li, Z.; Wang, J.; Derksen, J. Particle-resolved PIV experiments of solid-liquid mixing in a turbulent stirred tank. AIChE J. 2018, 64, 389–402. [Google Scholar] [CrossRef]
- Nouri, J.; Whitelaw, J. Particle velocity characteristics of dilute to moderately dense suspension flows in stirred reactors. Int. J. Multiph. Flow 1992, 18, 21–33. [Google Scholar] [CrossRef]
- Kohnen, C.; Bohnet, M. Measurement and simulation of fluid flow in agitated solid/liquid suspensions. Chem. Eng. Technol. Ind. Chem. Plant Equip. Process Eng. Biotechnol. 2001, 24, 639–643. [Google Scholar] [CrossRef]
- Micheletti, M.; Yianneskis, M. Study of Fluid Velocity Characteristics in Stirred Solid—Liquid Suspensions With a Refractive Index Matching Technique. Proc. Inst. Mech. Eng. Part -J. Process Mech. Eng. 2004, 218, 191–204. [Google Scholar] [CrossRef]
- Virdung, T.; Rasmuson, A. Measurements of continuous phase velocities in solid–liquid flow at elevated concentrations in a stirred vessel using LDV. Chem. Eng. Res. Des. 2007, 85, 193–200. [Google Scholar] [CrossRef]
- Guiraud, P.; Costes, J.; Bertrand, J. Local measurements of fluid and particle velocities in a stirred suspension. Chem. Eng. J. 1997, 68, 75–86. [Google Scholar] [CrossRef]
- Sommer, A.E.; Rox, H.; Shi, P.; Eckert, K.; Rzehak, R. Solid-liquid flow in stirred tanks:“CFD-grade” experimental investigation. Chem. Eng. Sci. 2021, 245, 116743. [Google Scholar] [CrossRef]
- Ferrante, A.; Elghobashi, S. On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 2003, 15, 315–329. [Google Scholar] [CrossRef]
- Borrero-Echeverry, D.; Morrison, B.C.A. Aqueous ammonium thiocyanate solutions as refractive index-matching fluids with low density and viscosity. Exp. Fluids 2016, 57, 123. [Google Scholar] [CrossRef]
- Budwig, R. Refractive index matching methods for liquid flow investigations. Exp. Fluids 1994, 17, 350–355. [Google Scholar] [CrossRef]
- Wright, S.F.; Zadrazil, I.; Markides, C.N. A review of solid–fluid selection options for optical-based measurements in single-phase liquid, two-phase liquid–liquid and multiphase solid–liquid flows. Exp. Fluids 2017, 58, 108. [Google Scholar] [CrossRef]
- Sion, C.; Ghannoum, D.; Ebel, B.; Gallo, F.; de Isla, N.; Guedon, E.; Chevalot, I.; Olmos, E. A new perfusion mode of culture for WJ-MSCs expansion in a stirred and online monitored bioreactor. Biotechnol. Bioeng. 2021, 118, 4453–4464. [Google Scholar] [CrossRef]
- Wiederseiner, S.; Andreini, N.; Epely-Chauvin, G.; Ancey, C. Refractive-index and density matching in concentrated particle suspensions: A review. Exp. Fluids 2011, 50, 1183–1206. [Google Scholar] [CrossRef]
- Adrian, R.J. Image shifting technique to resolve directional ambiguity in double-pulsed velocimetry. Appl. Opt. 1986, 25, 3855–3858. [Google Scholar] [CrossRef]
- Chéron, J.; Loubière, C.; Delaunay, S.; Guezennec, A.G.; Olmos, E. CFD numerical simulation of particle suspension and hydromechanical stress in various designs of multi-stage bioleaching reactors. Hydrometallurgy 2020, 197, 105490. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent flows. Meas. Sci. Technol. 2001, 12, 2020–2021. [Google Scholar] [CrossRef]
- Simon, E.; Augier, F.; Morchain, J.; Pierson, J.L.; Liné, A. Investigation of the local apparent viscosity in a stirred tank with a shear-thinning fluid through particle image velocimetry. Chem. Eng. Res. Des. 2024, 206, 378–385. [Google Scholar] [CrossRef]
- Saarenrinne, P.; Piirto, M.; Eloranta, H. Experiences of turbulence measurement with PIV. Meas. Sci. Technol. 2001, 12, 1904. [Google Scholar] [CrossRef]
- Baldi, S.; Yianneskis, M. On the quantification of energy dissipation in the impeller stream of a stirred vessel from fluctuating velocity gradient measurements. Chem. Eng. Sci. 2004, 59, 2659–2671. [Google Scholar] [CrossRef]
- Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Owen, P. Turbulent flow and particle deposition in the trachea. In Ciba Foundation Symposium-Circulatory and Respiratory Mass Transport; Wiley Online Library: Hoboken, NJ, USA, 1969; pp. 236–255. [Google Scholar]
- Scharnowski, S.; Kähler, C.J. Particle image velocimetry-classical operating rules from today’s perspective. Opt. Lasers Eng. 2020, 135, 106185. [Google Scholar] [CrossRef]
- Gabriele, A.; Nienow, A.; Simmons, M. Use of angle resolved PIV to estimate local specific energy dissipation rates for up-and down-pumping pitched blade agitators in a stirred tank. Chem. Eng. Sci. 2009, 64, 126–143. [Google Scholar] [CrossRef]
- Liu, N.; Wang, W.; Han, J.; Zhang, M.; Angeli, P.; Wu, C.; Gong, J. A PIV investigation of the effect of disperse phase fraction on the turbulence characteristics of liquid–liquid mixing in a stirred tank. Chem. Eng. Sci. 2016, 152, 528–546. [Google Scholar] [CrossRef]
- Escudié, R.; Liné, A. Experimental analysis of hydrodynamics in a radially agitated tank. AIChE J. 2003, 49, 585–603. [Google Scholar] [CrossRef]
- Khan, F.R.; Rielly, C.D.; Brown, D.A.R. Angle-resolved stereo-PIV measurements close to a down-pumping pitched-blade turbine. Chem. Eng. Sci. 2006, 61, 2799–2806. [Google Scholar] [CrossRef]
- Chung, K.H.K.; Barigou, M.; Simmons, M.J.H. Reconstruction of 3-D Flow Field Inside Miniature Stirred Vessels Using a 2-D PIV Technique. Chem. Eng. Res. Des. 2007, 85, 560–567. [Google Scholar] [CrossRef]
- Fornari, W.; Formenti, A.; Picano, F.; Brandt, L. The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions. Phys. Fluids. 2016, 28, 033301. [Google Scholar] [CrossRef]
- Gore, R.; Crowe, C. Effect of particle size on modulating turbulent intensity. Int. J. Multiph. Flow 1989, 15, 279–285. [Google Scholar] [CrossRef]
- Tanaka, T.; Eaton, J.K. Classification of Turbulence Modification by Dispersed Spheres Using a Novel Dimensionless Number. Phys. Rev. Lett. 2008, 101, 114502. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, J.D.; Schwarzkopf, M.; Sommerfeld, Y.; Crowe, C.T. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Delafosse, A.; Collignon, M.L.; Crine, M.; Toye, D. Estimation of the turbulent kinetic energy dissipation rate from 2D-PIV measurements in a vessel stirred by an axial Mixel TTP impeller. Chem. Eng. Sci. 2011, 66, 1728–1737. [Google Scholar] [CrossRef]
- Gai, G.; Hadjadj, A.; Kudriakov, S.; Thomine, O. Particles-induced turbulence: A critical review of physical concepts, numerical modelings and experimental investigations. Theor. Appl. Mech. Lett. 2020, 10, 241–248. [Google Scholar] [CrossRef]





| Study | Technique | Agitator | (μm) | (v%) | Re | n max () | |
|---|---|---|---|---|---|---|---|
| Nouri & Whitelaw [30] | LDA | RT | 590/730 | 2.5 | 0.75 | 54,000 | 0.233 |
| Virdung & Rasmuson [24] | PIV | PBT | 1000 | 1.5 | 0.40 | 7500 | 0.0286 |
| Micheletti & Yianneskis [32] | LDA | RT | 186 | 2.0 | 0.99 | 20,000 | 5.936 |
| Unadkat et al. [25] | PIV | PBT | 1000 | 0.5 | 0.40 | 30,800 | 0.0096 |
| Montante et al. [28] | PIV | RT | 115/774 | 0.2 | 0.40 | 88,000 | 2.512 |
| Li et al. [29] | PIV | PBT | 7000 | 8.0 | 0.45 | 10,000 | 0.00045 |
| This work | PIV | HTPGD | 168 | 3.0 | 0.96 | 5000 | 12 |
| Properties | Cytodex-1/Water | PMMA/SCN |
|---|---|---|
| (−) | ≈0.97 | ≈0.96 |
| mPa·s | 1 | 1.94 |
| μm | 170 | 168 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madani, M.; Delafosse, A.; Calvo, S.; Toye, D. RIM-PIV Measurements of Solid–Liquid Flow in a Stirred Tank Used for Mesenchymal Stem Cell Culture. Fluids 2025, 10, 272. https://doi.org/10.3390/fluids10100272
Madani M, Delafosse A, Calvo S, Toye D. RIM-PIV Measurements of Solid–Liquid Flow in a Stirred Tank Used for Mesenchymal Stem Cell Culture. Fluids. 2025; 10(10):272. https://doi.org/10.3390/fluids10100272
Chicago/Turabian StyleMadani, Mohamad, Angélique Delafosse, Sébastien Calvo, and Dominique Toye. 2025. "RIM-PIV Measurements of Solid–Liquid Flow in a Stirred Tank Used for Mesenchymal Stem Cell Culture" Fluids 10, no. 10: 272. https://doi.org/10.3390/fluids10100272
APA StyleMadani, M., Delafosse, A., Calvo, S., & Toye, D. (2025). RIM-PIV Measurements of Solid–Liquid Flow in a Stirred Tank Used for Mesenchymal Stem Cell Culture. Fluids, 10(10), 272. https://doi.org/10.3390/fluids10100272







