Enhanced Rupture Force in a Cut-Dispersed Double-Network Hydrogel
Abstract
1. Introduction
2. Results and Discussion
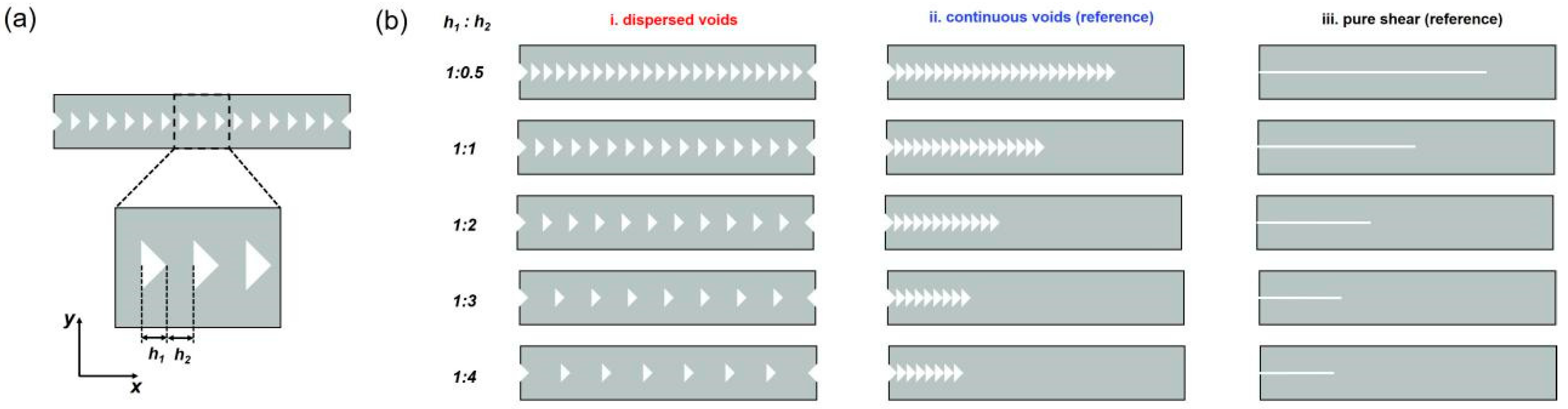
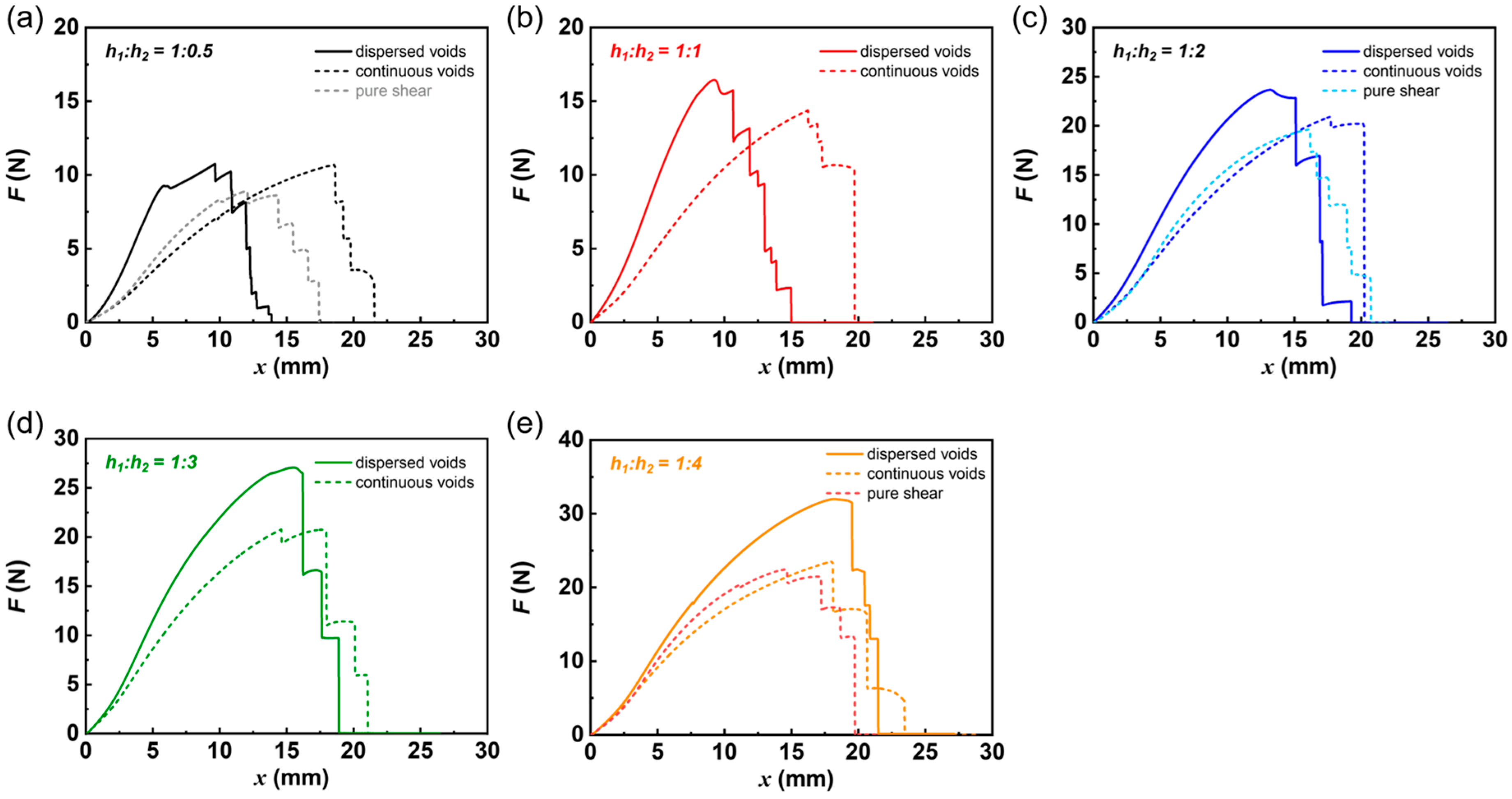
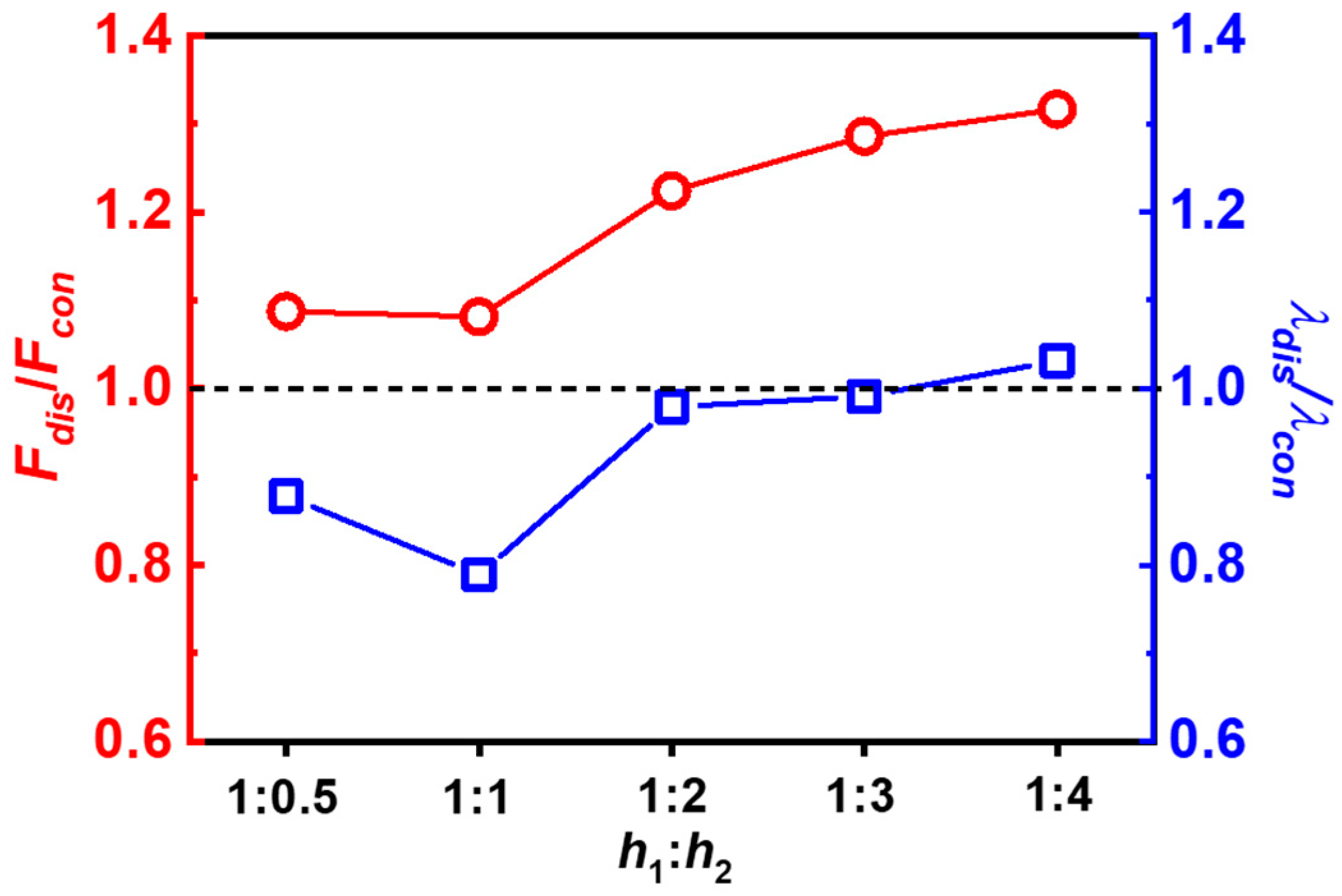
2.1. Effect of Dispersed Cuts on the Fracture Behavior of DN Hydrogel Specimens
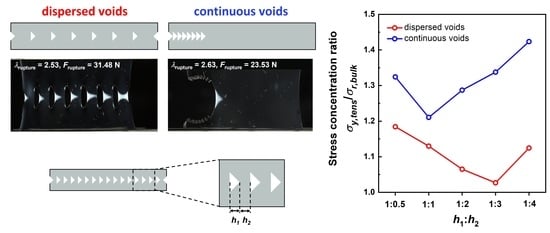
2.2. Birefringence Observation on the Rupture of Specimens Containing Dispersed Cuts and Continuous Cuts
2.3. Characteristic Fracture Structure of the DN Gels with Dispersed and Continuous Cuts
3. Conclusions
4. Materials and Methods
4.1. Materials
4.2. Synthesis of DN Hydrogels
4.3. Preparation of Various Cuts Patterns in DN Hydrogel Specimens
4.4. Real-Time Birefringence Observation on the Fracture Tests
4.5. Tensile Test
4.6. Microscopic Observation of Cuts in the DN Gels
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Chen, X.; Yuk, H.; Lin, S.; Liu, X.; Parada, G. Soft Materials by Design: Unconventional Polymer Networks Give Extreme Properties. Chem. Rev. 2021, 121, 4309–4372. [Google Scholar] [CrossRef] [PubMed]
- Pinnaratip, R.; Bhuiyan, M.S.A.; Meyers, K.; Rajachar, R.M.; Lee, B.P. Multifunctional biomedical adhesives. Adv. Healthc. Mater. 2019, 8, 1801568. [Google Scholar] [CrossRef] [PubMed]
- Freedman, B.R.; Kuttler, A.; Beckmann, N.; Nam, S.; Kent, D.; Schuleit, M.; Ramazani, F.; Accart, N.; Rock, A.; Li, J. Enhanced tendon healing by a tough hydrogel with an adhesive side and high drug-loading capacity. Nat. Biomed. Eng. 2022, 6, 1167–1179. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Bourquard, C.; Gao, Q.; Jiang, S.; De Iure-Grimmel, T.; Huo, R.; Li, X.; He, Z.; Yang, Z.; Yang, G. Controlled tough bioadhesion mediated by ultrasound. Science 2022, 377, 751–755. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Yuk, H.; Wu, J.; Nabzdyk, C.S.; Zhao, X. Instant tough bioadhesive with triggerable benign detachment. Proc. Natl. Acad. Sci. USA 2020, 117, 15497–15503. [Google Scholar] [CrossRef] [PubMed]
- Yoda, R. Elastomers for biomedical applications. J. Biomater. Sci. Polym. Ed. 1998, 9, 561–626. [Google Scholar] [CrossRef] [PubMed]
- Caliari, S.R.; Burdick, J.A. A practical guide to hydrogels for cell culture. Nat. Methods 2016, 13, 405–414. [Google Scholar] [CrossRef] [PubMed]
- Thiele, J.; Ma, Y.; Bruekers, S.M.; Ma, S.; Huck, W.T. 25th anniversary article: Designer hydrogels for cell cultures: A materials selection guide. Adv. Mater. 2014, 26, 125–148. [Google Scholar] [CrossRef] [PubMed]
- Tibbitt, M.W.; Anseth, K.S. Hydrogels as extracellular matrix mimics for 3D cell culture. Biotechnol. Bioeng. 2009, 103, 655–663. [Google Scholar] [CrossRef]
- Lee, K.Y.; Mooney, D.J. Hydrogels for tissue engineering. Chem. Rev. 2001, 101, 1869–1880. [Google Scholar] [CrossRef]
- Nguyen, K.T.; West, J.L. Photopolymerizable hydrogels for tissue engineering applications. Biomaterials 2002, 23, 4307–4314. [Google Scholar] [CrossRef] [PubMed]
- Drury, J.L.; Mooney, D.J. Hydrogels for tissue engineering: Scaffold design variables and applications. Biomaterials 2003, 24, 4337–4351. [Google Scholar] [CrossRef] [PubMed]
- Yuk, H.; Lin, S.; Ma, C.; Takaffoli, M.; Fang, N.X.; Zhao, X. Hydraulic hydrogel actuators and robots optically and sonically camouflaged in water. Nat. Commun. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Li, T.; Li, G.; Liang, Y.; Cheng, T.; Dai, J.; Yang, X.; Liu, B.; Zeng, Z.; Huang, Z.; Luo, Y. Fast-moving soft electronic fish. Sci. Adv. 2017, 3, e1602045. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.S.; Liu, M.; Ishida, Y.; Ebina, Y.; Osada, M.; Sasaki, T.; Hikima, T.; Takata, M.; Aida, T. Thermoresponsive actuation enabled by permittivity switching in an electrostatically anisotropic hydrogel. Nat. Mater. 2015, 14, 1002–1007. [Google Scholar] [CrossRef] [PubMed]
- Shian, S.; Bertoldi, K.; Clarke, D.R. Dielectric elastomer based “grippers” for soft robotics. Adv. Mater. 2015, 27, 6814–6819. [Google Scholar] [CrossRef] [PubMed]
- Marchese, A.D.; Katzschmann, R.K.; Rus, D. A recipe for soft fluidic elastomer robots. Soft Robot. 2015, 2, 7–25. [Google Scholar] [CrossRef]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and mechanics for stretchable electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Yuk, H.; Zhang, T.; Parada, G.A.; Koo, H.; Yu, C.; Zhao, X. Stretchable hydrogel electronics and devices. Adv. Mater. 2016, 28, 4497–4505. [Google Scholar] [CrossRef]
- Yang, C.; Suo, Z. Hydrogel ionotronics. Nat. Rev. Mater. 2018, 3, 125–142. [Google Scholar] [CrossRef]
- Brooks, A.K.; Chakravarty, S.; Ali, M.; Yadavalli, V.K. Kirigami-Inspired Biodesign for Applications in Healthcare. Adv. Mater. 2022, 34, 2109550. [Google Scholar] [CrossRef]
- Hao, X.P.; Xu, Z.; Li, C.Y.; Hong, W.; Zheng, Q.; Wu, Z.L. Kirigami-design-enabled hydrogel multimorphs with application as a multistate switch. Adv. Mater. 2020, 32, 2000781. [Google Scholar] [CrossRef] [PubMed]
- Callens, S.J.; Zadpoor, A.A. From flat sheets to curved geometries: Origami and kirigami approaches. Mater. Today 2018, 21, 241–264. [Google Scholar] [CrossRef]
- Tao, J.; Khosravi, H.; Deshpande, V.; Li, S. Engineering by Cuts: How Kirigami Principle Enables Unique Mechanical Properties and Functionalities. Adv. Sci. 2022, 10, 2204733. [Google Scholar] [CrossRef] [PubMed]
- Rafsanjani, A.; Zhang, Y.; Liu, B.; Rubinstein, S.M.; Bertoldi, K. Kirigami skins make a simple soft actuator crawl. Sci. Robot. 2018, 3, eaar7555. [Google Scholar] [CrossRef]
- Sakai, T.; Matsunaga, T.; Yamamoto, Y.; Ito, C.; Yoshida, R.; Suzuki, S.; Sasaki, N.; Shibayama, M.; Chung, U.-I. Design and fabrication of a high-strength hydrogel with ideally homogeneous network structure from tetrahedron-like macromonomers. Macromolecules 2008, 41, 5379–5384. [Google Scholar] [CrossRef]
- Gong, J.P.; Katsuyama, Y.; Kurokawa, T.; Osada, Y. Double-network hydrogels with extremely high mechanical strength. Adv. Mater. 2003, 15, 1155–1158. [Google Scholar] [CrossRef]
- Okumura, Y.; Ito, K. The polyrotaxane gel: A topological gel by figure-of-eight cross-links. Adv. Mater. 2001, 13, 485–487. [Google Scholar] [CrossRef]
- Creton, C. 50th anniversary perspective: Networks and gels: Soft but dynamic and tough. Macromolecules 2017, 50, 8297–8316. [Google Scholar] [CrossRef]
- Ge, G.; Wang, Q.; Zhang, Y.Z.; Alshareef, H.N.; Dong, X. 3D printing of hydrogels for stretchable ionotronic devices. Adv. Funct. Mater. 2021, 31, 2107437. [Google Scholar] [CrossRef]
- Huang, X.; Ge, G.; She, M.; Ma, Q.; Lu, Y.; Zhao, W.; Shen, Q.; Wang, Q.; Shao, J. Self-healing hydrogel with multiple dynamic interactions for multifunctional epidermal sensor. Appl. Surf. Sci. 2022, 598, 153803. [Google Scholar] [CrossRef]
- Nakajima, T. Generalization of the sacrificial bond principle for gel and elastomer toughening. Polym. J. 2017, 49, 477–485. [Google Scholar] [CrossRef]
- Ducrot, E.; Chen, Y.; Bulters, M.; Sijbesma, R.P.; Creton, C. Toughening elastomers with sacrificial bonds and watching them break. Science 2014, 344, 186–189. [Google Scholar] [CrossRef]
- Sun, T.L.; Kurokawa, T.; Kuroda, S.; Ihsan, A.B.; Akasaki, T.; Sato, K.; Haque, M.A.; Nakajima, T.; Gong, J.P. Physical hydrogels composed of polyampholytes demonstrate high toughness and viscoelasticity. Nat. Mater. 2013, 12, 932–937. [Google Scholar] [CrossRef] [PubMed]
- Gong, J.P. Why are double network hydrogels so tough? Soft Matter 2010, 6, 2583–2590. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, L.; Zhao, C.; Wang, Q.; Zheng, J. A robust, one-pot synthesis of highly mechanical and recoverable double network hydrogels using thermoreversible sol-gel polysaccharide. Adv. Mater. 2013, 25, 4171–4176. [Google Scholar] [CrossRef] [PubMed]
- Illeperuma, W.R.; Sun, J.-Y.; Suo, Z.; Vlassak, J.J. Fiber-reinforced tough hydrogels. Extrem. Mech. Lett. 2014, 1, 90–96. [Google Scholar] [CrossRef]
- Lin, S.; Cao, C.; Wang, Q.; Gonzalez, M.; Dolbow, J.E.; Zhao, X. Design of stiff, tough and stretchy hydrogel composites via nanoscale hybrid crosslinking and macroscale fiber reinforcement. Soft Matter 2014, 10, 7519–7527. [Google Scholar] [CrossRef]
- Kazem, N.; Bartlett, M.D.; Majidi, C. Extreme toughening of soft materials with liquid metal. Adv. Mater. 2018, 30, 1706594. [Google Scholar] [CrossRef]
- Lin, W.-C.; Fan, W.; Marcellan, A.; Hourdet, D.; Creton, C. Large strain and fracture properties of poly (dimethylacrylamide)/silica hybrid hydrogels. Macromolecules 2010, 43, 2554–2563. [Google Scholar] [CrossRef]
- Harito, C.; Bavykin, D.V.; Yuliarto, B.; Dipojono, H.K.; Walsh, F.C. Polymer nanocomposites having a high filler content: Synthesis, structures, properties, and applications. Nanoscale 2019, 11, 4653–4682. [Google Scholar] [CrossRef] [PubMed]
- Rothon, R. Fillers for Polymer Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Utech, S.; Boccaccini, A.R. A review of hydrogel-based composites for biomedical applications: Enhancement of hydrogel properties by addition of rigid inorganic fillers. J. Mater. Sci. 2016, 51, 271–310. [Google Scholar] [CrossRef]
- Dannenberg, E. The effects of surface chemical interactions on the properties of filler-reinforced rubbers. Rubber Chem. Technol. 1975, 48, 410–444. [Google Scholar] [CrossRef]
- Haraguchi, K.; Takehisa, T. Nanocomposite hydrogels: A unique organic–inorganic network structure with extraordinary mechanical, optical, and swelling/de-swelling properties. Adv. Mater. 2002, 14, 1120–1124. [Google Scholar] [CrossRef]
- Haraguchi, K.; Takehisa, T.; Fan, S. Effects of clay content on the properties of nanocomposite hydrogels composed of poly (N-isopropylacrylamide) and clay. Macromolecules 2002, 35, 10162–10171. [Google Scholar] [CrossRef]
- Millereau, P.; Ducrot, E.; Clough, J.M.; Wiseman, M.E.; Brown, H.R.; Sijbesma, R.P.; Creton, C. Mechanics of elastomeric molecular composites. Proc. Natl. Acad. Sci. USA 2018, 115, 9110–9115. [Google Scholar] [CrossRef]
- Zheng, Y.; Kiyama, R.; Matsuda, T.; Cui, K.; Li, X.; Cui, W.; Guo, Y.; Nakajima, T.; Kurokawa, T.; Gong, J.P. Nanophase Separation in Immiscible Double Network Elastomers Induces Synergetic Strengthening, Toughening, and Fatigue Resistance. Chem. Mater. 2021, 33, 3321–3334. [Google Scholar] [CrossRef]
- Matsuda, T.; Nakajima, T.; Gong, J.P. Fabrication of tough and stretchable hybrid double-network elastomers using ionic dissociation of polyelectrolyte in nonaqueous media. Chem. Mater. 2019, 31, 3766–3776. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhuo, S.; Fang, R.; Zhang, L.; Zhou, X.; Xu, Y.; Zhang, J.; Dong, Z.; Jiang, L.; Liu, M. Dual-Programmable Shape-Morphing and Self-Healing Organohydrogels Through Orthogonal Supramolecular Heteronetworks. Adv. Mater. 2018, 30, 1804435. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Y.; Zhang, K.; Zhuo, S.; Fang, R.; Zhang, J.; Jiang, L.; Liu, M. Biphasic Synergistic Gel Materials with Switchable Mechanics and Self-Healing Capacity. Angew. Chem. Int. Ed. 2017, 56, 13464–13469. [Google Scholar] [CrossRef]
- Morikawa, Y.; Yamagiwa, S.; Sawahata, H.; Numano, R.; Koida, K.; Ishida, M.; Kawano, T. Ultrastretchable kirigami bioprobes. Adv. Healthc. Mater. 2018, 7, 1701100. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.C.; Hao, X.P.; Zhang, C.W.; Zheng, S.Y.; Du, M.; Liang, S.; Wu, Z.L.; Zheng, Q. Engineering tough metallosupramolecular hydrogel films with kirigami structures for compliant soft electronics. Small 2021, 17, 2103836. [Google Scholar] [CrossRef] [PubMed]
- Cao, W.; Geng, Z.Z.; Wang, N.; Pan, Q.; Guo, S.; Xu, S.; Zhou, J.; Liu, W.R. A reversible chemogenetic switch for chimeric antigen receptor T cells. Angew. Chem. Int. Ed. 2022, 61, e202109550. [Google Scholar]
- Jangizehi, A.; Schmid, F.; Besenius, P.; Kremer, K.; Seiffert, S. Defects and defect engineering in Soft Matter. Soft Matter 2020, 16, 10809–10859. [Google Scholar] [CrossRef]
- Zheng, Y.; Matsuda, T.; Nakajima, T.; Cui, W.; Zhang, Y.; Hui, C.-Y.; Kurokawa, T.; Gong, J.P. How chain dynamics affects crack initiation in double-network gels. Proc. Natl. Acad. Sci. USA 2021, 118, e2111880118. [Google Scholar] [CrossRef]
- Liang, S.; Wu, Z.L.; Hu, J.; Kurokawa, T.; Yu, Q.M.; Gong, J.P. Direct observation on the surface fracture of ultrathin film double-network hydrogels. Macromolecules 2011, 44, 3016–3020. [Google Scholar] [CrossRef]
- Ahmed, S.; Nakajima, T.; Kurokawa, T.; Haque, M.A.; Gong, J.P. Brittle–ductile transition of double network hydrogels: Mechanical balance of two networks as the key factor. Polymer 2014, 55, 914–923. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Yan, D.; Chen, L.; Wang, Y.; Zhu, F.; Ye, Y.; Zheng, Y.; Yu, W.; Zheng, Q. Enhanced Rupture Force in a Cut-Dispersed Double-Network Hydrogel. Gels 2023, 9, 158. https://doi.org/10.3390/gels9020158
Zhu S, Yan D, Chen L, Wang Y, Zhu F, Ye Y, Zheng Y, Yu W, Zheng Q. Enhanced Rupture Force in a Cut-Dispersed Double-Network Hydrogel. Gels. 2023; 9(2):158. https://doi.org/10.3390/gels9020158
Chicago/Turabian StyleZhu, Shilei, Dongdong Yan, Lin Chen, Yan Wang, Fengbo Zhu, Yanan Ye, Yong Zheng, Wenwen Yu, and Qiang Zheng. 2023. "Enhanced Rupture Force in a Cut-Dispersed Double-Network Hydrogel" Gels 9, no. 2: 158. https://doi.org/10.3390/gels9020158
APA StyleZhu, S., Yan, D., Chen, L., Wang, Y., Zhu, F., Ye, Y., Zheng, Y., Yu, W., & Zheng, Q. (2023). Enhanced Rupture Force in a Cut-Dispersed Double-Network Hydrogel. Gels, 9(2), 158. https://doi.org/10.3390/gels9020158