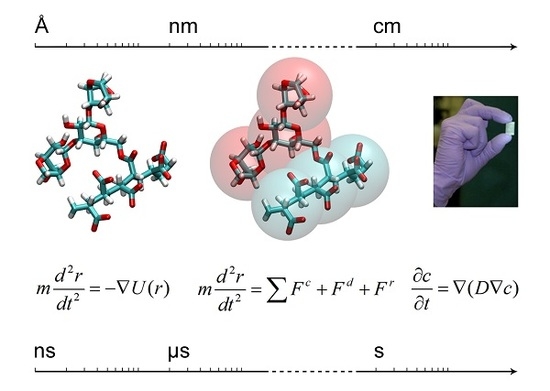
From Microscale to Macroscale: Nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery
Abstract
1. Introduction
2. Modeling Approaches—Brief Theoretical Background
2.1. Molecular Dynamics Simulations
2.2. Coarse-Grained Models
- At simulation step n, the computed system energy is Un;
- At stimulation step n + 1, randomly-chosen particles attempt to perform a random displacement Δr;
- A new energy value Un+1, deriving from such displacement, is computed;
- Displacement attempt is accepted with a probability:
- In order to decide whether to accept or reject the random displacement, a random number x is generated from a uniform distribution in the interval [0, 1]. If acc(n → n+1) ≥ x, the move is accepted; otherwise, it is rejected.
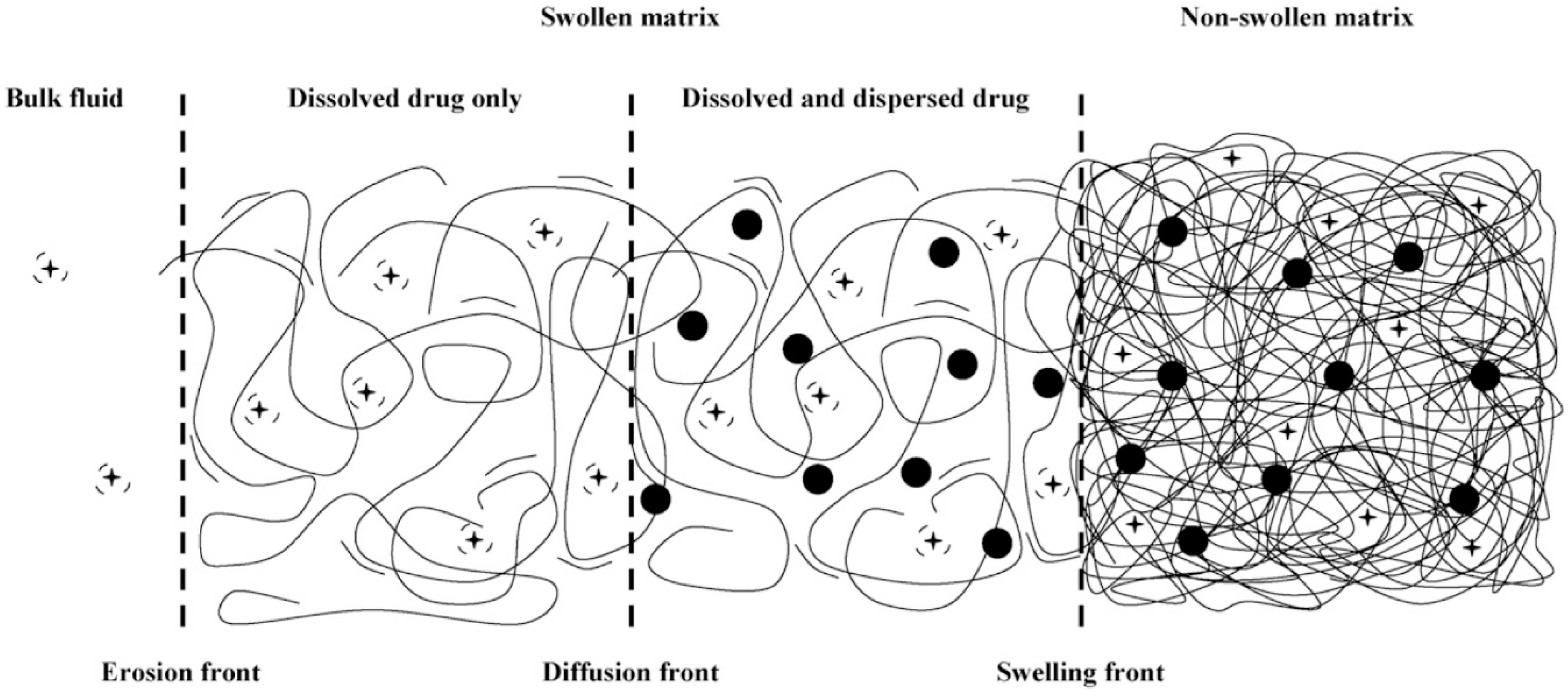
2.3. Macroscale Models
- Models based on obstruction effects: Polymer chains are assumed motionless if compared with the diffusant, by virtue of their lower self-diffusion coefficient. Polymer matrix is thus modeled as a rigid and impenetrable network, whose effect is the increasing of the mean diffusive path. These models are suitable for small molecules and low polymer concentrations, while they do not provide reliable results at high polymer concentration, since solute/network interactions cannot be neglected anymore.
- Models based on hydrodynamic theories: Polymer chains are still assumed to be motionless with respect to the solute, which is modeled as a hard sphere moving at constant velocity in a continuum and experiencing a frictional drag, according to Stokes–Einstein formalism. Polymer chains enhance the frictional drag by slowing down the surrounding fluid.
- Models based on free volume theory: Free volume can be defined as the volume of the system at a given temperature minus the volume of the same system at 0 K or, in a more straightforward way, as the volume not occupied by matter. These models are based on the assumption that diffusion phenomena are governed by free volume arrangements that create pores and path where solute and solvent molecules can move.
- The drug is covalently linked to polymer chains through cleavable spacers, and the rate-determining step is the kinetics of bond cleavage;
- Drug release is mainly due to surface erosion;
- Drug diffusion is hindered by polymer chains and the rate-determining step is polymer degradation, which creates new and wider diffusive paths;
- The active compound is not covalently bound to polymer chains and the rate-determining step is the binding equilibrium.
3. Applications
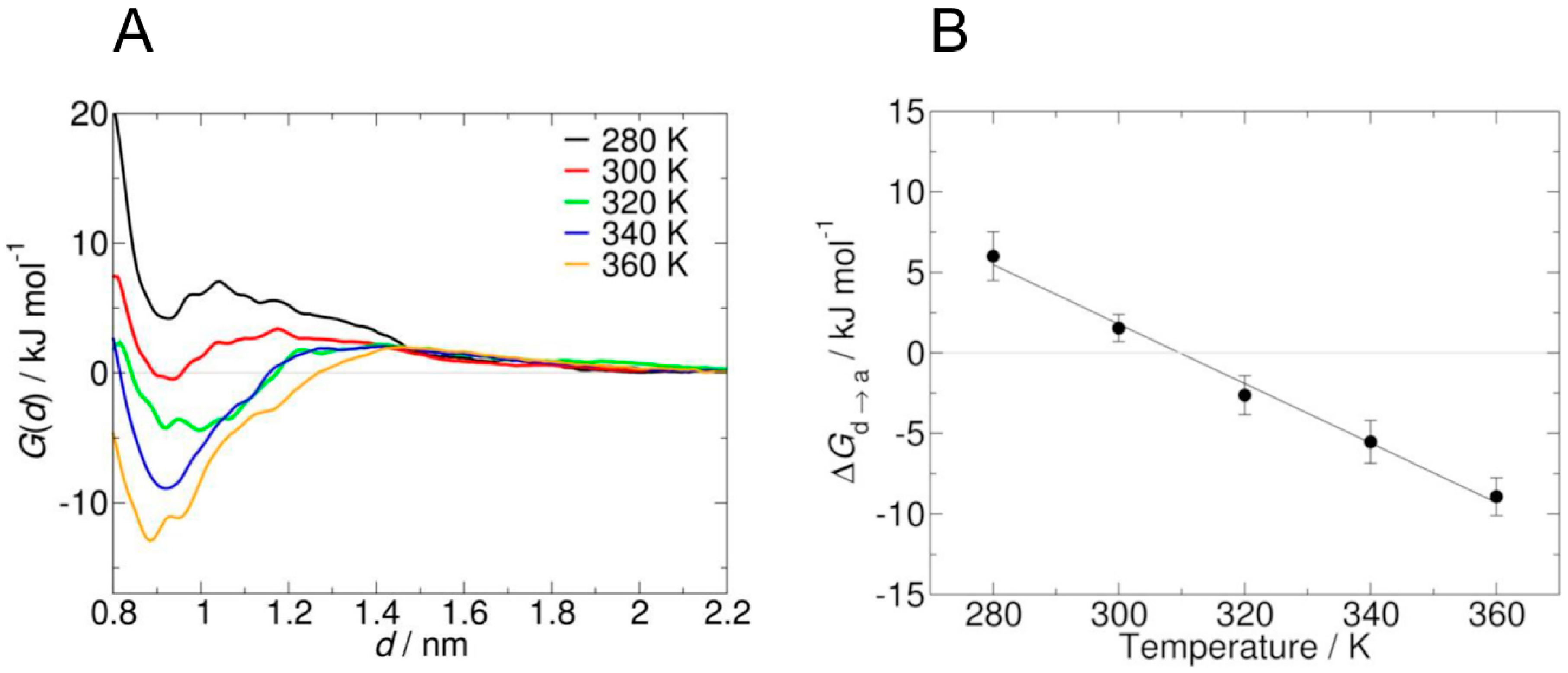
3.1. Molecular Dynamics Simulations
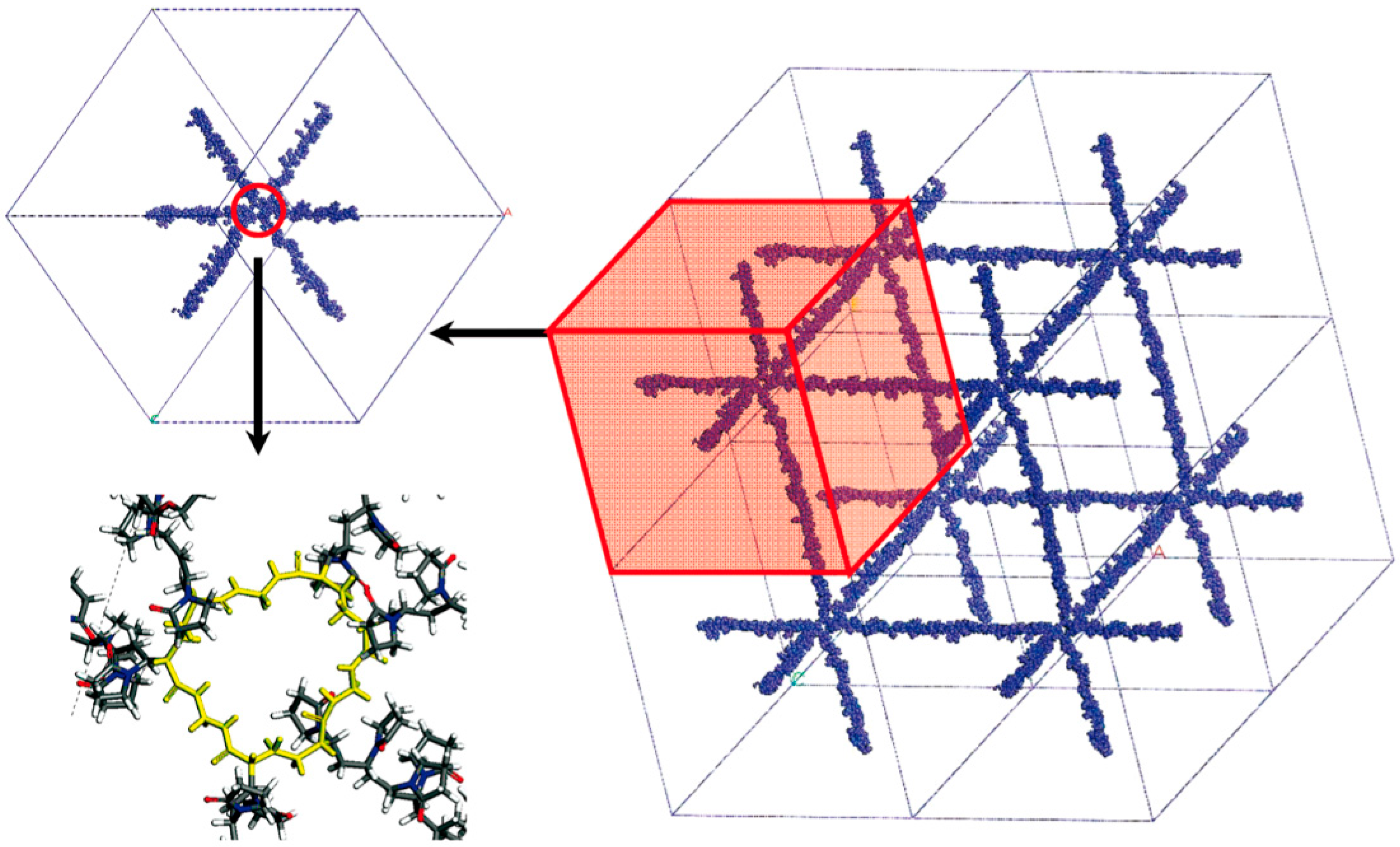
3.2. Coarse-Grained Models
3.3. Coarse-Grained Molecular Dynamics
3.4. Brownian Dynamics and Langevin Dynamics
3.5. Dissipative Particle Dynamics
3.6. Monte Carlo Simulations
3.7. Macroscale Models
3.8. Diffusion-Controlled Systems
3.9. Swelling-Controlled Systems
3.10. Chemically Controlled Systems
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Wichterle, O.; Lim, D. Hydrophilic gels in biologic use. Nature 1960, 185, 117–118. [Google Scholar] [CrossRef]
- Slaughter, B.V.; Khurshid, S.S.; Fisher, O.Z.; Khademhosseini, A.; Peppas, N.A. Hydrogels in Regenerative Medicine. Adv. Mater. 2009, 21, 3307–3329. [Google Scholar] [CrossRef] [PubMed]
- Peppas, N.A.; Hilt, J.Z.; Khademhosseini, A.; Langer, R. Hydrogels in biology and medicine: From molecular principles to bionanotechnology. Adv. Mater. 2006, 18, 1345–1360. [Google Scholar] [CrossRef]
- Peppas, N.A. Hydrogels and drug delivery. Curr. Opin. Colloid Interface Sci. 1997, 2, 531–537. [Google Scholar] [CrossRef]
- Koetting, M.C.; Peters, J.T.; Steichen, S.D.; Peppas, N.A. Stimulus-responsive hydrogels: Theory, modern advances, and applications. Mater. Sci. Eng. R 2015, 93, 1–49. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953; 672p. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Riniker, S. Fixed-Charge Atomistic Force Fields for Molecular Dynamics Simulations in the Condensed Phase: An Overview. J. Chem. Inf. Model. 2018, 58, 565–578. [Google Scholar] [CrossRef] [PubMed]
- Bochicchio, D.; Pavan, G.M. Molecular modelling of supramolecular polymers. Adv. Phys. X 2018, 3, 315–337. [Google Scholar] [CrossRef]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingolfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational Modeling of Realistic Cell Membranes. Chem. Rev. 2019. [Google Scholar] [CrossRef]
- Paidikondala, M.; Rangasami, V.K.; Nawale, G.N.; Casalini, T.; Perale, G.; Kadekar, S.; Mohanty, G.; Salminen, T.; Oommen, O.P.; Varghese, O.P. An Unexpected Role of Hyaluronic Acid in Trafficking siRNA Across the Cellular Barrier: The First Biomimetic, Anionic, Non-Viral Transfection Method. Angew. Chem. Int. Ed. Engl. 2019, 58, 2815–2819. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, A.; Coote, M.L.; Barakat, K. Molecular dynamics-driven drug discovery: Leaping forward with confidence. Drug Discov. Today 2017, 22, 249–269. [Google Scholar] [CrossRef] [PubMed]
- Salvalaglio, M.; Vetter, T.; Mazzotti, M.; Parrinello, M. Controlling and predicting crystal shapes: The case of urea. Angew. Chem. Int. Ed. Engl. 2013, 52, 13369–13372. [Google Scholar] [CrossRef] [PubMed]
- Tiwary, P.; Limongelli, V.; Salvalaglio, M.; Parrinello, M. Kinetics of protein-ligand unbinding: Predicting pathways, rates, and rate-limiting steps. Proc. Natl. Acad. Sci. USA 2015, 112, E386–E391. [Google Scholar] [CrossRef]
- Einstein, A. On the Motion of Small Particles Suspended in Stationary Liquids Required by the Molecular—Kinetic Theory of Heat. Annalen der Physik 1905, 17, 549–560. [Google Scholar] [CrossRef]
- Lee, S.G.; Koh, W.; Brunello, G.F.; Choi, J.I.; Bucknall, D.G.; Jang, S.S. Effect of monomeric sequence on transport properties of D-glucose and ascorbic acid in poly(VP-co-HEMA) hydrogels with various water contents: Molecular dynamics simulation approach. Theor. Chem. Acc. 2012, 131. [Google Scholar] [CrossRef]
- Tabatabaei, F.; Lenz, O.; Holm, C. Simulational study of anomalous tracer diffusion in hydrogels. Colloid Polym. Sci. 2011, 289, 523–534. [Google Scholar] [CrossRef]
- Azurmendi, H.F.; Ramia, M.E. Anomalous diffusion of water in a hydrogel of sucrose and diepoxide monomers. J. Chem. Phys. 2001, 114, 9657–9662. [Google Scholar] [CrossRef]
- Di Meo, C.; Coviello, T.; Matricardi, P.; Alhaique, F.; Capitani, D.; Lamanna, R. Anisotropic enhanced water diffusion in scleroglucan gel tablets. Soft Matter 2011, 7, 6068–6075. [Google Scholar] [CrossRef]
- Ramirez, J.; Dursch, T.J.; Olsen, B.D. A Molecular Explanation for Anomalous Diffusion in Supramolecular Polymer Networks. Macromolecules 2018, 51, 2517–2525. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801–6822. [Google Scholar] [CrossRef] [PubMed]
- Arnarez, C.; Uusitalo, J.J.; Masman, M.F.; Ingolfsson, H.I.; de Jong, D.H.; Melo, M.N.; Periole, X.; de Vries, A.H.; Marrink, S.J. Dry Martini, a Coarse-Grained Force Field for Lipid Membrane Simblations with Implicit Solvent. J. Chem. Theory Comput. 2015, 11, 260–275. [Google Scholar] [CrossRef] [PubMed]
- Espanol, P.; Warren, P.B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146. [Google Scholar] [CrossRef] [PubMed]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Masaro, L.; Zhu, X.X. Physical models of diffusion for polymer solutions, gels and solids. Prog. Polym. Sci. 1999, 24, 731–775. [Google Scholar] [CrossRef]
- Fatin-Rouge, N.; Milon, A.; Buffle, J.; Goulet, R.R.; Tessier, A. Diffusion and partitioning of solutes in agarose hydrogels: The relative influence of electrostatic and specific interactions. J. Phys. Chem. B 2003, 107, 12126–12137. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharmaceut. 2008, 364, 328–343. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.C.; Metters, A.T. Hydrogels in controlled release formulations: Network design and mathematical modeling. Adv. Drug Deliv. Rev. 2006, 58, 1379–1408. [Google Scholar] [CrossRef]
- Chiessi, E.; Cavalieri, F.; Paradossi, G. Supercooled water in PVA matrixes. II. A molecular dynamics simulation study and comparison with QENS results. J. Phys. Chem. B 2005, 109, 8091–8096. [Google Scholar] [CrossRef]
- Chiessi, E.; Cavalieri, F.; Paradossi, G. Water and polymer dynamics in chemically cross-linked hydrogels of poly(vinyl alcohol): A molecular dynamics simulation study. J. Phys. Chem. B 2007, 111, 2820–2827. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.S.; Goddard, W.A.; Kalani, M.Y.S. Mechanical and transport properties of the poly(ethylene oxide)-poly(acrylic acid) double network hydrogel from molecular dynamic simulations. J. Phys. Chem. B 2007, 111, 1729–1737. [Google Scholar] [CrossRef]
- Lee, S.G.; Brunello, G.F.; Jang, S.S.; Lee, J.H.; Bucknall, D.G. Effect of Monomeric Sequence on Mechanical Properties of P(VP-co-HEMA) Hydrogels at Low Hydration. J. Phys. Chem. B 2009, 113, 6604–6612. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.G.; Brunello, G.F.; Jang, S.S.; Bucknall, D.G. Molecular dynamics simulation study of P (VP-co-HEMA) hydrogels: Effect of water content on equilibrium structures and mechanical properties. Biomaterials 2009, 30, 6130–6141. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo-Botero, A.; Blanco, M.; Li, Y.Y.; McGuinness, G.; Goddard, W.A. First-Principles Based Approaches to Nano-Mechanical and Biomimetic Characterization of Polymer-Based Hydrogel Networks for Cartilage Scaffold-Supported Therapies. J. Comput. Theor. Nanosci. 2010, 7, 1238–1256. [Google Scholar] [CrossRef]
- He, Y.; Shao, Q.; Tsao, H.K.; Chen, S.F.; Goddard, W.A.; Jiang, S.Y. Understanding Three Hydration-Dependent Transitions of Zwitterionic Carboxybetaine Hydrogel by Molecular Dynamics Simulations. J. Phys. Chem. B 2011, 115, 11575–11580. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Tsao, H.K.; Jiang, S.Y. Improved Mechanical Properties of Zwitterionic Hydrogels with Hydroxyl Groups. J. Phys. Chem. B 2012, 116, 5766–5770. [Google Scholar] [CrossRef] [PubMed]
- Pascal, T.A.; He, Y.; Jiang, S.Y.; Goddard, W.A. Thermodynamics of Water Stabilization of Carboxybetaine Hydrogels from Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2011, 2, 1757–1760. [Google Scholar] [CrossRef]
- Wu, Y.B.; Joseph, S.; Aluru, N.R. Effect of Cross-Linking on the Diffusion of Water, Ions, and Small Molecules in Hydrogels. J. Phys. Chem. B 2009, 113, 3512–3520. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.Y.; Liang, L.J.; Wang, Q.; Laaksonen, A.; Wu, T. A molecular dynamics study on pH response of protein adsorbed on peptide-modified polyvinyl alcohol hydrogel. Biomater. Sci. 2014, 2, 419–426. [Google Scholar] [CrossRef]
- Walter, J.; Ermatchkov, V.; Vrabec, J.; Hasse, H. Molecular dynamics and experimental study of conformation change of poly(N-isopropylacrylamide) hydrogels in water. Fluid Phase Equilibria 2010, 296, 164–172. [Google Scholar] [CrossRef]
- Walter, J.; Sehrt, J.; Vrabec, J.; Hasse, H. Molecular Dynamics and Experimental Study of Conformation Change of Poly(N-isopropylacrylamide) Hydrogels in Mixtures of Water and Methanol. J. Phys. Chem. B 2012, 116, 5251–5259. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, S.; Mooney, D.A.; McDermott, T.; Kulkarni, S.; MacElroy, J.M.D. Molecular modeling of thermo-responsive hydrogels: Observation of lower critical solution temperature. Soft Matter 2009, 5, 1514–1521. [Google Scholar] [CrossRef]
- Deshmukh, S.; Mooney, D.A.; MacElroy, J.M.D. Molecular simulation study of the effect of cross-linker on the properties of poly(N-isopropyl acrylamide) hydrogel. Mol. Simul. 2011, 37, 846–854. [Google Scholar] [CrossRef]
- Alaghemandi, M.; Spohr, E. Molecular Dynamics Investigation of the Thermo-Responsive Polymer Poly(N-isopropylacrylamide). Macromol. Theor. Simul. 2012, 21, 106–112. [Google Scholar] [CrossRef]
- Tonsing, T.; Oldiges, C. Molecular dynamic simulation study on structure of water in crosslinked poly(N-isopropylacrylamide) hydrogels. Phys. Chem. Chem. Phys. 2001, 3, 5542–5549. [Google Scholar] [CrossRef]
- De Oliveira, T.E.; Marques, C.M.; Netz, P.A. Molecular dynamics study of the LCST transition in aqueous poly(N-n-propylacrylamide). Phys. Chem. Chem. Phys. 2018, 20, 10100–10107. [Google Scholar] [CrossRef] [PubMed]
- Garcia, E.J.; Bhandary, D.; Horsch, M.T.; Hasse, H. A molecular dynamics simulation scenario for studying solvent-mediated interactions of polymers and application to thermoresponse of poly(N-isopropylacrylamide) in water. J. Mol. Liq. 2018, 268, 294–302. [Google Scholar] [CrossRef]
- Du, H.B.; Qian, X.H. Molecular Dynamics Simulations of PNIPAM-co-PEGMA Copolymer Hydrophilic to Hydrophobic Transition in NaCl Solution. J. Polym. Sci. Polym. Phys. 2011, 49, 1112–1122. [Google Scholar] [CrossRef]
- Chiessi, E.; Lonardi, A.; Paradossi, G. Toward Modeling Thermoresponsive Polymer Networks: A Molecular Dynamics Simulation Study of N-Isopropyl Acrylamide Co-oligomers. J. Phys. Chem. B 2010, 114, 8301–8312. [Google Scholar] [CrossRef] [PubMed]
- Oldiges, C.; Tonsing, T. Molecular dynamic simulation of structural, mobility effects between dilute aqueous CH3CN solution and crosslinked PAA—Part 1. Structure. Phys. Chem. Chem. Phys. 2002, 4, 1628–1636. [Google Scholar] [CrossRef]
- Oldiges, C.; Tonsing, T.; Wittler, K. Molecular dynamics simulation of structural, mobility effects between dilute aqueous CH3CN solution and crosslinked PAA—Part 2. Dynamics. Phys. Chem. Chem. Phys. 2002, 4, 5135–5141. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, C.Y.; Han, Q. Molecular dynamic simulation on the state of water in poly(vinyl alcohol) hydrogel. Comput. Theor. Chem. 2017, 1102, 15–21. [Google Scholar] [CrossRef]
- Zhang, Q.G.; Liu, Q.L.; Chen, Y.; Wu, J.Y.; Zhu, A.M. Microstructure dependent diffusion of water-ethanol in swollen poly(vinyl alcohol): A molecular dynamics simulation study. Chem. Eng. Sci. 2009, 64, 334–340. [Google Scholar] [CrossRef]
- Paradossi, G.; Finelli, I.; Natali, F.; Telling, M.T.F.; Chiessi, E. Polymer and Water Dynamics in Poly(vinyl alcohol)/Poly(methacrylate) Networks. A Molecular Dynamics Simulation and Incoherent Neutron Scattering Investigation. Polymers 2011, 3, 1805–1832. [Google Scholar] [CrossRef]
- Avila-Salas, F.; Nunez, Y.A.R.; Marican, A.; Castro, R.I.; Villasenor, J.; Santos, L.S.; Wehinger, S.; Duran-Lara, E.F. Rational Development of a Novel Hydrogel as a pH-Sensitive Controlled Release System for Nifedipine. Polymers 2018, 10, 806. [Google Scholar] [CrossRef] [PubMed]
- Valdes, O.; Avila-Salas, F.; Marican, A.; Fuentealba, N.; Villasenor, J.; Arenas-Salinas, M.; Argandona, Y.; Duran-Lara, E.F. Methamidophos removal from aqueous solutions using a super adsorbent based on crosslinked poly(vinyl alcohol) hydrogel. J. Appl. Polym. Sci. 2018, 135. [Google Scholar] [CrossRef]
- Avila-Salas, F.; Marican, A.; Villasenor, J.; Arenas-Salinas, M.; Argandona, Y.; Caballero, J.; Duran-Lara, E.F. In-Silico Design, Synthesis and Evaluation of a Nanostructured Hydrogel as a Dimethoate Removal Agent. Nanomaterials 2018, 8, 23. [Google Scholar] [CrossRef] [PubMed]
- Ou, X.; Han, Q.; Dai, H.H.; Wang, J. Molecular dynamic simulations of the water absorbency of hydrogels. J. Mol. Model. 2015, 21. [Google Scholar] [CrossRef] [PubMed]
- Baker, C.A.; Schudel, B.; Chaudhari, M.I.; Wu, K.; Dunford, D.; Singh, A.K.; Rempe, S.B.; Hatch, A.V. Nanoporous Hydrogels for the Observation of Anthrax Exotoxin Translocation Dynamics. ACS Appl. Mater. Interfaces 2018, 10, 13342–13349. [Google Scholar] [CrossRef]
- Angelerou, M.G.F.; Frederix, P.W.J.M.; Wallace, M.; Yang, B.; Rodger, A.; Adams, D.J.; Marlow, M.; Zelzer, M. Supramolecular Nucleoside-Based Gel: Molecular Dynamics Simulation and Characterization of Its Nanoarchitecture and Self-Assembly Mechanism. Langmuir 2018, 34, 6912–6921. [Google Scholar] [CrossRef] [PubMed]
- Eckes, K.M.; Mu, X.J.; Ruehle, M.A.; Ren, P.Y.; Suggs, L.J. beta Sheets Not Required: Combined Experimental and Computational Studies of Self-Assembly and Gelation of the Ester-Containing Analogue of an Fmoc-Dipeptide Hydrogelator. Langmuir 2014, 30, 5287–5296. [Google Scholar] [CrossRef] [PubMed]
- Sathaye, S.; Zhang, H.X.; Sonmez, C.; Schneider, J.P.; MacDermaid, C.M.; Von Bargen, C.D.; Saven, J.G.; Pochan, D.J. Engineering Complementary Hydrophobic Interactions to Control beta-Hairpin Peptide Self-Assembly, Network Branching, and Hydrogel Properties. Biomacromolecules 2014, 15, 3891–3900. [Google Scholar] [CrossRef] [PubMed]
- Miller, Y.; Ma, B.Y.; Nussinov, R. Polymorphism in Self-Assembly of Peptide-Based beta-Hairpin Contributes to Network Morphology and Hydrogel Mechanical Rigidity. J. Phys. Chem. B 2015, 119, 482–490. [Google Scholar] [CrossRef] [PubMed]
- Gautieri, A.; Vesentini, S.; Redaelli, A. How to predict diffusion of medium-sized molecules in polymer matrices. From atomistic to coarse grain simulations. J. Mol. Model. 2010, 16, 1845–1851. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zadok, I.; Srebnik, S. Coarse-Grained Simulation of Protein-Imprinted Hydrogels. J. Phys. Chem. B 2018, 122, 7091–7101. [Google Scholar] [CrossRef] [PubMed]
- Salahshoor, H.; Rahbar, N. Multi-scale mechanical and transport properties of a hydrogel. J. Mech. Behav. Biomed. 2014, 37, 299–306. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, H.; Xu, G.Y.; Yuan, S.L. A molecular dynamics simulation of N-(fluorenyl-9-methoxycarbonyl)-dipeptides supramolecular hydrogel. Colloid Surf. A 2013, 417, 217–223. [Google Scholar] [CrossRef]
- Brown, N.; Lei, J.T.; Zhan, C.D.; Shimon, L.J.W.; Adler-Abramovich, L.; Wei, G.H.; Gazit, E. Structural Polymorphism in a Self-Assembled Tri-Aromatic Peptide System. ACS Nano 2018, 12, 3253–3262. [Google Scholar] [CrossRef] [PubMed]
- Frederix, P.W.; Scott, G.G.; Abul-Haija, Y.M.; Kalafatovic, D.; Pappas, C.G.; Javid, N.; Hunt, N.T.; Ulijn, R.V.; Tuttle, T. Exploring the sequence space for (tri-)peptide self-assembly to design and discover new hydrogels. Nat. Chem. 2015, 7, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Fu, I.W.; Markegard, C.B.; Chu, B.K.; Nguyen, H.D. Role of Hydrophobicity on Self-Assembly by Peptide Amphiphiles via Molecular Dynamics Simulations. Langmuir 2014, 30, 7745–7754. [Google Scholar] [CrossRef] [PubMed]
- Fu, I.W.; Markegard, C.B.; Chu, B.K.; Nguyen, H.D. The Role of Electrostatics and Temperature on Morphological Transitions of Hydrogel Nanostructures Self-Assembled by Peptide Amphiphiles Via Molecular Dynamics Simulations. Adv. Healthc. Mater. 2013, 2, 1388–1400. [Google Scholar] [CrossRef] [PubMed]
- Fu, I.W.; Markegard, C.B.; Nguyen, H.D. Solvent Effects on Kinetic Mechanisms of Self-Assembly by Peptide Amphiphiles via Molecular Dynamics Simulations. Langmuir 2015, 31, 315–324. [Google Scholar] [CrossRef] [PubMed]
- Kosovan, P.; Richter, T.; Holm, C. Modeling of Polyelectrolyte Gels in Equilibrium with Salt Solutions. Macromolecules 2015, 48, 7698–7708. [Google Scholar] [CrossRef]
- Mann, B.A.F.; Kremer, K.; Lenz, O.; Holm, C. Hydrogels in Poor Solvents: A Molecular Dynamics Study. Macromol. Theor. Simul. 2011, 20, 721–734. [Google Scholar] [CrossRef]
- Mann, B.A.; Kremer, K.; Holm, C. The swelling behavior of charged hydrogels. Macromol. Symp. 2006, 237, 90–107. [Google Scholar] [CrossRef]
- Ghelichi, M.; Qazvini, N.T. Self-organization of hydrophobic-capped triblock copolymers with a polyelectrolyte midblock: A coarse-grained molecular dynamics simulation study. Soft Matter 2016, 12, 4611–4620. [Google Scholar] [CrossRef] [PubMed]
- Hansing, J.; Netz, R.R. Hydrodynamic Effects on Particle Diffusion in Polymeric Hydrogels with Steric and Electrostatic Particle-Gel Interactions. Macromolecules 2018, 51, 7608–7620. [Google Scholar] [CrossRef]
- Sandrin, D.; Wagner, D.; Sitta, C.E.; Thoma, R.; Felekyan, S.; Hermes, H.E.; Janiak, C.; Amadeu, N.D.; Kuhnemuth, R.; Lowen, H.; et al. Diffusion of macromolecules in a polymer hydrogel: From microscopic to macroscopic scales. Phys. Chem. Chem. Phys. 2016, 18, 12860–12876. [Google Scholar] [CrossRef] [PubMed]
- Pei, H.; Allison, S.; Haynes, B.M.H.; Augustin, D. Brownian Dynamics Simulation of the Diffusion of Rods and Wormlike Chains in a Gel Modeled as a Cubic Lattice: Application to DNA. J. Phys. Chem. B 2009, 113, 2564–2571. [Google Scholar] [CrossRef] [PubMed]
- Kvarnstrom, M.; Westergard, A.; Loren, N.; Nyden, M. Brownian dynamics simulations in hydrogels using an adaptive time-stepping algorithm. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, S.B. Brownian dynamics simulation of tracer diffusion in a cross-linked network. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef]
- Rapp, P.B.; Omar, A.K.; Shen, J.J.; Buck, M.E.; Wang, Z.G.; Tirrell, D.A. Analysis and Control of Chain Mobility in Protein Hydrogels. J. Am. Chem. Soc. 2017, 139, 3796–3804. [Google Scholar] [CrossRef]
- Chen, S.S.; Yong, X. Dissipative particle dynamics modeling of hydrogel swelling by osmotic ensemble method. J. Chem. Phys. 2018, 149. [Google Scholar] [CrossRef] [PubMed]
- Nikolov, S.; Fernandez-Nieves, A.; Alexeev, A. Mesoscale modeling of microgel mechanics and kinetics through the swelling transition. Appl. Math. Mech. 2018, 39, 47–62. [Google Scholar] [CrossRef]
- Rudyak, V.Y.; Gavrilov, A.A.; Kozhunova, E.Y.; Chertovich, A.V. Shell-corona microgels from double interpenetrating networks. Soft Matter 2018, 14, 2777–2781. [Google Scholar] [CrossRef] [PubMed]
- Masoud, H.; Alexeev, A. Controlled Release of Nanoparticles and Macromolecules from Responsive Microgel Capsules. ACS Nano 2012, 6, 212–219. [Google Scholar] [CrossRef] [PubMed]
- Yong, X.; Simakova, A.; Averick, S.; Gutierrez, J.; Kuksenok, O.; Balazs, A.C.; Matyjaszewski, K. Stackable, Covalently Fused Gels: Repair and Composite Formation. Macromolecules 2015, 48, 1169–1178. [Google Scholar] [CrossRef]
- Edgecombe, S.; Linse, P. Monte Carlo simulation of two interpenetrating polymer networks: Structure, swelling, and mechanical properties. Polymer 2008, 49, 1981–1992. [Google Scholar] [CrossRef]
- Ahualli, S.; Martin-Molina, A.; Maroto-Centeno, J.A.; Quesada-Perez, M. Interaction between Ideal Neutral Nanogels: A Monte Carlo Simulation Study. Macromolecules 2017, 50, 2229–2238. [Google Scholar] [CrossRef]
- Quesada-Perez, M.; Adroher-Benitez, I.; Maroto-Centeno, J.A. Size-exclusion partitioning of neutral solutes in crosslinked polymer networks: A Monte Carlo simulation study. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef]
- Perez-Mas, L.; Martin-Molina, A.; Quesada-Perez, M.; Moncho-Jorda, A. Maximizing the absorption of small cosolutes inside neutral hydrogels: Steric exclusion versus hydrophobic adhesion. Phys. Chem. Chem. Phys. 2018, 20, 2814–2825. [Google Scholar] [CrossRef] [PubMed]
- Rizzi, L.G.; Levin, Y. Influence of network topology on the swelling of polyelectrolyte nanogels. J. Chem. Phys. 2016, 144. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.L.; de Pablo, J.J. Monte Carlo simulation of a coarse-grained model of polyelectrolyte networks. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Yin, D.W.; Horkay, F.; Douglas, J.F.; de Pablo, J.J. Molecular simulation of the swelling of polyelectrolyte gels by monovalent and divalent counterions. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.; Linse, P. Swelling of cross-linked polyelectrolyte gels. Eur. Phys. J. E 2002, 8, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Edgecombe, S.; Schneider, S.; Linse, P. Monte Carlo simulations of defect-free cross-linked gels in the presence of salt. Macromolecules 2004, 37, 10089–10100. [Google Scholar] [CrossRef]
- Edgecombe, S.; Linse, P. Monte Carlo simulations of cross-linked polyelectrolyte gels with oppositely charged macroions. Langmuir 2006, 22, 3836–3843. [Google Scholar] [CrossRef] [PubMed]
- Edgecombe, S.; Linse, P. Monte Carlo simulation of polyelectrolyte gels: Effects of polydispersity and topological defects. Macromolecules 2007, 40, 3868–3875. [Google Scholar] [CrossRef]
- Quesada-Perez, M.; Martin-Molina, A. Monte Carlo simulation of thermo-responsive charged nanogels in salt-free solutions. Soft Matter 2013, 9, 7086–7094. [Google Scholar] [CrossRef]
- Quesada-Perez, M.; Ahualli, S.; Martin-Molina, A. Temperature-sensitive nanogels in the presence of salt: Explicit coarse-grained simulations. J. Chem. Phys. 2014, 141. [Google Scholar] [CrossRef] [PubMed]
- Quesada-Perez, M.; Ahualli, S.; Martin-Molina, A. Thermo-responsive Gels in the Presence of Monovalent Salt at Physiological Concentrations: A Monte Carlo Simulation Study. J. Polym. Sci. Polym. Phys. 2014, 52, 1403–1411. [Google Scholar] [CrossRef]
- Adroher-Benitez, I.; Martin-Molina, A.; Ahualli, S.; Quesada-Perez, M.; Odriozola, G.; Moncho-Jorda, A. Competition between excluded-volume and electrostatic interactions for nanogel swelling: Effects of the counterion valence and nanogel charge. Phys. Chem. Chem. Phys. 2017, 19, 6838–6848. [Google Scholar] [CrossRef] [PubMed]
- Quesada-Perez, M.; Maroto-Centeno, J.A.; Martin-Molina, A.; Moncho-Jorda, A. Direct determination of forces between charged nanogels through coarse-grained simulations. Phys. Rev. E 2018, 97. [Google Scholar] [CrossRef] [PubMed]
- Brannonpeppas, L.; Peppas, N.A. Equilibrium Swelling Behavior of Dilute Ionic Hydrogels in Electrolytic Solutions. J. Control. Release 1991, 16, 319–330. [Google Scholar] [CrossRef]
- Peppas, N.A. Hydrogels in Medicine and Pharmacy; CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar]
- Siepmann, J.; Peppas, N.A. Modeling of drug release from delivery systems based on hydroxypropyl methylcellulose (HPMC). Adv. Drug Deliv. Rev. 2001, 48, 139–157. [Google Scholar] [CrossRef]
- Peppas, N.A.; Sahlin, J.J. A Simple Equation for the Description of Solute Release. 3. Coupling of Diffusion and Relaxation. Int. J. Pharmaceut. 1989, 57, 169–172. [Google Scholar] [CrossRef]
- Fu, J.C.; Hagemeir, C.; Moyer, D.L. A unified mathematical model for diffusion from drug-polymer composite tablets. J. Biomed. Mater. Res. 1976, 10, 743–758. [Google Scholar] [CrossRef] [PubMed]
- Peppas, N.A.; Bures, P.; Leobandung, W.; Ichikawa, H. Hydrogels in pharmaceutical formulations. Eur. J. Pharm. Biopharm. 2000, 50, 27–46. [Google Scholar] [CrossRef]
- Amsden, B. Solute diffusion within hydrogels. Mechanisms and models. Macromolecules 1998, 31, 8382–8395. [Google Scholar] [CrossRef]
- Peppas, N.A.; Reinhart, C.T. Solute Diffusion in Swollen Membranes. 1. A New Theory. J. Membrane Sci. 1983, 15, 275–287. [Google Scholar] [CrossRef]
- Lustig, S.R.; Peppas, N.A. Solute Diffusion in Swollen Membranes. 9. Scaling Laws for Solute Diffusion in Gels. J. Appl. Polym. Sci. 1988, 36, 735–747. [Google Scholar] [CrossRef]
- Cukier, R.I. Diffusion of Brownian Spheres in Semidilute Polymer-Solutions. Macromolecules 1984, 17, 252–255. [Google Scholar] [CrossRef]
- Phillips, R.J.; Deen, W.M.; Brady, J.F. Hindered Transport of Spherical Macromolecules in Fibrous Membranes and Gels. AICHE J. 1989, 35, 1761–1769. [Google Scholar] [CrossRef]
- Jackson, G.W.; James, D.F. The Permeability of Fibrous Porous-Media. Can. J. Chem. Eng. 1986, 64, 364–374. [Google Scholar] [CrossRef]
- Ogston, A.G. The Spaces in a Uniform Random Suspension of Fibres. Trans. Faraday Soc. 1958, 54, 1754–1757. [Google Scholar] [CrossRef]
- Johansson, L.; Elvingson, C.; Lofroth, J.E. Diffusion and Interaction in Gels and Solutions. 3. Theoretical Results on the Obstruction Effect. Macromolecules 1991, 24, 6024–6029. [Google Scholar] [CrossRef]
- Tsai, D.S.; Strieder, W. Effective Conductivities of Random Fiber Beds. Chem. Eng. Commun. 1986, 40, 207–218. [Google Scholar] [CrossRef]
- Amsden, B. Solute diffusion in hydrogels. An examination of the retardation effect. Polym. Gels Netw. 1998, 6, 13–43. [Google Scholar] [CrossRef]
- Johnson, E.M.; Berk, D.A.; Jain, R.K.; Deen, W.M. Hindered diffusion in agarose gels: Test of effective medium model. Biophys. J. 1996, 70, 1017–1023. [Google Scholar] [CrossRef]
- Clague, D.S.; Phillips, R.J. Hindered diffusion of spherical macromolecules through dilute fibrous media. Phys. Fluids 1996, 8, 1720–1731. [Google Scholar] [CrossRef]
- Peppas, N.A.; Gurny, R.; Doelker, E.; Buri, P. Modeling of Drug Diffusion through Swellable Polymeric Systems. J. Membrane Sci. 1980, 7, 241–253. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Lustig, S.R.; Peppas, N.A. Solute and Penetrant Diffusion in Swellable Polymers. 1. Mathematical-Modeling. J. Polym. Sci. Polym. Phys. 1986, 24, 395–408. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Vonmeerwall, E.; Peppas, N.A. Solute and Penetrant Diffusion in Swellable Polymers. 2. Verification of Theoretical-Models. J. Polym. Sci. Polym. Phys. 1986, 24, 409–434. [Google Scholar] [CrossRef]
- Ju, R.T.C.; Nixon, P.R.; Patel, M.V. Drug-Release from Hydrophilic Matrices. 1. New Scaling Laws for Predicting Polymer and Drug-Release Based on the Polymer Disentanglement Concentration and the Diffusion Layer. J. Pharm. Sci. 1995, 84, 1455–1463. [Google Scholar] [CrossRef] [PubMed]
- Ju, R.T.C.; Nixon, P.R.; Patel, M.V.; Tong, D.M. Drug-Release from Hydrophilic Matrices. 2. A Mathematical-Model Based on the Polymer Disentanglement Concentration and the Diffusion Layer. J. Pharm. Sci. 1995, 84, 1464–1477. [Google Scholar] [CrossRef] [PubMed]
- Ju, R.T.C.; Nixon, P.R.; Patel, M.V. Diffusion coefficients of polymer chains in the diffusion layer adjacent to a swollen hydrophilic matrix. J. Pharm. Sci. 1997, 86, 1293–1298. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.; Peppas, N.A. Hydrophilic matrices for controlled drug delivery: An improved mathematical model to predict the resulting drug release kinetics (the “sequential layer” model). Pharm. Res. 2000, 17, 1290–1298. [Google Scholar] [CrossRef] [PubMed]
- Pitt, C.G.; Schindler, A. The Kinetics of Drug Cleavage and Release from Matrices Containing Covalent Polymer-Drug Conjugates. J. Control. Release 1995, 33, 391–395. [Google Scholar] [CrossRef]
- DuBose, J.W.; Cutshall, C.; Metters, A.T. Controlled release of tethered molecules via engineered hydrogel degradation: Model development and validation. J. Biomed. Mater. Res. A 2005, 74a, 104–116. [Google Scholar] [CrossRef] [PubMed]
- Reid, R.; Sgobba, M.; Raveh, B.; Rastelli, G.; Sali, A.; Santi, D.V. Analytical and Simulation-Based Models for Drug Release and Gel-Degradation in a Tetra-PEG Hydrogel Drug-Delivery System. Macromolecules 2015, 48, 7359–7369. [Google Scholar] [CrossRef]
- Ehrbar, M.; Metters, A.; Zammaretti, P.; Hubbell, J.A.; Zisch, A.H. Endothelial cell proliferation and progenitor maturation by fibrin-bound VEGF variants with differential susceptibilities to local cellular activity. J. Control. Release 2005, 101, 93–109. [Google Scholar] [CrossRef] [PubMed]
- Griffin, D.R.; Patterson, J.T.; Kasko, A.M. Photodegradation as a Mechanism for Controlled Drug Delivery. Biotechnol. Bioeng. 2010, 107, 1012–1019. [Google Scholar] [CrossRef]
- Sackett, C.K.; Narasimhan, B. Mathematical modeling of polymer erosion: Consequences for drug delivery. Int. J. Pharmaceut. 2011, 418, 104–114. [Google Scholar] [CrossRef]
- Lee, P.I. Diffusional Release of a Solute from a Polymeric Matrix—Approximate Analytical Solutions. J. Membrane Sci. 1980, 7, 255–275. [Google Scholar]
- Hopfenberg, H.B. Controlled Release from Erodible Slabs, Cylinders, and Spheres. In Controlled Release Polymeric Formulations; ACS Symposium Series; American Chemical Society: Washington, DC, USA, 1976; pp. 26–32. [Google Scholar]
- Katzhendler, I.; Hoffman, A.; Goldberger, A.; Friedman, M. Modeling of drug release from erodible tablets. J. Pharm. Sci. 1997, 86, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Gopferich, A.; Langer, R. Modeling of Polymer Erosion. Macromolecules 1993, 26, 4105–4112. [Google Scholar] [CrossRef]
- Mason, M.N.; Metters, A.T.; Bowman, C.N.; Anseth, K.S. Predicting controlled-release behavior of degradable PLA-b-PEG-b-PLA hydrogels. Macromolecules 2001, 34, 4630–4635. [Google Scholar] [CrossRef]
- Lin, C.C.; Anseth, K.S. PEG Hydrogels for the Controlled Release of Biomolecules in Regenerative Medicine. Pharm. Res. 2009, 26, 631–643. [Google Scholar] [CrossRef] [PubMed]
- Tibbitt, M.W.; Kloxin, A.M.; Sawicki, L.A.; Anseth, K.S. Mechanical Properties and Degradation of Chain and Step-Polymerized Photodegradable Hydrogels. Macromolecules 2013, 46, 2785–2792. [Google Scholar] [CrossRef] [PubMed]
- Metters, A.T.; Bowman, C.N.; Anseth, K.S. A statistical kinetic model for the bulk degradation of PLA-b-PEG-b-PLA hydrogel networks. J. Phys. Chem. B 2000, 104, 7043–7049. [Google Scholar] [CrossRef]
- Metters, A.T.; Anseth, K.S.; Bowman, C.N. A statistical kinetic model for the bulk degradation of PLA-b-PEG-b-PLA hydrogel networks: Incorporating network non-idealities. J. Phys. Chem. B 2001, 105, 8069–8076. [Google Scholar] [CrossRef]
- Metters, A.; Hubbell, J. Network formation and degradation behavior of hydrogels formed by Michael-type addition reactions. Biomacromolecules 2005, 6, 290–301. [Google Scholar] [CrossRef] [PubMed]
- Shih, H.; Lin, C.C. Cross-Linking and Degradation of Step-Growth Hydrogels Formed by Thiol-Ene Photoclick Chemistry. Biomacromolecules 2012, 13, 2003–2012. [Google Scholar] [CrossRef]
- Tibbitt, M.W.; Kloxin, A.M.; Anseth, K.S. Modeling controlled photodegradation in optically thick hydrogels. J. Polym. Sci. Pol. Chem. 2013, 51, 1899–1911. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.; Faisant, N.; Benoit, J.P. A new mathematical model quantifying drug release from bioerodible microparticles using Monte Carlo simulations. Pharm. Res. 2002, 19, 1885–1893. [Google Scholar] [CrossRef] [PubMed]
- Vlugt-Wensink, K.D.F.; Vlugt, T.J.H.; Jiskoot, W.; Crommelin, D.J.A.; Verrijk, R.; Hennink, W.E. Modeling the release of proteins from degrading crosslinked dextran microspheres using kinetic Monte Carlo simulations. J. Control. Release 2006, 111, 117–127. [Google Scholar] [CrossRef]
- Peppas, N.A.; Wright, S.L. Drug diffusion and binding in ionizable interpenetrating networks from poly(vinyl alcohol) and poly(acrylic acid). Eur. J. Pharm. Biopharm. 1998, 46, 15–29. [Google Scholar] [CrossRef]
- Liu, D.E.; Dursch, T.J.; Taylor, N.O.; Chan, S.Y.; Bregante, D.T.; Radke, C.J. Diffusion of water-soluble sorptive drugs in HEMA/MAA hydrogels. J. Control. Release 2016, 239, 242–248. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Lumpkin, J.A.; Rosenblatt, J. Mathematical-Modeling of Drug-Release from Hydrogel Matrices Via a Diffusion Coupled with Desorption Mechanism. J. Control. Release 1994, 32, 17–25. [Google Scholar] [CrossRef]
- Rossi, F.; Castiglione, F.; Ferro, M.; Marchini, P.; Mauri, E.; Moioli, M.; Mele, A.; Masi, M. Drug-Polymer Interactions in Hydrogel-based Drug-Delivery Systems: An Experimental and Theoretical Study. Chemphyschem 2015, 16, 2818–2825. [Google Scholar] [CrossRef] [PubMed]
- Vulic, K.; Pakulska, M.M.; Sonthalia, R.; Ramachandran, A.; Shoichet, M.S. Mathematical model accurately predicts protein release from an affinity-based delivery system. J. Control. Release 2015, 197, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Sakiyama-Elbert, S.E.; Hubbell, J.A. Development of fibrin derivatives for controlled release of heparin-binding growth factors. J. Control. Release 2000, 65, 389–402. [Google Scholar] [CrossRef]
- Yan, H.J.; Casalini, T.; Hulsart-Billstrom, G.; Wang, S.J.; Oommen, O.P.; Salvalaglio, M.; Larsson, S.; Hilborn, J.; Varghese, O.P. Synthetic design of growth factor sequestering extracellular matrix mimetic hydrogel for promoting in vivo bone formation. Biomaterials 2018, 161, 190–202. [Google Scholar] [CrossRef] [PubMed]
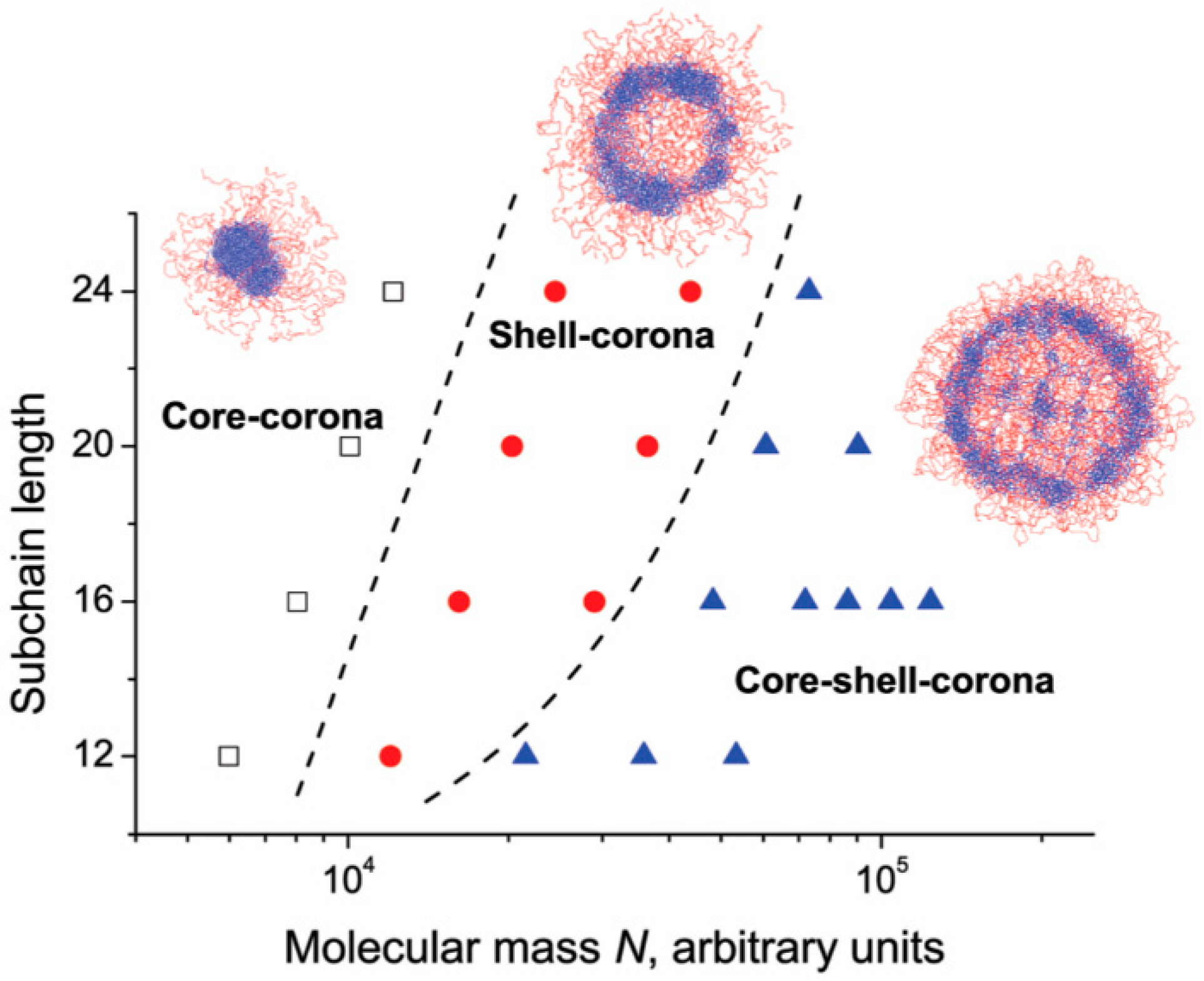
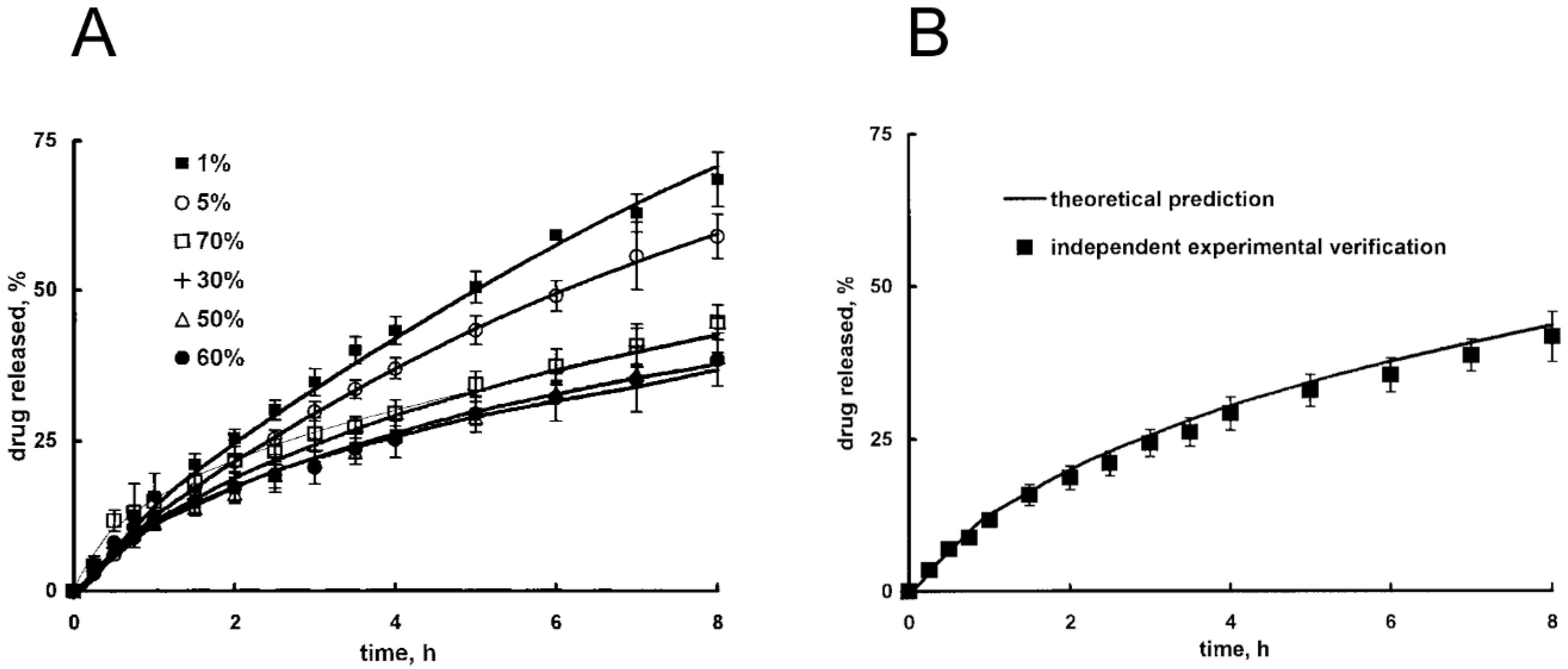
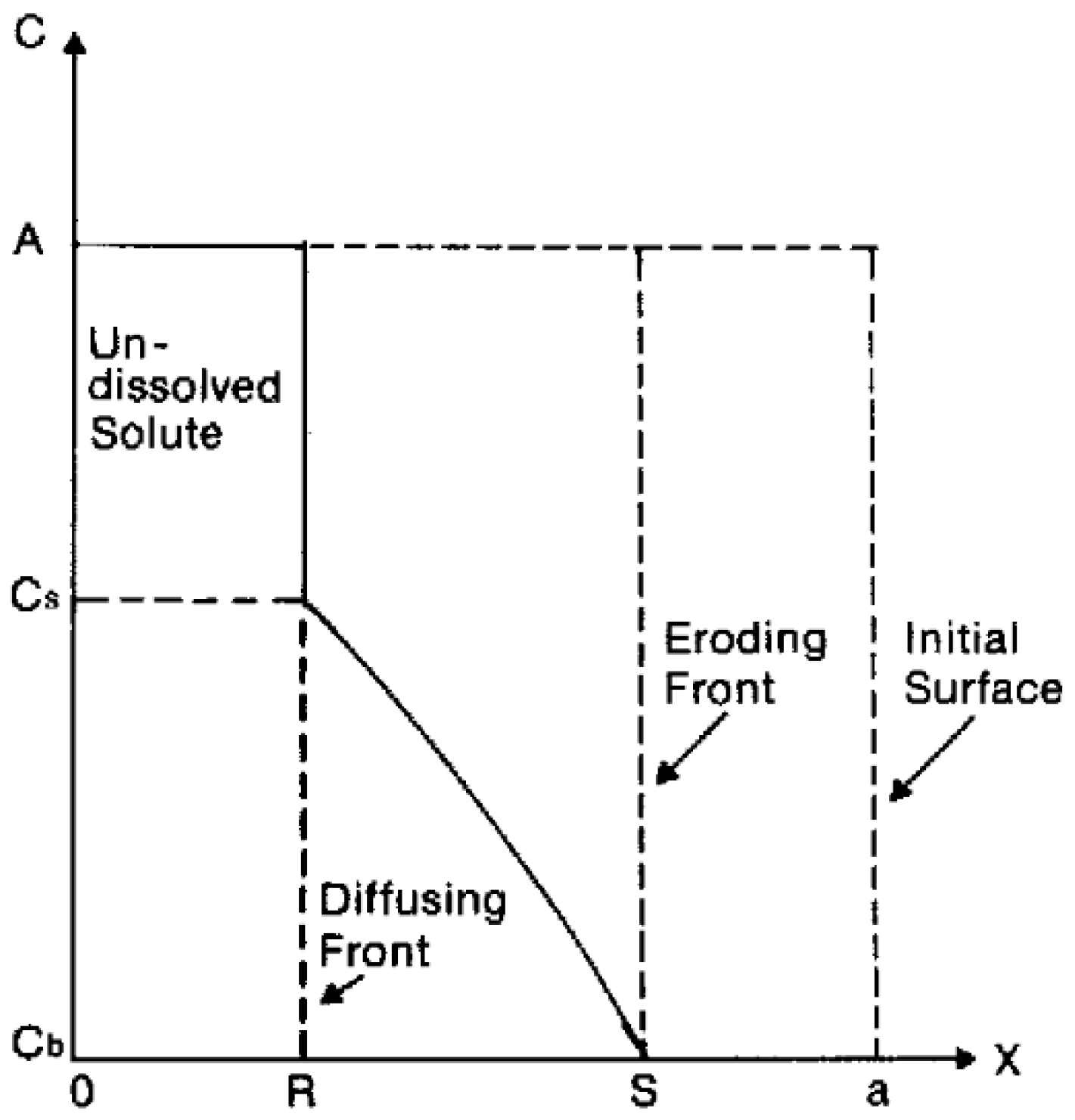
| Method | Time Scale | Length Scale | Applications |
|---|---|---|---|
| Molecular dynamics simulations | Nanoseconds | Nanometers (tenth) | Transport phenomena Chain conformation |
| Coarse-grained models | Microseconds | Nanometers (up to hundredth) | Transport phenomena Network structure Swelling equilibrium |
| Macroscale models | Seconds | Meters | Structural parameters Swelling dynamics Degradation kinetics Release rate |
| n [-] | Release Mechanism | ||
|---|---|---|---|
| Thin Film | Cylinder | Sphere | |
| 0.5 | 0.45 | 0.43 | Fickian diffusion |
| 0.5 < n < 1.0 | 0.45 < n < 0.89 | 0.43 < n < 0.85 | Anomalous transport |
| 1.0 | 0.89 | 0.85 | Case II transport |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casalini, T.; Perale, G. From Microscale to Macroscale: Nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery. Gels 2019, 5, 28. https://doi.org/10.3390/gels5020028
Casalini T, Perale G. From Microscale to Macroscale: Nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery. Gels. 2019; 5(2):28. https://doi.org/10.3390/gels5020028
Chicago/Turabian StyleCasalini, Tommaso, and Giuseppe Perale. 2019. "From Microscale to Macroscale: Nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery" Gels 5, no. 2: 28. https://doi.org/10.3390/gels5020028
APA StyleCasalini, T., & Perale, G. (2019). From Microscale to Macroscale: Nine Orders of Magnitude for a Comprehensive Modeling of Hydrogels for Controlled Drug Delivery. Gels, 5(2), 28. https://doi.org/10.3390/gels5020028