Unveiling the Effect of Aqueous-Phase Dynamics on Chitosan Hydrogel Film Mechanical Properties Through AFM Nanoindentation and Tensile Testing
Abstract
1. Introduction
2. Results and Discussion
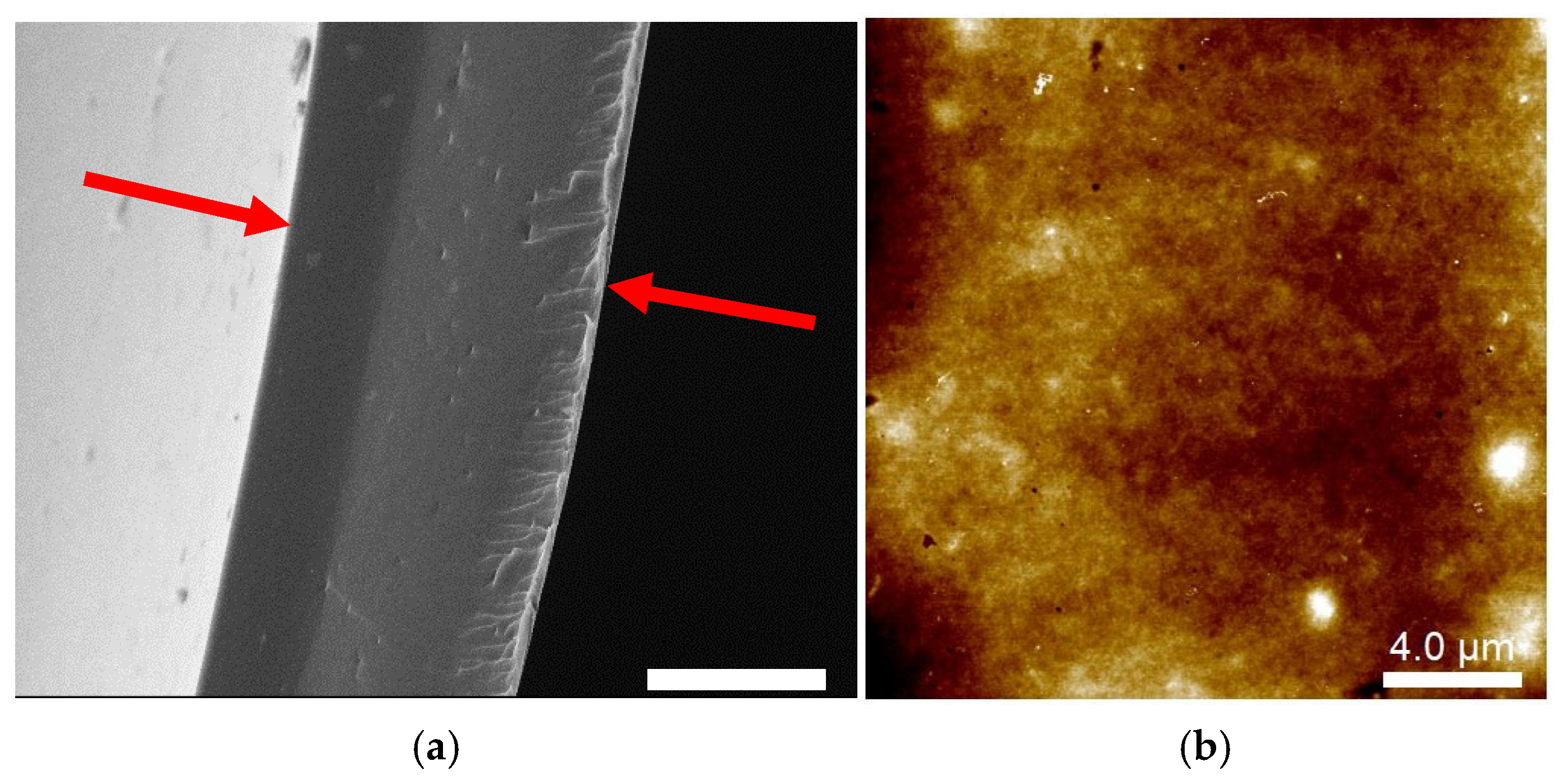
2.1. Microstructure of Cast-Dried CHI Films
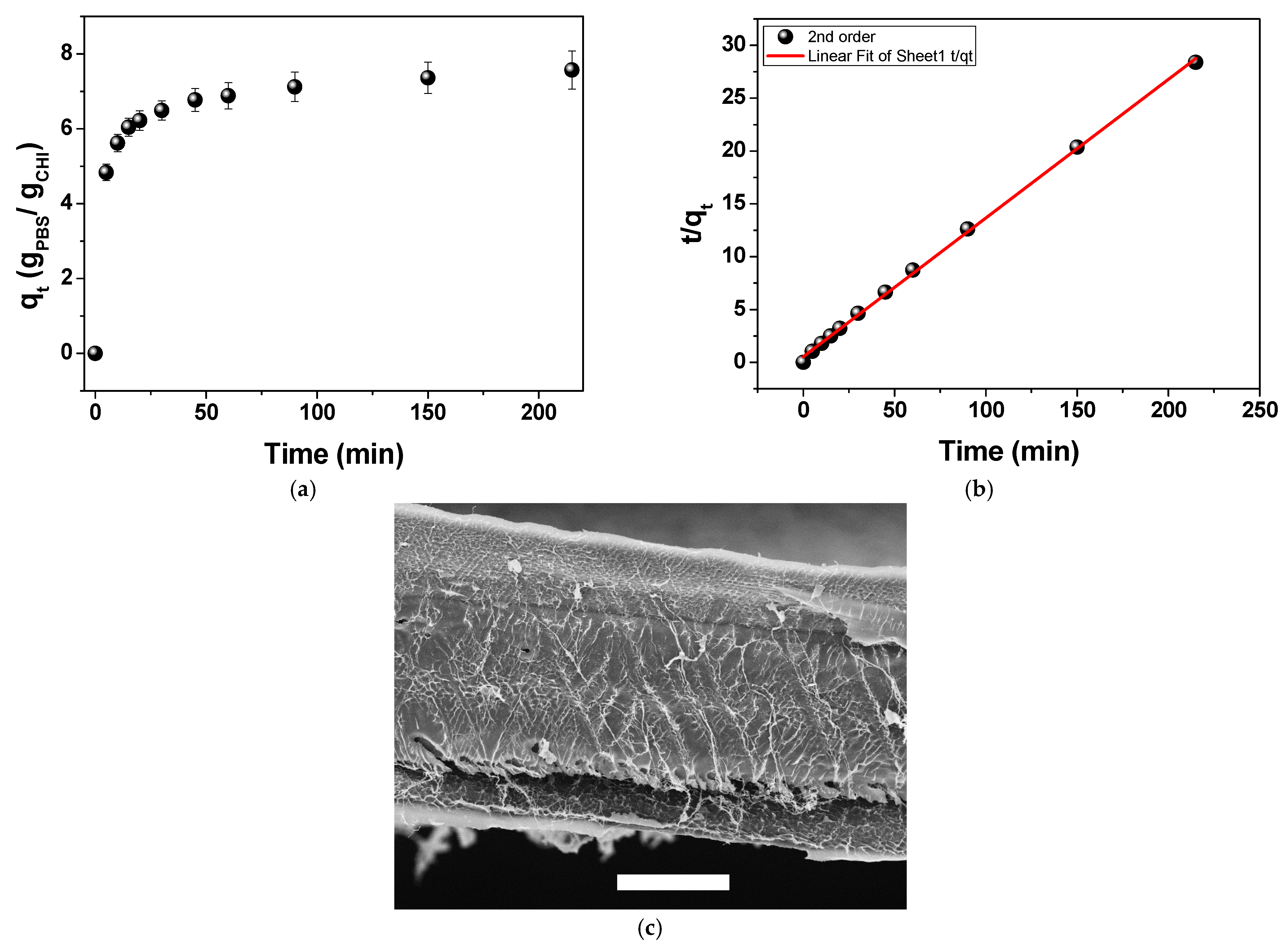
2.2. Aqueous-Phase Sorption Studies
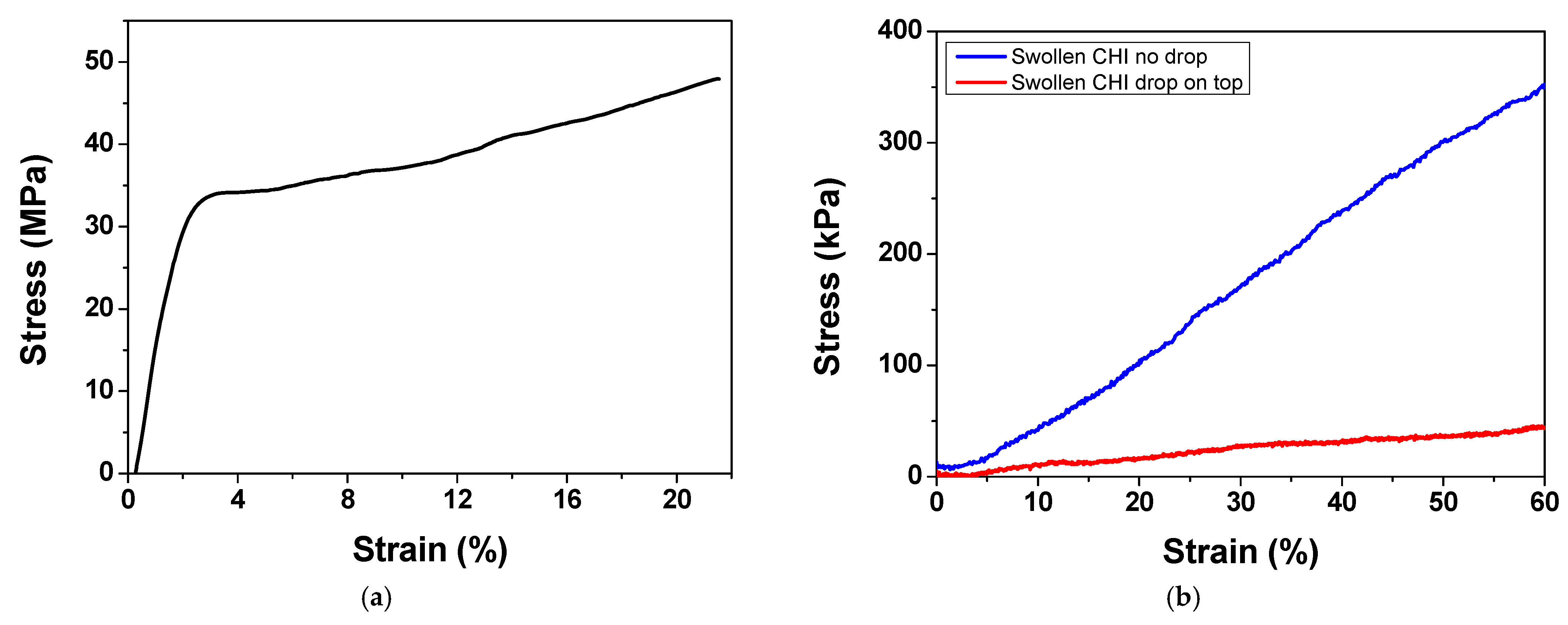
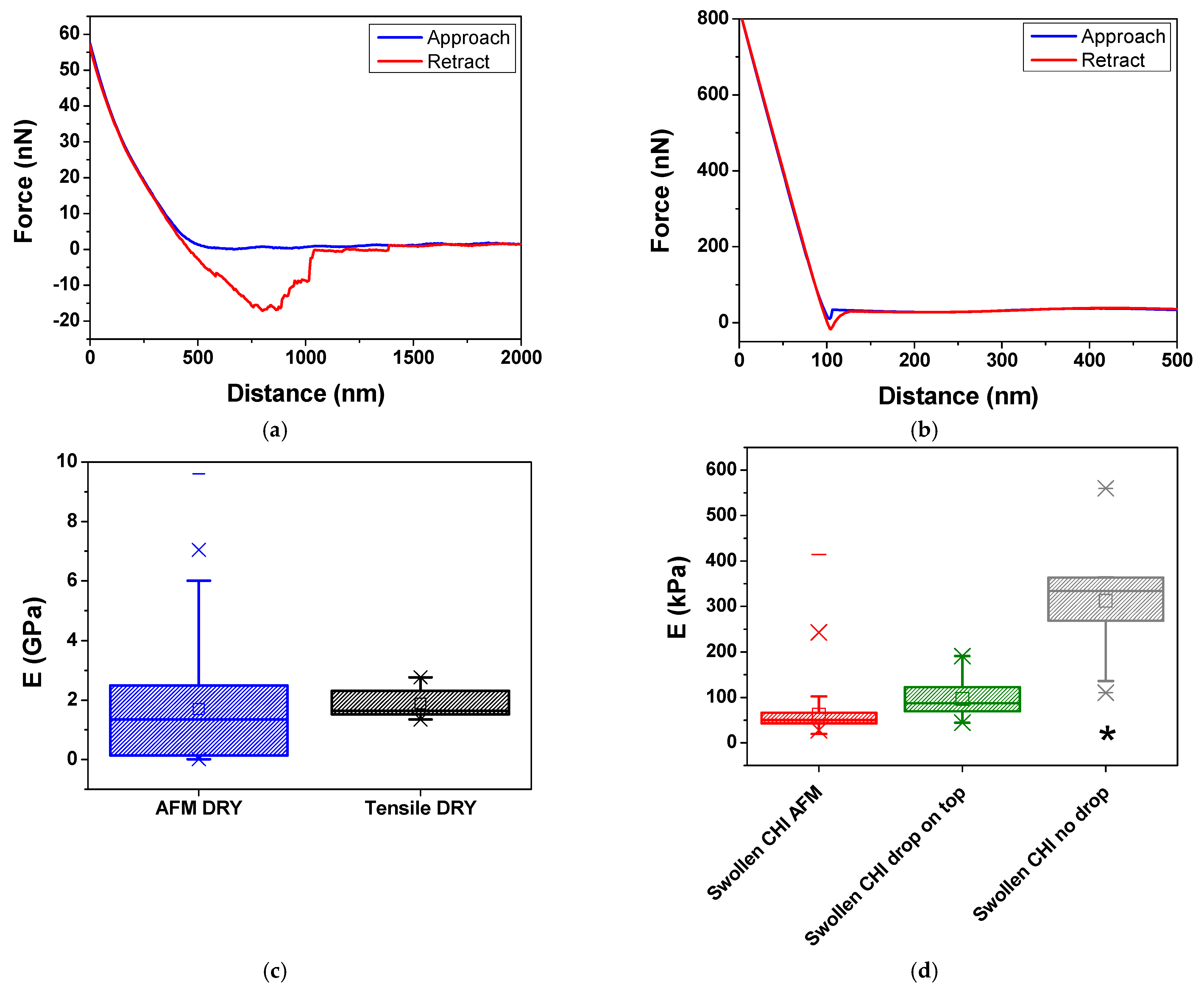
2.3. Film Mechanical Characterization
2.3.1. Tensile Testing
2.3.2. AFM Nanoindentation
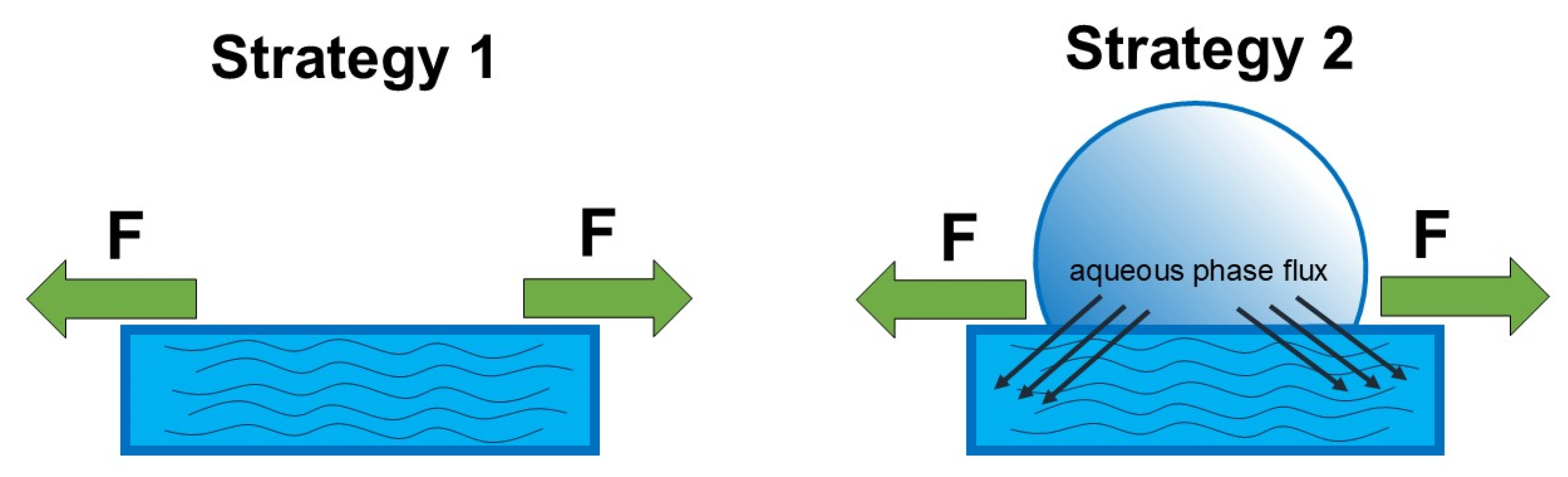
2.4. Aqueous-Phase Dynamics Studies
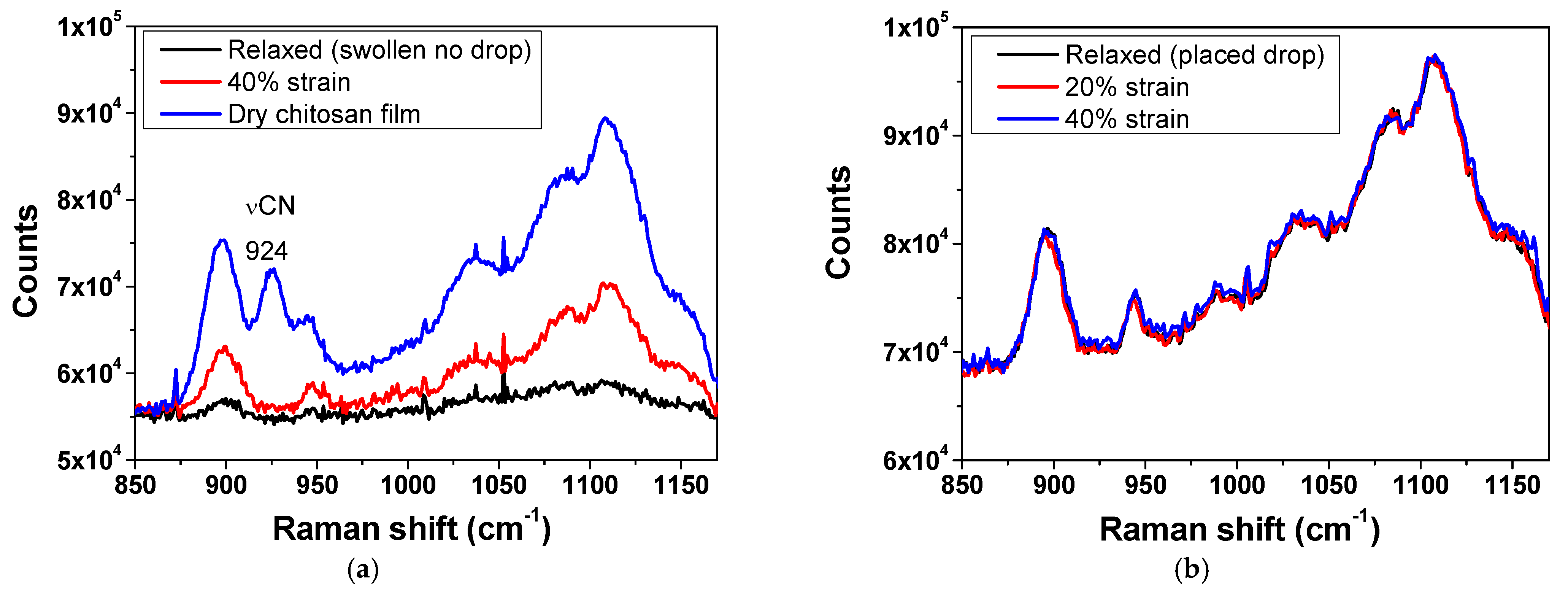
2.4.1. Raman Spectroscopy
2.4.2. Gravimetrical Analysis
3. Conclusions
4. Materials and Methods
4.1. Chitosan Film Preparation
4.2. Sorption Kinetics
4.3. Macro Mechanical Testing
4.4. Micro Mechanical Testing
4.5. Spectroscopic Characterization
4.6. Aqueous-Phase Loss Evaluation
4.7. Statistical Analysis
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guimarães, C.F.; Gasperini, L.; Marques, A.P.; Reis, R.L. The Stiffness of Living Tissues and Its Implications for Tissue Engineering. Nat. Rev. Mater. 2020, 5, 351–370. [Google Scholar] [CrossRef]
- Wang, L.; Wang, C.; Wu, S.; Fan, Y.; Li, X. Influence of the Mechanical Properties of Biomaterials on Degradability, Cell Behaviors and Signaling Pathways: Current Progress and Challenges. Biomater. Sci. 2020, 8, 2714–2733. [Google Scholar] [CrossRef] [PubMed]
- Yi, B.; Xu, Q.; Liu, W. An Overview of Substrate Stiffness Guided Cellular Response and Its Applications in Tissue Regeneration. Bioact. Mater. 2022, 15, 82–102. [Google Scholar] [CrossRef] [PubMed]
- Ye, K.; Wang, X.; Cao, L.; Li, S.; Li, Z.; Yu, L.; Ding, J. Matrix Stiffness and Nanoscale Spatial Organization of Cell-Adhesive Ligands Direct Stem Cell Fate. Nano Lett. 2015, 15, 4720–4729. [Google Scholar] [CrossRef]
- Zhou, Q.; Ge, L.; Guimarães, C.F.; Kühn, P.T.; Yang, L.; van Rijn, P. Development of a Novel Orthogonal Double Gradient for High-Throughput Screening of Mesenchymal Stem Cells–Materials Interaction. Adv. Mater. Interfaces 2018, 5, 1800504. [Google Scholar] [CrossRef]
- Garreta, E.; Prado, P.; Tarantino, C.; Oria, R.; Fanlo, L.; Martí, E.; Zalvidea, D.; Trepat, X.; Roca-Cusachs, P.; Gavaldà-Navarro, A.; et al. Fine Tuning the Extracellular Environment Accelerates the Derivation of Kidney Organoids from Human Pluripotent Stem Cells. Nat. Mater. 2019, 18, 397–405. [Google Scholar] [CrossRef]
- Uynuk-Ool, T.; Rothdiener, M.; Walters, B.; Hegemann, M.; Palm, J.; Nguyen, P.; Seeger, T.; Stöckle, U.; Stegemann, J.P.; Aicher, W.K.; et al. The Geometrical Shape of Mesenchymal Stromal Cells Measured by Quantitative Shape Descriptors Is Determined by the Stiffness of the Biomaterial and by Cyclic Tensile Forces. J. Tissue Eng. Regen. Med. 2017, 11, 3508–3522. [Google Scholar] [CrossRef]
- Branco da Cunha, C.; Klumpers, D.D.; Li, W.A.; Koshy, S.T.; Weaver, J.C.; Chaudhuri, O.; Granja, P.L.; Mooney, D.J. Influence of the Stiffness of Three-Dimensional Alginate/Collagen-I Interpenetrating Networks on Fibroblast Biology. Biomaterials 2014, 35, 8927–8936. [Google Scholar] [CrossRef]
- Lv, H.; Wang, H.; Zhang, Z.; Yang, W.; Liu, W.; Li, Y.; Li, L. Biomaterial Stiffness Determines Stem Cell Fate. Life Sci. 2017, 178, 42–48. [Google Scholar] [CrossRef]
- Sun, A.X.; Lin, H.; Fritch, M.R.; Shen, H.; Alexander, P.G.; DeHart, M.; Tuan, R.S. Chondrogenesis of Human Bone Marrow Mesenchymal Stem Cells in 3-Dimensional, Photocrosslinked Hydrogel Constructs: Effect of Cell Seeding Density and Material Stiffness. Acta Biomater. 2017, 58, 302–311. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, D.; Zhou, C.; Yuan, Q.; Ye, L.; Zhou, X. Substrate Elasticity Regulates Adipose-Derived Stromal Cell Differentiation towards Osteogenesis and Adipogenesis through β-Catenin Transduction. Acta Biomater. 2018, 79, 83–95. [Google Scholar] [CrossRef] [PubMed]
- McKee, C.T.; Last, J.A.; Russell, P.; Murphy, C.J. Indentation Versus Tensile Measurements of Young’s Modulus for Soft Biological Tissues. Tissue Eng. Part B Rev. 2011, 17, 155–164. [Google Scholar] [CrossRef]
- Perić, D.; de Souza Neto, E.A.; Feijóo, R.A.; Partovi, M.; Molina, A.J.C. On Micro-to-Macro Transitions for Multi-Scale Analysis of Non-Linear Heterogeneous Materials: Unified Variational Basis and Finite Element Implementation. Int. J. Numer. Methods Eng. 2011, 87, 149–170. [Google Scholar] [CrossRef]
- Abazari, A.M.; Safavi, S.M.; Rezazadeh, G.; Villanueva, L.G. Modelling the Size Effects on the Mechanical Properties of Micro/Nano Structures. Sensors 2015, 15, 28543–28562. [Google Scholar] [CrossRef]
- McNamara, L.E.; Burchmore, R.; Riehle, M.O.; Herzyk, P.; Biggs, M.J.P.; Wilkinson, C.D.W.; Curtis, A.S.G.; Dalby, M.J. The Role of Microtopography in Cellular Mechanotransduction. Biomaterials 2012, 33, 2835–2847. [Google Scholar] [CrossRef]
- Qian, L.; Zhao, H. Nanoindentation of Soft Biological Materials. Micromachines 2018, 9, 654. [Google Scholar] [CrossRef]
- Jacot, J.G.; Dianis, S.; Schnall, J.; Wong, J.Y. A Simple Microindentation Technique for Mapping the Microscale Compliance of Soft Hydrated Materials and Tissues. J. Biomed. Mater. Res. A 2006, 79A, 485–494. [Google Scholar] [CrossRef]
- Constantinides, G.; Kalcioglu, Z.I.; McFarland, M.; Smith, J.F.; Van Vliet, K.J. Probing Mechanical Properties of Fully Hydrated Gels and Biological Tissues. J. Biomech. 2008, 41, 3285–3289. [Google Scholar] [CrossRef]
- Torres, F.G.; Troncoso, O.P.; Montes, M.R. The Effect of Temperature on the Mechanical Properties of a Protein-Based Biopolymer Network. J. Therm. Anal. Calorim. 2013, 111, 1921–1925. [Google Scholar] [CrossRef]
- Zhou, C.; Guo, H.; Li, J.; Huang, S.; Li, H.; Meng, Y.; Yu, D.; de Claville Christiansen, J.; Jiang, S. Temperature Dependence of Poly(Lactic Acid) Mechanical Properties. RSC Adv. 2016, 6, 113762–113772. [Google Scholar] [CrossRef]
- Johnston, A.; Callanan, A. Recent Methods for Modifying Mechanical Properties of Tissue-Engineered Scaffolds for Clinical Applications. Biomimetics 2023, 8, 205. [Google Scholar] [CrossRef] [PubMed]
- Kolipaka, A.; Wassenaar, P.A.; Cha, S.; Marashdeh, W.M.; Mo, X.; Kalra, P.; Gans, B.; Raterman, B.; Bourekas, E. Magnetic Resonance Elastography to Estimate Brain Stiffness: Measurement Reproducibility and Its Estimate in Pseudotumor Cerebri Patients. Clin. Imaging 2018, 51, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhu, M.; Thomas, E.; Hopyan, S.; Sun, Y. Existing and Potential Applications of Elastography for Measuring the Viscoelasticity of Biological Tissues In Vivo. Front. Phys. 2021, 9, 670571. [Google Scholar] [CrossRef]
- Buffinton, C.M.; Tong, K.J.; Blaho, R.A.; Buffinton, E.M.; Ebenstein, D.M. Comparison of Mechanical Testing Methods for Biomaterials: Pipette Aspiration, Nanoindentation, and Macroscale Testing. J. Mech. Behav. Biomed. Mater. 2015, 51, 367–379. [Google Scholar] [CrossRef]
- Casanova, M.; Balmelli, A.; Carnelli, D.; Courty, D.; Schneider, P.; Müller, R. Nanoindentation Analysis of the Micromechanical Anisotropy in Mouse Cortical Bone. R. Soc. Open Sci. 2017, 4, 160971. [Google Scholar] [CrossRef]
- Sadyrin, E.; Lapitskaya, V.; Kuznetsova, T.; Yogina, D.; Maksyukov, S.; Aizikovich, S. Nanoindentation and Atomic Force Microscopy Derived Mechanical and Microgeometrical Properties of Tooth Root Cementum. Micro 2022, 2, 575–588. [Google Scholar] [CrossRef]
- Xu, D.; Hernandez Miranda, M.L.; Evans, N.D.; Sengers, B.G.; Browne, M.; Cook, R.B. Depth Profiling via Nanoindentation for Characterisation of the Elastic Modulus and Hydraulic Properties of Thin Hydrogel Layers. J. Mech. Behav. Biomed. Mater. 2023, 148, 106195. [Google Scholar] [CrossRef]
- Kain, L.; Andriotis, O.G.; Gruber, P.; Frank, M.; Markovic, M.; Grech, D.; Nedelkovski, V.; Stolz, M.; Ovsianikov, A.; Thurner, P.J. Calibration of Colloidal Probes with Atomic Force Microscopy for Micromechanical Assessment. J. Mech. Behav. Biomed. Mater. 2018, 85, 225–236. [Google Scholar] [CrossRef]
- Collinson, D.W.; Sheridan, R.J.; Palmeri, M.J.; Brinson, L.C. Best Practices and Recommendations for Accurate Nanomechanical Characterization of Heterogeneous Polymer Systems with Atomic Force Microscopy. Prog. Polym. Sci. 2021, 119, 101420. [Google Scholar] [CrossRef]
- Bose, S.; Li, S.; Mele, E.; Williams, C.J.; Silberschmidt, V.V. Stability and Mechanical Performance of Collagen Films under Different Environmental Conditions. Polym. Degrad. Stab. 2022, 197, 109853. [Google Scholar] [CrossRef]
- Grant, C.A.; Brockwell, D.J.; Radford, S.E.; Thomson, N.H. Effects of Hydration on the Mechanical Response of Individual Collagen Fibrils. Appl. Phys. Lett. 2008, 92, 233902. [Google Scholar] [CrossRef]
- Bose, S.; Li, S.; Mele, E.; Silberschmidt, V.V. Dry vs. Wet: Properties and Performance of Collagen Films. Part I. Mechanical Behaviour and Strain-Rate Effect. J. Mech. Behav. Biomed. Mater. 2020, 111, 103983. [Google Scholar] [CrossRef] [PubMed]
- Aryaei, A.; Jayatissa, A.H.; Jayasuriya, A.C. Nano and Micro Mechanical Properties of Uncross-Linked and Cross-Linked Chitosan Films. J. Mech. Behav. Biomed. Mater. 2012, 5, 82–89. [Google Scholar] [CrossRef]
- Breda, C.A.; Morgado, D.L.; Assis, O.B.G.; Duarte, M.C.T. Processing and Characterization of Chitosan Films with Incorporation of Ethanolic Extract from “Pequi” Peels. Macromol. Res. 2017, 25, 1049–1056. [Google Scholar] [CrossRef]
- da Silva, R.L.C.G.; Bernardinelli, O.D.; Frachini, E.C.G.; Ulrich, H.; Sabadini, E.; Petri, D.F.S. Vanillin Crosslinked Chitosan Films: The States of Water and the Effect of Carriers on Curcumin Uptake. Carbohydr. Polym. 2022, 292, 119725. [Google Scholar] [CrossRef]
- da Silva, R.L.C.G.; Bezjak, D.; Corrales, T.P.; Kappl, M.; Petri, D.F.S. Chitosan/Vanillin/Polydimethylsiloxane Scaffolds with Tunable Stiffness for Muscle Cell Proliferation. Int. J. Biol. Macromol. 2025, 286, 138445. [Google Scholar] [CrossRef]
- Miles, K.B.; Ball, R.L.; Matthew, H.W.T. Chitosan Films with Improved Tensile Strength and Toughness from N-Acetyl-Cysteine Mediated Disulfide Bonds. Carbohydr. Polym. 2016, 139, 1–9. [Google Scholar] [CrossRef]
- Miras, J.; Liu, C.; Blomberg, E.; Thormann, E.; Vílchez, S.; Esquena, J. PH-Responsive Chitosan Nanofilms Crosslinked with Genipin. Colloids Surf. A Physicochem. Eng. Asp. 2021, 616, 126229. [Google Scholar] [CrossRef]
- Luna, R.; Touhami, F.; Uddin, M.J.; Touhami, A. Effect of Temperature and PH on Nanostructural and Nanomechanical Properties of Chitosan Films. Surf. Interfaces 2022, 29, 101706. [Google Scholar] [CrossRef]
- Eivazzadeh-Keihan, R.; Radinekiyan, F.; Aliabadi, H.A.M.; Sukhtezari, S.; Tahmasebi, B.; Maleki, A.; Madanchi, H. Chitosan Hydrogel/Silk Fibroin/Mg(OH)2 Nanobiocomposite as a Novel Scaffold with Antimicrobial Activity and Improved Mechanical Properties. Sci. Rep. 2021, 11, 650. [Google Scholar] [CrossRef]
- Marangoni Júnior, L.; Jamróz, E.; de Ávila Gonçalves, S.A.; da Silva, R.G.; Alves, R.M.V.; Vieira, R.P. Preparation and Characterization of Sodium Alginate Films with Propolis Extract and Nano-SiO2. Food Hydrocoll. Health 2022, 2, 100094. [Google Scholar] [CrossRef]
- Nützl, M.; Schrottenbaum, M.; Müller, T.; Müller, R. Mechanical Properties and Chemical Stability of Alginate-Based Anisotropic Capillary Hydrogels. J. Mech. Behav. Biomed. Mater. 2022, 134, 105397. [Google Scholar] [CrossRef] [PubMed]
- Alavarse, A.C.; da Silva, R.L.C.G.; Ghaffari Bohlouli, P.; Cornejo, D.; Ulrich, H.; Shavandi, A.; Petri, D.F.S. Magnetic Force Microscopy and Nanoindentation on 3D Printed Magnetic Scaffolds for Neuronal Cell Growth. ACS Appl. Polym. Mater. 2024, 6, 1410–1421. [Google Scholar] [CrossRef]
- Kaklamani, G.; Cheneler, D.; Grover, L.M.; Adams, M.J.; Bowen, J. Mechanical Properties of Alginate Hydrogels Manufactured Using External Gelation. J. Mech. Behav. Biomed. Mater. 2014, 36, 135–142. [Google Scholar] [CrossRef]
- Wang, L.-F.; Shankar, S.; Rhim, J.-W. Properties of Alginate-Based Films Reinforced with Cellulose Fibers and Cellulose Nanowhiskers Isolated from Mulberry Pulp. Food Hydrocoll. 2017, 63, 201–208. [Google Scholar] [CrossRef]
- Aussel, A.; Montembault, A.; Malaise, S.; Foulc, M.P.; Faure, W.; Cornet, S.; Aid, R.; Chaouat, M.; Delair, T.; Letourneur, D.; et al. In Vitro Mechanical Property Evaluation of Chitosan-Based Hydrogels Intended for Vascular Graft Development. J. Cardiovasc. Transl. Res 2017, 10, 480–488. [Google Scholar] [CrossRef]
- Rosova, E.; Zoolshoev, Z.; Vyrezkova, E.; Vlasova, E.; Smirnova, N.; Kolbe, K.; Saprykina, N.; Kuryndin, I. Preparation and Characterization of Biocompatible Hydrogels Based on a Chitosan-Polyacrylamide Copolymer. Biomater. Connect 2025, 2, 0014. [Google Scholar] [CrossRef]
- Lee, S.Y.; Pereira, B.P.; Yusof, N.; Selvaratnam, L.; Yu, Z.; Abbas, A.A.; Kamarul, T. Unconfined Compression Properties of a Porous Poly(Vinyl Alcohol)-Chitosan-Based Hydrogel after Hydration. Acta Biomater. 2009, 5, 1919–1925. [Google Scholar] [CrossRef]
- Xin, L.; Cai, Y.; Liu, J.; Jia, W.; Fang, L.; Liu, C. Design and in Vitro/in Vivo Evaluation of Chitosan-Polyvinyl Alcohol Copolymer Material Cross-Linked by Dynamic Borate Ester Covalent for Pregabalin Film-Forming Delivery System. Int. J. Biol. Macromol. 2024, 281, 136433. [Google Scholar] [CrossRef]
- Uma Thanu Krishnan Neela, N.; Szewczyk, P.K.; Karbowniczek, J.E.; Polak, M.; Knapczyk-Korczak, J.; Stachewicz, U. Improving Stability and Mechanical Strength of Electrospun Chitosan-Polycaprolactone Scaffolds Using Genipin Cross-Linking for Biomedical Applications. Macromol. Rapid Commun. 2024, 2400869. [Google Scholar] [CrossRef]
- Rubina, M.; Elmanovich, I.; Vasil’kov, A. AFM Studies of Chitosan, Gold-Chitosan, and Silver-Chitosan Films Morphology. Macromol. Symp. 2020, 389, 1900068. [Google Scholar] [CrossRef]
- Pigaleva, M.A.; Portnov, I.V.; Rudov, A.A.; Blagodatskikh, I.V.; Grigoriev, T.E.; Gallyamov, M.O.; Potemkin, I.I. Stabilization of Chitosan Aggregates at the Nanoscale in Solutions in Carbonic Acid. Macromolecules 2014, 47, 5749–5758. [Google Scholar] [CrossRef]
- Assis, O.B.G.; Bernardes-Filho, R.; Vieira, D.C.; Filho, S.P.C. AFM Characterization of Chitosan Self-Assembled Films. Int. J. Polym. Mater. Polym. Biomater. 2002, 51, 633–638. [Google Scholar] [CrossRef]
- Madihally, S.V.; Matthew, H.W.T. Porous Chitosan Scaffolds for Tissue Engineering. Biomaterials 1999, 20, 1133–1142. [Google Scholar] [CrossRef]
- Gautieri, A.; Pate, M.I.; Vesentini, S.; Redaelli, A.; Buehler, M.J. Hydration and Distance Dependence of Intermolecular Shearing between Collagen Molecules in a Model Microfibril. J. Biomech. 2012, 45, 2079–2083. [Google Scholar] [CrossRef]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Schaible, E.; Stewart, P.; Ritchie, R.O.; Meyers, M.A. On the Tear Resistance of Skin. Nat. Commun. 2015, 6, 6649. [Google Scholar] [CrossRef]
- Bose, S.; Li, S.; Mele, E.; Silberschmidt, V.V. Exploring the Mechanical Properties and Performance of Type-I Collagen at Various Length Scales: A Progress Report. Materials 2022, 15, 2753. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, S.-H.; Chuang, W.-T.; Dai, N.-T.; Hsu, S. Biomimetic Strain-Stiffening in Chitosan Self-Healing Hydrogels. ACS Appl. Mater. Interfaces 2022, 14, 16032–16046. [Google Scholar] [CrossRef]
- Chan, E.P.; Hu, Y.; Johnson, P.M.; Suo, Z.; Stafford, C.M. Spherical Indentation Testing of Poroelastic Relaxations in Thin Hydrogel Layers. Soft Matter 2012, 8, 1492–1498. [Google Scholar] [CrossRef]
- Kim, S.; Byun, K.M.; Lee, S.Y. Influence of Water Content on Raman Spectroscopy Characterization of Skin Sample. Biomed. Opt. Express 2017, 8, 1130–1138. [Google Scholar] [CrossRef]
- Zając, A.; Hanuza, J.; Wandas, M.; Dymińska, L. Determination of N-Acetylation Degree in Chitosan Using Raman Spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2015, 134, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Addis, J.; Mohammed, N.; Rotimi, O.; Magee, D.; Jha, A.; Subramanian, V. Raman Spectroscopy of Endoscopic Colonic Biopsies from Patients with Ulcerative Colitis to Identify Mucosal Inflammation and Healing. Biomed. Opt. Express 2016, 7, 2022–2035. [Google Scholar] [CrossRef] [PubMed]
- Simič, R.; Yetkin, M.; Zhang, K.; Spencer, N.D. Importance of Hydration and Surface Structure for Friction of Acrylamide Hydrogels. Tribol. Lett. 2020, 68, 64. [Google Scholar] [CrossRef]
- Toledo, P.V.O.; Bernardinelli, O.D.; Sabadini, E.; Petri, D.F.S. The States of Water in Tryptophan Grafted Hydroxypropyl Methylcellulose Hydrogels and Their Effect on the Adsorption of Methylene Blue and Rhodamine B. Carbohydr. Polym. 2020, 248, 116765. [Google Scholar] [CrossRef]
- Wang, H.; Cui, H.; Wang, X.; Lin, C.; Xia, S.; Hayat, K.; Hussain, S.; Tahir, M.U.; Zhang, X. Metal Complexed-Enzymatic Hydrolyzed Chitosan Improves Moisture Retention of Fiber Papers by Migrating Immobilized Water to Bound State. Carbohydr. Polym. 2020, 235, 115967. [Google Scholar] [CrossRef]
| System | Form | E (GPa) | Testing Method | Ref. | |
|---|---|---|---|---|---|
| Wet | Dry | ||||
| Collagen | Film | 0.006–0.009 | 8.5 ± 4.2 | Nanoindentation | [30] |
| Fibril | 0.0012 ± 0.0001 | 1.9 ± 0.5 | AFM | [31] | |
| Film | 0.00274 ± 0.001 | 0.0757 ± 0.0157 | Tensile testing | [32] | |
| Chitosan | Film | - | 1.5 | Nanoindentation | [33] |
| Film | - | 0.1344 ± 0.0174 | Tensile testing | [34] | |
| Film | - | 0.236 ± 0.027 | Tensile testing | [35] | |
| Film | 0.000137 0.000062 | 0.275 - | Tensile testing Nanoindentation | [36] | |
| Film | 0.00348 ± 0.00024 | - | Tensile testing | [37] | |
| Thin film | 0.3–0.7 | AFM | [38] | ||
| Film | - | 1–3 | AFM | [39] | |
| Hydrogel | 0.00006542 | - | Compression | [40] | |
| Sodium Alginate | Film | - | 0.0129 ± 0.0012 | Tensile testing | [41] |
| Hydrogel | 0.000015–0.000045 | - | AFM | [42] | |
| 3D-printed | - | - | AFM | [43] | |
| hydrogel | 0.00015–0.00055 | - | Nanoindentation | [44] | |
| film | 0.0456 ± 0.0041 | Tensile testing | [45] | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, R.L.C.G.; Ando, R.A.; Petri, D.F.S. Unveiling the Effect of Aqueous-Phase Dynamics on Chitosan Hydrogel Film Mechanical Properties Through AFM Nanoindentation and Tensile Testing. Gels 2025, 11, 496. https://doi.org/10.3390/gels11070496
da Silva RLCG, Ando RA, Petri DFS. Unveiling the Effect of Aqueous-Phase Dynamics on Chitosan Hydrogel Film Mechanical Properties Through AFM Nanoindentation and Tensile Testing. Gels. 2025; 11(7):496. https://doi.org/10.3390/gels11070496
Chicago/Turabian Styleda Silva, Rafael L. C. G., Rômulo Augusto Ando, and Denise F. S. Petri. 2025. "Unveiling the Effect of Aqueous-Phase Dynamics on Chitosan Hydrogel Film Mechanical Properties Through AFM Nanoindentation and Tensile Testing" Gels 11, no. 7: 496. https://doi.org/10.3390/gels11070496
APA Styleda Silva, R. L. C. G., Ando, R. A., & Petri, D. F. S. (2025). Unveiling the Effect of Aqueous-Phase Dynamics on Chitosan Hydrogel Film Mechanical Properties Through AFM Nanoindentation and Tensile Testing. Gels, 11(7), 496. https://doi.org/10.3390/gels11070496








