A Probabilistic Bag-to-Class Approach to Multiple-Instance Learning
Abstract
1. Introduction
1.1. Classification of Weakly Supervised Data
1.2. Multi-Instance Learning
1.3. Bag Density and Class Sparsity
1.4. A Probabilistic Bag-to-Class Approach to Multi-Instance Learning
- presenting the hierarchical model for general, non-standard MI assumptions (Section 3.3),
- introduction of bag-to-class dissimilarity measures (Section 3.5), and
- identification of two properties for bag-to-class divergence (Section 4.1).
2. Related Work and State-of-the-Art
3. Theoretical Background and Intuitions
3.1. Notation
- X: instance random vector
- C: class, either or
- B: bag
- : probability distribution
- : feature vector (instance) in set k,
- : set of feature vectors k of size
- : bag label
- : sample space for instances
- : sample space for positive instances
- : sample space for negative instances
- : sample space of positive bags
- : sample space of negative bags
- : posterior class probability, given instance sample
- : parameter random vector
- : parameter vector
- : probability distribution for instances in bag B
- : parameterized probability distribution of bag k
- : probability distribution for instances from the positive class
- : probability distribution for instances from the negative class
- : instance label
- : probability of positive instances
- : divergence from to
- : probability density function (PDF) for bag k
- : divergence from to
3.2. The Non-Vectorial Space of Probability Functions
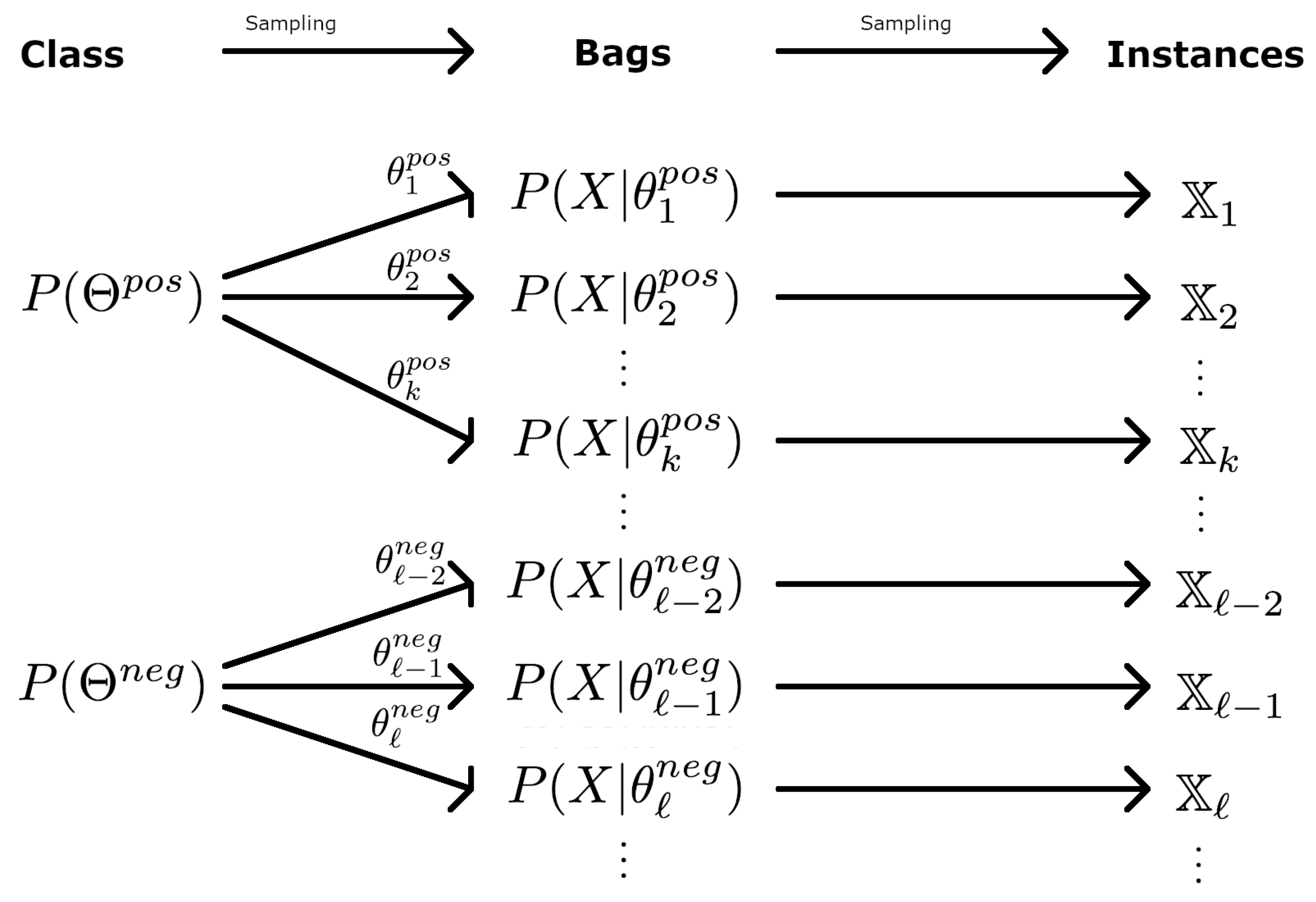
3.3. Hierarchical Distributions
- Step 1: Draw from , from , and from . These three parameters define the bag.
- Step 2: For , draw from , draw from if , and from otherwise.
3.4. Dissimilarities in MI Learning
- Equality and orthogonality: An f-divergence takes its minimum when the two probability functions are equal and its maximum when they are orthogonal. This means that two identical bags will have minimum dissimilarity between them, and that two bags without shared sample space will have maximum dissimilarity. A definition of orthogonal distributions can be found in [47].
- Monotonicity: The f-divergences possess a monotonicity property that can be thought of as an equivalent to the triangle property for distances: For a family of densities with monotone likelihood ratio, if , then . This is valid, e.g., for Gaussian densities with equal variance and mean . This means that if the distance between and is larger than the distance between and , the divergence is larger or equal. The f-divergences are not symmetric by definition, but some of them are.
3.5. Bag-to-Class Dissimilarity
4. Properties for Bag-Level Classification
4.1. Properties for Bag-to-Class Divergences
4.2. A Class-Conditional Dissimilarity for MI Classification
4.3. Bag-Level Divergence Classification
5. Experiments
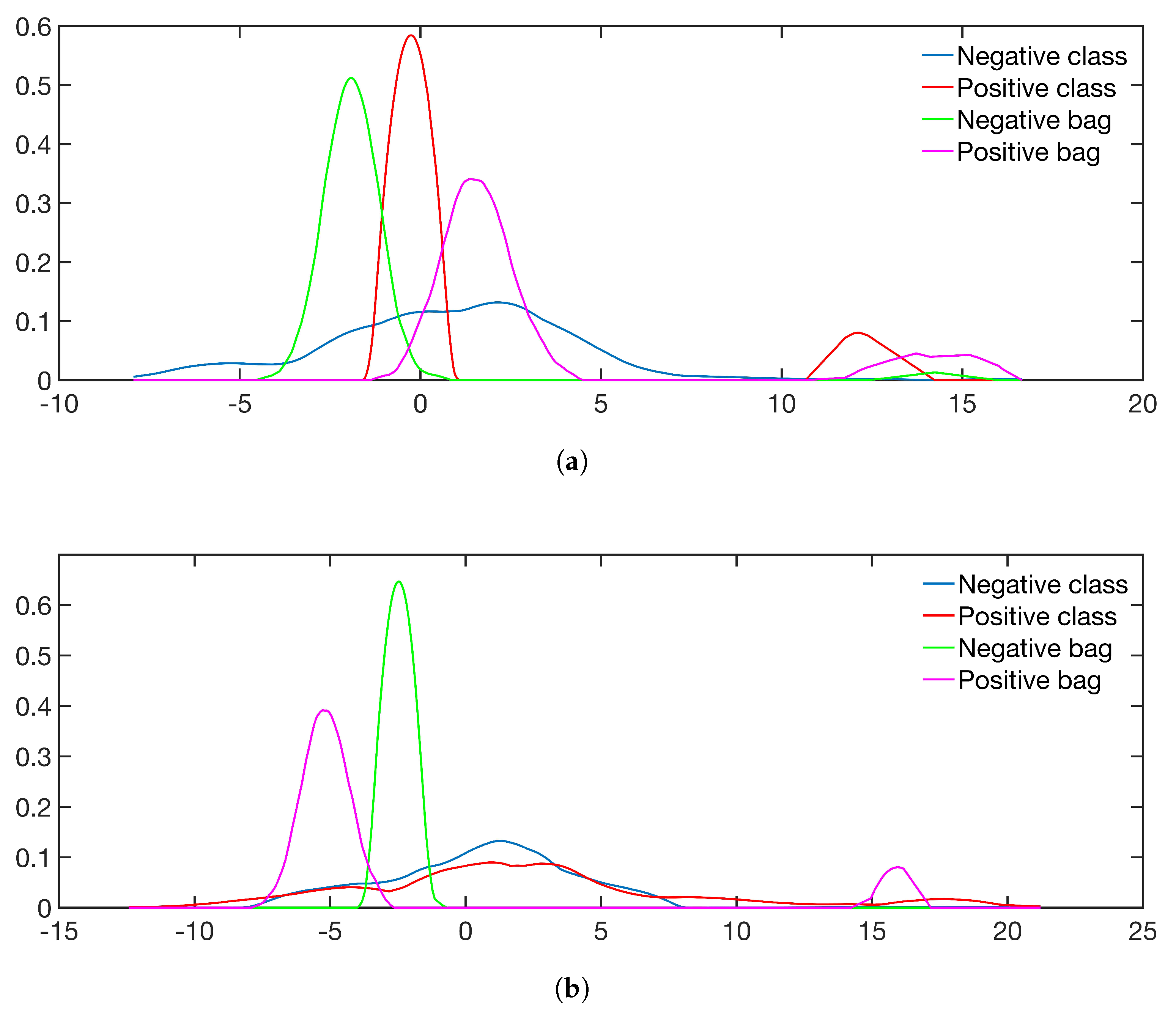
5.1. Simulated Data and Class Sparsity
- Sim 1: : No positive instances in negative bags.
- Sim 2: : Positive instances in negative bags.
- Sim 3: : Positive and negative instances have the same expectation of the mean, but unequal variance.
- Sim 4: : Positive instances are sampled from two distributions with unequal mean expectation.
5.2. The Impact of Pdf Estimation and Comparison to Other Methods
5.3. Comparison to State-of-the-Art Methods
- GMMs are fitted with components, and the number of components is chosen by minimum AIC. To save computation time, the number of components is estimated for 10 bags sampled from the training set. The median number of components is used to fit the bag PDFs in the rest of the algorithm, see Table 4. For the class PDFs, a random subsample of 10% of the instances is taken from each bag, to reduce computation time.
- Integrals: Importance sampling.
- Classification: To estimate the threshold, t, the training set is used to estimate and , and the divergences between the bags in the validation set and and are calculated. The threshold, , that gives the highest accuracy will then serve as threshold for the test set.
5.4. Results
6. Discussion
6.1. Point-of-View
6.2. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MI | multi-instance |
| probability density function | |
| IS | instance space |
| ES | embedded space |
| BS | bag space |
| KL | Kullback–Leibler |
| SVM | support vector machine |
| AIC | Akaike Information Criterion |
| GMM | Gaussian mixture models |
| KDE | kernel density estimation |
| ROC | receiver operating characteristic |
| AUC | area under the ROC curve |
Appendix A
Appendix A.1. Non-Symmetric Divergences
Appendix A.2. Class-Conditional Bag-to-Class Divergence
References
- Cheplygina, V.; de Bruijne, M.; Pluim, J.P. Not-so-supervised: A survey of semi-supervised, multi-instance, and transfer learning in medical image analysis. Med. Image Anal. 2019, 54, 280–296. [Google Scholar] [CrossRef]
- Gelasca, E.D.; Byun, J.; Obara, B.; Manjunath, B.S. Evaluation and Benchmark for Biological Image Segmentation. In Proceedings of the IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 1816–1819. [Google Scholar] [CrossRef]
- Kandemir, M.; Zhang, C.; Hamprecht, F.A. Empowering Multiple Instance Histopathology Cancer Diagnosis by Cell Graphs. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention—MICCAI 2014, Boston, MA, USA, 14–18 September 2014; pp. 228–235. [Google Scholar] [CrossRef]
- Doran, G.; Ray, S. Multiple-Instance Learning from Distributions. J. Mach. Learn. Res. 2016, 17, 1–50. [Google Scholar]
- Zhang, M.L.; Zhou, Z.H. Multi-instance clustering with applications to multi-instance prediction. Appl. Intell. 2009, 31, 47–68. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Zhang, M.L.; Huang, S.J.; Li, Y.F. Multi-instance multi-label learning. Artif. Intell. 2012, 176, 2291–2320. [Google Scholar] [CrossRef]
- Tang, P.; Wang, X.; Huang, Z.; Bai, X.; Liu, W. Deep patch learning for weakly supervised object classification and discovery. Pattern Recognit. 2017, 71, 446–459. [Google Scholar] [CrossRef]
- Wang, X.; Yan, Y.; Tang, P.; Bai, X.; Liu, W. Revisiting multiple instance neural networks. Pattern Recognit. 2018, 74, 15–24. [Google Scholar] [CrossRef]
- Dietterich, T.G.; Lathrop, R.H.; Lozano-Pérez, T. Solving the multiple instance problem with axis-parallel rectangles. Artif. Intell. 1997, 89, 31–71. [Google Scholar] [CrossRef]
- Xu, Y.Y. Multiple-instance learning based decision neural networks for image retrieval and classification. Neurocomputing 2016, 171, 826–836. [Google Scholar] [CrossRef]
- Qiao, M.; Liu, L.; Yu, J.; Xu, C.; Tao, D. Diversified dictionaries for multi-instance learning. Pattern Recognit. 2017, 64, 407–416. [Google Scholar] [CrossRef]
- Weidmann, N.; Frank, E.; Pfahringer, B. A Two-Level Learning Method for Generalized Multi-instance Problems. In Proceedings of the European Conference on Machine Learning, Cavtat-Dubrovnik, Croatia, 22–26 September 2003; pp. 468–479. [Google Scholar] [CrossRef]
- Foulds, J.; Frank, E. A review of multi-instance learning assumptions. Knowl. Eng. Rev. 2010, 25, 1–25. [Google Scholar] [CrossRef]
- Cheplygina, V.; Tax, D.M.J.; Loog, M. Multiple Instance Learning with Bag Dissimilarities. Pattern Recognit. 2015, 48, 264–275. [Google Scholar] [CrossRef]
- Amores, J. Multiple Instance Classification: Review, Taxonomy and Comparative Study. Artif. Intell. 2013, 201, 81–105. [Google Scholar] [CrossRef]
- Carbonneau, M.A.; Cheplygina, V.; Granger, E.; Gagnon, G. Multiple Instance Learning: A survey of Problem Characteristics and Applications. Pattern Recognit. 2018, 77, 329–353. [Google Scholar] [CrossRef]
- Maron, O.; Lozano-Pérez, T. A framework for multiple-instance learning. In Advances in Neural Information Processing Systems, Denver, CO, USA, 30 November–5 December 1998; MIT Press: Cambridge, MA, USA, 1998; Volume 10, pp. 570–576. [Google Scholar]
- Xu, X.; Frank, E. Logistic Regression and Boosting for Labeled Bags of Instances; Lecture Notes in Computer Science; Dai, H., Srikant, R., Zhang, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 272–281. [Google Scholar] [CrossRef]
- Tax, D.M.J.; Loog, M.; Duin, R.P.W.; Cheplygina, V.; Lee, W.J. Bag Dissimilarities for Multiple Instance Learning. In Similarity-Based Pattern Recognition; Lecture Notes in Computer Science; Pelillo, M., Hancock, E.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 7005, pp. 222–234. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Sun, Y.Y.; Li, Y.F. Multi-instance Learning by Treating Instances As non-I.I.D. Samples. In Proceedings of the 26th Annual International Conference on Machine Learning—ICML ’09, Montreal, QC, Canada, 14–18 June 2009; pp. 1249–1256. [Google Scholar] [CrossRef]
- Cheplygina, V.; Tax, D.M.J.; Loog, M. Dissimilarity-Based Ensembles for Multiple Instance Learning. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1379–1391. [Google Scholar] [CrossRef]
- Boiman, O.; Shechtman, E.; Irani, M. In defense of Nearest-Neighbor based image classification. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Lee, W.J.; Cheplygina, V.; Tax, D.M.J.; Loog, M.; Duin, R.P.W. Bridging structure and feature representations in graph matching. Int. J. Patten Recognit. Artif. Intell. 2012, 26, 1260005. [Google Scholar] [CrossRef]
- Scott, S.; Zhang, J.; Brown, J. On generalized multiple-instance learning. Int. J. Comput. Intell. Appl. 2005, 5, 21–35. [Google Scholar] [CrossRef]
- Ruiz-Muñoz, J.F.; Castellanos-Dominguez, G.; Orozco-Alzate, M. Enhancing the dissimilarity-based classification of birdsong recordings. Ecol. Inform. 2016, 33, 75–84. [Google Scholar] [CrossRef]
- Sørensen, L.; Loog, M.; Tax, D.M.J.; Lee, W.J.; de Bruijne, M.; Duin, R.P.W. Dissimilarity-Based Multiple Instance Learning. In Structural, Syntactic, and Statistical Pattern Recognition; Hancock, E.R., Wilson, R.C., Windeatt, T., Ulusoy, I., Escolano, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 129–138. [Google Scholar] [CrossRef]
- Schölkopf, B. The Kernel Trick for Distances. In Proceedings of the 13th International Conference on Neural Information Processing Systems, Denver, CO, USA, 27 November–2 December 2000; MIT Press: Cambridge, MA, USA, 2000; pp. 283–289. [Google Scholar]
- Wei, X.S.; Wu, J.; Zhou, Z.H. Scalable Algorithms for Multi-Instance Learning. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 975–987. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Sahu, S.K.; Cheng, R.C.H. A fast distance-based approach for determining the number of components in mixtures. Can. J. Stat. 2003, 31, 3–22. [Google Scholar] [CrossRef]
- Sudharshan, P.; Petitjean, C.; Spanhol, F.; Oliveira, L.E.; Heutte, L.; Honeine, P. Multiple instance learning for histopathological breast cancer image classification. Expert Syst. Appl. 2019, 117, 103–111. [Google Scholar] [CrossRef]
- Zhang, G.; Yin, J.; Li, Z.; Su, X.; Li, G.; Zhang, H. Automated skin biopsy histopathological image annotation using multi-instance representation and learning. BMC Med. Genom. 2013, 6, S10. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, W.; Zhang, J.; McKenna, S.J. Multiple instance cancer detection by boosting regularised trees. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Basel, Switzerland, 2015; Volume 9349, pp. 645–652. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Ilse, M.; Welling, M. Deep Learning with Permutation-invariant Operator for Multi-instance Histopathology Classification. arXiv 2017, arXiv:1712.00310. [Google Scholar]
- Mercan, C.; Aksoy, S.; Mercan, E.; Shapiro, L.G.; Weaver, D.L.; Elmore, J.G. Multi-Instance Multi-Label Learning for Multi-Class Classification of Whole Slide Breast Histopathology Images. IEEE Trans. Med. Imaging 2018, 37, 316–325. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, J.Y.; Chang, E.I.; Lai, M.; Tu, Z. Weakly supervised histopathology cancer image segmentation and classification. Med. Image Anal. 2014, 18, 591–604. [Google Scholar] [CrossRef] [PubMed]
- McCann, M.T.; Bhagavatula, R.; Fickus, M.C.; Ozolek, J.A.; Kovaĉević, J. Automated colitis detection from endoscopic biopsies as a tissue screening tool in diagnostic pathology. In Proceedings of the 2012 19th IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 2809–2812. [Google Scholar] [CrossRef]
- Dundar, M.M.; Badve, S.; Raykar, V.C.; Jain, R.K.; Sertel, O.; Gurcan, M.N. A multiple instance learning approach toward optimal classification of pathology slides. In Proceedings of the International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2732–2735. [Google Scholar] [CrossRef]
- Samsudin, N.A.; Bradley, A.P. Nearest neighbour group-based classification. Pattern Recognit. 2010, 43, 3458–3467. [Google Scholar] [CrossRef]
- Kraus, O.Z.; Ba, J.L.; Frey, B.J. Classifying and segmenting microscopy imageswith deep multiple instance learning. Bioinformatics 2016, 32, i52–i59. [Google Scholar] [CrossRef]
- Hou, L.; Samaras, D.; Kurc, T.M.; Gao, Y.; Davis, J.E.; Saltz, J.H. Efficient Multiple Instance Convolutional Neural Networks for GigapixelResolution Image Classification. arXiv 2015, arXiv:1504.07947. [Google Scholar]
- Jia, Z.; Huang, X.; Chang, E.I.; Xu, Y. Constrained Deep Weak Supervision for Histopathology Image Segmentation. IEEE Trans. Med. Imaging 2017, 36, 2376–2388. [Google Scholar] [CrossRef]
- Jiang, B.; Pei, J.; Tao, Y.; Lin, X. Clustering Uncertain Data Based on Probability Distribution Similarity. IEEE Trans. Knowl. Data Eng. 2013, 25, 751–763. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Pfeifle, M. Density-based Clustering of Uncertain Data. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery in Data Mining KDD ’05, Chicago, IL, USA, 21–24 August 2005; pp. 672–677. [Google Scholar] [CrossRef]
- Ali, S.M.; Silvey, S.D. A General Class of Coefficients of Divergence of One Distribution from Another. J. R. Stat. Soc. Ser. B (Methodol.) 1966, 28, 131–142. [Google Scholar] [CrossRef]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observations. Studia Scientiarum Mathematicarum Hungarica 1967, 2, 299–318. [Google Scholar]
- Berger, A. On orthogonal probability measures. Proc. Am. Math. Soc. 1953, 4, 800–806. [Google Scholar] [CrossRef]
- Gibbs, A.L.; Su, F.E. On Choosing and Bounding Probability Metrics. Int. Stat. Rev. 2002, 70, 419–435. [Google Scholar] [CrossRef]
- Møllersen, K.; Dhar, S.S.; Godtliebsen, F. On Data-Independent Properties for Density-Based Dissimilarity Measures in Hybrid Clustering. Appl. Math. 2016, 07, 1674–1706. [Google Scholar] [CrossRef]
- Møllersen, K.; Hardeberg, J.Y.; Godtliebsen, F. Divergence-based colour features for melanoma detection. In Proceedings of the 2015 Colour and Visual Computing Symposium (CVCS), Gjøvik, Norway, 25–26 August 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Eguchi, S.; Copas, J. Interpreting Kullback-Leibler Divergence with the Neyman-Pearson Lemma. J. Multivar. Anal. 2006, 97, 2034–2040. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Taneja, I.J.; Kumar, P. Generalized non-symmetric divergence measures and inequaities. J. Interdiscip. Math. 2006, 9, 581–599. [Google Scholar] [CrossRef]
- McLachlan, G.; Peel, D. Finite Mixture Models; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar] [CrossRef]
- Sheather, S.J.; Jones, M.C. A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation. J. R. Stat. Soc. Ser. B (Methodol.) 1991, 53, 683–690. [Google Scholar] [CrossRef]
- Wei, X.S.; Zhou, Z.H. An empirical study on image bag generators for multi-instance learning. Mach. Learn. 2016, 105, 155–198. [Google Scholar] [CrossRef]
- Andrews, S.; Andrews, S.; Tsochantaridis, I.; Hofmann, T. Support vector machines for multiple-instance learning. Adv. Neural Inf. Process. Syst. 2003, 15, 561–568. [Google Scholar]
- Venkatesan, R.; Chandakkar, P.; Li, B. Simpler Non-Parametric Methods Provide as Good or Better Results to Multiple-Instance Learning. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Sun, M.; Han, T.X.; Liu, M.-C.; Khodayari-Rostamabad, A. Multiple Instance Learning Convolutional Neural Networks for object recognition. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 3270–3275. [Google Scholar] [CrossRef]



| Bags | : 5 | : 10 | : 25 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sim: | : | |||||||||
| 1 | 61 | 69 | 85 | 62 | 72 | 89 | 61 | 73 | 92 | |
| 1 | 5 | 63 | 75 | 86 | 64 | 82 | 94 | 68 | 84 | 97 |
| 10 | 69 | 86 | 87 | 73 | 91 | 95 | 75 | 91 | 98 | |
| 1 | 57 | 61 | 75 | 59 | 61 | 78 | 58 | 55 | 75 | |
| 2 | 5 | 59 | 67 | 79 | 60 | 68 | 84 | 62 | 63 | 85 |
| 10 | 64 | 77 | 80 | 66 | 78 | 86 | 68 | 72 | 86 | |
| 1 | 51 | 55 | 71 | 52 | 58 | 73 | 50 | 57 | 74 | |
| 3 | 5 | 53 | 61 | 76 | 53 | 66 | 81 | 52 | 65 | 83 |
| 10 | 58 | 73 | 78 | 58 | 76 | 84 | 57 | 76 | 87 | |
| 1 | 55 | 61 | 70 | 56 | 62 | 73 | 56 | 58 | 69 | |
| 4 | 5 | 56 | 63 | 75 | 57 | 64 | 81 | 59 | 59 | 80 |
| 10 | 60 | 74 | 77 | 62 | 76 | 85 | 63 | 69 | 84 | |
| 1 | 64 | 61 | 62 | 67 | 63 | 66 | 64 | 62 | 67 | |
| 5 | 5 | 73 | 69 | 63 | 74 | 70 | 67 | 75 | 71 | 72 |
| 10 | 74 | 70 | 62 | 75 | 73 | 69 | 76 | 74 | 72 | |
| 1 | 68 | 68 | 67 | 66 | 68 | 68 | 68 | 71 | 68 | |
| 6 | 5 | 65 | 64 | 67 | 68 | 68 | 69 | 70 | 71 | 74 |
| 10 | 66 | 64 | 66 | 70 | 69 | 72 | 72 | 73 | 74 | |
| KDE (Epan.) | KDE (Gauss.) | GMMs | |
|---|---|---|---|
| 90 | 92 | 94 | |
| 82 | 92 | 96 |
| Method | AUC |
|---|---|
| 94 | |
| 96 | |
| DEEPISR-MIL [34] | 90 |
| Li et al. [33] | 93 |
| GPMIL [3] | 86 |
| RGPMIL [3] | 90 |
| Data Set | ||||
|---|---|---|---|---|
| Dimension | 23 | 26 | 25 | 24 |
| Rep 1 | 66 | 55 | 52 | 70 |
| Rep 2 | 58 | 49 | 69 | 71 |
| Rep 3 | 59 | 50 | 50 | 70 |
| Rep 4 | 47 | 49 | 58 | 73 |
| Rep 5 | 63 | 59 | 72 | 74 |
| Data Set (Magnification) | ||||
|---|---|---|---|---|
| MI-SVM poly [57] | 86.2 (2.8) | 82.8 (4.8) | 81.7 (4.4) | 82.7 (3.8) |
| Non-parametric [58] | 87.8 (5.6) | 85.6 (4.3) | 80.8 (2.8) | 82.9 (4.1) |
| MILCNN [59] | 86.1 (4.2) | 83.8 (3.1) | 80.2 (2.6) | 80.6 (4.6) |
| CNN [31] | 85.6 (4.8) | 83.5 (3.9) | 83.1 (1.9) | 80.8 (3.0) |
| SVM [31] | 79.9 (3.7) | 77.1 (5.5) | 84.2 (1.6) | 81.2 (3.6) |
| rKL | 83.4 (4.1) | 84.9 (4.2) | 88.3 (3.6) | 84.0 (2.8) |
| cKL | 81.5 (3.2) | 85.2 (3.5) | 88.1 (3.6) | 85.0 (3.5) |
| Data Set (Magnification) | ||||
|---|---|---|---|---|
| rKL | 91.4 (2.4) | 91.3 (2.2) | 94.4 (1.9) | 91.6 (1.7) |
| cKL | 88.4 (2.6) | 89.7 (1.6) | 91.9 (2.7) | 91.7 (2.4) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Møllersen, K.; Hardeberg, J.Y.; Godtliebsen, F. A Probabilistic Bag-to-Class Approach to Multiple-Instance Learning. Data 2020, 5, 56. https://doi.org/10.3390/data5020056
Møllersen K, Hardeberg JY, Godtliebsen F. A Probabilistic Bag-to-Class Approach to Multiple-Instance Learning. Data. 2020; 5(2):56. https://doi.org/10.3390/data5020056
Chicago/Turabian StyleMøllersen, Kajsa, Jon Yngve Hardeberg, and Fred Godtliebsen. 2020. "A Probabilistic Bag-to-Class Approach to Multiple-Instance Learning" Data 5, no. 2: 56. https://doi.org/10.3390/data5020056
APA StyleMøllersen, K., Hardeberg, J. Y., & Godtliebsen, F. (2020). A Probabilistic Bag-to-Class Approach to Multiple-Instance Learning. Data, 5(2), 56. https://doi.org/10.3390/data5020056







