Handling Data Gaps in Reported Field Measurements of Short Rotation Forestry
Abstract
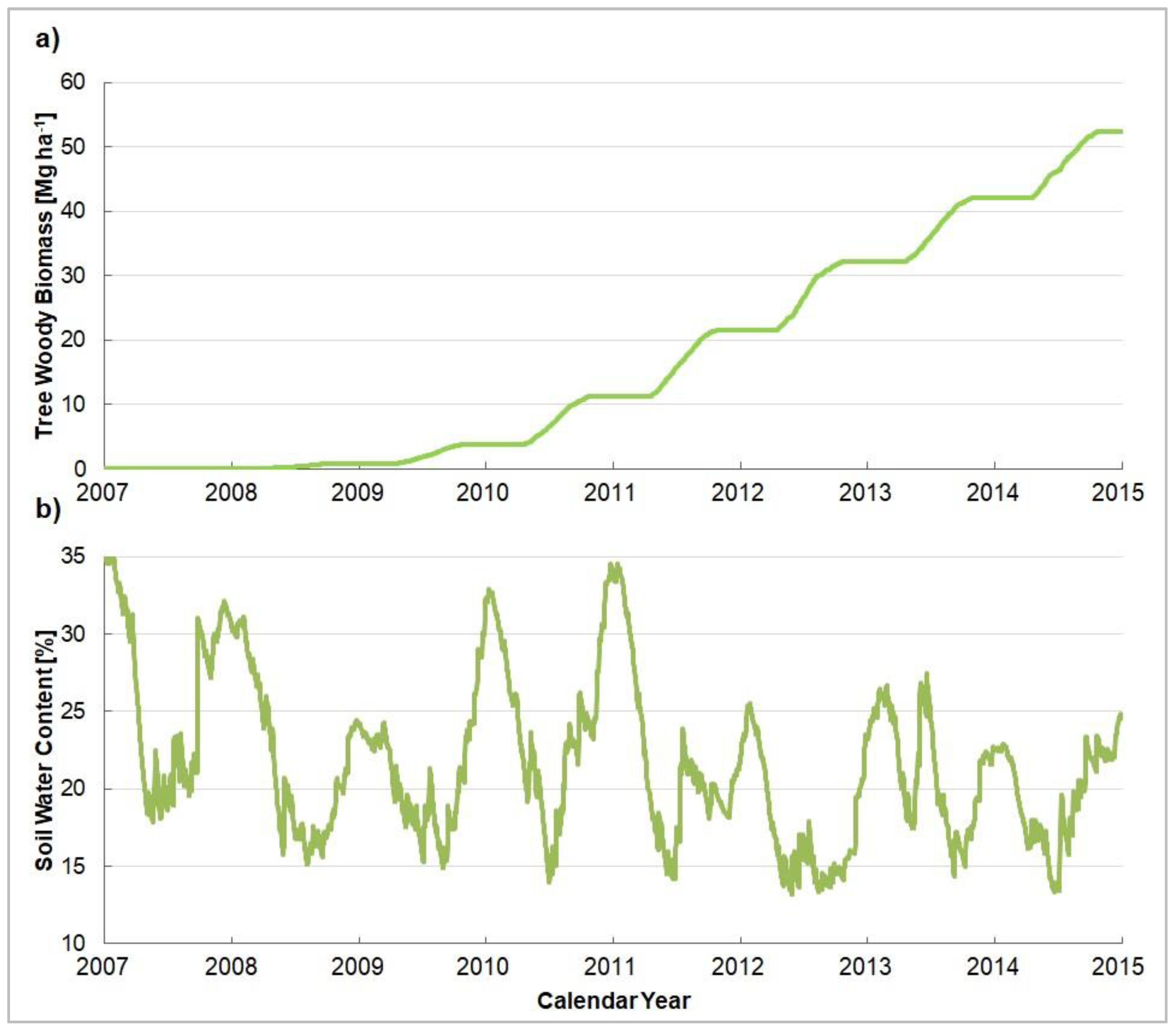
:1. Background and Summary
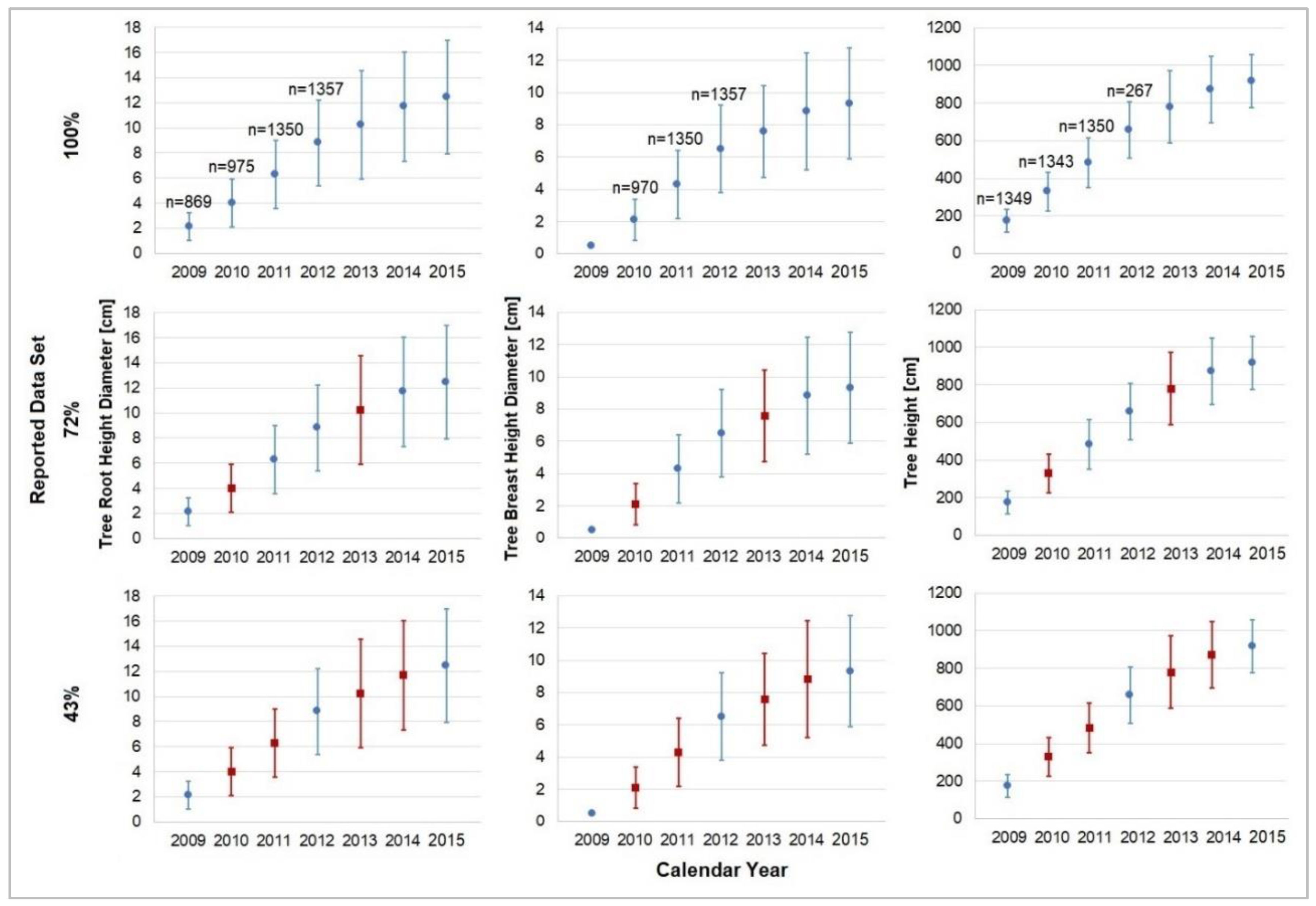
2. Data Description
3. Methods
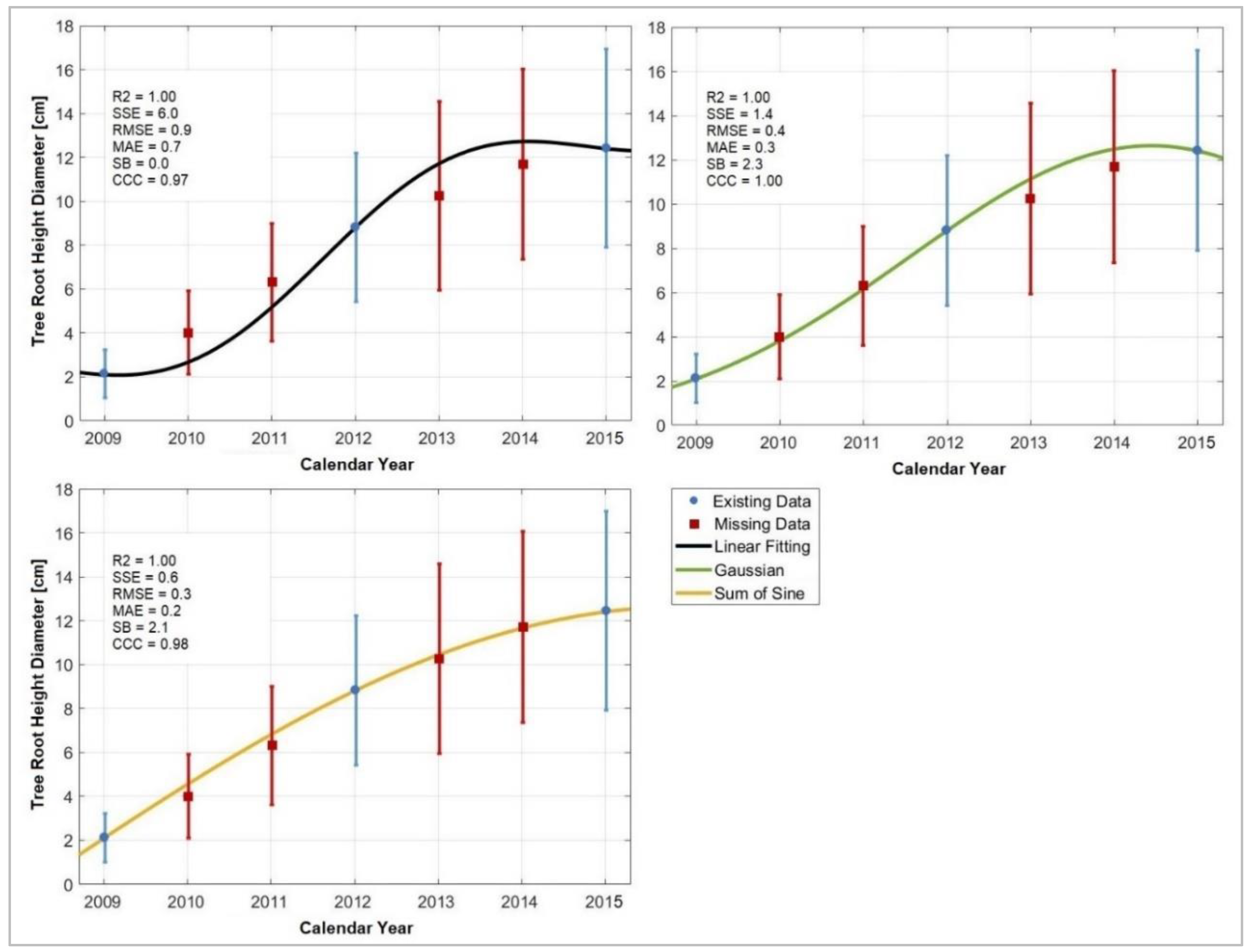
3.1. Regression Analysis
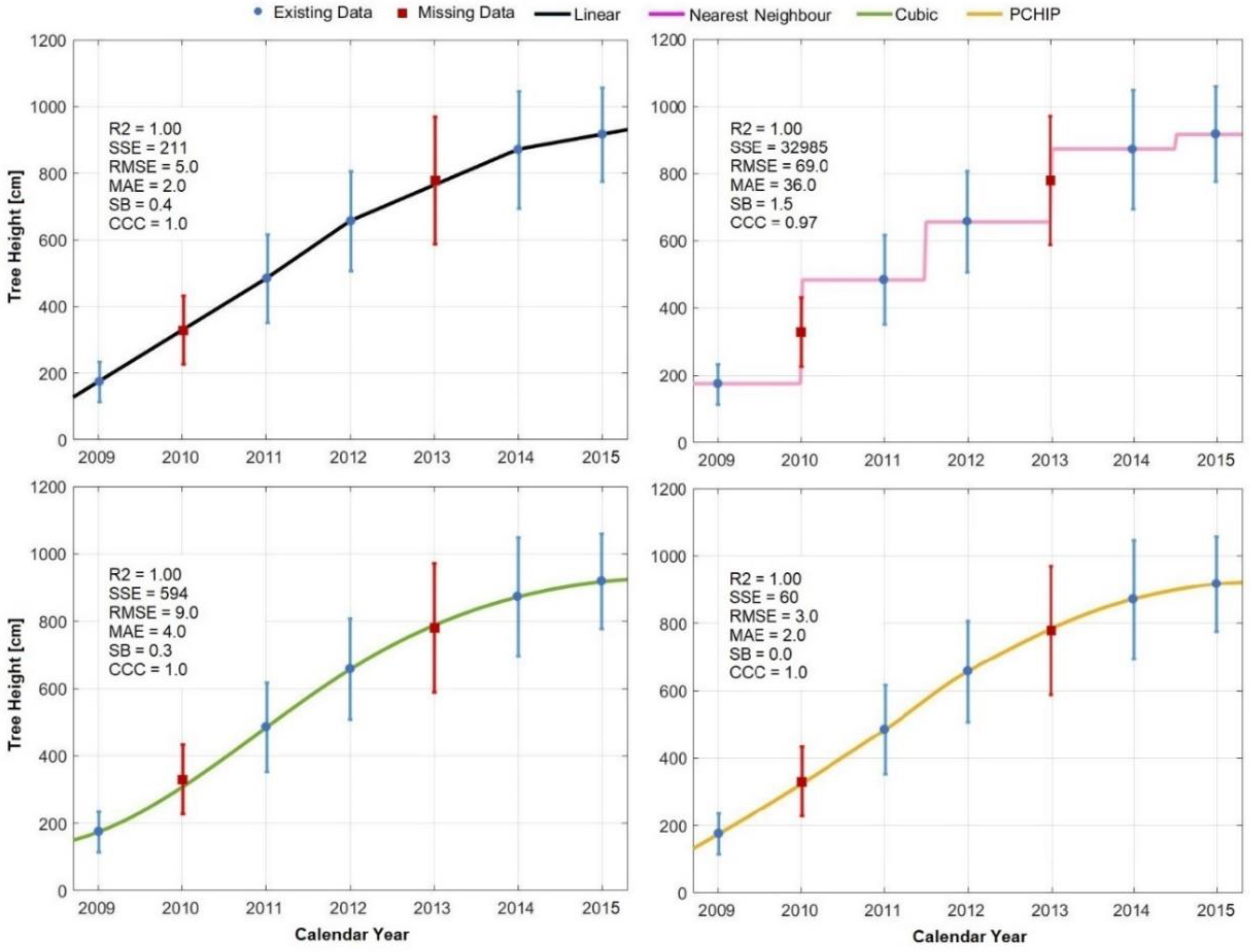
3.2. Interpolation
3.3. Multiple Imputation
3.4. Forest Growth Functions
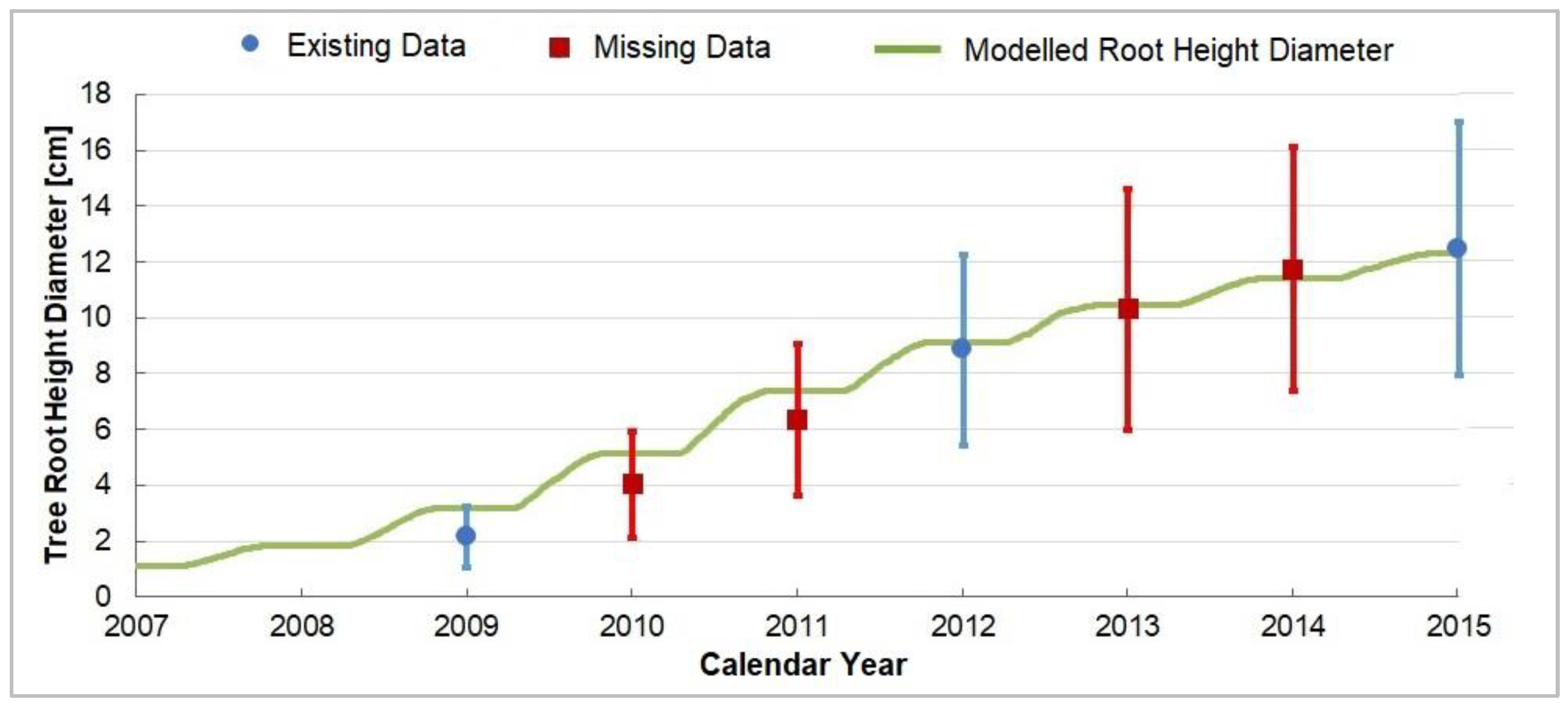
3.5. Process-Oriented Tree Growth Model
3.6. Statistical Analysis
4. Results and Discussion
4.1. Regression Analysis
4.2. Interpolation
4.3. Multiple Imputation
4.4. Forest Growth Functions
4.5. Process-Oriented Growth Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BHD | breast height diameter |
| H | height |
| MAR | missing at random |
| MCAR | missing completely at random |
| RHD | root height diameter |
| SRF | short rotation forestry |
Appendix A
| Symbol | Description | Unit | Value | Source |
|---|---|---|---|---|
| nShoots0 | Initial number of shoots per tree | tree−1 | 1.0 | Own data |
| Bt0 | Initial tree biomass | g tree−1 | 40 | [38] |
| LAt0 | Initial tree leaf area | m2 tree−1 | 0.0 | [28,29] |
| εt | Radiation use efficiency | g MJ−1 | 1.04 | Own data |
| Kt | Light extinction coefficient | – | 0.5 | Own data |
| tt | The number of days after budburst at which the leaf area has reached 63.2% of its maximum leaf area LAssmax | d | 10 | [28,29] |
| LAssmax | Maximum leaf area for a single shoot | m2 | 0.05 | [28,29] |
| nShootsmax | Maximum number of shoots per tree | tree−1 | 10,000 | [28,29] |
| Kmain | Relative attrition rate of tree biomass | d−1 | 10−4 | [28,29] |
| γt | Transpiration coefficient of the trees | m3 g−1 | 0.0002 | [38] |
| (pFcrit)t | Critical pF value for trees | log (cm) | 4.0 | [29] |
| (pFpwp)t | pF value at permanent wilting point | log (cm) | 4.2 | [29] |
| DOYbudburst, DOYleaffall | Day of year for budburst and leaffall | DOY | 105, 300 | [38] |
| ρt | Planting density | trees ha−1 | 2200 | [14] |
| θ0 | Initial volumetric water content | m3 m−3 | 0.35 | [34] |
| δeva | Potential evaporation per unit energy | mm MJ−1 | 0.15 | [29] |
| D | Depth of the soil compartment | mm | 1000 | [34] |
| α | Van Genuchten parameter | – | 0.0083 | [34] |
| nsoil | Van Genuchten parameter | – | 1.2539 | [34] |
| δ | Parameter affecting the drainage rate below the root zone | – | 0.07 | [34] |
| PWP | Permanent wilting point | log (cm) | 4.2 | [28,29] |
| (pFcrit)E | Critical pF value for evaporation | log (cm) | 2.3 | [28,29] |
| pFFC | Water tension at field capacity | log (cm) | 2.3 | [28,29] |
| Ks | Soil hydraulic conductivity at saturation | mm d−1 | 2.272 | [34] |
| θs | Saturated volumetric water content | m3 m−3 | 0.43 | [34] |
| θr | Residual volumetric water content | m3 m−3 | 0.01 | [34] |
| Model | Variable | Data Gap Representation | R2 | SSE | RMSE | MAE | SB [%] | CCC | Label |
|---|---|---|---|---|---|---|---|---|---|
| Exponential | RHD | 72 | 0.90 | 10.3 | 1.2 | 1.1 | 1.0 | 0.93 | Acceptable |
| 43 | −3.31 * | 534.3 | 8.7 | 7.9 | na | na | Na | ||
| BHD | 72 | −3.32 * | 287.1 | 6.4 | 5.6 | na | na | Na | |
| 43 | −2.19 * | 287.1 | 6.4 | 5.6 | na | na | Na | ||
| Height | 72 | 0.90 | 51,868 | 86 | 78 | 0.7 | 0.94 | Satisfactory | |
| 43 | −3.58 * | 3,013,195 | 656 | 602 | na | na | Na | ||
| BHD & RHD | 72 | 0.97 | 2.4 | 0.6 | 0.5 | 1.3 | 0.99 | Very good | |
| 43 | 0.97 | 2.8 | 0.6 | 0.5 | 2.7 | 0.98 | Satisfactory | ||
| Height & BHD | 72 | 0.93 | 4.0 | 0.8 | 0.6 | 1.9 | 0.97 | Poor | |
| 43 | 0.92 | 4.1 | 0.8 | 0.6 | 1.0 | 0.95 | Satisfactory | ||
| Height & RHD | 72 | 0.96 | 3.0 | 0.7 | 0.5 | 0.3 | 0.99 | Very good | |
| 43 | 0.96 | 3.0 | 0.7 | 0.5 | 1.4 | 0.99 | Satisfactory | ||
| Fourier | RHD | 72 | 1.00 | 0.3 | 0.2 | 0.2 | 0.3 | 0.99 | Very good |
| 43 | na | na | na | na | na | na | Na | ||
| BHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.5 | 0.99 | Satisfactory | |
| 43 | na | na | na | na | na | na | Na | ||
| Height | 72 | 1.00 | 185 | 5.0 | 5.0 | 0.0 | 1.00 | Very good | |
| 43 | na | na | na | na | na | na | Na | ||
| BHD & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 1.4 | 1.00 | Very good | |
| 43 | na | na | na | na | na | na | Na | ||
| Height & BHD | 72 | 1.00 | 0.2 | 0.1 | 0.1 | 1.4 | 0.99 | Satisfactory | |
| 43 | na | na | na | na | na | na | Na | ||
| Height & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.2 | 1.00 | Very good | |
| 43 | na | na | na | na | na | na | Na | ||
| Gauss | RHD | 72 | 0.99 | 0.4 | 0.2 | 0.2 | 0.1 | 0.99 | Very good |
| 43 | 1.00 | 1.4 | 0.4 | 0.3 | 2.3 | 1.00 | Very good | ||
| BHD | 72 | 0.98 | 1.2 | 0.4 | 0.4 | 2.9 | 0.99 | Very good | |
| 43 | 1.00 | 7.1 | 1.0 | 0.7 | 5.5 | 0.96 | Acceptable | ||
| Height | 72 | 1.00 | 1627 | 15 | 15 | 0.3 | 1.00 | Very good | |
| 43 | 1.00 | 4578 | 26 | 18 | 1.1 | 1.00 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.4 | 0.2 | 0.2 | 1.4 | 1.00 | Very good | |
| 43 | 1.00 | 0.6 | 0.3 | 0.2 | 1.7 | 0.99 | Satisfactory | ||
| Height & BHD | 72 | 0.99 | 0.8 | 0.3 | 0.3 | 2.0 | 0.99 | Very good | |
| 43 | 1.00 | 1.9 | 0.5 | 0.4 | 0.6 | 0.98 | Acceptable | ||
| Height & RHD | 72 | 1.00 | 0.3 | 0.2 | 0.2 | 0.2 | 1.00 | Very good | |
| 43 | 1.00 | 0.4 | 0.3 | 0.2 | 0.1 | 1.00 | Very good | ||
| Power: one term | RHD | 72 | na | na | na | na | na | na | Na |
| 43 | na | na | na | na | na | na | Na | ||
| BHD | 72 | na | na | na | na | na | na | Na | |
| 43 | na | na | na | na | na | na | Na | ||
| Height | 72 | na | na | na | na | na | na | Na | |
| 43 | na | na | na | na | na | na | Na | ||
| BHD & RHD | 72 | 0.98 | 1.2 | 0.4 | 0.3 | 1.8 | 0.99 | Very good | |
| 43 | 0.99 | 1.6 | 0.5 | 0.4 | 1.8 | 1.00 | Satisfactory | ||
| Height & BHD | 72 | 0.99 | 0.7 | 0.3 | 0.3 | 2.1 | 0.99 | Acceptable | |
| 43 | 0.99 | 0.7 | 0.3 | 0.3 | 1.2 | 0.99 | Satisfactory | ||
| Height & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.2 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.0 | 1.00 | Very good | ||
| Power: two terms | RHD | 72 | 0.98 | 2.5 | 0.6 | 0.6 | 1.3 | 0.99 | Satisfactory |
| 43 | 0.97 | 2.6 | 0.6 | 0.6 | 2.2 | 0.98 | Very good | ||
| BHD | 72 | 0.96 | 2.4 | 0.6 | 0.5 | 0.0 | 0.98 | Acceptable | |
| 43 | 0.96 | 2.6 | 0.6 | 0.6 | 2.7 | 0.96 | Satisfactory | ||
| Height | 72 | 0.97 | 12,883 | 43 | 38 | 1.0 | 0.99 | Very good | |
| 43 | 0.97 | 15,558 | 47 | 41 | 3.1 | 0.98 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.2 | 0.1 | 0.1 | 1.4 | 1.00 | Very good | |
| 43 | 1.00 | 0.2 | 0.2 | 0.1 | 1.0 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.5 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.4 | 0.2 | 0.1 | 2.5 | 0.98 | Acceptable | ||
| Height & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.2 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.1 | 1.00 | Very good | ||
| Rational | RHD | 72 | 1.00 | 0.8 | 0.3 | 0.3 | 0.3 | 0.99 | Satisfactory |
| 43 | 1.00 | 1.5 | 0.5 | 0.3 | 2.3 | 0.99 | Acceptable | ||
| BHD | 72 | 0.99 | 0.8 | 0.3 | 0.3 | 1.5 | 0.98 | Poor | |
| 43 | 1.00 | 1.7 | 0.5 | 0.3 | 4.0 | 0.98 | Poor | ||
| Height | 72 | 0.00 | 479,485 | 262 | 231 | 3.1 | 0.00 | Poor | |
| 43 | 0.00 | 480,081 | 262 | 236 | 3.2 | 0.00 | Poor | ||
| BHD & RHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.2 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 0.0 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.5 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.3 | 0.2 | 0.1 | 2.4 | 0.99 | Acceptable | ||
| Height & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.2 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.2 | 1.00 | Very good | ||
| Sum of Sine | RHD | 72 | 1.00 | 0.4 | 0.2 | 0.2 | 0.3 | 0.99 | Very good |
| 43 | 1.00 | 0.6 | 0.3 | 0.2 | 2.1 | 0.99 | Satisfactory | ||
| BHD | 72 | 1.00 | 0.3 | 0.2 | 0.2 | 1.5 | 0.98 | Acceptable | |
| 43 | 1.00 | 0.6 | 0.3 | 0.2 | 3.5 | 0.98 | Acceptable | ||
| Height | 72 | 1.00 | 921 | 11 | 11 | 0.0 | 1.00 | Very good | |
| 43 | 1.00 | 1421 | 14 | 9.0 | 0.9 | 1.00 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.3 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 0.0 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.5 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.3 | 0.2 | 0.1 | 2.2 | 0.99 | Satisfactory | ||
| Height & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.2 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.2 | 1.00 | Very good | ||
| Linear Fit | RHD | 72 | 0.98 | 1.0 | 0.4 | 0.3 | 1.0 | 0.99 | Very good |
| 43 | 1.00 | 6.0 | 0.9 | 0.7 | 0.0 | 0.97 | Poor | ||
| BHD | 72 | 0.98 | 1.2 | 0.4 | 0.4 | 0.6 | 0.99 | Very good | |
| 43 | 1.00 | 7.1 | 1.0 | 0.8 | 3.5 | 0.98 | Poor | ||
| Height | 72 | 0.99 | 6198 | 30 | 27 | 0.6 | 0.99 | Satisfactory | |
| 43 | 1.00 | 33,105 | 69 | 51 | 1.1 | 0.97 | Poor | ||
| BHD & RHD | 72 | 0.95 | 6.4 | 1.0 | 0.8 | 3.9 | 0.97 | Poor | |
| 43 | 1.00 | 6552.4 | 30.6 | 21.3 | 45.1 | −0.03 | Poor | ||
| Height & BHD | 72 | 0.97 | 1.8 | 0.5 | 0.4 | 2.0 | 0.98 | Acceptable | |
| 43 | 1.00 | 65.9 | 3.1 | 2.2 | 17.6 | 0.55 | Poor | ||
| Height & RHD | 72 | 0.98 | 1.7 | 0.5 | 0.4 | 0.4 | 0.99 | Satisfactory | |
| 43 | 1.00 | 60.3 | 2.9 | 2.1 | 11.6 | 0.68 | Poor | ||
| Polynomial: first degree | RHD | 72 | 0.98 | 2.6 | 0.6 | 0.6 | 1.3 | 0.99 | Satisfactory |
| 43 | 0.97 | 2.7 | 0.6 | 0.6 | 2.2 | 0.98 | Very good | ||
| BHD | 72 | 0.96 | 2.4 | 0.6 | 0.5 | 0.0 | 0.98 | Acceptable | |
| 43 | 0.96 | 2.7 | 0.6 | 0.6 | 2.7 | 0.96 | Satisfactory | ||
| Height | 72 | 0.97 | 13,187 | 43 | 39 | 1.0 | 0.99 | Very good | |
| 43 | 0.97 | 15,939 | 48 | 42 | 3.2 | 0.98 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.3 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 0.0 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.3 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.2 | 0.2 | 0.1 | 1.4 | 0.99 | Acceptable | ||
| Height & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.3 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.1 | 1.00 | Very good | ||
| Polynomial: second degree | RHD | 72 | 1.00 | 0.6 | 0.3 | 0.2 | 0.3 | 0.99 | Satisfactory |
| 43 | 1.00 | 0.9 | 0.4 | 0.2 | 2.1 | 0.99 | Satisfactory | ||
| BHD | 72 | 1.00 | 0.5 | 0.3 | 0.2 | 1.5 | 0.98 | Acceptable | |
| 43 | 1.00 | 0.9 | 0.4 | 0.2 | 3.6 | 0.98 | Poor | ||
| Height | 72 | 1.00 | 1774 | 16 | 15 | 0.0 | 1.00 | Very good | |
| 43 | 1.00 | 2636 | 19 | 13 | 0.9 | 1.00 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 1.4 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 0.8 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 1.5 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.3 | 0.2 | 0.1 | 2.3 | 0.99 | Acceptable | ||
| Height & RHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.2 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.1 | 1.00 | Very good |
| Model | Variable | Data Gap Representation | R2 | SSE | RMSE | MAE | SB [%] | CCC | Label |
|---|---|---|---|---|---|---|---|---|---|
| Interpolant: Nearest Neighbor | RHD | 72 | 1.00 | 4.8 | 0.8 | 0.5 | 2.3 | 0.97 | Poor |
| 43 | 1.00 | 12.6 | 1.3 | 0.9 | 0.4 | 0.93 | Poor | ||
| BHD | 72 | 1.00 | 4.0 | 0.8 | 0.4 | 1.0 | 0.97 | Poor | |
| 43 | 1.00 | 8.9 | 1.1 | 0.8 | 0.0 | 0.92 | Poor | ||
| Height | 72 | 1.00 | 32,985 | 69 | 36 | 1.5 | 0.97 | Poor | |
| 43 | 1.00 | 71,174 | 101 | 71 | 1.4 | 0.93 | Poor | ||
| BHD & RHD | 72 | 1.00 | 6.0 | 0.9 | 0.5 | 6.8 | 0.97 | Poor | |
| 43 | 1.00 | 12.6 | 1.3 | 0.9 | 0.4 | 0.93 | Poor | ||
| Height & BHD | 72 | 1.00 | 6.3 | 0.9 | 0.5 | 8.7 | 0.95 | Poor | |
| 43 | 1.00 | 8.9 | 1.1 | 0.8 | 0.0 | 0.92 | Poor | ||
| Height & RHD | 72 | 1.00 | 6.5 | 1.0 | 0.5 | 5.2 | 0.97 | Poor | |
| 43 | 1.00 | 12.6 | 1.3 | 0.9 | 0.4 | 0.93 | Poor | ||
| Interpolant: Linear | RHD | 72 | 1.00 | 0.3 | 0.2 | 0.1 | 0.8 | 1.00 | Very good |
| 43 | 1.00 | 0.5 | 0.3 | 0.2 | 0.4 | 0.99 | Very good | ||
| BHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.9 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.4 | 0.2 | 0.2 | 0.0 | 0.98 | Satisfactory | ||
| Height | 72 | 1.00 | 211 | 5.0 | 2.0 | 0.4 | 1.00 | Very good | |
| 43 | 1.00 | 3154 | 21 | 13 | 1.4 | 1.00 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.3 | 0.2 | 0.1 | 1.5 | 1.00 | Very good | |
| 43 | 1.00 | 0.0 | 0.1 | 0.0 | 0.2 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 1.3 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.2 | 0.2 | 0.1 | 1.6 | 0.99 | Satisfactory | ||
| Height & RHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 0.5 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.1 | 1.00 | Very good | ||
| Interpolant: Cubic | RHD | 72 | 1.00 | 0.3 | 0.2 | 0.1 | 1.2 | 1.00 | Very good |
| 43 | 1.00 | 0.9 | 0.4 | 0.2 | 2.1 | 0.99 | Satisfactory | ||
| BHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 0.7 | 0.99 | Very good | |
| 43 | 1.00 | 0.9 | 0.4 | 0.2 | 3.6 | 0.98 | Poor | ||
| Height | 72 | 1.00 | 594 | 9.0 | 4.0 | 0.3 | 1.00 | Very good | |
| 43 | 1.00 | 2636 | 19 | 13 | 0.9 | 1.00 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.7 | 0.3 | 0.2 | 2.6 | 1.00 | Satisfactory | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 0.8 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 1.0 | 0.99 | Very good | |
| 43 | 1.00 | 0.3 | 0.2 | 0.1 | 2.3 | 0.99 | Acceptable | ||
| Height & RHD | 72 | 1.00 | 0.4 | 0.2 | 0.1 | 1.8 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.1 | 1.00 | Very good | ||
| Interpolant: PCHIP | RHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 0.8 | 1.00 | Very good |
| 43 | 1.00 | 1.0 | 0.4 | 0.2 | 2.1 | 0.99 | Satisfactory | ||
| BHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 1.2 | 0.99 | Satisfactory | |
| 43 | 1.00 | 1.1 | 0.4 | 0.2 | 3.6 | 0.98 | Poor | ||
| Height | 72 | 1.00 | 60 | 3.0 | 2.0 | 0.0 | 1.00 | Very good | |
| 43 | 1.00 | 3398 | 22 | 16 | 0.9 | 1.00 | Very good | ||
| BHD & RHD | 72 | 1.00 | 0.4 | 0.2 | 0.1 | 1.8 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 0.8 | 1.00 | Very good | ||
| Height & BHD | 72 | 1.00 | 0.1 | 0.1 | 0.1 | 1.3 | 0.99 | Satisfactory | |
| 43 | 1.00 | 0.3 | 0.2 | 0.1 | 2.3 | 0.99 | Acceptable | ||
| Height & RHD | 72 | 1.00 | 0.2 | 0.2 | 0.1 | 0.8 | 1.00 | Very good | |
| 43 | 1.00 | 0.1 | 0.1 | 0.1 | 1.1 | 1.00 | Very good |
References
- Strelher, A. Technologies of wood combustion. Ecol. Eng. 2000, 16, 25–40. [Google Scholar] [CrossRef]
- BWE. Bekanntmachung über die Förderung von Forschung und Entwicklung zur kosten- und energieeffizienten Nutzung von Biomasse im Strom- und Wärmemarkt, Energetische Biomassenutzung. BAnz AT 2005, B1, 1–7. [Google Scholar]
- Christersson, L.; Verma, K. Short-rotation forestry—A complement to “conventional” forestry. Unasylva 2006, 223, 34–39. [Google Scholar]
- Tsonkova, P.; Böhm, C.; Quinkenstein, A.; Freese, D. Ecological benefits provided by alley cropping systems for production of woody biomass in the temperate region: A review. Agrofor. Syst. 2012, 85, 133–152. [Google Scholar] [CrossRef]
- Carl, C.; Biber, P.; Landgraf, D.; Buras, A.; Pretzsch, H. Allometric Models to Predict Aboveground Woody Biomass of Black Locust (Robinia pseudoacacia L.) in Short Rotation Coppice in Previous Mining and Agricultural Areas in Germany. Forests 2017, 8, 328. [Google Scholar] [CrossRef]
- Ceulemans, R.; McDonald, A.J.S.; Pereira, J.S.A. A comparison among eucalypt, poplar and willow characteristics with particular reference to a coppice, growth-modelling approach. Biomass Bioenergy 1996, 11, 215–231. [Google Scholar] [CrossRef]
- Walle, I.V.; Camp, N.V.; Van de Casteele, L.; Verheyen, K.; Lemeur, R. Short-rotation forestry of birch, maple, poplar and willow in Flanders (Belgium) II. Energy production and CO2 emission reduction potential. Biomass Bioenergy 2007, 31, 276–283. [Google Scholar] [CrossRef]
- Sims, R.E.H.; Maiava, T.G.; Bullock, B.T. Short rotation coppice tree species selection for woody biomass production in New Zealand. Biomass Bioenergy 2001, 20, 329–335. [Google Scholar] [CrossRef]
- Aravanopoulos, F.A.; Kimb, K.H.; Zsuffa, L. Genetic diversity of superior Salix clones selected for intensive forestry plantations. Biomass Bioenergy 1999, 16, 249–255. [Google Scholar] [CrossRef]
- Zewdie, M.; Olsson, M.; Verwijst, T. Above-ground biomass production and allometric relations of Eucalyptus globulus Labill coppice plantations along a chronosequence in the central highlands of Ethiopia. Biomass Bioenergy 2009, 33, 421–428. [Google Scholar] [CrossRef]
- Sochacki, S.J.; Harper, R.J.; Smettem, K.R.J. Estimation of woody biomass production from a short-rotation bio-energy system in semi-arid Australia. Biomass Bioenergy 2007, 31, 608–616. [Google Scholar] [CrossRef]
- Diamantopolou, M.J. Filling gaps in diameter measurements on standing tree boles in the urban forest of Thessaloniki, Greece. Environ. Model. Softw. 2016, 25, 1857–1865. [Google Scholar] [CrossRef]
- Wang, G.; Garcia, D.; Liu, Y.; de Jeu, R.; Dolman, A.J. A three-dimensional gap filling method for large geophysical datasets: Application to global satellite soil moisture observations. Environ. Model. Softw. 2012, 30, 139–142. [Google Scholar] [CrossRef]
- Bärwolf, M.; Jung, L.; Harzendorf, D.; Prüfer, M.; Mürter, S. Schlussbericht zum Verbundvorhaben AgroForstEnergie II.; Teilvorhaben 1: Ertragseffekte und Ökonomie; Abschlußbericht; Fachagentur für Nachwachsende Rohstoffe: Gülzow, Germany, 2016; 263p.
- Pretzsch, H. Forest Dynamics, Growth and Yield. from Measurement to Model; Springer: Freising, Germany, 2009; 671p. [Google Scholar] [CrossRef]
- Takanashi, M. Statistical Inference in Missing Data by MCMC and Non-MCMC Multiple Imputation Algorithms: Assessing the Effects of Between-Imputation Iterations. Data Sci. J. 2017, 16, 37. [Google Scholar] [CrossRef]
- Linder, A. Statistische Methoden für Naturwissenschaftler, Mediziner und Ingenieure, 2nd ed.; Verlag Birkhäuser: Basel, Switzerland, 1951; 238p. [Google Scholar]
- Mudra, A. StatistischeMethoden für landwirtschaftliche Versuche; Verlag Paul Parey: Berlin/Hamburg, Germany, 1958; 336p. [Google Scholar]
- Rasch, D. Einf¨uhrung in die Biostatistik, 2nd ed.; Verlag Harri Deutsch: Frankfurt am Main, Germany, 1987; 276p. [Google Scholar]
- Honaker, J.; King, G.; Blackwell, M. Amelia II: A Program for Missing Data. J. Stat. Softw. 2011, 45, 47. [Google Scholar] [CrossRef]
- Assmann, E. Untersuchungen über die Höhenkurven von Fichtenbeständen. Allg. Forst-und Jagdztg. 1943, 119, 77–88, 105–123, 133–151. [Google Scholar]
- Korsun, H. Zivot normalniho porostu ve vzoroich (Das Leben des normalen Waldes in Formeln). Lesnicka Pr. 1935, 14, 289–300. [Google Scholar]
- Michailoff, I. Zahlenmäßiges Verfahren für die Ausf¨uhrung der Bestandeshöhenkurven. Forstw. Cbl. 1943, 6, 273–279. [Google Scholar]
- Petterson, H. Die Massenproduktion des Nadelwaldes. Mitt. d. schwed. Forstl. 1955, 45, 189. [Google Scholar]
- Prodan, M. Messung der Waldbestände; JD Sauerländer’s Verlag: Frankfurt am Main, Germany, 1951; p. 260. [Google Scholar]
- Pretzsch, H.; Forrester, D.I.; Rötzer, T. Representation of species mixing in forest growth models. A review and perspective. Ecol. Model. 2015, 313, 276–292. [Google Scholar] [CrossRef] [Green Version]
- Van der Werf, W.; Keesman, K.; Burgess, P.J.; Graves, A.R.; Pilbeam, D.; Incoll, L.D.; Metselaar, K.; Mayus, M.; Stappers, R.; van Keulen, H.; et al. Yield-SAFE: A parameter-sparse, process-based dynamic model for predicting resource capture, growth, and production in agroforestry systems. Ecol. Eng. 2007, 29, 419–433. [Google Scholar] [CrossRef] [Green Version]
- Graves, A.R.; Burgess, P.J.; Palma, J.; Keesman, K.J.; van der Werf, W.; Dupraz, C.; van Keulen, H.; Herzog, F.; Mayus, M. Implementation and calibration of the parameter-sparse Yield-SAFE model to predict production and land equivalent ratio in mixed tree and crop systems under two contrasting production situations in Europe. Ecol. Model. 2010, 221, 1744–1756. [Google Scholar] [CrossRef] [Green Version]
- Keesman, K.J.; Graves, A.; van der Werf, W.; Burgess, P.; Palma, J.; Dupraz, C.; van Keulen, H. A system identification approach for developing and parameterising an agroforestry system model under constrained availability of data. Environ. Model. Softw. 2011, 26, 1540–1553. [Google Scholar] [CrossRef]
- Burgess, P.J.; Graves, A.; Metselaar, K.; Stappers, R.; Keesman, K.; Palma, J.; Mayus, M.; van der Werf, W. Description of Plot-SAFE Version 0.3; Cranfield University: Silsoe, Bedfordshire, 15 September 2004; 52p, Unpublished work. [Google Scholar]
- Burgess, P.; Graves, A.; Palma, J.; Herzog, F.; Keesman, K.; van der Werf, W. EU SAFE Project Deliverable 6.4: Parametrization of the Yield-SAFE Model and Its Use to Determine Yields at the Landscape Test Sites; Cranfield University-Institute of Water and Environment: Silsoe, UK, 2005. [Google Scholar]
- Palma, J.H.N.; Graves, A.R.; Bunce, R.G.H.; Burgess, P.J.; de Filippi, R.; Keesman, K.J.; van Keulen, H.; Liagre, F.; Mayus, M.; Reisner, Y.; et al. Modeling environmental benefits of silvoarable agroforestry in Europe. Agric. Ecosyst. Environ. 2007, 119, 320–334. [Google Scholar] [CrossRef] [Green Version]
- Palma, J.H.N.; Paulo, J.A.; Tome, M. Carbon sequestration of modern Quercus suber L. silvoarable agroforestry systems in Portugal: A YieldSAFE-based estimation. Agrofor. Syst. 2014, 88, 791–801. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Ojeda, J.J.; Volenec, J.J.; Brouder, S.M.; Caviglia, O.P.; Agnusdei, M.G. Evaluation of Agricultural Production Systems Simulator (APSIM) as yield predictor of Panicum virgatum and Miscanthus x giganteus in several US environments. GCB Bioenergy 2017, 9, 796–816. [Google Scholar] [CrossRef]
- Kanzler, M.; Böhm, C. Nachhaltige Erzeugung von Energieholz in Agroforstsystemen (AgroForstEnergie II): Teilvorhaben 2: Bodenschutz, Bodenfruchtbarkeit, Wasserhaushalt und Mikroklima Schlußbericht. In Fachgebiet für Bodenschutz und Rekultivierung; Brandenburgische Technische Universität Cottbus-Senftenberg: Cottbus, Germany, 2016. [Google Scholar]
- Lamerre, J.; Langhof, M.; Sevke-Masur, K.; Schwarz, K.U.; von Wühlisch, G.; Swieter, A.; Greef, J.M.; Dauber, J.; Hirschberg, F.; Joormann, I.; et al. Nachhaltige Erzeugung von Energieholz in Agroforstsystemen: Teilprojekt 3: Standort Niedersachsen, Strukturvielfalt und Biodiversität. Schlußbericht. In Institut für Pflanzenbau und Bodenkunde; Julius Kühn-Institut Bundesforschungsinstitut für Kulturpflanzen (JKI): Braunschweig, Germany, 2016. [Google Scholar]
- Crous-Duran, J.; Graves, A.R.; Paulo, J.A.; Mirck, J.; Oliveira, T.S.; Kay, S.; García de Jalón, S.; Palma, J.H.N. Modelling tree density effects on provisioning ecosystem services in Europe. Agrofor. Syst. 2018, 1–23. [Google Scholar] [CrossRef]
| Model Name | General Model |
|---|---|
| Exponential | a × exp(b × x) |
| Fourier | a0 + a1 × cos(x × w) + b1 × sin(x × w) |
| Gaussian | a1 × exp( − ((x − b1)/c1)^2) |
| Power: one term | a × x^b |
| Power: two terms | a × x^b + c |
| Rational | (p1)/(x + q1) |
| Sum of Sine | a1 × sin(b1 × x + c1) |
| Linear Fit | a × (sin(x − pi)) + b × ((x − 10)^2) + c |
| Polynomial: first degree | p1 × x + p2 |
| Polynomial: second degree | p1 × x^2 + p2 × x + p3 |
| Model Name | General Model |
|---|---|
| Interpolant: Nearest Neighbor | Piecewise polynomial computed from p. |
| Interpolant: Linear | |
| Interpolant: Cubic | |
| Interpolant: PCHIP (Piecewise Cubic Hermite Interpolation) |
| Model Name | General Model |
|---|---|
| Assmann [21] | H = a + b × lnD |
| Korsun [22] | H = exp(a0 + a1 × ln(D) + a2 × ln(D)^2) |
| Michailoff [23] | H = a0 × exp(− a1/D) + 1.3 |
| Petterson [24] | H = (D/(a0 + a1 × D))^3 + 1.3 |
| Prodan [25] | H = D^2/(a0 + a1 × D + a2 × D^2) + 1.3 |
| Model | Variable | Data Gap Representation | R2 | SSE | RMSE | MAE | SB [%] | CCC | Label |
|---|---|---|---|---|---|---|---|---|---|
| Amelia II | RHD | 72 | 1.00 | 0.2 | 0.3 | 0.3 | 6.4 | 1.00 | Satisfactory |
| 43 | 1.00 | 4.1 | 1.0 | 0.8 | 14.9 | 0.00 | Poor | ||
| BHD | 72 | 0.99 | 0.7 | 0.6 | 0.6 | 11.5 | 0.97 | Poor | |
| 43 | 0.99 | 0.4 | 0.3 | 0.3 | 5.5 | 0.99 | Acceptable | ||
| Height | 72 | 0.99 | 10,110.2 | 71.1 | 57.3 | 14.1 | 0.94 | Poor | |
| 43 | 0.99 | 24,478.6 | 78.2 | 70.4 | 4.3 | 0.92 | Satisfactory | ||
| BHD & | 72 | 1.00 | 0.9 | 0.7 | 0.6 | 15.1 | 0.97 | Poor | |
| RHD | 43 | 0.99 | 5.0 | 1.1 | 1.0 | 3.6 | 0.44 | Poor | |
| Height & | 72 | 1.00 | 1627.5 | 20.5 | 20.4 | 10.1 | 0.98 | Poor | |
| BHD | 43 | 0.98 | 2986.8 | 19.6 | 16.7 | 7.6 | 0.98 | Poor | |
| Height & | 72 | 1.00 | 1214.8 | 17.7 | 17.3 | 3.6 | 0.99 | Poor | |
| RHD | 43 | 0.99 | 3065.4 | 19.8 | 17.9 | 4.7 | 0.49 | Poor |
| Model | Variable | Data Gap Representation | R2 | SSE | RMSE | MAE | SB [%] | CCC | Label |
|---|---|---|---|---|---|---|---|---|---|
| Assmann [21] | Height | 72 | 0.99 | 3.68 | 0.73 | 0.64 | 3.8 | 0.97 | Poor |
| BHD | 43 | 0.98 | 4.77 | 0.83 | 0.66 | 7.5 | 0.96 | Poor | |
| Height | 72 | 0.99 | 5.49 | 0.89 | 0.79 | 1.8 | 0.75 | Poor | |
| RHD | 43 | 0.99 | 7.10 | 1.01 | 0.84 | 6.1 | 0.70 | Poor | |
| Prodan [25] | Height | 72 | 0.98 | 1.51 | 0.46 | 0.34 | 4.3 | 0.99 | Satisfactory |
| BHD | 43 | 0.98 | 91.19 | 3.61 | 2.22 | 25.1 | 0.68 | Poor | |
| Height | 72 | 1.00 | 0.10 | 0.12 | 0.10 | −0.3 | 1.00 | Very good | |
| RHD | 43 | 1.00 | 0.13 | 0.14 | 0.10 | 0.2 | 1.00 | Very good | |
| Petterson [24] | Height | 72 | 0.97 | 1.70 | 0.49 | 0.33 | 4.2 | 0.99 | Acceptable |
| BHD | 43 | 0.97 | 1.65 | 0.49 | 0.34 | 4.0 | 0.99 | Acceptable | |
| Height | 72 | 1.00 | 0.10 | 0.12 | 0.08 | −0.5 | 1.00 | Very good | |
| RHD | 43 | 1.00 | 0.10 | 0.12 | 0.09 | 0.3 | 1.00 | Very good | |
| Korsun [22] | Height | 72 | 1.00 | 0.11 | 0.13 | 0.08 | 1.1 | 1.00 | Very good |
| BHD | 43 | 1.00 | 0.11 | 0.13 | 0.07 | 1.0 | 1.00 | Very good | |
| Height | 72 | 1.00 | 0.12 | 0.13 | 0.11 | −0.2 | 1.00 | Very good | |
| RHD | 43 | 1.00 | 0.11 | 0.13 | 0.09 | 1.1 | 1.00 | Very good | |
| Michailoff [23] | Height | 72 | 0.99 | 0.92 | 0.36 | 0.23 | 3.5 | 0.99 | Satisfactory |
| BHD | 43 | 0.98 | 0.90 | 0.36 | 0.25 | 3.2 | 0.99 | Satisfactory | |
| Height | 72 | 0.99 | 0.62 | 0.30 | 0.25 | −1.7 | 1.00 | Very good | |
| RHD | 43 | 0.99 | 0.76 | 0.33 | 0.27 | −1.2 | 1.00 | Satisfactory |
| Model | Variable | Data Gap Representation | R2 | SSE | RMSE | MAE | SB [%] | CCC | Label |
|---|---|---|---|---|---|---|---|---|---|
| Yield-SAFE | RHD | 72 | 1.00 | 3.7 | 1.0 | 0.9 | 12.4 | 0.99 | Satisfactory |
| 43 | 1.00 | 4.0 | 1.1 | 1.1 | 15.1 | 0.99 | Satisfactory |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seserman, D.-M.; Freese, D. Handling Data Gaps in Reported Field Measurements of Short Rotation Forestry. Data 2019, 4, 132. https://doi.org/10.3390/data4040132
Seserman D-M, Freese D. Handling Data Gaps in Reported Field Measurements of Short Rotation Forestry. Data. 2019; 4(4):132. https://doi.org/10.3390/data4040132
Chicago/Turabian StyleSeserman, Diana-Maria, and Dirk Freese. 2019. "Handling Data Gaps in Reported Field Measurements of Short Rotation Forestry" Data 4, no. 4: 132. https://doi.org/10.3390/data4040132





