Next Article in Journal
Homisland-IO: Homogeneous Land Use/Land Cover over the Small Islands of the Indian Ocean
Previous Article in Journal
Survey Data for Measuring Musical Creativity and the Impact of Information
Previous Article in Special Issue
Ensemble Based Classification of Sentiments Using Forest Optimization Algorithm
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Data
Volume 4
Issue 2
10.3390/data4020081
data-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Graph Theoretic and Pearson Correlation-Based Discovery of Network Biomarkers for Cancer

by
Raihanul Bari Tanvir
,
Tasmia Aqila
,
Mona Maharjan
,
Abdullah Al Mamun
and
Ananda Mohan Mondal
*
School of Computing and Information Sciences, Florida International University, Miami, FL 33199, USA
*
Author to whom correspondence should be addressed.
Data 2019, 4(2), 81; https://doi.org/10.3390/data4020081
Submission received: 16 April 2019 / Revised: 30 May 2019 / Accepted: 3 June 2019 / Published: 5 June 2019
(This article belongs to the Special Issue Big Network Inference, Integration and Analysis for Precision Medicine (BigDataNetAnalysis))
Browse Figures
Versions Notes

Abstract

:
Two graph theoretic concepts—clique and bipartite graphs—are explored to identify the network biomarkers for cancer at the gene network level. The rationale is that a group of genes work together by forming a cluster or a clique-like structures to initiate a cancer. After initiation, the disease signal goes to the next group of genes related to the second stage of a cancer, which can be represented as a bipartite graph. In other words, bipartite graphs represent the cross-talk among the genes between two disease stages. To prove this hypothesis, gene expression values for three cancers— breast invasive carcinoma (BRCA), colorectal adenocarcinoma (COAD) and glioblastoma multiforme (GBM)—are used for analysis. First, a co-expression gene network is generated with highly correlated gene pairs with a Pearson correlation coefficient ≥ 0.9. Second, clique structures of all sizes are isolated from the co-expression network. Then combining these cliques, three different biomarker modules are developed—maximal clique-like modules, 2-clique-1-bipartite modules, and 3-clique-2-bipartite modules. The list of biomarker genes discovered from these network modules are validated as the essential genes for causing a cancer in terms of network properties and survival analysis. This list of biomarker genes will help biologists to design wet lab experiments for further elucidating the complex mechanism of cancer.

1. Introduction

The present work is motivated by the prospective applications of protein-protein interaction (PPI) networks to diseases and other dynamic processes. Ideker and Sharan [1] enumerated four different applications of protein networks to diseases: i) identifying new disease genes, ii) studying the network properties of disease genes, iii) classifying diseases based on protein network, and iv) identifying disease-related subnetworks. Genome-wide PPI networks come with rich information about the dynamic processes such as the behavior of genetic networks in response to DNA damage [2] and exposure to arsenic [3], the prediction of protein function [4], genetic interaction [5], protein subcellular localization [6,7,8,9,10,11], the process of aging [12], and protein network biomarkers [13,14,15].
One of the widely used methods for elucidating biomarkers for diseases is through protein-protein interaction (PPI) or gene co-expression networks based on “guilt by association” concept. In a gene co-expression network, nodes represent the genes and edges represent the connection between genes due to significantly similar expression patterns over different samples. Several methods exist for inferring edges in gene networks. Pearson correlation is one of the most common co-expression measures employed in various studies [16,17]. Another common method, Mutual Information (MI) [18] is an information theoretic measure for measuring nonlinear relationship between genes or other variables. A threshold is applied after constructing the co-expression network to retain the most biologically significant correlations between genes.
The main purpose of analyzing gene co-expression networks is to identify the biologically significant modules consist of groups of genes with dense interactions. Usually, highly connected groups have a higher within-group homogeneity and can be considered as biologically significant modules performing a common task, such as shared regulatory inputs or functional pathways. Clustering is a popular method for finding relevant modules from gene co-expression networks. Weighted Gene Correlation Network Analysis (WGCNA) is the most widely used package for module finding [19] which applies hierarchical clustering to find modules. It applies a soft threshold during construction of a gene co-expression network. Several researchers have identified key differentially expressed genes associated with different cancers, such as breast, cervical, colon, esophageal, osteosarcoma and ovarian cancers [20,21,22,23,24,25,26], using WGCNA.
Lui et al. [27] used differential entropy technique to identify key genes in diabetes using rat’s time-series gene expression data from case and control samples. Guan et al. [28], developed a prediction model using Bayes discriminant method to predict the prognosis of hepatocellular carcinoma based on gene co-expression network.
Graph theoretic methods are also applied for analysis of gene co-expression networks. Shi et.al. [29], proposed an algorithm named Iterative clique enumeration technique (ICE) to discover relatively independent maximal cliques for breast cancer on GEO dataset and found some highly correlated modules that may indicate the tumor grades. Similarly, Perkins et al. used spectral graph theory on Homo sapiens and Saccharomyces cerevisiae microarray data for clustering at various thresholds [30]. Zhang et al. [31], discovered the top five hub genes for bladder cancer using the centrality analysis method.
None of the previous studies used clique and bipartite combination to identify the biologically significant modules. The main goal of this paper is to explore the existence of clique-bipartite-like network modules in actual gene network for cancer. Mondal et al. [32] showed that clique-like structures and bipartite graphs could be the building blocks for disease progression, Figure 2 in [32]. The rationale is that a group of proteins or genes work together by forming a network (a clique-like structure) to accomplish a specific function, which could be related to a disease stage [32] and bipartite structure represents the cross-talk among genes between two disease stages.
In this study, gene co-expression network was constructed using highly correlated gene pairs with PCC ≥ 0.9. Three network modules—maximal clique-like graph, 2-clique-1-bipartite graph, and 3-clique-2-bipartite graph—are identified. Finally, the effectiveness of the key genes discovered from these network modules was validated using pathway and survival analyses.

2. Results

Three different types of cancers—breast invasive carcinoma (BRCA), colorectal adenocarcinoma (COAD), and glioblastoma multiforme (GBM)—are considered in the present study to identify network biomarkers. Gene correlation networks based on gene expression profiles of BRCA (20,155 genes for 1093 samples), COAD (19,828 genes for 379 samples), and GBM (19,660 genes for 153 samples) are developed with highly correlated gene pairs (PCC ≥ 0.9). From these networks, three types of gene network modules, considered as network biomarkers, are isolated: i) Single clique-like module based on maximal cliques named as “maximal clique-like” module, ii) clique-bipartite-like modules with two cliques and one bipartite graph named as “2-clique-1-bipartite” modules, which are discovered based on two cliques connected with maximum number of inter-clique connections, and iii) clique-bipartite-like modules with three cliques (A, B, C) and two bipartite graphs (A-B and B-C) named as “3-clique-2-bipartite” modules, which are discovered based on two bipartite graphs having relatively more edges compare to others.
This section is organized in following subsections: Section 2.1—results with the topology of gene co-expression networks; Section 2.2—results with cliques and maximal clique-like modules; Section 2.3—results with 2-clique-1-bipartite modules; and Section 2.4—results with 3-clique-2-bipartite modules.

2.1. Topology of Gene Co-Expression Networks

Table 1 shows the topology of gene co-expression networks for three cancers—BRCA, COAD, and GBM—generated using gene pairs with PCC ≥ 0.9. The network for COAD is the largest and densest composed of 607 genes and 3651 interactions with an average degree of 12. The network for BRCA is the smallest composed of 380 genes and 1034 interactions, which is a sparse network with an average degree of 5.4. The network for GBM is the sparsest with an average degree of 4.9.

2.2. Cliques and Maximal Clique-Like Modules

NetworkX [33], a python package, was used to discover cliques of all possible sizes. The total number of cliques are 209, 1535, and 322 for BRCA, COAD, and GBM, respectively. The size of cliques and the corresponding number of cliques (frequency) for each cancer are presented in Supplementary Table S1. It is clear from this table that small-sized cliques (3-node, 4-node, etc.) appear more than the cliques of larger size, as expected. The gene co-expression networks for BRCA, COAD, and GBM have 3, 10, and 6 maximal cliques with 17, 19, and 11 genes, respectively, Supplementary Table S1.
For a particular cancer, most of the genes in maximal cliques are in common, Supplementary Table S2. Thus, it is better to combine the maximal cliques for a cancer to have a single maximal clique-like module for further analysis. The maximal clique-like modules for three cancers—BRCA, COAD, and GBM—are shown in Supplementary Figure S1. Finally, the maximal clique-like modules have 19, 30, and 14 genes for BRCA, COAD, and GBM, respectively, as shown in Table 2. Based on these modules, COAD and GBM cancers share six genes—CD4, HCK, ITGB2, LAIR1, LAPTM5, and SPI1. However, BRCA does not share any genes with the other two cancers. It can be concluded from the maximal clique-like modules that BRCA cancer has a unique behavior which is different from COAD and GBM, whereas COAD and GBM might have some common characteristics.

2.3. 2-Clique-1-Bipartite Modules

Figure 1 shows clique-bipartite-like modules composed of two cliques and one bipartite graph for BRCA, COAD, and GBM. The nodes in two cliques are represented by yellow (Clique-1) and gray (Clique-2) colors. Intra-clique connections are blue and inter-clique connections, forming a bipartite graph, are red. In identifying clique-to-clique connections, it is made sure that the two cliques do not have any gene in common. Finding the interconnected cliques is a combinatorial problem. Usually, cliques or cluster of genes representing different stages of a disease are more likely to have cross-talks or interconnections between two cliques. Bipartite graphs between genes of two stages represent the cross-talks. This study focuses on identifying cliques with maximal connections (cross-talks) only. There are 59, 145, and 44 edges that are connecting two cliques in Figure 1a–c, which are the highest in three respective cancers.
Table 3 shows the list of genes discovered from these clique-bipartite-like modules. Based on these modules, COAD and GBM cancers share many genes in common. The common genes—in clique1 for both cancers are HCK, ITGB2, LAIR1, and LRRC25, and for clique2 are CD4, CD53, LILRB1, NCKAP1L, and SPI1. LAPTM5 is the only common gene between clique1 of GBM and clique2 of COAD. On the other hand, BRCA does not share any gene in common. It can be concluded from 2-clique-1-bipartite modules that BRCA cancer has unique behavior, which is different from COAD and GBM cancers, whereas COAD and GBM might have some common characteristics.

2.4. 3-Clique-2-Bipartite Modules

The top three modules of 3-clique-2-bipartite from each cancer are considered for further analysis. Table 4 summarizes these modules in terms of clique size and the number of inter-clique connections. For example, BRCA-Module1 consists of three cliques of 13, seven, and four genes connected by two bipartite graphs of 56 and 13 connections.
Figure 2 shows the top three 3-clique-2Clique-2-bipartite modules for BRCA. Modules for COAD and GBM are shown in Figure S2. The nodes in three cliques are represented by yellow (clique-A), grey (clique-B) and orange (clique-C) colors. Intra-clique edges are colored blue and inter-clique edges are colored red.
The complete lists of genes that are present in each of the top three 3-clique-2-bipartite modules for BRCA, COAD, and GBM are presented in Supplementary Table S3. Observation of these list reveals that there are many genes in common in three modules of a particular cancer. Table 5 shows the combined list—44, 48, and 32 genes for BRCA, COAD, and GBM respectively. Three cancers share four genes—CD53, DOCK2, IKZF1, and NCKAP1L. Other than these four genes, BRCA and COAD share three more genes—ITK, PTPRC, and TBC1D10C; COAD and GBM share 10 more genes—ARHGAP30, CD4, CD86, CSF1R, HCK, ITGB2, LAIR1, LAPTM5, SASH3, and SPI; and BRCA and GBM do not share any more genes. Thus, BRCA and COAD share a total of seven genes; COAD and GBM share a total of 14 genes; and BRCA and GBM share only four genes. Again, based on 3-clique-bipapartite modules, COAD and GBM shares many genes, which means that they might have some common cause for cancer development. These lists of common genes might provide better insight from lab experiments.

3. Discussion

This section discusses the validation of key genes related to three cancers—BRCA, COAD, and GBM—discovered from three network modules—maximal clique-like modules, 2-clique-1-bipartite modules, and 3-clique-2-bipartite modules. First, since the key genes are discovered via network modules, this paper used a network-based app, CytoHubba [34] for validation. The app, CytoHubba, is capable of ranking genes in a network using 12 different graph-theoretic algorithms. The reason for using CytoHubba is that it produces successful results in predicting essential proteins from the yeast protein-protein interaction network [34]. Similarly, in a cancer gene co-expression network, the genes that cause cancer can be thought of as the essential genes for causing that cancer and most likely will have the similar network properties as essential proteins in PPI network. Second, a survival analysis is conducted to show the effectiveness of the key genes discovered using network modules. Finally, pathway and GO term enrichment analyses are conducted for the key genes.

3.1. Validation Using CytoHubba

Figure 3 shows the validation process using two validation metrics—Top 20 genes and Top 50 genes—developed using CytoHubba. The original or base gene network (network created with PCC ≥ 0.9) are analyzed using 12 scoring methods—betweenness, bottleneck, closeness, clustering coefficient (CC), degree, density of maximum neighborhood component (DMNC), eccentricity (EcC), edge percolated component (EPC), maximal clique centrality (MCC), maximum neighborhood component (MNC), radiality, and stress—of CytoHubba to create the list of genes as the benchmark for validation.
Metric-1 (Top-20 Genes): First, Top-20 genes are taken from each of the 12 scoring methods. Then, the genes that appear in two or more scoring methods are considered as the benchmark for validation. The benchmarks for BRCA, COAD, and GBM cancers consist of 41, 53, and 42 genes, respectively, see Supplementary Table S4.
Metric-2 (Top-50 Genes): Similarly, Top-50 genes are taken from each of the 12 scoring methods. Then, the genes that appear in two or more scoring methods are considered as the benchmark for validation. The benchmarks for BRCA, COAD, and GBM cancers consist of 92, 130, and 99 genes respectively, see Supplementary Table S4.
Table 6 shows the number of key genes obtained by combining the unique genes from three modules and the number of these key genes validated by metric-1 and metric-2. For example, 47 key genes were discovered from three network modules of BRCA. These 47 key genes were then compared with the benchmark genes in metric-1 and metric-2. Out of 47 key genes, 26 and 45 genes were found to be common in metric-1 and metric-2, respectively. This validation supports that the list of genes discovered using three modules—maximal clique-like modules, 2-clique-1-bipartite modules, and 3-clique-2-bipartite modules—are essential genes for causing a cancer. This also supports the proposed hypotheses that there exist clique-like and clique-bipartite-like structures, which can be considered as network biomarkers for cancers.

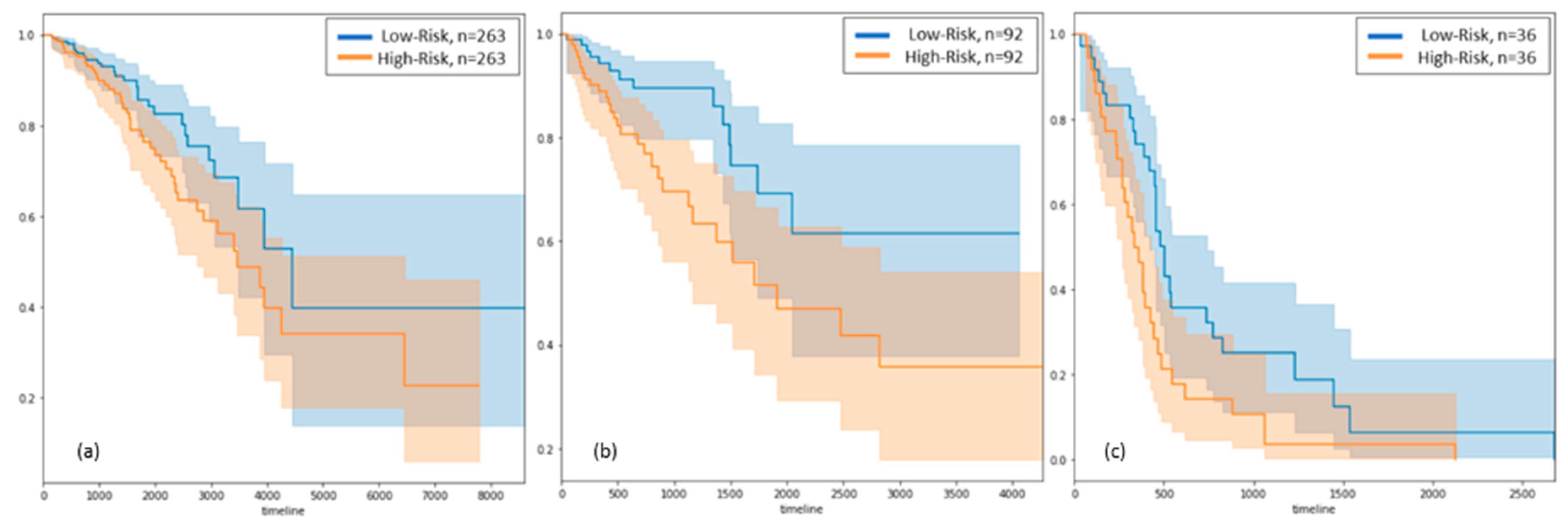
3.2. Survival Analysis

Cox proportional hazard regression [35], a semi-parametric method was used for calculating the Cox coefficients of the key genes (Supplemental Table S5). It can adjust survival rate estimation to quantify the effect to predictor variables, which are key genes in the present study. The clinical data of cancer patients (obtained from TCGA) were divided into two equal groups such that each group had the same ratio of dead and alive. One of the groups were used as training set for calculation of Cox coefficients of the key genes. Then, the prognostic risk of each patient in the test set was calculated based on the expression values of key genes using the gene expression grade index (GGI) [36]. The following equation calculates the risk:
GGI Risk Score = ∑ x i − ∑ y i
where, x i and yi are the expression level of genes with positive and negative cox coefficient.
According to GGI risk score, patients in the test were divided into two groups, as high and low risk groups. The patients with a top 50% GGI risk score are in the high-risk group and others are in the low-risk group. Then a log-rank test was performed to see if there are significant difference in the real survival risks between the two groups.
The survival analysis of key genes of three cancers is shown in Figure 4. It is clear from this figure that the key genes of BRCA, COAD, and GBM are capable of distinguishing between cancer patients in terms of survival in the respective cancers. The log rank p-values between high-risk and low-risk groups were 0.0411, 0.0100, and 0.0171. Log-rank p-values below 0.05 means there is a significant difference between the two groups in consideration. The hazard ratios between high-risk groups and low-risk groups are 1.6478, 2.1627, and 1.6569 for cancer patients of BRCA, COAD, and GBM. This means, for example, high-risk groups of COAD patients are 2.1627 more likely to die than low-risk patients.

3.3. Pathway and Gene Ontology Enrichment of Key Genes

The pathway and Gene Ontology (GO) enrichment analyses are also performed for validation of key genes (List of key genes can be found in Supplementary Table S5). Pathway analysis was performed in ReactomeFIViz [37], a Cytoscape app. The false discovery rate (FDR) was calculated based on P-values using Benjamini–Hochberg method. The top ten pathways enriched in three cancers were compared. The pathways enriched in at least two cancers is listed in Supplementary Table S6. TCR signaling in -ve CD4+ T cells is enriched in all three cancers. There are five other pathways- Neutrophil degranulation, Osteoclast differentiation, Staphylococcus aureus infection, Natural killer cell mediated cytotoxicity and Fc gamma R-mediated phagocytosis are enriched in both COAD and GBM. This may be due to genes in common between COAD and GBM in maximal clique-like modules and 2-clique-1 bipartite modules. BRCA showed unique behavior in both modules. In 3-clique-2-bipartite module, BRCA had three genes in common with other two cancers and three more in common with COAD. The pathway T cell receptor signaling pathway is the only pathway enriched in both BRCA and GBM. In all three modules, COAD and GBM shared the same number genes. This is further observed in the enriched pathways they share in common.
A Cytoscape app, BiNGO [38] was used for GO enrichment analysis in three categories- biological process (BP), cellular component (CC), and molecular function (MF). BiNGO uses the Benjamini and Hochberg (false discovery rate) statistical method for multiple testing correction. The top ten enriched GO terms in three cancers were compared. GO terms common in at least two cancers are listed in Supplementary Table S7.
The biological processes enriched in all three cancers are Immune system process, regulation of immune system process, positive regulation of immune system, and T cell activation. Three more biological processes are enriched in both BRCA and GBM, and two more are in COAD and GBM. Most of the common enriched BPs are related to immune system. It is an accepted fact that immune cells have the ability to influence cancer [39]. This is another validation of the key genes discovered in the present study.
There are five cellular components enriched in all three cancers—plasma membrane, plasma membrane part, integral to plasma membrane, intrinsic to plasma membrane, and receptor complex. The dysregulation of the structural integrity of plasma membrane or its domain is known to promote oncogenic signaling [40]. Three other pathways—T cell receptor complex, membrane, and cell surface—are enriched in at least two of three cancers.
The three molecular functions enriched in all three cancers are molecular transducer activity, signal transducer activity, and protein binding. Two other molecular functions—GTPase regulatory activity and nucleoside-triphosphatase regulator activity—are enriched in COAD and GBM while receptor activity and non-membrane spanning protein tyrosine kinase are enriched in BRCA and COAD.

3.4. Future Direction

This study discovers key genes related to cancers from gene co-expression networks. There are three epigenetic factors that drive the cancer via gene expression of cancer genes, which are: i) DNA methylation, ii) histone modification, and iii) miRNA dysregulation. Future study will be conducted to determine how these three epigenetic factors are related to the genes discovered in this study. A study will be conducted for further analysis of the clique-like disease progression to identify the core clique, which could be a clique of three or more genes, for initiating a cancer utilizing the information from three epigenetic factors. Finally, we will explore how the core clique expands to a maximal clique-like structure in the final stage of a cancer.

4. Materials and Methods

4.1. Dataset Preparation

Gene expression data for BRCA, COAD, and GBM are obtained from LinkedOmics [41]. The datasets consist of gene expression values of 20155 genes for 1093 samples, 19,828 genes for 379 samples, and 19,660 genes for 153 samples, respectively, for BRCA, COAD, and GBM as mentioned in Table 7. In these datasets, all samples are cancer patients.
The missing values were imputed using the fancyimpute package in Python employing the k-nearest neighbors algorithm. The number of genes in the reduced datasets are 16,011, 15,769, and 16,186, respectively, for BRCA, COAD, and GBM. For the present study, highly correlated positive gene pairs, PCC ≥ 0.9 in each cancer are considered for creating the base networks for further analysis.

4.2. Method to Identify Clique and Clique-Bipartite-Like Modules

To discover the cluster of genes or cliques and how they are connected to each other by forming bipartite graphs, Python package NetworkX [33] is used. First, list of cliques with different sizes are discovered. Then, using the list of cliques and the original network (network created with PCC ≥ 0.9), three types of gene network modules, considered as network biomarkers, are discovered—i) maximal clique-like modules, ii) 2-clique-1Clique-1-bipartite modules, and iii) 3-clique-2Clique-2-bipartite modules.
Maximal clique-like module: The discovered cliques are organized in a list based on their size and frequency of occurrence. From the sorted list, the size and number of maximal (largest) cliques in each cancer are found and then combined together to get the maximal clique-like module. This process generates a single maximal clique-like module for each cancer.
2-Clique-1-bipartite module: These are clique-bipartite-like modules with two cliques and one bipartite graph, which are discovered based on two cliques connected with maximum number of inter-clique connections.
3-Clique-2-bipartite module: With the list of cliques and the original network (network created with PCC ≥ 0.9), a list of three connected cliques A, B, and C is generated in a way such that clique A is connected to clique B and clique B is connected to clique C, but cliques A, B, and C do not have any common genes. This process takes longer than usual because of the high number of cliques and the problem is combinatorial in nature. Every combination of three cliques is being checked to see whether it fulfills the condition. These modules are identified by first sorting the list by number of edges connecting cliques A and B and then sorting by number of edges connecting cliques B and C. It is observed that if one of the edge-count (between cliques A and B) has the highest value then the other edge-count (between cliques B and C) has very low value. Finally, from the sorted list, structures having both the edge-counts higher than others are selected as the possible network modules for a cancer. The top three structures from each cancer are considered for further analysis.

5. Conclusions

This paper used two graph theoretic concepts—clique and bipartite graphs—to identify the network biomarkers for cancer from gene co-expression networks developed with highly correlated gene pairs. The gene expression profiles of three cancers—BRCA, COAD, and GBM—are considered for experiment. Results show that three types of network modules—maximal clique-like, 2-clique-1-bipartite, and 3-clique-2-bipartite graphs—derived using the simple graph theoretic concepts clique and bipartite graph are capable of representing cancer dynamics at the gene network level. The combined list of genes from three network modules for a particular cancer are validated with the benchmark developed from a network-based tools CytoHubba. The effectiveness of the key genes is also validated by survival and pathway analyses.
The discovered gene network modules provide a short list of genes related to cancer that can be used by the biologist to design wet lab experiment for further elucidation of the complex mechanism of cancer.

Supplementary Materials

The following are available online at https://www.mdpi.com/2306-5729/4/2/81/s1; Figure S1. Maximal clique-like modules; Figure S2. Top three 3-clique-2-bipartite modules for COAD and GBM; Table S1. Frequency of cliques according to sizes; Table S2. List of genes in maximal cliques; Table S3. List of genes for top three 3-clique-2-bipartite modules; Table S4. List of benchmark genes in top-20 and top-50 metrics; Table S5. List of genes combining three network modules; Table S6. Enriched pathways with key genes; Table S7. GO term enrichment analysis.

Author Contributions

Conceptualization: A.M.M. and R.B.T.; methodology: A.M.M., R.B.T., and T.A.; software: R.B.T. and T.A.; validation: A.A.M. and M.M.; formal analysis: R.B.T. and T.A.; investigation: R.B.T., T.A., M.M., and A.A.M.; resources: R.B.T., T.A., M.M., and A.A.M.; data curation: T.A. and R.B.T.; writing—original draft preparation: A.M.M.; writing—review and editing: A.M.M., T.A., R.B.T., M.M., and A.A.M.; visualization: A.M.M., R.B.T., M.M., and A.A.M.; supervision: A.M.M.; project administration: A.M.M.; funding acquisition: A.M.M.

Funding

This research is funded by NSF CAREER award #1651917 (transferred to #1901628) to AMM.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ideker, T.; Sharan, R. Protein networks in disease. Genome Res. 2008, 18, 644–652. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Bandyopadhyay, S.; Mehta, M.; Kuo, D.; Sung, M.-K.; Chuang, R.; Jaehnig, E.J.; Bodenmiller, B.; Licon, K.; Copeland, W.; Shales, M.; et al. Rewiring of Genetic Networks in Response to DNA Damage. Science 2010, 330, 1385–1389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Haugen, A.C.; Kelley, R.; Collins, J.B.; Tucker, C.J.; Deng, C.; Afshari, C.A.; Brown, J.M.; Ideker, T.; Van Houten, B. Integrating phenotypic and expression profiles to map arsenic-response networks. Genome Boil. 2004, 5, R95. [Google Scholar] [CrossRef] [PubMed]
  4. Lee, H.; Tu, Z.; Deng, M.; Sun, F.; Chen, T. Diffusion Kernel-Based Logistic Regression Models for Protein Function Prediction. OMICS A J. Integr. Boil. 2006, 10, 40–55. [Google Scholar] [CrossRef] [PubMed]
  5. Qi, Y.; Suhail, Y.; Lin, Y.; Boeke, J.D.; Bader, J.S. Finding friends and enemies in an enemies-only network: A graph diffusion kernel for predicting novel genetic interactions and co-complex membership from yeast genetic interactions. Genome Res. 2008, 18, 1991–2004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Ananda, M.M.; Hu, J. NetLoc: Network based protein localization prediction using protein-protein interaction and co-expression networks. In Proceedings of the 2010 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Hong Kong, China, 18–21 December 2010; pp. 142–148. [Google Scholar]
  7. Mondal, A.; Lin, J.-R.; Hu, J. Network based subcellular localization prediction for multi-label proteins. In Proceedings of the 2011 IEEE International Conference on Bioinformatics and Biomedicine Workshops (BIBMW), Atlanta, GA, USA, 12–15 November 2011. [Google Scholar]
  8. Mondal, A.M.; Hu, J. Protein Localization by Integrating Multiple Protein Correlation Networks. Proceedings of The 2012 International Conference on Bioinformatics & Computational Biology (BIOCOMP’12), Las Vegas, NV, USA, 16–19 July 2012; pp. 82–88. [Google Scholar]
  9. Lin, J.-R.; Mondal, A.M.; Liu, R.; Hu, J. Minimalist ensemble algorithms for genome-wide protein localization prediction. BMC Bioinform. 2012, 13, 157. [Google Scholar] [CrossRef]
  10. Mondal, A.; Hu, J. Scored Protein-Protein Interaction to Predict Subcellular Localizations for Yeast Using Diffusion Kernel. In International Conference on Pattern Recognition and Machine Intelligence; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
  11. Mondal, A.; Hu, J. Network based prediction of protein localisation using diffusion kernel. Int. J. Data Min. Bioinform. 2014, 9, 386–400. [Google Scholar] [CrossRef]
  12. Faisal, F.E.; Milenkovic, T. Dynamic networks reveal key players in aging. Bioinformatics 2014, 30, 1721–1729. [Google Scholar] [CrossRef] [Green Version]
  13. Kevin, C.; Andrews, A.; Ananda, M. Protein Subnetwork Biomarkers for Yeast Using Brute Force Method. In Proceedings of the International Conference on Bioinformatics & Computational Biology (BIOCOMP), Las Vagas, NV, USA, 22–25 July 2013; pp. 218–223. [Google Scholar]
  14. Timalsina, P.; Charles, K.; Mondal, A.M. STRING PPI Score to Characterize Protein Subnetwork Biomarkers for Human Diseases and Pathways. In Proceedings of the 2014 IEEE International Conference on Bioinformatics and Bioengineering, Boca Raton, FL, USA, 10–12 November 2014; pp. 251–256. [Google Scholar]
  15. Maharjan, M.; Tanvir, R.B.; Chowdhury, K.; Mondal, A.M. Determination of Biomarkers for Diagnosis of Lung Cancer Using Cytoscape-based GO and Pathway Analysis. In Proceedings of the 20th International Conference on Bioinformatics & Computational Biology (BIOCOMP’19), Las Vegas, NV, USA, 29 July–01 Aug 2019. (Accepted). [Google Scholar]
  16. Eisen, M.B.; Spellman, P.T.; Brown, P.O.; Botstein, D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 1998, 95, 14863–14868. [Google Scholar] [CrossRef] [Green Version]
  17. Wolfe, C.J.; Kohane, I.S.; Butte, A.J. Systematic survey reveals general applicability of ‘guilt-by-association’ within gene coexpression networks. BMC Bioinform. 2005, 6, 227. [Google Scholar] [CrossRef]
  18. Butte, A.J.; Kohane, I.S. Mutual information relevance networks: Functional genomic clustering using pairwise entropy measurements. Pac. Symp. Biocomput. 2000, 418–429. [Google Scholar]
  19. Zhang, B.; Horvath, S. A general framework for weighted gene co-expression network analysis. Stat. Appl. Genet. Mol. Biol. 2005, 4, 17. [Google Scholar] [CrossRef]
  20. Tang, J.; Lu, M.; Cui, Q.; Zhang, D.; Kong, D.; Liao, X.; Ren, J.; Gong, Y.; Wu, G. Overexpression of ASPM, CDC20, and TTK Confer a Poorer Prognosis in Breast Cancer Identified by Gene Co-expression Network Analysis. Front. Oncol. 2019, 9, 310. [Google Scholar] [CrossRef]
  21. Lalremmawia, H.; Tiwary, B.K. Identification of Molecular Biomarkers for Ovarian Cancer using Computational Approaches. Carcinogenesis 2019. [Google Scholar] [CrossRef]
  22. Maertens, A.M.; Tran, V.; Kleensang, A.; Hartung, T. Weighted Gene Correlation Network Analysis (WGCNA) Reveals Novel Transcription Factors Associated With Bisphenol A Dose-Response. Front. Genet. 2018, 9, 508. [Google Scholar] [CrossRef] [Green Version]
  23. Shi, H.; Zhang, L.; Qu, Y.; Hou, L.; Wang, L.; Zheng, M. Prognostic genes of breast cancer revealed by gene co-expression network analysis. Oncol. Lett. 2017, 14, 4535–4542. [Google Scholar] [CrossRef]
  24. Liu, X.; Hu, A.-X.; Zhao, J.-L.; Chen, F. Identification of Key Gene Modules in Human Osteosarcoma by Co-Expression Analysis Weighted Gene Co-Expression Network Analysis (WGCNA). J. Cell. Biochem. 2017, 118, 3953–3959. [Google Scholar] [CrossRef]
  25. Zhang, C.; Sun, Q. Weighted gene co-expression network analysis of gene modules for the prognosis of esophageal cancer. J. Huazhong Univ. Sci. Technol. [Med. Sci.] 2017, 37, 319–325. [Google Scholar] [CrossRef]
  26. Liu, R.; Zhang, W.; Liu, Z.; Zhou, H. Associating transcriptional modules with colon cancer survival through weighted gene co-expression network analysis. BMC Genom. 2017, 18, 361. [Google Scholar] [CrossRef]
  27. Liu, Z.-P.; Gao, R. Detecting pathway biomarkers of diabetic progression with differential entropy. J. Biomed. Inform. 2018, 82, 143–153. [Google Scholar] [CrossRef]
  28. Guan, L.; Luo, Q.; Liang, N.; Liu, H. A prognostic prediction system for hepatocellular carcinoma based on gene co-expression network. Exp. Ther. Med. 2019, 17, 4506–4516. [Google Scholar] [CrossRef]
  29. Shi, Z.; Derow, C.K.; Zhang, B. Co-expression module analysis reveals biological processes, genomic gain, and regulatory mechanisms associated with breast cancer progression. BMC Syst. Biol. 2010, 4, 74. [Google Scholar] [CrossRef]
  30. Perkins, A.D.; Langston, M.A. Threshold selection in gene co-expression networks using spectral graph theory techniques. BMC Bioinform. 2009, 10, S4. [Google Scholar] [CrossRef]
  31. Zhang, D.-Q.; Zhou, C.; Chen, S.-Z.; Yang, Y.; Shi, B. Identification of hub genes and pathways associated with bladder cancer based on co-expression network analysis. Oncol. Lett. 2017, 14, 1115–1122. [Google Scholar] [CrossRef]
  32. Mondal, A.M.; Schultz, C.A.; Sheppard, M.; Carson, J.; Tanvir, R.B.; Aqila, T. Graph Theoretic Concepts as the Building Blocks for Disease Initiation and Progression at Protein Network Level: Identification and Challenges. In Proceedings of the 2018 IEEE International Conference on Bioinformatics and Biomedicine, BIBM, Madrid, Spain, 3–6 December 2018. [Google Scholar]
  33. Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy), Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
  34. Chin, C.-H.; Chen, S.-H.; Wu, H.-H.; Ho, C.-W.; Ko, M.-T.; Lin, C.-Y. cytoHubba: Identifying hub objects and sub-networks from complex interactome. BMC Syst. Biol. 2014, 8 (Suppl. 4), S11. [Google Scholar] [CrossRef]
  35. Mauger, E.A.; Wolfe, R.A.; Port, F.K. Transient effects in the cox proportional hazards regression model. Stat. Med. 1995, 14, 1553–1565. [Google Scholar] [CrossRef]
  36. Sotiriou, C.; Wirapati, P.; Loi, S.; Harris, A.; Fox, S.; Smeds, J.; Nordgren, H.; Farmer, P.; Praz, V.; Haibe-Kains, B.; et al. Gene Expression Profiling in Breast Cancer: Understanding the Molecular Basis of Histologic Grade to Improve Prognosis. J. Natl. Cancer Inst. 2006, 98, 262–272. [Google Scholar] [CrossRef]
  37. Wu, G.; Dawson, E.; Duong, A.; Haw, R.; Stein, L. ReactomeFIViz: The Reactome FI Cytoscape app for pathway and network-based data analysis. F1000Research 2014, 3, 146. [Google Scholar] [CrossRef]
  38. Maere, S.; Heymans, K.; Kuiper, M. BiNGO: A Cytoscape plugin to assess overrepresentation of Gene Ontology categories in Biological Networks. Bioinformatics 2005, 21, 3448–3449. [Google Scholar] [CrossRef]
  39. Monette, A.; Bergeron, D.; Ben Amor, A.; Meunier, L.; Caron, C.; Mes-Masson, A.-M.; Kchir, N.; Hamzaoui, K.; Jurisica, I.; Lapointe, R. Immune-enrichment of non-small cell lung cancer baseline biopsies for multiplex profiling define prognostic immune checkpoint combinations for patient stratification. J. Immunother. Cancer 2019, 7, 86. [Google Scholar] [CrossRef]
  40. Erazo-Oliveras, A.; Fuentes, N.R.; Wright, R.C.; Chapkin, R.S. Functional link between plasma membrane spatiotemporal dynamics, cancer biology, and dietary membrane-altering agents. Cancer Metastasis Rev. 2018, 37, 519–544. [Google Scholar] [CrossRef]
  41. Vasaikar, S.V.; Straub, P.; Wang, J.; Zhang, B. LinkedOmics: Analyzing multi-omics data within and across 32 cancer types. Nucleic Acids Res. 2017, 46, D956–D963. [Google Scholar] [CrossRef]
Data 04 00081 g001 550
Figure 1. Clique-bipartite-like modules with maximal interconnections between two cliques. (a) BRCA; (b) COAD; and (c) GBM. Nodes in Clique-1 are yellow and nodes in Clique-2 are grey colored. Intra-clique connections are blue and inter-clique connections (a bipartite graph) are red.
Figure 1. Clique-bipartite-like modules with maximal interconnections between two cliques. (a) BRCA; (b) COAD; and (c) GBM. Nodes in Clique-1 are yellow and nodes in Clique-2 are grey colored. Intra-clique connections are blue and inter-clique connections (a bipartite graph) are red.
Data 04 00081 g001
Data 04 00081 g002 550
Figure 2. Top three 3-clique-2-bipartite modules for BRCA. Yellow nodes: Clique-A, gray nodes: Clique-B, Orange nodes: Clique-C. Blue: Intra-clique edges, Red: Inter-clique edges. (a) Cliques A, B, and C have 13, 7, and 4 nodes respectively. There are 56 connecting edges between cliques A and B and 13 connecting edges between cliques B and C.; (b) Cliques A, B, and C have 11, 7, and 4 nodes respectively. There are 35 connecting edges between cliques A and B and 10 connecting edges between cliques B and C.; (c) Cliques A, B, and C have 8, 6, and 6 nodes respectively. There are 8 connecting edges between cliques A and B and 18 connecting edges between cliques B and C.
Figure 2. Top three 3-clique-2-bipartite modules for BRCA. Yellow nodes: Clique-A, gray nodes: Clique-B, Orange nodes: Clique-C. Blue: Intra-clique edges, Red: Inter-clique edges. (a) Cliques A, B, and C have 13, 7, and 4 nodes respectively. There are 56 connecting edges between cliques A and B and 13 connecting edges between cliques B and C.; (b) Cliques A, B, and C have 11, 7, and 4 nodes respectively. There are 35 connecting edges between cliques A and B and 10 connecting edges between cliques B and C.; (c) Cliques A, B, and C have 8, 6, and 6 nodes respectively. There are 8 connecting edges between cliques A and B and 18 connecting edges between cliques B and C.
Data 04 00081 g002
Data 04 00081 g003 550
Figure 3. Validation process using two metrics. Metric-1: Top-20 genes from 12 scoring methods of CytoHubba; Metric-2: Top-50 genes from 12 scoring methods of CytoHubba.
Figure 3. Validation process using two metrics. Metric-1: Top-20 genes from 12 scoring methods of CytoHubba; Metric-2: Top-50 genes from 12 scoring methods of CytoHubba.
Data 04 00081 g003
Data 04 00081 g004 550
Figure 4. Survival Analysis in data sets of BRCA (a), COAD (b), and GBM (c) cancer patients, using their respective key genes as prognostic factors. The Kaplan–Meyer curve in blue is for the low-risk group and in orange for the high-risk group. The shaded blue and orange regions around their respective lines indicate the confidence interval. The y-axis is the probability of survival and the x-axis is the duration in days.
Figure 4. Survival Analysis in data sets of BRCA (a), COAD (b), and GBM (c) cancer patients, using their respective key genes as prognostic factors. The Kaplan–Meyer curve in blue is for the low-risk group and in orange for the high-risk group. The shaded blue and orange regions around their respective lines indicate the confidence interval. The y-axis is the probability of survival and the x-axis is the duration in days.
Data 04 00081 g004
Table
Table 1. Topology of gene co-expression network with PCC > 0.9.
Table 1. Topology of gene co-expression network with PCC > 0.9.
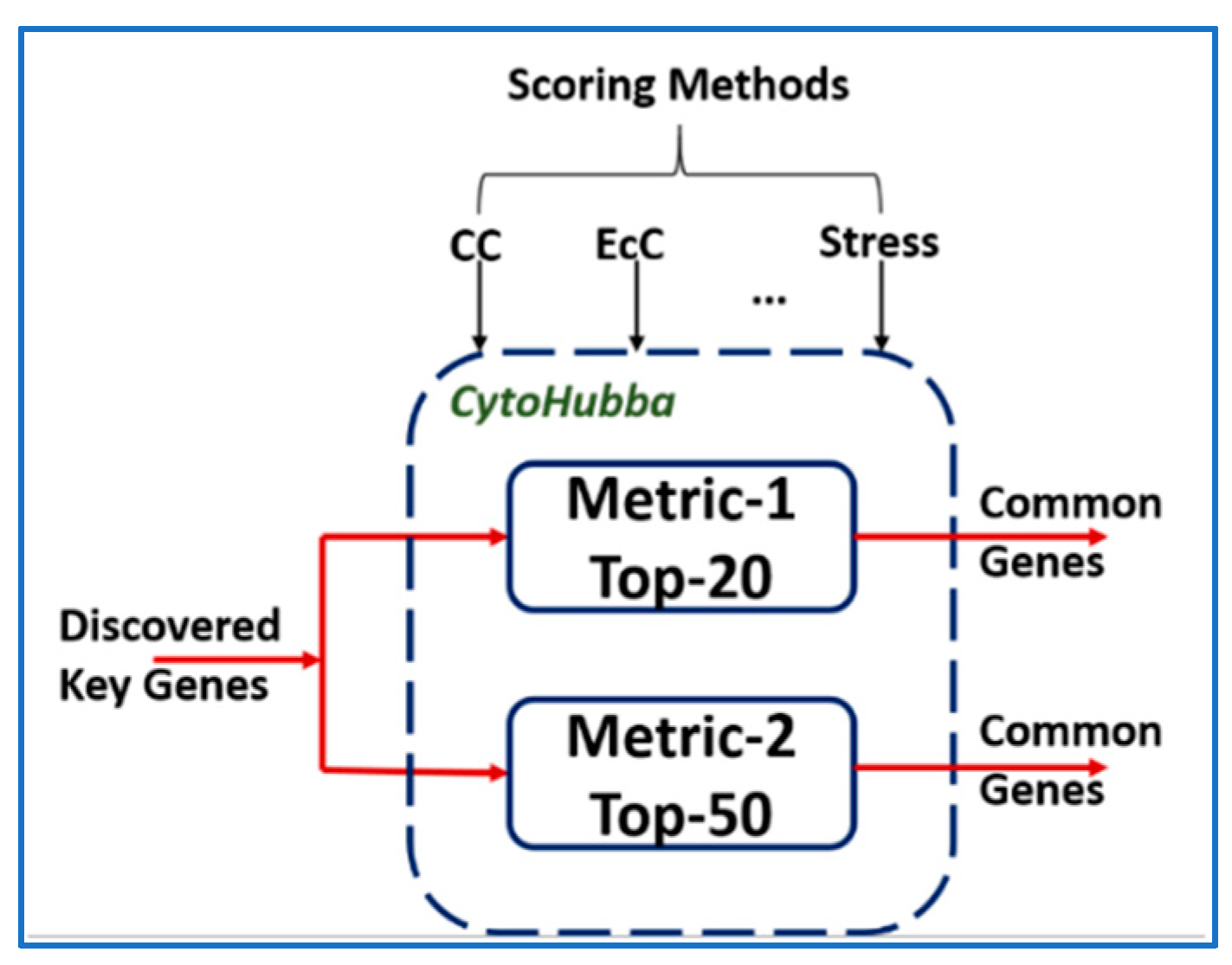
Cancer Name# Of Genes# Of EdgesMax DegreeMin DegreeAvg Degree
BRCA38010343915.4
COAD607365175112.0
GBM50612434914.9
Table
Table 2. List of genes in maximal clique-like modules for three Cancers—BRCA, COAD, and GBM.
Table 2. List of genes in maximal clique-like modules for three Cancers—BRCA, COAD, and GBM.
CancerList of Genes in Maximal Clique-Like Modules
BRCACD2, CD247, CD3D, CD3E, CD5, CD96, CXCR3, IL2RG, LCK, LY9, PTPN7, SH2D1A, SIRPG, SIT1, SLA2, SLAMF1, SLAMF6, TBX21, UBASH3A
COADC1QB, C1QC, C3AR1, CD300A, CD4, CD53, CD86, CLEC7A, CSF1R, CYBB, CYTH4, DOK2, FCER1G, FPR3, HAVCR2, HCK, ITGB2, LAIR1, LAPTM5, LILRB1, LILRB4, LRRC25, MS4A4A, PDCD1LG2, SIGLEC7, SIGLEC9, SLAMF8, SPI1, TFEC, TYROBP
GBMALOX5, CD4, FERMT3, HCK, ITGB2, LAIR1, LAPTM5, NCKAP1L, PTPN6, SASH3, SPI1, STXBP2, VAV1, WAS
Table
Table 3. List of genes in 2-clique-1-bipartite modules.
Table 3. List of genes in 2-clique-1-bipartite modules.
BRCACOADGBM
Clique1CCL5, CD2, CD247, CD3D, CD3E, CXCR3, GZMA, IL2RG, SIRPG, SLA2, TBX21C1QB, C1QC, C3AR1, CD163, CLEC7A, CMKLR1, CSF1R, FPR3, HCK, ITGB2, LAIR1, LILRB2, LRRC25, SIGLEC7, SLAMF8, TLR8CD68, FERMT3, HCK, ITGB2, LAIR1, LAPTM5, LRRC25, SIGLEC9
Clique2BTLA, ITK, LY9, PYHIN1, SH2D1A, SLAMF1, SLAMF6, TRAT1, ZNF831CD4, CD53, CD86, CYBB, CYTH4, DOCK2, DOK2, LAPTM5, LCP2, LILRB1, NCKAP1L, SLA, SPI1CD4, CD53, LILRB4, NCKAP1L, PTPN6, SASH3, SPI1, VAV1
Table
Table 4. Summary statistics of 3-clique-2-bipartite modules.
Table 4. Summary statistics of 3-clique-2-bipartite modules.
Clique-AClique-BClique-CConnections A-BConnections B-C
BRCA-Module1 13745613
BRCA-Module211743510
BRCA-Module3866818
COAD-Module1161478553
COAD-Module21614611151
COAD-Module3161276940
GBM-Module19953019
GBM-Module29762223
GBM-Module39743614
Table
Table 5. Combined list of genes from top three 3-clique-2 bipartite modules.
Table 5. Combined list of genes from top three 3-clique-2 bipartite modules.
List of Genes
BRCA-ModulesACAP1, CCL5, CD2, CD247, CD3D, CD3E, CD3G, CD5, CD53, CD96, CXCR3, CXCR6, DOCK2, EVI2B, FYB, GZMA, GZMM, IKZF1, IL2RG, ITK, LCP2, LY9, NCKAP1L, PLEK, PRF1, PRKCB, PTPRC, PTPRCAP, PYHIN1, S1PR4, SH2D1A, SIRPG, SIT1, SLA2, SLAMF1, SLAMF6, SPN, TBC1D10C, TBX21, THEMIS, TRAT1, UBASH3A, ZAP70, ZNF831
COAD-ModulesAPBB1IP, ARHGAP30, ARHGAP9, BTK, C3AR1, CD163, CD4, CD53, CD84, CD86, CLEC7A, CSF1R, CYBB, CYTH4, DOCK10, DOCK2, FPR3, HAVCR2, HCK, HCLS1, IKZF1, IL10RA, ITGAL, ITGB2, ITK, KLHL6, LAIR1, LAPTM5, LILRB1, LILRB4, LRRC25, MAP4K1, MNDA, MYO1G, NCKAP1L, PIK3R5, PTPRC, RASAL3, SASH3, SIGLEC7, SIGLEC9, SIRPB2, SLA, SLAMF8, SPI1, TBC1D10C, TRAF3IP3, WAS
GBM-ModulesARHGAP30, ARL11, C1QA, C1QB, C1QC, CD33, CD4, CD53, CD68, CD86, CSF1R, DOCK2, DOCK8, FCER1G, FCGR3A, FERMT3, HCK, IKZF1, ITGB2, LAIR1, LAPTM5, MYO1F, NCF4, NCKAP1L, PLCG2, SASH3, SPI1, STXBP2, SYK, TYROBP, VAMP8, VAV1
Table
Table 6. Summary of validation.
Table 6. Summary of validation.
Dataset.Key GenesKeys Genes Common with
Metric-1Metric-2
BRCA472645
COAD612353
GBM382536
Table
Table 7. Summary of gene expression data for BRCA, COAD, and GBM.
Table 7. Summary of gene expression data for BRCA, COAD, and GBM.
Cancer No of GenesNo of SamplesReduced no of Genes
Breast invasive carcinoma (BRCA)20,155109316,011
Colorectal adenocarcinoma (COAD)19,82837915,769
Glioblastoma multiforme (GBM)19,66015316,186

Share and Cite

MDPI and ACS Style

Tanvir, R.B.; Aqila, T.; Maharjan, M.; Mamun, A.A.; Mondal, A.M. Graph Theoretic and Pearson Correlation-Based Discovery of Network Biomarkers for Cancer. Data 2019, 4, 81. https://doi.org/10.3390/data4020081

AMA Style

Tanvir RB, Aqila T, Maharjan M, Mamun AA, Mondal AM. Graph Theoretic and Pearson Correlation-Based Discovery of Network Biomarkers for Cancer. Data. 2019; 4(2):81. https://doi.org/10.3390/data4020081

Chicago/Turabian Style

Tanvir, Raihanul Bari, Tasmia Aqila, Mona Maharjan, Abdullah Al Mamun, and Ananda Mohan Mondal. 2019. "Graph Theoretic and Pearson Correlation-Based Discovery of Network Biomarkers for Cancer" Data 4, no. 2: 81. https://doi.org/10.3390/data4020081

Article Metrics

Back to TopTop