Machine Learning in Classification Time Series with Fractal Properties †
Abstract
1. Introduction
2. Materials and Methods
2.1. Characteristics and Models of Fractal Random Processes
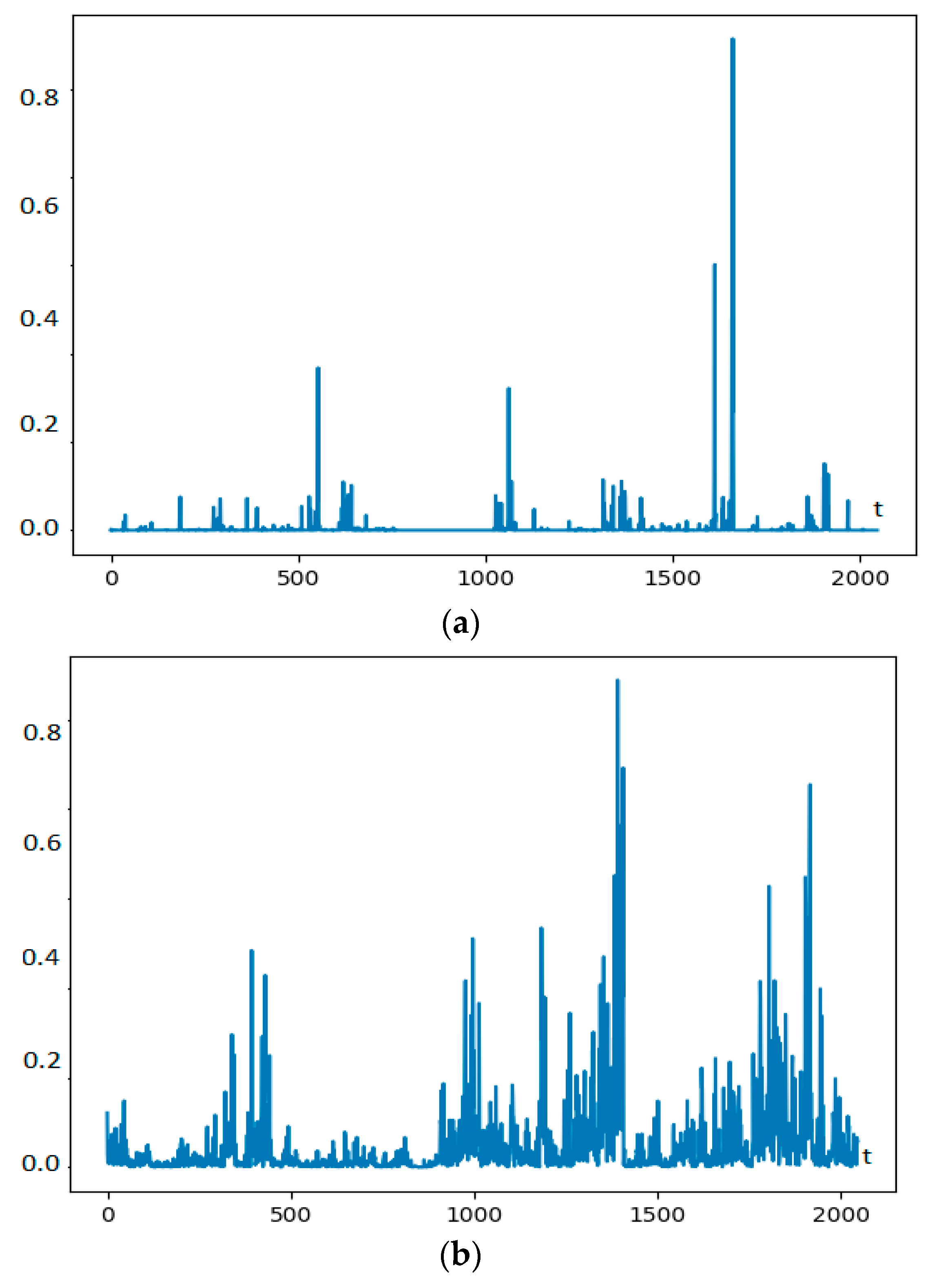
2.2. Time Series Estimation of Fractal Characteristics
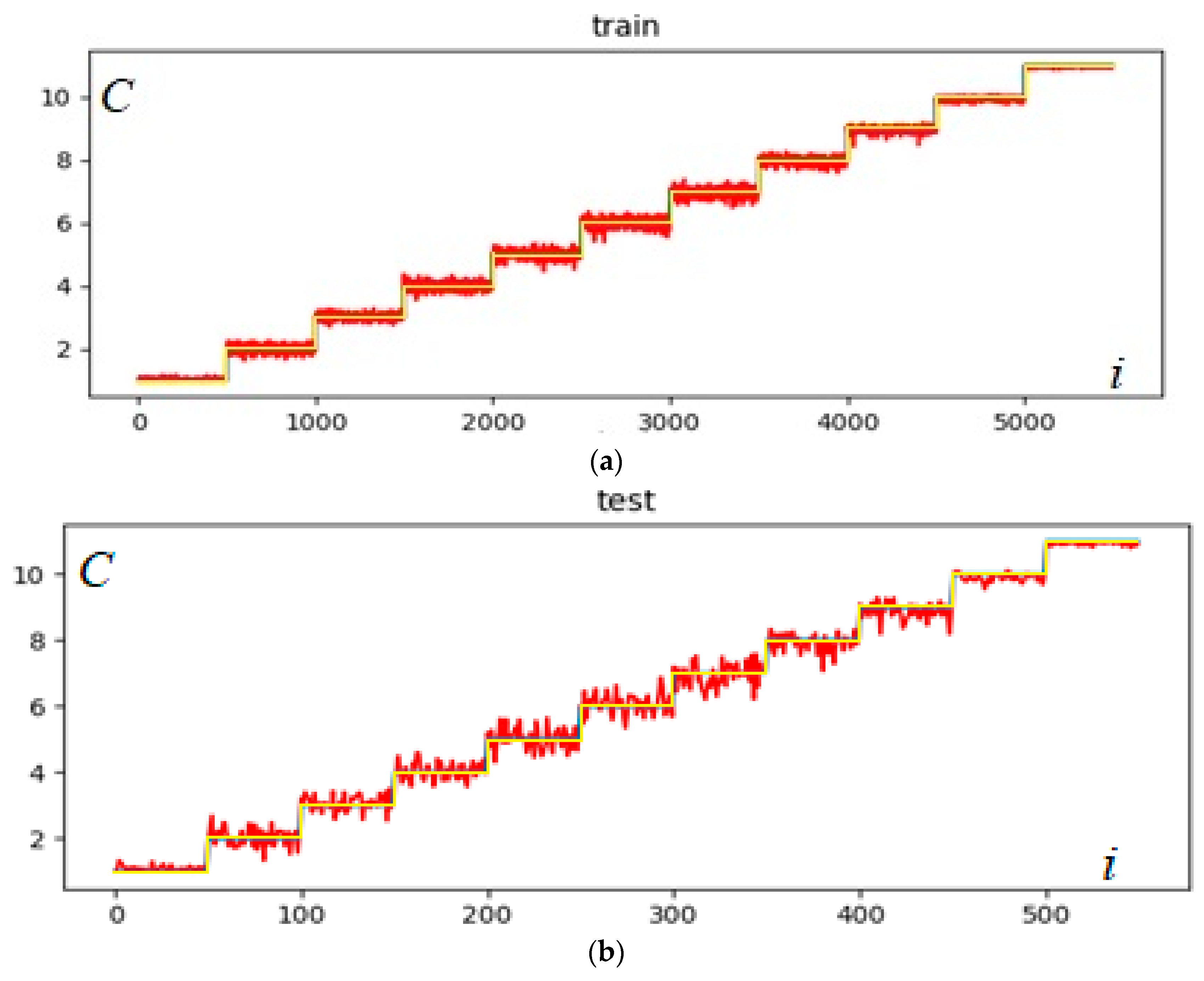
2.3. Time Series Classification Using Decision Tree Methods
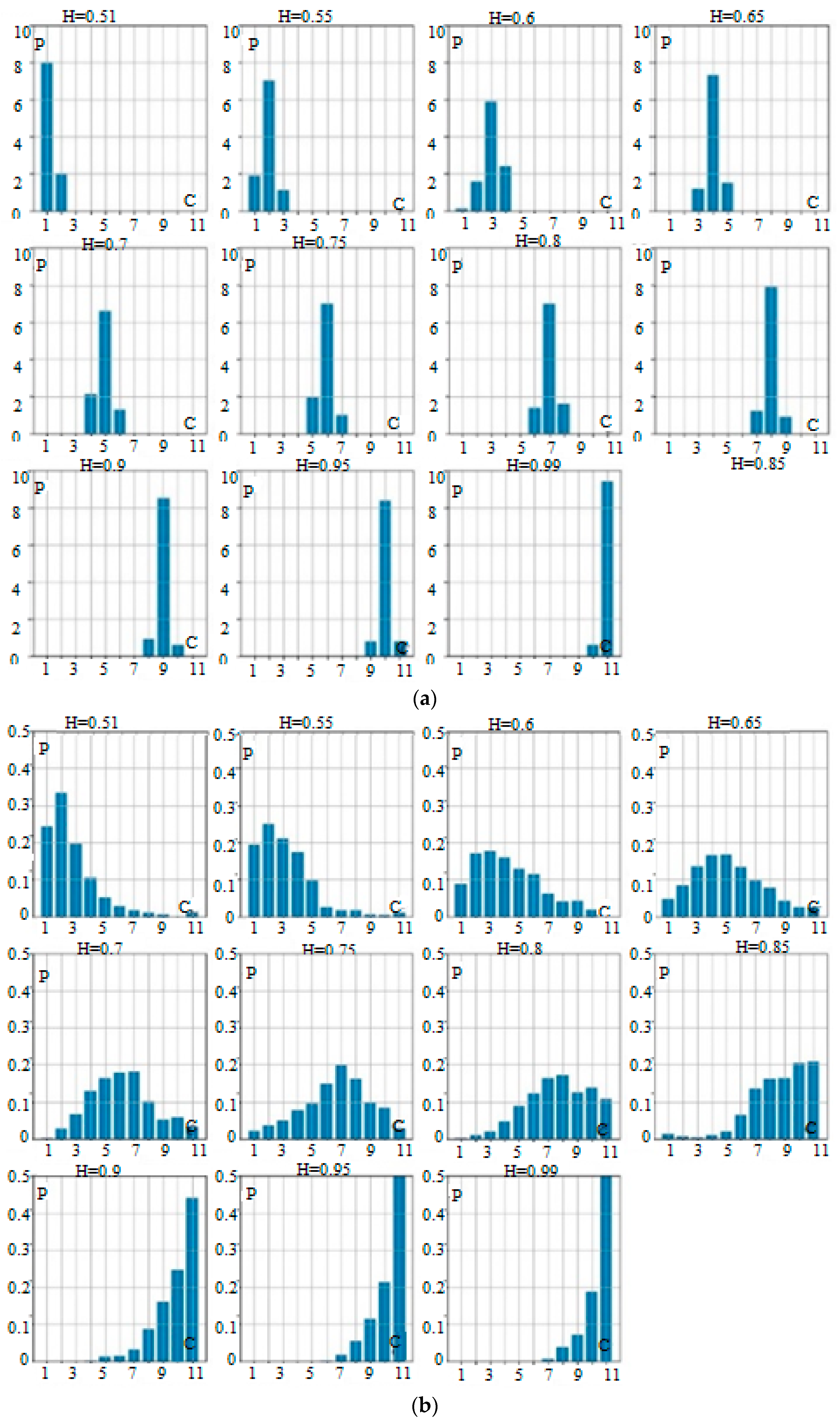
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Esling, P.; Agon, C. Time series data mining. ACM Comput. Surv. 2012, 45, 12:1–12:34. [Google Scholar] [CrossRef]
- Ben, D. Feature-Based Time-Series Analysis. 2017. Available online: https://arxiv.org/abs/1709.08055 (accessed on 26 October 2018).
- Bagnall, A.; Lines, J.; Bostrom, A.; Large, J.; Keogh, E. The great time series classification bake off: A review and experimental evaluation of recent algorithmic advances. Data Min. Knowl. Discov. 2017, 31, 606–660. [Google Scholar] [CrossRef]
- Kirichenko, L.; Radivilova, T.; Zinkevich, I. Comparative Analysis of Conversion Series Forecasting in E-commerce Tasks. In Advances in Intelligent Systems and Computing II. CSIT 2017; Shakhovska, N., Stepashko, V., Eds.; Springer: Cham, Switzerland, 2018; Volume 689, pp. 230–242. [Google Scholar] [CrossRef]
- Brambila, F. Fractal Analysis—Applications in Physics, Engineering and Technology. Available online: https://www.intechopen.com/books/fractal-analysis-applications-in-physics-engineering-and-technology (accessed on 28 October 2018).
- Coelho, A.L.V.; Lima, C.A.M. Assessing fractal dimension methods as feature extractors for EMG signal classification. Eng. Appl. Artif. Intell. 2014, 36, 81–98. [Google Scholar] [CrossRef]
- Symeon, S. Sentiment analysis via fractal dimension. In Proceedings of the 6th Symposium on Future Directions in Information Access, Thessaloniki, Greece, 2 September 2015; pp. 48–50. [Google Scholar] [CrossRef]
- Arjunan, S.P.; Kumar, D.K.; Naik, G.R. A machine learning based method for classification of fractal features of forearm sEMG using Twin Support vector machines. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 4821–4824. [Google Scholar] [CrossRef]
- Tyralis, H.; Dimitriadis, P.; Koutsoyiannis, D.; O’Connell, P.E.; Tzouka, K.; Iliopoulou, T. On the long-range dependence properties of annual precipitation using a global network of instrumental measurements. Adv. Water Resour. 2018, 111, 301–318. [Google Scholar] [CrossRef]
- Bulakh, V.; Kirichenko, L.; Radivilova, T. Classification of Multifractal Time Series by Decision Tree Methods. In Proceedings of the 14th International Conference ICTERI 2018 ICT in Education, Research, and Industrial Applications, Kyiv, Ukraine, 14–17 May 2018; pp. 1–4. [Google Scholar]
- Bulakh, V.; Kirichenko, L.; Radivilova, T. Time Series Classification Based on Fractal Properties. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 198–201. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Shelukhin, O.I.; Smolskiy, S.M.; Osin, A.V. Self-Similar Processes in Telecommunications; John Wiley & Sons: New York, NY, USA, 2007; 320p. [Google Scholar]
- Kaur, G.; Saxena, V.; Gupta, J. Detection of TCP targeted high bandwidth attacks using self-similarity. J. King Saud Univ. Comput. Inf. Sci. 2017. [Google Scholar] [CrossRef]
- Deka, R.; Bhattacharyya, D. Self-similarity based DDoS attack detection using Hurst parameter. Secur. Commun. Netw. 2016, 9, 4468–4481. [Google Scholar] [CrossRef]
- Popa, S.M.; Manea, G.M. Using Traffic Self-Similarity for Network Anomalies Detection. In Proceedings of the 2015 20th International Conference on Control Systems and Computer Science, Bucharest, Romania, 27–29 May 2015; pp. 639–644. [Google Scholar] [CrossRef]
- Bulakh, V.; Kirichenko, L.; Radivilova, T.; Ageiev, D. Intrusion Detection of Traffic Realizations Based on Maching Learning using Fractal Properties. In Proceedings of the 2018 International Conference on Information and Telecommunication Technologies and Radio Electronics (UkrMiCo), Odessa, Ukraine, 10–14 September 2018; pp. 1–4. [Google Scholar]
- Riedi, R.H. Multifractal Processes. Available online: https://www.researchgate.net/publication/2839202_Multifractal_Processes (accessed on 27 December 2018).
- Kirichenko, L.; Radivilova, T.; Kayali, E. Modeling telecommunications traffic using the stochastic multifractal cascade process. Radio Electron. Comput. Sci. Control 2012, 55–63. [Google Scholar] [CrossRef]
- Kantelhardt, J. W.; Zschiegner, S. A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Taqqu, M.; Teverovsky, V.; Willinger, W. Estimators for long-range dependence: An empirical study. Fractals 1995, 3, 785–798. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D. Simultaneous estimation of the parameters of the Hurst–Kolmogorov stochastic process. Stoch. Environ. Res. Risk Assess. 2011, 25, 21–33. [Google Scholar] [CrossRef]
- Rea, W.; Oxley, L.; Reale, M.; Brown, J. Estimators for long range dependence: An empirical study. Electron. J. Stat. 2009. Available online: https://arxiv.org/pdf/0901.0762.pdf (accessed on 10 December 2018).
- Kantelhardt, J.W. Fractal and Multifractal Time Series. 2008. Available online: https://arxiv.org/abs/0804.0747 (accessed on 2 December 2018).
- Tyralis, H.; Koutsoyiannis, D. A Bayesian statistical model for deriving the predictive distribution of hydroclimatic variables. Clim. Dyn. 2014, 42, 2867–2883. [Google Scholar] [CrossRef]
- Kirichenko, L.; Radivilova, T.; Bulakh, V. Generalized approach to Hurst exponent estimating by time series. Inform. Autom. Pomiary Gospod. Ochr. Środowiska 2018, 8, 28–31. [Google Scholar] [CrossRef]
- Kirichenko, L.; Radivilova, T.; Deineko, Z. Comparative Analysis for Estimating of the Hurst Exponent for Stationary and Nonstationary Time Series. Inf. Technol. Knowl. 2011, 5, 371–388. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993; 302p. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cielen, D.; Meysman, A.; Ali, M. Introducing Data Science: Big Data, Machine Learning, and More, Using Python Tools; Manning Publications: Shelter Island, NY, USA, 2016; ISBN 9781633430037. [Google Scholar]
- Chicco, D. Ten quick tips for machine learning in computational biology. Biodata Min. 2017. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Series in Statistics; Springer: New York, NY, USA, 2009; 764p. [Google Scholar] [CrossRef]
- Al-kasassbeh, M.; Al-Naymat, G.; Al-Hawari, E. Towards Generating Realistic SNMP-MIB Dataset for Network Anomaly Detection. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 1162–1185. [Google Scholar]
- Ivanisenko, I.; Kirichenko, L.; Radivilova, T. Investigation of self-similar properties of additive data traffic. In Proceedings of the 2015 Xth International Scientific and Technical Conference “Computer Sciences and Information Technologies” (CSIT), Lviv, Ukraine, 14–17 September 2015; pp. 169–171. [Google Scholar] [CrossRef]
- Ivanisenko, I.; Kirichenko, L.; Radivilova, T. Investigation of multifractal properties of additive data stream. In Proceedings of the 2016 IEEE First International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 23–27 August 2016; pp. 305–308. [Google Scholar] [CrossRef]

| 500 | 1000 | 2000 | 4000 | |
| 0.085 | 0.07 | 0.055 | 0.045 |
| Time Series Length | Bagging | Random Forest | ||
|---|---|---|---|---|
| Classification Trees | Regression Trees | Classification Trees | Regression Trees | |
| 512 | 0.635 | 0.777 | 0.811 | 0.835 |
| 1024 | 0.644 | 0.842 | 0.822 | 0.882 |
| 2048 | 0.665 | 0.834 | 0.834 | 0.912 |
| 4096 | 0.701 | 0.878 | 0.851 | 0.922 |
| Length | Random Forest | Time Series Estimate H | |
|---|---|---|---|
| P | P | ||
| 11 classes | 512 | 0.72 | 0.18 |
| 4096 | 0.76 | 0.25 | |
| 2 classes | 512 | 0.94 | 0.75 |
| 4096 | 0.96 | 0.78 |
| H | 0.51–0.6 | 0.6–0.7 | 0.7–0.8 | 0.8–0.9 | 0.9–0.99 |
| Probability | 0.96 | 0.91 | 0.85 | 0.76 | 0.68 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirichenko, L.; Radivilova, T.; Bulakh, V. Machine Learning in Classification Time Series with Fractal Properties. Data 2019, 4, 5. https://doi.org/10.3390/data4010005
Kirichenko L, Radivilova T, Bulakh V. Machine Learning in Classification Time Series with Fractal Properties. Data. 2019; 4(1):5. https://doi.org/10.3390/data4010005
Chicago/Turabian StyleKirichenko, Lyudmyla, Tamara Radivilova, and Vitalii Bulakh. 2019. "Machine Learning in Classification Time Series with Fractal Properties" Data 4, no. 1: 5. https://doi.org/10.3390/data4010005
APA StyleKirichenko, L., Radivilova, T., & Bulakh, V. (2019). Machine Learning in Classification Time Series with Fractal Properties. Data, 4(1), 5. https://doi.org/10.3390/data4010005





