1. Introduction
Classification and clustering relate to the main tasks in data stream analysis. They mean the distribution of objects between groups with not known properties in advance. In video analytics, there is a task that arises often; when it needs to find the specified objects the video sequence and track their movement in the frame. Another problem is the object state changes detection, which remains within the frame for a long time. Video streams are characterized by a non-Gaussian nature. Many methods of clustering and classification have been developed for their analysis. Among these methods, a large group consists of methods based on the use of ANNs. A classic approach can be found in [
1]. Modern classification and clustering systems often use SVM, which provide high accuracy [
2,
3,
4,
5]. Solutions were also obtained for weighted fuzzy support vector regression [
6], radial basis networks [
7].
Specifically, Deep Neural Networks (DNN) [
8,
9,
10,
11] have been given in terms of classification accuracy. This line of research turned out to be very promising, convolutional neural networks (CNN) and deep learning are widely used in the pattern recognition tasks, especially for image, audio and video streams classifying and clustering. For recognition of Chinese characters, a convolutional network with the RNN Framework is proposed in [
12]. The Levenberg–Marquardt network [
13] is used in the diagnostic task for medical photos. Deep recurrent architecture was at the heart of the system for remote sensing image classification [
14]. However, DNNs are not prone to certain shortcomings, with a low speed of multiepoch learning being the major limitation, leading to their inefficiency in a subclass Data Stream Mining tasks, when information is fed to the system in a sequential mode (quite large volume of training sets that are not always available). Furthermore, in real-world tasks, image clusters are often mutually overlapped, which calls for L. Zadeh’s fuzzy logic classification methods. In this case, hybrid systems of computational intelligence [
15,
16] come in handy, since they both possess the learning capabilities of ANN and DNN and, being a fuzzy systems, are capable of distinguishing overlapping classes. The training speed of such systems calls for attention which requires the use of non-standard neurons, architectures and teaching methods.
In [
17], the mixed fuzzy clustering algorithm for health care problems where time series analysis is necessary was proposed. Another hybrid structure discussed in [
18] is the deep TSK classifier which uses interpreted linguistic rules for a fuzzy inference system.
The high training speed of the hybrid systems requires the use of non-standard neurons, architectures and teaching methods.
In this paper, we consider an approach to constructing a hybrid system that performs the multidimensional data classification using neo-fuzzy neurons. The structure was developed for the problem of emotion estimation by images and video streams. Therefore,
Section 2 describes previous works that are relevant to this task.
Section 3 describes in detail the architecture of classification system.
Section 4 is devoted to the learning algorithm of the neo-fuzzy structure.
Section 5 discusses the results of experiments, and the conclusions are presented in
Section 6.
2. Related Work
Many important practical tasks in the video analytics, such as health care and life support, crowd analytics, surveillance, man-machine interface and so on, are now associated with systems capable to recognize the emotional status [
19]. Researches in this area are connected with primary data gathering methods on video and audio streams [
20,
21] and with methods for human emotions online classification, clustering and recognition [
22,
23,
24]. Artificial neural networks are particularly effective in analyzing nonlinear processes in real-time; so, many researchers use them to identify human facial expressions. In [
25,
26], the use of genetic algorithms is considered; in [
27] the use of cascaded continuous regression; in [
28] the use of shallow neural networks. Reference [
6] describes a fuzzy system for emotional intent classifying, while [
29] describes the affect estimation by audio stream using ensemble of ordinal classifiers. Many works have been devoted to the recognition of emotions from photos and videos using deep CNN, for example [
30,
31].
The proposed system is based on the neo-fuzzy approach [
32,
33,
34], which provides high approximating properties and, therefore, can be applied in solving a number of real practical tasks [
35,
36]. It is also important to note that a neo-fuzzy system learning rate can be optimized [
37], which allows using it in real-time Data Stream Mining tasks.
3. The Architecture of the Neo-Fuzzy Classification System
Neo-fuzzy neuron modifications, such as extended neo-fuzzy neurons (ENFN) [
38,
39,
40] and neo-fuzzy units (NFU) [
41,
42,
43] with nonlinear activation (sigmoidal) functions have significantly improved approximating capabilities. In the system proposed here, we suggest utilizing a hybrid neo-fuzzy unit, which is a modification of an NFU which replaces the standard nonlinear synapses (NS) with extended nonlinear synapses (ENS) taking advantage of the neuro-fuzzy Takagi-Sugeno–Kang arbitrary order system properties.
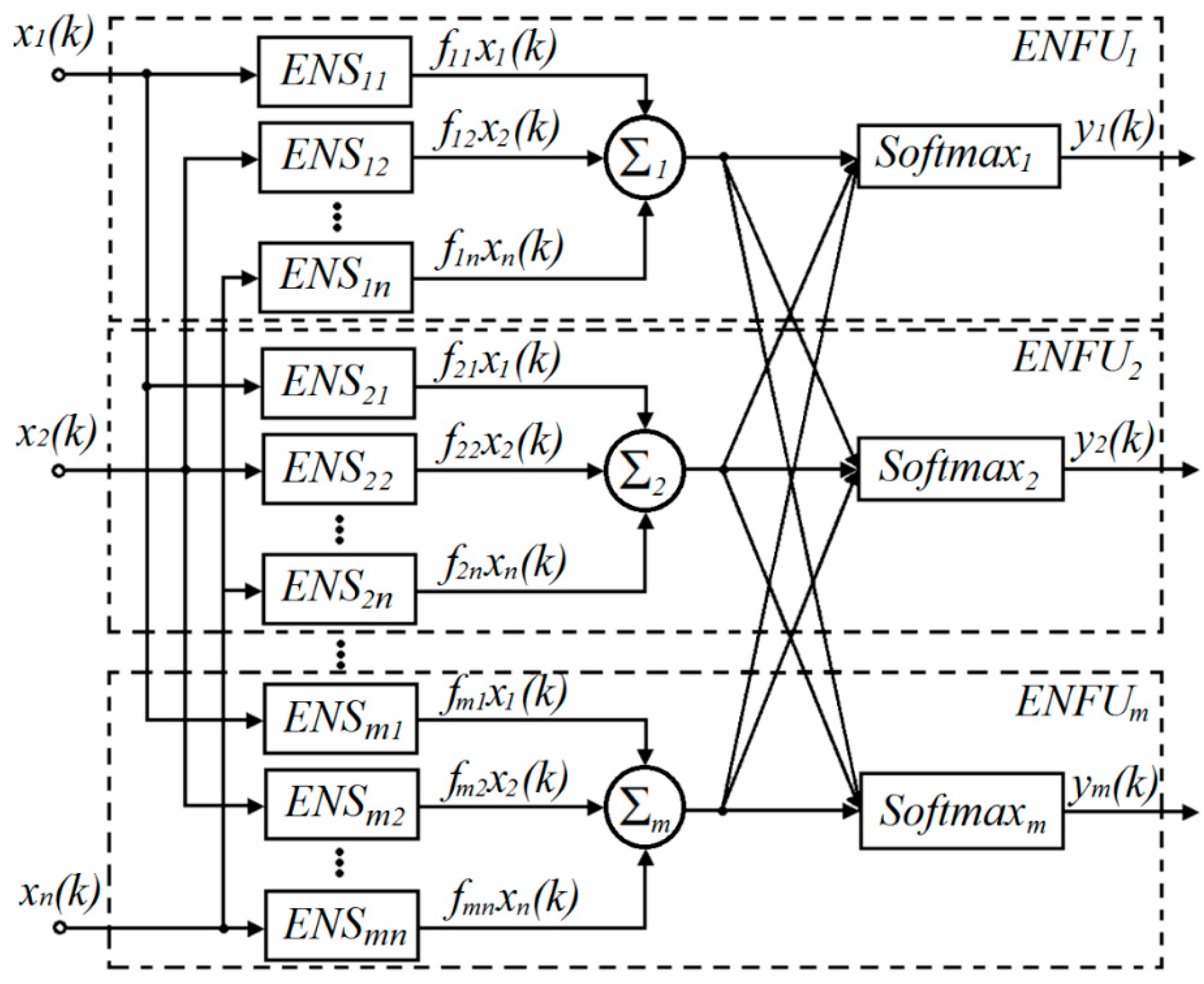
Figure 1 shows the proposed extended multidimensional neo-fuzzy system (EMNFS) architecture with two information processing layers.
The vector signal
of images to be classified is fed to the inputs of the system, where
is the index of the current discrete time. The first layer of the system is formed by extended nonlinear synapses (ENS), where
, m is the number of possible classes. For each
j-th class, n such synapses ENS
j1, ENS
j2,..., ENS
jn, whose output signals
are fed to the summation blocks
, are used. ENS
ji synapses and adders
form extended neo-fuzzy neurons (ENFN) [
38,
39]. ENFN output signals are fed to the second output layer of the system, formed by nonlinear softmax activation functions:
which are the generalization of traditional sigmoidal activation functions
for classification systems with many outputs [
10]. ENFN
j together with functions
form extended neo-fuzzy units (ENFU), which are a generalization of neo-fuzzy units introduced in [
40,
41]. Output signals of the system
specify the levels of presented input image
fuzzy membership to each of the possible m classes.
As is known [
32,
33,
34], the standard neo-fuzzy neuron is formed by n nonlinear synapses; each of them implements the fuzzy derivation of the Takagi–Sugeno–Kang of zero order (Wang–Mendel reasoning)
where h is the number of membership functions
in the nonlinear synapse,
adjustable synaptic weights,
synapse number in the neo-fuzzy neuron.
The extended nonlinear synapse introduced in [
38,
39] implements the Takagi–Sugeno–Kang inference of arbitrary order, that is:
By introducing for ENS
ji a vector of synaptic weights
and fuzzyficated signals
of dimensionality
, we can write the output of this synapse in the form
Further, it is easy to write the output of each ENFN
j as a whole in the form
Introducing the vectors of ENFN
j synaptic weights
and fuzzyficated inputs
of the
dimensionality, the output signal ENFN
j can be rewritten in compact form:
This signal is then fed to the activation function of the output layer, and a whole resulting system output form the values of the fuzzy membership levels of the presented image
to the
j-th class:
where
are the values of the synaptic weights obtained as a result of learning on previous
images.
4. Learning of the Extended Multidimensional Neo-Fuzzy System in the Pattern Recognition Task
To learn the considered system, it is advisable to use the cross-entropy learning criterion [
1,
33]
and the one-hot coding of the reference signal, when the vector external reference signal
is formed by zeros and a single unit located in a position corresponding to the “correct” class.
Minimizing the criterion (3) with the standard gradient procedure leads to the δ-rule setting of the synaptic weights of each ENFU
j in the form
where
is the learning rate parameter of
j-th ENFU,
a learning error, while the
j-th component of vector reference signal
can take only two values—0 or 1.
Algorithm (4) can be given both filtering and tracking properties, if the parameter
is chosen in accordance with the relation [
37]
where
is the forgetting factor. Depending on the value of α, procedures (4),(5) can take stochastic approximation properties for α = 1 (Goodwin–Ramadge–Caines algorithm) [
42] or for α = 0 the procedure takes the form of the optimal Kaczmarz–Widrow–Hoff algorithm [
43], which provides the maximal speed of convergence to optimal solution.
5. Experiments
Among the areas where real-time recognition results are extremely important, we highlight human–computer interfaces of various kinds. In many situations, the psycho-emotional state of one person, for example, wakefulness of vehicles drivers and nuclear objects operators are crucial. Just as in the care of seriously ill or lonely patients, it is sometimes necessary to carry out continuous monitoring of their condition and timely detection of deviations.
The problem of emotional status recognition is further complicated by the fact that people often perceive not one, but a whole range of emotions. In this range, individual emotions can be expressed in varying degrees, forming a certain combination. In communication, people “read” these degrees of individual emotion expression, and, by their specific weight, they form an idea of the state of the interlocutor. Thus, the basic emotions can be represented in the form of fuzzy variables, which are expressed by their membership value, which lies within the limits [0; 1]. Obviously, the automatic recognition system should then produce the appropriate output signal. The advantage of the approach proposed in this paper is that the output layer of the extended multidimensional neo-fuzzy system forms a vector whose elements are in the desired range [
1].
To study the designed architecture and learning algorithm an experiment on basic emotions recognition was performed. The images from PICS and CK+ open databases [
44,
45] were used as the objects for recognition. PICS image database consists of single images of individuals in different emotional states. The CK+ database contains separate frames from video sequences with transitions between different emotional states of dozens of people. In all the photos, people are photographed from the front, without tilting the head, in standard lighting, with the same distance from the camera. 87 photos were taken from the base of the CK+, 257 from the PICS base; on the selected images, there are reflections of pure emotions only.
Using some contour detectors like SURF, BRISK or Shi-Tomasi [
46,
47,
48], we had obtain feature points for every selected image. Input data vector contain X and Y coordinates of 35 features, including such points like, for example:
The point’s placement can indicate the basic facial actions of the FACS system in the facial dynamics (
Figure 2). Chosen feature points are connected with Facial action units and allow recognizing investigated emotions.
The output vector corresponds to a set of seven simplest emotions (neutral, exasperation; distaste; anxiety; grief; astonishment; joy). The number of neo-fuzzy neurons in the first layer varying from 3 to 11.
The learning data contains 344 images, learning repeated from 10 to 10,000 epochs. This paper deals with the case when the data for learning is small. To assess whether the proposed architecture is able to recognize facial expressions, small sets of photos are used. Each set contained no more than 100 pictures.
The network was being learned to recognize emotions by a set of photos grouped for one given facial expression. Then, the system was put into fuzzy-reasoning mode. Proposed architecture approximating ability was examined on an integrated data set, where photos with different emotions were mixed, and their total number was 344. The learning set consists of 60% of all photos, selected randomly from 344. To test the model used the remaining 40%. The experiments were carried out more than 30 times; before each run, the initial data was smashed so that in different experiments the learning and testing data did not coincide. The final results of the experiments are quite close to each other, and the difference did not exceed 2–3%.
The network learning error is shown in
Table 1 as number of unrecognized emotions depending on the number of learning epochs and the number of neo-fuzzy neurons. The number of membership functions in every nonlinear synapse in neo-fuzzy neuron was 3.
6. Conclusions
This article proposes an extended multidimensional system, based on neo-fuzzy neuron modifications, specifically, extended multidimensional neo-fuzzy units, with improved approximating properties.
Experiments have shown that three to five neo-fuzzy neurons in the classification system input layer provides low accuracy, which cannot be enhanced only by learning epochs number increasing. At the same time, an increment of a neo-fuzzy neuron number in the input layer dramatically increases the classification accuracy. The experiments also varied the number of terms in nonlinear synapses from three to seven and changed the Takagi–Sugeno’s fuzzy inference order. However, this factor did not have a significant impact on improving the classification accuracy and, therefore, the results of these experiments are not given in the table.
The proposed system is designed to solve image recognition problems, including overlapping classes tasks, when information is submitted for processing in an online mode. The proposed learning algorithm demonstrates both high conversion rate and additional filtering properties. Carried out experiments proved the proposed system to be efficient in solving emotion recognition tasks as well as its declared simplicity.
Author Contributions
Y.B.: conceptualization, formal analysis, methodology, writing—original draft; N.K.: data curation, investigation, validation; O.C.: visualization, writing—review & editing.
Funding
This research received no external funding.
Acknowledgments
The authors thank the administration of the Kharkov National University of Radio Electronics for the administrative support of the research performed.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bishop, C.M. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK, 1995; 482p, ISBN 354064928X, 9783540649281. [Google Scholar]
- Lin, S.-B.; Zeng, J.; Chang, X. Learning rates for classification with Gaussian kernels. Neural Comput. 2017, 29, 3353–3380. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.; Wang, Z.; Zhuo, L.; Wang, J.; Chi, Z.; Feng, D. Learning realistic facial expressions from web images. Pattern Recognit. 2013, 46, 2144–2155. [Google Scholar] [CrossRef]
- Madani, A.; Yusof, R. Traffic sign recognition based on color, shape, and pictogram classification using support vector machines. Neural Comput. Appl. 2018, 30, 2807–2817. [Google Scholar] [CrossRef]
- Furkan, A.; Ali, A.; Davut, H. Leaf recognition based on artificial neural network. In Proceedings of the 2017 International Artificial Intelligence and Data Processing Symposium (IDAP), Malatya, Turkey, 16–17 September 2017. [Google Scholar]
- Chen, L.; Zhou, M.; Wu, M.; She, J.; Liu, Z.; Dong, F.; Hirota, K. Three-layer weighted fuzzy support vector regression for emotional intention understanding in human–robot interaction. IEEE Trans. Fuzzy Syst. 2018, 26, 2524–2538. [Google Scholar] [CrossRef]
- Vantigodi, S.; Radhakrishnan, V.B. Action recognition from motion capture data using Meta-Cognitive RBF network classifier. In Proceedings of the 2014 IEEE Ninth International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Singapore, 21–24 April 2014. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Goodfellow, J.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 9780262035613. [Google Scholar]
- Graupe, D. Deep Learning Neural Networks Design and Case Studies; World Scientific: Singapore, 2016; ISBN 9813146451. [Google Scholar]
- Zhang, X.-Y.; Yin, F.; Zhang, Y.-M.; Liu, C.-L.; Bengio, Y. Drawing and recognizing chinese characters with recurrent neural network. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 849–862. [Google Scholar] [CrossRef]
- Rundo, F.; Conoci, S.; Banna, G.L.; Ortis, A.; Stanco, F.; Battiato, S. Evaluation of Levenberg–Marquardt neural networks and stacked autoencoders clustering for skin lesion analysis, screening and follow-up. IET Comput. Vis. 2017, 12, 957–962. [Google Scholar] [CrossRef]
- Lakhal, M.I.; Çevikalp, H.; Escalera, S.; Ofli, F. Recurrent neural networks for remote sensing image classification. IET Comput. Vis. 2018, 12, 1040–1045. [Google Scholar] [CrossRef]
- Mumford, C.L.; Jain, L.C. Computational Intelligence; Springer: Berlin, Germany, 2009. [Google Scholar]
- Springer Handbook on Computational Intelligence; Kacprzyk, J., Pedricz, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 978-3-662-43504-5. [Google Scholar]
- Salgado, C.M.; Viegas, J.L.; Azevedo, C.S.; Ferreira, M.C.; Vieira, S.M.; Sousa, J.M.C. Takagi–Sugeno fuzzy modeling using mixed fuzzy clustering. IEEE Trans. Fuzzy Syst. 2017, 25, 1417–1429. [Google Scholar] [CrossRef]
- Zhang, Y.; Ishibuchi, H.; Wang, S. Deep Takagi–Sugeno–Kang fuzzy classifier with shared linguistic fuzzy rules. IEEE Trans. Fuzzy Syst. 2018, 26, 1535–1549. [Google Scholar] [CrossRef]
- Sariyanidi, E.; Gunes, H.; Cavallaro, A. Automatic analysis of facial affect: A survey of registration, representation, and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1113–1133. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Hua, G. Probabilistic elastic part model: A pose-invariant representation for real-world face verification. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 918–930. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Lu, J.; Feng, J.; Zhou, J. Context-aware local binary feature learning for face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1139–1153. [Google Scholar] [CrossRef] [PubMed]
- Meier, B.B.; Elezi, I.; Amirian, M.; Dürr, O.; Stadelmann, T. Learning neural models for end-to-end clustering. In Artificial Neural Networks in Pattern Recognition. ANNPR 2018. Lecture Notes in Computer Science; Pancioni, L., Schwenker, F., Trentin, E., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Pal, S.K.; Ray, S.S.; Ganivada, A. Classification using fuzzy rough granular neural networks. In Granular Neural Networks, Pattern Recognition and Bioinformatics. Studies in Computational Intelligence; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Day, M. Emotion recognition with boosted tree classifiers. In Proceedings of the 15th ACM on International Conference on Multimodal Interaction, Sydney, Australia, 9–13 December 2013. [Google Scholar]
- Barakova, E.I.; Gorbunov, R.; Rauterberg, M. Automatic interpretation of affective facial expressions in the context of interpersonal interaction. IEEE Trans. Hum.-Mach. Syst. 2015, 45, 409–418. [Google Scholar] [CrossRef]
- Mistry, K.; Zhang, L.; Neoh, S.C.; Lim, C.P.; Fielding, B. A Micro-GA embedded PSO feature selection approach to intelligent facial emotion recognition. IEEE Trans. Cybern. 2016, 99, 1–14. [Google Scholar] [CrossRef]
- Sánchez-Lozano, E.; Tzimiropoulos, G.; Martinez, B.; De la Torre, F.; Valstar, M. A functional regression approach to facial landmark tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2037–2050. [Google Scholar] [CrossRef]
- Gogić, I.; Manhart, M.; Pandžić, I.S. Fast facial expression recognition using local binary features and shallow neural networks. Vis. Comput. 2018. [Google Scholar] [CrossRef]
- Sazadaly, M.; Pinchon, P.; Fagot, A.; Prevost, L.; Maumy-Bertrand, M. Cascade of ordinal classification and local regression for audio-based affect estimation. In Artificial Neural Networks in Pattern Recognition, Proceedings of the 8th IAPR TC3 Workshop, ANNPR 2018, Siena, Italy, 19–21 September 2018; Pancioni, L., Schwenker, F., Trentin, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Tan, Z.; Wan, J.; Lei, Z.; Zhi, R.; Guo, G.; Li, S.Z. Efficient group-n encoding and decoding for facial age estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2610–2623. [Google Scholar] [CrossRef]
- Wu, Y.; Hassner, T.; Kim, K.; Medioni, G.; Natarajan, P. Facial landmark detection with tweaked convolutional neural networks. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- Yamakawa, J.; Uchino, E.; Miki, J.; Kusanagi, H. A neo-fuzzy neuron and its application to system identification and prediction of the system behavior. In Proceedings of the 2nd International Conference on Fuzzy Logic & Neural Networks, Iizuka, Japan, 17–22 July 1992. [Google Scholar]
- Uchino, E.; Yamakawa, J. Soft computing based signal prediction, restoration and filtering. In Intelligent Hybrid Systems: Fuzzy Logic, Neural Networks and Genetic Algorithms; Ruan, D., Ed.; Kluwer Academic Publishers: Boston, MA, USA, 1997; pp. 331–349. [Google Scholar]
- Miki, J.; Yamakawa, J. Analog implementation of neo-fuzzy neuron and its on-board learning. In Computational Intelligence and Applications; Mastorakis, N.E., Ed.; WSES Press: Piraeus, Greece, 1999; pp. 144–149. [Google Scholar]
- Zurita, D.; Delgado, M.; Carino, J.A.; Ortega, J.A.; Clerc, G. Industrial Time Series Modelling by Means of the Neo-Fuzzy Neuron. IEEE Access 2016, 4, 6151–6160. [Google Scholar] [CrossRef]
- Pandit, M.; Srivastava, L.; Singh, V. On-line voltage security assessment using modified neo-fuzzy neuron based classifier. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006. [Google Scholar]
- Bodyanskiy, Y.; Kokshenev, I.; Kolodyazhniy, V. An adaptive learning algorithm for a neo-fuzzy neuron. In Proceedings of the 3rd Conference of the European Society for Fuzzy Logic and Technology, Zittau, Germany, 10–12 September 2003. [Google Scholar]
- Bodyanskiy, Y.V.; Kulishova, N.Y. Extended neo-fuzzy neuron in the task of images filtering. Radioelectron. Comput. Sci. Control 2014, 1, 112–119. [Google Scholar] [CrossRef]
- Bodyanskiy, Y.; Kulishova, N.; Malysheva, D. The Extended Neo-Fuzzy System of Computational Intelligence and its Fast Learning for Emotions Online Recognition. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018. [Google Scholar]
- Bodyanskiy, Y.; Popov, S. Multilayer network of neuro-fuzzy units in forecasting applications. Knowl. Acquis. Manag. 2008, 25, 9–14. [Google Scholar]
- Bodyanskiy, Y.; Popov, S.; Titov, M. Robust learning algorithm for networks of neuro-fuzzy units. In Innovation and Advances in Computer Sciences and Engineering; Sobh, T., Ed.; Springer: Dordrecht, Germany, 2010; pp. 343–346. [Google Scholar]
- Goodwin, G.C.; Ramage, P.J.; Caines, P.E. Discrete time stochastic adaptive control. SIAM J. Control Optim. 1981, 19, 829–853. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks. A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1999; 842p, ISBN 0780334949, 9780780334946. [Google Scholar]
- 2D face sets. Available online: http://pics.psych.stir.ac.uk/2D_face_sets.htm (accessed on 3 October 2018).
- Lucey, P.; Cohn, J.F.; Kanade, T.; Saragih, J.; Ambadar, Z.; Matthews, I. The Extended Cohn-Kanade Dataset (CK+): A complete dataset for action unit and emotion-specified expression. In Proceedings of the IEEE workshop on CVPR for Human Communicative Behavior Analysis, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. SURF: Speeded up robust features. Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Leutenegger, S.; Chli, M.; Siegwart, R. BRISK: Binary Robust Invariant Scalable Keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Shi, J.; Tomasi, C. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).