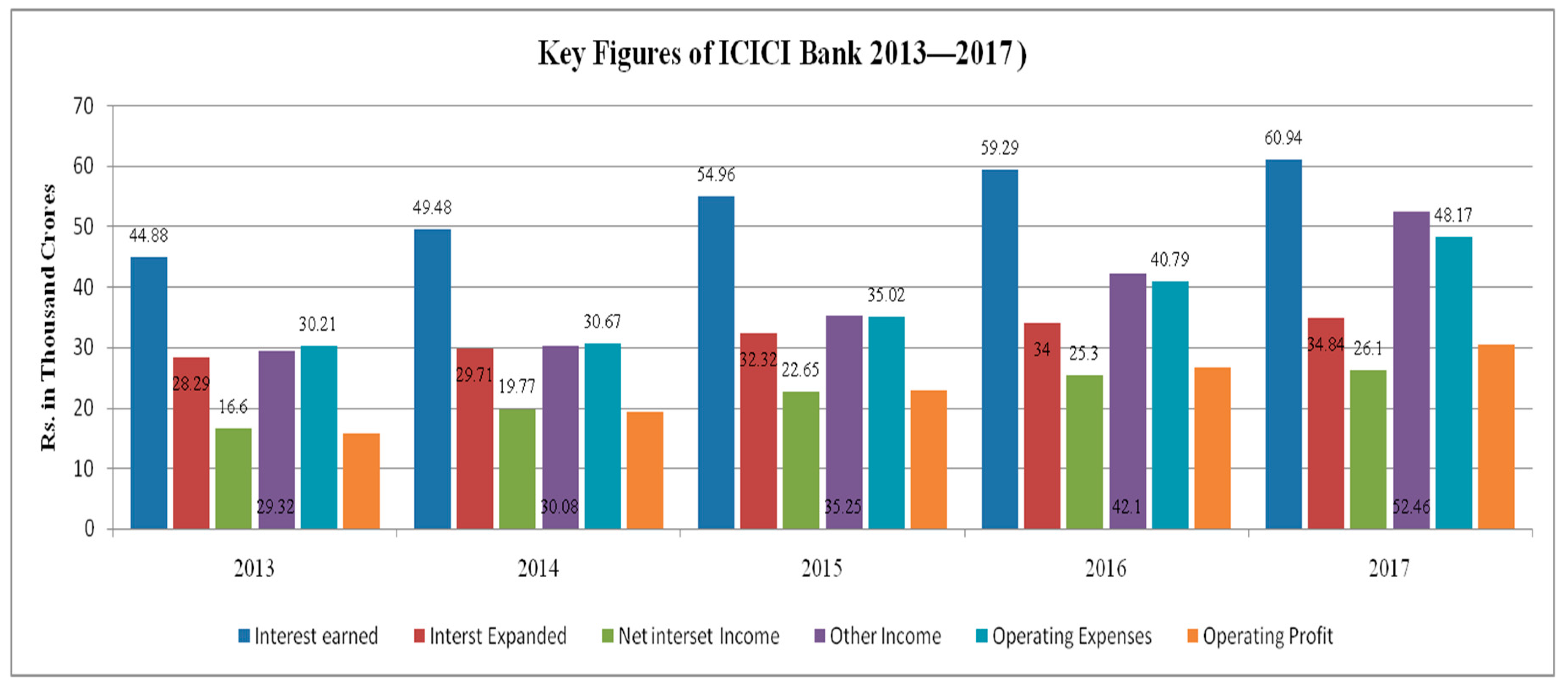
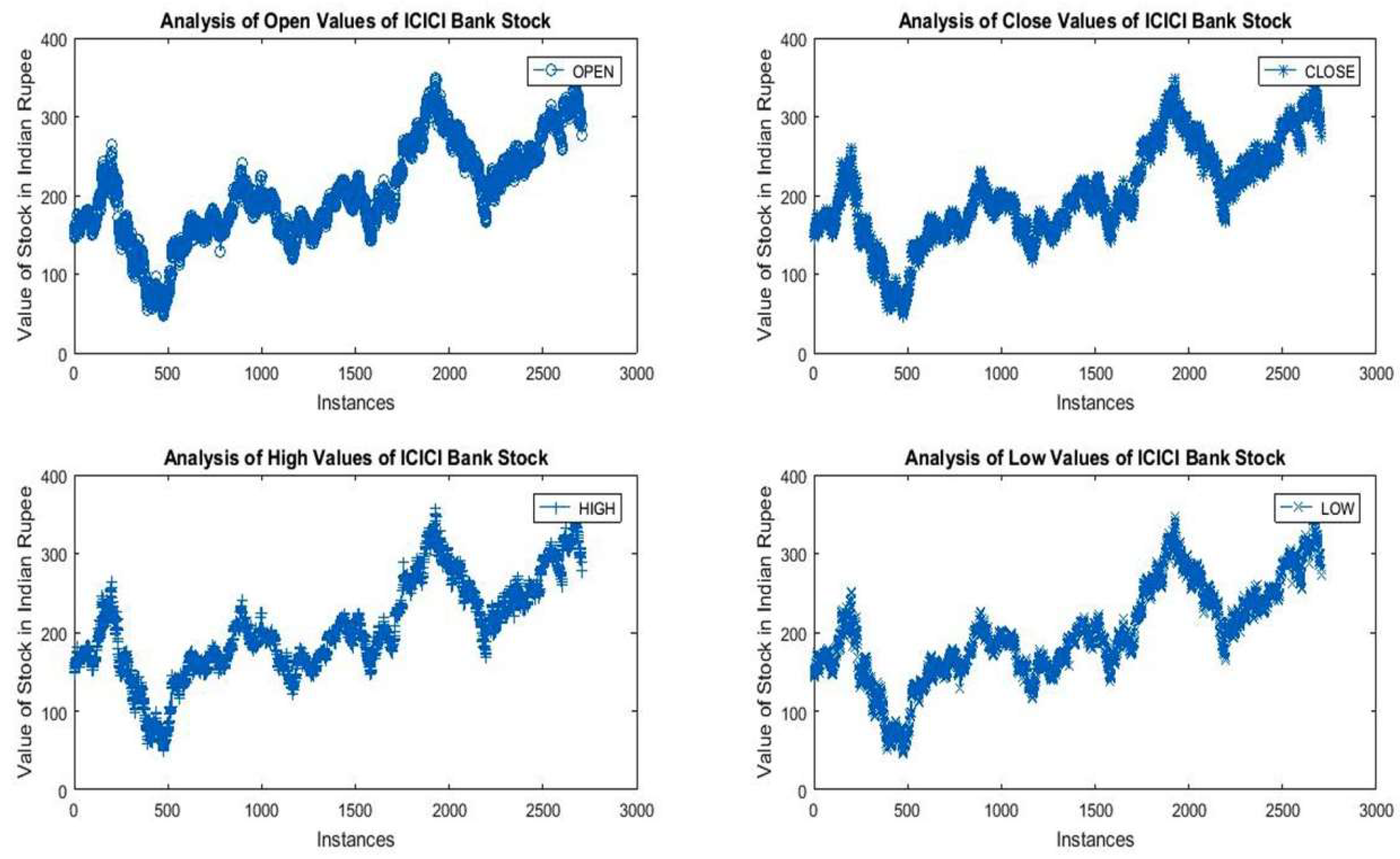
It was found that the average value of open, close, low, and high attributes of ICICI Bank’s stock lies between 198.43 to 204.79. As per statistical results, the 95% confidence interval range (mean) for open attribute reveals that the average value of open attribute lies between 199.50 to 204.13. From standard deviation, it was found that in the last twelve years, 68% of opening values lie between 140.47 and 263.17, 95% lie between 79.12 and 324.52, and 99.7% lie between 17.77 and 285.87. The negative kurtosis values of open, close, low, and high attributes represent that the distribution curve is platy curtic and more flat in nature.
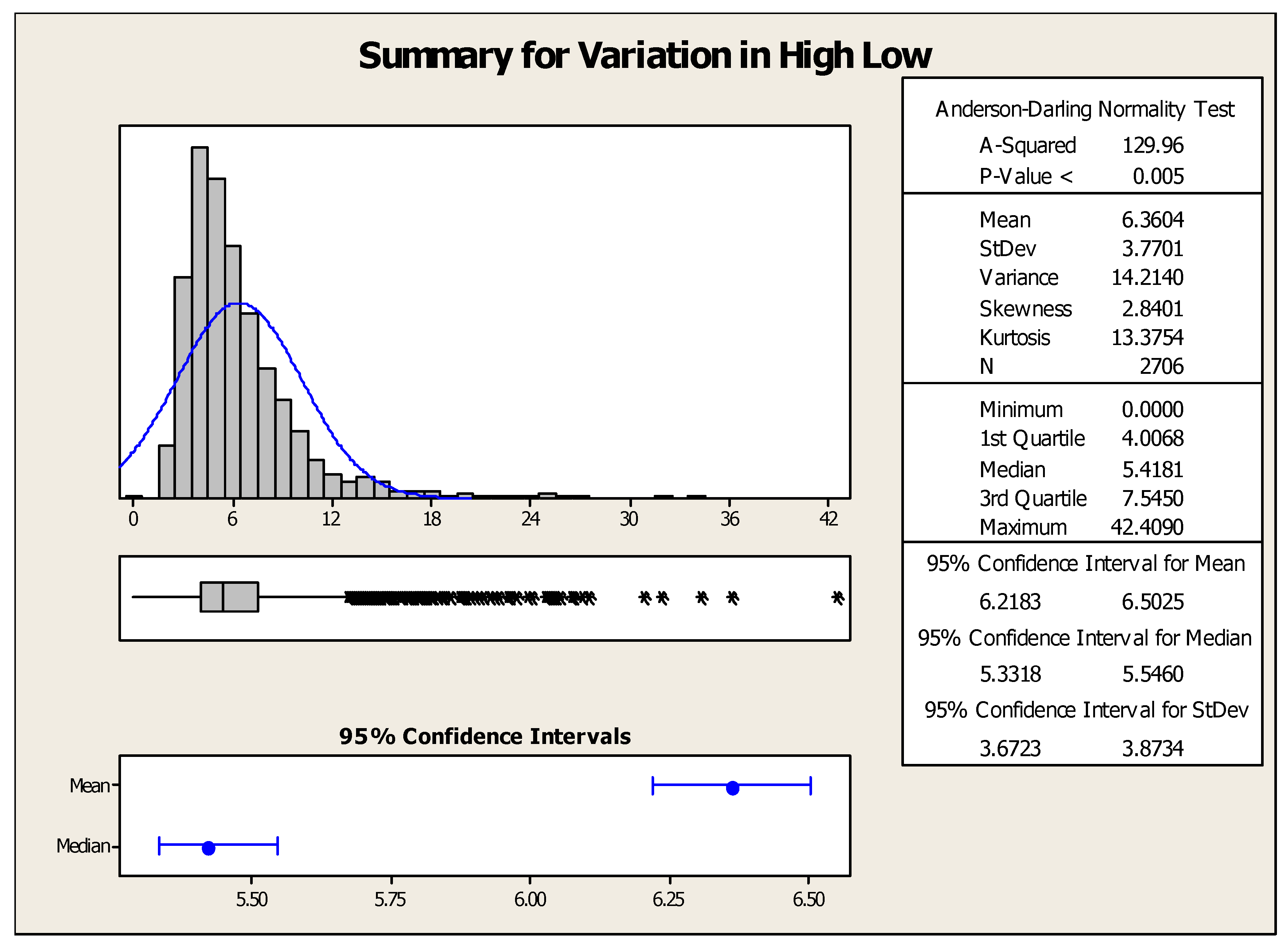
From the data, it is also clear that maximum and minimum low–high variations are recorded in 2008 and 2013, respectively. However, the common range of variation lies between 90 and 120.
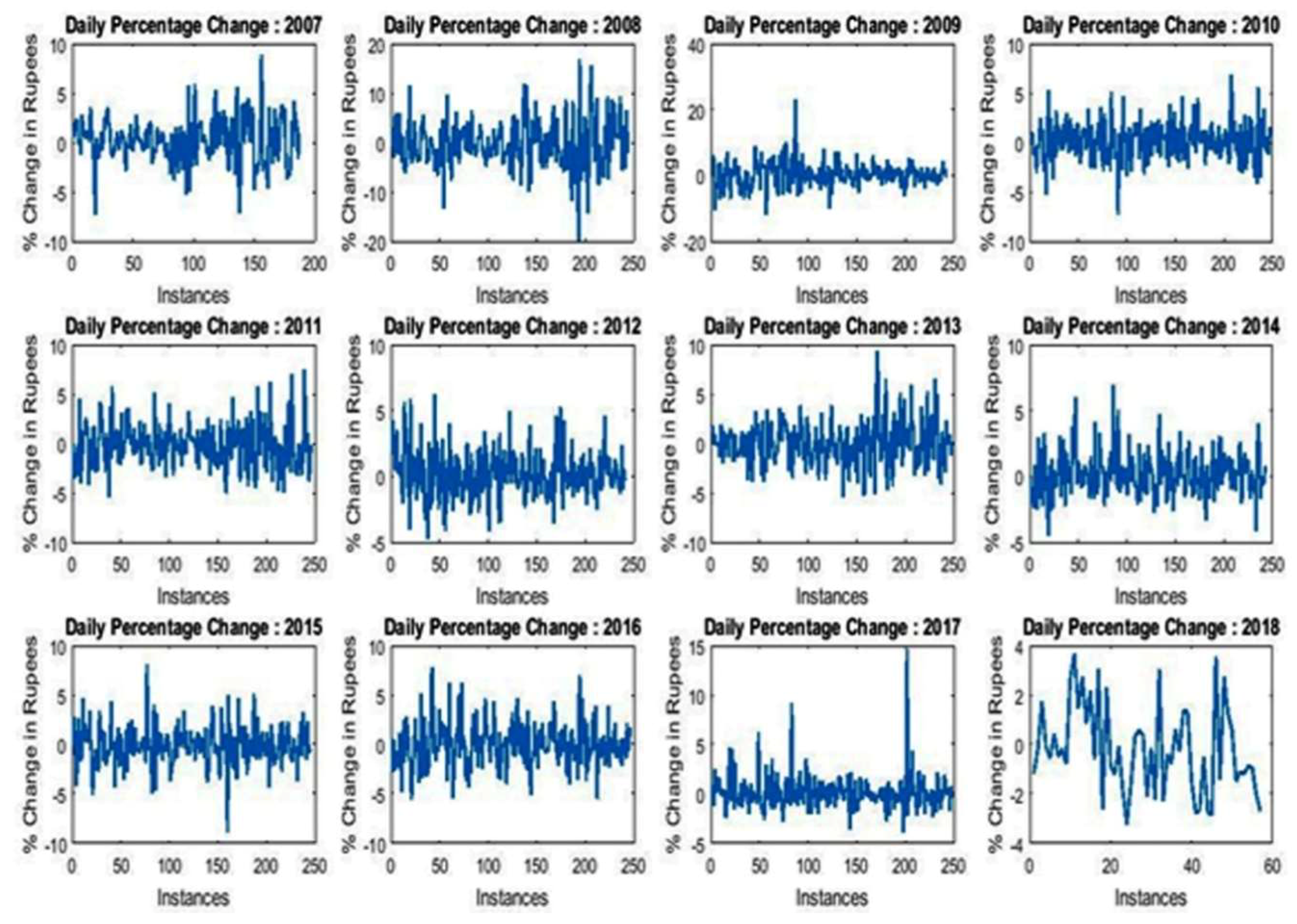
Figure 3 depicts the daily percentage change recorded over the last 12 years. It is observed that in the years 2008, 2011, 2015, 2016, and 2017, large numbers of negative daily percentage changes were witnessed.
Furthermore, in the last twelve years, the year 2009 seems to be very negative for the sellers as it had the lowest minimum and maximum opening values. However, the variation between minimum and maximum was found to be significant (264.2%). The year 2018 represents a sound state for investors who invested their money in previous years as the maximum opening value (Rs. 360.8) was achieved in this year. Additionally, the maximum and minimum variation in opening balance was recorded in the years 2008 and 2013, respectively.
Figure 4 represents the summary of descriptive statistical measures for low–high variation of ICICI Bank’s stock. The mean, minimum, and maximum values of high–low variation were found to be 6.36, 0, and 42.4, respectively. This means the maximum intraday variation in ICICI Bank’s stock lies between 0 and 42.4 Indian rupees.
4.1. Evaluation Criterions and Analysis of Different Classifiers
The performance of predictive classification models is based upon the values of correctly and incorrectly classified instances. A confusion matrix represents the performance metrics of classifiers that highlight the number and types of errors made during data classification and are related to the following conditions:
Positive instances classified as positive (TP)
Positive instances classified as negative (FP)
Negative instances classified as negative (TN)
Negative instances classified as positive (FN)
Some metrics from the confusion matrix, such as accuracy, precision, recall, F1-score, specificity, and sensitivity, can be computed to determine the performance of classifiers from a different perspective.
Accuracy is the most instinctive performance metric that represents the ratio of correctly foretold observation to the total observations, that is,
The rate of misclassification is an important measure of classification techniques. The rate of misclassification is based upon three major parameters of classification matrix, namely, true positive, true negative, and a total number of instances. A classifier that has zero rates of misclassification would be perfect and preferred. However, because of the presence of noise in data, it is difficult to find such a type of classifier. Mathematically, the rate of misclassification, which is denoted as err, is computed as
Here, TP, TN, and N represent true positive, true negative, and total number of instances, respectively.
Sensitivity and specificity are computed to examine the rate of true positive and true negative instances. Mathematically,
Additionally, the precision and recall can be computed to determine the exactness and completeness property of the classifier.
Mean absolute error (MAE) represents the magnitude of the average absolute error. Mathematically,
F1 denotes the weighted average of recall and precision. It should be noted that a higher value of F1-score does not guarantee that the classifier is performing well. Rather, it depends upon the circumstances.
In this section, the performance of ten different classifiers has been examined in classifying the instance of ICICI Bank’s stock data.
Table 2,
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10 and
Table 11 representthe values of different metrics like FP, TP, TN, and FN, along with the number of correctly and incorrectly classified instances, accuracy, precision, recall, and an F1-score of different supervised classifiers in analyzing the data set of ICICI Bank’s stock. From
Table 2,
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10 and
Table 11, it is observed that rates of classification of naïve Bayes; C4.5; random forest; logistic regression; linear discriminant; and linear, quadratic, cubic, fine and medium Gaussian support vector machines lie between 47.6% and 48.9%, 53.6% and 53.6%, 53.0% and 53.6%, 99.7% and 99.8%, 53.6% and 53.6%, 98.7% and 99.8%, 91.0% and 93.9%, 75.0% and 91.7%, 78.2% and 79.9%, and 69.6% and 72.4%, respectively. To precisely examine the performance of different classifiers, the K-fold cross-validation mechanism was used. In K-fold validation, initially, the data have to be decomposed into K mutually exclusive equal sized folds or subsets. In 5-fold, the data are decomposed into giving subsets also known as folds (F1, F2, F3, F4, and F5). Testing and training are carried out five times. In the first iteration, the fold F1 acts as the test set and the remaining four subsets as training sets. Similarly, in the second iteration, F2 acts as testing and the remaining subgroups are used for drilling. The process is repeated five times. The data were mined by varying the folds from 5 to 10.
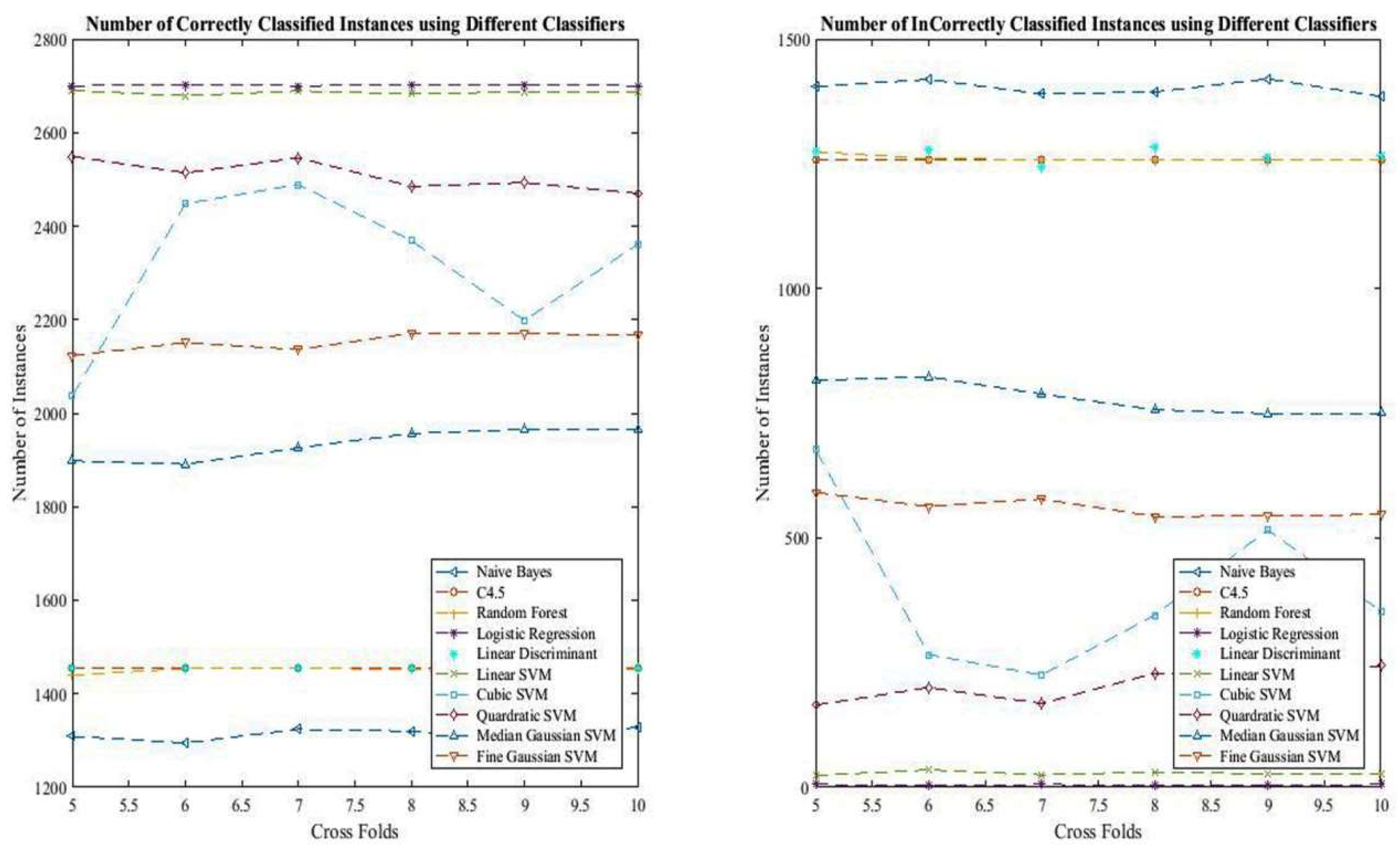
The experimental analysis shows that logistic regression, followed by linear SVM, was found to be best suited as a classifier for ICICI Bank’s stock analysis. NB, C4.5, RF, LD, and CSVM merely act as a random guessing machine. The rate of accuracy achieved using logistic regression lies in between 99.7% and 99.8%. Moreover, this classifier had a higher rate of precision, as well as recall. It was found that naïve Bayes seems to merely guessing machine, as it has the lowest rate of accuracy among all the classifiers. The rate of classification in classifying correct and incorrect instances using naïve Bayes was found to be 47.6% and 48.9%, respectively. In addition, when precision was considered, C4.5 seemed to be the best classifier.
The value of precision accomplished using six to ten cross-fold remained constant and, surprisingly, was 100%. However, this classifier utterly failed to classify true negative cases. Additionally, the rate of identifying false negative cases using naïve Bayes was extremely high. Like accuracy, logistic regression also showed outstanding performance as far as F1 values were concerned.
The rates of correctly and incorrectly classified instances achieved using different classifiers are depicted in
Figure 5.
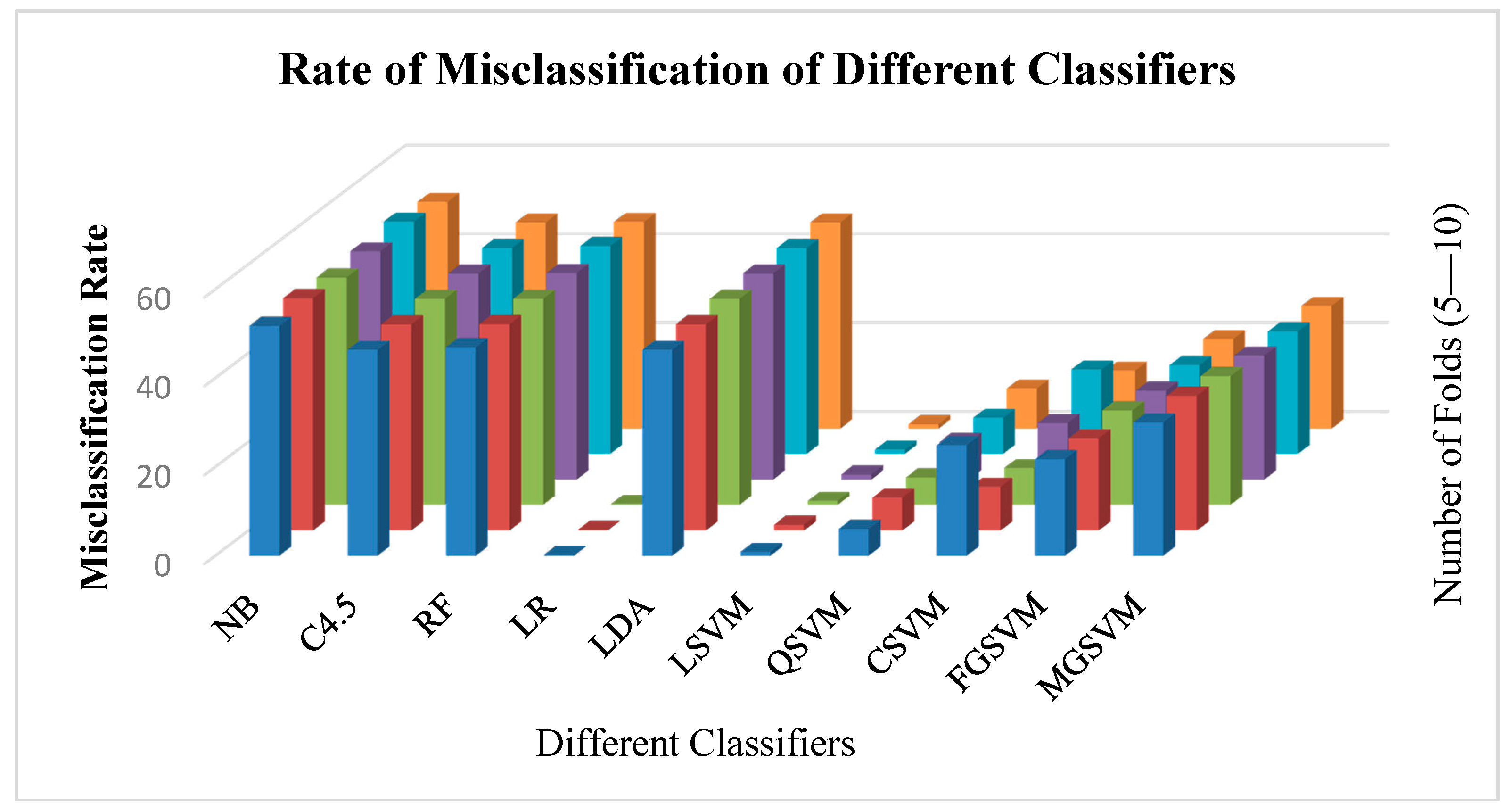
Figure 6 depicts the rate of misclassification of different classifiers. It is observed that naïve Bayes had the highest rate of misclassification, whereas logistic regression and linear SVM were found to have the lowest misclassification rate.
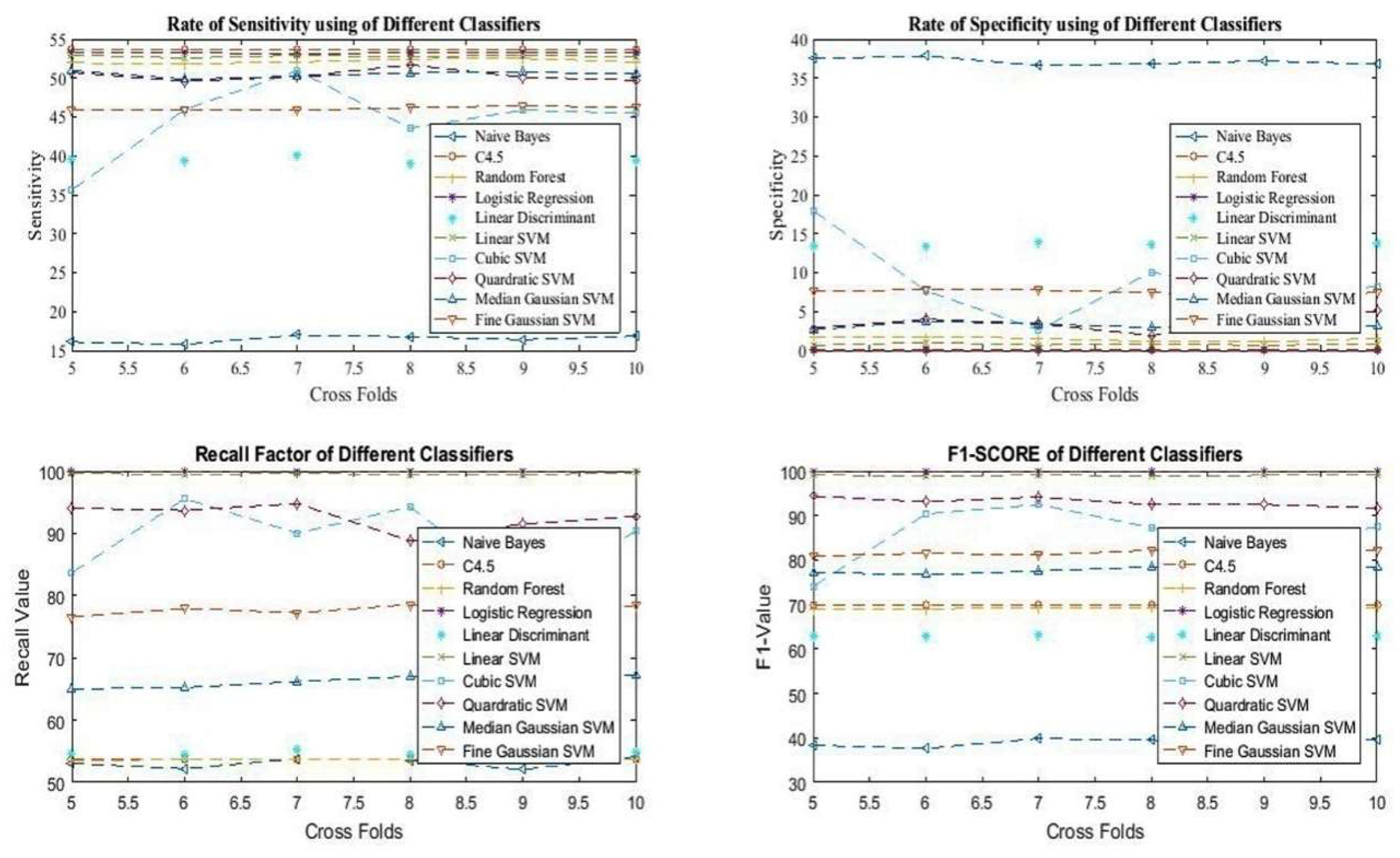
Additinally, the analysis of sensitivty, specificity, F1 score and recall has been presntedin
Figure 7.
4.2. Ranking Using MCD Techniques
Table 12 represents the summarized performance of different classifiers in classifying ICICI Bank’s stock data. It represents a multi-criterion decision problem with ten different approaches having seven different performance criterions. This table has been created from
Table 4 by taking the best possible value from different cross folds.
This MCD problem has been solved using two different statistical techniques, called TOPSIS (technique for order preference by similarity to ideal solution) and WSA (weighted sum approach) [
51,
52]. The ranking of different approaches based upon seven different criterions is presented in
Table 13.
The working of the WSA method is based on the utility maximization principle. It helps in finding the ranks of the alternatives on the basis of their total utility by considering all the chosen criteria. In TOPSIS, d
i+ and d
i− represent the distance of ideal and basal variants. Here,
Hj and
Dj are the maximum or minimum values corresponding to the ideal or basal distances.
Finally, the relative closeness to the ideal solution C
i is calculated as mentioned below:
In order to get the real picture of predicted rate of return, the ICICI stock data were also predicted using linear and multiple regression.
Table 14 represents the difference between the rate of actual and predicted return value obtained using both linear and multiple regression. Here, the rate of return was computed for the month of February 2018. The buy-and-hold time was fixed at one month.
From
Table 14, it was found that the results obtained using linear regression were more precise when compared with results obtained using multiple regression, as the difference between actual and predicted rate of return was very small for linear regression.