1. Introduction
Competent environmental resource management based on reliable information about the properties of natural and geotechnical systems is the most important approach to improve environmental, economic, and social sustainability. Identifying land surface plots that are relatively homogeneous in terms of geophysical and geochemical properties (the geological environment, geological, and geomorphological, as well as hydrological processes, the development of vegetation phenological phases, etc.) allows evaluating the sustainability of lands and predicting their resistance to technogenous load and natural or technogeneous emergencies. Data collected by Earth remote sensing (ERS), as well as the analysis of such data using automated classification methods and land cover (LC) map creation, are becoming more and more important for research and practice activities related to assessing the spatio-temporal structure of the Earth’s surface. This approach is important because it allows extracting the necessary objective data to make science-based management decisions.
Instrumental analysis of multispectral space images is based on the methods and algorithms of data signal analysis [
1,
2,
3,
4,
5,
6,
7,
8], diagnosis of the types and properties of objects on the basis of systemic linkages in their spectral properties and structural characteristics [
9], statistical classification [
10], neural networks [
11,
12,
13,
14], support vector machines [
15,
16], ensemble systems [
17,
18,
19,
20].
Land cover information is a significant data for environmental planning, ecology, or forest management and monitoring in regional and global scales. Obtaining LC information from satellite imagery is a non-trivial task that depends on the complexity of landscapes and the resolution of the imagery being used [
21]. Over regional scales, LC maps are produced using medium spectral resolution imagery, such as Landsat 7 and 8 [
22]. While these remote sensing data are inadequate for detailed mapping, it is useful for producing well-generalized landscape maps and important for approbation of the accurate approaches that are suitable for the landscapes classification.
Since space images are a multidimensional matrix of pixels, traditional LC-mapping has been based on a pixel-based approach [
23] that uses different classification techniques that assign a pixel to a class by the spectral similarities [
24]. The object-oriented classification approach is a relatively new method: it not only relies on the spectral parameters, but more on their geometric and structural information (such as neighborhood descriptors), artificially extracted from remote sensing data [
25,
26].
Object-oriented image analysis is based on homogeneous image regions that are generated by segmentation process. The image content is represented as a network of image objects, connecting all the regions of it [
27,
28]. These image objects act as the building blocks for the following image analysis. In comparison to pixels, image objects carry much more information. Many researchers have successfully used object-oriented methods for different purposes: change detection [
28], and analysis underlying texture in both panchromatic and multispectral bands [
29]. It is promising to carry out experiments aimed at improving the efficiency of multispectral space image interpretation based on the Ensemble Learning concept, combined with the use of contextual information through various synthetic descriptors [
17,
18].
The study described below made it possible to obtain an effective methodology for classifying land using neighborhood descriptors. The second chapter presents the formalization of the task of analyzing Earth remote sensing data, its main features are identified, the choice of the initial materials for the study, and the means for implementing it are made. The third part describes in detail the proposed methodology and proposes a list of descriptors, the calculation of which is informative in the analysis of territories. Finally, in the fourth part, approbation of the proposed methodology on the test polygon system is carried out and conclusions are drawn about its effectiveness.
2. Formulation of the Problem
The problem consists in automating the ERS data analysis to monitor the sustainability of lands and predict emergent natural processes; the solution to this problem should be based on the presence of objective linkages between the spectral properties of the areal model and the characteristics thereof. Physical surfaces can reflect and radiate electromagnetic waves in various ways. The measured value of the spectral brightness coefficient is affected by the conditions of the atmosphere, as well as the physical-chemical and geometrical parameters of the area. The dependency of the spectral brightness coefficient on the wavelength is an important objective characteristic reflecting the properties of the area under research. The analysis of this dependency can provide information not only on the type of surface, but also on its properties [
19].
Available multispectral and hyperspectral ERS data allow studying the optical properties of the geophysical shell in different spectral bands. This significantly expands the analysis capabilities: if in a particular spectral band different land types can have similar reflectivity, one can identify their regular objective differences taking into account the imagery of different channels. On the contrary, geophysical shells of the same class feature similar properties of spectral curves. Analysis and classification of Earth remote sensing data should be based on extensive use of automatic and automated methods as a key research tool. To solve the problems in this area more efficiently, one has to determine the key characteristics of input data. Given the importance of the spectral characteristics of a geophysical surface, initial approximation reduces the problem of remote sensing data interpretation to finding a functional dependency of following type:
where
X is the desired characteristics of the object displayed;
B (
λ) is the spectral characteristics of the object displayed.
Spectral brightness is the most important parameter obtained from remote sensing data and characterizing the areal objects under research; however, it is not the only such parameter. Additional data such as the characteristics of the neighborhood of an object, its heterogeneity and sustainability are obtainable from ERS data by a synthetic method using numeric algorithms and mathematical modeling methods. Taking such parameters into account allows achieving greater accuracy and efficiency when determining the characteristics of the objects displayed:
where
D is additional spatial information obtained from ERS data.
Various factors affect the value of the spectral brightness coefficient, which, on the one hand, allows determining a number of characteristics of the area under analysis, while, on the other hand, this makes it difficult to identify the surface type. One needs a priori information about such an area to take into account how such factors as noise exposure, atmospheric impact, and light affect the spectral properties of an object.
A priori information about natural and anthropogenic objects is obtained by various measurements that supplement satellite imagery. This information is found in statistical data, cartographic materials, as well as field research output. A priori information may affect the results of determining the properties of an object on the basis of its ERS-based characteristics, which makes the functional dependency suggested above considerably more complex yet more objective:
where
I is a priori information about the object displayed.
Remote sensing allows collecting objective data in dangerous and inaccessible areas without costly and lengthy field research. However, analysis of remote sensing data always has to rely on a priori information about the research object. Therefore, solving the inverse ERS problem is reduced to analyzing the spectral characteristics of the objects displayed, algorithmically extracted spatial data, and a priori information about the research object. The functional dependency
f (
B (
λ),
D,
I) is non-linear and rather complex due to the complexity and ambiguity of the object; the solution of the inverse RS problem is difficult to formalize. It is virtually impossible to identify a dependency that would provide exceptionally true and optimal results. At the same time, it is pivotal to enhance the objectivity of the results. That is why research and development of algorithms and methods for ERS data analysis are relevant and multidirectional. This area of research employs statistical, neuronetic, and fuzzy algorithms, while the creation of new and integrated approaches to solving the inverse ERS problem remains a relevant and open question in the field of sustainable ecology [
30,
31,
32,
33,
34].
The diversity of the existing types of space images determines the possibility of using them to solve a number of problems; however, it also implies a conscious approach to selecting the most informative material. In selecting ERS data, the basis should be the objective set and the problems to be solved. Availability of data is also an important factor. Analysis of the satellite imagery market allowed choosing data from Landsat 7 and Landsat 8 as the input data for our experiments.
It is advisable to use integrated computing and modeling software for the analysis of satellite imagery. We chose MATLAB, a software suite for computational calculations, whose applications are theme-grouped: Image Processing Toolbox, Neural Network Toolbox, and Statistics Toolbox. That is convenient for a wide range of experiments related to supervised and unsupervised training, as well as the construction of ensemble systems. Finally, MATLAB allows assessing the classification made, as well as the quality of the algorithms used.
3. ERS Data Classification Algorithm Taking into Account Neighborhood Descriptors
To obtain an integrated spatio-temporal description of the conditions of lands, as well as to assess sustainability and predict the emergent processes, it is advisable to rely on systematic analysis of data which characterize the dynamic and invariant conditions of the area surrounding the geophysical plot, as analyzing the properties of the neighborhood is important for determining the class of the area, as are the spectral characteristics. The neighborhood of a geophysical object is an area within a certain distance from the center of an object.
The invariant properties of a geophysical object are identifiable by studying the morphometric maps of the terrain, which irreversibly changes over a very long time. Data on the dynamics of the geophysical shell could be taken from the ERS data by analyzing the spectral characteristics. When solving the problem of classifying geophysical areas, the characteristics of the neighborhood should be taken into account on par with the spectral properties. The experiment carried out helped to find the answer to the question of how such neighborhood analysis could affect the classification output [
20]. The description of the developed methodology for the integrated accounting of the different neighborhood descriptors is presented below. First, a description of the separate neighborhood parameters is given, then a technique for combining them using the Fisher vector is described.
Local entropy of the neighborhood. This parameter allows describing the geophysical heterogeneity and sustainability of an area and is an authentic metric that identifies the type of the geophysical complex. This parameter is not new, but it is easy to calculate, and we will show that its use is effective in combination with other descriptors through calculation of the Fisher vector. Local entropy of the neighborhood is calculated as follows:
where
is the number of pixels of certain spectral brightness
i in this neighborhood;
is the radiometric resolution of the image;
is the area of the neighborhood; and
r is the radius of the neighborhood.
Deviation. This parameter describes the variation of spectral brightness relative to the mean value. Geophysical complexes of different structures have different spatial structures, resulting in different standard deviation values. This metric is calculable according to this formula:
where
is the mean value of the spectral brightness of the local geophysical complex, N is the number of pixels in a neighborhood of the radius r. In the case of a circular neighborhood, this parameter is approximately equal to
.
Analyzing the color properties of an image is an important stage of spatial object analysis. It is advisable to use such properties that are invariant to undesirable color changes like shadow imposition or light-striking.
Color moment, a parameter that describes the probabilistic distribution of colors in the region and is determined by a tuple of mean, dispersion, and the skewness coefficient, which combine to give an authentic and stable color description to associate the distribution of that color with the space:
where
is the color moment;
is the mean pixel brightness;
is the pixel brightness dispersion;
is the pixel brightness coefficient of skewness;
is the number of pixels in the neighborhood of the radius
r.
Histogram of shades calculated for all the pixels in the region is the informative descriptor of a geophysical object. The metric value of a shade is calculated based on the brightness of the object in the three spectral bands under research. The shade can be represented as the proportion of the distance around the edge of the hexagon which passes through the projected point. Mathematically, this definition of hue is written piecewise:
where
H is the shade; and
ci is the spectral brightness in the ith band.
Parameter
ci can be a spectral brightness from any analyzed band. This formula allows the calculation of shade as a value uniformly distributed in polar coordinates. Color tags are associated based on mapping the 3D space of colors into the scalar color attribute. This descriptor features good photometric invariance, because an object of the same nature can have different shade values, but the same color tag. The color tuple is constructed as follows:
where
is the color tuple;
p(
Ci) is the probability of a pixel of the
ith color emerging in the neighborhood region;
Ni is the number of pixels of the
ith color in the neighborhood; and
N is the total number of pixels in the neighborhood of the radius
r.
When making a classification, it is advisable to compute the Fisher vector for integrated handling of the neighborhood descriptors. The Fisher vector is a special case of the Fisher kernel. It is designed to encode the local peculiarities of images in a format suitable for efficient learning and comparison to simple metrics. The Fisher vector is the representation of an image by combining the local peculiarities, or descriptors, of that image, which is why it is advisable to use this kernel as a descriptor for an image or a part thereof when classifying lands.
An image or a part thereof can be represented as a set of D-dimensional descriptor vectors algorithmically extracted from an image:
where
I is the image; and
xi is the
ith image descriptor.
Given these
parameters of a model combining Gaussian distributions (
α is the a priori probability,
μ is the mathematical expectation,
σ is the standard deviation,
σ2 is the variance) based on a descriptor distribution, each vector
x1 maps into mode
j with a force defined by the a posteriori probability:
For each mode
j, the vectors of mathematical expectation (
M) and standard deviation (Σ) can be calculated:
where
covers the dimensionality of the vector.
The Fisher vector of image
I is therefore constructed as follows:
Now E (entropy), S (deviation), M (color moment), H (shade), and CC (color tuple) can be integrated with a Fisher vector. For this it is necessary to form the vector I using the calculated descriptors. When classifying lands taking into account the neighborhood descriptors, each basic component of space imagery has to be associated with both its spectral properties and the metric descriptors of its surroundings. We propose a classification of spatial objects based on a vector of these parameters to be used to construct the geophysical model of vegetation sustainability.
We designed an experiment to classify a space image taking into account the neighborhood parameters; the experiment was carried out as follows:
- (1)
define the problem and identify the purpose of creating a cartographic model;
- (2)
choose input data for analysis and determine the form of the output of the classifying process, i.e., the nomenclature of classes that the objects on such space image will be classified into;
- (3)
pre-process the image: calculate the neighborhood parameters: to perform this operation, the value of the neighborhood radius and the form of the neighborhood, as well as the informational descriptors of the neighborhood need to be empirically and expertly identified;
- (4)
associate each atomic plot of ERS data with the vector of its properties: X = [Λ Μ], where Λ = [λ1, …, λn] is the vector of the spectral parameters of the plot, and Μ = [μ1, …, μk] is the vector of the neighborhood parameters;
- (5)
choose an algorithm for trainable data classification (a neural network, SVM, decision trees, and ensembles), determine its architecture and the properties of its implementation;
- (6)
prepare a training and testing sample to train the algorithm on the basis of a priori information about the area under research;
- (7)
train the classifier;
- (8)
classify the ERS data;
- (9)
assess the quality of such classification on the basis of objective metrics and the output by means of an expert assessment; make a conclusion on the quality of the solution to the problem of classifying ERS data taking into account the neighborhood parameters;
- (10)
repeat steps 3 through 9 varying the neighborhood parameters, the calculable property vectors, and the architecture of the algorithm; make a conclusion on how taking into account the neighborhood properties affects the classification process and its output.
To test the remote sensing data classification algorithm based on the neighborhood descriptors, a system of research polygons was deployed in the Republic of Mordovia (Russia). In the experiment the efficiency of various neighborhood descriptors was analyzed. The study results are given in the next chapter.
4. Experiment and Discussion of Results
To develop technologies for decoding multispectral space images, the development of a test polygon system is of great scientific and practical importance. In the scheme of physical-geographical zoning, most of the territory of Mordovia belongs to the province of the forest-steppe of the Volga Upland, which, in the northwest and west of the republic is replaced by the province of mixed forests of the Oka-Don lowland. When detailing the properties of the territory, a hierarchical system of taxonomic units is singled out on the electronic general scientific map of GIS Mordovia: systems, subsystems, classes, subclasses, types, subtypes, genera, and subgenera of landscapes. Approbation of the ERS data analysis algorithm taking into account the neighborhood descriptors was carried out on four test polygons: Inerka, Smolny, Mamangino, and Cheberchinka.
The “Inerka” polygon (center: 54°3′52.21″ N, 45°53′11.20″ E) reflects the interaction of paragenetic systems of the remnant-watershed massives of the erosion-denudation plain and the valley of the river Sura. The formation of the Sura valley began during the period of active epeirogenic uplifts that swept the Volga Upland at the end of the Paleogene. Due to the peculiarities of the tectonics of sedimentary rocks, the slope of the indigenous rocks in the direction of the Ulyanovsk-Saratov trough, Sura, during long geological time, meanders to the south, southeast. This led to the formation of an asymmetric valley with a high “upland” right-side board and a very gentle left bank. The development and deepening of the valley was significantly influenced by water-glacial flows of the Don glacier, which formed the most ancient sandy and sandy loamy east of the village of Bolshie Berezniki.
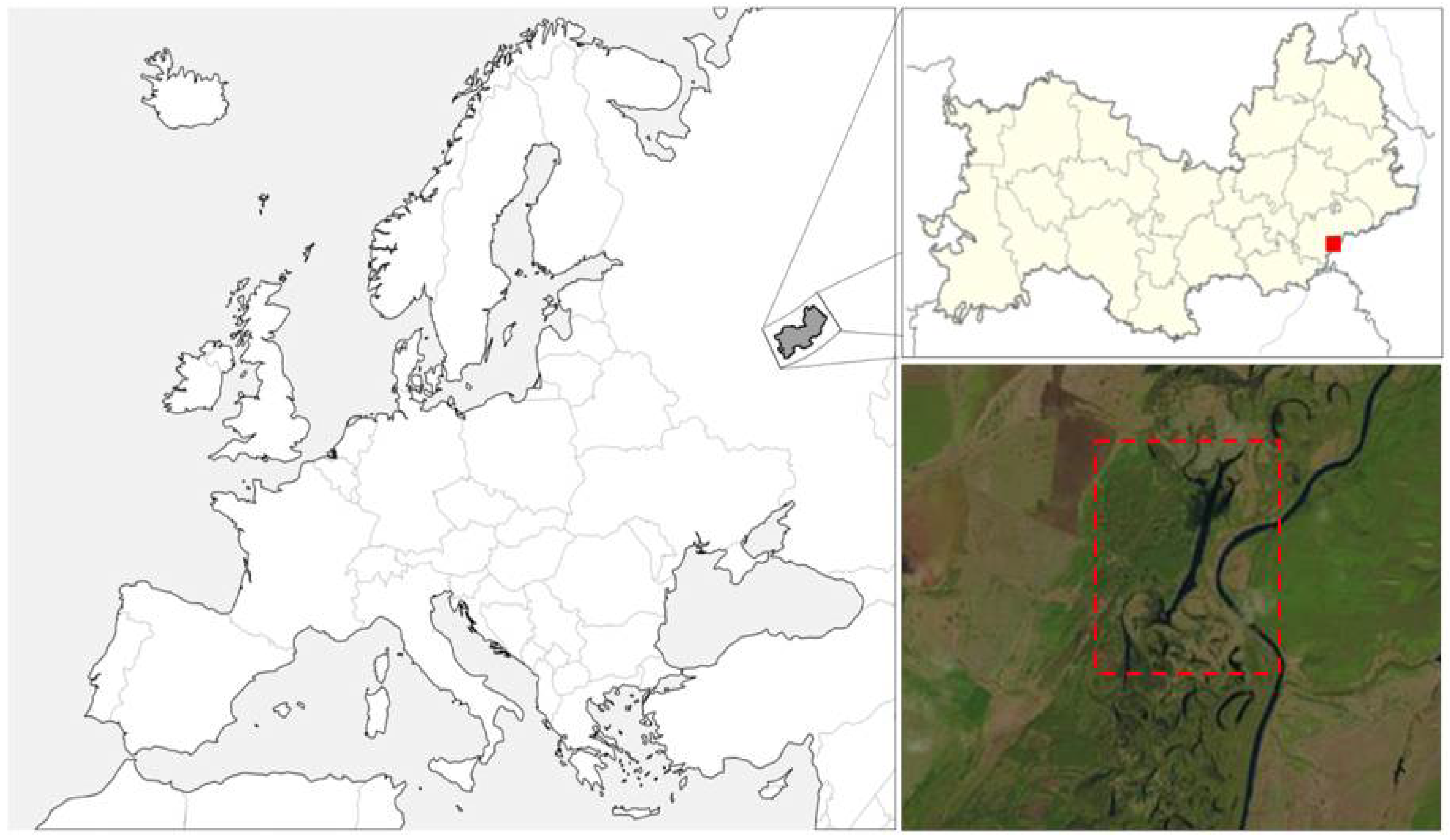
To conduct studies on research polygon “Inerka”, we chose Landsat 8 images (acquisition date: 5 May 2017; path: 173; row: 22). The location of the research polygon “Inerka” is shown in
Figure 1. Research polygon reflects the interaction of paragenetic systems of the remnant-watershed massifs of the erosion-denudation plain and the valley of the Sura River. On the third and second terraces of the Sura, dune-shaped relief forms are common, in the depressions between which swamps are widespread. The first terrace passes to the floodplain, the width of which reaches 4–5 km. Throughout the Mordovia Rebublic it is sandy, with the buttes of floodplain terraces, heavily changed by aeolian processes, numerous meanders, and oxbow lakes.
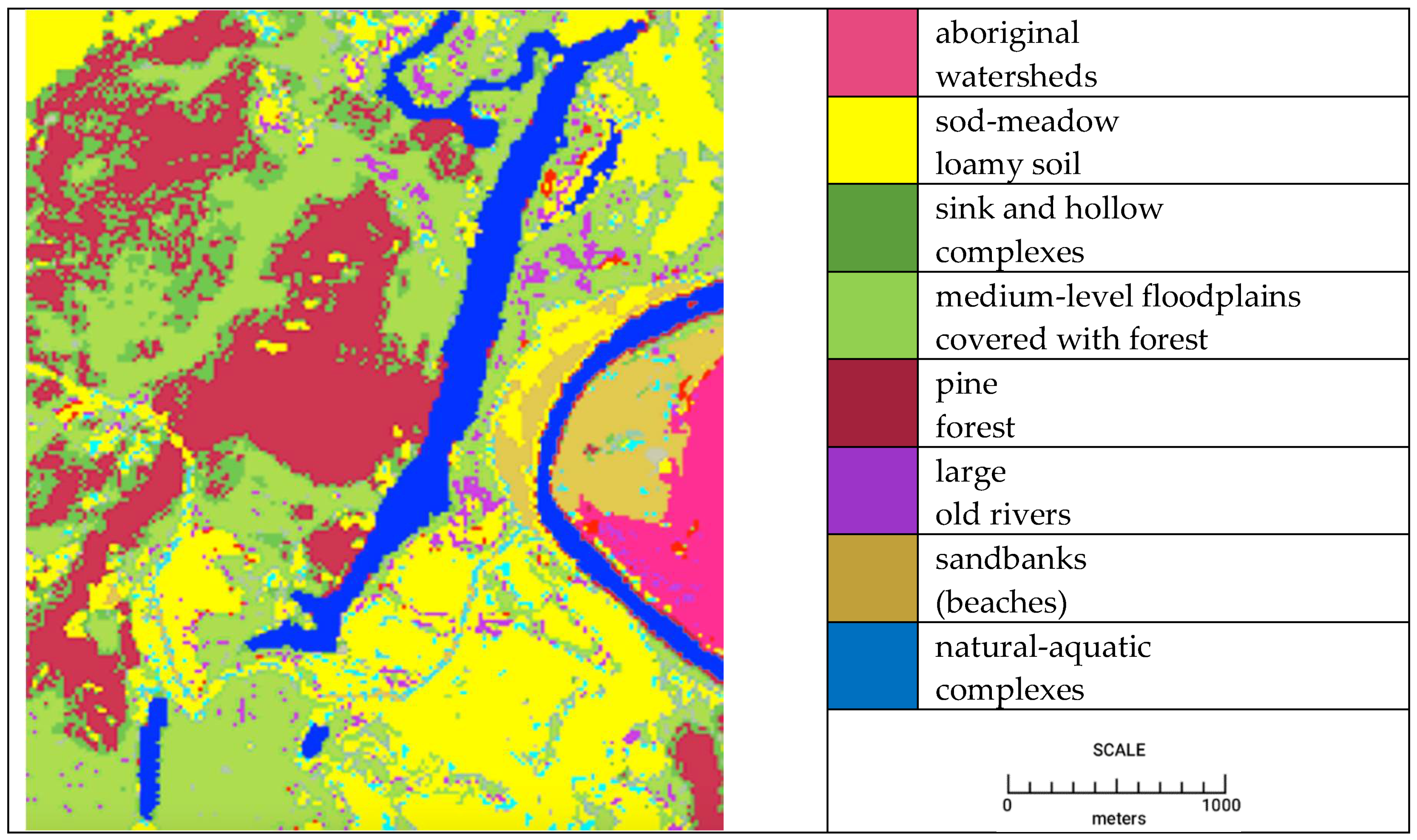
We collected training, test, and validation data for neural network training for the following classes: aboriginal watersheds, sod-meadow loamy soil, sink and hollow complexes, broad-leaved forest, pine forest, large old rivers, sandbanks (beaches), and natural-aquatic complexes. These lands form the landscapes of the explored polygon. To classify the presented data, we used a feedforward neural network [
30] with one hidden layer. The transfer function is sigmoid:
We use the backpropagation training method [
30] with cross-entropy measure of error:
where
is the target value of the output of the network
i when applying the example
q;
is the real value of the output of the network
i when applying the example
q;
is the number of examples in the training set;
is the number of network outputs.
The network was trained on various datasets independently generated from the common data bank. Expert processed 9882 samples, which were divided as follows: training data—7900 samples; test data—1600 samples; validation data—382 samples. The lands covered by clouds and shadows were not included in the test, training and validation samples and was not involved in the assessment of classification accuracy. Therefore, each classifier, trained on various samples, have a unique ability to classify the geosystems of specific classes. Neural Network has a medium-capacity (five neurons) internal neural layer.
The analysis of remote sensing data, which involves the processing of large volumes of data, particularly requires a tool that allows an assessment of the classification performed. For these purposes, the methodology of error matrices and metrics computed on its basis is perfectly suitable. Error matrices are often used to describe the performance of classification models based on the evaluation of the classification of test data for which the true values of the belonging of objects to classes are known. To build the error matrix, it is necessary to classify the test data by the analyzed classifier and compile a contingency table based on the results of its work. The number of rows and columns of this table is determined by the number of classes allocated for classification. The rows of the matrix form a real error classes, which include a test sample items, and columns—classes predicted classifications. In other words, the Mij-element of the error matrix indicates how many objects of class i have been classified as objects of class j.
Elements of the matrix of its main diagonal (for which i = j) characterize the number of correctly classified classes, and the rest, on the contrary, are the errors admitted by the classifier. The element TPi (hit) characterizes the number of objects of class i, which are defined correctly by the classifier. Element FNij is the number of objects of class i, erroneously classified as belonging to class j. In the good case, the sum of the values of the elements that do not belong to the main diagonal should be as small as possible, at best—should be zero.
The error matrix allows, based on the ratio of the values of its elements, to calculate various metrics that characterize the success, accuracy, and inaccuracy of the classifier. The value of these metrics is that they are able to evaluate both the effectiveness of the classification algorithm in general, and its ability to classify correctly objects of a certain class. Metrics calculated on the basis of the error matrix are inherently objective in nature, but their reliability, in turn, directly depends on the quality of the test set of objects, the compilation of which is subjective. This fact suggests that the test sample should be formed as representative as possible, with a minimum of errors. Only in this case the matrix of errors and the metrics computed on its basis will give a qualitative assessment of the efficiency of the classifier.
We now turn to the consideration of the metric, the computation of which will be useful and informative in evaluating the effectiveness of classification in the experiment. It starts with absolute characteristics: the sum of all elements of the error matrix (total) is equal to the volume of the test sample. Parameter FPi is referred to in the literature as an error of the first kind or as a false positive. It is calculated as the sum of the elements of column i, excluding the element of the main diagonal. The FNi metric is a type II error, or a classifier miss when class i objects are detected. Unlike the previous case, it is calculated as the sum of the elements of the string. The true deviation of TNi is equal to the number of objects correctly classified as not belonging to class i.
The overall accuracy of the classifier is characterized by the ratio of the total number of correctly classified objects to the total number of test sample objects:
The value of this metric is measured in the range from 0 (none of the objects is classified correctly) to 1 (all objects are classified correctly). The overall accuracy of the classifier gives an estimate of the performance of the model as a whole. To determine how qualitatively the classifier defines objects of specific classes, you must enter other metrics. It is advisable to take into account parameters that are of a relative nature, normalized in their meaning by the upper and lower thresholds. The set of described metrics can be divided into two categories: characterizing the correctness and error. The values of the metrics of the first block should be maximized, the second, on the contrary, minimized to zero.
To assess the quality of classification it is advisable to introduce metrics integrating the properties of several indicators of the correctness of the classifier. Thus, it is useful to introduce the value of harmonic mean accuracy and sensitivity:
This indicator, calculated on the basis of sensitivity and accuracy parameters, characterizes the ability of the classifier to correctly classify objects of a certain class, while avoiding errors of the I and II types. The values of this metric are calculated from 0 to 100. It is logical to use to estimate the accuracy of classification in the experiment.
Experiments have shown that the analysis of the authenticity of the surrounding areas enables a more objective classification of land plots on the basis of spatial patterns. The output excludes identification of geophysical areas that do not fit into the general spatial model, thanks to which a material classification based on the parameters of a greater neighborhood is suitable for mapping a geophysical shell of a smaller scale. Combined use of various environmental descriptors (see
Table 1) enables high-quality handling of neighborhood properties, as each descriptor provides its own specific information about a geospatial system.
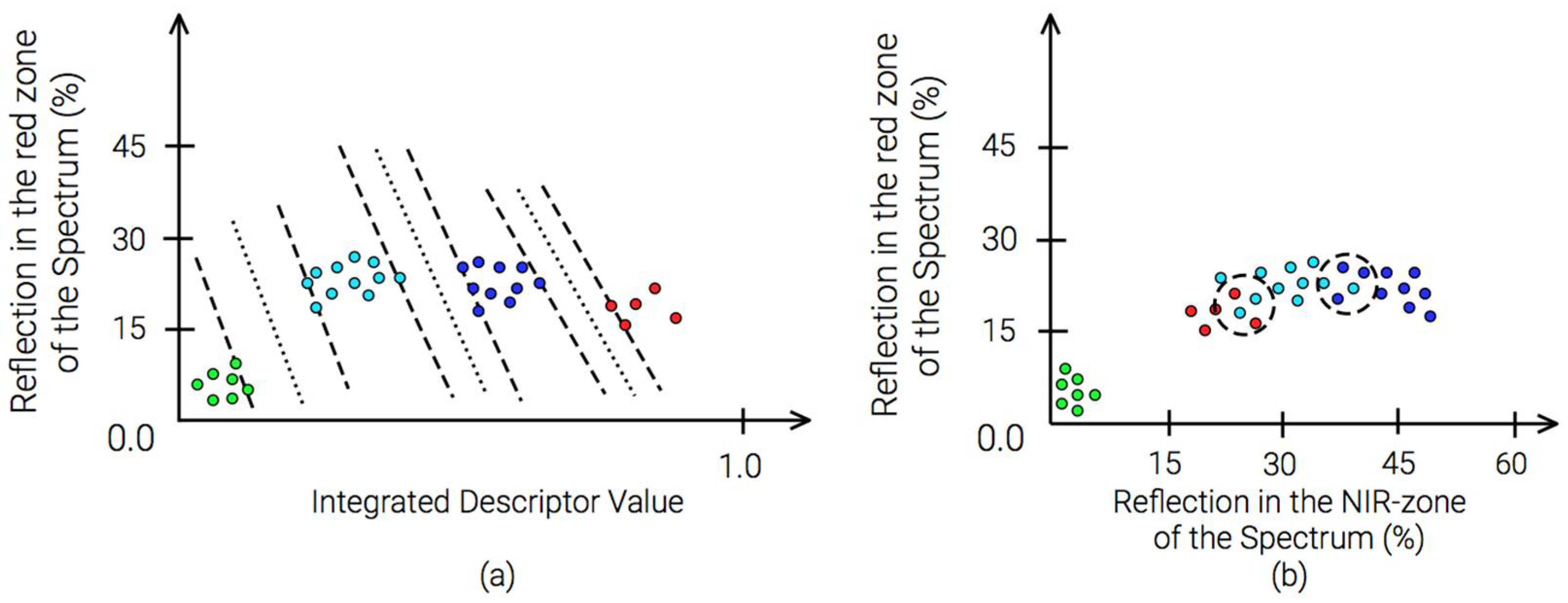
As a data classifier, a neural network of direct propagation was used. Training, validation, and test samples were prepared in conjunction with the expert. When analysing space images, direct, indirect, and complex deciphering features are used. Direct signs of interpretation allow directly, by analyzing remote sensing data, to identify terrain objects, natural contours. Direct forms include the shape, size, color, structure, texture of the image. The interrelationships between natural components are specific and valid only within certain regions, therefore, the signs of interpretation are also established only within specific test ranges with a similar physico-geographical situation. Usually, in the process of remote sensing data analysis, the expert selects combinations of deciphering characteristics of the objects under study. These complexes vary greatly depending on natural conditions, season, time of day, and other reasons. The use of synthetic neighborhood descriptors as attributes of the classified land makes it possible to obtain compact clusters of feature vectors that form locally-bounded domains in the feature space (
Figure 2).
Classification with taking into account the parameters of a neighborhood made it possible to separate aboriginal watersheds and sink and hollow complexes, sink and hollow complexes, and medium-level floodplains covered with broad-leaved forest. This became possible due to the consideration of the unique properties of the neighborhood, manifested in this scale. The result of the classification of the problem site of the Inerka test polygon is shown in
Figure 3.
The “Cheberchinka” polygon (center: 54°27′36.46″ N, 46°18′50.60″ E) reflects the originality of the development of forest-steppe landscapes of erosion-denudation plains of the polygon is associated with active tectonic inversions in the Neogene-Quaternary period. The minimum absolute heights in the Cheberchinka estuary are 98 m. The slopes and river valleys have an asymmetric structure. The slopes of the western and southern expositions are steep, while the eastern and northern slopes are gently sloping. In the Cheberchinka valley, the first floodplain terrace is fragmented. In the lower reaches it has a width of up to 1 km, upstream the width decreases. The height of the terrain is 3–5 m above the level of the floodplain. The profile line has a maximum mark of 278 m, a minimum of 131 m, and an average of 174 m.
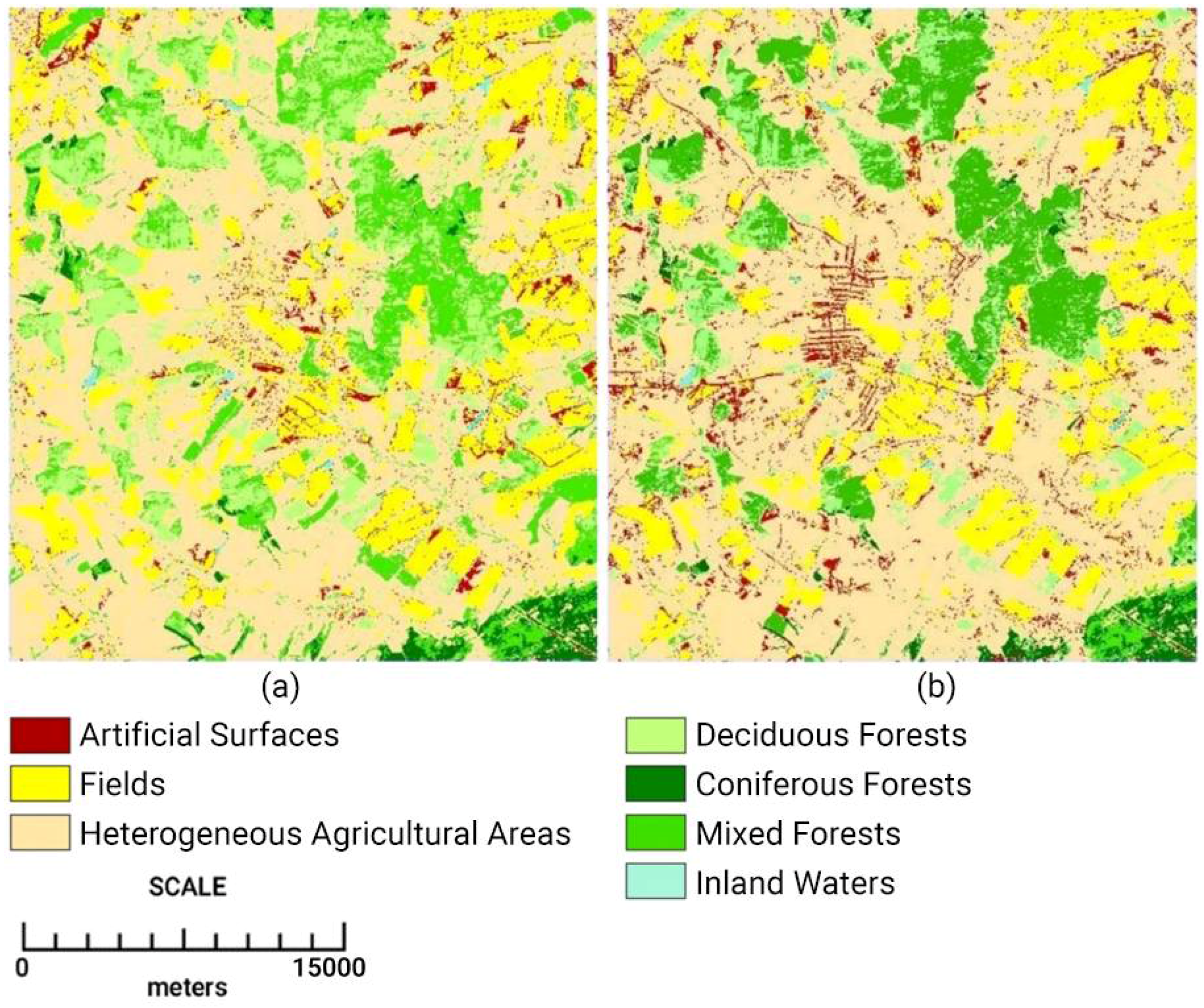
Diagnostics of authentic properties of the internal structure of spatial objects on the basis of analysis of the characteristics of the neighborhood allows to achieve noise suppression, generalization of the result and a general increase in the accuracy of classification. During the classification, the following territories were identified: artificial surfaces, fields, heterogeneous agricultural areas, deciduous forests, coniferous forests, mixed forests, and inland waters.
Figure 4 shows the results of the classification of the problem site of the Cheberchinka test polygon both with simple spectral parameter-based and neuborhood descriptors-based classification. The experiment showed that the classification of geospatial data, taking into account the parameters of the neighborhood descriptors, allows:
- -
to carry out flexible adjustment of the resulting result without increasing errors and reducing the efficiency of classification;
- -
minimize the negative noise impact associated with distortion of the original satellite information;
- -
to classify land areas with greater objective accuracy due to the analysis of the authenticity of the surrounding territories on the basis of spatial regularities; and
- -
exclude the allocation of geophysical territories that do not fit into the overall spatial model.
The “Smolny” polygon (center: 54°42′18.72″ N, 45°18′33.79″ E) is isolated in the interaction zone of forest-steppe geosystems of secondary moraine, forest landscapes of water-glacial and ancient alluvial plains. The valley of Alatyr is subtirally extended in Northeastern Mordovia from west to east. It was formed in a system of tectonic faults. During the Don glaciation period, it was expanded and deepened by water-glacial flows moving from the Moksha Basin to the Sura basin. Large layers of fluvioglacial sands were deposited on the bottom of the erosion form, which, in some areas, were significantly altered by eolian processes. Subsequently, this ancient valley of the river was inherited by modern Alatyr. On the above-floodplain terraces are traced boggy hollows and depressions of thermokarst and suffosion origin, the gullies that crash into the slopes of the watersheds. The right root, washed by Alatyr, is complicated by deep ravines and beams with numerous manifestations of landslide processes. The floodplain has a width of up to 4–5 km.
Landsat 7 space images were chosen as the initial data. Thus, for the analysis of the lands of the National Park “Smolny” it was initially assumed that the nomenclature of the classification result will be based on the division of vegetation classes, including coniferous, broad-leaved, small-leaved forests, as well as lands not covered with vegetation. For efficient analysis of remote sensing data, it is reasonable to choose a combination of short-wave infrared, near infrared, and red channels from Landsat 7. The combination of these spectral zones is informative in solving the problem of classifying lands covered with vegetation.
The calculation of the descriptors of the neighborhood was carried out. To make an estimate of the effect of the size of the analyzed neighborhood on the result of the classification, experiments were carried out taking into account the characteristics of the descriptors of the radius neighborhood of 10 px (300 m), 50 px (1500 m), 100 px (3000 m), and without taking these parameters into account. As a data classifier, a neural network of direct distribution was used, together with an expert for it, training, validation, and test samples were prepared. The thematic interpretation of space survey materials by neural networks trained on these samples allowed generation of vegetation maps and allocating sites corresponding to lands covered with coniferous, broad-leaved, small-leaved forests, as well as open sands. Classification, taking into account the descriptors of the neighborhood with a radius of 300 m, resulted in a generalized result in solving the problem of land classification. Classification of remote sensing data, taking into account the descriptors of the neighborhood with a radius of 1.5 km, made it possible to identify sandy areas that were not covered by vegetation, which were little emphasized in the results of the remaining experiments.
Experiments have shown that classifying geodata with the inclusion of the neighborhood descriptors enables a more flexible configuration of the final output while also providing better accuracy in some cases. Since the proposed method is based on the analysis of the neighborhood, the radius of it is determined empirically. The classification accuracies with varying radius on different test polygons are illustrated in
Table 2.
It is noteworthy that the classification, with taking into account a neighborhood with a radius of 300 m, led to some generalization in solving the problem of classifying geophysical shells. Qualitative consideration of the properties of a neighborhood is possible with the combined use of various environmental descriptors, since each of them provides various information about geospatial systems.
5. Conclusions
The set of geophysical shell analysis algorithms developed is the prototype of an ERS data classification system written in MATLAB and consists of two subsystems: (1) the analysis of data describing the invariant geophysical properties while identifying their borders; and (2) the analysis of the dynamic properties of geophysical plots to study the sustainability of the internal structure of geophysical plots.
The study showed that for interpretation of remote sensing data, allocation of landscapes and types of land, it is expedient to use both spectral data and synthetic spatial information about the territory and its neighborhood. It is important to note that the spectral features contain information about the properties of the territory, while the neighborhood descriptors reflect the spatial distribution of this information containing information about the structure and statistical properties of the territory. The spectral features and descriptors of the neighborhood are interdependent, but their joint use allows one to take into account the emergent properties of the internal structure of landscapes. In the analysis of the territory based on neighborhood descriptors, it is necessary to identify the most informative features of the territory that must be taken into account when training a classifier capable of predicting the class to which the image area belongs. Careful selection of textual descriptors containing the greatest amount of information makes it possible to identify well-shared attributes of landscapes.
The application of the developed methodology in the analysis of different areas should be based on an algorithm that includes the following steps: (1) definition of the problem and the purpose of study; (2) selection of input data for analysis and determination the the form of the output of the classifying process; (3) pre-processing of the image, which includes calculation of the neighborhood parameters; (4) choice of the algorithm for trainable data classification, determination of its architecture, and the properties of its implementation; (5) preparing a training and testing samples; (6) training the classifier; (7) classification of remote sensing data using a trained algorithm; and (8) quality assessment of the classification on the basis of metrics described in the article.
The developed technique for assessing the properties of the geophysical shell based on remote sensing data is based on taking into account the spectral characteristics of the territory and synthetic descriptors in the vicinity, it allows to achieve: (a) reducing the noise impact; (b) obtaining a generalized result; and (c) improving the accuracy of classification.
The presented technique makes it possible to calculate an informative complex descriptor of the territory with low computational costs in order to diagnose emergent properties of the internal structure of the geophysical site through analysis of the diversity of the neighborhood descriptors.
To solve this problem, it is expedient to use algorithms for assessing the geophysical diversity of the area by calculating of the boundary descriptor, heterogeneity, color descriptor, and integrated descriptor. When analyzing images obtained as a result of remote sensing, the most informative was the integrated descriptor. It is also worth noting that images are often evaluated visually in RGB format and, in this connection, the histogram of the shades described in the article was quite informative. In turn, a further search of informative territory descriptors will be carried out in the course of further investigation.
Due to the analysis of the properties of not only the atomic section, but also its surrounding territories, the negative noise effect associated with the distortions of the initial satellite information is minimized. The analysis of the authenticity of the surrounding territories allows the classification of land plots on the basis of spatial regularities with greater objective accuracy.
The final result excludes the allocation of geophysical territories that do not fit into the overall spatial model, so the classification of materials based on the parameters of a larger neighborhood is suitable for mapping small-scale geophysical shells. An excessive increase in the radius of the neighborhood can lead to a decrease in the accuracy of the classification. The algorithm was tested in the system of the test polygon and demonstrated some variation in the accuracy of the classification, which was between 81‒88% (neighborhood excluded) or 87‒96% (neighborhood included). It was also discovered that a significantly greater radius of the neighborhood under analysis makes the resulting classification less accurate.
Due to the system analysis of the properties of not only the atomic site, but also its nearby territories, the negative noise impact associated with the distortions of the initial satellite information is minimized. The analysis of the authenticity of the surrounding territories allows the classification of land plots on the basis of spatial regularities with greater objective accuracy. The final result excludes the allocation of geophysical territories that do not fit into the overall spatial model, so the classification of materials based on the parameters of a larger neighborhood is suitable for mapping small-scale geophysical shells.