Prediction of Ethanol Content and Total Extract Using Densimetry and Refractometry
Abstract
1. Introduction
- 1.
- Establish patterns of changes in refractometer readings during the fermentation of grape must and develop a way to control the fermentation process by registering changes in °Brix refractometer readings;
- 2.
- To develop a rapid, non-destructive method for determining the volume fraction of ethanol in liquid homogeneous products of grape winemaking, based on measuring the density and refractive index. This will be conducted using a device suitable for implementation in production conditions (i.e., using standard laboratory equipment that would be available at a winery’s laboratory) and based on a clear algorithm of actions and calculations that ensures sufficient accuracy and unambiguity of the determined result.
2. Materials and Methods
2.1. Materials
2.2. Fermentation Process and Monitoring
2.3. Production and Measurements of Model Solutions
2.4. Data Analysis
3. Results and Discussion
3.1. Background
3.2. Determination of the Dynamics of Changes in the Readings of the Refractometer Scale during Alcoholic Fermentation
3.3. Example Calculation
3.4. Determination of the Volume Fraction of Ethanol
- b1 = α00,
- b2 = (α10 − α00)/(p1 − p0),
- b3 = (α01 − α00)/(B1 − B0),
- b4 = (α00 − α10 − α01 + α11)/(p1 − p0) × (B1 − B0)
3.5. Example Calculation
- b1 = α00 = 18.6
- b2 = = = −0.367
- b3 = = = 1.57
- b4 = = = 0.0
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- dos Santos, C.A.T.; Páscoa, R.N.M.J.; Lopes, J.A. A review on the application of vibrational spectroscopy in the wine industry: From soil to bottle. TrAC Trends Anal. Chem. 2017, 88, 100–118. [Google Scholar] [CrossRef]
- Debebe, A.; Redi-Abshiro, M.; Chandravanshi, B.S. Non-destructive determination of ethanol levels in fermented alcoholic beverages using Fourier transform mid-infrared spectroscopy. Chem. Cent. J. 2017, 11, 27. [Google Scholar] [CrossRef] [PubMed]
- Green, D.W.; Southard, M.Z. Perry’s Chemical Engineers’ Handbook; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Magwaza, L.S.; Opara, U.L. Analytical methods for determination of sugars and sweetness of horticultural products—A review. Sci. Hortic. 2015, 184, 179–192. [Google Scholar] [CrossRef]
- Iland, P.; Ewart, A.; Sitters, J.; Markides, A.; Bruer, N. Techniques for Accurate Chemical Analysis and Quality Monitoring during Winemaking; Patrick Iland Promotions: Campbell Town, Australia, 2000. [Google Scholar]
- Gayda, G.; Stasyuk, N.; Klepach, H.; Gonchar, M.; Nisnevitch, M. 12—Promising Bioanalytical Approaches to Wine Analysis. In Quality Control in the Beverage Industry; Grumezescu, A.M., Holban, A.M., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 419–457. [Google Scholar] [CrossRef]
- Wine, I.O. Compendium of International Methods of Wine and Must Analysis; International Organisation of Vine and Wine: Dijon, France, 2021. [Google Scholar]
- Bavčar, D.; Košmerl, T. Determination of alcohol and total dry extract in Slovenian wines by empirical relations. Food Technol. Biotechnol. 2002, 40, 321–329. [Google Scholar]
- Taylor, J. Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Cozzolino, D.; Cynkar, W.; Shah, N.; Dambergs, R.; Smith, P. A brief introduction to multivariate methods in grape and wine analysis. Int. J. Wine Res. 2009, 1, 123–130. [Google Scholar] [CrossRef]
- Khodasevich, M.; Scorbanov, E.; Rogovaya, M. Application of multivariate analysis of broadband transmission spectra for calibration of physico-chemical parameters of wines. Devices Methods Meas. 2019, 10, 198–206. [Google Scholar] [CrossRef]
- Timofeev, R. Refractodensimetric method for determining the volume fraction of ethyl alcohol in wines and winy beverages. Proc. Voronezh State Univ. Eng. Technol. 2020, 82, 104–109. [Google Scholar] [CrossRef]
- Noiseux, I.; Long, W.; Cournoyer, A.; Vernon, M. Simple fiber-optic-based sensors for process monitoring: An application in wine quality control monitoring. Appl. Spectrosc. 2004, 58, 1010–1019. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Miles, R.E.H.; Cotterell, M.I.; Marsh, A.; Rovelli, G.; Rickards, A.M.J.; Zhang, Y.-H.; Reid, J.P. Comparison of Methods for Predicting the Compositional Dependence of the Density and Refractive Index of Organic-Aqueous Aerosols. J. Phys. Chem. A 2016, 120, 6604–6617. [Google Scholar] [CrossRef] [PubMed]
- Martens, M.; Hadrich, M.J.; Nestler, F.; Ouda, M.; Schaadt, A. Combination of Refractometry and Densimetry—A Promising Option for Fast Raw Methanol Analysis. Chem. Ing. Tech. 2020, 92, 1474–1481. [Google Scholar] [CrossRef]
- Regmi, U.; Rai, K.P.; Palma, M. Determination of organic acids in wine and spirit drinks by fourier transform infrared (FT-IR) spectroscopy. J. Food Sci. Technol. Nepal 2012, 7, 36–43. [Google Scholar] [CrossRef]
- Fu, Q.; Wang, J.; Lin, G.; Suo, H.; Zhao, C. Short-wave near-infrared spectrometer for alcohol determination and temperature correction. J. Anal. Methods Chem. 2012, 2012, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Peng, B.; Ge, N.; Cui, L.; Zhao, H. Monitoring of alcohol strength and titratable acidity of apple wine during fermentation using near-infrared spectroscopy. LWT-Food Sci. Technol. 2016, 66, 86–92. [Google Scholar] [CrossRef]
- Pretorius, F.; Focke, W.W.; Androsch, R.; du Toit, E. Estimating binary liquid composition from density and refractive index measurements: A comprehensive review of mixing rules. J. Mol. Liq. 2021, 332, 115893. [Google Scholar] [CrossRef]
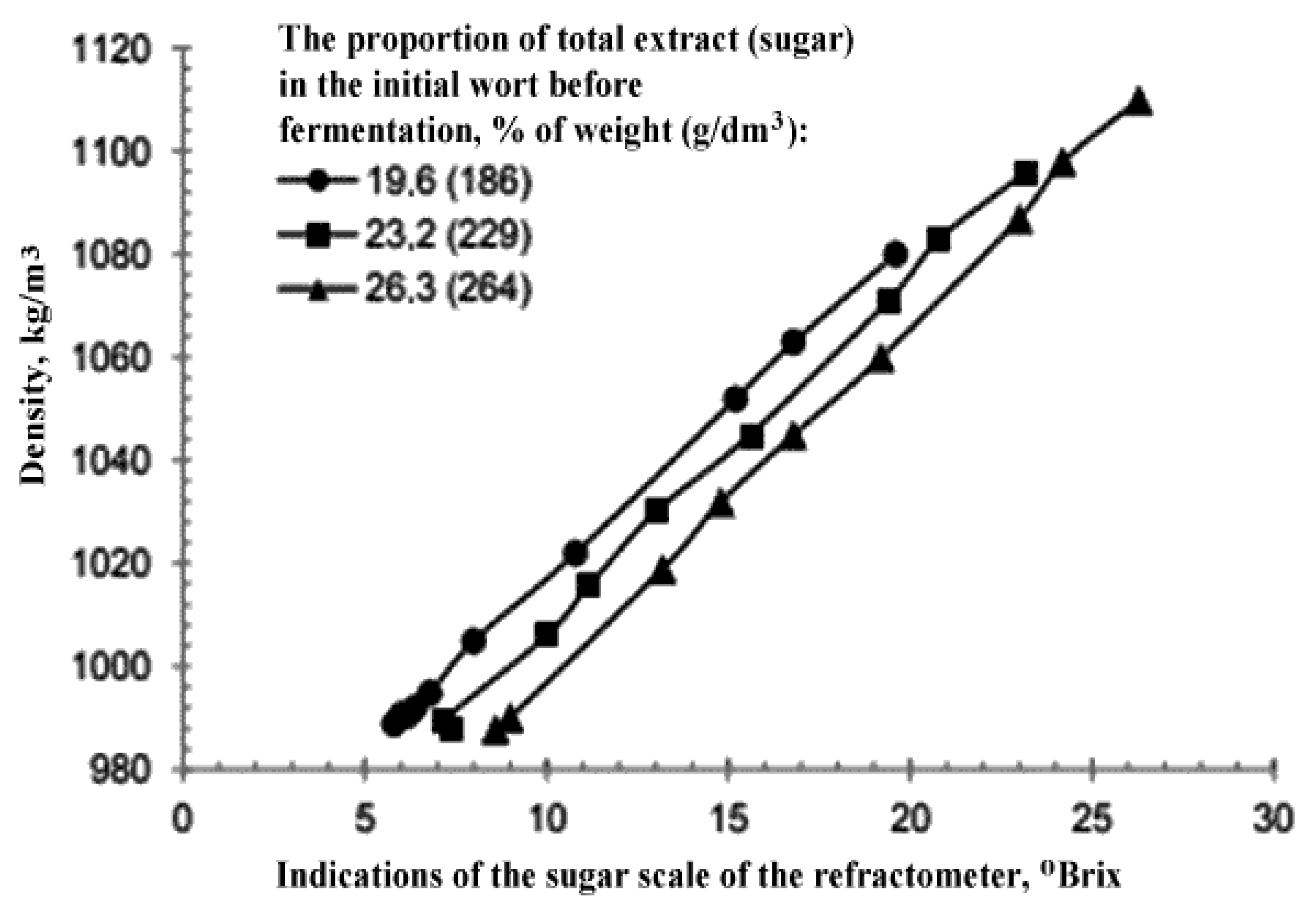
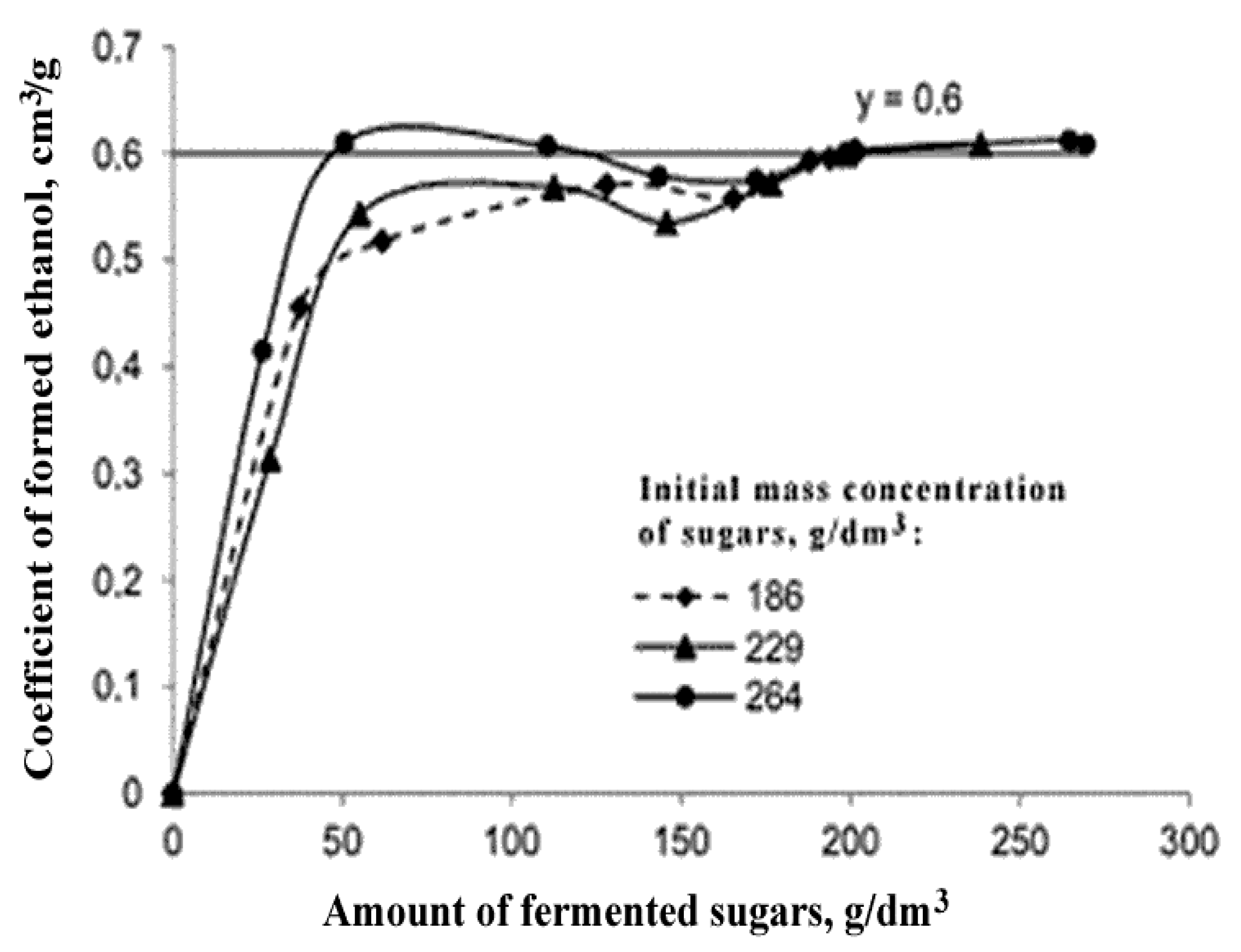

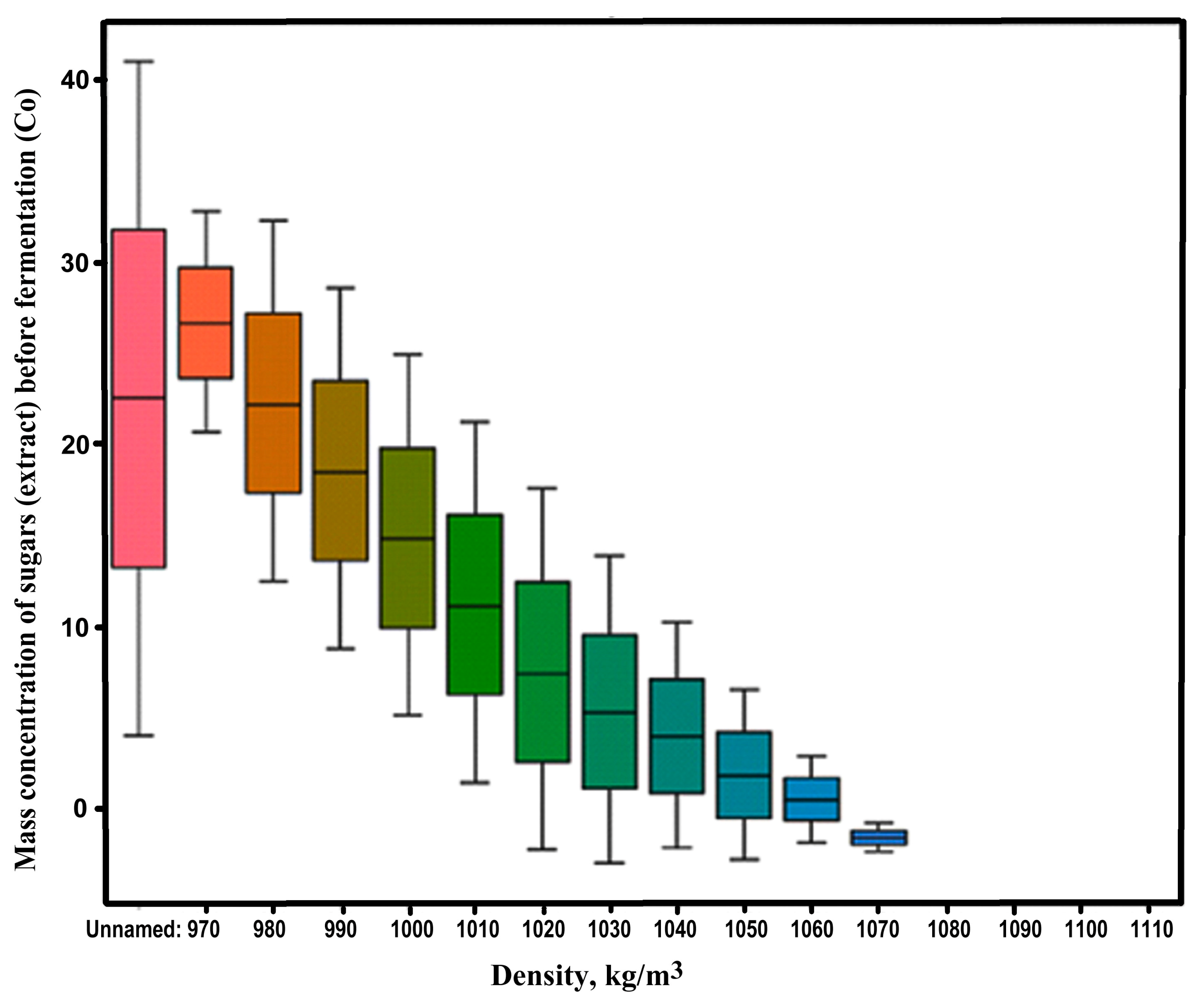
| Amount of Discarded Sugars, g/dm3 | Alcohol Yield Coefficient, cm3/g (Mean ± 95% Confidence Interval) |
|---|---|
| 30 | 0.40 ± 0.12 |
| 50 | 0.54 ± 0.10 |
| 80 | 0.58 ± 0.04 |
| 150 | 0.56 ± 0.03 |
| >200 | 0.60 ± 0.01 |
| B0 | C0 | α | B0 | C0 | α | B0 | C0 | α |
|---|---|---|---|---|---|---|---|---|
| 10.0 | 82 | 14.16 | 16.8 | 155 | 14.76 | 23.6 | 233 | 15.41 |
| 10.2 | 84 | 14.17 | 17.0 | 158 | 14.78 | 23.8 | 235 | 15.43 |
| 10.4 | 86 | 14.19 | 17.2 | 160 | 14.80 | 24.0 | 238 | 15.44 |
| 10.6 | 88 | 14.21 | 17.4 | 162 | 14.81 | 24.2 | 240 | 15.46 |
| 10.8 | 90 | 14.23 | 17.6 | 164 | 14.83 | 24.4 | 242 | 15.48 |
| 11.0 | 92 | 14.24 | 17.8 | 167 | 14.85 | 24.6 | 245 | 15.50 |
| 11.2 | 94 | 14.26 | 18.0 | 169 | 14.87 | 24.8 | 247 | 15.52 |
| 11.4 | 97 | 14.28 | 18.2 | 171 | 14.89 | 25.0 | 249 | 15.54 |
| 11.6 | 99 | 14.29 | 18.4 | 173 | 14.91 | 25.2 | 252 | 15.56 |
| 11.8 | 101 | 14.31 | 18.6 | 176 | 14.93 | 25.4 | 254 | 15.58 |
| 12.0 | 103 | 14.33 | 18.8 | 178 | 14.94 | 25.6 | 256 | 15.60 |
| 12.2 | 105 | 14.35 | 19.0 | 180 | 14.96 | 25.8 | 259 | 15.62 |
| 12.4 | 107 | 14.36 | 19.2 | 182 | 14.98 | 26.0 | 261 | 15.64 |
| 12.6 | 109 | 14.38 | 19.4 | 185 | 15.00 | 26.2 | 263 | 15.66 |
| 12.8 | 112 | 14.40 | 19.6 | 187 | 15.02 | 26.4 | 266 | 15.68 |
| 13.0 | 114 | 14.42 | 19.8 | 189 | 15.04 | 26.6 | 268 | 15.71 |
| 13.2 | 116 | 14.43 | 20.0 | 192 | 15.06 | 26.8 | 270 | 15.73 |
| 13.4 | 118 | 14.45 | 20.2 | 194 | 15.08 | 27.0 | 273 | 15.75 |
| 13.6 | 120 | 14.47 | 20.4 | 196 | 15.10 | 27.2 | 275 | 15.77 |
| 13.8 | 122 | 14.49 | 20.6 | 198 | 15.11 | 27.4 | 277 | 15.79 |
| 14.0 | 125 | 14.51 | 20.8 | 201 | 15.13 | 27.6 | 280 | 15.81 |
| 14.2 | 127 | 14.52 | 21.0 | 203 | 15.15 | 27.8 | 282 | 15.83 |
| 14.4 | 129 | 14.54 | 21.2 | 205 | 15.17 | 28.0 | 284 | 15.85 |
| 14.6 | 131 | 14.56 | 21.4 | 208 | 15.19 | 28.2 | 287 | 15.87 |
| 14.8 | 133 | 14.58 | 21.6 | 210 | 15.21 | 28.4 | 289 | 15.89 |
| 15.0 | 135 | 14.59 | 21.8 | 212 | 15.23 | 28.6 | 292 | 15.91 |
| 15.2 | 138 | 14.61 | 22.0 | 215 | 15.25 | 28.8 | 294 | 15.93 |
| 15.4 | 140 | 14.63 | 22.2 | 217 | 15.27 | 29.0 | 296 | 15.95 |
| 15.6 | 142 | 14.65 | 22.4 | 219 | 15.29 | 29.2 | 299 | 15.97 |
| 15.8 | 144 | 14.67 | 22.6 | 221 | 15.31 | 29.4 | 301 | 15.99 |
| 16.0 | 147 | 14.69 | 22.8 | 224 | 15.33 | 29.6 | 303 | 16.01 |
| 16.2 | 149 | 14.70 | 23.0 | 226 | 15.35 | 29.8 | 306 | 16.03 |
| 16.4 | 151 | 14.72 | 23.2 | 228 | 15.37 | 30.0 | 308 | 16.06 |
| 16.6 | 153 | 14.74 | 23.4 | 231 | 15.39 |
| Density, kg/m3 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B, % mass | 970 | 980 | 990 | 1000 | 1010 | 1020 | 1030 | 1040 | 1050 | 1060 | 1070 | 1080 | 1090 | 1100 | 1110 | 1120 | 1130 |
| 4.0 | - | 12.48 | 8.79 | 5.11 | 1.43 | −2.25 | - | - | - | - | - | - | - | - | - | - | - |
| 5.0 | - | 13.96 | 10.27 | 6.59 | 2.91 | −0.77 | - | - | - | - | - | - | - | - | - | - | - |
| 6.0 | - | 15.44 | 11.75 | 8.07 | 4.39 | 0.71 | −2.96 | - | - | - | - | - | - | - | - | - | - |
| 7.0 | 20.61 | 16.92 | 13.23 | 9.55 | 5.87 | 2.19 | −1.48 | - | - | - | - | - | - | - | - | - | - |
| 8.0 | 22.09 | 18.40 | 14.71 | 11.03 | 7.35 | 3.67 | 0.00 | - | - | - | - | - | - | - | - | - | - |
| 9.0 | 23.56 | 19.88 | 16.19 | 12.51 | 8.83 | 5.15 | 1.48 | −2.19 | - | - | - | - | - | - | - | - | - |
| 10.0 | 25.04 | 21.35 | 17.67 | 13.98 | 10.31 | 6.63 | 2.96 | −0.71 | - | - | - | - | - | - | - | - | - |
| 11.0 | 26.61 | 22.92 | 19.24 | 15.56 | 11.88 | 8.20 | 4.53 | 0.86 | −2.81 | - | - | - | - | - | - | - | - |
| 12.0 | 28.08 | 24.40 | 20.71 | 17.03 | 13.36 | 9.68 | 6.01 | 2.34 | −1.33 | - | - | - | - | - | - | - | - |
| 13.0 | 29.65 | 25.97 | 22.28 | 18.60 | 14.93 | 11.25 | 7.58 | 3.91 | 0.24 | - | - | - | - | - | - | - | - |
| 14.0 | 31.22 | 27.54 | 23.85 | 20.17 | 16.50 | 12.82 | 9.15 | 5.48 | 1.82 | −1.85 | - | - | - | - | - | - | - |
| 15.0 | 32 | 29.10 | 25.42 | 21.74 | 18.07 | 14.39 | 10.72 | 7.05 | 3.39 | −0.28 | - | - | - | - | - | - | - |
| 16.0 | - | 30.67 | 26.99 | 23.31 | 19.04 | 15.96 | 12.29 | 8.62 | 4.96 | 1.29 | −2.37 | - | - | - | - | - | - |
| 17.0 | - | 32.23 | 28.55 | 24.88 | 21.20 | 17.53 | 13.86 | 10.19 | 6.53 | 2.86 | −0.80 | - | - | - | - | - | - |
| 18.0 | - | - | 30.12 | 26.44 | 22.77 | 19.10 | 15.43 | 11.76 | 8.09 | 4.43 | 0.77 | −2.89 | - | - | - | - | - |
| 19.0 | - | - | 31.78 | 28.10 | 24.43 | 20.76 | 17.09 | 13.42 | 9.76 | 6.10 | 2.44 | −1.22 | - | - | - | - | - |
| 20.0 | - | - | - | 29.66 | 25.99 | 22.32 | 18.65 | 14.99 | 11.32 | 7.66 | 4.00 | 0.34 | −3.31 | - | - | - | - |
| 21.0 | - | - | - | 31.32 | 27.65 | 23.98 | 20.31 | 16.65 | 12.98 | 9.32 | 5.66 | 2.01 | −1.65 | - | - | - | - |
| 22.0 | - | - | - | 32.98 | 29.31 | 25.64 | 21.97 | 18.31 | 14.64 | 10.98 | 7.32 | 3.67 | 0.01 | - | - | - | - |
| 23.0 | - | - | - | - | 30.96 | 27.29 | 23.63 | 19.96 | 16.30 | 12.64 | 8.98 | 5.33 | 1.67 | - | - | - | - |
| 24.0 | - | - | - | - | 32.61 | 28.95 | 25.28 | 21.62 | 17.96 | 14.30 | 10.64 | 6.99 | 3.33 | −0.32 | - | - | - |
| 25.0 | - | - | - | - | - | 30.60 | 26.94 | 23.27 | 19.61 | 15.95 | 12.30 | 8.64 | 4.99 | 1.34 | −2.31 | - | - |
| 26.0 | - | - | - | - | - | 32.25 | 28.59 | 24.93 | 21.27 | 17.61 | 13.95 | 10.30 | 6.65 | 2.99 | −0.65 | - | - |
| 27.0 | - | - | - | - | - | - | 30.29 | 26.62 | 22.97 | 19.31 | 15.65 | 12.00 | 8.35 | 4.70 | 1.05 | - | - |
| 28.0 | - | - | - | - | - | - | 31.98 | 28.32 | 24.66 | 21.01 | 17.35 | 13.70 | 10.05 | 6.40 | 2.75 | −0.90 | - |
| 29.0 | - | - | - | - | - | - | - | 30.07 | 26.41 | 22.75 | 19.10 | 15.45 | 11.80 | 8.15 | 4.50 | 0.85 | −2.79 |
| 30.0 | - | - | - | - | - | - | - | 31.81 | 28.15 | 24.50 | 20.84 | 17.19 | 13.54 | 9.89 | 6.25 | 2.60 | −1.04 |
| 31.0 | - | - | - | - | - | - | - | - | 29.89 | 26.24 | 22.59 | 18.94 | 15.29 | 11.64 | 7.99 | 4.35 | 0.70 |
| P0 = 990 | P1 = 1000 | |||
|---|---|---|---|---|
| … | … | … | … | … |
| B0 = 7.0 | … | α00 = 18.60 | α10 = 14.93 | … |
| B0 = 8.0 | … | α01 = 20.17 | α11 = 16.50 | … |
| … | … | … | … | … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plugatar, Y.; Johnson, J.B.; Timofeev, R.; Korzin, V.; Kazak, A.; Nekhaychuk, D.; Borisova, E.; Rotanov, G. Prediction of Ethanol Content and Total Extract Using Densimetry and Refractometry. Beverages 2023, 9, 31. https://doi.org/10.3390/beverages9020031
Plugatar Y, Johnson JB, Timofeev R, Korzin V, Kazak A, Nekhaychuk D, Borisova E, Rotanov G. Prediction of Ethanol Content and Total Extract Using Densimetry and Refractometry. Beverages. 2023; 9(2):31. https://doi.org/10.3390/beverages9020031
Chicago/Turabian StylePlugatar, Yurij, Joel B. Johnson, Ruslan Timofeev, Vadim Korzin, Anatoliy Kazak, Dmitry Nekhaychuk, Elvira Borisova, and Gennady Rotanov. 2023. "Prediction of Ethanol Content and Total Extract Using Densimetry and Refractometry" Beverages 9, no. 2: 31. https://doi.org/10.3390/beverages9020031
APA StylePlugatar, Y., Johnson, J. B., Timofeev, R., Korzin, V., Kazak, A., Nekhaychuk, D., Borisova, E., & Rotanov, G. (2023). Prediction of Ethanol Content and Total Extract Using Densimetry and Refractometry. Beverages, 9(2), 31. https://doi.org/10.3390/beverages9020031







