Exploration of Data Fusion Strategies Using Principal Component Analysis and Multiple Factor Analysis
Abstract
1. Introduction
- The choice of model can be difficult due to the large number of available techniques and their variants;
- The execution of some models is difficult due to the availability of software and may often require advanced programming skills. In addition to this, a lack of transparency when it comes to the different stages of data handling creates reproducibility issues among the science community;
- Evaluating the performance of unsupervised data models is often descriptive of the data, but does not include descriptions of the model.
2. Materials and Methods
2.1. Experimental Design
2.2. Sensory Data Methodology
2.3. Chemical Data Collection and Capturing
2.4. Statistical Analysis
3. Results
3.1. Curation of Data Blocks
3.1.1. Assessment of Pre-Modelling Processing
3.1.2. Performance of Individual Block Models
3.2. Low-Level Data Fusion
3.3. Mid-Level Data Fusion
3.3.1. Principal Component Analysis (PCA)
3.3.2. Multiple Factor Analysis (MFA)
3.4. General Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Gagolewski, M. Data Fusion. Theory, Methods, and Applications; Hryniewicz, O., Mielniczuk, J., Penczek, W., Waniewski, J., Eds.; Institute of Computer Science, Polish Academy of Sciences: Warsaw, Poland, 2015; ISBN 9788363159207. [Google Scholar]
- Lahat, D.; Adalı, T.; Jutten, C. Multimodal Data Fusion: An Overview of Methods, Challenges and Prospects. Inst. Electr. Electron. Eng. 2015, 103, 1449–1477. [Google Scholar] [CrossRef]
- Cocchi, M. Data fusion methodology and applications. In Data Handling in Science and Technology; Cocchi, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 31, pp. 1–370. ISBN 9780444639844. [Google Scholar]
- Arvanitoyannis, I.S.; Katsota, M.N.; Psarra, E.P.; Soufleros, E.H.; Kallithraka, S. Application of quality control methods for assessing wine authenticity: Use of multivariate analysis (chemometrics). Trends Food Sci. Technol. 1999, 10, 321–336. [Google Scholar] [CrossRef]
- Iorgulescu, E.; Voicu, V.A.; Sârbu, C.; Tache, F.; Albu, F.; Medvedovici, A. Experimental variability and data pre-processing as factors affecting the discrimination power of some chemometric approaches (PCA, CA and a new algorithm based on linear regression) applied to (+/-)ESI/MS and RPLC/UV data: Application on green tea extrac. Talanta 2016, 155, 133–144. [Google Scholar] [CrossRef] [PubMed]
- Silvestri, M.; Elia, A.; Bertelli, D.; Salvatore, E.; Durante, C.; Li Vigni, M.; Marchetti, A.; Cocchi, M. A mid level data fusion strategy for the Varietal Classification of Lambrusco PDO wines. Chemom. Intell. Lab. Syst. 2014, 137, 181–189. [Google Scholar] [CrossRef]
- Alañón, M.; Pérez-Coello, M.; Marina, M. Wine science in the metabolomics era. Trends Anal. Chem. 2015, 74, 1–20. [Google Scholar] [CrossRef]
- Valentin, D.; Chollet, S.; Lelièvre, M.; Abdi, H. Quick and dirty but still pretty good: A review of new descriptive methods in food science. Int. J. Food Sci. Technol. 2012, 47, 1563–1578. [Google Scholar] [CrossRef]
- Granato, D.; de Araújo Calado, V.M.; Jarvis, B. Observations on the use of statistical methods in Food Science and Technology. Food Res. Int. 2014, 55, 137–149. [Google Scholar] [CrossRef]
- Cocchi, M. Introduction: Ways and Means to Deal With Data From Multiple Sources. In Data Handling in Science and Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 2019; Volume 31, pp. 1–26. [Google Scholar]
- Brand, J. Rapid Sensory Profiling Methods for Wine: Workflow Optimisation for Research and Industry Applications. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2019. [Google Scholar]
- Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- López-Rituerto, E.; Savorani, F.; Avenoza, A.; Busto, J.H.; Peregrina, J.M.; Engelsen, S.B. Investigations of la Rioja terroir for wine production using 1H NMR metabolomics. J. Agric. Food Chem. 2012, 60, 3452–3461. [Google Scholar] [CrossRef]
- Ragone, R.; Crupi, P.; Piccinonna, S.; Bergamini, C.; Mazzone, F.; Fanizzi, F.P.; Schena, F.P.; Antonacci, D. Classification and Chemometric Study of Southern Italy Monovarietal Wines Based on NMR and HPLC-DAD-MS. Food Sci. Biotechnol. 2015, 24, 817–826. [Google Scholar] [CrossRef]
- Borràs, E.; Ferré, J.; Boqué, R.; Mestres, M.; Aceña, L.; Busto, O. Data fusion methodologies for food and beverage authentication and quality assessment-A review. Anal. Chim. Acta 2015, 891, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Brand, J.; Panzeri, V.; Buica, A. Wine quality drivers: A case study on South African chenin blanc and pinotage wines. Foods 2020, 9, 805. [Google Scholar] [CrossRef] [PubMed]
- Biancolillo, A.; Boqué, R.; Cocchi, M.; Marini, F. Data Fusion Strategies in Food Analysis. In Data Handling in Science and Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 2019; Volume 31, pp. 271–310. [Google Scholar]
- Pereira, A.C.; Carvalho, M.J.; Miranda, A.; Leça, J.M.; Pereira, V.; Albuquerque, F.; Marques, J.C.; Reis, M.S. Modelling the ageing process: A novel strategy to analyze the wine evolution towards the expected features. Chemom. Intell. Lab. Syst. 2016, 154, 176–184. [Google Scholar] [CrossRef]
- Valente, C.C.; Bauer, F.F.; Venter, F.; Watson, B.; Nieuwoudt, H.H. Modelling the sensory space of varietal wines: Mining of large, unstructured text data and visualisation of style patterns. Sci. Rep. 2018, 8, 4987. [Google Scholar] [CrossRef] [PubMed]
- Ballabio, D.; Todeschini, R.; Consonni, V. Recent Advances in High-Level Fusion Methods to Classify Multiple Analytical Chemical Data. In Data Handling in Science and Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 2019; Volume 31, pp. 129–155. [Google Scholar]
- Pagés, J.; Husson, F. Multiple factor analysis with confidence ellipses: A methodology to study the relationships between sensory and instrumental data. J. Chemom. 2005, 19, 138–144. [Google Scholar] [CrossRef]
- Salkind, J.; Kristin, R. Encyclopidia of Measurement and Statistics; Salkind, N.J., Ed.; Sage: Newcastle upon Tyne, UK, 2007; ISBN 9781412916110. [Google Scholar]
- McKillup, S. Statistics Explained: An Introductory Guide for Life Scientists, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012; ISBN 9781107005518. [Google Scholar]
- Borgognone, M.G.; Bussi, J.; Hough, G. Principal component analysis in sensory analysis: Covariance or correlation matrix? Food Qual. Prefer. 2001, 12, 323–326. [Google Scholar] [CrossRef]
- Pagès, J. Collection and analysis of perceived product inter-distances using multiple factor analysis: Application to the study of 10 white wines from the Loire Valley. Food Qual. Prefer. 2005, 16, 642–649. [Google Scholar] [CrossRef]
- Abdi, H.; Valentin, D. Multiple Factor Analysis (MFA). Encycl. Meas. Stat. 2007, 1, 657–663. [Google Scholar]
- de Tayrac, M.; Lê, S.; Aubry, M.; Mosser, J.; Husson, F. Simultaneous analysis of distinct Omics data sets with integration of biological knowledge: Multiple Factor Analysis approach. BMC Genom. 2009, 10, 32. [Google Scholar] [CrossRef]
- Baldwin, E.; Han, J.; Luo, W.; Zhou, J.; An, L.; Liu, J.; Zhang, H.H.; Li, H. On fusion methods for knowledge discovery from multi-omics datasets. Comput. Struct. Biotechnol. J. 2020, 18, 509–517. [Google Scholar] [CrossRef]
- Pagès, J. Multiple factor analysis: Main features and application to sensory data. Rev. Colomb. Estad. 2004, 27, 1–26. [Google Scholar]
- Cadena, R.S.; Cruz, A.G.; Netto, R.R.; Castro, W.F.; Faria, J.D.A.F.; Bolini, H.M.A. Sensory profile and physicochemical characteristics of mango nectar sweetened with high intensity sweeteners throughout storage time. Food Res. Int. 2013, 54, 1670–1679. [Google Scholar] [CrossRef]
- Mafata, M.; Brand, J.; Medvedovici, A.; Buica, A.; Mafata, M.; Brand, J.; Medvedovici, A.; Buica, A. Chemometric and sensometric techniques in enological data analysis. Crit. Rev. Food Sci. Nutr. 2022, 1–15. [Google Scholar] [CrossRef]
- Le Dien, S.; Pagès, J. Hierarchical Multiple Factor Analysis: Application to the comparison of sensory profiles. Food Qual. Prefer. 2003, 14, 397–403. [Google Scholar] [CrossRef]
- Abdi, H. RV Coefficient and Congruence Coefficient. Encycl. Meas. Stat. 2007, 1, 849–853. [Google Scholar]
- Mafata, M.; Brand, J.; Panzeri, V.; Kidd, M.; Buica, A. A multivariate approach to evaluating the chemical and sensorial evolution of South African Sauvignon Blanc and Chenin Blanc wines under different bottle storage conditions. Food Res. Int. 2019, 125, 108515. [Google Scholar] [CrossRef] [PubMed]
- Antúnez, L.; Salvador, A.; de Saldamando, L.; Varela, P.; Giménez, A.; Ares, G. Evaluation of Data Aggregation in Polarized Sensory Positioning. J. Sens. Stud. 2015, 30, 46–55. [Google Scholar] [CrossRef]
- Fleming, E.E.; Ziegler, G.R.; Hayes, J.E. Check-all-that-apply (CATA), sorting, and polarized sensory positioning (PSP) with astringent stimuli. Food Qual. Prefer. 2015, 45, 41–49. [Google Scholar] [CrossRef]
- Thuillier, B.; Valentin, D.; Marchal, R.; Dacremont, C. Pivot© profile: A new descriptive method based on free description. Food Qual. Prefer. 2015, 42, 66–77. [Google Scholar] [CrossRef]
- Lelièvre-Desmas, M.; Valentin, D.; Chollet, S. Pivot profile method: What is the influence of the pivot and product space? Food Qual. Prefer. 2017, 61, 6–14. [Google Scholar] [CrossRef]
- Aben, N.; Westerhuis, J.A.; Song, Y.; Kiers, H.A.L.; Michaut, M.; Smilde, A.K.; Wessels, L.F.A. iTOP: Inferring the topology of omics data. Bioinformatics 2018, 34, 988–996. [Google Scholar] [CrossRef] [PubMed]
- Engel, J.; Gerretzen, J.; Szymańska, E.; Jansen, J.J.; Downey, G.; Blanchet, L.; Buydens, L.M. Breaking with trends in pre-processing? Trends Anal. Chem. 2013, 50, 96–106. [Google Scholar] [CrossRef]
- Smilde, A.K.; Van Mechelen, I. A Framework for Low-Level Data Fusion. In Data Handling in Science and Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 2019; Volume 31, pp. 27–50. [Google Scholar]
- Umetrics, M. User Guide to SIMCA 13. Umetrics 2012, 13, 1–661. [Google Scholar] [CrossRef]
- Gishen, M.; Dambergs, R.G.; Cozzolino, D. Grape and wine analysis-enhancing the power of spectroscopy with chemometrics. Aust. J. Grape Wine Res. 2005, 11, 296–305. [Google Scholar] [CrossRef]
- Stevenson, T. The-New-Sothebys-Wine-Encyclopedia, 4th ed.; Dorling Kindersley Limited: London, UK, 2005. [Google Scholar]
- Ríos-Reina, R.; Callejón, R.M.; Savorani, F.; Amigo, J.M.; Cocchi, M. Data fusion approaches in spectroscopic characterization and classification of PDO wine vinegars. Talanta 2019, 198, 560–572. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.W. Practical Handbook of Spectroscopy; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781351422789. [Google Scholar]
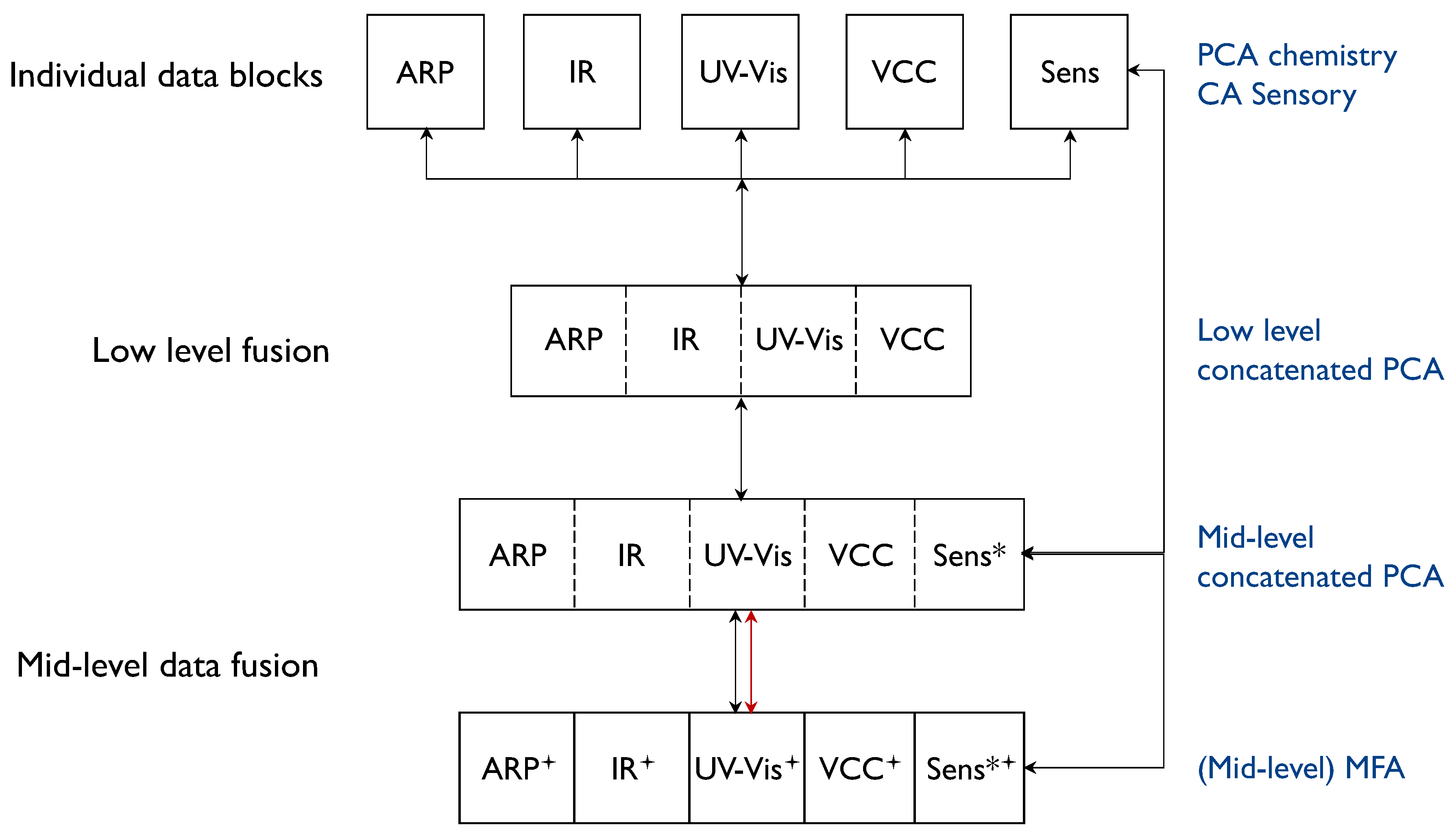
| Level | Blocks | Input | Pre-Processing | Modelling | Model Output | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Description | Value Type | Matrix Type | Row | Column | Modelled Matrix | Model Type | Output Matrix Type | Output Matrix Row | Output Matrix Column | Model Performance Parameters | |||
| Individual Data Blocks | ARP | Concentrations, absorbance values | Discreet | Correlation | Samples | Concentrations, AU | None | Raw data | PCA | Scores | Samples | Principal components | EV%, eigenvalue, decay slope R2 |
| IR | Spectral, reflectance | Continuous | Continuous | Samples | Wavenumber | None * | Raw data | PCA | Scores | Samples | Principal components | ||
| UV-Vis | Spectral, absorbance | Continuous | Continuous | Samples | Absorbance wavelengths | None | Raw data | PCA | Scores | Samples | Principal components | ||
| VCC | Concentrations | Discreet | Correlation | Samples | Concentrations | None | Raw data | PCA | Scores | Samples | Principal components | ||
| Sensory | Pivot profile reference-based method | Discreet | Rating | Samples | Ratings (−1, 0, 1) | Conversion to frequency matrix | Positive FC | CA | Scores | Samples | Factors | ||
| Standardized deviates | Samples | Variables | |||||||||||
| Low | ARP + IR + UV-Vis + VCC | Block concatenation | Mixed | Mixed | Samples | See individual data blocks | Matrix concatenation | Concatenated matrix | PCA | Scores | Samples | Principal components | EV%, eigenvalue, decay slope R2 |
| Mid | ARP + IR + UV-Vis + VCC + Sensory ‡ | Block concatenation | Mixed | Mixed | Samples | See individual data blocks except ‡ | Matrix concatenation | Concatenated matrix | PCA | Scores | Samples | Principal components | EV%, eigenvalue, decay slope R2 |
| ARP + IR + UV-Vis + VCC + Sensory ‡ | Blocks | Mixed | Multiblock | Samples | See individual data blocks except ‡ | PCA per block on raw data except ‡ | Multiblock standardized deviates from individual PCA | MFA | Scores | Samples | MFA dimensions | EV%, eigenvalue, decay slope R2 | |
| Loadings | Blocks | MFA dimensions | |||||||||||
| Data Set | Raw | 1st Deriv | MSC | 1st Deriv + MSC | MSC + 1st Deriv | |
|---|---|---|---|---|---|---|
| Chenin Blanc | AVN | 82 | 52 | 73 | 51 | 53 |
| CDB | 72 | 57 | 61 | 52 | 52 | |
| DTK | 97 | 62 | 97 | 72 | 73 | |
| FRV | 76 | 52 | 68 | 50 | 53 | |
| KZC | 96 | 79 | 100 | 100 | 100 | |
| PDB | 81 | 54 | 88 | 50 | 60 | |
| Average | 84 | 59 | 81 | 63 | 65 | |
| Stdev | 9 | 9 | 15 | 18 | 17 | |
| Sauvignon Blanc | AVN | 72 | 43 | 55 | 40 | 39 |
| CDB | 74 | 54 | 63 | 51 | 51 | |
| DTK | 63 | 45 | 46 | 39 | 40 | |
| FRV | 74 | 50 | 51 | 40 | 41 | |
| KZC | 62 | 43 | 51 | 38 | 39 | |
| PDB | 77 | 45 | 52 | 38 | 39 | |
| Average | 70 | 47 | 53 | 41 | 42 | |
| Stdev | 6 | 4 | 5 | 5 | 4 | |
| Overall | Low | 62 | 43 | 46 | 38 | 39 |
| High | 97 | 79 | 100 | 100 | 100 | |
| Average | 77 | 53 | 67 | 52 | 53 | |
| Stdev | 10 | 10 | 18 | 17 | 17 |
| Cumulative %EV per PC | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cultivar | Data Set | Total Stress (Eigenvalue) | Slope | R² | F1 | F2 | F3 | F4 | F5 | F6 |
| Chenin Blanc | AVN | 589 | 0.55 | 0.989 | 41 | 68 | 84 | 92 | 97 | 100 |
| CDB | 591 | 0.46 | 0.970 | 41 | 69 | 82 | 90 | 95 | 100 | |
| DTK | 742 | 0.88 | 0.966 | 52 | 85 | 93 | 98 | 99 | 100 | |
| FRV | 688 | 0.44 | 0.926 | 48 | 69 | 81 | 88 | 95 | 100 | |
| KZC | 962 | 0.87 | 0.947 | 67 | 89 | 95 | 98 | 99 | 100 | |
| PDB | 837 | 0.56 | 0.910 | 59 | 78 | 86 | 92 | 97 | 100 | |
| Sauvignon Blanc | AVN | 617 | 0.47 | 0.962 | 43 | 70 | 82 | 90 | 95 | 100 |
| CDB | 716 | 0.54 | 0.966 | 50 | 74 | 84 | 92 | 97 | 100 | |
| DTK | 541 | 0.38 | 0.932 | 38 | 65 | 78 | 86 | 93 | 100 | |
| FRV | 556 | 0.55 | 0.934 | 39 | 76 | 85 | 92 | 97 | 100 | |
| KZC | 800 | 0.41 | 0.813 | 56 | 70 | 79 | 88 | 95 | 100 | |
| PDB | 653 | 0.46 | 0.946 | 46 | 70 | 82 | 89 | 95 | 100 | |
| Range | Min | 541 | 0.38 | 0.813 | 38 | 65 | 78 | 86 | 93 | 100 |
| Max | 962 | 0.88 | 0.989 | 67 | 89 | 95 | 98 | 99 | 100 | |
| Cumulative %EV per PC | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data Set | Observations | Total Stress (Eigenvalue) | Slope | R² | F1 | F2 | F3 | F4 | F5 | F6 | |
| Chenin Blanc | AVN | 1458 | 601 | 0.45 | 0.97 | 41 | 68 | 81 | 89 | 95 | 100 |
| CDB | 1463 | 595 | 0.53 | 0.99 | 41 | 67 | 83 | 91 | 97 | 100 | |
| DTK | 1461 | 747 | 0.83 | 0.96 | 51 | 84 | 92 | 97 | 99 | 100 | |
| FRV | 1463 | 698 | 0.43 | 0.92 | 48 | 68 | 80 | 88 | 95 | 100 | |
| KZC | 1458 | 968 | 0.82 | 0.94 | 66 | 89 | 95 | 97 | 99 | 100 | |
| PDB | 1461 | 847 | 0.54 | 0.90 | 58 | 77 | 85 | 91 | 97 | 100 | |
| Sauvignon Blanc | AVN | 1459 | 661 | 0.45 | 0.94 | 45 | 69 | 81 | 89 | 95 | 100 |
| CDB | 1457 | 721 | 0.53 | 0.97 | 50 | 73 | 84 | 92 | 97 | 100 | |
| DTK | 1464 | 544 | 0.37 | 0.93 | 37 | 64 | 77 | 86 | 93 | 100 | |
| FRV | 1463 | 561 | 0.53 | 0.93 | 38 | 75 | 84 | 92 | 97 | 100 | |
| KZC | 1464 | 805 | 0.40 | 0.80 | 55 | 69 | 78 | 87 | 95 | 100 | |
| PDB | 1458 | 661 | 0.45 | 0.94 | 45 | 69 | 81 | 89 | 95 | 100 | |
| Range | Min | 1457 | 544 | 0.37 | 0.80 | 37 | 64 | 77 | 86 | 93 | 100 |
| Max | 1464 | 968 | 0.83 | 0.99 | 66 | 89 | 95 | 97 | 99 | 100 | |
| Chenin Blanc | Sauvignon Blanc | ||
|---|---|---|---|
| AVN | IR | ↑0.90 | ↗0.88 |
| ARP | ↘0.67 | ↘0.61 | |
| VCC | ↗0.80 | ↓0.45 | |
| UV-Vis | →0.76 | ↗0.82 | |
| Sensory | →0.73 | ↘0.68 | |
| CDB | IR | ↗0.88 | ↗0.86 |
| ARP | →0.75 | ↗0.83 | |
| VCC | ↘0.60 | →0.72 | |
| UV-Vis | →0.78 | →0.76 | |
| Sensory | ↗0.84 | →0.74 | |
| DTK | IR | ↗0.88 | ↑0.93 |
| ARP | ↘0.57 | ↘0.68 | |
| VCC | ↘0.65 | ↘0.64 | |
| UV-Vis | ↘0.56 | ↗0.86 | |
| Sensory | ↘0.66 | →0.73 | |
| FRV | IR | ↑0.95 | ↗0.83 |
| ARP | ↗0.85 | →0.75 | |
| VCC | →0.74 | →0.72 | |
| UV-Vis | ↗0.86 | →0.72 | |
| Sensory | ↗0.84 | →0.71 | |
| KZC | IR | ↑0.96 | ↑0.96 |
| ARP | ↘0.53 | →0.79 | |
| VCC | ↘0.52 | ↓0.46 | |
| UV-Vis | →0.78 | ↑0.93 | |
| Sensory | ↘0.63 | ↘0.61 | |
| PDB | IR | ↑0.92 | ↑0.93 |
| ARP | ↗0.88 | ↗0.86 | |
| VCC | ↘0.69 | ↘0.55 | |
| UV-Vis | ↗0.88 | ↗0.86 | |
| Sensory | ↗0.82 | →0.75 |
| Cumulative %EV | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample Set | Total Stress (Eigenvalue) | Slope | R² | C1 | C2 | C3 | C4 | C5 | C6 | |
| Chenin Blanc | AVN | 9.8952 | 0.43 | 0.96 | 40 | 67 | 79 | 89 | 95 | 100 |
| CDB | 9.7308 | 0.35 | 0.94 | 40 | 61 | 75 | 86 | 93 | 100 | |
| DTK | 9.0578 | 0.43 | 0.99 | 41 | 64 | 78 | 89 | 96 | 100 | |
| FRV | 9.7637 | 0.38 | 0.96 | 42 | 63 | 77 | 87 | 94 | 100 | |
| KZC | 8.9517 | 0.47 | 0.97 | 42 | 68 | 82 | 90 | 96 | 100 | |
| PDB | 9.0879 | 0.37 | 0.84 | 49 | 64 | 76 | 86 | 95 | 100 | |
| Sauvignon Blanc | AVN | 9.3392 | 0.30 | 0.85 | 39 | 60 | 72 | 82 | 92 | 100 |
| CDB | 10.6642 | 0.37 | 0.99 | 33 | 58 | 76 | 86 | 94 | 100 | |
| DTK | 10.3854 | 0.33 | 0.94 | 38 | 57 | 75 | 85 | 93 | 100 | |
| FRV | 9.3328 | 0.35 | 0.93 | 39 | 63 | 75 | 85 | 94 | 100 | |
| KZC | 10.7258 | 0.32 | 0.98 | 33 | 58 | 73 | 84 | 93 | 100 | |
| PDB | 9.21612 | 0.27 | 0.71 | 43 | 56 | 70 | 82 | 93 | 100 | |
| Range | Min | 8.9517 | 0.27 | 0.71 | 33 | 56 | 70 | 82 | 92 | 100 |
| Max | 10.7258 | 0.47 | 0.99 | 49 | 68 | 82 | 90 | 96 | 100 | |
| SAMPLE SET | RV | ITOP RV | |
|---|---|---|---|
| Chenin Blanc | AVN | ↗0.82 | →0.70 |
| CDB | ↗0.82 | →0.75 | |
| DTK | ↗0.80 | ↘0.62 | |
| FRV | ↑0.94 | ↑0.93 | |
| KZC | ↗0.85 | ↗0.80 | |
| PDB | ↑0.96 | ↑0.95 | |
| Sauvignon Blanc | AVN | →0.78 | →0.77 |
| CDB | ↑0.93 | ↑0.92 | |
| DTK | ↗0.81 | →0.70 | |
| FRV | ↗0.89 | ↗0.85 | |
| KZC | ↗0.84 | →0.79 | |
| PDB | ↗0.81 | ↗0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mafata, M.; Brand, J.; Kidd, M.; Medvedovici, A.; Buica, A. Exploration of Data Fusion Strategies Using Principal Component Analysis and Multiple Factor Analysis. Beverages 2022, 8, 66. https://doi.org/10.3390/beverages8040066
Mafata M, Brand J, Kidd M, Medvedovici A, Buica A. Exploration of Data Fusion Strategies Using Principal Component Analysis and Multiple Factor Analysis. Beverages. 2022; 8(4):66. https://doi.org/10.3390/beverages8040066
Chicago/Turabian StyleMafata, Mpho, Jeanne Brand, Martin Kidd, Andrei Medvedovici, and Astrid Buica. 2022. "Exploration of Data Fusion Strategies Using Principal Component Analysis and Multiple Factor Analysis" Beverages 8, no. 4: 66. https://doi.org/10.3390/beverages8040066
APA StyleMafata, M., Brand, J., Kidd, M., Medvedovici, A., & Buica, A. (2022). Exploration of Data Fusion Strategies Using Principal Component Analysis and Multiple Factor Analysis. Beverages, 8(4), 66. https://doi.org/10.3390/beverages8040066









