Multiscale Characterization of Type I Collagen Fibril Stress–Strain Behavior under Tensile Load: Analytical vs. MD Approaches
Abstract
1. Introduction
2. Methodology
2.1. Stress–Strain Curve for the Tropocollagen Molecule
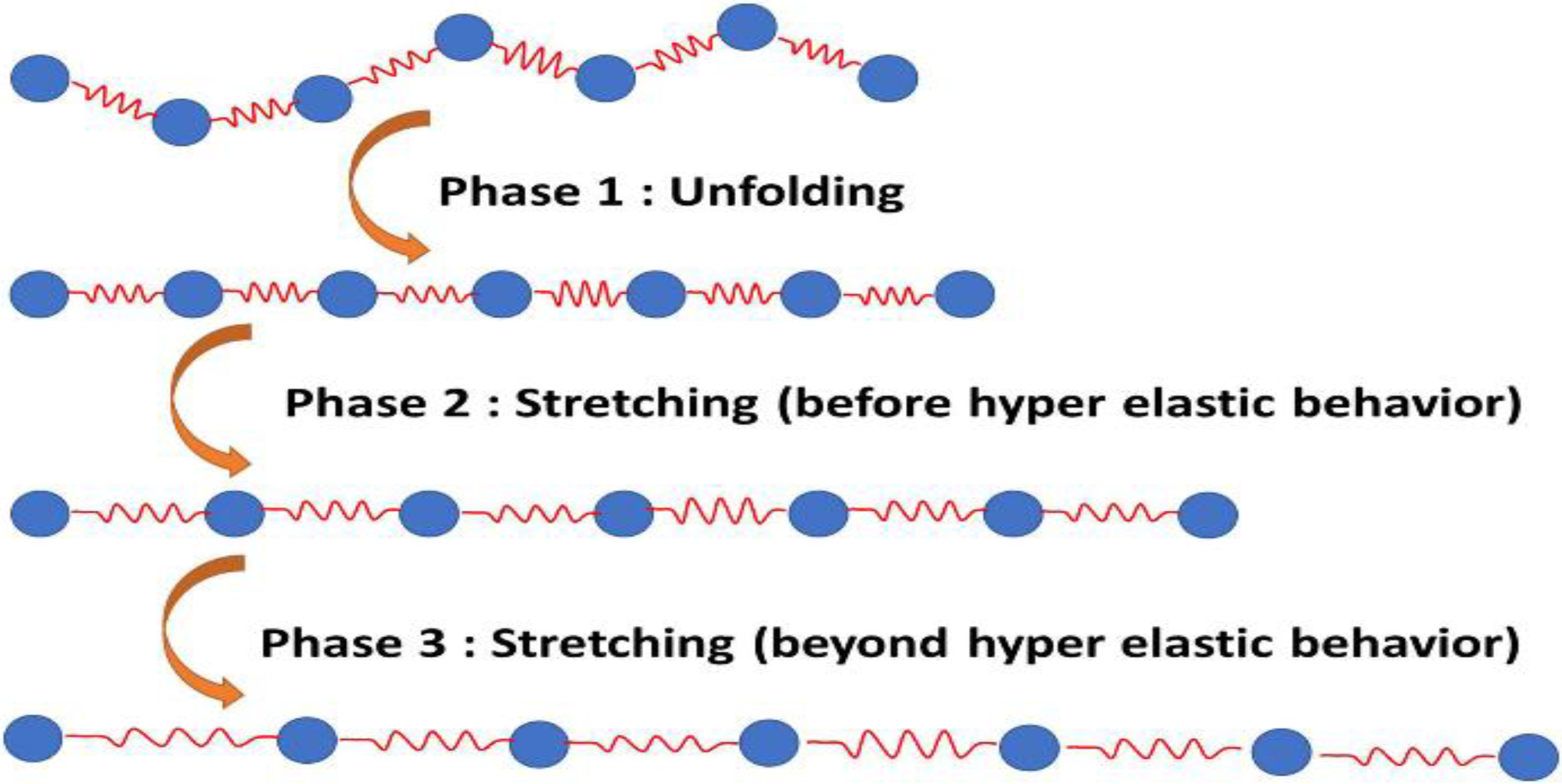
2.1.1. Stage 1: Unfolding of the Molecule
2.1.2. Stage 2: Molecule Stretching before the Hyperelastic Limit
2.1.3. Stage 3: Molecule Stretching after the Hyperelastic Limit
2.2. Stress–Strain Curve for Collagen Fibril with No Crosslinks
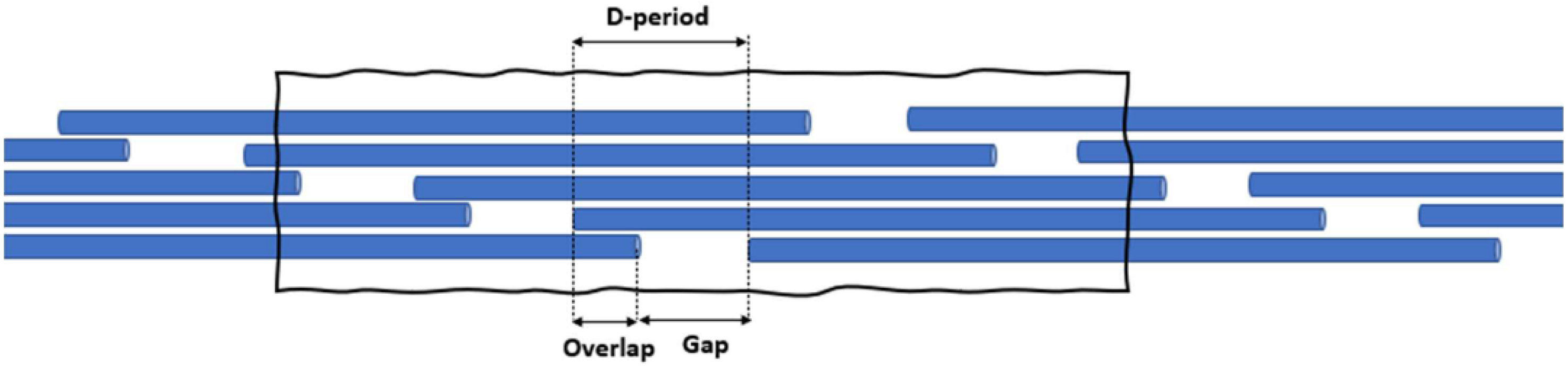
2.2.1. Stage 1: Unfolding of the Fibril
2.2.2. Stage 2: Stretching of the Fibril
2.2.3. Stage 3: Sliding of Molecules
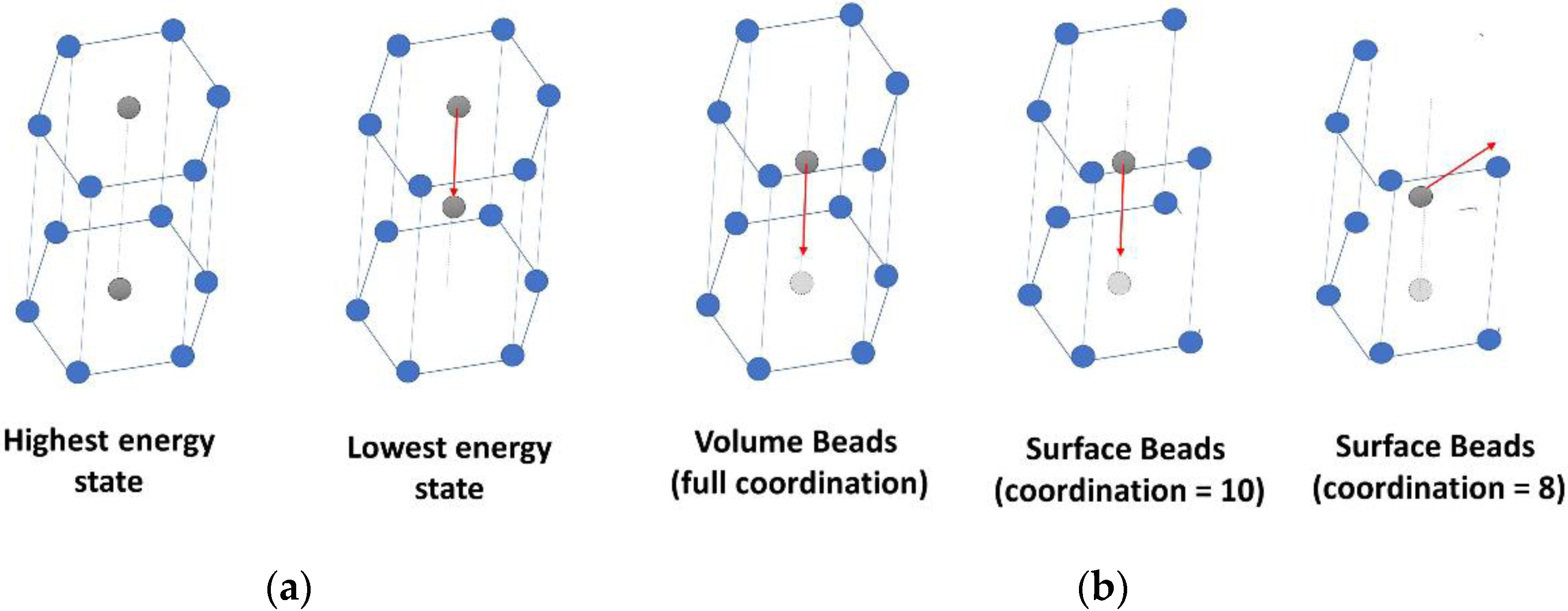
2.3. Stress–Strain Curve for a Fully Crosslinked Collagen Fibril
2.3.1. Stage 1: Unfolding of the Fibril
2.3.2. Stage 2: Fibril Stretching before the Hyperelastic Limit
2.3.3. Stage 3: Fibril Stretching beyond the Hyperelastic Limit
2.3.4. Stage 4: Sliding of the Molecules
2.4. Stress–Strain Curve for a Partially Crosslinked Collagen Fibril
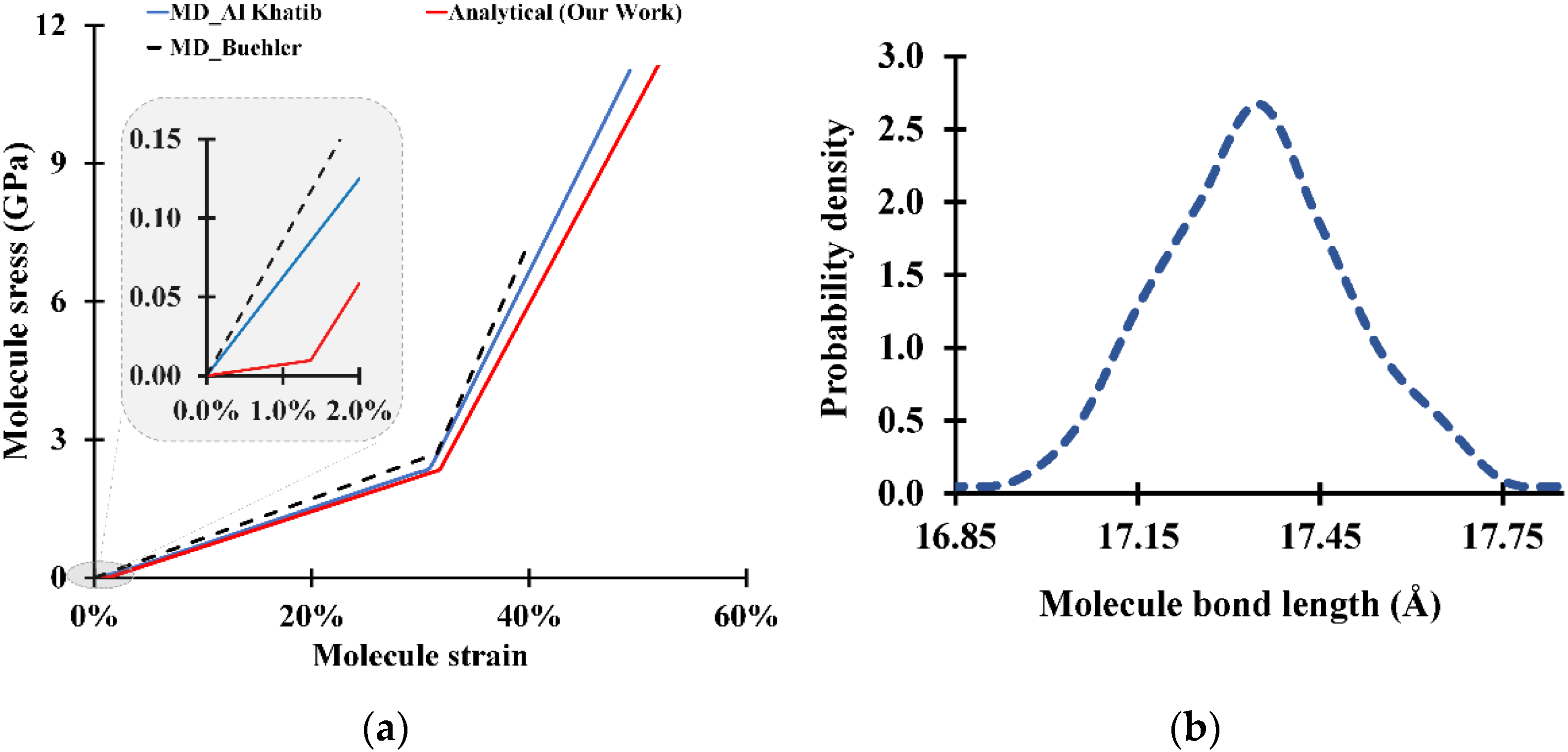
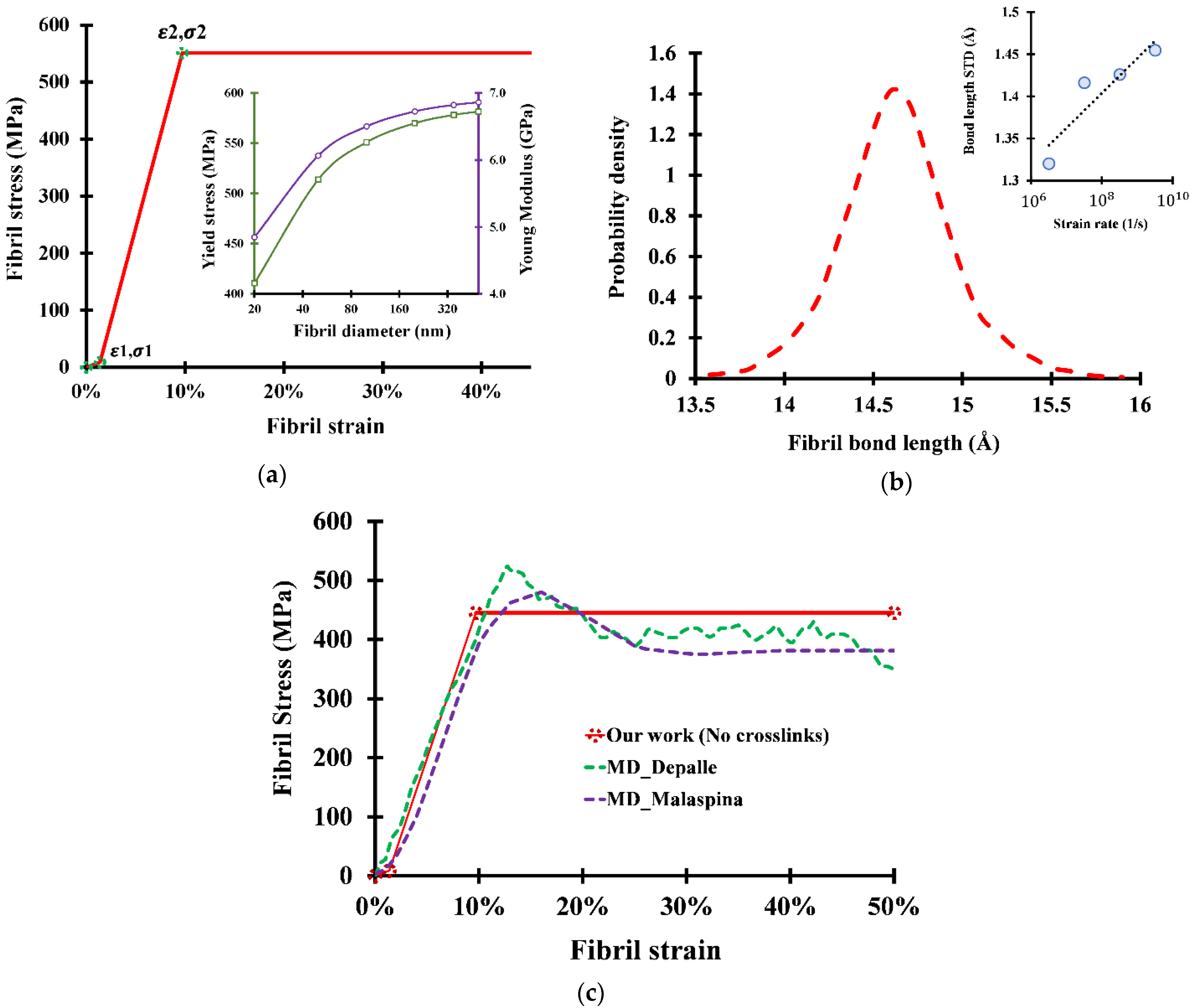
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ricard-Blum, S. The collagen family. Cold Spring Harb. Perspect. Biol. 2011, 3, a004978. [Google Scholar] [CrossRef] [PubMed]
- Buckley, M.R.; Evans, E.B.; Matuszewski, P.E.; Chen, Y.-L.; Satchel, L.N.; Elliott, D.M.; Soslowsky, L.J.; Dodge, G.R. Distributions of types I, II and III collagen by region in the human supraspinatus tendon. Connect. Tissue Res. 2013, 54, 374–379. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.L.; Rui, H.; Mosler, S.; Notbohm, H.; Sawaryn, A.; Müller, P.K. Collagen II from articular cartilage and annulus fibrosus: Structural land functional implication of tissue specific posttranslational modifications of collagen molecules. Eur. J. Biochem. 1993, 213, 1297–1302. [Google Scholar] [CrossRef] [PubMed]
- Kuivaniemi, H.; Tromp, G. Type III collagen (COL3A1): Gene and protein structure, tissue distribution, and associated diseases. Gene 2019, 707, 151–171. [Google Scholar] [CrossRef]
- Abreu-Velez, A.M.; Howard, M.S. Collagen IV in normal skin and in pathological processes. N. Am. J. Med. Sci. 2012, 4, 1–8. [Google Scholar] [CrossRef]
- Mak, K.M.; Png, C.Y.M.; Lee, D.J. Type V collagen in health, disease, and fibrosis. Anatomical Record 2016, 299, 613–629. [Google Scholar] [CrossRef]
- Wenger, M.P.; Bozec, L.; Horton, M.A.; Mesquida, P. Mechanical properties of collagen fibrils. Biophys. J. 2007, 93, 1255–1263. [Google Scholar] [CrossRef]
- Svensson, R.B.; Eriksen, C.S.; Tran, P.H.; Kjaer, M.; Magnusson, S.P. Mechanical properties of human patellar tendon collagen fibrils. An exploratory study of aging and sex. J. Mech. Behav. Biomed. Mater. 2021, 124, 104864. [Google Scholar] [CrossRef]
- Manssor, N.A.S.; Radzi, Z.; Yahya, N.A.; Yusof, L.M.; Hariri, F.; Khairuddin, N.H.; Kasim, N.H.A.; Czernuszka, J.T. Characteristics and young’s modulus of collagen fibrils from expanded skin using anisotropic controlled rate self-inflating tissue expander. Ski. Pharmacol. Physiol. 2016, 29, 55–62. [Google Scholar] [CrossRef]
- Goh, K.L.; Holmes, D.F.; Lu, Y.H.; Kadler, K.E.; Purslow, P.P. Age-related dataset on the mechanical properties and collagen fibril structure of tendons from a murine model. Sci. Data 2018, 5, 180140. [Google Scholar] [CrossRef]
- Antipova, O.; Orgel, J.P. Non-enzymatic decomposition of collagen fibers by a biglycan antibody and a plausible mechanism for rheumatoid arthritis. PLoS ONE 2012, 7, e32241. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fessel, G.; Georgiadis, M.; Snedeker, J.G. Advanced glycation end-products diminish tendon collagen fiber sliding. Matrix Biol. 2013, 32, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Aso, Y.; Inukai, T.; Tayama, K.; Takemura, Y. Serum concentrations of advanced glycation endproducts are associated with the development of atherosclerosis as well as diabetic microangiopathy in patients with type 2 diabetes. Acta Diabetol. 2000, 37, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Chavoshnejad, P.; Foroughi, A.H.; Dhandapani, N.; German, G.K.; Razavi, M.J. Effect of collagen degradation on the mechanical behavior and wrinkling of skin. Phys. Rev. E 2021, 104, 034406. [Google Scholar] [CrossRef]
- Tonge, T.K.; Ruberti, J.W.; Nguyen, T.D. Micromechanical modeling study of mechanical inhibition of enzymatic degradation of collagen tissues. Biophys. J. 2015, 109, 2689–2700. [Google Scholar] [CrossRef]
- Cerami, A.; Vlassara, H.; Brownlee, M. Glucose and aging. Sci. Am. 1987, 256, 90–97. [Google Scholar] [CrossRef]
- Cooper, M.E. Importance of advanced glycation end products in diabetes-associated cardiovascular and renal disease. Am. J. Hypertens. 2004, 17, 31S–38S. [Google Scholar] [CrossRef]
- Depalle, B.; Qin, Z.; Shefelbine, S.J.; Buehler, M.J. Influence of cross-link structure, density and mechanical properties in the mesoscale deformation mechanisms of collagen fibrils. J. Mech. Behav. Biomed. Mater. 2015, 52, 1–13. [Google Scholar] [CrossRef]
- Couppe, C.; Hansen, P.; Kongsgaard, M.; Kovanen, V.; Suetta, C.; Aagaard, P.; Kjaer, M.; Magnusson, S.P. Mechanical properties and collagen cross-linking of the patellar tendon in old and young men. J. Appl. Physiol. 2009, 107, 880–886. [Google Scholar] [CrossRef]
- Svensson, R.B.; Hassenkam, T.; Grant, C.A.; Magnusson, S.P. Tensile properties of human collagen fibrils and fascicles are insensitive to environmental salts. Biophys. J. 2010, 99, 4020–4027. [Google Scholar] [CrossRef]
- Liu, Y.; Ballarini, R.; Eppell, S.J. Tension tests on mammalian collagen fibrils. Interface Focus 2016, 6, 20150080. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, N. Tensile strength of single collagen fibrils isolated from tendons. Eur. J. Biophys. 2017, 5, 1–6. [Google Scholar] [CrossRef]
- Yamamoto, N.; Nakamura, S. Relationships between the tensile strength and diameter of collagen fibrils isolated from mouse tail tendons. J. Biomech. Sci. Eng. 2017, 12, 16-00511. [Google Scholar] [CrossRef][Green Version]
- Gahunia, H.; Gross, A.; Pritzker, K.; Babyn, P.; Murnaghan, L. Articular Cartilage of the Knee: Health, Disease and Therapy; Springer: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Saitoh, K.-I.; Sato, T.; Takuma, M.; Takahashi, Y. Molecular Dynamics Study of Collagen Fibrils: Relation between Mechanical Properties and Molecular Chirality. J. Biomater. Nanobiotechnol. 2020, 11, 260–278. [Google Scholar] [CrossRef]
- Ndlovu, H.; Ashcroft, A.E.; Radford, S.E.; Harris, S.A. Effect of sequence variation on the mechanical response of amyloid fibrils probed by steered molecular dynamics simulation. Biophys. J. 2012, 102, 587–596. [Google Scholar] [CrossRef] [PubMed]
- Malaspina, D.C.; Szleifer, I.; Dhaher, Y. Mechanical properties of a collagen fibril under simulated degradation. J. Mech. Behav. Biomed. Mater. 2017, 75, 549–557. [Google Scholar] [CrossRef] [PubMed]
- Adouni, M.; Gouissem, A.; Al Khatib, F.; Eilaghi, A. Biomechanics of the anterior cruciate ligament under simulated molecular degradation. Eur. Cells Mater. 2022, 43, 22–38. [Google Scholar] [CrossRef]
- Khatib, F.A.; Gouissem, A.; Eilaghi, A.; Adouni, M. The Effect of Enzymatic Crosslink Degradation on the Mechanics of the Anterior Cruciate Ligament: A Hybrid Multi-Domain Model. Appl. Sci. 2021, 11, 8580. [Google Scholar] [CrossRef]
- Buehler, M.J. Nature designs tough collagen: Explaining the nanostructure of collagen fibrils. Proc. Natl. Acad. Sci. USA 2006, 103, 12285–12290. [Google Scholar] [CrossRef]
- Fang, M.; Holl, M.M.B. Variation in type I collagen fibril nanomorphology: The significance and origin. BoneKEy Rep. 2013, 2, 394. [Google Scholar] [CrossRef]
- Orgel, J.P.; Irving, T.C.; Miller, A.; Wess, T.J. Microfibrillar structure of type I collagen in situ. Proc. Natl. Acad. Sci. USA 2006, 103, 9001–9005. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, S.M.; Orgel, J.P.; Fertala, A.; McAuliffe, J.D.; Turner, K.R.; Di Lullo, G.A.; Chen, S.; Antipova, O.; Perumal, S.; Ala-Kokko, L. Candidate cell and matrix interaction domains on the collagen fibril, the predominant protein of vertebrates. J. Biol. Chem. 2008, 283, 21187–21197. [Google Scholar] [CrossRef] [PubMed]
- Gautieri, A.; Vesentini, S.; Redaelli, A.; Buehler, M.J. Hierarchical structure and nanomechanics of collagen microfibrils from the atomistic scale up. Nano Lett. 2011, 11, 757–766. [Google Scholar] [CrossRef] [PubMed]
- Watanabe-Nakayama, T.; Itami, M.; Kodera, N.; Ando, T.; Konno, H. High-speed atomic force microscopy reveals strongly polarized movement of clostridial collagenase along collagen fibrils. Sci. Rep. 2016, 6, 28975. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Jiang, H.; Kim, M.; Vink, J.; Cremers, S.; Paik, D.; Wapner, R.; Mahendroo, M.; Myers, K. Quantitative evaluation of collagen crosslinks and corresponding tensile mechanical properties in mouse cervical tissue during normal pregnancy. PLoS ONE 2014, 9, e112391. [Google Scholar] [CrossRef]
- Hudson, D.M.; Archer, M.; Rai, J.; Weis, M.; Fernandes, R.J.; Eyre, D.R. Age-related type I collagen modifications reveal tissue-defining differences between ligament and tendon. Matrix Biol. Plus 2021, 12, 100070. [Google Scholar] [CrossRef]
- Gaar, J.; Naffa, R.; Brimble, M. Enzymatic and non-enzymatic crosslinks found in collagen and elastin and their chemical synthesis. Org. Chem. Front. 2020, 7, 2789–2814. [Google Scholar] [CrossRef]
- Li, S.-T. Biologic biomaterials: Tissue-derived biomaterials (collagen). In Biomedical Engineering Fundamentals; CRC Press: Boca Raton, FL, USA, 2014; pp. 637–660. [Google Scholar]
- Gautieri, A.; Redaelli, A.; Buehler, M.J.; Vesentini, S. Age- and diabetes-related nonenzymatic crosslinks in collagen fibrils: Candidate amino acids involved in advanced glycation end-products. Matrix Biol. 2014, 34, 89–95. [Google Scholar] [CrossRef]
- Snedeker, J.G.; Gautieri, A. The role of collagen crosslinks in ageing and diabetes-the good, the bad, and the ugly. Muscles Ligaments Tendons J. 2014, 4, 303–308. [Google Scholar] [CrossRef]
- Buehler, M.J.; Wong, S.Y. Entropic elasticity controls nanomechanics of single tropocollagen molecules. Biophys. J. 2007, 93, 37–43. [Google Scholar] [CrossRef]
- Gineyts, E.; Borel, O.; Chapurlat, R.; Garnero, P. Quantification of immature and mature collagen crosslinks by liquid chromatography–electrospray ionization mass spectrometry in connective tissues. J. Chromatogr. B 2010, 878, 1449–1454. [Google Scholar] [CrossRef] [PubMed]
- Naffa, R.; Edwards, P.J.; Norris, G. Isolation and characterization of collagen type I crosslink from skin: High-resolution NMR reveals diastereomers of hydroxylysinonorleucine crosslink. Amino Acids 2019, 51, 705–715. [Google Scholar] [CrossRef] [PubMed]
- Gupta, H.; Messmer, P.; Roschger, P.; Bernstorff, S.; Klaushofer, K.; Fratzl, P. Synchrotron diffraction study of deformation mechanisms in mineralized tendon. Phys. Rev. Lett. 2004, 93, 158101. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.L.; Dodge, M.R.; Kahn, H.; Ballarini, R.; Eppell, S.J. Stress-strain experiments on individual collagen fibrils. Biophys. J. 2008, 95, 3956–3963. [Google Scholar] [CrossRef]
- Graham, J.S.; Vomund, A.N.; Phillips, C.L.; Grandbois, M. Structural changes in human type I collagen fibrils investigated by force spectroscopy. Exp. Cell Res. 2004, 299, 335–342. [Google Scholar] [CrossRef]
- Eppell, S.J.; Smith, B.N.; Kahn, H.; Ballarini, R. Nano measurements with micro-devices: Mechanical properties of hydrated collagen fibrils. J. R. Soc. Interface 2006, 3, 117–121. [Google Scholar] [CrossRef]
- Tang, M.; Li, T.; Gandhi, N.S.; Burrage, K.; Gu, Y. Heterogeneous nanomechanical properties of type I collagen in longitudinal direction. Biomech. Model. Mechanobiol. 2017, 16, 1023–1033. [Google Scholar] [CrossRef]
- Minary-Jolandan, M.; Yu, M.-F. Nanomechanical heterogeneity in the gap and overlap regions of type I collagen fibrils with implications for bone heterogeneity. Biomacromolecules 2009, 10, 2565–2570. [Google Scholar] [CrossRef]
- Ratiu, C.; Brocks, M.; Costea, T.; Moldovan, L.; Cavalu, S. PRGF-modified collagen membranes for guided bone regeneration: Spectroscopic, microscopic and nano-mechanical investigations. Appl. Sci. 2019, 9, 1035. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Molecule number of amino acids | 3134 |
| Molecule total mass [g/mol] | 287,000 |
| Number of beads per molecule | 218 |
| Mass of each bead [g/mol] | 1316 |
| Length along principal axis [Å] | 3011 |
| Parameter | Value |
|---|---|
| —Equilibrium distance [Å] | 14.00 |
| —Critical hyperplastic distance [Å] | 18.20 |
| —Bond breaking distance [Å] | 21.00 |
| —Stretching strength constant [Kcal/mol] | 17.13 |
| —Stretching strength constant [Kcal/mol] | 97.66 |
| —Equilibrium bending angle [degree] | 164–180 |
| —Equilibrium bending constant [Kcal/mol/rad2] | 14.98 |
| Parameter | Value |
|---|---|
| —Lennard-Jones energy [Kcal/mol] | 6.87 |
| —Lennard-Jones equilibrium distance [Å] | 14.72 |
| Parameter | Divalent Crosslinks | Trivalent Crosslinks |
|---|---|---|
| r0—Equilibrium distance [Å] | 10.00 | 8.60 |
| r1—Critical hyperplastic distance [Å] | 12.00 | 12.20 |
| rb—Bond breaking distance [Å] | 14.68 | 14.89 |
| KT0—Stretching strength constant [Kcal/mol] | 0.20 | 0.20 |
| KT1—Stretching strength constant [Kcal/mol] | 41.84 | 54.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gouissem, A.; Mbarki, R.; Al Khatib, F.; Adouni, M. Multiscale Characterization of Type I Collagen Fibril Stress–Strain Behavior under Tensile Load: Analytical vs. MD Approaches. Bioengineering 2022, 9, 193. https://doi.org/10.3390/bioengineering9050193
Gouissem A, Mbarki R, Al Khatib F, Adouni M. Multiscale Characterization of Type I Collagen Fibril Stress–Strain Behavior under Tensile Load: Analytical vs. MD Approaches. Bioengineering. 2022; 9(5):193. https://doi.org/10.3390/bioengineering9050193
Chicago/Turabian StyleGouissem, Afif, Raouf Mbarki, Fadi Al Khatib, and Malek Adouni. 2022. "Multiscale Characterization of Type I Collagen Fibril Stress–Strain Behavior under Tensile Load: Analytical vs. MD Approaches" Bioengineering 9, no. 5: 193. https://doi.org/10.3390/bioengineering9050193
APA StyleGouissem, A., Mbarki, R., Al Khatib, F., & Adouni, M. (2022). Multiscale Characterization of Type I Collagen Fibril Stress–Strain Behavior under Tensile Load: Analytical vs. MD Approaches. Bioengineering, 9(5), 193. https://doi.org/10.3390/bioengineering9050193






