Biologically Inspired Optimal Terminal Iterative Learning Control for the Swing Phase of Gait in a Hybrid Neuroprosthesis: A Modeling Study
Abstract
:1. Introduction
2. Materials and Methods
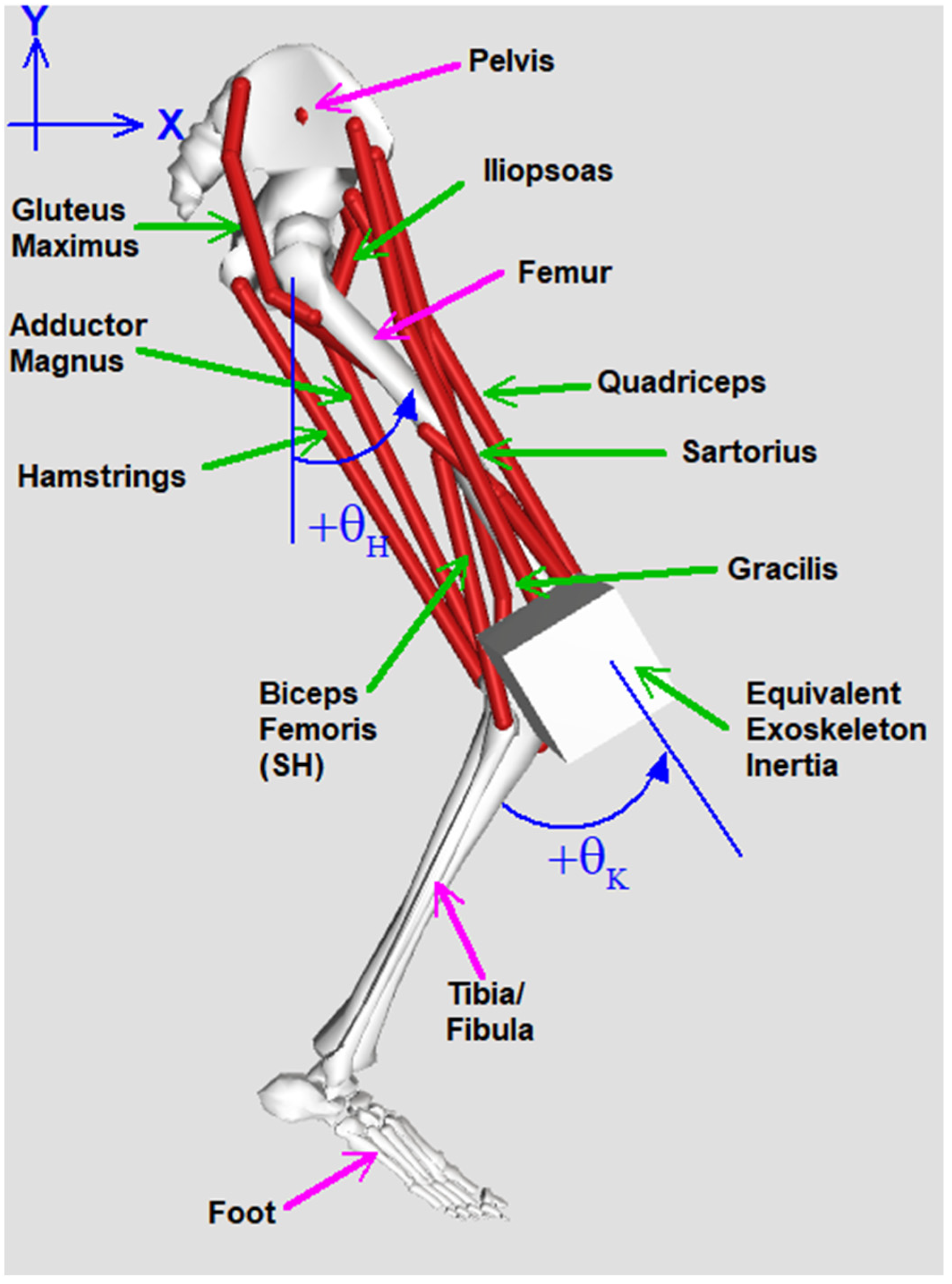
2.1. Device and Simulation Design
2.2. Controller Design
2.3. Simulation Implementation
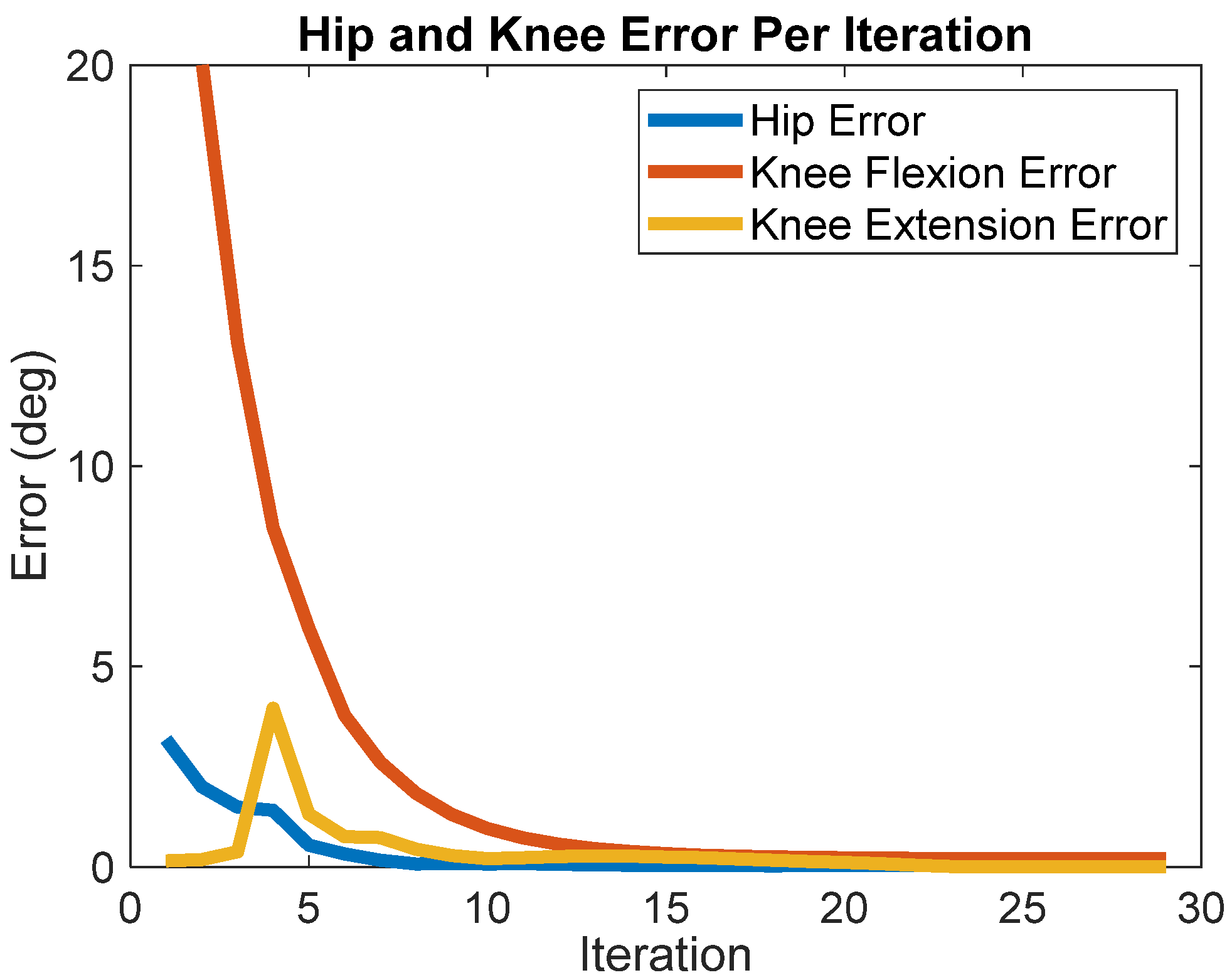
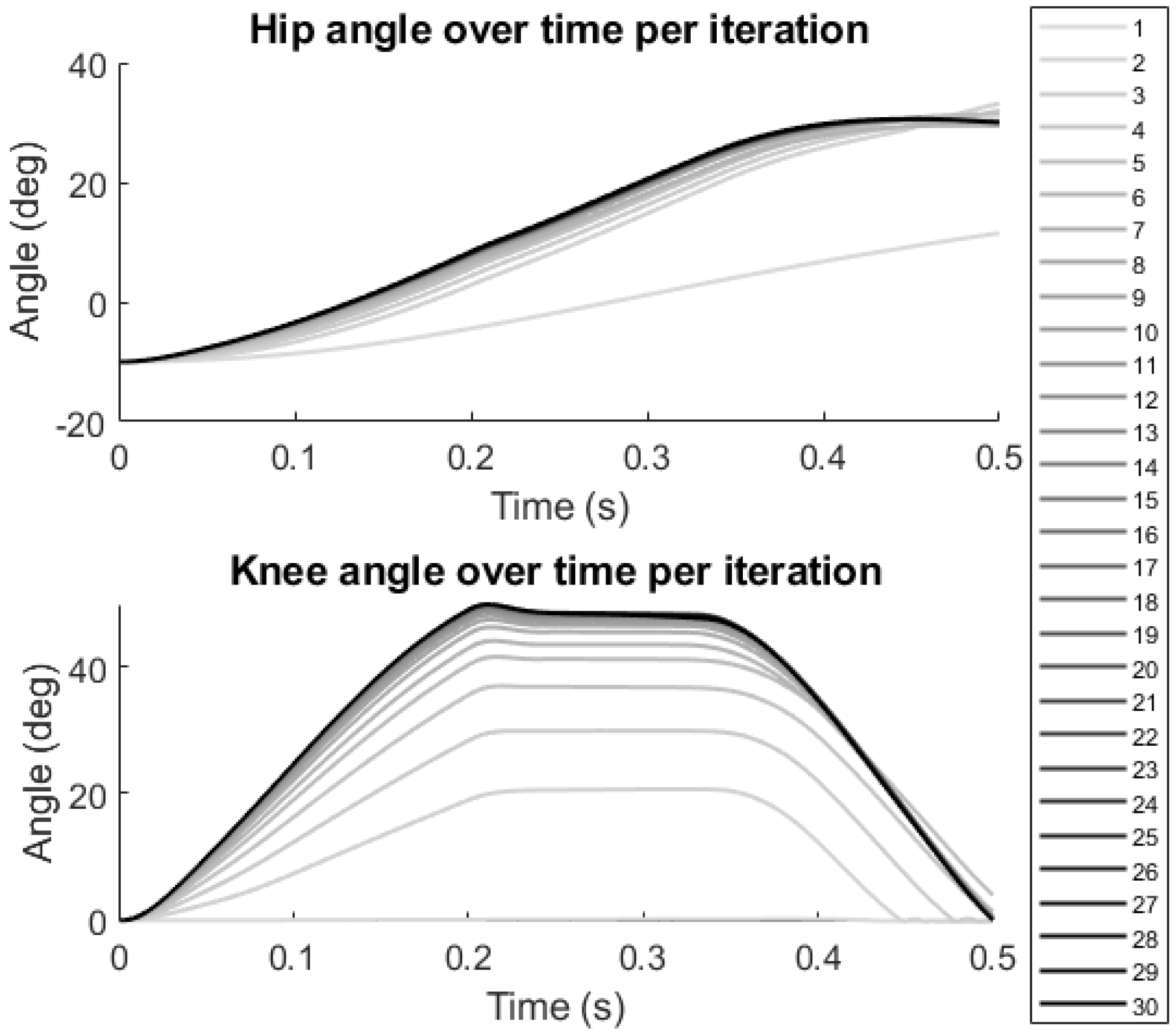
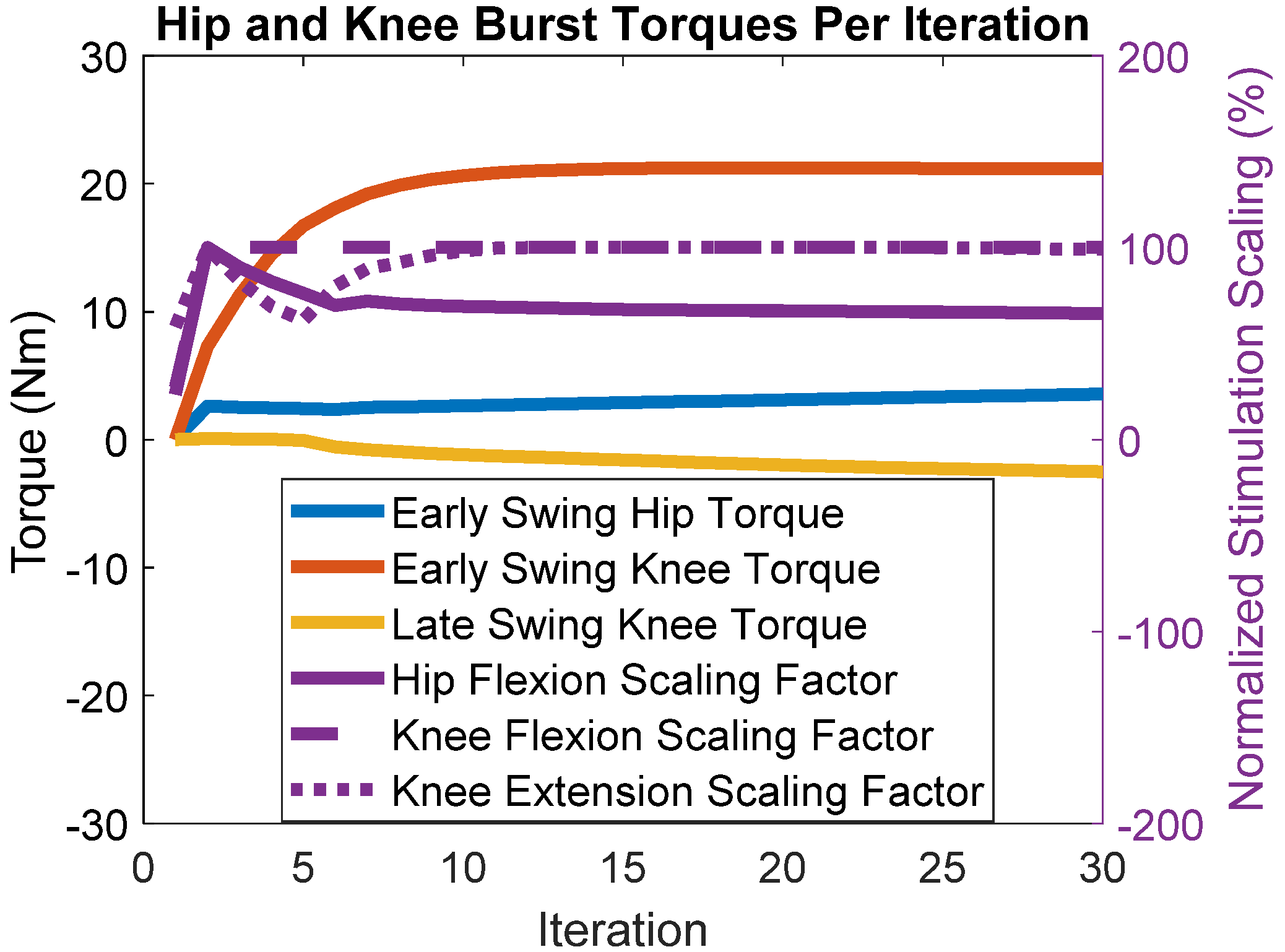
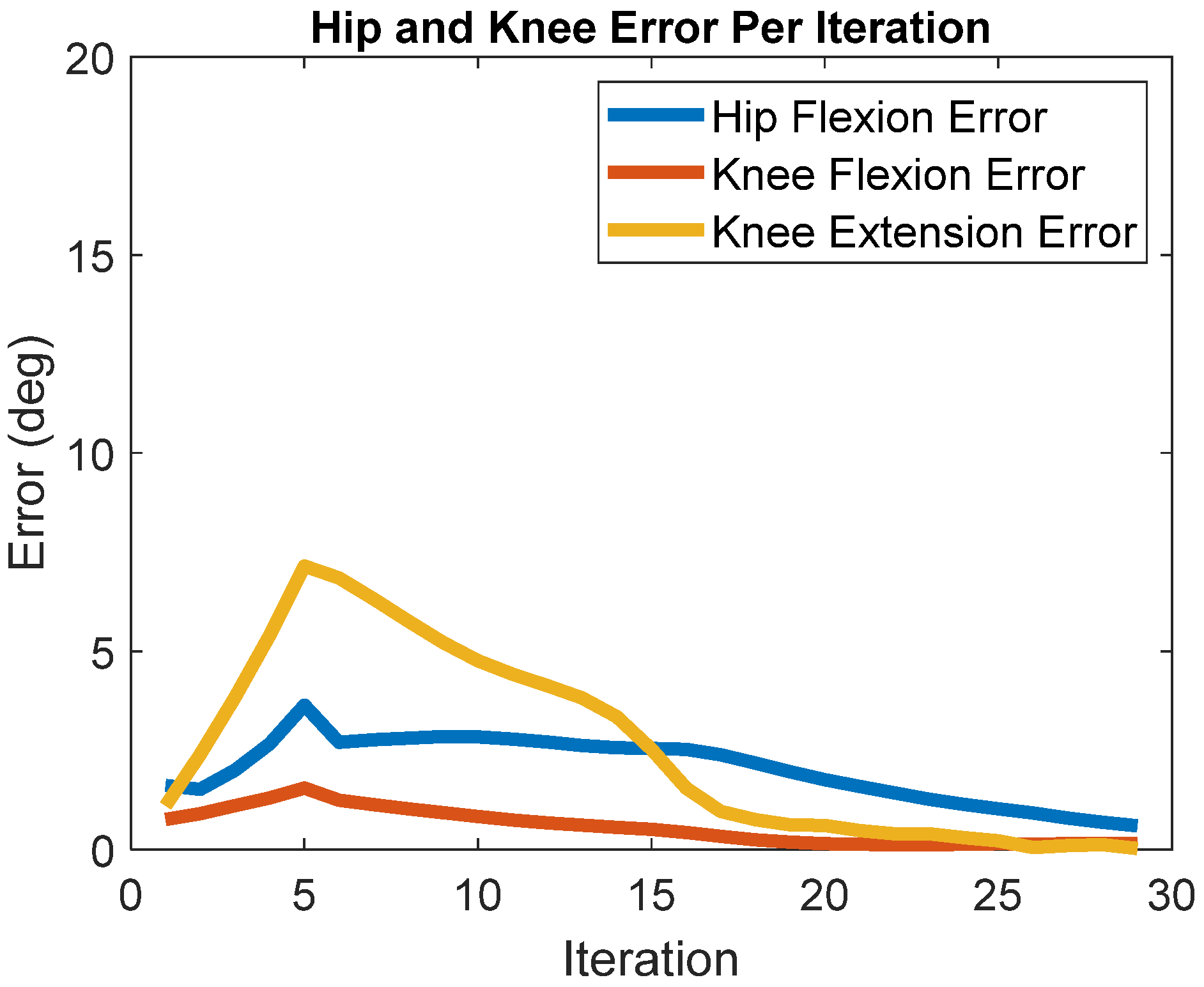
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Controller Derivation
Appendix A.1.1. Variables
Appendix A.1.2. Parameters
Appendix A.1.3. Derivation
References
- Anderson, K.D. Targeting Recovery: Priorities of the Spinal Cord-Injured Population. J. Neurotrauma 2004, 21, 1371–1383. [Google Scholar] [CrossRef] [PubMed]
- Gardner, A.D.; Potgieter, J.; Noble, F.K. A Review of Commercially Available Exoskeletons’ Capabilities. In Proceedings of the 2017 24th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 21–23 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Baronchelli, F.; Zucchella, C.; Serrao, M.; Intiso, D.; Bartolo, M. The Effect of Robotic Assisted Gait Training With Lokomat® on Balance Control After Stroke: Systematic Review and Meta-Analysis. Front. Neurol. 2021, 12, 661815. [Google Scholar] [CrossRef] [PubMed]
- Miller, L.; Zimmermann, A.; Herbert, W. Clinical Effectiveness and Safety of Powered Exoskeleton-Assisted Walking in Patients with Spinal Cord Injury: Systematic Review with Meta-Analysis. Med. Devices Evid. Res. 2016, 9, 455. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anaya, F.; Thangavel, P.; Yu, H. Hybrid FES–Robotic Gait Rehabilitation Technologies: A Review on Mechanical Design, Actuation, and Control Strategies. Int. J. Intell. Robot. Appl. 2018, 2, 1–28. [Google Scholar] [CrossRef]
- del-Ama, A.J.; Koutsou, A.D.; Moreno, J.C.; de-los-Reyes, A.; Gil-Agudo, Á.; Pons, J.L. Review of Hybrid Exoskeletons to Restore Gait Following Spinal Cord Injury. J. Rehabil. Res. Dev. 2012, 49, 497. [Google Scholar] [CrossRef]
- Alibeji, N.A.; Molazadeh, V.; Dicianno, B.E.; Sharma, N. A Control Scheme That Uses Dynamic Postural Synergies to Coordinate a Hybrid Walking Neuroprosthesis: Theory and Experiments. Front. Neurosci. 2018, 12, 159. [Google Scholar] [CrossRef]
- Ekelem, A.; Goldfarb, M. Supplemental Stimulation Improves Swing Phase Kinematics During Exoskeleton Assisted Gait of SCI Subjects With Severe Muscle Spasticity. Front. Neurosci. 2018, 12, 374. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Z.; Molazadeh, V.; Sharma, N. Hybrid Dynamical System Model and Robust Control of a Hybrid Neuroprosthesis under Fatigue Based Switching. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; Volume 6. [Google Scholar]
- Zhang, D.; Ren, Y.; Gui, K.; Jia, J.; Xu, W. Cooperative Control for A Hybrid Rehabilitation System Combining Functional Electrical Stimulation and Robotic Exoskeleton. Front. Neurosci. 2017, 11, 725. [Google Scholar] [CrossRef] [Green Version]
- Romero-Sánchez, F.; Bermejo-García, J.; Barrios-Muriel, J.; Alonso, F.J. Design of the Cooperative Actuation in Hybrid Orthoses: A Theoretical Approach Based on Muscle Models. Front. Neurorobot. 2019, 13, 58. [Google Scholar] [CrossRef] [Green Version]
- Alouane, M.A.; Rifai, H.; Kim, K.; Amirat, Y.; Mohammed, S. Hybrid Impedance Control of a Knee Joint Orthosis. Ind. Robot Int. J. Robot. Res. Appl. 2019, 46, 192–201. [Google Scholar] [CrossRef]
- Vallery, H.; Stützle, T.; Buss, M.; Abel, D. Control of a hybrid motor prosthesis for the knee joint. IFAC Proc. Vol. 2005, 38, 76–81. [Google Scholar] [CrossRef] [Green Version]
- Kirsch, N.A.; Bao, X.; Alibeji, N.A.; Dicianno, B.E.; Sharma, N. Model-Based Dynamic Control Allocation in a Hybrid Neuroprosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Bao, X.; Kirsch, N.; Sharma, N. Dynamic Control Allocation of a Feedback Linearized Hybrid Neuroprosthetic System. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 3976–3981. [Google Scholar] [CrossRef]
- Alibeji, N.; Kirsch, N.; Sharma, N. An Adaptive Low-Dimensional Control to Compensate for Actuator Redundancy and FES-Induced Muscle Fatigue in a Hybrid Neuroprosthesis. Control Eng. Pract. 2017, 59, 204–219. [Google Scholar] [CrossRef] [Green Version]
- Bao, X.; Sun, Z.; Sharma, N. A Recurrent Neural Network Based MPC for a Hybrid Neuroprosthesis System. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, 12–15 December 2017; pp. 4715–4720. [Google Scholar] [CrossRef]
- Takegaki, M.; Arimoto, S. A New Feedback Method for Dynamic Control of Manipulators. J. Dyn. Syst. Meas. Control 1981, 103, 119–125. [Google Scholar] [CrossRef]
- Bristow, D.; Tharayil, M.; Alleyne, A. A Survey of Iterative Learning Control. IEEE Control Syst. 2006, 26, 96–114. [Google Scholar] [CrossRef]
- Xu, J.-X.; Chen, Y.; Lee, T.H.; Yamamoto, S. Terminal Iterative Learning Control with an Application to RTPCVD Thickness Control. Automatica 1999, 35, 1535–1542. [Google Scholar] [CrossRef]
- Hou, Z.; Wang, Y.; Yin, C.; Tang, T. Terminal Iterative Learning Control Based Station Stop Control of a Train. Int. J. Control 2011, 84, 1263–1274. [Google Scholar] [CrossRef]
- Johansen, S.V.; Jensen, M.R.; Chu, B.; Bendtsen, J.D.; Mogensen, J.; Rogers, E. Broiler FCR Optimization Using Norm Optimal Terminal Iterative Learning Control. IEEE Trans. Control Syst. Technol. 2021, 29, 580–592. [Google Scholar] [CrossRef]
- Müller, P.; Del Ama, A.J.; Moreno, J.C.; Schauer, T. Adaptive Multichannel FES Neuroprosthesis with Learning Control and Automatic Gait Assessment. J. Neuroeng. Rehabil. 2020, 17, 36. [Google Scholar] [CrossRef]
- Ha, K.H.; Murray, S.A.; Goldfarb, M. An Approach for the Cooperative Control of FES With a Powered Exoskeleton During Level Walking for Persons With Paraplegia. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 455–466. [Google Scholar] [CrossRef]
- Del-Ama, A.J.; Gil-Agudo, A.; Pons, J.L.; Moreno, J.C. Hybrid FES-Robot Cooperative Control of Ambulatory Gait Rehabilitation Exoskeleton. J. NeuroEng. Rehabil. 2014, 11, 27. [Google Scholar] [CrossRef] [PubMed]
- Molazadeh, V.; Sheng, Z.; Bao, X.; Sharma, N. A Robust Iterative Learning Switching Controller for Following Virtual Constraints: Application to a Hybrid Neuroprosthesis. IFAC-PapersOnLine 2019, 51, 28–33. [Google Scholar] [CrossRef]
- Molazadeh, V.; Zhang, Q.; Sharma, N. Neural-network based iterative learning control of a hybrid exoskeleton with an mpc allocation strategy. In Dynamic Systems and Control Conference; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59148, p. V001T05A011. [Google Scholar]
- Reyes, R.-D.; Kobetic, R.; Nandor, M.; Makowski, N.; Audu, M.; Quinn, R.; Triolo, R. Effect of Joint Friction Compensation on a “Muscle-First” Motor-Assisted Hybrid Neuroprosthesis. Front. Neurorobot. 2020, 14, 588950. [Google Scholar] [CrossRef] [PubMed]
- Nandor, M.; Kobetic, R.; Audu, M.; Triolo, R.; Quinn, R. A Muscle-First, Electromechanical Hybrid Gait Restoration System in People with Spinal Cord Injury. Front. Robot. AI Sect. Biomed. Robot. 2021, 8, 645588. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.R.; Kobetic, R.; Triolo, R.J. Effect of Exoskeletal Joint Constraint and Passive Resistance on Metabolic Energy Expenditure: Implications for Walking in Paraplegia. PLoS ONE 2017, 12, e0183125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, S.R.; Nandor, M.J.; Kobetic, R.; Foglyano, K.M.; Quinn, R.D.; Triolo, R.J. Improving Stand-to-Sit Maneuver for Individuals with Spinal Cord Injury. J. NeuroEng. Rehabil. 2016, 13, 27. [Google Scholar] [CrossRef] [Green Version]
- Chi, R. Data-Driven Optimal Terminal Iterative Learning Control. J. Process Control 2012, 12, 2026–2037. [Google Scholar] [CrossRef]
- Mochon, S.; McMahon, T.A. Ballistic Walking. J. Biomech. 1980, 13, 49–57. [Google Scholar] [CrossRef]
- Rose, J.; Gamble, J.G. (Eds.) Human Walking, 3rd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2006. [Google Scholar]
- Kobetic, R.; Triolo, R.J.; Marsolais, E.B. Muscle Selection and Walking Performance of Multichannel FES Systems for Ambulation in Paraplegia. IEEE Trans. Rehabil. Eng. 1997, 5, 23–29. [Google Scholar] [CrossRef]
- Xu, J.; Huang, D.; Wang, W. Ballistic Learning Control: Formulation, Analysis and Convergence. J. Control Theory Appl. 2013, 11, 325–335. [Google Scholar] [CrossRef]
- Xu, J.-X.; Huang, D. Iterative Learning in Ballistic Control: Formulation of Spatial Learning Processes for Endpoint Control. J. Dyn. Syst. Meas. Control 2013, 135, 024501. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Ding, J.; Wexler, A.S.; Binder-Macleod, S.A. Mathematical Models for Fatigue Minimization during Functional Electrical Stimulation. J. Electromyogr. Kinesiol. Off. J. Int. Soc. Electrophysiol. Kinesiol. 2003, 13, 575–588. [Google Scholar] [CrossRef]
- Alibeji, N.A.; Kirsch, N.A.; Sharma, N. A Muscle Synergy-Inspired Adaptive Control Scheme for a Hybrid Walking Neuroprosthesis. Front. Bioeng. Biotechnol. 2015, 3, 203. [Google Scholar] [CrossRef]
- Alibeji, N.; Kirsch, N.; Farrokhi, S.; Sharma, N. Further Results on Predictor-Based Control of Neuromuscular Electrical Stimulation. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1095–1105. [Google Scholar] [CrossRef]
- Molazadeh, V.; Zhang, Q.; Bao, X.; Sharma, N. An Iterative Learning Controller for a Switched Cooperative Allocation Strategy During Sit-to-Stand Tasks with a Hybrid Exoskeleton. IEEE Trans. Control Syst. Technol. 2021, 1–16. [Google Scholar] [CrossRef]
- Xu, X.; Xie, H.; Wen, K.; He, R.; Hong, W.; Shi, J. Iterative Learning Control Guided Reinforcement Learning Control Scheme for Batch Processes. Authorea 2020. [Google Scholar] [CrossRef]
- Emken, J.L.; Benitez, R.; Reinkensmeyer, D.J. Human-Robot Cooperative Movement Training: Learning a Novel Sensory Motor Transformation during Walking with Robotic Assistance-as-Needed. J. Neuroeng. Rehabil. 2007, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Lin, N.; Liang, H.; Lv, Y.; Chi, R. A Forgetting-Factor Based Data-Driven Optimal Terminal Iterative Learning Control with Applications to Product Concentration Control of Ethanol Fermentation Processes. Trans. Inst. Meas. Control 2019, 41, 3936–3942. [Google Scholar] [CrossRef]
- Chi, R.; Liu, Y.; Hou, Z.; Jin, S. Data-driven Terminal Iterative Learning Control with High-order Learning Law for a Class of Non-linear Discrete-time Multiple-input–Multiple Output Systems. IET Control Theory Appl. 2015, 9, 1075–1082. [Google Scholar] [CrossRef]
- Son, T.D.; Ahn, H.-S.; Moore, K.L. Iterative Learning Control in Optimal Tracking Problems with Specified Data Points. Automatica 2013, 49, 1465–1472. [Google Scholar] [CrossRef]
- Chi, R.; Huang, B.; Wang, D.; Zhang, R.; Feng, Y. Data-driven Optimal Terminal Iterative Learning Control with Initial Value Dynamic Compensation. IET Control Theory Appl. 2016, 10, 1357–1364. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Anlysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]

| Characteristic | Quantity | Description |
|---|---|---|
| Actuator Masses | 2.2 kg | |
| Actuator Torque Limits | Nm | Peak torque limit |
| Viscous Damping Model | Results in <6 Nm of torque required to backdrive actuator at joint speeds of [28]. , is a scaled and shifted sigmoid to center the torque at zero. and represent the polynomial fit terms for the friction model for each actuator. | |
| Feedforward Friction Compensation | Compensator derived in [28]. and are tuning parameters to account for errors in the polynomial fit and reduce sensitivity to noise when operating near zero speed. | |
| Actuator Electrical Current Dynamics | is the current, is the current setpoint, resulting in a current rise time of 10 ms. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makowski, N.S.; Fitzpatrick, M.N.; Triolo, R.J.; Reyes, R.-D.; Quinn, R.D.; Audu, M. Biologically Inspired Optimal Terminal Iterative Learning Control for the Swing Phase of Gait in a Hybrid Neuroprosthesis: A Modeling Study. Bioengineering 2022, 9, 71. https://doi.org/10.3390/bioengineering9020071
Makowski NS, Fitzpatrick MN, Triolo RJ, Reyes R-D, Quinn RD, Audu M. Biologically Inspired Optimal Terminal Iterative Learning Control for the Swing Phase of Gait in a Hybrid Neuroprosthesis: A Modeling Study. Bioengineering. 2022; 9(2):71. https://doi.org/10.3390/bioengineering9020071
Chicago/Turabian StyleMakowski, Nathaniel S., Marshaun N. Fitzpatrick, Ronald J. Triolo, Ryan-David Reyes, Roger D. Quinn, and Musa Audu. 2022. "Biologically Inspired Optimal Terminal Iterative Learning Control for the Swing Phase of Gait in a Hybrid Neuroprosthesis: A Modeling Study" Bioengineering 9, no. 2: 71. https://doi.org/10.3390/bioengineering9020071
APA StyleMakowski, N. S., Fitzpatrick, M. N., Triolo, R. J., Reyes, R.-D., Quinn, R. D., & Audu, M. (2022). Biologically Inspired Optimal Terminal Iterative Learning Control for the Swing Phase of Gait in a Hybrid Neuroprosthesis: A Modeling Study. Bioengineering, 9(2), 71. https://doi.org/10.3390/bioengineering9020071





