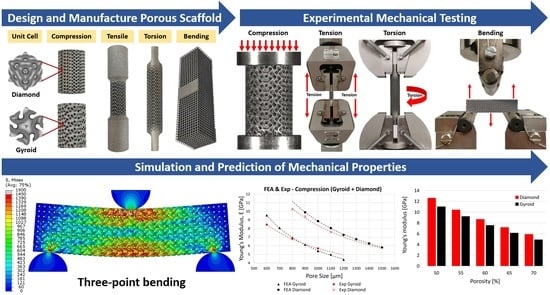
Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration
Abstract
:1. Introduction
2. Materials and Methods
2.1. Design and Manufacturing of Porous Titanium Scaffolds
2.1.1. Micro-Structure-Driven Design of the Scaffolds
2.1.2. Powder Material
2.1.3. Manufacturing of Testing Specimens
2.2. Morphological and Mechanical Characterisations
2.2.1. Morphological Examinations
2.2.2. Mechanical Tests
2.3. Finite Element Modelling
2.3.1. Geometry and Mesh Convergence
2.3.2. Material Properties
2.3.3. Loading and Boundary Conditions
3. Results and Discussion
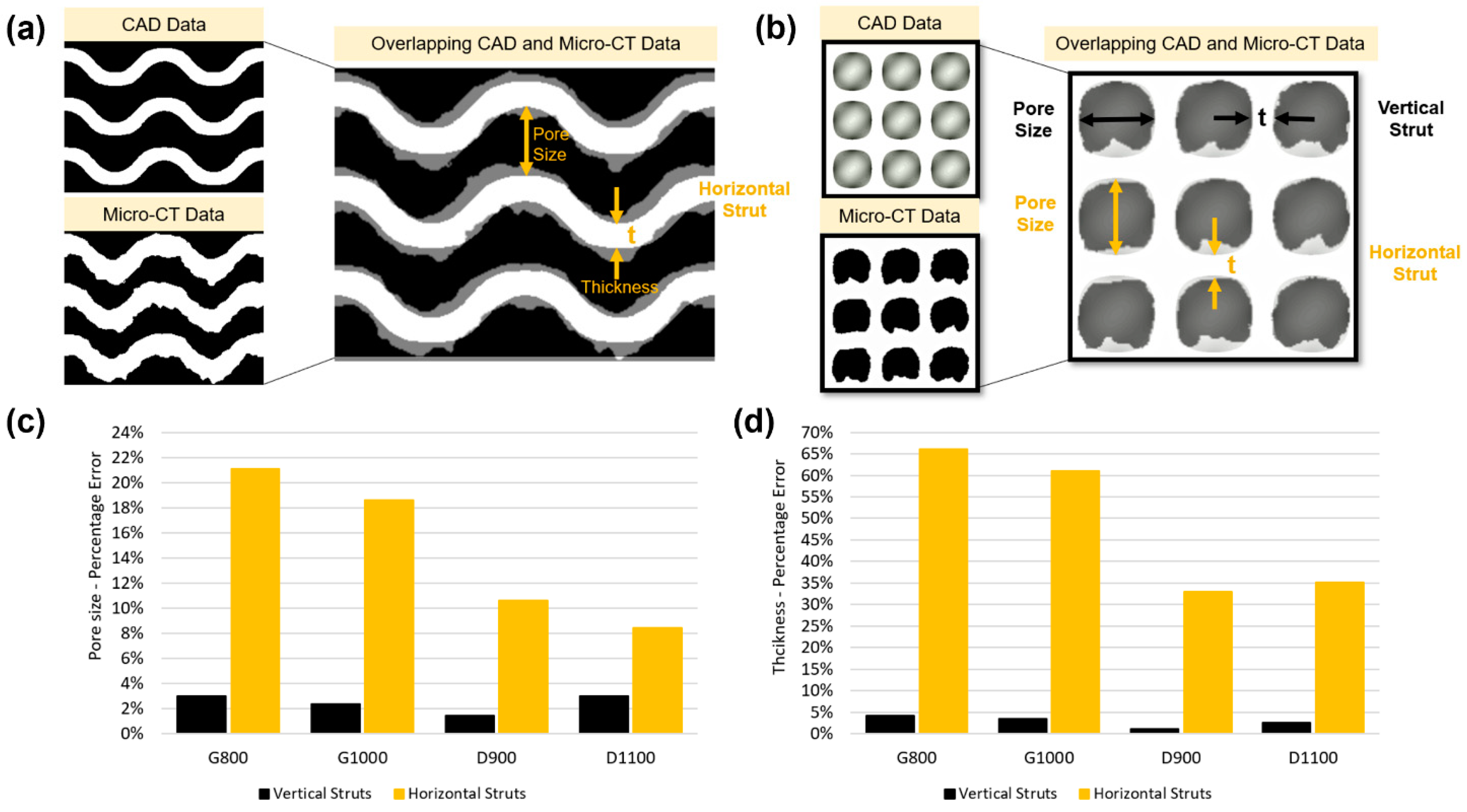
3.1. Morphological Deviation of Additive Manufacturing Specimens from Designs
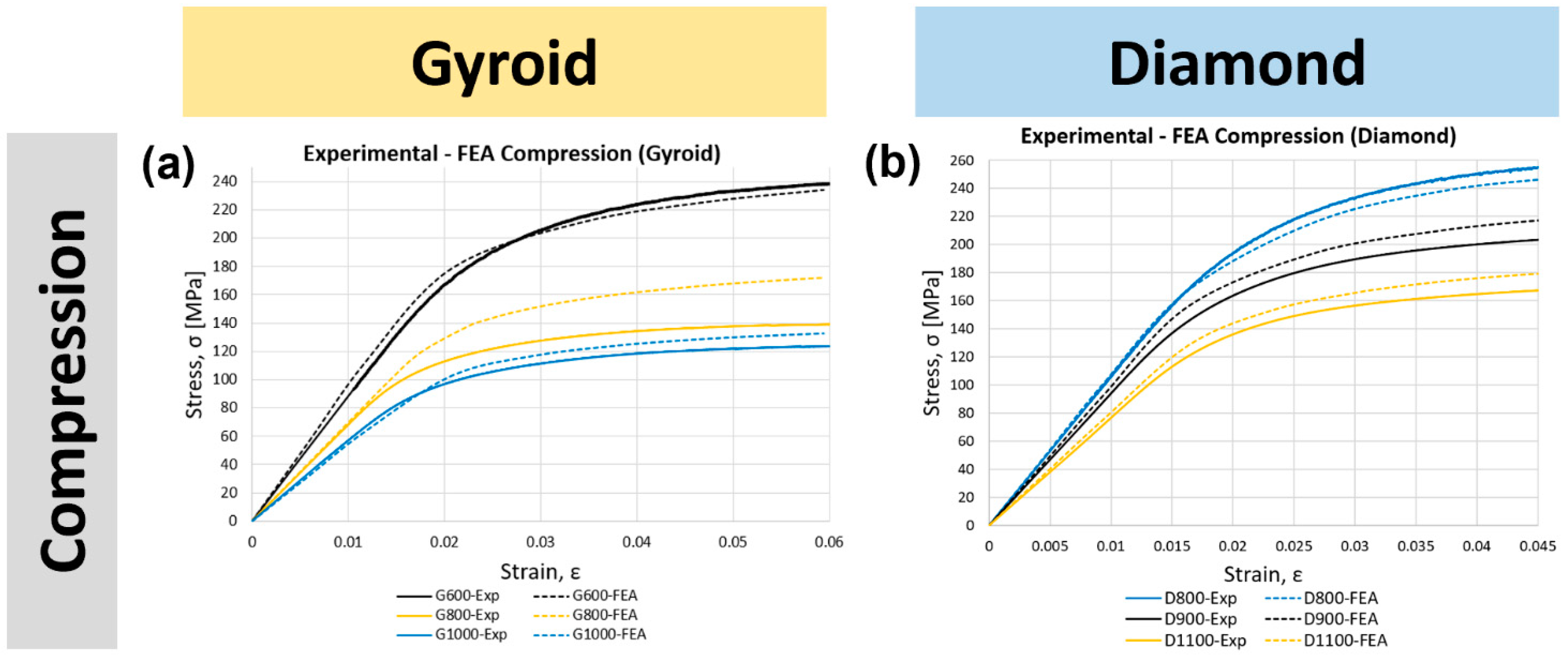
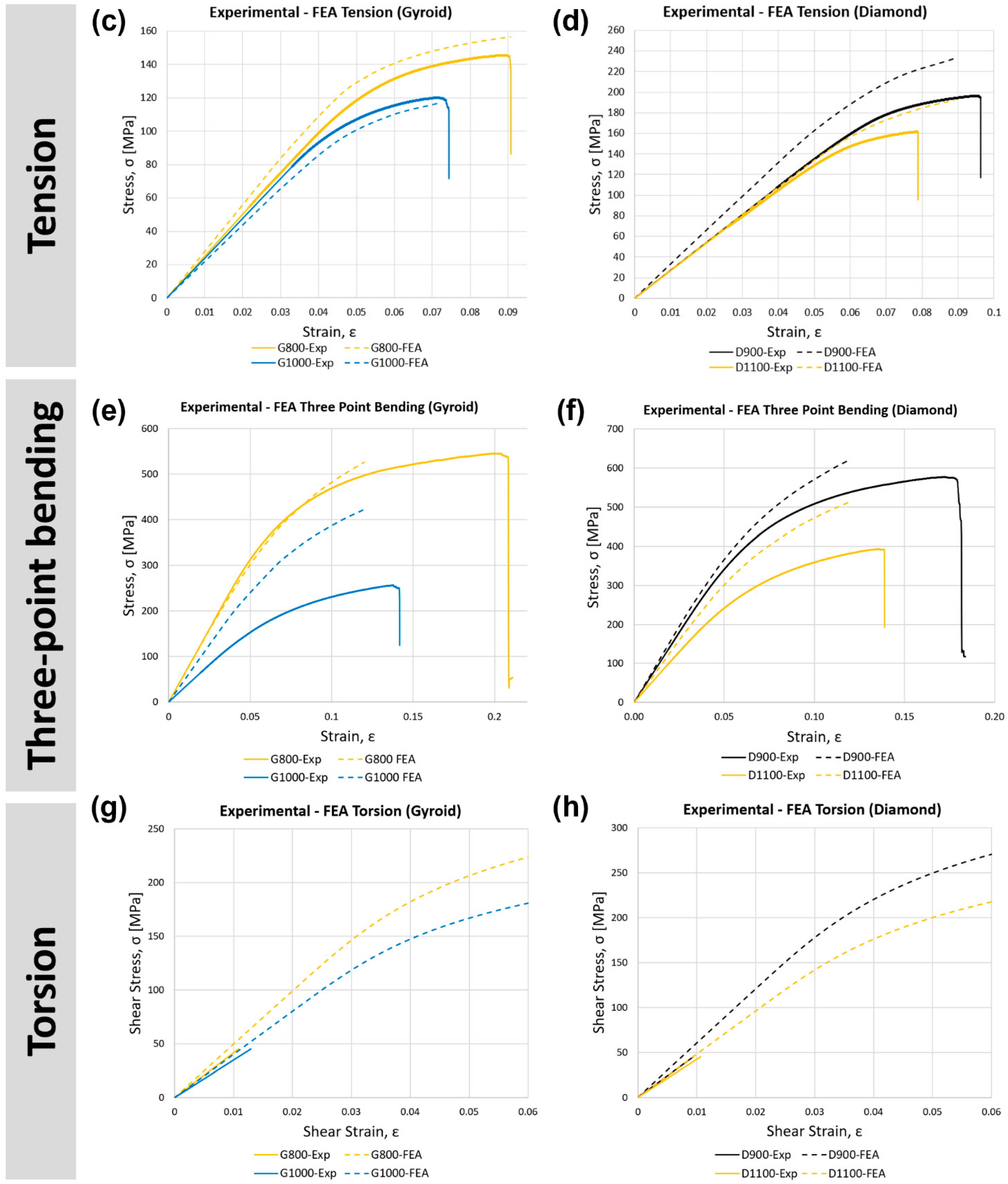
3.2. Validation of the Finite Element Model
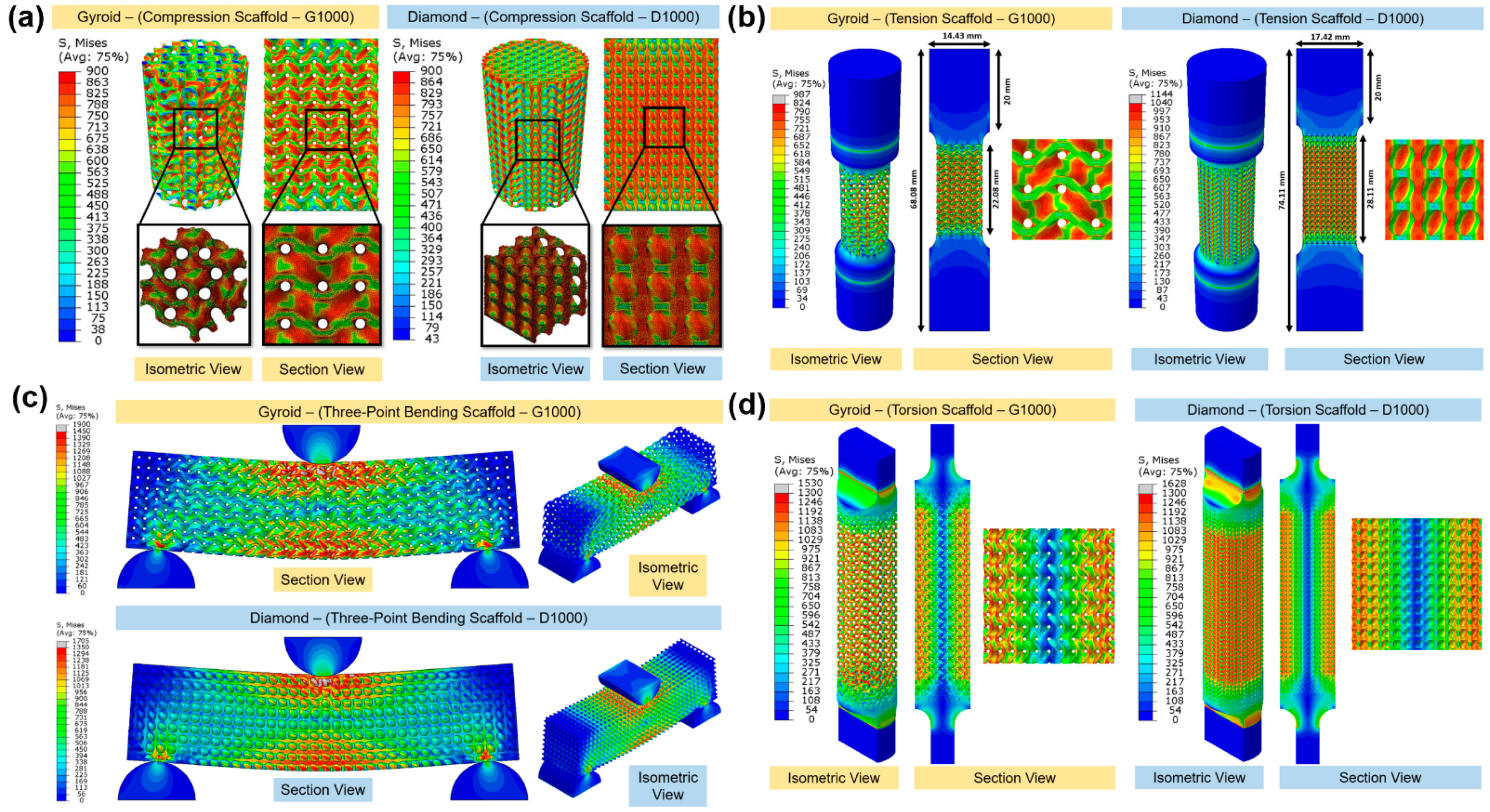
3.3. Finite Element Analysis of the Mechanical Behaviour of Gyroid and Diamond Topologies
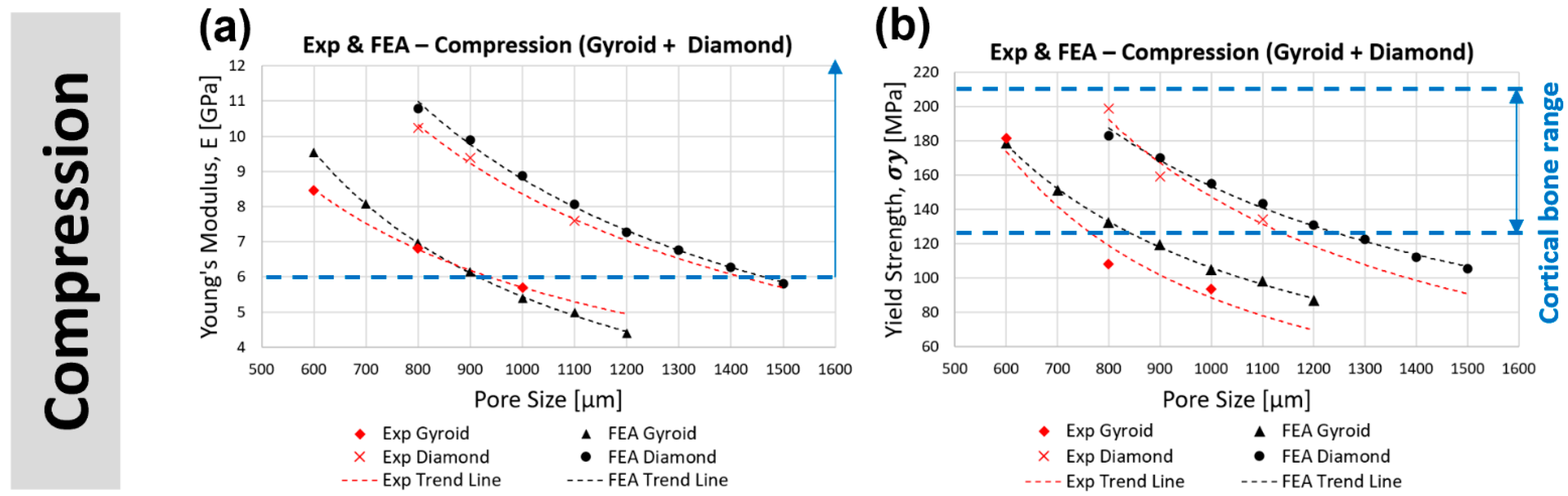
3.3.1. Compression
3.3.2. Tension
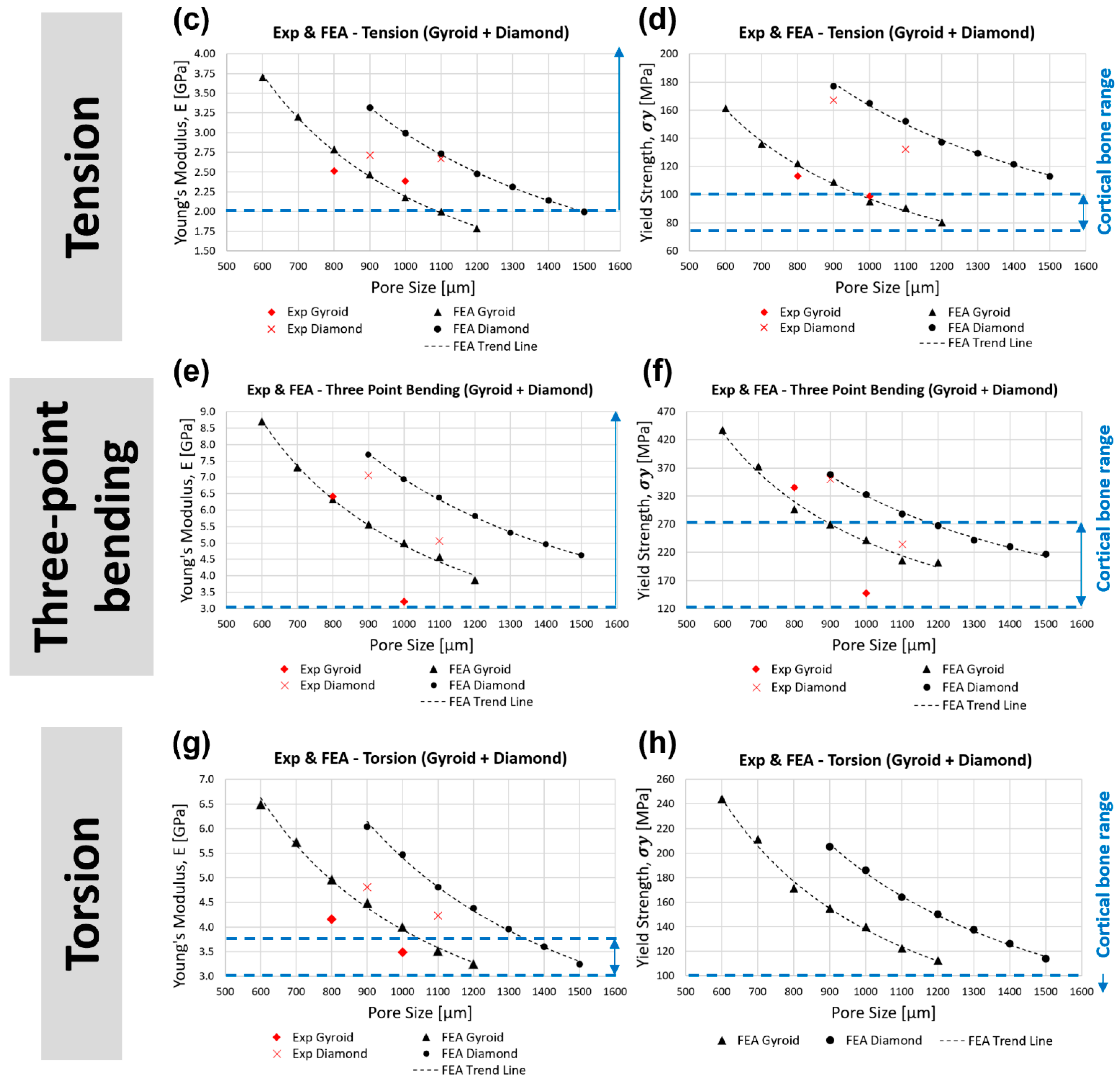
3.3.3. Three-Point Bending
3.3.4. Torsion
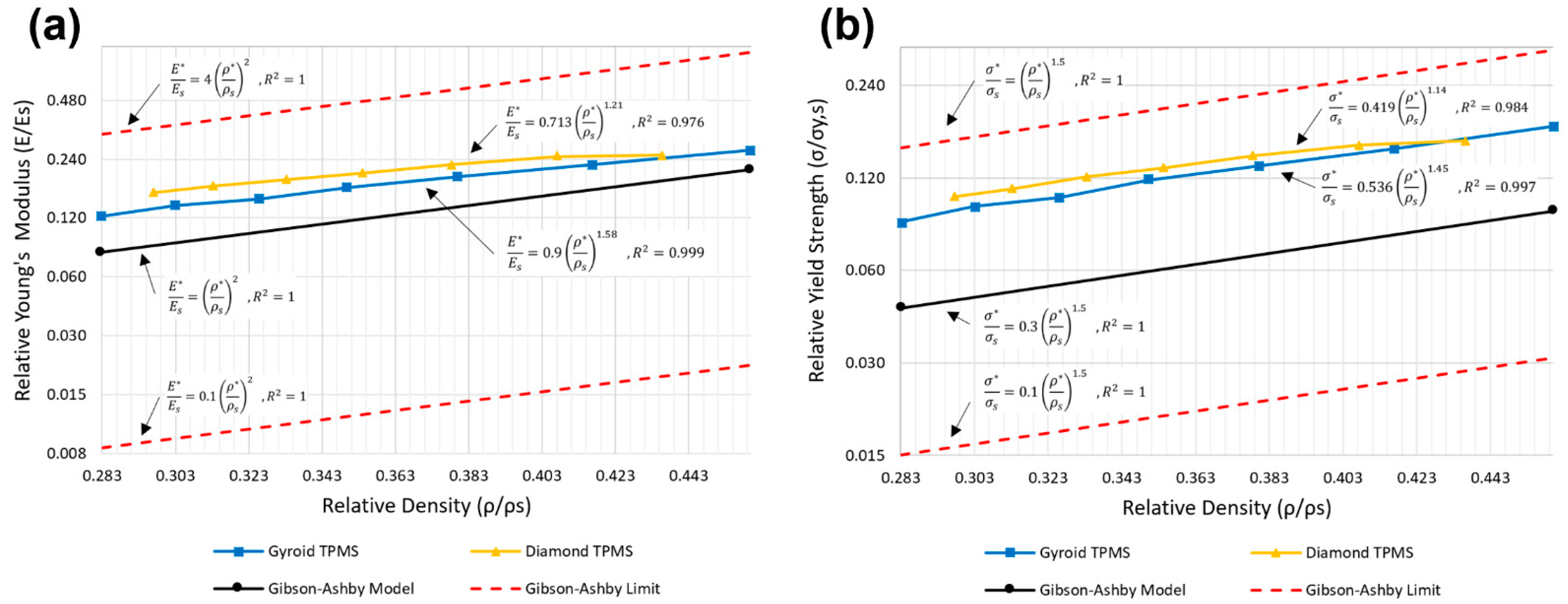
3.4. Comparison of Compressive Properties with the Classical Gibson–Ashby Model
3.5. Failure Mechanism and Deformation Mode
3.6. Limitations
4. Conclusions
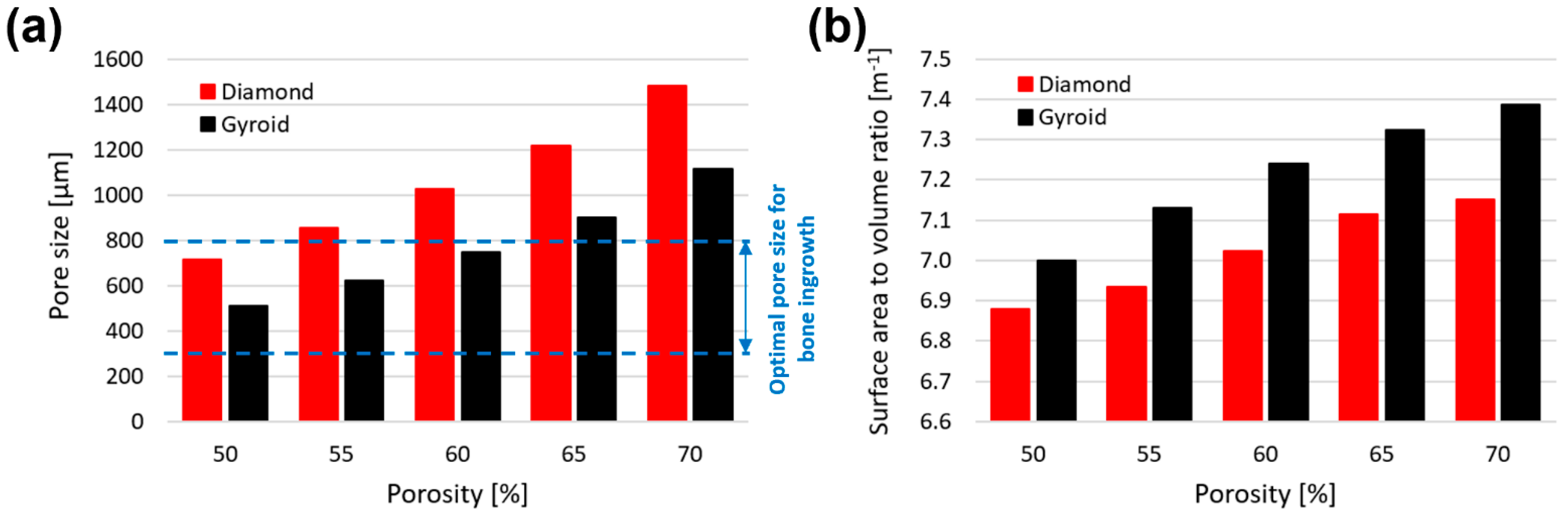
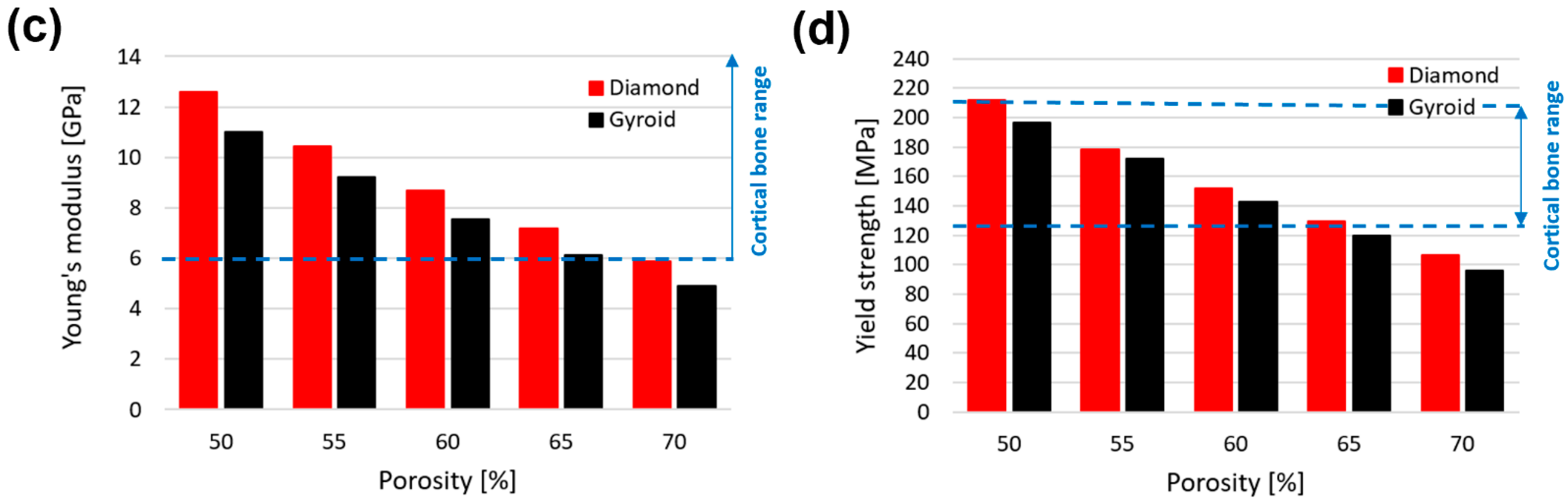
- In compression, gyroid with a pore size less than 800 μm (stiffness > 6.96 GPa, yield strength > 133 MPa) and diamond with a pore size less than 1200 μm (stiffness > 7.27 GPa, yield strength > 131 MPa) are within the acceptable lower range of cortical bone stiffness (6–30 GPa) and yield strength (125–210 MPa). At the same pore size, the diamond scaffold is stiffer (by approximately 65%) and stronger (by approximately 48%) than the gyroid in compression.
- In tension, gyroid with a pore size less than 1000 μm (stiffness > 2.18 GPa, yield strength > 95 MPa) and diamond with a pore size less than 1400 μm (stiffness > 2.14 GPa, yield strength > 122 MPa) are within the acceptable range of cortical bone stiffness (2–16 GPa) and greater than the acceptable cortical bone tensile yield strength (77–98 MPa). At the same pore size, the diamond scaffold is stiffer (by approximately 37%) and stronger (by approximately 74%) than the gyroid in tension.
- In bending, gyroid with a pore size less than 1200 μm (stiffness > 3.86 GPa, yield strength > 202 MPa) and diamond with a pore size less than 1500 μm (stiffness > 4.62 GPa, yield strength > 216 MPa) are within the acceptable range of cortical bone bending stiffness (3–15 GPa) and yield strength (45–270 GPa). At the same pore size, diamond is stiffer (by approximately 39%) and stronger (by approximately 37%) than gyroid in bending.
- In torsion, gyroid with a pore size of between 1100 and 1200 μm (3.24 < stiffness < 3.51 GPa, 113 < yield strength < 123 MPa) and diamond with a pore size of between 1400 and 1500 μm (3.24 < stiffness < 3.60 GPa, 114 < yield strength < 126 MPa) are within the acceptable range of cortical bone torsional stiffness (3.1–3.7 GPa) and greater than the acceptable cortical bone torsional yield strength (49–98 MPa). At the same pore size, diamond is stiffer (by approximately 37%) and stronger (by approximately 33%) than gyroid in torsion.
- Mechanical and morphological deviation between the designed and printed scaffolds are originated from the over melting of the struts, where horizontal and vertical struts are generally thicker than their designed values. Horizontal struts have a greater deviation (about 64% for gyroid and 34% for diamond) when compared to the vertical struts (about 4% for gyroid and 2% for diamond).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Subic, A.; Kovacs, J. Design and Materials in Snowboarding; Elsevier Ltd.: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Rochus, P.; Plesseria, J.Y.; van Elsen, M.; Kruth, J.P.; Carrus, R.; Dormal, T. New applications of rapid prototyping and rapid manufacturing (RP/RM) technologies for space instrumentation. Acta Astronaut. 2007, 61, 352–359. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Tamaddon, M.; Blunn, G.; Tan, R.; Yang, P.; Sun, X.; Chen, S.M.; Luo, J.; Liu, Z.; Wang, L.; Li, D.; et al. In vivo evaluation of additively manufactured multi-layered scaffold for the repair of large osteochondral defects. Bio-Des. Manuf. 2022, 5, 481–496. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Xu, W.; Lu, X.; Tamaddon, M.; Chen, M.; Dong, J.; Liu, Y.; Guo, L.; Zhang, J.; Qu, X.; et al. The Optimization of Ti Gradient Porous Structure Involves the Finite Element Simulation Analysis. Froniters Mater. 2021, 8, 226. [Google Scholar] [CrossRef]
- Xu, W.; Yu, A.; Lu, X.; Tamaddon, M.; Wang, M.; Zhang, J.; Zhang, J.; Qu, X.; Liu, C.; Su, B. Design and performance evaluation of additively manufactured composite lattice structures of commercially pure Ti (CP-Ti). Bioact. Mater. 2021, 6, 1215–1222. [Google Scholar] [CrossRef]
- Brennan-Craddock, J.; Brackett, D.; Wildman, R.; Hague, R. The design of impact absorbing structures for additive manufacture. J. Phys. Conf. Ser. 2012, 382, 2–9. [Google Scholar] [CrossRef]
- Lee Ventola, C. Medical Applications for 3D Printing: Current and Projected Uses. Pharm. Ther. 2014, 39, 704–711. [Google Scholar]
- Liu, S.; Shin, Y.C. Additive manufacturing of Ti6Al4V alloy: A review. Mater. Des. 2019, 164, 107552. [Google Scholar] [CrossRef]
- Irsen, S.H.; Milz, S.; Tille, C.; Schieker, M.; Seitz, H. Hydroxyapatite scaffolds for bone tissue engineering made by 3D printing. J. Mater. Sci. Mater. Med. 2005, 6, 1121–1124. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Bagheri, A.; Petit-Rojo, O. 3D printing of porous scaffolds with controlled porosity and pore size values. Materials 2018, 11, 1532. [Google Scholar] [CrossRef]
- Liu, X.; Chu, P.K.; Ding, C. Surface modification of titanium, titanium alloys, and related materials for biomedical applications. Mater. Sci. Eng. R Rep. 2004, 47, 49–121. [Google Scholar] [CrossRef]
- Szabo, E.; Rimnac, C. Biomechanics of immature human cortical bone: A systematic review. J. Mech. Behav. Biomed. Mater. 2022, 125, 104889. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, S.; Zhou, S.; Xu, W.; Leary, M.; Choong, P.; Qian, M.; Brandt, M.; Xie, Y.M. Topological design and additive manufacturing of porous metals for bone scaffolds and orthopaedic implants: A review. Biomaterials 2016, 83, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Niinomi, M.; Nakai, M. Titanium-based biomaterials for preventing stress shielding between implant devices and bone. Int. J. Biomater. 2011, 2011, 836587. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.C.; Kuo, C.N.; Shie, M.Y.; Su, Y.L.; Wei, L.J.; Chen, S.Y.; Huang, J.C. Structural design and mechanical response of gradient porous Ti-6Al-4V fabricated by electron beam additive manufacturing. Mater. Des. 2018, 158, 256–265. [Google Scholar] [CrossRef]
- Geetha, M.; Singh, A.K.; Asokamani, R.; Gogia, A.K. Ti based biomaterials, the ultimate choice for orthopaedic implants—A review. Prog. Mater. Sci. 2009, 54, 397–425. [Google Scholar] [CrossRef]
- Gibson, L.J.; Sh, M.F.A.; Schajerj, J.G.S. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Loud. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Miao, X.; Sun, D. Graded/gradient porous biomaterials. Materials 2010, 3, 26. [Google Scholar] [CrossRef]
- Fousová, M.; Vojtěch, D.; Kubásek, J.; Jablonská, E.; Fojt, J. Promising characteristics of gradient porosity Ti-6Al-4V alloy prepared by SLM process. J. Mech. Behav. Biomed. Mater. 2017, 69, 368–376. [Google Scholar] [CrossRef]
- Migliorini, F.; la Padula, G.; Torsiello, E.; Spiezia, F.; Oliva, F.; Maffulli, N. Strategies for large bone defect reconstruction after trauma, infections or tumour excision: A comprehensive review of the literature. Eur. J. Med. Res. 2021, 26, 118. [Google Scholar] [CrossRef]
- Guo, X.; Zheng, X.; Yang, Y.; Yang, X.; Yi, Y. Mechanical behavior of TPMS-based scaffolds: A comparison between minimal surfaces and their lattice structures. SN Appl. Sci. 2019, 1, 1145. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Bone tissue regeneration: The role of scaffold geometry. Biomater. Sci. 2015, 3, 231–245. [Google Scholar] [CrossRef] [PubMed]
- Brentel, A.S.; de Vasconcellos, L.M.; Oliveira, M.V.; Graca, M.L.; de Vasconcellos, L.G.; Cairo, C.A.; Carvalho, Y.R. Histomorphometric Analysis of Pure Titanium Implants With Porous Surface Versus Rough Surface. J. Appl. Oral Sci. 2006, 14, 213–218. [Google Scholar] [CrossRef]
- Oliveira, M.V.; Pereira, L.C.; Cairo, C.A.A. Porous Structure Characterization in Titanium Coating for Surgical Implants. Mater. Res. 2002, 5, 269–273. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical evaluation of porous titanium (Ti6Al4V) structures with electron beam melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Bubb, S.L.; Young, P.; Raymont, D. Evaluation of light-weight AlSi10Mg periodic cellular lattice structures fabricated via direct metal laser sintering. J. Mater. Process. Technol. 2014, 214, 856–864. [Google Scholar] [CrossRef]
- Ma, S.; Tang, Q.; Han, X.; Feng, Q.; Song, J.; Setchi, R.; Liu, Y.; Liu, Y.; Goulas, A.; Engstrøm, D.S.; et al. Manufacturability, Mechanical Properties, Mass-Transport Properties and Biocompatibility of Triply Periodic Minimal Surface (TPMS) Porous Scaffolds Fabricated by Selective Laser Melting. Mater. Des. 2020, 195, 109034. [Google Scholar] [CrossRef]
- du Plessis, A.; Yadroitsava, I.; Yadroitsev, I.; le Roux, S.G.; Blaine, D.C. Numerical comparison of lattice unit cell designs for medical implants by additive manufacturing. Virtual Phys. Prototyp. 2018, 13, 266–281. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Zhao, X.; Li, S.; Zhang, M.; Liu, Y.; Sercombe, T.B.; Wang, S.; Hao, Y.; Yang, R.; Murr, L.E. Comparison of the microstructures and mechanical properties of Ti-6Al-4V fabricated by selective laser melting and electron beam melting. Mater. Des. 2016, 95, 21–31. [Google Scholar] [CrossRef]
- Sing, S.L.; An, J.; Yeong, W.Y.; Wiria, F.E. Laser and electron-beam powder-bed additive manufacturing of metallic implants: A review on processes, materials and designs. J. Orthop. Res. 2016, 34, 369–385. [Google Scholar] [CrossRef] [PubMed]
- Arabnejad, S.; Johnston, R.B.; Pura, J.A.; Singh, B.; Tanzer, M.; Pasini, D. High-strength porous biomaterials for bone replacement: A strategy to assess the interplay between cell morphology, mechanical properties, bone ingrowth and manufacturing constraints. Acta Biomater. 2016, 30, 345–356. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Hao, L.; Hussein, A.; Raymont, D. Evaluations of cellular lattice structures manufactured using selective laser melting. Int. J. Mach. Tools Manuf. 2012, 62, 32–38. [Google Scholar] [CrossRef]
- Bagheri, Z.S.; Melancon, D.; Liu, L.; Johnston, R.B.; Pasini, D. Compensation strategy to reduce geometry and mechanics mismatches in porous biomaterials built with Selective Laser Melting. J. Mech. Behav. Biomed. Mater. 2017, 70, 17–27. [Google Scholar] [CrossRef]
- Yu, G.; Li, Z.; Li, S.; Zhang, Q.; Hua, Y.; Liu, H.; Zhao, X.; Dhaidhai, D.T.; Li, W.; Wang, X. The select of internal architecture for porous Ti alloy scaffold: A compromise between mechanical properties and permeability. Mater. Des. 2020, 192, 108754. [Google Scholar] [CrossRef]
- Hameed, P.; Liu, C.F.; Ummethala, R.; Singh, N.; Huang, H.H.; Manivasagam, G.; Prashanth, K.G. Biomorphic porous Ti6Al4V gyroid scaffolds for bone implant applications fabricated by selective laser melting. Prog. Addit. Manuf. 2021, 6, 455–469. [Google Scholar] [CrossRef]
- Ge, J.; Huang, J.; Lei, Y.; O’Reilly, P.; Ahmed, M.; Zhang, C.; Yan, X.; Yin, S. Microstructural features and compressive properties of SLM Ti6Al4V lattice structures. Surf. Coatings Technol. 2020, 403, 126419. [Google Scholar] [CrossRef]
- Li, Y.; Shi, J.; Jahr, H.; Zhou, J.; Zadpoor, A.A.; Wang, L. Improving the Mechanical Properties of Additively Manufactured Micro-Architected Biodegradable Metals. Jom 2021, 73, 4188–4198. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Zhou, X.; Zhang, M.; Zhang, P.; Wang, L. Innovative design and additive manufacturing of regenerative cooling thermal protection system based on the triply periodic minimal surface porous structure. CMES—Comput. Model. Eng. Sci. 2020, 123, 495–508. [Google Scholar] [CrossRef]
- Polley, C.; Radlof, W.; Hauschulz, F.; Benz, C.; Sander, M.; Seitz, H. Morphological and mechanical characterisation of three-dimensional gyroid structures fabricated by electron beam melting for the use as a porous biomaterial. J. Mech. Behav. Biomed. Mater. 2022, 125, 104882. [Google Scholar] [CrossRef] [PubMed]
- Khrapov, D.; Kozadayeva, M.; Manabaev, K.; Panin, A.; Sjöström, W.; Koptyug, A.; Mishurova, T.; Evsevleev, S.; Meinel, D.; Bruno, G.; et al. Different approaches for manufacturing ti-6al-4v alloy with triply periodic minimal surface sheet-based structures by electron beam melting. Materials 2021, 14, 4912. [Google Scholar] [CrossRef] [PubMed]
- Horn, T.J.; Harrysson, O.L.A.; Marcellin-Little, D.J.; West, H.A.; Lascelles, B.D.X.; Aman, R. Flexural properties of Ti6Al4V rhombic dodecahedron open cellular structures fabricated with electron beam melting. Addit. Manuf. 2014, 1, 2–11. [Google Scholar] [CrossRef]
- Korshunova, N.; Alaimo, G.; Hosseini, S.B.; Carraturo, M.; Reali, A.; Niiranen, J.; Auricchio, F.; Rank, E.; Kollmannsberger, S. Bending behavior of octet-truss lattice structures: Modelling options, numerical characterization and experimental validation. Mater. Des. 2021, 205, 109693. [Google Scholar] [CrossRef]
- Mohammadhosseini, A.; Masood, S.H.; Fraser, D.; Jahedi, M.; Gulizia, S. Flexural Behaviour of titanium cellular structures produced by Electron Beam Melting. Mater. Today Proc. 2017, 4, 8260–8268. [Google Scholar] [CrossRef]
- O’Masta, M.R.; Dong, L.; St-Pierre, L.; Wadley, H.N.G.; Deshpande, V.S. The fracture toughness of octet-truss lattices. J. Mech. Phys. Solids 2017, 98, 271–289. [Google Scholar] [CrossRef]
- Audibert, C.; Chaves-Jacob, J.; Linares, J.M.; Lopez, Q.A. Bio-inspired method based on bone architecture to optimize the structure of mechanical workspieces. Mater. Des. 2018, 160, 708–717. [Google Scholar] [CrossRef]
- Rashid, R.A.R.; Mallavarapu, J.; Palanisamy, S.; Masood, S.H. A comparative study of flexural properties of additively manufactured aluminium lattice structures. Mater. Today Proc. 2017, 4, 8597–8604. [Google Scholar] [CrossRef]
- Imwinkelried, T. Mechanical properties of open-pore titanium foam. J. Biomed. Mater. Res. Part A 2007, 81, 964–970. [Google Scholar] [CrossRef]
- Yánez, A.; Cuadrado, A.; Martel, O.; Afonso, H.; Monopoli, D. Gyroid porous titanium structures: A versatile solution to be used as scaffolds in bone defect reconstruction. Mater. Des. 2018, 140, 21–29. [Google Scholar] [CrossRef]
- Cansizoglu, O.; Harrysson, O.; Cormier, D.; West, H.; Mahale, T. Properties of Ti-6Al-4V non-stochastic lattice structures fabricated via electron beam melting. Mater. Sci. Eng. A 2008, 492, 468–474. [Google Scholar] [CrossRef]
- Naghavi, S.A.; Sun, C.; Hejazi, M.; Tamaddon, M.; Zheng, J.; Wang, L.; Zhang, C.; Varma, S.N.; Li, D.; Moazen, M.; et al. On the mechanical aspect of additive manufactured polyether-ether-ketone scaffold for repair of large bone defects. Biomater. Transl. 2022, 3, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Soro, N.; Saintier, N.; Attar, H.; Dargusch, M.S. Surface and morphological modification of selectively laser melted titanium lattices using a chemical post treatment. Surf. Coat. Technol. 2020, 393, 125794. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Babamiri, B.B.; Zhou, Y.; Dargusch, M.; Hazeli, K.; Zhang, M.-X. Enhancing specific energy absorption of additively manufactured titanium lattice structures through simultaneous manipulation of architecture and constituent material. Addit. Manuf. 2022, 55, 102887. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.O.; Panesar, A.; Williams, C.B.; Tuck, C.J.; Wildman, R.D.; Ashcroft, I.A.; Hague, R.J.M. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2018, 152, 62–71. [Google Scholar] [CrossRef]
- Barnes, B.; Babamiri, B.B.; Demeneghi, G.; Soltani-Tehrani, A.; Shamsaei, N.; Hazeli, K. Quasi-static and dynamic behavior of additively manufactured lattice structures with hybrid topologies. Addit. Manuf. 2021, 48, 102466. [Google Scholar] [CrossRef]
- ISO 6892-1:2019; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Bsi: London, UK, 2019. Available online: https://www.iso.org/standard/78322.html (accessed on 23 July 2020).
- ASTM E143-13; Standard Test Method for Shear Modulus at Room Temperature. ASTM International: West Conshohocken, PA, USA, 2008; Volume 2, p. 545-545. Available online: https://www.astm.org/standards/e143 (accessed on 27 July 2020).
- ISO 17340-2014; Metallic Materials—Ductility Testing—High Speed Compression Test for Porous and Cellular Metals. International Organization for Standardization: Geneva, Switzerland, 2014. Available online: https://www.iso.org/standard/59594.html (accessed on 13 November 2020).
- ISO 13314-2011; Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals. 2011. Available online: https://www.iso.org/standard/53669.html (accessed on 13 November 2020).
- ASTM C1674-16; Standard Test Method for Flexural Strength of Advanced Ceramics with Engineered Porosity (Honeycomb Cellular Channels) at Ambient. ASTM International: West Conshohocken, PA, USA, 2010; pp. 1–26. Available online: https://www.astm.org/c1674-16.html (accessed on 18 November 2020).
- van Bael, S.; Kerckhofs, G.; Moesen, M.; Pyka, G.; Schrooten, J.; Kruth, J.-P. Micro-CT-based improvement of geometrical and mechanical controllability of selective laser melted Ti6Al4V porous structures. Mater. Sci. Eng. A 2011, 528, 7423–7431. [Google Scholar] [CrossRef]
- Pyka, G.; Kerckhofs, G.; Papantoniou, I.; Speirs, M.; Schrooten, J.; Wevers, M. Surface roughness and morphology customization of additive manufactured open porous Ti6Al4V structures. Materials 2013, 6, 4737. [Google Scholar] [CrossRef]
- Taniguchi, N.; Fujibayashi, S.; Takemoto, M.; Sasaki, K.; Otsuki, B.; Nakamura, T.; Matsushita, T.; Kokubo, T.; Matsuda, S. Effect of pore size on bone ingrowth into porous titanium implants fabricated by additive manufacturing: An in vivo experiment. Mater. Sci. Eng. C 2016, 59, 690–701. [Google Scholar] [CrossRef]
- van Bael, S.; Chai, Y.C.; Truscello, S.; Moesen, M.; Kerckhofs, G.; van Oosterwyck, H.; Kruth, J.P.; Schrooten, J. The effect of pore geometry on the in vitro biological behavior of human periosteum-derived cells seeded on selective laser-melted Ti6Al4V bone scaffolds. Acta Biomater. 2012, 8, 2824–2834. [Google Scholar] [CrossRef]
- Fukuda, A.; Takemoto, M.; Saito, T.; Fujibayashi, S.; Neo, M.; Pattanayak, D.K.; Matsushita, T.; Sasaki, K.; Nishida, N.; Kokubo, T.; et al. Osteoinduction of porous Ti implants with a channel structure fabricated by selective laser melting. Acta Biomater. 2011, 7, 2327–2336. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.H.; Li, Y.; Zhang, Y.Q.; Li, X.K.; Yuan, C.F.; Hao, Y.L.; Zhang, Z.Y.; Guo, Z. Porous Titanium-6 Aluminum-4 Vanadium Cage Has Better Osseointegration and Less Micromotion Than a Poly-Ether-Ether-Ketone Cage in Sheep Vertebral Fusion. Artif. Organs. 2013, 37, E191–E201. [Google Scholar] [CrossRef]
- Barba, D.; Alabort, E.; Reed, R.C. Synthetic bone: Design by additive manufacturing. Acta Biomater. 2019, 97, 637–656. [Google Scholar] [CrossRef]
- Naghavi, S.A.; Wang, H.; Varma, S.N.; Tamaddon, M.; Marghoub, A.; Galbraith, R.; Galbraith, J.; Moazen, M.; Hua, J.; Xu, W.; et al. On the Morphological Deviation in Additive Manufacturing of Porous Ti6Al4V Scaffold: A Design Consideration. Materials 2022, 15, 4729. [Google Scholar] [CrossRef]
- Caeiro, J.R.; González, P.; Guede, D. Biomechanics and bone (& II): Trials in different hierarchical levels of bone and alternative tools for the determination of bone strength. Rev. Osteoporos Y Metab. Miner. 2013, 5, 99–108. Available online: http://revistadeosteoporosisymetabolismomineral.com/2017/07/11/biomechanics-and-bone-ii-trials-in-different-hierarchical-levels-of-bone-and-alternative-tools-for-the-determination-of-bone-strength/ (accessed on 8 February 2022).
- Bobbert, F.S.L.; Lietaert, K.; Eftekhari, A.A.; Pouran, B.; Ahmadi, S.M.; Weinans, H.; Zadpoor, A.A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [PubMed]
- Barber, H.; Kelly, C.N.; Nelson, K.; Gall, K. Compressive anisotropy of sheet and strut based porous Ti–6Al–4V scaffolds. J. Mech. Behav. Biomed. Mater. 2021, 115, 104243. [Google Scholar] [CrossRef] [PubMed]
- Shimko, D.A.; Shimko, V.F.; Sander, E.A.; Dickson, K.F.; Nauman, E.A. Effect of porosity on the fluid flow characteristics and mechanical properties of tantalum scaffolds. J. Biomed. Mater. Res.-Part B Appl. Biomater. 2005, 73, 315–324. [Google Scholar] [CrossRef]
- Kelly, C.N.; Francovich, J.; Julmi, S.; Safranski, D.; Guldberg, R.E.; Maier, H.J.; Gall, K. Fatigue behavior of As-built selective laser melted titanium scaffolds with sheet-based gyroid microarchitecture for bone tissue engineering. Acta Biomater. 2019, 94, 610–626. [Google Scholar] [CrossRef]
- Ashby, M.F. Mechanical Properties of Cellular Solids. Metall. Trans. A Phys. Metall. Mater. Sci. 1983, 14, 1755–1769. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, T.; Fleck, N.A.; Hutchinson, J.W.; Wadley, H.N.G.; Gibson, L.J. Metal Foams, A Design Guide; Elsevier, Butterworth Heinemann: Stoneham, MA, USA, 2000. [Google Scholar]
- Ashby, M.F.; Gibson, L.J. Cellular Solids Structure and Properties; Cambridge University Press: Cambridge, UK, 1997; pp. 175–231. [Google Scholar]
- Vijayavenkataraman, S.; Zhang, L.; Zhang, S.; Fuh, J.Y.H.; Lu, W.F. Triply periodic minimal surfaces sheet scaffolds for tissue engineering applications: An optimization approach toward biomimetic scaffold design. ACS Appl. Bio Mater. 2018, 1, 259–269. [Google Scholar] [CrossRef] [PubMed]
- Babamiri, B.B.; Askari, H.; Hazeli, K. Deformation mechanisms and post-yielding behavior of additively manufactured lattice structures. Mater. Des. 2020, 188, 108443. [Google Scholar] [CrossRef]
- Babamiri, B.B.; Barnes, B.; Soltani-Tehrani, A.; Shamsaei, N.; Hazeli, K. Designing additively manufactured lattice structures based on deformation mechanisms. Addit. Manuf. 2021, 46, 102143. [Google Scholar] [CrossRef]
- Hazeli, K.; June, D.; Anantwar, P.; Babamiri, B.B. Mechanical behavior of additively manufactured GRCop-84 copper alloy lattice structures. Addit. Manuf. 2022, 56, 102928. [Google Scholar] [CrossRef]
- Babamiri, B.B.; Mayeur, J.R.; Hazeli, K. Synchronous involvement of topology and microstructure to design additively manufactured lattice structures. Addit. Manuf. 2022, 52, 102618. [Google Scholar] [CrossRef]
- Hazeli, K.; Babamiri, B.B.; Indeck, J.; Minor, A.; Askari, H. Microstructure-topology relationship effects on the quasi-static and dynamic behavior of additively manufactured lattice structures. Mater. Des. 2019, 176, 107826. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Jia, G.; Zeng, H.; Yuan, G. Fatigue and dynamic biodegradation behavior of additively manufactured Mg scaffolds. Acta Biomater. 2021, 135, 705–722. [Google Scholar] [CrossRef] [PubMed]
- Grimm, M.J.; Williams, J.L. Measurements of permeability in human calcaneal trabecular bone. J. Biomech. 1997, 30, 743–745. [Google Scholar] [CrossRef]
- Karande, T.S.; Ong, J.L.; Agrawal, C.M. Diffusion in musculoskeletal tissue engineering scaffolds: Design issues related to porosity, permeability, architecture, and nutrient mixing. Ann. Biomed. Eng. 2004, 32, 1728–1743. [Google Scholar] [CrossRef]
- O’Brien, F.J.; Harley, B.A.; Waller, M.A.; Yannas, I.V.; Gibson, L.J.; Prendergast, P.J. The effect of pore size on permeability and cell attachment in collagen scaffolds for tissue engineering. Technol. Health Care 2007, 15, 3–17. [Google Scholar] [CrossRef]


| Element | C | O | N | H | Fe | Al | V | Ti |
|---|---|---|---|---|---|---|---|---|
| Standard values (mass %) | ≤0.08 | ≤0.20 | ≤0.05 | ≤0.015 | ≤0.3 | ≤5.5–6.75 | ≤3.5–4.5 | Balance |
| Measured values (mass %) | 0.01 | 0.09 | 0.02 | 0.0022 | 0.22 | 6.44 | 4 | Balance |
| Parameter | Laser Power (W) | Layer Thickness (µm) | Scan Speed (mm/s) | Spot Size (µm) | Energy Density (J/mm3) | Hatch Distance (µm) |
|---|---|---|---|---|---|---|
| Value | 190 | 30 | 1000 | 90 | 85 | 110 |
| Structure | Scaffold ID | Sheet Thickness (mm) | Pore Size (μm) | Unit Cell (mm) | Porosity (%) |
|---|---|---|---|---|---|
| Gyroid | G600 | 0.3 | 600 | 1.808 | 54.0 |
| G800 | 800 | 2.208 | 62.0 | ||
| G1000 | 1000 | 2.608 | 67.4 | ||
| Diamond | D800 | 0.3 | 800 | 2.195 | 52.7 |
| D900 | 900 | 2.400 | 56.4 | ||
| D1100 | 1100 | 2.811 | 62.2 |
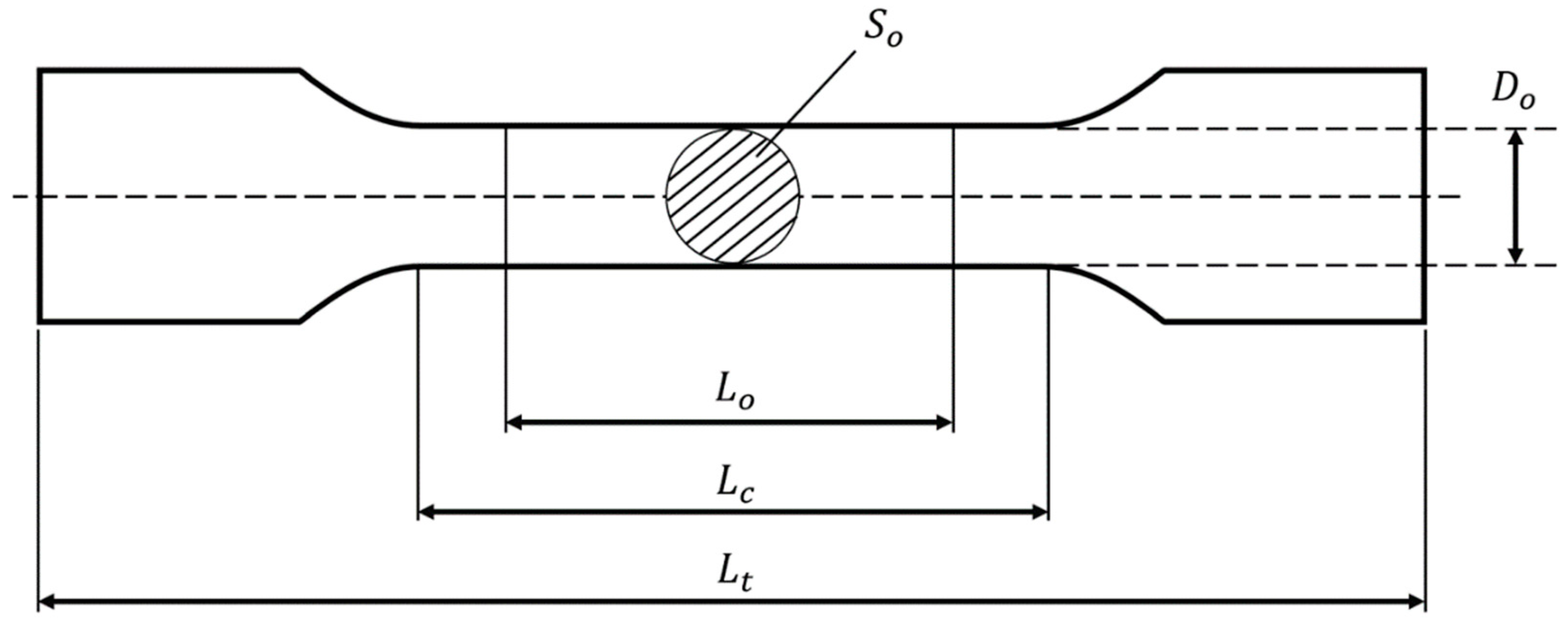
| Scaffold | Total Length (Lt) mm | Parallel Length (Lc) mm | Gauge Length (Lo) mm | Diameter (Do) mm | Cross-Sectional area (So) cm2 |
|---|---|---|---|---|---|
| Gyroid | 68.08 | 22.08 | 14.72 | 11.04 | 95.73 |
| Diamond | 74.11 | 28.11 | 18.74 | 14.06 | 155.26 |
| Pore Size (µm) | Porosity (%) | Sheet Thickness (µm) | Unit Cell Size (mm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit cell | CAD | Micro-CT (Vertical) | % Error | Micro-CT (Horizontal) | % Error | CAD | Micro-CT | % Error | CAD | Micro-CT (Vertical) | % Error | Micro-CT (Horizontal) | % Error | |
| Gyroid | 800 | 776.2 ± 18.3 | 3% | 631.3 ± 33.8 | 21% | 62.00 | 54.9 | 11% | 300 | 312.6 ± 17.3 | 4% | 498.6 ± 37.1 | 66% | 2.208 |
| 1000 | 976.4 ± 22.4 | 2% | 814.2 ± 35.8 | 19% | 67.40 | 61.8 | 8% | 310.4 ± 14.5 | 3% | 482.8 ± 24.3 | 61% | 2.608 | ||
| Diamond | 900 | 887.1 ± 17.3 | 1% | 804.7 ± 16.4 | 11% | 56.40 | 47.4 | 13% | 300 | 303.5 ± 13.2 | 1% | 399.1 ± 32.7 | 33% | 2.400 |
| 1100 | 1066.9 ± 18.9 | 3% | 1007.2 ± 18.9 | 8% | 62.15 | 55.2 | 11% | 307.5 ± 18.5 | 3% | 405.4 ± 19.5 | 35% | 2.811 | ||
| Test | Sample Name | Young’s Modulus (GPa) | Yield Stress (MPa) | ||||
|---|---|---|---|---|---|---|---|
| Experimental | Simulation | % Error | Experimental | Simulation | % Error | ||
| G600 | 8.46 ± 0.43 | 9.54 | 12% | 181 ± 3 | 179 | 2% | |
| Compression | G800 | 6.81 | 6.96 | 2% | 108 | 133 | 23% |
| G1000 | 5.69 | 5.39 | 5% | 94 | 105 | 12% | |
| D800 | 10.22 ± 0.31 | 10.78 | 5% | 199 ± 3 | 183 | 8% | |
| D900 | 9.37 | 9.89 | 6% | 159 | 170 | 7% | |
| D1100 | 7.59 | 8.06 | 6% | 134 | 144 | 7% | |
| Cortical Bone | 6–30 | - | - | 125–210 | - | - | |
| Tension | G800 | 2.51 | 2.78 | 11% | 113 | 122 | 8% |
| G1000 | 2.39 | 2.18 | 9% | 99 | 95 | 4% | |
| D900 | 2.71 | 3.32 | 22% | 167 | 177 | 6% | |
| D1100 | 2.67 | 2.73 | 2% | 132 | 152 | 15% | |
| Cortical Bone | 2–16 | - | - | 77–98 | - | - | |
| Three-point bending | G800 | 6.41 | 6.32 | 2% | 335 | 296 | 12% |
| G1000 | 3.21 | 5.00 | 56% | 147 | 242 | 65% | |
| D900 | 7.06 | 7.68 | 9% | 350 | 358 | 2% | |
| D1100 | 5.07 | 6.37 | 26% | 234 | 287 | 23% | |
| Cortical Bone | 3–15 | - | - | 45–270 | - | - | |
| Torsion | G800 | 4.16 | 4.96 | 19% | - | 171 | - |
| G1000 | 3.48 | 4.00 | 15% | - | 140 | - | |
| D900 | 4.80 | 6.04 | 26% | - | 205 | - | |
| D1100 | 4.23 | 4.81 | 14% | - | 164 | - | |
| Cortical Bone | 3.1–3.7 | - | - | 49–98 | - | - | |
| Relative Young’s Modulus | Relative Yield Strength | |
|---|---|---|
| Gibson−Ashby | ||
| Gyroid sheet TPMS | ||
| Diamond sheet TPMS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naghavi, S.A.; Tamaddon, M.; Marghoub, A.; Wang, K.; Babamiri, B.B.; Hazeli, K.; Xu, W.; Lu, X.; Sun, C.; Wang, L.; et al. Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration. Bioengineering 2022, 9, 504. https://doi.org/10.3390/bioengineering9100504
Naghavi SA, Tamaddon M, Marghoub A, Wang K, Babamiri BB, Hazeli K, Xu W, Lu X, Sun C, Wang L, et al. Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration. Bioengineering. 2022; 9(10):504. https://doi.org/10.3390/bioengineering9100504
Chicago/Turabian StyleNaghavi, Seyed Ataollah, Maryam Tamaddon, Arsalan Marghoub, Katherine Wang, Behzad Bahrami Babamiri, Kavan Hazeli, Wei Xu, Xin Lu, Changning Sun, Liqing Wang, and et al. 2022. "Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration" Bioengineering 9, no. 10: 504. https://doi.org/10.3390/bioengineering9100504
APA StyleNaghavi, S. A., Tamaddon, M., Marghoub, A., Wang, K., Babamiri, B. B., Hazeli, K., Xu, W., Lu, X., Sun, C., Wang, L., Moazen, M., Wang, L., Li, D., & Liu, C. (2022). Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration. Bioengineering, 9(10), 504. https://doi.org/10.3390/bioengineering9100504