1. Introduction
Cell-based products receiving market approval are increasing over the last years. The European Medicine Agency (EMA) has approved 14 medicinal products based on gene therapies, cell therapies or tissue engineering, also called advanced therapies for the European market [
1]. The U.S. Food and Drug Administration (FDA) has approved 17 cellular or gene therapy products [
2]. Compared to other pharmaceuticals such as small molecule drugs or biologics, the active pharmaceutical ingredient (API) of these cell-based therapies is living cells. An example of such a cell-based therapy is chimeric antigen receptor (CAR) T-cell therapy, where the patient is injected with human immune cells, which are modified to target cancer cells [
3]. Another type of cell-based therapy is skeletal tissue engineering, where a cell-based implant is used to regenerate cartilage or bone in the patient instead of using a prosthetic implant, which has the disadvantage that it will need to be replaced within 10–15 years [
4]. Besides being the active component of the final medicinal product, cells can also be used as a tool in the manufacturing process to produce the final product, such as extracellular vesicles [
5].
With the introduction of this promising group of cell-based or cell-derived products, the necessity to transform the emerging cell therapy and regenerative medicine industrial sector towards a BioPharma 4.0 sector is growing. This revolution should build on a strong IT infrastructure combined with automation technologies in order to use continuous data to steer and optimise bioprocesses in real-time without the need for human interaction [
6]. Closely monitoring and controlling the bioprocess tackles the challenge of irreproducible manufacturing processes that are often seen for (personalised) cell-based therapies. This bioprocess variability is inherent to donor variability, the time-varying characteristics of progenitor cells (such as phenotype) and the complexity of living systems [
7].
Progenitor cell expansion is a crucial process step whereby clinically relevant numbers are produced typically ranging between 5 × 10
7–10
8 [
8,
9]. Currently, progenitor cell expansion relies on fixed protocols which do not take into account the particularities of the cell type, donor characteristics or the batch, leading to suboptimal outcomes [
10]. In order to reduce this variability, the process has to remain within predefined boundaries during the whole production process, which is possible by actively adapting critical process parameters (CPP) during the cell expansion process, based on the characteristics and individual needs of a batch. The retuning of the process parameters should be done in a way that would enable the process to follow a predefined (reference) trajectory, providing optimal conditions for the cultured cells. Due to the inherent variability of cells and the time-varying dynamics of the process, modelling and controlling the cell growth is challenging [
11].
Active control of cell culture bioprocesses will also result in lower batch-to-batch variability. Without any monitoring or control of cell culture, there could be a high amount of batch rejections due to results of in-process or finished product testing falling out of the predefined boundaries of the validated process. These specifications are described in quality control documents approved by health authorities and are set to assure product quality and safety. The amount of “out of specifications” test results of two different commercial cell therapies was recently described in the biologics license application (BLA) submission of Kymriah
® and Yescarta
®. Novartis reported 7% and 9% manufacturing failures for Kymriah batches, whereas Kite reported 1% for Yescarta batches [
12]. Novartis disclosed that all out of specifications (OOS) results were caused by viability problems, resulting in final products with a viability lower than 80%. The challenge lies in the nature of cell products having an inherent variability and complexity.
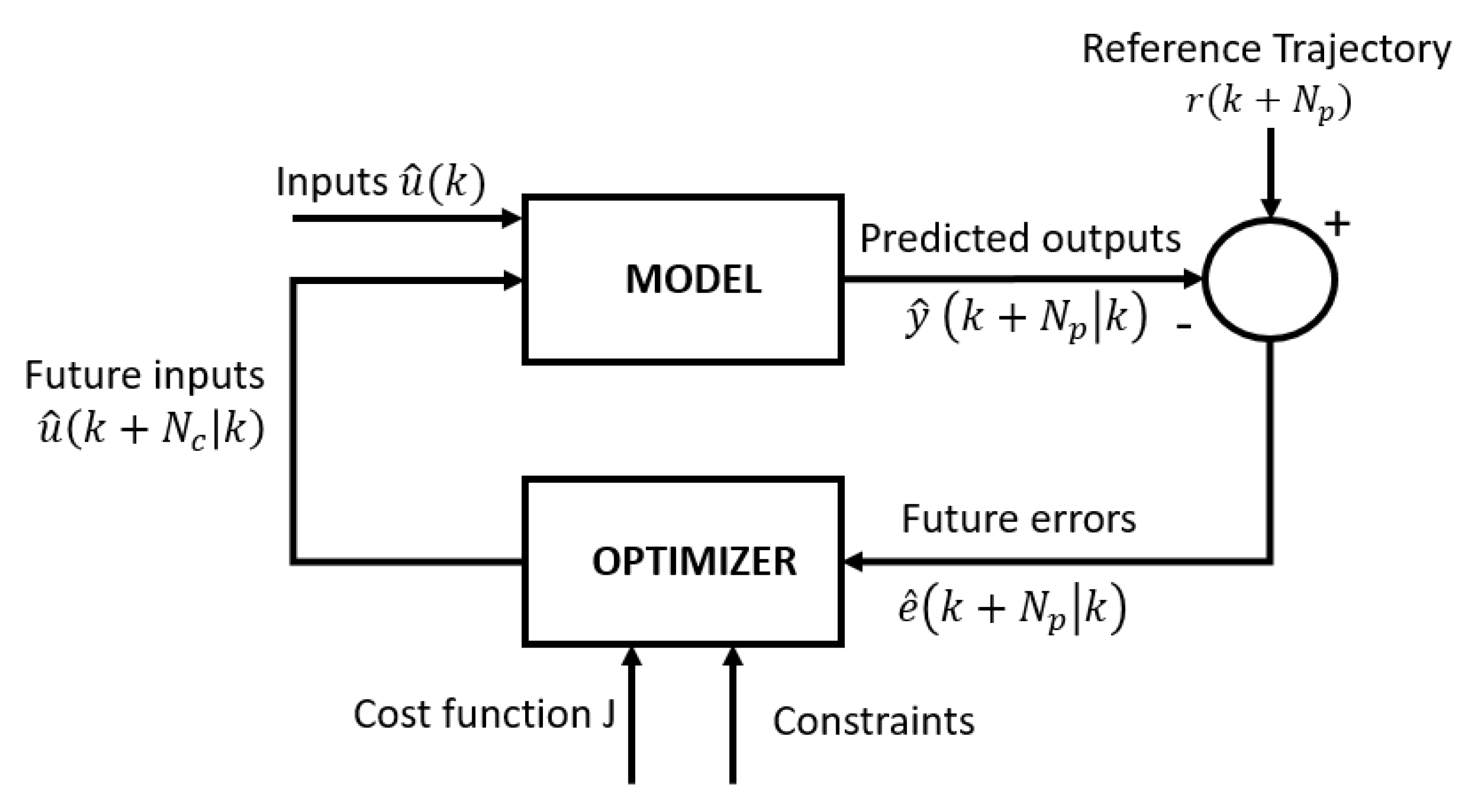
Therefore, in this work, a model-based predictive control (MPC) system is proposed as a potential solution to the aforementioned challenges of inherent variability and time-varying dynamics of the cell culture process [
13]. MPC exhibits several interesting features, such as intuitive concepts, easy tuning and the ability to control a range of simple and complex phenomena, including systems with time delays, non-minimum phase dynamics, dead times, multivariable cases and instability [
14]. While dealing with all these challenges, the MPC can easily incorporate constraints and tailor formulated control objectives [
12,
13]. Model predictive control offers several important advantages: (1) the process model captures the dynamic and static interactions between input, output and disturbance variables; (2) constraints on inputs and outputs are considered in a systematic manner in the cost function and (3) accurate model predictions can provide early warnings of potential problems [
13].
Several studies have investigated the benefits of controlling the environment of cell culture vessels such as dissolved oxygen tension (dO
2), temperature and CO
2 [
15]. Instead of using these standard physicochemical process parameters to control the bioprocess, this paper will develop a method to control the metabolic responses of the cells. This metabolic response is measured off-line and is used as an indication of the cell growth, which can only be measured at the end of the bioprocess of adherent cells. An interesting metabolic response to use as an indirect measure for cell growth in a high glucose medium is the cumulative lactate production of the cells over the culture period. Using lactate measures has the advantage, in an environment with excess amount of glucose, that the ratio between lactate production and glucose consumption is a known value (two) based on the anaerobic glycolysis pathway [
16]. In high glucose environments, measurements of glucose have a low sensitivity compared to lactate. Lactate concentrations are low in fresh medium and are produced by the cells, resulting in higher sensitivity and indication of whether or not cells are alive. Another advantage is controlling the pH, since this is related to the lactate concentration [
17,
18]. The control of this pH is important because an increase in extracellular acidosis, i.e., a value below 6.7, leads to a higher amount of apoptosis [
19,
20].
Furthermore, lowering the lactate concentration by replacing the media for 100%, 50% or 0% of the total working volume has been reported to have a significant effect on the cell growth [
15].
The aim of this paper is to describe a framework for controlling process parameters of the cell expansion process based on lactate measurements in combination with a model predictive control approach. As a proof of concept we used lactate measures, but depending on the considered application, the input and output could be chosen differently, taking into account specific process parameters and quality attributes. For example, in low glucose environments, it would be interesting to change the measurement to glucose. By controlling the process parameters, the cell growth can be directed towards a predefined reference trajectory. This research demonstrated the intended goal using experimental data in combination with control strategy simulations.
4. Discussion
Monitoring and controlling the cell growth is crucial when developing a large-scale reproducible cell culture process. However, there are currently no standardised methods to sample the amount of cells during a cell culture expansion in tissue flasks or hollow fibre bioreactors. Previous studies have therefore investigated the benefits of controlling the environment of the cell culture vessels using standard physicochemical process parameters [
15]. In addition, other studies developed potential soft sensors using the metabolic responses of the cells to control the process, mostly glucose concentration [
33,
34]. This work used this metabolic soft sensor concept by measuring the lactate concentration off-line and used it as an indication of the cell growth, which can otherwise only be measured at the end of the bioprocess.
Choosing the correct control strategy for this framework results in high accuracy between the experimental data and the simulated data. Many different control strategies have been explored in fermentation processes [
35], some for mammalian cells [
15,
17], and a few for human cells [
36]. These control strategies are built on either user experience, a process model or historical data [
35]. Each strategy has its own benefits and disadvantages. Using an approach based only on user experience has the advantage that it can be quickly applied to a new system without the need for historical data or a process model. However, these approaches, such as probing control [
37] or fuzzy control [
38], are running behind the action, because they act when the current state is not ideal, without an optimal strategy for the whole process. When there is a large amount of historical data, interesting approaches are artificial neural networks [
20,
21] or statistical process controls [
39]. However, for cell therapy bioprocesses this is mostly not the case, since these data are very process-specific and cannot be extrapolated for different cell types, batch sizes or in autologous applications, which are donor-specific. Mechanistic mathematical approaches encounter the same difficulty, because their specific sets of kinetic parameters have to be redefined for each specific process, requiring many specific data sets. A mathematical model, for example, one that describes the exponential growth of cells in combination with consumption nutrients and production waste products [
36], is useful for the prediction of an average control strategy for that cell type. However, the downside of these mathematical models is that they contain cell-lineage-specific kinetics parameters from literature and should be updated for every stage of that cell lineage, e.g., proliferation or differentiation [
40].
In cases where there is a process model available, the preferred choice would be to use model-based predictive control (MPC), because it can deal with non-linear dynamics, unpredictable disturbances and provides insight for the user [
35]. Other attempts at controlling bioprocesses using an MPC have been made. One of them consisted of controlling the glucose concentration to maintain more than a certain threshold of 11 mM in a 15 L fed-batch system [
34]. To achieve this, they used a non-linear model-based predictive control to adapt the feed rate based on a mechanistic mathematical model which describes the cell growth and metabolism. However, the main problem was the process–model mismatch, which is inherent to the variability of a bioprocess. They also compared an off-line measurement method with 12 h between samples to an on-line spectroscopy technique sampling every six minutes. The problem with on-line glucose methods was a high sample-to-noise ratio. Another study tried to avoid this problem of the high cost and noise of on-line glucose sensors by developing a soft sensor [
33]. This soft sensor uses cumulative oxygen transfer rates, calculated using several on-line measured variables. It defines the correlation between the on-line soft sensor and the real glucose concentration by comparing off-line measures of glucose every 24 h to recalculate the correlation.
What was still missing from most current control strategies is the combination of a model predictive control with an adaptive control strategy to avoid the process–model mismatch [
34]. Therefore, this paper uses the MPC approach and implements an adaptive prediction model. This allows the model to predict the next input to achieve the desired output based on all previous inputs and outputs, taking into account unpredictable disturbances or inherent batch variability in bioprocesses by updating the model parameters in real-time. The accuracy of the model fit when using the same model over different medium replacement conditions or different donors can even be below 50%. This is represented in
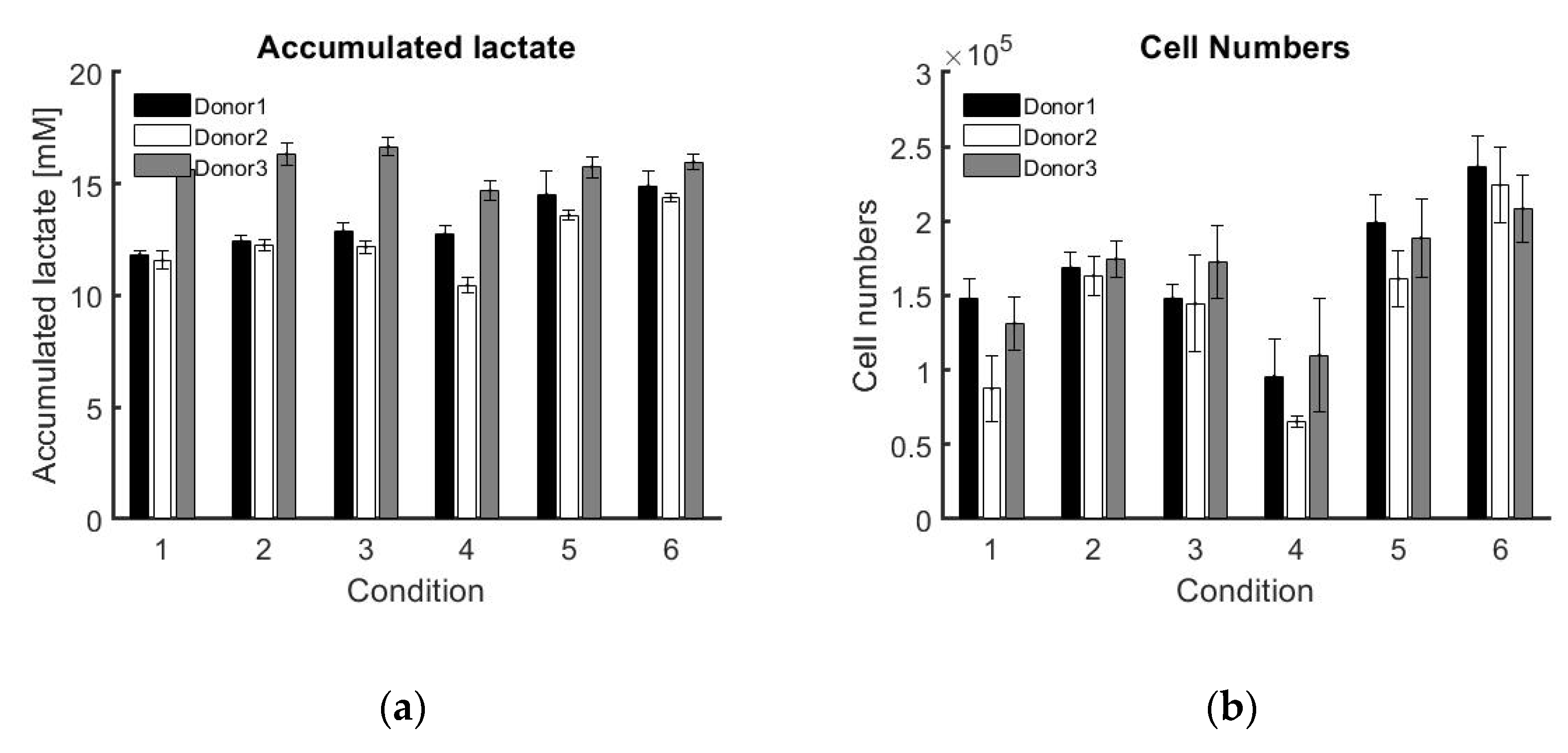
Table A1 where the model for donor 2 is fitted on data of donor 3. This points out the variability between donors and realisations. However, the potential of the approach developed in this work is that the model is estimated and adapted in real-time solely using data for that specific realisation/individual, and thus guarantees a personalised approach.
This work also uses the concept of a soft sensor by using another measurable variable (lactate concentration) to estimate a desired critical quality attribute of the bioprocess (cell number). The flexibility of the controller to react to disturbances as well as process variability is shown by successfully applying the controller to three different donors and six different control strategies in triplicate.
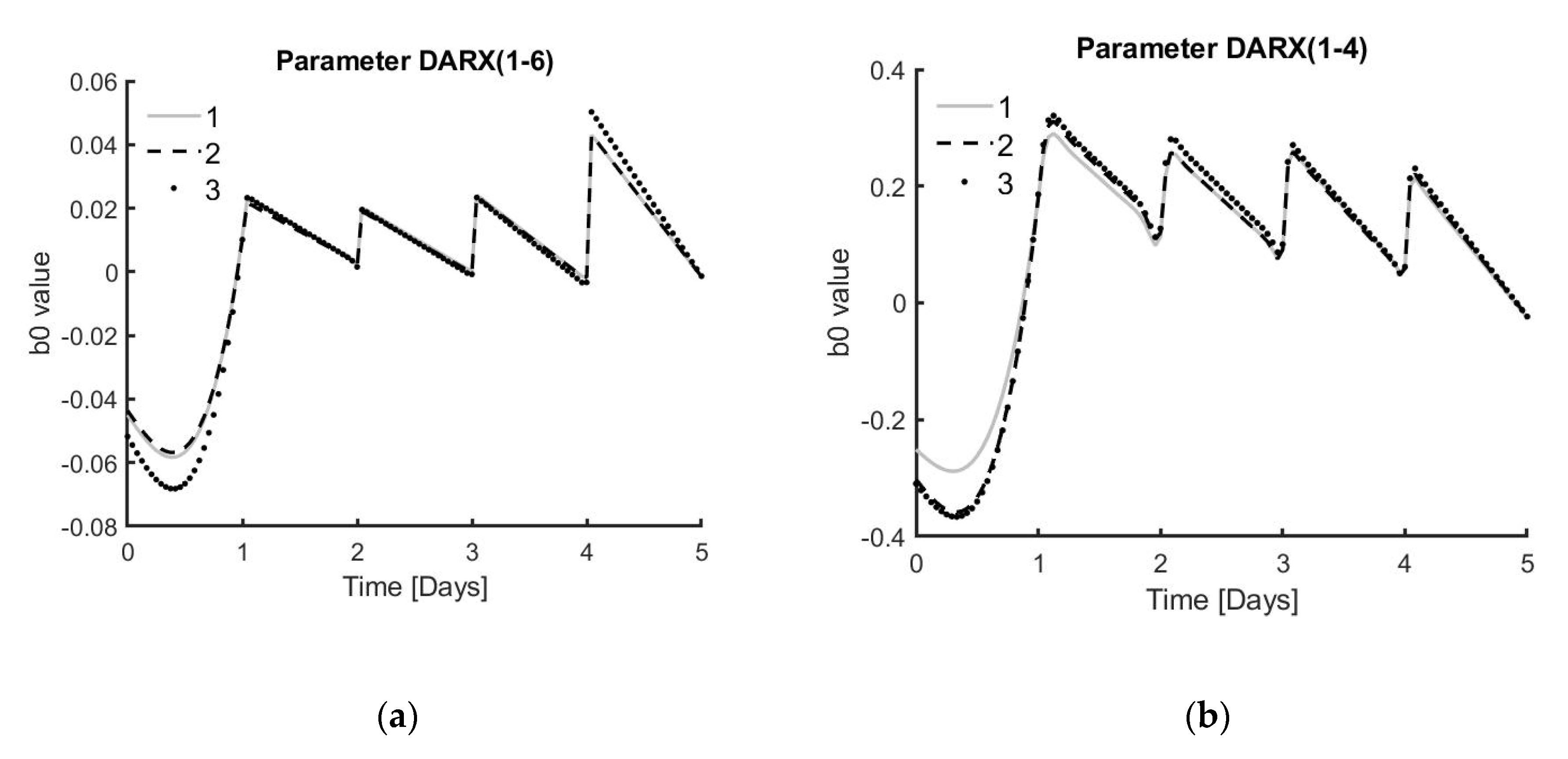
The next step for this work is to implement the controller in real-time to the system and re-evaluate the performance of the controller. The prediction model will be updated with every new data point received from the current experimental run. In future experiments, the idea is to start from the known model structure, which was found to be the best representation for that bioprocess. In this case, the model would be a DARX model with a fixed parameter and a variable over time. After gathering enough data points, depending on the measuring frequency, this could be one day. The model will be developed based on the parameters defined by the process at hand. After this initial data gathering period, the model and controller will be updated in real-time using only the data from the current experiment. Using only the fixed model structure from previous experiments would lead to better results compared to other modelling techniques, where the parameter values of previous experiments are also used without tuning them based on experiment-specific data. The MPC approach presented in this work, which uses the data of each specific realisation, results in a model that adapts well to the process at hand.
In addition, this MPC model could potentially address a case study based on giving the process just enough medium to reach a certain percentage of the maximum cell number at harvest. This maximum cell number is estimated when supplying the process with 100% medium every day. However, to practically perform such a controlled process, additional knowledge about the system is required, which can be gained by performing follow-up experiments. One strategy to consider for these experiments is to observe the values of the DARX model, which is continuously re-estimated with every new data point collected from the experiment at hand. Further analysis could lead to finding certain thresholds for this parameter that would result in reaching a predefined percentage of the maximum achievable cell number at harvest.
Another additional path to explore is to correlate the cumulative lactate produced back to the biomass growth, in order to use the measurements as a soft sensor and estimate the amount of biomass at each lactate sample time point. However, the relation between the number of cells and lactate produced can differ not only between cell types, but also between different medium replacement strategies. In cases where cells receive a very low amount of medium, cells could die due to nutrient and growth factor depletion. Another possibility which could lead to a change in the relation between the amount of cells and the amount of lactate produced is a metabolic alteration (a by-product of glycolysis) by the cells when the amount of replaced medium is low [
41]. Therefore, it would also be important in additional experiments to assess different quality attributes of the cells to check whether all process parameters are possible or if certain thresholds on medium replacement are required to avoid changing the quality and characteristics of the cells. The quality could be assessed with live/dead analysis, additional measures such as Lactate Dehydrogenase (LDH) and flow cytometry for MSC markers or the trilineage potential, determining the osteogenic, chondrogenic or adipogenic potential.
When these two steps of real time implementation and translation into cell numbers are combined, the controller could potentially solve case studies using an adaptive reference trajectory where a specific number of cells is required by a specific realistic time period using a minimal amount of medium. This approach is also capable of implementing different manipulated and controlled variables, in case new sensor techniques come onto the market.
Finally, instead of using well plates as a way to keep process costs low and experimental time short for a large amount of experiments, we envisage the use of such tools for suspension bioreactors where progenitor cell populations can be scaled-up for clinical production, allowing, at the same time, the capacity for real-time process adaptation [
10,
40].
5. Conclusions
The model predictive controller developed in this work is a generic algorithm which requires minimal effort to implement different process parameters and different responses of the system. This controller has the potential to be an inexpensive tool to minimise the costs and time of cell expansions in combination with assured product quality by design (QbD) [
42]. Using cumulative lactate concentrations as an output measurement of the controller has proven to be useful in this specific bioprocess setting, where high glucose DMEM was used. However, it is important, when applying this method to a different bioprocess, to first assess which output measurement and related process parameter would suit that specific bioprocess.
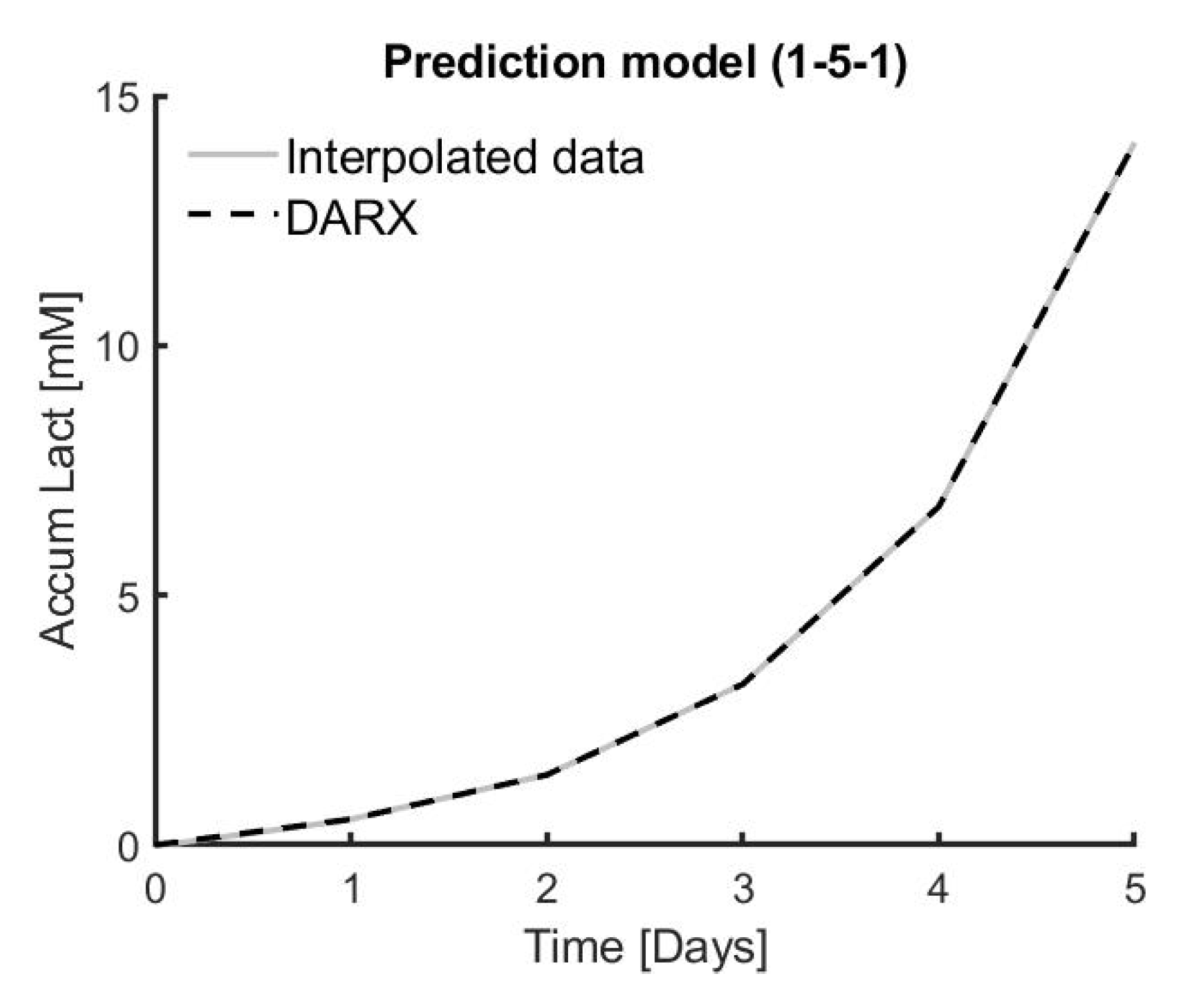
Six different combinations of medium replacement were tested on three different donors in triplicate in order to model the dynamical response of medium replacement on cell proliferation. This dynamic response is best modelled using a DARX prediction model, resulting in an overall high R2 of 99.80% ± 0.02% for the DARX model on the same experimental data. The process–model mismatch is also low when applying a model based on experimental data from one triplicate to experimental data from another one of the triplicates. The average fit for the triplicates in DARX models on all the triplicates of experimental data is 96.57% ± 3.26%.
Based on simulations, the model predictive controller designed in this work shows promising results to accurately predict the effect of medium replacement on cell growth. The medium change input suggested by the simulation has a 86.45% ± 0.78% accuracy compared to the real experimental data, whereas the accumulated lactate output has an accuracy of 98.64% ± 0.10% compared to the target experimental data.
The results in this work show that this lactate-based model predictive controller can be applied to different donors as well as different medium-replacement strategies. The parameters are estimated for each individual experimental run, resulting in a high accuracy fit between the simulated data and the experimental data. Using these individualised parameters is the main advantage compared to other control strategies, which are more focused on a suitable prediction for the average bioprocess [
14,
17].