Biomechanical Restoration Potential of Pentagalloyl Glucose after Arterial Extracellular Matrix Degeneration
Abstract
1. Introduction
2. Materials and Methods
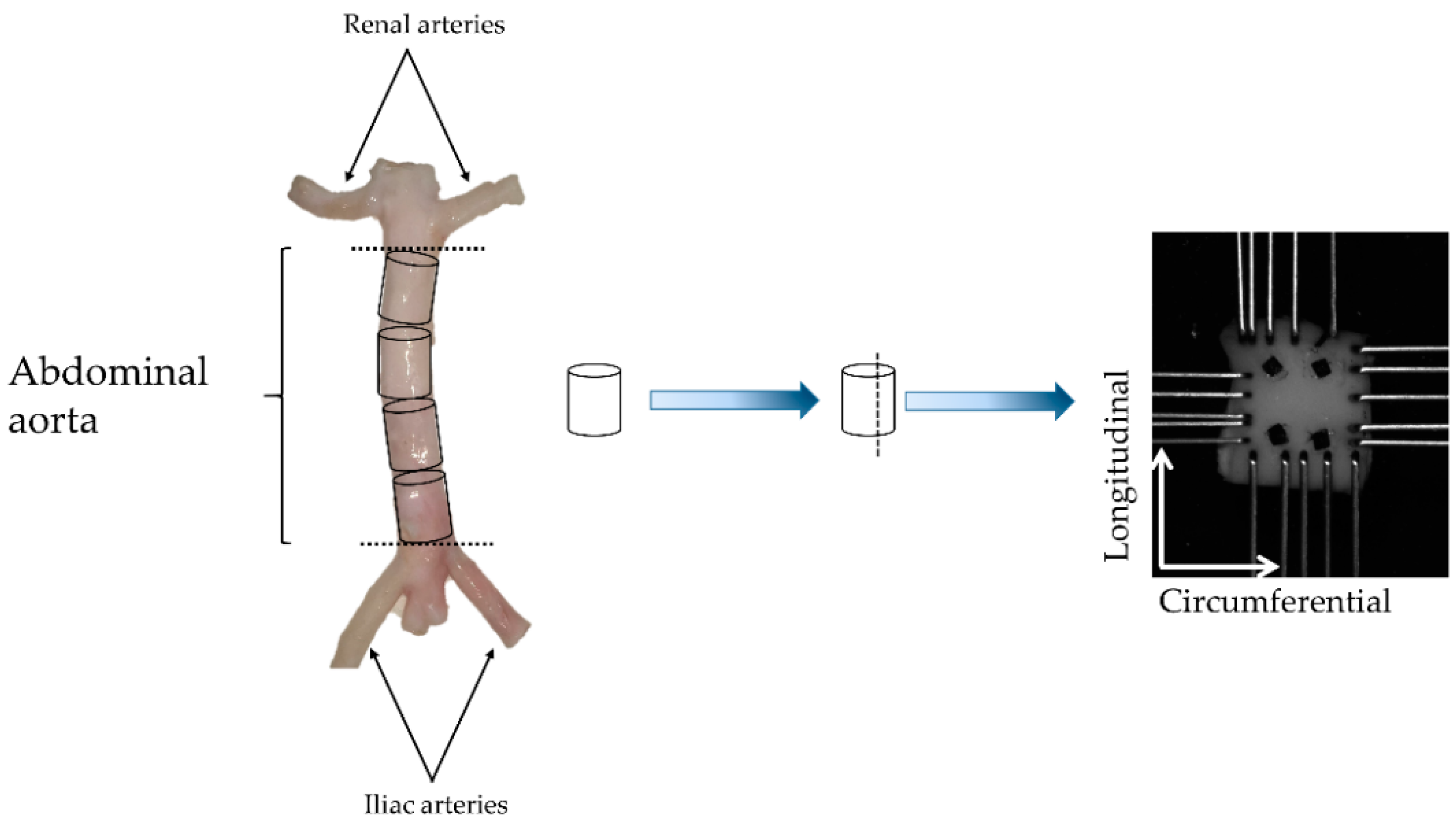
2.1. Biomechanical Testing
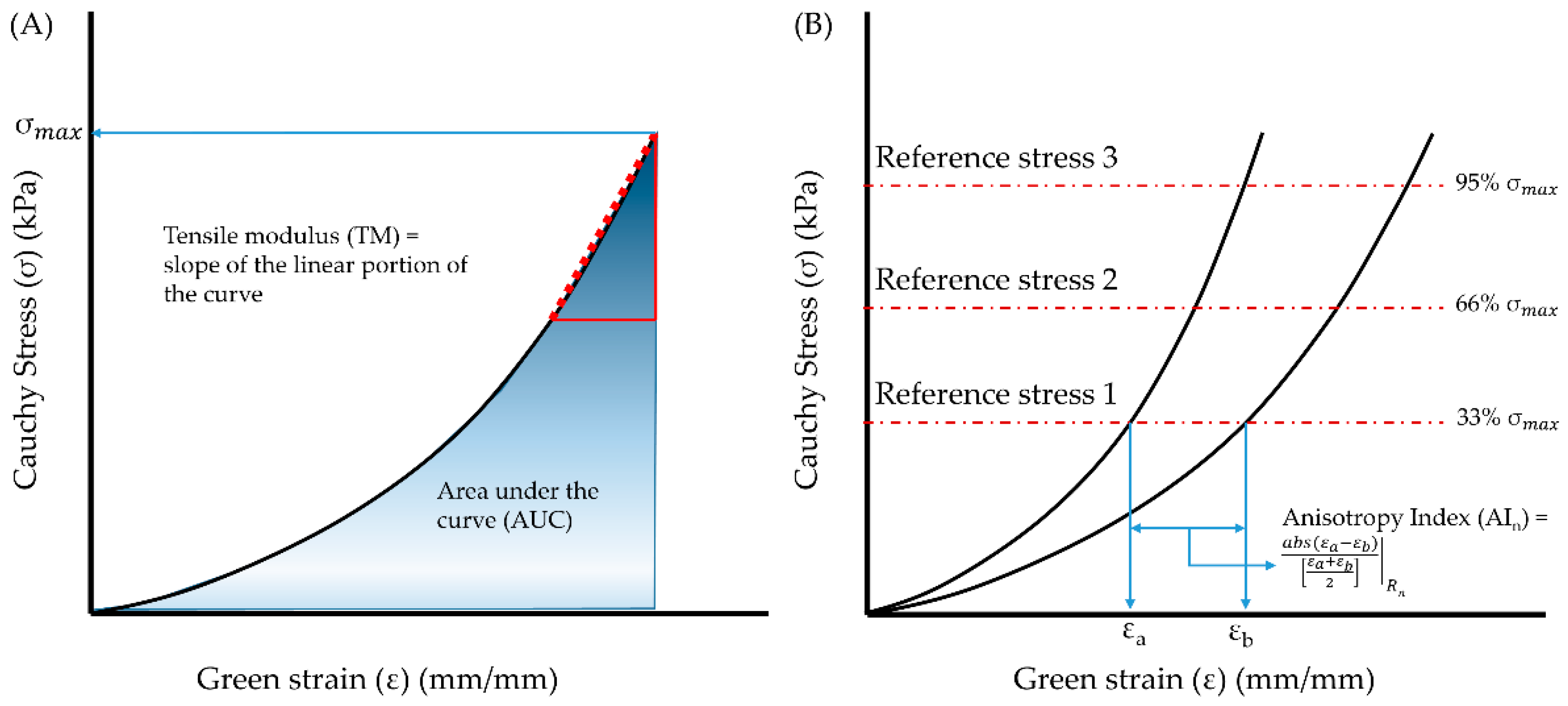
2.2. Data Analysis
2.3. Constitutive Modeling
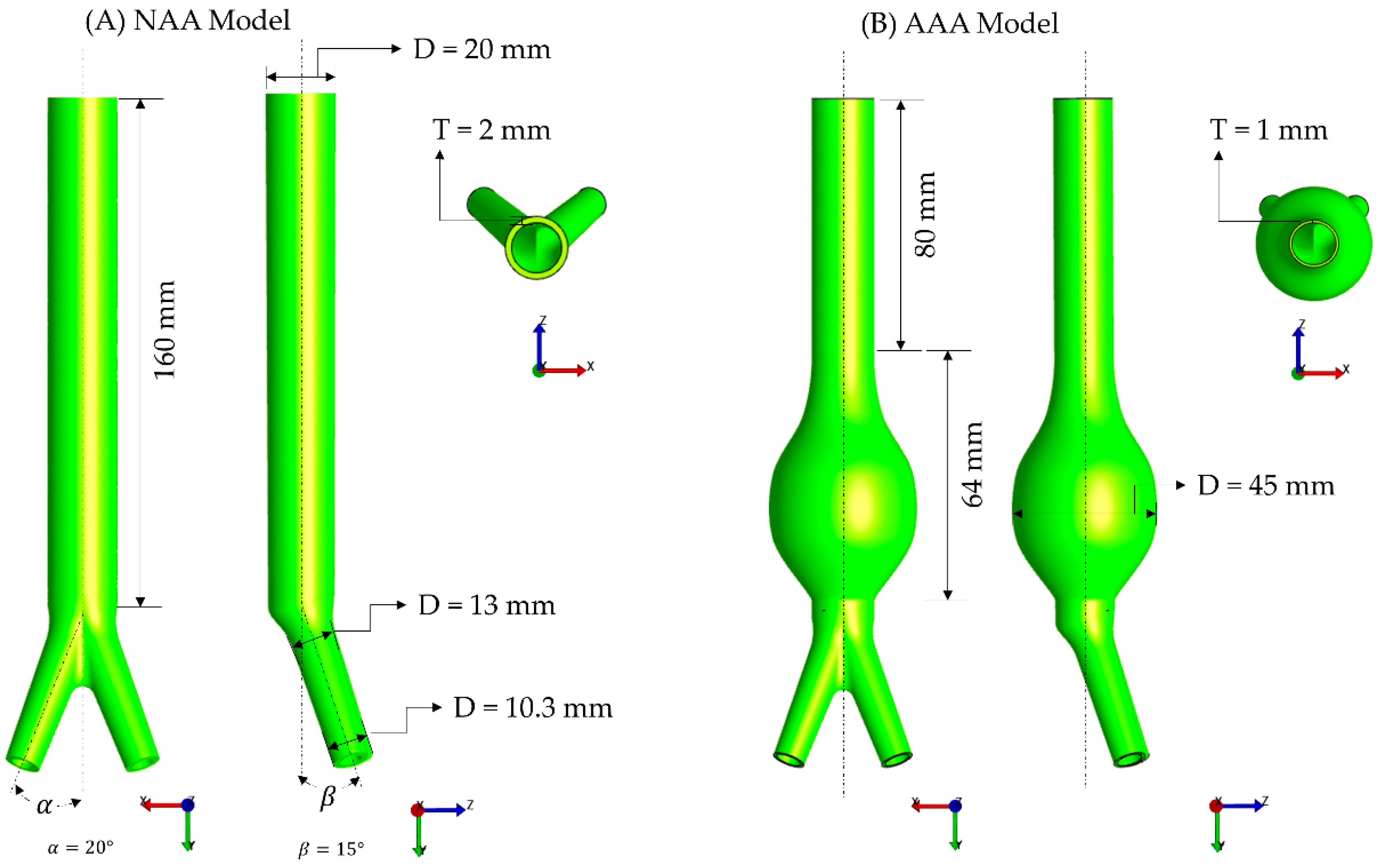
2.4. Finite Element Modeling
2.5. Statistical Analysis
3. Results
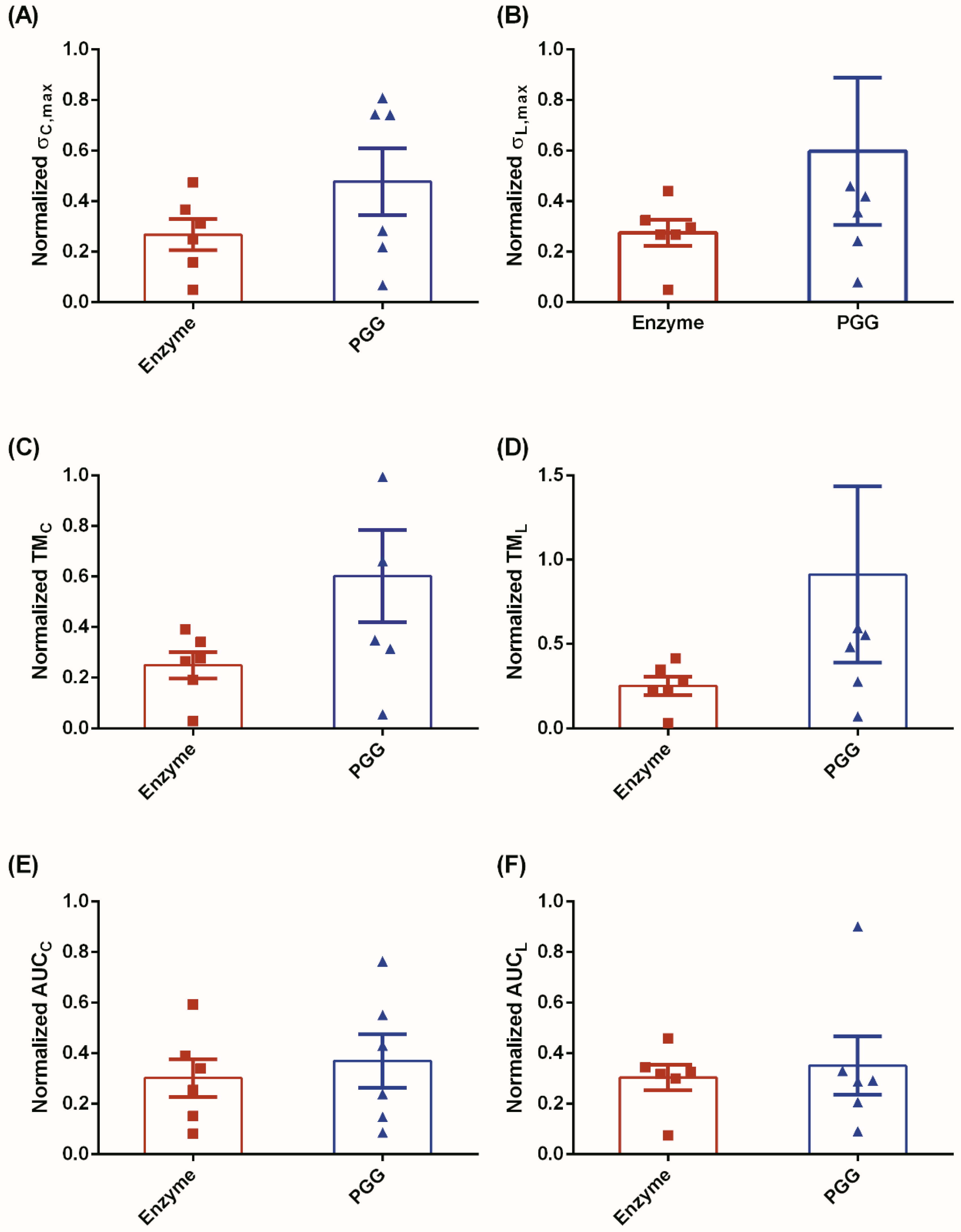
3.1. Biomechanical Testing
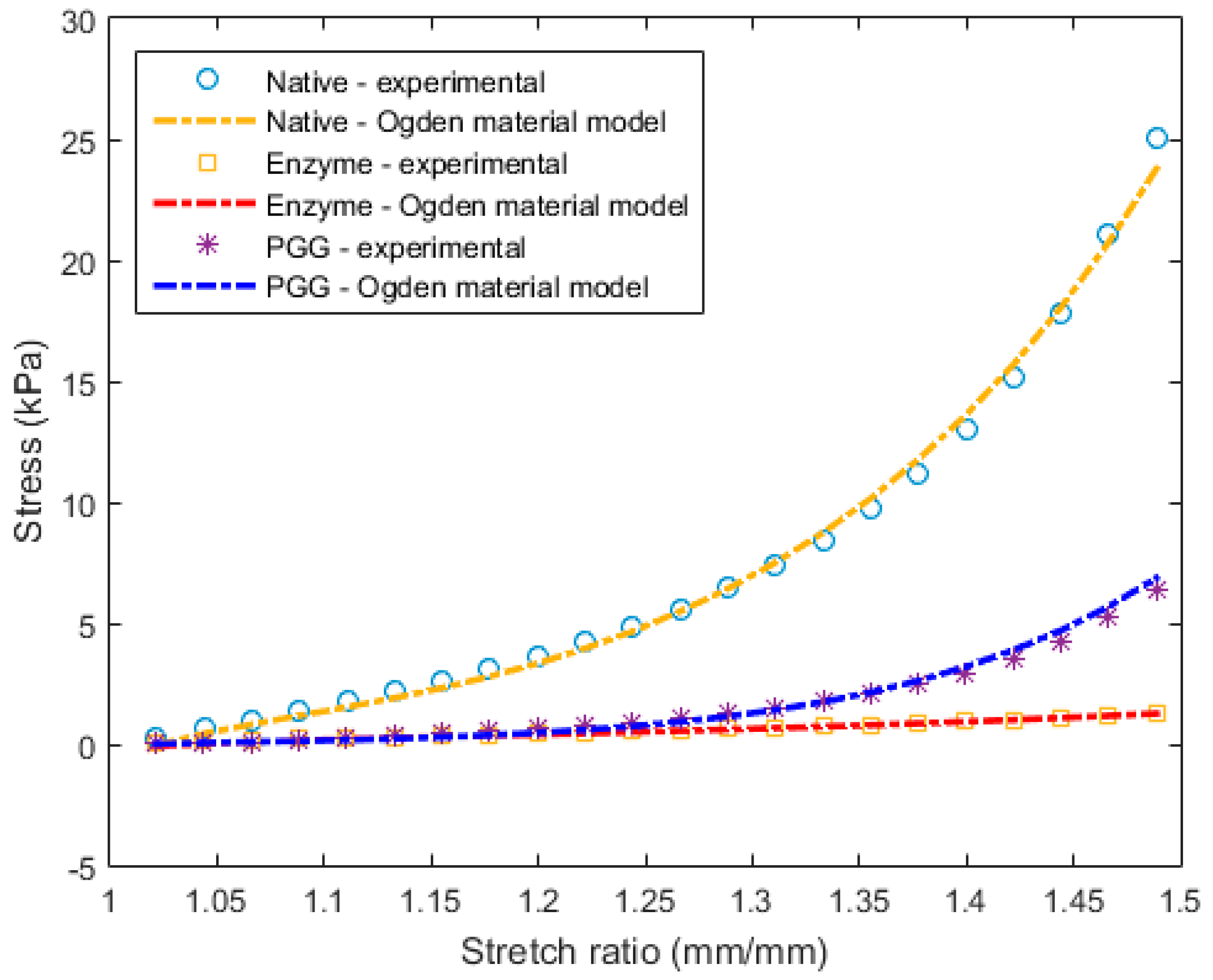
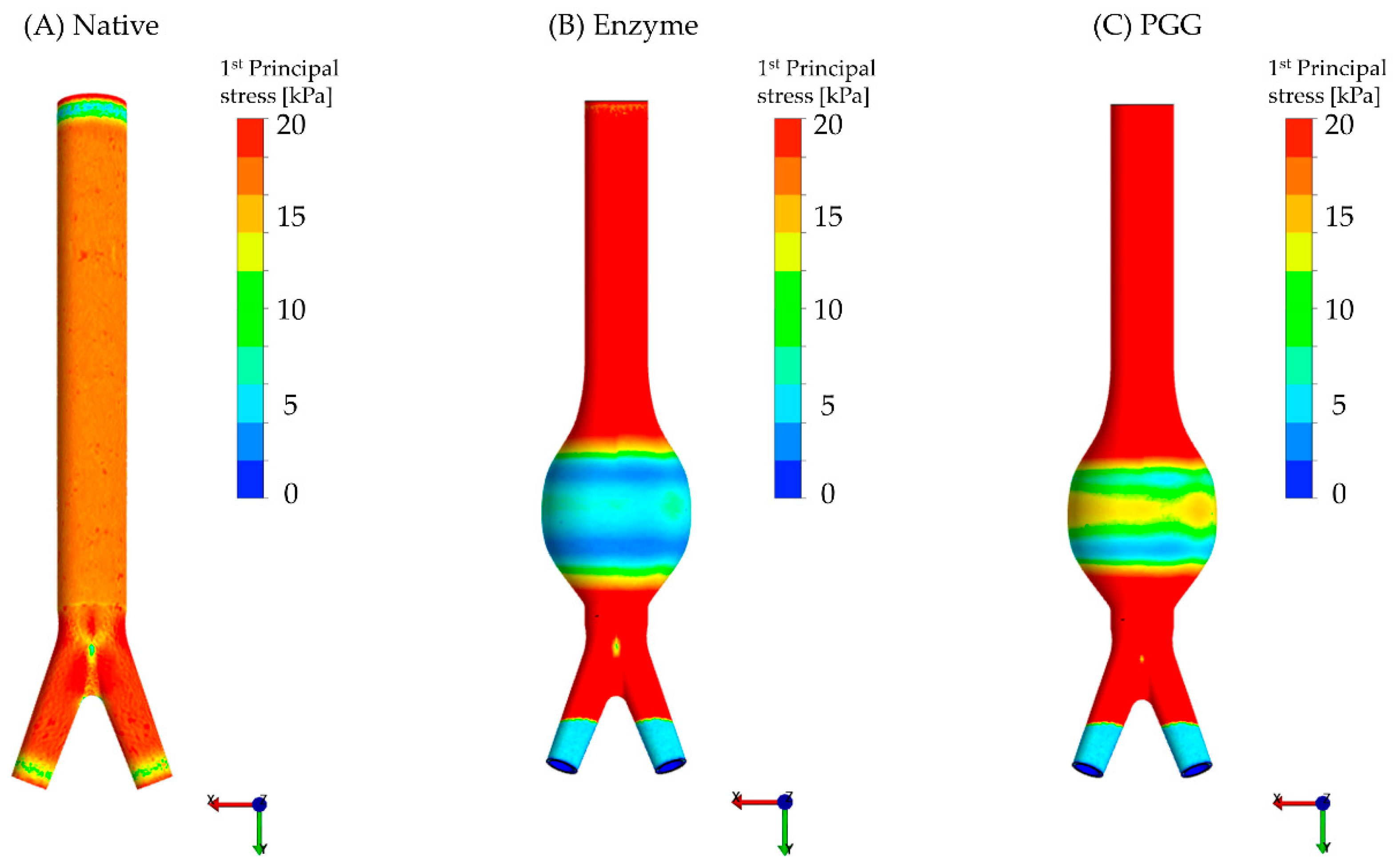
3.2. Constitutive Modeling and Finite Element Analyses
4. Discussion
4.1. Biomechanical Restoration Potential of PGG
4.2. Binding of PGG to Degenerated Arterial ECM
4.3. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Samarth, S.R.; Santanu, C.; Judy, S.; Christopher, B.W.; Satish, C.M.; Ender, A.F.; Jose, F.R. Biological, geometric and biomechanical factors influencing abdominal aortic aneurysm rupture risk: A comprehensive review. Recent Pat. Med. Imaging 2013, 3, 44–59. [Google Scholar]
- Raut, S.S.; Chandra, S.; Shum, J.; Finol, E.A. The role of geometric and biomechanical factors in abdominal aortic aneurysm rupture risk assessment. Ann. Biomed. Eng. 2013, 41, 1459–1477. [Google Scholar] [CrossRef] [PubMed]
- Golledge, J.; Norman, P.E.; Murphy, M.P.; Dalman, R.L. Challenges and opportunities in limiting abdominal aortic aneurysm growth. J. Vasc. Surg. 2017, 65, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Carmo, M.; Colombo, L.; Bruno, A.; Corsi, F.R.M.; Roncoroni, L.; Cuttin, M.S.; Radice, F.; Mussini, E.; Settembrini, P.G. Alteration of elastin, collagen and their cross-links in abdominal aortic aneurysms. Eur. J. Vasc. Endovasc. Surg. 2002, 23, 543–549. [Google Scholar] [CrossRef] [PubMed]
- White, J.V.; Haas, K.; Phillips, S.; Comerota, A.J. Adventitial elastolysis is a primary event in aneurysm formation. J. Vasc. Surg. 1993, 17, 371–380. [Google Scholar] [CrossRef]
- Cohen, J.R.; Mandell, C.; Chang, J.B.; Wise, L. Elastin metabolism of the infrarenal aorta. J. Vasc. Surg. 1988, 7, 210–214. [Google Scholar] [CrossRef][Green Version]
- Tanios, F.; Gee, M.W.; Pelisek, J.; Kehl, S.; Biehler, J.; Grabher-Meier, V.; Wall, W.A.; Eckstein, H.H.; Reeps, C. Interaction of biomechanics with extracellular matrix components in abdominal aortic aneurysm wall. Eur. J. Vasc. Endovasc. Surg. 2015, 50, 167–174. [Google Scholar] [CrossRef]
- Thompson, R.W.; Baxter, B.T. MMP inhibition in abdominal aortic aneurysms. Rationale for a prospective randomized clinical trial. Ann. N. Y. Acad. Sci. 1999, 878, 159–178. [Google Scholar] [CrossRef]
- Swedenborg, J.; Eriksson, P. The intraluminal thrombus as a source of proteolytic activity. Ann. N. Y. Acad. Sci. 2006, 1085, 133–138. [Google Scholar] [CrossRef]
- Vorp, D.A.; Lee, P.C.; Wang, D.H.; Makaroun, M.S.; Nemoto, E.M.; Ogawa, S.; Webster, M.W. Association of intraluminal thrombus in abdominal aortic aneurysm with local hypoxia and wall weakening. J. Vasc. Surg. 2001, 34, 291–299. [Google Scholar] [CrossRef]
- Roy, J.; Labruto, F.; Beckman, M.O.; Danielson, J.; Johansson, G.; Swedenborg, J. Bleeding into the intraluminal thrombus in abdominal aortic aneurysms is associated with rupture. J. Vasc. Surg. 2008, 48, 1108–1113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, L.; Kim, S.H.; Hagerman, A.E.; Lu, J. Anti-cancer, anti-diabetic and other pharmacologic and biological activities of penta-galloyl-glucose. Pharm. Res. 2009, 26, 2066–2080. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Himmeldirk, K.B.; Qian, Y.; Ren, Y.; Malki, A.; Chen, X. Biological and biomedical functions of Penta-O-galloyl-D-glucose and its derivatives. J. Nat. Med. 2014, 68, 465–472. [Google Scholar] [CrossRef] [PubMed]
- Patnaik, S.S.; Simionescu, D.T.; Goergen, C.J.; Hoyt, K.; Sirsi, S.; Finol, E.A. Pentagalloyl Glucose and Its Functional Role in Vascular Health: Biomechanics and Drug-Delivery Characteristics. Ann. Biomed. Eng. 2019, 47, 39–59. [Google Scholar] [CrossRef] [PubMed]
- Luck, G.; Liao, H.; Murray, N.J.; Grimmer, H.R.; Warminski, E.E.; Williamson, M.P.; Lilley, T.H.; Haslam, E. Polyphenols, astringency and proline-rich proteins. Phytochemistry 1994, 37, 357–371. [Google Scholar] [CrossRef]
- Dobreva, M.A.; Frazier, R.A.; Mueller-Harvey, I.; Clifton, L.A.; Gea, A.; Green, R.J. Binding of pentagalloyl glucose to two globular proteins occurs via multiple surface sites. Biomacromolecules 2011, 12, 710–715. [Google Scholar] [CrossRef] [PubMed]
- Isenburg, J.C.; Simionescu, D.T.; Starcher, B.C.; Vyavahare, N.R. Elastin stabilization for treatment of abdominal aortic aneurysms. Circulation 2007, 115, 1729–1737. [Google Scholar] [CrossRef] [PubMed]
- Nosoudi, N.; Chowdhury, A.; Siclari, S.; Karamched, S.; Parasaram, V.; Parrish, J.; Gerard, P.; Vyavahare, N. Reversal of Vascular Calcification and Aneurysms in a Rat Model Using Dual Targeted Therapy with EDTA- and PGG-Loaded Nanoparticles. Theranostics 2016, 6, 1975–1987. [Google Scholar] [CrossRef]
- Nosoudi, N.; Chowdhury, A.; Siclari, S.; Parasaram, V.; Karamched, S.; Vyavahare, N. Systemic Delivery of Nanoparticles Loaded with Pentagalloyl Glucose Protects Elastic Lamina and Prevents Abdominal Aortic Aneurysm in Rats. J. Cardiovasc. Transl. Res. 2016, 9, 445–455. [Google Scholar] [CrossRef] [PubMed]
- Sinha, A.; Nosoudi, N.; Vyavahare, N. Elasto-regenerative properties of polyphenols. Biochem. Biophys. Res. Commun. 2014, 444, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Thirugnanasambandam, M.; Simionescu, D.T.; Escobar, P.G.; Sprague, E.; Goins, B.; Clarke, G.D.; Han, H.-C.; Amezcua, K.L.; Adeyinka, O.R.; Goergen, C.J.; et al. The Effect of Pentagalloyl Glucose on the Wall Mechanics and Inflammatory Activity of Rat Abdominal Aortic Aneurysms. J. Biomech. Eng. 2018, 140, 084502. [Google Scholar] [CrossRef] [PubMed]
- Kloster, B.O.; Lund, L.; Lindholt, J.S. Inhibition of early AAA formation by aortic intraluminal pentagalloyl glucose (PGG) infusion in a novel porcine AAA model. Ann. Med. Surg. 2016, 7, 65–70. [Google Scholar] [CrossRef] [PubMed]
- Hynecek, R.L.; DeRubertis, B.G.; Trocciola, S.M.; Zhang, H.; Prince, M.R.; Ennis, T.L.; Kent, K.C.; Faries, P.L. The creation of an infrarenal aneurysm within the native abdominal aorta of swine. Surgery 2007, 142, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Sadek, M.; Hynecek, R.L.; Goldenberg, S.; Kent, K.C.; Marin, M.L.; Faries, P.L. Gene expression analysis of a porcine native abdominal aortic aneurysm model. Surgery 2008, 144, 252–258. [Google Scholar] [CrossRef] [PubMed]
- Czerski, A.; Bujok, J.; Gnus, J.; Hauzer, W.; Ratajczak, K.; Nowak, M.; Janeczek, M.; Zawadzki, W.; Witkiewicz, W.; Rusiecka, A. Experimental methods of abdominal aortic aneurysm creation in swine as a large animal model. J. Physiol. Pharmacol. 2013, 64, 185–192. [Google Scholar] [PubMed]
- Hauzer, W.; Czerski, A.; Zawadzki, W.; Gnus, J.; Ratajczak, K.; Nowak, M.; Janeczek, M.; Witkiewicz, W.; Niespielak, P. The effects of aneurysm repair using an aortic prosthesis on the electrical parameters of the muscular layer of the abdominal aorta. J. Physiol. Pharmacol. 2014, 65, 853–858. [Google Scholar] [PubMed]
- Lysgaard Poulsen, J.; Stubbe, J.; Lindholt, J.S. Animal Models Used to Explore Abdominal Aortic Aneurysms: A Systematic Review. Eur. J. Vasc. Endovasc. Surg. 2016, 52, 487–499. [Google Scholar] [CrossRef]
- Kratzberg, J.A.; Walker, P.J.; Rikkers, E.; Raghavan, M.L. The effect of proteolytic treatment on plastic deformation of porcine aortic tissue. J. Mech. Behav. Biomed. Mater. 2009, 2, 65–72. [Google Scholar] [CrossRef]
- Chow, M.J.; Choi, M.; Yun, S.H.; Zhang, Y. The effect of static stretch on elastin degradation in arteries. PLoS ONE 2013, 8, e81951. [Google Scholar] [CrossRef]
- Gundiah, N.; Babu, A.R.; Pruitt, L.A. Effects of elastase and collagenase on the nonlinearity and anisotropy of porcine aorta. Physiol. Meas. 2013, 34, 1657–1673. [Google Scholar] [CrossRef]
- Riches, K.; Angelini, T.G.; Mudhar, G.S.; Kaye, J.; Clark, E.; Bailey, M.A.; Sohrabi, S.; Korossis, S.; Walker, P.G.; Scott, D.J.; et al. Exploring smooth muscle phenotype and function in a bioreactor model of abdominal aortic aneurysm. J. Transl. Med. 2013, 11, 208. [Google Scholar] [CrossRef] [PubMed]
- Zeinali-Davarani, S.; Chow, M.J.; Turcotte, R.; Zhang, Y. Characterization of biaxial mechanical behavior of porcine aorta under gradual elastin degradation. Ann. Biomed. Eng. 2013, 41, 1528–1538. [Google Scholar] [CrossRef] [PubMed]
- Schriefl, A.J.; Schmidt, T.; Balzani, D.; Sommer, G.; Holzapfel, G.A. Selective enzymatic removal of elastin and collagen from human abdominal aortas: Uniaxial mechanical response and constitutive modeling. Acta Biomater. 2015, 17, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Vande Geest, J.P.; Sacks, M.S.; Vorp, D.A. The effects of aneurysm on the biaxial mechanical behavior of human abdominal aorta. J. Biomech. 2006, 39, 1324–1334. [Google Scholar] [CrossRef] [PubMed]
- Matthews, P.B.; Azadani, A.N.; Jhun, C.S.; Ge, L.; Guy, T.S.; Guccione, J.M.; Tseng, E.E. Comparison of porcine pulmonary and aortic root material properties. Ann. Thorac. Surg. 2010, 89, 1981–1988. [Google Scholar] [CrossRef] [PubMed]
- O’Leary, S.A.; Kavanagh, E.G.; Grace, P.A.; McGloughlin, T.M.; Doyle, B.J. The biaxial mechanical behaviour of abdominal aortic aneurysm intraluminal thrombus: Classification of morphology and the determination of layer and region specific properties. J. Biomech. 2014, 47, 1430–1437. [Google Scholar] [CrossRef] [PubMed]
- Vande Geest, J.P.; Sacks, M.S.; Vorp, D.A. Age dependency of the biaxial biomechanical behavior of human abdominal aorta. J. Biomech. Eng. 2004, 126, 815–822. [Google Scholar] [CrossRef]
- Macrae, R.A.; Miller, K.; Doyle, B.J. Methods in Mechanical Testing of Arterial Tissue: A Review. Strain 2016, 52, 380–399. [Google Scholar] [CrossRef]
- Lee, J.M.; Ku, M.; Haberer, S.A. The bovine pericardial xenograft: III. Effect of uniaxial and sequential biaxial stress during fixation on the tensile viscoelastic properties of bovine pericardium. J. Biomed. Mater. Res. 1989, 23, 491–506. [Google Scholar] [CrossRef]
- Langdon, S.E.; Chernecky, R.; Pereira, C.A.; Abdulla, D.; Lee, J.M. Biaxial mechanical/structural effects of equibiaxial strain during crosslinking of bovine pericardial xenograft materials. Biomaterials 1999, 20, 137–153. [Google Scholar] [CrossRef]
- Ogden, R.W. Large Deformation Isotropic Elasticity: On the Correlation of Theory and Experiment for Compressible Rubberlike Solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1972, 328, 567–583. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Callanan, A.; Morris, L.G.; McGloughlin, T.M. Finite element and photoelastic modelling of an abdominal aortic aneurysm: A comparative study. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Azar, D.; Ohadi, D.; Rachev, A.; Eberth, J.F.; Uline, M.J.; Shazly, T. Mechanical and geometrical determinants of wall stress in abdominal aortic aneurysms: A computational study. PLoS ONE 2018, 13, e0192032. [Google Scholar] [CrossRef] [PubMed]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Si, H. TetGen, a Delaunay-Based Quality Tetrahedral Mesh Generator. ACM Trans. Math. Softw. 2015, 41, 1–36. [Google Scholar] [CrossRef]
- Maas, S.A.; Ellis, B.J.; Ateshian, G.A.; Weiss, J.A. FEBio: Finite elements for biomechanics. J. Biomech. Eng. 2012, 134, 011005. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, S.S.; Gutierrez, C.A.; Thirugnanasambandam, M.; De Oliveira, V.; Muluk, S.C.; Eskandari, M.K.; Finol, E.A. The Association Between Geometry and Wall Stress in Emergently Repaired Abdominal Aortic Aneurysms. Ann. Biomed. Eng. 2017, 45, 1908–1916. [Google Scholar] [CrossRef] [PubMed]
- Isenburg, J.C.; Karamchandani, N.V.; Simionescu, D.T.; Vyavahare, N.R. Structural requirements for stabilization of vascular elastin by polyphenolic tannins. Biomaterials 2006, 27, 3645–3651. [Google Scholar] [CrossRef] [PubMed]
- Charlton, A.J.; Baxter, N.J.; Khan, M.L.; Moir, A.J.; Haslam, E.; Davies, A.P.; Williamson, M.P. Polyphenol/peptide binding and precipitation. J. Agric. Food Chem. 2002, 50, 1593–1601. [Google Scholar] [CrossRef] [PubMed]
- Chow, M.J.; Mondonedo, J.R.; Johnson, V.M.; Zhang, Y. Progressive structural and biomechanical changes in elastin degraded aorta. Biomech. Model. Mechanobiol. 2013, 12, 361–372. [Google Scholar] [CrossRef]
- Baxter, N.J.; Lilley, T.H.; Haslam, E.; Williamson, M.P. Multiple interactions between polyphenols and a salivary proline-rich protein repeat result in complexation and precipitation. Biochemistry 1997, 36, 5566–5577. [Google Scholar] [CrossRef] [PubMed]
- Bennick, A. Interaction of plant polyphenols with salivary proteins. Crit. Rev. Oral Biol. Med. 2002, 13, 184–196. [Google Scholar] [CrossRef] [PubMed]
- Zulliger, M.A.; Stergiopulos, N. Structural strain energy function applied to the ageing of the human aorta. J. Biomech. 2007, 40, 3061–3069. [Google Scholar] [CrossRef] [PubMed]
- Owen, B.; Bojdo, N.; Jivkov, A.; Keavney, B.; Revell, A. Structural modelling of the cardiovascular system. Biomech. Model. Mechanobiol. 2018, 17, 1217–1242. [Google Scholar] [CrossRef] [PubMed]
- Niestrawska, J.A.; Ch Haspinger, D.; Holzapfel, G.A. The influence of fiber dispersion on the mechanical response of aortic tissues in health and disease: A computational study. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 99–112. [Google Scholar] [CrossRef] [PubMed]
- Kang, D.G.; Moon, M.K.; Choi, D.H.; Lee, J.K.; Kwon, T.O.; Lee, H.S. Vasodilatory and anti-inflammatory effects of the 1,2,3,4,6-penta-O-galloyl-beta-D-glucose (PGG) via a nitric oxide-cGMP pathway. Eur. J. Pharmacol. 2005, 524, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Mendonca, P.; Taka, E.; Bauer, D.; Cobourne-Duval, M.; Soliman, K.F. The attenuating effects of 1,2,3,4,6 penta-O-galloyl-beta-d-glucose on inflammatory cytokines release from activated BV-2 microglial cells. J. Neuroimmunol. 2017, 305, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Mendonca, P.; Taka, E.; Bauer, D.; Reams, R.R.; Soliman, K.F.A. The attenuating effects of 1,2,3,4,6 penta-O-galloyl-β-d-glucose on pro-inflammatory responses of LPS/IFNγ-activated BV-2 microglial cells through NFƙB and MAPK signaling pathways. J. Neuroimmunol. 2018, 324, 43–53. [Google Scholar] [CrossRef]
- Lu, Y.; Deng, Y.; Liu, W.; Jiang, M.; Bai, G. Searching for calcium antagonists for hypertension disease therapy from Moutan Cortex, using bioactivity integrated UHPLC-QTOF-MS. Phytochem. Anal. 2019, 30, 456–463. [Google Scholar] [CrossRef]
- Adolph, R.; Vorp, D.A.; Steed, D.L.; Webster, M.W.; Kameneva, M.V.; Watkins, S.C. Cellular content and permeability of intraluminal thrombus in abdominal aortic aneurysm. J. Vasc. Surg. 1997, 25, 916–926. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. On planar biaxial tests for anisotropic nonlinearly elastic solids. A continuum mechanical framework. Math. Mech. Solids 2008, 14, 474–489. [Google Scholar] [CrossRef]
- Sommer, G.; Haspinger, D.; Andra, M.; Sacherer, M.; Viertler, C.; Regitnig, P.; Holzapfel, G.A. Quantification of Shear Deformations and Corresponding Stresses in the Biaxially Tested Human Myocardium. Ann. Biomed. Eng. 2015, 43, 2334–2348. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Feng, Y.; Lee, C.H.; Billiar, K.L.; Sacks, M.S. A generalized method for the analysis of planar biaxial mechanical data using tethered testing configurations. J. Biomech. Eng. 2015, 137, 064501. [Google Scholar] [CrossRef] [PubMed]
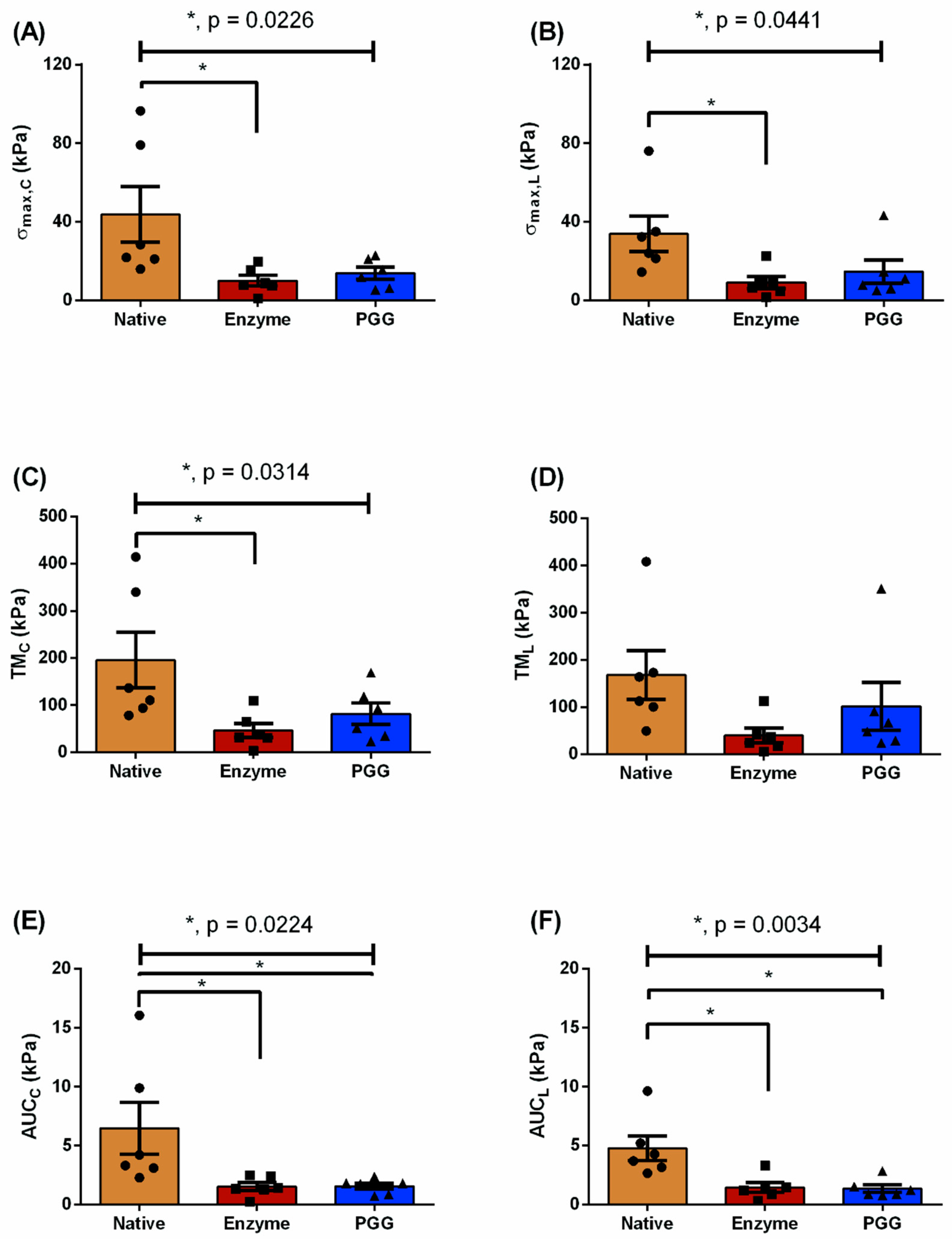
| Testing Protocol | Biomechanical Parameters (kPa) | N | E | P | p-Value |
|---|---|---|---|---|---|
| = 1:1 | 43.78 ± 14.18 | 10.03 ± 2.66 | 13.85 ± 3.02 | 0.0226 a | |
| 33.89 ± 8.98 | 9.04 ± 2.97 | 14.69 ± 5.88 | 0.0441 a | ||
| TMC | 195.6 ± 58.72 | 46.51 ± 15.04 | 81.8 ± 22.76 | 0.0314 a | |
| TML | 168.0 ± 51.53 | 39.75 ± 15.56 | 101.6 ± 50.87 | n.s. | |
| AUCC | 6.48 ± 2.22 | 1.55 ± 0.34 | 1.56 ± 0.26 | 0.0224 a,b | |
| AUCL | 4.77 ± 1.04 | 1.45 ± 0.42 | 1.35 ± 0.32 | 0.0034 a,b | |
| = 0.5:1 | 7.6 ± 1.35 | 2.65 ± 0.54 | 1.51 ± 0.14 | 0.0004 a,b | |
| 18.66 ± 3.78 | 5.71 ± 1.92 | 4.05 ± 1.04 | 0.0013 a,b | ||
| TMC | 67.46 ± 12.94 | 22.19 ± 5.63 | 16.86 ± 2.73 | 0.0011 a,b | |
| TML | 101.9 ± 30.18 | 26.11 ± 10.26 | 31.61 ± 12.91 | 0.0273 a | |
| AUCC | 0.63 ± 0.12 | 0.24 ± 0.04 | 0.1 ± 0.01 | 0.0006 a,b | |
| AUCL | 2.84 ± 0.41 | 0.93 ± 0.3 | 0.48 ± 0.07 | <0.0001 a,b | |
| = 1:0.5 | 19.84 ± 5.14 | 5.84 ± 1.44 | 3.1 ± 0.73 | 0.0034 a,b | |
| 6.99 ± 2.71 | 2.28 ± 1.299 | 0.8 ± 0.08 | <0.0001 a,b | ||
| TMC | 125.3 ± 38.93 | 30.08 ± 9.42 | 22.37 ± 6.28 | 0.0102 a,b | |
| TML | 60.95 ± 12.84 | 18.15 ± 4.11 | 7.6 ± 1.38 | 0.0007 a,b | |
| AUCC | 2.64 ± 0.57 | 0.91 ± 0.18 | 0.37 ± 0.09 | 0.011 a,b | |
| AUCL | 0.59 ± 0.08 | 0.19 ± 0.05 | 0.06 ± 0.007 | <0.0001 a,b |
| Group | (kPa) | (−) |
|---|---|---|
| N | 0.96 ± 0.025 | 10.06 ± 0.38 |
| E | 0.37 ± 0.06 | 8.53 ± 0.67 |
| P | 0.09 ± 0.03 | 13.57 ± 0.87 |
| Group | Maximum Wall Stress (kPa) | Average Wall Stress (kPa) | Minimum Wall Stress (kPa) |
|---|---|---|---|
| N | 35 ± 4.0 | 26 ± 4.0 | 20 ± 4.0 |
| E | 13 ± 1.0 | 8.0 ± 0.4 | 3.0 ± 0.2 |
| P | 16 ± 0.5 | 10 ± 0.5 | 5.0 ± 0.3 |
| p-value | 0.0002 ab | 0.0003 ab | 0.0002 ab |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patnaik, S.S.; Piskin, S.; Pillalamarri, N.R.; Romero, G.; Escobar, G.P.; Sprague, E.; Finol, E.A. Biomechanical Restoration Potential of Pentagalloyl Glucose after Arterial Extracellular Matrix Degeneration. Bioengineering 2019, 6, 58. https://doi.org/10.3390/bioengineering6030058
Patnaik SS, Piskin S, Pillalamarri NR, Romero G, Escobar GP, Sprague E, Finol EA. Biomechanical Restoration Potential of Pentagalloyl Glucose after Arterial Extracellular Matrix Degeneration. Bioengineering. 2019; 6(3):58. https://doi.org/10.3390/bioengineering6030058
Chicago/Turabian StylePatnaik, Sourav S., Senol Piskin, Narasimha Rao Pillalamarri, Gabriela Romero, G. Patricia Escobar, Eugene Sprague, and Ender A. Finol. 2019. "Biomechanical Restoration Potential of Pentagalloyl Glucose after Arterial Extracellular Matrix Degeneration" Bioengineering 6, no. 3: 58. https://doi.org/10.3390/bioengineering6030058
APA StylePatnaik, S. S., Piskin, S., Pillalamarri, N. R., Romero, G., Escobar, G. P., Sprague, E., & Finol, E. A. (2019). Biomechanical Restoration Potential of Pentagalloyl Glucose after Arterial Extracellular Matrix Degeneration. Bioengineering, 6(3), 58. https://doi.org/10.3390/bioengineering6030058







