Mechanics of the Tricuspid Valve—From Clinical Diagnosis/Treatment, In-Vivo and In-Vitro Investigations, to Patient-Specific Biomechanical Modeling
Abstract
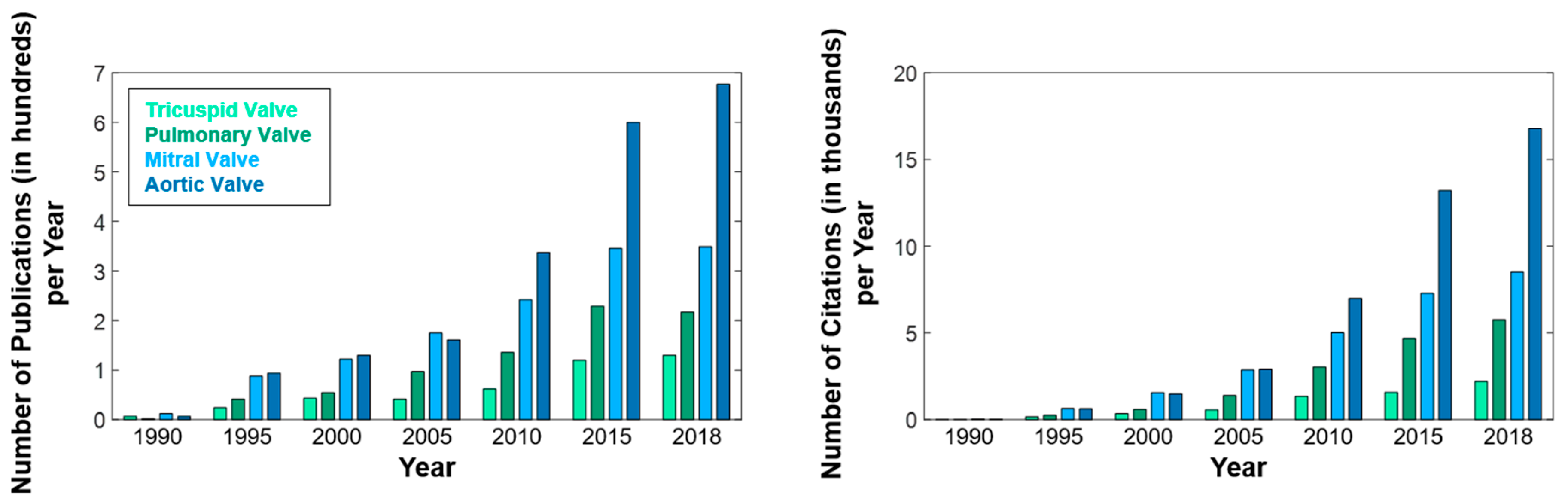
1. Introduction
2. Functional Tricuspid Regurgitation: Diagnosis and Treatment Options
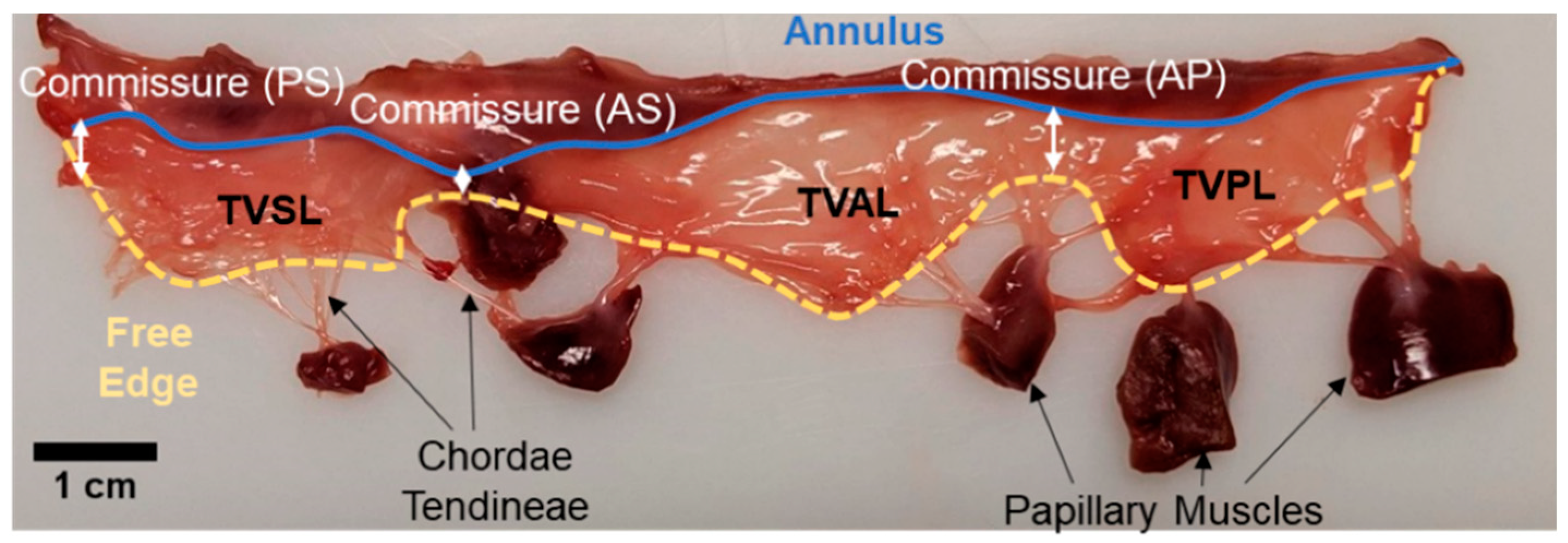
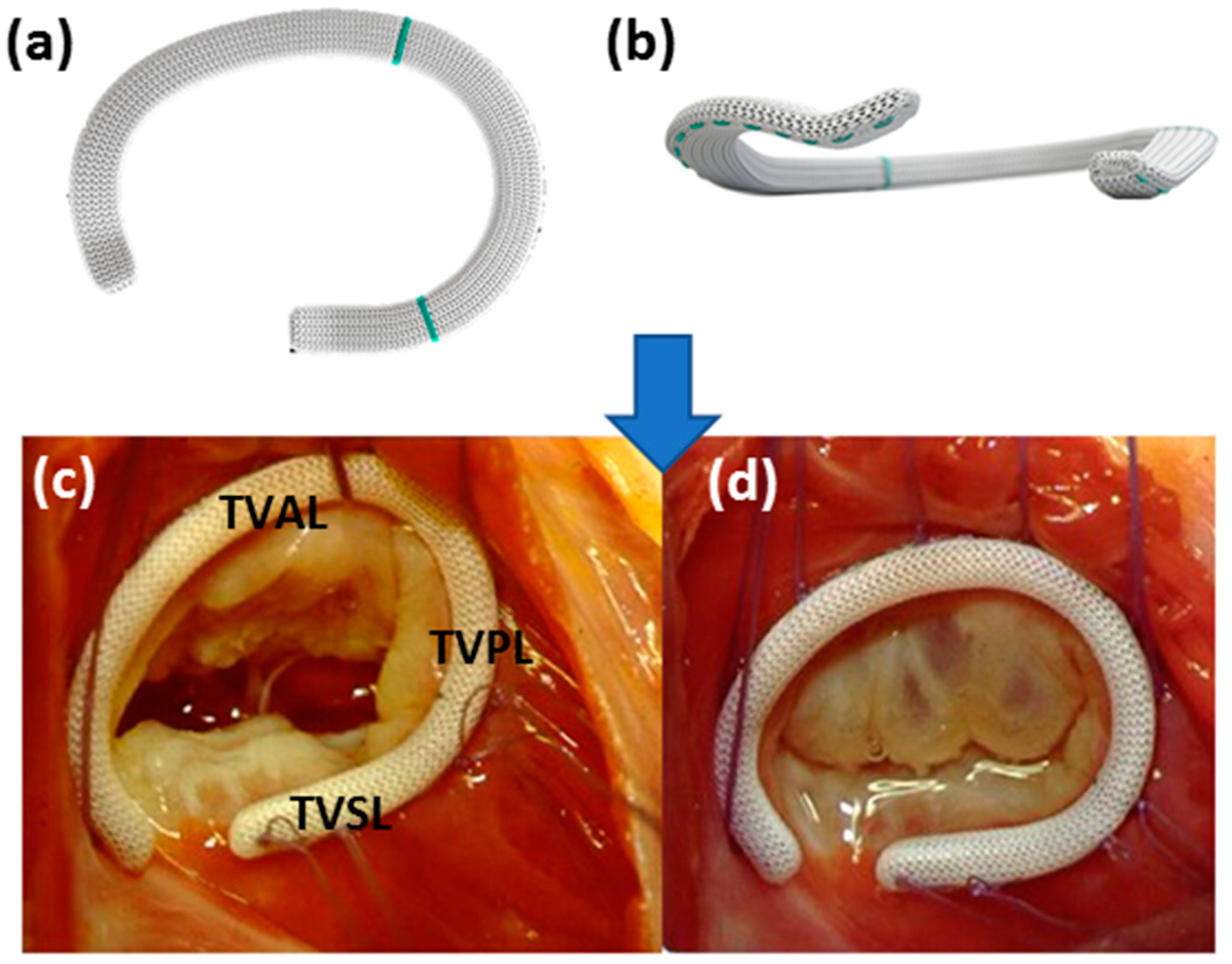
2.1. Sub-Valvular Structures and Components of the TV
2.1.1. TV Annulus
2.1.2. TV Leaflets
2.1.3. TV Chordae Tendineae
2.2. Imaging Modalities for Assessing FTR
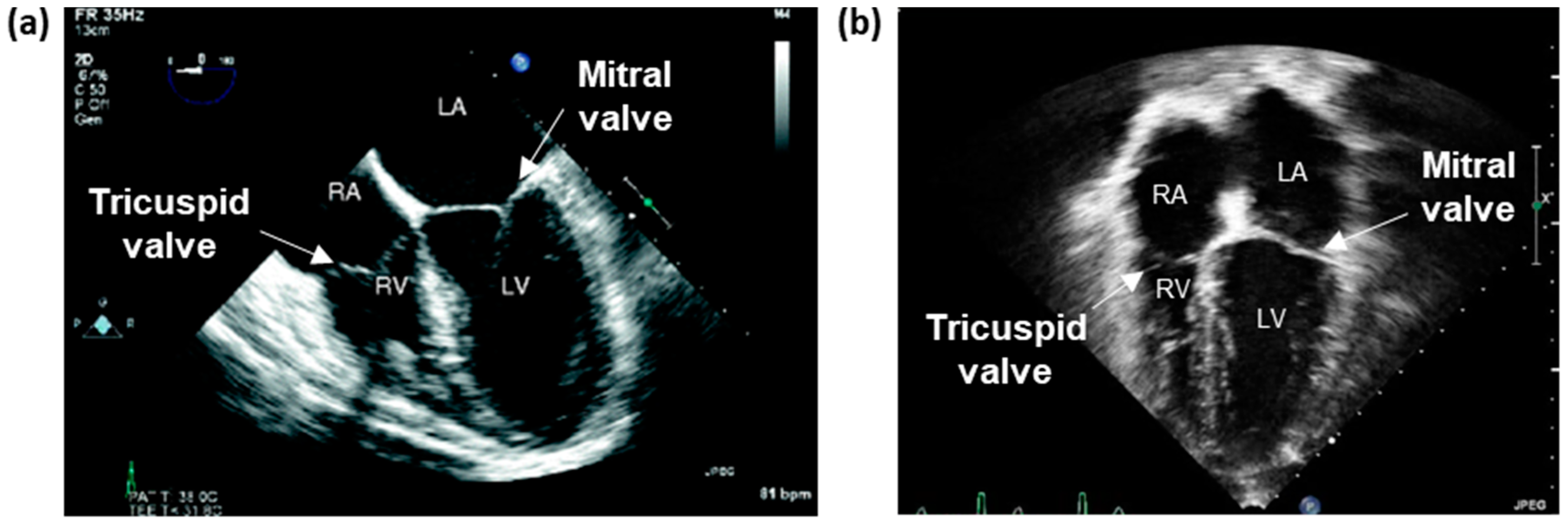
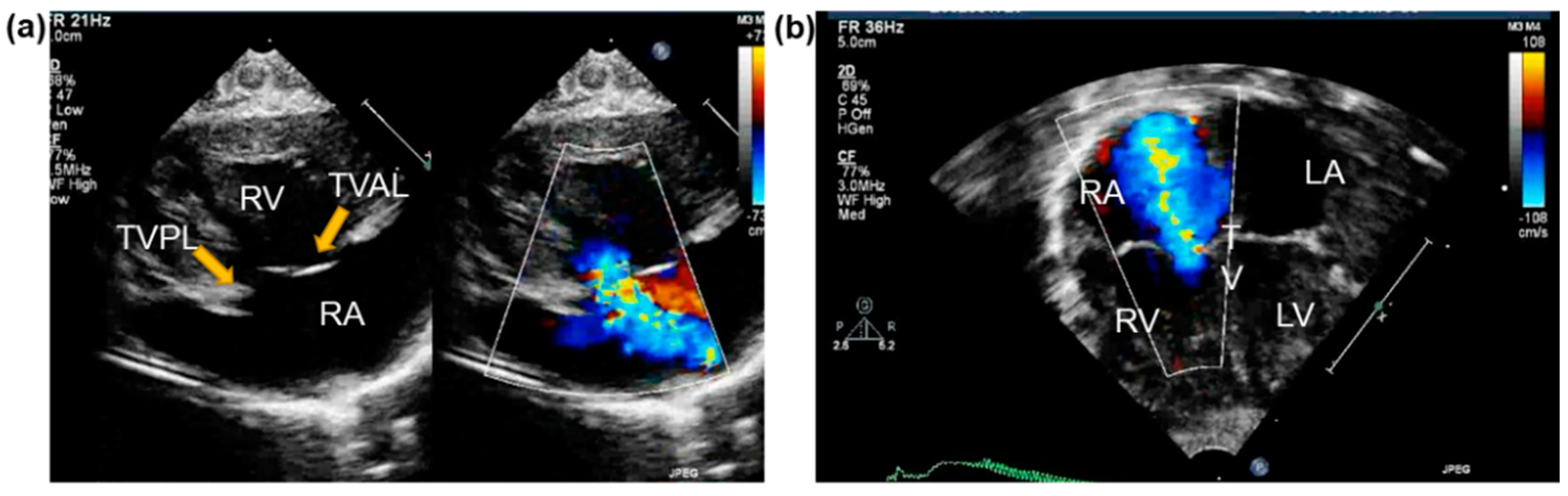
2.2.1. Echocardiography
Two-Dimensional Imaging Modalities
Standard Echocardiography Imaging Windows
Three-Dimensional Imaging Modalities
2.2.2. CMRI
2.2.3. Cardiac CT
2.3. Parameters for Grading TR Severity
2.3.1. Regurgitant Jet Area
2.3.2. VC Width
2.3.3. Proximal Isovelocity Surface Area (PISA)
2.3.4. TA Diameter
2.3.5. Proposed Revisions to The Current TR Severity’s Grading Recommendations
2.4. Surgical Interventions
2.4.1. Repair Methods for Surgical Treatment of FTR
2.4.2. Replacement Methods for Surgical Treatment of FTR
3. In-Vivo and In-Vitro Investigations
3.1. In-Vivo Dynamics and Strains of the TV Annulus
3.2. In-Vitro Flow and Pressure Systems
3.2.1. In-Vitro Flow Systems
3.2.2. In-Vitro Pressure Systems
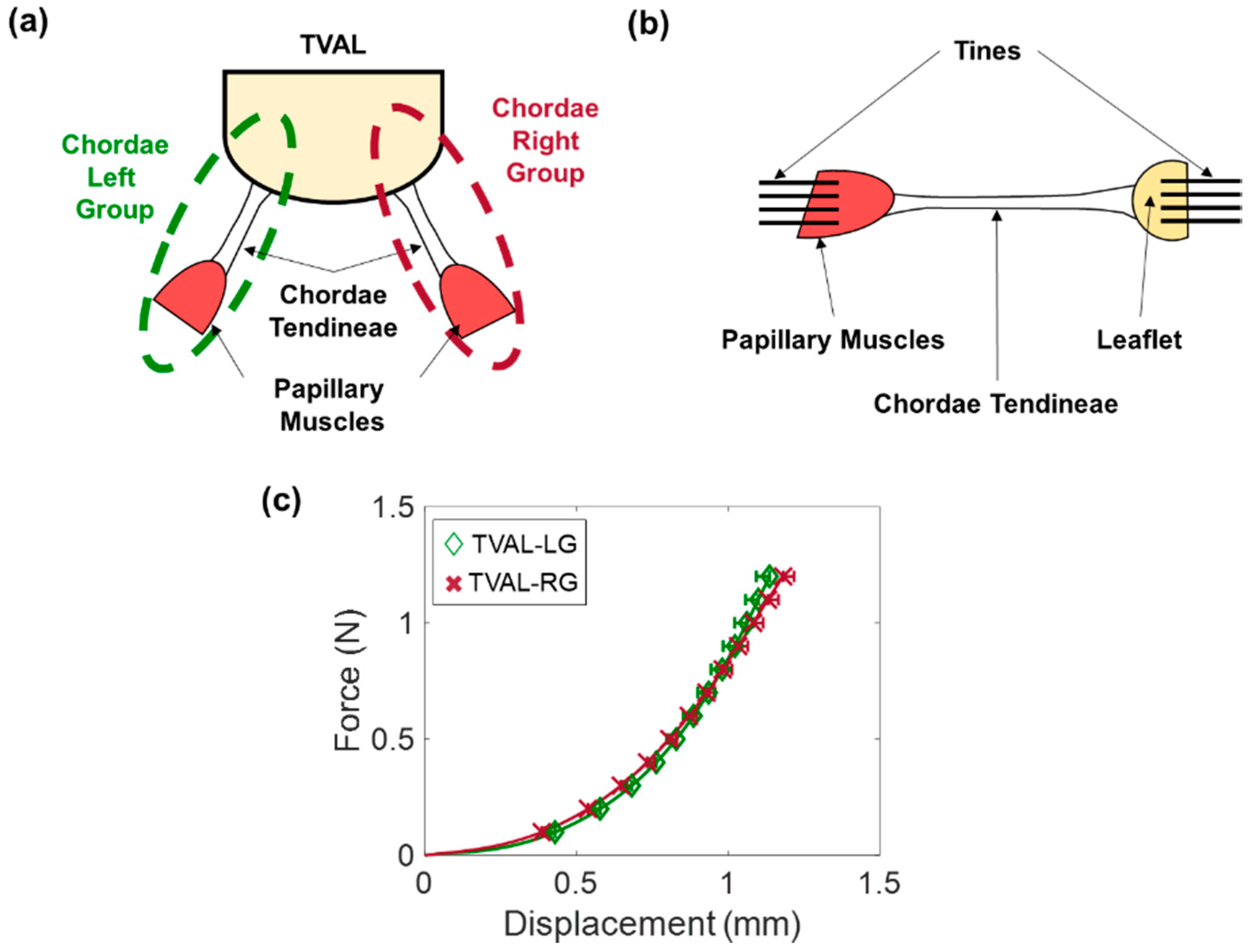
3.3. Chordae Tendineae Force Measurements
3.4. Biomechanical Quantifications of the Subvalvlar Structures of the TV
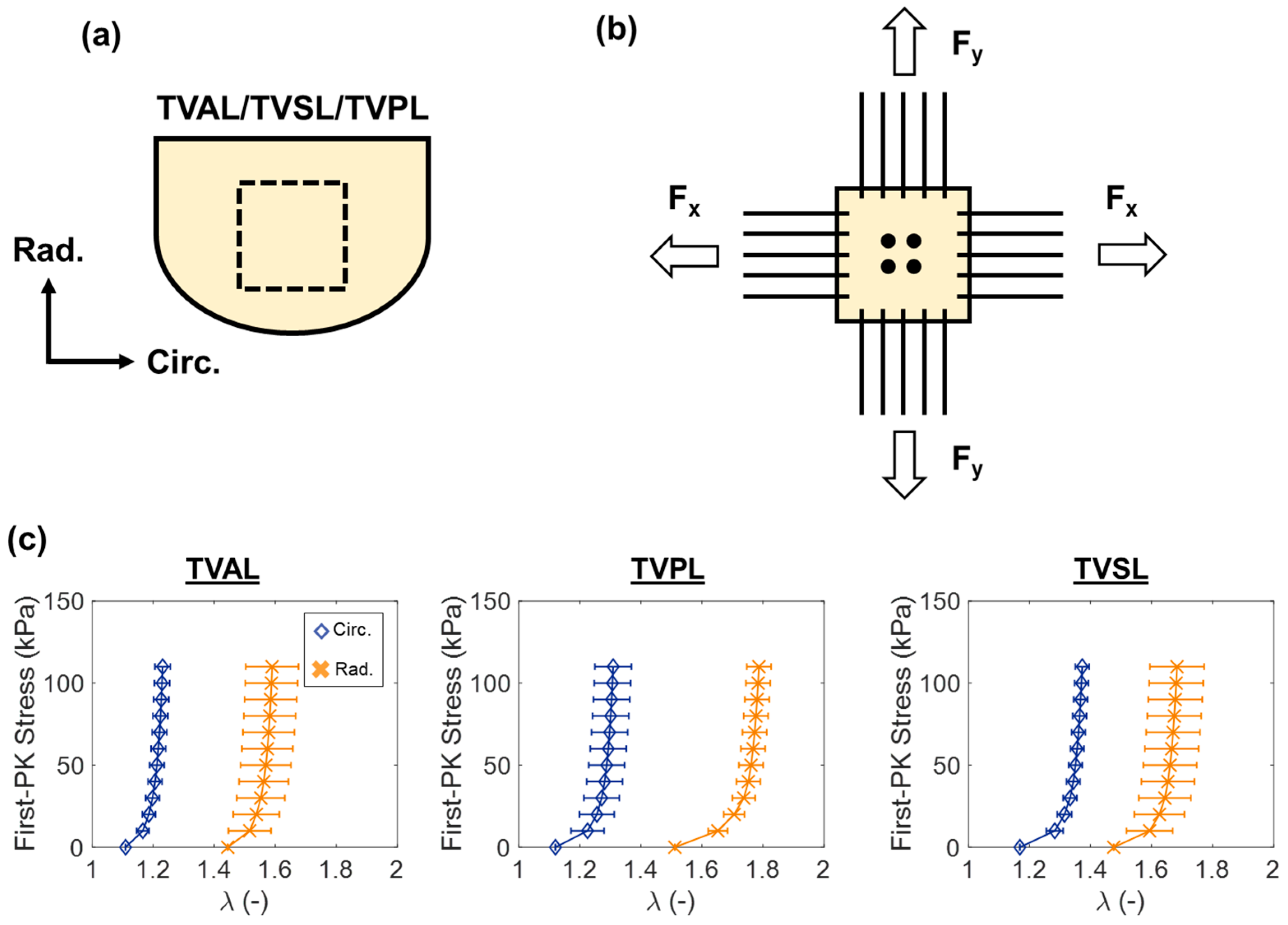
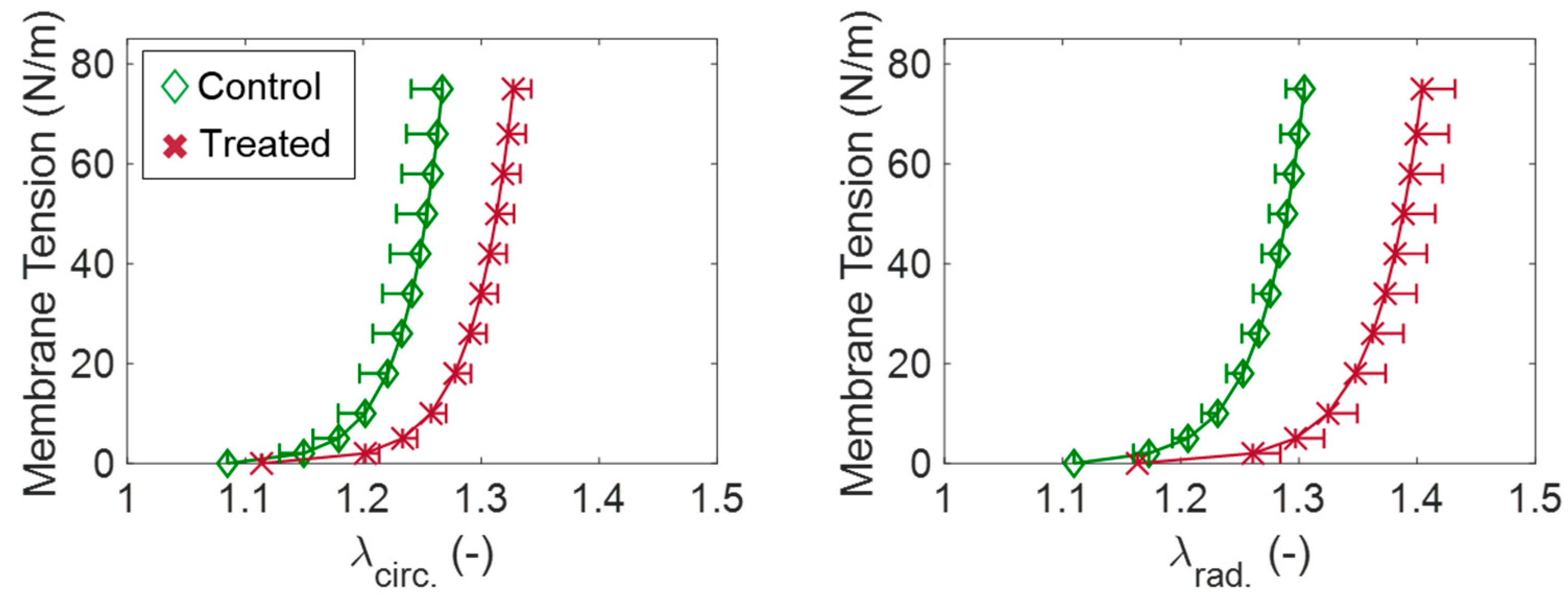
3.4.1. Biaxial and Uniaxial Mechanical Properties of the TV Leaflets
3.4.2. Bending Properties of the TV Leaflets
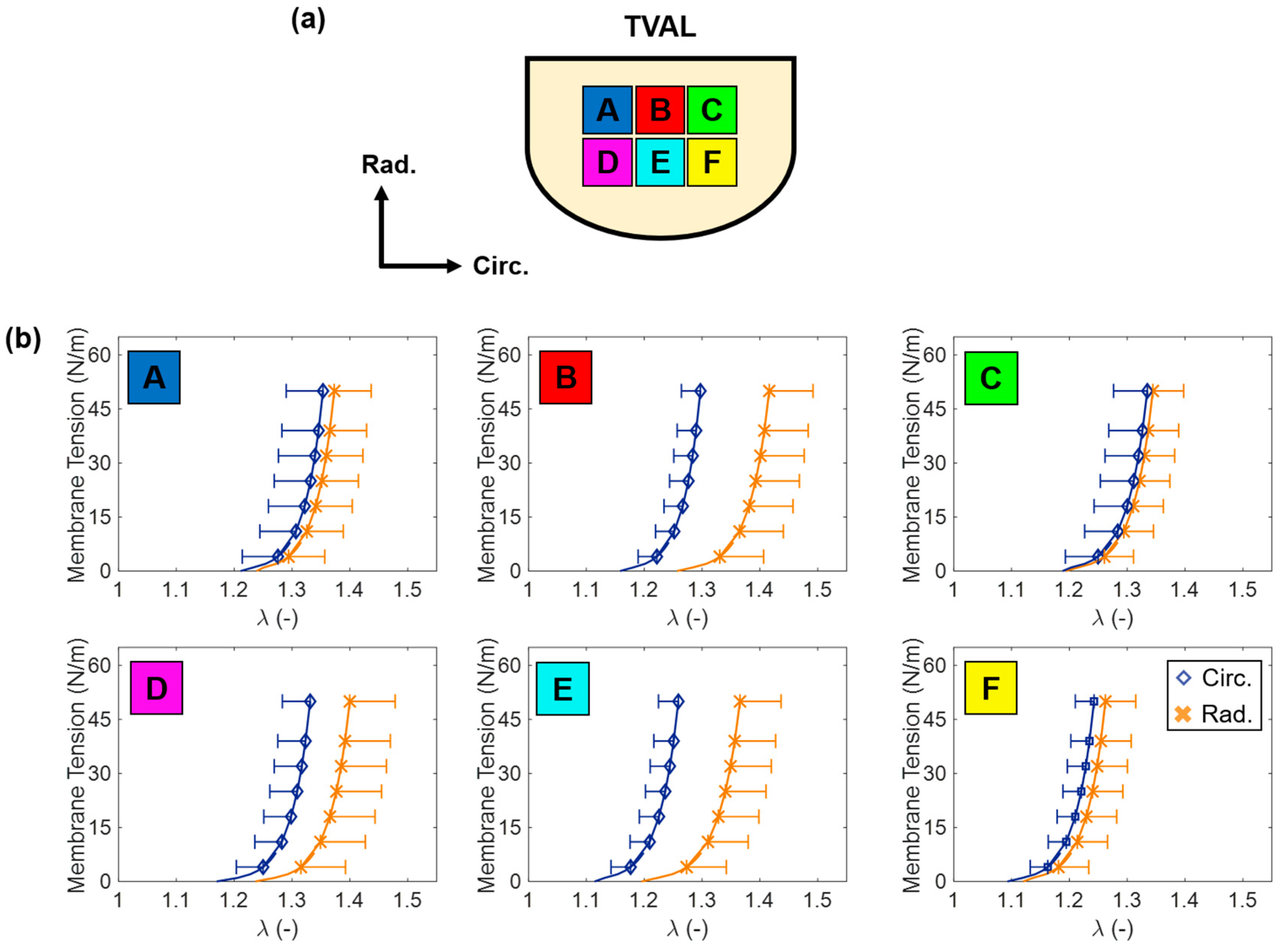
3.4.3. Spatial Variations in Tissue Mechanics of TV Leaflets
3.4.4. Microstructural Constituent’s Contributions to Tissue Mechanics of the TV Leaflet
3.4.5. Mechanics of TV Chordae Tendineae
4. Computational Biomechanical Modeling of the TV
4.1. Disparity of Computational Models for the Left-Sided and Right-Sided Heart Valves
4.2. Geometrical Modeling of the TV
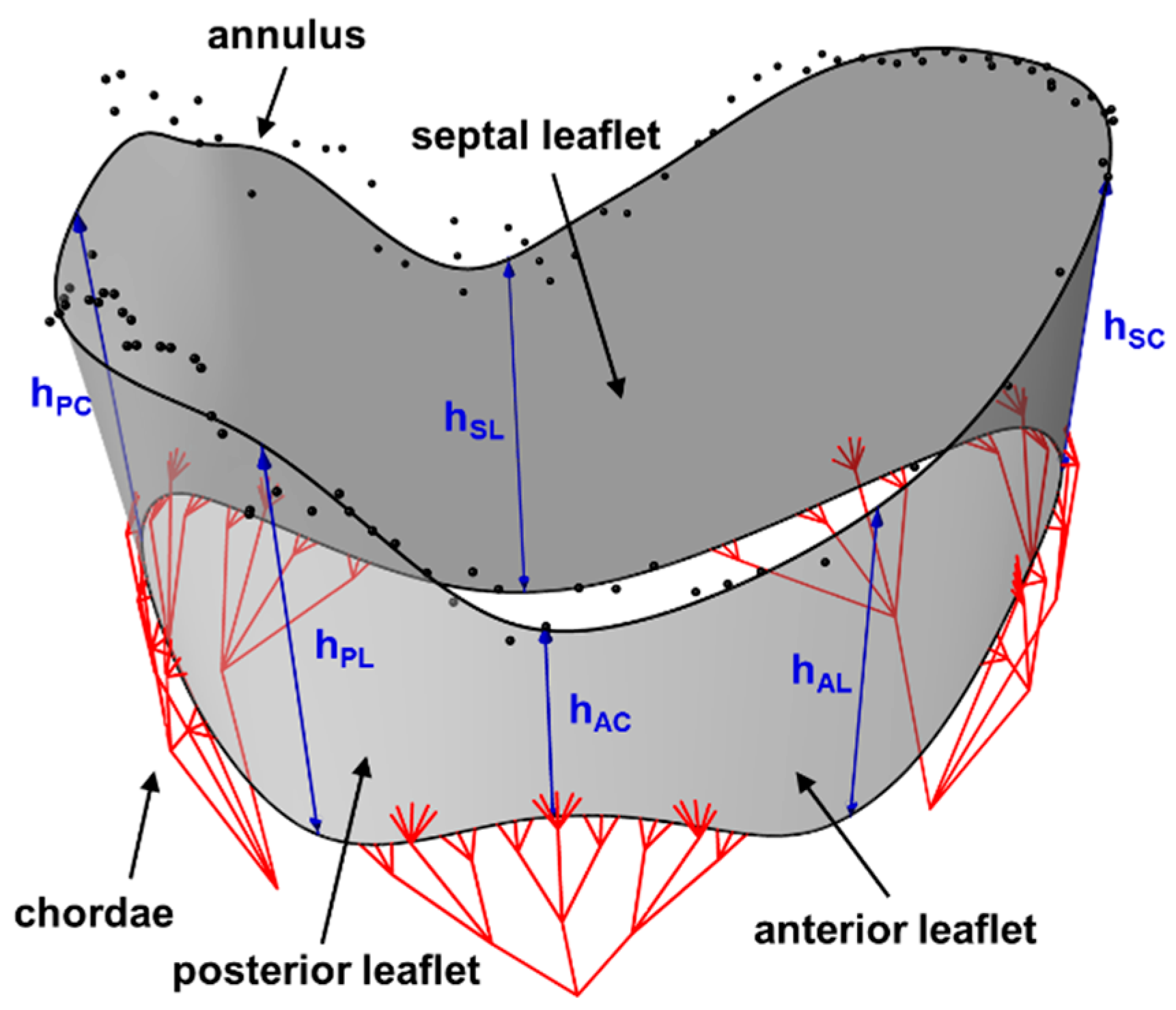
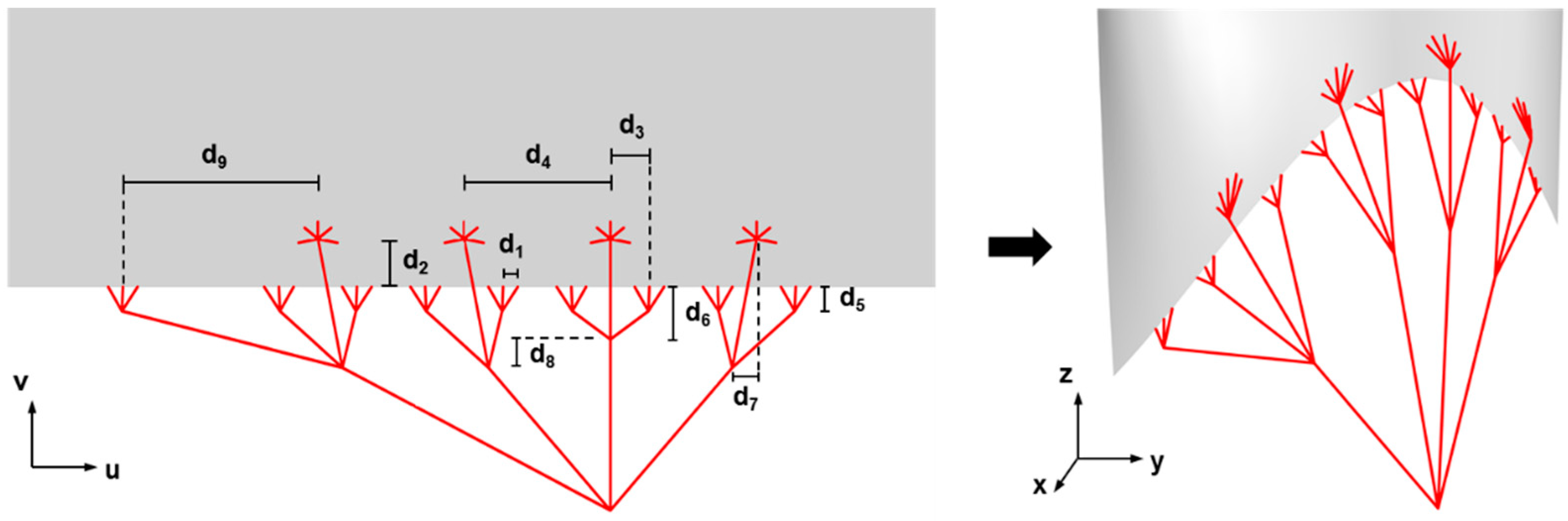
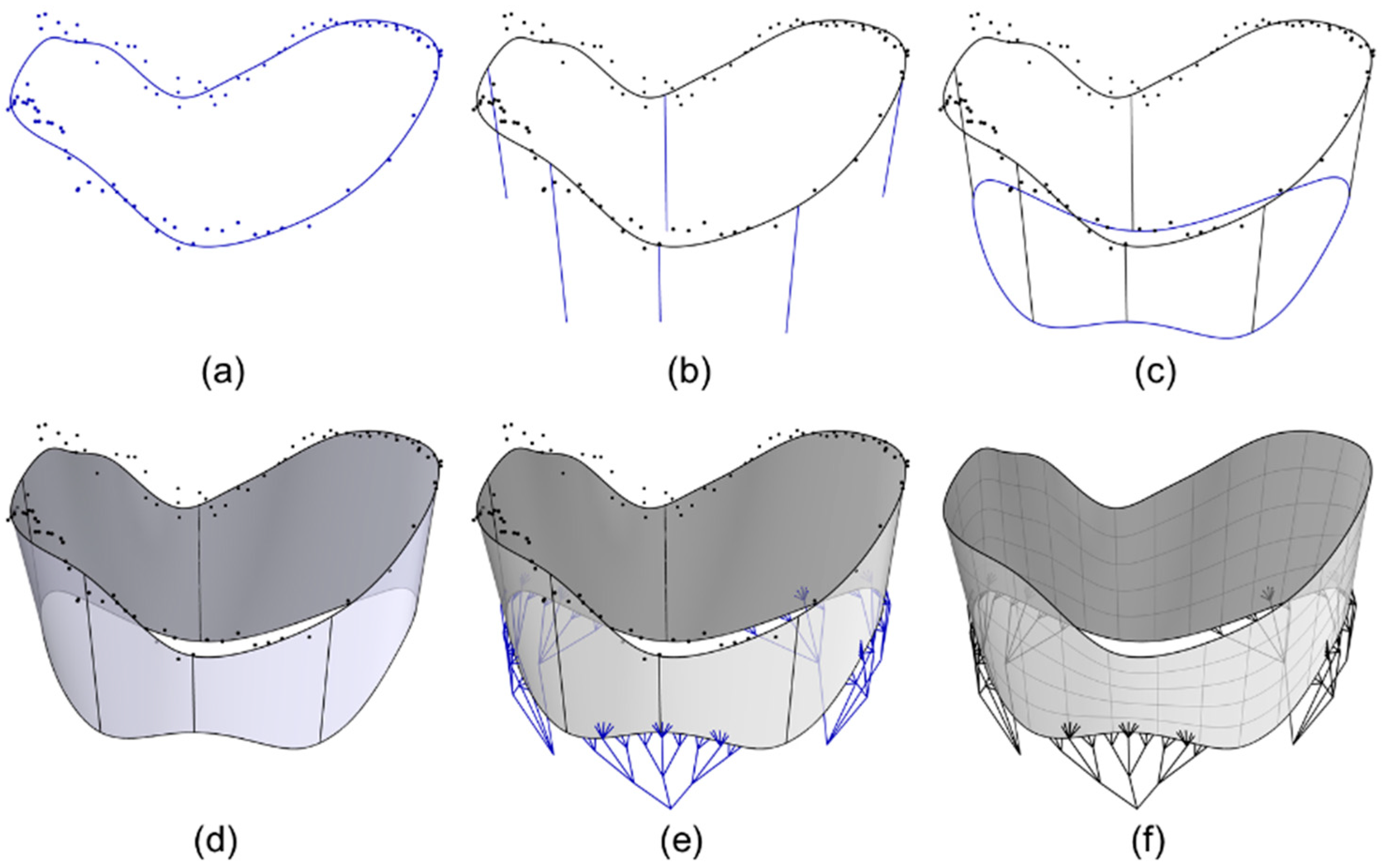
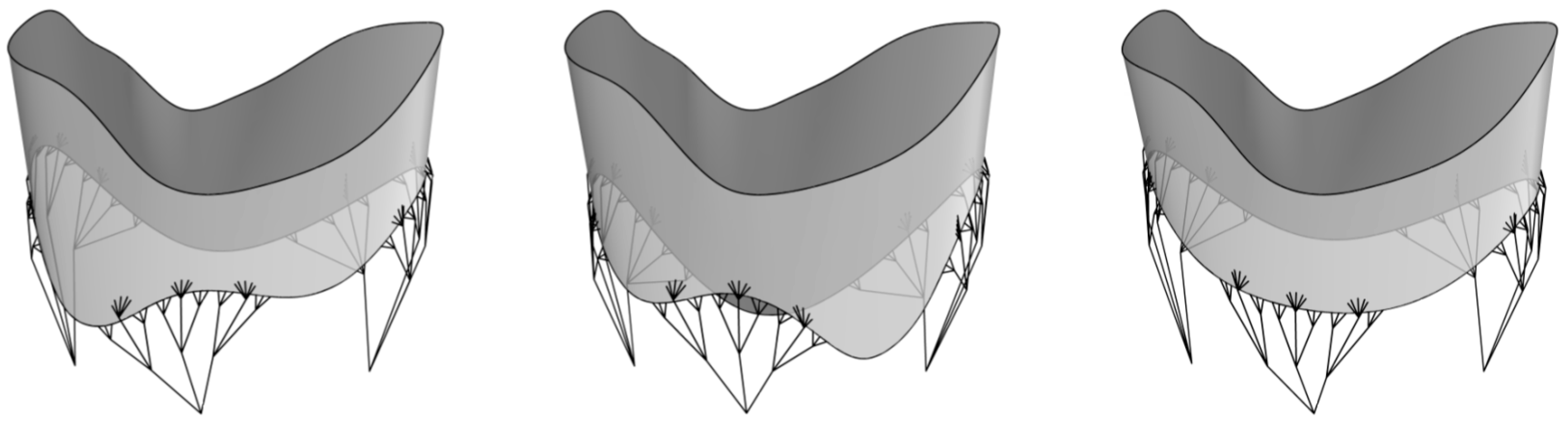
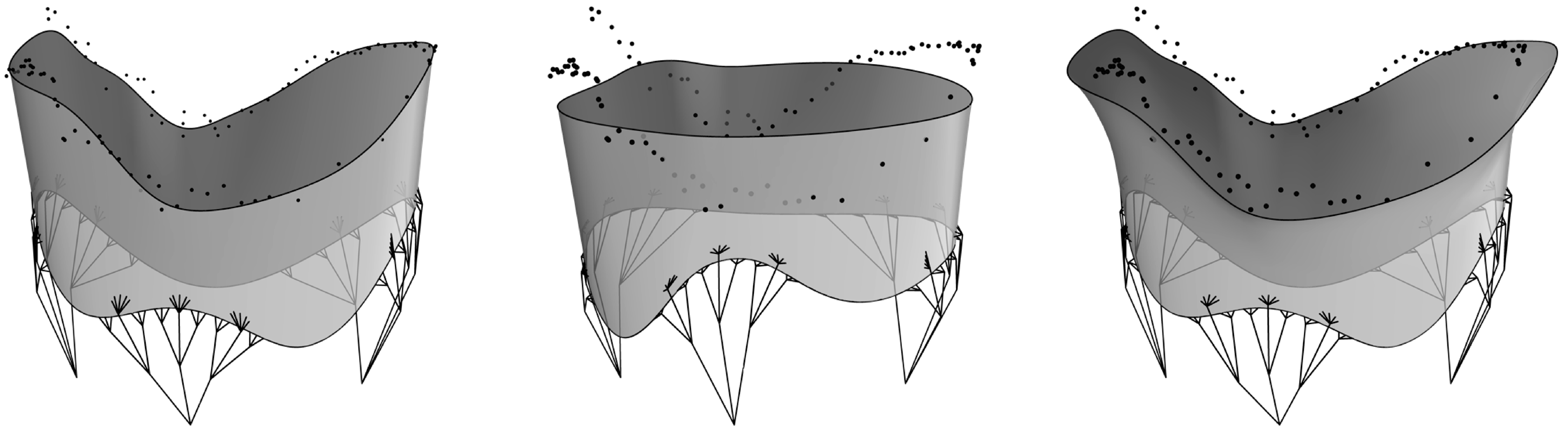
4.2.1. Modeling the TV Geometry
4.2.2. Parametric Design of Heart Valve Geometries
4.3. Constitutive Modeling of the TV Leaflets
4.4. Computational Models of the TV
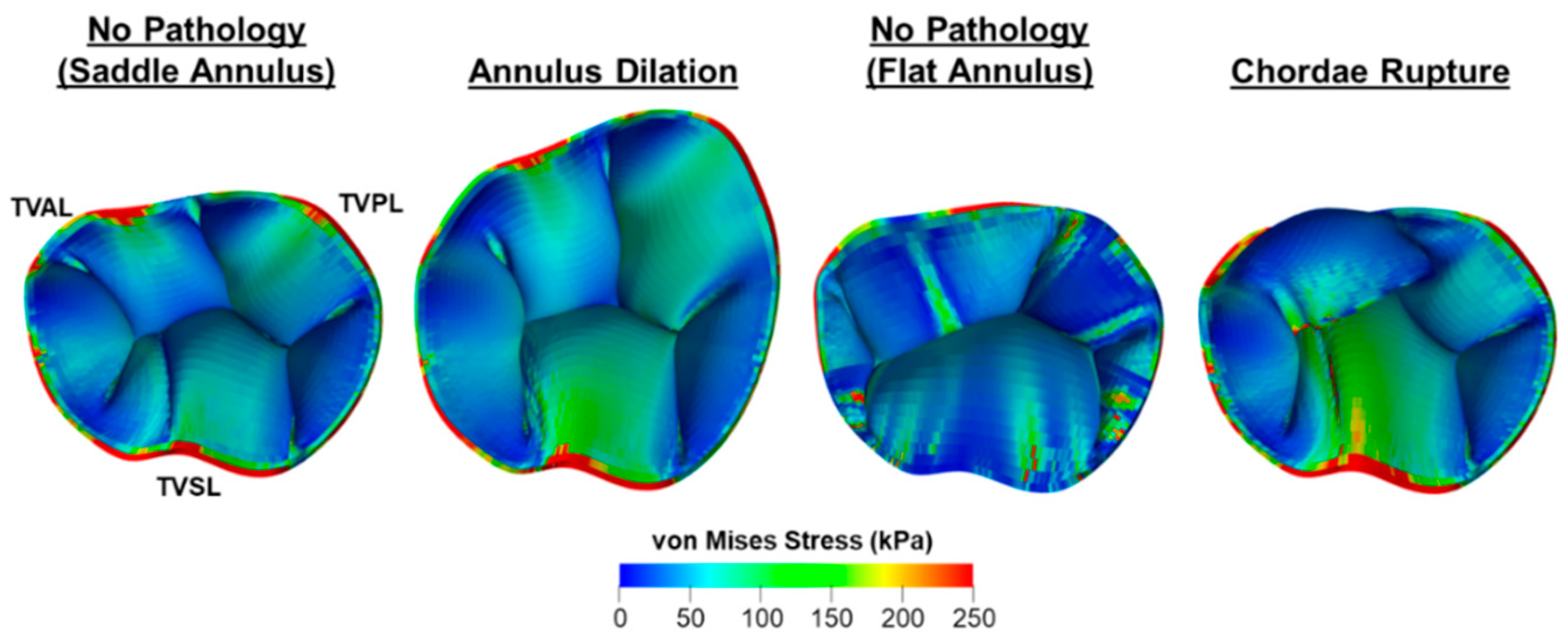
4.4.1. Bio-Solid Models of the TV
4.4.2. FSI Model of the TV
5. Closing Remarks and Future Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Badano, L.P.; Muraru, D.; Enriquez-Sarano, M. Assessment of functional tricuspid regurgitation. Eur. Heart J. 2013, 34, 1875–1885. [Google Scholar] [CrossRef]
- Anwar, A.M.; Folkert, J.; Soliman, O.I. Clinical recognition of tricuspid valve disease. In Practical Manual of Tricuspid Valve Diseases; Springer: Berlin, Germany, 2018; pp. 25–48. [Google Scholar]
- Nishimura, R.A.; Otto, C.M.; Bonow, R.O.; Carabello, B.A.; Erwin, J.P.; Guyton, R.A.; O’Gara, P.T.; Ruiz, C.E.; Skubas, N.J.; Sorajja, P. 2014 AHA/ACC guideline for the management of patients with valvular heart disease: Executive summary: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. J. Am. Coll. Cardiol. 2014, 63, 2438–2488. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.-P.; O’Gara, P.T. Epidemiology, anatomy, pathophysiology and clinical evaluation of functional tricuspid regurgitation. Minerva Cardioangiol. 2017, 65, 469–479. [Google Scholar] [PubMed]
- Badano, L.P.; Ginghina, C.; Easaw, J.; Muraru, D.; Grillo, M.T.; Lancellotti, P.; Pinamonti, B.; Coghlan, G.; Marra, M.P.; Popescu, B.A. Right ventricle in pulmonary arterial hypertension: Haemodynamics, structural changes, imaging, and proposal of a study protocol aimed to assess remodelling and treatment effects. Eur. J. Echocardiogr. 2009, 11, 27–37. [Google Scholar] [CrossRef]
- Spinner, E.M.; Lerakis, S.; Higginson, J.; Pernetz, M.; Howell, S.; Veledar, E.; Yoganathan, A.P. Correlates of tricuspid regurgitation as determined by 3D echocardiography: Pulmonary arterial pressure, ventricle geometry, annular dilatation, and papillary muscle displacement. Circ. Cardiovasc. Imaging 2012, 5, 43–50. [Google Scholar] [CrossRef]
- Hinderliter, A.L.; Willis, P.W.; Long, W.A.; Clarke, W.R.; Ralph, D.; Caldwell, E.J.; Williams, W.; Ettinger, N.A.; Hill, N.S.; Summer, W.R. Frequency and severity of tricuspid regurgitation determined by Doppler echocardiography in primary pulmonary hypertension. Am. J. Cardiol. 2003, 91, 1033–1037. [Google Scholar] [CrossRef]
- Come, P.C.; Riley, M.F. Tricuspid anular dilatation and failure of tricuspid leaflet coaptation in tricuspid regurgitation. Am. J. Cardiol. 1985, 55, 599–601. [Google Scholar] [CrossRef]
- Ton-Nu, T.-T.; Levine, R.A.; Handschumacher, M.D.; Dorer, D.J.; Yosefy, C.; Fan, D.; Hua, L.; Jiang, L.; Hung, J. Geometric determinants of functional tricuspid regurgitation: Insights from 3-dimensional echocardiography. Circulation 2006, 114, 143–149. [Google Scholar] [CrossRef]
- 1Song, J.-M.; Jang, M.-K.; Kim, Y.-J.; Kim, D.-H.; Kang, D.-H.; Song, J.-K. Right ventricular remodeling determines tricuspid valve geometry and the severity of functional tricuspid regurgitation: A real-time 3-dimensional echocardiography study. Korean Circ. J. 2010, 40, 448–453. [Google Scholar]
- Stuge, O.; Liddicoat, J. Emerging opportunities for cardiac surgeons within structural heart disease. J. Thorac. Cardiovasc. Surg. 2006, 132, 1258–1261. [Google Scholar] [CrossRef]
- Taramasso, M.; Pozzoli, A.; Guidotti, A.; Nietlispach, F.; Inderbitzin, D.T.; Benussi, S.; Alfieri, O.; Maisano, F. Percutaneous tricuspid valve therapies: The new frontier. Eur. Heart J. 2016, 38, 639–647. [Google Scholar] [CrossRef]
- Braunwald, N.S.; Ross, J., Jr.; Morrow, A.G. Conservative management of tricuspid regurgitation in patients undergoing mitral valve replacement. Circulation 1967, 35, I-63–I-69. [Google Scholar] [CrossRef]
- Dreyfus, G.D.; Corbi, P.J.; Chan, K.M.J.; Bahrami, T. Secondary tricuspid regurgitation or dilatation: Which should be the criteria for surgical repair? Ann. Thorac. Surg. 2005, 79, 127–132. [Google Scholar] [CrossRef]
- Anyanwu, A.C.; Adams, D.H. Functional tricuspid regurgitation in mitral valve disease: Epidemiology and prognostic implications. Semin. Thoracic Cardiovasc. Surg. 2010, 22, 69–75. [Google Scholar] [CrossRef]
- Navia, J.L.; Nowicki, E.R.; Blackstone, E.H.; Brozzi, N.A.; Nento, D.E.; Atik, F.A.; Rajeswaran, J.; Gillinov, A.M.; Svensson, L.G.; Lytle, B.W. Surgical management of secondary tricuspid valve regurgitation: Annulus, commissure, or leaflet procedure? J. Thorac. Cardiovasc. Surg. 2010, 139, 1473–1482. [Google Scholar] [CrossRef] [PubMed]
- Navia, J.L.; Brozzi, N.A.; Klein, A.L.; Ling, L.F.; Kittayarak, C.; Nowicki, E.R.; Batizy, L.H.; Zhong, J.; Blackstone, E.H. Moderate tricuspid regurgitation with left-sided degenerative heart valve disease: To repair or not to repair? Ann. Thorac. Surg. 2012, 93, 59–69. [Google Scholar] [CrossRef]
- Di Mauro, M.; Bezante, G.P.; Di Baldassarre, A.; Clemente, D.; Cardinali, A.; Acitelli, A.; Salerni, S.; Penco, M.; Calafiore, A.M.; Gallina, S. Functional tricuspid regurgitation: An underestimated issue. Int. J. Cardiol. 2013, 168, 707–715. [Google Scholar] [CrossRef]
- Chan, V.; Burwash, I.G.; Lam, B.-K.; Auyeung, T.; Tran, A.; Mesana, T.G.; Ruel, M. Clinical and echocardiographic impact of functional tricuspid regurgitation repair at the time of mitral valve replacement. Ann. Thorac. Surg. 2009, 88, 1209–1215. [Google Scholar] [CrossRef]
- Calafiore, A.M.; Gallina, S.; Iacò, A.L.; Contini, M.; Bivona, A.; Gagliardi, M.; Bosco, P.; Di Mauro, M. Mitral valve surgery for functional mitral regurgitation: Should moderate-or-more tricuspid regurgitation be treated? A propensity score analysis. Ann. Thorac. Surg. 2009, 87, 698–703. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.H.; Bolling, S.F. The tricuspid valve: Current perspective and evolving management of tricuspid regurgitation. Circulation 2009, 119, 2718–2725. [Google Scholar] [CrossRef]
- Antunes, M.J.; Barlow, J.B. Management of tricuspid valve regurgitation. Heart 2007, 93, 271–276. [Google Scholar] [CrossRef][Green Version]
- Fukuda, S.; Song, J.-M.; Gillinov, A.M.; McCarthy, P.M.; Daimon, M.; Kongsaerepong, V.; Thomas, J.D.; Shiota, T. Tricuspid valve tethering predicts residual tricuspid regurgitation after tricuspid annuloplasty. Circulation 2005, 111, 975–979. [Google Scholar] [CrossRef]
- Matsuyama, K.; Matsumoto, M.; Sugita, T.; Nishizawa, J.; Tokuda, Y.; Matsuo, T. Predictors of residual tricuspid regurgitation after mitral valve surgery. Ann. Thorac. Surg. 2003, 75, 1826–1828. [Google Scholar] [CrossRef]
- Tang, G.H.L.; David, T.E.; Singh, S.K.; Maganti, M.D.; Armstrong, S.; Borger, M.A. Tricuspid valve repair with an annuloplasty ring results in improved long-term outcomes. Circulation 2006, 114, I-577–I-581. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Kwon, D.-A.; Kim, H.-K.; Park, J.-S.; Hahn, S.; Kim, K.-H.; Kim, K.-B.; Sohn, D.-W.; Ahn, H.; Oh, B.-H. Determinants of surgical outcome in patients with isolated tricuspid regurgitation. Circulation 2009, 120, 1672–1678. [Google Scholar] [CrossRef] [PubMed]
- Onoda, K.; Yasuda, F.; Takao, M.; Shimono, T.; Tanaka, K.; Shimpo, H.; Yada, I. Long-term follow-up after Carpentier-Edwards ring annuloplasty for tricuspid regurgitation. Ann. Thorac. Surg. 2000, 70, 796–799. [Google Scholar] [CrossRef]
- Fukuda, S.; Gillinov, A.M.; McCarthy, P.M.; Matsumura, Y.; Thomas, J.D.; Shiota, T. Echocardiographic follow-up of tricuspid annuloplasty with a new three-dimensional ring in patients with functional tricuspid regurgitation. J. Am. Soc. Echocardiogr. 2007, 20, 1236–1242. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.B.; Jung, S.-H.; Choo, S.J.; Chung, C.H.; Lee, J.W. Clinical and echocardiographic outcomes after surgery for severe isolated tricuspid regurgitation. J. Thorac. Cardiovasc. Surg. 2013, 146, 278–284. [Google Scholar] [CrossRef]
- Fukuda, S.; Gillinov, A.M.; Song, J.-M.; Daimon, M.; Kongsaerepong, V.; Thomas, J.D.; Shiota, T. Echocardiographic insights into atrial and ventricular mechanisms of functional tricuspid regurgitation. Am. Heart J. 2006, 152, 1208–1214. [Google Scholar] [CrossRef] [PubMed]
- Min, S.-Y.; Song, J.-M.; Kim, J.-H.; Jang, M.-K.; Kim, Y.-J.; Song, H.; Kim, D.-H.; Lee, J.W.; Kang, D.-H.; Song, J.-K. Geometric changes after tricuspid annuloplasty and predictors of residual tricuspid regurgitation: A real-time three-dimensional echocardiography study. Eur. Heart J. 2010, 31, 2871–2880. [Google Scholar] [CrossRef] [PubMed]
- Meador, W.D.; Mathur, M.; Rausch, M.K. Tricuspid valve biomechanics: A brief review. In Advances in Heart Valve Biomechanics; Springer: Berlin, Germany, 2018; pp. 105–114. [Google Scholar]
- Hiro, M.E.; Jouan, J.; Pagel, M.R.; Lansac, E.; Lim, K.H.; Lim, H.-S.; Duran, C.M.G. Sonometric study of the normal tricuspid valve annulus in sheep. J. Heart. Valve Dis. 2004, 13, 452–460. [Google Scholar]
- Deloche, A.; Guérinon, J.; Fabiani, J.; Morillo, F.; Caramanian, M.; Carpentier, A.; Maurice, P.; Dubost, C. Anatomical study of rheumatic tricuspid valvulopathies. Applications to the critical study of various methods of annuloplasty. Arch. Mal. Coeur Vaiss. 1974, 67, 497. [Google Scholar]
- Chandra, S.; Powell, K.; Breburda, C.; Mikic, I.; Shekhar, R.; Morehead, A.; Cosgrove, D.; Thomas, J. Three dimensional reconstruction (shape and motion) of tricuspid annulus in normals and in patients after tricuspid annuloplasty with a flexible ring. Comput. Cardiol. 1996, 693–696. [Google Scholar] [CrossRef]
- Jouan, J.; Pagel, M.R.; Hiro, M.E.; Lim, K.H.; Lansac, E.; Duran, C.M. Further information from a sonometric study of the normal tricuspid valve annulus in sheep: geometric changes during the cardiac cycle. J. Heart. Valve Dis. 2007, 16, 511. [Google Scholar]
- Jensen, M.O.; Jensen, H.; Levine, R.A.; Yoganathan, A.P.; Andersen, N.T.; Nygaard, H.; Hasenkam, J.M.; Nielsen, S.L. Saddle-shaped mitral valve annuloplasty rings improve leaflet coaptation geometry. J. Thorac. Cardiovasc. Surg. 2011, 142, 697–703. [Google Scholar] [CrossRef][Green Version]
- Salgo, I.S.; Gorman, J.H., III; Gorman, R.C.; Jackson, B.M.; Bowen, F.W.; Plappert, T.; St John Sutton, M.G.; Edmunds, L.H., Jr. Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation 2002, 106, 711–717. [Google Scholar] [CrossRef]
- Dwivedi, G.; Mahadevan, G.; Jimenez, D.; Frenneaux, M.; Steeds, R.P. Reference values for mitral and tricuspid annular dimensions using two-dimensional echocardiography. Echo Res. Pr. 2014, 1, 43–50. [Google Scholar] [CrossRef]
- Spinner, E.M.; Buice, D.; Yap, C.H.; Yoganathan, A.P. The effects of a three-dimensional, saddle-shaped annulus on anterior and posterior leaflet stretch and regurgitation of the tricuspid valve. Ann. Biomed. Eng. 2012, 40, 996–1005. [Google Scholar] [CrossRef]
- Angelini, A.; Ho, S.; Anderson, R.H.; Davies, M.J.; Becker, A.E. A histological study of the atrioventricular junction in hearts with normal and prolapsed leaflets of the mitral valve. Heart 1988, 59, 712–716. [Google Scholar] [CrossRef]
- Keith, A.; Flack, M. The form and nature of the muscular connections between the primary divisions of the vertebrate heart. J. Anat. Physiol. 1907, 41, 172. [Google Scholar]
- Racker, D.K.; Ursell, P.C.; Hoffman, B.F. Anatomy of the tricuspid annulus. Circumferential myofibers as the structural basis for atrial flutter in a canine model. Circulation 1991, 84, 841–851. [Google Scholar] [CrossRef] [PubMed]
- Dudziak, M.; Skwarek, M.; Hreczecha, J.; Jerzemowski, J.; Grzybiak, M. Microscopic study of right fibrous annulus. Folia Morphol. (Praha) 2009, 68, 32–35. [Google Scholar]
- Silver, M.D.; Lam, J.H.C.; Ranganathan, N.; Wigle, E.D. Morphology of the human tricuspid valve. Circulation 1971, 43, 333–348. [Google Scholar] [CrossRef]
- Jett, S.; Laurence, D.; Kunkel, R.; Babu, A.R.; Kramer, K.; Baumwart, R.; Towner, R.; Wu, Y.; Lee, C.-H. An investigation of the anisotropic mechanical properties and anatomical structure of porcine atrioventricular heart valves. J. Mech. Behav. Biomed. Mater. 2018, 87, 155–171. [Google Scholar] [CrossRef]
- Gross, L.; Kugel, M.A. Topographic anatomy and histology of the valves in the human heart. Am. J. Pathol. 1931, 7, 445. [Google Scholar] [PubMed]
- Sacks, M.S.; Yoganathan, A.P. Heart valve function: A biomechanical perspective. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2007, 362, 1369–1391. [Google Scholar] [CrossRef] [PubMed]
- Eckert, C.E.; Fan, R.; Mikulis, B.; Barron, M.; Carruthers, C.A.; Friebe, V.M.; Vyavahare, N.R.; Sacks, M.S. On the biomechanical role of glycosaminoglycans in the aortic heart valve leaflet. Acta Biomater. 2013, 9, 4653–4660. [Google Scholar] [CrossRef] [PubMed]
- Lovekamp, J.J.; Simionescu, D.T.; Mercuri, J.J.; Zubiate, B.; Sacks, M.S.; Vyavahare, N.R. Stability and function of glycosaminoglycans in porcine bioprosthetic heart valves. Biomaterials 2006, 27, 1507–1518. [Google Scholar] [CrossRef] [PubMed]
- Marron, K.; Yacoub, M.H.; Polak, J.M.; Sheppard, M.N.; Fagan, D.; Whitehead, B.F.; de Leval, M.R.; Anderson, R.H.; Wharton, J. Innervation of human atrioventricular and arterial valves. Circulation 1996, 94, 368–375. [Google Scholar] [CrossRef]
- Merryman, W.D.; Youn, I.; Lukoff, H.D.; Krueger, P.M.; Guilak, F.; Hopkins, R.A.; Sacks, M.S. Correlation between heart valve interstitial cell stiffness and transvalvular pressure: Implications for collagen biosynthesis. Am. J. Physiol. Heart Circ. Physiol. 2006, 290, H224–H231. [Google Scholar] [CrossRef]
- Messier, R.H., Jr.; Bass, B.L.; Aly, H.M.; Jones, J.L.; Domkowski, P.W.; Wallace, R.B.; Hopkins, R.A. Dual structural and functional phenotypes of the porcine aortic valve interstitial population: Characteristics of the leaflet myofibroblast. J. Surg. Res. 1994, 57, 1–21. [Google Scholar] [CrossRef]
- Lam, J.H.C.; Ranganathan, N.; Wigle, E.D.; Silver, M.D. Morphology of the human mitral valve: I. Chordae tendineae: A new classification. Circulation 1970, 41, 449–458. [Google Scholar] [CrossRef]
- Millington-Sanders, C.; Meir, A.; Lawrence, L.; Stolinski, C. Structure of chordae tendineae in the left ventricle of the human heart. J. Anat. 1998, 192, 573–581. [Google Scholar] [CrossRef]
- Casado, J.A.; Diego, S.; Ferreño, D.; Ruiz, E.; Carrascal, I.; Méndez, D.; Revuelta, J.M.; Pontón, A.; Icardo, J.M.; Gutiérrez-Solana, F. Determination of the mechanical properties of normal and calcified human mitral chordae tendineae. J. Mech. Behav. Biomed. Mater. 2012, 13, 1–13. [Google Scholar] [CrossRef]
- Kunzelman, K.S.; Cochran, K.P. Mechanical properties of basal and marginal mitral valve chordae tendineae. ASAIO J. 1990, 36, M405–M407. [Google Scholar]
- 5Humphries, J.A.; Kramer, C.J.; Sengupta, P.P.; Khandheria, B.K. Transesophageal echocardiography. In Case Based Echocardiography; Springer: Berlin, Germany, 2010; pp. 85–101. [Google Scholar]
- Addetia, K.; Yamat, M.; Mediratta, A.; Medvedofsky, D.; Patel, M.; Ferrara, P.; Mor-Avi, V.; Lang, R.M. Comprehensive two-dimensional interrogation of the tricuspid valve using knowledge derived from three-dimensional echocardiography. J. Am. Soc. Echocardiogr. 2016, 29, 74–82. [Google Scholar] [CrossRef]
- Anwar, A.M.; Geleijnse, M.L.; Soliman, O.I.; McGhie, J.S.; Frowijn, R.; Nemes, A.; van den Bosch, A.E.; Galema, T.W.; Folkert, J. Assessment of normal tricuspid valve anatomy in adults by real-time three-dimensional echocardiography. Int. J. Cardiovasc. Imaging 2007, 23, 717–724. [Google Scholar] [CrossRef]
- Badano, L.P.; Agricola, E.; de Isla, L.P.; Gianfagna, P.; Zamorano, J.L. Evaluation of the tricuspid valve morphology and function by transthoracic real-time three-dimensional echocardiography. Eur. J. Echocardiogr. 2009, 10, 477–484. [Google Scholar] [CrossRef]
- Anwar, A.M.; Geleijnse, M.L.; ten Cate, F.J.; Meijboom, F.J. Assessment of tricuspid valve annulus size, shape and function using real-time three-dimensional echocardiography. Interact. Cardiovasc. Thorac. Surg. 2006, 5, 683–687. [Google Scholar] [CrossRef]
- Kwan, J.; Kim, G.-C.; Jeon, M.-J.; Kim, D.-H.; Shiota, T.; Thomas, J.D.; Park, K.-S.; Lee, W.-H. 3D geometry of a normal tricuspid annulus during systole: A comparison study with the mitral annulus using real-time 3D echocardiography. Eur. J. Echocardiogr. 2007, 8, 375–383. [Google Scholar] [CrossRef][Green Version]
- Vegas, A. Three-dimensional transesophageal echocardiography: Principles and clinical applications. Ann. Card. Anaesth. 2016, 19, S35. [Google Scholar] [CrossRef] [PubMed]
- Rivera, R.; Duran, E.; Ajuria, M. Carpentier’s flexible ring versus De Vega’s annuloplasty. A prospective randomized study. J. Thorac. Cardiovasc. Surg. 1985, 89, 196–203. [Google Scholar]
- Pennell, D.J.; Sechtem, U.P.; Higgins, C.B.; Manning, W.J.; Pohost, G.M.; Rademakers, F.E.; van Rossum, A.C.; Shaw, L.J.; Kent Yucel, E. Clinical indications for cardiovascular magnetic resonance (CMR): Consensus Panel report. J. Cardiovasc. Magn. Reson. 2004, 6, 727–765. [Google Scholar] [CrossRef]
- Van Praet, K.M.; Stamm, C.; Starck, C.T.; Sündermann, S.; Meyer, A.; Montagner, M.; Nazari Shafti, T.Z.; Unbehaun, A.; Jacobs, S.; Falk, V. An overview of surgical treatment modalities and emerging transcatheter interventions in the management of tricuspid valve regurgitation. Expert Rev. Cardiovasc. Ther. 2018, 16, 75–89. [Google Scholar] [CrossRef]
- Huttin, O.; Voilliot, D.; Mandry, D.; Venner, C.; Juillière, Y.; Selton-Suty, C. All you need to know about the tricuspid valve: Tricuspid valve imaging and tricuspid regurgitation analysis. Arch. Cardiovasc. Dis. 2016, 109, 67–80. [Google Scholar] [CrossRef]
- Kabasawa, M.; Kohno, H.; Ishizaka, T.; Ishida, K.; Funabashi, N.; Kataoka, A.; Matsumiya, G. Assessment of functional tricuspid regurgitation using 320-detector-row multislice computed tomography: Risk factor analysis for recurrent regurgitation after tricuspid annuloplasty. J. Thorac. Cardiovasc. Surg. 2014, 147, 312–320. [Google Scholar] [CrossRef]
- Nemoto, N.; Lesser, J.R.; Pedersen, W.R.; Sorajja, P.; Spinner, E.; Garberich, R.F.; Vock, D.M.; Schwartz, R.S. Pathogenic structural heart changes in early tricuspid regurgitation. J. Thorac. Cardiovasc. Surg. 2015, 150, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Gopalan, D. Right heart on multidetector CT. Br. J. Radiol. 2011, 84, S306–S323. [Google Scholar] [CrossRef]
- Go, Y.Y.; Dulgheru, R.; Lancellotti, P. The conundrum of tricuspid regurgitation grading. Front. Cardiovasc. Med. 2018, 5, 164. [Google Scholar] [CrossRef] [PubMed]
- Lancellotti, P.; Moura, L.; Pierard, L.A.; Agricola, E.; Popescu, B.A.; Tribouilloy, C.; Hagendorff, A.; Monin, J.-L.; Badano, L.; Zamorano, J.L. European Association of Echocardiography recommendations for the assessment of valvular regurgitation. Part 2: Mitral and tricuspid regurgitation (native valve disease). Eur. J. Echocardiogr. 2010, 11, 307–332. [Google Scholar] [CrossRef]
- Tribouilloy, C.M.; Enriquez-Sarano, M.; Bailey, K.R.; Tajik, A.J.; Seward, J.B. Quantification of tricuspid regurgitation by measuring the width of the vena contracta with Doppler color flow imaging: A clinical study. J. Am. Coll. Cardiol. 2000, 36, 472–478. [Google Scholar] [CrossRef]
- Lambert, A.S. Proximal isovelocity surface area should be routinely measured in evaluating mitral regurgitation: A core review. Anesth. Analg. 2007, 105, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Hahn, R.T.; Zamorano, J.L. The need for a new tricuspid regurgitation grading scheme. Eur. Heart J. Cardiovasc. Imaging 2017, 18, 1342–1343. [Google Scholar] [CrossRef] [PubMed]
- Izgi, I.A.; Acar, E.; Kilicgedik, A.; Guler, A.; Cakmak, E.O.; Demirel, M.; Izci, S.; Yilmaz, M.F.; Inanir, M.; Kirma, C. A new and simple method for clarifying the severity of tricuspid regurgitation. Echocardiography 2017, 34, 328–333. [Google Scholar] [CrossRef]
- Chikwe, J.; Anyanwu, A.C. Surgical strategies for functional tricuspid regurgitation. Semin. Thorac. Cardiovasc. Surg. 2010, 22, 90–96. [Google Scholar] [CrossRef] [PubMed]
- Pinney, S.P. The role of tricuspid valve repair and replacement in right heart failure. Curr. Opin. Cardiol. 2012, 27, 288–295. [Google Scholar] [CrossRef]
- Chang, H.W.; Jeong, D.S.; Cho, Y.H.; Sung, K.; Kim, W.S.; Lee, Y.T.; Park, P.W. Tricuspid valve replacement vs. repair in severe tricuspid regurgitation. Circ. J. 2017, 81, 330–338. [Google Scholar] [CrossRef]
- Kay, J.H.; Maselli-Campagna, G.; Tsuji, H.K. Surgical treatment of tricuspid insufficiency. Ann. Surg. 1965, 162, 53–58. [Google Scholar] [CrossRef]
- De Vega, N.; De Rabago, G.; Castillon, L.; Moreno, T.; Azpitarte, J. A new tricuspid repair. Short-term clinical results in 23 cases. J. Cardiovasc. Surg. (Torino) 1973, 14, 384–386. [Google Scholar]
- Antunes, M.J.; Girdwood, R.W. Tricuspid annuloplasty: A modified technique. Ann. Thorac. Surg. 1983, 35, 676–678. [Google Scholar] [CrossRef]
- Raja, S.G.; Dreyfus, G.D. Basis for intervention on functional tricuspid regurgitation. Semin. Thorac. Cardiovasc. Surg. 2010, 22, 79–83. [Google Scholar] [CrossRef] [PubMed]
- Carpentier, A. A new reconstructive operation for correction of mitral and tricuspid insufficiency. J. Thorac. Cardiovasc. Surg. 1971, 61, 1–13. [Google Scholar] [PubMed]
- Pfannmüller, B.; Doenst, T.; Eberhardt, K.; Seeburger, J.; Borger, M.A.; Mohr, F.W. Increased risk of dehiscence after tricuspid valve repair with rigid annuloplasty rings. J. Thorac. Cardiovasc. Surg. 2012, 143, 10501055. [Google Scholar] [CrossRef]
- Huang, X.; Gu, C.; Men, X.; Zhang, J.; You, B.; Zhang, H.; Wei, H.; Li, J. Repair of functional tricuspid regurgitation: Comparison between suture annuloplasty and rings annuloplasty. Ann. Thorac. Surg. 2014, 97, 1286–1292. [Google Scholar] [CrossRef] [PubMed]
- Filsoufi, F.; Salzberg, S.P.; Coutu, M.; Adams, D.H. A three-dimensional ring annuloplasty for the treatment of tricuspid regurgitation. Ann. Thorac. Surg. 2006, 81, 2273–2277. [Google Scholar] [CrossRef] [PubMed]
- Mas, P.T.; Rodríguez-Palomares, J.F.; Antunes, M.J. Secondary tricuspid valve regurgitation: A forgotten entity. Heart 2015, 101, 1840–1848. [Google Scholar]
- Bernal, J.M.; Gutiérrez-Morlote, J.; Llorca, J.; San José, J.M.; Morales, D.; Revuelta, J.M. Tricuspid valve repair: An old disease, a modern experience. Ann. Thorac. Surg. 2004, 78, 2069–2074. [Google Scholar] [CrossRef] [PubMed]
- Charfeddine, S.; Hammami, R.; Triki, F.; Abid, L.; Hentati, M.; Frikha, I.; Kammoun, S. Plastic repair of tricuspid valve: Carpentier’s ring annuloplasty versus De VEGA technique. Pan Afr. Med. J. 2017, 27, 119. [Google Scholar] [CrossRef] [PubMed]
- Dreyfus, G.D.; Raja, S.G.; John Chan, K.M. Tricuspid leaflet augmentation to address severe tethering in functional tricuspid regurgitation. Eur. J. Cardiothorac. Surg. 2008, 34, 908–910. [Google Scholar] [CrossRef]
- Lapenna, E.; De Bonis, M.; Verzini, A.; La Canna, G.; Ferrara, D.; Calabrese, M.C.; Taramasso, M.; Alfieri, O. The clover technique for the treatment of complex tricuspid valve insufficiency: Midterm clinical and echocardiographic results in 66 patients. Eur. J. Cardiothorac. Surg. 2010, 37, 1297–1303. [Google Scholar] [CrossRef]
- Belluschi, I.; Del Forno, B.; Lapenna, E.; Nisi, T.; Iaci, G.; Ferrara, D.; Castiglioni, A.; Alfieri, O.; De Bonis, M. Surgical techniques for tricuspid valve disease. Front. Cardiovasc. Med. 2018, 5, 118. [Google Scholar] [CrossRef]
- Bloomfield, P. Choice of heart valve prosthesis. Heart 2002, 87, 583–589. [Google Scholar] [CrossRef]
- Hammarström, E.; Wranne, B.; Pinto, F.J.; Puryear, J.; Popp, R.L. Tricuspid annular motion. J. Am. Soc. Echocardiogr. 1991, 4, 131–139. [Google Scholar] [CrossRef]
- Ring, L.; Rana, B.S.; Kydd, A.; Boyd, J.; Parker, K.; Rusk, R.A. Dynamics of the tricuspid valve annulus in normal and dilated right hearts: a three-dimensional transoesophageal echocardiography study. Eur. Heart J. Cardiovasc. Imaging 2012, 13, 756–762. [Google Scholar] [CrossRef]
- Malinowski, M.; Wilton, P.; Khaghani, A.; Langholz, D.; Hooker, V.; Eberhart, L.; Hooker, R.L.; Timek, T.A. The effect of pulmonary hypertension on ovine tricuspid annular dynamics. Eur. J. Cardiothorac. Surg. 2015, 49, 40–45. [Google Scholar] [CrossRef]
- Malinowski, M.; Schubert, H.; Wodarek, J.; Ferguson, H.; Eberhart, L.; Langholz, D.; Jazwiec, T.; Rausch, M.K.; Timek, T.A. Tricuspid annular geometry and strain after suture annuloplasty in acute ovine right heart failure. Ann. Thorac. Surg. 2018, 106, 1804–1811. [Google Scholar] [CrossRef]
- Rausch, M.K.; Malinowski, M.; Wilton, P.; Khaghani, A.; Timek, T.A. Engineering analysis of tricuspid annular dynamics in the beating ovine heart. Ann. Biomed. Eng. 2018, 46, 443–451. [Google Scholar] [CrossRef]
- Fawzy, H.; Fukamachi, K.; Mazer, C.D.; Harrington, A.; Latter, D.; Bonneau, D.; Errett, L. Complete mapping of the tricuspid valve apparatus using three-dimensional sonomicrometry. J. Thorac. Cardiovasc. Surg. 2011, 141, 1037–1043. [Google Scholar] [CrossRef]
- Mathur, M.; Jazwiec, T.; Meador, W.D.; Malinowski, M.; Goehler, M.; Ferguson, H.; Timek, T.A.; Rausch, M.K. Tricuspid valve leaflet strains in the beating ovine heart. Biomech. Model. Mechanobiol. 2019, 1–11. [Google Scholar] [CrossRef]
- Malinowski, M.; Proudfoot, A.G.; Eberhart, L.; Schubert, H.; Wodarek, J.; Langholz, D.; Rausch, M.K.; Timek, T.A. Large animal model of acute right ventricular failure with functional tricuspid regurgitation. Int. J. Cardiol. 2018, 264, 124–129. [Google Scholar] [CrossRef]
- Rausch, M.K.; Malinowski, M.; Meador, W.D.; Wilton, P.; Khaghani, A.; Timek, T.A. The Effect of Acute Pulmonary Hypertension on Tricuspid Annular Height, Strain, and Curvature in Sheep. Cardiovasc. Eng. Technol. 2018, 9, 365–376. [Google Scholar] [CrossRef] [PubMed]
- Malinowski, M.; Jaźwiec, T.; Goehler, M.; Bush, J.; Quay, N.; Ferguson, H.; Rausch, M.K.; Timek, T.A. Impact of tricuspid annular size reduction on right ventricular function, geometry and strain. Eur. J. Cardiothorac. Surg. 2019. [Google Scholar] [CrossRef]
- Schechter, M.A.; Southerland, K.W.; Feger, B.J.; Linder, D., Jr.; Ali, A.A.; Njoroge, L.; Milano, C.A.; Bowles, D.E. An isolated working heart system for large animal models. J. Vis. Exp. 2014. [Google Scholar] [CrossRef] [PubMed]
- Khoiy, K.A.; Pant, A.D.; Amini, R. Quantification of material constants for a phenomenological constitutive model of porcine tricuspid valve leaflets for simulation applications. J. Biomech. Eng. 2018, 140, 094503. [Google Scholar] [CrossRef] [PubMed]
- Khoiy, K.A.; Biswas, D.; Decker, T.N.; Asgarian, K.T.; Loth, F.; Amini, R. Surface strains of porcine tricuspid valve septal leaflets measured in ex vivo beating hearts. J. Biomech. Eng. 2016, 138, 111006. [Google Scholar] [CrossRef]
- Spinner, E.M.; Shannon, P.; Buice, D.; Jimenez, J.H.; Veledar, E.; del Nido, P.J.; Adams, D.H.; Yoganathan, A.P. In-vitro characterization of the mechanisms responsible for functional tricuspid regurgitation. Circulation 2011, 124, 920–929. [Google Scholar] [CrossRef]
- Malinowski, M.; Jazwiec, T.; Goehler, M.; Quay, N.; Bush, J.; Jovinge, S.; Rausch, M.K.; Timek, T.A. Sonomicrometry-derived 3-dimensional geometry of the human tricuspid annulus. J. Thorac. Cardiovasc. Surg. 2019, 157, 1452–1461. [Google Scholar] [CrossRef]
- Pant, A.D.; Thomas, V.S.; Black, A.L.; Verba, T.; Lesicko, J.G.; Amini, R. Pressure-induced microstructural changes in porcine tricuspid valve leaflets. Acta Biomater. 2018, 67, 248–258. [Google Scholar] [CrossRef]
- Basu, A.; He, Z. Annulus tension on the tricuspid valve: an in-vitro study. Cardiovasc. Eng. Technol. 2016, 7, 270–279. [Google Scholar] [CrossRef]
- Troxler, L.G.; Spinner, E.M.; Yoganathan, A.P. Measurement of strut chordal forces of the tricuspid valve using miniature C ring transducers. J. Biomech. 2012, 45, 1084–1091. [Google Scholar] [CrossRef]
- Arts, T.; Meerbaum, S.; Reneman, R.; Corday, E. Stresses in the closed mitral valve: A model study. J. Biomech. 1983, 16, 539–547. [Google Scholar] [CrossRef]
- Khoiy, K.A.; Amini, R. On the biaxial mechanical response of porcine tricuspid valve leaflets. J. Biomech. Eng. 2016, 138, 104504–104506. [Google Scholar] [CrossRef]
- Aggarwal, A.; Ferrari, G.; Joyce, E.; Daniels, M.J.; Sainger, R.; Gorman, J.H., III; Gorman, R.; Sacks, M.S. Architectural trends in the human normal and bicuspid aortic valve leaflet and its relevance to valve disease. Ann. Biomed. Eng. 2014, 42, 986–998. [Google Scholar] [CrossRef]
- Aggarwal, A.; Sacks, M.S. A framework for determination of heart valves’ mechanical properties using inverse-modeling approach. In Proceedings of the International Conference on Functional Imaging and Modeling of the Heart, Maastricht, The Netherlands, 25–27 June 2015; pp. 285–294. [Google Scholar]
- Aggarwal, A.; Sacks, M.S. An inverse modeling approach for semilunar heart valve leaflet mechanics: Exploitation of tissue structure. Biomech. Model. Mechanobiol. 2016, 15, 909–932. [Google Scholar] [CrossRef]
- Abbasi, M.; Barakat, M.S.; Dvir, D.; Azadani, A.N. A non-invasive material characterization framework for bioprosthetic heart valves. Ann. Biomed. Eng. 2019, 47, 97–112. [Google Scholar] [CrossRef]
- Jett, S.; Laurence, D.; Kunkel, R.; Babu, A.R.; Kramer, K.; Baumwart, R.; Towner, R.; Wu, Y.; Lee, C.-H. Biaxial mechanical data of porcine atrioventricular valve leaflets. Data in Brief 2018, 21, 358–363. [Google Scholar] [CrossRef]
- Pokutta-Paskaleva, A.; Sulejmani, F.; DelRocini, M.; Sun, W. Comparative mechanical, morphological, and microstructural characterization of porcine mitral and tricuspid leaflets and chordae tendineae. Acta Biomater. 2019, 85, 241–252. [Google Scholar] [CrossRef]
- Ross, C.; Laurence, D.; Wu, Y.; Lee, C.-H. Biaxial mechanical characterizations of atrioventricular heart valves. J. Vis. Exp. 2019, 146, e59170. [Google Scholar] [CrossRef]
- Pham, T.; Sulejmani, F.; Shin, E.; Wang, D.; Sun, W. Quantification and comparison of the mechanical properties of four human cardiac valves. Acta Biomater. 2017, 54, 345–355. [Google Scholar] [CrossRef]
- Laurence, D.; Ross, C.; Jett, S.; Johns, C.; Echols, A.; Baumwart, R.; Towner, R.; Liao, J.; Bajona, P.; Wu, Y.; et al. An investigation of regional variations in the biaxial mechanical properties and stress relaxation behaviors of porcine atrioventricular heart valve leaflets. J. Biomech. 2019, 83, 16–27. [Google Scholar] [CrossRef]
- Kunzelman, K.S.; Cochran, R.P.; Murphree, S.S.; Ring, W.S.; Verrier, E.D.; Eberhart, R.C. Differential collagen distribution in the mitral valve and its influence on biomechanical behaviour. J. Heart. Valve Dis. 1993, 2, 236–244. [Google Scholar]
- Lee, C.-H.; Rabbah, J.-P.; Yoganathan, A.P.; Gorman, R.C.; Gorman, J.H., III; Sacks, M.S. On the effects of leaflet microstructure and constitutive model on the closing behavior of the mitral valve. Biomech. Model. Mechanobiol. 2015, 14, 1281–1302. [Google Scholar] [CrossRef]
- Goth, W.; Potter, S.; Allen, A.C.B.; Zoldan, J.; Sacks, M.S.; Tunnell, J.W. Non-destructive reflectance mapping of collagen fiber alignment in heart valve leaflets. Ann. Biomed. Eng. 2019, 47, 1250–1264. [Google Scholar] [CrossRef]
- Alavi, S.H.; Sinha, A.; Steward, E.; Milliken, J.C.; Kheradvar, A. Load-dependent extracellular matrix organization in atrioventricular heart valves: Differences and similarities. Am. J. Physiol. Heart Circ. Physiol. 2015, 309, H276–H284. [Google Scholar] [CrossRef]
- Basu, A.; Lacerda, C.; He, Z. Mechanical Properties and Composition of the Basal Leaflet-Annulus Region of the Tricuspid Valve. Cardiovasc. Eng. Technol. 2018, 9, 217–225. [Google Scholar] [CrossRef]
- Fu, J.-T.; Popal, M.S.; Jiao, Y.-Q.; Zhang, H.-B.; Zheng, S.; Hu, Q.-M.; Han, W.; Meng, X. A predictor for mitral valve repair in patient with rheumatic heart disease: the bending angle of anterior mitral leaflet. J. Thorac. Dis. 2018, 10, 2908. [Google Scholar] [CrossRef]
- Merryman, W.D.; Engelmayr, G.C., Jr.; Liao, J.; Sacks, M.S. Defining biomechanical endpoints for tissue engineered heart valve leaflets from native leaflet properties. Prog. Pediatr. Cardiol. 2006, 21, 153–160. [Google Scholar] [CrossRef]
- Brazile, B.; Wang, B.; Wang, G.; Bertucci, R.; Prabhu, R.; Patnaik, S.S.; Butler, J.R.; Claude, A.; Brinkman-Ferguson, E.; Williams, L.N. On the bending properties of porcine mitral, tricuspid, aortic, and pulmonary valve leaflets. J. Long Term Effects Med. Implants 2015, 25, 41–53. [Google Scholar] [CrossRef]
- Amoroso, N.J.; D’Amore, A.; Hong, Y.; Rivera, C.P.; Sacks, M.S.; Wagner, W.R. Microstructural manipulation of electrospun scaffolds for specific bending stiffness for heart valve tissue engineering. Acta Biomater. 2012, 8, 4268–4277. [Google Scholar] [CrossRef]
- Amini, R.; Eckert, C.E.; Koomalsingh, K.; McGarvey, J.; Minakawa, M.; Gorman, J.H., III; Gorman, R.C.; Sacks, M.S. On the in-vivo deformation of the mitral valve anterior leaflet: effects of annular geometry and referential configuration. Ann. Biomed. Eng. 2012, 40, 1455–1467. [Google Scholar] [CrossRef]
- Arzani, A.; Mofrad, M.R.K. A strain-based finite element model for calcification progression in aortic valves. J. Biomech. 2017, 65, 216–220. [Google Scholar] [CrossRef]
- Kunzelman, K.S.; Reimink, M.S.; Cochran, R.P. Annular dilatation increases stress in the mitral valve and delays coaptation: A finite element computer model. Cardiovasc. Surg. 1997, 5, 427–434. [Google Scholar] [CrossRef]
- Lee, C.-H.; Carruthers, C.A.; Ayoub, S.; Gorman, R.C.; Gorman, J.H., III; Sacks, M.S. Quantification and simulation of layer-specific mitral valve interstitial cells deformation under physiological loading. J. Theor. Biol. 2015, 373, 26–39. [Google Scholar] [CrossRef]
- Li, J.; Luo, X.Y.; Kuang, Z.B. A nonlinear anisotropic model for porcine aortic heart valves. J. Biomech. 2001, 34, 1279–1289. [Google Scholar] [CrossRef]
- Prot, V.; Skallerud, B. Nonlinear solid finite element analysis of mitral valves with heterogeneous leaflet layers. Comput. Mech. 2009, 43, 353–368. [Google Scholar] [CrossRef]
- Rego, B.V.; Sacks, M.S. A functionally graded material model for the transmural stress distribution of the aortic valve leaflet. J. Biomech. 2017, 54, 88–95. [Google Scholar] [CrossRef]
- Sacks, M.S. Incorporation of experimentally-derived fiber orientation into a structural constitutive model for planar collagenous tissues. J. Biomech. Eng. 2003, 125, 280–287. [Google Scholar] [CrossRef]
- Shah, S.R.; Vyavahare, N.R. The effect of glycosaminoglycan stabilization on tissue buckling in bioprosthetic heart valves. Biomaterials 2008, 29, 1645–1653. [Google Scholar] [CrossRef]
- Rodriguez, K.J.; Piechura, L.M.; Porras, A.M.; Masters, K.S. Manipulation of valve composition to elucidate the role of collagen in aortic valve calcification. BMC Cardiovasc. Disord. 2014, 14, 29. [Google Scholar] [CrossRef]
- Kramer, K.; Ross, C.; Laurence, D.; Babu, A.; Wu, Y.; Towner, R.; Mir, A.; Burkhart, H.M.; Holzapfel, G.A.; Lee, C.-H. An investigation of layer-specific tissue biomechanics of porcine atrioventricular heart valve leaflets. Acta Biomater. Under review.
- Lim, K.O. Mechanical properties and ultrastructure of normal human tricuspid valve chordae tendineae. Jpn. J. Physiol. 1980, 30, 455–464. [Google Scholar] [CrossRef]
- Lim, K.O.; Boughner, D.R. Mechanical properties of human mitral valve chordae tendineae: Variation with size and strain rate. Can. J. Physiol. Pharmacol. 1975, 53, 330–339. [Google Scholar] [CrossRef]
- Ritchie, J.; Jimenez, J.; He, Z.; Sacks, M.S.; Yoganathan, A.P. The material properties of the native porcine mitral valve chordae tendineae: An in-vitro investigation. J. Biomech. 2006, 39, 1129–1135. [Google Scholar] [CrossRef]
- Roberts, N.; Morticelli, L.; Jin, Z.; Ingham, E.; Korossis, S. Regional biomechanical and histological characterization of the mitral valve apparatus: Implications for mitral repair strategies. J. Biomech. 2016, 49, 2491–2501. [Google Scholar] [CrossRef]
- Sedransk, K.L.; Grande-Allen, K.J.; Vesely, I. Failure mechanics of mitral valve chordae tendineae. J. Heart. Valve Dis. 2002, 11, 644–650. [Google Scholar] [PubMed]
- Wilcox, A.G.; Buchan, K.G.; Espino, D.M. Frequency and diameter dependent viscoelastic properties of mitral valve chordae tendineae. J. Mech. Behav. Biomed. Mater. 2014, 30, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Zuo, K.; Pham, T.; Li, K.; Martin, C.; He, Z.; Sun, W. Characterization of biomechanical properties of aged human and ovine mitral valve chordae tendineae. J. Mech. Behav. Biomed. Mater. 2016, 62, 607–618. [Google Scholar] [CrossRef]
- Kunzelman, K.S.; Cochran, R.P.; Chuong, C.; Ring, W.S.; Verrier, E.D.; Eberhart, R.D. Finite element analysis of the mitral valve. J. Heart. Valve Dis. 1993, 2, 326–340. [Google Scholar]
- Hamid, M.S.; Sabbah, H.N.; Stein, P.D. Vibrational analysis of bioprosthetic heart valve leaflets using numerical models: Effects of leaflet stiffening, calcification, and perforation. Circul. Res. 1987, 61, 687–694. [Google Scholar] [CrossRef]
- Lee, C.-H.; Amini, R.; Gorman, R.C.; Gorman, J.H., 3rd; Sacks, M.S. An inverse modeling approach for stress estimation in mitral valve anterior leaflet valvuloplasty for in-vivo valvular biomaterial assessment. J. Biomech. 2014, 47, 2055–2063. [Google Scholar] [CrossRef]
- Prot, V.; Skallerud, B.; Sommer, G.; Holzapfel, G.A. On modelling and analysis of healthy and pathological human mitral valves: Two case studies. J. Mech. Behav. Biomed. Mater. 2010, 3, 167–177. [Google Scholar] [CrossRef]
- Lee, C.-H.; Amini, R.; Sakamoto, Y.; Carruthers, C.A.; Aggarwal, A.; Gorman, R.C.; Gorman, J.H., III; Sacks, M.S. Mitral valves: A computational framework. In Multiscale Modeling in Biomechanics and Mechanobiology; Springer: Berlin, Germany, 2015; pp. 223–255. [Google Scholar]
- Lee, C.-H.; Oomen, P.J.A.; Rabbah, J.P.; Yoganathan, A.; Gorman, R.C.; Gorman, J.H., III; Amini, R.; Sacks, M.S. A high-fidelity and micro-anatomically accurate 3D finite element model for simulations of functional mitral valve. In Proceedings of the International Conference on Functional Imaging and Modeling of the Heart, London, UK, 20–22 June 2013; pp. 416–424. [Google Scholar]
- Wang, Q.; Sun, W. Finite element modeling of mitral valve dynamic deformation using patient-specific multi-slices computed tomography scans. Ann. Biomed. Eng. 2013, 41, 142–153. [Google Scholar] [CrossRef]
- Kunzelman, K.S.; Einstein, D.R.; Cochran, R.P. Fluid–structure interaction models of the mitral valve: function in normal and pathological states. Philos. Trans. R. Soc. B: Biol. Sci. 2007, 362, 1393–1406. [Google Scholar] [CrossRef]
- Lau, K.D.; Diaz, V.; Scambler, P.; Burriesci, G. Mitral valve dynamics in structural and fluid–structure interaction models. Med. Eng. Phys. 2010, 32, 1057–1064. [Google Scholar] [CrossRef]
- De Hart, J.; Peters, G.W.M.; Schreurs, P.J.G.; Baaijens, F.P.T. A three-dimensional computational analysis of fluid–structure interaction in the aortic valve. J. Biomech. 2003, 36, 103–112. [Google Scholar] [CrossRef]
- Hsu, M.-C.; Kamensky, D.; Bazilevs, Y.; Sacks, M.S.; Hughes, T.J. Fluid–structure interaction analysis of bioprosthetic heart valves: Significance of arterial wall deformation. Comput. Mech. 2014, 54, 1055–1071. [Google Scholar] [CrossRef]
- Hsu, M.-C.; Kamensky, D.; Xu, F.; Kiendl, J.; Wang, C.; Wu, M.C.; Mineroff, J.; Reali, A.; Bazilevs, Y.; Sacks, M.S. Dynamic and fluid–structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung-type material models. Comput. Mech. 2015, 55, 1211–1225. [Google Scholar] [CrossRef]
- Billiar, K.L.; Sacks, M.S. Biaxial mechanical properties of the native and glutaraldehyde-treated aortic valve cusp: Part II—A structural constitutive model. J. Biomech. Eng. 2000, 122, 327–335. [Google Scholar] [CrossRef]
- Morganti, S.; Conti, M.; Aiello, M.; Valentini, A.; Mazzola, A.; Reali, A.; Auricchio, F. Simulation of transcatheter aortic valve implantation through patient-specific finite element analysis: Two clinical cases. J. Biomech. 2014, 47, 2547–2555. [Google Scholar] [CrossRef]
- Wang, Q.; Sirois, E.; Sun, W. Patient-specific modeling of biomechanical interaction in transcatheter aortic valve deployment. J. Biomech. 2012, 45, 1965–1971. [Google Scholar] [CrossRef]
- Nicosia, M.A.; Cochran, R.P.; Einstein, D.R.; Rutland, C.J.; Kunzelman, K.S. A coupled fluid-structure finite element model of the aortic valve and root. J. Heart. Valve Dis. 2003, 12, 781–789. [Google Scholar] [PubMed]
- Haj-Ali, R.; Marom, G.; Zekry, S.B.; Rosenfeld, M.; Raanani, E. A general three-dimensional parametric geometry of the native aortic valve and root for biomechanical modeling. J. Biomech. 2012, 45, 2392–2397. [Google Scholar] [CrossRef]
- Stevanella, M.; Votta, E.; Lemma, M.; Antona, C.; Redaelli, A. Finite element modelling of the tricuspid valve: A preliminary study. Med. Eng. Phys. 2010, 32, 1213–1223. [Google Scholar] [CrossRef]
- Votta, E.; Caiani, E.; Veronesi, F.; Soncini, M.; Montevecchi, F.M.; Redaelli, A. Mitral valve finite-element modelling from ultrasound data: A pilot study for a new approach to understand mitral function and clinical scenarios. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2008, 366, 3411–3434. [Google Scholar] [CrossRef]
- Aversa, A.; Careddu, E. Image-Based Analysis of Tricuspid Valve Biomechanics: Towards a Novel Approach Integrating In-vitro 3D-Echocardiography and Finite Element Modelling. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2017. [Google Scholar]
- Kong, F.; Pham, T.; Martin, C.; McKay, R.; Primiano, C.; Hashim, S.; Kodali, S.; Sun, W. Finite element analysis of tricuspid valve deformation from multi-slice computed tomography images. Ann. Biomed. Eng. 2018, 46, 1112–1127. [Google Scholar] [CrossRef]
- Pouch, A.M.; Aly, A.H.; Lasso, A.; Nguyen, A.V.; Scanlan, A.B.; McGowan, F.X.; Fichtinger, G.; Gorman, R.C.; Gorman, J.H.; Yushkevich, P.A. Image segmentation and modeling of the pediatric tricuspid valve in hypoplastic left heart syndrome. In Proceedings of the International Conference on Functional Imaging and Modeling of the Heart, Toronto, ON, Canada, 11–13 June 2017; pp. 95–105. [Google Scholar]
- Kamensky, D.; Xu, F.; Lee, C.-H.; Yan, J.; Bazilevs, Y.; Hsu, M.-C. A contact formulation based on a volumetric potential: Application to isogeometric simulations of atrioventricular valves. Comput. Meth. Appl. Mech. Eng. 2018, 330, 522–546. [Google Scholar] [CrossRef]
- Thubrikar, M. Geometry of the aortic valve. In The Aortic Valve; CRC Press: Boca Raton, FL, USA, 1990; pp. 1–20. [Google Scholar]
- Labrosse, M.R.; Beller, C.J.; Robicsek, F.; Thubrikar, M.J. Geometric modeling of functional trileaflet aortic valves: Development and clinical applications. J. Biomech. 2006, 39, 2665–2672. [Google Scholar] [CrossRef] [PubMed]
- Kouhi, E.; Morsi, Y.S. A parametric study on mathematical formulation and geometrical construction of a stentless aortic heart valve. J. Artificial Organs 2013, 16, 425–442. [Google Scholar] [CrossRef]
- Fan, R.; Bayoumi, A.S.; Chen, P.; Hobson, C.M.; Wagner, W.R.; Mayer, J.E., Jr.; Sacks, M.S. Optimal elastomeric scaffold leaflet shape for pulmonary heart valve leaflet replacement. J. Biomech. 2013, 46, 662–669. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Sun, W. Simulated transcatheter aortic valve deformation: A parametric study on the impact of leaflet geometry on valve peak stress. Int. J. Numer. Method. Biomed. Eng. 2017, 33, e02814. [Google Scholar] [CrossRef]
- Xu, F.; Morganti, S.; Zakerzadeh, R.; Kamensky, D.; Auricchio, F.; Reali, A.; Hughes, T.J.; Sacks, M.S.; Hsu, M.C. A framework for designing patient-specific bioprosthetic heart valves using immersogeometric fluid–structure interaction analysis. Int. J. Numer. Method. Biomed. Eng. 2018, 34, e2938. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Meth. Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar]
- Prot, V.; Skallerud, B.; Holzapfel, G.A. Transversely isotropic membrane shells with application to mitral valve mechanics. Constitutive modelling and finite element implementation. Int. J. Numer. Meth. Eng. 2007, 71, 987–1008. [Google Scholar] [CrossRef]
- Zhang, W.; Ayoub, S.; Liao, J.; Sacks, M.S. A meso-scale layer-specific structural constitutive model of the mitral heart valve leaflets. Acta Biomater. 2016, 32, 238–255. [Google Scholar] [CrossRef]
- Singh-Gryzbon, S.; Sadri, V.; Toma, M.; Pierce, E.L.; Wei, Z.A.; Yoganathan, A.P. Development of a computational method for simulating tricuspid valve dynamics. Ann. Biomed. Eng. 2019, 47, 1422–1434. [Google Scholar] [CrossRef]
- Laurence, D.; Johnson, E.; Hsu, M.-C.; Mir, A.; Burkhart, H.M.; Wu, Y.; Lee, C.-H. Finite element simulation framework for investigating pathological effects on organ-level tricuspid valve biomechanical function. In Proceedings of the Summer Biomechanics, Bioengineering and Biotransport Conference, Seven Springs, PA, USA, 25–28 June 2019. [Google Scholar]
- Toma, M.; Bloodworth, C.H.; Einstein, D.R.; Pierce, E.L.; Cochran, R.P.; Yoganathan, A.P.; Kunzelman, K.S. High-resolution subject-specific mitral valve imaging and modeling: Experimental and computational methods. Biomech. Model. Mechanobiol. 2016, 15, 1619–1630. [Google Scholar] [CrossRef]
- Collé, A.; Limido, J.; Vila, J.-P. An accurate SPH scheme for dynamic fragmentation modelling. In Proceedings of the EPJ Web of Conferences, Arcachon, France, 9–14 September 2018; p. 01030. [Google Scholar]
- Lanson, N.; Vila, J.P. Meshless methods for conservation laws. Math. Comput. Sim. 2001, 55, 493–501. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Gingold, R.A. Shock simulation by the particle method SPH. JCoPh 1983, 52, 374–389. [Google Scholar] [CrossRef]
- Sun, P.; Colagrossi, A.; Marrone, S.; Antuono, M.; Zhang, A.M. Multi-resolution Delta-plus-SPH with tensile instability control: Towards high Reynolds number flows. CoPhC 2018, 224, 63–80. [Google Scholar] [CrossRef]
- Borazjani, I. Fluid–structure interaction, immersed boundary-finite element method simulations of bio-prosthetic heart valves. Comput. Meth. Appl. Mech. Eng. 2013, 257, 103–116. [Google Scholar] [CrossRef]
- Griffith, B.E.; Luo, X.; McQueen, D.M.; Peskin, C.S. Simulating the fluid dynamics of natural and prosthetic heart valves using the immersed boundary method. Int. J. Appl. Mech. 2009, 1, 137–177. [Google Scholar] [CrossRef]
- Griffith, B.E. Immersed boundary model of aortic heart valve dynamics with physiological driving and loading conditions. Int. J. Numer. Method. Biomed. Eng. 2012, 28, 317–345. [Google Scholar] [CrossRef]
- Espino, D.M.; Shepherd, D.E.T.; Hukins, D.W.L. Evaluation of a transient, simultaneous, arbitrary Lagrange–Euler based multi-physics method for simulating the mitral heart valve. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 450–458. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Inage, A.; Rebeyka, I.M.; Ross, D.B.; Thompson, R.B.; Mackie, A.S.; Smallhorn, J.F. Real-time 3-dimensional echocardiography provides new insight into mechanisms of tricuspid valve regurgitation in patients with hypoplastic left heart syndrome. Circulation 2009, 120, 1091. [Google Scholar] [CrossRef] [PubMed]
- Nii, M.; Guerra, V.; Roman, K.S.; Macgowan, C.K.; Smallhorn, J.F. Three-dimensional tricuspid annular function provides insight into the mechanisms of tricuspid valve regurgitation in classic hypoplastic left heart syndrome. J. Am. Soc. Echocardiogr. 2006, 19, 391–402. [Google Scholar] [CrossRef]
- Reyes, A., 2nd; Bove, E.L.; Mosca, R.S.; Kulik, T.J.; Ludomirsky, A. Tricuspid valve repair in children with hypoplastic left heart syndrome during staged surgical reconstruction. Circulation 1997, 96, II-341-3–II-344-5. [Google Scholar] [PubMed]
- Apitz, C.; Webb, G.D.; Redington, A.N. Tetralogy of Fallot. Lancet 2009, 374, 1462–1471. [Google Scholar] [CrossRef]
- Bertranou, E.G.; Blackstone, E.H.; Hazelrig, J.B.; Turner, M.E., Jr.; Kirklin, J.W. Life expectancy without surgery in Tetralogy of Fallot. Am. J. Cardiol. 1978, 42, 458–466. [Google Scholar] [CrossRef]
- Maglogiannis, I.; Loukis, E.; Zafiropoulos, E.; Stasis, A. Support vectors machine-based identification of heart valve diseases using heart sounds. Comput. Methods Programs Biomed. 2009, 95, 47–61. [Google Scholar] [CrossRef]
- Das, R.; Sengur, A. Evaluation of ensemble methods for diagnosing of valvular heart disease. Expert Syst. Appl. 2010, 37, 5110–5115. [Google Scholar] [CrossRef]


| Abbreviation | Description | |
|---|---|---|
| Anatomy | AP | Antero-posterior |
| AV | Aortic valve | |
| MV | Mitral valve | |
| PV | Pulmonary valve | |
| RA | Right atrium | |
| RV | Right ventricle | |
| SL | Septo-lateral | |
| TA | Tricuspid valve annulus | |
| TV | Tricuspid valve | |
| TVAL | Tricuspid valve anterior leaflet | |
| TVPL | Tricuspid valve posterior leaflet | |
| TVSL | Tricuspid valve septal leaflet | |
| VC | Vena contracta | |
| Computational Modeling | CAD | Computer-aided design |
| FE | Finite element | |
| FSI | Fluid-structure interaction | |
| IGA | Isogeometric analysis | |
| SPH | Smooth particle hydrodynamics | |
| Disease/Pathology | FTR | Functional tricuspid regurgitation |
| HLHS | Hypoplastic left heart syndrome | |
| ToF | Tetralogy of Fallot | |
| TR | Tricuspid regurgitation | |
| Imaging and Grading of the TR Severity | 2DE | Two-dimensional echocardiography |
| 3DE | Three-dimensional echocardiography | |
| A4C | Apical four-chamber view | |
| CT | Computed tomography | |
| CMRI | Cardiac magnetic resonance imaging | |
| EROA | Effective regurgitant orifice area | |
| ME | Mid-esophageal | |
| PISA | Proximal isovelocity surface area | |
| PLAX | Parasternal long axis | |
| PSAX | Parasternal short axis | |
| RT3DE | Real-time three-dimensional echocardiography | |
| RVEIO | Right ventricular early inflow-outflow | |
| RVF | Right ventricular-focused | |
| RVIF | Right ventricular inflow | |
| R Vol | Regurgitant jet volume | |
| TEE | Transesophageal echocardiography | |
| TTE | Transthoracic echocardiography | |
| Mechanics | C | Right Cauchy-Green tensor |
| ECC | Green strain in the tissue’s circumferential direction | |
| ERR | Green strain in the tissue’s radial direction | |
| Fx | Force in the x-direction | |
| Fy | Force in the y-direction | |
| I1 | First invariant of the right Cauchy-Green tensor C | |
| I4 | Fourth invariant of the right Cauchy-Green tensor C | |
| λ | Stretch ratio | |
| Tcirc | Membrane tension in the circumferential direction | |
| Trad | Membrane tension in the radial direction | |
| Microstructure | A | Atrialis layer |
| ECM | Extracellular matrix | |
| F | Fibrosa layer | |
| GAGs | Glycosaminoglycans | |
| PGs | Proteoglycans | |
| S | Spongiosa layer | |
| SMC | Smooth muscle cell | |
| V | Ventricularis layer | |
| VIC | Valvular interstitial cell | |
| Specimen Labels | -C | Control specimen |
| -T | Treated specimen | |
| A/S | Atrialis/spongiosa layer | |
| F/V | Fibrosa/ventricularis layer | |
| LG | Left chordae group | |
| RG | Right chordae group |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-H.; Laurence, D.W.; Ross, C.J.; Kramer, K.E.; Babu, A.R.; Johnson, E.L.; Hsu, M.-C.; Aggarwal, A.; Mir, A.; Burkhart, H.M.; et al. Mechanics of the Tricuspid Valve—From Clinical Diagnosis/Treatment, In-Vivo and In-Vitro Investigations, to Patient-Specific Biomechanical Modeling. Bioengineering 2019, 6, 47. https://doi.org/10.3390/bioengineering6020047
Lee C-H, Laurence DW, Ross CJ, Kramer KE, Babu AR, Johnson EL, Hsu M-C, Aggarwal A, Mir A, Burkhart HM, et al. Mechanics of the Tricuspid Valve—From Clinical Diagnosis/Treatment, In-Vivo and In-Vitro Investigations, to Patient-Specific Biomechanical Modeling. Bioengineering. 2019; 6(2):47. https://doi.org/10.3390/bioengineering6020047
Chicago/Turabian StyleLee, Chung-Hao, Devin W. Laurence, Colton J. Ross, Katherine E. Kramer, Anju R. Babu, Emily L. Johnson, Ming-Chen Hsu, Ankush Aggarwal, Arshid Mir, Harold M. Burkhart, and et al. 2019. "Mechanics of the Tricuspid Valve—From Clinical Diagnosis/Treatment, In-Vivo and In-Vitro Investigations, to Patient-Specific Biomechanical Modeling" Bioengineering 6, no. 2: 47. https://doi.org/10.3390/bioengineering6020047
APA StyleLee, C.-H., Laurence, D. W., Ross, C. J., Kramer, K. E., Babu, A. R., Johnson, E. L., Hsu, M.-C., Aggarwal, A., Mir, A., Burkhart, H. M., Towner, R. A., Baumwart, R., & Wu, Y. (2019). Mechanics of the Tricuspid Valve—From Clinical Diagnosis/Treatment, In-Vivo and In-Vitro Investigations, to Patient-Specific Biomechanical Modeling. Bioengineering, 6(2), 47. https://doi.org/10.3390/bioengineering6020047







