A Study of the Biomechanical Behavior of the Implantation Method of Inverted Shoulder Prosthesis (BIO–RSA) under Different Abduction Movements
Abstract
:1. Introduction
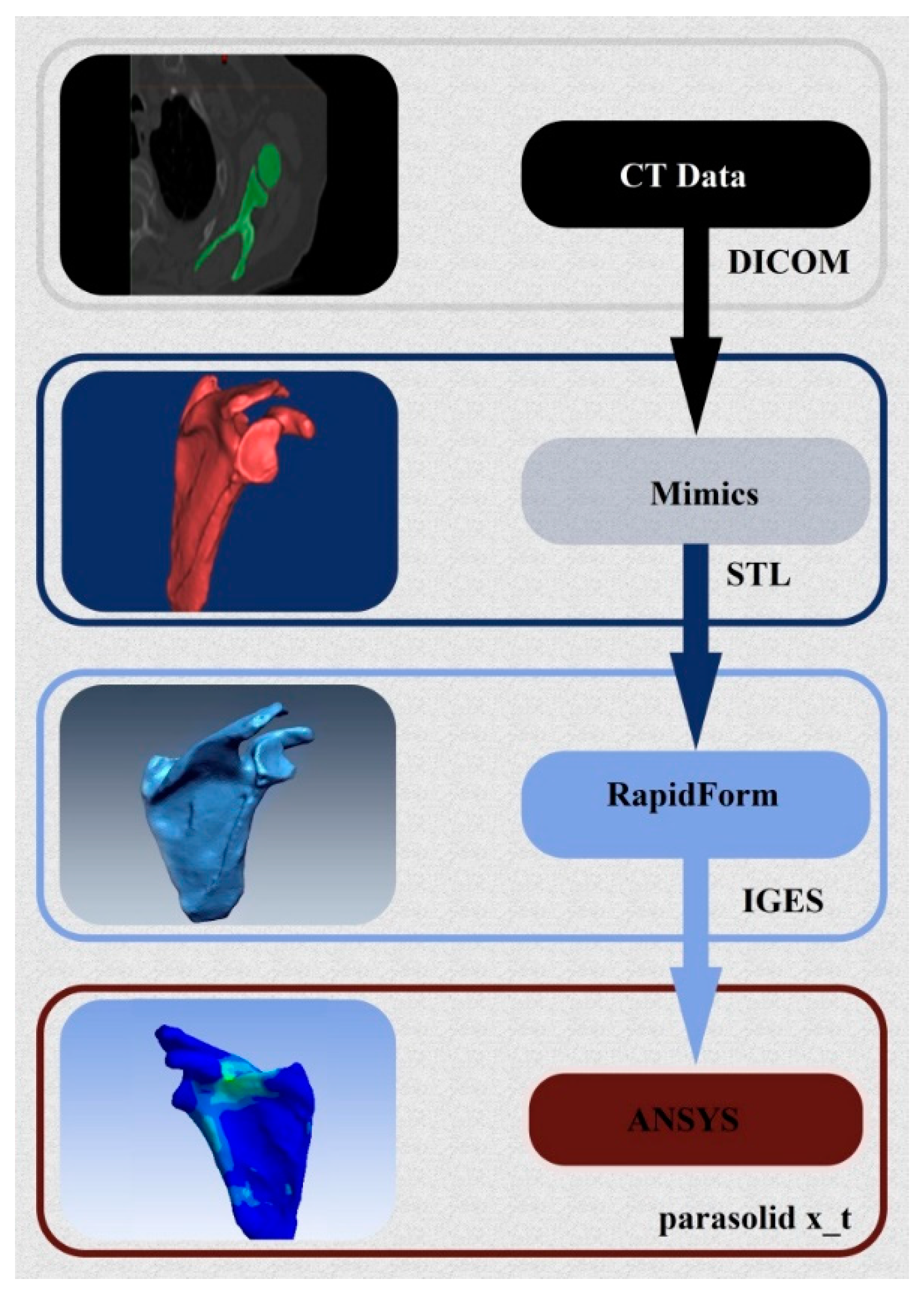
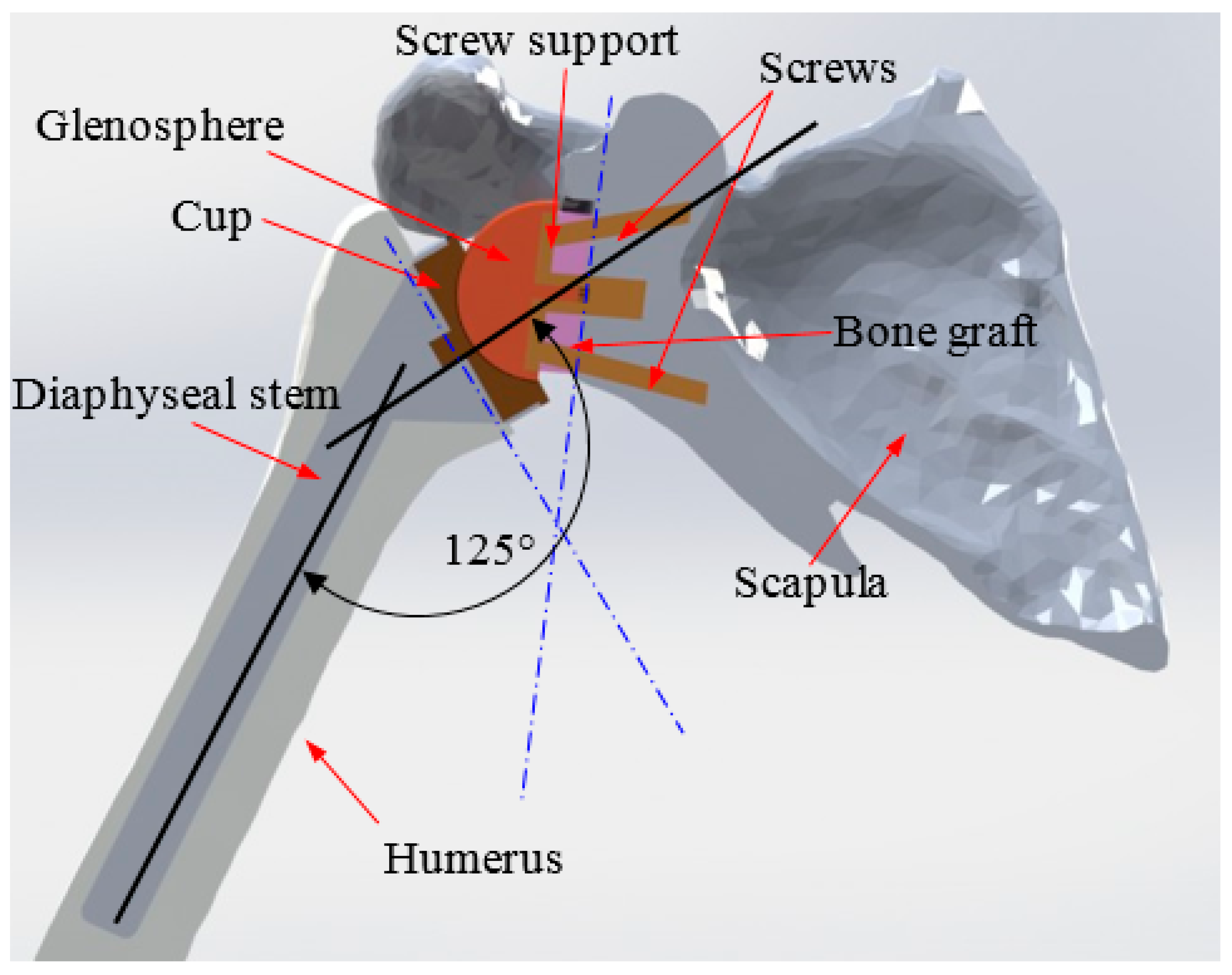
2. 3D Reconstruction and Conception of the Shoulder Prosthesis
3. Finite Element Modeling
3.1. Mechanical Properties
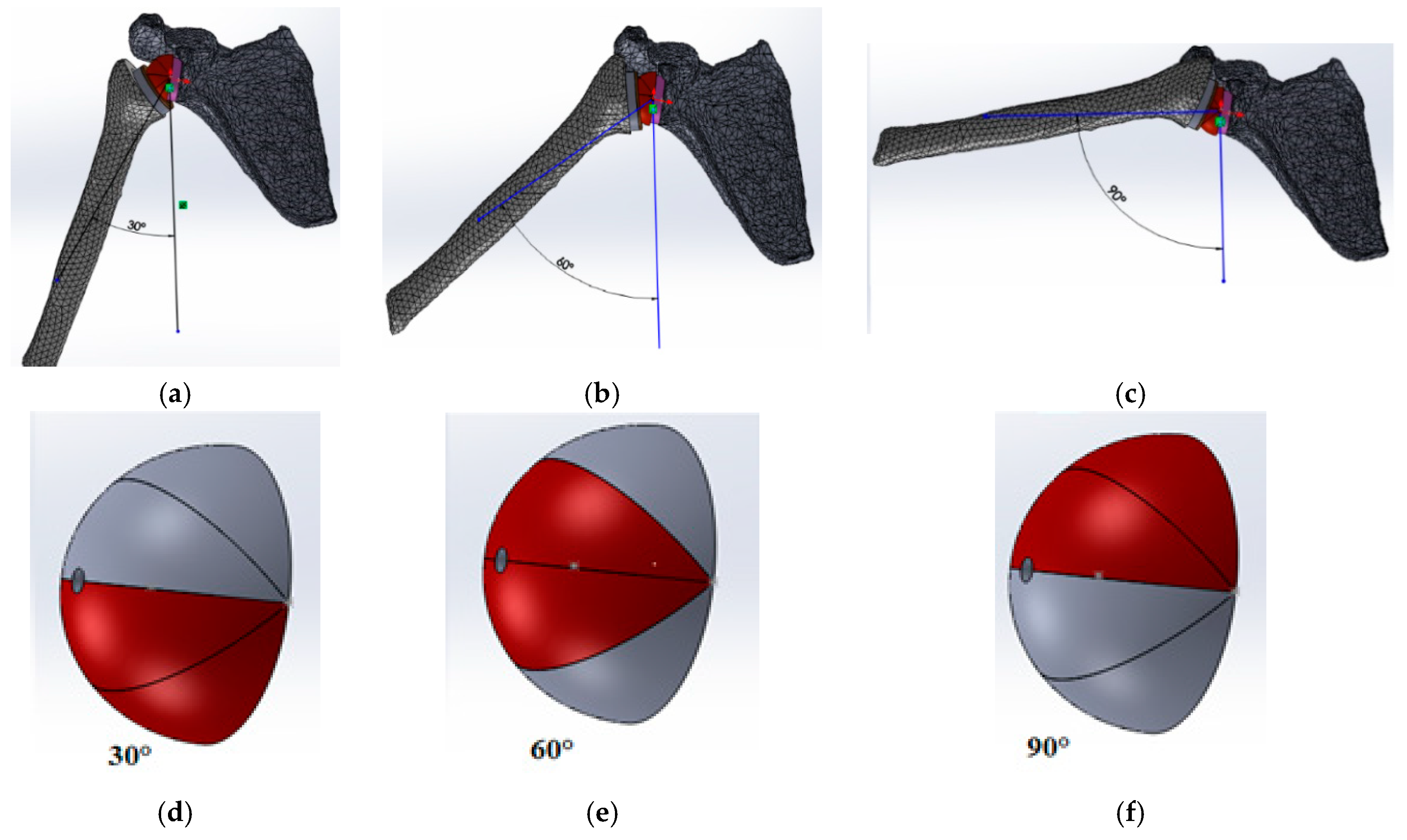
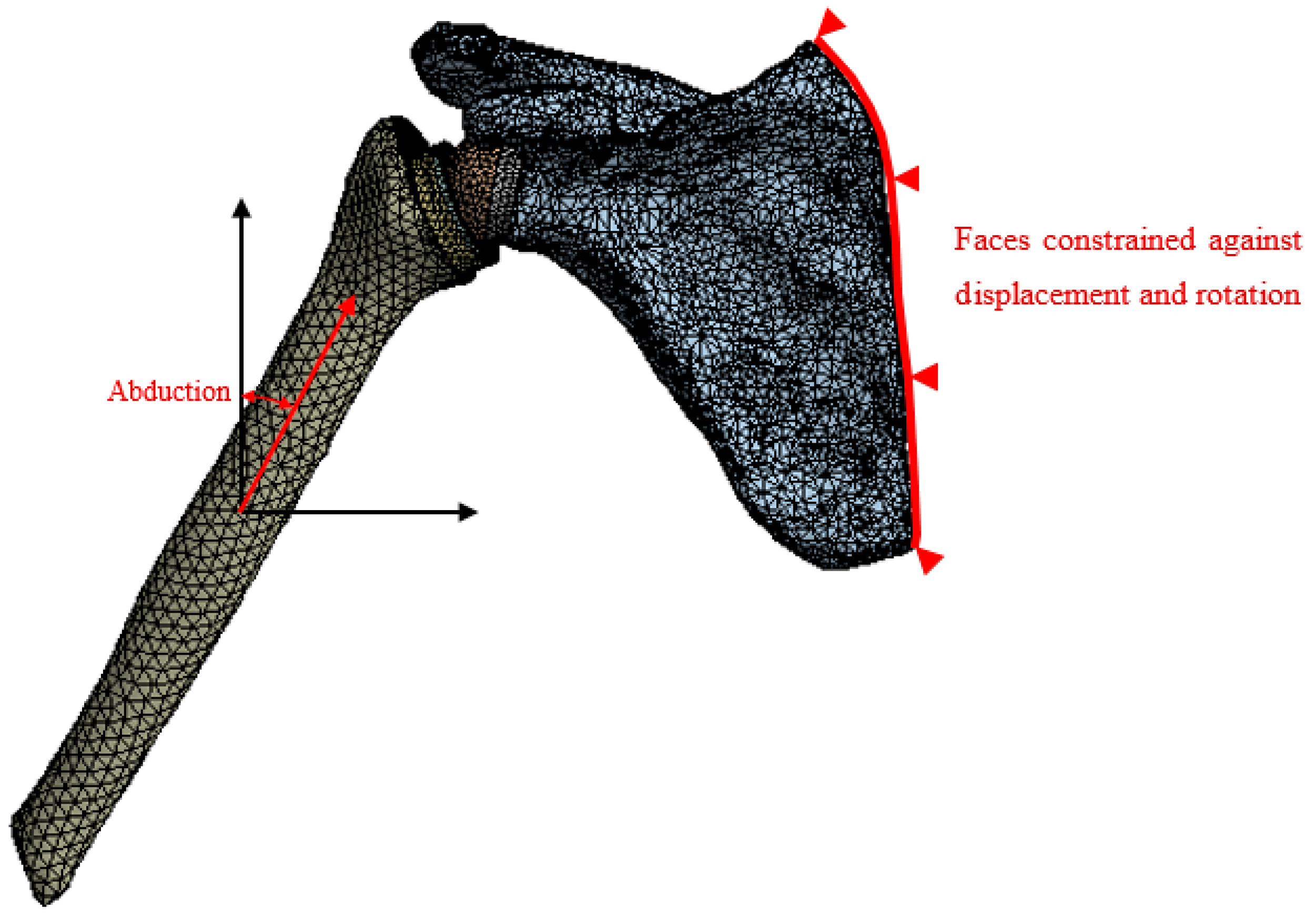
3.2. Loading Conditions
4. Results and Discussion
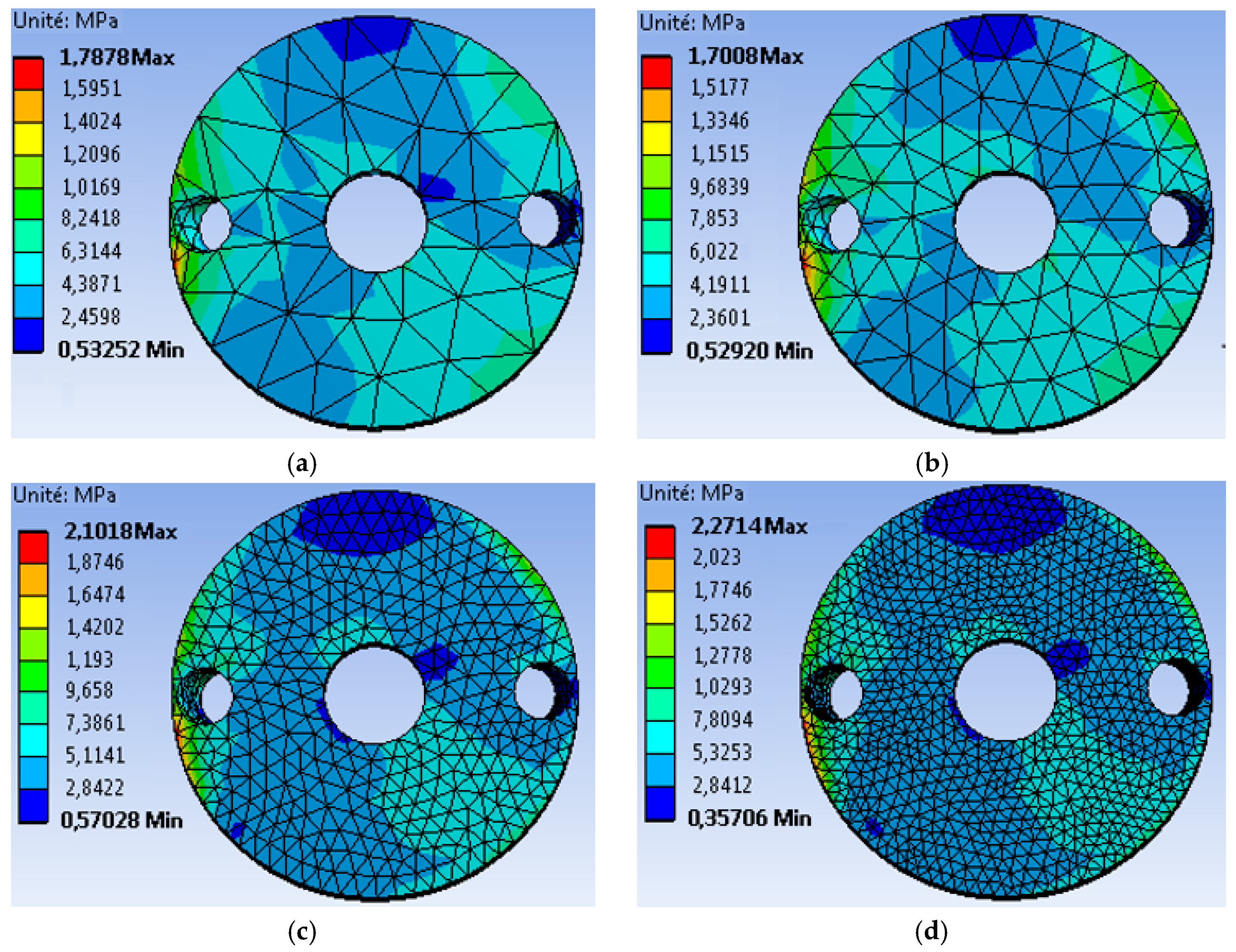
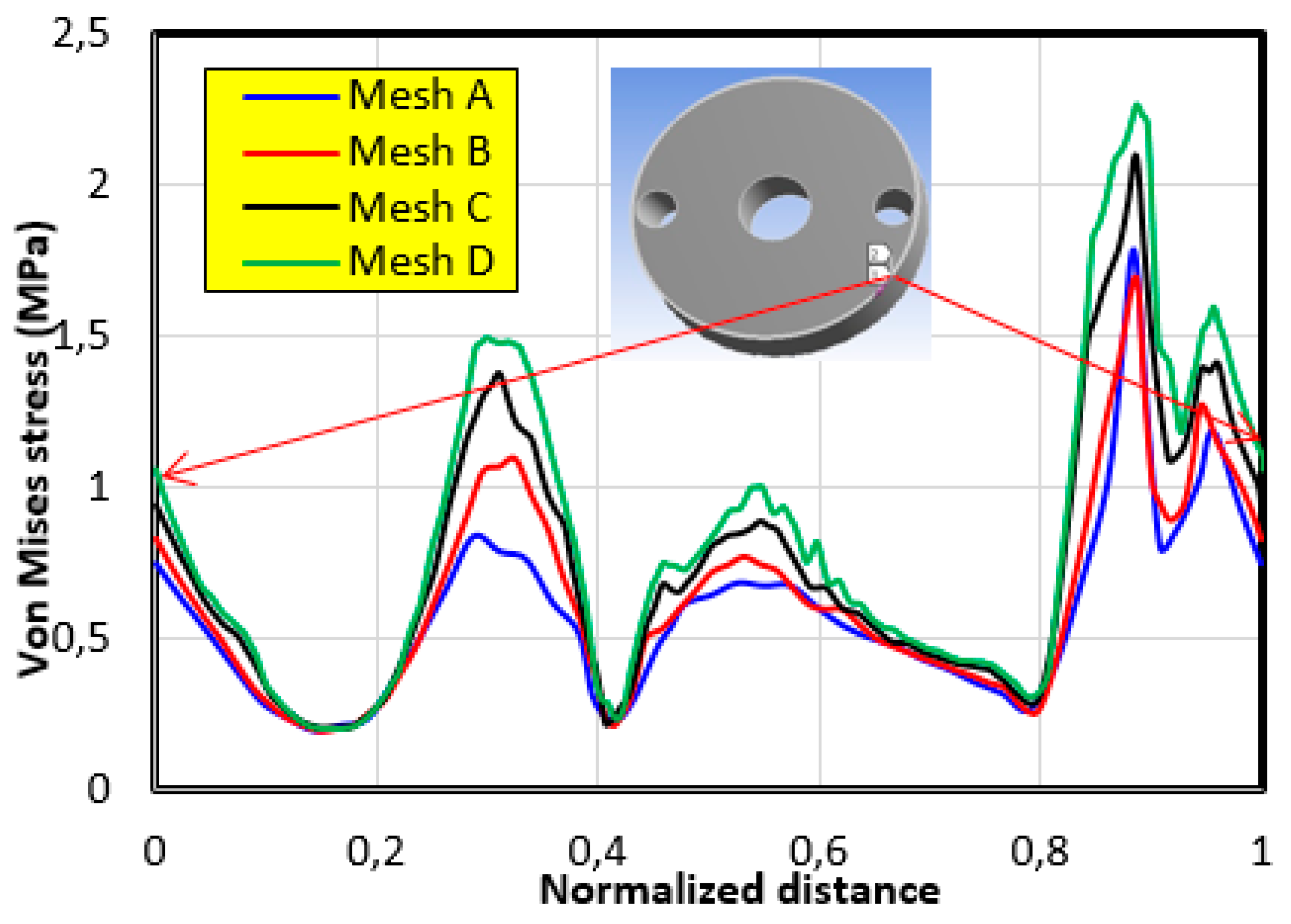
4.1. The Mesh Sensitivity Study
- The first mesh (a) of a size of 5 mm was composed of 49,866 tetrahedral elements with 86,186 nodes.
- The second mesh (b) of a medium size (3 mm) was composed of 51,061 tetrahedral elements with 88,109 nodes.
- The third mesh (c) of a fine size (1.5 mm) was composed of 62,567 tetrahedral elements with 105261 nodes.
- The fourth mesh (d) of a very fine size (1 mm) was composed of 93,929 tetrahedral elements with 150,252 nodes.
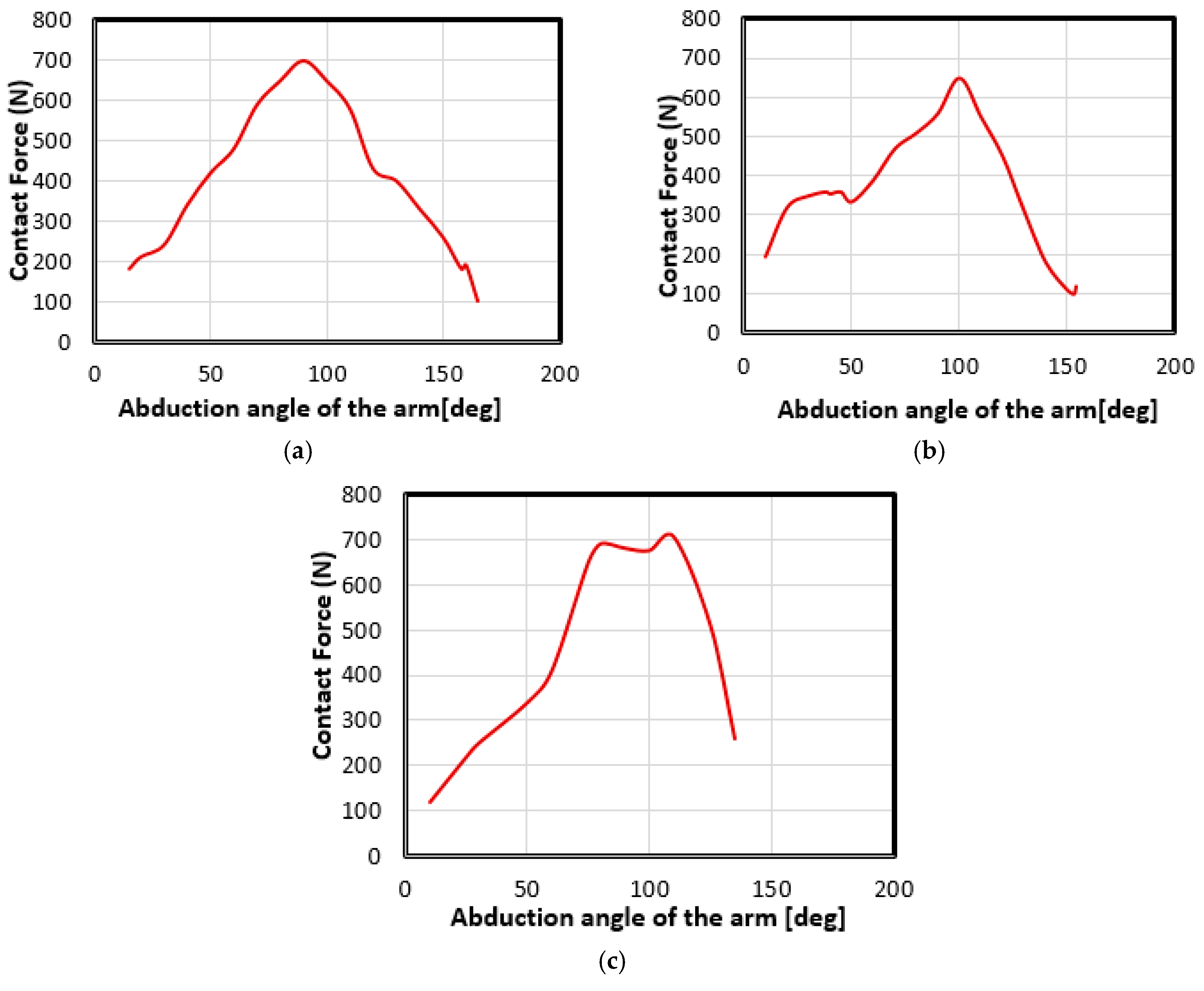
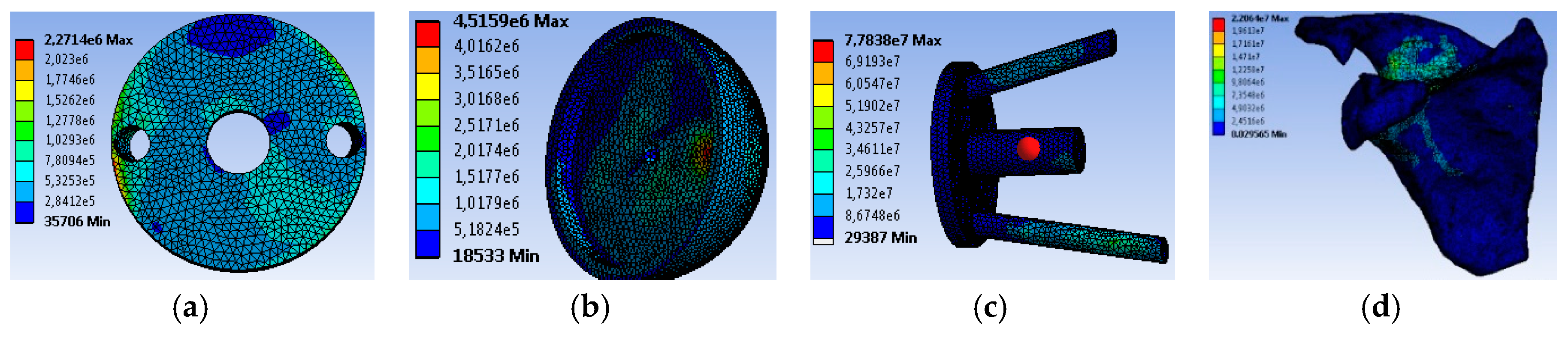
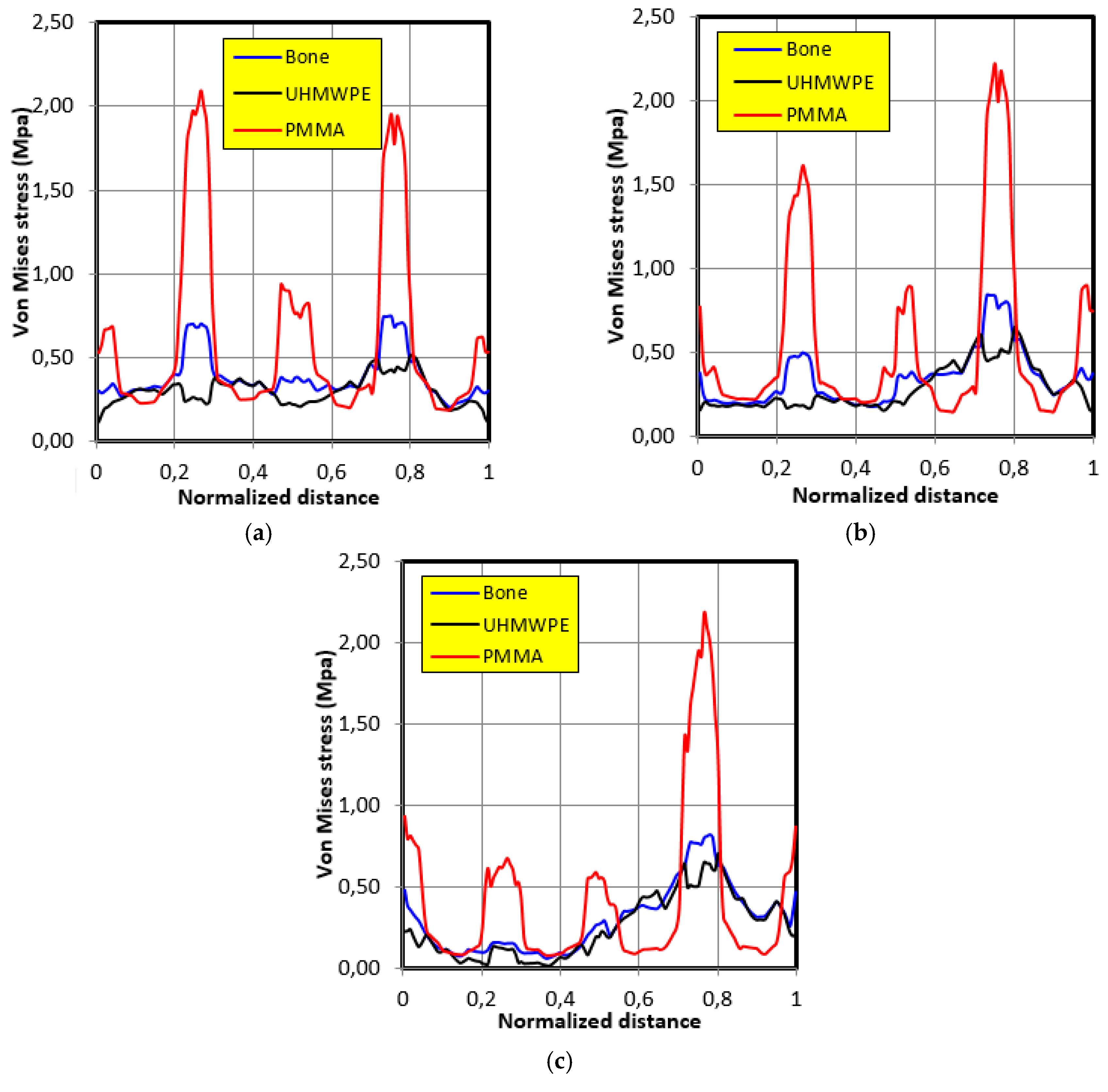
4.2. Movement Case of Individual 1
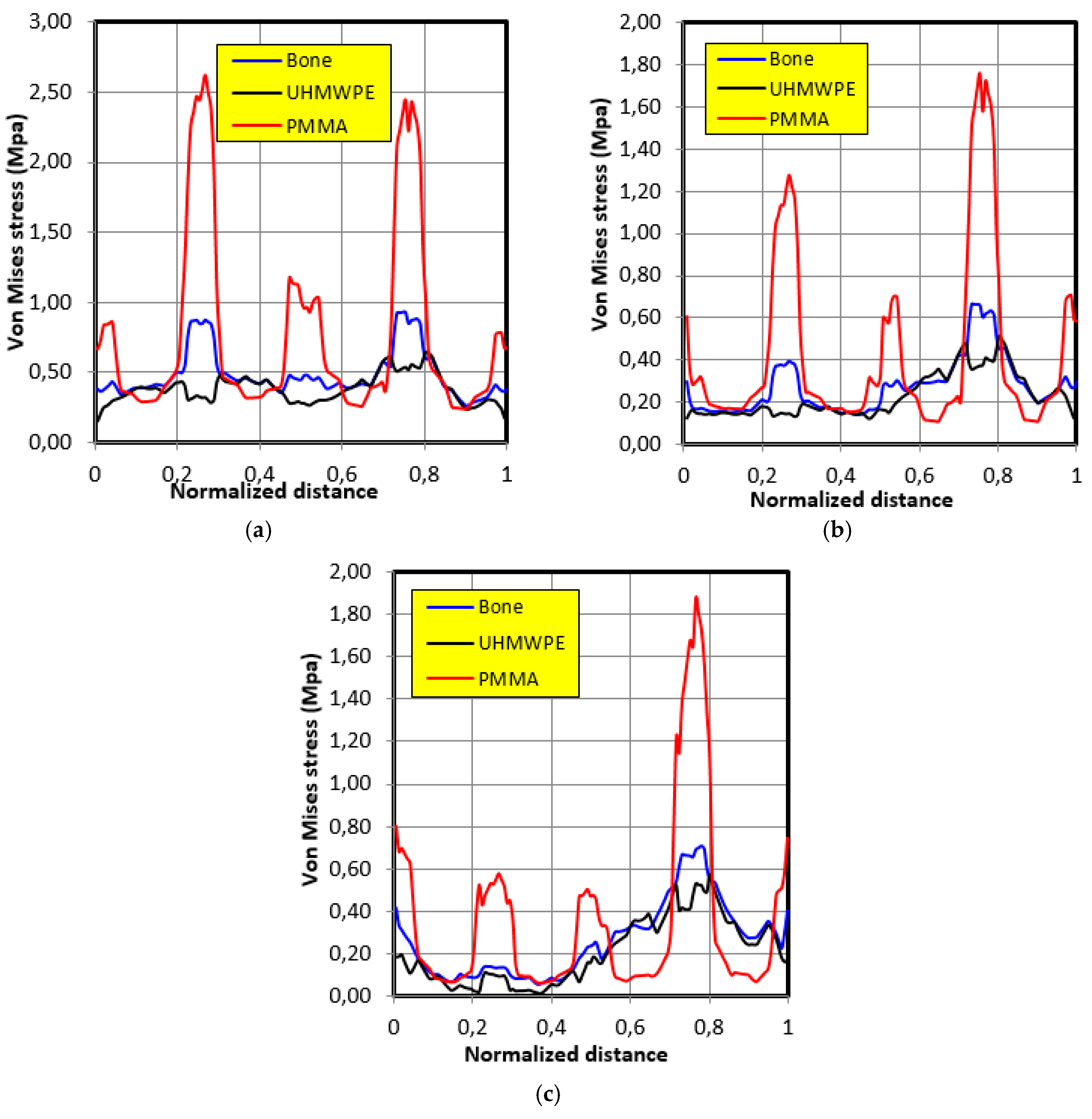
4.3. Movement Case of Individual 2
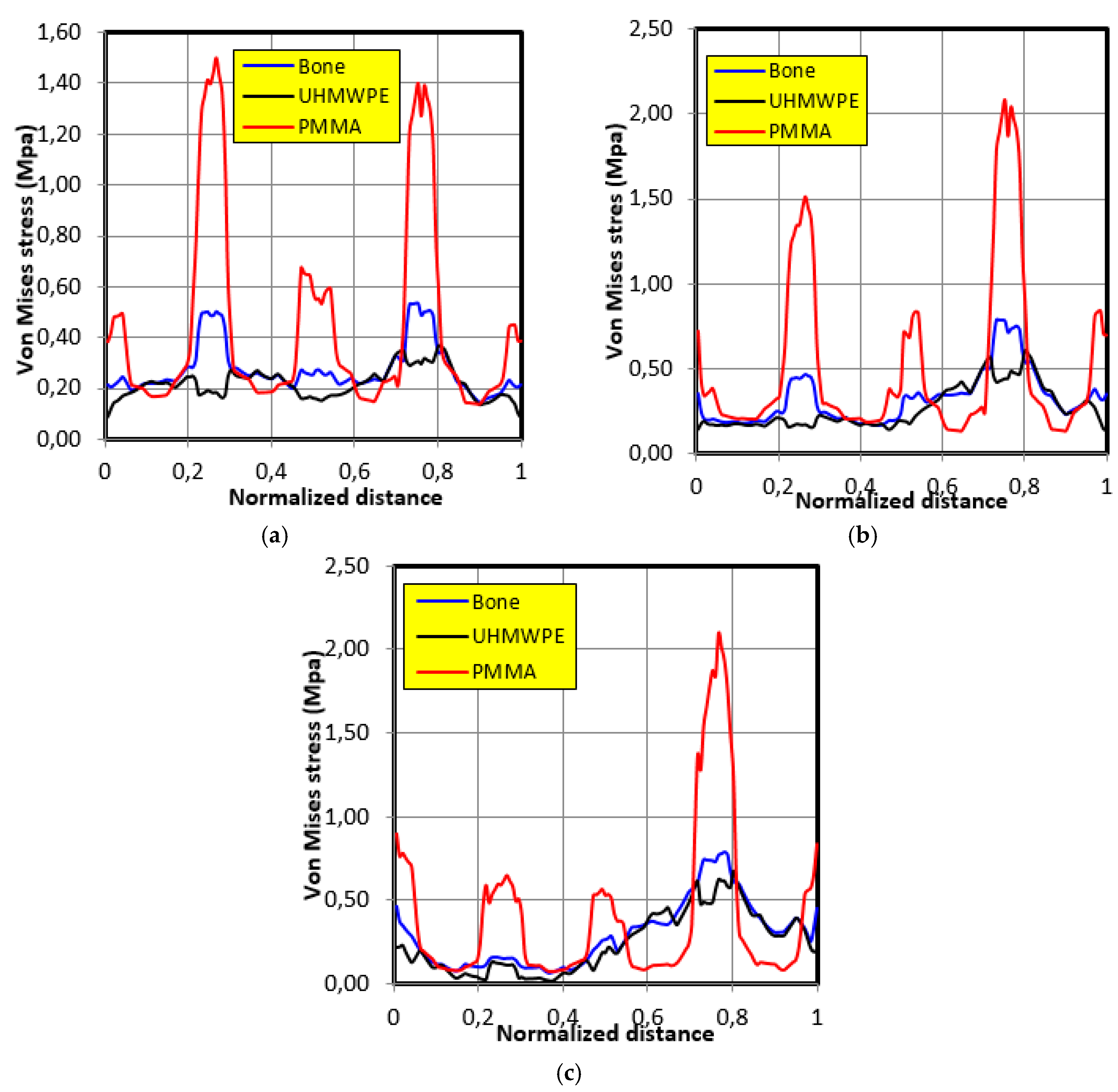
4.4. Movement Case of Individual 3
5. Conclusion
- To obtain reliable results, we must use bio-faithful geometric models with a fine mesh.
- The graft of ultra-high molecular weight polyethylene (UHMWPE) has a closer mechanical response to that of bone compared to poly methacrylate (PMMA). So, grafts made of UHMWPE minimize stress and better protect the prosthesis from the risk of fatigue failure.
- The maximum stress on the graft varies significantly depending on the properties of the graft, the position of the contact surface and the individual.
Author Contributions
Funding
Conflicts of Interest
References
- Astier, V.; Arnoux, P.J.; Thollon, L.; Mouret, F.; Brunet, C. Finite element simulation of humeral intramedullary nailing: Case of torsion loading. Presented at 2nd European Hyperworks Technology Conference Strasbourg, Strasbourg, France, September 2008. [Google Scholar]
- Walch, G.; Edwards, T.B.; Boulahia, A.; Nové-Josserand, L.; Neyton, L.; Szabo, I. Arthroscopic tenotomy of the long head of the biceps in the treatment of rotator cuff tears: Clinical and radiographic results of 307 cases. J. Shoulder Elbow Surg. 2005, 14, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Lévigne, C.; Lacroix, P. Jérome Shoulder arthroplasty in 2010 anatomical or reversed, prosthesis? Indications and contra-indications. Rev. Rhum. Monogr. 2010, 77, 195–200. [Google Scholar]
- Boussakri, H.; Alassaf, I.; Hammoudi, S.; Elidrissi, M.; Shimi, M.; Elibrahimi, A.; Elmrini, A.; Dumez, J.F. Total bilateral reverse shoulder prosthesis: About two cases. Pan Afr. Med. J. 2015, 20, 272. [Google Scholar] [PubMed]
- Lock, C.; Allgar, V.; Jones, K.; Marples, G.; Chandler, C.; Dawson, P. Prevalence of back, neck and shoulder problems in the inner city. Physiother. Res. Int. 1999, 4, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Boileau, P. Complications and revision of reverse total shoulder arthroplasty. Orthop. Traumatol. Surg. Res. 2016, 102, S33–S43. [Google Scholar] [CrossRef]
- Frankle, M.; Siegal, S.; Pupello, D.; Saleem, A.; Mighell, M.; Vasey, M. The Reverse Shoulder Prosthesis for glenohumeral arthritis associated with severe rotator cuff deficiency. A minimum two-year follow-up study of sixty patients. J. Bone Jt. Surg. Am. 2005, 87, 1697–1705. [Google Scholar] [CrossRef] [PubMed]
- Kolmodin, J.; Davidson, I.U.; Jun, B.J.; Sodhi, N.; Subhas, N.; Patterson, T.E.; Li, Z.M.; Iannotti, J.P.; Ricchetti, E.T. Scapular Notching After Reverse Total Shoulder Arthroplasty. J. Bone Jt. Surg. 2018, 100, 1095–1103. [Google Scholar] [CrossRef] [PubMed]
- Boileau, P.; Balg, F. The reverse shoulder prosthesis: Biomechanical principles, concept and evolution Prothèses D’épaule. État Actuel 2008, 153–168. [Google Scholar] [CrossRef]
- Kirzner, N.; Paul, E.; Moaveni, A. Reverse shoulder arthroplasty vs BIO-RSA: Clinical and radiographic outcomes at short term follow-up. J. Orthop. Surg. Res. 2018, 13, 256. [Google Scholar] [CrossRef]
- Ahir, S.P.; Walker, P.S.; Squire-Taylor, C.J.; Blunn, G.W.; Bayley, J.I. Analysis of glenoid fixation for a reversed anatomy fixed-fulcrum shoulder replacement. J. Biomech. 2004, 37, 1699–1708. [Google Scholar] [CrossRef]
- Couteau, B.; Mansat, P.; Darmana, R.; Mansat, M.; Egan, J. Morphological and mechanical analysis of the glenoid by the geometric reconstruction using computed tomography. Clin. Biomech. 2000, 15, 8–12. [Google Scholar] [CrossRef]
- Terrier, A.; Buchler, P.; Farron, A. Bone-cement interface of the glenoid component: Stress analysis for varying cement thickness. Clin. Biomech. 2005, 20, 710–717. [Google Scholar] [CrossRef] [PubMed]
- Lacroix, D.; Murphy, L.A.; Prendergast, P.J. Three-dimensional finite element analysis of glenoid replacement prosthesis; a comparison of keeled and pegged anchorage systems. J. Biomech. Eng. 2000, 122, 430–436. [Google Scholar] [CrossRef] [PubMed]
- Murphy, L.A.; Prendergast, P.J.; Resch, H. Structural analysis of an offset-keel design glenoid component compared with a center-keel design. J. Shoulder Elbow Surg. 2001, 10, 568–579. [Google Scholar] [CrossRef] [PubMed]
- Clavert, P.; Zerah, M.; Krier, J.; Mille, P.; Kempf, J.F.; Kahn, J.L. Finite element analysis of the strain distribution in the humeral head tubercles during abduction: Comparison of young and osteoporotic bone. Surg. Radiol. Anat. 2006, 28, 581–587. [Google Scholar] [CrossRef]
- Büchler, P.; Farron, A. Benefits of an anatomical reconstruction of the humeral head during shoulder arthroplasty, a finite element analysis. J. Biomech. 2004, 19, 16–23. [Google Scholar] [CrossRef]
- Terrier, A.; Farron, A. Biomechanical analysis of reversed shoulder prosthesis: Benefit of the inferior position of the glenoid base plate. In Proceedings of the 52nd Annual Meeting of the Orthopaedic Research Society, Chicago, IL, USA, 19–22 March 2006. [Google Scholar]
- Langohr, G.D.; Willing, R.; Medley, J.B.; Athwal, G.S.; Johnson, J.A. Contact mechanics of reverse total shoulder arthroplasty during abduction: The effect of neck-shaft angle, humeral cup depth, and glenosphere diameter. J. Shoulder Elbow Surg. 2015, 25, 589–597. [Google Scholar] [CrossRef]
- Chae, S.-W.; Lee, H.; Kim, S.M.; Lee, J.; Han, S.-H.; Kim, S.-Y. Primary Stability of Inferior Tilt Fixation of the Glenoid Component in Reverse Total Shoulder Arthroplasty: A Finite Element Study. J. Orthop. Res. 2016, 34, 1061–1068. [Google Scholar] [CrossRef]
- Berliner, J.L.; Regalado-Magdos, A.; Ma, C.B.; Feeley, B.T. biomechanics of reverse total shoulder arthroplasty. J. Shoulder Elbow Surg. 2015, 24, 150–160. [Google Scholar] [CrossRef]
- Permeswaran, V.N.; Goetz, J.E.; Rudert, M.J.; Hettrich, C.M.; Anderson, D.D. Cadaveric validation of a finite element modeling approach for studying scapular notching in reverse shoulder arthroplasty. J. Biomech. 2016, 49, 3069–3073. [Google Scholar] [CrossRef]
- Ingrassia, T.; Nalbone, L.; Nigrelli, V.; Ricotta, V.; Pisciotta, D. Biomechanical analysis of the humeral tray positioning in reverse shoulder arthroplasty design. Int. J. Interact. Des. Manuf. 2018, 12, 3069–3073. [Google Scholar] [CrossRef]
- Ansari, F.; Lee, T.; Malito, L.; Martin, A.; Gunther, S.B.; Harmsen, S.; Norris, T.R.; Ries, M.; van Citters, D.; Pruitt, L. Analysis of severely fractured glenoid components: Clinical consequences of biomechanics, design, and materials selection on implant performance. J. Shoulder Elbow Surg. 2016, 25, 1041–1050. [Google Scholar] [CrossRef] [PubMed]
- Saini, M.; Singh, Y.; Arora, P.; Arora, V.; Jain, K. Implant biomaterials: A comprehensive review. World J. Clin. Cases 2015, 3, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.-W.; Nicholson, T.A.; Hoffler, C.E.; Williams, G., Jr.; Getz, C. Metal Allergy as a Cause of Implant Failure in Shoulder Arthroplasty. Orthopedics 2017, 40, e844–e848. [Google Scholar] [CrossRef] [PubMed]
- Ghadikolaei, A.D.; Vahdati, M. Experimental study on the effect of finishing parameters on surface roughness in magneto-rheological abrasive flow finishing process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014. [Google Scholar] [CrossRef]
- Ibrahim, H.; Jahadakbar, A.; Dehghan, A.; Moghaddam, N.S.; Amerinatanzi, A.; Elahinia, M. In Vitro Corrosion Assessment of Additively Manufactured Porous NiTi Structures for Bone Fixation Applications. Metals 2018, 8, 164. [Google Scholar] [CrossRef]
- Amerinatanzi, A.; Mehrabi, R.; Ibrahim, H.; Dehghan, A.; Moghaddam, N.S.; Elahinia, M. Predicting the Biodegradation of Magnesium Alloy Implants: Modeling, Parameter Identification, and Validation. Bioengineering 2018, 5, 105. [Google Scholar] [CrossRef]
- Clark, J.C.; Ritchie, J.; Frederick; Song, S.; Kissenberth, M.J.; Tolan, S.J.; Hart, N.D.; Hawkins, R.J. Complication rates, dislocation, pain, and postoperative range of motion after reverse shoulder arthroplasty in patients with and without repair of the subscapularis. J. Shoulder Elbow Surg 2012, 21, 36–41. [Google Scholar] [CrossRef]
- Astier, V.; Thollon, L.; Arnoux, P.J.; Mouret, F.; Brunet, C. Development of a finite element model of the shoulder: Application during a side impact. Int. J. Crashworth. 2008, 13, 301–312. [Google Scholar] [CrossRef]
- Quental, C.; Folgado, J.; Fernandes, P.R.; Monteiro, J. Computational analysis of polyethylene wear in anatomical and reverse shoulder prostheses. Med. Biol. Eng. Comput. 2015, 53, 111–122. [Google Scholar] [CrossRef]
- Isabelle, P.; Silvio, R.; Cyntia, D.; Alexandre, T. Analyse Cinématique et Biomécanique de l’épaule lors d’activités de la vie Quotidienne. EPFL Scientific Publications. 2009. Available online: http://ibi.epfl.ch/files/content/sites/sti/files/shared/sgm/masterprojects/Poster_Pretre.pdf (accessed on 13 October 2018).
- Sarshari, E. A Closed-Loop EMG-Assisted Shoulder Model. Es Sciences. Ph.D. Thesis, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2018. [Google Scholar]

| Elements | Materials | Young Modulus E(MPa) | Poisson Coefficient ν | Density (g/mm3) |
|---|---|---|---|---|
| Scapula | Cortical bone | 8000 | 0.3 | 1.3 × 10−3 |
| Screws and Screws Holder | Titanium | 110,000 | 0.33 | 4.5 × 10−3 |
| Glenosphere | Stainless steel | 230,000 | 0.3 | 8.01 × 10−3 |
| Graft | PMMA | 2000 | 0.22 | - |
| UHMWPE | 500 | 0.4 | - | |
| Bone | 450 | 0.3 | - |
| Contact Force (N) | 280 | 480 | 710 |
| Elevation of the Humerus (Degrees) | 30 | 60 | 90 |
| Contact Force (N) | 350 | 390 | 560 |
| Elevation of the Humerus (Degrees) | 30 | 60 | 90 |
| Contact Force (N) | 250 | 410 | 680 |
| Elevation of the Humerus (Degrees) | 30 | 60 | 90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mebarki, S.; Aour, B.; Jourdan, F.; Malachanne, E.; Belaghit, A.H. A Study of the Biomechanical Behavior of the Implantation Method of Inverted Shoulder Prosthesis (BIO–RSA) under Different Abduction Movements. Bioengineering 2019, 6, 19. https://doi.org/10.3390/bioengineering6010019
Mebarki S, Aour B, Jourdan F, Malachanne E, Belaghit AH. A Study of the Biomechanical Behavior of the Implantation Method of Inverted Shoulder Prosthesis (BIO–RSA) under Different Abduction Movements. Bioengineering. 2019; 6(1):19. https://doi.org/10.3390/bioengineering6010019
Chicago/Turabian StyleMebarki, Salah, Benaoumeur Aour, Franck Jourdan, Etienne Malachanne, and Abdel Hakem Belaghit. 2019. "A Study of the Biomechanical Behavior of the Implantation Method of Inverted Shoulder Prosthesis (BIO–RSA) under Different Abduction Movements" Bioengineering 6, no. 1: 19. https://doi.org/10.3390/bioengineering6010019
APA StyleMebarki, S., Aour, B., Jourdan, F., Malachanne, E., & Belaghit, A. H. (2019). A Study of the Biomechanical Behavior of the Implantation Method of Inverted Shoulder Prosthesis (BIO–RSA) under Different Abduction Movements. Bioengineering, 6(1), 19. https://doi.org/10.3390/bioengineering6010019






