Predicting the Biodegradation of Magnesium Alloy Implants: Modeling, Parameter Identification, and Validation
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and In Vitro Immersion Corrosion Testing
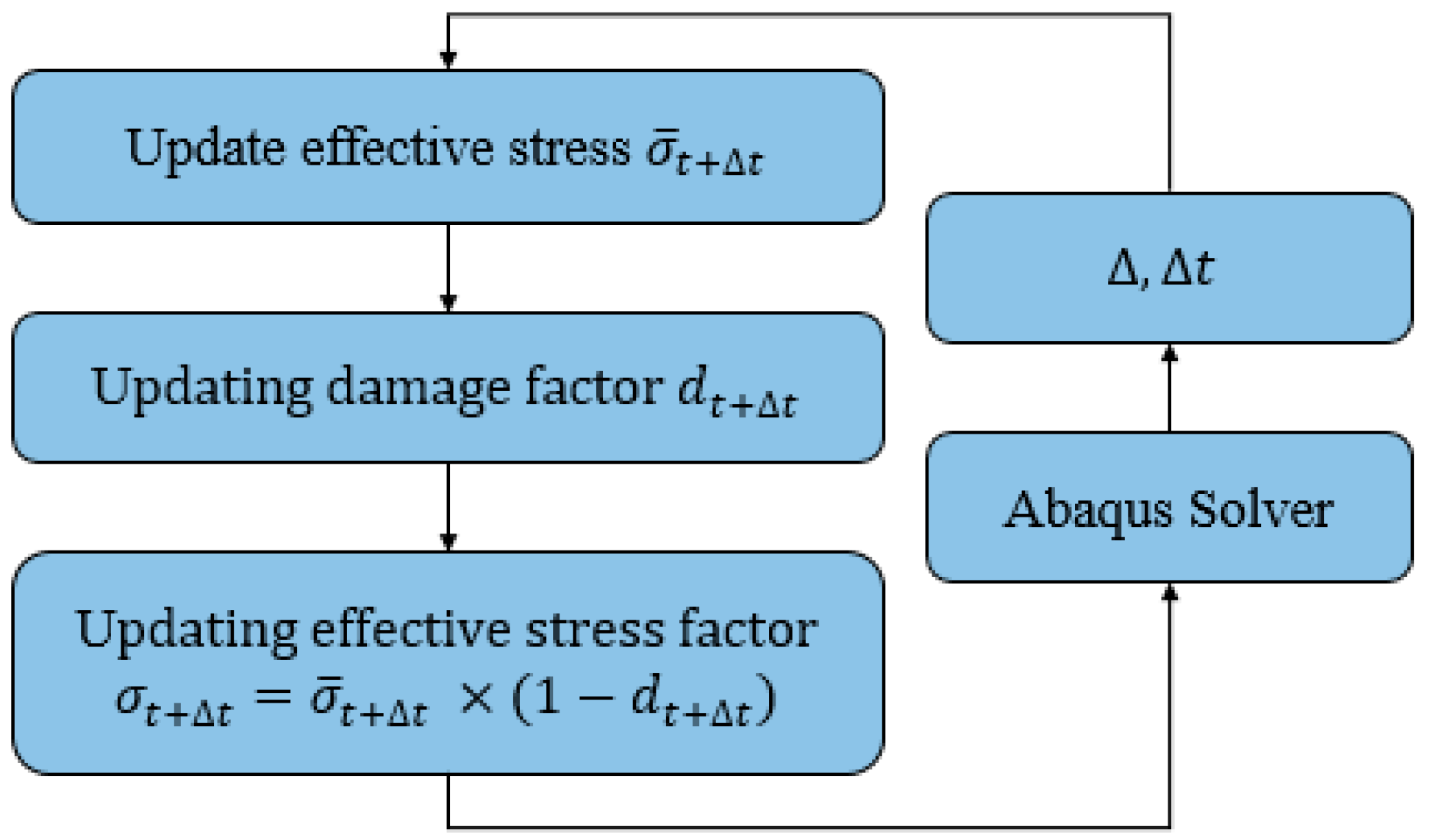
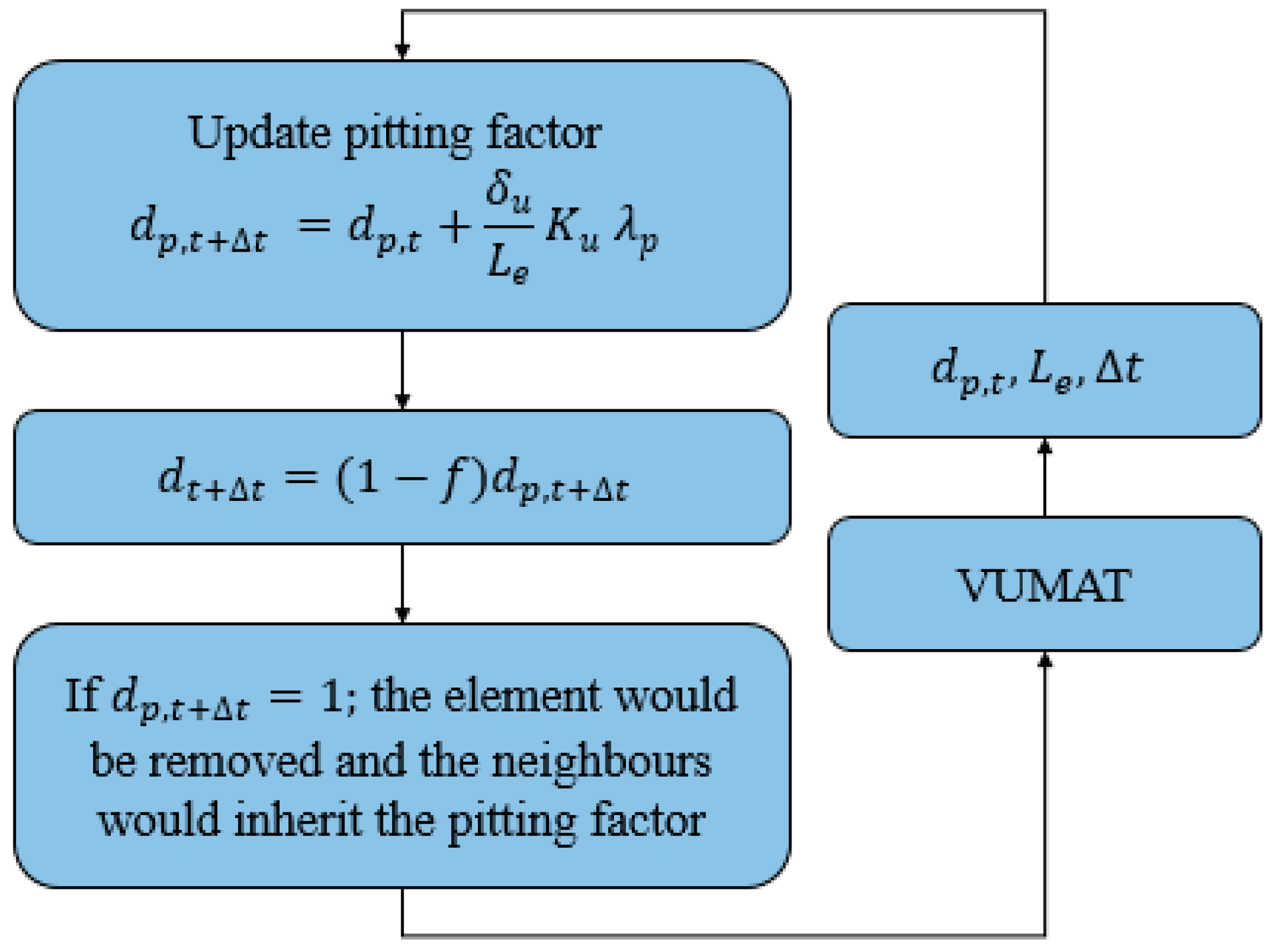
2.2. Damage Model Development
2.3. Boundary Conditions and Simulations
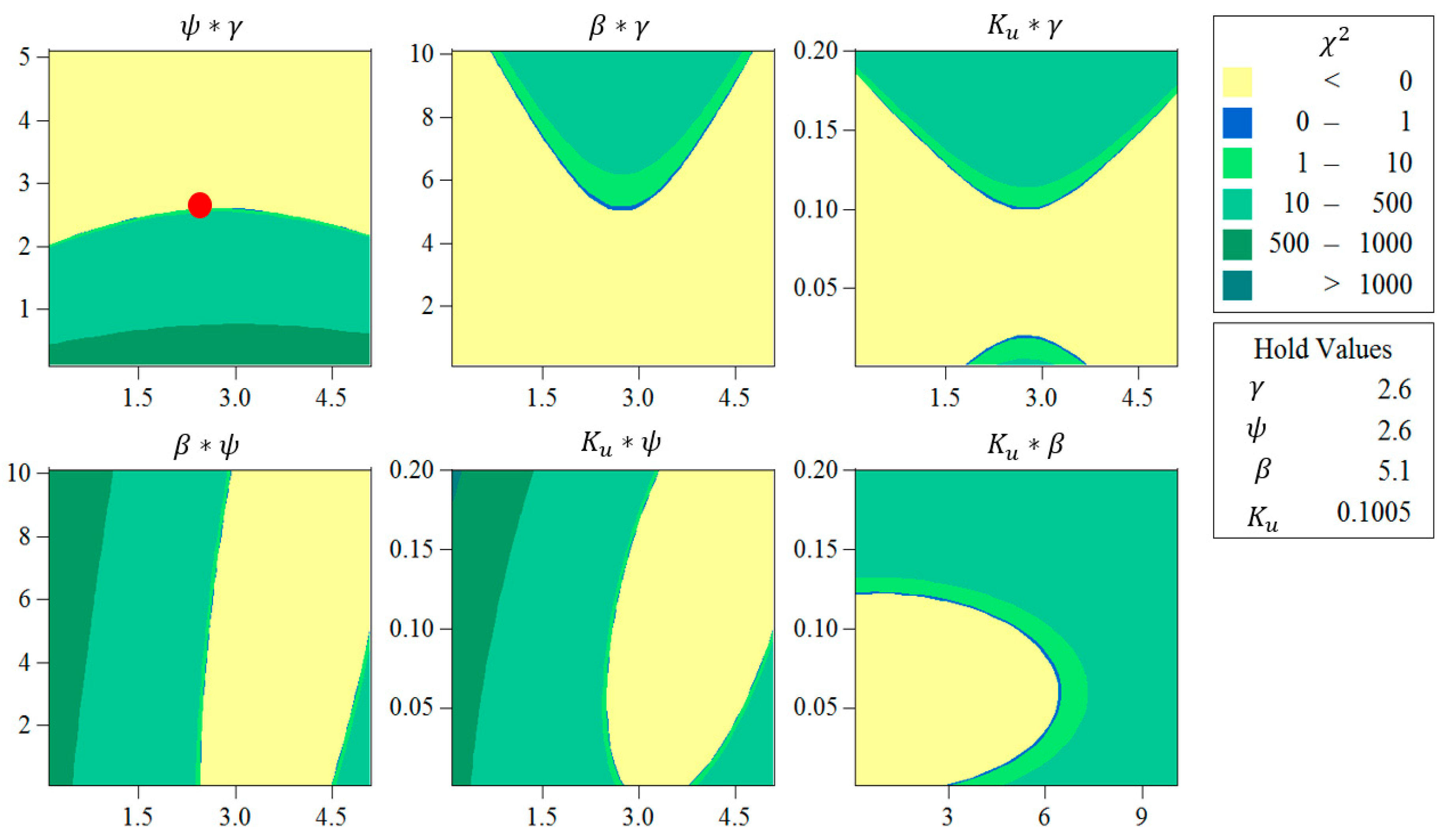
2.4. Calibration Strategy through RSM
3. Results
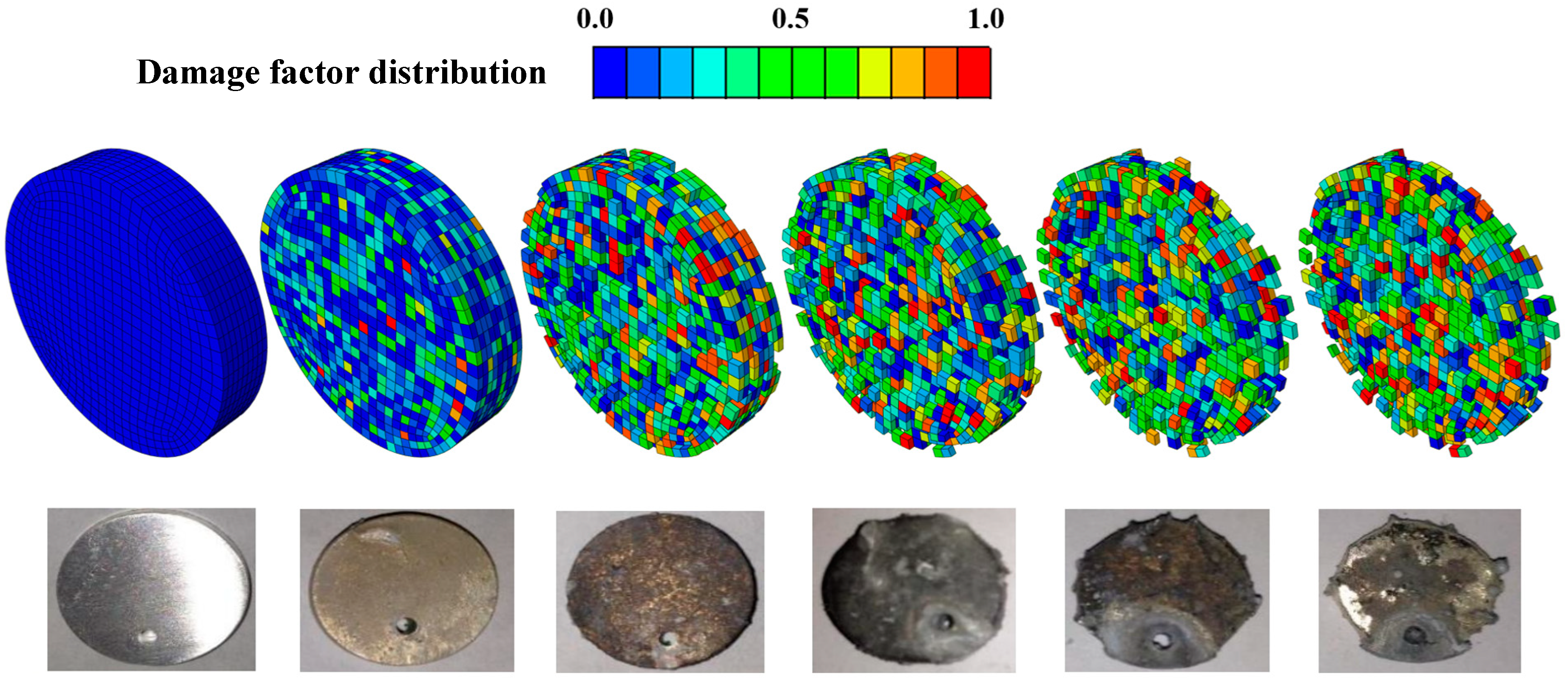
3.1. Degradation Behavior of Mg–Zn–Ca Alloy
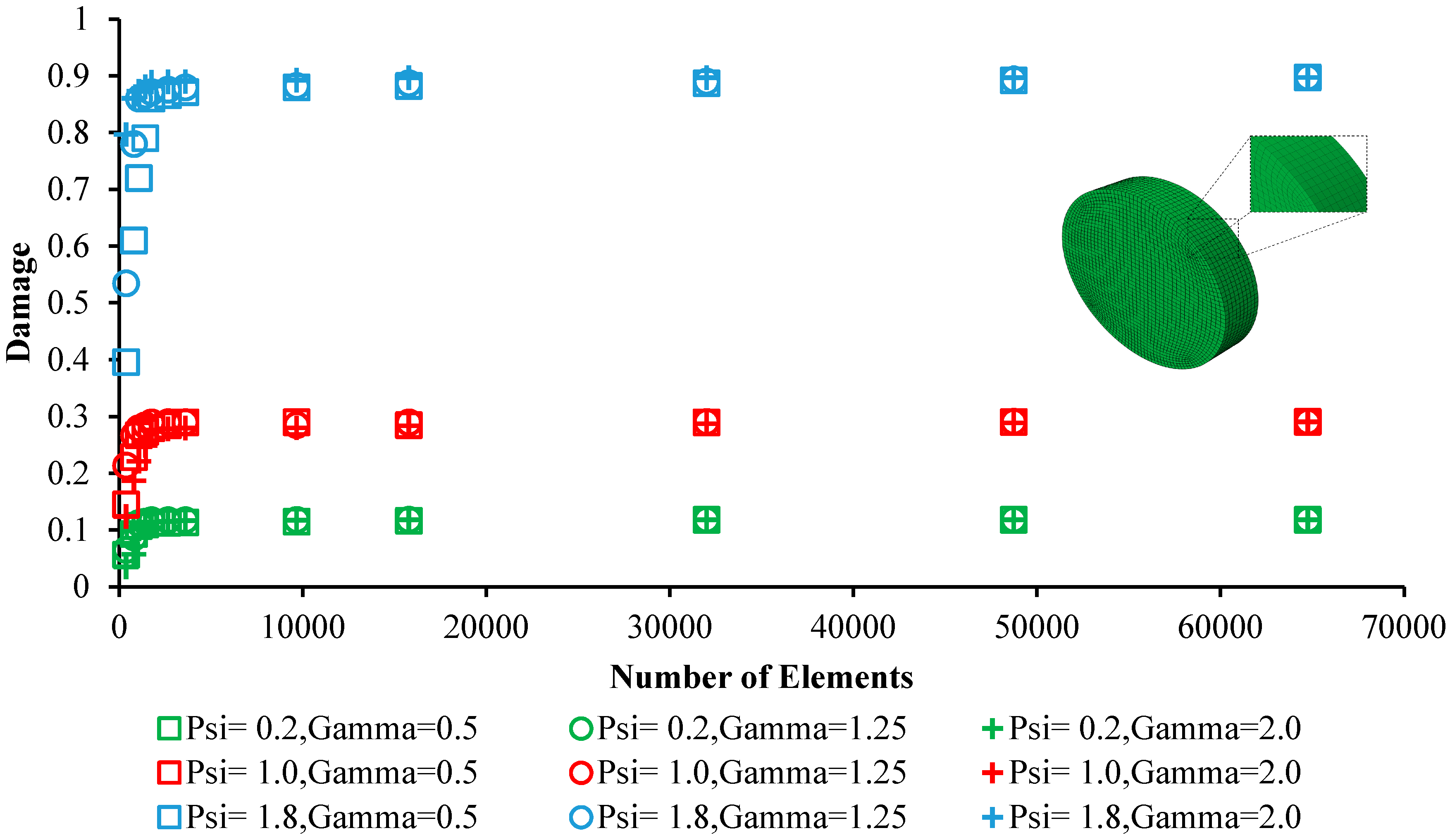
3.2. Mesh Analysis
3.3. Determination of Model Parameters
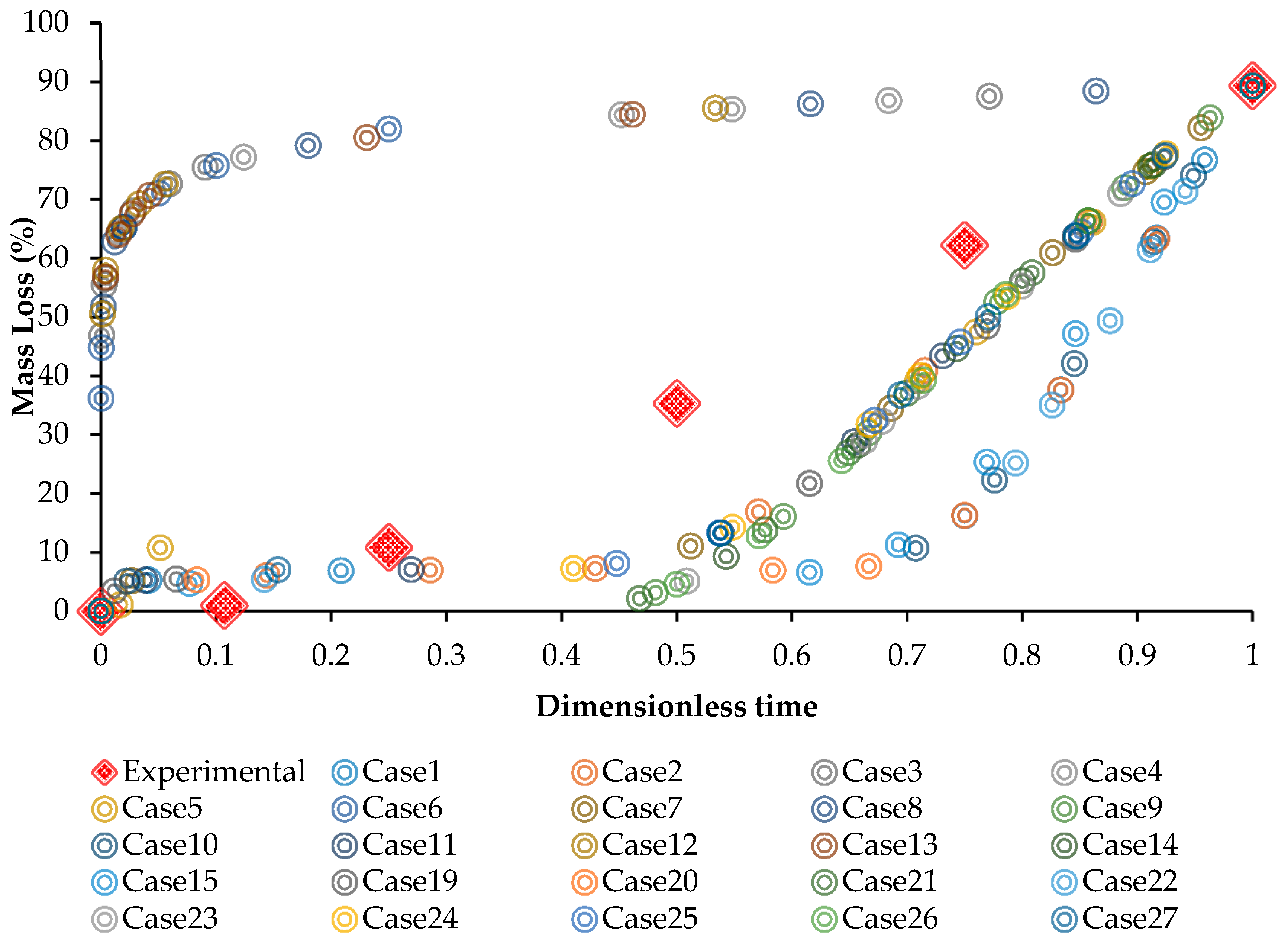
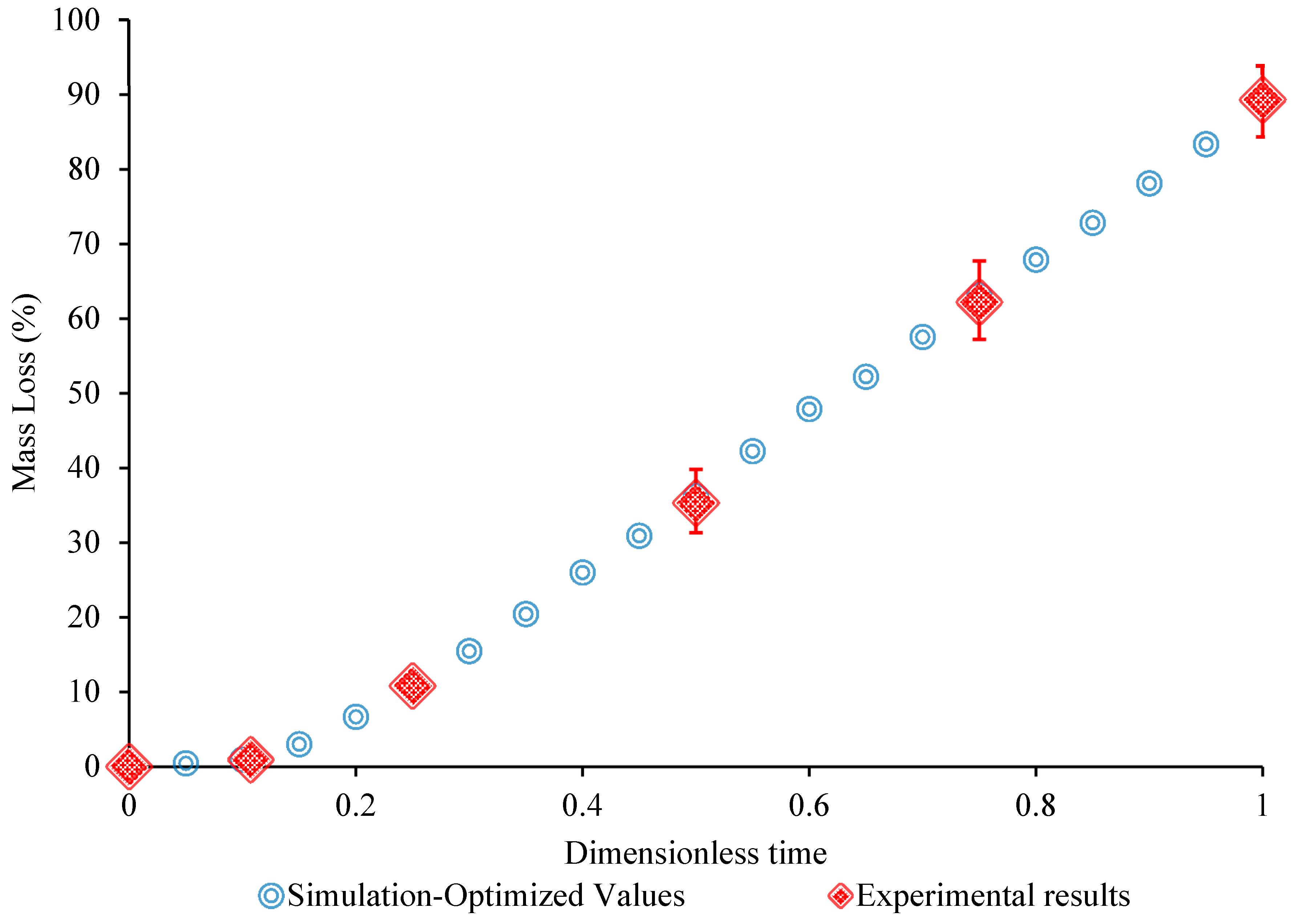
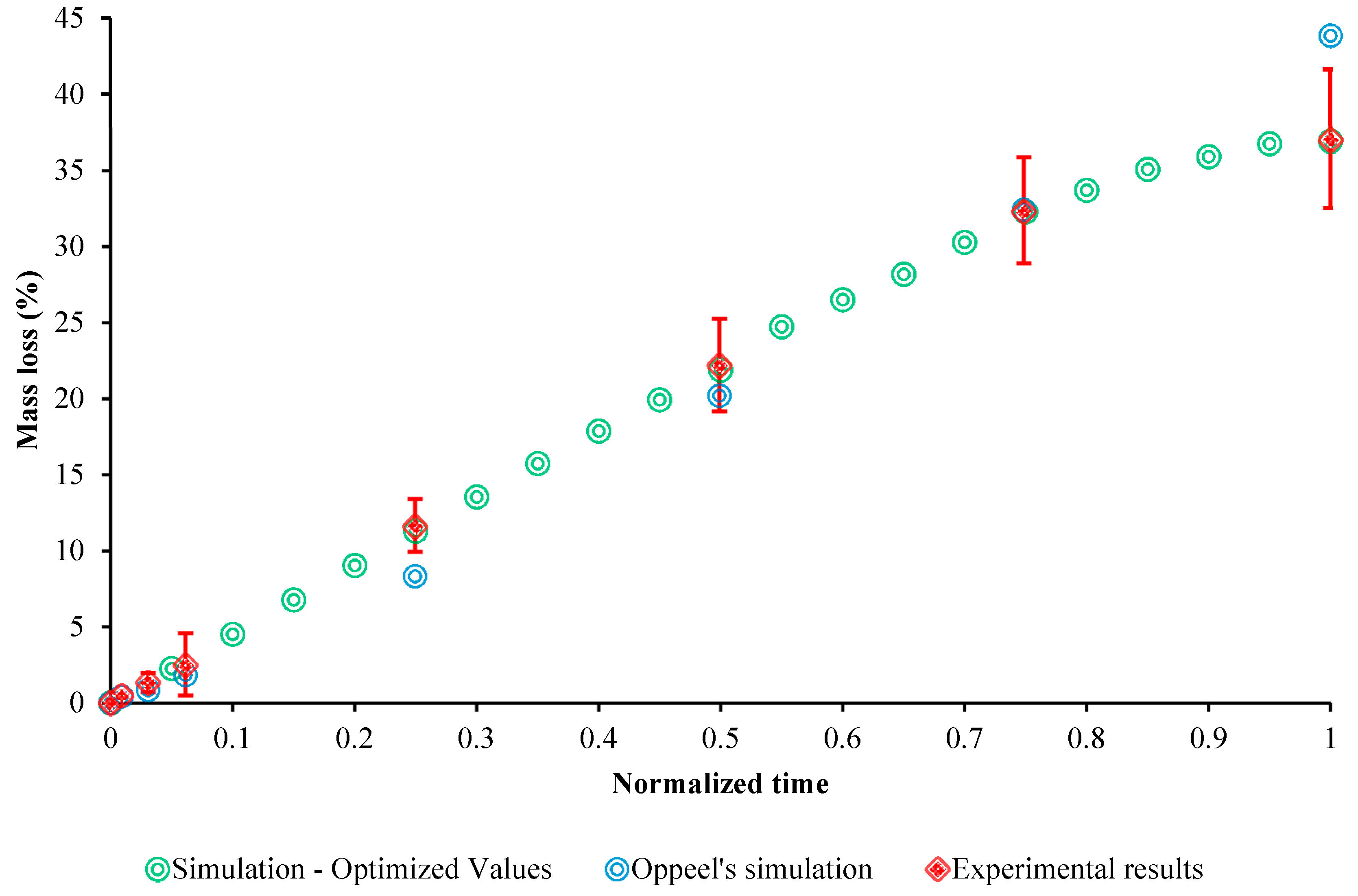
3.4. Evaluation of the Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, Y.; Gu, X.; Witte, F. Biodegradable metals. Mater. Sci. Eng. R Rep. 2014, 77, 1–34. [Google Scholar] [CrossRef]
- Ibrahim, H.; Esfahani, S.N.; Poorganji, B.; Dean, D.; Elahinia, M. Resorbable bone fixation alloys, forming, and post-fabrication treatments. Mater. Sci. Eng. C 2017, 70, 870–888. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, N.S.; Jahadakbar, A.; Amerinatanzi, A.; Elahinia, M.; Miller, M.; Dean, D. Metallic fixation of mandibular segmental defects: Graft immobilization and orofacial functional maintenance. Plast. Reconstr. Surg. Glob. Open 2016, 4, e858. [Google Scholar] [CrossRef] [PubMed]
- Zberg, B.; Uggowitzer, P.J.; Löffler, J.F. MgZnCa glasses without clinically observable hydrogen evolution for biodegradable implants. Nat. Mater. 2009, 8, 887. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Chen, D.; Niu, J.; Zhang, J.; Wang, Y.; Zhu, Z.; Yuan, G.; He, Y.; Jiang, Y. In vitro degradation and mechanical properties of polyporous CaHPO4-coated Mg–Nd–Zn–Zr alloy as potential tissue engineering scaffold. Mater. Lett. 2013, 100, 306–308. [Google Scholar] [CrossRef]
- Farraro, K.F.; Kim, K.E.; Woo, S.L.; Flowers, J.R.; McCullough, M.B. Revolutionizing orthopaedic biomaterials: The potential of biodegradable and bioresorbable magnesium-based materials for functional tissue engineering. J. Biomech. 2014, 47, 1979–1986. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Chan, K.; Jiang, X.; Zhang, H.; Zhang, D.; Wang, J.; Jiang, B.; Pan, F. Atmospheric RE-free Mg-based bulk metallic glass with high bio-corrosion resistance. J. Non-Cryst. Solids 2013, 379, 107–111. [Google Scholar] [CrossRef]
- Witte, F.; Eliezer, A. Biodegradable metals. In Degradation of Implant Materials; Eliaz, N., Ed.; Springer: New York, NY, USA, 2012; pp. 93–109. [Google Scholar]
- Ibasco, S. Magnesium Phosphate Precipitates and Coatings for Biomedical Applications. Master’s Thesis, McGill University, Montreal, QC, Canada, 2009. [Google Scholar]
- Elahinia, M.; Moghaddam, N.S.; Andani, M.T.; Amerinatanzi, A.; Bimber, B.A.; Hamilton, R.F. Fabrication of NiTi through additive manufacturing: A review. Progress Mater. Sci. 2016, 83, 630–663. [Google Scholar] [CrossRef]
- Jahadakbar, A.; Shayesteh Moghaddam, N.; Amerinatanzi, A.; Dean, D.; Karaca, H.E.; Elahinia, M. Finite element simulation and additive manufacturing of stiffness-matched NiTi fixation hardware for mandibular reconstruction surgery. Bioengineering 2016, 3, 36. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, N.S.; Skoracki, R.; Miller, M.; Elahinia, M.; Dean, D. Three dimensional printing of stiffness-tuned, nitinol skeletal fixation hardware with an example of mandibular segmental defect repair. Procedia CIRP 2016, 49, 45–50. [Google Scholar] [CrossRef]
- Song, G. Control of biodegradation of biocompatable magnesium alloys. Corros. Sci. 2007, 49, 1696–1701. [Google Scholar] [CrossRef]
- Kim, M.; Carman, C.V.; Springer, T.A. Bidirectional transmembrane signaling by cytoplasmic domain separation in integrins. Science 2003, 301, 1720–1725. [Google Scholar] [CrossRef] [PubMed]
- Witte, F.; Kaese, V.; Haferkamp, H.; Switzer, E.; Meyer-Lindenberg, A.; Wirth, C.; Windhagen, H. In vivo corrosion of four magnesium alloys and the associated bone response. Biomaterials 2005, 26, 3557–3563. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, H.; Jahadakbar, A.; Dehghan, A.; Moghaddam, N.S.; Amerinatanzi, A.; Elahinia, M. In Vitro Corrosion Assessment of Additively Manufactured Porous NiTi Structures for Bone Fixation Applications. Metals 2018, 8, 164. [Google Scholar] [CrossRef]
- Cosmi, F.; Steimberg, N.; Mazzoleni, G. A mesoscale study of the degradation of bone structural properties in modeled microgravity conditions. J. Mech. Behav. Biomed. Mater. 2015, 44, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, N.S.; Andani, M.T.; Amerinatanzi, A.; Haberland, C.; Huff, S.; Miller, M.; Elahinia, M.; Dean, D. Metals for bone implants: Safety, design, and efficacy. Biomanuf. Rev. 2016, 1, 1. [Google Scholar] [CrossRef]
- Namdari, N.; Dehghan, A. Natural frequencies and mode shapes for vibrations of rectangular and circular membranes: A numerical study. Int. Res. J. Adv. Eng. Sci. 2018, 3, 30–34. [Google Scholar]
- Grogan, J.; O’Brien, B.; Leen, S.; McHugh, P. A corrosion model for bioabsorbable metallic stents. Acta Biomater. 2011, 7, 3523–3533. [Google Scholar] [CrossRef] [PubMed]
- Lippmann, H.; Lemaitre, J. A Course on Damage Mechanics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures; Springer Science & Business Media: Berlin, Germany, 2005. [Google Scholar]
- Dehghanghadikolaei, A.; Ansary, J.; Ghoreishi, R. Sol-gel process applications: A mini-review. Proc. Nat. Res. Soc. 2018, 2, 02008. [Google Scholar] [CrossRef]
- Wenman, M.; Trethewey, K.; Jarman, S.; Chard-Tuckey, P. A finite-element computational model of chloride-induced transgranular stress-corrosion cracking of austenitic stainless steel. Acta Mater. 2008, 56, 4125–4136. [Google Scholar] [CrossRef]
- Gastaldi, D.; Sassi, V.; Petrini, L.; Vedani, M.; Trasatti, S.; Migliavacca, F. Continuum damage model for bioresorbable magnesium alloy devices—Application to coronary stents. J. Mech. Behav. Biomed. Mater. 2011, 4, 352–365. [Google Scholar] [CrossRef] [PubMed]
- Oppeal, A. Experimental Characterisation and Finite Element Modeling of Biodegradable Magnesium Stents. Master’s Thesis, Universiteit Gent, Ghent, Belgium, 2015. [Google Scholar]
- Ibrahim, H.; Klarner, A.D.; Poorganji, B.; Dean, D.; Luo, A.A.; Elahinia, M. Microstructural, mechanical and corrosion characteristics of heat-treated Mg-1.2 Zn-0.5 Ca (wt %) alloy for use as resorbable bone fixation material. J. Mech. Behave. Biomed. Mater. 2017, 69, 203–212. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, H.; Moghaddam, N.; Elahinia, M. Mechanical and in vitro corrosion properties of a heat-treated Mg-Zn-Ca-Mn alloy as a potential bioresorbable material. Sci. Pages Metall. Mater. Eng. 2017, 1, 1–7. [Google Scholar]
- Oyane, A.; Kim, H.M.; Furuya, T.; Kokubo, T.; Miyazaki, T.; Nakamura, T. Preparation and assessment of revised simulated body fluids. J. Biomed. Mater. Res. A 2003, 65, 188–195. [Google Scholar] [CrossRef] [PubMed]
- Kirkland, N.T.; Birbilis, N.; Staiger, M. Assessing the corrosion of biodegradable magnesium implants: A critical review of current methodologies and their limitations. Acta Biomater. 2012, 8, 925–936. [Google Scholar] [CrossRef] [PubMed]
- Agha, N.A.; Feyerabend, F.; Mihailova, B.; Heidrich, S.; Bismayer, U.; Willumeit-Römer, R. Magnesium degradation influenced by buffering salts in concentrations typical of in vitro and in vivo models. Mater. Sci. Eng. C 2016, 58, 817–825. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Huang, J.; Zhang, B.; Yang, K. Preliminary study of biodegradation of AZ31B magnesium alloy. Front. Mater. Sci. Ch. 2007, 1, 401–404. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Shayesteh Moghaddam, N.; Jahadakbar, A.; Amerinatanzi, A.; Skoracki, R.; Miller, M.; Dean, D.; Elahinia, M. Fixation release and the bone bandaid: A new bone fixation device paradigm. Bioengineering 2017, 4, 5. [Google Scholar] [CrossRef] [PubMed]


| Reagent | Amount |
|---|---|
| NaCl | 5.403 g |
| NaHCO3 | 0.504 g |
| Na2CO3 | 0.426 g |
| KCl | 0.225 g |
| K2HPO4·3H2O | 0.23 g |
| MgCl2·6H2O | 0.311 g |
| 0.2 mol L−1 NaOH | 100 mL |
| HEPES | 17.892 g |
| CaCl2 | 0.293 g |
| Na2SO4 | 0.072 g |
| 1 mol L−1 NaOH | 15 mL |
| Variables, Unit | Range and Levels | ||
|---|---|---|---|
| 0 | |||
| 0.1 | 2.6 | 5.1 | |
| 0.1 | 2.6 | 5.1 | |
| 0.1 | 5.1 | 10.1 | |
| 0.001 | 0.1005 | 0.2 | |
| Case | () | () | (β) | Ku |
|---|---|---|---|---|
| 1 | 2.6 | 5.1 | 5.1 | 0.001 |
| 2 | 2.6 | 2.6 | 5.1 | 0.1005 |
| 3 | 2.6 | 0.1 | 5.1 | 0.2 |
| 4 | 0.1 | 0.1 | 5.1 | 0.1005 |
| 5 | 5.1 | 2.6 | 5.1 | 0.2 |
| 6 | 2.6 | 0.1 | 5.1 | 0.001 |
| 7 | 0.1 | 2.6 | 5.1 | 0.2 |
| 8 | 5.1 | 0.1 | 5.1 | 0.1005 |
| 9 | 2.6 | 2.6 | 0.1 | 0.001 |
| 10 | 2.6 | 5.1 | 10.1 | 0.1005 |
| 11 | 2.6 | 2.6 | 10.1 | 0.001 |
| 12 | 2.6 | 0.1 | 10.1 | 0.1005 |
| 13 | 2.6 | 2.6 | 5.1 | 0.1005 |
| 14 | 0.1 | 2.6 | 0.1 | 0.1005 |
| 15 | 0.1 | 5.1 | 5.1 | 0.1005 |
| 16 | 2.6 | 2.6 | 5.1 | 0.1005 |
| 17 | 0.1 | 2.6 | 5.1 | 0.001 |
| 18 | 2.6 | 0.1 | 0.1 | 0.1005 |
| 19 | 5.1 | 2.6 | 5.1 | 0.001 |
| 20 | 2.6 | 5.1 | 5.1 | 0.2 |
| 21 | 5.1 | 2.6 | 0.1 | 0.1005 |
| 22 | 5.1 | 5.1 | 5.1 | 0.1005 |
| 23 | 2.6 | 2.6 | 0.1 | 0.2 |
| 24 | 5.1 | 2.6 | 10.1 | 0.1005 |
| 25 | 0.1 | 2.6 | 10.1 | 0.1005 |
| 26 | 2.6 | 5.1 | 0.1 | 0.1005 |
| 27 | 2.6 | 2.6 | 10.1 | 0.2 |
| Case | () | () | (β) | Ku | |
|---|---|---|---|---|---|
| 1 | 2.6 | 5.1 | 5.1 | 0.001 | 1.42 |
| 2 | 2.6 | 2.6 | 5.1 | 0.1005 | 0.43 |
| 3 | 2.6 | 0.1 | 5.1 | 0.2 | 1409.05 |
| 4 | 0.1 | 0.1 | 5.1 | 0.1005 | 342.21 |
| 5 | 5.1 | 2.6 | 5.1 | 0.2 | 6.31 |
| 6 | 2.6 | 0.1 | 5.1 | 0.001 | 703.62 |
| 7 | 0.1 | 2.6 | 5.1 | 0.2 | 0.96 |
| 8 | 5.1 | 0.1 | 5.1 | 0.1005 | 460.68 |
| 9 | 2.6 | 2.6 | 0.1 | 0.001 | 0.59 |
| 10 | 2.6 | 5.1 | 10.1 | 0.1005 | 1.52 |
| 11 | 2.6 | 2.6 | 10.1 | 0.001 | 1.16 |
| 12 | 2.6 | 0.1 | 10.1 | 0.1005 | 1096.31 |
| 13 | 2.6 | 2.6 | 5.1 | 0.1005 | 0.43 |
| 14 | 0.1 | 2.6 | 0.1 | 0.1005 | 0.42 |
| 15 | 0.1 | 5.1 | 5.1 | 0.1005 | 1.67 |
| 16 | 2.6 | 2.6 | 5.1 | 0.1005 | 0.43 |
| 17 | 0.1 | 2.6 | 5.1 | 0.001 | 0.36 |
| 18 | 2.6 | 0.1 | 0.1 | 0.1005 | 634.60 |
| 19 | 5.1 | 2.6 | 5.1 | 0.001 | 6.41 |
| 20 | 2.6 | 5.1 | 5.1 | 0.2 | 1.71 |
| 21 | 5.1 | 2.6 | 0.1 | 0.1005 | 0.68 |
| 22 | 5.1 | 5.1 | 5.1 | 0.1005 | 0.59 |
| 23 | 2.6 | 2.6 | 0.1 | 0.2 | 0.56 |
| 24 | 5.1 | 2.6 | 10.1 | 0.1005 | 0.47 |
| 25 | 0.1 | 2.6 | 10.1 | 0.1005 | 0.47 |
| 26 | 2.6 | 5.1 | 0.1 | 0.1005 | 0.70 |
| 27 | 2.6 | 2.6 | 10.1 | 0.2 | 0.32 |
| Optimized | 2.74898 | 2.60477 | 5.1 | 0.1005 | 0.034 |
| Parameter | Grogan et al. [20] | Gastaldi et al. [25] | Oppeel et al. [26] | Our Simulation | |
|---|---|---|---|---|---|
| Material | AZ31 | AZ31 | AZ31 | Mg-Zn-Ca | AZ31 |
| (−) | 0.2 | - | 0.2 | 2.74898 | 0.5846 |
| (−) | - | - | - | 2.60477 | 0.93003 |
| (−) | 0.8 | - | 0.5 | 5.1 | 0.2505 |
| Ku (h−1) | 0.00042 | 0.00500 | 0.00650 | 0.1005 | 0.005 |
| 34.83 | 48.73 | 25.14 | 0.034 | 0.0399 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amerinatanzi, A.; Mehrabi, R.; Ibrahim, H.; Dehghan, A.; Shayesteh Moghaddam, N.; Elahinia, M. Predicting the Biodegradation of Magnesium Alloy Implants: Modeling, Parameter Identification, and Validation. Bioengineering 2018, 5, 105. https://doi.org/10.3390/bioengineering5040105
Amerinatanzi A, Mehrabi R, Ibrahim H, Dehghan A, Shayesteh Moghaddam N, Elahinia M. Predicting the Biodegradation of Magnesium Alloy Implants: Modeling, Parameter Identification, and Validation. Bioengineering. 2018; 5(4):105. https://doi.org/10.3390/bioengineering5040105
Chicago/Turabian StyleAmerinatanzi, Amirhesam, Reza Mehrabi, Hamdy Ibrahim, Amir Dehghan, Narges Shayesteh Moghaddam, and Mohammad Elahinia. 2018. "Predicting the Biodegradation of Magnesium Alloy Implants: Modeling, Parameter Identification, and Validation" Bioengineering 5, no. 4: 105. https://doi.org/10.3390/bioengineering5040105
APA StyleAmerinatanzi, A., Mehrabi, R., Ibrahim, H., Dehghan, A., Shayesteh Moghaddam, N., & Elahinia, M. (2018). Predicting the Biodegradation of Magnesium Alloy Implants: Modeling, Parameter Identification, and Validation. Bioengineering, 5(4), 105. https://doi.org/10.3390/bioengineering5040105







