Finite Element Analysis of the Effects of Different Shapes of Adult Cranial Sutures on Their Mechanical Behavior
Abstract
1. Introduction
2. Materials and Methods
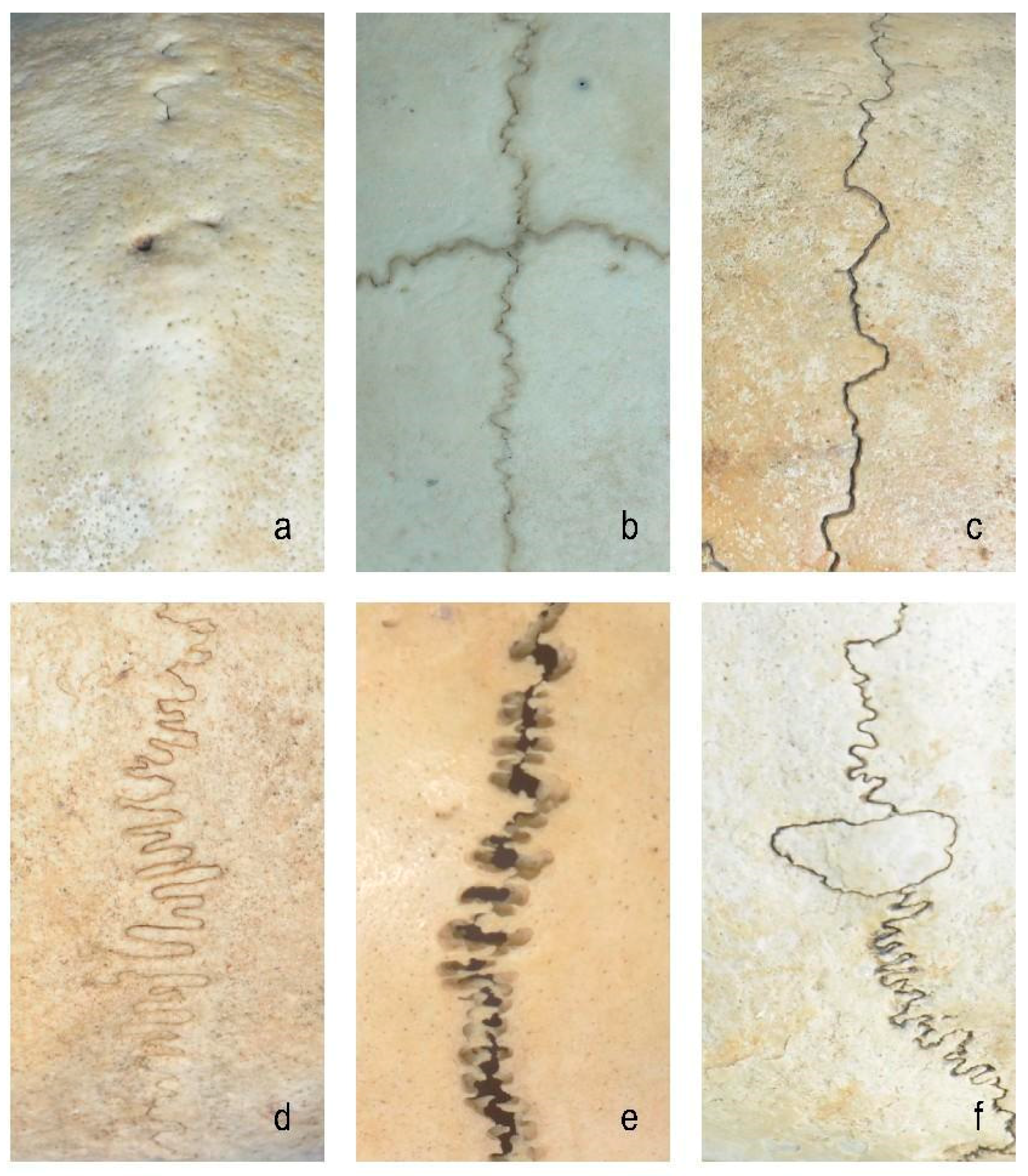
2.1. FE Modeling of Cranial Sutures
- (1)
- Closed group: fully ossified sutures with complete bone fusion;
- (2)
- Straight suture group: simulating the straight line morphology of the cranial suture;
- (3)
- Sine wave group: simulating the cranial suture as a standard sinusoidal waveform (bone–suture–bone contact surfaces are smooth with continuous mesh nodes between materials [3]; wavelength λ = 2 mm, amplitude A = 0.25 mm);
- (4)
- Tight sinusoidal wave group: high-frequency sinusoids in which the angular velocity ω of the sine wave becomes larger, the waveform shrinks on the X-axis, and the wave number becomes greater compared to the sine wave group;
- (5)
- Layered sinusoidal wave group: the structure of the cranial suture is the same as that of the standard sine wave group, but the amplitude and wavelength are different. This group is composed of two layers of sinusoidal waves, with multiple small sinusoids working together to form a large sinusoidal wave (the bone–suture–bone contact surfaces are rough);
- (6)
- Layered sinusoidal wave + sutural bone group: hybrid structure combining sinusoidal patterns with sutural bone elements (sutural bone refers to small, irregularly shaped bone fragments or plates found within cranial sutures—the fibrous joints connecting the bones of the skull), becoming the most complex and irregular waveforms.
2.2. Model Construction
2.3. Meshing and Analysis
3. Results
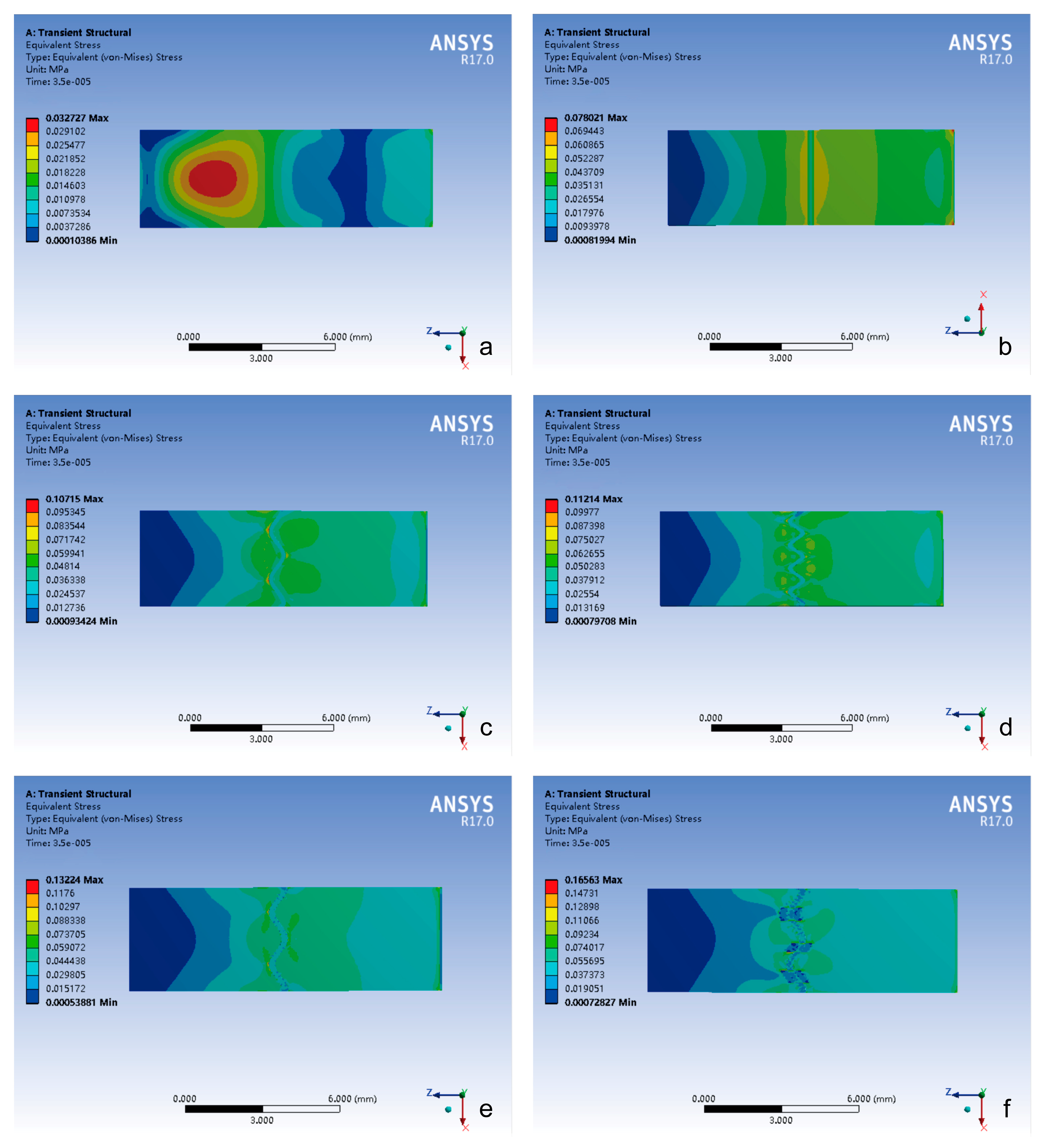
3.1. Von Mises Stress Changes of Different Cranial Suture Morphologies Under Impact and Tensile Loads
3.1.1. Impact Loading Conditions
- (1)
- Temporal delay effect: in the cranial suture groups (excluding closed sutures), peak stress occurrence was significantly delayed compared to the closed group.
- (2)
- Morphological equivalence: the straight suture, sine wave, and tight sinusoidal wave groups exhibited similar stress evolution trends and peak magnitudes.
- (3)
- Hierarchical enhancement: the layered sinusoidal wave group and the layered sinusoidal wave + sutural bone group demonstrated the highest peak stresses (296.31 kPa and 282.9 kPa, respectively), surpassing all other configurations by 19–36%.
- (1)
- The closed group exhibited stress localization primarily at the impact side or center of the composite structure.
- (2)
- The stress of the cranial suture groups showed stress concentration on both sides of the cranial suture, with peak stress magnitude positively correlated with the complexity of the suture–bone interface.
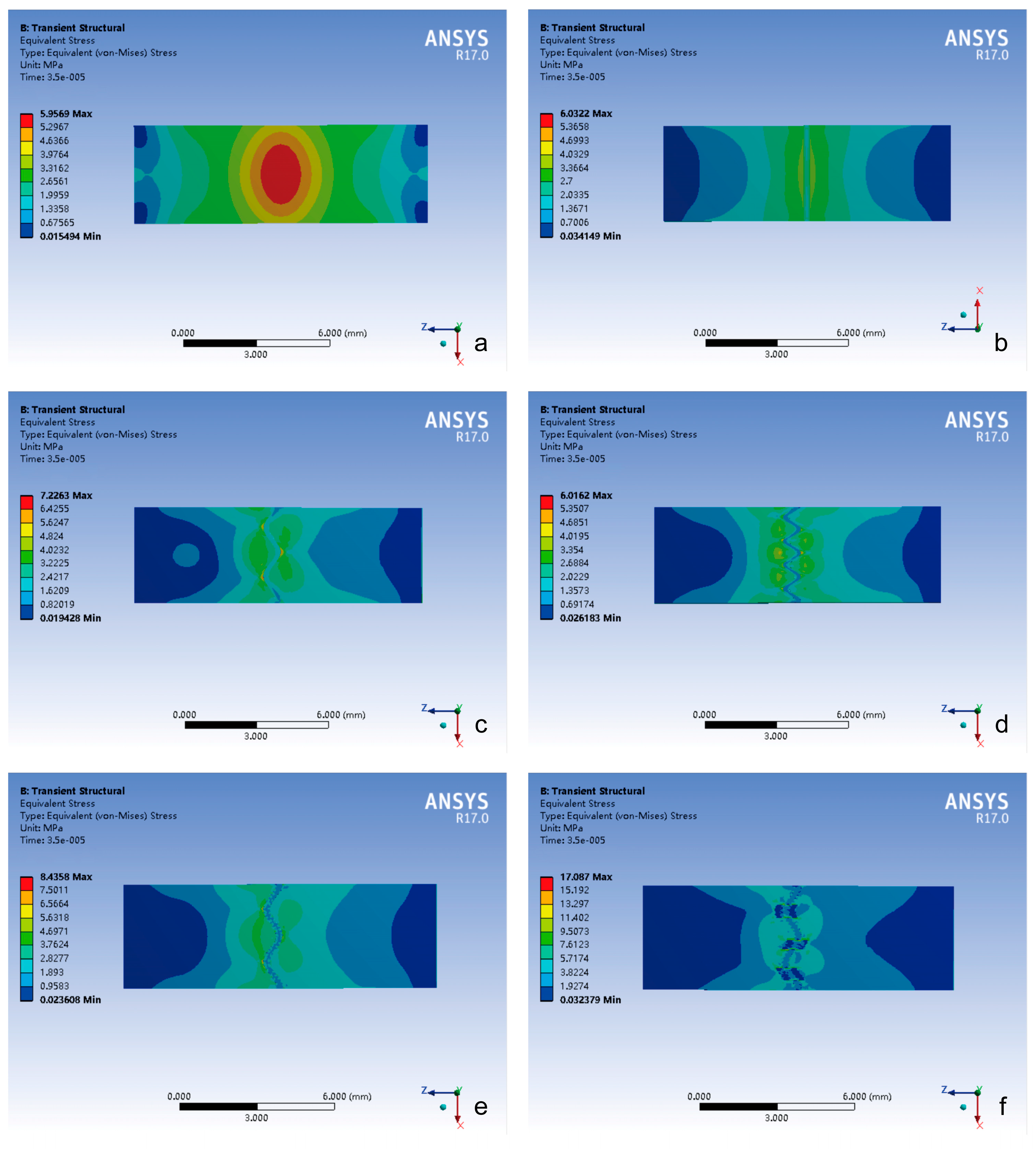
3.1.2. Tensile Loading Conditions
- (1)
- All groups exhibited comparable peak stress timing.
- (2)
- The layered sinusoidal wave + sutural bone group achieved the highest peak stress (56,577 kPa), followed closely by the layered sinusoidal wave group (40,611 kPa). Straight, sine, and tight sinusoidal wave groups showed nearly identical stress profiles (29,950 kPa, 30,334 kPa, 31,087 kPa), while the closed group exhibited the lowest peak stress (11,722 kPa).
- (1)
- The closed group maintained centralized stress distribution.
- (2)
- The stress of the cranial suture groups exhibited bilateral stress localization around cranial sutures, with peak stress magnitude again positively correlated with the complexity of the suture–bone interface.
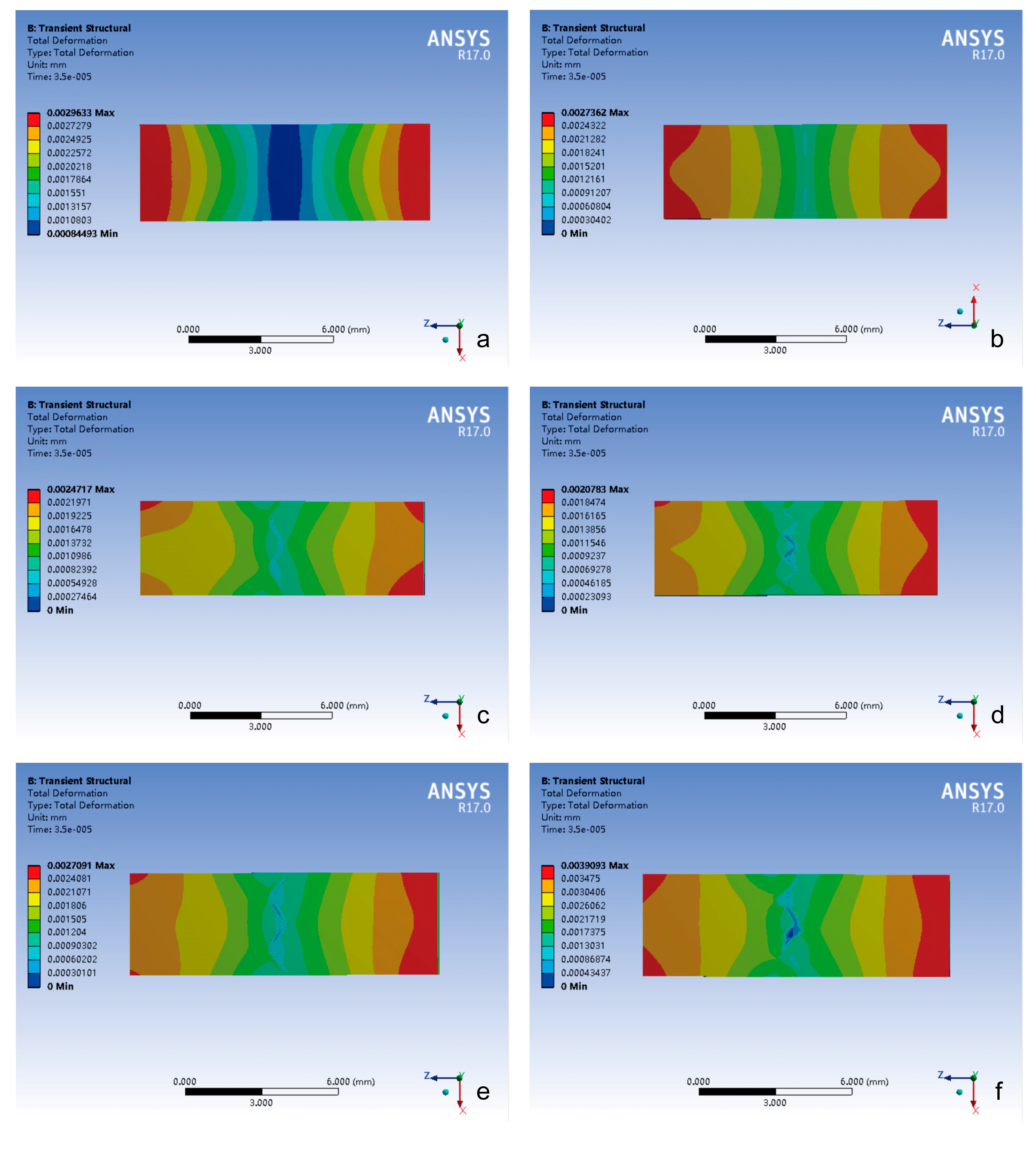
3.2. Total Deformation Changes of Different Cranial Suture Morphologies Under Impact and Tensile Loads
3.2.1. Temporal Deformation Analysis
- (1)
- Peak deformation timing: the cranial suture groups exhibited delayed peak deformation compared to closed groups under the impact and tensile loading conditions.
- (2)
- Deformation magnitude hierarchy: the closed group demonstrated minimal deformation (impact: 0.14 μm; tensile: 9.25 μm); the peak value of total deformation in the cranial suture groups was significantly higher than that in the closed group, but with no inter-group differences (p > 0.05).
- (3)
- Loading mode effect: the highest total deformation in all groups was only 0.2 μm under impact load and 11 μm under tensile load, and the total deformation under tensile loading is greater than that under impact loading.
3.2.2. Spatial Deformation Patterns
- (1)
- Impact-side deformation concentration: the closed group exhibited the largest total deformation localized within the most limited impact zone, demonstrating constrained energy absorption characteristics.
- (2)
- Attenuation gradient distribution trend: all groups showed peak total deformation concentrated on the impact side, which gradually decreased in a step-like manner.
- (3)
- Suture-mediated deformation modulation: the presence of cranial sutures can significantly increase both peak magnitude and the spatial extent of the total deformation.
- (4)
- Morphology–deformation correlation: the total deformation of the cranial suture was related to its morphology.
- (1)
- Bimodal strain distribution: the total deformation of all groups exhibited symmetrical “double-peaked” distribution with maximum values at both ends and minimum values in the center.
- (2)
- Interface complexity-driven irregularity: the distribution trend of the total deformation in the closed group maintained regular deformation distribution, whereas cranial suture groups exhibited progressive pattern irregularity proportional to suture–bone interface complexity.
4. Discussion
4.1. Morphology–Environment Correlation: Mechanical Responses of Sutures Reflect Their Biomechanical Context
4.2. Suture Function Under Contrasting Loading Regimes
4.3. Clinical and Evolutionary Implications
5. Conclusions
6. Study Limitations and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- White, H.E.; Clavel, J.; Tucker, A.S.; Goswami, A. A comparison of metrics for quantifying cranial suture complexity. J. R. Soc. Interface 2020, 17, 20200476. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- White, H.E.; Goswami, A.; Tucker, A.S. The Intertwined Evolution and Development of Sutures and Cranial Morphology. Front. Cell Dev. Biol. 2021, 9, 653579. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Zhang, Z.Q.; Yang, J.L. Biomechanical Dynamics of Cranial Sutures during Simulated Impulsive Loading. Appl. Bionics Biomech. 2015, 2015, 596843. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Remesz, R.; Khurelbaatar, T.; Grotski, M.; Popowics, T.; Rafferty, K.; Herring, S.W.; Addison, O.; Doschak, M.R.; Romanyk, D.L. Cranial suture morphometry and mechanical response to loading: 2D vs. 3D assumptions and characterization. Biomech. Model. Mechanobiol. 2022, 21, 1251–1265. [Google Scholar] [CrossRef] [PubMed]
- Sharp, A.C.; Dutel, H.; Watson, P.J.; Gröning, F.; Crumpton, N.; Fagan, M.J.; Evans, S.E. Assessment of the mechanical role of cranial sutures in the mammalian skull: Computational biomechanical modelling of the rat skull. J. Morphol. 2023, 284, e21555. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Wang, Q.; Smith, A.L.; Strait, D.S.; Wright, B.W.; Richmond, B.G.; Grosse, I.R.; Byron, C.D.; Zapata, U. The global impact of sutures assessed in a finite element model of a macaque cranium. Anat. Rec. 2010, 293, 1477–1491. [Google Scholar] [CrossRef] [PubMed]
- Rayfield, E.J. Using finite-element analysis to investigate suture morphology: A case study using large carnivorous dinosaurs. Anat. Rec. A Discov. Mol. Cell Evol. Biol. 2005, 283, 349–365. [Google Scholar] [CrossRef] [PubMed]
- Jasinoski, S.C.; Reddy, B.D.; Louw, K.K.; Chinsamy, A. Mechanics of cranial sutures using the finite element method. J. Biomech. 2010, 43, 3104–3111. [Google Scholar] [CrossRef] [PubMed]
- Maloul, A.; Fialkov, J.; Wagner, D.; Whyne, C.M. Characterization of craniofacial sutures using the finite element method. J. Biomech. 2014, 47, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, Z.; Zhong, W.; Yang, H.; Li, Y. A study of 285 cases of cranial vault suture closure in Chinese adults. Surg. Radiol. Anat. 2022, 44, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Li, J.H.; Chen, Z.J.; Zhong, W.X.; Yang, H.; Liu, D.; Li, Y.K. Anatomical characteristics and significance of the metopism and Wormian bones in dry adult-Chinese skulls. Folia Morphol. 2023, 82, 166–175. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.S.; Witt, P.L. The controversy of cranial bone motion. J. Orthop. Sports Phys. Ther. 1997, 26, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Downey, P.A.; Barbano, T.; Kapur-Wadhwa, R.; Sciote, J.J.; Siegel, M.I.; Mooney, M.P. Craniosacral therapy: The effects of cranial manipulation on intracranial pressure and cranial bone movement. J. Orthop. Sports Phys. Ther. 2006, 36, 845–853. [Google Scholar] [CrossRef] [PubMed]
- Corega, C.; Vaida, L.; Băciuţ, M.; Serbănescu, A.; Palaghiţă-Banias, L. Three-dimensional cranial suture morphology analysis. Rom. J. Morphol. Embryol. 2010, 51, 123–127. [Google Scholar] [PubMed]
- Ashman, R.B.; Van Buskirk, W.C. The elastic properties of a human mandible. Adv. Dent. Res. 1987, 1, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Coats, B.; Margulies, S.S. Material properties of human infant skull and suture at high rates. J. Neurotrauma 2006, 23, 1222–1232. [Google Scholar] [CrossRef] [PubMed]
- Jaslow, C.R. Mechanical properties of cranial sutures. J. Biomech. 1990, 23, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Zollikofer, C.P.; Weissmann, J.D. A bidirectional interface growth model for cranial interosseous suture morphogenesis. J. Anat. 2011, 219, 100–114. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Herring, S.W.; Mucci, R.J. In vivo strain in cranial sutures: The zygomatic arch. J. Morphol. 1991, 207, 225–239. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Tanaka, E.; Miyawaki, Y.; del Pozo, R.; Tanne, K. Changes in the biomechanical properties of the rat interparietal suture incident to continuous tensile force application. Arch. Oral. Biol. 2000, 45, 1059–1064. [Google Scholar] [CrossRef] [PubMed]
- Ox, R.H. Wave propagation through a newtonian fluid contained within a thick-walled, viscoelastic tube. Biophys. J. 1968, 8, 691–709. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Herring, S.W.; Ochareon, P. Bone–special problems of the craniofacial region. Orthod. Craniofacial Res. 2005, 8, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Losken, H.W.; Mooney, M.P.; Zoldos, J.; Tschakaloff, A.; Burrows, A.M.; Smith, T.D.; Cano, G.; Arnott, R.; Sherwood, C.; Dechant, J.; et al. Coronal suture response to distraction osteogenesis in rabbits with delayed-onset craniosynostosis. J. Craniofacial Surg. 1999, 10, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Ruengdit, S.; Troy Case, D.; Mahakkanukrauh, P. Cranial suture closure as an age indicator: A review. Forensic Sci. Int. 2020, 307, 110111. [Google Scholar] [CrossRef] [PubMed]
- Di Ieva, A.; Bruner, E.; Davidson, J.; Pisano, P.; Haider, T.; Stone, S.S.; Cusimano, M.D.; Tschabitscher, M.; Grizzi, F. Cranial sutures: A multidisciplinary review. Childs Nerv. Syst. 2013, 29, 893–905. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, L.R.; Lessa, L.G. Comparative analysis of cranial suture complexity in the genus Caiman (Crocodylia, Alligatoridae). Braz. J. Biol. 2000, 60, 689–694. [Google Scholar] [CrossRef] [PubMed]
- Henderson, J.H.; Chang, L.Y.; Song, H.M.; Longaker, M.T.; Carter, D.R. Age-dependent properties and quasi-static strain in the rat sagittal suture. J. Biomech. 2005, 38, 2294–2301. [Google Scholar] [CrossRef] [PubMed]
- Nicolay, C.W.; Vaders, M.J. Cranial suture complexity in white-tailed deer (Odocoileus virginianus). J. Morphol. 2006, 267, 841–849. [Google Scholar] [CrossRef] [PubMed]
- Wood, C. The age-related emergence of cranial morphological variation. Forensic Sci. Int. 2015, 251, 220.e1–220.e20. [Google Scholar] [CrossRef] [PubMed]
- Herring, S.W.; Teng, S. Strain in the braincase and its sutures during function. Am. J. Phys. Anthropol. 2000, 112, 575–593. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Byron, C.D.; Borke, J.; Yu, J.; Pashley, D.; Wingard, C.J.; Hamrick, M. Effects of increased muscle mass on mouse sagittal suture morphology and mechanics. Anat. Rec. A Discov. Mol. Cell Evol. Biol. 2004, 279, 676–684. [Google Scholar] [CrossRef] [PubMed]
- Buezas, G.; Becerra, F.; Vassallo, A. Cranial suture complexity in caviomorph rodents (Rodentia; Ctenohystrica). J. Morphol. 2017, 278, 1125–1136. [Google Scholar] [CrossRef] [PubMed]
- Byron, C.; Segreti, M.; Hawkinson, K.; Herman, K.; Patel, S. Dietary material properties shape cranial suture morphology in the mouse calvarium. J. Anat. 2018, 233, 807–813. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Opperman, L.A. Cranial sutures as intramembranous bone growth sites. Dev. Dyn. 2000, 219, 472–485. [Google Scholar] [CrossRef] [PubMed]
- Geiger, M.; Haussman, S. Cranial Suture Closure in Domestic Dog Breeds and Its Relationships to Skull Morphology. Anat. Rec. 2016, 299, 412–420. [Google Scholar] [CrossRef] [PubMed]
- Hukki, J.; Saarinen, P.; Kangasniemi, M. Single suture craniosynostosis: Diagnosis and imaging. Front. Oral. Biol. 2008, 12, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Curtis, N.; Jones, M.E.; Evans, S.E.; O’Higgins, P.; Fagan, M.J. Cranial sutures work collectively to distribute strain throughout the reptile skull. J. R. Soc. Interface 2013, 10, 20130442. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
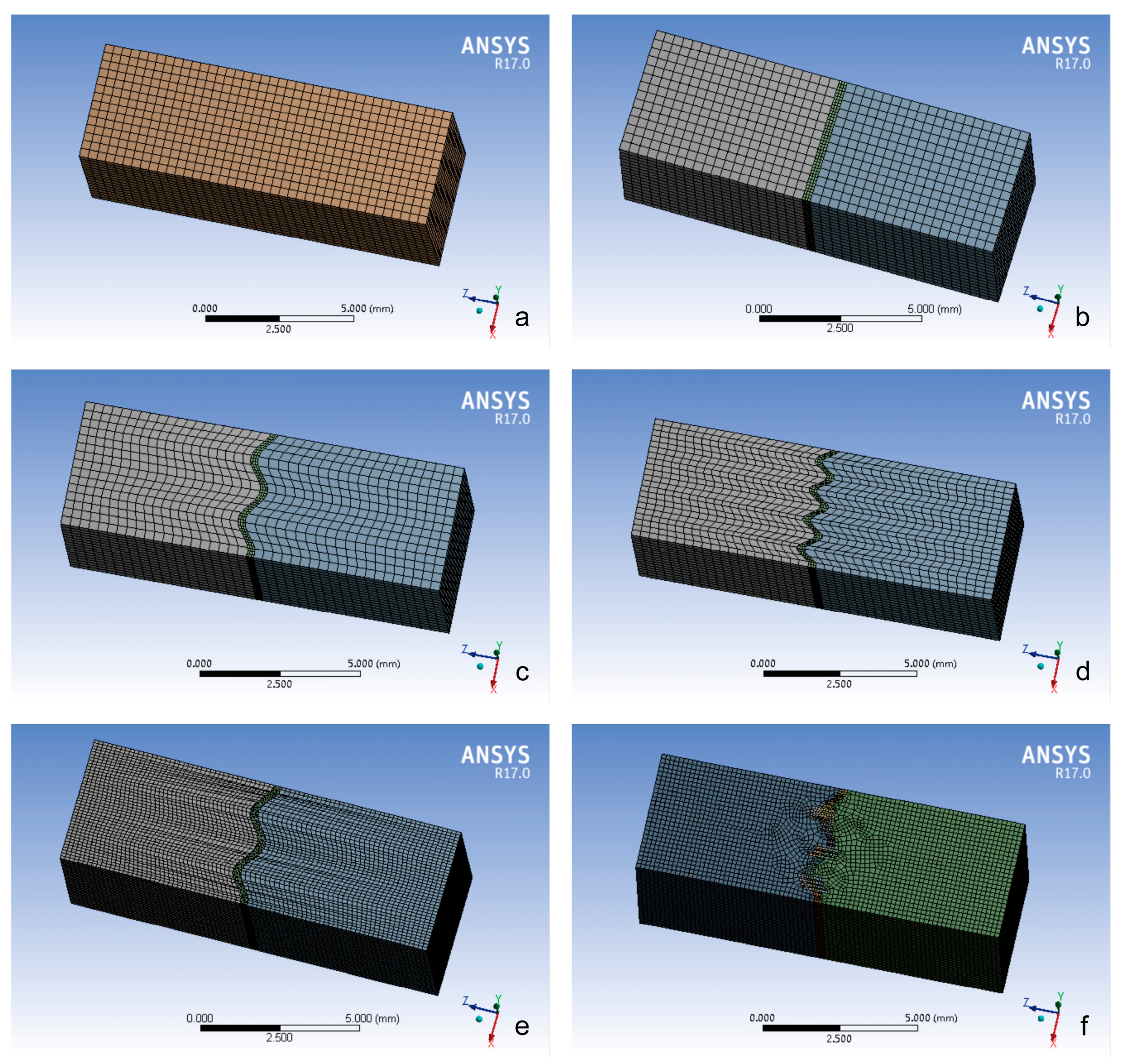



| Model Group | Component | Nodes | Elements | Element Size (mm) |
|---|---|---|---|---|
| Closed Group | Cranial Bone | 42,657 | 9520 | Bone: 0.3 |
| Straight Suture Group | Bone | 21,717 | 4760 | Bone: 0.15 |
| Suture | 30,997 | 6000 | Suture: 0.1 | |
| Sine Wave Group | Bone | 23,190 | 5100 | Bone: 0.15 |
| Suture | 35,563 | 6900 | Suture: 0.1 | |
| Tight Sinusoidal Wave Group | Bone | 32,028 | 7140 | Bone: 0.15 |
| Suture | 45,456 | 8850 | Suture: 0.1 | |
| Layered Sinusoidal Wave Group | Bone (Side 1) | 236,453 | 55,760 | Bone: 0.3 |
| Bone (Side 2) | 230,780 | 54,400 | Bone: 0.3 | |
| Suture | 78,325 | 48,854 | Suture: 0.1 | |
| Layered Sinusoidal & Sutural Bone Group | Bone (Side 1) | 162,296 | 37,570 | Bone: 0.15 |
| Bone (Side 2) | 174,076 | 40,426 | Bone: 0.15 | |
| Sutural Bone 1 | 5884–7406 | 1050–1350 | Suture: 0.1 | |
| Sutural Bone 2 | 5884–7406 | 1050–1350 | Suture: 0.1 | |
| Sutural Bone 3 | 5884–7406 | 1050–1350 | Suture: 0.1 | |
| Remaining Suture Segments | ~6000 | ~1100 | Suture: 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Yuan, S.; Yan, Y.; Zhou, L.; Zheng, C.; Li, Y.; Li, J. Finite Element Analysis of the Effects of Different Shapes of Adult Cranial Sutures on Their Mechanical Behavior. Bioengineering 2025, 12, 318. https://doi.org/10.3390/bioengineering12030318
Yang H, Yuan S, Yan Y, Zhou L, Zheng C, Li Y, Li J. Finite Element Analysis of the Effects of Different Shapes of Adult Cranial Sutures on Their Mechanical Behavior. Bioengineering. 2025; 12(3):318. https://doi.org/10.3390/bioengineering12030318
Chicago/Turabian StyleYang, Han, Shiguo Yuan, Yuan Yan, Li Zhou, Chao Zheng, Yikai Li, and Junhua Li. 2025. "Finite Element Analysis of the Effects of Different Shapes of Adult Cranial Sutures on Their Mechanical Behavior" Bioengineering 12, no. 3: 318. https://doi.org/10.3390/bioengineering12030318
APA StyleYang, H., Yuan, S., Yan, Y., Zhou, L., Zheng, C., Li, Y., & Li, J. (2025). Finite Element Analysis of the Effects of Different Shapes of Adult Cranial Sutures on Their Mechanical Behavior. Bioengineering, 12(3), 318. https://doi.org/10.3390/bioengineering12030318








