A Monte Carlo-Based 3D Whole Lung Model for Aerosol Deposition Studies: Implementation and Validation
Abstract
1. Introduction
- Realistic patient-specific bronchial trees can be constructed. Their proximal airways can be efficiently and automatically extracted from large CT-scan databases thanks to recently developed machine learning-based algorithms [22,23,24,25]. If the lobe or sub-lobe volumes can also be extracted from CT-scans, volume-filling algorithms can be adopted to stochastically grow the deeper airways within them [26,27,28,29,30]. Complete bronchial trees with 23 or more generations can be easily constructed with realistic shapes and physiologically sound morphometric statistical distributions.
- Mathematical models can be applied to healthy pre-constructed trees to simulate different types and severities of lung diseases. Geometric or functional modifications can be applied to specific ducts or distributed along the tree, and deposition simulations can reveal how drug delivery is impaired by the progression of a disease. Thanks to recent advances in functional respiratory imaging, the disease progression can be modeled in a realistic and patient-specific way [36].
2. Model Description and Code Implementation
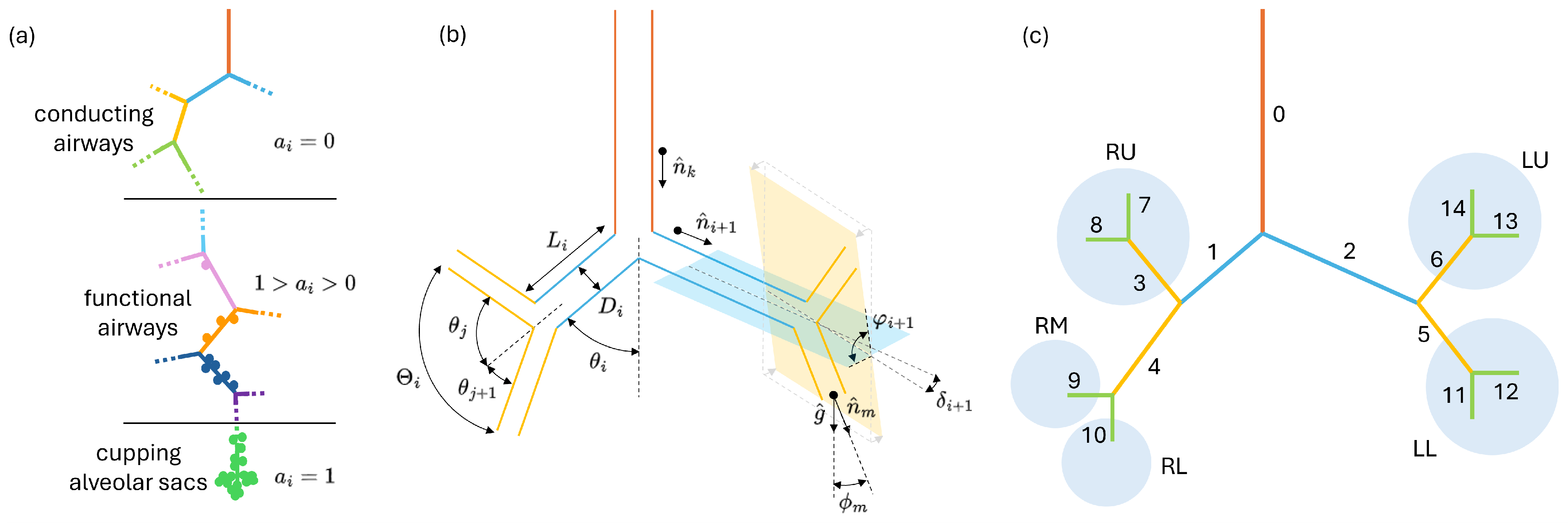
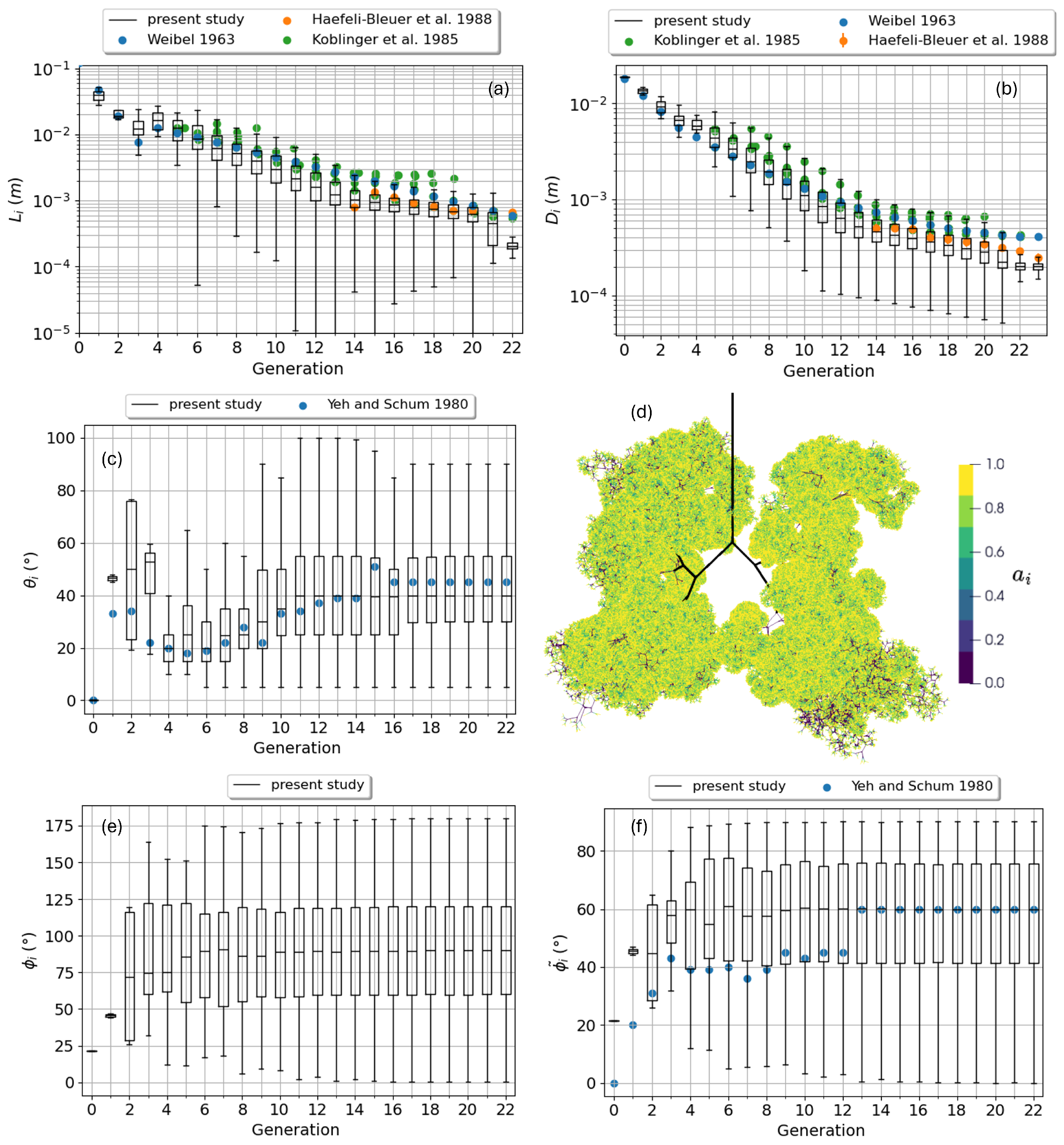
2.1. Bronchial Tree Construction
2.2. Airflow Behavior in the Bronchial Tree
- the total volume of the ducts can be computed, after the bronchial tree is generated, as follows:where the volume of each individual duct has been assumed cylindrical;
- subtracting the duct volume to the total lung volume one can compute the total alveolar volume ;
- must now be distributed in the alveolated ducts based on their local alveolation index , to this aim one can define which is the fraction of the total alveolar volume corresponding to each value as follows:Now the total alveolar volume downstream the i-th duct can be computed as follows:with subset of all the ducts downstream the i-th one, i.e., the sub-tree generated from the i-th duct. is a functional factor representing the efficiency of the alveoli if the j-th duct to stretch and recall air. can be used to represent diffuse or localized losses of lung function due to diseases (e.g., fibrosis or emphysema) or to account for a different local deformation of the alveoli due to a different elasticity/stretchability of parenchyma. According to Equation (8) ventilation anisotropy can thus be induced in a tree by acting on both , i.e., on the local alveolar density, and . Being interested in modeling homogeneous and healthy lungs, unless explicitly stated, in all the calculations presented in this work is set to one for all the ducts of the bronchial trees.
2.3. Aerosol Transport and Deposition
2.3.1. Input Parameters
2.3.2. Algorithm Description
- A particle can deposit in a conducting airway (1).
- A particle can deposit in a functional airway. A random number is extracted in the interval and compared to the local alveolation index which, being normalized to 1, works as the probability to enter an alveolus. If the particle deposits on the airway wall (2), otherwise it enters a local alveolus or a capping alveolar sac (3).
- Once in an alveolus a particle can deposit therein driven by settling or diffusion (4), no inertial impaction is contemplated as the air velocity is supposed to be negligible.
- Lastly, at the end of an inhalation phase, a particle can still be traveling in a conducting or functional duct (5) or floating in an alveouls (6).
- A particle starting in condition (5) can deposit in a conducting (7) or a functional (8) duct. In the latter case the same procedure described for condition (2) applies.
- A particle starting in condition (6) can deposit in the alveolus like in (4).
- As for inhalation, particles can still survive the breath-holding phase remaining suspended in a duct (5) or in an alveolus (6).
- All particles are expelled from the alveoli, as in condition (9). Particles within a capping alveolar sac will start the exhalation phase in its parent duct; particles within a side alveolus will be re-assigned to the corresponding functional duct.
- A particle traveling the airways can deposit in conducting (11) or functional (10) ducts. In the latter case the same procedure described for condition (2) applies.
- A particle can survive until the next inhalation phase, in which case the conditions of Figure 4c apply again. Or, in its ascent, a particle can escape the trachea, condition (12), and reach the extra-thoracic airways. Another attempt for particle deposition is made against the nasal or oropharyngeal probability functions, in case of failure the particle is eventually exhaled in the atmosphere.
2.3.3. Output Analysis
2.3.4. Aerosol Deposition Probabilities
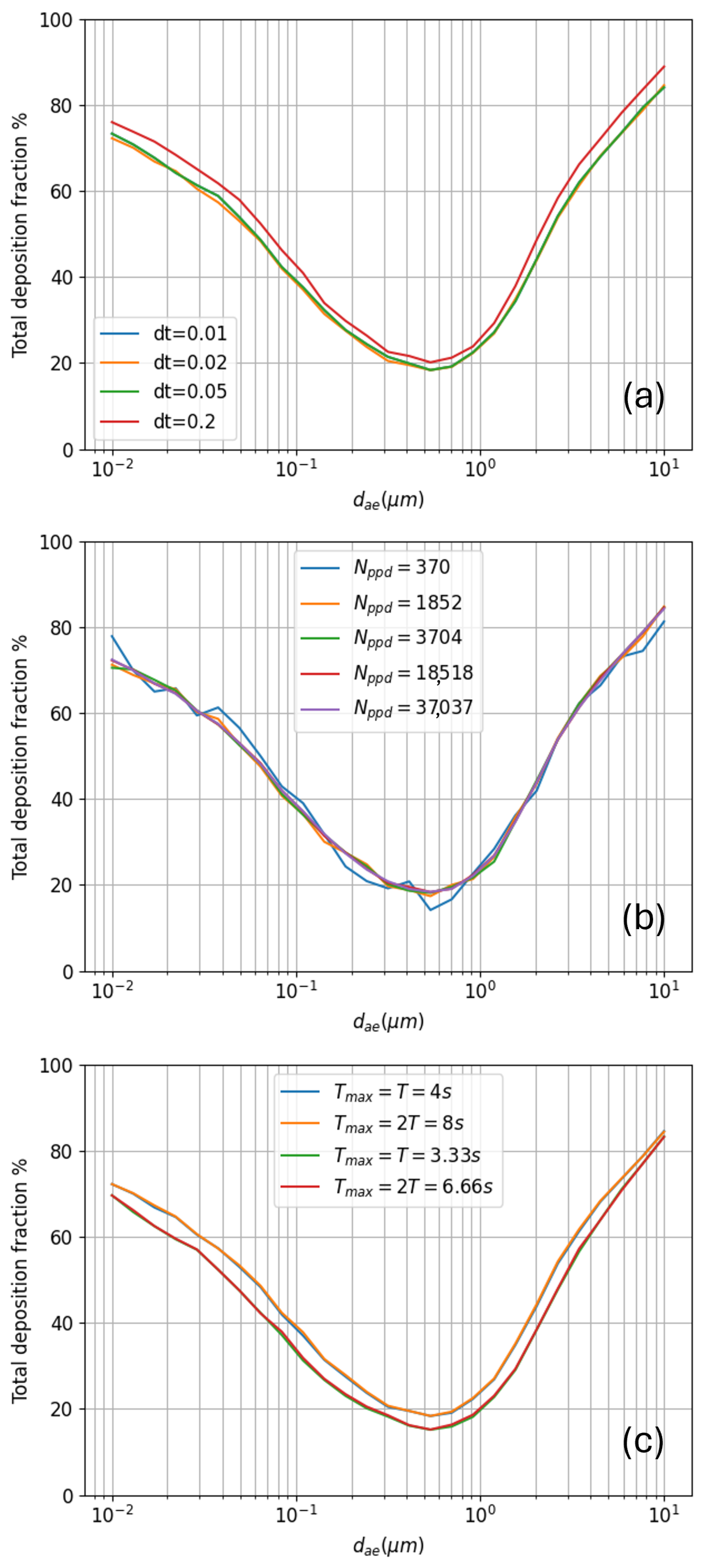
2.3.5. Model Sensitivity Analysis
3. Model Validation
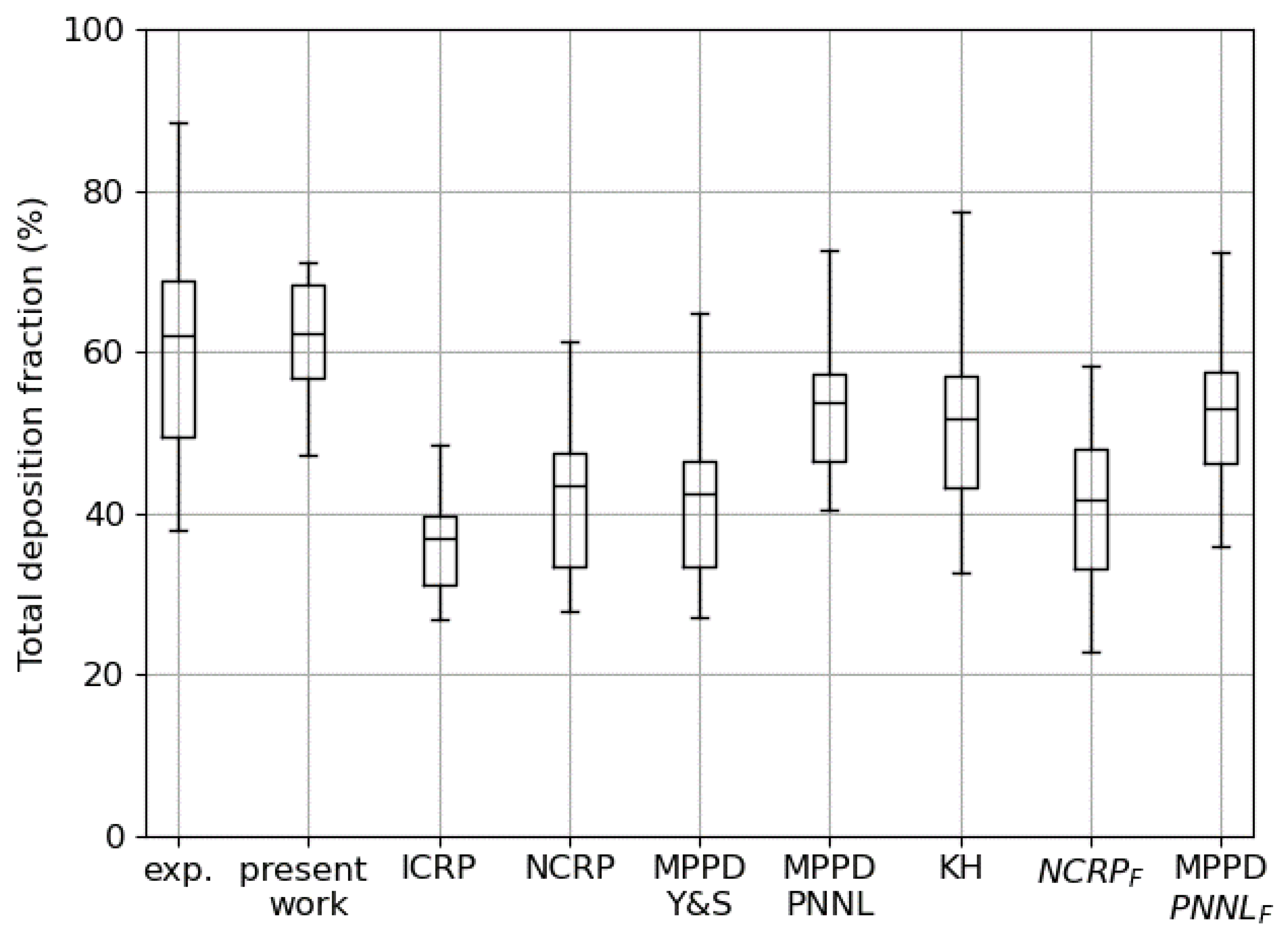
3.1. Total Deposition
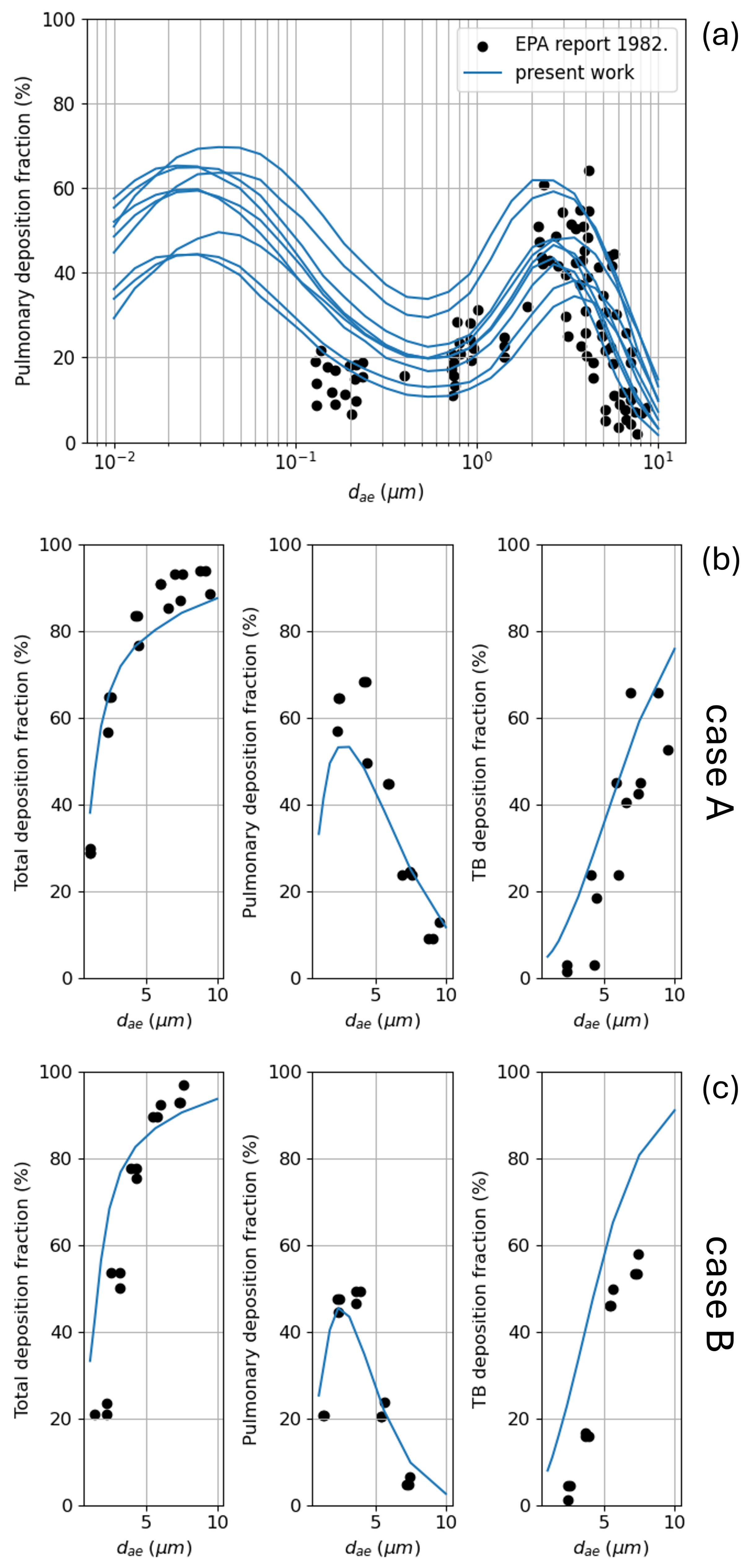
3.2. Regional Deposition
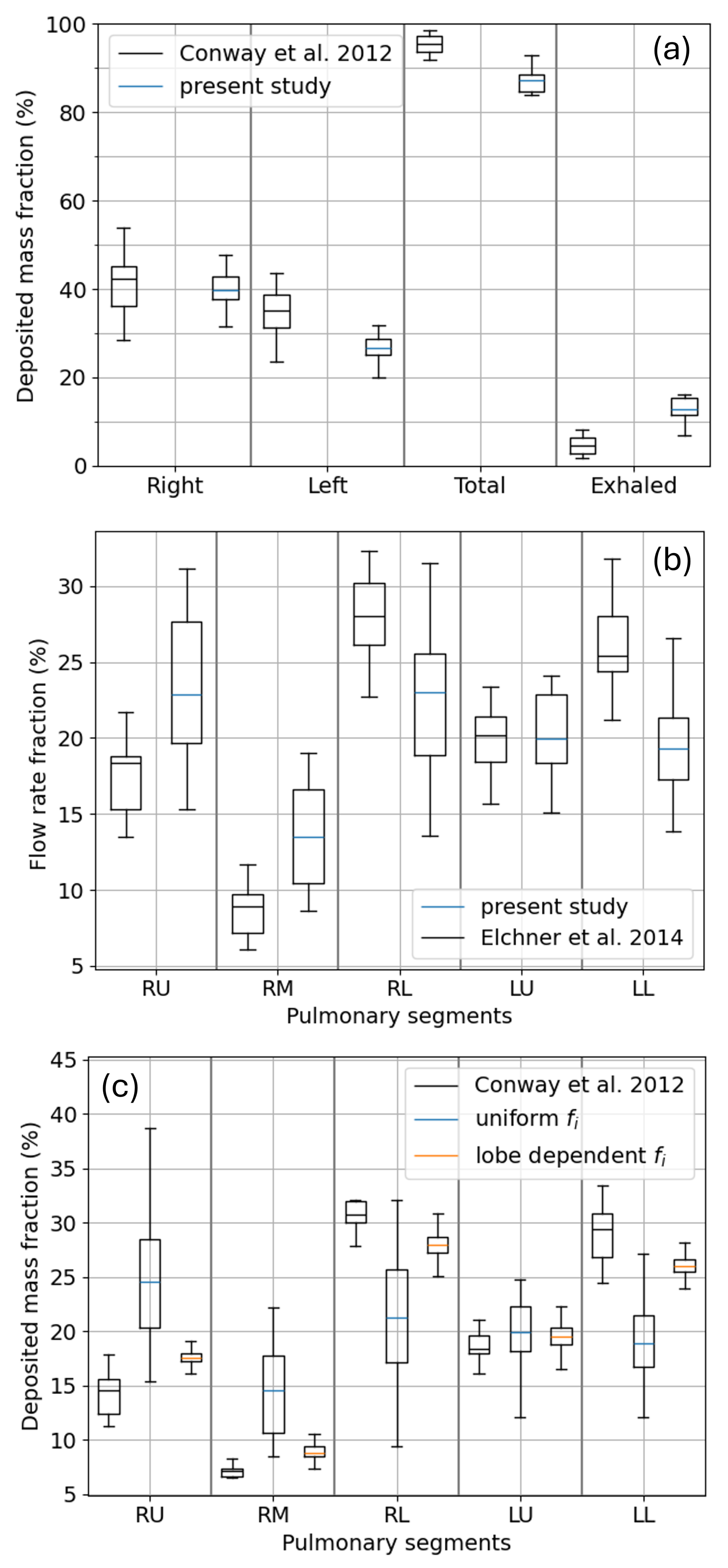
3.3. Lobar and Sub-Lobar Deposition
4. Conclusions and Future Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
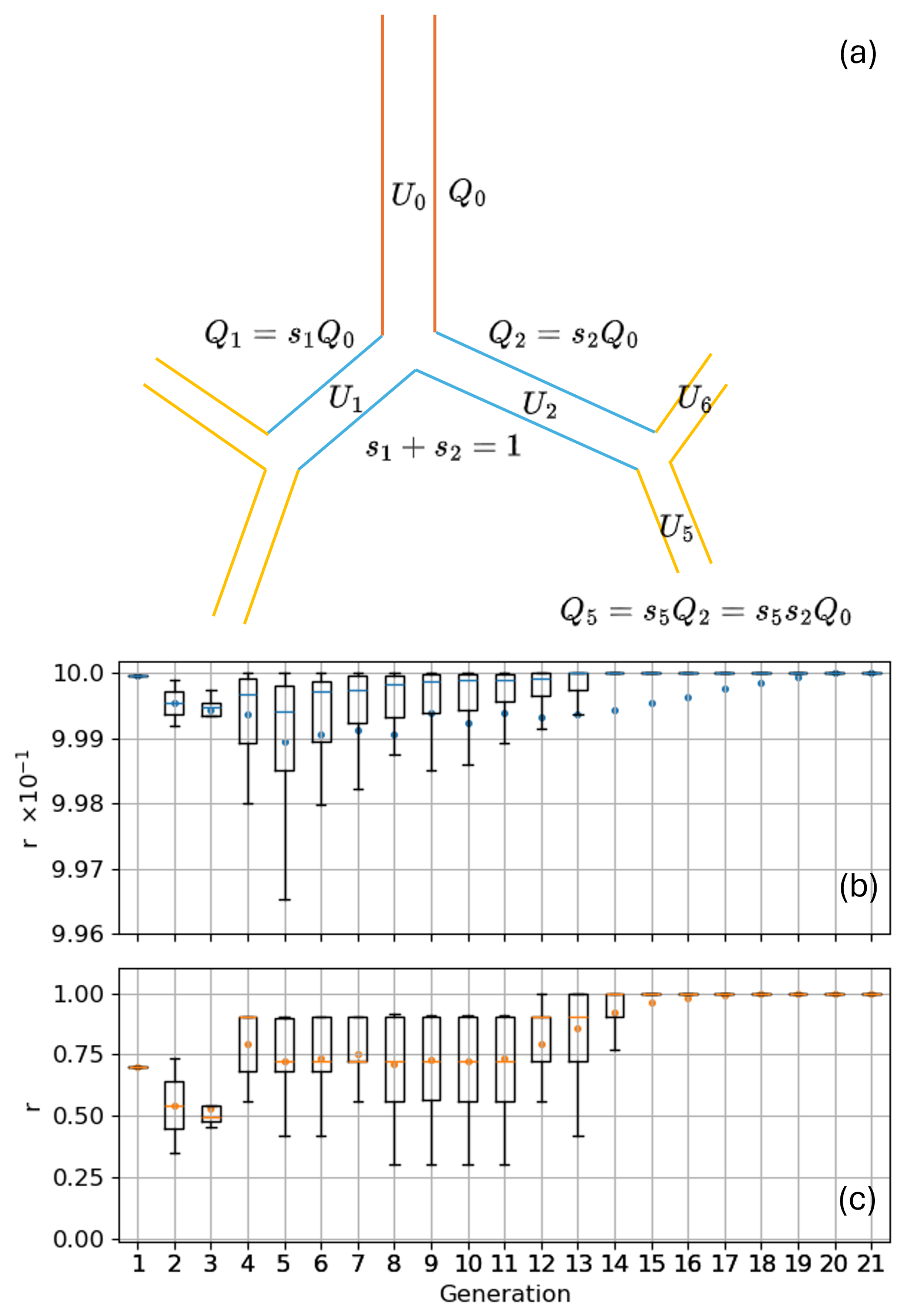
Appendix A. Indexes Relations
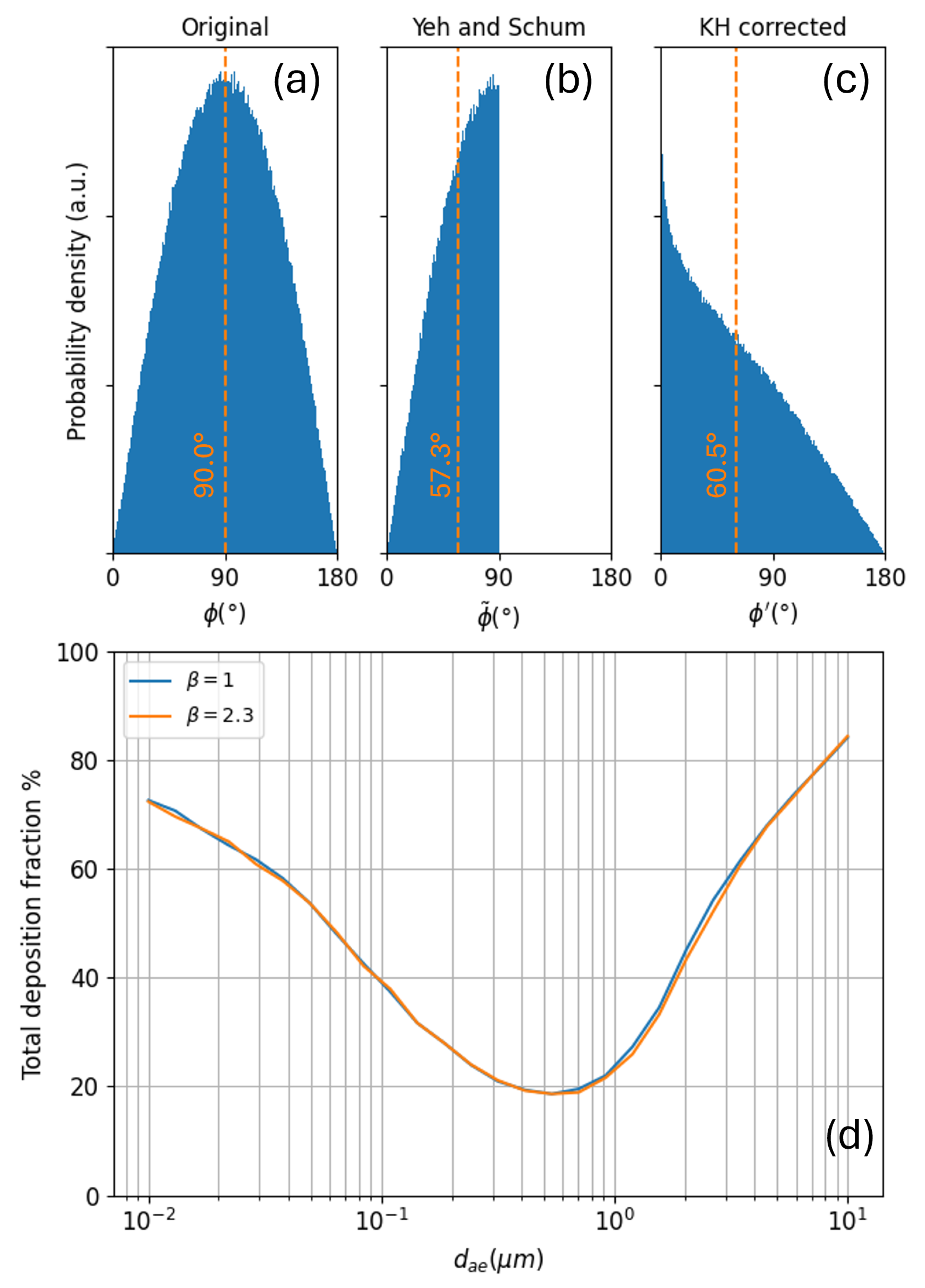
Appendix B. Details on KH-like Tree Generation
Appendix C. Time Integration of the Aerosol Particle Trajectory
Appendix D. Detailed Implementation of Deposition Probability Equations
Appendix E. List of Symbols Adopted in the Paper
| Symbol | Meaning |
|---|---|
| N | number of generations composing the bronchial tree |
| number of ducts composing the bronchial tree | |
| number of bifurcations composing the bronchial tree | |
| versor indicating the i-th duct direction | |
| average diameter of the i-th duct | |
| length of the i-th duct | |
| branching angle of the i-th duct | |
| (angle between and its parent versor ) | |
| bifurcation angle of the i-th duct | |
| (angle between its two child duct versor and ) | |
| gravity angle of the i-th duct | |
| (angle between the gravity versor and ) | |
| rotation angle of the i-th duct | |
| (angle between the plane containing i-th and -th ducts | |
| and the one containing the i-th children) | |
| non-planarity angle of the i-th duct | |
| (angle between the plane containing the i-th duct and the one | |
| containing its two children) | |
| alveolation index of the i-th duct |
| Symbol | Meaning |
|---|---|
| total lung volume | |
| volume of the cylindrical ducts | |
| total alveolar volume | |
| tidal volume | |
| average air velocity in the i-th duct | |
| airflow rate in the i-th duct | |
| airflow rate at the mouth and trachea () | |
| splitting coefficient of the i-th duct | |
| cumulative splitting coefficient of the i-th duct | |
| air density at 37 °C | |
| air dynamic viscosity at 37 °C |
| Symbol | Meaning |
|---|---|
| d | diameter of aerosol particle/droplet |
| aerodynamic diameter of aerosol particle/droplet | |
| density of the aerosol particle/droplets | |
| aerosol particle/droplet size number distribution | |
| aerosol particle/droplet size mass distribution | |
| total duration of the simulation deposition | |
| duration of inhalation phase | |
| duration of breath-holding phase | |
| duration of exhalation phase | |
| T | period of the tidal breathing sinusoid |
| air volume inhaled and exhaled during a tidal period | |
| time instant of particle/droplet insertion | |
| time interval for aerosol insertion | |
| particle/droplet flight time | |
| particle/droplet crossing time for the i-th duct | |
| inertial impaction deposition probability in the i-th duct | |
| gravitational settling deposition probability in the i-th duct | |
| Brownian diffusion deposition probability in the i-th duct | |
| joint probability to survive deposition in the i-th duct |
References
- Subramani, P.K.; Remya, P.; Narayanasamy, D. The Role of Pulmonary Drug Delivery in Modern Therapeutics: An Overview. Cureus 2024, 16, e68639. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Wang, L.; Yang, Q.; Zhang, Y.; Qinglai, T.; Yang, X.; Xiao, Z.; Lei, L.; Li, S. Pulmonary inhalation for disease treatment: Basic research and clinical translations. Mater. Today Bio 2024, 25, 100966. [Google Scholar] [CrossRef]
- Anonymous. First inhaled lentiviral gene therapy enters cystic fibrosis trial. Nat. Biotechnol. 2025, 43, 288. [Google Scholar] [CrossRef]
- Kassinos, S.; Bäckman, P.; Conway, J.; Hickey, A.J. Inhaled Medicines; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Neelakantan, S.; Xin, Y.; Gaver, D.; Cereda, M.; Rizi, R.; Smith, B.; Avazmohammadi, R. Computational lung modelling in respiratory medicine. J. R. Soc. Interface 2022, 19, 20220062. [Google Scholar] [CrossRef]
- Spasov, G.; Rossi, R.; Vanossi, A.; Cottini, C.; Benassi, A. A critical analysis of the CFD-DEM simulation of pharmaceutical aerosols deposition in extra-thoracic airways. Int. J. Pharm. 2022, 629, 122331. [Google Scholar] [CrossRef]
- Spasov, G.; Rossi, R.; Vanossi, A.; Cottini, C.; Benassi, A. A critical analysis of the CFD-DEM simulation of pharmaceutical aerosols deposition in upper intra-thoracic airways: Considerations on air flow. Comput. Biol. Med. 2024, 170, 107948. [Google Scholar] [CrossRef]
- Spasov, G.H.; Rossi, R.; Vanossi, A.; Cottini, C.; Benassi, A. A Critical Analysis of the CFD-DEM Simulation of Pharmaceutical Aerosols Deposition in Upper Intra-Thoracic Airways: Considerations on Aerosol Transport and Deposition. Pharmaceutics 2024, 16, 1119. [Google Scholar] [CrossRef]
- Koullapis, P.; Hofemeier, P.; Sznitman, J.; Kassinos, S. An efficient computational fluid-particle dynamics method to predict deposition in a simplified approximation of the deep lung. Eur. J. Pharm. Sci. 2018, 113, 132–144. [Google Scholar] [CrossRef] [PubMed]
- Longest, P.W.; Tian, G.; Delvadia, R.; Hindle, M. Development of a Stochastic Individual Path (SIP) Model for Predicting the Deposition of Pharmaceutical Aerosols: Effects of Turbulence, Polydisperse Aerosol Size, and Evaluation of Multiple Lung Lobes. Aerosol Sci. Technol. 2012, 46, 1271–1285. [Google Scholar] [CrossRef]
- Tian, G.; Longest, P.W.; Su, G.; Walenga, R.L.; Hindle, M. Development of a stochastic individual path (SIP) model for predicting the tracheobronchial deposition of pharmaceutical aerosols: Effects of transient inhalation and sampling the airways. J. Aerosol Sci. 2011, 42, 781–799. [Google Scholar] [CrossRef]
- Atzori, M.; Gallorini, E.; Cottini, C.; Benassi, A.; Quadrio, M. Direct numerical simulations of inhalation in a 23-generation lung model. arXiv 2025. [Google Scholar] [CrossRef]
- Hofmann, W. Regional Deposition: Deposition Models. J. Aerosol Med. Pulm. Drug Deliv. 2020, 33, 239–248. [Google Scholar] [CrossRef]
- Yeh, H.C.; Schum, G.M. Models of human lung airways and their application to inhaled particle deposition. Bull. Math. Biol. 1980, 42, 461–480. [Google Scholar] [CrossRef]
- Miller, F.J.; Asgharian, B.; Schroeter, J.D.; Price, O. Improvements and additions to the Multiple Path Particle Dosimetry model. J. Aerosol Sci. 2016, 99, 14–26. [Google Scholar] [CrossRef]
- Anjilvel, S.; Asgharian, B. A Multiple-Path Model of Particle Deposition in the Rat Lung. Fundam. Appl. Toxicol. 1995, 28, 41–50. [Google Scholar] [CrossRef]
- Koblinger, L.; Hofmann, W. Monte Carlo modeling of aerosol deposition in human lungs. Part I: Simulation of particle transport in a stochastic lung structure. J. Aerosol Sci. 1990, 21, 661–674. [Google Scholar] [CrossRef]
- Koblinger, L. Analysis of human lung morphometric data for stochastic aerosol deposition calculations. Phys. Med. Biol. 1985, 30, 541. [Google Scholar] [CrossRef] [PubMed]
- Kundu, D.; Panchagnula, M.V. Stochastic asymmetric bronchial tree models for population-scale variability in dosimetry. J. Aerosol Sci. 2025, 189, 106622. [Google Scholar] [CrossRef]
- Jin, G.; Kumar, H.; Clark, A.R.; Burrowes, K.S.; Hoffman, E.A.; Tawhai, M.H. Evaluating the role of sex-related structure-function differences on airway aerosol transport and deposition. J. Appl. Physiol. 2024, 137, 1285–1300. [Google Scholar] [CrossRef] [PubMed]
- Asgharian, B.; Hofmann, W.; Bergmann, R. Particle Deposition in a Multiple-Path Model of the Human Lung. Aerosol Sci. Technol. 2001, 34, 332–339. [Google Scholar] [CrossRef]
- Zhang, M.; Gu, Y. Towards Connectivity-Aware Pulmonary Airway Segmentation. IEEE J. Biomed. Health Inform. 2024, 28, 321–332. [Google Scholar] [CrossRef]
- Tang, Z.; Nan, Y.; Walsh, S.; Yang, G. Adversarial Transformer for Repairing Human Airway Segmentation. IEEE J. Biomed. Health Inform. 2023, 27, 5015–5022. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Y.; Zhang, H.; Qin, Y.; Zheng, H.; Tang, W.; Arnold, C.; Pei, C.; Yu, P.; Nan, Y.; et al. Multi-site, Multi-domain Airway Tree Modeling. Med Image Anal. 2023, 90, 102957. [Google Scholar] [CrossRef]
- Garcia-Uceda, A.; Selvan, R.; Saghir, Z.; Tiddens, H.; De Bruijne, M. Automatic airway segmentation from computed tomography using robust and efficient 3-D convolutional neural networks. Sci. Rep. 2021, 11, 16001. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Qiu, W.; Li, L.; Chen, R.; Kang, Y.; Ruan, S. A novel approach to pulmonary bronchial tree model construction and performance index study. Front. Pharmacol. 2023, 14, 1254804. [Google Scholar] [CrossRef]
- Nousias, S.; Zacharaki, E.; Moustakas, K. AVATREE: An open-source computational modelling framework modelling Anatomically Valid Airway TREE conformations. PLoS ONE 2020, 15, e0230259. [Google Scholar] [CrossRef]
- Montesantos, S.; Katz, I.; Pichelin, M.; Caillibotte, G. The Creation and Statistical Evaluation of a Deterministic Model of the Human Bronchial Tree from HRCT Images. PLoS ONE 2016, 11, e0168026. [Google Scholar] [CrossRef] [PubMed]
- Bordas, R.; Lefevre, C.; Veeckmans, B.; Pitt-Francis, J.; Fetita, C.; Brightling, C.; Kay, D.; Siddiqui, S.; Burrowes, K. Development and Analysis of Patient-Based Complete Conducting Airways Models. PLoS ONE 2015, 10, e0144105. [Google Scholar] [CrossRef]
- Tawhai, M.; Pullan, A.; Hunter, P. Generation of an Anatomically Based Three-Dimensional Model of the Conducting Airways. Ann. Biomed. Eng. 2000, 28, 793–802. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Kumar, H.; Tawhai, M.; Veiga, C.; Szmul, A.; Landau, D.; McClelland, J.; Lao, L.; Burrowes, K. In Silico Ventilation Within the Dose-Volume is Predictive of Lung Function Post-radiation Therapy in Patients with Lung Cancer. Ann. Biomed. Eng. 2021, 49, 1416–1431. [Google Scholar] [CrossRef]
- Yoon, S.; Tam, T.M.; Rajaraman, P.K.; Lin, C.L.; Tawhai, M.; Hoffman, E.A.; Choi, S. An integrated 1D breathing lung simulation with relative hysteresis of airway structure and regional pressure for healthy and asthmatic human lungs. J. Appl. Physiol. 2020, 129, 732–747. [Google Scholar] [CrossRef]
- Roth, C.J.; Yoshihara, L.; Ismail, M.; Wall, W.A. Computational modelling of the respiratory system: Discussion of coupled modelling approaches and two recent extensions. Comput. Methods Appl. Mech. Eng. 2017, 314, 473–493. [Google Scholar] [CrossRef]
- Roth, C.J.; Becher, T.; Frerichs, I.; Weiler, N.; Wall, W.A. Coupling of EIT with computational lung modeling for predicting patient-specific ventilatory responses. J. Appl. Physiol. 2017, 122, 855–867. [Google Scholar] [CrossRef]
- Pozin, N.; Montesantos, S.; Katz, I.; Pichelin, M.; Vignon-Clementel, I.; Grandmont, C. A tree-parenchyma coupled model for lung ventilation simulation. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2873. [Google Scholar] [CrossRef]
- Bayat, S.; Wild, J.; Winkler, T. Lung functional imaging. Breathe 2023, 19, 220272. [Google Scholar] [CrossRef]
- Hansen, J.E.; Ampaya, E.P. Human air space shapes, sizes, areas, and volumes. J. Appl. Physiol. 1975, 38, 990–995. [Google Scholar] [CrossRef]
- Haefeli-Bleuer, B.; Weibel, E.R. Morphometry of the human pulmonary acinus. Anat. Rec. 1988, 220, 401–414. [Google Scholar] [CrossRef] [PubMed]
- Kitaoka, H.; Takaki, R.; Suki, B. A three-dimensional model of the human airway tree. J. Appl. Physiol. 1999, 87, 2207–2217. [Google Scholar] [CrossRef]
- Ochs, M.; Nyengaard, J.R.; Jung, A.; Knudsen, L.; Voigt, M.; Wahlers, T.; Richter, J.; Gundersen, H.J.G. The Number of Alveoli in the Human Lung. Am. J. Respir. Crit. Care Med. 2004, 169, 120–124. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R. Morphometry of the Human Lung; Springer: Berlin/Heidelberg, Germany. [CrossRef]
- Pedley, T.; Schroter, R.; Sudlow, M. Energy losses and pressure drop in models of human airways. Respir. Physiol. 1970, 9, 371–386. [Google Scholar] [CrossRef] [PubMed]
- Pedley, T.; Schroter, R.; Sudlow, M. The prediction of pressure drop and variation of resistance within the human bronchial airways. Respir. Physiol. 1970, 9, 387–405. [Google Scholar] [CrossRef]
- van Ertbruggen, C.; Hirsch, C.; Paiva, M. Anatomically based three-dimensional model of airways to simulate flow and particle transport using computational fluid dynamics. J. Appl. Physiol. 2005, 98, 970–980. [Google Scholar] [CrossRef]
- Elcner, J.; Chovancova, M.; Jicha, M. The influence of boundary conditions to the flow through model of upper part of human respiratory system. EPJ Web Conf. 2014, 67, 02025. [Google Scholar] [CrossRef]
- Finlay, W.H. The Mechanics of Inhaled Pharmaceutical Aerosols; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Cheng, Y.S. Aerosol Deposition in the Extrathoracic Region. Aerosol Sci. Technol. 2003, 37, 659–671. [Google Scholar] [CrossRef]
- Yeh, H.; Phalen, R.; Raabe, O. Factors influencing the deposition of inhaled particles. Environ. Health Perspect. 1976, 15, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Monjezi, M.; Dastanpour, R.; Saidi, M.; Pishevar, A. Prediction of particle deposition in the respiratory track using 3D–1D modeling. Sci. Iran. 2012, 19, 1479–1486. [Google Scholar] [CrossRef]
- Sonnenberg, A.H.; Herrmann, J.; Grinstaff, M.W.; Suki, B. A Markov chain model of particle deposition in the lung. Sci.Rep. 2020, 10, 13573. [Google Scholar] [CrossRef]
- Darquenne, C. Aerosol Deposition in Health and Disease. J. Aerosol Med. Pulm. Drug Deliv. 2012, 25, 140–147. [Google Scholar] [CrossRef] [PubMed]
- Altshuler, B.; Yarmus, L.; Palmes, E.; Nelson, N. Aerosol deposition in the human respiratory tract. I. Experimental procedures and total deposition. AMA Arch. Ind. Health 1957, 15, 293–303. [Google Scholar]
- Landahl, H.; Tracewell, T.; Lassen, W. On the retention of airborne particulates in the human lung: II. AMA Arch. Ind. Hyg. Occup. Med. 1951, 3, 359–366. [Google Scholar]
- Swift, D.; Shanty, F.; O’Neil, J. Human Respiratory Deposition Pattern of Fume-Like Particles. Am. Ind. Hyg. Conf. 1977. [Google Scholar]
- Rissler, J.; Nicklasson, H.; Gudmundsson, A.; Wollmer, P.; Swietlicki, E.; Löndahl, J. A Set-up for Respiratory Tract Deposition Efficiency Measurements (15-5000 nm) and First Results for a Group of Children and Adults. Aerosol Air Qual. Res. 2017, 17, 1244–1255. [Google Scholar] [CrossRef]
- Brand, P.; Friemel, I.; Meyer, T.; Schulz, H.; Heyder, J.; Häußinger, K. Total Deposition of Therapeutic Particles During Spontaneous and Controlled Inhalations. J. Pharm. Sci. 2000, 89, 724–731. [Google Scholar] [CrossRef]
- Rissler, J.; Sjögren, M.P.; Linell, J.; Hurtig, A.L.; Wollmer, P.; Löndahl, J. An experimental study on lung deposition of inhaled 2 μm particles in relation to lung characteristics and deposition models. Part. Fibre Toxicol. 2023, 20, 40. [Google Scholar] [CrossRef]
- Guha, S.; Hariharan, P.; Myers, M.R. Enhancement of ICRP’s Lung Deposition Model for Pathogenic Bioaerosols. Aerosol Sci. Technol. 2014, 48, 1226–1235. [Google Scholar] [CrossRef]
- Anonymous. Human respiratory tract model for radiological protection. A report of a Task Group of the International Commission on Radiological Protection. Ann. ICRP 1994, 24, 1–482. [Google Scholar]
- U.S. Environmental Protection Agency. Air Quality Criteria for Particulate Matter and Sulfur Oxides: Volume III; U.S. Environmental Protection Agency: Washington, DC, USA, 1982.
- Stahlhofen, W.; Gebhart, J.; Heyder, J. Experimental determination of the regional deposition of aerosol particles in the human respiratory tract. Am. Ind. Hyg. Assoc. J. 1980, 41, 385–398a. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.; Fleming, J.; Majoral, C.; Katz, I.; Perchet, D.; Peebles, C.; Tossici-Bolt, L.; Collier, L.; Caillibotte, G.; Pichelin, M.; et al. Controlled, parametric, individualized, 2-D and 3-D imaging measurements of aerosol deposition in the respiratory tract of healthy human subjects for model validation. J. Aerosol Sci. 2012, 52, 1–17. [Google Scholar] [CrossRef]
- Grill, M.J.; Biehler, J.; Wichmann, K.R.; Rudlstorfer, D.; Rixner, M.; Brei, M.; Richter, J.; Bügel, J.; Pischke, N.; Wall, W.A.; et al. In silico high-resolution whole lung model to predict the locally delivered dose of inhaled drugs. arXiv 2023. [Google Scholar] [CrossRef]
- Winkler-Heil, R.; Hussain, M.; Hofmann, W. Predictions of inter- and intra-lobar deposition patterns of inhaled particles in a five-lobe lung model. Inhal. Toxicol. 2021, 33, 96–112. [Google Scholar] [CrossRef]
- Phillips, C.; Kaye, S. On the asymmetry of bifurcations in the bronchial tree. Respir. Physiol. 1997, 107, 85–98. [Google Scholar] [CrossRef]
- Hofmann, W.; Koblinger, L. Monte Carlo modeling of aerosol deposition in human lungs. Part II: Deposition fractions and their sensitivity to parameter variations. J. Aerosol Sci. 1990, 21, 675–688. [Google Scholar] [CrossRef]
- Ponzini, R.; Da Vià, R.; Bnà, S.; Cottini, C.; Benassi, A. Coupled CFD-DEM model for dry powder inhalers simulation: Validation and sensitivity analysis for the main model parameters. Powder Technol. 2021, 385, 199–226. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Cui, Y.; Schmalfuß, S. Potential and constraints for the application of CFD combined with Lagrangian particle tracking to dry powder inhalers. Eur. J. Pharm. Sci. 2019, 128, 299–324. [Google Scholar] [CrossRef]
- Suwandecha, T.; Wongpoowarak, W.; Srichana, T. Computer-aided design of dry powder inhalers using computational fluid dynamics to assess performance. Pharm. Dev. Technol. 2016, 21, 54–60. [Google Scholar] [CrossRef] [PubMed]
- Wong, W.; Fletcher, D.F.; Traini, D.; Chan, H.K.; Young, P.M. The use of computational approaches in inhaler development. Adv. Drug Deliv. Rev. 2012, 64, 312–322. [Google Scholar] [CrossRef] [PubMed]
- Ruzycki, C.A.; Javaheri, E.; Finlay, W.H. The use of computational fluid dynamics in inhaler design. Expert Opin. Drug Deliv. 2013, 10, 307–323. [Google Scholar] [CrossRef]
- Feng, Y.; Zhao, J.; Hayati, H.; Sperry, T.; Yi, H. Tutorial: Understanding the transport, deposition, and translocation of particles in human respiratory systems using Computational Fluid-Particle Dynamics and Physiologically Based Toxicokinetic models. J. Aerosol Sci. 2021, 151, 105672. [Google Scholar] [CrossRef]
- Vulovic, A.; Sustersic, T.; Cvijic, S.; Ibric, S.; Filipovic, N. Coupled in silico platform: Computational fluid dynamics (CFD) and physiologically-based pharmacokinetic (PBPK) modelling. Eur. J. Pharm. Sci. 2018, 113, 171–184. [Google Scholar] [CrossRef]
- Winkler-Heil, R.; Hofmann, W. Modeling particle deposition in the Balb/c mouse respiratory tract. Inhal. Toxicol. 2016, 28, 180–191. [Google Scholar] [CrossRef]
- Monfared, M.; Mohammadzadeheydgahi, M.; Farshidfar, Z.; Mehrabi, S.; Sadrizadeh, S.; Abouali, O. Morphometric variation in central airways of ten different human lung. Biomed. Phys. Eng. Express 2025, 11, 025054. [Google Scholar] [CrossRef] [PubMed]
- Yeh, H.C.; Schum, G.M.; Duggan, M.T. Anatomic Models of the tracheobronchial and pulmonary regions of the rat. Anat. Rec. 1979, 195, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Davies, C.N. Definitive equations for the fluid resistance of spheres. Proc. Phys. Soc. 1945, 57, 259. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spasov, G.H.; Cottini, C.; Benassi, A. A Monte Carlo-Based 3D Whole Lung Model for Aerosol Deposition Studies: Implementation and Validation. Bioengineering 2025, 12, 1092. https://doi.org/10.3390/bioengineering12101092
Spasov GH, Cottini C, Benassi A. A Monte Carlo-Based 3D Whole Lung Model for Aerosol Deposition Studies: Implementation and Validation. Bioengineering. 2025; 12(10):1092. https://doi.org/10.3390/bioengineering12101092
Chicago/Turabian StyleSpasov, Georgi Hristov, Ciro Cottini, and Andrea Benassi. 2025. "A Monte Carlo-Based 3D Whole Lung Model for Aerosol Deposition Studies: Implementation and Validation" Bioengineering 12, no. 10: 1092. https://doi.org/10.3390/bioengineering12101092
APA StyleSpasov, G. H., Cottini, C., & Benassi, A. (2025). A Monte Carlo-Based 3D Whole Lung Model for Aerosol Deposition Studies: Implementation and Validation. Bioengineering, 12(10), 1092. https://doi.org/10.3390/bioengineering12101092






