1. Introduction
According to the World Health Organization (WHO), 17.9 million people die each year due to cardiovascular disease (CVDs), and four out of five of these deaths are due to heart attacks and strokes. In contrast, one-third of these deaths occur prematurely in people under 70 years of age. Identifying those at the highest risk of CVDs and ensuring they receive appropriate treatment can prevent premature deaths [
1]. Typically, to diagnose a CVD or cardiac abnormality, an electrocardiogram (ECG) signal is acquired in a clinical setting, then manually analyzed by an experienced cardiologist. However, some CVDs, such as arrhythmia, may not appear in a short trace of ECG and may require extended monitoring. Holter monitors are used for extended monitoring as subjects do their normal activities. However, such monitors are bulky and inconvenient to use, may restrict the activities that can be performed, and require hospital visits when electrodes detach from the skin. With the advent of miniaturized wearable health devices (WHDs), continuous monitoring of ECG signals is possible. WHDs can be implemented on small-footprint circuits with low power consumption in a fabric, and the wireless sensor network can be integrated into a garment [
2], making them comfortable and not bulky and a convenient alternative to Holter monitors [
3,
4,
5]. However, as WHDs are implemented using low-power microcontrollers with limited memory and battery power, only a limited amount of data can be acquired and stored. This may be highly restrictive for continuous monitoring; therefore, WHDs may have to communicate to a central node for storage and manipulation of the acquired data. Since data transmission represents the most demanding task in terms of energy consumption for a WHD node [
6], to deal with these limitations, the state of the art proposes the use of compression techniques to reduce the data rate toward the central node. Compression techniques or algorithms are usually divided into the following two main categories: (i) lossless and (ii) lossy algorithms. Lossless techniques, such as the Lempel–Ziv–Welch [
7] and Huffman [
8] methods, can compress the ECG signal without substantial loss of information but generally have Compression Ratio (CR) values of 2 or 4 (the number of samples is reduced by a factor of 2 or 4, respectively). On the other hand, lossy techniques can reach a much greater compression ratio (between 10 and 20) but with the possibility of losing portions of significant information. Among the lossy techniques for ECG compression, transformation techniques such as Discrete Wavelet Transform (DWT) [
9,
10,
11] and Fourier transform [
12] are widely used, since they can compress the signal without loss of clinical information. These techniques impose a heavy computational load on the node of the WHD, so they are not suitable for use with a wearable device. Among the lossy methods, Compressed Sensing (CS) has great potential to be used in WHDs, as it has a low computational load in the signal compression phase. Consequently, compression can be performed directly on the WHD nodes, while the reconstruction of the signal, which has a significantly higher computational requirement, can be performed by a receiver node. The main challenge in developing CS frameworks for the compression and reconstruction of ECG signals is finding compression (sensing matrix) and reconstruction (dictionary matrix) matrices that offer the best trade-off between the quality of reconstruction and achievable compression [
13,
14,
15,
16]. Besides acquiring and compressing the ECG signal, WHD can also be considered as part of a system that can detect cardiac anomalies. As anomaly detection and classification are performed in real time, a cardiologist can be promptly warned through an alert system in case of a positive detection [
17].
In this paper, a new method for the classification of ECG signal arrhythmias from their compressed representations obtained using CS is presented. The method works on compressed heartbeat waveforms obtained by segmenting the ECG signal according to the R-peak position and compressing it with a Deterministic Binary Block Diagonal (DBBD) matrix. The method evaluates the discrete cosine transform (DCT) coefficients of each compressed heartbeat and identifies the heartbeat type among the considered categories. For the classification of the beats, a combination of ensembled k-Nearest Neighbor (KNN) classifiers was used, working in parallel. Before validating the method in a real-life scenario with the ECG signals acquired from a wearable device, a preliminary evaluation phase was performed using signals from the MIT-BIH database to compare the performance of the proposed method with literature results. Among different datasets, the MIT-BIH database was chosen because it has been used most studies regarding ECG anomaly detection. In this preliminary phase, five heartbeat classes were considered, as they are the most commonly considered in the literature regarding ECG anomaly detection, namely Atrial Premature Beat (APB, labeled as A), Premature Ventricular Contraction (PVC, labeled as V), normal beats (labeled as N), Right-Branch Block Beat (RBBB, labeled as R), and Left-Branch Block Beat (LBBB, labeled as L), whose characteristic waveforms are shown in
Figure 1.
It is important to clarify a fundamental point. This article aims to carry out the classification of ECG beats, not of the entire trace, based on tags inserted by cardiologists. This research is not intended to be a replacement for medical diagnosis but can be used as a support for diagnosis alongside the expertise of cardiologists. The following are the contributions of this paper:
A classification methodology is proposed for distinguishing different arrhythmias in ECG signals acquired by compressed sensing using an ensemble of classifiers and a small set of features.
The proposed methodology can perform classification without the need to reconstruct the signal. This makes it particularly suitable for use in combination with WHDs that can work with limited energy resources.
The rest of the paper is organized as follows.
Section 2 reports the state of the art for ECG classification using machine learning (ML), while
Section 3 provides an overview of CS.
Section 4 presents the proposed method for the classification of ECG arrhythmias, while
Section 5 presents the experimental evaluation and the limitations of the proposed method. Finally,
Section 6 provides the conclusion and possible directions for future work.
2. Background
To classify the beats of the ECG signal, features need to be defined and extracted. Typically, the features considered in the state of the art can be mainly divided into the following four categories [
18]: features in the time domain (e.g., Principal Component Analysis (PCA) [
19,
20,
21,
22], Linear Discriminant Analysis (LDA) [
20], and Independent Component Analysis (ICA) [
23,
24]), features in the frequency domain (e.g., Discrete Fourier Transform (DFT) coefficients, DCT [
25], and Power Spectral Density (PSD) [
26]), statistical measures or measurement based on the signal morphology [
27], and nonlinear methods (e.g., wavelet transform coefficients [
21,
22], Higher-Order Statistics (HOS) [
28,
29], and empirical mode decomposition [
30]).
In [
27], Chazal et al. used a set of time-domain features combined with the morphological features of an ECG signal. Some of the used features included pre-RR intervals, post-RR intervals, mean RR, local RR, QRS duration, T-wave duration, P-wave presence, QRS, normalized QRS, T wave, and normalized T wave. The classifier was trained on the signals from the MIT-BIH arrhythmia database, from which 44 ECG signals were extracted from different subjects without a pacemaker. The classifier model is based on linear decomposition, and 12 different classifier configurations were used. In particular, eight configurations present a classifier trained on a single ECG lead, while the other four present two classifiers trained on two ECG leads. The final classification of a beat is carried out by combining the outputs of the two classifiers with a maximum likelihood combiner. The classifier groups the ECG signals into the following five different classes defined by the Advancement of Medical Instrumentation (AAMI) guidelines: normal beats and bundle branch block beats (tagged as N), supraventricular ectopic beats (SVEBs) (tagged as S), ventricular ectopic beats (VEBs) (tagged as V), beats that result from fusing normal beats and VEBs (tagged as F), and unknown beats (tagged as Q). Considering the exhibited performance, the best achieved accuracy was 96.4%.
In [
26], Plawiak used PSD obtained using the Welsh method combined with the discrete Fourier transform of the ECG signal, which was normalized by applying a logarithmic function to the transformed signal. To reduce the data, speed up the classification, and eliminate features that contain non-significant information, Rutkowski et. al. [
31] proposed a system for the automatic classification of ECG signal anomalies with a feature selection phase using a Genetic Algorithm (GA). The proposed method can classify 17 types of beats, using 1000 10-second-long ECG segments from the MIT-BIH database as training signals. The method was tested using dour classifiers, namely Support Vector Machine (SVM), k-Nearest Neighbor (KNN), Probabilistic Neural Network (PNN), and Radial Basis Function Neural Network (RBFNN), managing to achieve an accuracy of 98.85%.
In [
25], Roshat et al. proposed a method for the classification of ECG arrhythmias that uses the DCT features of the signal. Signals from the MIT-BIH database were used for classification. Initially, there is a signal preprocessing phase, in which a wavelet-based denoising technique is used to clean up the signal of noise. Subsequently, a Pan–Tompkins algorithm [
32] is used to detect the R peak. Following this, 200 samples are taken around the peak (100 before the peak and 99 after the peak), and the DCT is applied. A PCA-based feature selection phase is used to eliminate redundant or non-significant features. The system is able to recognize five types of beats (same classes as [
27]), and the method has been tested using the following six classifiers: a neural network (NN), PNN, SVM, and radial basis functions (linear, quadratic, and polynomial). The authors reported a maximum accuracy of 99.52% using a PNN classifier.
Turker et al. [
33] used morphological wavelet transform features projected onto a lower dimensional feature space using PCA and temporal ECG features. The proposed classifier is a fully connected artificial neural network optimized patient-wise using a multidimensional particle swarm optimization technique. Following the AAMI guidelines, it discriminated five classes and was able to achieve an average accuracy of 98.58%.
Osowski et al. [
34] proposed a neural network classifier based on hybrid fuzzy logic, using HOS as the feature set to discriminate the following seven ECG classes: normal beats, LBBB, RBBB, APB, PVC, ventricular flutter waves, and ventricular escape beats. The average accuracy is 96.06%.
Isin et. al. [
35], developed a deep learning framework that was able to carry out the automatic classification and diagnosis of arrhythmias in ECG signals. The deep learning framework was trained on a general image dataset, after which it carries out automatic ECG arrhythmia diagnostics. A transferred deep convolutional neural network (namely, AlexNet) is used as a feature extractor, and the extracted features are fed into a simple back-propagation neural network to carry out the final classification. The authors used the MIT-BIH arrhythmia database as their dataset and selected three different conditions of ECG, namely (i) normal beats, (ii) paced beats, and (iii) right-branch block beats. The authors obtained a test accuracy of 92.44%.
In addition to methods and algorithmic improvements in ECG analysis, there is still room for improvement in terms of its applications, for example, in IoMT and telehealth devices [
18]. The methods presented above are focused on increasing the accuracy of classification without considering that in IoMT and telemedicine applications, the devices used to acquire the signal are constrained in terms of power consumption, as they are battery-powered. This implies that in scenarios such as those described above, wearable devices cannot be used for long-term acquisition of ECG signals. Another limitation that can occur in these systems is that when multiple patients are analyzed, the transmission systems cannot support the necessary data rate. It is possible to apply compression techniques to the ECG signals and perform automatic classification directly from the compressed samples without carrying out reconstruction because the compressed signal contains all the information necessary to identify arrhythmias. This results in a reduction in power consumption compared to classical classification methods in which compression is followed by reconstruction before classification, enabling the use of wearable technologies, as, since the transmitted data are compressed, the data rate will be lower.
In [
36], Alvarado et al. proposed a new method for the classification of anomalies from ECG signals for WHD applications. The signal is first preprocessed through a bank of filters to eliminate baseline wandering, and the temporal features of the signal are extracted from a compressed version of the signal. Compression is applied using a model based on the Integrate and Fire (IF) sampler. The authors analyzed the ECG signals using the stream of pulses generated by the IF sampler, extracted the pulse features, and evaluated the classifier’s performance. Therefore, the ECG signal does not need to be reconstructed. The chosen classifier is based on an LDA model, and the proposed method achieves the dual purpose of compressing the data-intensive ECG signals and performing classification in the pulse domain, following the AAMI guidelines for classification, achieving an accuracy of 93.6%.
Zheng et al. [
37] proposed a method utilizing singular value decomposition (SVD) to compress ECG signals and feed the compressed data to a convolutional neural network (CNN) and SVM for classification. The system can discriminate among the following four classes: normal beats, PVC, RBBB, and LBBB. A total of 11 records were obtained from the MIT-BIH cardiac arrhythmia database and used for the training and testing phases, and a Pan–Tompkin algorithm was used to divide the ECG signals into frames (one for each heartbeat). The highest average accuracies were 99.39% with the CNN classifier and 99.21% with SVD compression.
In [
38], Huang et al. developed an accurate method for the classification arrhythmias in ECG signalsthat involves compressing the signal using the maximal overlap wavelet packed decomposition in order to decompose the ECG into sub-signals of different scales. They used the Fast Compression Residual Convolutional Neural Network (FCResNet) and were able to discriminate among the following five different beat types: LBBB, RBBB, PVC, normal beats, and APB, achieving an overall accuracy of 98.79%. When comparing the performance among these three methods, it is possible to observe that the methods presented in [
37,
38] achieve higher accuracies than the method reported in [
36], but since they are based on NNs, they have the following disadvantages: (i) the requirement of large quantities of data for training; (ii) computational complexity, which results in the use of specialized hardware; and (iii) the lack of interpretability.
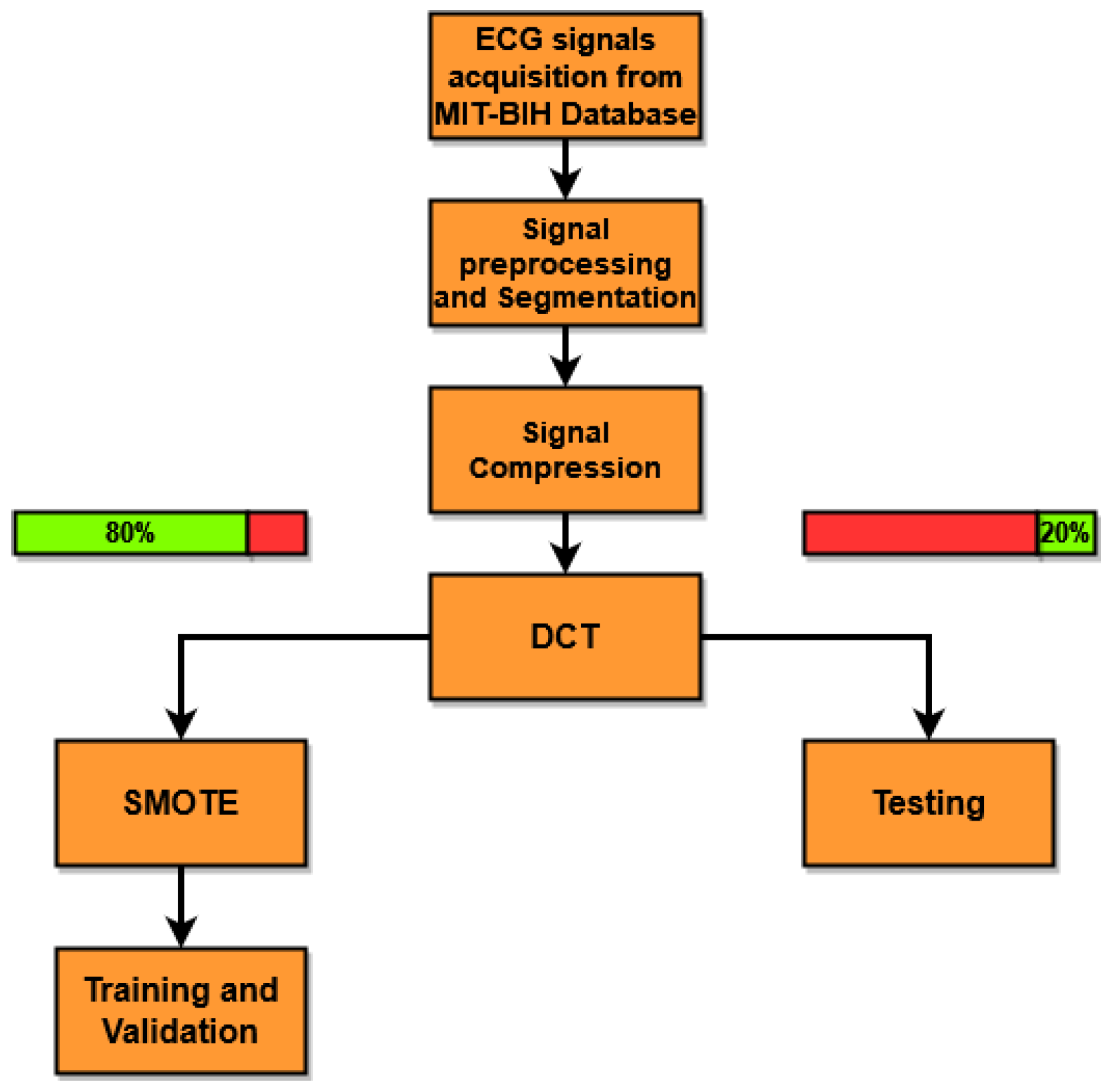
5. Experimental Evaluation
To carry out the experimental evaluation of the proposed method (see
Figure 2), the ECG signals were taken from the freely available online Physionet MIT-BIH Arrhythmia Database [
49]. The Physionet Database contains 48 ECG tracks from 47 ambulatory patients acquired through two channels for a period of half an hour. These acquisitions were made at a sampling frequency of 360 Hz, with a resolution of 11 bits per channel. Each ECG beat present in the database has been annotated by a cardiologist. This annotation is used to discriminate among the various beats and to select the desired heartbeat based on the classes discriminated by the classifier. For these tests, 44 out of the 48 available ECG tracks were used, where the 4 left-out tracks correspond to paced beats. As described in
Section 4, the QRS complexes were identified, the ECG signals were segmented into sub-signals centered on the R peak, each containing a beat of finite length equal to
samples. Two cascaded median filters were then applied to the segmented signals to eliminate the baseline. Since each beat has a label, only the beats that fall into one of the following five distinct classes are selected: normal beats (N), APB (A), LBBB (L), RBBB (R), and PVC (V). The signals are then compressed through CS, using a DBBD matrix (
4) with a compression ratio of
, where
M is the number of samples of the compressed signal. The experimental tests presented in this work were carried out by varying the CR to evaluate the classification performance and robustness of performance under various CRs. DCT is applied to the segmented and compressed signals, and its coefficients are used as features for classifier training. For the training phase, 80% of the signals for each class was selected randomly, and the remaining 20% was used for the testing phase. The SMOTE algorithm was used to handle data imbalance.
In
Table 1, the numbers of signals used for (i) training and validation without SMOTE, (ii) training and validation with SMOTE, and (iii) testing are presented. As can be seen, when dealing with the MIT-BIH dataset, there is a prevalence of normal beats (N) above all others. To reduce the unbalance, SMOTE was set to double the number of samples of the other classes, namely R, L, and V. Since the samples of class A are the smallest among all classes, the multiplicative coefficient was set to 2.5 (rounded down). Since the data used for the test must not be contaminated by artificial samples, in order to make the test data remain independent from those used in the training, SMOTE is applied only to the latter. To evaluate the performance of the proposed method, five commonly used figures of merit are calculated as follows:
Accuracy: The number of the correctly classified instances divided by the number of total instances (
7);
Sensitivity: the number of positive instances that are correctly classified divided by the sum of the number of positive instances that are correctly classified plus the number of positive instances that are wrongly classified (
8);
Specificity: the number of negative instances correctly classified divided by the sum of the number of negative instances correctly classified and the number of positive instances wrongly classified (
9);
Precision: the number of positive instances correctly classified divided by the total number of positive instances (
10);
F1 score: the harmonic mean of precision and sensitivity (
11).
5.1. Training and Validation Results
In order to not disrupt the flow of the main text of the article, all the tables referred to from now on can be found in
Appendix A. In
Table A1, the class-wise results from the training and validation of classifier C1 are reported for different values of CR. As can be seen from the presented results, the C1 classifier performs well during validation. Furthermore, the sensitivity, specificity, precision, and F1 score are higher in almost all cases (≥99%). As expected, as the CR increases, the number of cases of misclassification increases, and this leads to a degradation of the performance of the classifier. A decrease in accuracy with the CR is expected, as the DBBD matrix behaves as a low-pass filter on the signal, and by increasing the CR, the cut-off frequency of such a filter decreases. As a consequence, the information content of the signal is reduced. However, all figures of merit, once again, remain, for most cases, above 99%.
In
Table A2, the accuracy, average sensitivity, average precision, average specificity, and average F1 score are reported for C1. The performance of the classifier decreases only marginally as the CR changes. The classifier has an accuracy of 99.69% with a CR equal to 3, down to 99.60% with a CR equal to 9. Validation was carried out in the same way for the other four classifiers, and the results are presented in
Table A3,
Table A4,
Table A5,
Table A6,
Table A7,
Table A8,
Table A9 and
Table A10. In particular,
Table A3 and
Table A4 refer to classifier C2,
Table A5 and
Table A6 refer to classifier C3,
Table A7 and
Table A8 refer to classifier C4, and
Table A9 and
Table A10 refer to classifier C5. The performance is similar across all classifiers.
5.2. Testing Results
The results of the test phase are shown in
Table A11,
Table A12 and
Table A13. In
Table A11, the performance of the C1 classifier is reported, with similar results to what was presented in the validation phase. The figures of merit are calculated for each class and at different values of CR, while in
Table A12, the average performance of the classifier is shown. Again, as the CR changes, the combination of compressed DCT features and the ensemble classifier is robust, as the performance degradation due to the higher compression is only marginal. Classes A and V appear to be those with the most classification errors, and they are also the most affected by the increase in CR. In fact, class A attains a sensitivity of 90.18% with CR = 3, and this degrades to 87.92% with CR = 9, while for class V, the sensitivity degradation spans from 98.26% with CR = 3 to 96.30% with CR = 9. In particular, performance degradation is evident for class A. Referring to
Figure 1a,b, it is possible to note that the differences between a beat labeled as N and one labeled as A are minimal. This leads to very similar DCT coefficients, and consequently, it is harder for the classifier to discriminate between the two beat types. Classes N, R, and L have results similar to those seen in validation, with sensitivity, precision, and F1 scores higher than 99% for every CR value. Analyzing the average values in
Table A12, the accuracy of the classifier remains above 99% for all CR values, presenting a maximum of 99.39% with CR = 3.
Table A13 shows the results of the classifier after the decision maker. It is observed that for a CR equal to 3, the decision maker is unable to improve the performance of the classifier. However, as the CR value increases, it is possible to notice an increase in accuracy. In particular, in comparing the values between
Table A12 and
Table A13, the same performance as the classifier without the decision maker is achieved by the classifier with the decision maker using the next CR value utilized in the test. Following the use of the decision maker, the maximum accuracy of the proposed method is 99.40%, while the minimum is 99.15%. In
Table A14, a performance overview of studies regarding the classification of ECG signals is presented. All these studies use the MIT-BIH arrhythmia dataset, and the data size is also reported. Since in [
26,
38], the exact number of ECG beats was not reported, because both of the methods work with ECG 10 s segments chosen randomly from the database, an estimation of the ECG beats is reported, considering one heartbeat per second. In particular, in [
33,
37,
38], the classification of the ECG signal was carried out on its compressed representation. It can be noted that the proposed method has an accuracy in line with that reported in [
25], which is one of the highest values reported in the literature, while sensitivity was 1.27% lower, precision was 1.10% lower, and specificity was 0.23% lower. The proposed method outperforms all other classification methods using compressed ECG signals and is comparable with the method presented in [
38] in terms of accuracy. However, it should be noted that in [
38], class A was not used. Carrying out the same previously presented tests with only the N, L R, and V classes, the accuracy of the proposed method was determined to be 99.74%.
5.3. Limitations of the Proposed Method
Although the performance of the method in terms of accuracy is comparable with that of methods that do not use ECG signal compression and with those that use neural networks, it presents limitations listed in this subsection and that will be the subject of subsequent studies and future works. The method was tested for the classification of five types of beats, and not all possible arrhythmias or variations of arrhythmias were present in the dataset. The choice to use these five classes was made because they are the most used classes in the literature, with the aim of being able to validate the method and compare it with previously developed methods. The tests were carried out using signals that were acquired in medical scenarios, but these signals were not acquired by wearable devices. This means that in a scenario where a wearable is used, the presented accuracies could decrease, for example, due to motion artifacts. In this case, a possible solution is to carry out a quality assessment phase on the ECG signal to discard beats that are too corrupted by movement artifacts. Even though the method does not feature the use of NNs, it still uses five classifiers. This implies that the employed dataset must be large enough to ensure correct training of the method. Since the number of DCT features used to train the classifiers depends on the CR used to compress the ECG signals, they decrease as the CR increases. This implies a decrease in the duration of the training phase, but this means that every time a user wants to change the CR of the method, the classifiers must be retrained.
6. Conclusions
In this paper, a method for classifying compressed ECG beats is presented to be used in a WHD-based telemedicine system. The method operates based on heartbeats compressed by compressed sensing using a DBBD sensing matrix. To evaluate the performance of the classifier, accuracy, sensitivity, specificity, precision, and F1 score were calculated and compared with those of other classification methods found in the literature. In validation, the proposed method obtained an accuracy of 99.72%, a sensitivity of 99.74%, a precision of 99.71%, a specificity of 99.84%, and an F1 score of 99.73% for a CR value of 3, while these values dropped to 99.62%, 99.63%, 99.65%, 99.76%, and 99.64%, respectively, for a CR value of 9. In testing, an accuracy of 99.40%, a sensitivity of 97.42%, a precision of 98.48%, a specificity of 99.68%, and an F1 score of 97.96% for a CR value of 3 were observed, while for CR value of 9, these values dropped to 99.15%, 96.57%, 98.14%, 99.53%, and 97.15%, respectively. From these results, it is possible to conclude that the use of the KNN ensemble classifier and the DCT coefficients of the compressed signal is a robust solution for the classification of ECG signals in the compressed domain, without the need to reconstruct the signal. Comparison of the obtained results with the state of the art shows that the proposed method achieves comparable performance to that of methods that do not use compression and out-performs other methods classifying compressed ECG signals while only using the compressed DCT coefficients of the ECG signal. Future work will aim to improve the performance of the classifier, as it is clear from the tests that most of the classification errors are due to classes A and V. In particular, the use of other features that can be obtained from the compressed signal, such as PSD, should be taken into consideration. In addition, the decision maker will be improved to make a reasonable contribution, even with a low value of the CR. Furthermore, the system will be tested in a real-life scenario with the use of ECG signals acquired through the ATTICUS WHD reported in [
50] in both medical and real-life activity scenarios.