On Automated Object Grasping for Intelligent Prosthetic Hands Using Machine Learning
Abstract
1. Introduction
2. Background
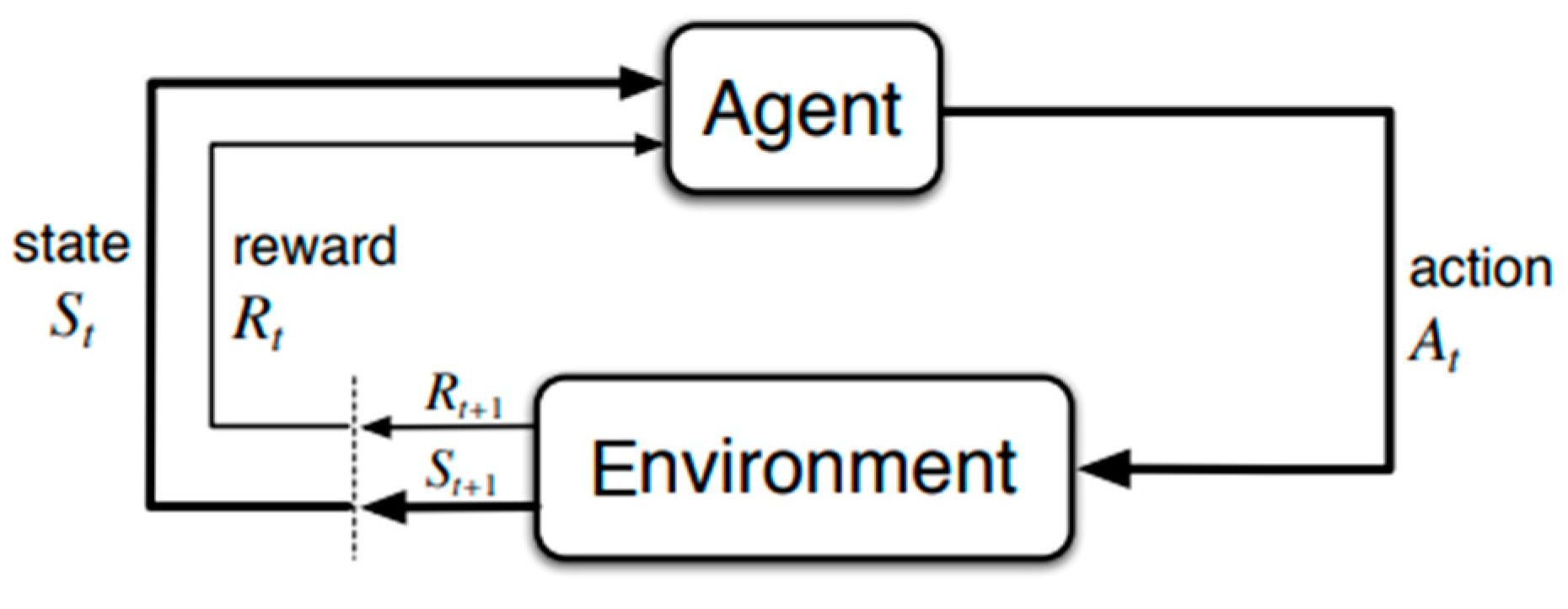
2.1. Reinforcement Learning
2.2. Soft Actor-Critic
| Algorithm 1. Soft Actor-Critic [21]. |
|
. for each iteration do for each iteration step do end for for each gradient step do end for end for |
2.3. Proximal Policy Optimization
| Algorithm 2. PPO, Actor-Critic style [22]. |
|
for each iteration do for each actor do in environment for T timessteps end for end for |
2.4. Deep Q-Networks
| Algorithm 3. Deep Q-learning with experience replay [24]. |
|
Initialize replay memory D to capacity N Initialize action-value function Q with random weights θ Initialize target action-value function with weights for episode 1, M do Initialize sequence and preprocessed sequence for t = 1, T do in D Sample random minibatch of experiences from D Perform a gradient descent step on with respect to the weights θ Every C steps reset end for end for |
3. Experiment
3.1. Experiment Process
Environment Assumptions
- (1)
- The simulation environment is deterministic, i.e., given the same initial state and actions, the environment will always produce the same outcome.
- (2)
- The action space and observation space of the environment are well-defined and consistent throughout the training and testing phases.
- (3)
- No external condition can cause the objects to move other than the gripper or other spawned objects in the environment.
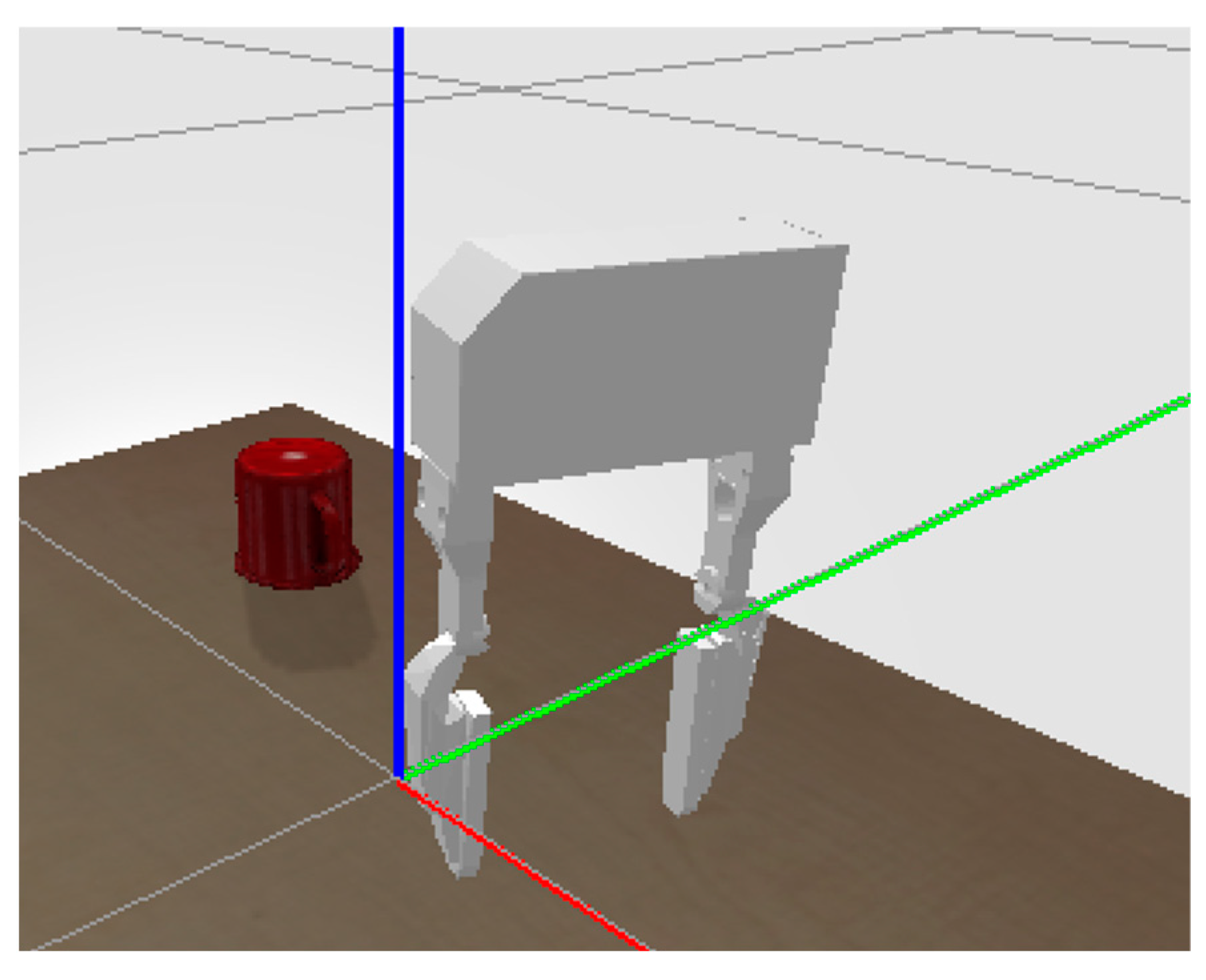
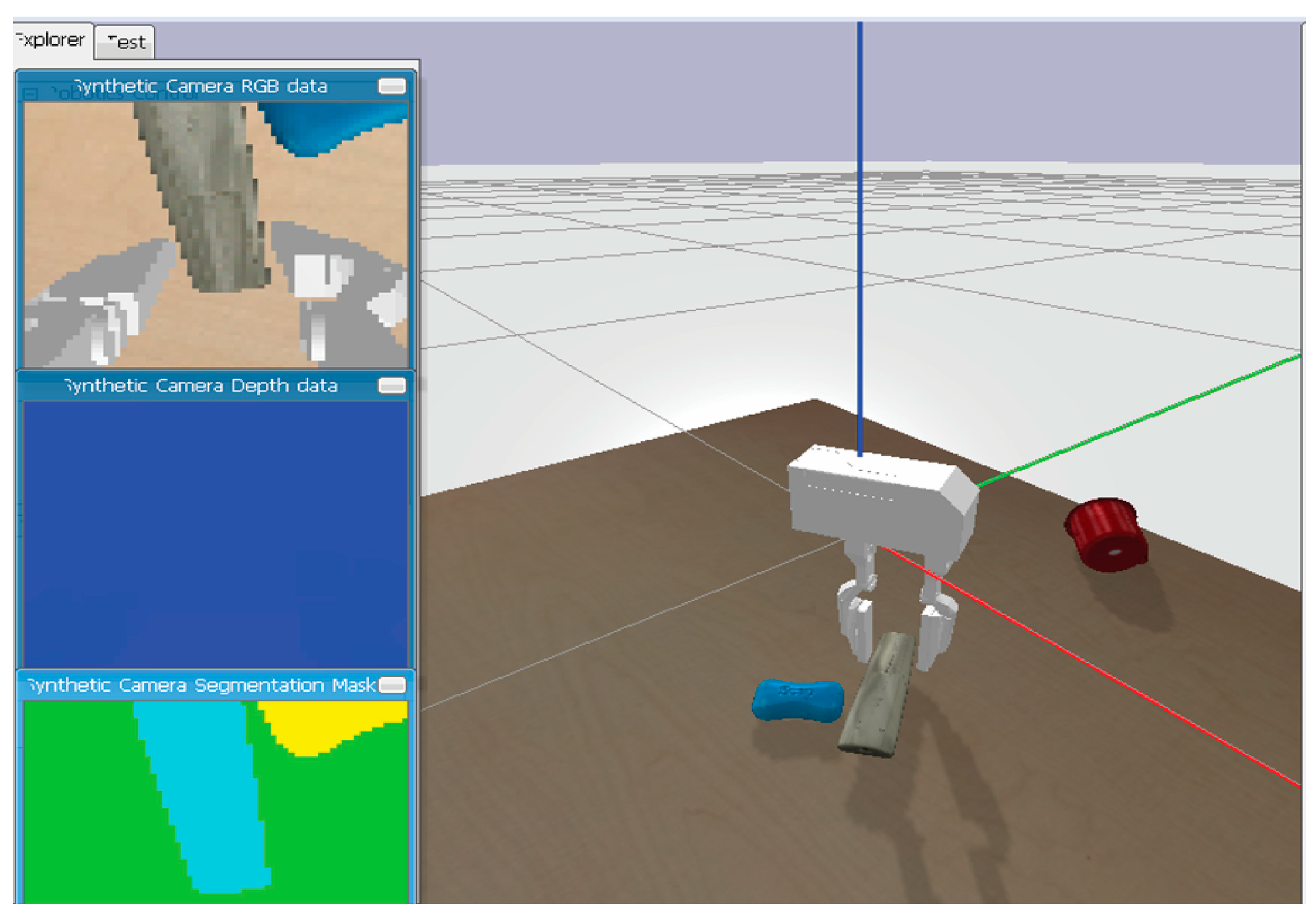
3.2. Sensor Setup
3.3. Sensor Setup
3.4. Sensor Setup
3.5. Reward Function
- (1)
- Lack of exploration: the reward function does not provide any incentives for the agent to explore the environment. This can lead to the agent getting stuck in local optima and failing to discover better solutions. To solve this, we introduced a random exploration component to the reward signal. This is important because it encourages the agent to take actions that it has not taken before, which can help it discover new ways to interact with the environment and achieve the task.
- (2)
- Sparse rewards: the reward function is designed to provide a large reward only when the arm lifts the object by the desired amount. This can make learning difficult for the agent, as it may take a long time to receive any useful feedback. By adding a distance penalty, we encourage the agent to move the object towards the target position. This helps to alleviate the issue of sparse rewards, as the agent can receive a small reward for making progress towards the goal, even if it has not fully achieved it yet.
3.6. Training Process
4. Results and Discussions
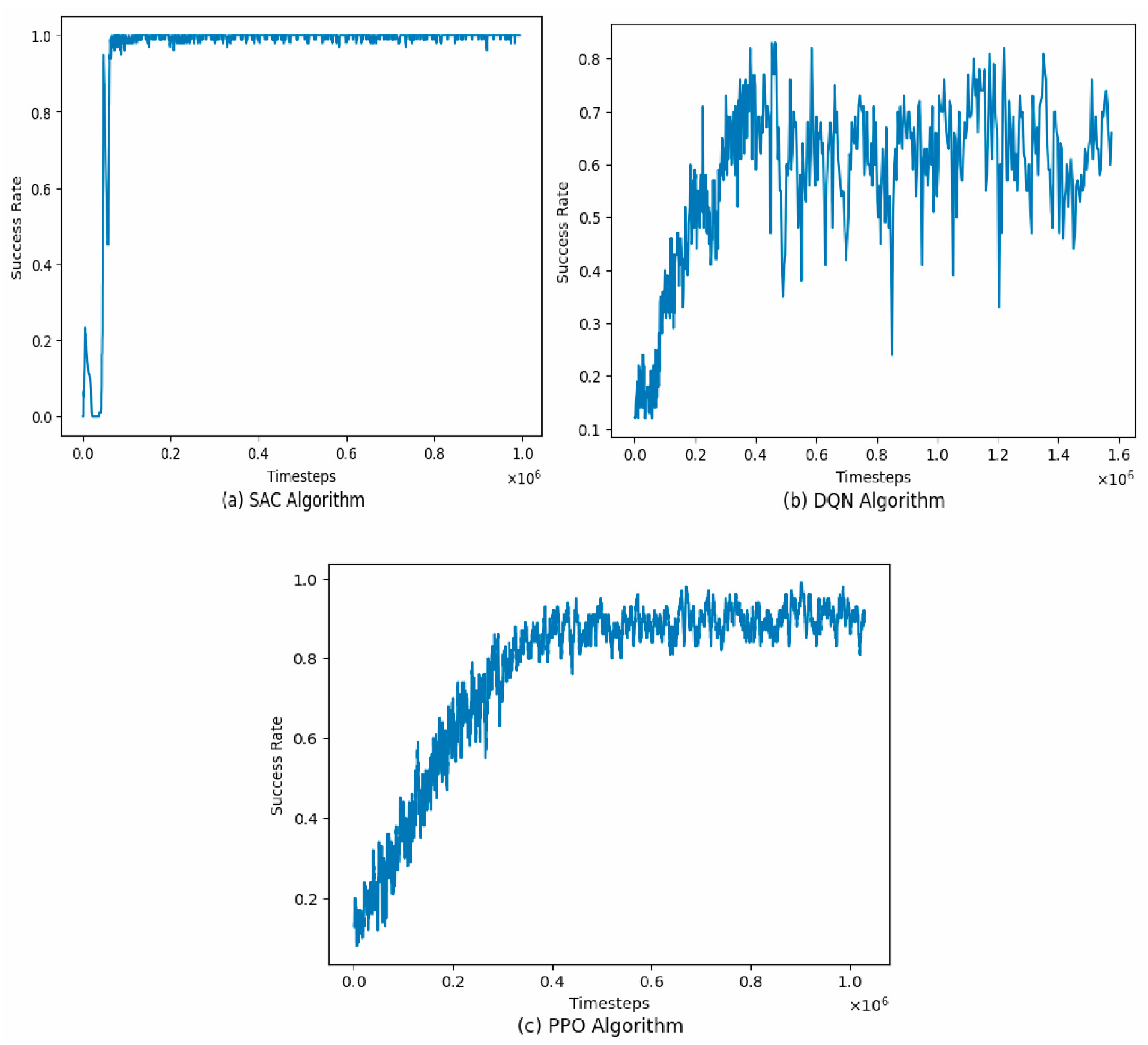
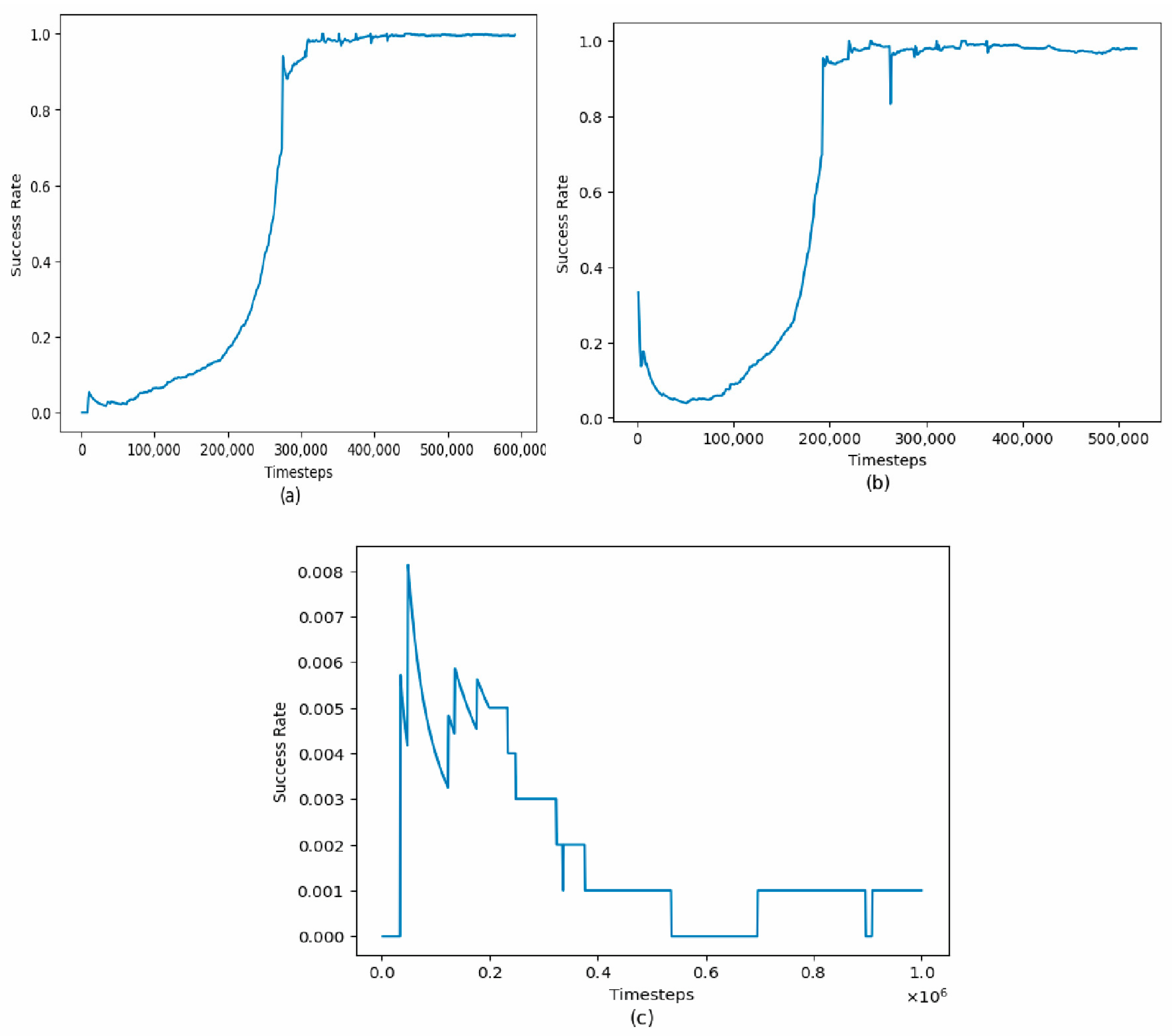
4.1. Algorithm-Specific Success Rate
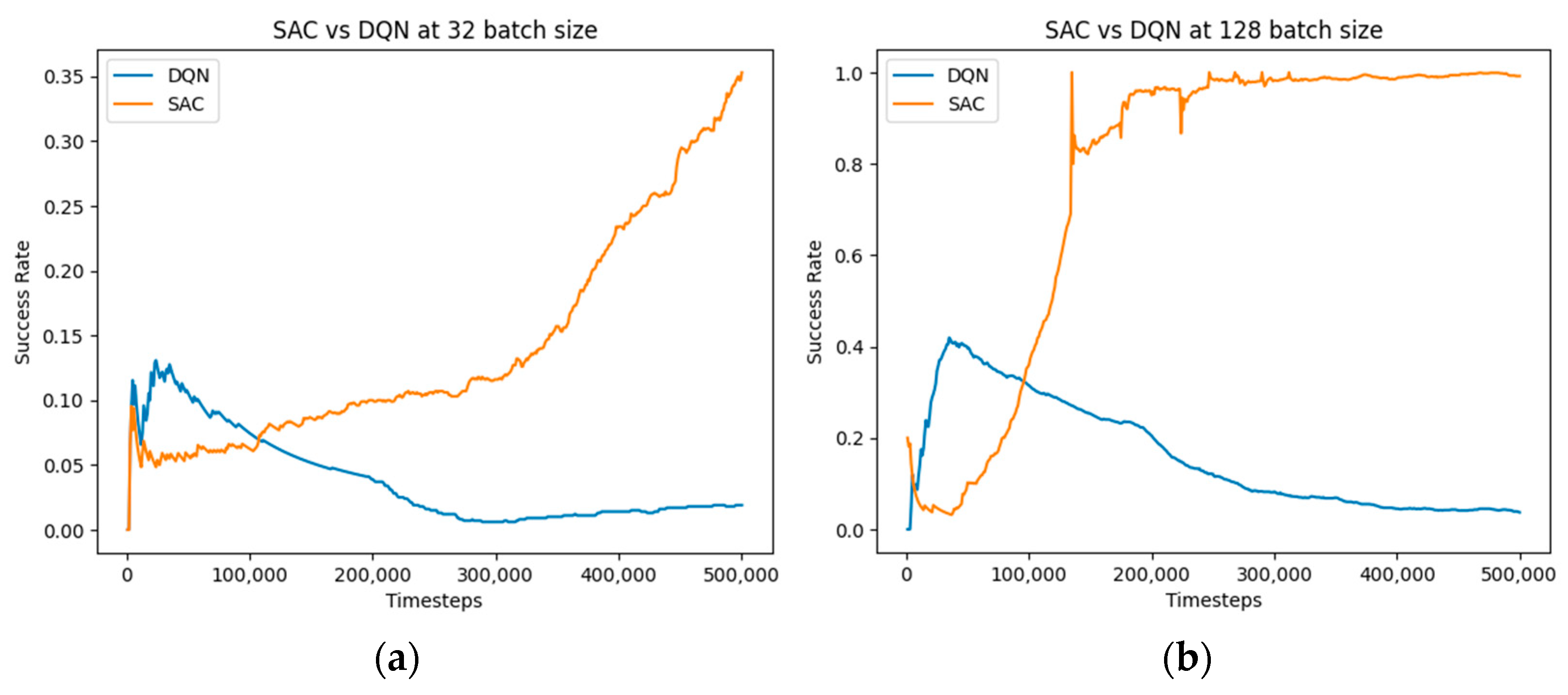
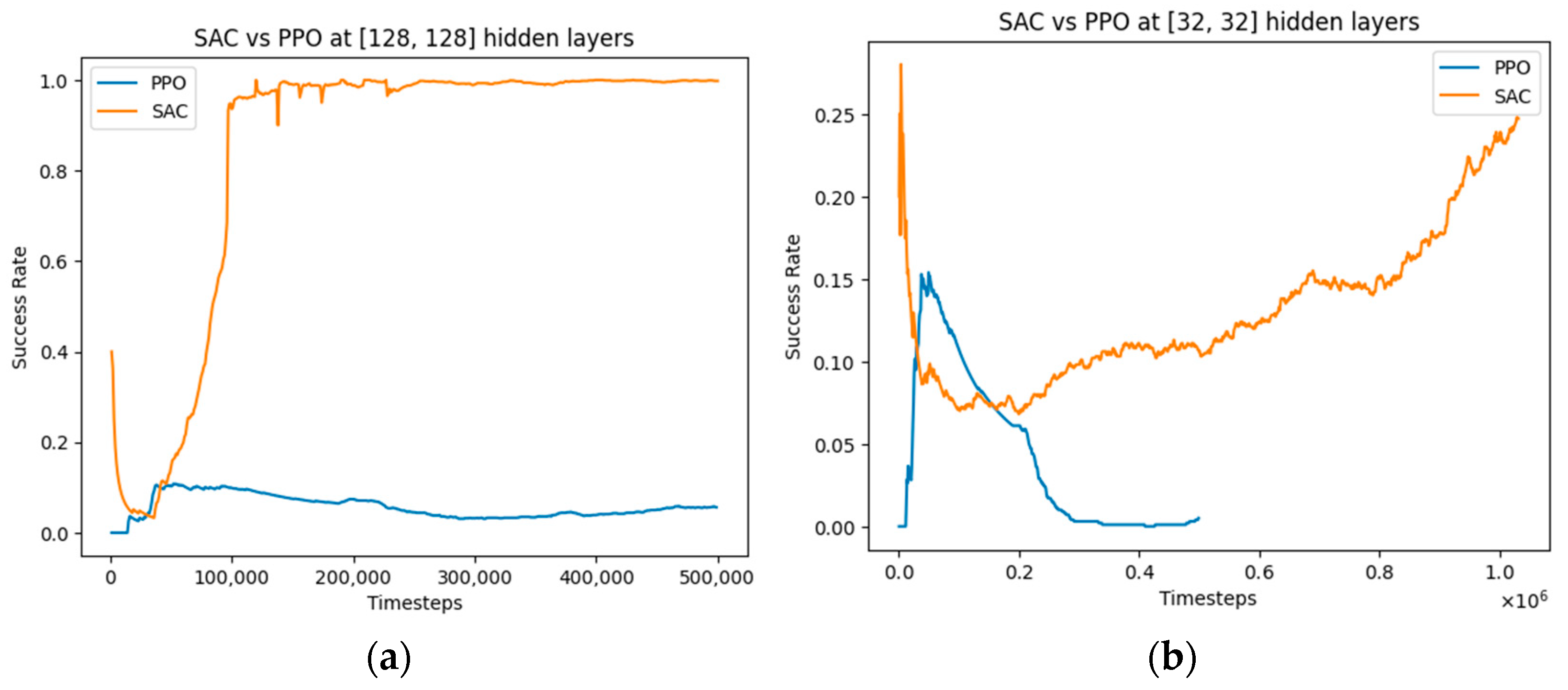
4.2. Comparative Analysis of SAC, PPO, and DQN for Object-Grasping–Hyperparameter Exploration
4.3. Object-Specific Success Rate
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Narumi, S.; Huang, X.; Lee, J.; Kambara, H.; Kang, Y.; Shin, D. A Design of Biomimetic Prosthetic Hand. Actuators 2022, 11, 167. [Google Scholar] [CrossRef]
- Jing, X.; Yong, X.; Jiang, Y.; Li, G.; Yokoi, H. Anthropomorphic Prosthetic Hand with Combination of Light Weight and Diversiform Motions. Appl. Sci. 2019, 9, 4203. [Google Scholar] [CrossRef]
- Stefanelli, E.; Cordella, F.; Gentile, C.; Zollo, L. Hand Prosthesis Sensorimotor Control Inspired by the Human Somatosensory System. Robotics 2023, 12, 136. [Google Scholar] [CrossRef]
- Malesevic, N.; Björkman, A.; Andersson, G.S.; Cipriani, C.; Antfolk, C. Evaluation of Simple Algorithms for Proportional Control of Prosthetic Hands Using Intramuscular Electromyography. Sensors 2022, 22, 5054. [Google Scholar] [CrossRef] [PubMed]
- Waris, A.; Niazi, I.K.; Jamil, M.; Englehart, K.; Jensen, W.; Kamavuako, E.N. Multiday Evaluation of Techniques for EMG-Based Classification of Hand Motions. IEEE J. Biomed. Health Inform. 2019, 23, 1526–1534. [Google Scholar] [CrossRef]
- Li, X.; Wen, R.; Duanmu, D.; Huang, W.; Wan, K.; Hu, Y. Finger Kinematics during Human Hand Grip and Release. Biomimetics 2023, 8, 244. [Google Scholar] [CrossRef] [PubMed]
- Van der Riet, D.; Stopforth, R.; Bright, G.; Diegel, O. An overview and comparison of upper limb prosthetics. In Proceedings of the AFRICON (Mauritius: IEEE), Pointe aux Piments, Mauritius, 9–12 September 2013; pp. 1–8. [Google Scholar]
- Kyberd, P.; Wartenberg, C.; Sandsjö, L.; Jönsson, S.; Gow, D.; Frid, J.; Sperling, L. Survey of Upper-Extremity Prosthesis Users in Sweden and the United Kingdom. JPO J. Prosthet. Orthot. 2007, 19, 55–62. Available online: https://journals.lww.com/jpojournal/Fulltext/2007/04000/Survey_of_Upper_Extremity_Prosthesis_Users_in.6.aspx (accessed on 23 March 2023). [CrossRef]
- Mihajlović, V.; Grundlehner, B.; Vullers, R.; Penders, J. Wearable, Wireless EEG Solutions in Daily Life Applications: What are we Missing? IEEE J. Biomed. Health Inform. 2015, 19, 6–21. [Google Scholar] [CrossRef]
- Abou Baker, N.; Zengeler, N.; Handmann, U. A Transfer Learning Evaluation of Deep Neural Networks for Image Classification. Mach. Learn. Knowl. Extr. 2022, 4, 22–41. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Y.; Lv, C. Affine Layer-Enabled Transfer Learning for Eye Tracking with Facial Feature Detection in Human–Machine Interactions. Machines 2022, 10, 853. [Google Scholar] [CrossRef]
- Hao, Z.; Charbel, T.; Gursel, A. A 3D Printed Soft Prosthetic Hand with Embedded Actuation and Soft Sensing Capabilities for Directly and Seamlessly Switching between Various Hand Gestures. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Delft, The Netherlands, 12–16 July 2021; pp. 75–80. [Google Scholar]
- Castro, M.; Pinheiro, W.; Rigolin, G. A Hybrid 3D Printed Hand Prosthesis Prototype Based on sEMG and a Fully Embedded Computer Vision System. Front. Neurorobotics 2022, 15, 751282. [Google Scholar] [CrossRef] [PubMed]
- Czimmermann, T.; Ciuti, G.; Milazzo, M.; Chiurazzi, M.; Roccella, S.; Oddo, C.; Dario, P. Visual-Based Defect Detection and Classification Approaches for Industrial Applications—A SURVEY. Sensors 2020, 20, 1459. [Google Scholar] [CrossRef]
- Abbasi, B.; Sharifzadeh, M.; Noohi, E.; Parastegari, S.; Žefran, M. Grasp Taxonomy for Robot Assistants Inferred from Finger Pressure and Flexion. In Proceedings of the 2019 International Symposium on Medical Robotics (ISMR), Atlanta, GA, USA, 3–5 April 2019. [Google Scholar]
- Wang, Y.; Wu, H.; Jhaveri, R.H.; Djenouri, Y. DRL-Based URLLC-Constraint and Energy-Efficient Task Offloading for Internet of Health Things. IEEE J. Biomed. Health Inform. 2023, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Kim, J.; Park, S.W.; Jin, S.-M.; Park, S.-M. Toward a Fully Automated Artificial Pancreas System Using a Bioinspired Reinforcement Learning Design: In Silico Validation. IEEE J. Biomed. Health Inform. 2021, 25, 536–546. [Google Scholar] [CrossRef] [PubMed]
- Owoeye, S.O.; Durodola, F.; Odeyemi, J. Object Detection and Tracking: Exploring a Deep Learning Approach and Other Techniques. In Video Data Analytics for Smart City Applications: Methods and Trends IoT and Big Data Analytics; Bentham Science Publishers: Sharjah, United Arab Emirates, 2023; pp. 37–53. Available online: https://www.eurekaselect.com/chapter/19138 (accessed on 9 December 2023). [CrossRef]
- Qian, Z.; Jing, W.; Lv, Y.; Zhang, W. Automatic Polyp Detection by Combining Conditional Generative Adversarial Network and Modified You-Only-Look-Once. IEEE Sens. J. 2022, 22, 10841–10849. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement Learning: A Survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. arXiv 2018. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017. [CrossRef]
- Mnih, V.K. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Roderick, M.; MacGlashan, J.; Tellex, S. Implementing the Deep Q-Network. arXiv 2017. [CrossRef]
- Collins, J.; McVicar, J.; Wedlock, D.; Brown, R.A.; Howard, D.; Leitner, J. Benchmarking Simulated Robotic Manipulation through a Real World Dataset. Arxiv Robot. 2019. Available online: https://arxiv.org/abs/1911.01557 (accessed on 15 April 2023). [CrossRef]
- Meyer, J.; Sendobry, A.; Kohlbrecher, S.; Klingauf, U.; Stryk, O.V. Comprehensive Simulation of Quadrotor UAVs Using ROS and Gazebo. 2012. Available online: http://gkmm.tu-darmstadt.de/publications/files/meyer2012quadrotorsimulation.pdf (accessed on 15 April 2023).
- Baris, Y. Branch Dueling Deep Q-Networks for Robotics Applications. Master’s Thesis, Department of Informatics, Technische Universität München, Munich, Germany, 2020. [Google Scholar]
- Liu, Z. OCRTOC: A Cloud-Based Competition and Benchmark for Robotic Grasping and Manipulation. IEEE Robot. Autom. Lett. 2021, 7, 486–493. [Google Scholar] [CrossRef]
- Breyer, M.; Furrer, F.; Novkovic, T.; Siegwart, R.; Nieto, J. Comparing Task Simplifications to Learn Closed-Loop Object Picking Using Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2019, 4, 1549–1556. [Google Scholar] [CrossRef]
- Nitish, S.; Geoffrey, H.; Alex, K.; Ilya, S.; Ruslan, S. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kim, B.; Kwon, G.; Park, C.; Kwon, N.K. The Task Decomposition and Dedicated Reward-System-Based Reinforcement Learning Algorithm for Pick-and-Place. Biomimetics 2023, 8, 240. [Google Scholar] [CrossRef]
- Han, B.; Liu, C.L.; Zhang, W.J. A Method to Measure the Resilience of Algorithm for Operation Management. In Proceedings of the 8th IFAC Conference on Manufacturing Modelling, Management and Control MIM 2016, Troyes, France, 28–30 June 2016. [Google Scholar]
- Raj, R.; Wang, J.W.; Nayak, A.; Tiwari, M.K.; Han, B.; Liu, C.L.; Zhang, W.J. Measuring Resilience of Supply Chain Systems using a Survival Model. IEEE Syst. J. 2017, 9, 377–381. [Google Scholar] [CrossRef]




| Environment | |
|---|---|
| Action space | 5 |
| Observation | RGBD and Depth data |
| Reward | Shaped reward |
| Discount factor | 0.99 |
| Non-Terminal State | Terminal State | |
|---|---|---|
| Object grasped? | ||
| Not grasped? | @timeout |
| Summary | Result |
|---|---|
| Mean success rate for DQN | 0.6021689086910577 |
| Mean success rate for SAC | 0.9903811107807406 |
| Mean success rate for PPO | 0.821488216618748 |
| DF | Pillai | F-Value | Den DF | Pr (>F) | |
|---|---|---|---|---|---|
| Algorithms | 2 | 0.57982 | 2040.7 | 19,994 | <2.2 × 10−16 *** |
| Residuals | 9997 |
| Group 1 | Group 2 | Mean Diff | P-adj | Lower | Upper | Reject |
|---|---|---|---|---|---|---|
| DQN | PPO | −0.2193 | 0.0 | −0.2295 | −0.2091 | True |
| DQN | SAC | 0.1689 | 0.0 | 0.1657 | 0.172 | True |
| PPO | SAC | 0.3882 | 0.0 | 0.3779 | 0.3985 | True |
| Result | |
|---|---|
| p-value | 0.0 |
| Q-value | 29,689.740691361738 |
| Algorithm | SAC | PPO | DQN |
|---|---|---|---|
| Convergence speed | Quickest to convergence | Slow convergence | Slow convergence |
| Hyperparameter sensitivity | Robust to hyperparameters, relatively easier to tune | Performance is heavily affected when deviating slightly from an optimal hyperparameter | Performance is also heavily affected |
| Training time | Takes the longest time to train | Lower training time than SAC | Requires the least amount of training time |
| DF | Pillai | F-Value | Den DF | Pr (>F) | |
|---|---|---|---|---|---|
| Algorithms | 2 | 0.6888 | 552.9 | 4210 | <2.2 × 10−16 *** |
| Residuals | 2105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odeyemi, J.; Ogbeyemi, A.; Wong, K.; Zhang, W. On Automated Object Grasping for Intelligent Prosthetic Hands Using Machine Learning. Bioengineering 2024, 11, 108. https://doi.org/10.3390/bioengineering11020108
Odeyemi J, Ogbeyemi A, Wong K, Zhang W. On Automated Object Grasping for Intelligent Prosthetic Hands Using Machine Learning. Bioengineering. 2024; 11(2):108. https://doi.org/10.3390/bioengineering11020108
Chicago/Turabian StyleOdeyemi, Jethro, Akinola Ogbeyemi, Kelvin Wong, and Wenjun Zhang. 2024. "On Automated Object Grasping for Intelligent Prosthetic Hands Using Machine Learning" Bioengineering 11, no. 2: 108. https://doi.org/10.3390/bioengineering11020108
APA StyleOdeyemi, J., Ogbeyemi, A., Wong, K., & Zhang, W. (2024). On Automated Object Grasping for Intelligent Prosthetic Hands Using Machine Learning. Bioengineering, 11(2), 108. https://doi.org/10.3390/bioengineering11020108








