Monte Carlo-Based Optical Simulation of Optical Distribution in Deep Brain Tissues Using Sixteen Optical Sources
Abstract
1. Introduction
2. Research Method
2.1. Optical Simulation Method
2.2. Brain Model
2.3. Various Types of Optical Sources
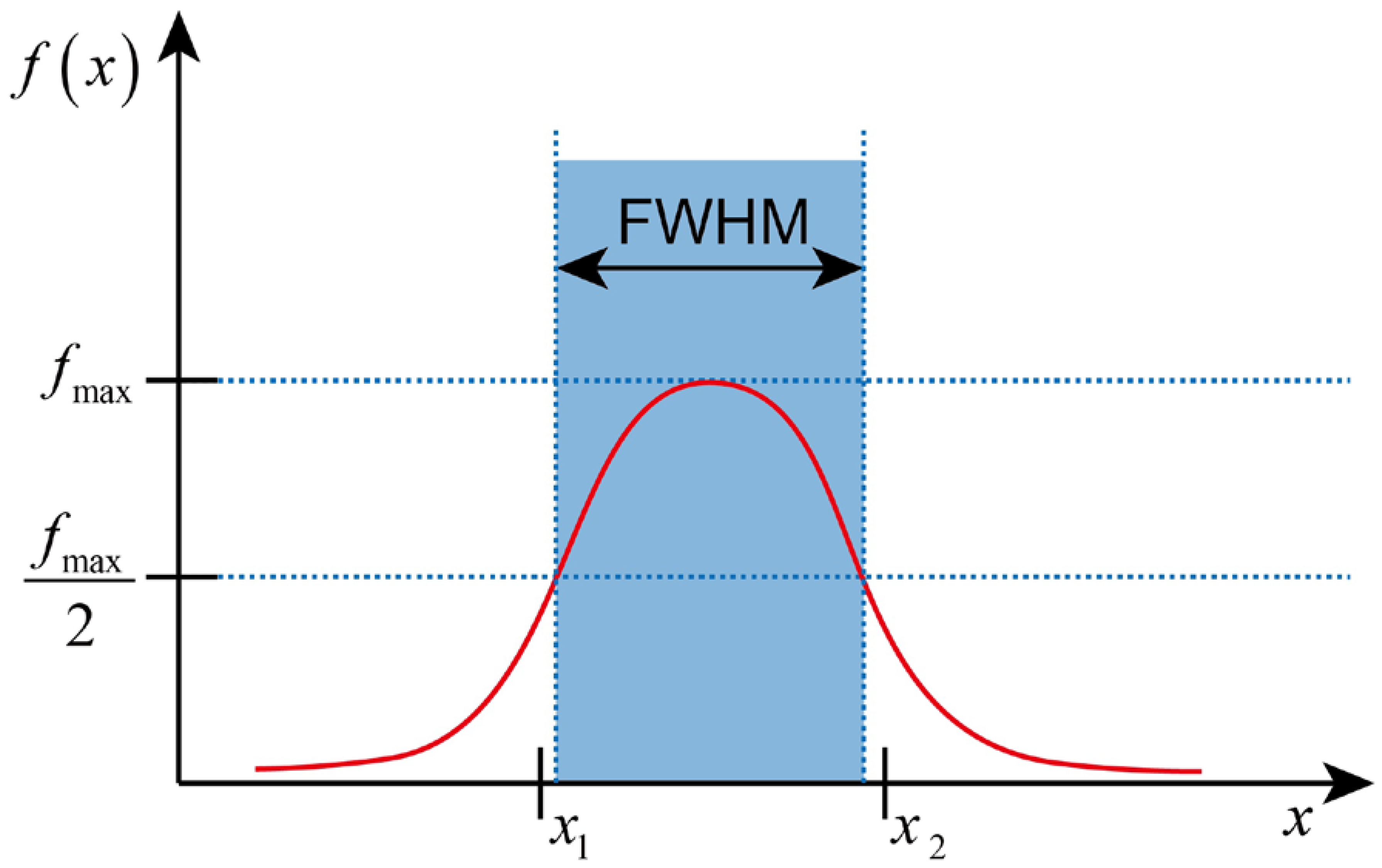
2.4. Propagating Depth and Field Width Quantitation
2.4.1. Data Preprocessing
2.4.2. Propagation Evaluation in Each Layer
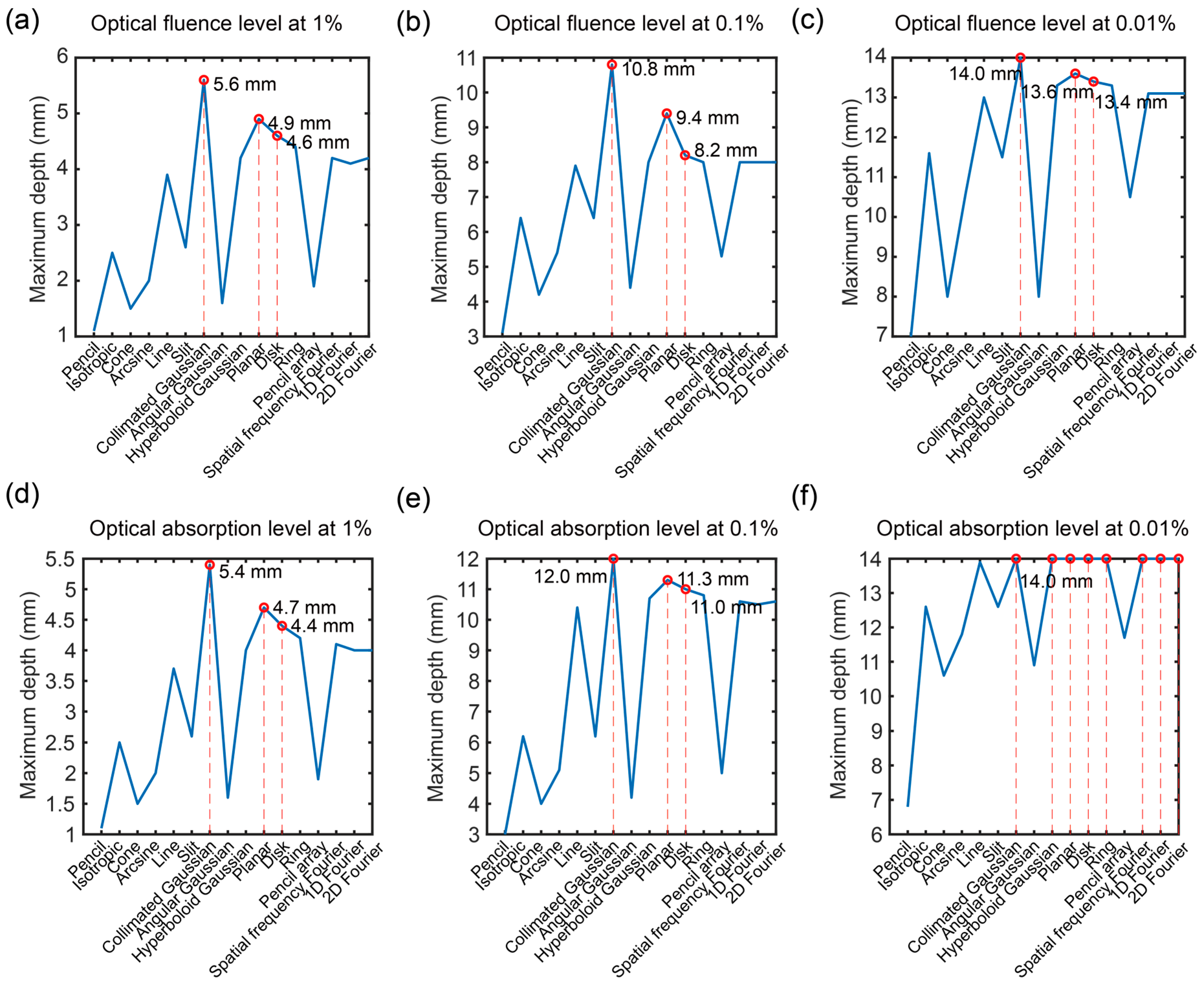
2.4.3. Propagating Depth Evaluation
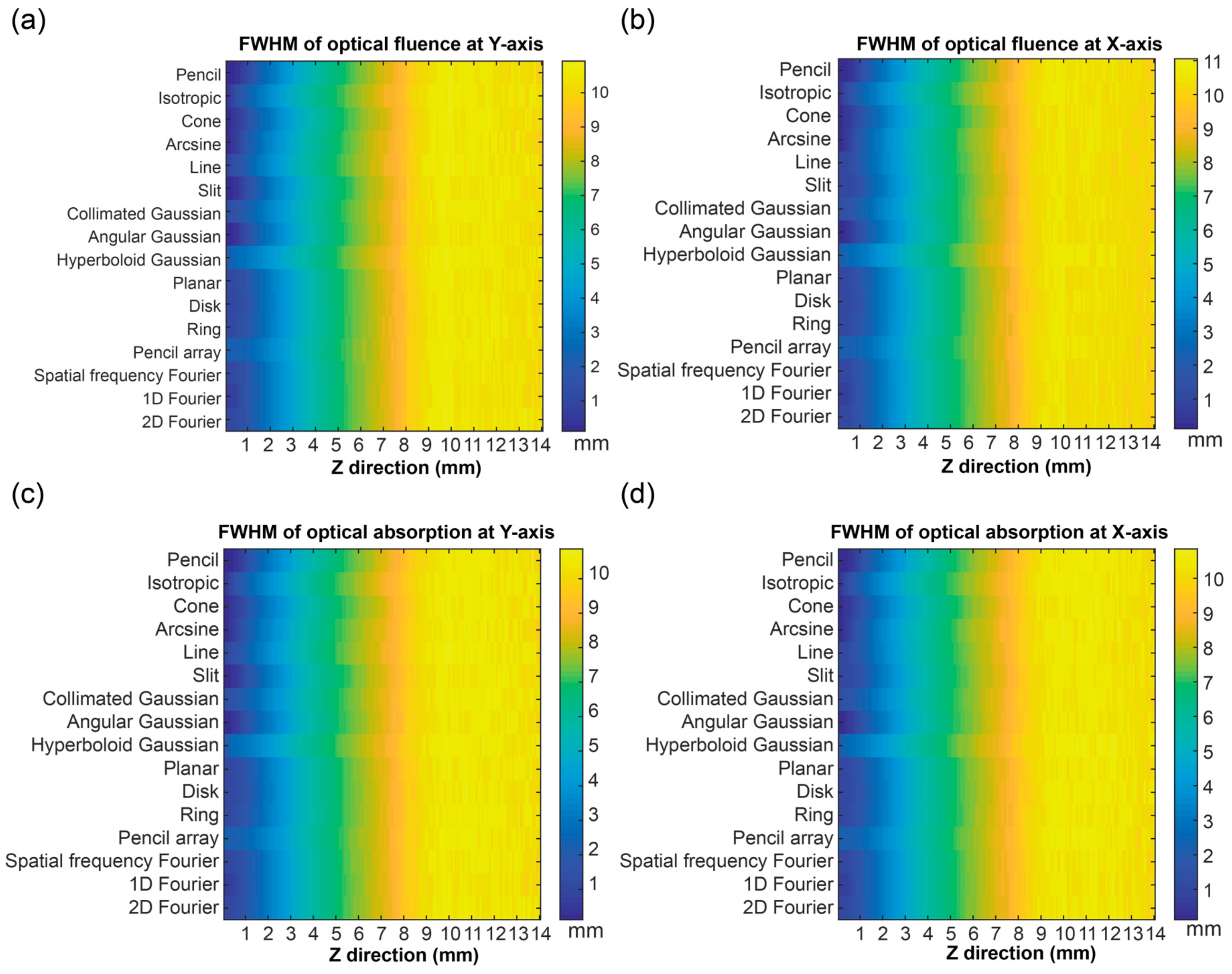
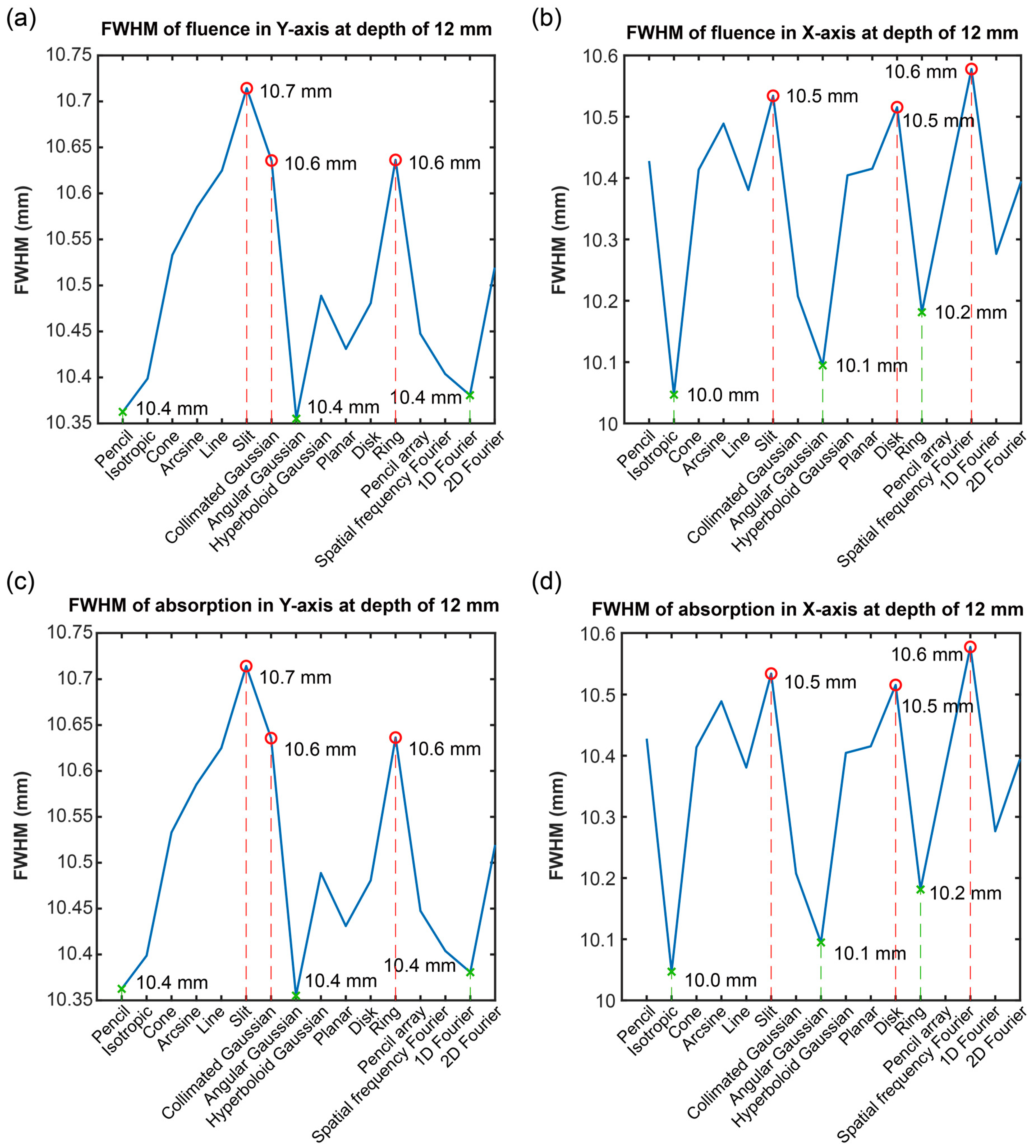
2.4.4. Optical Field Width Evaluation
3. Results and Discussion
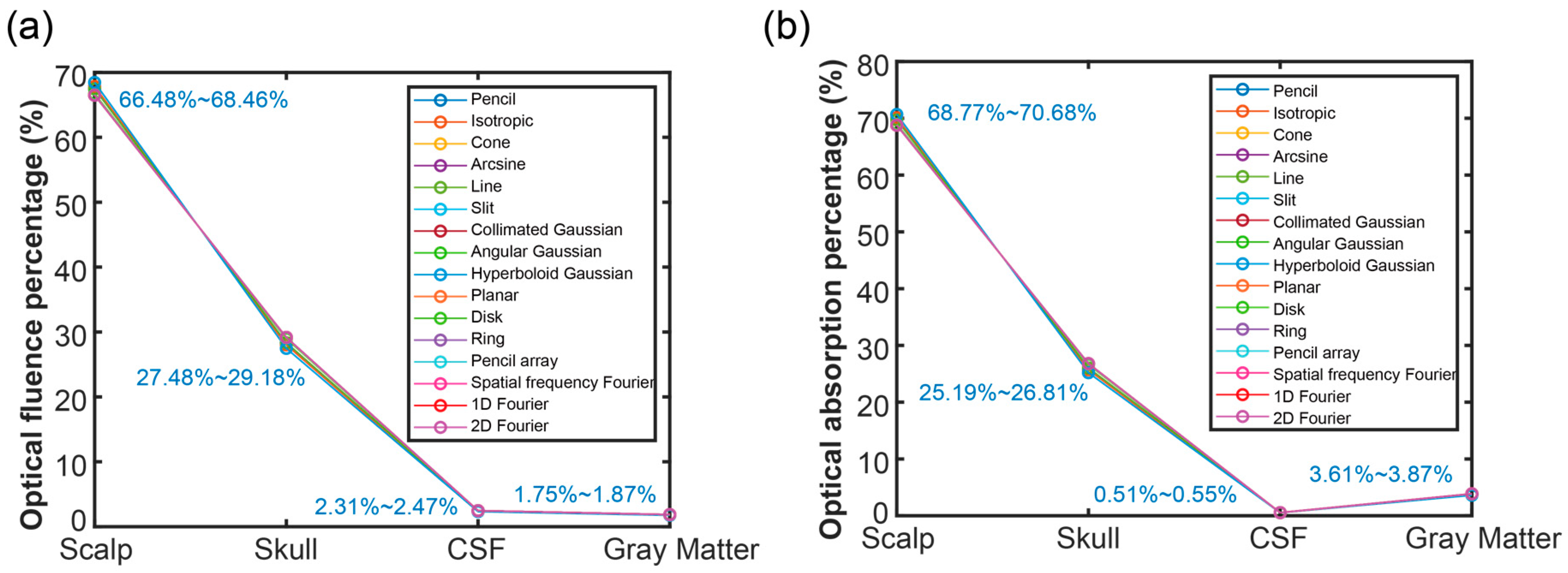
3.1. Optical Energy Percentage of Each Layer
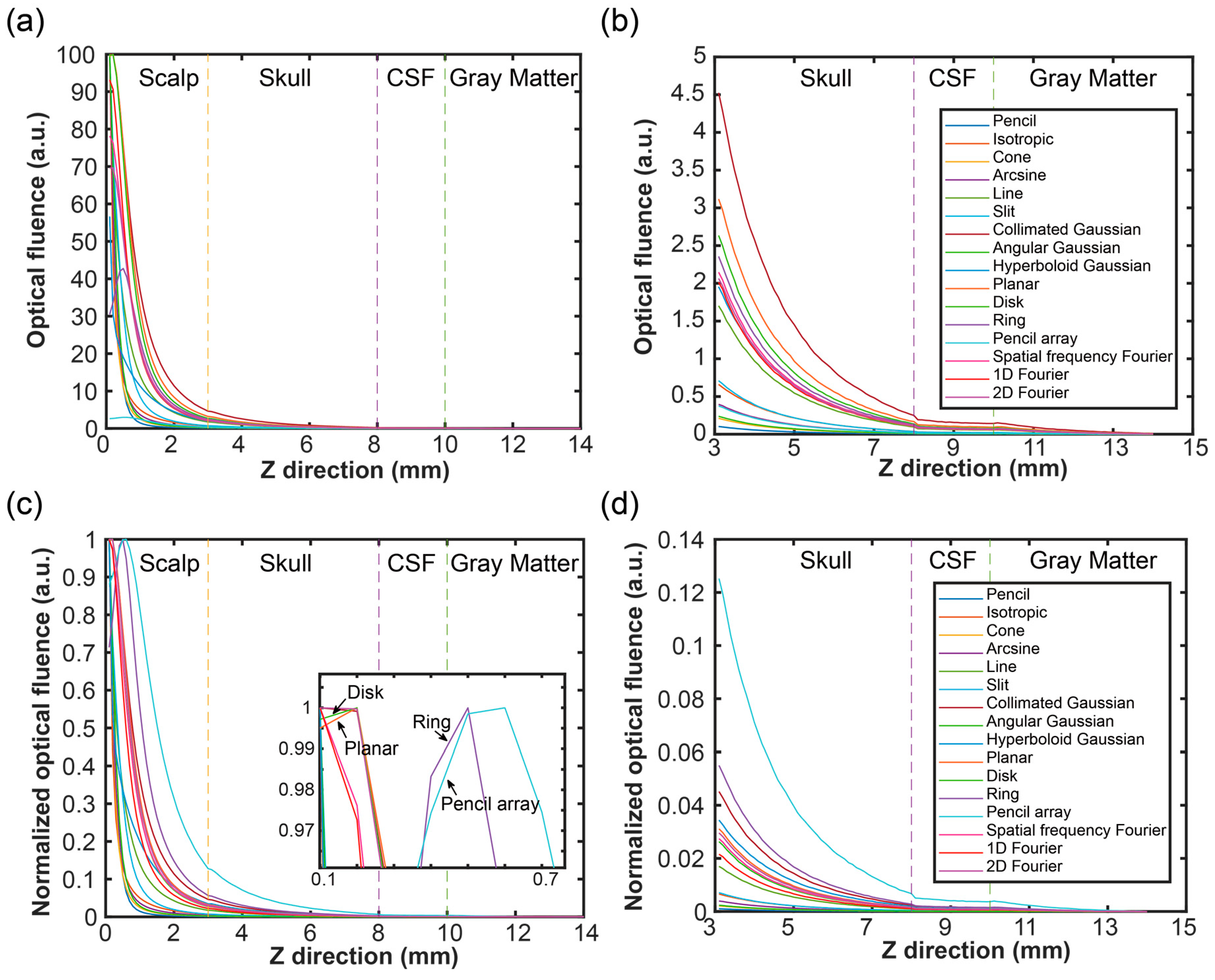
3.2. Optical Propagation in Vertical Direction
3.3. Optical Distribution in a Horizontal Direction
3.4. Discussion
3.5. Limitations and Prospects
- (1)
- Distribution size of the sources. Although the parameters of the optical sources are set as consistently as possible in this research, there is an obvious difference in the distribution size of the point, line, and surface sources. This phenomenon is due to the definition of the initial launch distribution and other settings of those source types. Therefore, the distribution size of line and surface sources can be researched and compared with point sources.
- (2)
- Increasing source number and intensity. In this manuscript, we found that the difference in propagating depth and FWHM of the different optical source types at the deep region is not as strong as in the surface region. Further, increasing source number and intensity can be researched for deep imaging under optical safety standards.
- (3)
- Experiment validation. The experimental validation allows us to validate the simulation model in real scenarios. However, due to the complex human brain tissues, in this paper we focused on the simulation exploration of the optical source types. The experiment validation can be conducted following the systematical analysis of the optical source.
- (4)
- Tissue uncertainty. Not only the properties of the tissues can impact the simulation research, but also the thickness and the distribution of each layer. The uncertainty of tissue is a very interesting topic to explore. This work only focused on one brain model with a referred property set. It is expected to research on the more complex brain model with variability.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| 1D | One dimensional |
| 2D | Two dimensional |
| 3D | Three dimensional |
| A | Optical absorption |
| AP | Optical absorption percentage |
| CSF | Cerebrospinal fluid |
| E | Optical energy |
| Ei | Optical energy like optical fluence or absorption |
| Emax | Maximum value of the energy |
| Emax xc, yc | Maximum value of the energy at the line of the position (x = 7 mm, y = 7 mm) |
| Emin | Minimum value of the energy |
| Emin xc, yc | Minimum value of the energy at the line at the position (x = 7 mm, y = 7 mm) |
| EN | Normalized energy (optical fluence or absorption) |
| ENZ | Normalized energy (optical fluence or absorption) |
| Ex,y,z | Energy at the position (x, y, z) |
| Exc, yc, z | Energy at the position (x = 7 mm, y = 7 mm, z) |
| EP | Optical energy percentage |
| F | Optical fluence |
| fNIRS | Functional near-infrared spectroscopy |
| FP | Optical fluence percentage |
| FWHM | Full width at half maximum |
| g | Anisotropy factor |
| n | Refractive index |
| NA | Not applicable |
| NIRS | Near-infrared spectroscopy |
| OCT | Optical coherence tomography |
| PAI | Photoacoustic imaging |
| Pi | Optical energy percentage in the ith layer |
| μa | Absorption coefficient |
| μs | Scattering coefficient |
References
- Scholkmann, F.; Kleiser, S.; Metz, A.J.; Zimmermann, R.; Mata Pavia, J.; Wolf, U.; Wolf, M. A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology. NeuroImage 2014, 85, 6–27. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Yang, J.; Wu, H.; Beier, K.T.; Sawan, M. Challenges and future trends in wearable closed-loop neuromodulation to efficiently treat methamphetamine addiction. Front. Psychiatry 2023, 14, 1085036. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Y.H.; Xia, F.; Sawan, M. Photoacoustic imaging for monitoring of stroke diseases: A review. Photoacoustics 2021, 23, 100287. [Google Scholar] [CrossRef]
- Pouliopoulos, A.N.; Murillo, M.F.; Noel, R.L.; Batts, A.J.; Ji, R.; Kwon, N.; Yu, H.; Tong, C.-K.; Gelinas, J.N.; Araghy, D.K.; et al. Non-invasive optogenetics with ultrasound-mediated gene delivery and red-light excitation. Brain Stimul. 2022, 15, 927–941. [Google Scholar] [CrossRef]
- Manwar, R.; Kratkiewicz, K.; Avanaki, K. Investigation of the Effect of the Skull in Transcranial Photoacoustic Imaging: A Preliminary Ex Vivo Study. Sensors 2020, 20, 4189. [Google Scholar] [CrossRef]
- Li, T.; Xue, C.; Wang, P.; Li, Y.; Wu, L. Photon penetration depth in human brain for light stimulation and treatment: A realistic Monte Carlo simulation study. J. Innov. Opt. Health Sci. 2017, 10, 1743002. [Google Scholar] [CrossRef]
- Sharma, A.; Srishti; Periyasamy, V.; Pramanik, M. Photoacoustic imaging depth comparison at 532-, 800-, and 1064-nm wavelengths: Monte Carlo simulation and experimental validation. J. Biomed. Opt. 2019, 24, 121904. [Google Scholar] [CrossRef]
- Tian, P.; Devor, A.; Sakadzic, S.; Dale, A.M.; Boas, D.A. Monte Carlo simulation of the spatial resolution and depth sensitivity of two-dimensional optical imaging of the brain. J. Biomed. Opt. 2011, 16, 016006. [Google Scholar] [CrossRef]
- Jacques, S.L. Light Distributions from Point, Line and Plane Sources for Photochemical Reactions and Fluorescence in Turbid Biological Tissues. Photochem. Photobiol. 1998, 67, 23–32. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, L. Accurate Monte Carlo simulation of frequency-domain optical coherence tomography. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3177. [Google Scholar] [CrossRef]
- Tang, Q.; Lin, J.; Tsytsarev, V.; Erzurumlu, R.; Liu, Y.; Chen, Y. Review of mesoscopic optical tomography for depth-resolved imaging of hemodynamic changes and neural activities. Neurophotonics 2016, 4, 011009. [Google Scholar] [CrossRef]
- Kao, T.-C.; Sung, K.-B. Quantifying tissue optical properties of human heads in vivo using continuous-wave near-infrared spectroscopy and subject-specific three-dimensional Monte Carlo models. J. Biomed. Opt. 2022, 27, 083021. [Google Scholar] [CrossRef]
- Tran, A.P.; Yan, S.; Fang, Q. Improving model-based functional near-infrared spectroscopy analysis using mesh-based anatomical and light-transport models. Neurophotonics 2020, 7, 015008. [Google Scholar] [CrossRef]
- Tang, Y.; Yao, J. 3D Monte Carlo simulation of light distribution in mouse brain in quantitative photoacoustic computed tomography. Quant. Imaging Med. Surg. 2021, 11, 1046–1059. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Y.H.; Sawan, M. Photoacoustic Generation in Human Brain with Embedded Blood Vessel: Modeling and Simulation. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 1145–1152. [Google Scholar]
- Wang, L.V.; Wu, H.-I. Biomedical Optics: Principles and Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Yu, L.; Nina-Paravecino, F.; Kaeli, D.; Fang, Q. Scalable and massively parallel Monte Carlo photon transport simulations for heterogeneous computing platforms. J. Biomed. Opt. 2018, 23, 010504. [Google Scholar] [CrossRef]
- Okada, E.; Delpy, D.T. Near-infrared light propagation in an adult head model. II. Effect of superficial tissue thickness on the sensitivity of the near-infrared spectroscopy signal. Appl. Opt. 2003, 42, 2915–2921. [Google Scholar] [CrossRef]
- Li, T.; Gong, H.; Luo, Q. Visualization of light propagation in visible Chinese human head for functional near-infrared spectroscopy. J. Biomed. Opt. 2011, 16, 045001. [Google Scholar] [CrossRef]
- Alles, E.J.; Noimark, S.; Zhang, E.; Beard, P.C.; Desjardins, A.E. Pencil beam all-optical ultrasound imaging. Biomed. Opt. Express 2016, 7, 3696–3704. [Google Scholar] [CrossRef]
- Park, S.; Brooks, F.; Villa, U.; Su, R.; Anastasio, M.; Oraevsky, A. Normalization of optical fluence distribution for three-dimensional functional optoacoustic tomography of the breast. J. Biomed. Opt. 2022, 27, 036001. [Google Scholar] [CrossRef]
- Liu, D.; Liu, X.; Zhang, Y.; Wang, Q.; Lu, J.; Sun, J. Imitation-tumor targeting based on continuous-wave near-infrared tomography. Comput. Assist. Surg. 2017, 22, 157–162. [Google Scholar] [CrossRef]
- Zheng, S.; Yingsa, H.; Meichen, S.; Qi, M. Quantitative photoacoustic tomography with light fluence compensation based on radiance Monte Carlo model. Phys. Med. Biol. 2023, 68, 065009. [Google Scholar] [CrossRef]
- Auderset, C.; Mazza, C.; Ruh, E.A. Angular Gaussian and Cauchy estimation. J. Multivar. Anal. 2005, 93, 180–197. [Google Scholar] [CrossRef]
- Mei, Z.; Lin, L.; Lei, Y. Research on Behavior of Micro-Particle in Turbid Phantom Based on Interferometry System. In Proceedings of the Recent Developments in Mechatronics and Intelligent Robotics, Cham, Switzerland, 05 October 2018; pp. 324–329. [Google Scholar]
- Kuniyil Ajith Singh, M.; Xia, W. Portable and Affordable Light Source-Based Photoacoustic Tomography. Sensors 2020, 20, 6173. [Google Scholar] [CrossRef]
- Hoerauf, H.; Wirbelauer, C.; Scholz, C.; Engelhardt, R.; Koch, P.; Laqua, H.; Birngruber, R. Slit-lamp-adapted optical coherence tomography of the anterior segment. Graefe’s Arch. Clin. Exp. Ophthalmol. 2000, 238, 8–18. [Google Scholar] [CrossRef]
- Rosenthal, A.; Ntziachristos, V.; Razansky, D. Model-based optoacoustic inversion with arbitrary-shape detectors. Med. Phys. 2011, 38, 4285–4295. [Google Scholar] [CrossRef]
- Liu, X.; Kuang, C.; Hao, X.; Pang, C.; Xu, P.; Li, H.; Liu, Y.; Yu, C.; Xu, Y.; Nan, D.; et al. Fluorescent Nanowire Ring Illumination for Wide-Field Far-Field Subdiffraction Imaging. Phys. Rev. Lett. 2017, 118, 076101. [Google Scholar] [CrossRef]
- Bähr, J.; Krackhardt, U.; Dietrich, D. Novel Ray-Optical Technique for Testing of Aspheric Reflecting Surfaces; SPIE: Strasbourg, France, 2006; Volume 6189. [Google Scholar]
- Torabzadeh, M.; Park, I.-Y.; Bartels, R.; Durkin, A.; Tromberg, B. Compressed single pixel imaging in the spatial frequency domain. J. Biomed. Opt. 2017, 22, 030501. [Google Scholar] [CrossRef]
- Tzang, O.; Niv, E.; Singh, S.; Labouesse, S.; Myatt, G.; Piestun, R. Wavefront shaping in complex media with a 350 kHz modulator via a 1D-to-2D transform. Nat. Photonics 2019, 13, 788–793. [Google Scholar] [CrossRef]
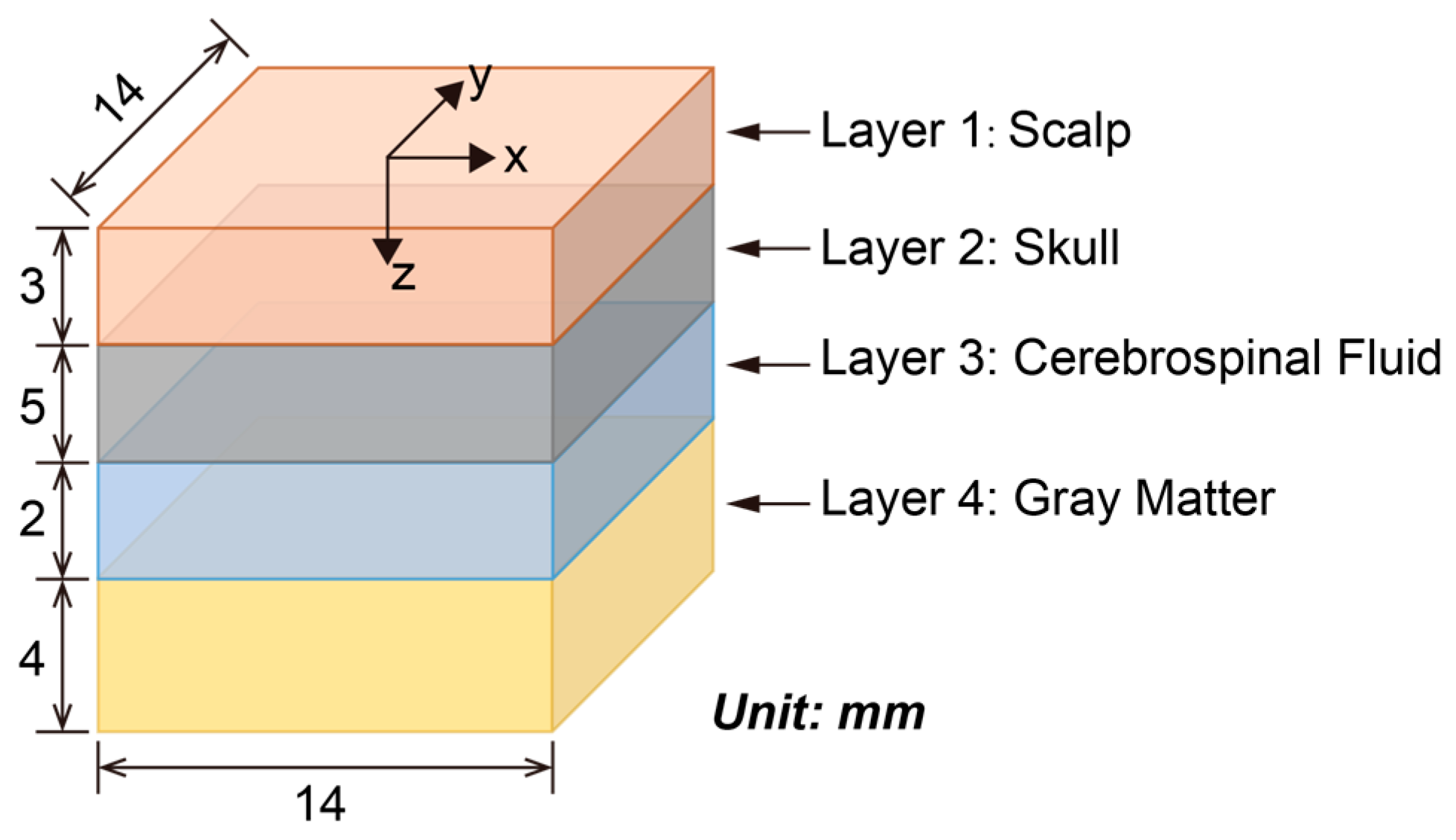




| Tissue Layers | Absorption Coefficient, μa (1/mm) | Scattering Coefficient, μs (1/mm) | Anisotropy Factor, g | Refractive Index, n |
|---|---|---|---|---|
| Scalp | 0.018 | 19.0 | 0.9 | 1.37 |
| Skull | 0.016 | 16.0 | 0.9 | 1.43 |
| Cerebrospinal fluid | 0.004 | 2.4 | 0.9 | 1.33 |
| Gray matter | 0.036 | 22.0 | 0.9 | 1.37 |
| No. | Source Type | Category | Characteristics | Parameter a |
|---|---|---|---|---|
| 1 | Pencil beam [20] | Point | Highly directional and focused with a narrow beam profile. | NA |
| 2 | Isotropic beam [9] | Point | Radiates equally in all directions with a spherical distribution. | NA |
| 3 | Cone beam [21] | Point | Uniformly expands in a conical shape. | Half-angle in radian: π/6 |
| 4 | Arcsine [22] | Point | Illuminates uniformly over a wide viewing angle with a cosine-squared distribution. | NA |
| 5 | Collimated Gaussian [23] | Surface | Bell-shaped intensity profile and uniform over a long distance; it is a parallel, collimated beam that is created by a collimating lens from a Gaussian beam. | Waist radius: 10 |
| 6 | Angular Gaussian [24] | Surface | Emits in a Gaussian distribution over a specific zenith angle. | Zenith angle: π/6 |
| 7 | Hyperboloid Gaussian [25] | Surface | Illuminates in a hyperboloid shape with Gaussian distributions, and it has differences in horizontal and vertical distributions. | Waist radius: 10 Distance between launch plane and focus: 1 Rayleigh range: π/6 |
| 8 | Line [26] | Line | Emits uniformly from the line region into the perpendicular direction. | Length: 10 |
| 9 | Slit [27] | Line | Emits with a collimated beam from the line region. | Length in X direction: 10 |
| 10 | Planar [9] | Surface | Illuminates uniformly from a 3D quadrilateral planar distribution. | Length in X and Y directions: 10 |
| 11 | Disk [28] | Surface | Illuminates uniformly from a 3D disk distribution pointing along the source direction. | Radius: 5 |
| 12 | Ring [29] | Surface | Illuminates uniformly from a 3D ring distribution, and it points along the source direction. | Outer radius: 5 Inner radius: 1 |
| 13 | Pencil array [30] | Surface | Distributes as a rectangular array of pencil beams. | Length in X and Y directions: 10 2 × 2 pencil beams |
| 14 | Spatial Frequency Fourier [31] | Surface | Illuminates in a spatial frequency domain distribution in a planar shape. | Length in X and Y directions: 10 X/Y frequencies: 2/2 |
| 15 | 1D Fourier [32] | Surface | Emits light in a general Fourier distribution in the x direction. | [v1x, v1y, v1z, |v2|] = [10, 0, 0, 10] b [kx, ky, phi0, M] = [1, 1, 0, 0] b |
| 16 | 2D Fourier [32] | Surface | Emits light in a general 2D Fourier distribution. | [v1x, v1y, v1z, |v2|] = [10, 0, 0, 10] b [kx, ky, phi0, M] = [1, 1, 0, 0] b |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Chai, C.; Zuo, H.; Chen, Y.-H.; Shi, J.; Ma, C.; Sawan, M. Monte Carlo-Based Optical Simulation of Optical Distribution in Deep Brain Tissues Using Sixteen Optical Sources. Bioengineering 2024, 11, 260. https://doi.org/10.3390/bioengineering11030260
Yang X, Chai C, Zuo H, Chen Y-H, Shi J, Ma C, Sawan M. Monte Carlo-Based Optical Simulation of Optical Distribution in Deep Brain Tissues Using Sixteen Optical Sources. Bioengineering. 2024; 11(3):260. https://doi.org/10.3390/bioengineering11030260
Chicago/Turabian StyleYang, Xi, Chengpeng Chai, Hongzhi Zuo, Yun-Hsuan Chen, Junhui Shi, Cheng Ma, and Mohamad Sawan. 2024. "Monte Carlo-Based Optical Simulation of Optical Distribution in Deep Brain Tissues Using Sixteen Optical Sources" Bioengineering 11, no. 3: 260. https://doi.org/10.3390/bioengineering11030260
APA StyleYang, X., Chai, C., Zuo, H., Chen, Y.-H., Shi, J., Ma, C., & Sawan, M. (2024). Monte Carlo-Based Optical Simulation of Optical Distribution in Deep Brain Tissues Using Sixteen Optical Sources. Bioengineering, 11(3), 260. https://doi.org/10.3390/bioengineering11030260









