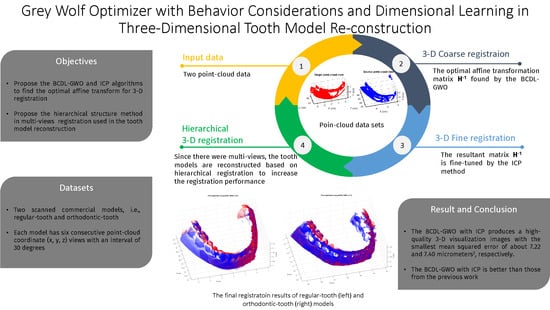
Grey Wolf Optimizer with Behavior Considerations and Dimensional Learning in Three-Dimensional Tooth Model Reconstruction
Abstract
1. Introduction
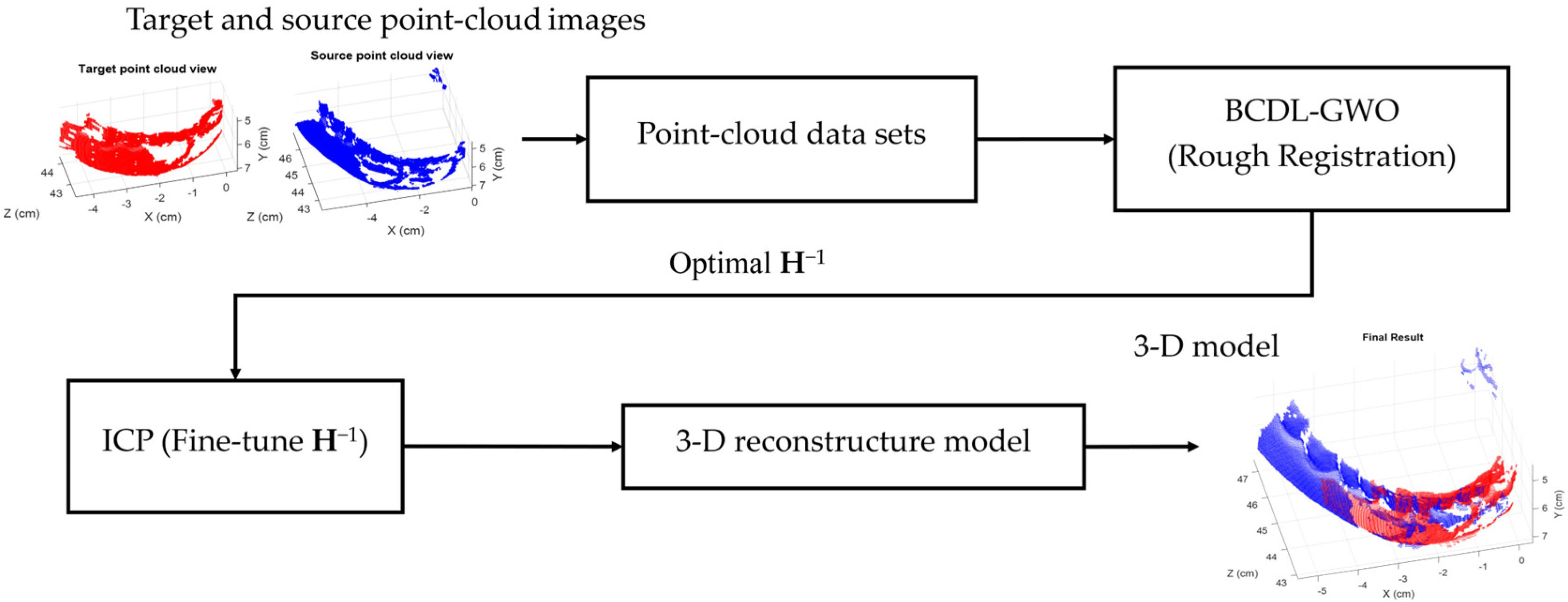
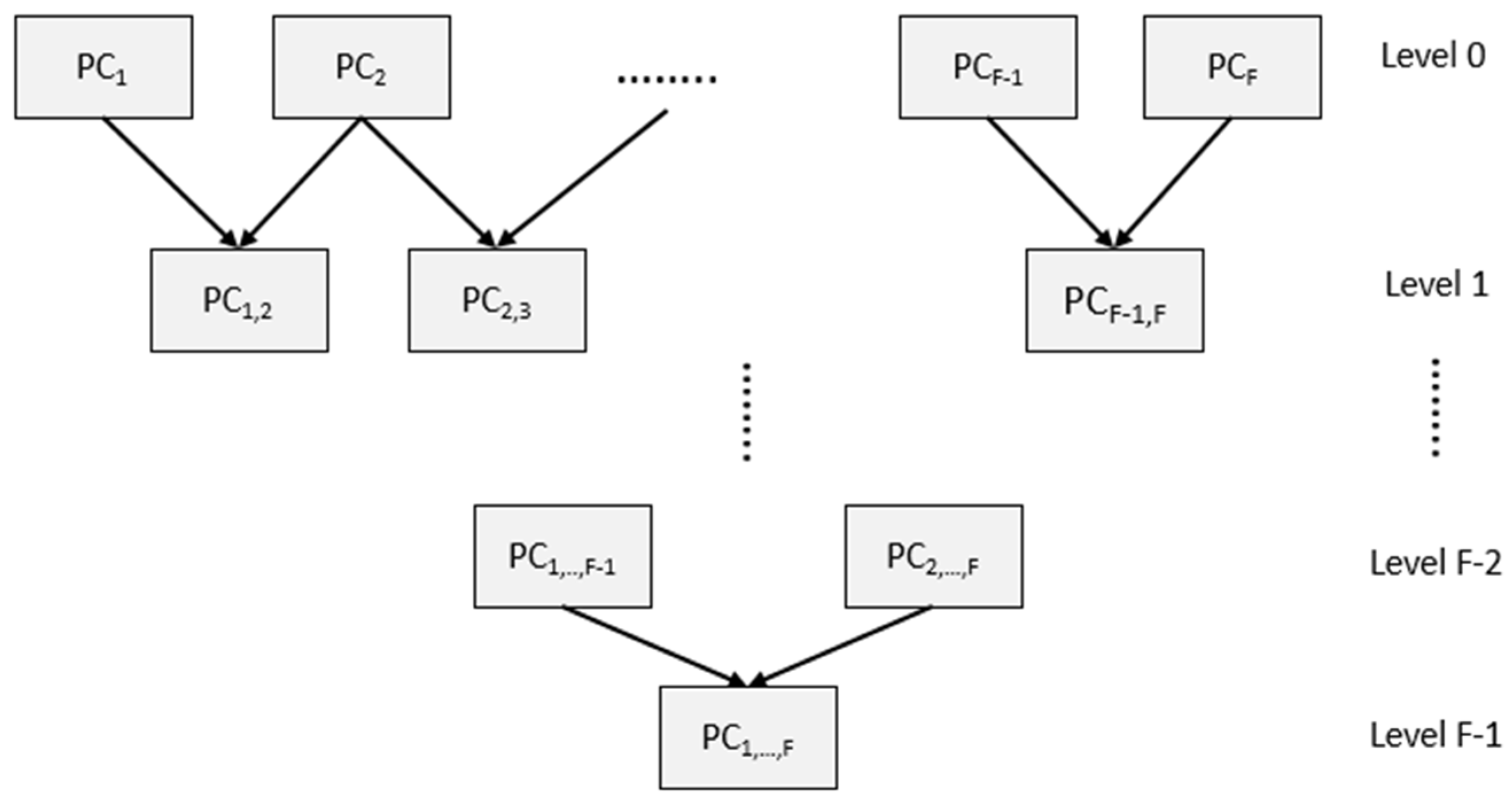
2. Registration Method
2.1. Overview of Grey Wolf Optimizer Algorithm (GWO)
2.2. The Modified GWO Algorithm with Behavior Considerations and Dimensional Learning (BCDL-GWO)
| Algorithm 1. BCDL-GWO algorithm |
| Input: K population size, maximum iterations T. Output: Optimal solution. Initial: K wolves, t = 0. While t ≤ T Evaluate fitness value for each wolf . Find three best leaders, i.e., . Update individual best positions . Update , and using Equations (10) and (11), respectively. For each wolf in GWO-SCA procedure Update current position using Equation (19). Evaluate fitness . End For For each wolf in behavior considerations procedure Generate new candidate solution using Equation (26). Evaluate fitness . Update using Equation (27). End For For each wolf in dimensional learning procedure Generate new candidate solution using equations (30). Evaluate fitness . Update using Equation (31). End For Update using Equation (32). t = t + 1 End While |
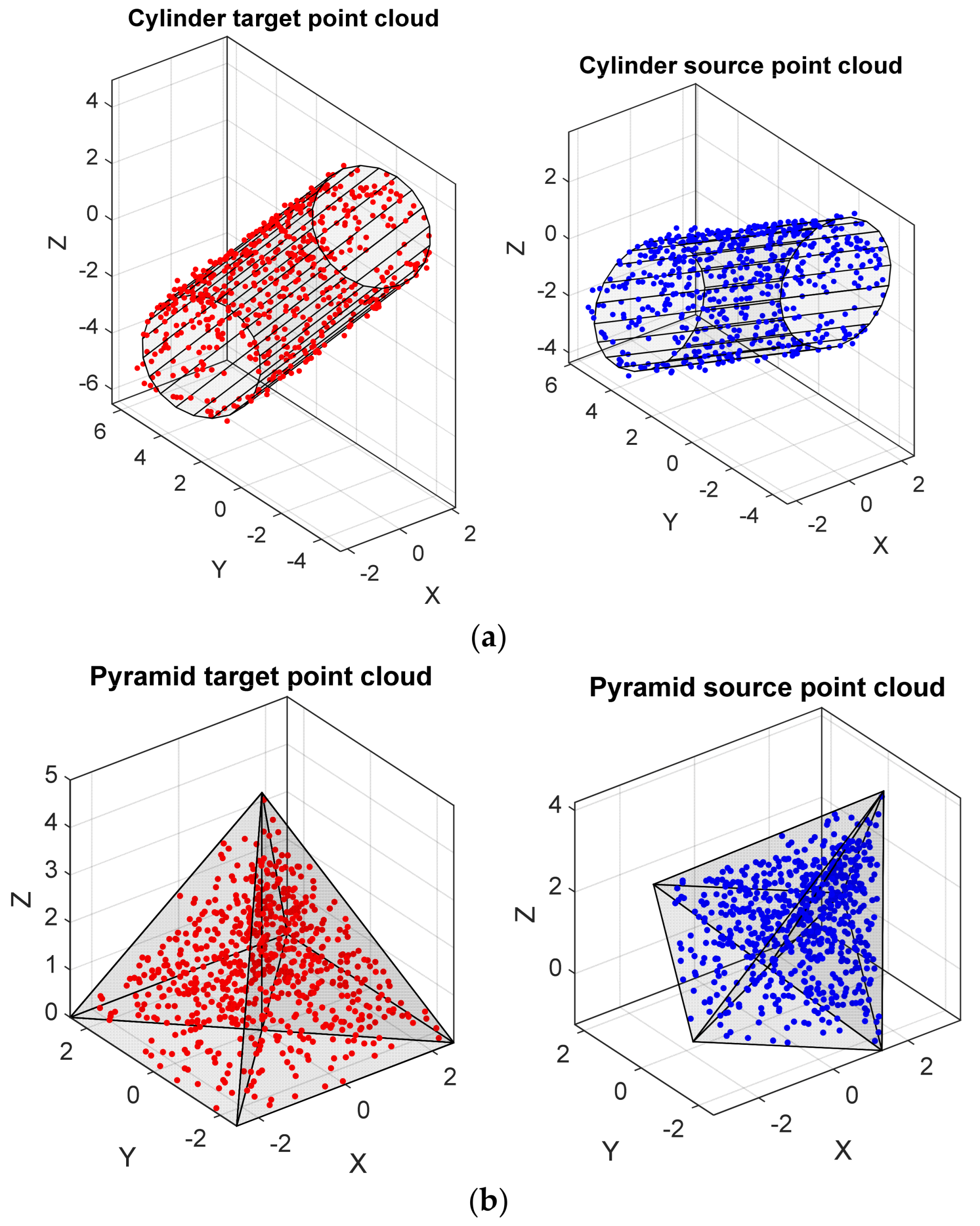
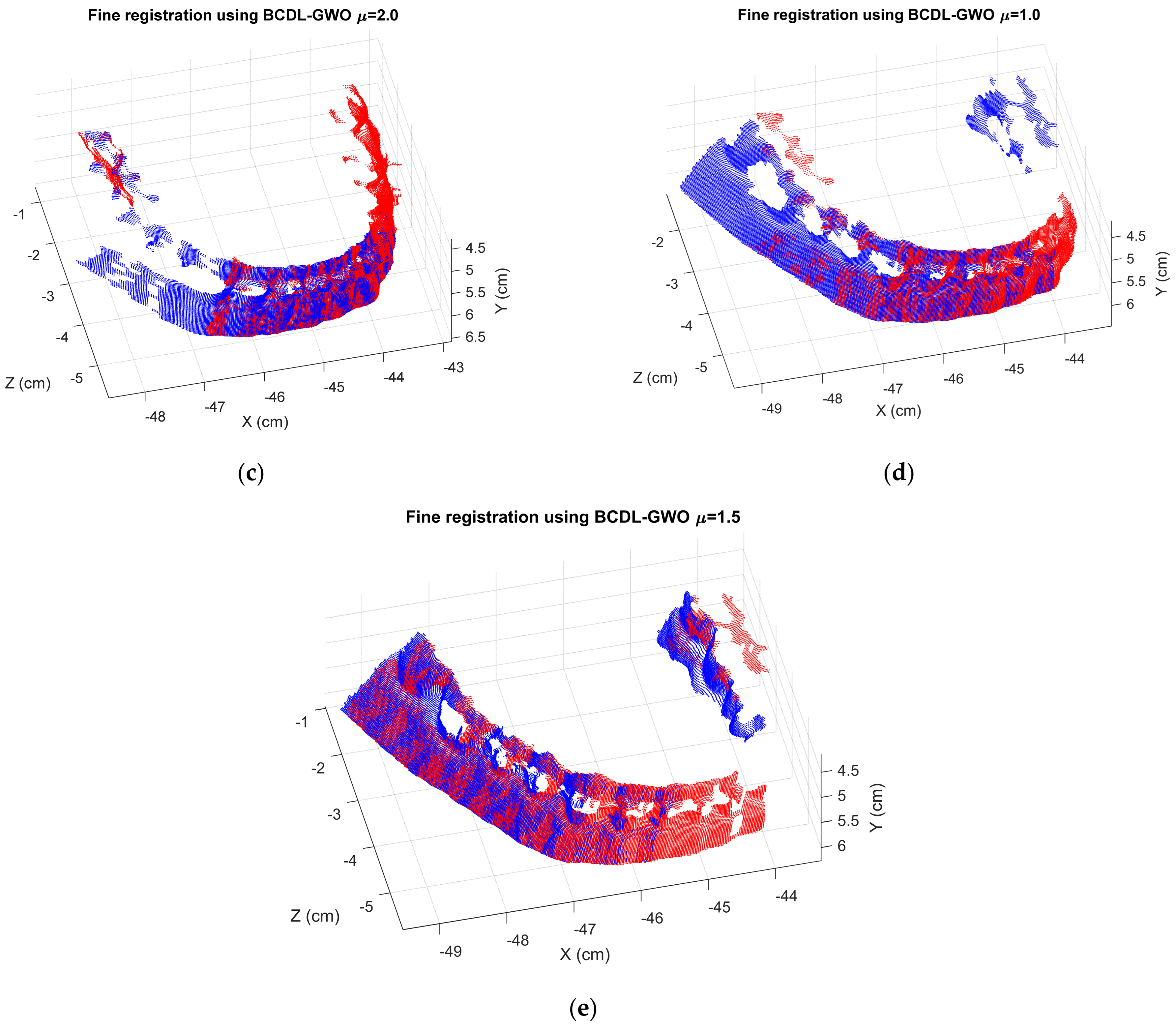
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sivakumar, A.; Thangaswamy, V.; Ravi, V. Treatment planning in conservative dentistry. J. Pharm. Bioallied Sci. 2012, 4 (Suppl. S2), S406–S409. [Google Scholar] [CrossRef] [PubMed]
- Stefanac, S.; Nesbit, S. Diagnosis and Treatment Planning in Dentistry, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 9780323287302. [Google Scholar]
- Hugar, S.M.; Sogi, H.P.S.; Nalawade, T.M.; Sinha, A.; Hugar, S.; Mallikarjuna, R.M. Knowledge, attitude, and practices of oral health care in prevention of early childhood caries among parents of children in Belagavi city: A Questionnaire study. J. Fam. Med. Prim. Care 2016, 5, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, R.; Sugaya, Y.; Kasahara, S.; Omachi, S. Tooth shape reconstruction from dental CT images with the region-growing method. Dentomaxillofacial Radiol. 2014, 43, 20140080. [Google Scholar] [CrossRef]
- Zhou, X.; Gan, Y.; Xiong, J.; Zhang, D.; Zhao, Q.; Xia, Z. A Method for Tooth Model Reconstruction Based on Integration of Multimodal Images. J. Healthc. Eng. 2018, 2018, 4950131. [Google Scholar] [CrossRef]
- Zhang, D.; Gan, Y.; Xiong, J.; Xia, Z. Three-dimensional tooth model reconstruction based on fusion of dental computed tomography images and laser-scanned images (Chineses Article). Shengwu Yixue Gongchengxue Zazhi 2017, 34, 7–14. (In Chinese) [Google Scholar]
- Yau, H.-T.; Yang, T.-J.; Chen, Y.-C. Tooth model reconstruction based upon data fusion for orthodontic treatment simulation. Comput. Biol. Med. 2014, 48, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Martorelli, M.; Ausiello, P. A novel approach for a complete 3D tooth reconstruction using only 3D crown data. Int. J. Interact. Des. Manuf. 2013, 7, 125–133. [Google Scholar] [CrossRef]
- Gan, Y.; Tan, J.; Zhao, Q.; Xia, Z. Automatic 3D Tooth Model Reconstruction from CT Images. In Proceedings of the 2014 International Association for Dental Research/Asia Pacific Region (IADR/APR), Cape Town, South Africa, 25 June 2014. [Google Scholar]
- Srisilapanan, P.; Nirunsittirat, A.; Roseman, J. Trends over Time in Dental Caries status in Urban and Rural Thai Children. J. Clin. Exp. Dent. 2017, 9, e1201–e1206. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Fakhry, A.E.; El-henawy, I.; Qiu, T.; Sangaiah, A.K. Feature and Intensity Based Medical Image Registration Using Particle Swarm Optimization. J. Med. Syst. 2017, 41, 197. [Google Scholar] [CrossRef]
- Sarvamangala, D.R.; Kulkarni, R.V. Swarm Intelligence Algorithms for Medical Image Registration: A Comparative Study. Commun. Comput. Inf. Sci. 2017, 776, 451–465. [Google Scholar] [CrossRef]
- Khan, M.K.; Nystrom, I. A Modified Particle Swarm Optimization Applied in Image Registration. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: Piscataway Township, NJ, USA, 2010; pp. 2302–2305. [Google Scholar]
- Jara, R.I.; Buchelly, F.J.; Meschino, G.; Ballarin, V.L. Improved Particle Swarm Optimization algorithm applied to rigid registration in medical images. In Proceedings of the VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, Santander, Colombia, 26–28 October 2016; IFMBE Proceedings. Torres, I., Bustamante, J., Sierra, D., Eds.; Springer: Singapore, 2016; Volume 60, pp. 161–164. [Google Scholar]
- Yonghong, Y.; Jiying, L.; Qiang, W.; Tao, Z. Improved Particle Swarm Optimization Image Registration Based on Mutual Information. In Proceedings of the 2019 11th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Qiqihar, China, 28–29 April 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 450–453. [Google Scholar]
- Ramirez, L.; Durdle, N.G.; Raso, V.J. A Parameters Selection Scheme for Medical Image Registration. In Proceedings of the Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), Montreal, QC, Canada, 3–6 June 2006; pp. 505–510. [Google Scholar]
- Sabuncu, M.R.; Ramadge, P.J. Spatial Information in Entropy-Based Image Registration. In WBIR 2003, Lecture Notes in Computer Science; Gee, J.C., Maintz, J.B.A., Vannier, M.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2717. [Google Scholar] [CrossRef]
- Kaur, A.; Kaur, L.; Gupta, S. Image Recognition using Coefficient of Correlation and Structural Similarity Index in Uncontrolled Environment. Int. J. Comput. Appl. 2012, 59, 32–39. [Google Scholar] [CrossRef]
- Daniel, E.; Anitha, J.; Kamaleshwaran, K.K.; Rani, I. Optimum spectrum mask based medical image fusion using Grey Wolf Optimization. Biomed. Signal Process. Control 2017, 34, 36–43. [Google Scholar] [CrossRef]
- Dida, H.; Charif, F.; Benchabane, A. Grey Wolf Optimizer for Multimodal Medical Image Registration. In Proceedings of the Fourth International Conference on Intelligent Computing in Data Sciences (ICDS), Fez, Morocco, 21–23 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Chakraborty, S.; Pradhan, R.; Ashour, A.S.; Moraru, L.; Dey, N. Grey-Wolf-Based Wang’s Demons for Retinal Image Registration. Entropy 2020, 22, 659. [Google Scholar] [CrossRef]
- Shaw, K.; Pandey, P.; Das, S.; Ghosh, D.; Malakar, P.; Dhabal, S. Image Registration using Bio-inspired Algorithms. In Proceedings of the 2020 IEEE 1st International Conference for Convergence in Engineering (ICCE), Kolkata, India, 5–6 September 2020; pp. 330–334. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, Y.; Zhang, D.; Hou, N. Multimodal image registration using histogram of oriented gradient distance and data-driven grey wolf optimizer. Neurocomputing 2020, 392, 108–120. [Google Scholar] [CrossRef]
- Lazar, Đ.; Jokic, A.; Petrovic, M.; Miljković, Z. Biologically Inspired Optimization Methods for Image Registration in Visual Servoing of a Mobile Robot. In Proceedings of the 7th International Conference on Electrical, Electronic and Computing Engineering (IcETRAN), Etno-Selo Stanišići, Republika Srpska, 28–30 September 2020. [Google Scholar]
- Kaur, K.; Budhiraja, S.; Sharma, N. Multimodal Medical Image Fusion based on Gray Wolf Optimization and Hilbert Transform. Biomed. Pharmacol. J. 2019, 12, 2091–2098. [Google Scholar] [CrossRef]
- Dida, H.; Charif, F.; Benchabane, A. Registration of computed tomography images of a lung infected with COVID-19 based in the new meta-heuristic algorithm HPSGWO. Multimed. Tools Appl. 2022, 81, 18955–18976. [Google Scholar] [CrossRef]
- Wachowiak, M.P.; Smolíková, R.; Zheng, Y.; Zurada, J.M.; Elmaghraby, A.S. An Approach to Multimodal Biomedical Im-age Registration Utilizing Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 289–301. [Google Scholar] [CrossRef]
- Chen, Y.-W.; Mimori, A. Hybrid Particle Swarm Optimization for Medical Image Registration. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjian, China, 14–16 August 2009; IEEE: Piscataway Township, NJ, USA, 2009; Volume 6, pp. 26–30. [Google Scholar]
- Abduo, J.; Bennamoun, M. Three-dimensional image registration as a tool for forensic odontology: A preliminary investigation. Am. J. Forensic Med. Pathol. 2013, 34, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Bradley, D.; Garrido, P.; Zollhöfer, M.; Theobalt, C.; Gross, M.; Beeler, T. Model-based teeth reconstruction. ACM Trans. Graph. 2016, 35, 220. [Google Scholar] [CrossRef]
- Yamany, S.M.; Farag, A.A.; Tasman, D.; Farman, A.G. A 3-D reconstruction system for the human jaw using a sequence of optical images. IEEE Trans. Med. Imaging 2000, 19, 538–547. [Google Scholar] [CrossRef] [PubMed]
- Zhan, X.; Cai, Y.; He, P. A three-dimensional point cloud registration based on entropy and particle swarm optimization. Adv. Mech. Eng. 2018, 10, 1687814018814330. [Google Scholar] [CrossRef]
- Zhan, X.; Cai, Y.; Li, H.; Li, Y.; He, P. A point-cloud registration algorithm based on normal vector and particle swarm optimization. Meas. Control 2019, 53, 265–275. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, B.; Nie, J.; Sun, B. A point cloud registration method combining enhanced particle swarm optimization and iterative closest point method. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; IEEE: Piscataway Township, NJ, USA, 2016; pp. 2810–2815. [Google Scholar]
- Yousry, M.; Youssef, B.A.B.; El Aziz, M.A.; Sidky, F.I. 3D Point-cloud Registration Using Particle Swarm Optimization Based on Different Descriptors. Int. J. Sci. Eng. Res. 2017, 8, 558–564. [Google Scholar]
- John, V.; Xu, Y.; Mita, S.; Long, Q.; Liu, Z.; Tan, Y.; Takagi, H.; Shi, Y. Registration of GPS and Stereo Vision for Point Cloud Localization in Intelligent Vehicles Using Particle Swarm Optimization. In Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 10385, pp. 209–217. [Google Scholar]
- Zhang, L.; Yang, B.; Wang, L.; Zhao, X.; Zhou, J.; Li, M.; Han, Y. Three-dimensional Cement Image Registration Based on Multi-layer PSO and Mutual Information. In Proceedings of the 2016 3rd International Conference on Informative and Cybernetics for Computational Social Systems (ICCSS), Jinzhou, China, 26–29 August 2016. [Google Scholar]
- Feng, Y.; Tang, J.; Su, B.; Su, Q.; Zhou, Z. Point Cloud Registration Algorithm Based on the Grey Wolf Optimizer. IEEE Access 2020, 8, 143375–143382. [Google Scholar] [CrossRef]
- Wongkhuenkaew, R.; Auephanwiriyakul, S.; Chaiworawitkul, M.; Theera-Umpon, N. Three-Dimensional Tooth Model Reconstruction Using Statistical Randomization-Based Particle Swarm Optimization. Appl. Sci. 2021, 11, 2363. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Singh, N.; Singh, S.B. A novel hybrid GWO-SCA approach for optimization problems. Eng. Sci. Technol. Int. J. 2017, 20, 1586–1601. [Google Scholar] [CrossRef]
- Heidari, A.A.; Pahlavani, P. An efficient modified grey wolf optimizer with Lévy flight for optimization tasks. Appl. Soft Comput. 2017, 60, 115–134. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Cai, S.; Xu, M. A Random Opposition-Based Learning Grey Wolf Optimizer. IEEE Access 2019, 7, 113810–113825. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Z. A survey of iterative closest point algorithm. In Proceedings of the Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 4395–4399. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; John Willey & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- FitzGibbon, A.W. Robust registration of 2D and 3D point sets. Image Vis. Comput. 2003, 21, 1145–1153. [Google Scholar] [CrossRef]
- Rezaei, F.; Safavi, H.R.; Abd Elaziz, M.; El-Sappagh, S.H.A.; Al-Betar, M.A.; Abuhmed, T. An Enhanced Grey Wolf Optimizer with a Velocity-Aided Global Search Mechanism. Mathematics 2022, 10, 351. [Google Scholar] [CrossRef]
- Long, W.; Jiao, J.; Liang, X.; Tang, M. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization. Eng. Appl. Artif. Intell. 2018, 68, 63–80. [Google Scholar] [CrossRef]
- Gao, Z.-M.; Zhao, J. An Improved Grey Wolf Optimization Algorithm with Variable Weights. Comput. Intell. Neurosci. 2019, 2019, 2981282. [Google Scholar] [CrossRef]
- Qiao, Y.; Hsu, H.-Y.; Pan, J.-S. Behavior-based Grey Wolf Optimizer for Wireless Sensor Network Deployment Problem. Int. J. Ad Hoc Ubiquitous Comput. 2022, 39, 70–82. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: England, UK, 2010; ISBN 1-905986-28-9. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks (ICNN), Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Asghar Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 111, 300–323. [Google Scholar] [CrossRef]
- Li, P.; Wang, R.; Wang, Y.; Gao, G. Fast Method of Registration for 3D RGB Point cloud with Improved Four Initial Point Pairs Algorithm. Sensors 2020, 20, 138. [Google Scholar] [CrossRef]
- Du, S.; Zheng, N.; Xiong, L.; Ying, S.; Xue, J. Scaling iterative closest point algorithm for registration of m–D point sets. J. Vis. Commun. Image Represent. 2010, 21, 442–452. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Ressl, C.; Briese, C. A correspondence framework for ALS strip adjustments based on variants of the ICP algorithm. J. Photogramm. Remote Sens. Geoinf. Sci. (PFG) 2015, 4, 275–289. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Ressl, C.; Briese, C. Rigorous Strip Adjustment of Airborne Laser scanning Data Based on the ICP Algorithm. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 73–80. [Google Scholar] [CrossRef]
- Point Cloud Tools for Matlab. Available online: www.geo.tuwien.ac.at/downloads/pg/pctools/pctools.html (accessed on 12 May 2022).
- Kalla, M.-P.; Economopoulos, T.L.; Matsopoulos, G.K. 3D dental image registration using exhaustive deformable models: A comparative study. Dentomaxillofacial Radiol. 2017, 46, 20160390. [Google Scholar] [CrossRef]
- Kim, M.; Chung, M.; Shin, Y.-G.; Kim, B. Automatic registration of dental CT and 3D scanned model using deep split jaw and surface curvature. Comput. Methods Programs Biomed. 2023, 233, 107467. [Google Scholar] [CrossRef]
- Kurniawan, A.; Yodokawa, K.; Kosaka, M.; Ito, K.; Sasaki, K.; Aoki, T.; Suzuki, T. Determining the effective number and surfaces of teeth for forensic dental identification through the 3D point cloud data analysis. Egypt. J. Forensic Sci. 2020, 10, 3. [Google Scholar] [CrossRef]
- Chung, M.; Lee, J.; Song, W.; Song, Y.; Yang, I.-H.; Lee, J.; Shin, Y.-G. Automatic Registration Between Dental Cone-Beam CT and Scanned Surface via Deep Pose Regression Neural Networks and Clustered Similarities. IEEE Trans. Med. Imaging 2020, 32, 3900–3909. [Google Scholar] [CrossRef]
- Porumb, I.C.; Leucuta, D.C.; Nigoghossian, M.; Culic, B.; Lucaciu, P.O.; Culic, C.; Badea, I.C.; Leghezeu, A.N.; Nicoara, A.G.; Simu, M.R. Caries Lesion Assessment Using 3D Virtual Models by Examiners with Different Degrees of Clinical Experience. Medicina 2023, 59, 2157. [Google Scholar] [CrossRef]








| Parameters | Lower Bound | Upper Bound |
|---|---|---|
| tx, ty, tz | −1.5 (cm) | 1.5 (cm) |
| ϕx, ϕy, ϕz | −45 (deg) | 45 (deg) |
| sx, sy, sz | 0.8 (20% downscaling) | 1.2 (20% upscaling) |
| sh1, sh2, sh3, sh4, sh5, sh6 | −0.5 (cm) | 0.5 (cm) |
| Parameters | Symbols | Values |
|---|---|---|
| Search agents (wolves) | K | 100 |
| Iterations | T | 2000 |
| Control parameter a | a0 | 2 |
| Control parameter c | c0 | 2 |
| Nonlinear exponent indices | μ | 0.5, 1.0, 1.5, 2.0 |
| Lévy distribution | β | 1.5 |
| Research work in [39] | α | |||
| α = 0.5 | α = 1.0 | α = 1.5 | α = 2.0 | |
| Without ICP | 7.68 × 10−2 | 9.23 × 10−2 | 3.22 × 10−31 | 9.68 × 10−2 |
| With ICP | 7.68 × 10−2 | 9.23 × 10−2 | 3.22 × 10−31 | 9.68 × 10−2 |
| BCDL-GWO | μ | |||
| 0.5 | 1.0 | 1.5 | 2.0 | |
| Without ICP | 1.90 × 10−9 | 5.37 × 10−11 | 3.46 × 10−13 | 3.23 × 10−12 |
| With ICP | 2.71 × 10−27 | 7.35 × 10−22 | 4.11 × 10−26 | 3.41 × 10−21 |
| SR-PSO [39] | α | |||
| α = 0.5 | α = 1.0 | α = 1.5 | α = 2.0 | |
| Without ICP | 1.14 × 10−3 | 1.18 × 10−4 | 5.71 × 10−30 | 1.70 × 10−4 |
| With ICP | 1.51 × 10−17 | 9.66 × 10−18 | 5.71 × 10−30 | 6.97 × 10−18 |
| BCDL-GWO | μ | |||
| 0.5 | 1.0 | 1.5 | 2.0 | |
| Without ICP | 9.37 × 10−10 | 3.40 × 10−10 | 1.96 × 10−13 | 1.95 × 10−12 |
| With ICP | 7.79 × 10−20 | 1.23 × 10−18 | 1.63 × 10−17 | 6.51 × 10−18 |
| SR-PSO [39] | α | |||
| α = 0.5 | α = 1.0 | α = 1.5 | α = 2.0 | |
| Without ICP | 5.38 × 10−2 ± 3.73 × 10−2 | 4.66 × 10−2 ± 4.05 × 10−2 | 3.84 × 10−2 ± 4.06 × 10−2 | 5.56 × 10−2 ± 3.90 × 10−2 |
| With ICP | 5.38 × 10−2 ± 3.73 × 10−2 | 4.66 × 10−2 ± 4.05 × 10−2 | 3.84 × 10−2 ± 4.06 × 10−2 | 5.56 × 10−2 ± 3.90 × 10−2 |
| BCDL-GWO | μ | |||
| 0.5 | 1.0 | 1.5 | 2.0 | |
| Without ICP | 2.91 × 10−9 ± 3.73 × 10−9 | 1.14 × 10−10 ± 1.7 × 10−10 | 1.07 × 10−11 ± 1.67 × 10−11 | 1.19 × 10−11 ± 2.26 × 10−11 |
| With ICP | 1.68 × 10−19 ± 4.48 × 10−19 | 4.26 × 10−22 ± 1.03 × 10−21 | 2.64 × 10−19 ± 8.31 × 10−19 | 5.69 × 10−20 ± 1.17 × 10−19 |
| SR-PSO [39] | α | |||
| α = 0.5 | α = 1.0 | α = 1.5 | α = 2.0 | |
| Without ICP | 1.65 × 10−4 ± 3.68 × 10−4 | 4.92 × 10−5 ± 1.08 × 10−4 | 1.92 × 10−6 ± 6.08 × 10−6 | 1.71 × 10−5 ± 5.38 × 10−5 |
| With ICP | 2.83 × 10−18 ± 5.91 × 10−18 | 4.90 × 10−19 ± 1.55 × 10−18 | 5.71 × 10−18 ± 1.81 × 10−17 | 9.92 × 10−18 ± 2.79 × 10−17 |
| BCDL-GWO | μ | |||
| 0.5 | 1.0 | 1.5 | 2.0 | |
| Without ICP | 2.30 × 10−9 ± 4.76 × 10−9 | 6.29 × 10−10 ± 9.14 × 10−10 | 2.49 × 10−10 ± 7.04 × 10−10 | 7.35 × 10−12 ± 1.76 × 10−11 |
| With ICP | 2.15 × 10−16 ± 6.56 × 10−16 | 3.79 × 10−18 ± 4.78 × 10−18 | 5.79 × 10−18 ± 9.57 × 10−18 | 6.93 × 10−19 ± 2.05 × 10−18 |
| BOA [57] | HNO [58] | SMA [59] | WOA [60] | SR-PSO [39] | BCDL-GWO | |
|---|---|---|---|---|---|---|
| Without ICP | 1.08 × 10−1 ± 3.83 × 10−3 | 9.63 × 10−2 ± 7.49 × 10−3 | 4.78 × 10−2 ± 4.70 × 10−2 | 7.27 × 10−2 ± 1.99 × 10−2 | 3.84 × 10−2 ± 4.06 × 10−2 | 1.07 × 10−11 ± 1.67 × 10−11 |
| With ICP | 8.58 × 10−2 ± 1.35 × 10−2 | 8.84 × 10−2 ± 1.09 × 10−2 | 4.54 × 10−2 ± 4.79 × 10−2 | 6.16 × 10−2 ± 3.38 × 10−2 | 3.84 × 10−2 ± 4.06 × 10−2 | 4.26 × 10−22 ± 1.03 × 10−21 |
| BOA [57] | HNO [58] | SMA [59] | WOA [60] | SR-PSO [39] | BCDL-GWO | |
|---|---|---|---|---|---|---|
| Without ICP | 4.14 × 10−2 ± 2.07 × 10−3 | 4.05 × 10−2 ± 8.42 × 10−3 | 7.92 × 10−3 ± 6.26 × 10−3 | 3.77 × 10−2 ± 8.85 × 10−3 | 1.92 × 10−6 ± 6.08 × 10−6 | 7.35 × 10−12 ± 1.76 × 10−11 |
| With ICP | 3.26 × 10−17 ± 8.08 × 10−17 | 4.19 × 10−17 ± 1.21 × 10−16 | 5.39 × 10−18 ± 1.08 × 10−17 | 3.08 × 10−16 ± 8.65 × 10−16 | 4.90 × 10−19 ± 1.55 × 10−18 | 6.93 × 10−19 ± 2.05 × 10−18 |
| Data Sets | Objects | Root Mean Squared Error (RMSE) | |
|---|---|---|---|
| Li et al. [61] | BCDL-GWO | ||
| SHOT | Super Mario | 4.422 × 10−1 | 4.06 × 10−3 |
| Doll | 4.9 × 10−3 | 4.01 × 10−3 | |
| Duck | 5.8 × 10−3 | 5.23 × 10−3 | |
| Frog | 4.1 × 10−3 | 3.83 × 10−3 | |
| Peter Rabbit | 3.9 × 10−3 | 4.05 × 10−3 | |
| Squirrel | 1.29 × 10−2 | 3.17 × 10−3 | |
| Stand ford | Du et al. [62] | BCDL-GWO | |
| Bunny | 1.9935 × 10−3 | 1.7912 × 10−3 | |
| Dragon | 1.841 × 10−3 | 1.7789 × 10−3 | |
| Happy Buddha | 2.0950 × 10−3 | 2.0279 × 10−3 | |
| Cow and Feet | Mean Squared Error (MSE) | ||
| Zhan et al. [33] | BCDL-GWO | ||
| Cow | 1.43 × 10−2 | 1.24 × 10−22 | |
| Feet of man | 3.78 × 10−16 | 2.13 × 10−18 | |
| Model | Object View | Object Name | Number of Points |
|---|---|---|---|
| Regular tooth model | 1 | Img0 | 28,807 |
| 2 | Img1 | 28,970 | |
| 3 | Img2 | 28,983 | |
| 4 | Img3 | 25,809 | |
| 5 | Img4 | 17,303 | |
| 6 | Img5 | 21,739 | |
| Total | Six views | 151,592 | |
| Orthodontic tooth model | 1 | Img0 | 25,301 |
| 2 | Img1 | 25,772 | |
| 3 | Img2 | 22,432 | |
| 4 | Img3 | 17,167 | |
| 5 | Img4 | 22,537 | |
| 6 | Img5 | 24,148 | |
| Total | Six views | 137,357 |
| View Pairs | MSE in Micrometer2 | |||
|---|---|---|---|---|
| μ = 0.5 | μ = 1.0 | μ = 1.5 | μ = 2.0 | |
| 1 vs. 2 | 5.8775 | 6.7106 | 5.8122 | 5.8169 |
| 2 vs. 3 | 5.0568 | 4.9923 | 4.9406 | 4.9582 |
| 3 vs. 4 | 5.3752 | 5.4111 | 5.4080 | 5.3940 |
| 4 vs. 5 | 5.5786 | 5.5135 | 5.5601 | 5.4953 |
| 5 vs. 6 | 5.9304 | 5.7735 | 5.7640 | 5.7808 |
| View Pairs | MSE in Micrometer2 | |||
|---|---|---|---|---|
| μ = 0.5 | μ = 1.0 | μ = 1.5 | μ = 2.0 | |
| 1 vs. 2 | 5.7533 | 5.7531 | 5.7327 | 5.7328 |
| 2 vs. 3 | 4.9278 | 4.9266 | 4.9291 | 4.9265 |
| 3 vs. 4 | 5.3558 | 5.3564 | 5.3854 | 5.3566 |
| 4 vs. 5 | 5.3860 | 5.3289 | 5.3320 | 5.3412 |
| 5 vs. 6 | 5.7269 | 5.7316 | 5.7331 | 5.7287 |
| View Pairs | MSE in Micrometer2 | |||
|---|---|---|---|---|
| Coarse Registration | Fine Registration | |||
| SR-PSO | BCDL-GWO | SR-PSO | BCDL-GWO | |
| 1 vs. 2 | 5.9300 | 5.8122 | 5.8628 | 5.7327 |
| 2 vs. 3 | 4.8937 | 4.9406 | 4.8860 | 4.9265 |
| 3 vs. 4 | 5.4310 | 5.3752 | 5.4017 | 5.3558 |
| 4 vs. 5 | 5.2666 | 5.4953 | 5.1253 | 5.3289 |
| 5 vs. 6 | 5.8166 | 5.7640 | 5.6828 | 5.7269 |
| SR-PSO with ICP | BCDL-GWO with ICP | |||
|---|---|---|---|---|
| α = 1.5 | μ = 0.5 | μ = 1.0 | μ = 1.5 | μ = 2.0 |
| 7.3666 | 7.2186 | 7.2188 | 7.2209 | 7.2189 |
| View pairs | MSE in Micrometer2 | |||
|---|---|---|---|---|
| μ = 0.5 | μ = 1.0 | μ = 1.5 | μ = 2.0 | |
| 1 vs. 2 | 5.5267 | 5.5227 | 5.6627 | 5.5413 |
| 2 vs. 3 | 6.2508 | 6.8335 | 6.2865 | 6.1815 |
| 3 vs. 4 | 5.5515 | 5.3939 | 5.6002 | 5.5869 |
| 4 vs. 5 | 6.4284 | 6.6458 | 6.4830 | 6.4737 |
| 5 vs. 6 | 6.1203 | 5.3183 | 5.4125 | 5.3231 |
| View Pairs | MSE in Micrometer2 | |||
|---|---|---|---|---|
| μ = 0.5 | μ = 1.0 | μ = 1.5 | μ = 2.0 | |
| 1 vs. 2 | 5.5104 | 5.5089 | 5.5108 | 5.5147 |
| 2 vs. 3 | 6.1425 | 6.1422 | 6.1423 | 6.1422 |
| 3 vs. 4 | 5.2838 | 5.2842 | 5.2842 | 5.2720 |
| 4 vs. 5 | 6.3988 | 6.3931 | 6.4010 | 6.4010 |
| 5 vs. 6 | 5.2861 | 5.2863 | 5.2804 | 5.2820 |
| View Pairs | MSE in Micrometer2 | |||
|---|---|---|---|---|
| Coarse Registration | Fine Registration | |||
| SR-PSO | BCDL-GWO | SR-PSO | BCDL-GWO | |
| 1 vs. 2 | 5.5553 | 5.5227 | 5.5093 | 5.5089 |
| 2 vs. 3 | 6.1613 | 6.1815 | 6.1440 | 6.1422 |
| 3 vs. 4 | 5.4687 | 5.3939 | 5.2706 | 5.2720 |
| 4 vs. 5 | 6.5847 | 6.4284 | 6.3945 | 6.3931 |
| 5 vs. 6 | 5.3262 | 5.3183 | 5.2801 | 5.2804 |
| SR-PSO with ICP | BCDL-GWO with ICP | |||
|---|---|---|---|---|
| α = 0.5 | μ = 0.5 | μ = 1.0 | μ = 1.5 | μ = 2.0 |
| 7.4130 | 7.4000 | 7.4008 | 7.3999 | 7.4001 |
| Research Works | Methods | Objective Functions | Data Sets | Transformations | Registration Errors |
|---|---|---|---|---|---|
| Kalla et al. [66] | Downhill simplex method and deformation techniques | Matt’s Mutual Information (MMI) | CT images | Non-Rigid | Pre-registered: 0.546 ± 0.233 Elastic-registered: 0.666 ± 0.286 |
| Kim et al. [67] | 2D CNN and ICP | Curvature variance of neighbor (CVN) | CT images and 3D scanned models | Rigid | Data set 1: 1.39 ± 2.67 mm Data set 2: 2.37 ± 3.43 mm Data set 3: 1.01 ± 2.10 mm |
| Kurniawan et al. [68] | ICP | Root Mean Squared Error (RMSE) | 3D point clouds | Rigid | Experiment 1: 0.182 ± 0.032 mm Experiment 2: 0.187 ± 0.041 mm |
| Chung et al. [69] | CNN and Downhill simplex method | Clustered similarity | CT images and 3D scanned models | Rigid | Surface-based error: 5.11 ± 2.54 mm Landmark-based error: 1.80 ± 0.84 mm |
| Our proposed method | BCDL-GWO and ICP | Mean Squared Error (MSE) | 3D point clouds | Non-Rigid | Tooth model 1: 7.22 × 10−3 mm Tooth model 2: 7.39 × 10−3 mm |
| Process | Time Complexities | |||||
|---|---|---|---|---|---|---|
| BCDL-GWO | SR-PSO [39] | BOA [57] | HHO [58] | SMA [59] | WOA [60] | |
| Initialization | O(K × D) * | O(K × D) | O(K × D) | O(K × D) | O(K × D) | O(K × D) |
| Control parameter calculations | O(K × D) | O(K × D) | O(K) | O(K) | O(K × D) | O(K × D) |
| Position update steps | O(K × D) | O(K × D) | O(K × D) | O(K × D) | O(K × D) | O(K × D) |
| New candidate generation steps | O(K × D2) | O(K × D) | - | - | - | - |
| Fitness evaluations | O(K × D) | O(K × D) | O(K × D) | O(K × D) | O(K × D) | O(K × D) |
| Fitness comparisons | O(K) | O(K) | O(K) | O(K) | O(KlogK) | O(K) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wongkhuenkaew, R.; Auephanwiriyakul, S.; Chaiworawitkul, M.; Theera-Umpon, N.; Yeesarapat, U. Grey Wolf Optimizer with Behavior Considerations and Dimensional Learning in Three-Dimensional Tooth Model Reconstruction. Bioengineering 2024, 11, 254. https://doi.org/10.3390/bioengineering11030254
Wongkhuenkaew R, Auephanwiriyakul S, Chaiworawitkul M, Theera-Umpon N, Yeesarapat U. Grey Wolf Optimizer with Behavior Considerations and Dimensional Learning in Three-Dimensional Tooth Model Reconstruction. Bioengineering. 2024; 11(3):254. https://doi.org/10.3390/bioengineering11030254
Chicago/Turabian StyleWongkhuenkaew, Ritipong, Sansanee Auephanwiriyakul, Marasri Chaiworawitkul, Nipon Theera-Umpon, and Uklid Yeesarapat. 2024. "Grey Wolf Optimizer with Behavior Considerations and Dimensional Learning in Three-Dimensional Tooth Model Reconstruction" Bioengineering 11, no. 3: 254. https://doi.org/10.3390/bioengineering11030254
APA StyleWongkhuenkaew, R., Auephanwiriyakul, S., Chaiworawitkul, M., Theera-Umpon, N., & Yeesarapat, U. (2024). Grey Wolf Optimizer with Behavior Considerations and Dimensional Learning in Three-Dimensional Tooth Model Reconstruction. Bioengineering, 11(3), 254. https://doi.org/10.3390/bioengineering11030254