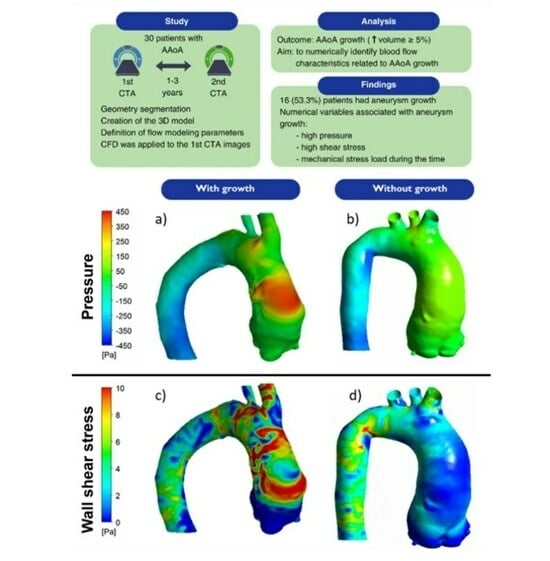
Stress Load and Ascending Aortic Aneurysms: An Observational, Longitudinal, Single-Center Study Using Computational Fluid Dynamics
Abstract
1. Introduction
2. Materials and Methods
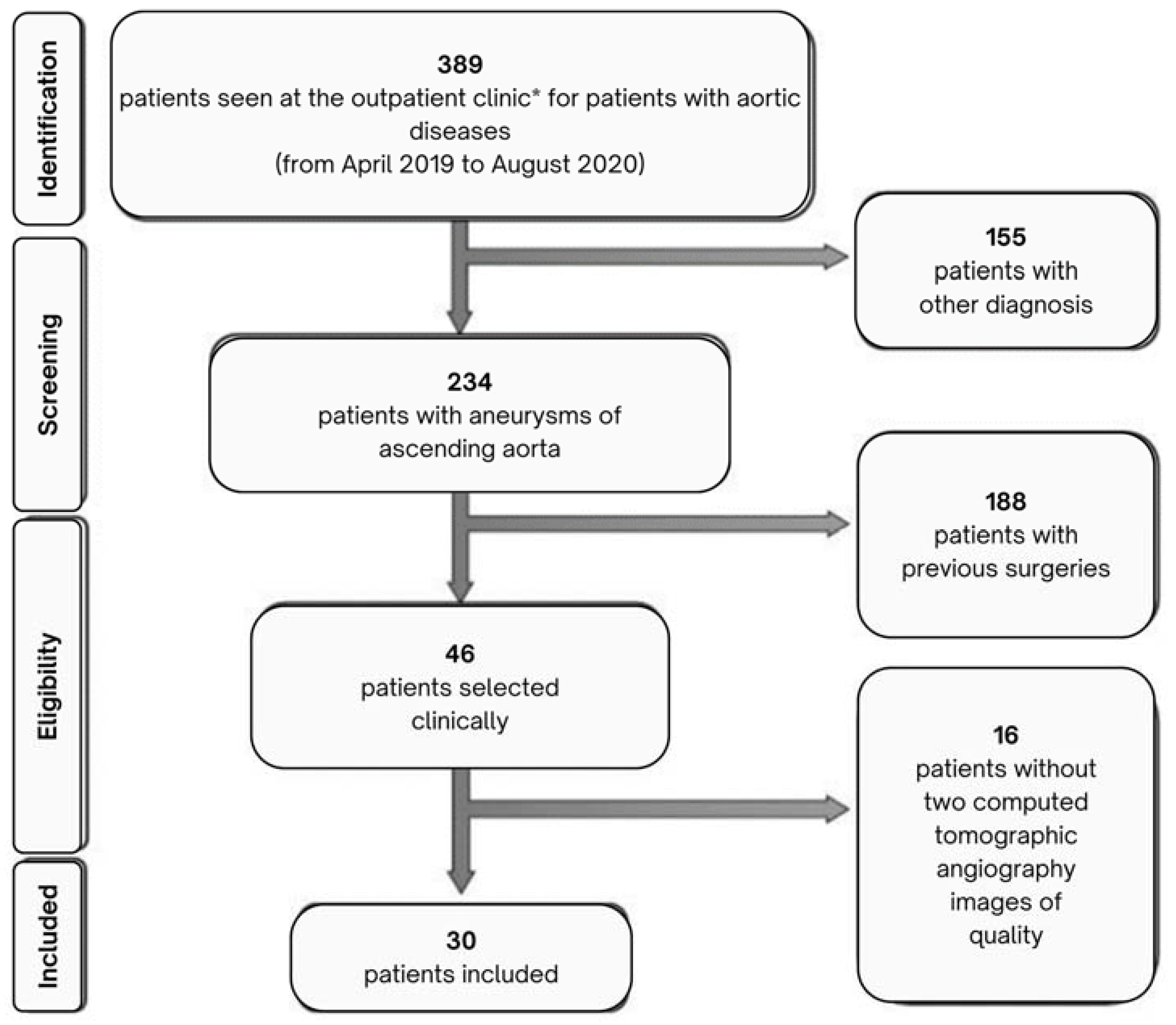
2.1. Patient Selection
2.2. Data Collection and Image Acquisition
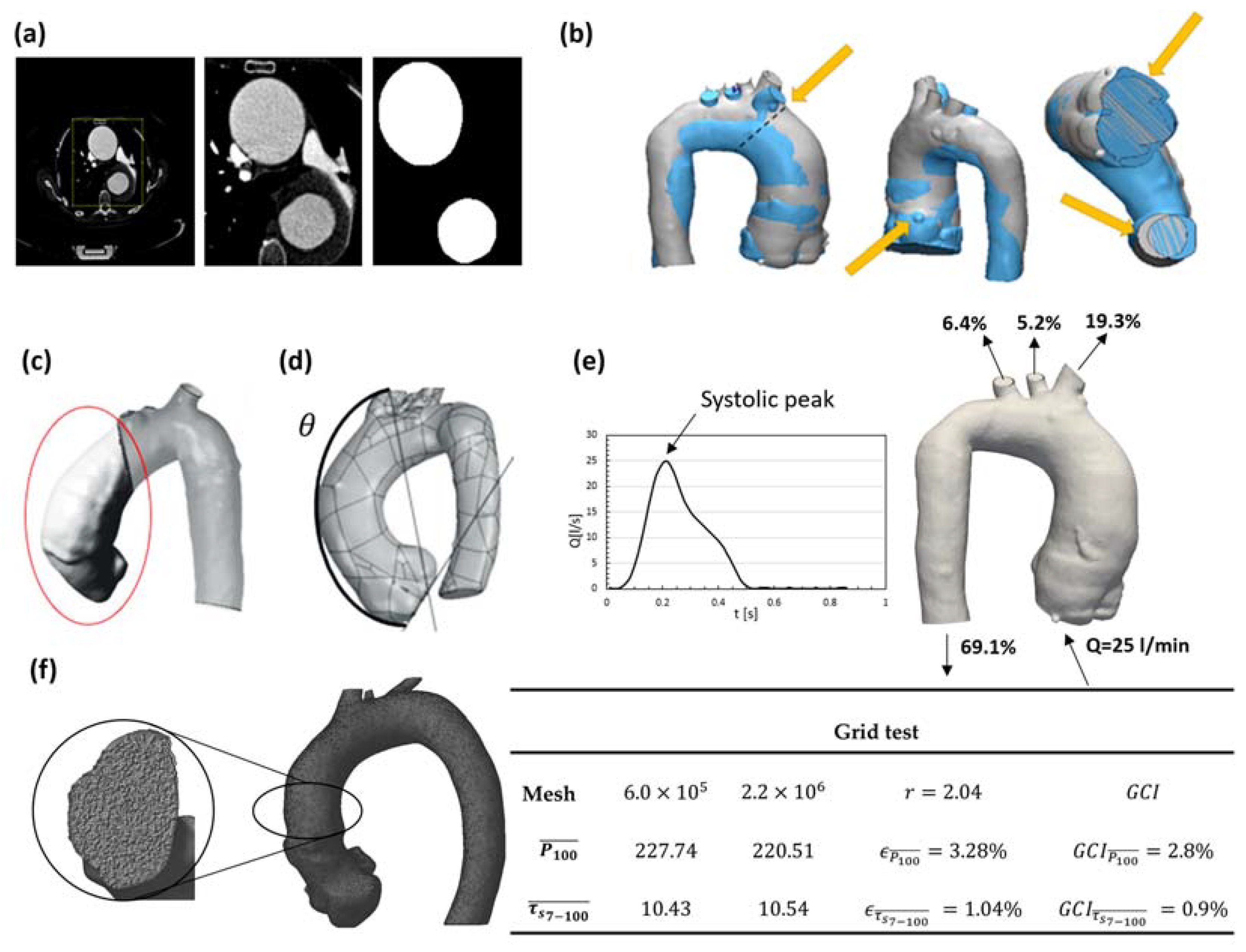
2.3. Geometry Segmentation and Three-Dimensional Computational Model
2.4. Patient Classification
2.5. Flow Modeling
2.6. Numerical Modeling
2.7. Postprocessing of the Data
2.8. Statistical Analysis
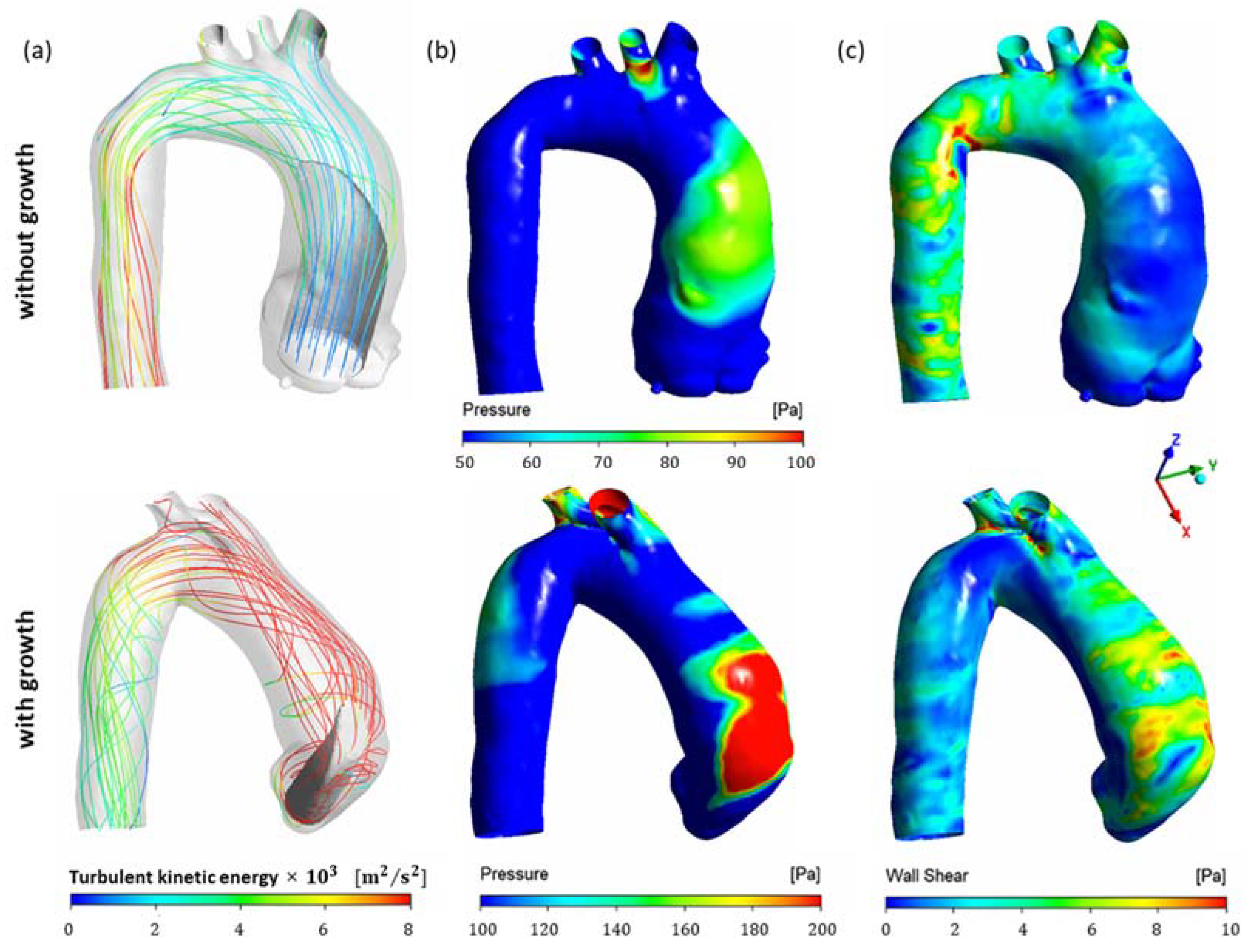
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vaduganathan, M.; Mensah, G.A.; Turco, J.V.; Fuster, V.; Roth, G.A. The Global Burden of Cardiovascular Diseases and Risk. J. Am. Coll. Cardiol. 2022, 80, 2361–2371. [Google Scholar] [CrossRef] [PubMed]
- Erbel, R.; Aboyans, V.; Boileau, C.; Bossone, E.; Bartolomeo, R.D.; Eggebrecht, H.; Evangelista, A.; Falk, V.; Frank, H.; Gaemperli, O.; et al. 2014 ESC Guidelines on the Diagnosis and Treatment of Aortic Diseases: Document Covering Acute and Chronic Aortic Diseases of the Thoracic and Abdominal Aorta of the Adult. The Task Force for the Diagnosis and Treatment of Aortic Diseases of the European Society of Cardiology (ESC). Eur. Heart J. 2014, 35, 2873–2926. [Google Scholar] [CrossRef] [PubMed]
- Isselbacher, E.M.; Preventza, O.; Black, J.H.; Augoustides, J.G.; Beck, A.W.; Bolen, M.A.; Braverman, A.C.; Bray, B.E.; Brown-Zimmerman, M.M.; Chen, E.P.; et al. 2022 ACC/AHA Guideline for the Diagnosis and Management of Aortic Disease: A Report of the American Heart Association/American College of Cardiology Joint Committee on Clinical Practice Guidelines. Circulation 2022, 146, e334–e482. [Google Scholar] [CrossRef] [PubMed]
- Dadras, R.; Jabbari, A.; Asl, N.K.; Soltani, M.; Rafiee, F.; Parsaee, M.; Golchin, S.; Pouraliakbar, H.; Sadeghipour, P.; Alimohammadi, M. In-Silico Investigations of Haemodynamic Parameters for a Blunt Thoracic Aortic Injury Case. Sci. Rep. 2023, 13, 8355. [Google Scholar] [CrossRef] [PubMed]
- Casas, B.; Lantz, J.; Viola, F.; Cedersund, G.; Bolger, A.F.; Carlhäll, C.-J.; Karlsson, M.; Ebbers, T. Bridging the Gap between Measurements and Modelling: A Cardiovascular Functional Avatar. Sci. Rep. 2017, 7, 6214. [Google Scholar] [CrossRef]
- Sadeghi, R.; Tomka, B.; Khodaei, S.; Daeian, M.; Gandhi, K.; Garcia, J.; Keshavarz-Motamed, Z. Impact of Extra-Anatomical Bypass on Coarctation Fluid Dynamics Using Patient-Specific Lumped Parameter and Lattice Boltzmann Modeling. Sci. Rep. 2022, 12, 9718. [Google Scholar] [CrossRef]
- Elefteriades, J.A.; Farkas, E.A. Thoracic Aortic Aneurysm Clinically Pertinent Controversies and Uncertainties. J. Am. Coll. Cardiol. 2010, 55, 841–857. [Google Scholar] [CrossRef]
- Harky, A.; Bashir, M.; Antoniou, A.; Francis, N.; Alhamdan, L.; Uppal, R. Size and Dissection: What Is the Relation? Indian J. Thorac. Cardiovasc. Surg. 2019, 35, 72–78. [Google Scholar] [CrossRef]
- den Hartog, A.W.; Franken, R.; de Witte, P.; Radonic, T.; Marquering, H.A.; van der Steen, W.E.; Timmermans, J.; Scholte, A.J.; van den Berg, M.P.; Zwinderman, A.H.; et al. Aortic Disease in Patients with Marfan Syndrome: Aortic Volume Assessment for Surveillance. Radiology 2013, 269, 370–377. [Google Scholar] [CrossRef] [PubMed]
- Renapurkar, R.D.; Setser, R.M.; O’Donnell, T.P.; Egger, J.; Lieber, M.L.; Desai, M.Y.; Stillman, A.E.; Schoenhagen, P.; Flamm, S.D. Aortic Volume as an Indicator of Disease Progression in Patients with Untreated Infrarenal Abdominal Aneurysm. Eur. J. Radiol. 2012, 81, e87–e93. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, M.L.; Vorp, D.A.; Federle, M.P.; Makaroun, M.S.; Webster, M.W. Wall Stress Distribution on Three-Dimensionally Reconstructed Models of Human Abdominal Aortic Aneurysm. J. Vasc. Surg. 2000, 31, 760–769. [Google Scholar] [CrossRef]
- Meyrignac, O.; Bal, L.; Zadro, C.; Vavasseur, A.; Sewonu, A.; Gaudry, M.; Saint-Lebes, B.; De Masi, M.; Revel-Mouroz, P.; Sommet, A.; et al. Combining Volumetric and Wall Shear Stress Analysis from CT to Assess Risk of Abdominal Aortic Aneurysm Progression. Radiology 2020, 295, 722–729. [Google Scholar] [CrossRef]
- Xiao, M.; Wu, J.; Chen, D.; Wang, C.; Wu, Y.; Sun, T.; Chen, J. Ascending Aortic Volume: A Feasible Indicator for Ascending Aortic Aneurysm Elective Surgery? Acta Biomater. 2023, 167, 100–108. [Google Scholar] [CrossRef]
- Guo, M.H.; Appoo, J.J.; Saczkowski, R.; Smith, H.N.; Ouzounian, M.; Gregory, A.J.; Herget, E.J.; Boodhwani, M. Association of Mortality and Acute Aortic Events with Ascending Aortic Aneurysm: A Systematic Review and Meta-Analysis. JAMA Netw. Open 2018, 1, e181281. [Google Scholar] [CrossRef] [PubMed]
- Landenhed, M.; Engström, G.; Gottsäter, A.; Caulfield, M.P.; Hedblad, B.; Newton-Cheh, C.; Melander, O.; Smith, J.G. Risk Profiles for Aortic Dissection and Ruptured or Surgically Treated Aneurysms: A Prospective Cohort Study. J. Am. Heart Assoc. 2015, 4, e001513. [Google Scholar] [CrossRef] [PubMed]
- Morris, P.D.; Narracott, A.; von Tengg-Kobligk, H.; Silva Soto, D.A.; Hsiao, S.; Lungu, A.; Evans, P.; Bressloff, N.W.; Lawford, P.V.; Hose, D.R.; et al. Computational Fluid Dynamics Modelling in Cardiovascular Medicine. Heart 2016, 102, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Chung, B.; Cebral, J.R. CFD for Evaluation and Treatment Planning of Aneurysms: Review of Proposed Clinical Uses and Their Challenges. Ann. Biomed. Eng. 2015, 43, 122–138. [Google Scholar] [CrossRef] [PubMed]
- Stokes, C.; Haupt, F.; Becker, D.; Muthurangu, V.; Von Tengg-Kobligk, H.; Balabani, S.; Díaz-Zuccarini, V. The Influence of Minor Aortic Branches in Patient-Specific Flow Simulations of Type-B Aortic Dissection. Ann. Biomed. Eng. 2023, 51, 1627–1644. [Google Scholar] [CrossRef]
- Bonfanti, M.; Franzetti, G.; Homer-Vanniasinkam, S.; Díaz-Zuccarini, V.; Balabani, S. A Combined In Vivo, In Vitro, In Silico Approach for Patient-Specific Haemodynamic Studies of Aortic Dissection. Ann. Biomed. Eng. 2020, 48, 2950–2964. [Google Scholar] [CrossRef]
- Moretti, S.; Tauro, F.; Orrico, M.; Mangialardi, N.; Facci, A.L. Comparative Analysis of Patient-Specific Aortic Dissections through Computational Fluid Dynamics Suggests Increased Likelihood of Degeneration in Partially Thrombosed False Lumen. Bioengineering 2023, 10, 316. [Google Scholar] [CrossRef]
- Ueda, T.; Suito, H.; Ota, H.; Takase, K. Computational Fluid Dynamics Modeling in Aortic Diseases. Cardiovasc. Imaging Asia 2018, 2, 58. [Google Scholar] [CrossRef][Green Version]
- Ong, C.W.; Wee, I.; Syn, N.; Ng, S.; Leo, H.L.; Richards, A.M.; Choong, A.M.T.L. Computational Fluid Dynamics Modeling of Hemodynamic Parameters in the Human Diseased Aorta: A Systematic Review. Ann. Vasc. Surg. 2020, 63, 336–381. [Google Scholar] [CrossRef]
- Aghilinejad, A.; Wei, H.; Magee, G.A.; Pahlevan, N.M. Model-Based Fluid-Structure Interaction Approach for Evaluation of Thoracic Endovascular Aortic Repair Endograft Length in Type B Aortic Dissection. Front. Bioeng. Biotechnol. 2022, 10, 825015. [Google Scholar] [CrossRef] [PubMed]
- Al-Jumaily, A.M.; Embong, A.H.B.; AL-Rawi, M.; Mahadevan, G.; Sugita, S. Aneurysm Rupture Prediction Based on Strain Energy-CFD Modelling. Bioengineering 2023, 10, 1231. [Google Scholar] [CrossRef]
- Simão, M.; Ferreira, J.; Tomás, A.C.; Fragata, J.; Ramos, H. Aorta Ascending Aneurysm Analysis Using CFD Models towards Possible Anomalies. Fluids 2017, 2, 31. [Google Scholar] [CrossRef]
- Almeida, C.G.; de Azevedo, B.A.; Azevedo, F.S.; Kalaun, K.; Ibanez, I.F.A.; Teixeira, P.S.; Gottlieb, I.; Melo, M.M.; de Oliveira, G.M.M.; Nieckele, A.O. Computational Fluid Dynamics to Assess the Future Risk of Ascending Aortic Aneurysms. Arq. Bras. Cardiol. 2022, 118, 448–460. [Google Scholar] [CrossRef] [PubMed]
- Salmasi, M.Y.; Pirola, S.; Mahuttanatan, S.; Fisichella, S.M.; Sengupta, S.; Jarral, O.A.; Oo, A.; O’Regan, D.; Xu, X.Y.; Athanasiou, T. Geometry and Flow in Ascending Aortic Aneurysms Are Influenced by Left Ventricular Outflow Tract Orientation: Detecting Increased Wall Shear Stress on the Outer Curve of Proximal Aortic Aneurysms. J. Thorac. Cardiovasc. Surg. 2023, 166, 11–21.e1. [Google Scholar] [CrossRef] [PubMed]
- Salmasi, M.Y.; Pirola, S.; Sasidharan, S.; Fisichella, S.M.; Redaelli, A.; Jarral, O.A.; O’Regan, D.P.; Oo, A.Y.; Moore, J.E.; Xu, X.Y.; et al. High Wall Shear Stress Can Predict Wall Degradation in Ascending Aortic Aneurysms: An Integrated Biomechanics Study. Front. Bioeng. Biotechnol. 2021, 9, 750656. [Google Scholar] [CrossRef] [PubMed]
- Boczar, K.E.; Boodhwani, M.; Beauchesne, L.; Dennie, C.; Chan, K.L.; Wells, G.A.; Coutinho, T. Aortic Stiffness, Central Blood Pressure, and Pulsatile Arterial Load Predict Future Thoracic Aortic Aneurysm Expansion. Hypertension 2021, 77, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Mirsadraee, S.; Asimakopoulos, G.; Gambaro, A.; Rosendahl, U.; Pepper, J.; Xu, X.Y. Association of Hemodynamic Factors and Progressive Aortic Dilatation Following Type A Aortic Dissection Surgical Repair. Sci. Rep. 2021, 11, 11521. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An Open-Source Platform for Biological-Image Analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Ibanez, I.; de Azevedo, B.A.; Nieckele, A.O. Effect of Percutaneous Aortic Valve Position on Stress Map in Ascending Aorta: A Fluid-Structure Interaction Analysis. Artif. Organs 2021, 45, O195–O206. [Google Scholar] [CrossRef] [PubMed]
- Long, D.S.; Smith, M.L.; Pries, A.R.; Ley, K.; Damiano, E.R. Microviscometry Reveals Reduced Blood Viscosity and Altered Shear Rate and Shear Stress Profiles in Microvessels after Hemodilution. Proc. Natl. Acad. Sci. USA 2004, 101, 10060–10065. [Google Scholar] [CrossRef] [PubMed]
- Thomas, B.; Sumam, K.S. Blood Flow in Human Arterial System-A Review. Procedia Technol. 2016, 24, 339–346. [Google Scholar] [CrossRef]
- Almeida, G.C.; Azevedo, B.N.; Silva, J.A.; Ibanez, I.F.A.; de Azevedo, B.A.; Nieckele, A.O.; Azevedo, F.S.; Oliveira, G.M.M. Impact of Viscosity on Blood Flow in Ascending Aortic Aneurysm. In Proceedings of the 26th International Congress of Mechanical Engineering, Florianópolis, Brazil, 22–26 November 2021. [Google Scholar] [CrossRef]
- Perocco, E.L.M. Analysis of the Blood Flow during the Cardiac Cycle in the Ascending Aorta. Master’s Thesis, Pontifical Catholic University of Rio de Janeiro, Rio de Janeiro, RJ, Brazil, 2022. [Google Scholar] [CrossRef]
- Malvindi, P.G.; Pasta, S.; Raffa, G.M.; Livesey, S. Computational Fluid Dynamics of the Ascending Aorta before the Onset of Type A Aortic Dissection. Eur. J. Cardio-Thorac. Surg. 2017, 51, 597–599. [Google Scholar] [CrossRef] [PubMed]
- Hellmeier, F.; Nordmeyer, S.; Yevtushenko, P.; Bruening, J.; Berger, F.; Kuehne, T.; Goubergrits, L.; Kelm, M. Hemodynamic Evaluation of a Biological and Mechanical Aortic Valve Prosthesis Using Patient-Specific MRI-Based CFD. Artif. Organs 2018, 42, 49–57. [Google Scholar] [CrossRef] [PubMed]
- May-Newman, K.; Hillen, B.; Dembitsky, W. Effect of Left Ventricular Assist Device Outflow Conduit Anastomosis Location on Flow Patterns in the Native Aorta. ASAIO J. 2006, 52, 132. [Google Scholar] [CrossRef] [PubMed]
- Geers, A.J.; Larrabide, I.; Morales, H.G.; Frangi, A.F. Comparison of Steady-State and Transient Blood Flow Simulations of Intracranial Aneurysms. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August 2010; pp. 2622–2625. Available online: https://academia.edu/download/53011957/Comparison_of_Steady-State_and_Transient20170505-3483-z401k3.pdf (accessed on 3 November 2023).
- Armour, C.H.; Guo, B.; Pirola, S.; Saitta, S.; Liu, Y.; Dong, Z.; Xu, X.Y. The Influence of Inlet Velocity Profile on Predicted Flow in Type B Aortic Dissection. Biomech. Model. Mechanobiol. 2021, 20, 481–490. [Google Scholar] [CrossRef]
- Saqr, K.M.; Tupin, S.; Rashad, S.; Endo, T.; Niizuma, K.; Tominaga, T.; Ohta, M. Physiologic Blood Flow Is Turbulent. Sci. Rep. 2020, 10, 15492. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Celis, D.F.T. Numerical Study of the Influence of Tilt Valve Angle on Blood Flow in an Aortic Model. Master’s Thesis, Pontifical Catholic University of Rio de Janeiro, Rio de Janeiro, RJ, Brazil, 2017. [Google Scholar] [CrossRef]
- de Azevedo, B.A.; Camargo, G.C.; dos Santos, J.R.L.; Azevedo, L.F.A.; Nieckele, A.O.; Siqueira-Filho, A.G.; de Oliveira, G.M.M. Influence of the Tilt Angle of Percutaneous Aortic Prosthesis on Velocity and Shear Stress Fields. Arq. Bras. Cardiol. 2017, 109, 231–240. [Google Scholar] [CrossRef]
- Madhavan, S.; Kemmerling, E.M.C. The Effect of Inlet and Outlet Boundary Conditions in Image-Based CFD Modeling of Aortic Flow. BioMed. Eng. OnLine 2018, 17, 66. [Google Scholar] [CrossRef] [PubMed]
- Alastruey, J.; Xiao, N.; Fok, H.; Schaeffter, T.; Figueroa, C.A. On the Impact of Modelling Assumptions in Multi-Scale, Subject-Specific Models of Aortic Haemodynamics. J. R. Soc. Interface 2016, 13, 20160073. [Google Scholar] [CrossRef] [PubMed]
- Faggiano, E.; Antiga, L.; Puppini, G.; Quarteroni, A.; Luciani, G.B.; Vergara, C. Helical Flows and Asymmetry of Blood Jet in Dilated Ascending Aorta with Normally Functioning Bicuspid Valve. Biomech. Model. Mechanobiol. 2013, 12, 801–813. [Google Scholar] [CrossRef]
- ANSYS, Inc. Ansys® Fluent, Release 1, Help System; User Guide Full 2020; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure of Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications–ScienceOpen. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Etli, M.; Canbolat, G.; Karahan, O.; Koru, M. Numerical Investigation of Patient-Specific Thoracic Aortic Aneurysms and Comparison with Normal Subject via Computational Fluid Dynamics (CFD). Med. Biol. Eng. Comput. 2021, 59, 71–84. [Google Scholar] [CrossRef] [PubMed]
- Rosner, B. Fundamentals of Biostatistics, 8th ed.; Cengage Learning: Boston, MA, USA, 2015; ISBN 978-1-305-26892-0. [Google Scholar]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Goldman, L.; Hashimoto, B.; Cook, E.F.; Loscalzo, A. Comparative Reproducibility and Validity of Systems for Assessing Cardiovascular Functional Class: Advantages of a New Specific Activity Scale. Circulation 1981, 64, 1227–1234. [Google Scholar] [CrossRef]
- Febina, J.; Sikkandar, M.Y.; Sudharsan, N.M. Wall Shear Stress Estimation of Thoracic Aortic Aneurysm Using Computational Fluid Dynamics. Comput. Math. Methods Med. 2018, 2018, 7126532. [Google Scholar] [CrossRef]
- Davies, P.F. Hemodynamic Shear Stress and the Endothelium in Cardiovascular Pathophysiology. Nat. Rev. Cardiol. 2009, 6, 16–26. [Google Scholar] [CrossRef]
- Mohamied, Y.; Rowland, E.M.; Bailey, E.L.; Sherwin, S.J.; Schwartz, M.A.; Weinberg, P.D. Change of Direction in the Biomechanics of Atherosclerosis. Ann. Biomed. Eng. 2015, 43, 16–25. [Google Scholar] [CrossRef]
- Caballero, A.D.; Laín, S. A Review on Computational Fluid Dynamics Modelling in Human Thoracic Aorta. Cardiovasc. Eng. Technol. 2013, 2, 103–130. [Google Scholar] [CrossRef]
- Petuchova, A.; Maknickas, A. Computational Analysis of Aortic Haemodynamics in the Presence of Ascending Aortic Aneurysm. Technol. Health Care 2022, 30, 187–200. [Google Scholar] [CrossRef]
- Taebi, A. Deep Learning for Computational Hemodynamics: A Brief Review of Recent Advances. Fluids 2022, 7, 197. [Google Scholar] [CrossRef]
- Kadem, M.; Garber, L.; Abdelkhalek, M.; Al-Khazraji, B.K.; Keshavarz-Motamed, Z. Hemodynamic Modeling, Medical Imaging, and Machine Learning and Their Applications to Cardiovascular Interventions. IEEE Rev. Biomed. Eng. 2023, 16, 403–423. [Google Scholar] [CrossRef]

| Variables | Total (n) | Values | Growth | p Value | |||
|---|---|---|---|---|---|---|---|
| No | Yes | ||||||
| Clinical data | Sex | Male—n (%) | 20 | 20 (66.7) | 10 (33.3) | 10 (33.3) | 0.709 |
| Female—n (%) | 10 | 10 (33.3) | 4 (13.3) | 6 (20) | |||
| Age (years)—mean ± SD | 30 | 64.5 ± 10.6 | 62.9 ± 12.3 (n = 14) | 65.9 ± 9 (n = 16) | 0.453 | ||
| Interval between CTAs (years)—mean ± SD | 30 | 1.9 ± 0.7 | 1.6 ± 0.7 (n = 13) | 2.1 ± 0.7 (n = 16) | 0.127 | ||
| Hypertension—n (%) | 28 | 24 (85.7) | 12 (42.9) | 12 (42.9) | 1.000 | ||
| Diabetes mellitus—n (%) | 28 | 7 (25) | 2 (7.1) | 5 (17.9) | 0.385 | ||
| Dyslipidemia—n (%) | 27 | 16 (59.3) | 8 (29.6) | 8 (29.6) | 1.000 | ||
| Chronic renal failure—n (%) | 28 | 4 (14.3) | 1 (3.6) | 3 (10.7) | 2.596 | ||
| Atrial fibrillation—n (%) | 28 | 6 (21.4) | 2 (7.1) | 4 (14.3) | 0.648 | ||
| Current or previous smoking—n (%) | 26 | 12 (46.1) | 5 (19.2) | 7 (26.9) | 0.695 | ||
| COPD—n (%) | 25 | 2 (8) | 0 (0) | 2 (8) | 0.480 | ||
| Obstructive CAD—n (%) | 27 | 6 (22.2) | 3 (11.1) | 3 (11.1) | 1.000 | ||
| Previous myocardial infarction—n (%) | 27 | 3 (11.1) | 2 (7.4) | 1 (3.7) | 1.000 | ||
| Stroke—n (%) | 28 | 2 (7.1) | 1 (3.6) | 1 (3.6) | 1.000 | ||
| Heart disease | Ischemic—n (%) | 28 | 5 (17.9) | 3 (10.7) | 2 (7.1) | 0.819 | |
| Valvar—n (%) | 5 (17.9) | 2 (7.1) | 3 (10.7) | ||||
| SBP (mmHg)—median [IQR] | 24 | 127 [120–140] | 132 [120–140] (n = 12) | 120 [120–130] (n = 12) | 0.875 | ||
| DBP (mmHg)—median [IQR] | 24 | 80 [70–80] | 80 [71.5–80] (n = 12) | 80 [70–82.5] (n = 12) | 0.200 | ||
| Heart rate (bpm)—mean ± SD | 23 | 67.2 ± 10.3 | 65.8 ± 9.9 (n = 11) | 68.4 ± 10.9 (n = 12) | 0.558 | ||
| Serum creatinine (mg/dL)—mean ± SD | 30 | 1.06 ± 0.34 | 1.01 ± 0.37 (n = 14) | 1.08 ± 0.32 (n = 16) | 0.691 | ||
| Echocardiographic data | LV EF (Teicholz, %)—mean ± SD | 29 | 64.6 ± 10.9 | 68.5 ± 6.5 (n = 14) | 60.9 ± 13 (n = 15) | 0.061 | |
| SDiam, LV (mm)—mean ± SD | 29 | 32.5 ± 6.2 | 30.5 ± 5 (n = 14) | 34.3 ± 6.8 (n = 15) | 0.097 | ||
| DDiam, LV (mm)—mean ± SD | 29 | 51.2 ± 6.8 | 50.7 ± 7.8 (n = 14) | 51.6 ± 6.1 (n = 15) | 0.734 | ||
| Septum (mm)—mean ± SD | 28 | 10.1 ± 1.6 | 9.6 ± 1.5 (n = 14) | 10.6 ± 1.5 (n = 14) | 0.120 | ||
| Posterior wall (mm)—mean ± SD | 28 | 9.4 ± 1.2 | 9.5 ± 1.2 (n = 14) | 9.3 ± 1.3 (n = 14) | 0.653 | ||
| Aorta (mm)—median [IQR] | 28 | 42 [35.7–49] | 42.5 [41.2–48] (n = 14) | 36.5 [32.2–49] (n = 14) | 0.112 | ||
| Left atrium (mm)—mean ± SD | 28 | 35.9 ± 6.8 | 34 ± 8.1 (n = 14) | 37.9 ± 4.7 (n = 14) | 0.136 | ||
| Aortic regurgitation | Absent or mild—n (%) | 29 | 18 (62) | 11 (37.9) | 7 (24.1) | 0.072 | |
| Moderate—n (%) | 7 (24.1) | 3 (10.3) | 4 (13.8) | ||||
| Severe—n (%) | 4 (13.8) | 0 (0) | 4 (13.8) | ||||
| Aortic stenosis | Absent or mild—n (%) | 29 | 27 (93.1) | 13 (44.7) | 14 (48.3) | 0.861 | |
| Severe—n (%) | 2 (6.9) | 1 (3.4) | 1 (3.4) | ||||
| Volume of the Ascending Aorta | Values (30 Patients) | Growth | p Value | |
|---|---|---|---|---|
| No (14 Patients) | Yes (16 Patients) | |||
| Volume first CTA (cm3)—median [IQR] | 143.80 [126.67–168.18] | 141.90 [127.38–164.75] | 149.28 [127.82–168.80] | 0.324 |
| Volume second CTA (cm3)—median [IQR] | 149.85 [123.32–176.45] | 132.73 [119.63–164.03] | 168.71 [144.35–191.12] | 0.006 |
| Percentile volume variation between the first and second CTA—mean ± SD | 4.53 ± 10.40 | [(−4.83) ± (5.86)] | 12.71 ± 5.20 | 0.004 |
| Maximum diameter at first CTA (cm)—mean ± SD | 50.41 ± 3.49 | 49.73 ± 3.89 | 51.01 ± 3.10 | - |
| Maximum diameter at second CTA (cm)—mean ± SD | 52.36 ± 5.17 | 49.71 ± 4.45 | 54.68 ± 4.71 | - |
| Diameter variation between the first and second CTA—mean ± SD | 1.65 [0.00–3.57] | 0.50 [(−1.00)–(1.22)] | 3.38 [1.50–5.00] | - |
| Variables | Stress (Pa) | Total (n) | First CTA Mean ± Standard Deviation | Growth | p Value | ||
|---|---|---|---|---|---|---|---|
| No | Yes | ||||||
| Pressure ≥100 Pa | Mean | 30 | 174.4 ± 51.4 | 154.1 ± 29.5 (n = 14) | 192.2 ± 60.3 (n = 16) | 0.041 | |
| Maximum | 30 | 321.0 ± 181.2 | 249.6 ± 100.5 (n = 14) | 383.4 ± 214.0 (n = 16) | 0.041 | ||
| Shear stress ≥5 Pa and ≥7 Pa | Mean | 30 | 7.1 ± 1.1 | 6.7 ± 0.7 (n = 14) | 7.4 ± 1.3 (n = 16) | 0.093 | |
| 30 | 8.9 ± 1.0 | 8.6 ± 0.7 (n = 14) | 9.1 ± 1.1 (n = 16) | 0.109 | |||
| Maximum | 30 | 18.5 ± 6.6 | 17.5 ± 6 (n = 14) | 19.5 ± 7.1 (n = 16) | 0.415 | ||
| 30 | 18.5 ± 6.6 | 17.5 ± 6 (n = 14) | 19.5 ± 7.1 (n = 16) | 0.415 | |||
| Intersection region | Mean value at intersection | 26 | 7 ± 1.3 | 6.5 ± 0.7 (n = 11) | 7.4 ± 1.4 (n = 15) | 0.063 | |
| 26 | 8.7 ± 1.1 | 8.2 ± 0.8 (n = 12) | 9.2 ± 1.2 (n = 14) | 0.023 | |||
| Maximum value at intersection | 27 | 15.8 ± 6.0 | 13.7 ± 4.5 (n = 12) | 17.5 ± 6.6 (n = 15) | 0.098 | ||
| 26 | 16.2 ± 5.9 | 13.6 ± 4.6 (n = 12) | 18.3 ± 6.2 (n = 14) | 0.041 | |||
| Variables from the First CTA × Δt | OR (95% CI) | p Value |
|---|---|---|
| 1.006 (CI: 1.000–1.013) | 0.057 | |
| 1.003 (CI: 1.000–1.006) | 0.042 | |
| 1.090 (CI: 0.946–1.250) | 0.241 | |
| 1.050 (CI: 0.985–1.110) | 0.138 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Azevedo, F.S.; Almeida, G.d.C.; Alvares de Azevedo, B.; Ibanez Aguilar, I.F.; Azevedo, B.N.; Teixeira, P.S.; Camargo, G.C.; Correia, M.G.; Nieckele, A.O.; Oliveira, G.M.M. Stress Load and Ascending Aortic Aneurysms: An Observational, Longitudinal, Single-Center Study Using Computational Fluid Dynamics. Bioengineering 2024, 11, 204. https://doi.org/10.3390/bioengineering11030204
de Azevedo FS, Almeida GdC, Alvares de Azevedo B, Ibanez Aguilar IF, Azevedo BN, Teixeira PS, Camargo GC, Correia MG, Nieckele AO, Oliveira GMM. Stress Load and Ascending Aortic Aneurysms: An Observational, Longitudinal, Single-Center Study Using Computational Fluid Dynamics. Bioengineering. 2024; 11(3):204. https://doi.org/10.3390/bioengineering11030204
Chicago/Turabian Stylede Azevedo, Fabiula Schwartz, Gabriela de Castro Almeida, Bruno Alvares de Azevedo, Ivan Fernney Ibanez Aguilar, Bruno Nieckele Azevedo, Pedro Soares Teixeira, Gabriel Cordeiro Camargo, Marcelo Goulart Correia, Angela Ourivio Nieckele, and Glaucia Maria Moraes Oliveira. 2024. "Stress Load and Ascending Aortic Aneurysms: An Observational, Longitudinal, Single-Center Study Using Computational Fluid Dynamics" Bioengineering 11, no. 3: 204. https://doi.org/10.3390/bioengineering11030204
APA Stylede Azevedo, F. S., Almeida, G. d. C., Alvares de Azevedo, B., Ibanez Aguilar, I. F., Azevedo, B. N., Teixeira, P. S., Camargo, G. C., Correia, M. G., Nieckele, A. O., & Oliveira, G. M. M. (2024). Stress Load and Ascending Aortic Aneurysms: An Observational, Longitudinal, Single-Center Study Using Computational Fluid Dynamics. Bioengineering, 11(3), 204. https://doi.org/10.3390/bioengineering11030204