Development of End-to-End Artificial Intelligence Models for Surgical Planning in Transforaminal Lumbar Interbody Fusion
Abstract
1. Introduction
2. Materials and Methods
2.1. Patient Selection
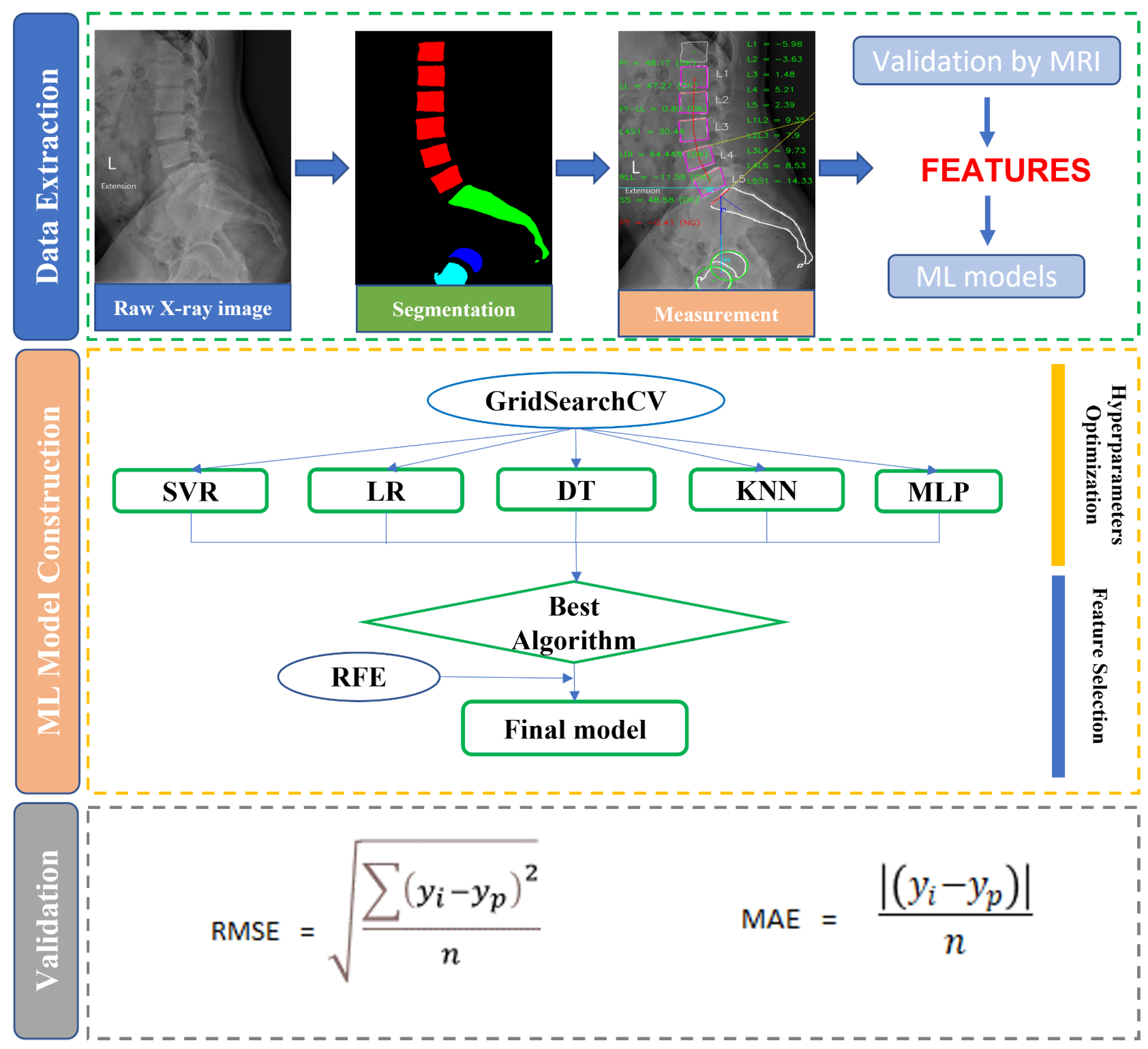
2.2. X-ray Segmentation and Feature Extraction
2.3. ML Implementation
2.3.1. Data Preprocessing
2.3.2. Regression Models
2.4. Statistical Analysis and Measurement Metrics
3. Results
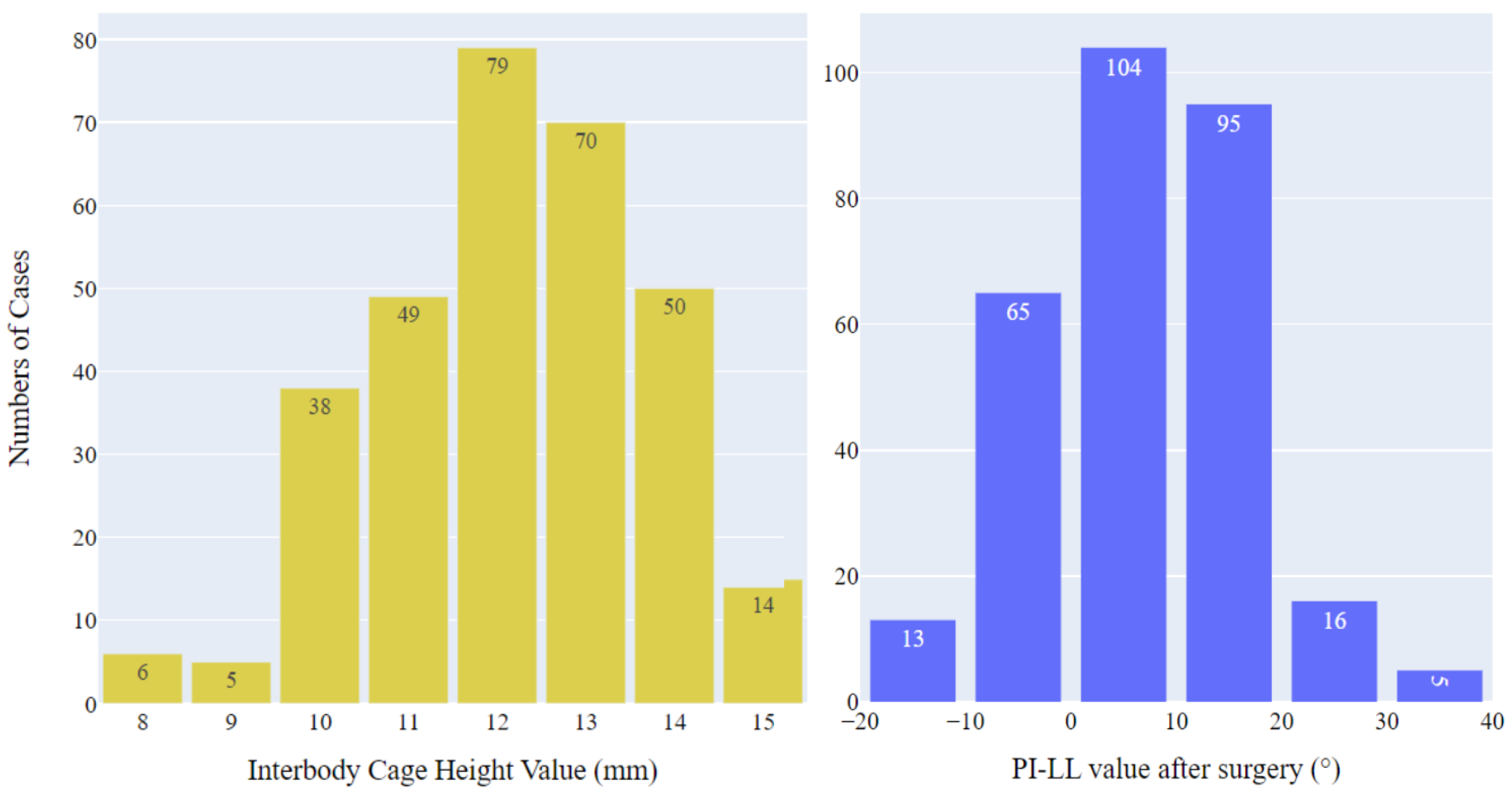
3.1. Patient Characteristics
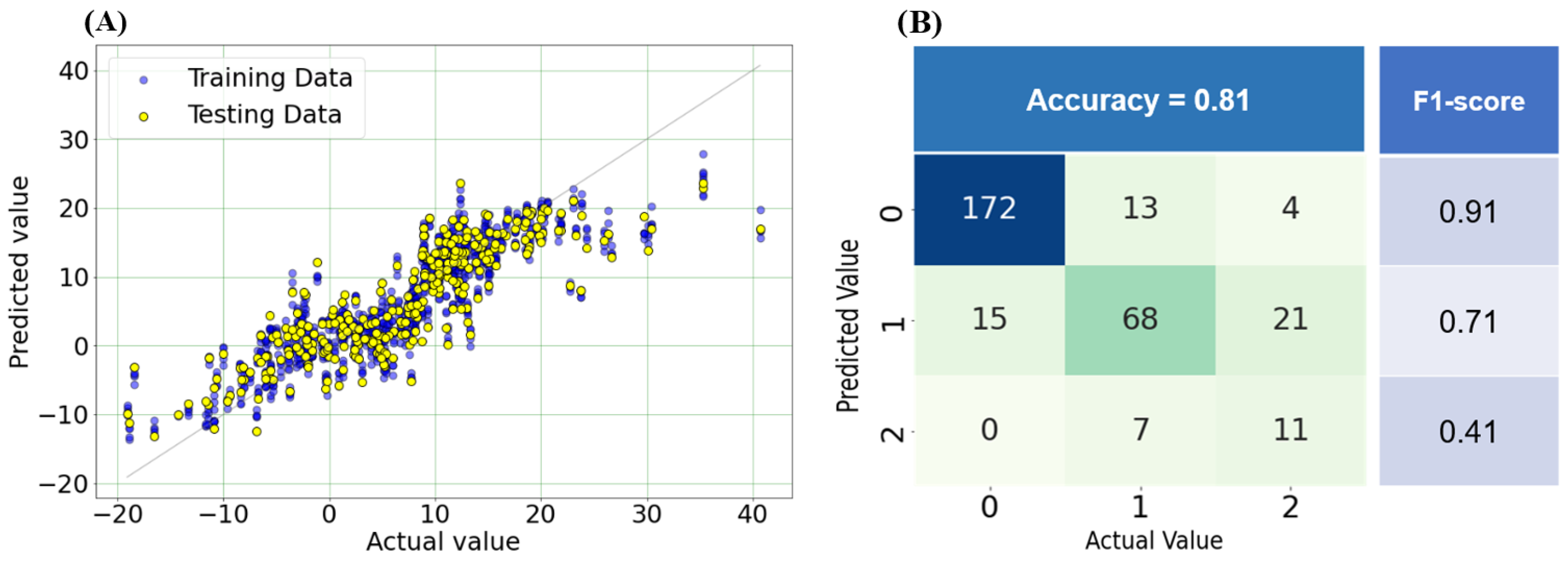
3.2. Performance of ML Algorithms
3.3. Final Model
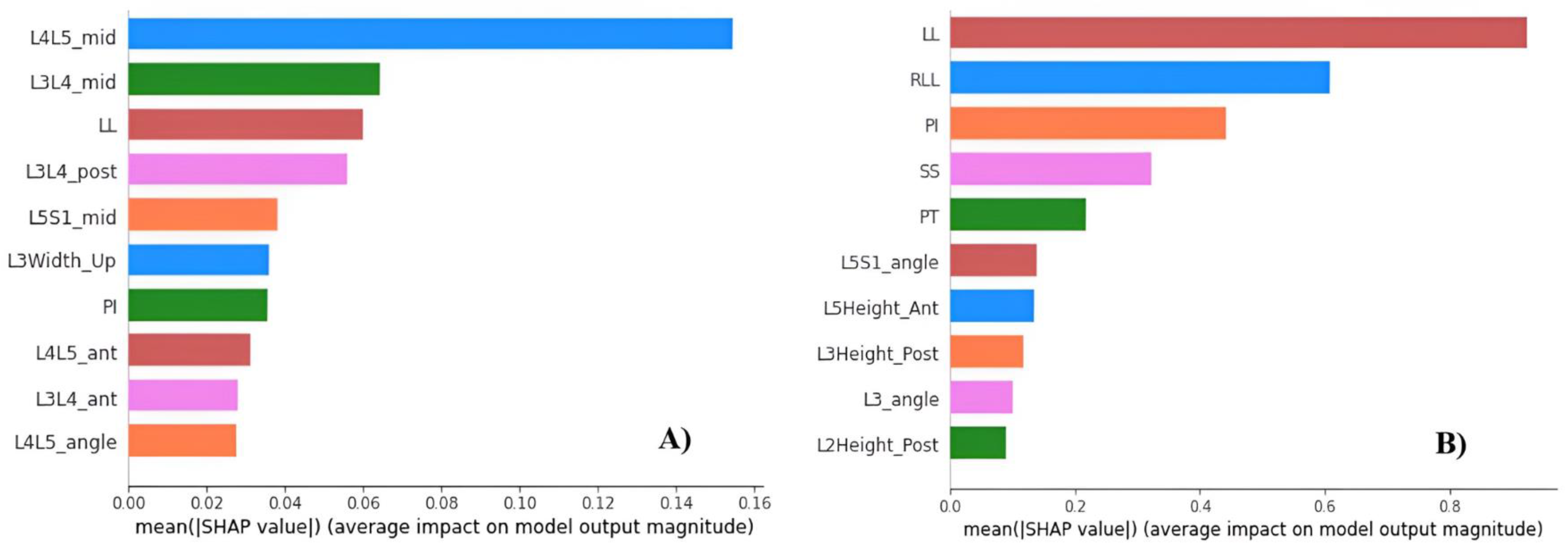
3.3.1. Feature Selection
3.3.2. Optimal Model Performance
3.3.3. Feature Importance
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mummaneni, P.V.; Dhall, S.S.; Eck, J.C.; Groff, M.W.; Ghogawala, Z.; Watters, W.C., 3rd; Dailey, A.T.; Resnick, D.K.; Choudhri, T.F.; Sharan, A.; et al. Guideline update for the performance of fusion procedures for degenerative disease of the lumbar spine. Part 11: Interbody techniques for lumbar fusion. J. Neurosurg. Spine 2014, 21, 67–74. [Google Scholar] [CrossRef]
- Noshchenko, A.; Hoffecker, L.; Lindley, E.M.; Burger, E.L.; Cain, C.M.; Patel, V.V. Perioperative and long-term clinical outcomes for bone morphogenetic protein versus iliac crest bone graft for lumbar fusion in degenerative disk disease: Systematic review with meta-analysis. J. Spinal Disord. Tech. 2014, 27, 117–135. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, F.; Chen, Q. Transforaminal lumbar interbody fusion with one cage and excised local bone. Arch. Orthop. Trauma Surg. 2010, 130, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Ould-Slimane, M.; Lenoir, T.; Dauzac, C.; Rillardon, L.; Hoffmann, E.; Guigui, P.; Ilharreborde, B. Influence of transforaminal lumbar interbody fusion procedures on spinal and pelvic parameters of sagittal balance. Eur. Spine J. 2012, 21, 1200–1206. [Google Scholar] [CrossRef]
- Watkins, R.G.t.; Hanna, R.; Chang, D.; Watkins, R.G., 3rd. Sagittal alignment after lumbar interbody fusion: Comparing anterior, lateral, and transforaminal approaches. J. Spinal Disord. Tech. 2014, 27, 253–256. [Google Scholar] [CrossRef]
- Yamasaki, K.; Hoshino, M.; Omori, K.; Igarashi, H.; Nemoto, Y.; Tsuruta, T.; Matsumoto, K.; Iriuchishima, T.; Ajiro, Y.; Matsuzaki, H. Risk Factors of Adjacent Segment Disease After Transforaminal Inter-Body Fusion for Degenerative Lumbar Disease. Spine 2017, 42, E86–E92. [Google Scholar] [CrossRef]
- Rothenfluh, D.A.; Mueller, D.A.; Rothenfluh, E.; Min, K. Pelvic incidence-lumbar lordosis mismatch predisposes to adjacent segment disease after lumbar spinal fusion. Eur. Spine J. 2015, 24, 1251–1258. [Google Scholar] [CrossRef]
- Aoki, Y.; Nakajima, A.; Takahashi, H.; Sonobe, M.; Terajima, F.; Saito, M.; Takahashi, K.; Ohtori, S.; Watanabe, A.; Nakajima, T.; et al. Influence of pelvic incidence-lumbar lordosis mismatch on surgical outcomes of short-segment transforaminal lumbar interbody fusion. BMC Musculoskelet. Disord. 2015, 16, 213. [Google Scholar] [CrossRef] [PubMed]
- Senteler, M.; Weisse, B.; Snedeker, J.G.; Rothenfluh, D.A. Pelvic incidence-lumbar lordosis mismatch results in increased segmental joint loads in the unfused and fused lumbar spine. Eur. Spine J. 2014, 23, 1384–1393. [Google Scholar] [CrossRef] [PubMed]
- Ailon, T.; Scheer, J.K.; Lafage, V.; Schwab, F.J.; Klineberg, E.; Sciubba, D.M.; Protopsaltis, T.S.; Zebala, L.; Hostin, R.; Obeid, I.; et al. Adult Spinal Deformity Surgeons Are Unable to Accurately Predict Postoperative Spinal Alignment Using Clinical Judgment Alone. Spine Deform. 2016, 4, 323–329. [Google Scholar] [CrossRef]
- Lafage, V.; Schwab, F.; Vira, S.; Patel, A.; Ungar, B.; Farcy, J.P. Spino-pelvic parameters after surgery can be predicted: A preliminary formula and validation of standing alignment. Spine 2011, 36, 1037–1045. [Google Scholar] [CrossRef]
- Lafage, R.; Pesenti, S.; Lafage, V.; Schwab, F.J. Self-learning computers for surgical planning and prediction of postoperative alignment. Eur. Spine J. 2018, 27, 123–128. [Google Scholar] [CrossRef]
- Abbushi, A.; Cabraja, M.; Thomale, U.W.; Woiciechowsky, C.; Kroppenstedt, S.N. The influence of cage positioning and cage type on cage migration and fusion rates in patients with monosegmental posterior lumbar interbody fusion and posterior fixation. Eur. Spine J. 2009, 18, 1621–1628. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Zhu, Y.; Ding, W.; Wang, Q. Incidence and risk factors of posterior cage migration following decompression and instrumented fusion for degenerative lumbar disorders. Medicine 2017, 96, e7804. [Google Scholar] [CrossRef] [PubMed]
- Aoki, Y.; Yamagata, M.; Nakajima, F.; Ikeda, Y.; Shimizu, K.; Yoshihara, M.; Iwasaki, J.; Toyone, T.; Nakagawa, K.; Nakajima, A.; et al. Examining risk factors for posterior migration of fusion cages following transforaminal lumbar interbody fusion: A possible limitation of unilateral pedicle screw fixation. J. Neurosurg. Spine 2010, 13, 381–387. [Google Scholar] [CrossRef]
- Wang, H.; Chen, W.; Jiang, J.; Lu, F.; Ma, X.; Xia, X. Analysis of the correlative factors in the selection of interbody fusion cage height in transforaminal lumbar interbody fusion. BMC Musculoskelet. Disord. 2016, 17, 9. [Google Scholar] [CrossRef]
- Makino, T.; Honda, H.; Fujiwara, H.; Yoshikawa, H.; Yonenobu, K.; Kaito, T. Low incidence of adjacent segment disease after posterior lumbar interbody fusion with minimum disc distraction: A preliminary report. Medicine 2018, 97, e9631. [Google Scholar] [CrossRef]
- Landham, P.R.; Don, A.S.; Robertson, P.A. Do position and size matter? An analysis of cage and placement variables for optimum lordosis in PLIF reconstruction. Eur. Spine J. 2017, 26, 2843–2850. [Google Scholar] [CrossRef] [PubMed]
- Cho, B.H.; Kaji, D.; Cheung, Z.B.; Ye, I.B.; Tang, R.; Ahn, A.; Carrillo, O.; Schwartz, J.T.; Valliani, A.A.; Oermann, E.K.; et al. Automated Measurement of Lumbar Lordosis on Radiographs Using Machine Learning and Computer Vision. Global Spine J. 2020, 10, 611–618. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Fan, T.; Yang, B.; Lin, Q.; Li, W.; Yang, M. Development and Internal Validation of Supervised Machine Learning Algorithms for Predicting the Risk of Surgical Site Infection Following Minimally Invasive Transforaminal Lumbar Interbody Fusion. Front. Med. 2021, 8, 771608. [Google Scholar] [CrossRef] [PubMed]
- Etzel, C.M.; Veeramani, A.; Zhang, A.S.; McDonald, C.L.; DiSilvestro, K.J.; Cohen, E.M.; Daniels, A.H. Supervised Machine Learning for Predicting Length of Stay After Lumbar Arthrodesis: A Comprehensive Artificial Intelligence Approach. J. Am. Acad. Orthop. Surg. 2022, 30, 125–132. [Google Scholar] [CrossRef]
- Misir, A.; Kizkapan, T.B.; Tas, S.K.; Yildiz, K.I.; Ozcamdalli, M.; Yetis, M. Lumbar spine posture and spinopelvic parameters change in various standing and sitting postures. Eur. Spine J. 2019, 28, 1072–1081. [Google Scholar] [CrossRef] [PubMed]
- Lim, T.K.; Lee, S.G.; Park, C.W.; Kim, W.K.; Son, S.; Lee, K. Comparative analysis of adjacent levels of degeneration and clinical outcomes between conventional pedicle screws and percutaneous pedicle screws in treatment of degenerative disease at l3-5; a preliminary report. Korean J. Spine 2012, 9, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Tran, V.; Lin, H.-Y.; Liu, H.-W.; Jang, F.-J.; Tseng, C.-H. BiLuNet: A Multi-Path Network for Semantic Segmentation on X-ray Images; IEEE: Piscataway, NJ, USA, 2021; pp. 10034–10041. [Google Scholar]
- Trinh, G.M.; Shao, H.C.; Hsieh, K.L.; Lee, C.Y.; Liu, H.W.; Lai, C.W.; Chou, S.Y.; Tsai, P.I.; Chen, K.J.; Chang, F.C.; et al. Detection of Lumbar Spondylolisthesis from X-ray Images Using Deep Learning Network. J. Clin. Med. 2022, 11, 5450. [Google Scholar] [CrossRef]
- Videman, T.; Battié, M.C.; Gibbons, L.E.; Gill, K. Aging changes in lumbar discs and vertebrae and their interaction: A 15-year follow-up study. Spine J. 2014, 14, 469–478. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Shalabi, L.A.; Shaaban, Z.; Kasasbeh, B. Data Mining: A Preprocessing Engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Schwab, F.; Ungar, B.; Blondel, B.; Buchowski, J.; Coe, J.; Deinlein, D.; DeWald, C.; Mehdian, H.; Shaffrey, C.; Tribus, C.; et al. Scoliosis Research Society-Schwab adult spinal deformity classification: A validation study. Spine 2012, 37, 1077–1082. [Google Scholar] [CrossRef]
- Terran, J.; Schwab, F.; Shaffrey, C.I.; Smith, J.S.; Devos, P.; Ames, C.P.; Fu, K.M.; Burton, D.; Hostin, R.; Klineberg, E.; et al. The SRS-Schwab adult spinal deformity classification: Assessment and clinical correlations based on a prospective operative and nonoperative cohort. Neurosurgery 2013, 73, 559–568. [Google Scholar] [CrossRef]
- Smith, J.S.; Klineberg, E.; Schwab, F.; Shaffrey, C.I.; Moal, B.; Ames, C.P.; Hostin, R.; Fu, K.M.; Burton, D.; Akbarnia, B.; et al. Change in classification grade by the SRS-Schwab Adult Spinal Deformity Classification predicts impact on health-related quality of life measures: Prospective analysis of operative and nonoperative treatment. Spine 2013, 38, 1663–1671. [Google Scholar] [CrossRef] [PubMed]
- Kong, L.D.; Zhang, Y.Z.; Wang, F.; Kong, F.L.; Ding, W.Y.; Shen, Y. Radiographic Restoration of Sagittal Spinopelvic Alignment After Posterior Lumbar Interbody Fusion in Degenerative Spondylolisthesis. Clin. Spine Surg. 2016, 29, E87–E92. [Google Scholar] [CrossRef] [PubMed]
- Glassman, S.D.; Berven, S.; Bridwell, K.; Horton, W.; Dimar, J.R. Correlation of radiographic parameters and clinical symptoms in adult scoliosis. Spine 2005, 30, 682–688. [Google Scholar] [CrossRef] [PubMed]
- Weisz, G.; Houang, M. Classification of the normal variation in the sagittal alignment of the human lumbar spine and pelvis in the standing position. Spine 2005, 30, 1558–1559. [Google Scholar] [CrossRef] [PubMed]
- Lafage, V.; Schwab, F.; Skalli, W.; Hawkinson, N.; Gagey, P.M.; Ondra, S.; Farcy, J.P. Standing balance and sagittal plane spinal deformity: Analysis of spinopelvic and gravity line parameters. Spine 2008, 33, 1572–1578. [Google Scholar] [CrossRef] [PubMed]
- Legaye, J.; Duval-Beaupère, G.; Hecquet, J.; Marty, C. Pelvic incidence: A fundamental pelvic parameter for three-dimensional regulation of spinal sagittal curves. Eur. Spine J. 1998, 7, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Chou, D. Commentary: Retrospective Review of Immediate Restoration of Lordosis in Single-Level Minimally Invasive Transforaminal Lumbar Interbody Fusion: A Comparison of Static and Expandable Interbody Cages. Oper. Neurosurg. 2020, 18, E153–E154. [Google Scholar] [CrossRef] [PubMed]
- McMordie, J.H.; Schmidt, K.P.; Gard, A.P.; Gillis, C.C. Clinical and Short-Term Radiographic Outcomes of Minimally Invasive Transforaminal Lumbar Interbody Fusion With Expandable Lordotic Devices. Neurosurgery 2020, 86, E147–E155. [Google Scholar] [CrossRef]
- Porche, K.; Dru, A.; Moor, R.; Kubilis, P.; Vaziri, S.; Hoh, D.J. Preoperative Radiographic Prediction Tool for Early Postoperative Segmental and Lumbar Lordosis Alignment After Transforaminal Lumbar Interbody Fusion. Cureus 2021, 13, e18175. [Google Scholar] [CrossRef]
- Schwab, F.; Lafage, V.; Patel, A.; Farcy, J.P. Sagittal plane considerations and the pelvis in the adult patient. Spine 2009, 34, 1828–1833. [Google Scholar] [CrossRef]
- Inami, S.; Moridaira, H.; Takeuchi, D.; Shiba, Y.; Nohara, Y.; Taneichi, H. Optimum pelvic incidence minus lumbar lordosis value can be determined by individual pelvic incidence. Eur. Spine J. 2016, 25, 3638–3643. [Google Scholar] [CrossRef]
- Schwab, F.; Patel, A.; Ungar, B.; Farcy, J.P.; Lafage, V. Adult spinal deformity-postoperative standing imbalance: How much can you tolerate? An overview of key parameters in assessing alignment and planning corrective surgery. Spine 2010, 35, 2224–2231. [Google Scholar] [CrossRef]
- Schwab, F.J.; Blondel, B.; Bess, S.; Hostin, R.; Shaffrey, C.I.; Smith, J.S.; Boachie-Adjei, O.; Burton, D.C.; Akbarnia, B.A.; Mundis, G.M.; et al. Radiographical spinopelvic parameters and disability in the setting of adult spinal deformity: A prospective multicenter analysis. Spine 2013, 38, E803–E812. [Google Scholar] [CrossRef]
- Berjano, P.; Aebi, M. Pedicle subtraction osteotomies (PSO) in the lumbar spine for sagittal deformities. Eur. Spine J. 2015, 24 (Suppl. S1), S49–S57. [Google Scholar] [CrossRef]
- Brink, R.C.; Colo, D.; Schlösser, T.P.C.; Vincken, K.L.; van Stralen, M.; Hui, S.C.N.; Shi, L.; Chu, W.C.W.; Cheng, J.C.Y.; Castelein, R.M. Upright, prone, and supine spinal morphology and alignment in adolescent idiopathic scoliosis. Scoliosis Spinal Disord. 2017, 12, 6. [Google Scholar] [CrossRef]
- Salem, W.; Coomans, Y.; Brismée, J.M.; Klein, P.; Sobczak, S.; Dugailly, P.M. Sagittal Thoracic and Lumbar Spine Profiles in Upright Standing and Lying Prone Positions Among Healthy Subjects: Influence of Various Biometric Features. Spine 2015, 40, E900–E908. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, H.; Suguro, T.; Yokoyama, Y.; Iida, Y.; Terashima, F.; Wada, A. Effect of cage geometry on sagittal alignment after posterior lumbar interbody fusion for degenerative disc disease. J. Orthop. Surg. 2010, 18, 139–142. [Google Scholar] [CrossRef] [PubMed]
- Kepler, C.K.; Rihn, J.A.; Radcliff, K.E.; Patel, A.A.; Anderson, D.G.; Vaccaro, A.R.; Hilibrand, A.S.; Albert, T.J. Restoration of lordosis and disk height after single-level transforaminal lumbar interbody fusion. Orthop. Surg. 2012, 4, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Faundez, A.A.; Mehbod, A.A.; Wu, C.; Wu, W.; Ploumis, A.; Transfeldt, E.E. Position of interbody spacer in transforaminal lumbar interbody fusion: Effect on 3-dimensional stability and sagittal lumbar contour. J. Spinal Disord. Tech. 2008, 21, 175–180. [Google Scholar] [CrossRef] [PubMed]
- Gambhir, S.; Wang, T.; Pelletier, M.H.; Walsh, W.R.; Ball, J.R. How Does Cage Lordosis Influence Postoperative Segmental Lordosis in Lumbar Interbody Fusion. World Neurosurg. 2019, 126, e606–e611. [Google Scholar] [CrossRef] [PubMed]
- Uribe, J.S.; Harris, J.E.; Beckman, J.M.; Turner, A.W.; Mundis, G.M.; Akbarnia, B.A. Finite element analysis of lordosis restoration with anterior longitudinal ligament release and lateral hyperlordotic cage placement. Eur. Spine J. 2015, 24 (Suppl. S3), 420–426. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S.; Bess, S.; Shaffrey, C.I.; Burton, D.C.; Hart, R.A.; Hostin, R.; Klineberg, E. Dynamic changes of the pelvis and spine are key to predicting postoperative sagittal alignment after pedicle subtraction osteotomy: A critical analysis of preoperative planning techniques. Spine 2012, 37, 845–853. [Google Scholar] [CrossRef] [PubMed]
- Legaye, J.; Duval-Beaupère, G. Sagittal plane alignment of the spine and gravity: A radiological and clinical evaluation. Acta Orthop. Belg. 2005, 71, 213–220. [Google Scholar] [PubMed]
- Langella, F.; Villafañe, J.H.; Damilano, M.; Cecchinato, R.; Pejrona, M.; Ismael, M.; Berjano, P. Predictive Accuracy of Surgimap Surgical Planning for Sagittal Imbalance: A Cohort Study. Spine 2017, 42, E1297–E1304. [Google Scholar] [CrossRef] [PubMed]
- Glassman, S.D.; Bridwell, K.; Dimar, J.R.; Horton, W.; Berven, S.; Schwab, F. The impact of positive sagittal balance in adult spinal deformity. Spine 2005, 30, 2024–2029. [Google Scholar] [CrossRef] [PubMed]
- Lafage, V.; Schwab, F.; Patel, A.; Hawkinson, N.; Farcy, J.P. Pelvic tilt and truncal inclination: Two key radiographic parameters in the setting of adults with spinal deformity. Spine 2009, 34, E599–E606. [Google Scholar] [CrossRef]
- Huang, M.; Zhou, S.; Chen, X.; Lai, H.; Feng, Q. Semi-supervised hybrid spine network for segmentation of spine MR images. Comput. Med. Imaging Graph. 2023, 107, 102245. [Google Scholar] [CrossRef]
- Lu, H.; Li, M.; Yu, K.; Zhang, Y.; Yu, L. Lumbar spine segmentation method based on deep learning. J. Appl. Clin. Med. Phys. 2023, 24, e13996. [Google Scholar] [CrossRef]


| ML Algorithm | Hyperparameter Ranges | Optimal Values for Cage Height Prediction | Optimal Values for PI-LL Prediction |
|---|---|---|---|
| LR | Alpha = [0, 1], interval = 0.001 | 0.001 | 0.01 |
| DT | Criterion = [squared_error, friedman_mse, absolute_error, poisson] min_samples_split = [10, 20, 30, 40, 50] min_samples_leaf = [5, 10, 20, 30, 40] | poisson 30 20 | squared_error 50 5 |
| SVR | kernels = [poly, linear, rbf, sigmoid] C = [0.1, 1, 10, 100] gamma = [0.001, 0.01, 0.1, 1] | sigmoid 10 0.001 | linear 0.1 1 |
| MLP | hidden_layer_sizes = [(50, 50, 50), (100, 100, 100), (200, 200, 200)] activation = [tanh, relu] solver = [sgd, adam, lbfgs] alpha = [0.0001, 0.001, 0.05] | (200, 200, 200) relu lbfgs 0.05 | (200, 200, 200) tanh sgd 0.0001 |
| KNN | n_neighbors = [5, 10, 20, 30, 40, 50] metric = [euclidean, manhattan, minkowski] weights = [uniform, distance] | 20 euclidean uniform | 5 euclidean distance |
| Algorithm | Cage Height | Postoperative PI-LL | ||
|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | |
| DT | 1.11 ± 0.042 | 0.85 ± 0.038 | 7.05 ± 0.85 | 5.39 ± 0.72 |
| LR | 1.06 ± 0.011 | 0.76 ± 0.01 | 5.42 ± 0.56 | 4.2 ± 0.42 |
| SVR | 1.09 ± 0.008 | 0.77 ± 0.01 | 5.4 ± 0.52 | 4.15 ± 0.48 |
| MLP | 1.16 ± 0.02 | 0.87 ± 0.016 | 6.36 ± 0.8 | 4.84 ± 0.76 |
| KNN | 1.11 ± 0.042 | 0.85 ± 0.038 | 7.05 ± 0.85 | 5.39 ± 0.72 |
| Baseline Model Performance | Optimal Model Performance | |||
|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | |
| Cage height prediction | 1.06 | 0.76 | 1.01 | 0.7 |
| Postoperative PI-LL prediction | 5.4 | 4.15 | 5.19 | 3.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, A.T.; Le, H.; Hoang, T.T.; Trinh, G.M.; Shao, H.-C.; Tsai, P.-I.; Chen, K.-J.; Hsieh, K.L.-C.; Huang, E.-W.; Hsu, C.-C.; et al. Development of End-to-End Artificial Intelligence Models for Surgical Planning in Transforaminal Lumbar Interbody Fusion. Bioengineering 2024, 11, 164. https://doi.org/10.3390/bioengineering11020164
Bui AT, Le H, Hoang TT, Trinh GM, Shao H-C, Tsai P-I, Chen K-J, Hsieh KL-C, Huang E-W, Hsu C-C, et al. Development of End-to-End Artificial Intelligence Models for Surgical Planning in Transforaminal Lumbar Interbody Fusion. Bioengineering. 2024; 11(2):164. https://doi.org/10.3390/bioengineering11020164
Chicago/Turabian StyleBui, Anh Tuan, Hieu Le, Tung Thanh Hoang, Giam Minh Trinh, Hao-Chiang Shao, Pei-I Tsai, Kuan-Jen Chen, Kevin Li-Chun Hsieh, E-Wen Huang, Ching-Chi Hsu, and et al. 2024. "Development of End-to-End Artificial Intelligence Models for Surgical Planning in Transforaminal Lumbar Interbody Fusion" Bioengineering 11, no. 2: 164. https://doi.org/10.3390/bioengineering11020164
APA StyleBui, A. T., Le, H., Hoang, T. T., Trinh, G. M., Shao, H.-C., Tsai, P.-I., Chen, K.-J., Hsieh, K. L.-C., Huang, E.-W., Hsu, C.-C., Mathew, M., Lee, C.-Y., Wang, P.-Y., Huang, T.-J., & Wu, M.-H. (2024). Development of End-to-End Artificial Intelligence Models for Surgical Planning in Transforaminal Lumbar Interbody Fusion. Bioengineering, 11(2), 164. https://doi.org/10.3390/bioengineering11020164









