Kinematic Analysis of Human Gait in Healthy Young Adults Using IMU Sensors: Exploring Relevant Machine Learning Features for Clinical Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Participants
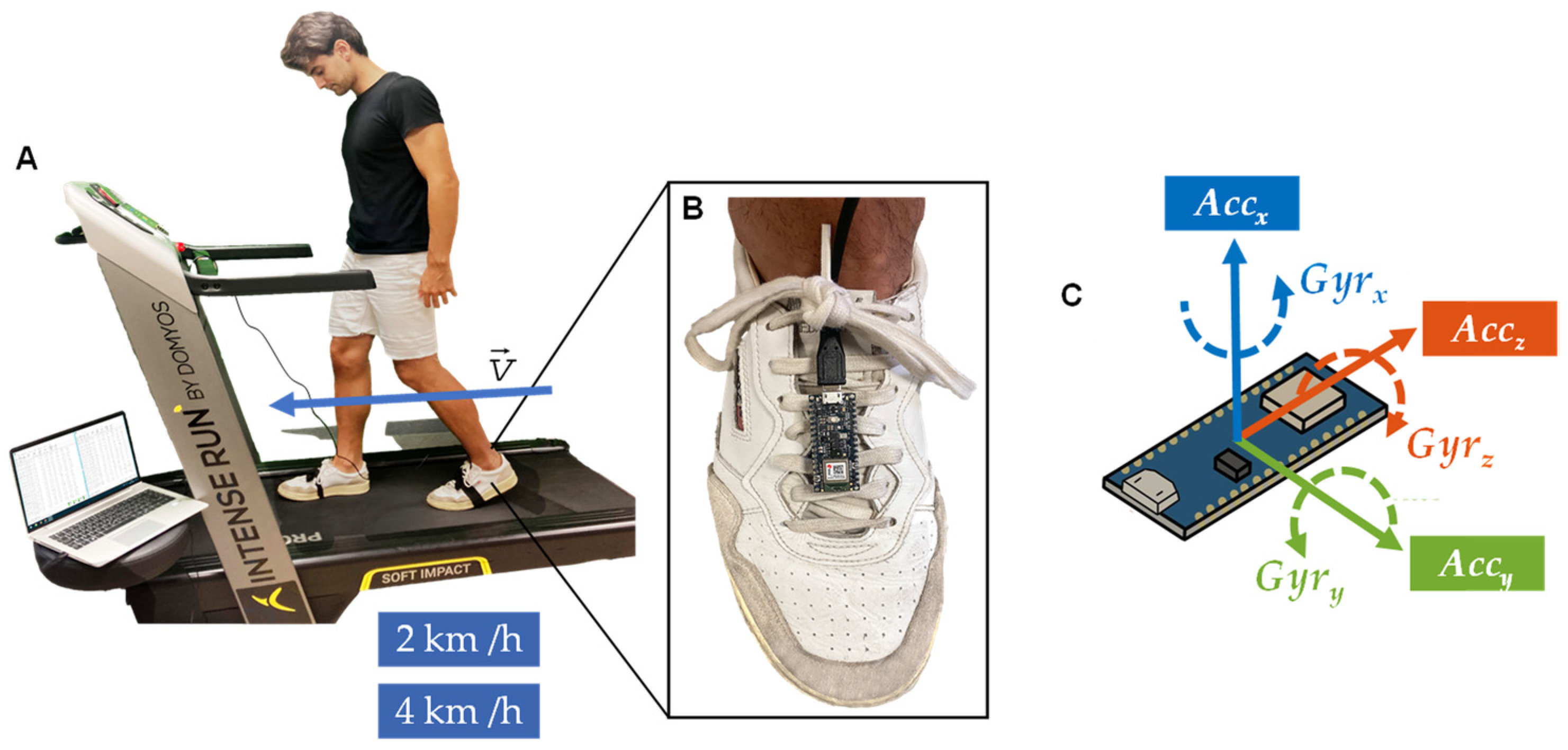
2.3. Data Collection
2.4. Procedure
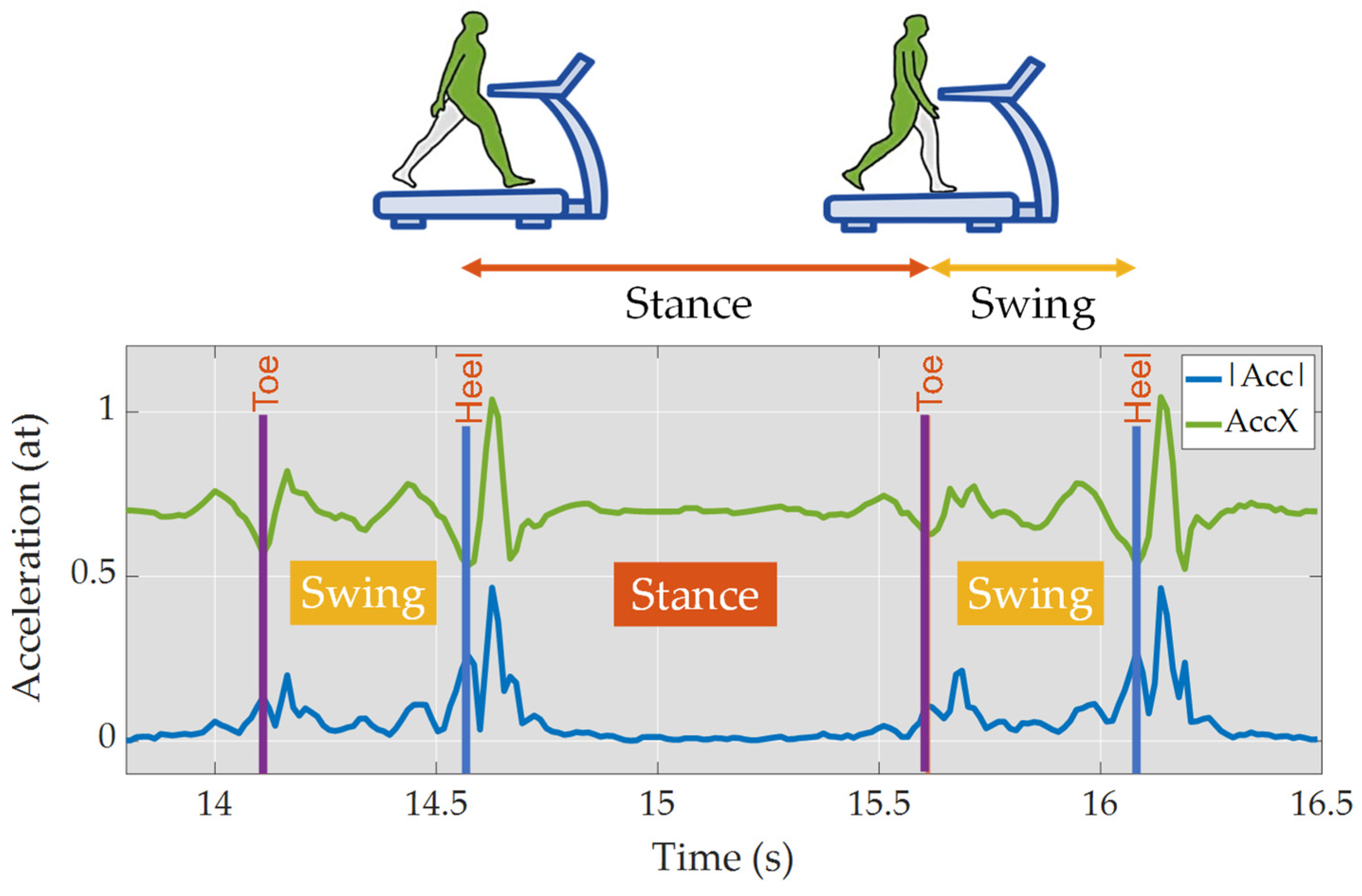
2.5. Data Processing
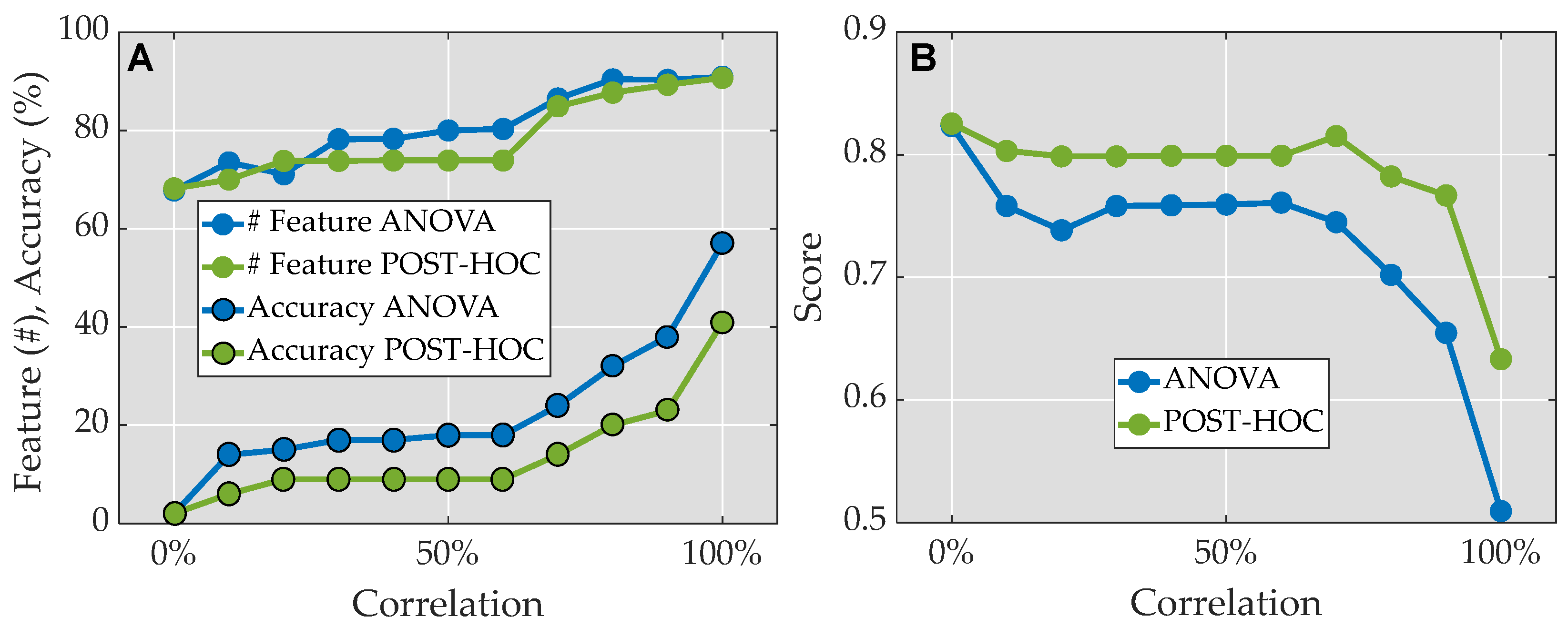
2.6. Feature Selection
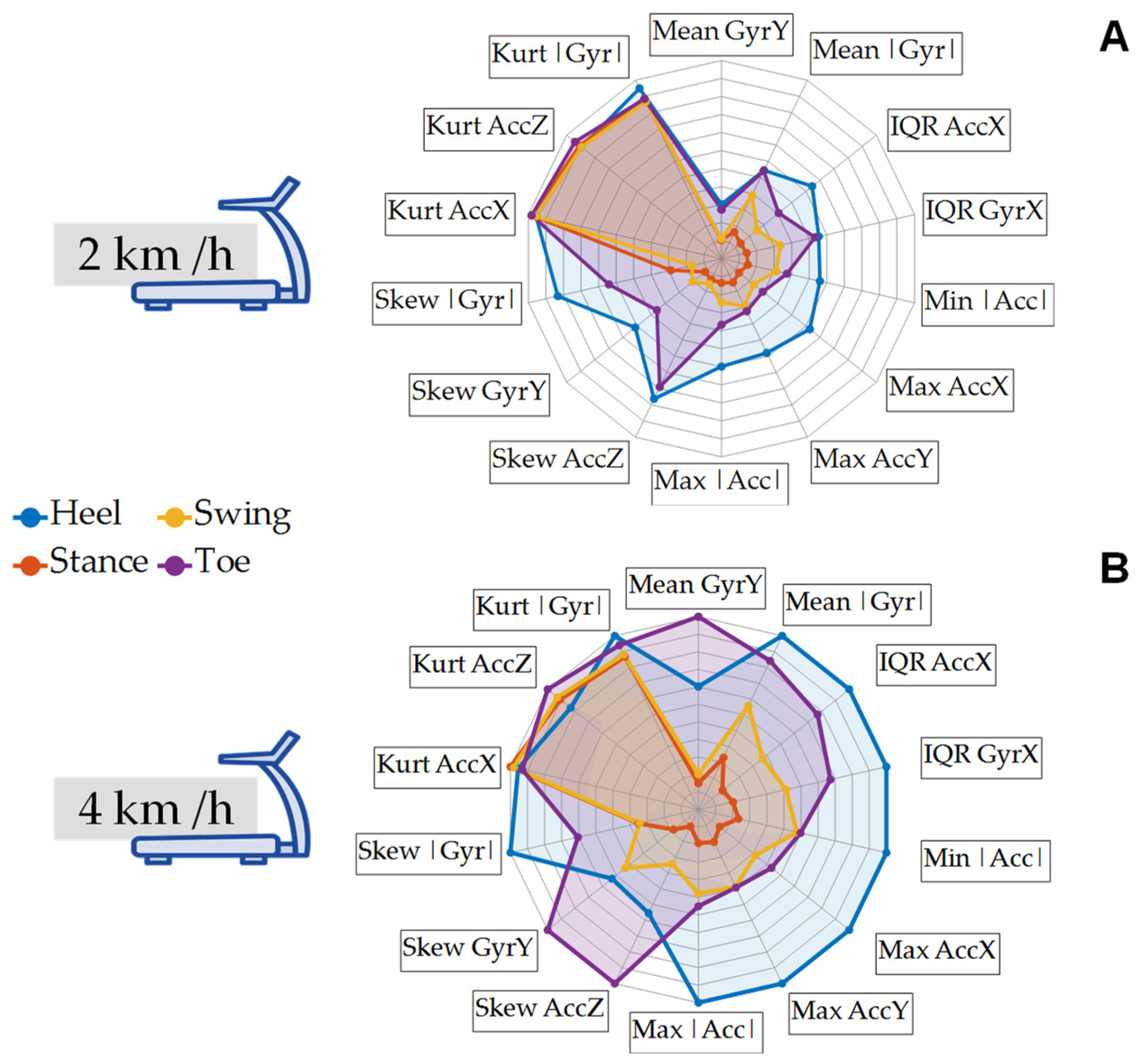
2.7. Spider Plots
2.8. Machine Learning Analysis
3. Results
3.1. Feature Reduction
- Mean of the magnitude of the gyroscope data (Mean |Gyr|)
- Maximum value of the magnitude of the acceleration data (Max |Acc|)
- Interquartile range of the gyroscope data in the x-axis (IQR GyrX)
- Minimum value of the magnitude of the acceleration data (Min |Acc|)
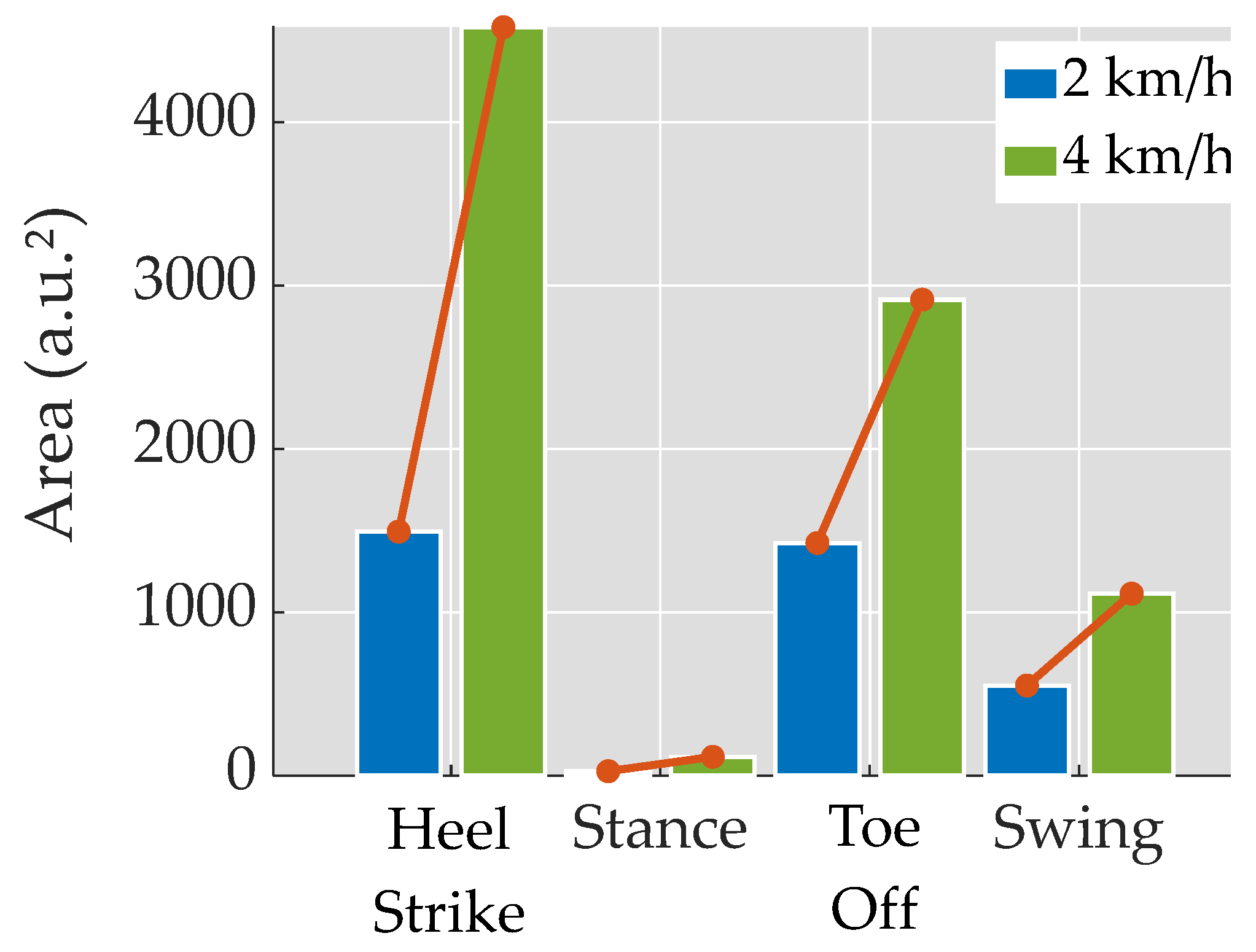
3.2. Spider Plots
3.3. Machine Learning Analysis
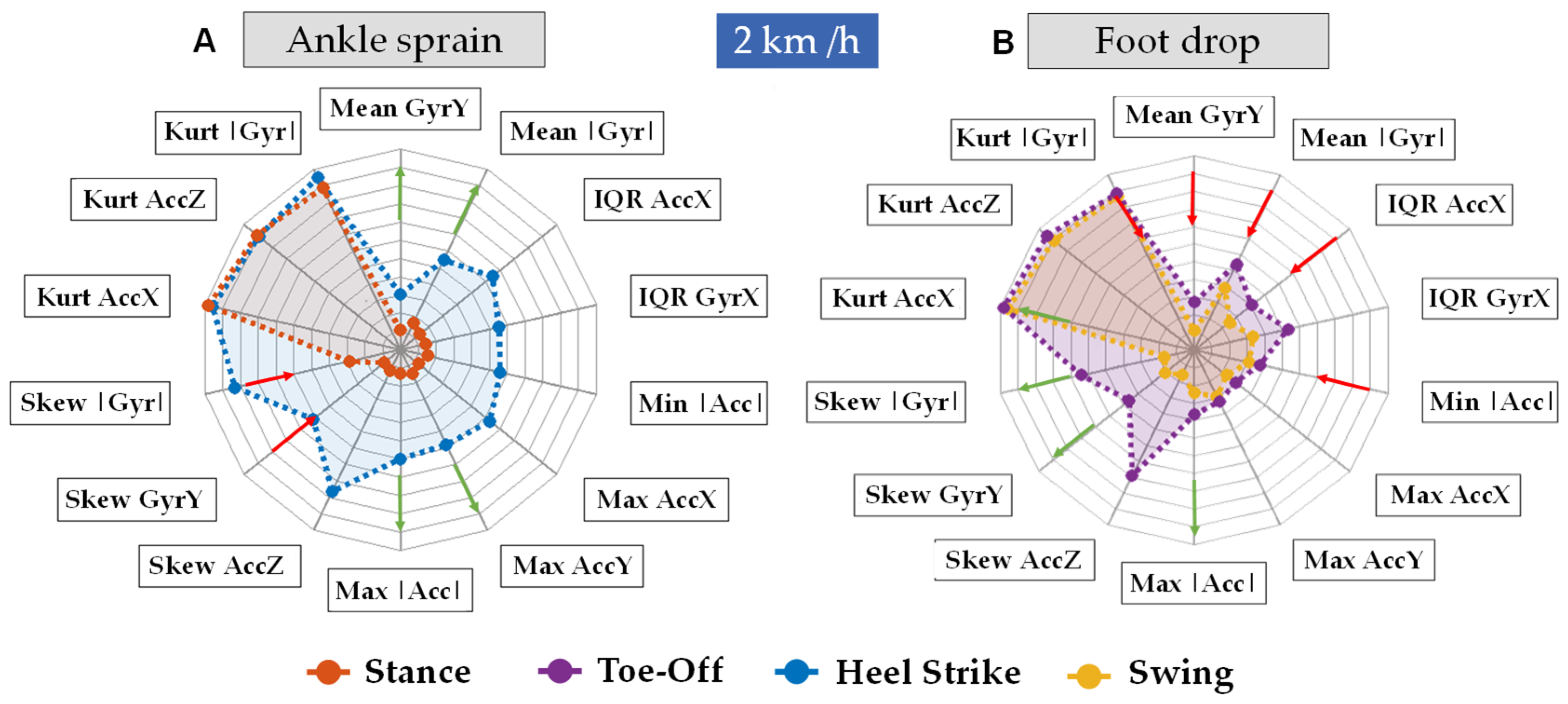
4. Discussion
5. Limitations, Conclusions and Future Directions
- Identifying abnormal gait patterns: High kurtosis or significant skewness may serve as indicators of deviations from the typical gait patterns, potentially suggesting the presence of underlying pathologies or impairments in the kinematic movement of the subject.
- Quantifying variability: Both kurtosis and skewness can express how variable the acceleration data are.
- Monitoring rehabilitation progress: These measures can also be used to track changes in gait over time. In the context of rehabilitation, a reduction in kurtosis and skewness may serve as an indicator of enhanced gait stability as the patient undergoes a rehabilitation intervention.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blacklock, R.E.; Rhodes, R.E.; Brown, S.G. Relationship Between Regular Walking, Physical Activity, and Health-Related Quality of Life. J. Phys. Act. Health 2007, 4, 138–152. [Google Scholar] [CrossRef]
- Manson, J.E.; Greenland, P.; LaCroix, A.Z.; Stefanick, M.L.; Mouton, C.P.; Oberman, A.; Perri, M.G.; Sheps, D.S.; Pettinger, M.B.; Siscovick, D.S. Walking Compared with Vigorous Exercise for the Prevention of Cardiovascular Events in Women. N. Engl. J. Med. 2002, 347, 716–725. [Google Scholar] [CrossRef]
- Jacquelin, P.; Judith, B. Gait Analysis: Normal and Pathological Function; Slack Inc.: New York, NY, USA, 2010. [Google Scholar]
- Takakusaki, K.; Saitoh, K.; Harada, H.; Kashiwayanagi, M. Role of Basal Ganglia–Brainstem Pathways in the Control of Motor Behaviors. Neurosci. Res. 2004, 50, 137–151. [Google Scholar] [CrossRef]
- Michael, W. Gait Analysis; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 9780750688833. [Google Scholar]
- Balaban, B.; Tok, F. Gait Disturbances in Patients With Stroke. PM&R 2014, 6, 635–642. [Google Scholar] [CrossRef]
- Roche, N.; Pradon, D.; Cosson, J.; Robertson, J.; Marchiori, C.; Zory, R. Categorization of Gait Patterns in Adults with Cerebral Palsy: A Clustering Approach. Gait Posture 2014, 39, 235–240. [Google Scholar] [CrossRef]
- Mukaino, M.; Ohtsuka, K.; Tanikawa, H.; Matsuda, F.; Yamada, J.; Itoh, N.; Saitoh, E. Clinical-Oriented Three-Dimensional Gait Analysis Method for Evaluating Gait Disorder. J. Vis. Exp. 2018, 133, e57063. [Google Scholar] [CrossRef]
- Vaishya, R.; Vaish, A. Falls in Older Adults Are Serious. Indian J. Orthop. 2020, 54, 69–74. [Google Scholar] [CrossRef]
- Tinetti, M.E.; Speechley, M.; Ginter, S.F. Risk Factors for Falls among Elderly Persons Living in the Community. N. Engl. J. Med. 1988, 319, 1701–1707. [Google Scholar] [CrossRef] [PubMed]
- Downton, J.H.; Andrews, K. Prevalence, Characteristics and Factors Associated with Falls among the Elderly Living at Home. Aging Clin. Exp. Res. 1991, 3, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Stalenhoef, P.A.; Diederiks, J.P.M.; Knottnerus, J.A.; Kester, A.D.M.; Crebolder, H.F.J.M. A Risk Model for the Prediction of Recurrent Falls in Community-Dwelling Elderly. J. Clin. Epidemiol. 2002, 55, 1088–1094. [Google Scholar] [CrossRef] [PubMed]
- James, S.L.; Lucchesi, L.R.; Bisignano, C.; Castle, C.D.; Dingels, Z.V.; Fox, J.T.; Hamilton, E.B.; Henry, N.J.; Krohn, K.J.; Liu, Z.; et al. The Global Burden of Falls: Global, Regional and National Estimates of Morbidity and Mortality from the Global Burden of Disease Study 2017. Inj. Prev. 2020, 26, i3–i11. [Google Scholar] [CrossRef]
- O’Mahony, D.; O’Sullivan, D.; Byrne, S.; O’Connor, M.N.; Ryan, C.; Gallagher, P. STOPP/START Criteria for Potentially Inappropriate Prescribing in Older People: Version 2. Age Ageing 2014, 44, 213–218. [Google Scholar] [CrossRef]
- Waterman, B.R.; Owens, B.D.; Davey, S.; Zacchilli, M.A.; Belmont, P.J. The Epidemiology of Ankle Sprains in the United States. J. Bone Jt. Surg. 2010, 92, 2279–2284. [Google Scholar] [CrossRef]
- Hølmer, P.; Søndergaard, L.; Konradsen, L.; Nielsen, P.T.; Jørgensen, L.N. Epidemiology of Sprains in the Lateral Ankle and Foot. Foot Ankle Int. 1994, 15, 72–74. [Google Scholar] [CrossRef]
- Newsham, K. The Ubiquitous Lateral Ankle Sprain: Time to Reconsider Our Management? J. Nurse Pract. 2019, 15, 343–346.e3. [Google Scholar] [CrossRef]
- Safran, M.R.; Zachazewski, J.E.; BenedettiI, R.S.; Bartolozzi, A.R.; Mandelbaum, R. Lateral Ankle Sprains: A Comprehensive Review Part 2: Treatment and Rehabilitation with an Emphasis on the Athlete. Med. Sci. Sports Exerc. 1999, 31, S438–S447. [Google Scholar] [CrossRef]
- Lytle, J.B.; Parikh, K.B.; Tarakemeh, A.; Vopat, B.G.; Mulcahey, M.K. Epidemiology of Foot and Ankle Injuries in NCAA Jumping Athletes in the United States During 2009–2014. Orthop. J. Sports Med. 2021, 9, 232596712199805. [Google Scholar] [CrossRef]
- Aminian, K.; Najafi, B.; Büla, C.; Leyvraz, P.-F.; Robert, P. Spatio-Temporal Parameters of Gait Measured by an Ambulatory System Using Miniature Gyroscopes. J. Biomech. 2002, 35, 689–699. [Google Scholar] [CrossRef] [PubMed]
- Baghdadi, A.; Cavuoto, L.A.; Crassidis, J.L. Hip and Trunk Kinematics Estimation in Gait Through Kalman Filter Using IMU Data at the Ankle. IEEE Sens. J. 2018, 18, 4253–4260. [Google Scholar] [CrossRef]
- Karatsidis, A. Kinetic Gait Analysis Using Inertial Motion Capture: New Tools for Knee Osteoarthritis; University of Twente: Enschede, The Netherlands, 2018. [Google Scholar]
- Slemenšek, J.; Fister, I.; Geršak, J.; Bratina, B.; van Midden, V.M.; Pirtošek, Z.; Šafarič, R. Human Gait Activity Recognition Machine Learning Methods. Sensors 2023, 23, 745. [Google Scholar] [CrossRef] [PubMed]
- Sprager, S.; Juric, M. Inertial Sensor-Based Gait Recognition: A Review. Sensors 2015, 15, 22089–22127. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, L.; Zhang, Y.; Hu, R.; He, C.; Tan, Y.; Zhang, J. A Wearable Real-Time Character Recognition System Based on Edge Computing-Enabled Deep Learning for Air-Writing. J. Sens. 2022, 2022, 8507706. [Google Scholar] [CrossRef]
- García-Villamil, G.; Neira-Álvarez, M.; Huertas-Hoyas, E.; Ramón-Jiménez, A.; Rodríguez-Sánchez, C. A Pilot Study to Validate a Wearable Inertial Sensor for Gait Assessment in Older Adults with Falls. Sensors 2021, 21, 4334. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Guo, Y.; Zanotto, D. Accurate Ambulatory Gait Analysis in Walking and Running Using Machine Learning Models. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 191–202. [Google Scholar] [CrossRef] [PubMed]
- Steffan, L.; Kaul, L.; Asfour, T. Online Stability Estimation Based on Inertial Sensor Data for Human and Humanoid Fall Prevention. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; pp. 171–177. [Google Scholar]
- Ordóñez, F.; Roggen, D. Deep Convolutional and LSTM Recurrent Neural Networks for Multimodal Wearable Activity Recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef]
- Sharifi Renani, M.; Myers, C.A.; Zandie, R.; Mahoor, M.H.; Davidson, B.S.; Clary, C.W. Deep Learning in Gait Parameter Prediction for OA and TKA Patients Wearing IMU Sensors. Sensors 2020, 20, 5553. [Google Scholar] [CrossRef]
- Hu, B.; Dixon, P.C.; Jacobs, J.V.; Dennerlein, J.T.; Schiffman, J.M. Machine Learning Algorithms Based on Signals from a Single Wearable Inertial Sensor Can Detect Surface- and Age-Related Differences in Walking. J. Biomech. 2018, 71, 37–42. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, M.; Ordieres-Meré, J. Comparison of Data Preprocessing Approaches for Applying Deep Learning to Human Activity Recognition in the Context of Industry 4.0. Sensors 2018, 18, 2146. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, S.; Li, J.; Komal, S.; Li, K. Reliability and Validity of a Wearable Inertial Sensor System for Gait Assessment in Healthy Young Adults. In Proceedings of the 2021 14th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 23–25 October 2021; pp. 1–6. [Google Scholar]
- Salchow-Hömmen, C.; Skrobot, M.; Jochner, M.C.E.; Schauer, T.; Kühn, A.A.; Wenger, N. Review—Emerging Portable Technologies for Gait Analysis in Neurological Disorders. Front. Hum. Neurosci. 2022, 16, 768575. [Google Scholar] [CrossRef]
- Galasso, S.; Baptista, R.; Molinara, M.; Pizzocaro, S.; Calabrò, R.S.; De Nunzio, A.M. Predicting Physical Activity Levels from Kinematic Gait Data Using Machine Learning Techniques. Eng. Appl. Artif. Intell. 2023, 123, 106487. [Google Scholar] [CrossRef]
- Gillani, S.I.; Azam, M.A.; Ehatisham-ul-Haq, M. Age Estimation and Gender Classification Based on Human Gait Analysis. In Proceedings of the 2020 International Conference on Emerging Trends in Smart Technologies (ICETST), Karachi, Pakistan, 26–27 March 2020; pp. 1–6. [Google Scholar]
- Tedaldi, D.; Pretto, A.; Menegatti, E. A Robust and Easy to Implement Method for IMU Calibration without External Equipments. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hongkong, China, 31 May–7 June 2014; pp. 3042–3049. [Google Scholar]
- Islam, M.R. Sample Size and Its Role in Central Limit Theorem (CLT). Int. J. Phys. Math. 2018, 1, 37–47. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Data Mining with Decision Trees; World Scientific: Singapore, 2014; Volume 81, ISBN 978-981-4590-07-5. [Google Scholar]
- Ferreira, P.J.S.; Cardoso, J.M.P.; Mendes-Moreira, J. KNN Prototyping Schemes for Embedded Human Activity Recognition with Online Learning. Computers 2020, 9, 96. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Weston, J. A User’s Guide to Support Vector Machines. In Data Mining Techniques for the Life Sciences; Springer: Berlin/Heidelberg, Germany, 2010; pp. 223–239. [Google Scholar]
- Muro-de-la-Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef]
- Hulleck, A.A.; Menoth Mohan, D.; Abdallah, N.; El Rich, M.; Khalaf, K. Present and Future of Gait Assessment in Clinical Practice: Towards the Application of Novel Trends and Technologies. Front. Med. Technol. 2022, 4, 901331. [Google Scholar] [CrossRef]
- Lim, A.C.Y.; Natarajan, P.; Fonseka, R.D.; Maharaj, M.; Mobbs, R.J. The Application of Artificial Intelligence and Custom Algorithms with Inertial Wearable Devices for Gait Analysis and Detection of Gait-Altering Pathologies in Adults: A Scoping Review of Literature. Digit. Health 2022, 8, 205520762210741. [Google Scholar] [CrossRef]
- Masum, H.; Chattopadhyay, S.; Ray, R.; Bhaumik, S. Spider Chart Based Pictographic Image Comparison in Walking Speed Estimation. In Proceedings of the 2019 Second International Conference on Advanced Computational and Communication Paradigms (ICACCP), Sikkim, India, 25–28 February 2019; pp. 1–4. [Google Scholar]
- Zhang, Y.; Hao, Z.; Wang, R.; Jin, D. A New Method for the Evaluation of Gait Pathology. In Proceedings of the 1st International Convention on Rehabilitation Engineering & Assistive Technology: In Conjunction with 1st Tan Tock Seng Hospital Neurorehabilitation Meeting, Singapore, 23–26 April 2007; ACM: New York, NY, USA, 2007; pp. 129–132. [Google Scholar]
- McGinnis, R.S.; Cain, S.M.; Davidson, S.P.; Vitali, R.V.; McLean, S.G.; Perkins, N.C. Inertial Sensor and Cluster Analysis for Discriminating Agility Run Technique and Quantifying Changes across Load. Biomed. Signal Process. Control 2017, 32, 150–156. [Google Scholar] [CrossRef]
- Trung, N.T.; Makihara, Y.; Nagahara, H.; Mukaigawa, Y.; Yagi, Y. Performance Evaluation of Gait Recognition Using the Largest Inertial Sensor-Based Gait Database. In Proceedings of the 2012 5th IAPR International Conference on Biometrics (ICB), New Delhi, India, 29 March–1 April 2012; pp. 360–366. [Google Scholar]
- Gao, D. Kinect-Based Gait Assessment Method for Hemiplegic Patients. In Proceedings of the 2021 3rd International Conference on Information Technology and Computer Communications, Guangzhou, China, 23–25 June 2021; ACM: New York, NY, USA, 2021; pp. 30–35. [Google Scholar]
- Sarhan, F.; Olivetto, M.; Ben Mansour, K.; Neiva, C.; Colin, E.; Choteau, B.; Marie, J.; Testelin, S.; Marin, F.; Dakpé, S. Quantified Analysis of Facial Movement: A Reference for Clinical Applications. Clin. Anat. 2023, 36, 492–502. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Qiu, S.; Wang, J.; Xu, F.; Wang, Z.; Shen, Y. Adaptive Gait Detection Based on Foot-Mounted Inertial Sensors and Multi-Sensor Fusion. Inf. Fusion 2019, 52, 157–166. [Google Scholar] [CrossRef]
- Rouhani, H.; Favre, J.; Crevoisier, X.; Aminian, K. A Wearable System for Multi-Segment Foot Kinetics Measurement. J. Biomech. 2014, 47, 1704–1711. [Google Scholar] [CrossRef] [PubMed]
- Lau, H.-Y.; Tong, K.-Y.; Zhu, H. Support Vector Machine for Classification of Walking Conditions Using Miniature Kinematic Sensors. Med. Biol. Eng. Comput. 2008, 46, 563–573. [Google Scholar] [CrossRef]
- Trabassi, D.; Serrao, M.; Varrecchia, T.; Ranavolo, A.; Coppola, G.; De Icco, R.; Tassorelli, C.; Castiglia, S.F. Machine Learning Approach to Support the Detection of Parkinson’s Disease in IMU-Based Gait Analysis. Sensors 2022, 22, 3700. [Google Scholar] [CrossRef]
- Kubota, K.J.; Chen, J.A.; Little, M.A. Machine Learning for Large-Scale Wearable Sensor Data in Parkinson’s Disease: Concepts, Promises, Pitfalls, and Futures. Mov. Disord. 2016, 31, 1314–1326. [Google Scholar] [CrossRef]
- Saboor, A.; Kask, T.; Kuusik, A.; Alam, M.M.; Le Moullec, Y.; Niazi, I.K.; Zoha, A.; Ahmad, R. Latest Research Trends in Gait Analysis Using Wearable Sensors and Machine Learning: A Systematic Review. IEEE Access 2020, 8, 167830–167864. [Google Scholar] [CrossRef]
- Ding, C.H.Q.; Dubchak, I. Multi-Class Protein Fold Recognition Using Support Vector Machines and Neural Networks. Bioinformatics 2001, 17, 349–358. [Google Scholar] [CrossRef]
- Aurélien, G. Hands-on Machine Learning with Scikit-Learn; O’Reilly Media, Inc.: Newton, MA, USA, 2019. [Google Scholar]
- Holzreiter, S.H.; Köhle, M.E. Assessment of Gait Patterns Using Neural Networks. J. Biomech. 1993, 26, 645–651. [Google Scholar] [CrossRef]
- Matovski, D.S.; Nixon, M.S.; Mahmoodi, S.; Carter, J.N. The Effect of Time on Gait Recognition Performance. IEEE Trans. Inf. Forensics Secur. 2012, 7, 543–552. [Google Scholar] [CrossRef]
- Liu, K.; Uygur, M.; Kaminski, T.W. Effect of Ankle Instability on Gait Parameters: A Systematic Review. Athl. Train. Sports Health Care 2012, 4, 275–281. [Google Scholar] [CrossRef]
- Nyska, M. Dynamic Force Distribution during Level Walking under the Feet of Patients with Chronic Ankle Instability. Br. J. Sports Med. 2003, 37, 495–497. [Google Scholar] [CrossRef]
- Ty Hopkins, J.; Coglianese, M.; Glasgow, P.; Reese, S.; Seeley, M.K. Alterations in Evertor/Invertor Muscle Activation and Center of Pressure Trajectory in Participants with Functional Ankle Instability. J. Electromyogr. Kinesiol. 2012, 22, 280–285. [Google Scholar] [CrossRef] [PubMed]
- Fereydounnia, S.; Shadmehr, A.; Talebian Moghadam, S.; Olyaei, G.; Jalaie, S.; Tahmasebi, A. Muscle Timing in Injured and Non-Injured Leg of Athletes with Chronic Ankle Instability in Response to a Visual Stimulus during Forward Jumping. J. Bodyw. Mov. Ther. 2016, 20, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Arnold, B.L.; Linens, S.W.; de la Motte, S.J.; Ross, S.E. Concentric Evertor Strength Differences and Functional Ankle Instability: A Meta-Analysis. J. Athl. Train. 2009, 44, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Hoch, M.C.; Mckeon, P.O. Peroneal Reaction Time after Ankle Sprain. Med. Sci. Sports Exerc. 2014, 46, 546–556. [Google Scholar] [CrossRef]
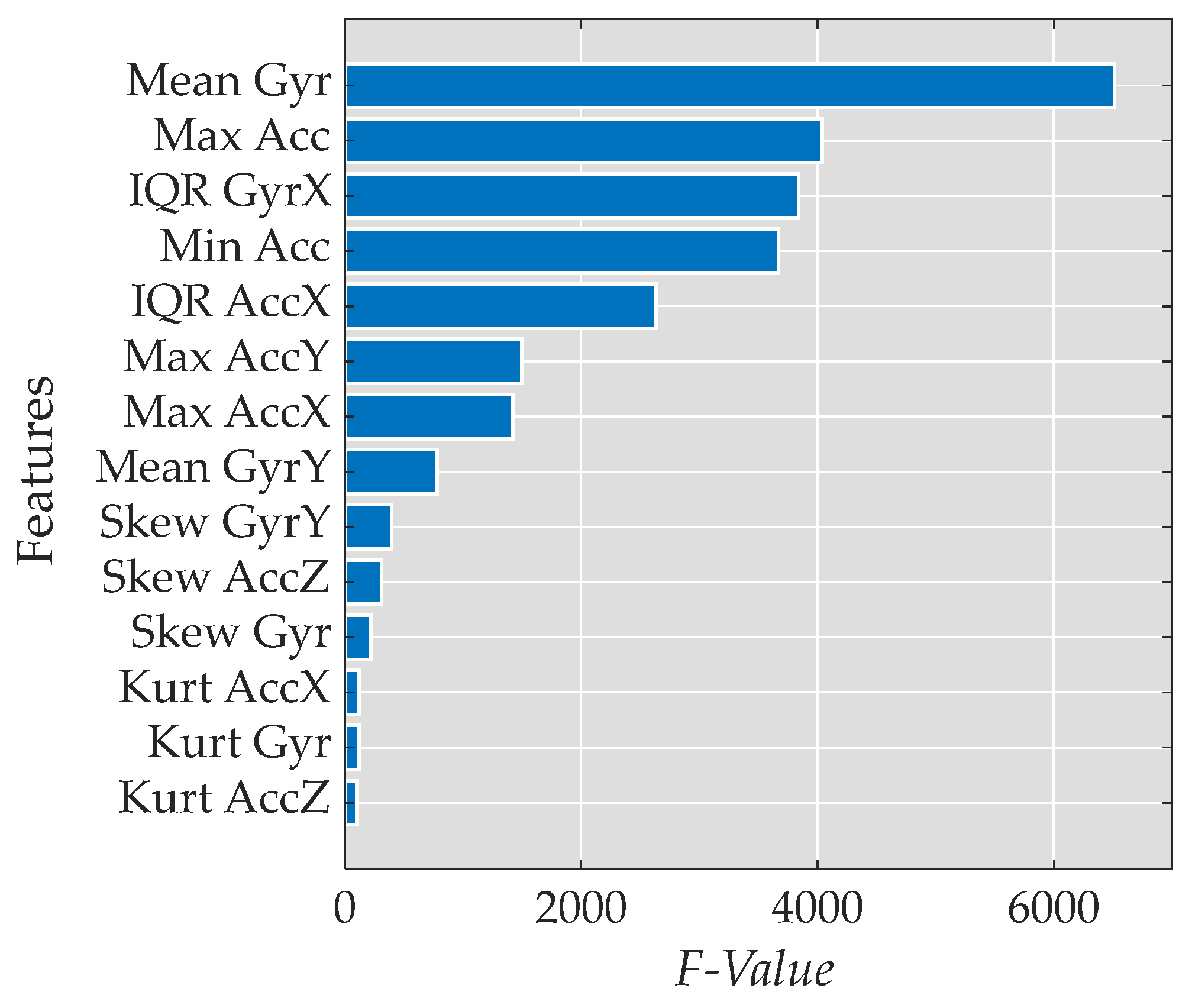

| Variables | Gender Leg Dominance | N | Mean (SD) | CI 95% | Shapiro-Wilk W |
|---|---|---|---|---|---|
| Age (years) | Male | 10 | 21.9 (1.85) | (20.6; 23.2) | 0.873 |
| Female | 22 | 22.2 (2.67) | (21.0; 23.4) | 0.909 | |
| Body mass (kg) | Male | 10 | 73.8 (5.87) | (69.6; 78.0) | 0.953 |
| Female | 22 | 59.9 (8.98) | (55.9; 63.9) | 0.969 | |
| Body height (cm) | Male | 10 | 183.2 (5.27) | (179.4; 187.0) | 0.917 |
| Female | 22 | 166.0 (4.31) | (164.0; 167.9) | 0.968 |
| Ranking | Features | Units * | Gait Event Phase | Mean (SD) | CI 95% |
|---|---|---|---|---|---|
| 1 | Mean |Gyr| | dps | Heel Strike | 2 (34.6) | (75.0; 77.5) |
| Stance | 20.4 (20.7) | (20.2; 20.7) | |||
| Toe-Off | 47.6 (28.2) | (47.1; 48.1) | |||
| Swing | 67.2 (30.4) | (66.2; 68.4) | |||
| 2 | Max |Acc| | at | Heel Strike | 0.44 (0.21) | (0.43; 0.45) |
| Stance | 0.08 (0.14) | (0.08; 0.09) | |||
| Toe-Off | 0.17 (0.12) | (0.17; 0.17) | |||
| Swing | 0.22 (0.12) | (0.21; 0.22) | |||
| 3 | IQR GyrX | dps | Heel Strike | 61.0 (42.7) | (59.5; 62.5) |
| Stance | 10.8 (16.3) | (10.6; 11.0) | |||
| Toe-Off | 31.0 (28.8) | (30.5; 31.6) | |||
| Swing | 47.1 (33.2) | (45.9; 48.3) | |||
| 4 | Min |Acc| | at | Heel Strike | 0.10 (0.07) | (0.10; 0.11) |
| Stance | 0.02 (0.03) | (0.02; 0.02) | |||
| Toe-Off | 0.05 (0.03) | (0.05; 0.05) | |||
| Swing | 0.05 (0.03) | (0.05; 0.05) |
| Model Type | Features | Accuracy | Prediction Speed [obs/s] |
|---|---|---|---|
| Fine Tree | 16/64 | 75.5% | 151,330 |
| 64/64 | 82.5% | 200,710 | |
| SVM Cubic | 16/64 | 87.1% | 9856 |
| 64/64 | 92.4% | 6100 | |
| SVM Median Gaussian | 16/64 | 86.4% | 3599 |
| 64/64 | 92.3% | 2772 | |
| Bagged Trees | 16/64 | 86.0% | 20,118 |
| 64/64 | 91.6% | 18,352 | |
| NN Medium | 16/64 | 86.6% | 171,405 |
| 64/64 | 91.5% | 166,463 | |
| NN Wide | 16/64 | 87.1% | 134,552 |
| 64/64 | 89.9% | 120,355 | |
| NN Bilayered | 16/64 | 85.5% | 159,197 |
| 64/64 | 91.5% | 174,773 | |
| NN Trilayered | 16/64 | 86.1% | 172,190 |
| 64/64 | 91.3% | 143,525 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marimon, X.; Mengual, I.; López-de-Celis, C.; Portela, A.; Rodríguez-Sanz, J.; Herráez, I.A.; Pérez-Bellmunt, A. Kinematic Analysis of Human Gait in Healthy Young Adults Using IMU Sensors: Exploring Relevant Machine Learning Features for Clinical Applications. Bioengineering 2024, 11, 105. https://doi.org/10.3390/bioengineering11020105
Marimon X, Mengual I, López-de-Celis C, Portela A, Rodríguez-Sanz J, Herráez IA, Pérez-Bellmunt A. Kinematic Analysis of Human Gait in Healthy Young Adults Using IMU Sensors: Exploring Relevant Machine Learning Features for Clinical Applications. Bioengineering. 2024; 11(2):105. https://doi.org/10.3390/bioengineering11020105
Chicago/Turabian StyleMarimon, Xavier, Itziar Mengual, Carlos López-de-Celis, Alejandro Portela, Jacobo Rodríguez-Sanz, Iria Andrea Herráez, and Albert Pérez-Bellmunt. 2024. "Kinematic Analysis of Human Gait in Healthy Young Adults Using IMU Sensors: Exploring Relevant Machine Learning Features for Clinical Applications" Bioengineering 11, no. 2: 105. https://doi.org/10.3390/bioengineering11020105
APA StyleMarimon, X., Mengual, I., López-de-Celis, C., Portela, A., Rodríguez-Sanz, J., Herráez, I. A., & Pérez-Bellmunt, A. (2024). Kinematic Analysis of Human Gait in Healthy Young Adults Using IMU Sensors: Exploring Relevant Machine Learning Features for Clinical Applications. Bioengineering, 11(2), 105. https://doi.org/10.3390/bioengineering11020105














