Modeling the Synergistic Impact of Yttrium 90 Radioembolization and Immune Checkpoint Inhibitors on Hepatocellular Carcinoma
Abstract
1. Introduction
2. Materials and Methods
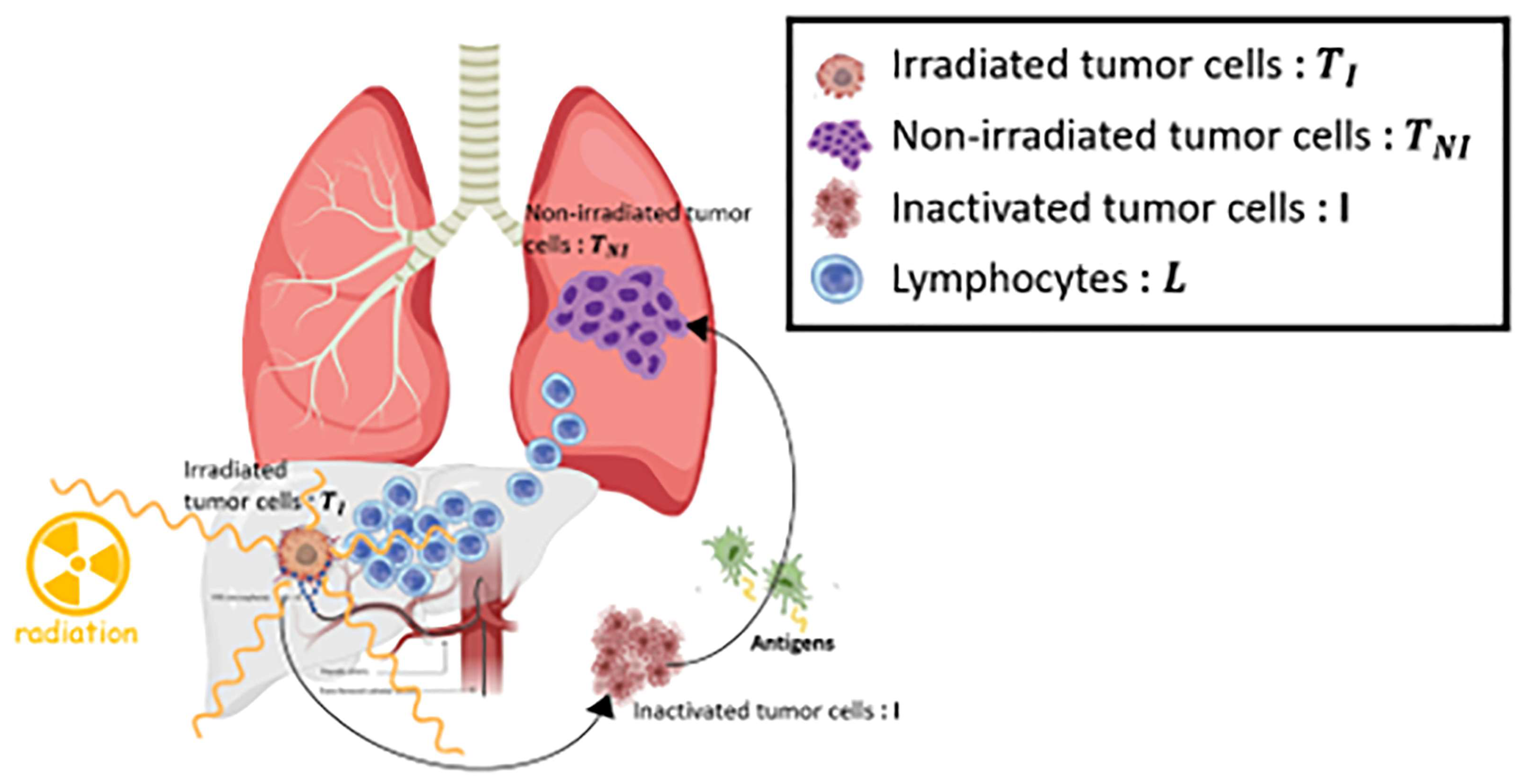
2.1. Mathematical Model Overview
2.2. Virtual Patient Cohort
2.3. Model Fitting to Yttrium 90 Radioembolization Therapy Response Data
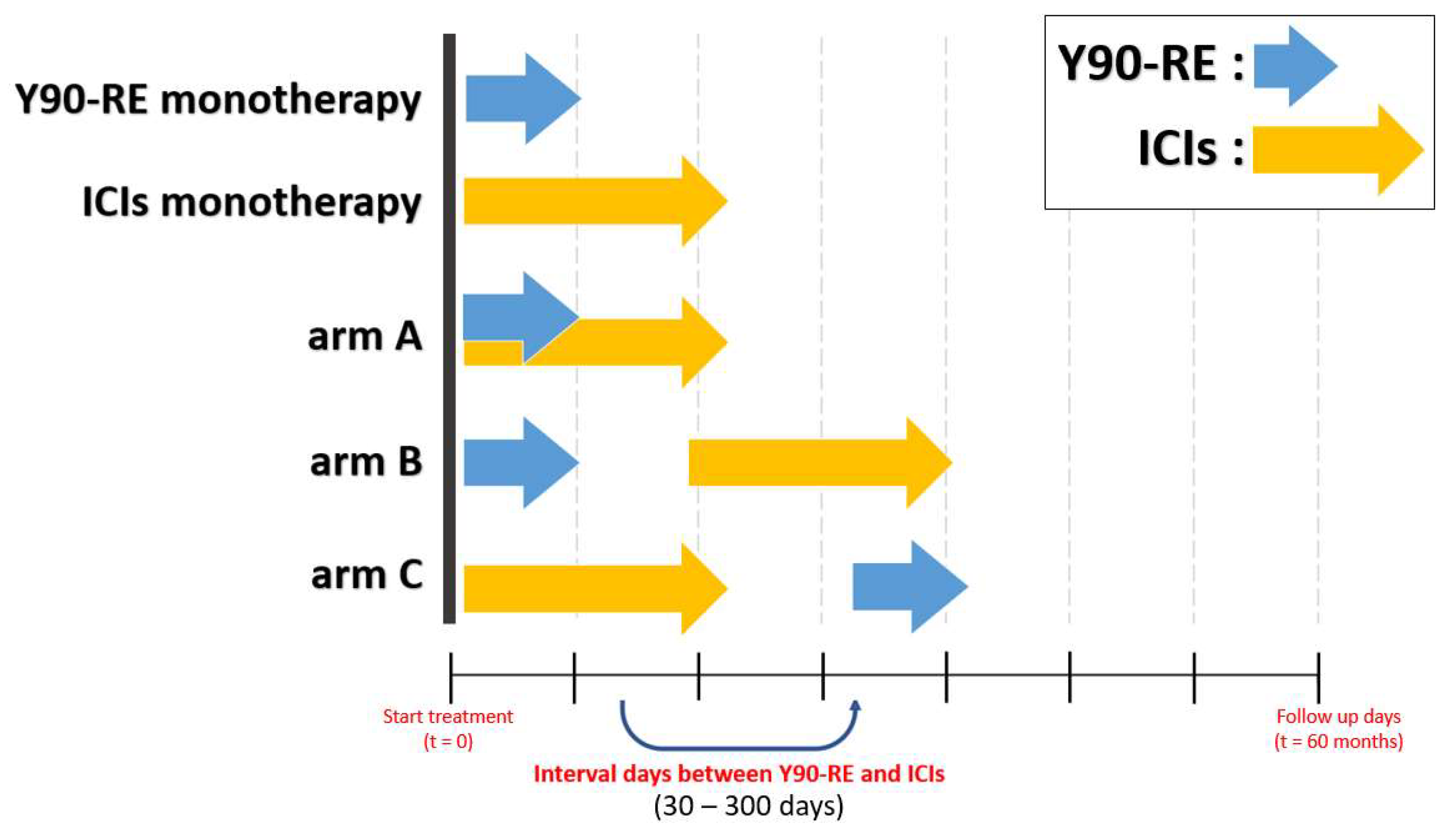
2.4. Virtual Clinical Trial and Outcome
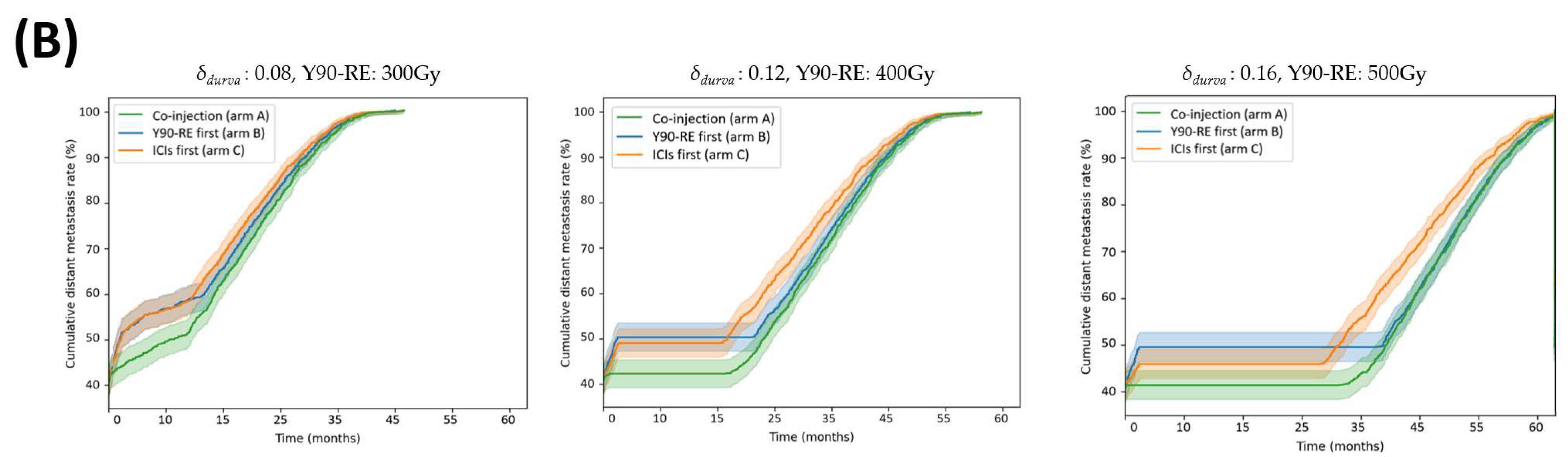
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lafaro, K.J.; Demirjian, A.N.; Pawlik, T.M. Epidemiology of Hepatocellular Carcinoma. Surg. Oncol. Clin. N. Am. 2015, 24, 1–17. [Google Scholar] [CrossRef] [PubMed]
- European Association for the Study of the Liver. European Organisation For Research And Treatment Of Cancer. EASL-EORTC Clinical Practice Guidelines: Management of Hepatocellular Carcinoma. J. Hepatol. 2012, 56, 908–943. [Google Scholar] [CrossRef] [PubMed]
- Yarchoan, M.; Agarwal, P.; Villanueva, A.; Rao, S.; Dawson, L.A.; Karasic, T.; Llovet, J.M.; Finn, R.S.; Groopman, J.D.; El-Serag, H.B.; et al. Recent Developments and Therapeutic Strategies against Hepatocellular Carcinoma. Cancer Res. 2019, 79, 4326–4330. [Google Scholar] [CrossRef] [PubMed]
- Murciano-Goroff, Y.R.; Warner, A.B.; Wolchok, J.D. The Future of Cancer Immunotherapy: Microenvironment-Targeting Combinations. Cell Res. 2020, 30, 507–519. [Google Scholar] [CrossRef] [PubMed]
- Asadian, S.; Piryaei, A.; Gheibi, N.; Aziz Kalantari, B.; Reza Davarpanah, M.; Azad, M.; Kapustina, V.; Alikhani, M.; Moghbeli Nejad, S.; Keshavarz Alikhani, H.; et al. Rhenium Perrhenate (188ReO4) Induced Apoptosis and Reduced Cancerous Phenotype in Liver Cancer Cells. Cells 2022, 11, 305. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.I.; Park, H.C. Radiotherapy as Valid Modality for Hepatocellular Carcinoma with Portal Vein Tumor Thrombosis. World J. Gastroenterol. 2016, 22, 6851. [Google Scholar] [CrossRef]
- Nault, J.-C.; Cheng, A.-L.; Sangro, B.; Llovet, J.M. Milestones in the Pathogenesis and Management of Primary Liver Cancer. J. Hepatol. 2020, 72, 209–214. [Google Scholar] [CrossRef]
- Ferlay, J.; Colombet, M.; Soerjomataram, I.; Parkin, D.M.; Piñeros, M.; Znaor, A.; Bray, F. Cancer Statistics for the Year 2020: An Overview. Int. J. Cancer 2021, 149, 778–789. [Google Scholar] [CrossRef]
- Bruix, J.; Sherman, M. Management of Hepatocellular Carcinoma. Hepatology 2005, 42, 1208–1236. [Google Scholar] [CrossRef]
- Kalbasi, A.; June, C.H.; Haas, N.; Vapiwala, N. Radiation and Immunotherapy: A Synergistic Combination. J. Clin. Investig. 2013, 123, 2756–2763. [Google Scholar] [CrossRef]
- Okusaka, T.; Ikeda, M. Immunotherapy for hepatocellular carcinoma: Current status and future perspectives. ESMO Open 2018, 3 (Suppl. 1), e000455. [Google Scholar] [CrossRef] [PubMed]
- Finn, R.S.; Qin, S.; Ikeda, M.; Galle, P.R.; Ducreux, M.; Kim, T.-Y.; Kudo, M.; Breder, V.; Merle, P.; Kaseb, A.O.; et al. Atezolizumab plus Bevacizumab in Unresectable Hepatocellular Carcinoma. N. Engl. J. Med. 2020, 382, 1894–1905. [Google Scholar] [CrossRef] [PubMed]
- Cheng, A.-L.; Qin, S.; Ikeda, M.; Galle, P.R.; Ducreux, M.; Kim, T.-Y.; Lim, H.Y.; Kudo, M.; Breder, V.; Merle, P.; et al. Updated Efficacy and Safety Data from IMbrave150: Atezolizumab plus Bevacizumab vs. Sorafenib for Unresectable Hepatocellular Carcinoma. J. Hepatol. 2021, 76, 862–873. [Google Scholar] [CrossRef] [PubMed]
- Abou-Alfa, G.K.; Lau, G.; Kudo, M.; Chan, S.L.; Kelley, R.K.; Furuse, J.; Sukeepaisarnjaroen, W.; Kang, Y.-K.; Van Dao, T.; De Toni, E.N.; et al. Tremelimumab plus Durvalumab in Unresectable Hepatocellular Carcinoma. NEJM Evid. 2022, 1, EVIDoa2100070. [Google Scholar] [CrossRef]
- Yau, T.; Park, J.-W.; Finn, R.S.; Cheng, A.-L.; Mathurin, P.; Edeline, J.; Kudo, M.; Harding, J.J.; Merle, P.; Rosmorduc, O.; et al. Nivolumab Versus Sorafenib Treatment in Advanced Hepatocellular Carcinoma (CheckMate 459): A Randomised, Multicentre, Open-Label, Phase 3 Trial. Lancet Oncol. 2022, 23, 77–90. [Google Scholar] [CrossRef] [PubMed]
- Rimassa, L.; Finn, R.S.; Sangro, B. Combination Immunotherapy for Hepatocellular Carcinoma. J. Hepatol. 2023, 79, 506–515. [Google Scholar] [CrossRef]
- Di Federico, A.; Rizzo, A.; Carloni, R.; De Giglio, A.; Bruno, R.; Ricci, D.; Brandi, G. Atezolizumab-Bevacizumab plus Y-90 TARE for the Treatment of Hepatocellular Carcinoma: Preclinical Rationale and Ongoing Clinical Trials. Expert Opin. Investig. Drugs 2021, 31, 361–369. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Chen, D.; Yu, J. Radiotherapy Combined with Immunotherapy: The Dawn of Cancer Treatment. Signal Transduct. Target. Ther. 2022, 7, 258. [Google Scholar] [CrossRef]
- Bernstein, M.B.; Krishnan, S.; Hodge, J.W.; Chang, J.Y. Immunotherapy and Stereotactic Ablative Radiotherapy (ISABR): A Curative Approach? Nat. Rev. Clin. Oncol. 2016, 13, 516–524. [Google Scholar] [CrossRef]
- Menon, H.; Ramapriyan, R.; Cushman, T.R.; Verma, V.; Kim, H.H.; Schoenhals, J.E.; Atalar, C.; Selek, U.; Chun, S.G.; Chang, J.Y.; et al. Role of Radiation Therapy in Modulation of the Tumor Stroma and Microenvironment. Front. Immunol. 2019, 10, 193. [Google Scholar] [CrossRef]
- Tai, D.; Loke, K.; Gogna, A.; Kaya, N.A.; Tan, S.H.; Hennedige, T.; Ng, D.; Irani, F.; Lee, J.; Lim, J.Q.; et al. Radioembolisation with Y90-Resin Microspheres Followed by Nivolumab for Advanced Hepatocellular Carcinoma (CA 209-678): A Single Arm, Single Centre, Phase 2 Trial. Lancet Gastroenterol. Hepatol. 2021, 6, 1025–1035. [Google Scholar] [CrossRef] [PubMed]
- de la Torre-Aláez, M.; Matilla, A.; Varela, M.; Iñarrairaegui, M.; Reig, M.; Lledó, J.L.; Arenas, J.I.; Lorente, S.; Testillano, M.; Márquez, L.; et al. Nivolumab after Selective Internal Radiation Therapy for the Treatment of Hepatocellular Carcinoma: A Phase 2, Single-Arm Study. J. ImmunoTherapy Cancer 2022, 10, e005457. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.J.; Kim, J.H.; Lee, S.J.; Lee, E.J.; Shin, E.C.; Seong, J. Radiation Improves Antitumor Effect of Immune Checkpoint Inhibitor in Murine Hepatocellular Carcinoma Model. Oncotarget 2017, 8, 41242. [Google Scholar] [CrossRef] [PubMed]
- Wehrenberg-Klee, E.; Goyal, L.; Dugan, M.C.; Zhu, A.X.; Ganguli, S. Y-90 Radioembolization Combined with a PD-1 Inhibitor for Advanced Hepatocellular Carcinoma. Cardiovasc. Interv. Radiol. 2018, 41, 1799–1802. [Google Scholar] [CrossRef]
- Valery, M.; Cervantes, B.; Samaha, R.; Gelli, M.; Smolenschi, C.; Fuerea, A.; Tselikas, L.; Klotz-Prieux, C.; Hollebecque, A.; Boige, V.; et al. Immunotherapy and Hepatocellular Cancer: Where Are We Now? Cancers 2022, 14, 4523. [Google Scholar] [CrossRef]
- Chew, V.; Lee, Y.H.; Pan, L.; Nasir, N.J.; Lim, C.J.; Chua, C.; Lai, L.; Hazirah, S.N.; Lim, T.K.; Goh, B.K.; et al. Immune Activation Underlies a Sustained Clinical Response to Yttrium-90 Radioembolisation in Hepatocellular Carcinoma. Gut 2018, 68, 335–346. [Google Scholar] [CrossRef]
- Zheng, J.; Irani, Z.; Lawrence, D.P.; Flaherty, K.T.; Arellano, R.S. Combined Effects of Yttrium-90 Transarterial Radioembolization around Immunotherapy for Hepatic Metastases from Uveal Melanoma: A Preliminary Retrospective Case Series. J. Vasc. Interv. Radiol. 2018, 29, 1369–1375. [Google Scholar] [CrossRef]
- Salem, R.; Greten, T.F. Interventional Radiology Meets Immuno-Oncology for Hepatocellular Carcinoma. J. Hepatol. 2022, S0168-8278(22)03003-3. [Google Scholar] [CrossRef]
- Zhan, C.; Ruohoniemi, D.M.; Shanbhogue, K.; Lee, J.; Welling, T.H.; Gu, P.; Park, J.S.; Dagher, N.N.; Taslakian, B.; Hickey, R. Safety of Combined Yttrium-90 Radioembolization and Immune Checkpoint Inhibitor Immunotherapy for Hepatocellular Carcinoma. J. Vasc. Interv. Radiol. 2020, 31, 25–34. [Google Scholar] [CrossRef]
- Ruohoniemi, D.M.; Zhan, C.; Wei, J.; Kulkarni, K.; Aaltonen, E.T.; Horn, J.C.; Hickey, R.M.; Taslakian, B. Safety and Effectiveness of Yttrium-90 Radioembolization around the Time of Immune Checkpoint Inhibitors for Unresectable Hepatic Metastases. J. Vasc. Interv. Radiol. JVIR 2020, 31, 1233–1241. [Google Scholar] [CrossRef]
- Sung, W.; Hong, T.S.; Poznansky, M.C.; Paganetti, H.; Grassberger, C. Mathematical Modeling to Simulate the Effect of Adding Radiation Therapy to Immunotherapy and Application to Hepatocellular Carcinoma. Int. J. Radiat. Oncol. Biol. Phys. 2022, 112, 1055–1062. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Pérez, D.; Sotolongo-Grau, O.; Espinosa Riquelme, R.; Sotolongo-Costa, O.; Santos Miranda, J.A.; Antoranz, J.C. Assessment of Cancer Immunotherapy Outcome in Terms of the Immune Response Time Features. Math. Med. Biol. A J. IMA 2007, 24, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Sotolongo-Costa, O.; Morales Molina, L.; Rodríguez Perez, D.; Antoranz, J.C.; Chacón Reyes, M. Behavior of Tumors under Nonstationary Therapy. Phys. D Nonlinear Phenom. 2003, 178, 242–253. [Google Scholar] [CrossRef]
- Sotolongo-Grau, O.; Rodríguez-Pérez, D.; Santos-Miranda, J.A.; Sotolongo-Costa, O.; Antoranz, J.C. Immune System-Tumour Efficiency Ratio as a New Oncological Index for Radiotherapy Treatment Optimization. Math. Med. Biol. A J. IMA 2009, 26, 297–307. [Google Scholar] [CrossRef]
- Loevinger, R. MIRD Primer for Absorbed Dose Calculations. Clin. Nucl. Med. 1989, 14, 723–724. [Google Scholar]
- Dezarn, W.A.; Cessna, J.T.; DeWerd, L.A.; Feng, W.; Gates, V.L.; Halama, J.; Kennedy, A.S.; Nag, S.; Sarfaraz, M.; Sehgal, V.; et al. Recommendations of the American Association of Physicists in Medicine on Dosimetry, Imaging, and Quality Assurance Procedures for 90Y Microsphere Brachytherapy in the Treatment of Hepatic Malignancies. Med. Phys. 2011, 38, 4824–4845. [Google Scholar] [CrossRef]
- Park, Y.; Choi, D.; Lim, H.K.; Rhim, H.; Kim, Y.-S.; Kim, S.H.; Lee, W.J. Growth Rate of New Hepatocellular Carcinoma after Percutaneous Radiofrequency Ablation: Evaluation with Multiphase CT. AJR Am. J. Roentgenol. 2008, 191, 215–220. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear Dynamics of Immunogenic Tumors: Parameter Estimation and Global Bifurcation Analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef]
- Tai, A.; Erickson, B.; Khater, K.A.; Li, X.A. Estimate of Radiobiologic Parameters from Clinical Data for Biologically Based Treatment Planning for Liver Irradiation. Int. J. Radiat. Oncol. Biol. Phys. 2008, 70, 900–907. [Google Scholar] [CrossRef]
- Serre, R.; Barlési, F.; Muracciole, X.; Barbolosi, D. Immunologically Effective Dose: A Practical Model for Immuno-Radiotherapy. Oncotarget 2018, 9, 31812–31819. [Google Scholar] [CrossRef][Green Version]
- Byun, H.K.; Kim, N.; Park, S.; Seong, J. Acute Severe Lymphopenia by Radiotherapy Is Associated with Reduced Overall Survival in Hepatocellular Carcinoma. Strahlenther. Onkol. 2019, 195, 1007–1017. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, N.; Kusunoki, Y.; Akiyama, M. Radiosensitivity of CD4 or CD8 Positive Human T-Lymphocytes by an In Vitro Colony Formation Assay. Radiat. Res. 1990, 123, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Walker, R.; Poleszczuk, J.; Pilon-Thomas, S.; Kim, S.; Anderson, A.A.R.A.; Czerniecki, B.J.; Harrison, L.B.; Moros, E.G.; Enderling, H. Immune Interconnectivity of Anatomically Distant Tumors as a Potential Mediator of Systemic Responses to Local Therapy. Sci. Rep. 2018, 8, 9474. [Google Scholar] [CrossRef] [PubMed]
- Basler, L.; Andratschke, N.; Ehrbar, S.; Guckenberger, M.; Tanadini-Lang, S. Modelling the Immunosuppressive Effect of Liver SBRT by Simulating the Dose to Circulating Lymphocytes: An In-Silico Planning Study. Radiat. Oncol. 2018, 13, 10. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Shen, K.; Zhu, C.; Li, Q.; Zhao, Y.; Ma, X. Safety and Efficacy of Durvalumab (MEDI4736) in Various Solid Tumors. Drug Des. Dev. Ther. 2018, 12, 2085–2096. [Google Scholar] [CrossRef]
- Sung, W.; Grassberger, C.; McNamara, A.L.; Basler, L.; Ehrbar, S.; Tanadini-Lang, S.; Hong, T.S.; Paganetti, H. A Tumor-Immune Interaction Model for Hepatocellular Carcinoma Based on Measured Lymphocyte Counts in Patients Undergoing Radiotherapy. Radiother. Oncol. 2020, 151, 73–81. [Google Scholar] [CrossRef]
- De la Garza-Ramos, C.; Montazeri, S.A.; Croome, K.P.; LeGout, J.D.; Sella, D.M.; Cleary, S.; Burns, J.; Mathur, A.K.; Overfield, C.J.; Frey, G.T.; et al. Radiation Segmentectomy for the Treatment of Solitary Hepatocellular Carcinoma: Outcomes Compared with Those of Surgical Resection. J. Vasc. Interv. Radiol. 2022, 33, 775–785.e2. [Google Scholar] [CrossRef]
- Toskich, B.; Vidal, L.L.; Olson, M.T.; Lewis, J.T.; LeGout, J.D.; Sella, D.M.; Montazeri, S.A.; Devcic, Z.; Lewis, A.R.; Frey, G.T.; et al. Pathologic Response of Hepatocellular Carcinoma Treated with Yttrium-90 Glass Microsphere Radiation Segmentectomy prior to Liver Transplantation: A Validation Study. J. Vasc. Interv. Radiol. 2021, 32, 518–526.e1. [Google Scholar] [CrossRef]
- McBride, S.; Sherman, E.; Tsai, C.J.; Baxi, S.; Aghalar, J.; Eng, J.; Zhi, W.I.; McFarland, D.; Michel, L.S.; Young, R.; et al. Randomized Phase II Trial of Nivolumab with Stereotactic Body Radiotherapy versus Nivolumab Alone in Metastatic Head and Neck Squamous Cell Carcinoma. J. Clin. Oncol. 2021, 39, 30–37. [Google Scholar] [CrossRef]
- Brooks, E.D.; Chang, J.Y. Time to Abandon Single-Site Irradiation for Inducing Abscopal Effects. Nat. Rev. Clin. Oncol. 2019, 16, 123–135. [Google Scholar] [CrossRef]
- Bertaglia, V.; Petrelli, F.; Porcu, M.; Saba, L.; Pearce, J.; Luciani, A.; Solinas, C.; Scartozzi, M. Assessment of Clinical Studies Evaluating Combinations of Immune Checkpoint Inhibitors with Locoregional Treatments in Solid Tumors. Cytokine Growth Factor Rev. 2022, 67, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Walker, R.; Schoenfeld, J.D.; Pilon-Thomas, S.; Poleszczuk, J.; Enderling, H. Evaluating the Potential for Maximized T Cell Redistribution Entropy to Improve Abscopal Responses to Radiotherapy. Converg. Sci. Phys. Oncol. 2017, 3, 034001. [Google Scholar] [CrossRef] [PubMed]
- Bekker, R.A.; Kim, S.; Pilon-Thomas, S.; Enderling, H. Mathematical Modeling of Radiotherapy and Its Impact on Tumor Interactions with the Immune System. Neoplasia 2022, 28, 100796. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Function | Value | Ref. |
|---|---|---|---|
| Tumor growth | [37] | ||
| Lymphocyte decay rate | [38] | ||
| Tumor—LQ cell death | [39] | ||
| Inactivated tumor cell decay rate | [40] | ||
| Tumor-directed lymphocyte efficiency | [33,34] | ||
| Tumor/inactivated tumor | |||
| Tumor–lymphocyte recruitment constant | [33,34] | ||
| Geometric saturation constant | [33,34] | ||
| Lymphocyte regeneration | [41] | ||
| Tumor—LQ cell death | Normally distributed | [39] | |
| Lymphocytes—LQ cell death | [42,43] | ||
| Cmax | Maximum concentration | 10 mg/kg | [44] |
| Half-life of immune checkpoint inhibitor (durvalumab) in the body | 21 days | [44] | |
| δdurva | Effectiveness of immune checkpoint Inhibitor (durvalumab) | Normally distributed (μ = 0.12 σ = 0.04) | [45] |
| Half-life of yttrium 90 in the body | 2.6 days | [36], added in this study | |
| q | Effectiveness of yttrium 90 | Normally distributed (μ = 0.12 σ = 0.04) | This study, added in this study |
| k | Constant to produce the dose rate in desired units | (0.9267 ) | [36], added in this study |
| <E> | Average energy emitted per nuclear transition | [36], added in this study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, M.; Shin, Y.; Kim, Y.; Ha, S.; Sung, W. Modeling the Synergistic Impact of Yttrium 90 Radioembolization and Immune Checkpoint Inhibitors on Hepatocellular Carcinoma. Bioengineering 2024, 11, 106. https://doi.org/10.3390/bioengineering11020106
Kang M, Shin Y, Kim Y, Ha S, Sung W. Modeling the Synergistic Impact of Yttrium 90 Radioembolization and Immune Checkpoint Inhibitors on Hepatocellular Carcinoma. Bioengineering. 2024; 11(2):106. https://doi.org/10.3390/bioengineering11020106
Chicago/Turabian StyleKang, Minah, Yerim Shin, Yeseul Kim, Sangseok Ha, and Wonmo Sung. 2024. "Modeling the Synergistic Impact of Yttrium 90 Radioembolization and Immune Checkpoint Inhibitors on Hepatocellular Carcinoma" Bioengineering 11, no. 2: 106. https://doi.org/10.3390/bioengineering11020106
APA StyleKang, M., Shin, Y., Kim, Y., Ha, S., & Sung, W. (2024). Modeling the Synergistic Impact of Yttrium 90 Radioembolization and Immune Checkpoint Inhibitors on Hepatocellular Carcinoma. Bioengineering, 11(2), 106. https://doi.org/10.3390/bioengineering11020106






