Characterization of Mechanical and Cellular Effects of Rhythmic Vertical Vibrations on Adherent Cell Cultures
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Culture
2.2. Experimental Design
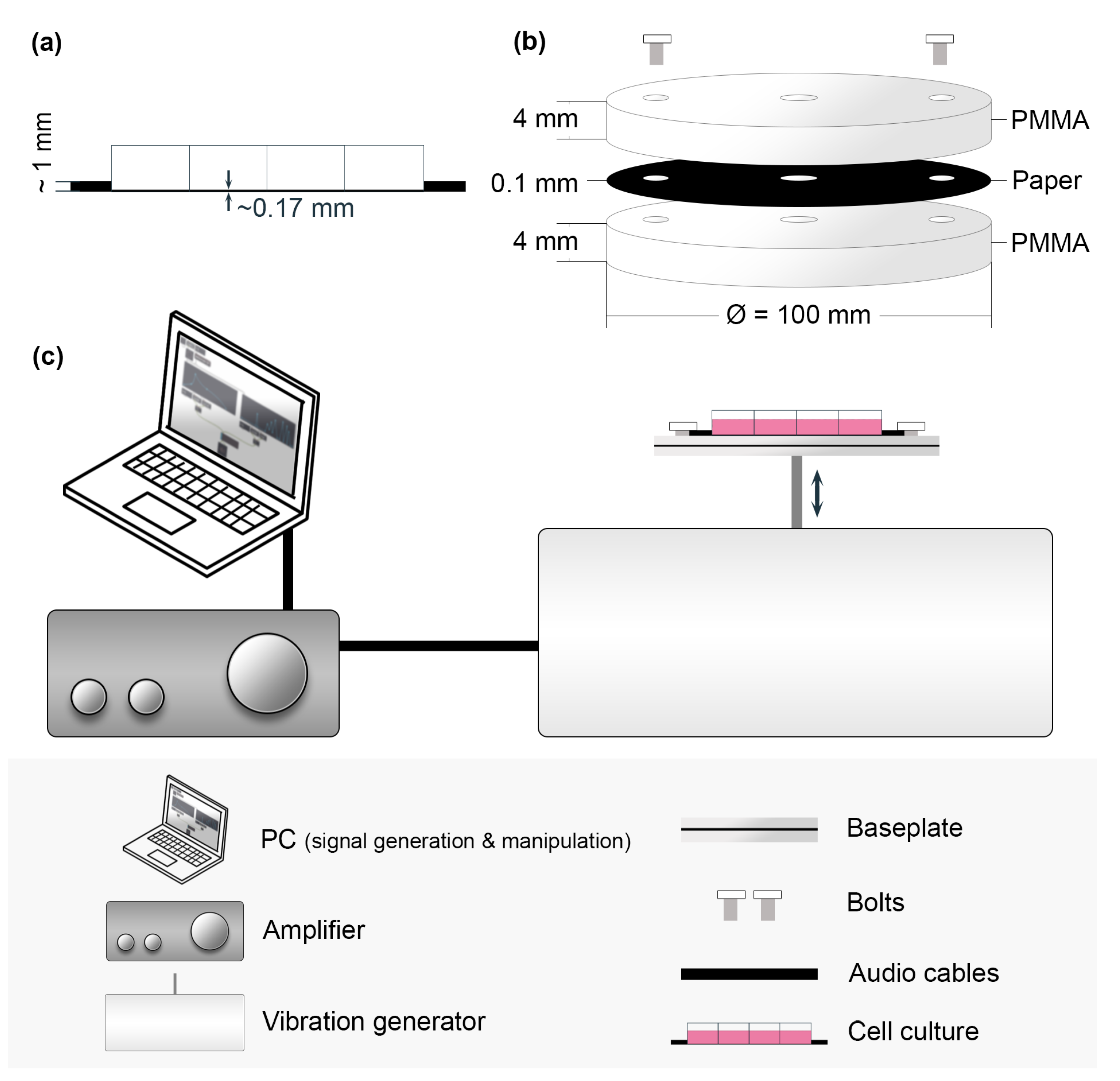
2.2.1. Vertical Vibration Setup
2.2.2. Experimental Conditions
- No Vibration (NV): control (static) condition;
- Continuous Vibration (CV): continuous (uninterrupted) sound vibration;
- Regular Pulse (RP): rigidly regular pulses with a fixed pulse duration and interval at 1000 ms;
- Variable Pulse (VP): irregular pulses with pulse durations and intervals varying unpredictably between 1000 and 1500 ms
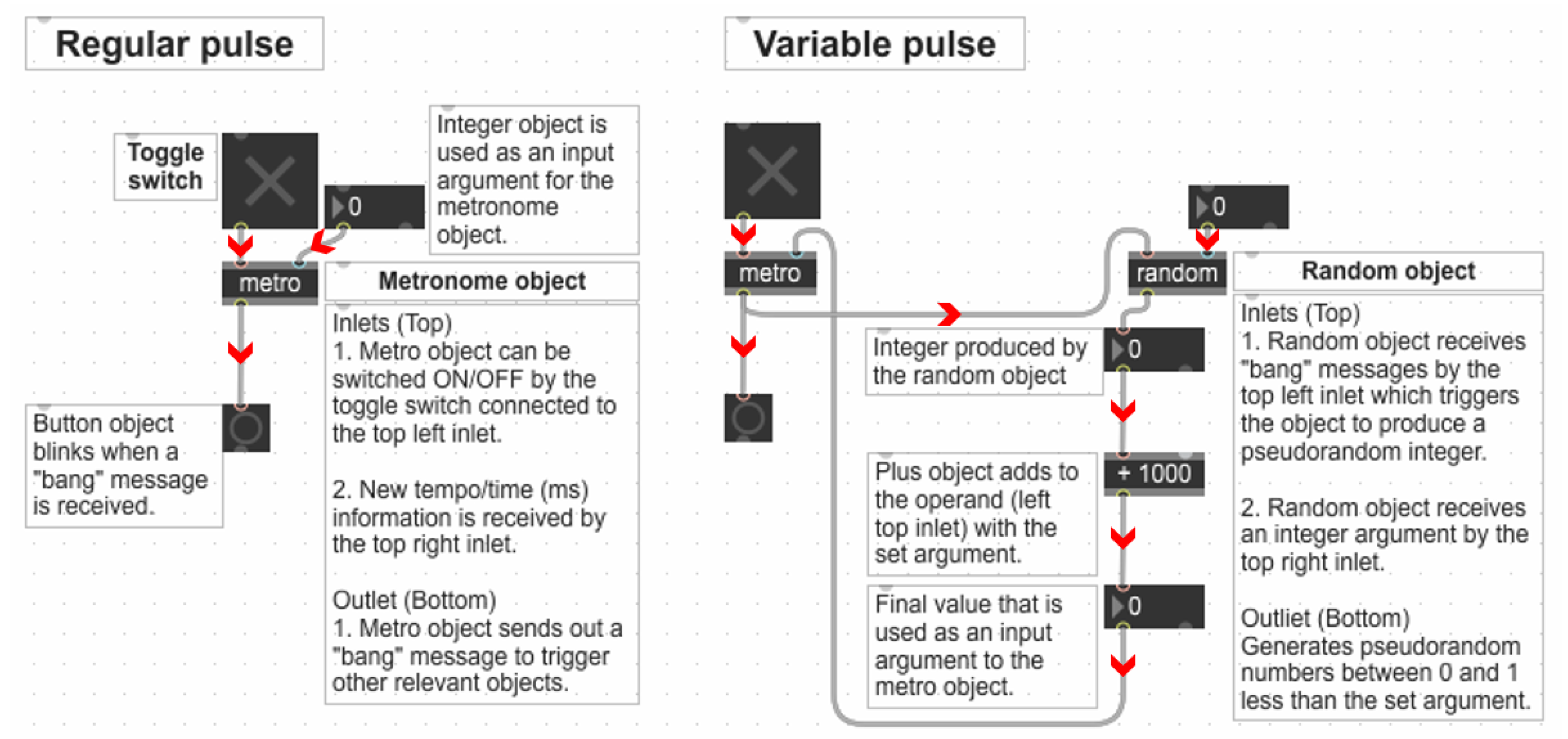
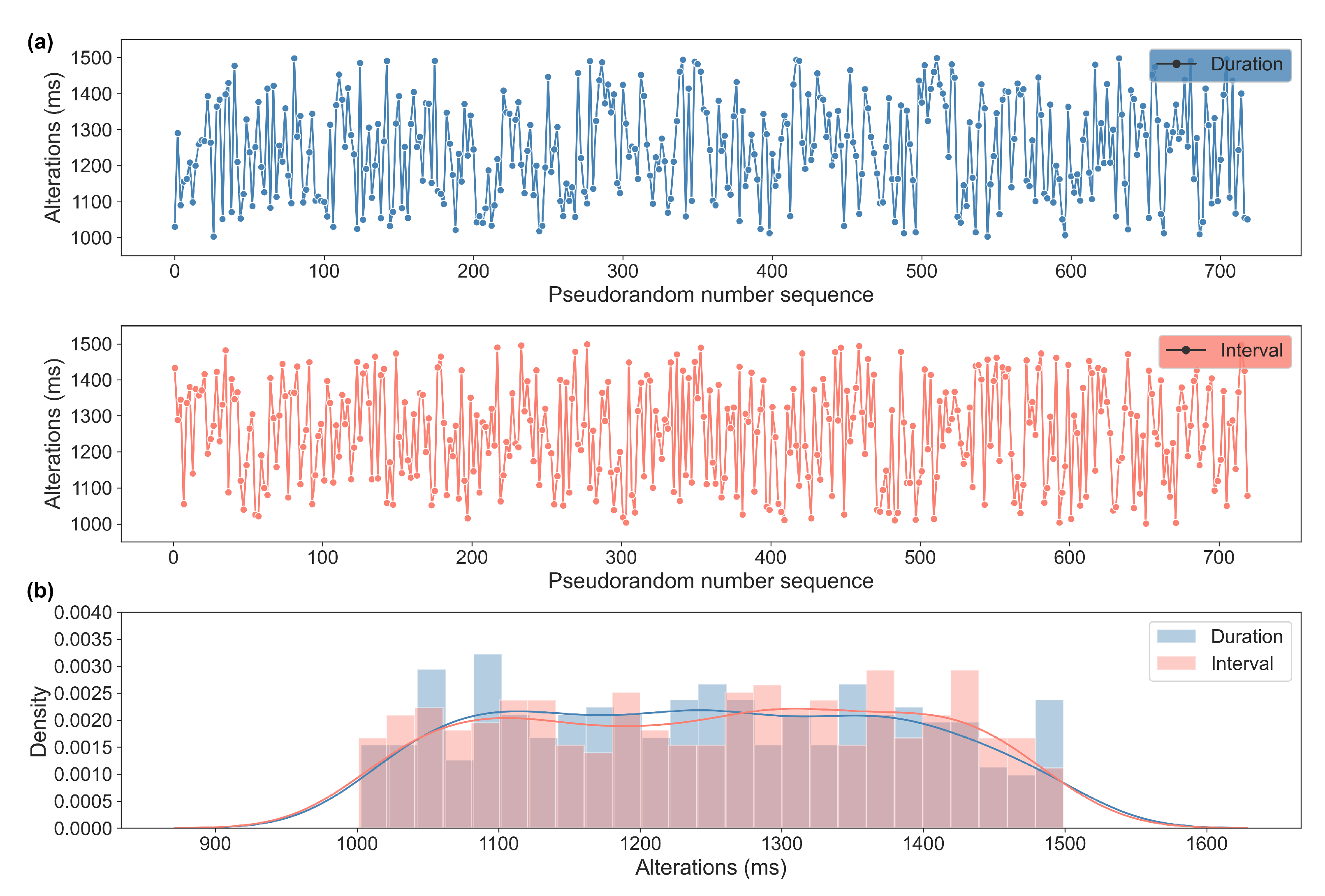
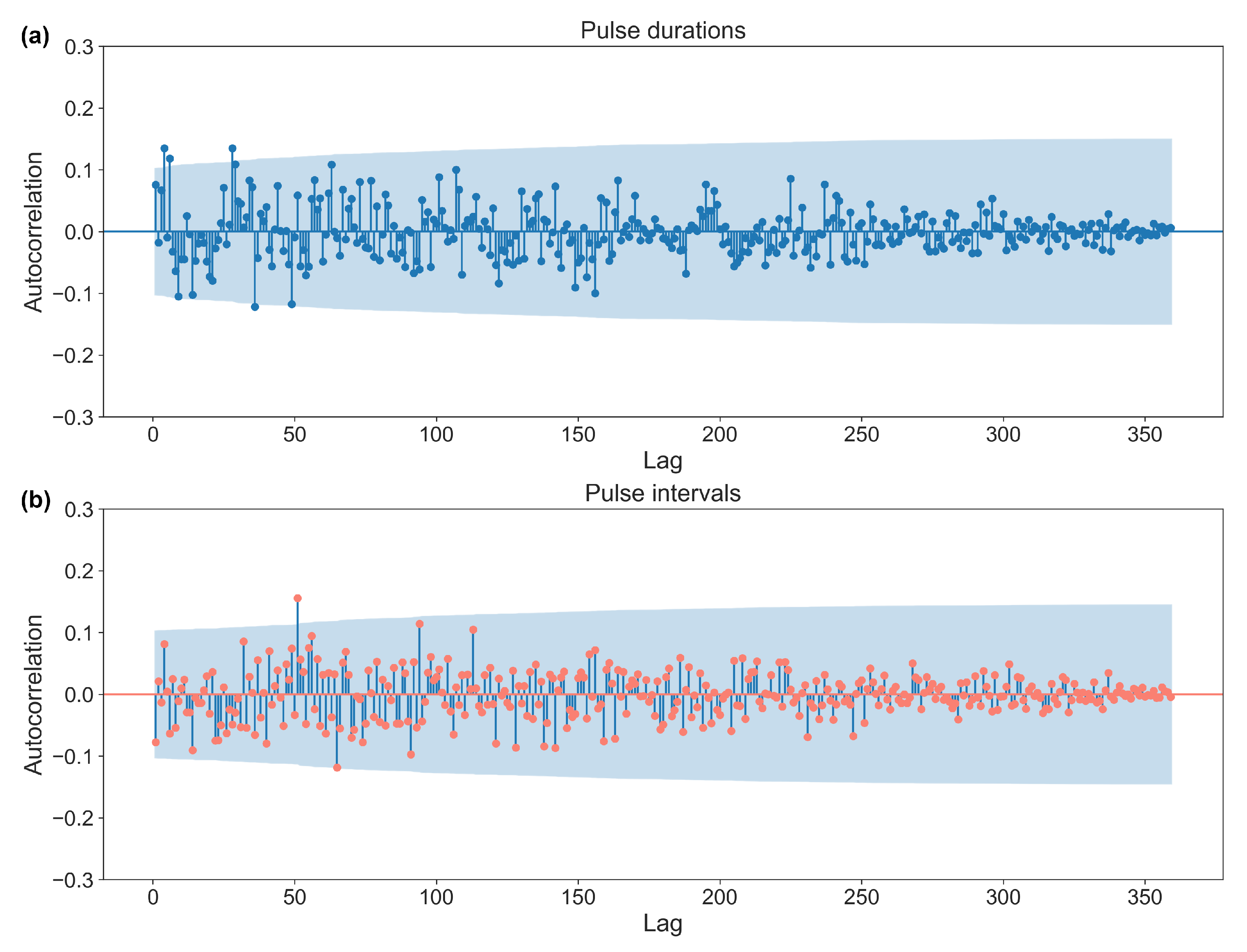
2.2.3. The Generation of Numerical Sequences for the Regular (RP) and Variable Pulse (VP) Conditions
2.3. Vibration Measurement
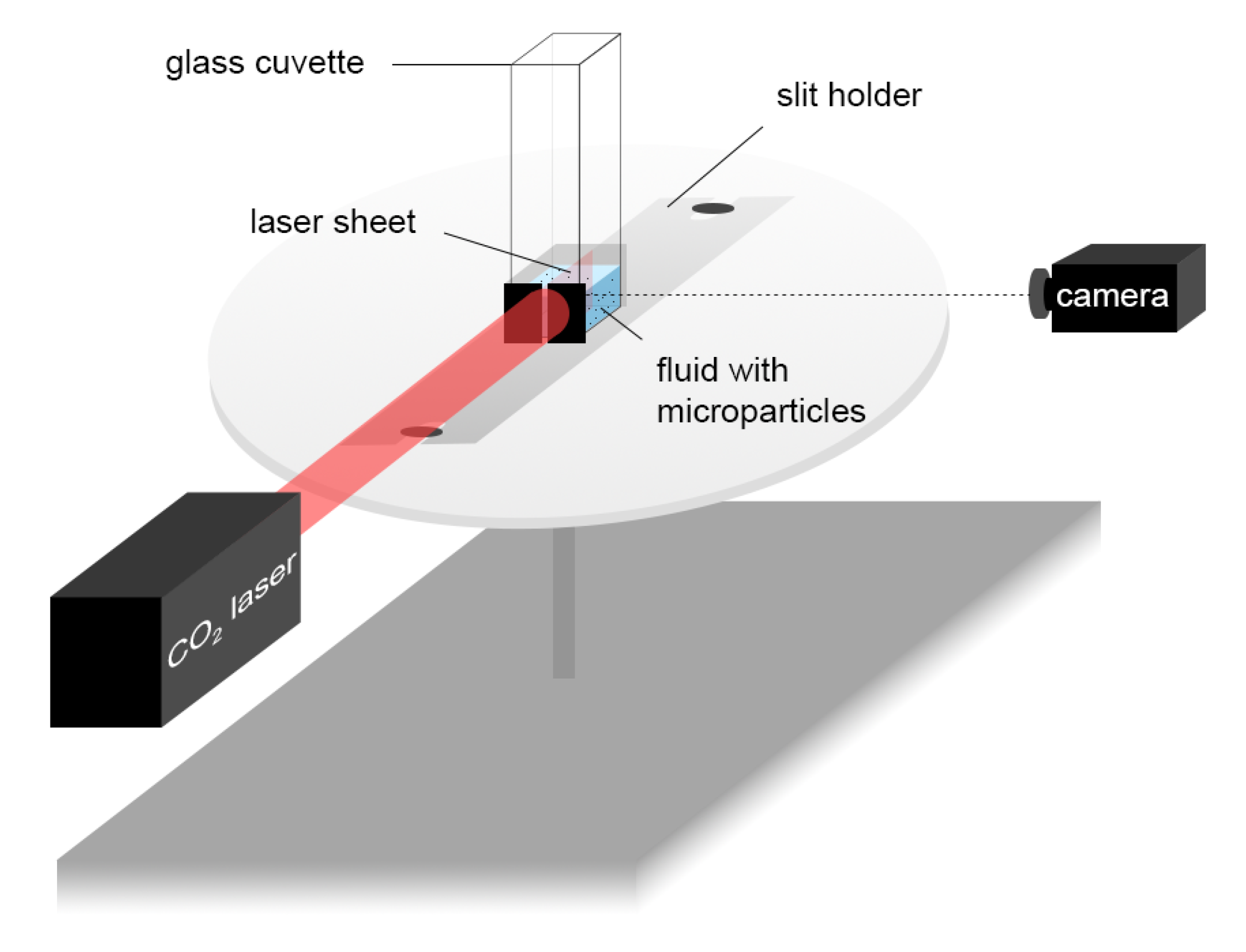
2.4. Particle Tracking Velocimetry (PTV) Measurement
- Shutter: 5 ms;
- Gain: 12 dB;
- Framerate: 25 FPS.
2.5. Staining of F-Actin Filaments
2.6. Microscopy and Image Acquisition
- Processing: manual;
- Noise filter: −4;
- SR frequency weighting: 1;
- Baseline cut, sectioning: 100/83/83;
- PSF: theoretical;
- Output: SR-SIM.
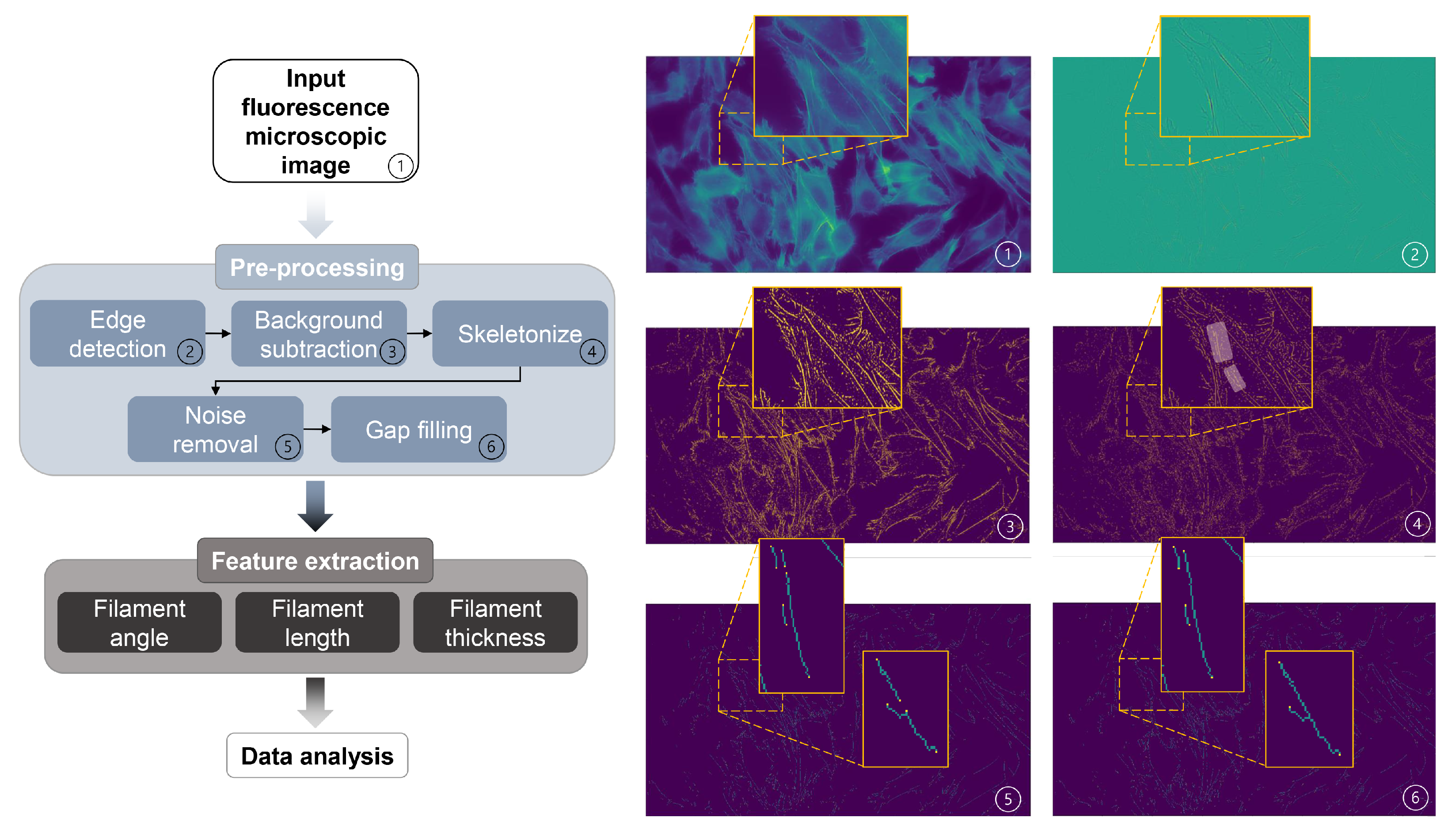
2.7. Image Analysis of F-Actin Filament Structures
2.8. Analysis of Cell Cycle Distribution
2.9. Statistical Analysis
3. Results
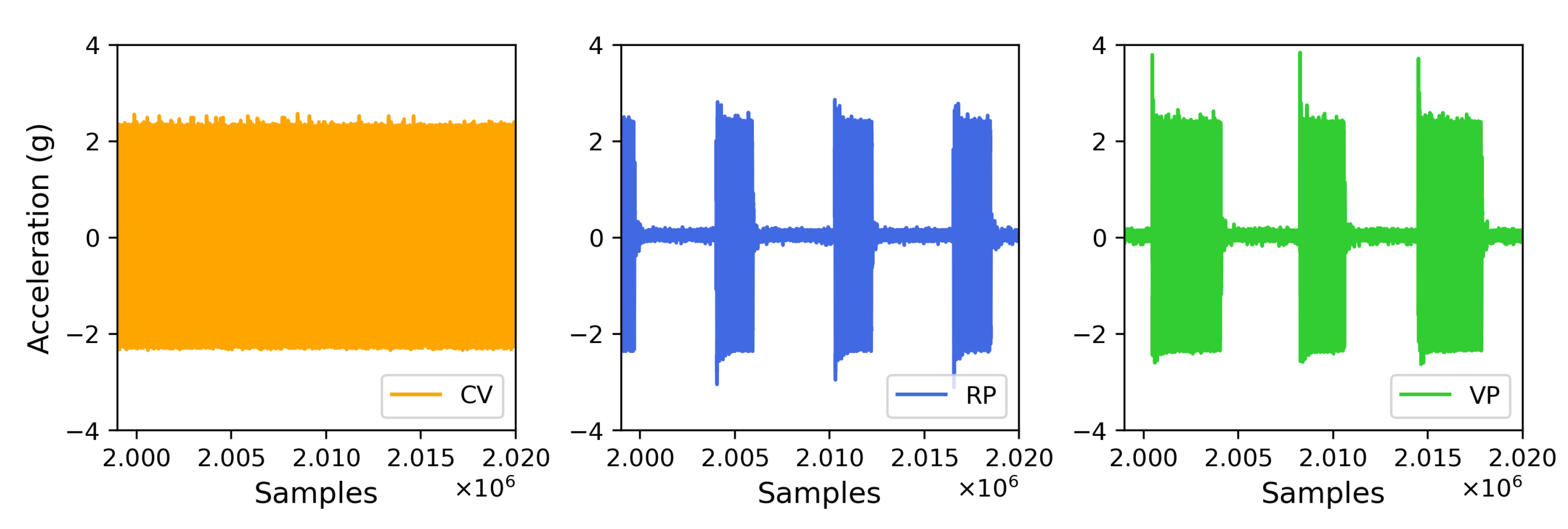
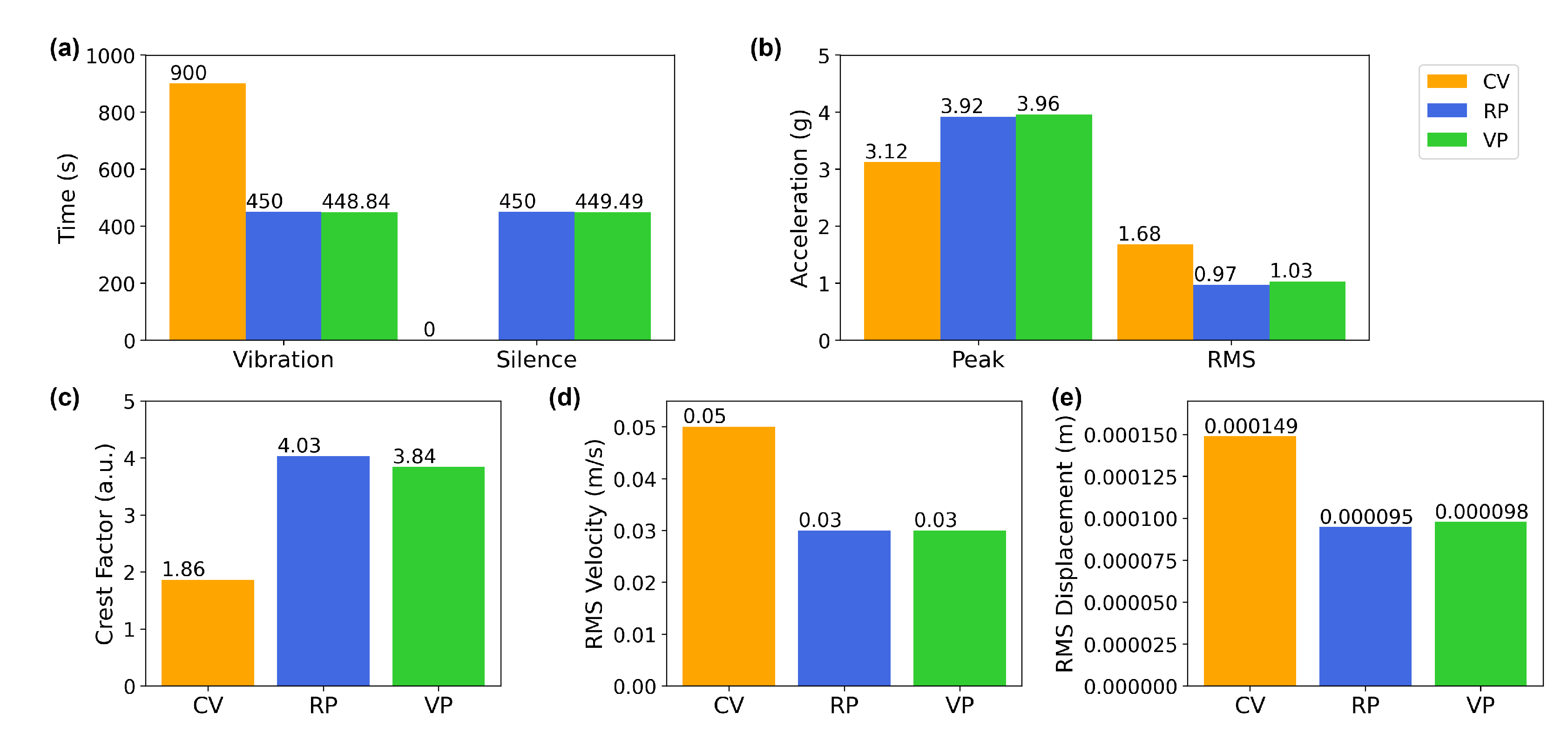
3.1. Characterization of Vertical Vibration in Terms of Acceleration Parameters
3.2. Fluid Flow Patterns and Shear Stress Estimation in the Wells of the Cell Culture Plate through the Particle Tracking Velocimetry (PTV) Method
3.3. Impact of Vertical Vibration on the F-Actin Filaments in HeLa Cells
3.4. Effect of Vertical Vibration on Cell Cycle Distribution
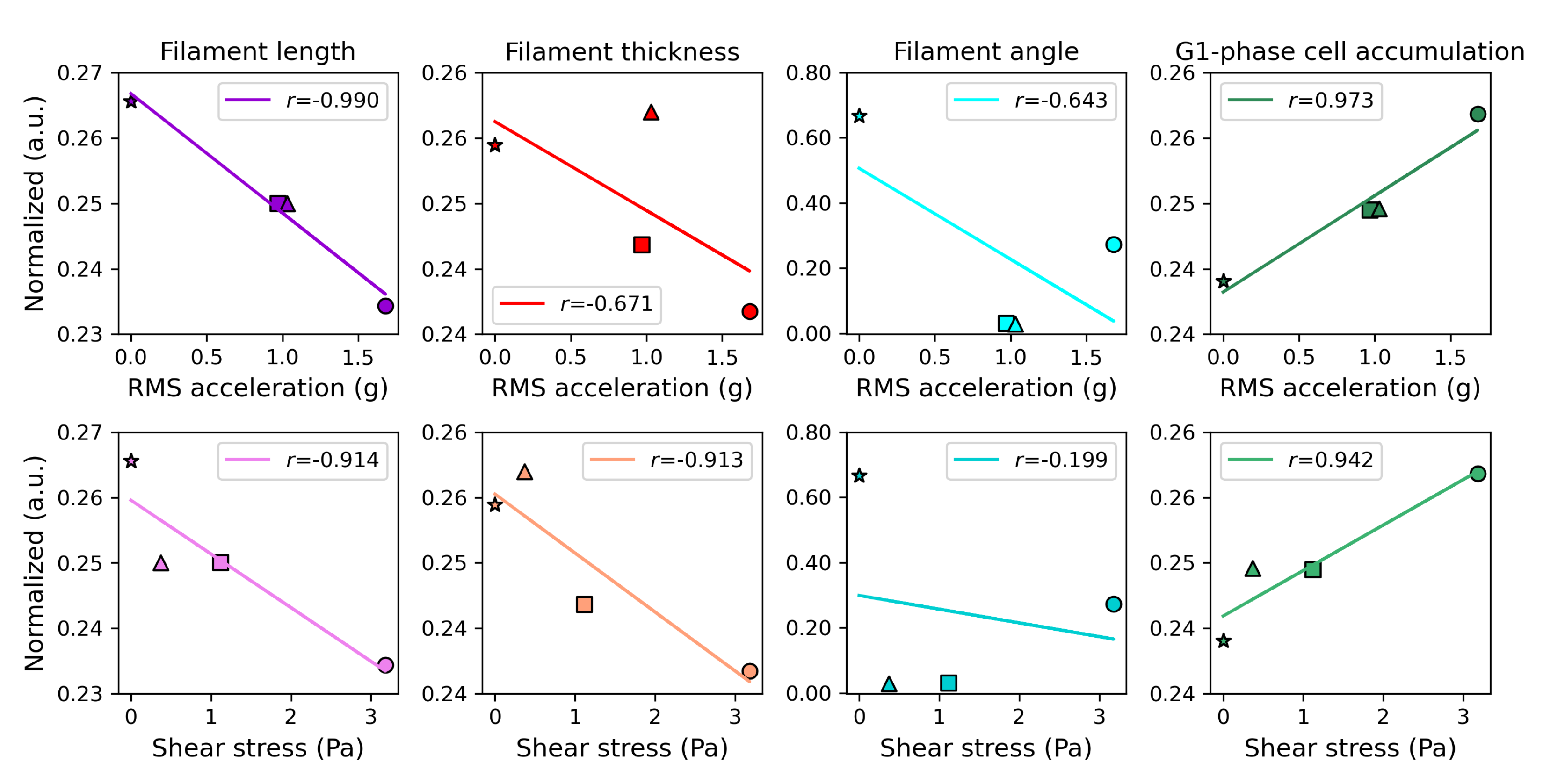
3.5. Correlations in Relation to the Magnitude of the Mechanical Stimuli
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammed, T.; Murphy, M.F.; Lilley, F.; Burton, D.R.; Bezombes, F. The effects of acoustic vibration on fibroblast cell migration. Mater. Sci. Eng. C 2016, 69, 1256–1262. [Google Scholar] [CrossRef]
- Yuan, H.; Xing, K.; Hsu, H.Y. Trinity of three-dimensional (3D) scaffold, vibration, and 3D printing on cell culture application: A systematic review and indicating future direction. Bioengineering 2018, 5, 57. [Google Scholar] [CrossRef]
- Wall, M.; Butler, D.; Haj, A.E.; Bodle, J.C.; Loboa, E.G.; Banes, A.J. Key developments that impacted the field of mechanobiology and mechanotransduction: Mechanobiology and signal transduction. J. Orthop. Res. 2017, 36, 605–619. [Google Scholar] [CrossRef] [PubMed]
- Matthews, B.D.; Overby, D.R.; Mannix, R.; Ingber, D.E. Cellular adaptation to mechanical stress: Role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Sci. 2006, 119, 508–518. [Google Scholar] [CrossRef] [PubMed]
- Enomoto, U.; Imashiro, C.; Takemura, K. Collective cell migration of fibroblasts is affected by horizontal vibration of the cell culture dish. Eng. Life Sci. 2020, 20, 402–411. [Google Scholar] [CrossRef]
- Kulkarni, R.N.; Voglewede, P.A.; Liu, D. Mechanical vibration inhibits osteoclast formation by reducing DC-STAMP receptor expression in osteoclast precursor cells. Bone 2013, 57, 493–498. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, M.; Fukunaga, T.; Sasaki, K.; Seiryu, M.; Yoshizawa, M.; Takeshita, N.; Takano-Yamamoto, T. Vibration enhances osteoclastogenesis by inducing RANKL expression via NF-kB signaling in osteocytes. Bone 2019, 123, 56–66. [Google Scholar] [CrossRef] [PubMed]
- Pravitharangul, A.; Suttapreyasri, S.; Leethanakul, C. Iliac and mandible osteoblasts exhibit varied responses to LMHF vibration: Sites affect bone cell responses to vibration. Cell Biol. Int. 2018, 42, 1349–1357. [Google Scholar] [CrossRef]
- Halonen, H.T.; Ihalainen, T.O.; Hyväri, L.; Miettinen, S.; Hyttinen, J.A.K. Cell adhesion and culture medium dependent changes in the high frequency mechanical vibration induced proliferation, osteogenesis, and intracellular organization of human adipose stem cells. J. Mech. Behav. Biomed. Mater. 2020, 101, 103419. [Google Scholar] [CrossRef]
- Tirkkonen, L.; Halonen, H.; Hyttinen, J.; Kuokkanen, H.; Sievänen, H.; Koivisto, A.M.; Mannerström, B.; Sándor, G.K.B.; Suuronen, R.; Miettinen, S.; et al. The effects of vibration loading on adipose stem cell number, viability and differentiation towards bone-forming cells. J. R. Soc. Interface 2011, 8, 1736–1747. [Google Scholar] [CrossRef]
- Cho, H.; Seo, Y.K.; Jeon, S.; Yoon, H.H.; Choi, Y.K.; Park, J.K. Neural differentiation of umbilical cord mesenchymal stem cells by sub-sonic vibration. Life Sci. 2012, 90, 591–599. [Google Scholar] [CrossRef] [PubMed]
- Kim, I.; Song, Y.; Lee, B.; Hwang, S. Human mesenchymal stromal cells are mechanosensitive to vibration stimuli. J. Dent. Res. 2012, 91, 1135–1140. [Google Scholar] [CrossRef] [PubMed]
- Kanie, K.; Sakai, T.; Imai, Y.; Yoshida, K.; Sugimoto, A.; Makino, H.; Kubo, H.; Kato, R. Effect of mechanical vibration stress in cell culture on human induced pluripotent stem cells. Regen. Ther. 2019, 12, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Terao, Y.; Kurashina, Y.; Tohyama, S.; Fukuma, Y.; Fukuda, K.; Fujita, J.; Takemura, K. An effective detachment system for human induced pluripotent stem cells cultured on multilayered cultivation substrates using resonance vibrations. Sci. Rep. 2019, 9, 15655. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, D.A.; Mullins, R.D. Cell mechanics and the cytoskeleton. Nature 2010, 463, 485–492. [Google Scholar] [CrossRef]
- Ingber, D.E.; Wang, N.; Stamenović, D. Tensegrity, cellular biophysics, and the mechanics of living systems. Rep. Prog. Phys. 2014, 77, 046603. [Google Scholar] [CrossRef]
- Reilly, C.B.; Ingber, D.E. Multi-scale modeling reveals use of hierarchical tensegrity principles at the molecular, multi-molecular, and cellular levels. Extrem. Mech. Lett. 2018, 20, 21–28. [Google Scholar] [CrossRef]
- Burridge, K.; Guilluy, C. Focal adhesions, stress fibers and mechanical tension. Exp. Cell Res. 2016, 343, 14–20. [Google Scholar] [CrossRef]
- Haque, F.; Lloyd, D.J.; Smallwood, D.T.; Dent, C.L.; Shanahan, C.M.; Fry, A.M.; Trembath, R.C.; Shackleton, S. SUN1 interacts with Nuclear Lamin A and Cytoplasmic Nesprins to provide a physical connection between the nuclear lamina and the cytoskeleton. Mol. Cell. Biol. 2006, 26, 3738–3751. [Google Scholar] [CrossRef]
- Wang, N.; Tytell, J.D.; Ingber, D.E. Mechanotransduction at a distance: Mechanically coupling the extracellular matrix with the nucleus. Nat. Rev. Mol. Cell Biol. 2009, 10, 75–82. [Google Scholar] [CrossRef]
- Goldbeter, A.; Gérard, C.; Gonze, D.; Leloup, J.C.; Dupont, G. Systems biology of cellular rhythms. FEBS Lett. 2012, 586, 2955–2965. [Google Scholar] [CrossRef] [PubMed]
- Kruse, K.; Jülicher, F. Oscillations in cell biology. Curr. Opin. Cell Biol. 2005, 17, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Hoyle, N.P.; Seinkmane, E.; Putker, M.; Feeney, K.A.; Krogager, T.P.; Chesham, J.E.; Bray, L.K.; Thomas, J.M.; Dunn, K.; Blaikley, J.; et al. Circadian actin dynamics drive rhythmic fibroblast mobilization during wound healing. Sci. Transl. Med. 2017, 9, eaal2774. [Google Scholar] [CrossRef] [PubMed]
- Rogers, E.H.; Fawcett, S.A.; Pekovic-Vaughan, V.; Hunt, J.A. Comparing circadian dynamics in primary derived stem cells from different sources of human adult tissue. Stem Cells Int. 2017, 2017, 2057168. [Google Scholar] [CrossRef] [PubMed]
- Vágó, J.; Katona, E.; Takács, R.; Dócs, K.; Hajdú, T.; Kovács, P.; Zákány, R.; van der Veen, D.R.; Matta, C. Cyclic uniaxial mechanical load enhances chondrogenesis through entraining the molecular circadian clock. J. Pineal Res. 2022, 73, e12827. [Google Scholar] [CrossRef]
- Kwak, D.; Olsen, P.A.; Danielsen, A.; Jensenius, A.R. A trio of biological rhythms and their relevance in rhythmic mechanical stimulation of cell cultures. Front. Psychol. 2022, 13, 867191. [Google Scholar] [CrossRef]
- De Belly, H.; Paluch, E.K.; Chalut, K.J. Interplay between mechanics and signalling in regulating cell fate. Nat. Rev. Mol. Cell Biol. 2022, 23, 465–480. [Google Scholar] [CrossRef]
- Jolley, M.J.; Russell, A.J.; Quinn, P.F.; Perks, M.T. Considerations When Applying Large-Scale PIV and PTV for Determining River Flow Velocity. Front. Water 2021, 3, 709269. [Google Scholar] [CrossRef]
- Scislo, L. Single-Point and Surface Quality Assessment Algorithm in Continuous Production with the Use of 3D Laser Doppler Scanning Vibrometry System. Sensors 2023, 23, 1263. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Tian, X. Vibration displacement measurement based on three axes accelerometer. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 2374–2378. [Google Scholar] [CrossRef]
- Day, M.A. The no-slip condition of fluid dynamics. Erkenntnis 1990, 33, 285–296. [Google Scholar] [CrossRef]
- Jensenius, A. Using motiongrams in the study of musical gestures. In Proceedings of the International Computer Music Conference, New Orlenas, LA, USA, 6–11 November 2006; pp. 499–502. [Google Scholar]
- Kueh, H.Y.; Brieher, W.M.; Mitchison, T.J. Dynamic stabilization of actin filaments. Proc. Natl. Acad. Sci. USA 2008, 105, 16531–16536. [Google Scholar] [CrossRef]
- Butt, T.; Mufti, T.; Humayun, A.; Rosenthal, P.B.; Khan, S.; Khan, S.; Molloy, J.E. Myosin motors drive long range alignment of actin filaments. J. Biol. Chem. 2010, 285, 4964–4974. [Google Scholar] [CrossRef]
- Gao, J.; He, L.; Zhou, L.; Jing, Y.; Wang, F.; Shi, Y.; Cai, M.; Sun, J.; Xu, H.; Jiang, J.; et al. Mechanical force regulation of YAP by F-actin and GPCR revealed by super-resolution imaging. Nanoscale 2020, 12, 2703–2714. [Google Scholar] [CrossRef] [PubMed]
- De La Cruz, E.M.; Gardel, M.L. Actin mechanics and fragmentation. J. Biol. Chem. 2015, 290, 17137–17144. [Google Scholar] [CrossRef] [PubMed]
- Yoshigi, M.; Hoffman, L.M.; Jensen, C.C.; Yost, H.J.; Beckerle, M.C. Mechanical force mobilizes zyxin from focal adhesions to actin filaments and regulates cytoskeletal reinforcement. J. Cell Biol. 2005, 171, 209–215. [Google Scholar] [CrossRef]
- Taïeb, H.M.; Garske, D.S.; Contzen, J.; Gossen, M.; Bertinetti, L.; Robinson, T.; Cipitria, A. Osmotic pressure modulates single cell cycle dynamics inducing reversible growth arrest and reactivation of human metastatic cells. Sci. Rep. 2021, 11, 13455. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.K.; Chaudhuri, O. Mechanical regulation of cell-cycle progression and division. Trends Cell Biol. 2022, 32, 773–785. [Google Scholar] [CrossRef]
- Tarannum, N.; Singh, R.; Woolner, S. Sculpting an Embryo: The Interplay between Mechanical Force and Cell Division. J. Dev. Biol. 2022, 10, 37. [Google Scholar] [CrossRef] [PubMed]


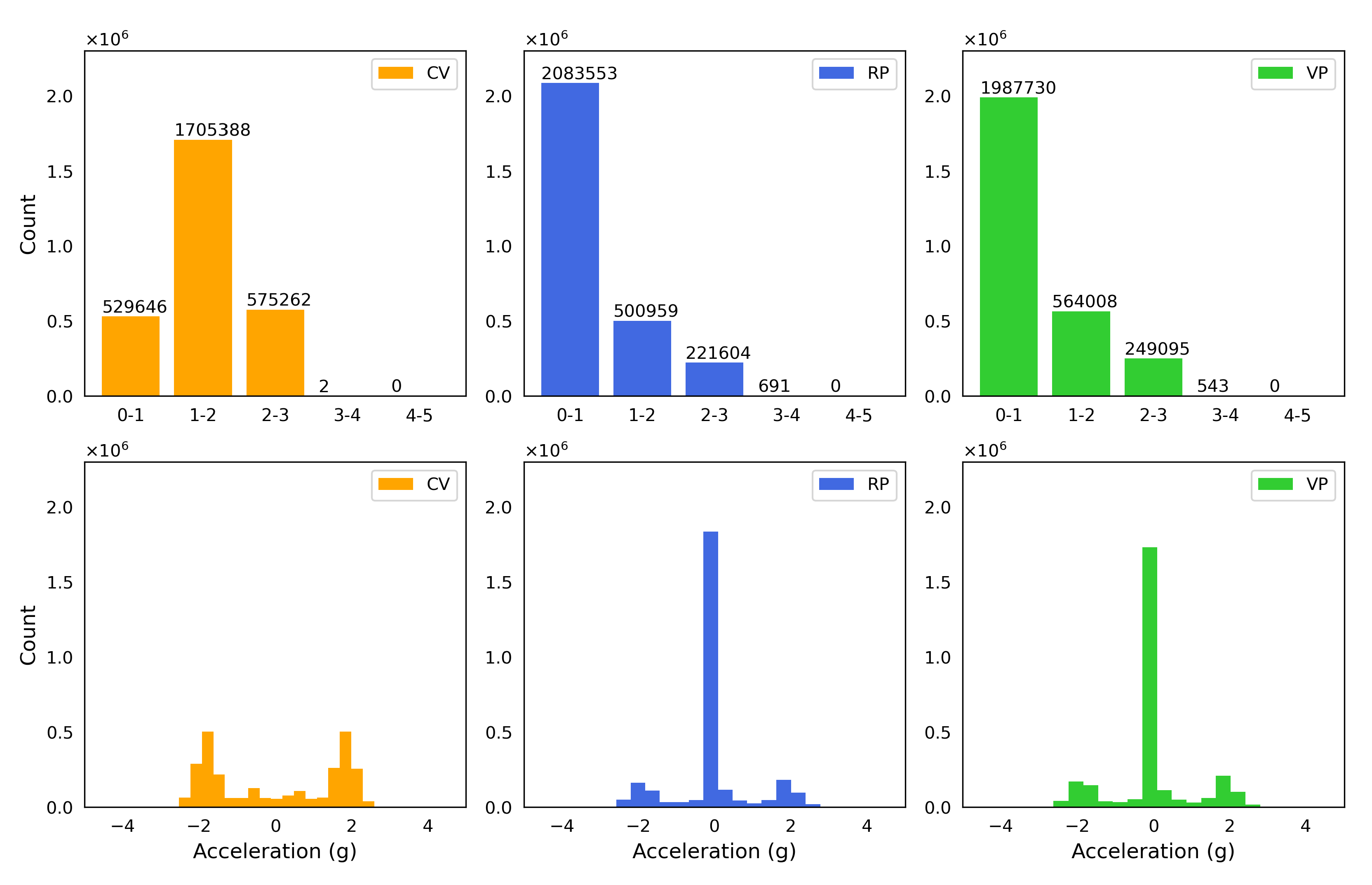
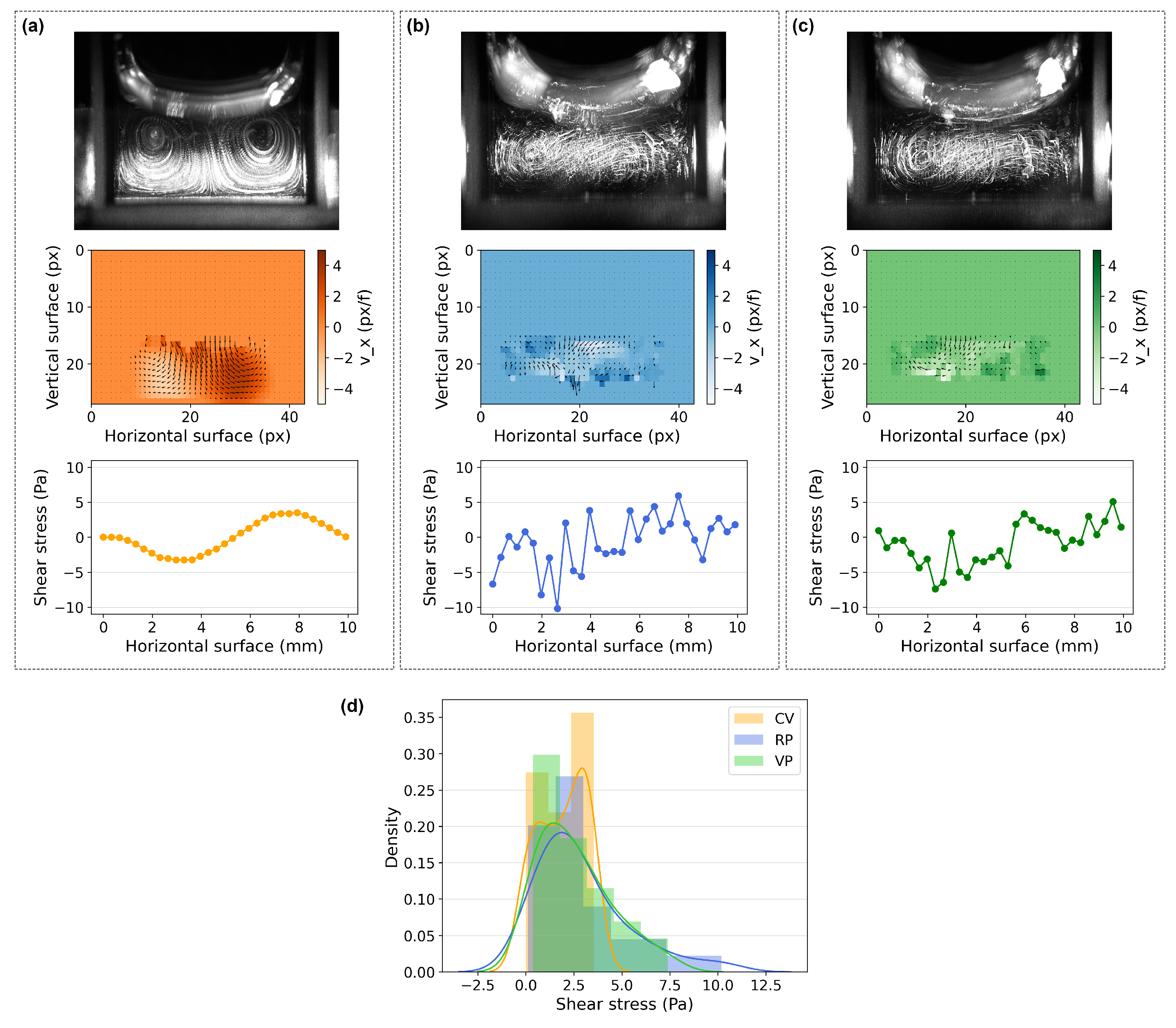

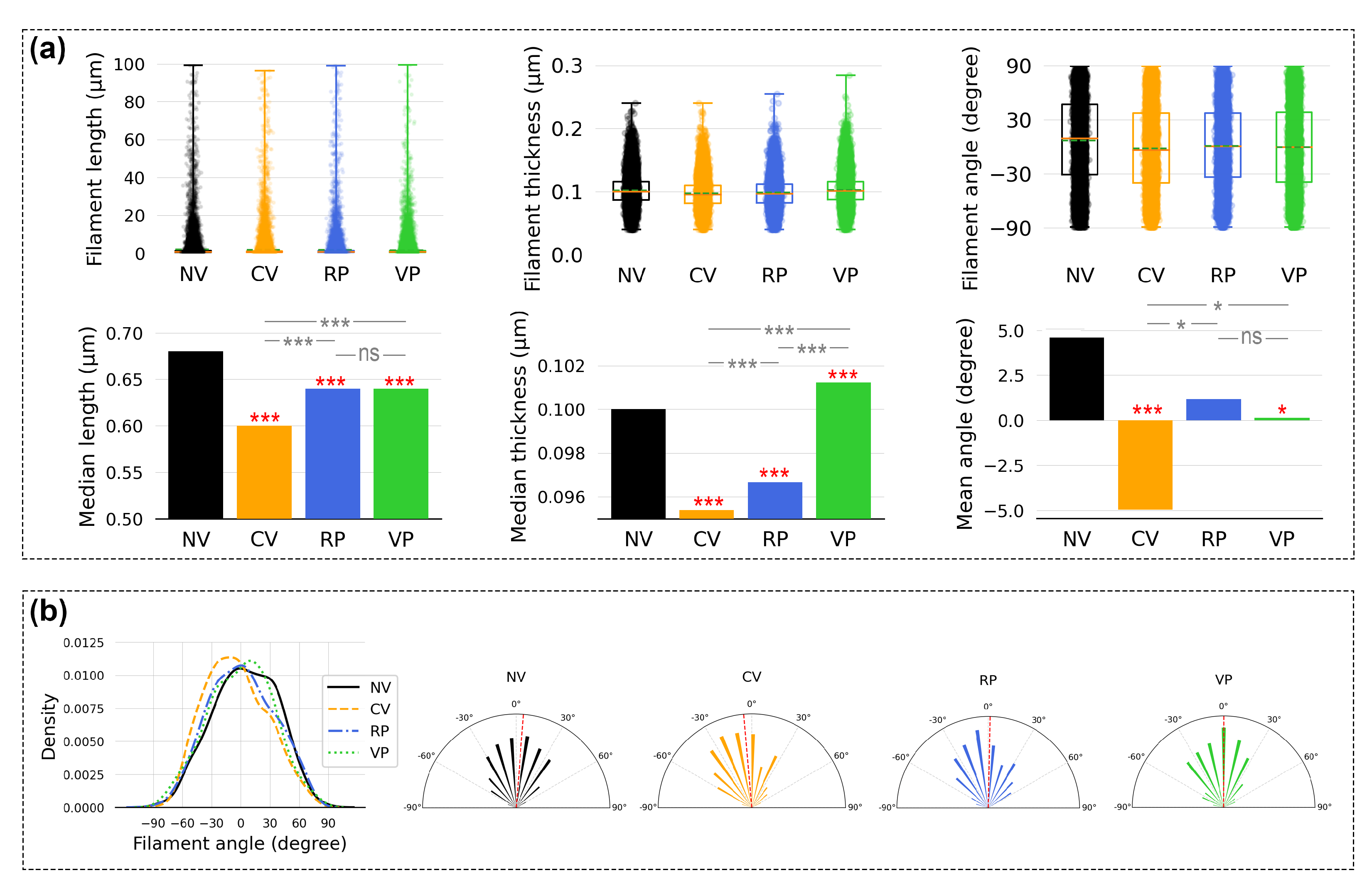
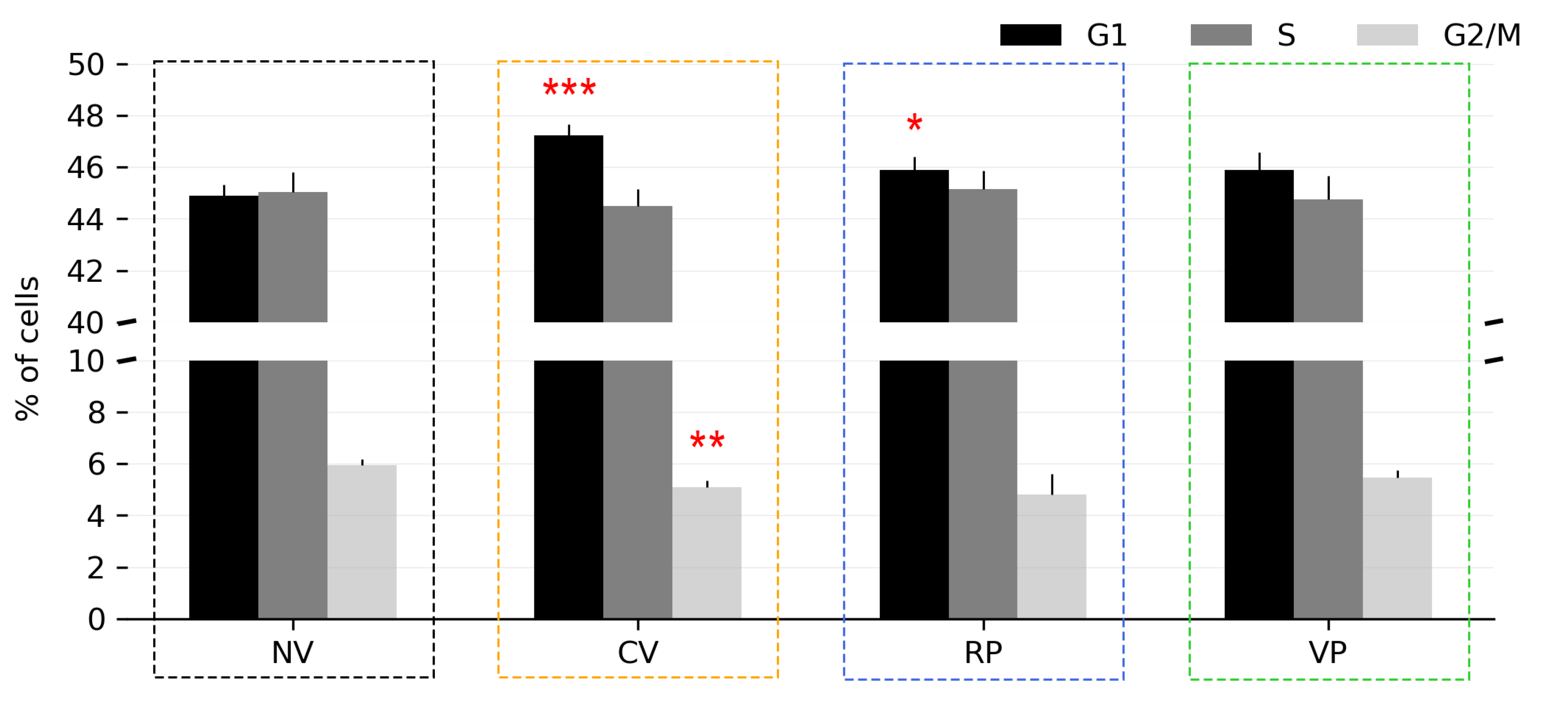
| n | Runs Test (p Value) | Entropy Max Value | Entropy Value | |
|---|---|---|---|---|
| Pulse duration | 360 | 0.4 | 5.89 | 5.27 |
| Pulse interval | 360 | 0.1 | 5.27 |
| Data Set | CV | RP | VP |
|---|---|---|---|
| Input frequency (Hz) | 50 | 50 | 50 |
| Measured fundamental frequency (Hz) | ∼51 | ∼51 | ∼51 |
| Total vibration time (s) | 900 | 450 | 448.84 |
| Total silence (intervals) time (s) | 0 | 450 | 451.16 |
| Acceleration peak (g) | 3.12 | 3.92 | 3.96 |
| Acceleration RMS (g) | 1.69 | 0.97 | 1.03 |
| Crest factor | 1.86 | 4.03 | 3.84 |
| Velocity RMS (m/s) | 0.049 | 0.029 | 0.031 |
| Displacement RMS (m) | 0.00015 | 0.0001 | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, D.; Combriat, T.; Jensenius, A.R.; Olsen, P.A. Characterization of Mechanical and Cellular Effects of Rhythmic Vertical Vibrations on Adherent Cell Cultures. Bioengineering 2023, 10, 811. https://doi.org/10.3390/bioengineering10070811
Kwak D, Combriat T, Jensenius AR, Olsen PA. Characterization of Mechanical and Cellular Effects of Rhythmic Vertical Vibrations on Adherent Cell Cultures. Bioengineering. 2023; 10(7):811. https://doi.org/10.3390/bioengineering10070811
Chicago/Turabian StyleKwak, Dongho, Thomas Combriat, Alexander Refsum Jensenius, and Petter Angell Olsen. 2023. "Characterization of Mechanical and Cellular Effects of Rhythmic Vertical Vibrations on Adherent Cell Cultures" Bioengineering 10, no. 7: 811. https://doi.org/10.3390/bioengineering10070811
APA StyleKwak, D., Combriat, T., Jensenius, A. R., & Olsen, P. A. (2023). Characterization of Mechanical and Cellular Effects of Rhythmic Vertical Vibrations on Adherent Cell Cultures. Bioengineering, 10(7), 811. https://doi.org/10.3390/bioengineering10070811







